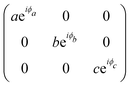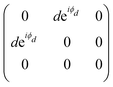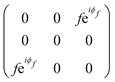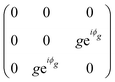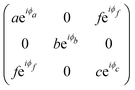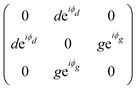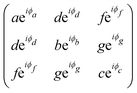Polarized Raman spectroscopy in low-symmetry 2D materials: angle-resolved experiments and complex number tensor elements
Marcos A.
Pimenta
 *a,
Geovani C.
Resende
a,
Henrique B.
Ribeiro
b and
Bruno R.
Carvalho
*a,
Geovani C.
Resende
a,
Henrique B.
Ribeiro
b and
Bruno R.
Carvalho
 *c
*c
aDepartamento de Física, Universidade Federal de Minas Gerais, Belo Horizonte, Minas Gerais 30123-970, Brazil. E-mail: mpimenta@fisica.ufmg.br
bDepartment of Applied Physics, Stanford University, Stanford, California 94305, USA
cDepartamento de Física, Universidade Federal do Rio Grande do Norte, Natal, Rio Grande do Norte 59078-970, Brazil. E-mail: brunorc@fisica.ufrn.br
First published on 16th October 2021
Abstract
In this perspective review, we discuss the power of polarized Raman spectroscopy to study optically anisotropic 2D materials, belonging to the orthorhombic, monoclinic and triclinic crystal families. We start by showing that the polarization dependence of the peak intensities is described by the Raman tensor that is unique for each phonon mode, and then we discuss how to determine the tensor elements from the angle-resolved polarized measurements by analyzing the intensities in both the parallel- and cross-polarized scattering configurations. We present specific examples of orthorhombic black phosphorus and monoclinic 1T′-MoTe2, where the Raman tensors have null elements and their principal axes coincide with the crystallographic ones, followed by a discussion on the results for triclinic ReS2 and ReSe2, where the axes of the Raman tensor do not coincide with the crystallographic axes and all elements are non-zero. We show that the Raman tensor elements are, in general, given by complex numbers and that phase differences between tensor elements are needed to describe the experimental results. We discuss the dependence of the Raman tensors on the excitation laser energy and thickness of the sample within the framework of the quantum model for the Raman intensities. We show that the wavevector dependence of the electron–phonon interaction is essential for explaining the distinct Raman tensor for each phonon mode. Finally, we close with our concluding remarks and perspectives to be explored using angle-resolved polarized Raman spectroscopy in optically anisotropic 2D materials.
1 Introduction
It is remarkable how the science of 2D materials has progressed since the isolation of graphene in 2004.1 Since then, a wide family of 2D materials has been uncovered and more are yet to be discovered.2–4 Knowledge from 3D systems has been spanned and explored in 2D materials, revealing the interesting physics limited to the atomic layer of 2D materials. There is a vast diversity of physical properties in the 2D family such as the wide range of electronic band gaps, ranging from semi-metallics to insulators.3,4 In low-symmetry 2D materials, crystalline symmetry structures play an important role since their optical, electronic and thermal properties are anisotropic in the layer plane.5,6A crystal can be classified into one of the six families of symmetry:7–9 cubic, hexagonal, tetragonal, orthorhombic, monoclinic and triclinic. This classification is based on the lengths and directions of the unitary vectors of the crystalline unit cell. A 2D material can belong to different families of symmetries. For instance, 2D transition metal dichalcogenides (TMDs) with a chemical formula MX2 (M is the transition metal and X is the chalcogen atom) can be found in different symmetry crystalline structures depending on the type and arrangement of the metal and chalcogen atoms and on the stacking of the different layers.10 Besides, some 2D TMDs such as MoS2, MoTe2, and WTe2 exhibit a structural polymorphism, meaning that they can exhibit different crystalline structures. For example, the MoS2 crystal can be arranged in hexagonal, tetragonal and orthorhombic structures.3,5,11
The 2D family also involves a large number of crystals made of different chemical elements and atomic structure, including h-BN, black phosphorus, transition metal monochalcogenides (MX, M = Ge, Sn; X = S, Se), transition metal trichalcogenides (MX3, M = Ti, Zr, Hf; X = S, Se, Te), group IV–V compounds (e.g., SiP, GeP, SiAs, GeAs and GeAs2), group III–VI compounds (GaSe and InSe, GaTe), and ternary transition metal chalcogenides (i.e., Ta2NiS5, TaIrTe4), among others. The low-symmetry 2D materials exhibit intriguing anisotropic in-plane electrical, optical, magnetic and phonon properties,12–22 and offer the opportunity to perform fundamental studies and be used in devices based on the anisotropic properties of electrons and phonons.
Raman spectroscopy is one of the most powerful tools to probe the fundamental properties of phonons and electrons in crystals. This technique has been widespread to characterize 3D semiconductors such as silicon,23–25 germanium,26,27 SiGe,28,29 GaAs30,31 and GaN,32 to name a few. Based on this development, Raman spectroscopy has been spanned to study 2D materials.33–36 Moreover, the possibility of tuning the excitation energy and performing resonant Raman spectroscopy provide further information about the electrons, phonons and their coupling in these systems.35,37–41 Although this technique has progressed through the years, it is essential to control different parameters of the experimental setup and data analysis treatment in order to understand the basic mechanism behind the Raman scattering process. In general, one needs to pay attention to the excitation energy, number of atomic layers, experimental polarized configuration, calibration and normalization of the spectra, and interference effects on the substrate, among others. In the case of low-symmetry 2D systems, we perform angle-resolved Raman measurements by controlling and changing the direction of polarization of the incident and scattered light with respect to the crystallographic axes. We will discuss in this work how the analysis of the angle-resolved experiments provides the determination of the Raman tensor elements of the crystal.19–21,42,43
The Raman tensor is unique for each Raman-active mode and allows complete characterization of a given Raman peak intensity as a function of polarization of the incident and scattered light. Nowadays, there is growing interest in the study of optically anisotropic 2D materials by angle-resolved polarized Raman spectroscopy since the unusual results in layered black phosphorus (BP) were explained by Ribeiro et al.21 considering that the Raman tensor elements are complex numbers and that phase differences between elements are needed to fit the experimental results. Ling et al.44 showed later that the tensor elements are strongly dependent on the flake thickness and the excitation energy, while Phaneuf-L’Heureux et al.45 determined the Raman tensors of few-layered BP (with 2, 3, 4, and 5 layers) using angle-resolved polarized Raman spectroscopy. Mao et al.46 performed polarized and resonance Raman measurements in the visible and ultraviolet energy ranges and observed from the Raman excitation profiles that the electron–phonon coupling in BP is symmetry-dependent. Also, Lin et al.47 used normal and oblique laser incidences to study black phosphorus and used depth-dependent polarized results to show that the Raman response is affected by birefringence, linear dichroism and interference effects in the multilayered structures. Zhu et al.48 performed angle-resolved polarized Raman measurements on both the basal and cross planes of black phosphorus and obtained the Raman tensors from the polarized spectra taken along the different crystal axes. Sriv et al.49 used polarized Raman spectroscopy with six different excitation energies to study the optical phonons in layered semiconductor alloys SnSe(1−x)Sx and observed distinct behavior for different symmetry modes. Wang et al.50 performed an angle-resolved Raman study of monoclinic 1T′-MoTe2 and obtained the Raman tensors using the excitation energies of 1.96 eV and 2.33 eV. Choi et al.51 investigated the angle-resolved polarized Raman response of few-layered ReS2 and ReSe2 and showed that it can distinguish the “up” and “down” orientations of the sample. Resende et al.19 performed angle-dependent polarized Raman spectroscopy of single-layer triclinic ReSe2, obtained the Raman tensor elements of all Raman modes, and explained the different behavior for each mode as due to the anisotropy of the electron–phonon coupling in low-symmetry 2D materials. Recently, Yu et al.52 used angle-resolved polarized Raman spectroscopy to study argon ion bombarded ReS2 samples and established the relationship between defect density and anisotropy.
There is widespread interest in unveiling the properties of optically anisotropic 2D materials and angle-resolved polarized Raman spectroscopy is a key to achieve this. In this context, we discuss in this perspective review the Raman tensor and the experimental setup used to determine its elements in low-symmetry 2D systems. We focus on the orthorhombic, monoclinic and triclinic symmetry classes discussing an example of each one of them. Interestingly, we show that some Raman modes in low-symmetry structures need to be adjusted by complex tensor elements. Therefore, a discussion of the real and imaginary parts of the Raman tensor elements is presented considering the quantum formalism for the Raman process. Finally, we shortly discuss some recent developments on the resonant angle-resolved Raman measurements in these low-symmetry structures that still need to be further explored.
1.1 The tensorial nature of the Raman intensity
When an incident laser beam hits the surface of a crystal, the electric field Ei of the incident light induces a polarization vector P in the material medium that can be written in terms of the incident field, in the linear regime, by the expression,53,54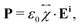 | (1) |
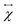 is the second-rank tensor electric susceptibility that accounts for the fact that the vectors P and Ei are not necessarily parallel. The induced oscillating polarization will emit light in different directions originating the scattering of light. Most of the light is elastically scattered but a small fraction of the light is inelastically scattered due to the creation or destruction of quanta of vibrations (phonons), giving rise to the Raman scattering process. Each cartesian component χij of the electric susceptibility tensor can be modulated by a vibrational mode μ described by the generalized normal coordinate qμ. The dependence of the elements χij on the normal coordinates qμ can be expanded using a Taylor series in the normal coordinates.54,55 The zeroth-order term of the Taylor series brings forth the Rayleigh (or elastic) scattering contribution (χ0ij) and the first-order term produces the Raman tensor elements written as,53,54
is the second-rank tensor electric susceptibility that accounts for the fact that the vectors P and Ei are not necessarily parallel. The induced oscillating polarization will emit light in different directions originating the scattering of light. Most of the light is elastically scattered but a small fraction of the light is inelastically scattered due to the creation or destruction of quanta of vibrations (phonons), giving rise to the Raman scattering process. Each cartesian component χij of the electric susceptibility tensor can be modulated by a vibrational mode μ described by the generalized normal coordinate qμ. The dependence of the elements χij on the normal coordinates qμ can be expanded using a Taylor series in the normal coordinates.54,55 The zeroth-order term of the Taylor series brings forth the Rayleigh (or elastic) scattering contribution (χ0ij) and the first-order term produces the Raman tensor elements written as,53,54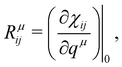 | (2) |
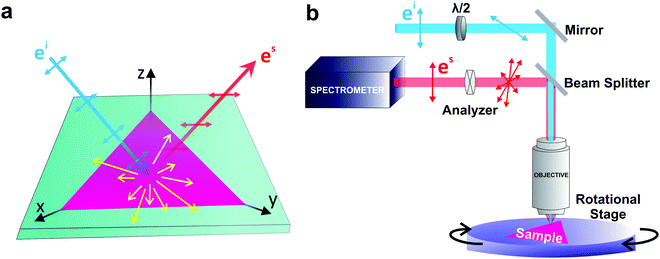
If the incident light is polarized along the direction of the unitary vector êi, the light scattered by phonons in crystals can exhibit different polarization. If we consider only the light scattered with polarization along the unitary vector ês, as shown in Fig. 1a, the theory of light scattering shows that the Raman intensity Iμ of the light scattered by a phonon μ is proportional to53,54
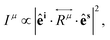 | (3) |
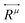 is the second-rank Raman tensor, specific for each Raman-active phonon μ. The symbol of proportionality in eqn (3) accounts for the fact that the experimental intensity also depends on instrumental parameters (see Fig. 1b), such as the efficiency of the spectrometer, the numerical aperture of the objective, intensity of the incident light, among others. The polarization vector êi of the incident light can be represented by a 1 × 3 row matrix, the polarization vector ês of the scattered light can be represented by a 3 × 1 column matrix, and eqn (3) can be rewritten as:53,54
is the second-rank Raman tensor, specific for each Raman-active phonon μ. The symbol of proportionality in eqn (3) accounts for the fact that the experimental intensity also depends on instrumental parameters (see Fig. 1b), such as the efficiency of the spectrometer, the numerical aperture of the objective, intensity of the incident light, among others. The polarization vector êi of the incident light can be represented by a 1 × 3 row matrix, the polarization vector ês of the scattered light can be represented by a 3 × 1 column matrix, and eqn (3) can be rewritten as:53,54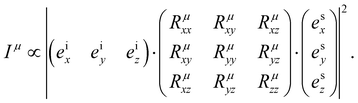 | (4) |
1.2 Classical formalism and complex Raman tensor elements
The simplest model for the classical electric susceptibility considers a damped oscillating electric dipole, with a resonance frequency ω0 and damping constant γ, forced to vibrate by the external electric field of the incident light, oscillating with a frequency ωi. In this case, the electric susceptibility can be written as,53,54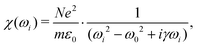 | (5) |
| χ(ω) = χ′(ω) + iχ′′(ω), | (6) |
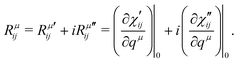 | (7) |
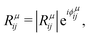 | (8) |
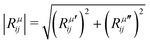 is the modulus of the element and
is the modulus of the element and 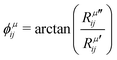 is its phase.53,54 In fact, as discussed below, we can only obtain the phase differences between the Raman tensor elements and this effect is only observed for the totally symmetric modes in low-symmetry systems. The complex nature of the Raman tensor elements has been reported in different systems of low-symmetry 2D materials19,21,44,45,51,56–59 For transparent 3D crystals, phase differences between tensor elements can also be associated with birefringence60 and, in this case, the phase difference is the same for all different Raman modes. Moreover, the birefringence contribution for the phase differences is only appreciable if the material's thickness is greater than the wavelength of the incident light, and this effect is negligible in 2D systems with few atomic layers.60 As discussed below, the observation of phase differences in single-layer low-symmetry materials is due to the resonance Raman effect, which is affected by the electron–phonon interaction, thus being specific for each Raman mode.
is its phase.53,54 In fact, as discussed below, we can only obtain the phase differences between the Raman tensor elements and this effect is only observed for the totally symmetric modes in low-symmetry systems. The complex nature of the Raman tensor elements has been reported in different systems of low-symmetry 2D materials19,21,44,45,51,56–59 For transparent 3D crystals, phase differences between tensor elements can also be associated with birefringence60 and, in this case, the phase difference is the same for all different Raman modes. Moreover, the birefringence contribution for the phase differences is only appreciable if the material's thickness is greater than the wavelength of the incident light, and this effect is negligible in 2D systems with few atomic layers.60 As discussed below, the observation of phase differences in single-layer low-symmetry materials is due to the resonance Raman effect, which is affected by the electron–phonon interaction, thus being specific for each Raman mode.
The electric susceptibility carries the symmetry properties of the kinetic coefficients given by χij(ω) = χji(ω), which is derived from Onsager's principle.54 Since the Raman tensor is given by the derivative of susceptibility with respect to the normal modes (see eqn (2)), it will also carry the property Rij(ω) = Rji(ω) if the medium is non-magnetic and if we neglect the slight frequency difference between the incident and scattered photon.54 An important consequence of the symmetry properties in the Raman tensor is the fact that the Raman tensor is not a Hermitian matrix. Therefore, we cannot diagonalize the Raman tensor when the elements are given by complex numbers. The orthogonal basis that diagonalizes the real part 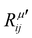 does not diagonalize the imaginary part
does not diagonalize the imaginary part 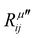 .
.
1.3 The quantum model for the Raman tensor
In this section, we will discuss the physical origin of the Raman tensor elements within the framework of the quantum model for the Raman effect, which is explained by the third-order process illustrated in Fig. 2a. In this approximation, we take explicitly into account not only the two optical transitions associated with the electron–hole creation and recombination, but also the quantum process associated with the creation or destruction of quanta of vibrations (phonons in crystals).53,54,61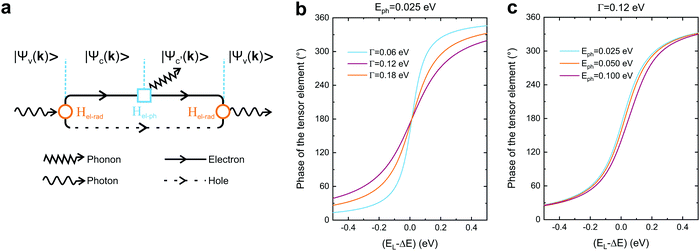 | ||
| Fig. 2 Quantum framework of the Raman tensor. (a) Feynman diagram of the quantum Raman scattering process. Calculated phase of the tensor element in the quantum framework (eqn (10)) considering the fixed values of the (b) phonon energy (Eph = 0.025 eV) and (c) damping (Γ = 0.12 eV). | ||
The Raman process starts with an optical transition from the electronic initial state |ψv〉 in the valence band to the first intermediate state |ψc〉 in the conduction band; the creation (or destruction) of a vibrational quantum (phonon in a crystal) takes the system to the second intermediate state |ψc′〉; finally, an optical transition is related to the electron–hole recombination, leaving the system in the initial electronic state |ψv〉 and giving rise to the scattered photon. The optical transitions are induced by the electron-radiation Hamiltonian (Hel-rad), and the creation of a phonon is induced by the electron–phonon Hamiltonian (Hel–ph). We will consider here the electric-dipole approximation for the electron-radiation Hamiltonian, which can be written as Hel-rad = −d·E, where d is the electric-dipole operator and E is the electric field of the radiation, which is polarized along the direction of the unitary vector ê.
The Raman intensity by a phonon belonging to branch μ is related to the probability of occurrence of the process illustrated in Fig. 2a, and is calculated by means of the Fermi golden rule transition probability for the third-order time-dependent perturbation process.53,54 In this approximation, the Raman tensor element Rμij depends on the excitation energy EL according to the expression:53,54
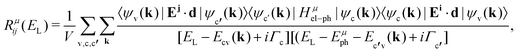 | (9) |
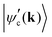 in the conduction band; and 〈ψv(k)|Ej·d|ψc′(k)〉 corresponds to the matrix element of the optical transition associated with the recombination of the electron–hole pair and emission of the scattered photon. In the denominator, Ecv(k) = Ec(k) − Ev(k) and Ec′v(k) = Ec′(k) − Ev(k) are the energy differences between the valence and conduction bands at a given wavevector k, Γc and Γc′ are the damping constants associated with the finite lifetime τ = ħ/2Γ of the photo-excited states |ψc(k)〉 and |ψc′(k)〉, respectively, and Eμph is the energy of phonon μ.19 The contribution of a specific process with wavevector k is inversely proportional to the difference EL − Ecv(k) that appears in the denominator of eqn (9).
in the conduction band; and 〈ψv(k)|Ej·d|ψc′(k)〉 corresponds to the matrix element of the optical transition associated with the recombination of the electron–hole pair and emission of the scattered photon. In the denominator, Ecv(k) = Ec(k) − Ev(k) and Ec′v(k) = Ec′(k) − Ev(k) are the energy differences between the valence and conduction bands at a given wavevector k, Γc and Γc′ are the damping constants associated with the finite lifetime τ = ħ/2Γ of the photo-excited states |ψc(k)〉 and |ψc′(k)〉, respectively, and Eμph is the energy of phonon μ.19 The contribution of a specific process with wavevector k is inversely proportional to the difference EL − Ecv(k) that appears in the denominator of eqn (9).
Let us consider the simplest particular case in eqn (9), where we ignore the two sums by restricting the optical transitions to one specific point k in the Brillouin zone and considering only one electronic state in the valence band (|ψv(k)〉), only one excited state in the conduction band (|ψc(k)〉), and Ecv(k) = ΔE. In this case, the phase ϕμij of the complex tensor element Rμij is given by:19
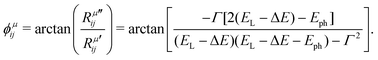 | (10) |
1.4 Raman tensors of low-symmetry 2D materials
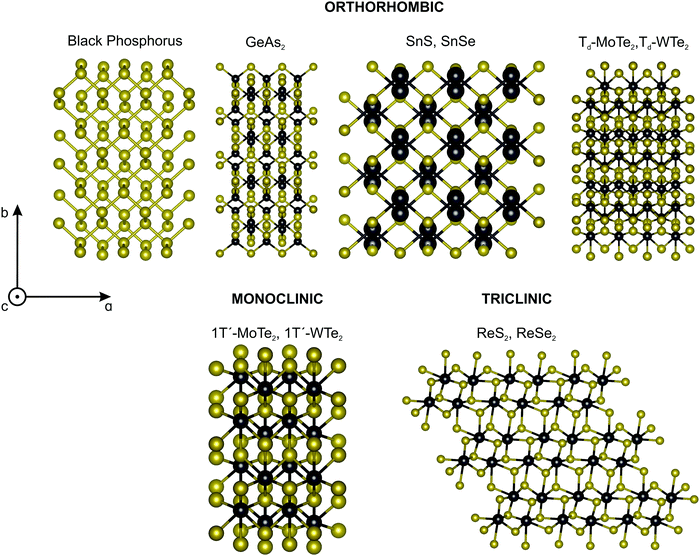
The most studied 2D materials, such as graphene and the semiconducting MoS2-type transition metal dichalcogenides, belong to the hexagonal crystal family, where the 6-fold or 3-fold symmetry is perpendicular to the layer plane.7,9 For these materials, the linear optical properties described by second-rank tensors are isotropic in the layer plane. In particular, their Raman spectrum is isotropic since the intensity of the Raman peaks do not depend on the direction of polarization of the light with respect to the crystallographic axes.62In the last years, several low-symmetry 2D materials from the orthorhombic,63–66 monoclinic67,68 and triclinic69,70 crystal families are being explored, and some examples are shown in Fig. 3. In these three families, the three crystallographic axes a, b, and c have unequal lengths. For the orthorhombic family, the three axes a, b, and c are perpendicular to each other.7–9 For the monoclinic family, one axis, say the a-axis, is perpendicular to the b-axis and c-axis, but the b-axis and c-axis are not perpendicular to each other.7–9 In the case of 2D monoclinic crystals, we have two possibilities: the a-axis can be in the plane of the layer or perpendicular to it.7–9 For the triclinic system, the three axes are inclined at non-orthogonal (non-perpendicular) angles relative to each other.7–9
The orthorhombic crystal family includes the point groups D2, C2v and D2h. Table 1 shows the four Raman tensors of the modes with different symmetries (different irreducible representation) for each point group of the orthorhombic crystal. Notice that in these three point groups, we have the totally symmetric representation A, A1 or Ag for the D2, C2v and D2h point groups, respectively, for which the Raman tensor is diagonal and the three elements in the diagonal are different. It also has three non-degenerate representations where the non-null elements are the off-diagonal terms xy, yz and xz.7
The monoclinic crystal family includes the point groups Cs, C2 and C2h. It has two Raman tensors for the modes with different symmetries (different irreducible representation) for each point group, as shown in Table 1. Here, we adopt the convention that the 2-fold axis is along the y-axis or the mirror plane is the xz plane. However, the reader should be aware that Raman tensors will be different if one adopts the convention that the 2-fold axis is along the z-axis or the mirror plane is the xy plane.7 We can observe for the monoclinic family that the Raman tensor of the totally symmetric representation A, A1 and Ag for the Cs, C2 and C2h point groups, respectively, is no longer a diagonal matrix, since the xz element is different from zero. For the other Raman tensors of the monoclinic systems, associated with the B, A2 and Bg modes for the Cs, C2 and C2h point groups, respectively, the diagonal elements are null and the non-null elements of the matrix are the off-diagonal terms xy and yz.
The triclinic crystal family includes the point groups C1 and Ci (or S2) where the only non-trivial symmetry operation is the inversion center.7 For the Ci point groups, the Raman-active modes belong to the totally symmetric Ag representation. In this case, all elements of the Raman tensor are different from zero, as shown in Table 1.
Among the vast types of low-symmetry 2D materials, this review will focus on one material of each crystal symmetry depicted in Fig. 3. In particular, we discuss the angle-resolved Raman spectra of the black phosphorus, 1T′-MoTe2 and ReSe2 in the following sections.
2 Angle-resolved polarized Raman spectra
2.1 Orthorhombic crystal: black phosphorus
Black phosphorus (BP) consists of atomically thin layers of phosphorus atoms covalently bonded to the neighboring atoms, forming a puckered honeycomb structure.71,72 The atomic structure of a monolayer BP exhibits an orthorhombic symmetry, which belongs to the D2h point (space group Pmna).73,74 By definition of the crystallographic axes of the BP structure,75 the a and c axes are, respectively, along the zigzag and armchair directions, and the b axis is perpendicular to the layer plane. A BP structure can be stacked in different manners,76–78 with the AB-stacking configuration being the most stable.22,77,79,80 The atomic structure of the bulk BP stacked in the AB configuration belongs to the D2h point group, but to the face-centered space group Cmce.81,82 In this case, the face-centered unit cell contains 8 atoms, but the primitive cell of the AB-stacked bulk BP only contains 4 atoms.81,83Group theory predicts 3 acoustic and 9 optical phonon branches for the monolayer and bulk BP, and the irreducible representations at the Brillouin zone center (Γ point) are8,9Γ = 2Ag ⊕ B1g ⊕ B2g ⊕ 2B3g ⊕ Au ⊕ 2B1u ⊕ 2B2u ⊕ B3u, where we considered the definition of the crystallographic axes aforementioned. Only the 2Ag ⊕ B1g ⊕ B2g ⊕ 2B3g phonons are Raman active.22,84–87 In a conventional back-scattering Raman configuration, where the light polarization is in the xz plane, only the A1g, A2g and B2g modes are observed in the Raman spectrum, as shown in Fig. 4. The B1g and B3g only appear in the spectrum where the incident light has a polarization component along the y-axis.21
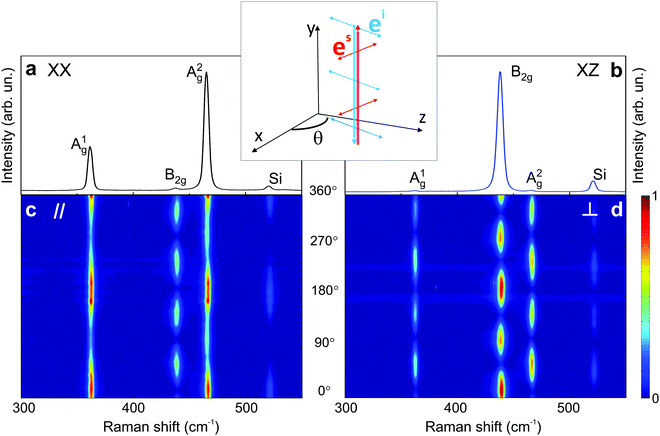 | ||
| Fig. 4 Characteristic Raman spectrum of the orthorhombic black phosphorus. Polarized Raman spectra in the (a) XX and (b) XZ configurations. Typical angle-resolved Raman map of BP in the (c) parallel (‖) and (d) crossed (⊥) configurations. These results are from an exfoliated BP flake. Adapted with permission from ref. 21. | ||
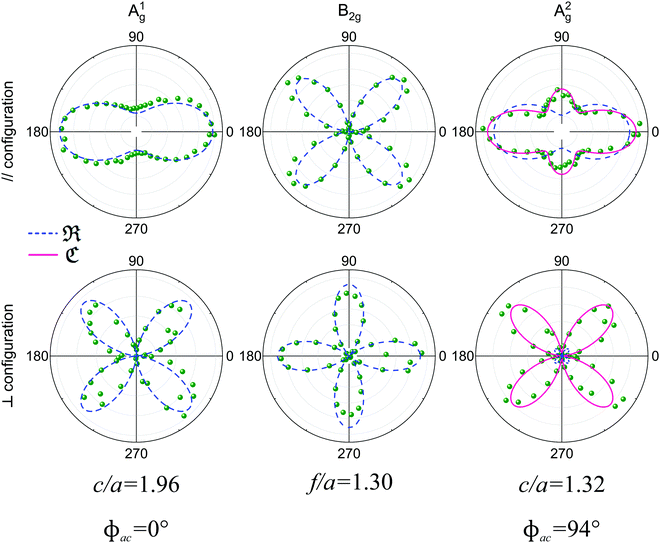
The angular dependence of the polarized Raman spectra can be performed by fixing the analyzer either parallel or perpendicular to the fixed incident polarization while the sample is rotated (see Fig. 1b).19,21,88 The polarized Raman spectra of a bulk BP in the XX and XZ configurations are shown in Fig. 4a and b. Notice that the intensities of the A1g, B2g and A2g modes vary in these configurations. Fig. 4c and d show the angle-resolved polarized Raman map excited with a 2.33 eV laser energy in the parallel and crossed polarized configurations, respectively. Here, the angle θ is between the incident light polarization and the x-axis, as shown in the inset of Fig. 4. The intensities of the A1g, B2g and A2g modes are given by the colorbar.21
The angular dependence of the Raman peak intensities shown in Fig. 4c and d can be explained considering eqn (3), the Raman tensors RAg and RB2g of the different modes, and the polarization vectors êi and ês of the incident and scattered light, respectively. The results shown in Fig. 4 were collected in the back-scattering configuration where the beam of the incident laser was along the y axis of bulk BP.21 Therefore, we only need to consider the Raman tensor elements related to the x and z axes, provided by the first and third rows (or columns) of the Raman tensors shown in Table 1. Thus, we consider the 2 × 2 blocks of the Ag and B2g modes in the xz plane, given by,53,54
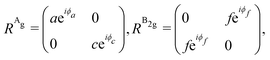 | (11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, sin
θ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), with θ being the angle between êi and the x-axis (see the inset of Fig. 4b). We also need to fix the scattered light polarization, described by the unit vector ês, to determine the Raman tensors elements. The polarized geometries of the unit vector ês are normally parallel and crossed (or perpendicular) to êi, and the unit vector ês can be expressed by a 2 × 1 matrix:
θ), with θ being the angle between êi and the x-axis (see the inset of Fig. 4b). We also need to fix the scattered light polarization, described by the unit vector ês, to determine the Raman tensors elements. The polarized geometries of the unit vector ês are normally parallel and crossed (or perpendicular) to êi, and the unit vector ês can be expressed by a 2 × 1 matrix: 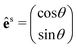 for the parallel configuration, and
for the parallel configuration, and 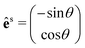 for the crossed configuration.
for the crossed configuration.
By introducing the expressions of the incident and scattered polarized unit vectors and the Raman tensor in eqn (3), we can obtain the angular dependence intensity equations for the Ag and B2g modes in the parallel (‖) and crossed (⊥) configurations, 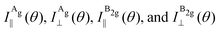 . As an example, we calculated the expression of the angular intensity of the Ag mode in the crossed configuration,53,54
. As an example, we calculated the expression of the angular intensity of the Ag mode in the crossed configuration,53,54
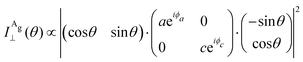 | (12a) |
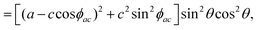 | (12b) |
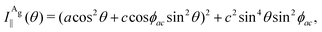 | (13a) |
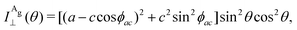 | (13b) |
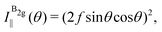 | (13c) |
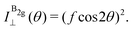 | (13d) |
To determine the Raman tensors of the A1g, B2g and A2g modes of BP, we need to fit the angular dependence of I‖(θ) and I⊥(θ), shown in Fig. 5, with the same set of elements for each mode. The curves in Fig. 5 represent the best fit of I‖ and I⊥ with the same set of tensor elements, respectively. The dashed blue curves represent the best fit considering only real numbers for the tensor elements, corresponding to the situation where the phase difference ϕac is zero (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕac = 0 and cos
ϕac = 0 and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕac = 1 in eqn (13a) and (13b)). Note from Fig. 5 that for the totally symmetric Ag modes, the angular dependence of I‖ exhibits a 2-fold symmetry (with periodicity of 180°), with the maxima at 0° and 180° and the minima (or secondary maxima) at 90° and 270°.21 The reason for this behavior is the fact that c/a < 1, and the opposite trend will occur when c/a > 1. On the other hand, the angular dependence of the cross-polarized intensity I⊥ for the totally symmetric Ag modes exhibits a 4-fold symmetry (with periodicity of 90°), with maxima at 45°, 135°, 225° and 315°. For the B2g-symmetry mode, its angular dependence in both I‖ and I⊥ exhibits a 4-fold symmetry, but the maxima of the I‖ are at 45°, 135°, 225° and 315°, whereas the maxima of the I⊥ are at 0°, 90°, 180° and 270°. The angular dependence behavior shown in Fig. 5 is characteristic of the orthorhombic symmetry of the BP crystal, where the principal axes of the real part of the susceptibility and Raman tensors are necessarily along the crystallographic axes.7,53
ϕac = 1 in eqn (13a) and (13b)). Note from Fig. 5 that for the totally symmetric Ag modes, the angular dependence of I‖ exhibits a 2-fold symmetry (with periodicity of 180°), with the maxima at 0° and 180° and the minima (or secondary maxima) at 90° and 270°.21 The reason for this behavior is the fact that c/a < 1, and the opposite trend will occur when c/a > 1. On the other hand, the angular dependence of the cross-polarized intensity I⊥ for the totally symmetric Ag modes exhibits a 4-fold symmetry (with periodicity of 90°), with maxima at 45°, 135°, 225° and 315°. For the B2g-symmetry mode, its angular dependence in both I‖ and I⊥ exhibits a 4-fold symmetry, but the maxima of the I‖ are at 45°, 135°, 225° and 315°, whereas the maxima of the I⊥ are at 0°, 90°, 180° and 270°. The angular dependence behavior shown in Fig. 5 is characteristic of the orthorhombic symmetry of the BP crystal, where the principal axes of the real part of the susceptibility and Raman tensors are necessarily along the crystallographic axes.7,53
 | ||
| Fig. 5 Angle-resolved Raman response of the orthorhombic black phosphorus. Angular dependence of the intensities of the A1g, B2g and A2g modes in the parallel (‖, top panel) and crossed (⊥, bottom panel) polarization configurations for an exfoliated BP flake for an excitation energy of 2.33 eV. The corresponding tensor element ratios and phase differences extracted from the fitting process are also shown. Adapted with permission from ref. 21. | ||
The experimental results of the B2g mode shown in Fig. 5 in both I‖ and I⊥ can be fitted by real number tensor elements, as expected from eqn (13c) and (13d) and shown by the dashed blue curves in Fig. 5. The results of I‖ and I⊥ for the A1g mode shown in Fig. 5 can also be fitted by real number elements, since ϕac = 0. However, for the A2g mode, the fit by real number elements fails dramatically, as shown by the dashed blue curves in Fig. 5. In this case, a phase difference ϕac is needed to fit the angular dependence of both I‖ and I⊥, as shown by the solid pink curves for the A2g mode in Fig. 5. The important consequences of introducing the phase difference ϕac are the appearance of a secondary maxima in the angular dependence of I‖, at 90° and 270°, and the significant enhancement of the intensities of I⊥ at 45°, 135°, 225° and 315°.
The angle-polarized Raman results mentioned above show the importance of properly measuring and analysing the angle-resolved intensities in the parallel (I‖) and crossed (I⊥) configurations. The determination of tensor elements only with the analysis of the parallel polarized intensities (I‖) can lead to misleading values for the Raman tensor elements.
2.2 Monoclinic crystals: 1T′-MoTe2 type compounds
In monoclinic crystals, one crystallographic axis is perpendicular to two other axes, which are not perpendicular to each other.7,9 The point groups that belong to the monoclinic system are C2 (2), C1h (m) and C2h (2/m). In the case of 2D monoclinic crystals, there are two possibilities: in one category of 2D monoclinic crystals, the 2-fold axis is perpendicular to the layer plane and in other case, the 2-fold axis is along the layer plane. Here, we discuss the monoclinic 1T′ structure of TMDs which includes MoTe2 and WTe2 and that belongs to the second category mentioned above.The monoclinic 1T′ structure of MoTe2 corresponds to a distortion of the 1T structure of TMD compounds, which has hexagonal symmetry.11 Differently from the MoS2-type TMDs, where the layer formed by the S (chalcogens) atoms, above and below the layer composed of Mo (transition metal) atoms, are on the top of each other, in the 1T structure the chalcogens are not on the top of each other, but instead rotated by 60°. The 1T′-MoTe2 structure belongs to the C2h point group and to the P121/m 1 space group. We have written the full notation for the space group to show that the 2-fold axis is along the y-direction. The notation 21 shows that the 2-fold axis is a screw axis.
We need to pay attention when analysing character tables and Raman tensors for monoclinic crystals, since the 2-fold axis in 1T′-MoTe2 is normally considered to be the y-axis and many textbooks assume that the 2-fold axis in monoclinic systems is along the z-direction. Thus, considering that the 2-fold axis is along the y-direction, the Ag symmetry Raman modes are expected to be observed in the XX, YY, ZZ and XZ polarized spectra, whereas the Bg modes appear in the XY and YZ spectra. Using the conventional back-scattering configuration with the incident light is along the z-axis, the Ag modes appear in the XX and YY parallel polarized spectra and the Bg modes in the crossed polarized XY spectrum.59,66,89
The unit cell of a monolayer 1T′-MoTe2 contains 6 atoms, while in its bulk form the unit cell contains 12 atoms.68 According to group theory predictions, 9 modes are expected to appear in the first-order Raman spectrum of monolayer 1T′-MoTe2 (6 Ag modes and 3 Bg modes). For bulk 1T′-MoTe2, 12 Ag modes and 6 Bg modes are predicted to appear in the first-order Raman spectra.68
Fig. 6 shows the angle-resolved polarized Raman map of a 4 nm thick sample of 1T′-MoTe2 in the parallel (‖) and crossed (⊥) configurations.50 The polar plots of the intensities I‖ and I⊥ for some Raman modes are shown in Fig. 6c. Note that in the parallel configuration, the A2g, A3g, A4g and A5g modes have a 2-fold symmetry with their maxima at 90° and 270°. The A1g and A6g modes also exhibit a 2-fold symmetry, but their maxima are at 0° and 180°. In the case of the Bg modes, they show a 4-fold symmetry on both configurations similarly to the B2g modes in orthorhombic BP (see Fig. 5).
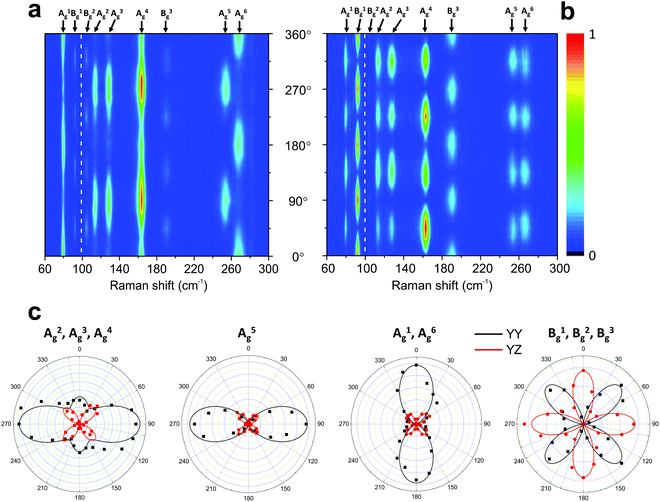 | ||
| Fig. 6 Typical angle-resolved Raman map of a monoclinic 1T′-MoTe2. Raman map in the (a) parallel (‖) and (b) crossed (⊥) polarization configurations. (c) Angular dependence of the intensities of the 1T′-MoTe2 peaks shown in (a) and (b). The angle-resolved Raman map was constructed using two excitation energies: 1.96 eV (below 100 cm−1) and 2.33 nm (above 100 cm−1). Adapted with permission from ref. 50. | ||
The Raman intensity for the Ag and Bg modes in the parallel and crossed polarization configurations is given by eqn (3) and the Raman tensor in Table 1 resulting in,53,54
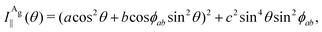 | (14a) |
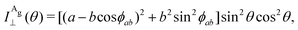 | (14b) |
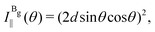 | (14c) |
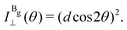 | (14d) |
2.3 Triclinic crystal: rhenium diselenide
The atomic structures of monolayer and bulk rhenium diselenide (ReSe2) belong to the triclinic Ci point group, which only has the identity and the inversion center as symmetry operations.70,90 In both cases, the unit cell has 12 atoms (4 rhenium and 8 selenium atoms) and exhibits diamond-shaped rhenium–rhenium bonds forming quasi-one-dimensional chains.57,70 Group theory predicts 3 acoustic branches and 33 optical branches in the phonon dispersion of ReSe2, and 18 zone-center modes with the Ag symmetry are Raman active.57,70Fig. 7a shows the Raman spectrum of the monolayer ReSe2, where the experimental data correspond to the blue dots and the orange curves represent the fit by Lorentzian curves, which allows us to identify the 18 Ag predicted Raman modes.19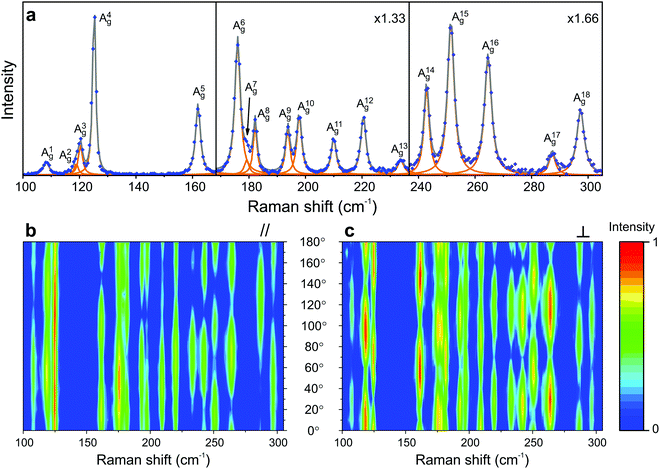 | ||
| Fig. 7 Characteristic Raman spectrum of the triclinic ReSe2; (a) Raman spectrum of a monolayer ReSe2 showing the 18 Ag modes predicted by group theory. Typical angle-resolved Raman map of ReSe2 in the (b) parallel (‖) and (c) crossed (⊥) configurations. The spectra and mapping were collected with a 2.33 eV laser energy. Adapted with permission from ref. 19. | ||
Fig. 7b and c show the angular dependence of the polarized Raman spectra of the monolayer ReSe2 in the parallel (‖) and crossed (⊥) configurations, respectively, where the angle θ is between the incident light polarization êi and the x-axis. The striking difference of these maps with respect to those of the orthorhombic and monoclinic crystals shown in Fig. 4 and 6 is the fact that the maxima and minima of both I‖ and I⊥ in Fig. 7b and c are not at fixed angles. Instead, they are at general angles which, in turn, are different for each mode.19 In fact, this is a consequence of the low-symmetry of the crystal, since all elements of the Raman tensor in triclinic systems are non-null.7 When the tensor has both diagonal and non-diagonal terms if written in the crystallographic axes of the systems, we can diagonalize the real part of the tensor and determine the principal axes. In this case, the principal axes are not along the crystallographic axes and, in turn, are at different angles for the different Raman modes.19
To analyze the results shown in Fig. 7, we need to introduce in eqn (3) the Raman tensor RAg of triclinic crystals and the polarization vectors êi and ês of the incident and scattered light, respectively. In the back-scattering geometry used in ref. 19, only the components of the first 2 × 2 block matrix associated with the x and y coordinates need to be considered since the laser beam is along the z-direction. The term aeiϕa can be put in evidence outside the matrix and we can write the Raman tensor considering only the 2 × 2 block in the xy plane as:53,54
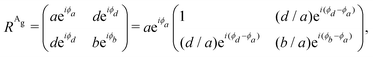 | (15) |
The polarized Raman intensities for the Ag modes in triclinic systems in the parallel (I‖) and crossed (I⊥) configurations, obtained by introducing the tensor in eqn (15) into eqn (3), are given by:53,54
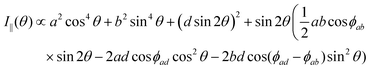 | (16a) |
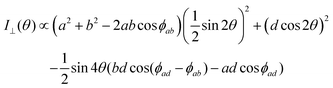 | (16b) |
Another interesting difference between orthorhombic and triclinic systems is related to the phases of Raman tensor elements, which are necessary to explain the experimental angular dependence of I‖ and I⊥ of the Ag symmetry modes.19 As shown in section 2.1, for orthorhombic crystals, we need to consider the phase difference ϕac = (ϕc − ϕa) between the diagonal elements of the tensor. However, for triclinic systems, we need to consider not only the phase difference ϕab = (ϕb − ϕa) between the diagonal elements but also the phase difference between the non-diagonal and one diagonal element, ϕad = (ϕd − ϕa).
Fig. 8 shows examples of the angular dependence of I‖(θ) and I⊥(θ) for six different Ag Raman modes of the monolayer ReSe2. The dots represent the experimental data, and the curves correspond to the best fitting by eqn (7) considering real and complex tensor elements. The dashed blue curves represent the best fit considering only real tensor elements, where the phase differences ϕab and ϕad are 0° or 180°. The solid pink curves in Fig. 8 represent the best fit of I‖ and I⊥ when the tensor elements are complex numbers and the phase differences ϕab and ϕad are included.
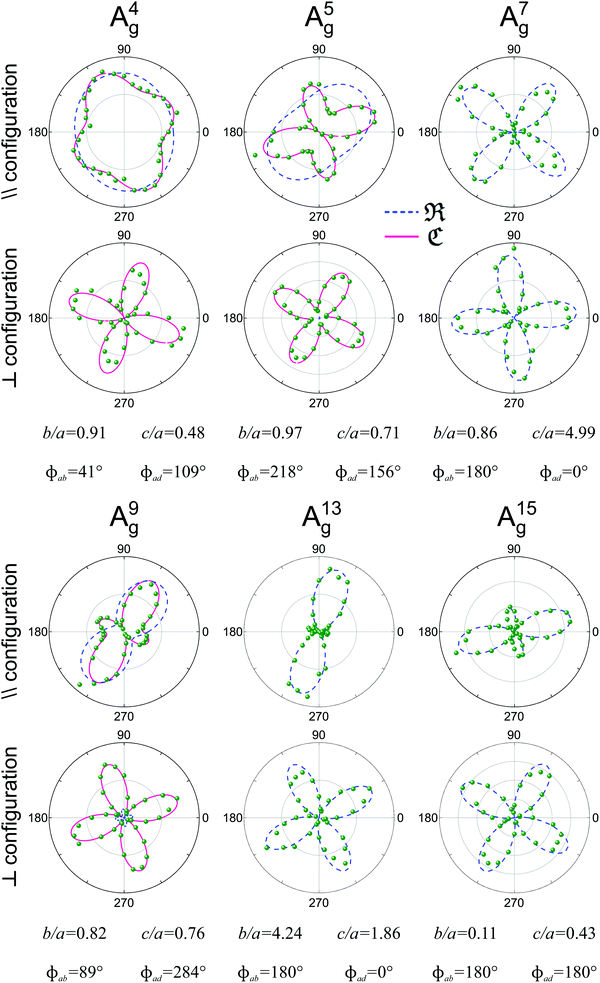 | ||
| Fig. 8 Typical Raman polar plots of a monolayer triclinic ReSe2. Angular dependence of the intensities of 6 Ag modes in the parallel (‖) and crossed (⊥) configurations for an exfoliated monolayer ReSe2 collected using an excitation energy of 2.33 eV. The corresponding tensor element ratios and phase differences extracted from the fitting process are also shown. Adapted with permission from ref. 19. | ||
We can observe in Fig. 8 that the angular dependence of I‖ and I⊥ of modes A7g, A13g and A15g can be fitted when the elements of the Raman tensors are real numbers, since the phase differences are 0° or 180°. However, for modes A4g, A5g and A9g, the disagreement between the experimental data and the fitting considering real numbers is evident, especially in the case of the crossed (I⊥) polarization results. The predicted minima of I⊥ considering real elements are zero, but the experimental results show that the minima of I⊥ are not zero. The effect of the phase of the tensor element also appears in the angular dependence of the parallel polarized intensity I‖. We conclude that the angular dependence of 2D triclinic crystals can only be explained if we consider that the tensor elements are complex numbers and if we introduce the phase differences ϕab and ϕad in eqn (16a) and (16b) to fit the angle-resolved polarized intensities.
Another important aspect of the Raman spectra in triclinic systems is the fact that they are different in the two different faces of the 2D sample. In fact, the atomic structure of ReX2 (X = S or Se) crystals lacks a rotation by π around any axis parallel to the layer plane, which results in two distinct vertical orientations, “up” or “down”.51,70,91 Hart et al. showed that it is possible to experimentally obtain crystals in these orientations in a controlled manner through mechanical exfoliation.91 They also have shown that for a rotation by π around the y-axis changes the sign of the xy and yz elements of the Raman tensors. Choi et al. performed angle-polarized Raman measurements on ReS2 and ReSe2 exfoliated crystals placed on a transparent quartz substrate in both “up” and “down” orientations,51 by turning the substrate upside down as schematized in Fig. 9a and b and shown in Fig. 9c and d. The ReS2 samples were excited by a 2.33 eV laser line. Fig. 9c and d show that the upside turn of the substrate is a π rotation around the 0° direction pointed in the optical images. Their angle-resolved polarized results in the “up” and “down” orientation are shown in Fig. 9e and f, respectively. As one can observe, for phonon modes of ReS2 labelled as mode 3 and mode 551 the polar plots in Fig. 9e are rotations of the polar plots in Fig. 9f around the vertical direction. The same trend was observed for ReSe2 samples.51
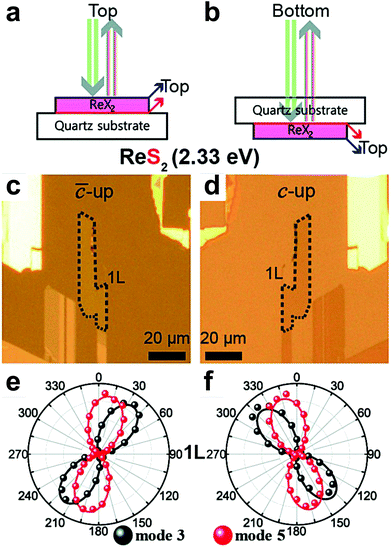 | ||
| Fig. 9 The flipping-like a coin behavior in triclinic 2D materials. Scheme of the laser beam to probe the vertical orientation in triclinic ReX2 (X = S or Se) in the (a) “up” and (b) “down” sample's orientation. Optical images of the monolayer ReS2 in the (c) “up” and (d) “down” orientation show in (a and b). Angle-polarized Raman response of modes 3 and 5 of monolayer ReS2 in the (e) “up” and (f) “down” orientations. Adapted with permission from ref. 51. | ||
3 Resonant Raman effects in low-symmetry 2D materials
3.1 Black phosphorus
Further investigation about the anisotropic Raman response of low-symmetry 2D materials has been provided by the combination of polarized Raman with resonant Raman spectroscopies. The latter has shown to be a powerful tool to probe the electronic structure, excitons and electron–phonon interactions in 2D materials, such as twisted-bilayer graphene,39 MoTe2,40 and MoS2,37,38 among others.34,35,62,92–95In few-layered black phosphorus, Mao et al. observed symmetry-dependent electron–phonon couplings in the experimental Raman excitation profiles of the different modes, which were supported by density functional theory calculations.46 It was shown in this work that, despite the fact that both Ag modes in black phosphorus exhibit in-plane and out-of-plane components, the “in-plane” vibrational A2g mode exhibits a stronger resonance in the visible range than the “out-of-plane” A1g mode, as shown in Fig. 10a and b. For excitation energies in the visible range, the A2g mode has a strong resonance behavior in the armchair and zigzag directions (see Fig. 10a and b), whereas the A1g mode exhibits a weak resonance in both directions, except when excited at the 2.70 eV and with polarization in the zigzag direction (see Fig. 10a and b).46 In addition, it was observed that, for excitation energies in the 2.60–2.73 eV range, the Raman response of the A1g mode is more intense in the zigzag than in the armchair direction as shown in Fig. 10c–f, despite the fact that the absorption is higher in the armchair direction in this energy range.46 This result is a strong indication that the electron–phonon coupling can be more relevant for the enhancement of Raman response than the intrinsic resonance effect in this range of excitation energies. Moreover, the difference in the resonance behavior for these two Ag modes increases in the UV region, where the intensity of A1g becomes very weak.
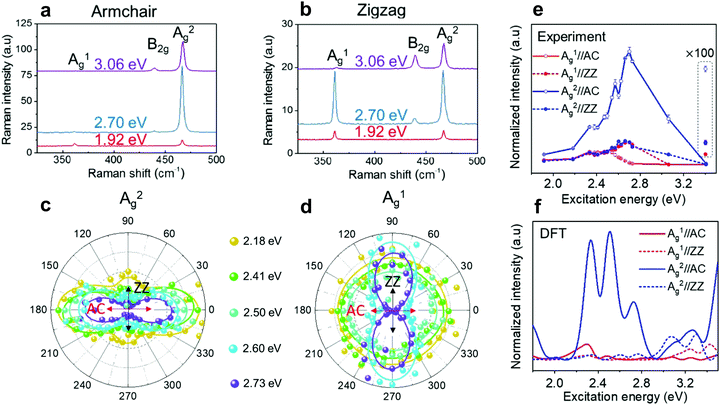 | ||
| Fig. 10 Resonant Raman response of an orthorhombic black phosphorus. Resonant Raman spectra of a 7.7 nm BP flake (∼14 layers) for the excitation energies of 1.92 eV, 2.70 eV and 3.06 eV along the (a) armchair and (b) zigzag directions. Resonant angle-resolved Raman results for different excitation energies of the (c) A2g and (d) A1g modes for a ∼10 nm BP flake. (e) Experimental and (f) calculated Raman excitation profiles of A1g (red curves) and A2g (blue curves) along the armchair (AC) and zigzag (ZZ) directions. Adapted with permission from ref. 46. | ||
These results can be understood considering the symmetry dependence of the exciton–phonon coupling, as observed in semiconducting 2D MoS238 and MoSe2.41 In the black phosphorus case, although both Ag modes share the same irreducible representation, the atoms vibrate along the armchair direction in the A2g mode, which therefore couples more efficiently with the optical transition for electric dipole along the same direction (see Fig. 10c). On the other hand, the A1g mode involves the vibration of atoms mainly in the out-of-plane direction and, therefore, does not exhibit such efficient coupling (see Fig. 10d). Similarly, the weak resonance for both Ag modes in the zigzag direction can be attributed to the fact that few-layered BP is almost transparent for visible light polarized in this direction.46 It is worth noting that few-layer black phosphorus absorbs UV light in the zigzag direction and, therefore, the stronger signal observed for the A2g mode suggests that the in-plane mode also couples more efficiently with in-plane electric dipole transition.
3.2 ReS2 and ReSe2 triclinic crystals
Fig. 8 shows that the orientation and shape of the polar plots of the angular-resolved dependence of the polarized Raman intensities in monolayer ReSe2 are distinct for each one of the 18 Raman modes.19,51 This is a consequence to the fact that all elements of the Raman tensor are non-null and, therefore, the presence of diagonal and non-diagonal terms makes the orientation of the tensors independent on the crystalline axes. In this section, we show that the orientation and shape of the polar plots for the Raman modes of the ReX2 (X = S or Se) also depend on the excitation laser energy and on the number of layers of the 2D materials.Choi et al. performed a systematic angle-resolved polarized Raman study of ReS2 and ReSe2 samples with one, two and three layers (1L, 2L and 3L) recorded with different excitation laser energies.51Fig. 11 shows the Raman intensity polar plots of the first five Ag modes in the monolayer (1L), bilayer (2L) and trilayer (3L) ReSe2, where the red, green and blue dots correspond to the intensities recorded, respectively, with the 1.96, 2.33 and 2.81 eV excitation laser energies in the “up” orientation of the sample.51 Note in the first row of Fig. 11 that both the orientation and shape of the polar plots of the 1L ReSe2 are distinct for each excitation energy. This result shows that the Raman tensor elements and the ratio between the non-diagonal to diagonal terms in triclinic systems depend on the excitation energy used to perform the angle-resolved experiments and also on the number of layers of the sample.
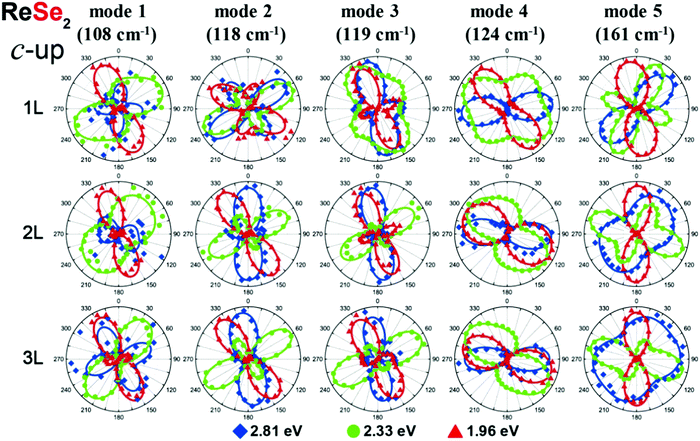 | ||
| Fig. 11 Resonant Raman response of a triclinic ReSe2. Resonant angle-resolved Raman dependence of some modes of a few-layered ReSe2 in the “up” orientation for excitation energies of 1.96, 2.33, and 2.81 eV, respectively. Adapted with permission from ref. 51. | ||
In a recent work, Resende et al. reported an angle-resolved polarized Raman study in 1L and bulk ReSe2 for the excitation energies of 1.92 eV and 2.34 eV, in order to investigate the effects of dimensionality and excitation energy on the Raman tensors of ReSe2.20 The Raman tensors for all 18 Ag modes were obtained considering a simultaneous fitting of the angular dependence in the parallel (I‖) and cross (I⊥) polarized intensities. It was observed that, as expected for a triclinic system excited near resonance conditions, the tensor elements are in general complex numbers and the angular dependence of the polarized Raman intensities is only fitted by considering phase differences between tensor elements.20Fig. 12a–d show, respectively, the Raman tensor element ratio (b/a and d/a) and the phase differences for the 1.92 eV and 2.34 eV laser energies for all 18 Ag modes of a monolayer ReSe2. We can observe that the phase differences of the 18 Ag modes in 1L ReSe2 vary between 0 and 180°, which in turn are different for the 1.92 eV and 2.34 eV excitation energies (see Fig. 12). In most cases, both the tensor elements and phases vary with the change of the excitation energy. For the tensor elements, the b/a ratio for the 2.34 eV laser energy is less scattered than the data for the 1.92 eV, and the c/a ratio is less scattered for both laser energies. Similar behavior can be observed for the phase differences. It was demonstrated in this work that the complex Raman tensor elements contain the contribution of the scattering process of a unique ReSe2 layer and other contribution related to the interference of the scattered light coming from the different layers of the material.20
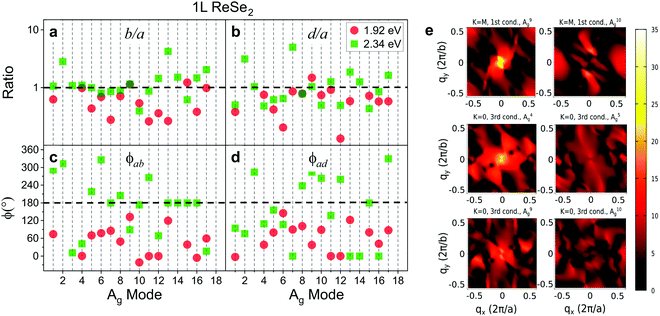 | ||
| Fig. 12 Raman tensor elements and phase differences of a monolayer ReSe2. (a and b) Ratio values of the Raman tensor elements (in a logarithmic scale) and (c and d) the phase differences for all 18 Ag of a monolayer ReSe2 for 1.92 eV and 2.34 eV excitation laser energies. (e) Calculated electron–phonon couplings for A9g and A10g between the lowest conduction band electronic states at the M point and for A4g, A5g, A9g, and A10g between the third lowest conduction band electronic stated at the G point. The color-bar scale is in units of meV. Images (a–d) were adapted with permission from ref. 20 and image (e) was adapted with permission from ref. 19. | ||
McCreary et al. investigated the resonant Raman behavior of rhenium disulfide (ReS2) for different number of layers (1L, 2L, 4L and bulk) using four excitation energies (1.58, 1.96, 2.41 and 2.54 eV).56 It was shown that most of the modes in ReS2 exhibit a maximum intensity peak when excited with the 1.58 eV energy, which is close to the excitonic transition for 2L, 4L and bulk, but a low-intensity response in the Raman spectrum of 1L ReS2 collected at the 1.58 eV energy.56 The peaks that exhibited the highest intensity are those associated with the S-atoms vibrations (e.g. A2g, A3g, A12g, A15g, A16g and A18g modes). A large intensity enhancement was observed for the modes related to the out-of-plane vibration of the Re atoms for the 1.58 eV excitation energy. However, the modes corresponding to the in-plane vibrations of the Re atoms (e.g. A6g and A7g modes) show a significant enhancement only when excited at 1.96 eV.56 The A1g and A8g modes, which are also related to Re in-plane vibrations, also present considerable intensity change but only for the 2L and 4L ReS2 samples.56
3.3 Origin of the complex Raman tensors and electron–phonon coupling
In this section, we will discuss the physical origin of the Raman tensor elements and the phase differences between tensor elements observed in low-symmetry crystals. We show that the dependence of the tensor elements on the laser excitation energy and on the number of layers in 2D materials is a consequence of the resonant Raman effect that occurs when the photons of the Raman process (absorption or emission) are in resonance with the optical transitions of the material.According to the expression for the Raman tensor elemens Rμij shown in eqn (9), the modulus of the tensor elements depends on the three matrix elements in the numerator and on the two resonant terms in the denominator of the expression. On the other hand, the phase ϕμij depends only on the terms in the denominator of eqn (9). Eqn (10) corresponds to the simplest expression for the phase ϕμij, where we ignore the sums in eqn (9), and considers only two electronic energy levels in the valence and conduction bands. The strong dependence of the phase ϕμij on the difference (EL − ΔE) observed in Fig. 2b explains why the modulus and phase differences of the Raman tensor elements observed in low-symmetry 2D materials depend on the laser excitation energy. It also explains why the Raman tensor elements are different in single-layered, few layered and bulk 2D materials, since the electronic band structure and excitonic optical transitions depend on the number of layers and are distinct in the single-layer, few-layers and bulk regimes.
The observed results that each Raman mode exhibits a distinct angle-resolved polarized Raman spectra and a specific Raman tensor in low-symmetry 2D materials cannot be explained by the weak dependence of ϕμij on the phonon frequency Eph shown in Fig. 2b. In fact, the distinct and particular behavior of each Raman mode is due to the dependence of the electron–phonon matrix element 〈ψc′(k)|Hel–μph|ψc(k)〉 on the wavevector k of the electronic state. Despite the fact that only q ∼ 0 phonons are involved in first-order Raman scattering, the vertical optical transitions occur for all electronic wavevectors k within the Brillouin zone. Fig. 12e shows the maps of the electron–phonon coupling as a function of the wavevector k over the entire Brillouin zone for six different normal modes of ReSe2.19 We can clearly observe in Fig. 12e that the maxima of the electron–phonon coupling for each Raman mode occur at different wavevectors k in the BZ. Therefore, the dependence of the electron–phonon matrix elements on k explains the distinct values of the modulus and phases of the Raman tensor elements for each Raman mode.
In summary, we can observe from eqn (9) that the modulus of the Raman tensor elements depends on the three matrix elements in the numerator of the expression, but the phases depend only on the terms in the denominator of eqn (10). For the two optical transitions, we need to take into account the electric fields E of the incident and scattered radiation polarized along the directions êi and êj, respectively, and the matrix elements of the electric dipole operator d between states in the valence and conduction bands. The sum in eqn (9) is performed over all wavevectors k within the first Brillouin zone, and the contribution of a specific process with wavevector k for the Raman intensity is directly proportional to the three matrix elements in the numerator of eqn (9) and inversely proportional to the difference [Ei − Ecv(k)] that appears in the denominator of eqn (9). We thus need to consider the dependence of all terms of eqn (9) on the wavevector k to explain the specific angular dependence for each Raman mode.
4 Concluding remarks
In the emerging field of 2D materials, new systems with different chemical elements and atomic structures are being extensively produced and studied. Raman spectroscopy is a fundamental experimental tool to investigate 2D materials that has been widespread in graphene and spanned to other 2D compounds such as the transition metal dichalcogenides. Raman spectra provide information about different physical properties of the sample, such as disorder, strain, presence of charges, number of layers, atomic structure of edges, and stacking arrangement, among others. Moreover, the possibility of using multiple excitation laser energies allows investigating the physics of excitons predominant in 2D layered materials and the electron–phonon interactions. In high symmetry 2D materials, such as graphene and MoS2, the intensity of the Raman peaks does not depend on the direction of the incident light polarization with respect to the crystallographic axes. However, in low-symmetry 2D systems belonging to the orthorhombic, monoclinic and triclinic crystal families, the intensity of each Raman mode depends on the polarization of the incident light with respect to the crystallographic axes of the material. The anisotropy on the Raman response in low-symmetry materials is described by the Raman tensor, which is specific for each Raman-active mode.In this perspective review, we started discussing the tensorial nature of the Raman response in crystals and the angle-resolved polarized Raman experiments, where one can vary the angle between the light polarization with respect to the crystalline axes. We have shown that it is of utmost importance to use a polarizer/analyzer to control the polarization of the scattered light to correctly determine the values of the Raman tensor elements from the analysis of the angle-resolved polarized intensities. In the most common configurations for the polarized Raman experiments, the polarization of the incident light can be parallel (‖) or perpendicular (⊥) to the polarization of the scattered light. The tensor elements are obtained by fitting the angular dependence of the parallel (I‖) and crossed (I⊥) Raman intensities with the same set of tensor elements for each mode. We have shown that the directions of the maxima and minima of I‖ for orthorhombic systems are along the crystalline axes and the maxima of I⊥ make an angle of 45° with respect to the crystalline axes. In monoclinic 1T′-MoTe2, the angle-resolved experiments are similar to the orthorhombic case since the 2-fold symmetry axis is in the layer plane. For triclinic systems, the maxima in the angular dependence of I‖ and I⊥ are at general orientations and distinct for each Raman mode. This behavior is a consequence of the fact that all elements of the Raman tensor in triclinic systems are different from zero. The co-existence of diagonal and non-diagonal elements in the Raman tensors makes the directions of the maxima of I‖ and I⊥ independent on the directions of the crystalline axes.
Most of the low-symmetry 2D materials studied so far, such as black-phosphorus and MoTe2, are semiconducting and the energies of the photons normally used in Raman spectroscopy are above their energy band gaps. Therefore, their Raman intensities are enhanced by the resonances of the photons with higher energy electronic (or excitonic) transitions. In this case, the Raman tensor elements are complex numbers, with a modulus and a phase. Information about the phases of the Raman tensor elements is lost in higher symmetry materials but is preserved in the case of low-symmetry materials. However, we can only obtain values of the phase differences between the elements of the Raman tensor from the analysis of the angle-resolved experiments. It was shown that the unusual angular dependence of the polarized spectra of black-phosphorus can be nicely explained by considering the phase difference between the two diagonal elements of the tensor associated with the totally symmetric A2g modes. In the case of triclinic and semiconducting materials such and ReS2 and ReSe2, it was shown that the complex nature of the tensor elements is observed for the majority of the modes, and phase differences between diagonal elements and between diagonal and non-diagonal elements are needed to fit the experimental angular dependence of I‖ and I⊥.
We have analyzed the results for the Raman tensors in low symmetry 2D materials within the framework of the quantum model for the Raman process, in which we consider explicitly not only the two optical transitions associated with the incident and scattered photons but also the matrix element of the electron–phonon process. For the determination of the Raman tensor, we need to sum the contribution over all k points in the Brillouin zone. Due to the resonance effect, the contribution of each k-vector for the Raman tensor element will be inversely proportional to the difference EL − ΔE(k) between the laser energy and the bandgap at this k point. Moreover, we also need to consider the contribution of the electron–phonon matrix element and its dependence on the wavevector k for the Raman tensor. The fact that the Raman tensor is different for each mode is a clear evidence that the dependence of the electron–phonon matrix elements on k plays a fundamental role to describe the angle-resolved polarized Raman spectra in low-symmetry 2D materials.
Finally, the possibility of performing measurements in samples of low-symmetry 2D materials with a different number of layers (1L, 2L, 3L and up to bulk) will allow the distinction of the contributions for the Raman tensor from a single atomic layer and from the light scattered by different layers of a multi-layered sample. Although there are some recent studies on the resonant Raman effect in low-symmetry 2D materials, most of the reports have used only a few laser excitation energies. A detailed multiple energy excitation Raman study, where we can tune the excitation laser energy across the excitonic transitions, will be needed to unveil the electron–phonon or exciton–phonon coupling mechanism in these materials. We stress that there is still a lot to be explored in these systems and the investigation of the polarized and resonant properties of the Raman spectra in low-symmetry 2D materials is still only at the beginning stage. For instance, some reports have recently demonstrated the emergence of anisotropic properties in twisted samples of graphene and semiconducting TMDs,96–101 due to the mismatch between the layers that breaks the axial symmetry. Angle-resolved polarized Raman spectroscopy may provide a new route to study symmetry lowering in twisted 2D structures. Also, the quantification of defects in 2D materials needs attention as it plays a major role in the physical properties of the material. Yu et al.52 reported a study of defects in anisotropic ReS2 created by argon irradiation and observed the correlation of the defect density and anisotropy. Future studies of defective anisotropic 2D materials may provide new and interesting results. We have only scratched a piece of the quantum formalism to investigate the modulus and phase of the Raman tensor elements and an integration of the Raman tensor expression over all valence and conduction bands and over all wavevectors k in the Brillouin zone will be needed to fully describe the experimental results. This review demonstrates the importance of angle-resolved polarized Raman spectroscopy to study the fundamental physics of low-symmetry materials, highlighting its uniqueness in the 2D materials field.
Author contributions
The authors researched, collated and wrote the manuscript. The authors discussed and modified the manuscript at all stages.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors acknowledge the financial support from the Brazilian agencies CNPq, CAPES, FAPEMIG and the Brazilian Institute for Science and Technology of Carbon Nanomaterials (INCT-Nanocarbono).References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306(5696), 666–669 CrossRef CAS PubMed.
- K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(30), 10451–10453 CrossRef CAS PubMed.
- M. Chhowalla, H. S. Shin, G. Eda, L.-J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5(4), 263 CrossRef PubMed.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13(3), 246 CrossRef CAS PubMed.
- S. Zhao, B. Dong, H. Wang, H. Wang, Y. Zhang, Z. V. Han and H. Zhang, Nanoscale Adv., 2020, 2(1), 109–139 RSC.
- S. Barraza-Lopez, F. Xia, W. Zhu and H. Wang, Beyond Graphene: Low-Symmetry and Anisotropic 2D Materials, 2020 Search PubMed.
- J. F. Nye, Physical properties of crystals: their representation by tensors and matrices, Oxford University Press, 1985 Search PubMed.
- M. S. Dresselhaus, G. Dresselhaus and A. Jorio, Group theory, Springer-Verlag, 1st edn, 2008 Search PubMed.
- M. Tinkham, Group Theory and Quantum Mechanics, Courier Corporation, 1st edn, 1992 Search PubMed.
- S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, Nat. Rev. Mater., 2017, 2(8), 17033 CrossRef CAS.
- Z. Lin, B. R. Carvalho, E. Kahn, R. Lv, R. Rao, H. Terrones, M. A. Pimenta and M. Terrones, 2D Mater., 2016, 3(2), 022002 CrossRef.
- H. Yuan, X. Liu, F. Afshinmanesh, W. Li, G. Xu, J. Sun, B. Lian, A. G. Curto, G. Ye and Y. Hikita, et al. , Nat. Nanotechnol., 2015, 10(8), 707–713 CrossRef CAS PubMed.
- F. Liu, S. Zheng, X. He, A. Chaturvedi, J. He, W. L. Chow, T. R. Mion, X. Wang, J. Zhou and Q. Fu, et al. , Adv. Funct. Mater., 2016, 26(8), 1169–1177 CrossRef CAS.
- X. Wang, A. M. Jones, K. L. Seyler, V. Tran, Y. Jia, H. Zhao, H. Wang, L. Yang, X. Xu and F. Xia, Nat. Nanotechnol., 2015, 10, 517 CrossRef CAS PubMed.
- H. Tian, Q. Guo, Y. Xie, H. Zhao, C. Li, J. J. Cha, F. Xia and H. Wang, Adv. Mater., 2016, 28(25), 4991–4997 CrossRef CAS PubMed.
- H. Wang, M.-L. Chen, M. Zhu, Y. Wang, B. Dong, X. Sun, X. Zhang, S. Cao, X. Li and J. Huang, et al. , Nat. Commun., 2019, 10(1), 1–8 CrossRef PubMed.
- M. N. Ali, J. Xiong, S. Flynn, J. Tao, Q. D. Gibson, L. M. Schoop, T. Liang, N. Haldolaarachchige, M. Hirschberger and N. P. Ong, et al. , Nature, 2014, 514(7521), 205–208 CrossRef CAS PubMed.
- A. D. Kent and D. C. Worledge, Nat. Nanotechnol., 2015, 10(3), 187–191 CrossRef CAS PubMed.
- G. C. Resende, G. A. S. Ribeiro, O. J. Silveira, J. S. Lemos, J. C. Brant, D. Rhodes, L. Balicas, M. Terrones, M. S. C. Mazzoni, C. Fantini, B. R. Carvalho and M. A. Pimenta, 2D Mater., 2021, 8(2), 025002 CrossRef CAS.
- G. C. Resende, G. A. S. Ribeiro, O. J. Silveira, J. S. Lemos, D. Rhodes, L. Balicas, M. Terrones, M. S. C. Mazzoni, C. Fantini, B. R. Carvalho and M. A. Pimenta, J. Raman Spectrosc., 2021 DOI:10.1002/jrs.6212.
- H. B. Ribeiro, M. A. Pimenta, C. J. S. de Matos, R. L. Moreira, A. S. Rodin, J. D. Zapata, E. A. T. de Souza and A. H. C. Neto, ACS Nano, 2015, 9(4), 4270–4276 CrossRef CAS PubMed.
- H. B. Ribeiro, C. E. P. Villegas, D. A. Bahamon, D. Muraca, A. H. C. Neto, E. A. T. de Souza, A. R. Rocha, M. A. Pimenta and C. J. S. de Matos, Nat. Commun., 2016, 7, 12191 CrossRef CAS PubMed.
- J. B. Renucci, R. N. Tyte and M. Cardona, Phys. Rev. B: Solid State, 1975, 11(10), 3885 CrossRef CAS.
- M. Cardona, J. Mol. Struct., 1986, 141, 93–107 CrossRef CAS.
- F. Widulle, T. Ruf, M. Konuma, I. Silier, M. Cardona, W. Kriegseis and V. I. Ozhogin, Solid State Commun., 2001, 118(1), 1–22 CrossRef CAS.
- F. Cerdeira, W. Dreybrodt and M. Cardona, Solid State Commun., 1972, 10(7), 591–595 CrossRef CAS.
- B. A. Weinstein and M. Cardona, Phys. Rev. B: Solid State, 1973, 7(6), 2545 CrossRef CAS.
- J. Menéndez, A. Pinczuk, J. Bevk and J. P. Mannaerts, J. Vac. Sci. Technol., B, 1988, 6(4), 1306–1309 CrossRef.
- A. Picco, E. Bonera, E. Grilli, M. Guzzi, M. Giarola, G. Mariotto, D. Chrastina and G. Isella, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(11), 115317 CrossRef.
- D. Olego and M. Cardona, Solid State Commun., 1981, 39(10), 1071–1075 CrossRef CAS.
- G. Burns, F. H. Dacol, C. R. Wie, E. Burstein and M. Cardona, Solid State Commun., 1987, 62(7), 449–454 CrossRef CAS.
- J. M. Zhang, T. Ruf, M. Cardona, O. Ambacher, M. Stutzmann, J.-M. Wagner and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56(22), 14399 CrossRef CAS.
- M. A. Pimenta, E. del Corro, B. R. Carvalho, C. Fantini and L. M. Malard, Acc. Chem. Res., 2015, 48(1), 41–47 CrossRef CAS PubMed.
- B. R. Carvalho and M. A. Pimenta, 2D Mater., 2020, 7(4), 042001 CrossRef CAS.
- L. M. Malard, M. A. Pimenta, G. Dresselhaus and M. S. Dresselhaus, Phys. Rep., 2009, 473(5), 51–87 CrossRef CAS.
- K. Fujisawa, B. R. Carvalho, T. Zhang, N. Perea-López, Z. Lin, V. Carozo, S. L. L. M. Ramos, E. Kahn, A. Bolotsky, H. Liu, A. L. Elías and M. Terrones, ACS Nano, 2021, 15(6), 9658–9669 CrossRef PubMed.
- B. R. Carvalho, Y. Wang, S. Mignuzzi, D. Roy, M. Terrones, C. Fantini, V. H. Crespi, L. M. Malard and M. A. Pimenta, Nat. Commun., 2017, 8(1), 1–8 CrossRef PubMed.
- B. R. Carvalho, L. M. Malard, J. M. Alves, C. Fantini and M. A. Pimenta, Phys. Rev. Lett., 2015, 114, 136403 CrossRef PubMed.
- G. S. N. Eliel, M. V. O. Moutinho, A. C. Gadelha, A. Righi, L. C. Campos, H. B. Ribeiro, P.-W. Chiu, K. Watanabe, T. Taniguchi, P. Puech, M. Paillet, T. Michel, P. Venezuela and M. A. Pimenta, Nat. Commun., 2018, 9(1), 1221 CrossRef CAS PubMed.
- H. Guo, T. Yang, M. Yamamoto, L. Zhou, R. Ishikawa, K. Ueno, K. Tsukagoshi, Z. Zhang, M. S. Dresselhaus and R. Saito, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 205415 CrossRef.
- P. Soubelet, A. E. Bruchhausen, A. Fainstein, K. Nogajewski and C. Faugeras, Phys. Rev. B, 2016, 93, 155407 CrossRef.
- T. Strach, J. Brunen, B. Lederle, J. Zegenhagen and M. Cardona, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1292–1297 CrossRef CAS.
- M. Cardona, Solid State Commun., 1971, 9(11), 819–822 CrossRef CAS.
- X. Ling, S. Huang, E. H. Hasdeo, L. Liang, W. M. Parkin, Y. Tatsumi, A. R. T. Nugraha, A. A. Puretzky, P. M. Das, B. G. Sumpter, D. B. Geohegan, J. Kong, R. Saito, M. Drndic, V. Meunier and M. S. Dresselhaus, Nano Lett., 2016, 16(4), 2260–2267 CrossRef CAS PubMed.
- A.-L. Phaneuf-L’Heureux, A. Favron, J.-F. Germain, P. Lavoie, P. Desjardins, R. Leonelli, R. Martel and S. Francoeur, Nano Lett., 2016, 16(12), 7761–7767 CrossRef PubMed.
- N. Mao, X. Wang, Y. Lin, B. G. Sumpter, Q. Ji, T. Palacios, S. Huang, V. Meunier, M. S. Dresselhaus, W. A. Tisdale, L. Liang, X. Ling and J. Kong, J. Am. Chem. Soc., 2019, 141(48), 18994–19001 CrossRef CAS PubMed.
- M.-L. Lin, Y.-C. Leng, X. Cong, D. Meng, J. Wang, X.-L. Li, B. Yu, X.-L. Liu, X.-F. Yu and P.-H. Tan, Sci. Bull., 2020, 65(22), 1894–1900 CrossRef CAS.
- Y. Zhu, W. Zheng, W. Wang, S. Zhu, L. Li, L. Cheng, M. Jin, Y. Ding and F. Huang, PhotoniX, 2020, 1(1), 1–9 CrossRef.
- T. Sriv, T. M. H. Nguyen, Y. Lee, S. Y. Lim, K. Kim, S. Cho and H. Cheong, et al. , Sci. Rep., 2020, 10(1), 1–9 CrossRef PubMed.
- J. Wang, X. Luo, S. Li, I. Verzhbitskiy, W. Zhao, S. Wang, S. Y. Quek and G. Eda, Adv. Funct. Mater., 2017, 27(14), 1604799 CrossRef.
- Y. Choi, K. Kim, S. Y. Lim, J. Kim, J. M. Park, J. H. Kim, Z. Lee and H. Cheong, Nanoscale Horiz., 2020, 5, 308–315 RSC.
- J. Yu, Y. Wang, J. Jiang, Y. Liang, Y. Liu, B. Zhong, S. Quan, M. Zhou, Z. Ni and S. Guo, Appl. Phys. Lett., 2021, 119(5), 053104 CrossRef CAS.
- R. Loudon, Adv. Phys., 1964, 13(52), 423–482 CrossRef CAS.
- P. Y. Yu and M. Cardona, Fundamentals of semiconductors, Springer-Verlag Berlin Heidelberg, 4th edn, 2010 Search PubMed.
- A. C. Albrecht, J. Chem. Phys., 1961, 34(5), 1476–1484 CrossRef CAS.
- A. McCreary, J. R. Simpson, Y. Wang, D. Rhodes, K. Fujisawa, L. Balicas, M. Dubey, V. H. Crespi, M. Terrones and A. R. Hight Walker, Nano Lett., 2017, 17(10), 5897–5907 CrossRef CAS PubMed.
- E. Lorchat, G. Froehlicher and S. Berciaud, ACS Nano, 2016, 10(2), 2752–2760 CrossRef CAS PubMed.
- Q. Song, X. Pan, H. Wang, K. Zhang, Q. Tan, P. Li, Y. Wan, Y. Wang, X. Xu, M. Lin, X. Wan, F. Song and L. Dai, Sci. Rep., 2016, 6, 29254 CrossRef PubMed.
- R. Beams, L. G. Cançado, S. Krylyuk, I. Kalish, B. Kalanyan, A. K. Singh, K. Choudhary, A. Bruma, P. M. Vora, F. Tavazza, A. V. Davydov and S. J. Stranick, ACS Nano, 2016, 10(10), 9626–9636 CrossRef CAS PubMed.
- C. Kranert, C. Sturm, R. Schmidt-Grund and M. Grundmann, Phys. Rev. Lett., 2016, 116, 127401 CrossRef PubMed.
- W. L. Peticolas, L. Nafie, P. Stein and B. Fanconi, J. Chem. Phys., 1970, 52(3), 1576–1584 CrossRef CAS.
- R. Saito, Y. Tatsumi, S. Huang, X. Ling and M. S. Dresselhaus, J. Phys.: Condens. Matter, 2016, 28(35), 353002 CrossRef CAS PubMed.
- F. Xia, H. Wang and Y. Jia, Nat. Commun., 2014, 5, 4458 CrossRef CAS PubMed.
- R. Fei, W. Li, J. Li and L. Yang, Appl. Phys. Lett., 2015, 107(17), 173104 CrossRef.
- Y. C. Jiang, J. Gao and L. Wang, Sci. Rep., 2016, 6(1), 19624 CrossRef CAS PubMed.
- K. Zhang, C. Bao, Q. Gu, X. Ren, H. Zhang, K. Deng, Y. Wu, Y. Li, J. Feng and S. Zhou, Nat. Commun., 2016, 7(1), 1–6 Search PubMed.
- J. Xia, D.-F. Li, J.-D. Zhou, P. Yu, J.-H. Lin, J.-L. Kuo, H.-B. Li, Z. Liu, J.-X. Yan and Z.-X. Shen, Small, 2017, 13(40), 1701887 CrossRef PubMed.
- Q. Song, H. Wang, X. Pan, X. Xu, Y. Wang, Y. Li, F. Song, X. Wan, Y. Ye and L. Dai, Sci. Rep., 2017, 7(1), 1–10 CrossRef PubMed.
- O. B. Aslan, D. A. Chenet, A. M. Van Der Zande, J. C. Hone and T. F. Heinz, ACS Photonics, 2016, 3(1), 96–101 CrossRef CAS.
- D. Wolverson, S. Crampin, A. S. Kazemi, A. Ilie and S. J. Bending, ACS Nano, 2014, 8(11), 11154–11164 CrossRef CAS PubMed.
- H. Fujihisa, Y. Akahama, H. Kawamura, Y. Ohishi, Y. Gotoh, H. Yamawaki, M. Sakashita, S. Takeya and K. Honda, Phys. Rev. Lett., 2007, 98, 175501 CrossRef.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9(5), 372–377 CrossRef CAS PubMed.
- C. A. Vanderborgh and D. Schiferl, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40(14), 9595 CrossRef CAS PubMed.
- A. Brown and S. Rundqvist, Acta Crystallogr., 1965, 19(4), 684–685 CrossRef CAS.
- S. Sugai and I. Shirotani, Solid State Commun., 1985, 53(9), 753–755 CrossRef CAS.
- D. Çakir, C. Sevik and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 165406 CrossRef.
- R. J. Wu, M. Topsakal, T. Low, M. C. Robbins, N. Haratipour, J. S. Jeong, R. M. Wentzcovitch, S. J. Koester and K. A. Mkhoyan, J. Vac. Sci. Technol., A, 2015, 33(6), 060604 CrossRef.
- H. Shu, Y. Li, X. Niu and J. Wang, Phys. Chem. Chem. Phys., 2016, 18(8), 6085–6091 RSC.
- J. Dai and X. C. Zeng, J. Phys. Chem. Lett., 2014, 5(7), 1289–1293 CrossRef CAS PubMed.
- A. Castellanos-Gomez, L. Vicarelli, E. Prada, J. O. Island, K. L. Narasimha-Acharya, S. I. Blanter, D. J. Groenendijk, M. Buscema, G. A. Steele and J. V. Alvarez, et al. , 2D Mater., 2014, 1(2), 025001 CrossRef CAS.
- J. Ribeiro-Soares, R. M. Almeida, L. G. Cançado, M. S. Dresselhaus and A. Jorio, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 205421 CrossRef.
- X. Ling, L. Liang, S. Huang, A. A. Puretzky, D. B. Geohegan, B. G. Sumpter, J. Kong, V. Meunier and M. S. Dresselhaus, Nano Lett., 2015, 15(6), 4080–4088 CrossRef CAS PubMed.
- J.-W. Jiang, B.-S. Wang and H. S. Park, J. Phys.: Condens. Matter, 2016, 28(16), 165401 CrossRef PubMed.
- J. Lannin and B. Shanabrook, Physics of Semiconductors, IOP Conf. Proc. Ser., vol. 43, 1979.
- S. Sugai, T. Ueda and K. Murase, J. Phys. Soc. Jpn., 1981, 50(10), 3356–3361 CrossRef CAS.
- S. Liu, N. Huo, S. Gan, Y. Li, Z. Wei, B. Huang, J. Liu, J. Li and H. Chen, J. Mater. Chem. C, 2015, 3(42), 10974–10980 RSC.
- C. Kaneta, H. Katayama-Yoshida and A. Morita, Solid State Commun., 1982, 44(5), 613–617 CrossRef CAS.
- J. Kim, J.-U. Lee, J. Lee, H. J. Park, Z. Lee, C. Lee and H. Cheong, Nanoscale, 2015, 7(44), 18708–18715 RSC.
- S.-Y. Chen, T. Goldstein, D. VenkataRaman, A. RamasubRamaniam and J. Yan, Nano Lett., 2016, 16(9), 5852–5860 CrossRef CAS PubMed.
- J. A. Wilson and A. D. Yoffe, Adv. Phys., 1969, 18(73), 193–335 CrossRef CAS.
- L. Hart, S. Dale, S. Hoye, J. L. Webb and D. Wolverson, Nano Lett., 2016, 16(2), 1381–1386 CrossRef CAS PubMed.
- E. del Corro, H. Terrones, A. Elias, C. Fantini, S. Feng, M. A. Nguyen, T. E. Mallouk, M. Terrones and M. A. Pimenta, ACS Nano, 2014, 8(9), 9629–9635 CrossRef CAS PubMed.
- E. del Corro, A. Botello-Méndez, Y. Gillet, A. L. Elias, H. Terrones, S. Feng, C. Fantini, D. Rhodes, N. Pradhan, L. Balicas, X. Gonze, J.-C. Charlier, M. Terrones and M. A. Pimenta, Nano Lett., 2016, 16(4), 2363–2368 CrossRef CAS PubMed.
- K. Golasa, M. Grzeszczyk, P. Leszczyński, C. Faugeras, A. A. L. Nicolet, A. Wysmolek, M. Potemski and A. Babiński, Appl. Phys. Lett., 2014, 104(9), 092106 CrossRef.
- H. Terrones, E. del Corro, S. Feng, J. M. Poumirol, D. Rhodes, D. Smirnov, N. R. Pradhan, Z. Lin, M. A. T. Nguyen, A. L. Elias, T. E. Mallouk, L. Balicas, M. A. Pimenta and M. Terrones, Sci. Rep., 2014, 4, 4215 CrossRef CAS PubMed.
- X. Zhang, R. Zhang, Y. Wang, Y. Zhang, T. Jiang, C. Deng, X. Zhang and S. Qin, Nanotechnology, 2019, 30(43), 435702 CrossRef CAS PubMed.
- H. Kim, H. Ko, S. M. Kim and H. Rho, J. Raman Spectrosc., 2020, 51(5), 774–780 CrossRef CAS.
- Y. Zhu, W. Zheng, W. Wang, S. Zhu, L. Cheng, L. Li, Z. Lin, Y. Ding, M. Jin and F. Huang, J. Raman Spectrosc., 2020, 51(8), 1324–1330 CrossRef CAS.
- M. Jin, W. Zheng, Y. Ding, Y. Zhu, W. Wang and F. Huang, J. Phys. Chem. Lett., 2020, 11(11), 4311–4316 CrossRef CAS PubMed.
- Y. Ding, W. Zheng, Z. Lin, R. Zhu, M. Jin, Y. Zhu and F. Huang, Sci. China Mater., 2020, 63, 1848–1854 CrossRef.
- Y. Ding, W. Zheng, M. Jin, Y. Zhu, R. Zhu, Z. Lin and F. Huang, Opt. Lett., 2020, 45(6), 1313–1316 CrossRef PubMed.
| This journal is © the Owner Societies 2021 |