An accurate full-dimensional potential energy surface for the reaction OH + SO → H + SO2
Jie
Qin
and
Jun
Li
 *
*
School of Chemistry and Chemical Engineering & Chongqing Key Laboratory of Theoretical and Computational Chemistry, Chongqing University, Chongqing 401331, China. E-mail: jli15@cqu.edu.cn
First published on 8th December 2020
Abstract
In this work, we report a full-dimensional accurate potential energy surface (PES-2020) for the reaction OH + SO → H + SO2, a prototype with deep complexes HOSO and HSO2. About 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 points are calculated at the level of UCCSD(T)-F12a/aug-cc-pVTZ and fitted by the permutation invariant polynomial-neural network (PIP-NN) approach. Particular attention is paid to the treatment of the electronic structure calculation so that the UCCSD(T)-F12a/aug-cc-pVTZ method can efficiently provide a reliable description for the ground electronic state of the title reaction. Comprehensive analyses and comparison show that the only available DMBE-PES is significantly different from the new PES-2020. Dynamics simulations on this new PES-2020 show that the reactivity decreases with the increase in collision energy. The isotropic product angular distributions remain within the studied collision energy range, 1–20 kcal mol−1, complying with the deep intermediates involved during the reaction process. The product energy partitioning is also analyzed. This accurate full-dimensional PES-2020 paves the way to fully understand the dynamics of the title reaction.
700 points are calculated at the level of UCCSD(T)-F12a/aug-cc-pVTZ and fitted by the permutation invariant polynomial-neural network (PIP-NN) approach. Particular attention is paid to the treatment of the electronic structure calculation so that the UCCSD(T)-F12a/aug-cc-pVTZ method can efficiently provide a reliable description for the ground electronic state of the title reaction. Comprehensive analyses and comparison show that the only available DMBE-PES is significantly different from the new PES-2020. Dynamics simulations on this new PES-2020 show that the reactivity decreases with the increase in collision energy. The isotropic product angular distributions remain within the studied collision energy range, 1–20 kcal mol−1, complying with the deep intermediates involved during the reaction process. The product energy partitioning is also analyzed. This accurate full-dimensional PES-2020 paves the way to fully understand the dynamics of the title reaction.
I. Introduction
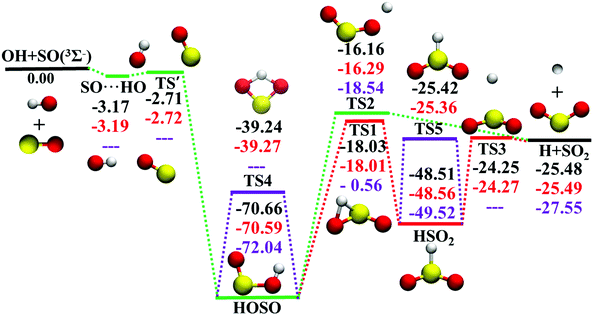
The potential energy surface (PES), a direct consequence of the Born–Oppenheimer approximation, plays a key role in chemistry. In either classical or quantum mechanics, the dynamics outcome is largely determined by the performance of the underlying PES. However, for a polyatomic reaction system, it is not always easy to develop its accurate full-dimensional PES, which is often quite rugged with intermediates, saddle points, and dissociation asymptotes.1 The title reaction represents such a typical example. As shown in Fig. 1, the topography of OH(2Π) + SO(3Σ−) → H(2S) + SO2 (1A1) (R1) on this ground electronic state is quite complicated. Starting from the separated reactants, OH and SO, they firstly form the SO⋯HO weakly interacted complex. Via the submerged barrier TS′, the orientation between SO and OH is altered to produce the deep intermediate HOSO, which can isomerize to another deep intermediate HSO2via the transition state TS1. Both intermediates HOSO and HSO2 can produce H and SO2via transition states, TS2 and TS3, respectively. The reaction profile of R1 is very similar to that of the reaction OH + CO → H + CO2,2–5 an important elementary reaction in both combustion and atmosphere.6Due to its significance in combustion and environment,7 the R1 reaction and its reverse R−1 have been extensively studied by theory8–23 and experiment.12,24–29 Rich information is available for its mechanism, kinetics and dynamics. Theoretically, various levels of theory were employed to study R1 and R−1.8,11,14,16,17,22,30 However, there was only one global full-dimensional PES (DMBE-PES), which was developed by the double many-body expansion (DMBE) method based on a small number of configurations computed at the full valence complete active space (CAS) and CASPT2 associated with Dunning's augmented correlation corrected valence double-zeta basis set (AVDZ) and AVTZ basis sets.16 With this DMBE-PES, the quasi-classical trajectory (QCT) method was employed to study the kinetics and dynamics of R1 and R−1.17,18,20,21,23,31 However, the computed rate coefficients were significantly higher17,20,21 than experimental measurements at temperatures above 500 K.27 Both the DMBE-PES and the experimental measurements have been doubted to account for such a disagreement. Indeed, the barrier height of TS1 was significantly overestimated on the DMBE-PES, 0.91 kcal mol−1. It is much higher than the benchmark value, −17.88 kcal mol−1, which was calculated at the unrestricted coupled cluster theory with single and double excitations and triple correction calculated by perturbation theory (UCCSD(T)) with energies refined by the complete basis set (CBS) extrapolation approach.22 This artificially high TS1 influences the kinetics and dynamics significantly, resulting in a small reaction probability through HSO2 for R1.17
Very recently, we developed a full-dimensional PES (denoted as PES-2019 hereafter)32 for the title reaction based on ca. 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 data points calculated at the explicitly correlated UCCSD(T) with the AVTZ basis set (UCCSD(T)-F12a/AVTZ).33,34 High-level ab initio calculations have been carried out at the explicitly correlated multi-reference configuration interaction (MRCI-F12)35–37 with the basis sets AVDZ and AVTZ, and revealed the complicated electronic structures along the R1 reaction.32 In particular for the entrance channel, the ground electronic state corresponds to OH(2Π) and SO(3Σ−) with three singly occupied orbitals, while other regions correspond to a doublet state with one singly occupied orbital. In our previous calculations, the UCCSD(T)-F12a/AVTZ calculations for a doublet state correspond to OH(2Π) + SO(a1Δ), which is 22.7 kcal mol−1 higher than the ground electronic state OH(X2Π) + SO(X3Σ−).32 Nonetheless, the PES-2019 was employed to study the collision energy transfer between H and SO2, which is expected to be adequately described since the OH + SO region is not accessed. At a collision energy of 59 kcal mol−1, the calculated vibrational energy populations of SO2 were well reproduced, compared with the recent experiment29 and simulation on the DMBE-PES.23 Detailed analysis showed that the dynamic mechanisms were significantly different between the PES-2019 and the DMBE-PES. On the DMBE-PES, the contributions of the trajectories via the HOSO dominate in the entire vibrational energy region, 84%, and the remaining 16% were HSO2 trajectories.23 On the PES-2019, there were several plausible mechanisms for the collision between H and SO2: the direct collision (66.8%) without passing through both wells HOSO and HSO2, the indirect collision through the HOSO complex (12.2%), or the HSO2 complex (11.4%), or through both HOSO and HSO2 complexes (9.6%). Apparently, these deviations were largely caused by the overestimated barrier of TS1, 0.91 kcal mol−1, on the DMBE-PES,16 significantly higher than −18.09 kcal mol−1 on the PES-2019,32 or −17.88 kcal mol−1 by the UCCSD(T)/CBS calculation.22
200 data points calculated at the explicitly correlated UCCSD(T) with the AVTZ basis set (UCCSD(T)-F12a/AVTZ).33,34 High-level ab initio calculations have been carried out at the explicitly correlated multi-reference configuration interaction (MRCI-F12)35–37 with the basis sets AVDZ and AVTZ, and revealed the complicated electronic structures along the R1 reaction.32 In particular for the entrance channel, the ground electronic state corresponds to OH(2Π) and SO(3Σ−) with three singly occupied orbitals, while other regions correspond to a doublet state with one singly occupied orbital. In our previous calculations, the UCCSD(T)-F12a/AVTZ calculations for a doublet state correspond to OH(2Π) + SO(a1Δ), which is 22.7 kcal mol−1 higher than the ground electronic state OH(X2Π) + SO(X3Σ−).32 Nonetheless, the PES-2019 was employed to study the collision energy transfer between H and SO2, which is expected to be adequately described since the OH + SO region is not accessed. At a collision energy of 59 kcal mol−1, the calculated vibrational energy populations of SO2 were well reproduced, compared with the recent experiment29 and simulation on the DMBE-PES.23 Detailed analysis showed that the dynamic mechanisms were significantly different between the PES-2019 and the DMBE-PES. On the DMBE-PES, the contributions of the trajectories via the HOSO dominate in the entire vibrational energy region, 84%, and the remaining 16% were HSO2 trajectories.23 On the PES-2019, there were several plausible mechanisms for the collision between H and SO2: the direct collision (66.8%) without passing through both wells HOSO and HSO2, the indirect collision through the HOSO complex (12.2%), or the HSO2 complex (11.4%), or through both HOSO and HSO2 complexes (9.6%). Apparently, these deviations were largely caused by the overestimated barrier of TS1, 0.91 kcal mol−1, on the DMBE-PES,16 significantly higher than −18.09 kcal mol−1 on the PES-2019,32 or −17.88 kcal mol−1 by the UCCSD(T)/CBS calculation.22
In this work, we report a new accurate full-dimensional PES (denoted as PES-2020) for the ground electronic state of the title reaction. In particular, the entrance channel is correctly described with careful treatment in the electronic structure calculations. A total of ca. 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 points are calculated at the UCCSD(T)-F12a/AVTZ level33,34 and fitted by the permutation invariant polynomial-neural network (PIP-NN) method,38–40 which has demonstrated its ultra-flexibility in fitting many polyatomic reactions, such as OH + H2O,41 OH + HO2,42,43 H/Cl/OH + CH4,44–46 F/Cl/H + CH3OH,47–51 N2O + C2H2,52 and the title reaction.32 Detailed analyses show that the PES-2020 can accurately reproduce the geometries, harmonic frequencies, and energies of the stationary points, the potentials of minimum energy paths (MEPs) along transition states, thanks to the small fitting error. Comprehensive comparison and analysis are also performed for the DMBE-PES. On the PES-2020, QCT calculations are then carried out to reveal the dynamics of the title reaction. The integral cross sections, product angular distributions and product energy populations are calculated and analyzed. The remainder of the publication is organized as follows. Section II describes the PES fitting and the QCT calculation details. The results are presented and discussed in Section III. A final summary is provided in Section IV.
700 points are calculated at the UCCSD(T)-F12a/AVTZ level33,34 and fitted by the permutation invariant polynomial-neural network (PIP-NN) method,38–40 which has demonstrated its ultra-flexibility in fitting many polyatomic reactions, such as OH + H2O,41 OH + HO2,42,43 H/Cl/OH + CH4,44–46 F/Cl/H + CH3OH,47–51 N2O + C2H2,52 and the title reaction.32 Detailed analyses show that the PES-2020 can accurately reproduce the geometries, harmonic frequencies, and energies of the stationary points, the potentials of minimum energy paths (MEPs) along transition states, thanks to the small fitting error. Comprehensive comparison and analysis are also performed for the DMBE-PES. On the PES-2020, QCT calculations are then carried out to reveal the dynamics of the title reaction. The integral cross sections, product angular distributions and product energy populations are calculated and analyzed. The remainder of the publication is organized as follows. Section II describes the PES fitting and the QCT calculation details. The results are presented and discussed in Section III. A final summary is provided in Section IV.
II. Calculation details
II-A. PES fitting
For the PES-2019,32ca. 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 points were sampled and calculated at the level of UCCSD(T)-F12a/AVTZ for a doublet state for the title reaction. As mentioned above, the entrance channel corresponds to OH(2Π) + SO(a1Δ) on the PES-2019, namely, the electronically excited state. As shown below, the UCCSD(T)-F12a/AVTZ calculation for a quartet state yields a correct description for the ground electronic state in the entrance channel, OH(2Π) + SO(3Σ−). Therefore, those points with the distance RHO⋯SO larger than 2.0 Å were selected and calculated again at the UCCSD(T)-F12a/AVTZ level for a quartet state. Compared with their energies for a doublet state, the lower energy is chosen for these points. Then, a primitive PES was fitted. To further explore regions that are not described well due to lacking points, trajectory calculations with various initial conditions were performed on this PES. New points were then added to patch up these regions. The PES was improved iteratively. Finally, a total of ca. 44
200 points were sampled and calculated at the level of UCCSD(T)-F12a/AVTZ for a doublet state for the title reaction. As mentioned above, the entrance channel corresponds to OH(2Π) + SO(a1Δ) on the PES-2019, namely, the electronically excited state. As shown below, the UCCSD(T)-F12a/AVTZ calculation for a quartet state yields a correct description for the ground electronic state in the entrance channel, OH(2Π) + SO(3Σ−). Therefore, those points with the distance RHO⋯SO larger than 2.0 Å were selected and calculated again at the UCCSD(T)-F12a/AVTZ level for a quartet state. Compared with their energies for a doublet state, the lower energy is chosen for these points. Then, a primitive PES was fitted. To further explore regions that are not described well due to lacking points, trajectory calculations with various initial conditions were performed on this PES. New points were then added to patch up these regions. The PES was improved iteratively. Finally, a total of ca. 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 points were calculated at the UCCSD(T)-F12a/AVTZ level and fitted by the permutation invariant polynomial-neural network (PIP-NN) method,38–40
700 points were calculated at the UCCSD(T)-F12a/AVTZ level and fitted by the permutation invariant polynomial-neural network (PIP-NN) method,38–40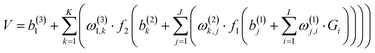 | (1) |
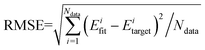 . The input layer of the NN consists of low-order PIPs,55 namely, symmetrized monomials of Morse-like variables of internuclear distances,
. The input layer of the NN consists of low-order PIPs,55 namely, symmetrized monomials of Morse-like variables of internuclear distances, 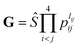 . In this work, the maximum order was selected to be 3, M = ∑lij ≤ 3, resulting in 49 terms (I = 49). pij = exp(−rij/α) are the Morse-like variables of the six internuclear distances (rij) with an adjustable constant α (α is fixed as 1.0 Å in this work). The symmetrization operator, Ŝ, contains the permutation operations between the two identical oxygen atoms of the title system.55
. In this work, the maximum order was selected to be 3, M = ∑lij ≤ 3, resulting in 49 terms (I = 49). pij = exp(−rij/α) are the Morse-like variables of the six internuclear distances (rij) with an adjustable constant α (α is fixed as 1.0 Å in this work). The symmetrization operator, Ŝ, contains the permutation operations between the two identical oxygen atoms of the title system.55
Different NN architectures, namely with different numbers of neurons in the two hidden layers, were tested. For each architecture, 100 different NN training calculations were launched with different initial parameters, and different training (90%), validation (5%), and test sets (5%). Only the training set was used in the fitting, while the validation set was used to terminate the fitting once the errors of the validation set started to increase, thus avoiding overfitting.56 The test set was used to provide an independent assessment of the quality of the fitting.
II-B. QCT calculation details
The QCT method was employed with the PES-2020 interfaced to the VENUS chemical dynamics program.57 The reactive integral cross section (ICS) at the collision energy Ec was computed according to the following formula:| σr(Ec) = πbmax2(Ec)Pr(Ec) | (2) |
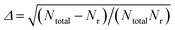 .
.
The differential cross section (DCS) provides information for the product angular distribution, which is related to the reaction mechanism. In this work, DCS was determined according to
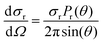 | (3) |
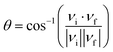 | (4) |
The trajectories were initiated with a reactant separation of 10.0 Å and terminated when products are separated by 8 Å, or when reactants are separated again by 10.5 Å. The maximal impact parameter was determined using 104 trajectories. The Monte Carlo approach, implemented in VENUS,58 was used to determine the scattering parameters including the impact parameter, vibrational phases, and the relative orientation between the initial reactants. The gradient of the PES with respect to atomic coordinates was computed numerically with a propagation time step of 0.05 fs. For the integration of the trajectories, the combined fourth-order Runge–Kutta and sixth-order Adams–Moulton algorithms were adopted. Almost all trajectories conserved energy to within a selected criterion (10−3 kcal mol−1).
III. Results and discussion
III-A. Stationary points
The ab initio calculation methods have been described in detail in our recent work on the PES-2019.32 Briefly, the MOLPRO package59 was used for all ab initio calculations. UCCSD(T)-F12a/AVnZ (n = D, T) were employed to determine the geometries, energies, and harmonic frequencies of all stationary.34Fig. 1 shows the calculated energy profile of R1 with the zero of energy being at the reactant asymptote OH(2Π) + SO(3Σ−). Many geometries and harmonic frequencies have been reported and analyzed in our previous work.32 The corresponding harmonic frequencies and energies are summarized in Table 1, with literature values included for comparison.15,16| Species | Note | E | Harmonic frequencies (cm−1) | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| a This work, the PIP-NN PES interfaced to POLYRATE. b This work, UCCSD(T)-F12a/AVTZ. c This work, the geometries were optimized with the DMBE-PES interfaced to POLYRATE. d QCISD(T)/6-311+G(3df,2p).15 e UCCSD(T)-F12a/AVTZ calculated single point energy with the geometries optimized on the PES-2020. | ||||||||
| OH(2Π) + SO(3Σ−) | PES-2020a | 0 | 1156 | 3743 | ||||
| Ab initio | 0 | 1108 | 3738 | |||||
| DMBE-PESc | 0 | 1142 | 3727 | |||||
| HOSO | PES-2020a | −70.66 | 92 | 395 | 803 | 1080 | 1226 | 3746 |
| Ab initio | −70.59 | 114 | 396 | 797 | 1086 | 1203 | 3748 | |
| DMBE-PESc | −72.04 | 451 | 687 | 853 | 1270 | 1331 | 3622 | |
| HSO2 | PES-2020a | −48.51 | 453 | 826 | 1004 | 1110 | 1332 | 2348 |
| Ab initio | −48.56 | 469 | 830 | 1003 | 1105 | 1326 | 2349 | |
| DMBE-PESc | −49.52 | 380 | 667 | 1012 | 1104 | 1316 | 1381 | |
| H + SO2 | PES-2020a | −25.48 | 521 | 1181 | 1378 | |||
| Ab initio | −25.49 | 522 | 1173 | 1383 | ||||
| DMBE-PESc | −27.54 | 522 | 1169 | 1381 | ||||
| TS1 | PES-2020a | −18.03 | i1545 | 418 | 638 | 916 | 1266 | 2072 |
| Ab initio | −18.01 | i1591 | 430 | 619 | 909 | 1260 | 2050 | |
| DMBE-PESc | −0.56 | i1912 | 219 | 737 | 1048 | 1399 | 1964 | |
| TS2 | PES-2020a | −16.16 | i1745 | 256 | 541 | 622 | 1099 | 1341 |
| Ab initio | −16.29 | i1746 | 292 | 498 | 552 | 1089 | 1306 | |
| DMBE-PESc | −18.54 | i2595 | 589 | 768 | 1372 | 1523 | 1888 | |
| TS3 | PES-2020a | −24.26 | i581 | 181 | 249 | 518 | 1177 | 1377 |
| Ab initio | −24.27 | i616 | 227 | 232 | 517 | 1172 | 1378 | |
| SO⋯HO | PIP-NNa | −3.17 | 17 | 107 | 218 | 239 | 1166 | 3715 |
| Ab initio | −3.19 | 25 | 125 | 292 | 341 | 1165 | 3712 | |
| −3.7 | ||||||||
| TS′ | PES-2020a | −2.71 | i98 | 101 | 171 | 267 | 1187 | 3741 |
| Ab initio | −2.72 | |||||||
| −2.3 | ||||||||
| HO⋯SO | PES-2020a | −1.75 | i78 | 57 | 70 | 170 | 1159 | 3744 |
| Ab initio | −1.73 | 51 | 73 | 80 | 110 | 1152 | 3736 | |
| TS4 | PES-2020a | −39.07 | i1950 | 668 | 980 | 1017 | 1035 | 2030 |
| Ab initio | −39.27 | i1933 | 673 | 1009 | 1017 | 1037 | 2058 | |
| TS5 | PES-2020a | −25.42 | i1436 | 466 | 857 | 1080 | 1351 | 2772 |
| Ab initio | −25.36 | i1657 | 79 | 217 | 937 | 1272 | 2364 | |
In the entrance channel, two van der Waals wells exist between OH and SO with different orientations, SO⋯HO and HO⋯SO, as shown in Fig. 2. They are −3.19 and −1.73 kcal mol−1, respectively, at the level of UCCSD(T)-F12a/AVTZ. The former, SO⋯HO, is relatively stable with a shorter intermolecular distance, 2.07 Å, and has been identified in the infrared spectroscopic experiment.60 With the geometries optimized at the level of B3LYP/6-31+G(d), McKee and Wine refined its energy to be −3.7 kcal mol−1 at the level of QCISD(T)/6-311+G(3df,2p).15 They also obtained a flexible transition state TS′, −2.30 kcal mol−1. Unfortunately, TS′ failed to locate by the UCCSD(T)-F12a/AVTZ computation. Its single-point energy is −2.72 kcal mol−1 based on the geometries optimized with the PES-2020 interfaced to POLYRATE.61 The other van der Waals well, HO⋯SO, with a 3.00 Å intermolecular distance, has never been reported in the literature, and awaits further theoretical and experimental investigations. The transition state TS4 accounts for the H-shift process, in which the hydrogen atom shifts from one oxygen to the other:  . Its geometry resembles the hydrogen-shift (H-shift) transition state for HOCO, TS5, which is much higher in energy and unlikely reachable in most cases for the reaction OH + CO.3 As shown in Fig. 1, TS4 is −39.3 kcal mol−1, relative to the reactant asymptote and the hydrogen atom lies at the middle of two oxygens, leading to TS4 a four-atom ring structure in a plane. TS5 is −25.42 kcal mol−1, a transition state of the planar structure which corresponds to the umbrella inversion of HSO2. Their geometric parameters, calculated at the UCCSD(T)-F12a/AVTZ level and PES-2020, are in good agreement with previous results computed at the level of ROCCSD(T)/aug-cc-pV(T+d)Z.22 Therefore, the H-shift process is expected to play an important role in the dynamics of the title system. On the DMBE-PES, however, SO⋯HO, HO⋯SO, TS3, TS4 and TS5 fail to locate. The energy discrepancies of the stationary points between PES-2020 and DMBE-PES are about 1–2 kcal mol−1 for HOSO, HSO2, H + SO2 and TS2. For TS1, it is −0.56 kcal mol−1 on the DMBE-PES, but −18.03 kcal mol−1 on the PES-2020. This huge distinction significantly affects reaction dynamics and kinetics properties, as shown below.
. Its geometry resembles the hydrogen-shift (H-shift) transition state for HOCO, TS5, which is much higher in energy and unlikely reachable in most cases for the reaction OH + CO.3 As shown in Fig. 1, TS4 is −39.3 kcal mol−1, relative to the reactant asymptote and the hydrogen atom lies at the middle of two oxygens, leading to TS4 a four-atom ring structure in a plane. TS5 is −25.42 kcal mol−1, a transition state of the planar structure which corresponds to the umbrella inversion of HSO2. Their geometric parameters, calculated at the UCCSD(T)-F12a/AVTZ level and PES-2020, are in good agreement with previous results computed at the level of ROCCSD(T)/aug-cc-pV(T+d)Z.22 Therefore, the H-shift process is expected to play an important role in the dynamics of the title system. On the DMBE-PES, however, SO⋯HO, HO⋯SO, TS3, TS4 and TS5 fail to locate. The energy discrepancies of the stationary points between PES-2020 and DMBE-PES are about 1–2 kcal mol−1 for HOSO, HSO2, H + SO2 and TS2. For TS1, it is −0.56 kcal mol−1 on the DMBE-PES, but −18.03 kcal mol−1 on the PES-2020. This huge distinction significantly affects reaction dynamics and kinetics properties, as shown below.
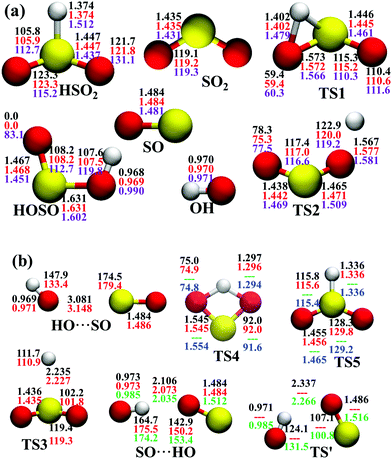 | ||
| Fig. 2 Geometries of the stationary points (angles in ° and distances in Å) at various levels, (a) PES-2020, UCCSD(T)-F12a/AVTZ, DMBE-PES; (b) PES-2020, UCCSD(T)-F12a/AVTZ, QCISD(T)/6-311+G(3df,2p),15 ROCCSD(T)/aug-cc-pV(T+d)Z level,22 from top to bottom. | ||
III-B. PES-2020
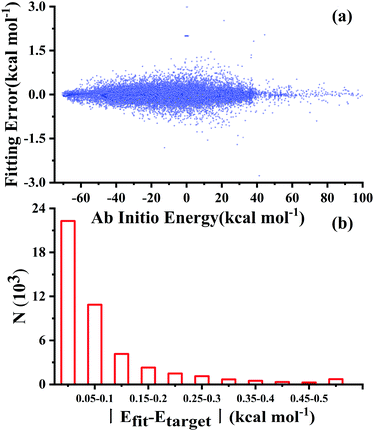
After testing, the optimal PES-2020 has two hidden layers, each with 40 and 85 neurons, respectively, resulting in 5571 parameters and a total RMSE of 0.16 kcal mol−1. The fitting errors and the distributions of the unsigned errors are depicted in Fig. 3(a) and (b), respectively. One can see that the small fitting errors are evenly distributed within the entire energy range: −71 to 100 kcal mol−1, and most of these points possess unsigned errors less than 0.1 kcal mol−1. As shown in Fig. 1 and 2, Table 1, the energies, geometries, and harmonic frequencies of the stationary points are all reproduced well on the PES-2020, compared to those computed directly at the UCCSD(T)-F12a/AVTZ level. The largest deviation for the energy of the stationary points is 0.20 kcal mol−1 for TS4. The internal coordinates are also well reproduced. Generally, the deviation on the PES-2020 and by the UCCSD(T)-F12a/AVTZ is less than 0.01 Å for bond distances or less than 0.5° for angles. For floppy coordinates, such as the distance HO⋯SO of the well HO⋯SO, the deviation can be as large as 0.07 Å.Fig. 4 presents the potential energy along the HO⋯SO distance (denoted as R, other coordinates fixed at the equilibrium of HOSO) on the PES-2020. The MRCI-F12 and UCCSD(T)-F12a calculated results, the corresponding data on the DMBE-PES and the PES-2019, which have been reported previously,32 are also included for comparison. The data on the PES-2019 correspond to HOSO → OH(2Π) + SO(a1Δ), 22.7 kcal mol−1 higher than the ground electronic state OH(2Π) + SO(3Σ−).32 PES-2020 correctly describes the entrance channel, compared with the UCCSD(T)-F12a calculation for a quartet state and the MRCI-F12 + Q/AVTZ calculated first state. When OH and SO approach each other further (R ≤ 2.5 Å), PES-2019 and PES-2020 become indistinguishable to each other. For “DMBE-PES/Ab Initio”, the energies were determined on the DMBE-PES with the HOSO geometries taken from the UCCSD(T)-F12a/AVTZ calculations. For “DMBE-PES”, the structural parameters of HOSO were obtained from the literature of the DMBE-PES.16 As shown in Fig. 2, the UCCSD(T)-F12a/AVTZ calculated geometries are different from those on the DMBE-PES, particularly for the dihedral angle.
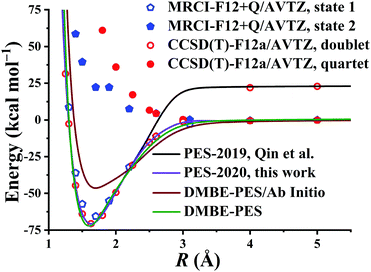 | ||
| Fig. 4 Potential energy dependence along RHO⋯SO at various levels of theory with other coordinates fixed at the HOSO equilibrium. See also details in the text. | ||
As shown in Fig. 4, the energy dependences are significantly different between “DMBE-PES” and “DMBE-PES/Ab Initio”. The potential curve of the DMBE-PES is in good agreement with the PES-2020 although the HOSO geometries are different for the two PESs.
Plenty of experimental62,63 and theoretical12,19,62,64–66 investigations have been done to study the geometries, harmonic frequencies, and energies of the HOSO species, a very important intermediate in sulfur-containing fuels. Fig. 5 plots the potential energy dependence along the HOSO dihedral angle (°) with other coordinates fixed at the HOSO equilibrium. For the PES-2020 and ab initio calculations, the HOSO equilibriums are identical, both from the UCCSD(T)-F12a/AVTZ optimized geometries. To evaluate the potential energy dependence on the DMBE-PES, two different HOSO geometries were used: UCCSD(T)-F12a/AVTZ calculated HOSO (DMBE-PES/Ab Initio) and the one optimized on the DMBE-PES (DMBE-PES).16 One can see that the dependences from DMBE-PES/Ab Initio deviate significantly from the PES-2020 and UCCSD(T)-F12a/AVTZ calculation. On the DMBE-PES, the HOSO minimum exists at a dihedral angle between 60 and 120°, far from the cis-like HOSO configuration on the PES-2020, UCCSD(T)-F12a/AVTZ calculation, and recent high level ab initio computations.12,65 Besides, the energy dependences along the HOSO dihedral angle were overestimated significantly by the DMBE-PES, particularly for regions between 120 and 240°. Although both PES-2020 and DMBE-PES predict that the configuration at 180° corresponds to a transition state, the one on the PES-2020 is only 2.6 kcal mol−1, consistent with high level calculations, 2.3,65 2.28 ± 0.1,19 and 1.82 kcal mol−1,12 all much lower than 16.5 kcal mol−1 predicted by the DMBE-PES, as shown in Fig. 5.
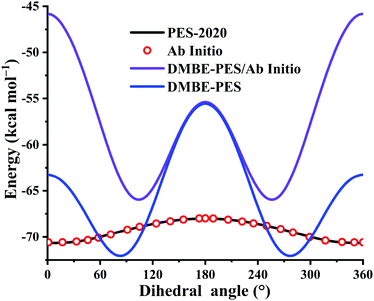 | ||
| Fig. 5 Potential energy dependence along the HOSO dihedral angle (°) with other coordinates fixed at the HOSO equilibrium. See also details in the text. | ||
Fig. 6 compares potential energies along MEPs of TS1, TS2, TS3, and TS4 on the PES-2020 and DMBE-PES (only available for TS1 and TS2), and those calculated directly by the UCCSD(T)-F12a/AVTZ. As shown in Fig. 1, HOSO and HSO2 isomers are 52.63 and 30.48 kcal mol−1 lower than TS1 on the PES-2020. The DMBE-PES overestimated the energy of TS1 significantly despite yielding reasonable energies for HOSO and HSO2. Accordingly, the energies around TS1 are much higher than those calculated by the UCCSD(T)-F12a/AVTZ and the PES-2020. TS2 connects HOSO and the products H + SO2, which is 1.72/1.87 kcal mol−1 above TS1 at the UCCSD(T)-F12a/AVTZ level or on the PES-2020. As shown in Fig. 6(b), the potential energy along the TS2 MEP on the DMBE-PES is lower than that calculated by the UCCSD(T)-F12a/AVTZ or PES-2020. As mentioned above, TS3 and TS4 failed to be optimized on the DMBE-PES.16 For these MEPs, the PES-2020 and UCCSD(T)-F12a/AVTZ are consistent with each other.
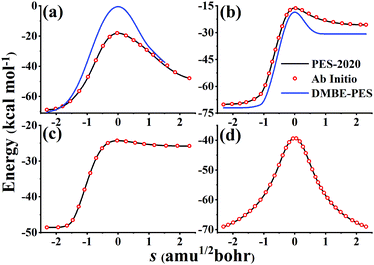 | ||
| Fig. 6 Potential energies along MEPs of TS1 (a), TS2 (b), TS3 (c), and TS4 (d) on the PES-2020, calculated directly by the UCCSD(T)-F12a/AVTZ and DMBE-PES. TS3 and TS4 fail to locate on the DMBE-PES. | ||
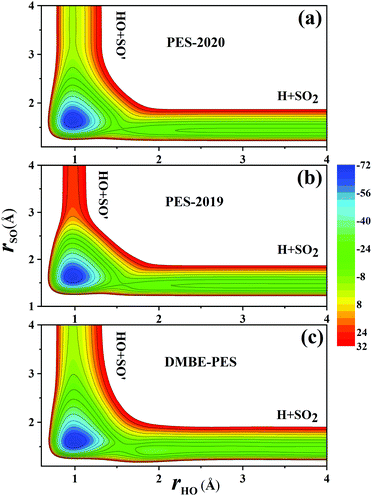
Fig. 7(a) and (b) compare the contour plots on the PES-201932 and the PES-2020 along the two bond distances rOH and rSO with other internal coordinates relaxed within a small range. Thus, the TS1 and HSO2 regions are not accessed. The regions for HOSO, TS2 and H + SO2 are essentially the same between two PESs, while the entrance on the PES-2020 is about 23 kcal mol−1 lower than on the PES-2019.32 The corresponding contour plot on the DMBE-PES shown in Fig. 7(c) is very similar to that on the PES-2020 despite with apparent deviations.
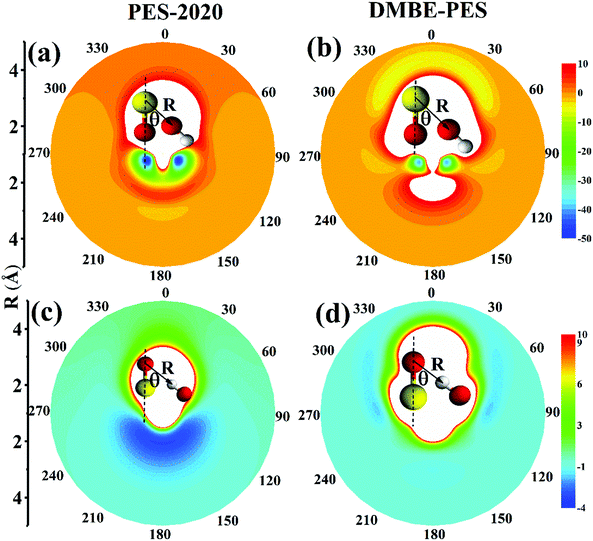
To illustrate the reactant asymptote of the PES, we plot in Fig. 8(a) and (c) contour plots for the interaction between OH and SO along two variables R and θ on the PES-2020 and Fig. 8(b) and (d) for the DMBE-PES.16R is the distance between the O atom of OH and the S atom of SO (Fig. 8(a) and (b)) or the H atom of OH and the O atom of SO (Fig. 8(c) and (d)). θ is the angle between R and the S–O bond axis. OH and SO are fixed at their respective equilibrium and placed within one plane.
On can see that, on the PES-2020, the interaction potentials are attractive for O of OH towards S of SO, as shown in Fig. 8(a). For 2.0 < R < 3 Å, this is the intersection region between doublet and quartet states where the electronic structure is extremely complicated, as described above. At R = 3.2 Å, there is a floppy potential well resembling the HO⋯SO complex. The two deep wells correspond to HOSO. If O of OH is toward O of SO, the interaction is repulsive. However, the interaction between OH and SO obtained by DMBE-PES is quite different. In Fig. 8(b), when O of OH is toward O of SO, the interaction is not repulsive but attractive to form a complex corresponding to SO⋯OH, which is −9.7 kcal mol−1 on the DMBE-PES.16 It is not an intermediate that connects directly to HOSO and OH + SO. It fails to be determined by using UCCSD(T)-F12a/AVTZ and PES-2020. When O of OH is toward S of SO, the interacted regions are repulsive, in contrast to that on the PES-2020. HO⋯SO is not shown on the DMBE-PES.
As shown in Fig. 8(c), the OH molecule is placed with H towards SO. Clearly, the top part, corresponding to OH⋯SO, is repulsive on the PES-2020. The lower part corresponds to the SO⋯HO complex, −3.2 kcal mol−1 at the UCCSD(T)-F12a/AVTZ level. Namely, this region is attractive. However, as shown in Fig. 8(d), the interaction potential energies are significantly different on the DMBE-PES. Most regions are repulsive with some weak attractive zones. These characterization studies in the entrance channel are expected to play a significant role in the subsequent reaction dynamics, particularly for low collision energy dynamics.
III-C. Dynamics calculations
As shown in Fig. 1, the title reaction is barrierless and exothermic. In other words, no energy is required to overcome a barrier in principle. However, if the approaching orientations between OH and SO are unfavorable, they might just rebound to the reactants directly without entering the HOSO well. Besides, for those that do enter the HOSO well, there is also a possibility to reenter the reactant channel. Indeed, 24.4%, 51.8%, 72.1%, and 93.5% trajectories form HOSO and go back to OH and SO at 1, 5, 10, and 20 kcal mol−1. Furthermore, it is very likely to observe some trajectories that undergo the H-shift process through TS4: OH + SO′ → HOSO′ → OSO′H → O′H + SO, which can be verified experimentally with different oxygen isotopes for the two oxygen atoms.According to the topography of the PES in Fig. 1, all reactive trajectories have to enter the HOSO well, after which there are two pathways to the products H + SO2. HOSO might go through the dissociation transition state, TS2, to arrive at the final products. Alternatively, it can overcome the isomerization barrier, TS1, which can be characterized as H migration from O to S, leading to the HSO2 species. The final H–S bond cleavage over TS3 results in the H + SO2 product. Since TS1 and TS2 are close to each other in energy, the portions of the two reaction pathways are expected to be similar. In contrast, no formation of HSO2 has occurred on the DMBE-PES, due to the much-overestimated isomerization barrier TS1 on that PES.17
Using the PES-2020, the reaction dynamics between OH and SO, both at ground rovibrational states, was studied by the QCT method with collision energies (Ec) of 1, 2, 3, 4, 5, 10, 15, and 20 kcal mol−1, respectively. For each Ec, 105 trajectories were calculated to make the statistical errors of the ICSs to H + SO2 less than 3%. For Ec = 20 kcal mol−1, 2 × 105 trajectories were computed since the reactivity is decreased significantly at this high collision energy. The calculated results are compared in Fig. 9 with those on the DMBE-PES.17 Both show similar trends, namely, they drop significantly along Ec, consistent with the barrierless nature of the title reaction, thus complying with a capture model. One can see that the reactivity of the title reaction is very high, supported by the large ICS values on both PESs. In contrast, the ICSs of the OH + CO → H + CO2 reaction increase as the collision energy goes up, consistent with the nearly equivalent bottlenecks in the entrance and exit channels.2,3 Quantitatively, the OH + SO reactive ICSs computed on our PES-2020 are smaller than those on the DMBE-PES17 for Ec < 10 kcal mol−1. Indeed, the difference between the two PESs is increased with decreasing Ec. At Ec = 1 kcal mol−1, the PES-2020 ICS is 32.9 Å2, much smaller than 86.8 Å2 on the DMBE-PES,17 signaling the deviations between two PESs, which have been discussed above. For Ec ≥ 10 kcal mol−1, both predictions from the two PESs are very close to each other. For instance, at Ec = 10 kcal mol−1, the ICSs are 5.7 and 5.2 Å2, respectively, on the PES-2020 and the DMBE-PES.17
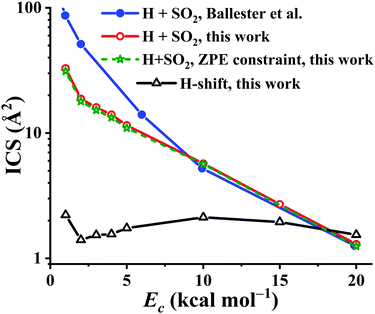 | ||
| Fig. 9 The integral cross section (ICS) for the reaction OH + SO → H + SO2 on the PES-2020 and DMBE-PES17 as a function of the collision energy (Ec, in kcal mol−1). The H-shift ICSs are also included. | ||
It is known that in QCT the leakage of the zero-point vibrational energy (ZPE) is allowed in principle during the reaction. Many techniques have been developed to remedy the ZPE issue in the QCT. In this work, the widely used ZPE constraint method67 is employed. In this method, only those trajectories yielding the SO2 product with vibrational energies not less than its ZPE (4.33 kcal mol−1) were taken into account. Due to the large exothermicity of the reaction, one can see that only a small portion of trajectories don’t meet this criterion and the ICSs are seldom affected, as shown in Fig. 9.
Starting from the reactant asymptote, the H-shift process is also available in principle, according to the low barrier TS4 in Fig. 1. The ICSs for this channel, OH + SO′ → HOSO′ → OSO′H → O′H + SO, were also computed, and shown in Fig. 9. One can see that the H-shift ICSs drop firstly from Ec = 1 to Ec = 2 kcal mol−1, then increase gradually to the peak, 2.1 Å2, at Ec = 10 kcal mol−1. Finally, they decrease slowly to 1.5 Å2 at Ec = 20 kcal mol−1. Overall, the H-shift ICSs are nearly constant, 1.4–2.2 Å2, within the collision energy range. Besides, it is noted that the ICSs to H + SO2 drop significantly at high Ec (18 kcal mol−1 above), even smaller than the H-shift ICSs.
Fig. 10 presents the calculated DCSs at Ec = 1, 5, 10 and 20 kcal mol−1 for the title reaction. Clearly, all these DCSs are isotropic, since the long-lived HOSO and/or HSO2 complex result in randomly scattering directions. The DCS results are different from those in the reaction OH + CO → H + CO2 with HOCO and HCO2 intermediates.4 In the latter reaction OH + CO, the forward scattering is more significant than the backward scattering. This can be attributed to differences between the two potential topologies. Particularly, the title reaction has no barriers for the entrance and exit channels essentially while OH + CO has nearly equivalent barrier heights for the entrance and exit channels. The HOSO is much deeper than HOCO, −70.59 vs. −29.59 kcal mol−1.3 The isomerization barrier between HOCO and HCO2 is not easily accessible due to that it is 8.78 kcal mol−1 higher in energy than the reactant OH + CO. In OH + SO, the corresponding isomerization TS1 is −18.01 kcal mol−1 relative to OH + SO.
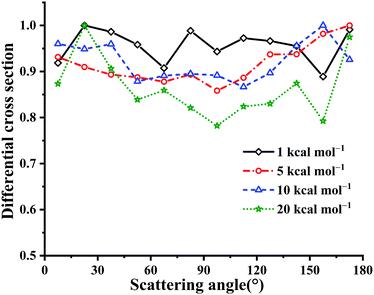 | ||
| Fig. 10 DCSs for the OH + SO → H + SO2 reaction at Ec = 1, 5, 10 and 20 kcal mol−1, respectively. The maximum distribution is scaled to be 1. | ||
As shown in Fig. 11, there is no correlation between the scattering angle and the impact parameter for the title reaction within the collision energy range. In addition, one can see that at Ec = 1 kcal mol−1, the bmax can be as large as 6.7 Å. This is expected since the long-range interaction between OH and SO can help guide their mutual orientations and increase the reactivity at low Ec. At Ec = 20 kcal mol−1, the bmax decreases to 3.6 Å.
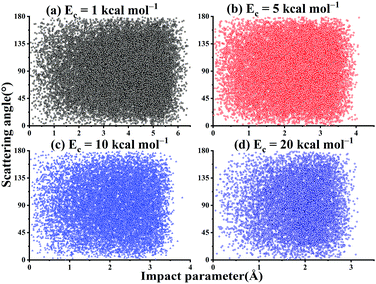 | ||
| Fig. 11 The scattered diagram between the impact parameters and the scattering angles for the reaction OH + SO → H + SO2 at Ec = 1, 5, 10, and 20 kcal mol−1, respectively. | ||
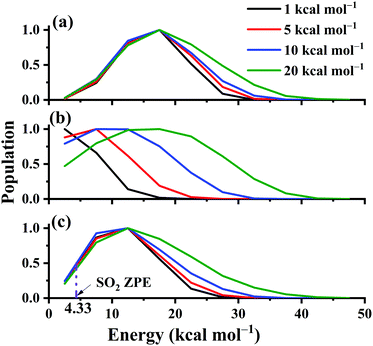
The distributions of the product translational energy, and SO2 rotational and vibrational energies are plotted in Fig. 12(a)–(c) for Ec = 1, 5, 10 and 20 kcal mol−1. One can see that in Fig. 12(b), the product rotational energy is increased significantly from Ec = 1 to 20 kcal mol−1. Not only the peak but also the shape is significantly shifted parallel to the high energy end. In contrast, the distributions of the translational and SO2 vibrational energies are not affected much with the collision energy increased, as shown in Fig. 12(a) and (c). Only the shapes of the distributions become a little wider with more collision energy available. Furthermore, the ZPE-violating fraction in the distribution seems to be small, as shown in Fig. 12(c), due to the exothermic nature of the reaction.
IV. Conclusions
The reaction OH + SO → H + SO2 presents a prototype with deep complex formation and no bottleneck. From the entrance channel OH + SO to the interaction region HOSO, the electronic structure varies significantly. The reactant asymptotic OH and SO feature three singly occupied orbitals, which become one for the strong interaction region and the product region. As a compromise between efficiency and cost, the UCCSD(T)-F12a/AVTZ method is employed to calculate the energies of the system. For regions with one singly occupied orbital, it corresponds to a doublet state. For the entrance channel with three singly occupied orbitals, it corresponds to a quartet state. For regions connecting them, both energies were calculated for a doublet state and for a quartet state. The lower energy was selected as for the ground electronic state. Careful analysis showed that this strategy provides a reliable description for the title reaction system efficiently. The UCCSD(T)-F12a/AVTZ calculated 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 points, corresponding to 89
700 points, corresponding to 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 points due to permutational symmetry with respect to the exchange between two identical O atoms, were fitted by the permutation invariant polynomial-neural network (PIP-NN) method, resulting in a RMSE of 0.16 kcal mol−1. This PES, named the PES-2020, is the most accurate full-dimensional PES for the ground electronic state of the title reaction, and can serve as a reliable platform for future kinetics and dynamics simulations. It should be noted that the spin–orbit correction of the OH species at the reactant asymptote is 0.19 kcal mol−1,68 and is expected to play negligible roles in the reaction dynamics of the title system.
400 points due to permutational symmetry with respect to the exchange between two identical O atoms, were fitted by the permutation invariant polynomial-neural network (PIP-NN) method, resulting in a RMSE of 0.16 kcal mol−1. This PES, named the PES-2020, is the most accurate full-dimensional PES for the ground electronic state of the title reaction, and can serve as a reliable platform for future kinetics and dynamics simulations. It should be noted that the spin–orbit correction of the OH species at the reactant asymptote is 0.19 kcal mol−1,68 and is expected to play negligible roles in the reaction dynamics of the title system.
Comprehensive analysis was made for the PES-2020 on the static properties, including the geometries, harmonic frequencies, and energies of the stationary points. Appropriate literature data were compared and discussed. The only available DMBE-PES has shown significant deficiencies. TS4 is the transition state of the hydrogen-shift (H-shift) process between two O atoms of HOSO. Its energy is lower than the that of the reactant asymptote. Hence it may play a significant role in the dynamics. Indeed, the ICSs of this channel are within 1.4–2.2 Å2 for the collision energy ranging 1–20 kcal mol−1, and even higher than the H + SO2 ICSs at collision energies higher than 18 kcal mol−1.
In comparison to DMBE-PES, the ICSs computed on our PES-2020 are much smaller for the collision energies less than 10 kcal mol−1. When the collision energies are equal to or greater than 10 kcal mol−1, the ICSs on the DMBE-PES agree well with those on the PES-2020. The ICSs on both PESs decrease significantly along with the collision energy due to the barrierless nature of the reaction. The DCSs on the PES-2020 are isotropic due to the long-lived HOSO and HSO2 complexes, which make the impact parameter and scattering angle have no correlation.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Contract No. 21973009) and the Chongqing Municipal Natural Science Foundation (Grant No. cstc2019jcyj-msxmX0087).References
- J. Li, B. Jiang, H. Song, J. Ma, B. Zhao, R. Dawes and H. Guo, J. Phys. Chem. A, 2015, 119, 4667–4687 CrossRef CAS PubMed.
- J. Li, Y. Wang, B. Jiang, J. Ma, R. Dawes, D. Xie, J. M. Bowman and H. Guo, J. Chem. Phys., 2012, 136, 041103 CrossRef PubMed.
- J. Li, C. Xie, J. Ma, Y. Wang, R. Dawes, D. Xie, J. M. Bowman and H. Guo, J. Phys. Chem. A, 2012, 116, 5057–5067 CrossRef CAS PubMed.
- A. Caracciolo, D. Lu, N. Balucani, G. Vanuzzo, D. Stranges, X. Wang, J. Li, H. Guo and P. Casavecchia, J. Phys. Chem. Lett., 2018, 9, 1229–1236 CrossRef CAS PubMed.
- J. Li, J. Chen, D. H. Zhang and H. Guo, J. Chem. Phys., 2014, 140, 044327 CrossRef PubMed.
- J. S. Francisco, J. T. Muckerman and H.-G. Yu, Acc. Chem. Res., 2010, 43, 1519–1526 CrossRef CAS PubMed.
- P. Glarborg, D. Kubel, K. DamJohansen, H. M. Chiang and J. W. Bozzelli, Int. J. Chem. Kinet., 1996, 28, 773–790 CrossRef CAS.
- D. Binns and P. Marshall, J. Chem. Phys., 1991, 95, 4940–4947 CrossRef CAS.
- T. Stoecklin, C. E. Dateo and D. C. Clary, J. Chem. Soc., Faraday Trans., 1991, 87, 1667–1679 RSC.
- D. C. Clary, T. S. Stoecklin and A. G. Wickham, J. Chem. Soc., Faraday Trans., 1993, 89, 2185–2191 RSC.
- V. R. Morris and W. M. Jackson, Chem. Phys. Lett., 1994, 223, 445–451 CrossRef CAS.
- A. J. Frank, M. Sadilek, J. G. Ferrier and F. Turecek, J. Am. Chem. Soc., 1997, 119, 12343–12353 CrossRef CAS.
- J. X. Qi, W. Q. Deng, K. L. Han and G. Z. He, J. Chem. Soc., Faraday Trans., 1997, 93, 25–28 RSC.
- A. Goumri, J. D. R. Rocha, D. Laakso, C. E. Smith and P. Marshall, J. Phys. Chem. A, 1999, 103, 11328–11335 CrossRef CAS.
- M. L. McKee and P. H. Wine, J. Am. Chem. Soc., 2001, 123, 2344–2353 CrossRef CAS PubMed.
- M. Y. Ballester and A. J. C. Varandas, Phys. Chem. Chem. Phys., 2005, 7, 2305–2317 RSC.
- M. Y. Ballester and A. J. C. Varandas, Chem. Phys. Lett., 2007, 433, 279–285 CrossRef CAS.
- M. Y. Ballester, P. J. S. B. Caridade and A. J. C. Varandas, Chem. Phys. Lett., 2007, 439, 301–307 CrossRef CAS.
- S. E. Wheeler and H. F. Schaefer, III, J. Phys. Chem. A, 2009, 113, 6779–6788 CrossRef CAS PubMed.
- M. Y. Ballester, Y. Orozco-Gonzalez, J. D. Garrido and H. F. Dos Santos, J. Chem. Phys., 2010, 132, 044310 CrossRef CAS PubMed.
- W. A. D. Pires, J. D. Garrido, M. A. C. Nascimento and M. Y. Ballester, Phys. Chem. Chem. Phys., 2014, 16, 12793–12801 RSC.
- D. Rodriguez-Linares, G. N. Freitas, M. Y. Ballester, M. A. Chaer Nascimento and J. D. Garrido, J. Phys. Chem. A, 2015, 119, 8734–8743 CrossRef CAS PubMed.
- R. S. da Silva, J. D. Garrido and M. Y. Ballester, J. Chem. Phys., 2017, 147, 084308 CrossRef PubMed.
- R. W. Fair and B. A. Thrush, Trans. Faraday Soc., 1969, 65, 1557–1570 RSC.
- J. L. Jourdain, G. Lebras and J. Combourieu, Int. J. Chem. Kinet., 1979, 11, 569–577 CrossRef CAS.
- V. R. Morris, K. L. Han and W. M. Jackson, J. Phys. Chem., 1995, 99, 10086–10091 CrossRef CAS.
- M. A. Blitz, K. W. McKee and M. J. Pilling, Proc. Combust. Inst., 2000, 28, 2491–2497 CrossRef CAS.
- M. U. Alzueta, R. Bilbao and P. Glarborg, Combust. Flame, 2001, 127, 2234–2251 CrossRef CAS.
- J. Ma, M. J. Wilhelm, J. M. Smith and H.-L. Dai, Phys. Rev. A, 2016, 93, 040702 CrossRef.
- G. N. Freitas, J. D. Garrido, M. Y. Ballester and M. A. Chaer Nascimento, J. Phys. Chem. A, 2012, 116, 7677–7685 CrossRef CAS PubMed.
- J. d. D. Garrido, S. Ellakkis and M. Y. Ballester, Mol. Phys., 2020, 118, e1751321 CrossRef.
- J. Qin, Y. Liu, D. Lu and J. Li, J. Phys. Chem. A, 2019, 123, 7218–7227 CrossRef CAS PubMed.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- T. Shiozaki, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 134, 034113 CrossRef PubMed.
- T. Shiozaki and H.-J. Werner, J. Chem. Phys., 2011, 134, 184104 CrossRef PubMed.
- T. Shiozaki and H.-J. Werner, Mol. Phys., 2013, 111, 607–630 CrossRef CAS.
- B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 054112 CrossRef PubMed.
- J. Li, B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 204103 CrossRef PubMed.
- B. Jiang, J. Li and H. Guo, Int. Rev. Phys. Chem., 2016, 35, 479–506 Search PubMed.
- M. Bai, D. Lu and J. Li, Phys. Chem. Chem. Phys., 2017, 19, 17718–17725 RSC.
- Y. Liu, M. Bai, H. Song, D. Xie and J. Li, Phys. Chem. Chem. Phys., 2019, 21, 12667–12675 RSC.
- Y. Liu, H. Song, D. Xie, J. Li and H. Guo, J. Am. Chem. Soc., 2020, 142, 3331–3335 CrossRef CAS PubMed.
- J. Li, J. Chen, Z. Zhao, D. Xie, D. H. Zhang and H. Guo, J. Chem. Phys., 2015, 142, 204302 CrossRef PubMed.
- Y. Liu and J. Li, Phys. Chem. Chem. Phys., 2020, 22, 344–353 RSC.
- J. Li and H. Guo, J. Chem. Phys., 2015, 143, 221103 CrossRef PubMed.
- M. L. Weichman, J. A. DeVine, M. C. Babin, J. Li, L. Guo, J. Ma, H. Guo and D. M. Neumark, Nat. Chem., 2017, 9, 950–955 CrossRef CAS PubMed.
- D. Lu, J. Li and H. Guo, Chem. Sci., 2019, 10, 7994–8001 RSC.
- D. Lu, C. Xie, J. Li and H. Guo, Chin. J. Chem. Phys., 2019, 32, 84–88 CrossRef CAS.
- D. Lu, J. Li and H. Guo, CCS Chem., 2020, 2, 882–894 CrossRef CAS.
- D. Lu, J. Behler and J. Li, J. Phys. Chem. A, 2020, 124, 5737–5745 CrossRef CAS PubMed.
- Y. Liu and J. Li, ACS Omega, 2020, 5, 23343–23350 CrossRef PubMed.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577–606 Search PubMed.
- C. Qu, Q. Yu and J. M. Bowman, Annu. Rev. Phys. Chem., 2018, 69, 151–175 CrossRef CAS PubMed.
- Z. Xie and J. M. Bowman, J. Chem. Theory Comput., 2010, 6, 26–34 CrossRef CAS PubMed.
- L. M. Raff, R. Komanduri, M. Hagan and S. T. S. Bukkapatnam, Neural Networks in Chemical Reaction Dynamics, Oxford University Press, Oxford, 2012 Search PubMed.
- W. L. Hase, K. Song and M. S. Gordon, Comput. Sci. Eng., 2003, 5, 36–44 CrossRef CAS.
- X. Hu, W. L. Hase and T. Pirraglia, J. Comput. Chem., 1991, 12, 1014–1024 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O’Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2015.1, a package of ab initio programs. See http://www.molpro.net.
- C. Chen, B. Lu, X. Zhao, W. Qian, J. Liu, T. Trabelsi, J. S. Francisco, J. Qin, J. Li, L. Wang and X. Zeng, J. Am. Chem. Soc., 2020, 142, 2175–2179 CrossRef CAS PubMed.
- J. Zheng, J. L. Bao, R. Meana-Pañeda, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. F. Ramos, B. A. Ellingson, V. S. Melissas, J. Villà, I. Rossi, E. L. Coitiño, J. Pu, T. V. Albu, A. Ratkiewicz, R. Steckler, B. C. Garrett, A. D. Isaacson and D. G. Truhlar, POLYRATE 2016-2A: Computer program for the calculation of chemical reaction rates for polatomics, University of Minnesota, Minneapolis, 2016 Search PubMed.
- B. Napolion and J. D. Watts, Chem. Phys. Lett., 2006, 421, 562–565 CrossRef CAS.
- D. J. Grant, D. A. Dixon, J. S. Francisco, D. Feller and K. A. Peterson, J. Phys. Chem. A, 2009, 113, 11343–11353 CrossRef CAS PubMed.
- D. Laakso, C. E. Smith, A. Goumri, J. D. R. Rocha and P. Marshall, Chem. Phys. Lett., 1994, 227, 377–383 CrossRef CAS.
- M. C. McCarthy, V. Lattanzi, O. Martinez, Jr., J. Gauss and S. Thorwirth, J. Phys. Chem. Lett., 2013, 4, 4074–4079 CrossRef CAS.
- R. C. Fortenberry, J. S. Francisco and T. J. Lee, J. Phys. Chem. A, 2017, 121, 8108–8114 CrossRef CAS PubMed.
- G. Czakó and J. M. Bowman, J. Chem. Phys., 2009, 131, 244302 CrossRef PubMed.
- B. Gruber and G. Czakó, Phys. Chem. Chem. Phys., 2020, 22, 14560–14569 RSC.
| This journal is © the Owner Societies 2021 |