Open Access Article
Open Access ArticleEntropy of stapled peptide inhibitors in free state is the major contributor to the improvement of binding affinity with the GK domain†
Ilona Christy
Unarta‡
ab,
Jianchao
Xu‡
c,
Yuan
Shang‡
 bd,
Carina Hey Pui
Cheung
c,
Ruichi
Zhu
bd,
Xudong
Chen
bd,
Siqin
Cao
be,
Peter Pak-Hang
Cheung
bc,
Donald
Bierer
f,
Mingjie
Zhang
*bd,
Xuhui
Huang
bd,
Carina Hey Pui
Cheung
c,
Ruichi
Zhu
bd,
Xudong
Chen
bd,
Siqin
Cao
be,
Peter Pak-Hang
Cheung
bc,
Donald
Bierer
f,
Mingjie
Zhang
*bd,
Xuhui
Huang
 *abeg and
Xuechen
Li
*abeg and
Xuechen
Li
 *c
*c
aBioengineering Graduate Program, Department of Biological and Chemical Engineering, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong. E-mail: xuhuihuang@ust.hk
bCentre of Systems Biology and Human Health, State Key Laboratory of Molecular Neuroscience, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong. E-mail: mzhang@ust.hk
cDepartment of Chemistry, State Key Lab of Synthetic Chemistry, The University of Hong Kong, Hong Kong. E-mail: xuechenl@hku.hk
dDivision of Life Science, The Hong Kong University of Science and Technology, Kowloon, Hong Kong
eDepartment of Chemistry, The Hong Kong University of Science and Technology, Kowloon, Hong Kong
fDepartment of Medicinal Chemistry, Bayer AG, Aprather Weg 18A, 42096 Wuppertal, Germany
gHong Kong Center for Neurodegenerative Diseases, Hong Kong Science Park, Hong Kong
First published on 25th June 2021
Abstract
Stapled peptides are promising protein–protein interaction (PPI) inhibitors that can increase the binding potency. Different from small-molecule inhibitors in which the binding mainly depends on energetic interactions with their protein targets, the binding of stapled peptides has long been suggested to be benefited from entropy. However, it remains challenging to reveal the molecular features that lead to this entropy gain, which could originate from the stabilization of the stapled peptide in solution or from the increased flexibility of the complex upon binding. This hinders the rational design of stapled peptides as PPI inhibitors. Using the guanylate kinase (GK) domain of the postsynaptic density protein 95 (PSD-95) as the target, we quantified the enthalpic and entropic contributions by combining isothermal titration calorimetry (ITC), X-ray crystallography, and free energy calculations based on all-atom molecular dynamics (MD) simulations. We successfully designed a stapled peptide inhibitor (staple 1) of the PSD-95 GK domain that led to a 25-fold increase in the binding affinity (from tens of μMs to 1.36 μM) with high cell permeability. We showed that entropy indeed greatly enhanced the binding affinity and the entropy gain was mainly due to the constrained-helix structure of the stapled peptide in solution (free state). Based on staple 1, we further designed two other stapled peptides (staple 2 and 3), which exerted even larger entropy gains compared to staple 1 because of their more flexible bound complexes (bound state). However, for staple 2 and 3, the overall binding affinities were not improved, as the loose binding in their bound states led to an enthalpic loss that largely compensated the excess entropy gain. Our work suggests that increasing the stability of the stapled peptide in free solution is an effective strategy for the rational design of stapled peptides as PPI inhibitors.
Introduction
Protein–protein interaction (PPI) facilitates many vital biological processes. Hence, it is of great importance to be able to target PPI for functional studies and drug development. Unfortunately, targeting PPI especially by using small chemical molecules is challenging because the interface of PPI is shallow but highly complex.1 Peptides represent a significant advancement in the design of inhibitors targeting PPI because they can be easily customized by simple modification of the residues to increase the specificity and biological potency of binding at the PPI interface. However, natural peptide ligands are prone to protease degradation, often have low cell permeability and bioavailability, and are unstable in the cellular environment.2 Additionally, peptides may adopt multiple conformations in solution, resulting in non-specific binding. Thus, to circumvent these limitations, stabilization of peptides in the bioactive states using methods such as peptide stapling has emerged to the forefront of peptide design.Peptide stapling is most commonly performed by tethering the side chains at i and i + 3, i and i + 4 or i and i + 7 residues via a chemical linker to chemically restrict the flexibility and maintain the α-helix structures of the short helical peptides in water.3 Stapled peptides have become a promising class of PPI inhibitors that have been reported to improve the cell permeability, protease resistance and biological potency.4–7 Most stapled peptides have also been shown to decrease the entropy penalty (−TΔS), leading to improvement in their binding affinity (ΔGbinding = ΔH − TΔS).8 Experimental techniques, such as ITC measurement and surface plasmon resonance, have been applied to measure the enthalpy and entropy differences (ΔH and ΔS) of the binding free energy. However, these thermodynamic measurements lack molecular interpretations, which hinders the rational design of stapled peptide PPI inhibitors. For example, it is well-known that stapled peptides can reduce the entropy penalty (−TΔS = −T(ΔSbound − Sfree)),8 which could be the result of a decrease of Sfree and/or increase of Sbound. Unfortunately, there is a lack of experimental techniques that can quantify the conformational ensemble of stapled peptides in the free state (separated from the bound state) to obtain this entropy (absolute entropy in the free state, Sfree). Lastly, it is even more challenging to identify the major molecular features influencing the thermodynamic contributions of stapled peptides to PPI binding. Molecular dynamics (MD) simulation is an ideal technique to address the above-mentioned challenges, as it can provide atomistic details of both the bound and free states. Ultimately, it will allow for the evaluation of individual thermodynamic contributions, which will help in correlating the molecular features with the specific thermodynamics terms, further guiding the rational design of stapled peptide PPI inhibitors.9
The PPI between postsynaptic density protein 95 (PSD-95) and the SAPAP/Shank complex serves as a great system for the development of stapled peptide PPI inhibitors. PSD-95 is a member of the DLG subfamily MAGUK scaffold.10 It forms a complex with SAPAP and Shank family proteins,11–13 and this complex has been shown to play a crucial role in synaptic development and transmission.14–17 During complex formation, the guanylate kinase (GK) domain of PSD-95 (referred to as GK domain hereinafter) functions as a phosphoprotein-binding module18–20 to recognize the SAPAP GK binding repeat (GBR) region.11,21 Previously, synthetic phosphor-peptides have been developed to block the PPI between the GK domain and SAPAP.22 However, phosphor-peptides have been shown to exhibit low cell penetrability23,24 and cellular instability. To resolve these problems, the unstable phosphor group has been replaced with glutamic acid to maintain the salt-bridge interactions between the phosphor group and its binding pocket. Unfortunately, this resulted in an order of magnitude decrease in binding affinity.22 Importantly, these synthetic phosphor-peptides adopt the α-helical conformation in the bound complex, and thus this system serves as an ideal target for the development of stapled peptide PPI inhibitors.
In the present work, we have successfully designed a hydrophilic staple peptide (staple 1) using our recently developed synthetic strategies25 to inhibit the GK domain with a 25-fold stronger binding affinity compared to that of the non-stapled (linear) peptide, accompanied by a high penetrability to mammalian cells. Using a combination of X-ray crystallography, ITC measurement and free energy calculations based on MD simulations, we further elucidated that it is the stabilization of the stapled peptide in the α-helical structure in the free state that greatly improves the binding of the stapled peptide. We further explored two additional staple peptides (staple 2 & 3). The ITC and MD simulations showed that staple 2 & 3 exhibited reduced entropy penalty to a larger extent than staple 1. Further investigations show that this excess entropy gain is mainly due to the increased flexibility of the bound complex, and this gain in entropy term is accompanied by the loss of enthalpy. As a result, the overall binding affinities of staple 2 and 3 are compared with that of staple 1. Our work elucidates the molecular mechanisms for the interplay between entropic and enthalpic contributions to the binding affinity of staple peptides for PPI inhibition.
Results and discussion
Optimization of stapling positions and peptide sequence
Replacement of phosphoserine with a phosphor-mimic residue, glutamic acid, in the linear natural ligand (p-SAPAP1) diminishes the binding with the GK domain (ESI,† Text). To improve the binding affinity, we propose the introduction of staple to the linear peptide, which can restrain the peptide in the α-helical structure mimicking the p-SAPAP1 ligand observed in the crystal structure of the GK domain bound with p-SAPAP1.22 First, we determined the position of the staple based on the crystal structure of the GK domain in complex with a phosphor linear peptide (phosphor-LGN, PDB ID: 3UAT18). We observed that three residues, at positions −1, 2, and 3, close to the phosphoserine (position 0) are facing away from the binding interface and are exposed to the solvent (Fig. 1). Therefore, we introduced our staple, either at i ∼ i + 3 (stapling at residues −1 and 2) or at i ∼ i + 4 (stapling at residues −1 and 3) to ensure that the staple is exposed to the solvent, avoiding any possible interference with the binding interface. Strikingly, the i ∼ i + 4 stapled peptide displayed detectable binding to the GK domain with Kd = 5.9 μM, while the i ∼ i + 3 stapled peptide behaved similarly to the linear peptide and did not bind to the GK domain (see Fig. S1, ESI†). We further performed several rounds of optimizations on the linear peptide sequence based on the binding surface of GK based on previously solved crystal structures18,19,22 (see ESI,† Section 2 for details). Upon these optimizations, we adopt the sequence of RIRREEYLKAIQ for further development of the stapled peptide. Our initial attempts to introduce the hydrocarbon linkers at i ∼ i + 4 positions were not successful, as they display poor solubility in aqueous solutions. To resolve this solubility issue, we designed our stapled peptide (staple 1) using our recently developed hydrophilic D–K(OH)25 lactam stapler (Fig. 2 and Fig. S2A and B, ESI†).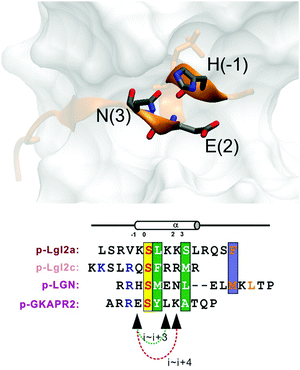 | ||
| Fig. 1 (a) MAGUK GK targets form helices in the complex. Positions (−1), (2) and (3) are not directly involved in complex binding, providing opportunity for stapling. | ||
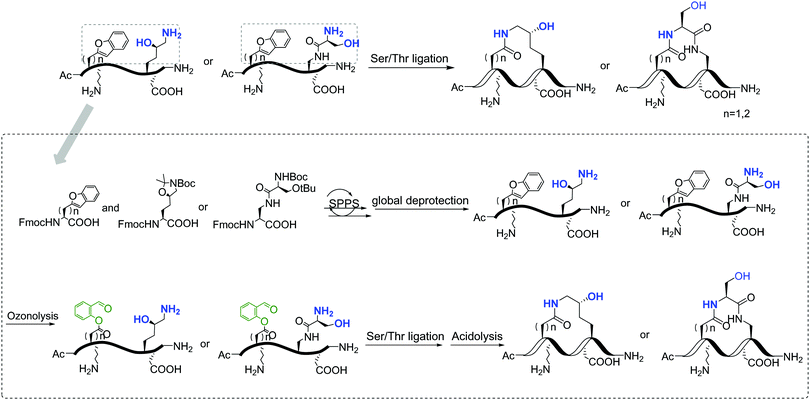 | ||
| Fig. 2 General synthetic route of the involved stapled peptides. Detailed synthetic pathways of staple 1, staple 2, and staple 3 are shown in Fig. S2, ESI.† | ||
Stapled peptide improves the binding affinity by 25-fold by the significant reduction of entropy penalty
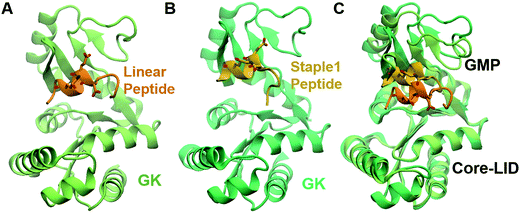
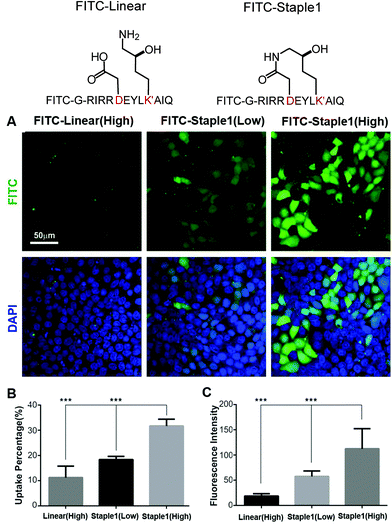
As shown in Fig. 3, staple 1 peptide greatly improved the binding affinity (ΔGbinding) by 25 fold to reach 1.36 μM. Furthermore, to elucidate the binding modes of the GK domain with both stapled and linear peptides, we solved the crystal structure of GK–linear and GK–staple 1 peptide complexes (Fig. 4). As shown in Fig. S4A and B (ESI†), the GK–linear peptide and GK–staple 1 peptide were crystallized in a similar binding pose with all the conserved binding interactions preserved. These interactions are similar in both GK–linear peptide and GK–staple 1 peptide complexes, suggesting that the enthalpy terms of both complexes are comparable and the improvement by one order of magnitude is entropy-driven. To further investigate the thermodynamic contributions to the enhancement of binding affinity of stapled peptides to the GK domain, we examined the entropic and enthalpic contributions using ITC measurements in combination with free energy calculations based on MD simulations.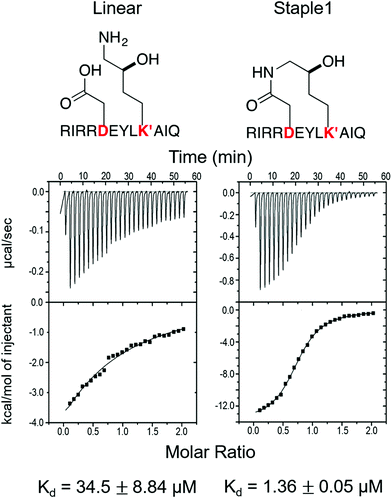 | ||
| Fig. 3 Functional groups of staples and ITC-based measurements showing the binding between the PSD95 GK domain and (A) linear and (B) staple 1 peptides. | ||
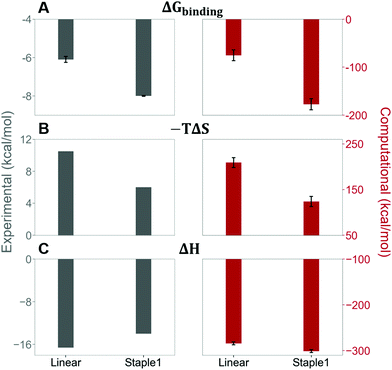
Our results show that the increase in binding affinity of the staple 1 peptide is due to the reduction in entropy penalty (−TΔS). The GK domain in complex with the staple 1 peptide has smaller entropy penalty, yet less favorable enthalpy contribution as derived by ITC-based binding experiments (Fig. 5B and C, gray bar). Specifically, the entropy term of the staple 1 peptide binding to the GK domain is stabilized by −4.5 kcal mol−1 and the enthalpy term is destabilized by 2.6 kcal mol−1 compared with the linear peptide (Table S1, ESI†). Nevertheless, the stabilization due to the entropy term significantly overrides the destabilization by the enthalpy term (|−TΔΔS| > |ΔΔH|), resulting in an order of magnitude improvement of Kd for the staple 1 peptide binding with the GK domain.
Constrained stapled peptide in the free state is the main contributor to the reduction of entropy penalty
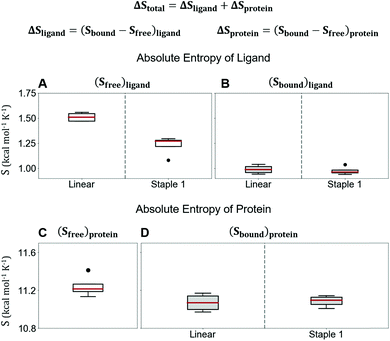
Using conformations from MD simulations, we further computed the binding free energy using a MM/PBSA and Quasi-Harmonic approximation. Our calculation results are in reasonable agreement with experimental observations within standard deviations for all thermodynamic terms: ΔGbinding, −TΔS, and ΔH (Fig. 5). Furthermore, we demonstrate that the improvement in the binding affinity of the GK domain to the staple 1 peptide is mainly due to the decrease in flexibility of the staple 1 peptide in free solution ((Sfree)ligand in Fig. 6A). Consistent with the small value of (Sfree)ligand, the staple 1 peptide has higher α-helical content according to both MD simulations and the CD Spectrum (Fig. 7). In sharp contrast, the linear peptide has lower α-helical content and is more flexible in the free state, leading to a substantially larger value of (Sfree)ligand (Fig. 7). These observations clearly indicate that the rigidification in the α-helix structure upon the introduction of the staple can significantly reduce the absolute entropy of the free peptide, resulting in much improved stabilization of binding to the GK domain. Interestingly, our calculations provide largely similar values for the absolute entropy of the bound state (Sbound) for both the protein and ligand (Fig. 6B and D), suggesting that there is no significant contribution from the bound state to the stabilization of binding affinity of the GK–staple 1 peptide complex.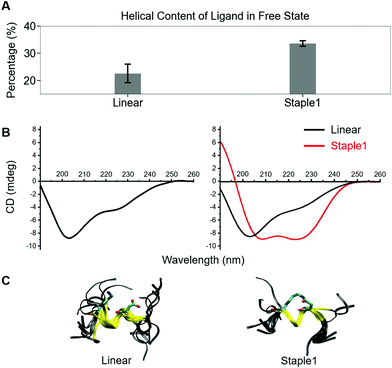 | ||
| Fig. 7 Helical content calculated from MD simulation (top), CD spectrum (middle) and overlaid structures from MD simulation (bottom) of (A) linear and (B) staple 1 ligands in the free state. | ||
Furthermore, we found that the GK domain has less stable interaction energy with the staple 1 peptide compared with the linear peptide (ΔEInteraction in Table S3, ESI†). Further analysis based on their crystal structures (Fig. 4C) and MD simulations (Fig. S5, ESI†) shows that the GK domain adopts a more open conformation when bound to the staple 1 peptide compared to the linear peptide. As shown in Fig. S6B (ESI†), the introduction of staple constrains the peptide in an α-helical conformation with a larger α-helix radius (Fig. S6B, ESI†). We speculate that this may subsequently induce the opening of the GK domain, leading to less stable interaction and eventually less favorable enthalpy between the GK domain and the stapled peptide than with the linear peptide.
Stapled peptide designs benefitting from increased bound state entropy could not improve the overall binding affinities due to the energy-entropy compensation
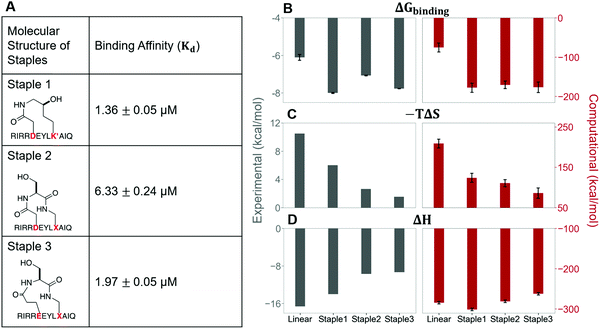
In this section, we synthesize two more stapled peptides, staple 2 and staple 3 peptides (Fig. 8A and Fig. S2C, ESI†). As shown in Fig. 8C and D, the experimental and free energy calculation results showed that the entropy penalty for the binding of staple 2 and 3 peptides is further reduced compared to the staple 1 peptide. Surprisingly, these two stapled peptides do not improve the overall binding affinity compared to the staple 1 peptide (Fig. 8). Further analysis reveals that the further reduction of the entropy penalty in staple 2 and 3 peptides is not due to (Sfree)ligand but due to the increase of the GK domain entropy in the bound state, (Sbound)protein (Fig. S7, ESI†). This increase in the flexibility of the GK domain in the bound state reflects a flexible binding mode with its ligand. Indeed, our calculations show that ΔH is less favorable for the binding of staple 2 and 3 peptides compared to the staple 1 peptide (Fig. 8C and D). As a result, the overall binding affinity is comparable for all three stapled peptides (Fig. 8). These results indicate that the stapled peptide design that increases the entropy of the bound state (Sbound) may not be effective due to the energy–entropy compensation.Stapled peptide penetrates the cell better than linear peptide
In this section, we further examined the cell penetrability of our novel staple using the staple 1 peptide. As shown in Fig. 9, the staple 1 peptide displays substantially better cell penetrability than the linear peptide. The cell penetrability of linear and staple 1 peptides was analyzed by treating MDCK cells with FITC-labelled peptides at 10 μM (low) or 20 μM (high) concentrations (calculated as the peptide concentration in culture media). There is a significantly higher percentage of uptake of the Staple 1 peptide by MDCK cells than the linear peptide (Fig. 9B). The average intensity of FITC in MDCK cells is also higher for the staple 1 peptide compared to the linear peptide, indicating that the staple 1 peptide can more effectively penetrate the cell membrane at a given concentration (e.g. 20 μM, Fig. 9C). This shows that our designed staple 1 peptide can indeed penetrate living cells with a high efficiency, indicating that this stapled peptide may be a promising tool to study PSD-95 and SAPAP interaction in vivo.In addition to stapled peptide designs that benefit from entropy, we expect that the binding affinity for the GK–domain inhibitors could also be improved by enhancing the interaction energies in the future. One promising strategy is to consider replacing the glutamic acid in our stapled peptides with non-natural amino acid with additional negative charges, which can further enhance its interactions with the phosphor-binding pocket because glutamic acid may not be sufficient to mimic the salt bridge between phosphoserine and the conserved binding site (e.g. residue R568 and R571 of the GK domain in Fig. S4, ESI†). For example, one could use a non-hydrolysable phosphoserine analog to further enhance the binding interactions.24
Conclusions
In this study, we successfully designed a stapled peptide (staple 1), which can bind to the PSD-95 GK domain with a 25-fold stronger binding affinity than its linear counterpart. To ensure good solubility of the stapled peptide, we employed a recently developed synthetic strategy to introduce hydrophilic groups into the staple.25 We also showed that the novel staple has better cell penetrability than the linear peptide, indicating its future applications for use in in vivo study. More importantly, we were able to quantitatively dissect the enthalpic and entropic contributions of binding affinity of peptide ligands to the GK domain, and further correlate molecular features with specific thermodynamics terms. We found that the stronger binding affinity of the staple 1 peptide is mainly due to the staple that constrained the peptide conformation in the free state, leading to a smaller absolute entropy of ligand in the free state ((Sfree)ligand). Based on staple 1, we further explored two other stapled peptides (staple 2 and 3), which exerted even larger entropy gains due to more flexible bound states ((Sbound)protein). Surprisingly, both staple 2 and 3 peptides display binding affinity comparable with that of the staple 1 peptide, due to the energy–entropy compensation of the bound state. Our results suggest that increasing the stability of the stapled peptide in free solution is an effective strategy for the rational design of stapled peptide inhibitors.Methods
Protein expression and purification
Expression and purification of human or rat PSD-95 GK have been described previously.18,19,26Peptide synthesis
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with 5% TFA in an ice bath. The solution was treated with O3, which was produced from an ozone generator, for 1 min. The resulting solution was diluted with H2O and ready for HPLC purification with a separation yield of 12–18% based on the loading of the resin.
1 with 5% TFA in an ice bath. The solution was treated with O3, which was produced from an ozone generator, for 1 min. The resulting solution was diluted with H2O and ready for HPLC purification with a separation yield of 12–18% based on the loading of the resin.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, mol mol−1) and the concentration of the peptide was adjusted to 0.5 mM. The resulting solution was stirred at room temperature for about 6 h and monitored by LC-MS. No dimer was formed but the product, and the solvent was blown off under a stream of condensed air, followed by treatment with the cocktail of TFA/H2O/TIPS = 95%/2.5%/2.5% for about 10 min. After precipitation with cold diethyl ether, the resulting peptide residue was ready for HPLC purification with a separation yield of 35–60%.
2, mol mol−1) and the concentration of the peptide was adjusted to 0.5 mM. The resulting solution was stirred at room temperature for about 6 h and monitored by LC-MS. No dimer was formed but the product, and the solvent was blown off under a stream of condensed air, followed by treatment with the cocktail of TFA/H2O/TIPS = 95%/2.5%/2.5% for about 10 min. After precipitation with cold diethyl ether, the resulting peptide residue was ready for HPLC purification with a separation yield of 35–60%.
CD spectrum
CD samples were dissolved in HPLC grade H2O at 200 μM concentration. CD spectra were acquired on a Jasco J-815 circular dichroism (CD) spectropolarimeter. Spectra were processed using OriginLab.Isothermal titration calorimetry assay
Isothermal titration calorimetry experiments were carried out on a MicroCal ITC200 calorimeter (Malvern) at 25 °C. The concentration of the injected samples (peptides) in the syringe was 200 μM, and the concentration of the samples in the cell was fixed at 20 μM. The sample in the syringe was sequentially injected into the sample cell with a time interval of 150 s (0.5 μL for the first injection and 2 μL each for the following 19 injections). The titration data were analyzed using the Origin 7.0 software and fitted with the one-site binding model.Crystallization, data collection and processing
Both crystals of rat DLG4 GK in complex with the synthesized peptide were obtained by the sitting drop vapor diffusion method at 16 °C. Freshly purified DLG4 GK protein was concentrated to 10 mg ml−1 before the addition of the synthesized peptide in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio.
1 molar ratio.
The GK/linear-peptide complex crystal was grown in solution containing (0.02 M citric acid, 0.08 M BIS-TRIS propane/pH 8.8), 16% w/v polyethylene glycol 3350. Glycerol (30%) was added as the cryo-protectant before the crystal was frozen in liquid nitrogen. The GK/stapled-peptide complex crystal was grown in solution containing 35% w/v PEP 629 and 100 mM HEPES (pH 7.5). This kind of crystal was frozen directly in liquid nitrogen. A 2.45 Å resolution X-ray data set for the GK/linear-peptide and a 2.60 Å resolution X-ray data set for the GK/stapled-peptide were collected at the beam-line BL19U1 or BL17U1 of the Shanghai Synchrotron Radiation Facility. The diffraction data sets were processed and scaled by HKL3000.
The data qualities were checked using phenix.xtriage, and pseudo-merohedral twinning was found in both data sets. Using the structure of the DLG1 GK domain (PDB id: 3UAT) as the search model, the initial structural models were solved using the molecular replacement method in PHASER for both GK/linear-peptide and GK/stapled-peptide complexes. The models were then refined by the phenix.refinement. Coot was used for peptide modelling and model adjustments. TLS refinement was applied at the final refinement stage. For the GK/linear-peptide complex, the data quality was largely improved by applying twin refinement (twin_fraction = 0.09, twin_law = h, -k, -h, -l). For the GK/Stapled-peptide complex, the model was also improved by applying twin refinement (twin_fraction = 0.07, twin_law = -k, -h, -l). The final structure was validated by phenix.model_vs_data validation tools. The final refinement statistics are listed in Table 1. The structure figures were prepared using the program VMD Molecular Graphic Viewer27 (http://www.ks.uiuc.edu/Research/vmd/). PDB id for the linear peptide/GK complex: 7F7G, PDB id for the stapled peptide/GK complex: 7F7I.
| Dataset | GK/linear peptide | GK/stapled peptide |
|---|---|---|
| Numbers in parentheses represent the value for the highest resolution shell.a Rmerge = ∑|Ii − Im|/∑Ii, where Ii is the intensity of the measured reflection and Im is the mean intensity of all symmetry related reflections.b Rcryst = ∑‖Fobs| − |Fcalc‖/∑|Fobs|, where Fobs and Fcalc are observed and calculated structure factors.c Rfree = ∑T‖Fobs| − |Fcalc‖/∑T|Fobs|, where T is a test data set of about 5% of the total reflections randomly chosen and set aside prior to refinement. | ||
| Data collection | ||
| Space group | p21 | p1 |
| Unit cell (a, b, c, Å) | 35.854, 61.579, 103.851 | 51.029, 51.954, 144.5 |
| Unit cell (α, β, γ, °) | 90.000, 98.29, 90.000 | 91.775, 91.429, 120.965 |
| Wavelength (Å) | 0.97774 | 0.97799 |
| Resolution range (Å) | 50.00–2.45 | 50.00–2.60 |
| (2.49–2.45) | (2.64–2.60) | |
| No. of unique reflections | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 628 (777) 628 (777) |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 969 (1893) 969 (1893) |
| Redundancy | 4.1(4.0) | 3.8(3.7) |
| I/σ | 8.5(1.8) | 9.9(1.9) |
| Completeness (%) | 93.9(96.2) | 97.2(97.1) |
| R merge (%)a | 13.9(41.3) | 14.7(69.4) |
| Structure refinement | ||
| Resolution, Å | 35.14–2.45 (2.53–2.45) | 33.14–2.60 (2.69–2.60) |
| R work /Rfreec (%) | 0.2094 (0.2755)/ 0.2706 (0.3731) | 0.2199 (0.2908)/ 0.2684 (0.3660) |
| Rmsd bonds/angles (Å/°) | 0.008/1.07 | 0.008/1.22 |
| Average B factor (Å2) | 37.98 | 48.9 |
| No. of protein atoms | 3210 | 9424 |
| No. of water molecules | 198 | 382 |
| No. of reflections | ||
| Working set | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 819 (1426) 819 (1426) |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 046 (3402) 046 (3402) |
| Test set | 792 (77) | 1906 (203) |
| Ramachandran plot (%) | ||
| Favored regions | 96.6 | 96.4 |
| Allowed regions | 3.4 | 3.4 |
| Outliers | 0 | 0.17 |
NMR spectrum
1D 1H water suppression NMR was performed in 90% H2O and 10% D2O. NMR spectra were acquired on a Bruker Avance DRX 500 FT-NMR spectrometer at 298 K and processed using TopSpin software.Cell culture and peptide cellular uptake
MDCK cells were cultured on 35 mm dishes with 10 mm diameter uncoated glass bottom (MatTek) in DMEM (Hyclone, SH30022.01B) supplemented with 10% fetal bovine serum (FBS; Hyclone, SH30084.03) and 50 μM penicillin–streptomycin. They were cultured in a 37 °C incubator with 5% CO2 for around 3 days after seeding.For the peptide cellular uptake experiment, the cells were rinsed three times with PBS to completely remove the medium. Peptides were dissolved in PBS with 1% glucose and diluted using DMEM with no FBS. Concentrations of the peptides were determined by measuring A280 and A488 using a NanoDrop spectrophotometer (Thermo Fisher Scientific). The cells were then applied with one milliliter of the medium containing 10 μM or 20 μM peptides at 37 °C for 4 hours. After the incubation, the cells were fixed using 4% PFA for the imaging.
Microscopy and data analysis
All the cell culture images were acquired on a Zeiss LSM 880 laser-scanning confocal microscope. Images were captured using a 40 × 1.4 oil objective with pinhole setting to 1 Airy unit. The obtained images were then analyzed with ImageJ software (http://imagej.nih.gov/ij/).Assignment of partial charges of staple peptides and hydroxylysine for MD simulation
As the stapled peptides and the linear peptide contain non-conventional amino acids, we performed geometry optimization and electrostatic potential calculation for each type of staple peptide (staple 1, staple 2, and staple 3) and hydroxylysine. For each type of staple peptide, we performed geometry optimization of the peptide with sequence, ACE-AXEYLXA-NME, where Xs are the stapled residues, ACE is acetyl to cap the N-terminal and NME is N-methyl to cap the C-terminal. For hydroxylysine, the amino acid is capped by ACE and NME. For these modelled structures, geometry optimizations were performed using Gaussian 0928 with the Becke, 3-parameter, Lee–Yang–Parr method and basis set 6-31g* (b3lyp/6-31G*). Electrostatic potential calculations were performed using the Hartree–Fock method with basis set 6-31g* (hf/6-31g*). The partial charges were then calculated by the RESP method using resp modules in AmberTools 13,29 where partial charges were determined by a two-stage RESP30 procedure. In the first stage, partial charges were fitted to the electrostatic potential while maintaining the partial charges of ACE, NME, Alanine, and -EYL- sequence, the same as AMBER 99SB-ILDN. In addition, the partial charges of N–H and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups of the stapled residues (X) were maintained to be the same as the non-charged residues in AMBER 99SB-ILDN. At the second stage, fitting was done for methylene and methyl groups while maintaining the partial charges of all the other atoms.
O groups of the stapled residues (X) were maintained to be the same as the non-charged residues in AMBER 99SB-ILDN. At the second stage, fitting was done for methylene and methyl groups while maintaining the partial charges of all the other atoms.
Molecular dynamics simulation of the GK–ligand complex
The crystal structures of the GK–linear complex and GK–staple 1 complex were used as the initial structures of Molecular Dynamics (MD) simulation. The complexes of GK–staple 2 and GK–staple 3 were modelled based on the GK–staple 1 crystal structure.All complexes were solvated in a dodecahedron box with TIP3P31 water molecules. To neutralize the system, Na+ and Cl− ions were added to 0.15 mol per liter salt concentration. We performed all MD simulations using the GROMACS 4.532 simulation package and the AMBER 99SB-ILDN33 force field along with the partial charges obtained by the RESP method for staple and non-conventional amino acids. Long-range electrostatic interactions were treated by the Particle-Mesh Ewald (PME) method34 and van der Waals short-range interactions were calculated using a cut-off of 10 Å.
Energy minimization was performed using the steepest descent method, followed by NVT equilibration for 1 ns with position restraints on the heavy atoms at 300 K using a V-rescale thermostat35 with a coupling constant of 0.1 ps. At this step, the positions of heavy atoms of the GK–ligand complex were restrained with a force constant of 1000 kJ mol−1 nm−1 and all bonds in protein molecules and water were constrained using the LINCS36 algorithm. NPT equilibration was then carried out for 1 ns using the Parrinello–Rahman barostat37 with a coupling constant = 0.2 ps to a reference pressure of 1 bar with position restraints on the heavy atoms of the GK–ligand complex using 1000 kJ mol−1 nm−1 force constant. The restraints were released by 200 kJ mol−1 nm−1 every 200 ps. Lastly, the position restraints were released and MD simulation was run for 400 ps under NPT conditions.
For each complex, four production MD simulations under NPT conditions were performed for 200 ns. In the succeeding MD simulations, we used the same simulation package, force field, non-bonded interaction calculation method, barostat, thermostat, and bond constraint. For the following analysis, the first 25 ns was removed from each simulation.
Molecular dynamics simulation of the GK domain
The starting structure for MD simulations was taken from the crystal structure of the GK–staple 1 complex with staple 1 removed. It was solvated in a dodecahedron box with 8797 TIP3P water molecules. The system also contains 30 Na+ ions and 27 Cl− ions to neutralize the system and creates a 0.15 mol per liter salt environment. Energy minimization was performed using the steepest descent method, followed by NVT equilibration for 100 ps with position restraints (force constant = 1000 kJ mol−1 nm−1) on the heavy atom of the GK domain at T = 300 K with coupling constant = 0.1 ps. NPT equilibration was then carried out for 100 ps with coupling constant = 0.2 ps to a reference pressure of 1 bar with position restraints on the heavy atoms of the GK domain. Four production NPT MD simulations were performed for 200 ns each. For the following analysis, the first 25 ns was removed from each simulation.Molecular dynamics simulation of peptide ligands
The starting structure for MD simulation was obtained from the GK–staple 1 complex for staple 1, staple 2, and staple 3 peptides and the GK–linear complex for the linear peptide, with the GK domain removed. It was solvated in a dodecahedron box with TIP3P water molecules, Na+ ions and Cl− ions to neutralize the system and creates a 0.15 mol per liter salt environment. Energy minimization was performed using the steepest descent method, followed by NVT equilibration for 100 ps with position restraints (force constant = 1000 kJ mol−1 nm−1) on the heavy atom of ligands at T = 300 K with coupling constant = 0.1 ps. NPT equilibration was then carried out for 100 ps with coupling constant = 0.2 ps to a reference pressure of 1 bar. Four production NPT MD simulations were performed for 200 ns each. For the following analysis, the first 25 ns was removed from each simulation.Computational thermodynamic property calculation
Binding free energy can be written as ΔGbinding = Gcomplex − Gligand − Gprotein. The free energies of the complex, protein and ligand (Gcomplex, Gligand, and Gprotein) were approximated by calculation of the solvation free energy, solute potential energy in a vacuum, and solute entropy, Gx = Gsolvation + EMM − TS, using the structures from the complex, protein and ligand MD simulations, respectively. Gsolvation was calculated by solving the linear Poisson–Boltzmann equation for the polar contribution (Gpolar) and the solvent accessible surface area equation for the non-polar (Gnon-polar)contribution, Gsolvation = Gpolar + Gnon-polar, using MM/PBSA implementation in GROMACS (g_mmpbsa,38,39). The box for Gpolar calculation was created by using the extreme coordinates of the complex in each dimension, then expanded it by 1.5-fold at each direction (cfac = 1.5). The ionic strength of the system is 0.15 M NaCl with 0.95 Å and 1.81 Å radii of Na+ and Cl−, respectively. Vacuum, solute and solvent dielectric constants were set as 1, 1, and 80, respectively. Non-polar solvation energy was calculated using the solvent accessible surface area method, with probe radius = 1.4 Å, γ = 0.022678 kJ mol−1 Å−2, and offset = 3.84982 kJ mol−1 Å−2.The potential energies of the protein, ligand, and complex in a vacuum, EMM, were calculated by GROMACS. The Coulomb interaction was calculated between all the atoms in each system using Coulomb's law. The potential energy consists of a bonded angle and dihedral energy, coulomb short range and 1–4, as well as Lennard-Jones short range and 1–4 interactions.
For each frame in the MD simulation of the complex, protein and ligand, Gsolvation + EMM was calculated. Then, to obtain the average and error bar, we combined all four simulations and just maintained the values at every 100th step, totalling 1400 values. Next, we did bootstrap of the 1400 values with 1400 samples. For each bootstrap sample, the mean was calculated. Then, the reported average is the average of 1400 bootstrap mean values and the error bar is the standard deviation from 1400 bootstrap mean values. Finally, the energy change, ΔGsolvation + ΔEMM, was obtained by subtracting the values from complex simulation (bound state) from the values from the protein and ligand simulation (free state). The values of ΔGsolvation + ΔEMM are compared with experimental ΔH measured by ITC shown in Fig. 5.
The conformational entropy, ΔS, was calculated by subtracting the absolute entropy of the protein/ligand in bound form from that of the protein/ligand in the free state, ΔS = (Sbound − Sfree)protein + (Sbound − Sfree)ligand. The absolute entropy was calculated by quasi-harmonic approximation40 with Cartesian coordinates, using g_covar and g_analyze modules in GROMACS. All the structures in MD simulation were first fitted to all Cα atoms of the GK domain and Cα of residues −1 to 3 of peptide ligands for calculation of entropy of the GK domain and peptide ligand, respectively. For each system (GK–ligand complex, GK, or peptide ligands), we performed four 200 ns simulations and calculated the absolute entropy (S) of the GK and ligand from each simulation. The Sbound value of the GK and ligand was calculated from the structures of the GK and ligand obtained by MD simulations of the GK–ligand complex, respectively. The Sfree value of the GK and ligand was calculated from the structures of the GK and ligand obtained by the MD simulation of the GK or ligand in solution, respectively. Thus, there are 4 × 4 combinations to subtract the absolute entropy of the bound state (Sbound) from that of the free state (Sfree) for the GK and ligand system, resulting in 16 ΔSprotein/ligand values. Then, bootstrapping of these 16 values was performed 800 times to calculate the average and error bar. The reported average in Fig. 5 is the addition of bootstrap average of entropy difference (ΔS) of the protein and ligand, ΔSligand + ΔSprotein, and the error bar is obtained by error propagation of standard deviation of bootstrap samples of ΔSprotein and ΔSligand.
Contribution
ICU and SC conducted the computation, JX and CHPC conducted the chemical synthesis, and YS, RZ, XC and PPHC conducted the biological experiment and structural biology. DB, MZ, XH and XL initiated and supervised the project. ICU, CHPC, YS, XH and XL wrote the manuscript with inputs from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the National Facility for Protein Science Shanghai (NFPS) for allowing us to use the BL19U1 beamline and the Shanghai Synchrotron Radiation Facility (SSRF) for X-ray beam time (BL17U1 beamline). This work was supported by the Hong Kong Research Grant Council (17309616, T13-605/18-W, AoE/M-09/12 and AoE/P-705/16), Innovation and Technology Commission (ITCPD/17-9), and a grant from the Asia Cancer Foundation. X. H. acknowledges the Padma Harilela Associate Professorship. MZ is a Kerry Holdings Professor in Science and a Senior Fellow of IAS at HKUST.References
- J. A. Wells and C. L. McClendon, Reaching for high-hanging fruit in drug discovery at protein-protein interfaces, Nature, 2007, 450(7172), 1001–1009 CrossRef CAS PubMed.
- P. Vlieghe, V. Lisowski, J. Martinez and M. Khrestchatisky, Synthetic therapeutic peptides: science and market, Drug DiscoveryToday, 2010, 15(1–2), 40–56 CrossRef CAS PubMed.
- T. A. Hill, N. E. Shepherd, F. Diness and D. P. Fairlie, Constraining cyclic peptides to mimic protein structure motifs, Angew. Chem., Int. Ed., 2014, 53(48), 13020–13041 CrossRef CAS PubMed.
- R. S. Harrison, et al., Novel helix-constrained nociceptin derivatives are potent agonists and antagonists of ERK phosphorylation and thermal analgesia in mice, J. Med. Chem., 2010, 53(23), 8400–8408 CrossRef CAS PubMed.
- Y. H. Lau, et al., ( 2015) Double Strain-Promoted Macrocyclization for the Rapid Selection of Cell-Active Stapled Peptides. Angew. Chem., Int. Ed. 54(51):15410–3 Search PubMed.
- R. S. Harrison, et al., Downsizing human, bacterial, and viral proteins to short water-stable alpha helices that maintain biological potency, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(26), 11686–11691 CrossRef CAS.
- T. K. Sawyer, et al., Macrocyclic α helical peptide therapeutic modality: A perspective of learnings and challenges, Bioorgan. Med. Chem., 2018, 26(10), 2807–2815 CrossRef CAS.
- Y. S. Tan, D. P. Lane and C. S. Verma, Stapled peptide design: principles and roles of computation, Drug Discovery Today, 2016, 21(10), 1642–1653 CrossRef CAS PubMed.
- J. A. Miles, et al., Hydrocarbon constrained peptides – understanding preorganisation and binding affini, Chem. Sci., 2016, 7, 3694–3702 RSC.
- J. Zhu, Y. Shang and M. Zhang, Mechanistic basis of MAGUK-organized complexes in synaptic development and signalling, Nat. Rev. Neurosci., 2016, 17(4), 209–223 CrossRef CAS PubMed.
- E. Kim, et al., GKAP, a novel synaptic protein that interacts with the guanylate kinase- like domain of the PSD-95/SAP90 family of channel clustering molecules, J. Cell Biol., 1997, 136(3), 669–678 CrossRef CAS PubMed.
- S. Naisbitt, et al., Characterization of guanylate kinase-associated protein, a postsynaptic density protein at excitatory synapses that interacts directly with postsynaptic density-95/synapse-associated protein 90, J. Neurosci., 1997, 17(15), 5687–5696 CrossRef CAS.
- M. Takeuchi, et al., SAPAPs. A family of PSD-95/SAP90-associated proteins localized at postsynaptic density, J. Biol. Chem., 1997, 272(18), 11943–11951 CrossRef CAS PubMed.
- S. G. N. Grant, Synaptopathies: Diseases of the synaptome, Curr. Opin. Neurobiol., 2012, 22(3), 522–529 CrossRef CAS.
- O. Marin, Interneuron dysfunction in psychiatric disorders, Nat. Rev. Neurosci., 2012, 13(2), 107–120 CrossRef CAS PubMed.
- P. Monteiro and G. Feng, SHANK proteins: Roles at the synapse and in autism spectrum disorder, Nat. Rev. Neurosci., 2017, 18(3), 147–157 CrossRef CAS.
- T. Bourgeron, From the genetic architecture to synaptic plasticity in autism spectrum disorder, Nat. Rev. Neurosci., 2015, 16(9), 551–563 CrossRef CAS.
- J. Zhu, et al., Guanylate kinase domains of the MAGUK family scaffold proteins as specific phospho-protein-binding modules, EMBO J., 2011, 30(24), 4986–4997 CrossRef CAS PubMed.
- J. Zhu, et al., Phosphorylation-dependent interaction between tumor suppressors Dlg and Lgl, Cell Res., 2014, 24(4), 451–463 CrossRef CAS PubMed.
- C. A. Johnston, C. Q. Doe and K. E. Prehoda, Structure of an enzyme-derived phosphoprotein recognition domain, PLoS One, 2012, 7(4), e36014 CrossRef CAS.
- K. Hirao, et al., A novel multiple PDZ domain-containing molecule interacting with N- methyl-D-aspartate receptors and neuronal cell adhesion proteins, J. Biol. Chem., 1998, 273(33), 21105–21110 CrossRef CAS.
- J. Zhu, et al., Synaptic Targeting and Function of SAPAPs Mediated by Phosphorylation-Dependent Binding to PSD-95 MAGUKs, Cell Rep., 2017, 21(13), 3781–3793 CrossRef CAS PubMed.
- D. J. Dunican and P. Doherty, Designing cell-permeant phosphopeptides to modulate intracellular signaling pathways, Biopolym. – Pept. Sci. Sect., 2001, 60(1), 45–60 CrossRef CAS.
- G. Ye, et al., Synthesis and evaluation of tripodal peptide analogues for cellular delivery of phosphopeptides, J. Med. Chem., 2007, 50(15), 3604–3617 CrossRef CAS PubMed.
- C. H. P. Cheung, et al., Construction of diverse peptide structure architectures via chemoselective peptide ligation, Chem. Sci., 2021, 12(20), 7091–7097 RSC.
- Y. Xia, Y. Shang, R. Zhang and J. Zhu, Structure of PSD-95/MAP1A complex reveals unique target recognition mode of MAGUK GK domain, Biochem. J., 2017, 474(16), 2817–2828 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian 09 A.02, Gaussian, Inc, Wallingford CT, 2009, DOI: 111 Search PubMed.
- D. A. Case, et al., AmberTools 13, Univ California, San Fr, 2013 Search PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly, P. A. Kollman and P. A. Kollmann, Application of RESP Charges To Calculate Conformational Energies, Hydrogen Bond Energies, and Free Energies of Solvation, J. Am. Chem. Soc., 1993, 115(7), 9620–9631 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79(2), 926–935 CrossRef CAS.
- S. Pronk, et al., GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit, Bioinformatics, 2013, 29(7), 845–854 CrossRef CAS PubMed.
- K. Lindorff-Larsen, et al., Improved side-chain torsion potentials for the Amber ff99SB protein force field, Proteins: Struct., Funct. Bioinf., 2010, 78(8), 1950–1958 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98(12), 10089 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126(1), 014101 CrossRef PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, LINCS: A Linear Constraint Solver for molecular simulations, J. Comput. Chem., 1997, 18(12), 1463–1472 CrossRef CAS.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52(12), 7182–7190 CrossRef CAS.
- R. Kumari, R. Kumar and A. Lynn, G-mmpbsa -A GROMACS tool for high-throughput MM-PBSA calculations, J. Chem. Inf. Model., 2014, 54(7), 1951–1962 CrossRef CAS PubMed.
- N. A. Baker, D. Sept, S. Joseph, M. J. Holst and J. A. McCammon, Electrostatics of nanosystems: Application to microtubules and the ribosome, Proc. Natl. Acad. Sci. U. S. A., 2001, 98(18), 10037–10041 CrossRef CAS PubMed.
- M. Karplus and J. N. Kushick, Method for Estimating the Configurational Entropy of Macromolecules, Macromolecules, 1981, 14(2), 325–332 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cb00087j |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |