Open Access Article
Open Access ArticleHyperpositive non-linear effects: enantiodivergence and modelling†
Yannick
Geiger
 ,
Thierry
Achard
,
Thierry
Achard
 ,
Aline
Maisse-François
and
Stéphane
Bellemin-Laponnaz
,
Aline
Maisse-François
and
Stéphane
Bellemin-Laponnaz
 *
*
Institut de Physique et Chimie des Matériaux de Strasbourg, Université de Strasbourg-CNRS, UMR 7504, Strasbourg, France. E-mail: bellemin@unistra.fr
First published on 7th October 2020
Abstract
The chiral ligand N-methylephedrine (NME) was found to catalyse the addition of dimethylzinc to benzaldehyde in an enantiodivergent way, with a monomeric and a homochiral dimeric complex both catalysing the reaction at a steady state and giving opposite product enantiomers. A change in the sign of the enantiomeric product was thus possible by simply varying the catalyst loading or the ligand ee, giving rise to an enantiodivergent non-linear effect. Simulations using a mathematical model confirmed the possibility of such behaviour and showed that this can lead to situations where a reaction gives racemic products, although the system is composed only of highly enantioselective individual catalysts. Furthermore, depending on the dimer's degree of participation in the catalytic conversion, enantiodivergence may or may not be observed experimentally, which raises questions about the possibility of enantiodivergence in other monomer/dimer-catalysed systems. Simulations of the reaction kinetics showed that the observed kinetic constant kobs is highly dependent on user-controlled parameters, such as the catalyst concentration and the ligand ee, and may thus vary in a distinct way from one experimental setup to another. This unusual dependency of kobs allowed us to confirm that a previously observed U-shaped catalyst order vs. catalyst loading-plot is linked to the simultaneous catalytic activity of both monomeric and dimeric complexes.
Introduction
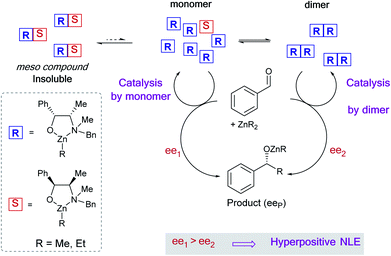
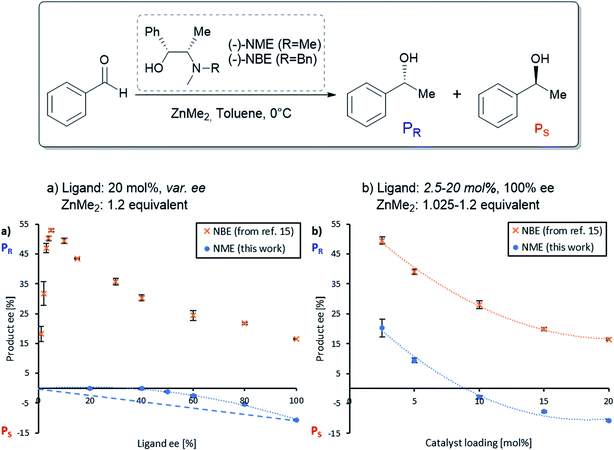
Non-linear effects (NLEs) in asymmetric catalysis refer to cases in which the enantiomeric excess of the product does not scale linearly with the enantiomeric excess of the catalyst.1 The first examples and models of such behavioural differences between scalemic and enantiomerically pure catalysts were established by Kagan in 1986.2 Since then NLEs are considered as ubiquitous phenomena that provide additional information regarding the aggregation state of the catalyst or the formation of multiligand species2,3 (cf. also reviews4,5 and some recent examples6–9). Not only being indicative of the catalytic system, NLEs also give clues to discussions on the origin of molecular homochirality in biology which is related to the origin of life.10Several models for NLEs have been described and discussed in the literature, all of them being the results of interactions between the enantiomers of the chiral catalyst thus generating diastereomeric perturbations of the entire system. A positive non-linear effect (i.e. asymmetric amplification, (+)-NLE) is essentially generated by the presence of a reservoir of racemic ideally catalytically inactive hetero-aggregate (meso),11–13 although pure homochiral aggregation can also lead to (+)-NLEs in certain cases.14 Amongst these models, Kagan established a hypothetical case wherein an unprecedented phenomenon could occur – that is, the chiral catalyst [would] be much more efficient when partially resolved than when enantiomerically pure. We recently have observed such a case, known as hyperpositive NLE, in the enantioselective addition of dialkylzincs to benzaldehyde when catalysed by the chiral N-benzylephedrine (NBE) ligand.15,16 Subsequent mechanistic investigations pointed towards a two-component catalysis where monomeric as well as homochiral dimeric catalysts are in equilibrium and in competition: both catalyse the reaction with different enantioselectivities, the dimeric catalyst being the less enantioselective one (Fig. 1). Through the precipitation of a heterochiral aggregate, variation of the ligand ee leads to a change of the overall catalyst concentration and, therefore, to a change of the monomer–dimer equilibrium. This favours the more enantioselective monomeric catalyst at low ligand ee and gives rise to the hyperpositive non-linear effect (Fig. 2a, orange crosses). These findings challenge the widely applied Noyori model for asymmetric dialkylzinc additions, where only monomers are catalytically active, and shows how complex systems with concurrent catalytic cycles can emerge from a minimum of components.13,17
 | ||
| Fig. 2 (a) NLE-curve and (b) eePvs. catalyst loading-plot of the (−)-NME- (blue dots) and (−)-NBE- (orange crosses, from ref. 11) catalyzed enantioselective addition of ZnMe2 to benzaldehyde at 0 °C. Each point is the mean of three independent experiments; the vertical bars depict standard deviations. The second-order polynomial fits (dotted lines) serve as visual guidelines. The dashed line in (a) simulates a linear eeP/eeL relationship for the NME-catalysed reaction. The product ee is defined as (PR − PS)/(PR + PS). | ||
In line with our studies on NLEs, we have explored additional ephedrine-based ligands in dialkylzinc addition reactions. The results presented in this work show that N-methylephedrine ligand (NME) follows the same model as the related NBE ligand, with monomer and dimer both catalysing the reaction, the only difference being that no meso aggregate precipitates in the case of NME. However, the homochiral dimer catalyst not only yields the product with a lower ee than the monomer catalyst, it selectively gives the opposite enantiomeric product. This enantiodivergent behaviour allowed us to switch between the preference for either enantiomer of the product, just by varying the catalyst loading. Variation of the enantiomeric excess of the ligand also allowed switching the selectivity of the product formation, leading to an enantiodivergent non-linear effect. In addition, we developed a theoretical model giving a closed mathematical expression which takes into account the concomitant catalysis by monomeric and dimeric species. From this we simulated [product ee vs. catalyst concentration] and [product ee vs. ligand ee]-plots which allowed us to gain a better understanding of the two-component catalytic system. Furthermore, the model also allowed us to analyse the reaction kinetics. Simulations showed that the observed kinetic constant of the system kobs is indeed not unique for each catalytic system, but depends on user-controlled parameters such as the total catalyst concentration and the ligand ee. This has confirmed the hypotheses made earlier and allowed the simulation of a U-shaped catalyst order vs. catalyst-curve, which had been previously observed experimentally in the NBE-catalysed reaction.15
The paper is organised as follows: we will (1) first present the experimental results obtained from the NME ligand, showing enantiodivergence in product ee (eeP) vs. ligand ee (eeL)- and eePvs. catalyst loading-plots, (2) then go on to a theoretical analysis where we present the mathematical model and discuss eePvs. catalyst concentration- and eePvs. eeL-plots, (3) this is followed by a kinetic analysis of the system in which we investigate the relationship of kobs with the catalyst concentration and eeL and simulate catalyst order vs. catalyst loading-plots. (4) Finally, we will discuss the impact of the simulations in a more general way and compare them with the experimental results.
Results & discussion
Nonlinear effect in the presence of N-methylephedrine as a chiral ligand
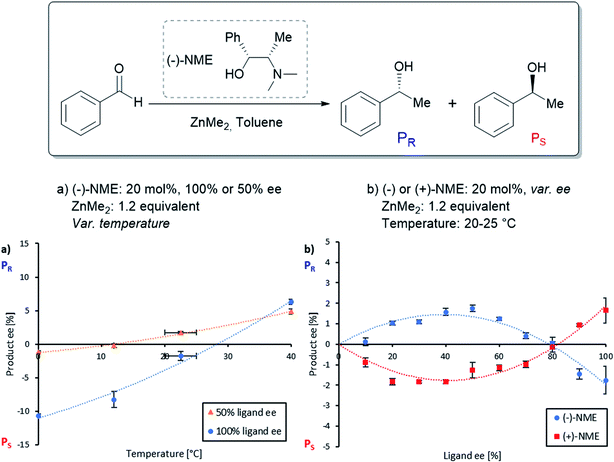
The NME and NBE ligands only differ by the N-methyl group being changed by an N-benzyl group. Therefore, we suspected that NME might generate diastereomeric and aggregation-induced perturbations in the same way as in Fig. 1 for the same reaction. The ligand has been previously applied in asymmetric alkylations using ZnEt2 as the reagent18–21 but, to the best of our knowledge, ZnMe2 has not been investigated so far. Knowing that the NBE ligand displays a more pronounced NLE with ZnMe2 than with ZnEt2,15 we suspected that NME might show an NLE in conjunction with ZnMe2, even though it had been shown previously that there is no apparent NLE with ZnEt2.22Fig. 2a displays the correlation between the enantiomeric excess of the product (eeP) and the enantiomeric excess of the ligand (eeL) for the asymmetric addition of dimethylzinc to benzaldehyde using chiral (−)-NME (blue dots). Although its (1R,2S)-configuration is identical to the one of (−)-NBE, it surprisingly yielded mainly the S-product (PS) while (−)-NBE (orange crosses) gave the R-product (PR) under similar reaction conditions. The NME-dataset in Fig. 2a generates a negative non-linear effect [(−)-NLE], albeit in an apparently inverted manner when compared to common representations of (−)-NLEs (this is due to eeP being defined here as the enantiomeric excess of PR, which leads to negative eeP values when PS is predominant).In parallel, we conducted a screening of the catalyst loading using enantiopure (−)-NME (Fig. 2b, blue dots). While a catalytic loading of 20 mol% (−)-NME gave the product in −11% ee (PS being predominant), lowering the catalyst loading progressively displaced eeP into the positive scale, giving PR in +18% ee at 2.5 mol%. The shape of the curve was found similar to the one observed when using NBE (orange crosses), as well as the eeP increase from 20 mol% to 2.5 mol% (NME: +31%; NBE: +33%).
Such behaviour with enantiopure NME, similar to what was observed with the NBE ligand, suggests that both systems follow an analogous catalytic scheme, where both monomeric and dimeric complexes are catalytically active. However, in contrast to NBE the catalytic runs with scalemic NME ligand were homogeneous with no apparent precipitate in the reaction mixture. This may account for the observed differences in NLE curves in Fig. 2a. While the hyperpositive NLE with NBE ligand was caused by the precipitation of the RS-dimer (leaving only R and RR complexes in solution and allowing high asymmetric amplification), the (−)-NLE with NME ligand might be the result of the presence of all catalytic species in solution (including S, SS and the meso dimer RS).
Moreover, the observed negative eeP at high catalyst loading unambiguously indicates that the dimeric NME-catalyst is not only less enantioselective, it even yields mainly the opposite enantiomeric product compared to the monomeric catalyst. Catalysis in which both enantiomeric products may be obtained from the same catalyst enantiomer is called enantiodivergent catalysis. It has attracted a lot of attention as a means to access easily both product enantiomers. Over the last two decades, many examples have been reported in which slight changes of the catalyst (substituent, metal, counter-ion, etc.) or of the reaction conditions (solvent, temperature, additive, ligand-to-metal ratio) have inverted the stereochemistry of the product.23–26 In our case, the switch which allows toggling between both product enantiomers is the catalyst concentration, a factor which has not been discussed in this context so far.27
These results made us wonder whether it is possible to switch the product enantiomer's sign within an NLE curve, i.e. by varying eeL instead of the catalyst loading. Such “enantiodivergent non-linear effect” has already been observed in other catalytic systems,28–30 but their origin has never been studied; even the possible presence of two catalysts yielding opposite enantiomers has not been proposed.31 Therefore, we continued our studies on NME by performing a temperature screening of the catalysis with the enantiopure ligand (Fig. 3a, blue dots) or only 50% eeL (orange triangles). At low temperature (0 °C), the product ee of the enantiopure ligand was well below the eeP of the scalemic sample, both being negative. Increasing the temperature increased eeP in both cases but not in the same manner: the difference between 100% and 50% eeL decreased progressively. At 40 °C the enantiopure ligand even surpassed the 50% eeL-sample.
However, an interesting situation occurred at room temperature (20–25 °C): here, (−)-NME in 50% ee gave positive eeP-values (i.e. R product), while the enantiopure ligand stayed negative (i.e. S product): this is nothing but the requirement for an enantiodivergent non-linear effect. The full NLE curve at room temperature (Fig. 3b, blue dots) confirmed this observation: the curve starts at 0% eeL in the positive eeP-range, reaches a maximum, then falls down to cross the eeL-axis (at eeL of ca. 80%) and ends up in the negative part of the eeP-scale. The use of (+)-NME (red squares) gave the appropriate mirror image of this curve. Thus, going to room temperature changes the (−)-NLE to a hyperpositive NLE, which in addition is also enantiodivergent.
Model studies: product ee vs. catalyst concentration (enantiopure system)
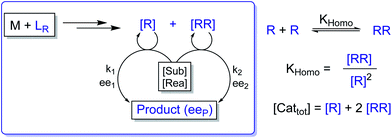
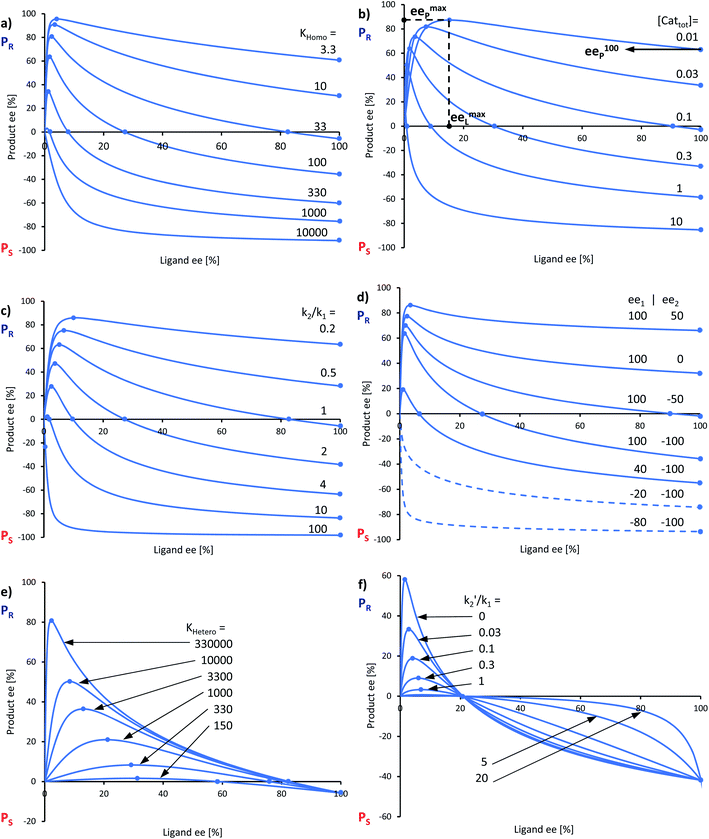
In the past, non-linear effects have been simulated and quantified using mathematical expressions of the considered models, such as the Kagan MLn models (catalysis by the aggregate)11 or the Noyori model (catalysis by the monomer, dimer acting as inactive reservoirs).13 These models have been further extended (electron-rich substrates,32 product inhibition33 for the Noyori model; monomers as reservoir species with catalytically active homochiral aggregates by Kagan14). However, to the best of our knowledge there has been no attempt to unify both approaches and to consider both monomers and dimers being simultaneously catalytically active.34 In order to fill this gap and to get a better understanding of hyperpositive and, in particular, enantiodivergent NLEs, we developed mathematical models which allow us to simulate eePvs. catalyst concentration- and eePvs. eeL-plots. We begin with Model I, which is based on an enantiopure system where an enantiopure ligand reacts with a metal to give monomeric and dimeric homochiral complexes (R and RR, respectively) both of which catalyse the reaction at different rates (k1 and k2) and with different enantioselectivities (ee1 and ee2), as shown in Fig. 4; [Cattot] represents the total catalyst concentration. For the sake of simplicity, we assume that both R and RR-catalysts follow a similar mechanism with a rate law of type −d[Sub]/dt = ki[Cati][Sub][Rea] (with ki and [Cati] being the respective rate constants and catalyst concentrations, [Sub] and [Rea] the substrate and reactant concentrations; all species are first-order). We also assume that the [RR]/[R]-ratio stays constant over the course of the reaction and depends only on the homochiral dimerization constant KHomo.35 This makes Model I reminiscent of Kagan's MLn model, which also considers the ratio between different catalytic species to be constant over time. The case of a time-dependent [RR]/[R]-ratio will be discussed at the end of this study.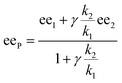 | (1) |
 | (2) |
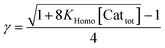
By combining the set of equations displayed in Fig. 4, it was possible to obtain eqn (1) and (2) which relate eeP to the parameters k2/k1, ee1, ee2, KHomo and [Cattot], and allowed us to compute eePvs. [Cattot]-curves. Fig. 5a displays the evolution of eeP for selected values of ee2 with fixed values of KHomo, k1 and k2 (k2/k1 was set to 1, ee1 to 100% and KHomo to 33, which corresponds to the association constant of DAIB-ZnMe).13,36 The graphs show that an enantiodivergent behaviour can indeed be observed by varying [Cattot], as long as ee2 has a sufficiently low and negative value. This is further favoured by high values of KHomo (Fig. 5b) and k2/k1 (Fig. 5c): the more the dimeric complex prevails over the monomer and the higher its relative activity, the more the curve becomes hyperbolic, pushing the point at which it crosses the [Cattot]-axis (i.e. eeP = 0, labelled [Cattot]0) to lower [Cattot]. [Cattot]0 corresponds to an overall catalytic system where R and RR catalysts compensate each other to yield an overall racemic product – even if both give independently enantiopure products.
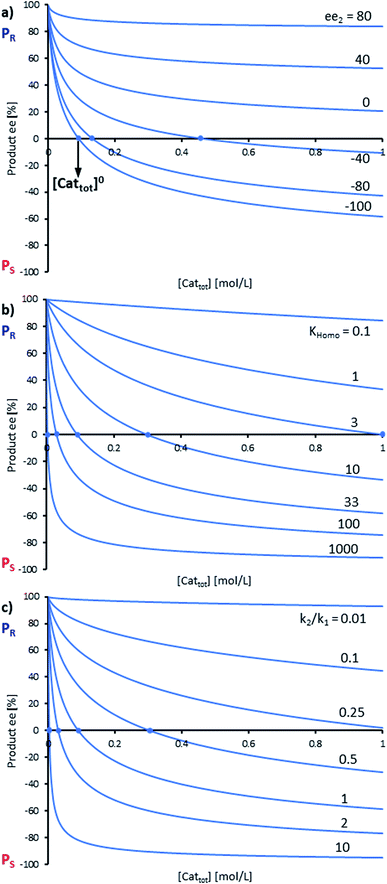 | ||
| Fig. 5 Simulation of the relationship between eeP and [Cattot] according to eqn (1) and (2). The basic set of parameters is ee1 = 100, ee2 = −100, KHomo = 33 and k2/k1 = 1. Each panel shows curves where one of the parameters has been varied: (a) ee2, (b) KHomo, (c) k2/k1. The product ee is defined as (PR − PS)/(PR + PS). | ||
Model studies: product ee vs. ligand ee (scalemic system)
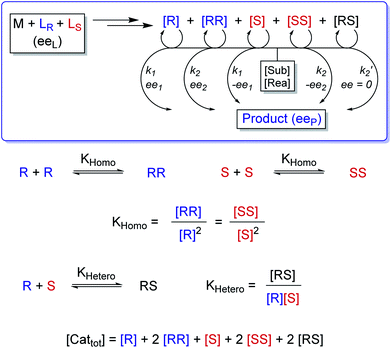
In order to also simulate NLE curves, we expanded Model I to non-enantiopure ligands, as shown in Fig. 6. The resulting system (Model II) now includes the catalytic species S and SS (which, like their enantiomeric counterparts, are linked through KHomo and catalyse with the kinetic constants k1 and k2) and also the heterochiral dimer RS, which is related to R and S through the dimerization constant KHetero and may generate racemic products with a rate constant k2′. Thus, a single scalemic ligand gives rise to 5 different catalytic species. To derive closed mathematical expressions, we followed the approach used by Noyori for the DAIB-model which consists in introducing α = [R] + [S] and β = [R][S] to simplify the equations. eeP and eeL are then given by eqn (3) and (4) as functions of α and β. Since β is itself a function of α [cf.eqn (5)], eeP and eeL are linked through α and depend only on the parameters KHomo, KHetero, k1, k2, k2′, ee1, ee2 and [Cattot]. After defining these parameters, eePvs. eeL-datasets could be obtained by choosing appropriate values for α (cf. ESI Methods† for the details of the calculations and the general expressions for the upper and lower limits of α). For this study, we will focus on the cases where the NLE is hyperpositive and potentially enantiodivergent – that is with KHetero > 2KHomo which is, as in the Noyori model, a necessary condition to obtain (+)-NLEs – and ee1 > ee2.13Fig. 7 shows several cases computed from Model II. To simplify the discussion we have set k2′ = 0 in all simulations except in Fig. 7f.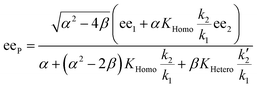 | (3) |
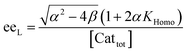 | (4) |
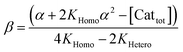 | (5) |
In all representations in Fig. 7, we selected conditions in which eeP100 could be negative and where the NLE curve crosses the eeL-axis, making it an enantiodivergent NLE. Lower the eeP100, lower the crossing point at which eeP = 0 (ee0L). At this point, the outcomes of all catalysts compensate each other to yield a racemic product. eemaxP diminishes as eeP100 decreases; the maximum's eeL-value (eemaxL) is only slightly affected by KHomo and, to a somewhat greater extent, by [Cattot] and k2/k1. This is seen nicely if, for a given set of parameters, KHomo is multiplied and [Cattot] divided by the same value: eeP100 remains unchanged but eemaxP and eemaxL do not (cf. ESI Fig. 1†). Fig. 7d shows the impact of ee1 and ee2 on eeP100: lower the ee2, lower the eeP100. This is also true for ee1; however, if both ee1 and ee2 are negative, the enantiodivergent NLE curve becomes a classic (+)-NLE for the S-product (PS, Fig. 7d, dashed curves); the same holds for the R-product (PR) if ee1 ≤ ee2 and if both are positive. In a similar way, very high KHomo-, [Cattot]- or k2/k1-values lead to apparent (+)-NLEs as eemaxP and eemaxL become exceedingly close to 0. Lowering the absolute amount of both a positive ee1 and a negative ee2 leads to a compression of the spectra (cf. ESI Fig. 2†).
Dynamic properties of models I and II
Apart from simulating eePvs. eeL-curves, NLE models have also been used to study the kinetic properties of the systems. This can be useful as some kinetic features may be characteristic for one or the other model, and thus be used as an additional probe to support the validity of a model for a specific catalytic reaction. Blackmond showed this in conjunction with the Kagan and Noyori models;37,38 Micheau and co-workers even built a toolset, using the different kinetic properties of both systems, which allows an easy distinction between monomer- and dimer-catalysed enantioselective systems (which is not necessarily possible on the basis of eePvs. eeL-curves alone)39 and verified the origin of the non-linearity in the Noyori model by a kinetic system based on differential equations.40 This prompted us to extend our work on Models I and II to a kinetic study.The mathematical expressions of the rate laws based on Models I and II turned out to correspond to a standard second-order rate law (eqn (6) and (7)), albeit with a more complex term for kobs (cf. ESI Methods† for the calculation details). For aggregate-free catalysed reactions, with 1st order in catalyst, kobs is the product of [Cattot] and the rate constant k1 (eqn (8)). According to Model I, where the monomer and dimer coexist and both of which are catalytically active, kobs depends on the parameters previously discussed: the (now absolute instead of relative) rate constants k1 and k2, KHomo and [Cattot] (eqn (9)). This holds for chiral, enantiopure catalysts as well as for achiral ones, since we consider only the system's kinetic behaviour and not a possible product ee. Non-enantiopure catalytic systems following Model II additionally depend on eeL, k2′ and KHetero (eqn (10)). For the sake of simplicity, we will consider here only the second-order rate law where the substrate and reactant concentrations are equal ([Sub] = [Rea]), however the following discussion applies also to its more general form where both differ from each other.
General second-order rate law (if [Sub] = [Rea]):
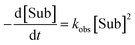 | (6) |
Integrated form of the second-order rate law:
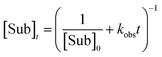 | (7) |
If only monomers exist:
| kobs = k1[Cattot] | (8) |
If monomers and dimers catalyse (Model I, achiral or enantiopure catalyst):
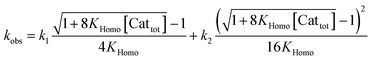 | (9) |
If monomers and dimers catalyse (Model II, chiral catalyst with any eeL):
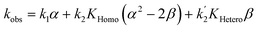 | (10) |
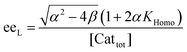 | (4) |
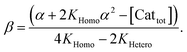 | (5) |
The interesting point here is that [Cattot] and eeL are user-controlled parameters, whose variation leads to singular changes in kobs. This can be seen in simulated kobs/[Cattot] vs. [Cattot]-plots: in the case of aggregate-free catalysed reactions (cf.eqn (8)) such a plot results in a flat line, whose y-intercept is equal to k1 (Fig. 8a, blue line). The same is observed for Model I (eqn (9)) in a special case that is when k2/k1 = 2: the loss of monomeric catalyst upon increase of [Cattot], because of dimeric aggregation, is then perfectly compensated by the higher activity of the dimer catalyst. Otherwise, an increase in [Cattot] leads to a significant change of kobs/[Cattot]: it increases if k2/k1 > 2 (grey dashed line) or decreases if k2/k1 < 2 (orange dotted line), which is symptomatic of the changing [RR]/[R]-ratio. At very low [Cattot] the amount of RR-catalyst becomes negligible and kobs/[Cattot] becomes equal to k1; on the other hand, kobs/[Cattot] = 0.5k2 at very high [Cattot] because of the prevalence of the dimeric catalyst. Thus, kobs/[Cattot] varies over changing [Cattot] even if R and RR catalyse with the same rate (k1 = k2, green dashed/dotted line). With non-enantiopure ligands kobs/[Cattot] varies in a similar way to that in Fig. 7a and depends, in addition, also on k2′ (cf. ESI Fig. 3† for a commented example with eeL = 0).
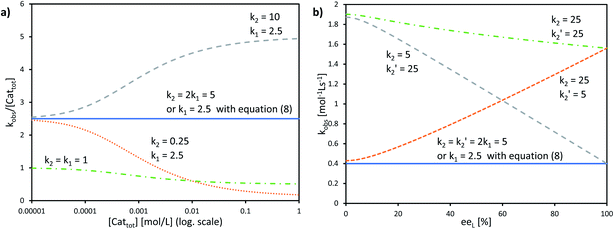 | ||
| Fig. 8 (a) Simulated kobs/[Cattot] vs. [Cattot]-plots computed from eqn (9) (KHomo = 1000, k1 and k2 as indicated) and (b) simulated kobsvs. eeL plots computed from eqn (10), (4) and (5) (KHomo = 30, KHetero = 3000, [Cattot] = 0.16, k1 = 2.5, k2 and k2′ as indicated). The full blue lines in a) and b) can also be obtained from eqn (8) (i.e. no aggregates are present in the system, the monomer is the only catalyst) using the indicated k1 value. | ||
The other user-controlled parameter, eeL, also influences kobs (at constant [Cattot]) as seen in kobsvs. eeL plots (Fig. 8b, computed from eqn (10)). kobs is constant if k2/k1 = k2′/k1 = 2 (blue full line). The case of k2/k1-values higher than 2 leads to an increase in kobs especially at high eeL, where the concentration of the homochiral dimers is also higher, and results in a positive slope (orange dotted line). On the other hand, increasing k2′/k1 gives a negative slope as it affects kobs mostly at low eeL, where the proportion of RS-dimers is highest (grey dashed line). A simultaneous increase of k2′/k1 and k2/k1 by the same amount also yields a negative slope if KHetero > 2KHomo (green dashed/dotted line). If the KHetero/KHomo-relationship is inverted then a positive slope is obtained, cf. ESI Fig. 4.†
In our previous study, we also determined the catalyst order c of the NBE-catalysed reaction when considering the system to follow the rate law −d[Sub]/dt = k[Cattot]c[Sub][Rea].15 For this, we had determined the catalyst order c using Variable Time-Normalised Analysis (VTNA)41–44 of rate profiles obtained from enantiopure NBE at different catalyst loadings. Plotting catalyst order c vs. catalyst loading gave an unusual U-shaped plot which we postulated to originate in a [Cattot]-induced change of kobs. The present kinetic model now allows us to verify this assumption, since Fig. 8a shows that kobs does indeed change with varying [Cattot]. To this end, we generated sets of rate profiles from eqn (7) and (9) by varying [Cattot] and leaving all other parameters unchanged. Then, c was determined from two different rate profiles at a time using VTNA; the results are shown in Fig. 9. In concordance with the previous discussion, k2/k1 = 2 gives a constant c value while varying the catalyst loading, since kobs is constant in that special case. k2/k1 < 2 gives a U-shaped curve, here with a minimum at c ≈ 0.7 (blue dots) and similar to the experimental one obtained from NBE. On the other hand k2/k1 > 2 gives a bell-shaped curve with a maximum at c ≈ 1.5 (grey triangles). Increasing KHomo displaces the curve's extremum to lower catalyst loading values (green crosses).
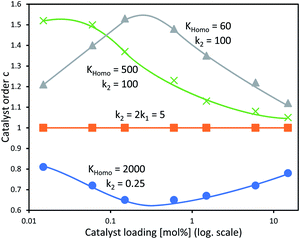 | ||
| Fig. 9 Simulated c vs. catalyst loading plot of a catalytic system following the kinetics of Model I and treated as if following the rate law −d[Sub]/dt = k[Cattot]c[Sub]a[Rea]b, with c as a variable partial order in catalyst, with undetermined rate constant k and partial substrate/reactant order a and b. Each datapoint relates the c-value obtained from two Model I-rate profiles via VTNA (from eqn (7) and (9), with [Sub]0 = 0.833, k1 = 2.5, KHomo and k2 as indicated, var. [Cattot]) with the mean of their catalyst loading values; the procedure is described in the ESI Methods†. The full lines are free-hand drawings which serve as visual guidelines. | ||
Discussion
Models I and II, although kept conceptually simple, allow us to gain a better understanding of several aspects of the NME- and NBE-catalysed reactions, which we will discuss in this section. Globally, the shape of the experimental curves (eePvs. catalyst loading as well as eePvs. eeL, Fig. 2 and 3) corresponds well with the computed curves in Fig. 5 and 7. Previously published graphs from reactions with NBE and ZnEt2 as the dialkylzinc reagent,16 giving a much weaker hyperpositive NLE than ZnMe2, also concord with the simulated ones in this study. The simulations have also given insights into the differences between the NME- and NBE-based catalysts: the overall lower eeP-values with NME may be due to lower ee1 or ee2 values, as well as to higher KHomo and/or k2/k1. The slight hyperpositive (and enantiodivergent) NLE with NME at room temperature (Fig. 3b) may arise from KHetero being only slightly higher than 2KHomo, since pronounced hyperpositive NLEs were simulated only when KHetero and KHomo are highly different (cf.Fig. 7e). At 0 °C (Fig. 2a), NME even generates a (−)-NLE which precludes that upon cooling, KHetero falls below the value of 2KHomo.In the case of NBE (Fig. 2a, orange crosses), the strong hyperpositive curve arises from the precipitation of the heterochiral dimer, which has an effect similar to an increase of KHetero. The simulations in Fig. 7 also reveal that, even if the dimeric catalyst gives the opposite product enantiomer in its pure form (ee2 = −100%), the NLE does not need to be enantiodivergent as long as the dimer's participation in the catalytic process is sufficiently low (due to low KHomo, [Cattot] or k2/k1, as seen in Fig. 7a–d). Therefore, dimeric NBE-ZnMe might yield the opposite enantiomer as well, even though its NLE and eePvs. catalyst loading-plot (Fig. 2, orange crosses) don't show direct evidence for that. This possibility is particularly interesting as it raises questions whether enantiodivergence between monomeric and dimeric catalysts might be a systematic phenomenon. There are various cases of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ligand-to-metal complexes which have been reported to yield the other product enantiomer than their 1
1 ligand-to-metal complexes which have been reported to yield the other product enantiomer than their 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 counterparts,45–53 Seebach's TADDOL-Ti-complexes being the first (but largely unnoticed) ones.46–48 2
1 counterparts,45–53 Seebach's TADDOL-Ti-complexes being the first (but largely unnoticed) ones.46–48 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes can be considered as analogues of dimeric complexes, both are even equivalent in Kagan's ML2 model.11
1 complexes can be considered as analogues of dimeric complexes, both are even equivalent in Kagan's ML2 model.11
Also, the models suggest that it is possible to obtain racemic products when working at a certain catalyst concentration ([Cattot]0, cf.Fig. 5) or ligand ee (ee0L, cf.Fig. 7), although the system consists of only highly enantioselective catalytic species. This is well exemplified with the results from NME-catalysed reactions at room temperature (Fig. 3b): the only 2% eeP yielded by the enantiopure catalyst may let one think that NME is a totally non-enantioselective catalyst in this reaction, which is definitely not the case.
Furthermore, the kinetic models show that the evolution in the ratios between the different catalytic species, when changing reaction parameters like [Cattot] or eeL, results in a variation of the rate constant kobs. This allowed us to confirm our previous assumption that a U-shaped curve for the catalyst order c vs. catalyst loading plot is consistent with Model I, assuming the monomer has more than half the catalytic activity of the dimer (k2/k1 < 2). However, this feature also shows the limitations of Model I and II: the simulated U-shaped c vs. catalyst loading-curve (Fig. 9) spans over several orders of magnitude of catalyst loading, whereas the experimental one obtained from NBE spans only from 20 to 2.5 mol%.15 For second order kinetic laws, plotting 1/[Sub]tvs. time gives a linear graph, however the corresponding experimental plots from NBE- and NME-catalysed reactions are mostly curved (cf. ESI Fig. 5†). This shows that kobs is not constant over time, most probably because of a change of the catalysts' concentrations (and their respective ratios) as the reaction goes on. It is known for DAIB-catalysed reactions that the reactants and, in certain cases, the reaction products have an influence on the catalyst composition, which results in altered reaction rates and non-constant eeP over time.13,33 Indeed, an increase of eeP over the course of the reaction was observed in the NBE-catalysed reaction.15 Therefore, further studies (and quantitative analyses in particular) of NME- and NBE-catalysed dialkylzinc additions will require more complex models, which include the concentrations of the starting materials and of the products and their possible influence on the catalyst distribution.
Conclusion
In summary, we have found an enantiodivergent behaviour in NME-catalysed reactions which may be explained by the monomer–dimer competition model, known for the parent ligand NBE. Simulation allowed us to confirm this and to get further insights into the model, such as the dependence of the observed kinetic constant kobs on the catalyst concentration and on the enantiomeric excess of the ligand. We expect this may serve as a basis for further research to understand past and future cases of enantiodivergent non-linear effects, as well as of asymmetric catalytic systems in general. Further work in our group will aim at the elucidation and the quantification of the different parameters governing reactions catalysed by ephedrine-derivatives, at the extension of the models in order to include the influence of reactants and products and at the investigation of aggregation-induced complex catalytic systems in a general way.Data availability
Synthetic and mathematical procedures, as well as additional data and chromatograms for every experimental catalytic run can be found in the ESI.† Detailed experimental data (reactant quantities, reaction conditions, raw and treated results for all catalytic runs, including reactions with NBE) and calculated data for all simulated graphs in this paper can be found in the respective excel files (SI_experimental_Data.xlsx, SI_Simulated_NLE.xlsx, SI_kinetic_model.xlsx).Author contributions
Y. G. performed the synthetic experiments and developed the catalytic models, along with their mathematical expressions. A. M.-F. and T. A. participated in data analyses. S. B.-L. conceptualized and supervised the study and wrote the manuscript with Y. G.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the French National Research Agency (ANR) through the Programme d'Investissement d'Avenir under contract ANR-11-LABX-0058_NIE within the Investissement d'Avenir program ANR-10-IDEX-0002-02.References
- H. B. Kagan and T. O. Luukas, in Comprehensive Asymmetric Catalysis, ed. E. N. Jacobsen, A. Pfaltz and H. Yamamoto, Springer-Verlag, Berlin, 1999, vol. I, pp. 101–118 Search PubMed.
- C. Puchot, O. Samuel, E. Dunach, S. Zhao, C. Agami and H. B. Kagan, Nonlinear effects in asymmetric synthesis. Examples in asymmetric oxidations and aldolization reactions, J. Am. Chem. Soc., 1986, 108, 2353–2357 CrossRef CAS.
- H. B. Kagan, Nonlinear Effects in Enantioselective Organometallic Catalysis, Oil Gas Sci. Technol., 2007, 62, 731–738 CrossRef CAS.
- C. Girard and H. B. Kagan, Nonlinear Effects in Asymmetric Synthesis and Stereoselective Reactions: Ten Years of Investigation, Angew. Chem., Int. Ed., 1998, 37, 2922–2959 CrossRef.
- T. Satyanarayana, S. Abraham and H. B. Kagan, Nonlinear Effects in Asymmetric Catalysis, Angew. Chem., Int. Ed., 2009, 48, 456–494 CrossRef CAS.
- Y. Hui, J. Jiang, W. Wang, W. Chen, Y. Cai, L. Lin, X. Liu and X. Feng, Highly Enantioselective Conjugate Addition of Thioglycolate to Chalcones Catalyzed by Lanthanum: Low Catalyst Loading and Remarkable Chiral Amplification, Angew. Chem., Int. Ed., 2010, 49, 4290–4293 CrossRef CAS.
- M. Magrez, J. Wencel-Delord, A. Alexakis, C. Crévisy and M. Mauduit, Significant Asymmetric Amplification in Enantioselective Cu/DiPPAM-catalyzed 1,6- and 1,4-Conjugate Additions of Diethylzinc to (Di)enones, Org. Lett., 2012, 14, 3576–3579 CrossRef CAS.
- S. Bellemin-Laponnaz, T. Achard, D. Bissessar, Y. Geiger and A. Maisse-François, Synthesis and application of dynamic self-supported enantioselective catalysts, Coord. Chem. Rev., 2017, 332, 38–47 CrossRef CAS.
- B. M. Armstrong, R. I. Sayler, B. H. Shupe, T. A. Stich, R. D. Britt and A. K. Franz, EPR Evidence for the Origin of Nonlinear Effects in an Enantioselective Cu(II)-Catalyzed Spiroannulation, ACS Catal., 2019, 9, 1224–1230 CrossRef CAS.
- D. G. Blackmond, The Origin of Biological Homochirality, Cold Spring Harbor Perspect. Biol., 2019, 11, a032540 CrossRef CAS.
- D. Guillaneux, S.-H. Zhao, O. Samuel, D. Rainford and H. B. Kagan, Nonlinear effects in asymmetric catalysis, J. Am. Chem. Soc., 1994, 116, 9430–9439 CrossRef CAS.
- M. Kitamura, S. Okada, S. Suga and R. Noyori, Enantioselective addition of dialkylzincs to aldehydes promoted by chiral amino alcohols. Mechanism and nonlinear effect, J. Am. Chem. Soc., 1989, 111, 4028–4036 CrossRef CAS.
- M. Kitamura, S. Suga, H. Oka and R. Noyori, Quantitative Analysis of the Chiral Amplification in the Amino Alcohol-Promoted Asymmetric Alkylation of Aldehydes with Dialkylzincs, J. Am. Chem. Soc., 1998, 120, 9800–9809 CrossRef CAS.
- M. Tsukamoto, K. Gopalaiah and H. B. Kagan, Equilibrium of Homochiral Oligomerization of a Mixture of Enantiomers. Its Relevance to Nonlinear Effects in Asymmetric Catalysis, J. Phys. Chem. B, 2008, 112, 15361–15368 CrossRef CAS.
- Y. Geiger, T. Achard, A. Maisse-François and S. Bellemin-Laponnaz, Hyperpositive nonlinear effects in asymmetric catalysis, Nat. Catal., 2020, 3, 422–426 CrossRef CAS.
- Y. Geiger, T. Achard, A. Maisse-François and S. Bellemin-Laponnaz, Observation of hyperpositive non-linear effect in catalytic asymmetric organozinc additions to aldehydes, Chirality, 2020, 32, 1250–1256 CrossRef CAS.
- R. Noyori, S. Suga, H. Oka and M. Kitamura, Self and nonself recognition of chiral catalysts: The origin of nonlinear effects in the amino-alcohol catalyzed asymmetric addition of diorganozincs to aldehydes, Chem. Rec., 2001, 1, 85–100 CrossRef CAS.
- A. Cruz, I. Irene Padilla-Martínez and M. Esther Bautista-Ramirez, N-Substituted Ephedrines as Chiral Auxiliaries in Enantioselective Alkylation Reactions of Carbonyl Compounds, Curr. Org. Synth., 2016, 13, 2–40 CrossRef CAS.
- C. Muchow, Y. Vannoorenberghe and G. Buono, Use of alkaloids and aminoalcohols in catalytic asymmetric induction:Temperature effect on the addition of diethylzinc to benzaldehyde, Tetrahedron Lett., 1987, 28, 6163–6166 CrossRef.
- P. A. Chaloner, E. Langadianou and S. A. R. Perera, Enantioselective reaction of diethylzinc with arenecarbaldehydes in the presence of ephedrine derivatives, J. Chem. Soc., Perkin Trans. 1, 1991,(0), 2731–2735 RSC.
- K. Soai, S. Yokohama and T. Hayasaka, Chiral N,N-Dialkylnorephedrines as Catalysts of the Highly Enantioselective Addition of Dialkylzincs to Aliphatic and Aromatic Aldehydes. The Asymmetric Synthesis of Secondary Aliphatic and Aromatic Alcohols of High Optical Purity, J. Org. Chem., 1991, 56, 4264–4268 CrossRef CAS.
- K. Fitzpatrick, R. Hulst and R. M. Kellogg, Thiol and disulfide derivatives of ephedra alkaloids 2: A mechanistic study of their effect on the addition of diethyl zinc to benzaldehyde, Tetrahedron: Asymmetry, 1995, 6, 1861–1864 CrossRef CAS.
- M. Sibi and M. Liu, Reversal of Stereochemistry in Enantioselective Transformations. Can they be Planned or are they Just Accidental?, Curr. Org. Chem., 2001, 5, 719–755 CrossRef CAS.
- J. Escorihuela, M. I. Burguete and S. V. Luis, New advances in dual stereocontrol for asymmetric reactions, Chem. Soc. Rev., 2013, 42, 5595–5617 RSC.
- I. P. Beletskaya, C. Nájera and M. Yus, Chem. Rev., 2018, 118, 5080–5200 CrossRef CAS.
- W. Cao, X. Feng and X. Liu, Reversal of enantioselectivity in chiral metal complex-catalyzed asymmetric reactions, Org. Biomol. Chem., 2019, 17, 6538–6550 RSC.
- The effect of catalyst concentration has been studied in one case, however it was the ligand-to-metal ratio which turned out to be the key factor to enantiodivergence there (cf.ref. 45).
- H. Du, J. Long, J. Hu, X. Li and K. Ding, 3,3′-Br2-BINOL-Zn Complex:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Highly Efficient Catalyst for the Enantioselective Hetero-Diels–Alder Reaction, Org. Lett., 2002, 4, 4349–4352 CrossRef CAS.
A Highly Efficient Catalyst for the Enantioselective Hetero-Diels–Alder Reaction, Org. Lett., 2002, 4, 4349–4352 CrossRef CAS. - H. Du, X. Zhang, Z. Wang and K. Ding, One catalyst for two distinct reactions: sequential asymmetric hetero Diels–Alder reaction and diethylzinc addition, Tetrahedron, 2005, 61, 9465–9477 CrossRef CAS.
- P. Wipf, N. Jayasuriya and S. Ribe, On the role of chiral catalysts in the alkenyl zirconocene/zinc addition to aldehydes: A study of ligand loading and asymmetric amplification, Chirality, 2003, 15, 208–212 CrossRef CAS.
- Only Kagan mentioned this briefly when discussing the general MLn model (cf.ref. 11).
- F. Buono, P. J. Walsh and D. G. Blackmond, Rationalization of Anomalous Nonlinear Effects in the Alkylation of Substituted Benzaldehydes, J. Am. Chem. Soc., 2002, 124, 13652–13653 CrossRef CAS.
- T. Rosner, P. J. Sears, W. A. Nugent and D. G. Blackmond, Kinetic Investigations of Product Inhibition in the Amino Alcohol-Catalyzed Asymmetric Alkylation of Benzaldehyde with Diethylzinc, Org. Lett., 2000, 2, 2511–2513 CrossRef CAS.
- Noble-Terán and co-workers discussed that possibility, but built their kinetic models for the two extreme cases were either only monomers or dimers catalyse, cf.ref. 39.
- K Homo in Models I and II should not be confused with Noyori's Khomo, which was defined as a dissociation constant (cf.ref. 13).
- M. Kitamura, S. Suga, M. Niwa, R. Noyori, Z.-X. Zhai and H. Suga, Enantiomer Recognition of Asymmetric Catalysts. Thermodynamic Properties of Homochiral and Heterochiral Dimers of the Methylzinc Alkoxide Formed from Dimethylzinc and Enantiomeric 3-exo-(Dimethylamino)isoborneol, J. Phys. Chem., 1994, 98, 12776–12781 CrossRef CAS.
- D. G. Blackmond, Mathematical Models of Nonlinear Effects in Asymmetric Catalysis:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) New Insights Based on the Role of Reaction Rate, J. Am. Chem. Soc., 1997, 119, 12934–12939 CrossRef CAS.
New Insights Based on the Role of Reaction Rate, J. Am. Chem. Soc., 1997, 119, 12934–12939 CrossRef CAS. - D. G. Blackmond, Kinetic aspects of non-linear effects in asymmetric synthesis, catalysis, and autocatalysis, Tetrahedron: Asymmetry, 2010, 21, 1630–1634 CrossRef CAS.
- M. E. Noble-Terán, T. Buhse, J.-M. Cruz, C. Coudret and J.-C. Micheau, Nonlinear Effects in Asymmetric Synthesis: A Practical Tool for the Discrimination between Monomer and Dimer Catalysis, ChemCatChem, 2016, 8, 1836–1845 CrossRef.
- J.-C. Micheau, T. Buhse, D. Lavabre and J. R. Islas, Kinetic understanding of asymmetric amplification in amino-alcohol catalyzed organozinc additions, Tetrahedron: Asymmetry, 2008, 19, 416–424 CrossRef CAS.
- J. Burés, A Simple Graphical Method to Determine the Order in Catalyst, Angew. Chem., Int. Ed., 2016, 55, 2028–2031 CrossRef.
- J. Burés, Variable Time Normalization Analysis: General Graphical Elucidation of Reaction Orders from Concentration Profiles, Angew. Chem., Int. Ed., 2016, 55, 16084–16087 CrossRef.
- C. D.-T. Nielsen and J. Burés, Visual kinetic analysis, Chem. Sci., 2019, 10, 348–353 RSC.
- J. Burés, What is the Order of a Reaction?, Top. Catal., 2017, 60, 631–633 CrossRef.
- A. M. Porte, J. Reibenspies and K. Burgess, Design and Optimization of New Phosphine Oxazoline Ligands via High-Throughput Catalyst Screening, J. Am. Chem. Soc., 1998, 120, 9180–9187 CrossRef CAS.
- B. Schmidt and D. Seebach, Katalytische und stöchiometrische enantioselektive Additionen von Diethylzink an Aldehyde mit Hilfe eines neuartigen chiralen Spirotitanats, Angew. Chem., 1991, 103, 100–101 CrossRef CAS.
- B. Schmidt and D. Seebach, 2,2-Dimethyl-α,α,α′,α′-tetra(naphth-2-yl)-1,3-dioxolan-4,5-dimethanol (DINOL) für die Titanat-vermittelte, enantioselektive Addition von Diethylzink an Aldehyde, Angew. Chem., 1991, 103, 1383–1385 CrossRef CAS.
- D. Seebach, D. A. Plattner, A. K. Beck, Y. M. Wang, D. Hunziker and W. Petter, On the Mechanisms of Enantioselective Reactions Using α,α,α′,α′-Tetraaryl-1,3-dioxolane-4,5-dimethanol(TADDOL)-Derived Titanates: Differences between C2- and C1-symmetrical TADDOLs – facts, implications and generalizations, Helv. Chim. Acta, 1992, 75, 2171–2209 CrossRef CAS.
- H. Danjo, M. Higuchi, M. Yada and T. Imamoto, P-stereogenic P/N hybrid ligands: a remarkable switch in enantioselectivity in palladium-catalyzed asymmetric allylation, Tetrahedron Lett., 2004, 45, 603–606 CrossRef CAS.
- Z. Shao, J. Wang, K. Ding and A. S. C. Chan, Unprecedented Effects of Additives and Ligand-to-Metal Ratio on the Enantiofacial Selection of Copper-Catalyzed Alkynylation of α-Imino Ester with Arylacetylenes, Adv. Synth. Catal., 2007, 349, 2375–2379 CrossRef CAS.
- F. Peng, Z. Shao and A. S. C. Chan, Copper(I)-catalyzed enantioselective alkynylation of α-imino esters: ligand-to-metal ratio effects and mechanistic studies, Tetrahedron: Asymmetry, 2010, 21, 465–468 CrossRef CAS.
- M. I. Burguete, M. Collado, J. Escorihuela and S. V. Luis, Efficient Chirality Switching in the Addition of Diethylzinc to Aldehydes in the Presence of Simple Chiral α-Amino Amides, Angew. Chem., Int. Ed., 2007, 46, 9002–9005 CrossRef CAS.
- J. Li, S.-S. Wang, P.-J. Xia, Q.-L. Zhao, J.-A. Xiao, H.-Y. Xiang, X.-Q. Chen and H. Yang, Unusual Ligand-to-Metal-Ratio-Controlled Bidirectional Enantioselectivity in Pd-Catalysed [3+3]-Annulation of Morita–Baylis–Hillman Acetate, Eur. J. Org. Chem., 2017, 2017, 6961–6965 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc04724d |
| This journal is © The Royal Society of Chemistry 2020 |