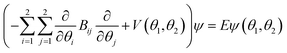Structures and internal dynamics of diphenylether and its aggregates with water†
M.
Fatima
 ab,
D.
Maué
c,
C.
Pérez
ab,
D.
Maué
c,
C.
Pérez
 ab,
D. S.
Tikhonov
ab,
D. S.
Tikhonov
 ab,
D.
Bernhard
c,
A.
Stamm
c,
C.
Medcraft‡
ab,
M.
Gerhards
ab,
D.
Bernhard
c,
A.
Stamm
c,
C.
Medcraft‡
ab,
M.
Gerhards
 *c and
M.
Schnell
*c and
M.
Schnell
 *ab
*ab
aDeutsches Elektronen-Synchrotron (DESY), Notkestr. 85, D-22607 Hamburg, Germany. E-mail: melanie.schnell@desy.de
bInstitute of Physical Chemistry, Christian-Albrechts-Universität zu Kiel, Max-Eyth-Str. 1, D-24118 Kiel, Germany
cTU Kaiserslautern, Fachbereich Chemie & Research Center Optimas, Erwin-Schroedinger-Str. 52, D-67663 Kaiserslautern, Germany. E-mail: gerhards@chemie.uni-kl.de
First published on 16th October 2020
Abstract
We report on a detailed multi-spectroscopic analysis of the structures and internal dynamics of diphenylether and its aggregates with up to three water molecules by employing molecular beam experiments. The application of stimulated Raman/UV and IR/UV double resonance methods as well as chirped-pulse Fourier transform microwave spectroscopy in combination with quantum-chemical computations yield the energetically preferred monomer and cluster geometries. Furthermore, the complex internal dynamics of the diphenylether monomer and the one-water clusters are analysed. In the cluster with three water molecules, water forms a cyclic structure similar to the isolated water trimer. The interactions ruling the structures of the higher-order water clusters are a combination of the ones identified for the two monohydrate isomers, with dispersion being a decisive contribution for systems that have a delicate energetic balance between different hydrogen-bonded arrangements of similar energy.
1. Introduction
The ability of molecules to adjust their structures according to their chemical environment can be of utmost importance for their chemical function. This ability is often represented by structural flexibility, resulting in conformational richness and/or large amplitude motions. As such, characterization of structural flexibility can be relevant when trying to understand the function of molecules, be it in chemical reactions or biological environments, for example.1–5 It is well known that structure and structural flexibility can be largely influenced by their environment, namely by interactions with other molecules. In some cases, the energy order of conformers of a specific molecule is significantly altered upon complexation with other species. For example, in the case of 15-crown-5 ether (15c5),6 when isolated in the gas phase, the 15c5 ring reduces its conformational flexibility to only two different open ring crown structures to maximize host–guest interactions. Here, already only one water molecule is able to drastically alter the conformational landscape of the 15c5 ring. The ability of 15c5 to change its overall shape by rotation around its C–C single bonds to optimize intermolecular interactions with its binding partner is a general effect observed in many molecular systems.Molecular spectroscopy techniques, complemented by quantum-chemistry computations, are ideally suited to investigate the structure, conformational flexibility, and intramolecular dynamics of molecules and molecular clusters. Employing a supersonic expansion in the gas phase provides internally cold molecules and complexes under collision-free and isolated conditions, which allows for their study independent on the environment. Interesting examples in this rich field include molecular and chirality recognition and microsolvation, among others.7–10
Recently, we studied the aggregation of diphenylether (DPE) with a series of alcohol molecules with increasing chain length and found a significant structural adjustment of the DPE to best accommodate the alcohol.11–13 In the isolated monomer, the two phenyl rings of DPE are arranged such that the two dihedral angles including the ether oxygen atom are of equal magnitude (about 40°), while they open to an almost perpendicular arrangement (90°) when complexed with the two bulky alcohols tert-butyl alcohol and adamantol. This structural rearrangement is important to explain an interesting change in binding preference of alcohols with increasing size to DPE. DPE offers two qualitatively different binding sites, the ether oxygen atom and the π clouds of the phenyl rings, which makes it a particularly interesting system to study. To date, it is still difficult to predict preferred intermolecular interaction sites. With increasing size of the side chain of the alcohol, we observe a preference towards the O binding site via hydrogen bonding. This can be explained with the geometrical opening of the DPE, which enables the alcohol to form a hydrogen bond to the ether oxygen atom and, at the same time, to generate dispersion interactions between the alcohol side chain and the phenyl rings.
Such a structural flexibility, however, can also manifest itself in rich internal dynamics, especially in systems with high symmetry. In high-resolution rotational spectroscopy, such internal motions typically result in characteristic line splittings. Their analysis allows for the determination of the corresponding tunnelling pathways and the associated barriers between equivalent forms. In the case of the isolated DPE monomer, the two phenyl rings can rotate around their respective C–O single bonds, hindered by low barriers. Indications of this have been reported before using different spectroscopic techniques, such as resonance-enhanced multi-photon ionization and NMR spectroscopy as well as quantum-chemical computations.14–21 However, once the molecule is complexed with another molecular species, internal dynamics are often not observed anymore, as in the case of DPE–CH3OH, DPE–tBuOH, DPE–adamantol, and also the DPE dimer.22 The reason is two-fold: in many cases the complexing molecules sterically hinder and thus “lock” the structure of the flexible molecule to a certain conformation, but a more general reason is that the symmetry is often broken upon complexation. Tunnelling occurs between equivalent minima. Complexation typically results in minima of different energies, i.e., it breaks the symmetry of the initial tunnelling problem.
Here, we use the double-resonance stimulated Raman methods (Ionization Gain Stimulated Raman Spectroscopy (IGSRS), Ionization Loss Stimulated Raman Spectroscopy (ILSRS)), and combined IR/UV spectroscopy as well as chirped-pulse Fourier transform microwave (CP-FTMW) spectroscopy to investigate the structure and internal dynamics of DPE and its complexes with up to three water molecules. Besides the rich tunnelling dynamics occurring in the DPE monomer, DPE–H2O is an interesting case for internal dynamics studies. Two isomers were observed for DPE–H2O: an OH–O and an OH–π bound one.12 For both isomers, characteristic tunnelling splittings are recorded in their rotational spectra, which differ qualitatively and quantitatively from each other and which will be analysed in more detail as part of this manuscript.
This manuscript is structured as follows: we first describe the experimental and computational approaches, in particular the ILSR and IGSR methods, applied for the first time to ether molecules and aggregates. We then describe the computational and spectroscopic results of the monomer, with a particular focus on structure and internal dynamics, followed by an analysis of the DPE–water clusters, including effects of dispersion interactions.
2. Experimental and computational details
2.1. Stimulated Raman spectroscopy and IR/UV methods
The Ionization Gain Stimulated Raman Spectroscopy (IGSRS) was introduced by Owyoung in 198323 for the examination of NO and was further developed by Felker,24 who also introduced the concept of the Ionization Loss Stimulated Raman Spectroscopy (ILSRS) for benzene, its dimers, and further molecules with aromatic units.25 In addition to these two groups, Ito26 and Bar27,28 performed additional improvements and applications. The stimulated Raman methods are complementary to the combined IR/UV technique cf. e.g.ref. 29–36 and offer further access (in combination with theoretical applications) to structural arrangements of isolated molecules. The class of ether molecules is investigated in this work for the first time with respect to stimulated Raman methods by using a new set-up in the Gerhards group. These investigations in combination with IR/UV and CP-FTMW spectroscopy are important to clarify structural arrangements of clusters of DPE with water.The concepts of the applied ILSR and IGSR methods are shown schematically in Fig. S1 (ESI†). A detailed description is given in the ESI.† The stimulated Raman spectra are plotted as a function of the ion signal vs. wavelength; the latter one results from the difference of νp (pump photon) and νs (Stokes photon for stimulated emission), see Fig. 3, 4, and Fig. S1 (ESI†). The experiments were performed by using tunable nanosecond laser systems. The UV laser radiation was generated via second harmonic generation in a BBO crystal using the output of a frequency-doubled dye laser (Sirah, Cobra-Stretch). The tunable dye laser was pumped by the second harmonic (532 nm) of a Nd:YAG laser (Innolas, SpitLight 600). The visible beams, required for the Raman methods, were obtained from an additional frequency doubled Nd:YAG laser (Innolas, SpitLight 1000). The output of the Nd:YAG laser was divided in a one-to-four ratio, so that 80% of the output pumped a tunable dye laser (Sirah, Precision Scan) to generate the visible, tunable Stokes beam (νs) and the 20% of the output provided as the pump photon (νp). For the IGSR and ILSR spectra, the “Stimulated Raman beams” were shifted by 30 ns prior to the UV beam. For both the IGSR and ILSR method, all beams are spatially overlapped.
The experimental spectra were recorded in a molecular beam apparatus consisting of a differentially pumped linear time-of-flight mass spectrometer (TOF-MS).33,34 The substance was brought into the carrier gases (neon or helium) via the gas flow over the sample. The supersonic molecular beam was generated by a pulsed valve (Series 9 and pulse driver Iota One, General Valve, 500 μm orifice). The DPE sample was purchased from Fluka (>99%) and used without further purification. In case of spectra of DPE/water aggregates, the carrier gas flowed both over a sample with DPE and a cooled sample with water.
2.2. Rotational spectroscopy
The rotational spectra of DPE and its water clusters were recorded with the Hamburg CP-FTMW spectrometer COMPACT in its 2–8 GHz low-frequency range. Experimental details are given elsewhere.37,38 DPE (stated purity ≥99%) was purchased from Sigma-Aldrich and used without further purification. The molecules were seeded into a supersonic expansion using a pulse nozzle (Parker General Valve, Series 9) equipped with a modified, heatable reservoir. DPE was placed into the reservoir, which is in front of the solenoid close to the valve orifice (diameter 1.1 mm), and heated to 85 °C. Neon (3 bar backing pressure) was used as a carrier gas to form a supersonic expansion into the vacuum chamber. For the observation of the water clusters, a second reservoir containing water was added upstream the neon gas line. To experimentally determine the position of the oxygen atom of the water molecules in the DPE–water complexes, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of H216O and H218O was used.
1 mixture of H216O and H218O was used.
For each gas pulse, the ensemble of molecules was polarized with a series of eight microwave chirps of 4 μs duration spanning 2–8 GHz.38 The chirps were generated with an arbitrary waveform generator (AWG), amplified by a 300 W travelling wave tube amplifier, and transmitted into the vacuum chamber with a horn antenna. Following each excitation chirp, 40 μs of the free induction decay (FID) of the macroscopic ensemble of polarized molecules were recorded, yielding a frequency resolution of 25 kHz. For the DPE monomer, a total of 6 million averages were co-added and Fourier transformed with a Kaiser–Bessel window function to give the broadband rotational spectrum in the frequency domain. For the DPE–water clusters, a total of 5 million averages were co-added and post-processed in the same way. To determine the position of the oxygen atom in the DPE–water complexes, an isotopically enriched sample of water with H218O was used, and a total of 10 million averages were co-added. All spectra were first fit to an asymmetric rotor Hamiltonian using the JB95 program.38,39 The transition frequencies were then refined using the AABS program suite, and the final asymmetric rotor Hamiltonian fits were completed with SPFIT.40,41 Line lists for all the assigned species are provided in the ESI† (Tables S16–S40).
The refinement of the r0-structure (see below) was performed in Cartesian coordinates constraining the overall C2 symmetry of DPE with soft restrictions by quantum-chemical calculations introduced via regularization42 using the UNEX software.43 The influence of the quantum-chemical parameters was calculated as given in ref. 44.
2.3. Computational details
The equilibrium structure of the DPE monomer was obtained at the B3LYP-D3(BJ)/def2-TZVP (using Gaussian 09) and SCS-MP2/def2-TZVPP levels of theory. The quantum-chemical computations to investigate the internal dynamics of the DPE monomer were performed using the Orca 4 software45 employing the def2-TZVPP basis set and the RI-JK approximation using the def2/JK basis set.46–49 A relaxed scan of the phenyl groups' internal rotation potential energy surface (PES) of DPE was obtained at the B3LYP-D3(BJ)/def2-TZVPP level50–52 with increments of 15°, and only the 42 unique points were computed. On the optimized geometries, DLPNO-CCSD(T)/def2-TZVPP53,54 single-point energies were calculated with TightPNO setting.The internal rotation levels were obtained from the solution of the 2D Schrödinger equation
The initial structures of the DPE–water clusters ((H2O)n, n = 1–3) were obtained using different procedures, including manual construction based on chemical intuition (n = 1–2) followed by MMFF94s57 force field optimizations and searches using the GFN-xTB program,58 which generates geometries by a simulated annealing conformational search (n = 3). In all cases, the obtained structures were optimized using the DFT hybrid functional B3LYP with Grimme's dispersion correction D3 and Becke–Johnson damping52 and the def2-TZVP basis set using Turbomole59,60 (for n = 1), by the application of the Berny algorithm of Gaussian 0961 using energies and gradients from Turbomole 7.0 for n = 2, and by using Gaussian 09 for n = 3. The geometries were confirmed as minimum structures by harmonic frequency calculations. Due to the neglected anharmonicity, the harmonically calculated vibrational frequencies based on DFT calculations have to be scaled. Typically, no unique scaling factor for the whole frequency range can be chosen, for the investigated spectral regions factors of 0.99 (C–O stretching region62,63) and 0.96 (CH stretching region64) are used. For DPE–H2O and DPE–(H2O)2, the harmonic frequency calculations were combined with calculated Raman activities (performed with Gaussian 09).61 These calculated Raman activities were converted to Raman intensities by the formula adapted by the work of Polavarapu and Prabavathi65,66 (cf. ESI†).
Transition states needed to describe the observed water internal motion of the OH–O isomer of the DPE complex with one water molecule were located using the nudged elastic band (NEB) method67 at the B97-3c level of theory. The energies of stationary points (equilibrium and transitions states) using the structures obtained with B97-3c68 were computed at the DLPNO-CCSD(T)/def2-TZVPP level of theory.
To guide our interpretation of the intermolecular binding contacts, we performed noncovalent interaction (NCI) analyses using NCIPLOT.69 This method assists in the interpretation of the types of intermolecular interactions present in large complexes. It investigates the electron density regions in which the reduced density gradient (RDG) vanishes at low electron densities. The RDG function is essentially a dimensionless form of the electron density gradient norm function. An NCI analysis provides useful iso-surfaces of the RDG. The sign of the second Hessian eigenvalue (λ2) of the density allows us to distinguish between different types of noncovalent interactions. The strength of the interaction can be derived from the electron density ρ in the corresponding region. To quantify the different types of interaction, symmetry adapted perturbation theory (SAPT) calculations70 were performed at the SAPT(0)/jun-cc-pVDZ and SAPT(2+3)/jun-cc-pVTZ levels of theory using the Psi4 program package.71–75 The basis set jun-cc-pVDZ corresponds to a reduced aug-cc-pVDZ basis set (without diffuse functions on hydrogen and without diffuse d functions on heavy atoms).
3. Results and discussion
3.1. The DPE monomer
The global minimum structure of DPE has C2 point group symmetry. It is highly flexible, with low barriers hindering internal rotations around the C–O single bonds. The full molecular symmetry group of DPE is G16, similar to N2H4 and N2O5.76 The redundant set of generators consists of (i) the rotation around the C2 symmetry axis (or (11′)(22′)(33′)(44′)(55′)(66′) in the notation of permutation-inversion group theory), with the symmetry axis C2 being the b-inertial axis of the molecule. This operation exchanges the two phenyl groups. (ii) Ca2 and Cb2 (or (26)(35) and (2′6′)(3′5′)) are 180° rotations of the individual phenyl groups a and b, respectively, and (iii) E* is the inversion operation. A mapping of G16(N2H4) to G16(DPE) is given in Fig. S2 (ESI†).
As mentioned, the equilibrium structure of DPE has an overall C2 symmetry with the two dihedral angles describing the arrangement of the phenyl groups being equal. Both B3LYP-D3 and DLPNO-CCSD(T) computations estimate an equilibrium angle of 40°–45°. The barrier for internal rotation within a valley is approx. 100 cm−1, whereas the energy needed to change from one valley to another is more than 1000 cm−1 (see Fig. 1(a)). As a consequence, rich internal dynamics can be expected for the DPE monomer due to anti-geared internal rotation within one valley, while torsional motion between the valleys are not expected to be feasible on the timescale and temperature of our experiment. Therefore, the full molecular symmetry group G16 can be reduced to the one that describes only the feasible motion inside a single valley. In case of DPE this group is not trivial. It consists of four elements: E, Ca2σh, Ca2Cb2, Cb2σh, where σh = E*C2. It is isomorphic to the C4 point group, which is a cyclic group and which has three irreducible representations A, B, and E (see ESI†). The μb dipole-moment component is the only non-zero component for DPE. Since it is anti-symmetric with respect to inversion, it belongs to the irreducible representation B. Each of the energy levels described by the C4 group are doubly degenerate due to the equivalent valleys. The splitting patterns and transition scheme are given in Fig. 1(b and c). The resulting tunneling splitting of the energy levels can be transferred to splittings of the experimentally observable rotational transitions, Fig. 1(e).
Due to the symmetry of the underlying PES, this shows a characteristic, equally spaced triplet splitting pattern with an expected intensity ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Note that line splittings due to large-amplitude motion scale inversely with the mass of the internally rotating moiety, resulting in comparatively small splittings for the heavy phenyl groups as internal rotors compared to lighter methyl groups, for example.
1. Note that line splittings due to large-amplitude motion scale inversely with the mass of the internally rotating moiety, resulting in comparatively small splittings for the heavy phenyl groups as internal rotors compared to lighter methyl groups, for example.
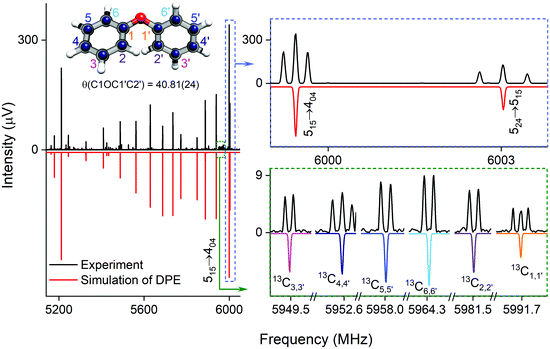 | ||
| Fig. 2 Parts of the rotational spectrum of the DPE monomer, where the zoom-ins highlight the characteristic triplet splitting pattern of DPE in both R and Q branches due to internal motions of the two phenyl groups (upper right blue box), and the triplet (C1,1′ and C4,4′) and doublet (C2,2′, C3,3′, C5,5′ and C6,6′) splitting patterns observed in the singly substituted 13C isotopologues in natural abundance due to the same motions, presented here for the J′Ka′,Kc ← JKaKc = 515 ← 404 rotational transition of DPE (lower right green box). In all spectra, the top, black trace shows the experimental spectrum, and the bottom traces give the simulated spectra based on the assigned rotational constants of DPE (red) and its 13C isotopologues (multi-color). The experimental structure of the DPE monomer (r(1)m fit, blue spheres) is also shown (top left, see also Fig. S4, ESI†), in comparison to the underlying grey structure computed at the B3LYP-D3(BJ)/def2-TZVP level of theory. | ||
As predicted (Fig. 1(e)), the rotational transitions of the DPE monomer are split due to internal motion of the two phenyl groups with respect to each other. As a two-C2 top program is not available, the components of the triplet pattern can only be fit individually using an asymmetric-rotor Hamiltonian without including large-amplitude motions (Table 1). However, the standard deviations for the low- and high-frequency tunneling components are around 90 kHz and thus significantly larger than for the centre frequency. This highlights that these two outer lines are strongly affected by the internal rotation. The signal-to-noise ratio of the spectrum was sufficient to also obtain the rotational spectra of all the six singly substituted 13C isotopologues of DPE in natural abundance. Due to the overall C2 symmetry, the isotopologue spectra have an increased intensity and are observed with about 2% of the intensity of the parent isotopologue (natural abundance of 13C is 1.1%). Note that the G16 molecular symmetry of DPE causes an interesting phenomenon. Single substitution of a 12C by a 13C atom often reduces the molecular symmetry, so that tunnelling would not occur between equivalent minima anymore. As a result, no spectral patterns for internal motion would be observed for such cases. In the case of DPE, however, we still observe tunnelling splittings for the singly substituted 13C isotopologues, which qualitatively depend on the position of the substituted atom. For the isotopologues with 13C single substitution in 1, 4, 1′ or 4′ position, we observe a similar triplet splitting pattern as for the parent isotopologue. For the 2, 3, 5, 6, 2′, 3′, 5′ or 6′ isotopologues, a doublet structure is observed. These patterns can also be explained with the group-theoretical considerations outlined above. The MS group of DPE is 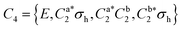 (see Fig. S3 in the ESI†), which is a subgroup of G16. We can restore this G16 group from the C4 group by adding a C2 symmetry element. The isotopic substitution in the positions 1, 4, 1′ or 4′ removes the C2 symmetry element, but since this is not contained in the C4 group in the first place, which describes the internal motion in the parent isotopologue, removal of the C2 element has no effect on the splitting pattern, and thus the same 1
(see Fig. S3 in the ESI†), which is a subgroup of G16. We can restore this G16 group from the C4 group by adding a C2 symmetry element. The isotopic substitution in the positions 1, 4, 1′ or 4′ removes the C2 symmetry element, but since this is not contained in the C4 group in the first place, which describes the internal motion in the parent isotopologue, removal of the C2 element has no effect on the splitting pattern, and thus the same 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 triplet splitting is observed for the species with 13C single substitution in 1, 4, 1′ or 4′ position as for the parent. For substitution in the other positions (2, 3, 5, 6, 2′, 3′, 5′, 6′), either the Ca2 or the Cb2 symmetry element (rotation of one of the two phenyl rings by 180°) is lost, therefore, C4 gets reduced to
1 triplet splitting is observed for the species with 13C single substitution in 1, 4, 1′ or 4′ position as for the parent. For substitution in the other positions (2, 3, 5, 6, 2′, 3′, 5′, 6′), either the Ca2 or the Cb2 symmetry element (rotation of one of the two phenyl rings by 180°) is lost, therefore, C4 gets reduced to 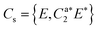 .
.
| Parameter | Low | Centre | High |
|---|---|---|---|
| a Number of fitted lines. | |||
| A (MHz) | 2361.873(27) | 2362.07003(92) | 2362.261(27) |
| B (MHz) | 437.9652(31) | 437.98867(21) | 438.0122(32) |
| C (MHz) | 412.4272(33) | 412.44316(22) | 412.4589(34) |
| Δ J (kHz) | 0.015(11) | 0.02706(77) | 0.038(11) |
| Δ JK (kHz) | 0.86(12) | 1.0058(78) | 1.14(12) |
| Δ K (kHz) | −13.7(57) | — | 12.5(58) |
| δ J (kHz) | −0.0048(17) | −0.00210(11) | 0.0007(17) |
| δ K (kHz) | −0.45(52) | 0.602(35) | 1.70(53) |
| N lines | 52 | 52 | 52 |
| σ (kHz) | 91 | 6.1 | 92 |
This symmetry reduction due to 13C substitution results in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 doublet, as observed. In Table S6 (ESI†), the fits of the rotational spectra of the singly substituted 13C isotopologues are summarized, where only the results for the centre frequencies are included. The additional sets of rotational constants allow for the determination of the positions of the individual carbon atoms with respect to the centre of mass of the molecule, thus resulting in an accurate experimental structure that can be compared with the results from quantum-chemical calculations, for example (see Fig. 2).
1 doublet, as observed. In Table S6 (ESI†), the fits of the rotational spectra of the singly substituted 13C isotopologues are summarized, where only the results for the centre frequencies are included. The additional sets of rotational constants allow for the determination of the positions of the individual carbon atoms with respect to the centre of mass of the molecule, thus resulting in an accurate experimental structure that can be compared with the results from quantum-chemical calculations, for example (see Fig. 2).
Different approaches for structure determination can be used. Kraitchman's equations provide the substitution structure, rs.77 It assumes that the structure does not change upon substitution. Least-squares fitting approaches, such as the so-called r0 and r(1)m methods,78 can also exploit multi-substitution and can account for structural changes upon substitution, which might be relevant in the case of the floppy DPE molecule. The structural parameters obtained from using the r0 approach employing least-squares fitting are summarized in Table 2 together with results from quantum-chemical calculations. The standard deviation of the r0 fit is quite high (27 kHz), which might be due to vibrational/torsional contributions due to the low-barrier motions. In order to account for such contributions, the r(1)m approach was employed, providing an improved standard deviation of the fit (17 kHz). Fig. 2 (top left) shows a comparison between the experimental carbon backbone structure (r(1)m fit, blue spheres) of the DPE monomer (left) with the structure calculated at the B3LYP-D3(BJ)/def2-TZVP level of theory (underlying grey structure), highlighting the good agreement.
| Parameter | r 0 fit | r (1)m fit | r e | r e |
|---|---|---|---|---|
| a B3LYP-D3(BJ)/def2-TZVP. b SCS-MP2/def2-TZVPP; the parameters have no measurable contribution from the regularization by the SCS-MP2/def2-TZVPP geometry. c wRMSD: weighted root-mean-square deviation of the model rotational constants from the experimental one. d Deviation of the fit (RMSD). | ||||
| B(CC) (Å) | 1.390(30) | 1.3891(28) | 1.39 | 1.395 |
| B(OC) (Å) | 1.406(35) | 1.37764(84) | 1.37 | 1.383 |
| A(CCC) (°) | 120(2) | 119.85(21) | 120 | 120 |
| A(COC) (°) | 116(3) | 119.467(99) | 120 | 117 |
| D(C1OC1′C2′) (°) | 43(2) | 40.81(29) | 40 | 44 |
| wRMSDc (kHz) | 27 | — | — | — |
| σ (kHz) | 98 | 17 | — | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 to 36
500 to 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (Fig. S4, ESI†). The spectrum exhibits an electronic origin at 35
000 cm−1 (Fig. S4, ESI†). The spectrum exhibits an electronic origin at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 cm−1 (S1 ← S0).
885 cm−1 (S1 ← S0).
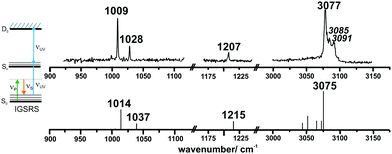
The ionization-gain stimulated Raman (IGSR) spectrum of DPE (cf.Fig. 3) is obtained by fixing the exciting UV laser at a wavenumber below the electronic origin, in this case 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 461 cm−1 is chosen. The IGSR spectrum exhibits two sharp, intense transitions at 1009 and 1028 cm−1, both corresponding to CH-bending vibrations of the phenyl rings. The fundamental of the C–O stretching mode is at 1207 cm−1.
461 cm−1 is chosen. The IGSR spectrum exhibits two sharp, intense transitions at 1009 and 1028 cm−1, both corresponding to CH-bending vibrations of the phenyl rings. The fundamental of the C–O stretching mode is at 1207 cm−1.
Both spectral regions exhibit a good agreement between experimentally observed and calculated CO stretching and the CH bending transitions. In the region above 3000 cm−1, the strong transition at 3077 cm−1 is in an excellent agreement to the calculated transition at 3075 cm−1. The listed frequencies of the DPE monomer (Tables S7 and S8, ESI†) and a comparison of the calculated frequencies to the experimental transitions are given in the ESI† (Table S9). The band around 3050 cm−1 shows no efficient Raman signal and may contribute to the experimentally observed broad background. The Raman spectra support the assignment of the DPE structure, and they are important for the further discussion of the clusters with water. Additionally, it is a proof of the stimulated Raman method with respect to ether molecules, which have not been investigated by this method before.
Interestingly, relatively strong transitions above 3077 cm−1 are observed although no vibrational transitions are theoretically predicted. A reason for these additional transitions in the IGSR spectrum of the DPE monomer can arise from fragmentation of hydrates on the mass channel of the monomer. Small traces of water can lead to formation of clusters, and a more detailed analysis of DPE–water clusters is described in the following.
3.2. The DPE–(H2O)n complexes (n = 1–3)
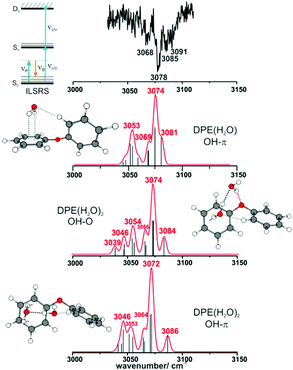
IR/R2PI spectra have been recorded for the DPE–(H2O)2 cluster in the OH stretching region (Fig. 5). The comparison of the calculated frequencies to the experimental transitions of DPE–(H2O) and DPE–(H2O)2 are given in Table S11 (ESI†). Several low-energy structures are obtained from geometry optimizations for the DPE–(H2O)2 and DPE–(H2O)3 clusters.
 | ||
Fig. 5 IR/R2PI spectrum of DPE–(H2O)2via the UV excitation energy of 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907 cm−1 using the carrier gas neon, compared to calculated vibrational frequencies for the two most stable clusters calculated at the B3LYP-D3(BJ)/def2-TZVP level. Scaling factor 0.96 (see also Fig. S9, ESI†). 907 cm−1 using the carrier gas neon, compared to calculated vibrational frequencies for the two most stable clusters calculated at the B3LYP-D3(BJ)/def2-TZVP level. Scaling factor 0.96 (see also Fig. S9, ESI†). | ||
The water molecules form a network with each other and with the DPE. In the case of DPE–(H2O)2, four structures below 4 kJ mol−1 are identified from geometry optimizations (Fig. S10, ESI†). They have clear structural similarities to the DPE–(H2O) isomers, i.e., the OH–π or the OH–O binding schemes or both are preserved. The two most stable structures obtained at the B3LYP-D3(BJ)/def2-TZVP level are included in Fig. 4 (Raman) and Fig. 5 (IR) along with their calculated and experimentally observed CH and OH stretching frequencies, respectively.
The OH–O structure consists of a water dimer bridging the ether oxygen and a phenyl ring of DPE. The π-bound water moiety gains additional stabilization from a CH⋯O contact. The OH–π structure is less stable than the OH–O arrangement by 1.5 kJ mol−1; it contains a water dimer moiety including two OH⋯π contacts for one of the water molecules, whereas the second water molecule is bound via a CH⋯O contact. The sum of the three H-bonds in the OH–O isomer (OH⋯π, OH⋯O, CH⋯O) leads to a slightly higher stabilization than the three H-bonds (two OH⋯π and one CH⋯O) of the OH–π isomer, which is also discussed in more detail below on the basis of SAPT and NCI calculations.
The comparison of the calculated and experimentally observed frequencies leads to the conclusion that both the OH⋯O and OH⋯π arrangement coexist. This assumption explains the experimentally observed Raman and IR spectra (Fig. 4 and 5) and yields an insight into the general structure of DPE with two water moieties.
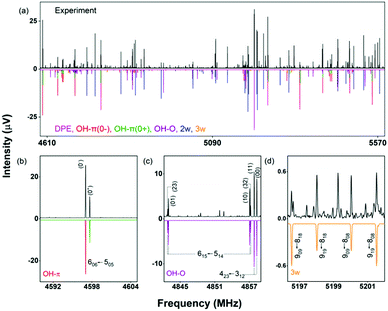
A section of the broadband rotational spectrum that we obtain when we add water in an additional reservoir is displayed in Fig. 6. The spectrum is rich, with dominant lines from the DPE monomer. Other strong lines in the spectrum belong to DPE complexed with more water molecules, such as DPE–(H2O)2 and DPE–(H2O)3. Sections b and c of Fig. 6 illustrate the line splitting caused by internal motion for the OH–O and the OH–π isomers of DPE–H2O. For OH–π, line splittings into two components (denoted as 0+ and 0−) are observed (Fig. 6b), while for OH–O, each rotational transition is split into four lines (Fig. 6c).
These different splitting patterns point to different tunneling pathways, as described below. Table 3 summarizes the results from fitting the doublet lines corresponding to the 0+ and 0− components separately to an asymmetric rotor Hamiltonian, in comparison with calculated rotational parameters for the OH–π DPE–H2O complex geometry.
| OH–π | OH–O | |||||
|---|---|---|---|---|---|---|
| State 0− | State 0+ | State 00 | State 11 | State 22 | State 33 | |
| a The theoretical rotational constants at the B3LYP-D3(BJ) level are given in the ESI. b Coriolis coupling constant. c Difference in vibrational energy between the tunnelling levels. d Number of lines included in the fit. | ||||||
| A (MHz) | 1359.68029(42) | 1362.4557(11) | 1062.18715(74) | 1062.18775(75) | 1062.2303(37) | 1062.2113(38) |
| B (MHz) | 409.24121(14) | 409.12297(45) | 433.3675(17) | 433.3673(16) | 433.4865(34) | 433.4865(34) |
| C (MHz) | 365.31297(13) | 365.43020(43) | 344.5387(17) | 344.5367(17) | 344.4217(33) | 344.4196(33) |
| Δ J (kHz) | 0.02233(85) | 0.0235(24) | — | — | 0.0127(23) | 0.0126(22) |
| Δ JK (kHz) | 0.2683(48) | 0.263(21) | 1.3776(87) | 1.291(32) | 1.3662(95) | 1.313(28) |
| F bc (MHz) | — | — | 9.1276(82) | 8.539(17) | ||
| ΔE(11)c (MHz) | — | — | 7.2508(31) | |||
| ΔE(33-22)c (MHz) | — | — | 7.4003(48) | |||
| σ (kHz) | 5.6 | 6.6 | 11.8 | |||
| N lines | 95 (y/n/y) | 78 (y/n/y) | 280 (y/y/n) | |||
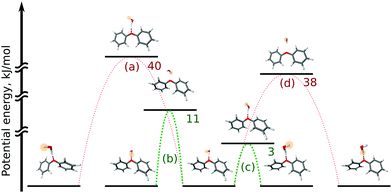
In the OH–π DPE–(H2O) cluster isomer, the water molecule can perform internal rotation around its C2 axis, which causes the characteristic tunneling splitting observed. To explain the observed splitting pattern for the OH–O DPE–(H2O) cluster, we have investigated four possible interconversion pathways between equal configurations (Fig. 8):
(a) antisymmetric internal rotation of the two phenyl groups, i.e., the motion that is causing the observed b-type tunnelling splitting in the case of the DPE monomer;
(b) water internal rotation that interchanges the positions of the protons, which can result in the observed splitting with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 intensity ratio;
3 intensity ratio;
(c) reorientation of the OH-group from one phenyl ring to the other;
(d) combination of motions (a) and (b).
Motion (a), which is the dominant one in the DPE monomer, is largely hindered by the water molecule in the OH–O DPE–(H2O) complex with a computed energy barrier of 40 kJ mol−1. The barriers for motions (b) and (c) are significantly lower (11 kJ mol−1 and 3 kJ mol−1, respectively) and are likely to be feasible on the timescale of our experiment. Motion (c) has a low barrier of 3 kJ mol−1, which is due to the fact that this interconversion pathway requires no motions of the phenyl rings, and water reorientation involves breaking of weak OH⋯π′ and O⋯(H–C)′′ interactions, that are transformed to OH⋯π′′ and O⋯(H–C)′ in the course of the tunnelling process (indexes ′ and ′′ denote first and second phenyl rings, respectively). This is associated with an inversion of the a-component (μa) of the dipole moment, which gives rise to the observed splitting in the a-type transitions with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 intensity ratio. It can thus be concluded that a combination of tunnelling pathways (b) and (c) cause the observed pattern.
1 intensity ratio. It can thus be concluded that a combination of tunnelling pathways (b) and (c) cause the observed pattern.
The difference in the observed splitting patterns of the rotational transitions for the two isomers and the tunnelling pathways can be better understood when investigating their respective intermolecular interactions. Fig. 7 summarizes the results of non-covalent interaction (NCI) calculations, which can help to visualize and characterize the different interactions present in the DPE complexes as hydrogen bonds (strong attraction, blue color), van der Waals (weak attraction, green color) and steric (strong repulsion, red color) interactions. The results are complemented with symmetry-adapted perturbation theory (SAPT) calculations using the Psi4 package, which provide the individual contributions from electrostatics, dispersion, and induction to the overall intermolecular interaction.
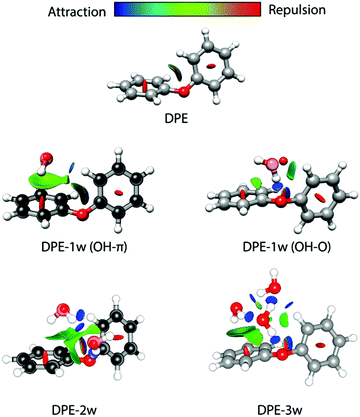 | ||
| Fig. 7 Non-covalent interaction (NCI) analysis for DPE and its experimentally observed complexes with one water (OH–π and OH–O isomers), two water (2w, OH–O structure, compare Fig. 4), and three water (3w) molecules. The structures of DPE–1w and DPE–2w are made transparent to show the experimental atom positions of carbon and oxygen determined from the r0 fit (for DPE–1w OH–π) and the rs structure (for DPE–1w OHO and DPE–2w). Blue and green colors identify the presence of hydrogen bonding (strong attraction, blue) and van der Waals interactions (weak attraction, green). Red indicates repulsive interactions. | ||
For the OH–O isomer, the NCI analysis reveals a dominant attractive interaction between one of the water hydrogen atoms with the ether oxygen, forming a strong hydrogen bond with an almost linear O–H–O angle. In addition, some weak interactions with the hydrogen atoms of the phenyl ring are revealed, resulting in a CH–O secondary interaction. For the OH–π isomer, the dominant (and compared to the OH–O form less directed) interaction of the water is with one of the two phenyl rings of the DPE, while also here a secondary interaction between the second phenyl ring and the oxygen atom of water is present. This is also resembled by the SAPT calculations (Table 4), which give a higher electrostatic contribution for the OH–O isomer with the strong hydrogen bond, while for the OH–π isomer the dispersion contribution is larger than for the OH–O isomer.
| Species | Isomer | E elec | E disp | E ind | E exch | E tot |
|---|---|---|---|---|---|---|
| DPE–H2O | OH–O | −29.8 | −12.6 | −7.6 | 30.2 | −19.9 |
| OH–π | −25.2 | −14.8 | −5.9 | 28.2 | −17.8 | |
| DPE–(H2O)2 | OH–O/isomer 1 | −54.4 | −24.9 | −15.5 | 57.6 | −37.1 |
| OH–π/isomer 2 | −38.7 | −19.2 | −13.2 | 42.0 | −29.1 | |
| OH–O/isomer 3 | −48.7 | −17.6 | −15.9 | 47.4 | −33.2 | |
| DPE–(H2O)3 | Isomer 1 | −46.3 | −27.8 | −11.9 | 50.7 | −35.3 |
| Isomer 2 | −43.4 | −27.0 | −11.3 | 47.0 | −34.3 | |
We also performed experiments with H218O instead of H216O, which allow us to determine the position of the water oxygen atom in the complex. The results of an r0 least-squares fit for the OH–π isomer are displayed on the left side of Fig. 7. The length of the hydrogen bond is determined to 2.4686(48) Å, which is indeed indicating a rather weak hydrogen bond. Interestingly, the dihedral angles in the DPE moiety change upon substitution with H2O for the OH–O isomer from equal values around 40° to 12° and 75° (Table S14, ESI†) for the two phenyl groups, respectively; DPE opens up to accommodate the water molecule on one of its phenyl rings. For the OH–π isomer, the dihedral angles for DPE remain close to the monomer values (52° and 31°, Table S14, ESI†).
3.2.2.1. Higher-order DPE–water clusters. We also observed the rotational spectra for DPE complexed with two and three water molecules, respectively (one observed isomer each). The experimental rotational constants for DPE–(H2O)2 and DPE–(H2O)3 are provided in Tables 5 and 6. For both DPE–(H2O)2 and DPE–(H2O)3, no line splittings due to internal motion of the water units or the DPE moiety are observed.
| Parameter | Theory | Experiment | ||
|---|---|---|---|---|
| Isomer 1 (OH–O) | Isomer 2 (OH–π) | Isomer 3 | ||
| A (MHz) | 865.3 | 845.0 | 681.4 | 823.80379(24) |
| B (MHz) | 390.7 | 378.1 | 403.6 | 390.51117(13) |
| C (MHz) | 338.7 | 302.2 | 289.0 | 334.18534(13) |
| Δ J (kHz) | — | — | — | 0.02964(86) |
| Δ JK (kHz) | — | — | — | 0.1766(34) |
| Δ K (kHz) | — | — | — | 0.6324(47) |
| δ j (kHz) | — | — | — | 0.00787(31) |
| μ a/μb/μc (D) | 1.5/−1.8/−1.3 | 1.2/−1.3/0.6 | −1.3/−1.9/−0.4 | — |
| μ tot (D) | 2.6 | 1.9 | 2.3 | |
| ΔE (kJ mol−1) | 0 | 1.5 | 1.9 | — |
| # lines (a/b/c) | — | — | — | 292 (y/y/y) |
| σ (kHz) | — | — | — | 9.9 |
| Parameter | Theory | Experiment | |
|---|---|---|---|
| Isomer 1 (anti-clockwise) | Isomer 2 (clockwise) | ||
| A (MHz) | 666.3 | 662.2 | 621.58779(33) |
| B (MHz) | 352.2 | 352.2 | 358.17136(13) |
| C (MHz) | 284.5 | 281.5 | 279.70640(12) |
| Δ J (kHz) | — | — | 0.02406(56) |
| Δ JK (kHz) | — | — | — |
| Δ K (kHz) | — | — | 0.331(11) |
| δ j (kHz) | — | — | 0.00814(37) |
| μ a/μb/μc (D) | 1.3/−1.7/−1.9 | −1.7/1.7/−1.6 | — |
| μ tot (D) | 2.9 | 2.9 | |
| ΔE (kJ mol−1) | 0.0 | 1.8 | — |
| # lines (a/b/c) | — | — | 190 (y/y/y) |
| σ (kHz) | — | — | 6.9 |
As described for the global minimum structure of DPE–(H2O)2, one water molecule anchors to the ether oxygen via a hydrogen bond (OH–O), thus acting as a hydrogen bond donor, while it also functions as a hydrogen bond acceptor for the second water molecule, which can result in cooperativity. This second water molecule connects to DPE via OH–π interactions similar to the OH–π one-water complex and makes another connection to DPE via a CH–O interaction (see also Fig. 7). The second low-energy DPE–(H2O)2 isomer does not have an OH–O interaction, but one water molecule binds via OH–π interactions of both protons to one of the phenyl rings, while the second water molecule is interacting via a CH–O bond to the second phenyl ring. This structure is calculated to be 1.5 kJ mol−1 higher in energy than the global minimum structure (Table 5).
The two isomers have quite similar rotational constants. While both isomers are assumed to contribute to the stimulated Raman and IR/R2PI spectra reported above (Fig. 4 and 5), only one DPE–(H2O)2 complex was observed using CP-FTMW spectroscopy. This difference might arise from different expansion conditions forming the supersonic jet in the two experiments.
A clear assignment of the experimentally observed structure to the calculated isomers 1 or 2 (OH–O and OH–π) is difficult based on the rotational constants alone, although B and C agree better with isomer 1. This, together with the fact that it is the calculated global minimum structure and that we observe all a-, b-, and c-type transitions in our experiment, supports an assignment as isomer 1 (OH–O) as the experimentally observed one. The structural assignment is further confirmed by performing a measurement with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of H216O
1 mixture of H216O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H218O. The experimental rotational constants of the 18O isotolopogues allow for the determination of the water–oxygen positions with respect to the centre of mass of the complex. The respective rs positions are included as red solid spheres in Fig. 7 and clearly agree with the OH–O isomer of DPE–(H2O)2. The dihedral angles of the phenyl groups of isomer 1 show a similar “opening up” as the OH–O DPE–1w isomer (Table S14, ESI†).
H218O. The experimental rotational constants of the 18O isotolopogues allow for the determination of the water–oxygen positions with respect to the centre of mass of the complex. The respective rs positions are included as red solid spheres in Fig. 7 and clearly agree with the OH–O isomer of DPE–(H2O)2. The dihedral angles of the phenyl groups of isomer 1 show a similar “opening up” as the OH–O DPE–1w isomer (Table S14, ESI†).
A third DPE–(H2O)2 isomer, about 1.9 kJ mol−1 higher in energy than the global minimum, consists of an OH–O bond of the first water and a CH–O bond of the second water molecule, highlighting again the importance of CH–O interactions for these kinds of systems. These interactions are also visualized using NCI analysis (Fig. S12, ESI†). The calculated rotational constants for the third isomer, however, are clearly different from the experimentally determined ones.
For the SAPT calculations of the higher-order clusters, the water dimer and trimer units were defined as one moiety, so that only the interactions between the water dimer/trimer as a whole and the DPE can be reproduced by the SAPT computations. As summarized in Table 4, the total interaction energy for isomer 1 of DPE–(H2O)2 is larger than for isomers 2 and 3. Isomer 2 is predicted here to have a lower interaction energy than isomer 3, while it was predicted to be somewhat lower in energy than isomer 3 using DFT. Such differences are likely to occur for clusters that are quite close in energy. As expected, isomers 1 and 3, which involve the OH–O hydrogen bond, have larger electrostatic contributions to the interaction energy than isomer 2. Isomer 3 has the lowest dispersion contribution because of the missing interaction with the π cloud.
For DPE–(H2O)3, geometry optimizations at the B3LYP-D3(BJ)/def2-TZVP level of theory predict ten low energy structures (including ZPE correction and BSSE) below 5 kJ mol−1. In all isomers, the water trimer adopts a cyclic structure. The first isomer with the water trimer forming a chain structure is about 5 kJ mol−1 higher in energy than the global minimum (Fig. S11, ESI†). The two lowest-energy isomers have very similar rotational constants and dipole-moment components (Table 6) and differ by about 2 kJ mol−1. It is thus not possible to unambiguously assign the experimentally observed structure to either one of these species. The three water molecules form a cyclic water network, where each water molecule is hydrogen bond donor and acceptor at the same time. This cyclic water network connects to the DPE via the known features, i.e., hydrogen bonding to the ether oxygen (OH–O), OH–π interactions to the phenyl rings of DPE, as well as CH–O interactions.
One obvious difference between the two low-energy structures is the orientation of the hydrogen bonds in the cyclic structure of the water trimer (Fig. S11 and S13, ESI†), which can either be clockwise or anti-clockwise, which is similar to our findings in the related case of diadamanthylether–(H2O)3,79 for example. A closer look reveals that this difference in the direction of the hydrogen bonds also results in a slight difference in the interactions between the water trimer moiety and the DPE for the two DPE–(H2O)3 isomers. For both structures, one water forms an OH–O bond to DPE, the second water in the network makes an OH–π interaction to one of the phenyl rings, and the third water an CH–O interaction to the other phenyl ring. Some small differences between the two isomers are revealed by the NCI analysis and the SAPT calculations: for example, for isomer 1 (anti-clockwise), there seems to be a more pronounced OH–π interaction of the second water molecule, with one of the hydrogen atoms being involved in both a hydrogen bond to the first water, and some OH–π interaction. For the clockwise arrangement in isomer 2, this is not the case.
The interaction energies between the water unit and the DPE monomer, as retrieved from SAPT calculations, are very similar for the two isomers. Overall, the total interaction energy for isomer 1 is about 1 kJ mol−1 larger than for isomer 2. This is in agreement with isomer 1 being identified as the global minimum by the DFT calculations. This larger total interaction energy arises from somewhat larger electrostatic and dispersion contributions for isomer 1, which indicate that for isomer 1 the water moiety can adjust better to the DPE unit. It should be noted, however, that the computed differences are clearly within the uncertainty of the approach.
Finally, it is interesting to note that the lowest-energy structures of DPE–(H2O)3 utilize the three different interaction types observed as low-energy structures for DPE–(H2O)2. Again, a CH–O interaction plays a decisive role.
4. Conclusions
A multi-spectroscopic and theoretical study of the DPE monomer and aggregates with up to three water molecules is presented. Structural assignments of the preferred docking motives are performed by combining CP-FTMW, stimulated Raman, IR/UV spectroscopy and theoretical analyses.The DPE monomer shows rich internal dynamics, resulting in a characteristic triplet splitting in the rotational spectrum. Using a combination of quantum-chemical computations and group theory, the corresponding tunnelling pathway can be identified as an anti-geared motion of the two phenyl rings within one valley of the potential energy surface. The stimulated Raman methods have not been applied to ether molecules before and support the assignment of the predicted DPE monomer structure. Furthermore, stimulated Raman spectra of the mono- and dihydrated clusters are obtained in the CH stretching region supplemented by IR/UV double resonance investigations in the OH stretching region. The comparison of the experimentally observed vibrational (Raman and IR) frequencies with calculated frequencies leads to the conclusion that for both the mono- and the dihydrate, the OH–O and OH–π arrangements coexist.
Broadband rotational spectroscopy on the DPE–water aggregates up to DPE–(H2O)3 provides further experimental structure information, for example by using isotopic substitution. Characteristic tunnelling splittings are observed for both isomers of the DPE–(H2O) complex, and tunnelling pathways are extracted based on group-theoretical considerations. Contrary to the stimulated Raman and IR/R2PI results, only the OH–O bound structure of the dihydrate is observed in the rotational spectrum. For the DPE–(H2O)3 cluster, the water trimer adopts a cyclic structure, where two different hydrogen-bond orientations, clockwise and anti-clockwise, are possible, with the anti-clockwise arrangement being about 2 kJ mol−1 lower in energy.
The stabilization due to London dispersion is found to be more pronounced in π-bound structures than in oxygen motifs, and the OH–O isomer has a higher electrostatic contribution, indicated by contributions extracted from both SAPT(0) calculations and an NCI analysis.
The combination of different spectroscopic and theory methods give a deeper insight in the structure and dynamics of DPE and its cluster with up to three water molecules. The small energetic balance between different types of isomers can be elucidated by our methods and emphasize the importance of dispersion interactions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Francis J. (Frank) Lovas and Fabian Dietrich for scientific discussions. Financial support in the context of the priority program SPP 1807 (Control of London dispersion interactions in molecular chemistry) of the Deutsche Forschungsgemeinschaft (DFG) (Ge 961/9-2; Schn 1280/4-2) is gratefully acknowledged. This work is part of the PhD theses of D. M. and D. B.Notes and references
- S. R. Domingos, A. Cnossen, W. J. Buma, W. R. Browne, B. L. Feringa and M. Schnell, Angew. Chem., 2017, 129, 11361–11364 CrossRef.
- S. R. Domingos, C. Pérez, C. Medcraft, P. Pinacho and M. Schnell, Phys. Chem. Chem. Phys., 2016, 18, 16682–16689 RSC.
- N. R. Pillsbury, J. A. Stearns, C. W. Müller, D. F. Plusquellic and T. S. Zwier, J. Chem. Phys., 2008, 129, 114301 CrossRef.
- A. M. Rijs, B. O. Crews, M. S. de Vries, J. S. Hannam, D. A. Leigh, M. Fanti, F. Zerbetto and W. J. Buma, Angew. Chem., Int. Ed., 2008, 47, 3174–3179 CrossRef CAS.
- R. Zhao, F. Qi, R.-Q. Zhang and M. A. van Hove, J. Phys. Chem. C, 2018, 122, 25067–25074 CrossRef CAS.
- J. C. López, C. Pérez, S. Blanco, V. A. Shubert, B. Temelso, G. C. Shields and M. Schnell, Phys. Chem. Chem. Phys., 2019, 21, 2875–2881 RSC.
- A. Zehnacker and M. A. Suhm, Angew. Chem., Int. Ed., 2008, 47, 6970–6992 CrossRef CAS.
- S. R. Domingos, C. Pérez and M. Schnell, J. Chem. Phys., 2016, 145, 161103 CrossRef.
- S. Oswald, N. A. Seifert, F. Bohle, M. Gawrilow, S. Grimme, W. Jäger, Y. Xu and M. A. Suhm, Angew. Chem., Int. Ed., 2019, 58, 5080–5084 CrossRef CAS.
- P. Pinacho, A. Krin, C. Pérez, S. Zinn, J. C. López, S. Blanco and M. Schnell, Phys. Chem. Chem. Phys., 2018, 20, 15635–15640 RSC.
- D. Bernhard, F. Dietrich, M. Fatima, C. Perez, A. Poblotzki, G. Jansen, M. A. Suhm, M. Schnell and M. Gerhards, Phys. Chem. Chem. Phys., 2017, 19, 18076–18088 RSC.
- F. Dietrich, D. Bernhard, M. Fatima, C. Pérez, M. Schnell and M. Gerhards, Angew. Chem., Int. Ed., 2018, 57, 9534–9537 CrossRef CAS.
- C. Medcraft, S. Zinn, M. Schnell, A. Poblotzki, J. Altnöder, M. Heger, M. A. Suhm, D. Bernhard, A. Stamm, F. Dietrich and M. Gerhards, Phys. Chem. Chem. Phys., 2016, 18, 25975–25983 RSC.
- A. C. S. Paiva, P. G. Kistemaker and T. L. Weeding, Int. J. Mass Spectrom., 2002, 221, 107–115 CrossRef CAS.
- K. Aimi, T. Fujiwara and S. Ando, J. Mol. Struct., 2002, 602–603, 405–416 CrossRef CAS.
- A. Almenningen, O. Bastiansen, L. Fernholt, B. N. Cyvin, S. J. Cyvin and S. Samdal, J. Mol. Struct., 1985, 128, 59–76 CrossRef CAS.
- M. Feigel, THEOCHEM, 1996, 366, 83–88 CrossRef CAS.
- M. Guerra, R. M. Pinto, J. P. Santos and A. C. S. Paiva, Mol. Phys., 2013, 111, 3311–3319 CrossRef CAS.
- C. J. Reid and J. K. Vij, J. Chem. Soc., Faraday Trans. 2, 1982, 78, 1649 RSC.
- T. Schaefer, G. H. Penner, C. Takeuchi and P. Tseki, Can. J. Chem., 1988, 66, 1647–1650 CrossRef CAS.
- T. Straßner, Can. J. Chem., 1997, 75, 1011–1022 CrossRef.
- M. Fatima, A. L. Steber, A. Poblotzki, C. Pérez, S. Zinn and M. Schnell, Angew. Chem., Int. Ed., 2019, 3108–3113 CrossRef CAS.
- P. Esherick and A. Owyoung, Chem. Phys. Lett., 1983, 103, 235–240 CrossRef CAS.
- B. F. Henson, G. V. Hartland, V. A. Venturo and P. M. Felker, J. Chem. Phys., 1989, 91, 2751–2753 CrossRef CAS.
- G. V. Hartland, B. F. Henson, V. A. Venturo, R. A. Hertz and P. M. Felker, J. Opt. Soc. Am. B, 1990, 7, 1950 CrossRef CAS.
- T. Ebata, M. Hamakado, S. Moriyama, Y. Morioka and M. Ito, Chem. Phys. Lett., 1992, 199, 33–41 CrossRef CAS.
- A. Golan, N. Mayorkas, S. Rosenwaks and I. Bar, J. Chem. Phys., 2009, 131, 24305 CrossRef.
- N. Mayorkas, H. Sachs, M. Schütz, S.-i. Ishiuchi, M. Fujii, O. Dopfer and I. Bar, Phys. Chem. Chem. Phys., 2016, 18, 1191–1201 RSC.
- R. H. Page, Y. R. Shen and Y. T. Lee, J. Chem. Phys., 1988, 88, 4621–4636 CrossRef CAS.
- C. Riehn, C. Lahmann, B. Wassermann and B. Brutschy, Chem. Phys. Lett., 1992, 197, 443–450 CrossRef CAS.
- S. Tanabe, T. Ebata, M. Fujii and N. Mikami, Chem. Phys. Lett., 1993, 215, 347–352 CrossRef CAS.
- T. S. Zwier, Annu. Rev. Phys. Chem., 1996, 47, 205–241 CrossRef CAS.
- C. Unterberg, A. Jansen and M. Gerhards, J. Chem. Phys., 2000, 113, 7945–7954 CrossRef CAS.
- M. Gerhards and C. Unterberg, Phys. Chem. Chem. Phys., 2002, 4, 1760–1765 RSC.
- W. Chin, F. Piuzzi, J.-P. Dognon, I. Dimicoli and M. Mons, J. Chem. Phys., 2005, 123, 84301 CrossRef.
- J. Mahé, D. J. Bakker, S. Jaeqx, A. M. Rijs and M.-P. Gaigeot, Phys. Chem. Chem. Phys., 2017, 19, 13778–13787 RSC.
- D. Schmitz, V. Alvin Shubert, T. Betz and M. Schnell, J. Mol. Spectrosc., 2012, 280, 77–84 CrossRef CAS.
- C. Pérez, A. Krin, A. L. Steber, J. C. López, Z. Kisiel and M. Schnell, J. Phys. Chem. Lett., 2016, 7, 154–160 CrossRef.
- D. F. Plusquellic, R. D. Suenram, B. Maté, J. O. Jensen and A. C. Samuels, J. Chem. Phys., 2001, 115, 3057–3067 CrossRef CAS.
- Z. Kisiel, L. Pszczółkowski, B. J. Drouin, C. S. Brauer, S. Yu, J. C. Pearson, I. R. Medvedev, S. Fortman and C. Neese, J. Mol. Spectrosc., 2012, 280, 134–144 CrossRef CAS.
- Z. Kisiel, L. Pszczółkowski, I. R. Medvedev, M. Winnewisser, F. C. de Lucia and E. Herbst, J. Mol. Spectrosc., 2005, 233, 231–243 CrossRef CAS.
- T. Baše, J. Holub, J. Fanfrlík, D. Hnyk, P. D. Lane, D. A. Wann, Y. V. Vishnevskiy, D. Tikhonov, C. G. Reuter and N. W. Mitzel, Chemistry, 2019, 25, 2313–2321 CrossRef.
- Y. V. Vishnevskiy, UNEX version 1.6, 2020 Search PubMed.
- D. S. Tikhonov, Y. V. Vishnevskiy, A. N. Rykov, O. E. Grikina and L. S. Khaikin, J. Mol. Struct., 2017, 1132, 20–27 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 73–78 CAS.
- S. Kossmann and F. Neese, Chem. Phys. Lett., 2009, 481, 240–243 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- D. G. Liakos and F. Neese, J. Chem. Theory Comput., 2015, 11, 4054–4063 CrossRef CAS.
- D. G. Liakos and F. Neese, J. Phys. Chem. A, 2012, 116, 4801–4816 CrossRef CAS.
- A. V. Kudich, V. A. Bataev, A. V. Abramenkov, V. I. Pupyshev and I. A. Godunov, THEOCHEM, 2003, 631, 39–51 CrossRef CAS.
- D. T. Colbert and W. H. Miller, J. Chem. Phys., 1992, 96, 1982–1991 CrossRef CAS.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519 CrossRef CAS.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS.
- s. 2. TURBOMOLE GmbH and available from http://www.turbomole.com, TURBOMOLE V7.3 2018, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Revision E.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- M. Gerhards, C. Unterberg and A. Gerlach, Phys. Chem. Chem. Phys., 2002, 4, 5563–5565 RSC.
- K. Bartl, A. Funk, K. Schwing, H. Fricke, G. Kock, H.-D. Martin and M. Gerhards, Phys. Chem. Chem. Phys., 2009, 11, 1173–1179 RSC.
- H. Fricke, K. Schwing, A. Gerlach, C. Unterberg and M. Gerhards, Phys. Chem. Chem. Phys., 2010, 12, 3511–3521 RSC.
- L. Polavarapu, J. Phys. Chem., 1990, 8106 CrossRef.
- V. Krishnak and N. Prabvathi, J. Raman Spectrosc., 2008, 679 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 64104 CrossRef.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke, M. L. Abrams, N. J. Russ, M. L. Leininger, C. L. Janssen, E. T. Seidl, W. D. Allen, H. F. Schaefer, R. A. King, E. F. Valeev, C. D. Sherrill and T. D. Crawford, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 556–565 CAS.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 3185–3197 CrossRef CAS.
- E. G. Hohenstein and C. D. Sherrill, J. Chem. Phys., 2010, 132, 184111 CrossRef.
- E. G. Hohenstein and C. D. Sherrill, J. Chem. Phys., 2010, 133, 104107 CrossRef.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 94106 CrossRef.
- J.-U. Grabow, A. M. Andrews, G. T. Fraser, K. K. Irikura, R. D. Suenram, F. J. Lovas, W. J. Lafferty and J. L. Domenech, J. Chem. Phys., 1996, 105, 7249–7262 CrossRef CAS.
- J. Kraitchman, Am. J. Phys., 1953, 21, 17–24 CrossRef CAS.
- Z. Kisiel, J. Mol. Spectrosc., 2003, 218, 58–67 CrossRef CAS.
- M. M. Quesada Moreno, P. Pinacho, C. Pérez, M. Šekutor, P. R. Schreiner and M. Schnell, Chem. – Eur. J., 2020, 26, 10817 CrossRef CAS.
- https://stash.desy.de/projects/MOLINC/repos/molinc/browse/DVR_solvers/2D_int_rot .
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04104a |
| ‡ Present address: School of Chemistry, UNSW Sydney, Sydney, New South Wales 2052, Australia. |
| This journal is © the Owner Societies 2020 |