Open Access Article
Open Access ArticleCO2 capture by Mn(I) and Re(I) complexes with a deprotonated triethanolamine ligand†
Hiroki
Koizumi
a,
Hiroyuki
Chiba
a,
Ayumi
Sugihara
b,
Munetaka
Iwamura
b,
Koichi
Nozaki
*b and
Osamu
Ishitani
 *a
*a
aDepartment of Chemistry, School of Science, Tokyo Institute of Technology, 2-12-1, NE-1 O-okayama, Meguro-ku, Tokyo 152-8550, Japan. E-mail: ishitani@chem.titech.ac.jp
bGraduate School of Science and Engineering, University of Toyama, 3190 Gofuku, Toyama 930-8555, Japan
First published on 17th January 2019
Abstract
CO2 capture at low concentration by catalysts is potentially useful for developing photocatalytic and electrocatalytic CO2 reduction systems. We investigated the CO2-capturing abilities of two complexes, fac-Mn(X2bpy)(CO)3(OCH2CH2NR2) and fac-Re(X2bpy)(CO)3(OCH2CH2NR2) (X2bpy = 4,4′-X2-2,2-bipyridine and R = –CH2CH2OH), which work as efficient catalysts for CO2 reduction. Both complexes could efficiently capture CO2 even from Ar gas containing only low concentration of CO2 such as 1% to be converted into fac-M(X2bpy)(CO)3(OC(O)OCH2CH2NR2) (M = Mn and Re). These CO2-capturing reactions proceeded reversibly and their equilibrium constants were >1000. The substituents of X2bpy strongly affected the CO2-capturing abilities of both Mn and Re complexes. The density functional theory (DFT) calculation could be used to estimate the CO2-capturing abilities of the metal complexes in the presence of triethanolamine.
Introduction
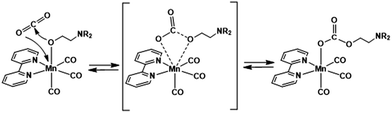
The catalytic conversion of CO2 into useful carbon resources by using sustainable energy such as sun light has attracted much attention as one of the technologies that address the issues of both global warming and the shortage of carbon-based resources. Transition metal complexes with ions such as Re(I),1 Mn(I),2 Ru(II),3 Ir(III),4 Ni(II),5,6 Fe(II),7–11 and Co(II)12,13 have been reported as catalysts for reducing CO2 to CO, formic acid, and/or methane. For example, fac-[Re(N^N)(CO)3(L)]n+ (N^N = diimine ligand and L = monodentate ligand) catalyses the selective conversion of CO2 into CO in a N,N-dimethylformamide (DMF) solution containing triethanolamine (TEOA) via photocatalytic reaction or a DMF solution containing H2O via electrocatalytic reaction.1,14fac-Mn(N^N)(CO)3Br has also been reported as an efficient CO2 reduction catalyst selectively giving CO or formic acid in electrocatalytic and photocatalytic systems, respectively.2,15–17We recently found that fac-Re(bpy)(CO)3(OCH2CH2NR2) (2Re-bpy: bpy = 2,2′-bipyridine and R = –CH2CH2OH), which has a deprotonated triethanolamine ligand, can capture a CO2 molecule even at low concentration of CO2 by CO2 insertion into the Re(I)–oxygen bond (Scheme 1).18 Since this CO2 insertion is a reversible reaction with a large equilibrium constant, more than 93% of the Re complex is converted into a CO2 adduct, i.e., fac-Re(bpy)(CO)3(OC(O)OCH2CH2NR2) (4Re-bpy), when bubbled with Ar gas containing only 10% CO2 (1.6 × 10−2 M in solution). This CO2 capture reaction by the Re(I) complex was successfully applied to photocatalytic CO2 reduction at low concentration of CO2.19 A Ru(II)–Re(I) photocatalyst consisting of a Ru photosensitiser unit and fac-Re(BL)(CO)3(OCH2CH2NR2) (BL = bridging ligand) as a catalyst unit shows almost same the photocatalytic efficiency and selectivity for CO2 reduction in an atmosphere of 10% CO2 as that in a 100% CO2 (0.13 M in solution) atmosphere. Even at 0.5% CO2 concentration, its photocatalytic efficiency was about 60% of that at 100% CO2 concentration. These results suggest that the ability of metal complex catalysts to capture CO2 using the deprotonated TEOA ligand potentially offers an effective method for reducing low-concentration CO2 atmospheres without the need for condensation.
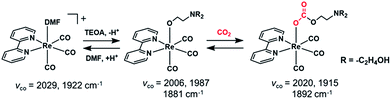 | ||
| Scheme 1 Ligand substitution and CO2 capture reactions of the Re(I) complex and the νCO values of the Re complexes. | ||
Although some similar CO2 insertion reactions into the M–OR bond of other alkoxide metal complexes, such as M = Mn(I)20,21 and Re(I)22,23 and R = –CH3 and –C2H5, have been reported,24–46 systematic and quantitative research, especially into the effects of different ligands and/or different central metal ions on the CO2 capture reactions, has not yet been reported to the best of our knowledge.
Here we report the CO2 capture abilities of Mn(I) 4,4′-X2-bpy tricarbonyl complexes, where X is any substituent of the corresponding Re(I) complexes, i.e., X = H, Br, and MeO; fac-Mn(X2bpy)(CO)3(OCH2CH2NR2) efficiently captured CO2 in the same manner as the Re(I) complexes but the corresponding W(0) bpy tricarbonyl complex did not. The abilities of the Mn(I) complexes to capture CO2 were different from those of the corresponding Re(I) complexes and the abilities of both the Mn(I) and Re(I) complexes were strongly dependent on the substituents on the diimine ligand. We successfully clarified the reasons for these dependences of the CO2 capture abilities by using density functional theory (DFT) calculations.
Results and discussion
Ligand substitution of fac-[M(X2bpy)(CO)3(MeCN)]+ in a DMF–TEOA mixed solution
As a typical example, fac-[Mn(bpy)(CO)3(MeCN)]+ (5.0 mM) was added to an Ar-saturated DMF solution containing TEOA (1.3 M), and the changes in the vibrational bands of the CO ligands (νCO) were followed by FT-IR. In Fig. 1, the peaks at νCO = 2046 and 1970 cm−1 were attributed to the starting complex and their intensity gradually decreased and new absorption bands appeared over time. After 30 min, there were no more changes in the IR spectrum and the main bands were observed at νCO = 2040, 1943, and 1936 cm−1, which are attributed to fac-[Mn(bpy)(CO)3(DMF)]+ (1Mn-bpy) based on the similarity of the highest wavenumber peaks to those of the starting complex in the case of the Re(I) complex.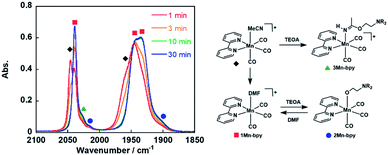 | ||
Fig. 1 Changes in the IR spectra of fac-[Mn(bpy)(CO)3(MeCN)]+ ( , 5.0 mM) in a DMF solution containing TEOA (1.3 M) under an Ar atmosphere over 30 min: , 5.0 mM) in a DMF solution containing TEOA (1.3 M) under an Ar atmosphere over 30 min:  , 1-Mnbpy; , 1-Mnbpy;  , 2-Mnbpy; , 2-Mnbpy;  , 3-Mnbpy. , 3-Mnbpy. | ||
Some shoulder peaks were also observed at νCO = 2020 and 1900 cm−1. Fig. 2a shows the IR spectra measured several hours after dissolving the same complex into DMF solutions containing different concentrations of TEOA. At higher concentration of TEOA, the intensity of the peaks at νCO = 2020 and 1900 cm−1 increased. We focussed on the totally symmetric vibrational bands around 2050–2010 cm−1 for understanding how many complexes were produced in the DMF–TEOA mixed solution. We could not reasonably fit these spectra by using curve-fitting with two components, but by using three components, we were able to identify three bands at νCO = 2040, 2030, and 2017 cm−1 (Fig. S1†). The peak at νCO = 2040 cm−1 was attributed to 1Mn-bpy. The peak at νCO = 2017 cm−1 can be attributed to fac-Mn(bpy)(CO)3(OCH2CH2NR2) (2Mn-bpy) because it became larger with increased TEOA concentration (Fig. 2a). The difference in the IR bands of 2Mn-bpy and 1Mn-bpy (Δν = 22 cm−1) was very similar to the difference between fac-Re(bpy)(CO)3(OCH2CH2NR2) and fac-[Re(bpy)(CO)3(DMF)]+ (Δν = 23 cm−1, Scheme 1). This kind of shift to a lower energy of νCO could be caused by an increase in π back donation from the Mn centre to the CO ligand because of the anionic alkoxide ligand instead of the neutral DMF. Fig. 2b shows the relationship between the peak area ratio of these complexes and the concentration of TEOA. The ratio of 1Mn-bpy decreased with increasing TEOA concentration; however, 2Mn-bpy showed a reverse correlation. From these results, it was concluded that 1Mn-bpy and 2Mn-bpy should be in equilibrium with each other in DMF–TEOA. On the other hand, the small peak at νCO = 2030 cm−1 did not strongly depend on the TEOA concentration. This was probably due to a Mn(I) complex with an imidate ester ligand, i.e., fac-[Mn(bpy)(CO)3(–NH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)–OCH2CH2NR2)]+ (3Mn-bpy), which is produced by the addition of deprotonated TEOA to the MeCN ligand (Fig. 1, right scheme). The difference in the totally symmetric vibrational band from fac-[Mn(bpy)(CO)3(MeCN)]+ was ΔνCO = 16 cm−1, and a similar peak shift was observed when fac-[Mn(bpy)(CO)3(MeCN)]+ was dissolved in a MeCN-TEOA (5
C(CH3)–OCH2CH2NR2)]+ (3Mn-bpy), which is produced by the addition of deprotonated TEOA to the MeCN ligand (Fig. 1, right scheme). The difference in the totally symmetric vibrational band from fac-[Mn(bpy)(CO)3(MeCN)]+ was ΔνCO = 16 cm−1, and a similar peak shift was observed when fac-[Mn(bpy)(CO)3(MeCN)]+ was dissolved in a MeCN-TEOA (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) solution (ΔνCO = 14 cm−1, Fig. S2†). This identification is also supported by the fact that the difference in νCO between fac-[Re(bpy)(CO)3(MeCN)]+ and fac-[Re(bpy)(CO)3(–NH
1, v/v) solution (ΔνCO = 14 cm−1, Fig. S2†). This identification is also supported by the fact that the difference in νCO between fac-[Re(bpy)(CO)3(MeCN)]+ and fac-[Re(bpy)(CO)3(–NH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)–OCH2CH2NR2)]+ was ΔνCO = 13 cm−1. This reaction was much slower in the case of the Mn(I) complex than that of the corresponding Re(I) complex. To further clarify the identity of this minor product, the following experiment was performed. fac-[Mn(bpy)(CO)3(MeCN)]+ was dissolved in a DMF solution containing 1.3 M TEOA. After 60 min, additional TEOA or DMF was added to this solution, i.e., the concentration of TEOA in the solution was changed from 1.3 to 3.9 or 0.65 M. The changes in the concentration of the solvent did not affect the concentration of the minor product in either case (Fig. S2†). This suggests that the minor product was 3Mn-bpy, which was only produced by the reaction between fac-[Mn(bpy)(CO)3(MeCN)]+ and TEOA, was stable in the solution. In other words, the presence of 3Mn-bpy in the solution should not affect the equilibrium between 1Mn-bpy and 2Mn-bpy. Therefore, in the following discussion, we consider only the equilibrium between the DMF and TEOA complexes.
C(CH3)–OCH2CH2NR2)]+ was ΔνCO = 13 cm−1. This reaction was much slower in the case of the Mn(I) complex than that of the corresponding Re(I) complex. To further clarify the identity of this minor product, the following experiment was performed. fac-[Mn(bpy)(CO)3(MeCN)]+ was dissolved in a DMF solution containing 1.3 M TEOA. After 60 min, additional TEOA or DMF was added to this solution, i.e., the concentration of TEOA in the solution was changed from 1.3 to 3.9 or 0.65 M. The changes in the concentration of the solvent did not affect the concentration of the minor product in either case (Fig. S2†). This suggests that the minor product was 3Mn-bpy, which was only produced by the reaction between fac-[Mn(bpy)(CO)3(MeCN)]+ and TEOA, was stable in the solution. In other words, the presence of 3Mn-bpy in the solution should not affect the equilibrium between 1Mn-bpy and 2Mn-bpy. Therefore, in the following discussion, we consider only the equilibrium between the DMF and TEOA complexes.
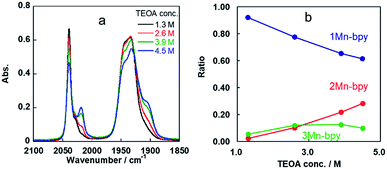 | ||
| Fig. 2 (a) IR spectra of fac-[Mn(bpy)(CO)3(MeCN)]+ in DMF solutions containing different concentrations of TEOA (1.3 M, black line; 2.6 M, red line; 3.9 M, green line; 4.5 M, blue line). (b) Ratios of 1Mn-bpy (blue), 2Mn-bpy (red) and 3Mn-bpy (green) obtained by curve-fitting of the IR spectra between 2000 and 2060 cm−1 (Fig. S1†). | ||
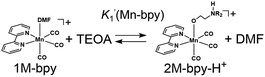
There are two possible equilibrium equations (eqn (1) and (3)) for the conversion of 1Mn-bpy into 2Mn-bpy. In the mechanism described in eqn (3), one TEOA molecule works as both a nucleophile and a base. In the case of eqn (1), two TEOA molecules contribute to the ligand substitution reaction, where proton capture from the TEOA interacting with the metal centre by the other TEOA molecule is considered. In this ligand substitution, the main mechanism is probably described in eqn (1) because the solution contained a very high concentration of TEOA (>1.3 M). Therefore, we chose eqn (1) for the DFT calculation as described below.‡
In eqn (2), the concentration of the protonated TEOA ([H–TEOA+]) was assumed to be the same as that of 2Mn-bpy because the proton that originated in the TEOA ligand should be captured by another TEOA molecule as described above. The concentrations of the Mn(I) complexes were calculated by curve-fitting of the IR spectra and were used to determine the equilibrium constant, i.e., K1(Mn-bpy) = (0.22 ± 0.03) × 10−3, by using eqn (2).
 | (1) |
 | (2) |
 | (3) |
When the Mn complexes with substituents at the 4,4′-position of the bpy ligand, i.e., fac-[Mn(X2bpy)(CO)3(MeCN)]+ (X = Br and OMe), were dissolved in the DMF–TEOA mixed solution, similar IR spectral changes were observed in both cases (Fig. S4†). However, the equilibrium constants were very different from K1(Mn-bpy). Electron-withdrawing substituents gave a larger constant, i.e., K1(Mn-Br2bpy) = (0.64 ± 0.03) × 10−3. On the other hand, electron-donating substituents gave a smaller constant, i.e., K1(Mn-(MeO)2bpy) = (0.12 ± 0.01) × 10−3. These results strongly suggest that stronger electron-withdrawing substituents on the X2bpy ligand give rise to higher stability of 2-Mn-X2bpy.
In the case of the corresponding Re(I) complex, fac-[Re(X2bpy)(CO)3(MeCN)]+ was converted into fac-[Re(X2bpy)(CO)3(DMF)]+ (1Re-X2bpy) by first dissolving in DMF § and then into fac-Re(X2bpy)(CO)3(OCH2CH2NR2) (2Re-X2bpy) by the addition of TEOA to the solution because this procedure could suppress the formation of [Re(bpy)(CO)3(–NH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)–OCH2CH2NR2)]+ (3Re-bpy).18¶ The equilibrium constants between 1Re-X2bpy and 2Re-X2bpy are summarised in Table 2. The values of K1(Re-X2bpy) are consistent with those of the corresponding Mn complexes as described above, i.e., the electron-withdrawing substituents on the X2bpy ligand yielded a larger equilibrium constant. The equilibrium constant of the Re complexes was much larger than that of the corresponding Mn complexes, for example, K1(Re-bpy) = (71 ± 1) × 10−3 and K1(Mn-bpy) = (0.64 ± 0.03) × 10−3, that is, the formation of 2Mn-X2bpy was thermodynamically less favourable compared to that of the corresponding Re(I) complex in the DMF–TEOA mixed solution.
C(CH3)–OCH2CH2NR2)]+ (3Re-bpy).18¶ The equilibrium constants between 1Re-X2bpy and 2Re-X2bpy are summarised in Table 2. The values of K1(Re-X2bpy) are consistent with those of the corresponding Mn complexes as described above, i.e., the electron-withdrawing substituents on the X2bpy ligand yielded a larger equilibrium constant. The equilibrium constant of the Re complexes was much larger than that of the corresponding Mn complexes, for example, K1(Re-bpy) = (71 ± 1) × 10−3 and K1(Mn-bpy) = (0.64 ± 0.03) × 10−3, that is, the formation of 2Mn-X2bpy was thermodynamically less favourable compared to that of the corresponding Re(I) complex in the DMF–TEOA mixed solution.
CO2 capture by fac-M(X2bpy)(CO)3(OCH2CH2NR2)
Introduction of CO2 into the DMF–TEOA solution containing the equilibrium mixture of 1Mn-bpy and 2Mn-bpy caused rapid disappearance of the νCO bands attributed to 1Mn-bpy and 2Mn-bpy and the appearance of three new νCO bands at 2028, 1936, and 1913 cm−1 (Fig. 3a). When this CO2-saturated solution was bubbled with Ar for 30 min, the original νCO bands of 1Mn-bpy and 2Mn-bpy were fully recovered (Fig. S5†). These IR spectral changes are very similar to those of the corresponding Re(I) complexes, where both 1Re-bpy and 2Re-bpy were converted into the CO2 adduct complex fac-Re(bpy)(CO)3(OC(O)OCH2CH2NR2) (4Re-bpy) upon bubbling with CO2.18 These results strongly suggest that CO2 capture by the Mn(I) complex proceeded well and that the reaction was reversible. Identification of the CO2 adduct was confirmed by 1H and 13C NMR experiments in a DMSO-d6 solution containing TEOA.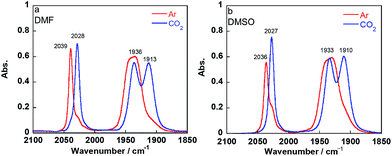 | ||
| Fig. 3 IR spectra of the equilibrated mixture of 1Mn-bpy and 2Mn-bpy in DMF (a) or DMSO (b) containing TEOA (1.3 M) after Ar bubbling (red line) and CO2 bubbling (blue line) for 15 min. | ||
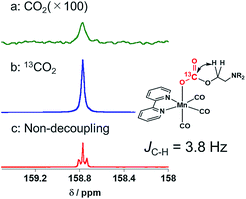
DMF-d7 was not used because the signal of a carbonate carbon (M–OC(O)O–R) is expected to be observed at a similar magnetic field to that of the amide carbon of DMF. We confirmed that even in a DMSO–TEOA mixed solution, similar IR spectral changes occurred to those in the DMF–TEOA solution (Fig. 3b). The 1H NMR spectra of the solution containing the Mn complexes were first measured under an Ar atmosphere and then measured again after bubbling with CO2 for 3 min (Fig. S6†). The 1H NMR signals attributed to the bpy ligands changed completely before and after bubbling with CO2; the proton peaks attributed to the bpy ligands of 1Mn-bpy and 2Mn-bpy, which were observed under an Ar atmosphere, disappeared and four new proton signals were observed at a higher magnetic field under a CO2 atmosphere. Fig. 4a shows the 13C NMR spectrum with proton decoupling; a singlet peak attributable to the carbonate carbon (M–OC(O)O–R) at 158.7 ppm was observed under the CO2 atmosphere. This signal was drastically enhanced by using 13CO2 (99% 13C content) instead of CO2 (Fig. 4b). Without proton decoupling, the signal at 158.7 ppm became a triplet with JC–H = 3.8 Hz (Fig. 4c). This is attributable to long-range coupling with the methylene group in the deprotonated TEOA moiety of the carbonate ester ligand (Fig. 4) because a similar signal was reported in the 13C NMR spectrum of 3Re-bpy (158.4 ppm, 3.6 Hz).18 These results strongly suggest that the insertion reaction of CO2 into the Mn–O bond in 2Mn-bpy gives the complex fac-[Mn(bpy)(CO)3(OC(O)OCH2CH2NR2)] (4Mn-bpy) (eqn (5)).
As shown in Fig. 5a, the ratios of the peaks changed with the CO2 concentration in the solution. We successfully conducted curve-fitting to obtain the concentrations of 1Mn-bpy, 2Mn-bpy and 4Mn-bpy as shown in Fig. 5b. Direct determination of K2(Mn-bpy) from the peak area of 2Mn-bpy showed a large experimental error because the peak of 2Mn-bpy was very small. Therefore, K2(Mn-bpy) was calculated by using eqn (7) with K1(Mn-bpy) and K3(Mn-bpy), which is the equilibrium constant between 1Mn-bpy and 4Mn-bpy (eqn (6) and (7)). In eqn (7), the concentration of the protonated TEOA ([H–TEOA+]) was assumed to be the same as the total concentrations of 2Mn-bpy and 4Mn-bpy because of the same reason in the case of eqn (2). This calculation method gave much lower experimental error; the value of K2(Mn-bpy) between 2Mn-bpy and 4Mn-bpy was obtained to be (61 ± 12) × 103 M−1.
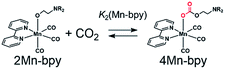 | (4) |
 | (5) |
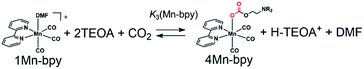 | (6) |
 | (7) |
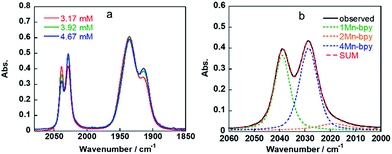 | ||
| Fig. 5 IR spectra of fac-[Mn(bpy)(CO)3(MeCN)]+ in DMF containing 1.3 M TEOA and different concentrations of CO2 (a) and the curve-fitting result for the observed spectra at 3.17 mM CO2 (b). | ||
The other Mn(I) complexes with the substituted bpy ligand also showed similar IR spectral changes during a similar experiment in the DMF–TEOA mixed solution (Fig. S7†). Therefore, these complexes also have the ability to capture CO2. The equilibrium constants are summarised in Table 1. It is noteworthy that the values of K2(Mn-X2bpy) are not drastically different from those of K1(Mn-X2bpy) of the three Mn complexes. The CO2 insertion between the Mn–O bond might be a concerted reaction between the nucleophilic attack of the oxygen atom in the ligand to the carbon in CO2 and the electrophilic attack of the central metal to the oxygen atom in CO2 (Scheme 2).22,31,47 Since a higher electronic density of the central metal should induce acceleration of the former process while obstructing the latter one, these conflicting effects might cancel each other out.
| Complex | K 1/10−3 | K 2/103 M−1 | K 3/M−1 | |
|---|---|---|---|---|
| Metal | X | |||
| Mn(I) | H | 0.22 ± 0.03 | 61 ± 12 | 14 ± 1 |
| Br | 0.64 ± 0.03 | 42 ± 8 | 27 ± 4 | |
| MeO | 0.12 ± 0.01 | 84 ± 15 | 10 ± 1 | |
All of the three 2Re-X2bpy complexes also efficiently captured CO2 even from gases containing low concentrations of CO2 (eqn (5)). The equilibrium constants for K2(Re-X2bpy) are summarised in Table 2. K2(Re-Br2bpy) was the largest of the three Re(I) complexes, while the difference between K2(Re-bpy) and K2(Re-(MeO)2bpy) was small.
| Complex | K 1/10−3 | K 2/103 M−1 | K 3/M−1 | |
|---|---|---|---|---|
| Metal | X | |||
| Re(I) | H | 71 ± 1 | 1.2 ± 0.2 | 88 ± 13 |
| Br | 128 ± 8 | 1.4 ± 0.1 | 179 ± 21 | |
| MeO | 30 ± 2 | 2.6 ± 0.1 | 79 ± 10 | |
Comparison of the CO2-capturing abilities of the Mn(I), Re(I) and W(0) complexes
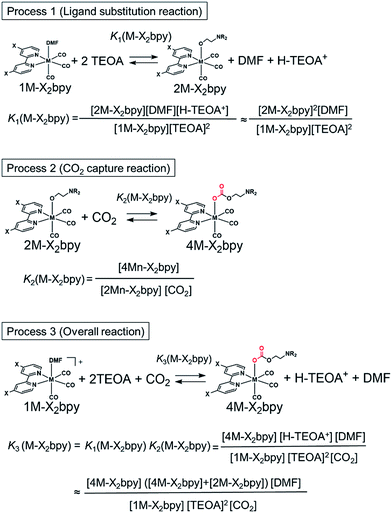
As described in the previous section, both series of the Mn(I) and Re(I) complexes have high CO2-capturing abilities (Scheme 3). The CO2 insertion reactions into 2Mn-X2bpy were more favourable than those into 2Re-X2bpy, equilibrium constants of which are defined as K2(M-X2bpy) (M = Mn and Re) (Process 2). However, the CO2-capturing ability of 1Mn-X2bpy in the presence of TEOA was lower than that of 1Re-X2bpy, and the equilibrium constants are defined as K3(M-X2bpy) (Process 3). This is because the formation of the TEOA adducts (2Mn-X2bpy and 2Re-X2bpy), i.e., Process 1, is much more favourable in the case of the Re complexes, the equilibrium constants of which are K1(M-X2bpy).
1Re-Br2bpy as the starting complex most efficiently captured CO2 from gases containing low concentrations of CO2 in DMF including 1.3 M TEOA where the volume ratio between DMF and TEOA is 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; bubbling air containing only 400 ppm of CO2 (1.7 × 10−4 M in solution) into the DMF–TEOA mixed solution containing 1Re-Br2bpy and 2Re-Br2bpy converted 31% of the Re complexes into the corresponding CO2 adduct, i.e., 4Re-Br2bpy. This conversion ratio increased by changing the solvent to DMSO. In a DMSO solution containing 1.3 M TEOA, 4Re-Br2bpy formed at a 47% ratio under air.
1; bubbling air containing only 400 ppm of CO2 (1.7 × 10−4 M in solution) into the DMF–TEOA mixed solution containing 1Re-Br2bpy and 2Re-Br2bpy converted 31% of the Re complexes into the corresponding CO2 adduct, i.e., 4Re-Br2bpy. This conversion ratio increased by changing the solvent to DMSO. In a DMSO solution containing 1.3 M TEOA, 4Re-Br2bpy formed at a 47% ratio under air.
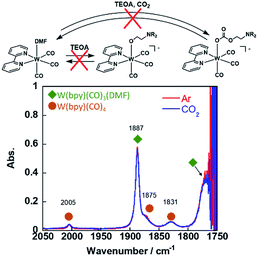
Since the W(0) complex with a structure similar to that of the Re(I) and Mn(I) complexes has been reported, we checked the ligand substitution and CO2-capturing ability of fac-W(bpy)(CO)3(MeCN). This complex was synthesised by dissolving W(bpy)(CO)4 into an MeCN solution, which was refluxed under an Ar atmosphere overnight. Evaporation of the solvent gave fac-W(bpy)(CO)3(MeCN) as a brown solid containing a small amount of W(bpy)(CO)4. Since fac-W(bpy)(CO)3(MeCN) was air-sensitive and W(bpy)(CO)4 did not affect the following experiments, we used this solid.||
The FT-IR spectrum of fac-W(bpy)(CO)3(MeCN) in an MeCN solution showed carbonyl vibration bands at νCO = 1898 and 1782 cm−1 (Fig. S8†), which are consistent with a previous report.48 This complex was dissolved in a DMF solution, and a CO vibration band at νCO = 1887 cm−1 attributable to fac-W(bpy)(CO)3(DMF) was observed (Fig. S9†). The other νCO bands overlapped with the carbonyl vibrational band of the DMF solvent and small absorption bands at νCO = 2005, 1875, and 1831 cm−1 were attributed to fac-W(bpy)(CO)4, which had the same wavelength and strength as those observed in the MeCN solution (Fig. 6). Addition of TEOA into the DMF solution containing W(bpy)(CO)3(DMF) did not affect the νCO band at all under an Ar atmosphere. In addition, the CO vibration of fac-W(bpy)(CO)3(DMF) in the IR spectra did not change after bubbling CO2 through this solution (Fig. 6). These results clearly indicate that fac-[W(bpy)(CO)3(OCH2CH2NR2)]− did not form from fac-W(bpy)(CO)3(DMF) even in the presence of 1.3 M TEOA, and the CO2-capturing reaction also did not proceed under these reaction conditions (refer the equation in Fig. 6).
Gibbs free energy change and DFT calculation
The Gibbs free energy (Gf) changes in Processes 1–3 were calculated by using the equilibrium constants (K1, K2, and K3) and are summarised in Table 3 (values in parentheses).| Metal | X | ΔG0/kJ mol−1 | ||
|---|---|---|---|---|
| Process 1 | Process 2 | Process 3 | ||
a Values in parentheses denote the experimental values calculated using ΔG0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K using T = 298 K and K1, K2 and K3. K using T = 298 K and K1, K2 and K3.
|
||||
| Mn(I) | H | 10.1 | −15.3 | −5.2 |
| (20.9) | (−27.3) | (−6.4) | ||
| Br | 8.9 | −15.0 | −6.1 | |
| (18.2) | (−26.4) | (−8.2) | ||
| OMe | 10.5 | −10.3 | +0.2 | |
| (22.4) | (−28.1) | (−5.7) | ||
| Re(I) | H | −8.0 | −2.6 | −10.6 |
| (6.55) | (−17.6) | (−11.1) | ||
| Br | 7.8 | −25.6 | −17.8 | |
| (5.09) | (−18.0) | (−12.9) | ||
| OMe | 11.2 | −16.7 | −5.5 | |
| (8.67) | (−19.5) | (−10.8) | ||
| W(0) | H | 21.8 | −9.0 | 12.8 |
The observed abilities of the metal tricarbonyl complexes in the CO2-capturing reactions involving TEOA were examined based on the DFT calculations. Selected geometrical parameters calculated at the def2-SVP/PBE1PBE level including solvent effects are depicted in Table S2.† All of the Mn–N(bpy) and Mn–C(CO) bond lengths were calculated for 1Mn-bpy, 2Mn-bpy and 4Mn-bpy with the singlet spin state and were in good agreement with those of the X-ray structure determined for fac-Mn(CO)3(bpy)I,49 supporting the accuracy of the DFT calculation. The geometrical optimisation of 1Re-bpy, 2Re-bpy and 4Re-bpy also gave molecular structures with geometrical parameters similar to those of the X-ray structure of fac-Re(CO)3(bpy)OC5H11.23
The CO stretching vibrational frequencies of the tricarbonyl complexes were calculated for the DFT-optimised structures and were corrected using the reported scaling factor (Tables S3 and S5†).50 While all of the calculated νCO values were slightly higher than the observed ones, the differences in νCO are almost constant for each series of the tricarbonyl complex: 31–50 cm−1 for Mn(I) complexes and 16–23 cm−1 for Re(I) complexes. The constant deviation in the calculated νCO supports the experimental identification of the species involved in the CO2-capturing reactions.
The changes in Gibbs free energy (ΔG0) of each process for the Mn(I) and Re(I) complexes were then calculated based on the DFT calculations (Table 3). For the overall reaction (Process 3), these calculated ΔG0 values are in good agreement with those obtained by the experiments with an error of 5 kJ mol−1 (∼1 kcal mol−1).
For CO2 capture by the Mn complexes, the calculated ΔG0 for reaction 1 is about 9–14 kJ mol−1 lower than the observed value, while those for Process 2 are 13–17 kJ mol−1 higher. This trend is also seen in the Re complexes even though the differences are smaller compared to those of the Mn complexes. These results are probably caused by an overestimation of the free energy of formation for the M–TEOA complexes (2M-X2bpy). The TEOA moiety with three ethanol groups has several conformation isomers. The geometrical optimisation of 2Mn-X2bpy and 4Mn-X2bpy gave somewhat compact structures due to intramolecular hydrogen bonding between the metal-coordinating O atom and the two remaining OH groups in the TEOA moiety.
The lengths of the hydrogen bonds in 4Mn-X2bpy are around 1.76–1.81 Å. On the other hand, in the case of 2Mn-X2bpy, the hydrogen bonds between the anionic O atom, which is attached to the metal ion, and the OH groups are considerably short (1.50–1.59 Å) (Fig. S10†). The same effects were observed in the Re complexes as well. Such strong intramolecular hydrogen bonding in 2M-X2bpy is one of the reasons for the overestimation of their stabilisation energies because, in the DMF–TEOA mixed solution, intermolecular hydrogen bonds with other TEOA molecules could break such a compact conformation and several other stable conformations would be formed. A more accurate prediction of ΔG0 for the CO2 insertion reaction therefore requires the evaluation of the TEOA conformational distribution including explicit interactions with other TEOA molecules. It should be noted that this uncertainty should not affect the ΔG0 values of Process 3 because 2Mn-X2bpy and 2Re-X2bpy do not contribute to this process as shown in the equation for determining K3 (Scheme 3). In other words, the errors based on the overestimation of the stabilisation energy of 2Mn-X2bpy and 2Re-X2bpy can be cancelled between Processes 1 and 2.
As described in the previous section, there are two possible equilibrium equations [eqn (1) and (3)] for the ligand substitution of DMF by TEOA. However, in solutions containing high concentration of TEOA (1.3 M), the reaction with one TEOA molecule acting as both a nucleophile and a base is considered unfavourable. The DFT calculation also supports this consideration because the observed vCO values (1902, 1918 and 2017 cm−1) are close to those calculated for 2M-bpy rather than for 2M-bpy-H+ (see Tables S3 and S4†). In addition, the calculated ΔG0 corresponding to eqn (3) (14.5 kJ mol−1) is higher than the ΔG0 value for Process 1 (10.1 kJ mol−1), which also indicates the favourability of eqn (1).
For the CO2-capturing reaction of the corresponding W(CO)3(bpy)X species, the ΔG0 values for Processes 1, 2, and 3 are calculated to be +21.8, −9.0, and +12.8 kJ mol−1, respectively. The calculated large positive ΔG0 value of Process 3 is consistent with the results showing that the W(0) complex was less reactive for the CO2-capturing reaction in the presence of TEOA compared to the Re(I) and Mn(I) complexes.
As shown for the three series of metal complexes consisting of different metal ions and different ligands, DFT was able to calculate the ΔG0 values for the overall CO2-capturing reaction (Process 3) with good accuracy (∼5 kJ mol−1). We can use this method for estimating the CO2-capturing abilities of other metal complexes and to examine the mechanism of CO2-capturing reactions.
Experimental section
General procedures
FT-IR spectra were measured using a JASCO FT/IR-610 or 6600 spectrometer at 1 cm−1 resolution. 1H NMR and 13C NMR spectra were measured in acetonitrile-d3, DMF-d7 or DMSO-d6 using a JEOL ECA400-II at 400 and 100 MHz, respectively. Electrospray ionisation mass spectroscopy (ESI-MS) was performed using a Shimadzu LCMS-2010A system with acetonitrile as the mobile phase.Materials
DMF was distilled under reduced pressure after pre-drying using activated molecular sieves of 4 Å and stored under Ar in a glove box. TEOA was distilled under reduced pressure and stored under Ar in a glove box. DMSO was distilled under reduced pressure after pre-drying overnight with CaH2 under Ar. Acetonitrile was distilled three times over P2O5 and distilled again by CaH2 before use. All other reagents of reagent-grade quality were used without further purification.Calculation of equilibrium constants
Preparation procedures of the solutions for the measurements were performed in a glove box (UNICO, UN-650F) with a gas circulation dehydration device (DGE-05) under Ar (water content was less than 376 ppm). Concentrations of the complexes in solutions were obtained by the peak areas of νCO at the highest wavenumber (2000–2060 cm−1) in the IR spectra. The peak areas attributed to each complex were obtained by curve-fitting using a linear combination of the Gaussian and the Lorentzian functions.18,19Ligand substitution reaction
The Mn(I) and W(0) diimine tricarbonyl acetonitrile complexes were dissolved in DMF solutions containing different concentrations of TEOA. The solutions were kept at room temperature in the dark for several hours and then their IR spectra were measured. In the case of the Re(I) complexes, the complexes with an acetonitrile ligand were dissolved in DMF to avoid the formation of 3Re-X2bpy. The solutions were kept at room temperature in the dark for several hours (>3 h), when all of the complexes were converted into 1Re-X2bpy, and then TEOA was added to these solutions. After keeping the solutions at room temperature in the dark for 2 h, the IR spectra of the equilibrium mixtures were recorded.CO2-capturing reactions
Various amounts (0.020–0.025 mL) of a CO2-saturated DMF solution (the concentration of CO2 is 0.20 M)18,19 were added to DMF solutions (1.8 mL) containing TEOA (1.3 M) and the equilibrium mixture of the metal complexes in a shielded sample tube by using a micro-syringe in a glove box. After the solutions were kept at room temperature for several hours, the IR spectra were measured.Synthesis
fac-Re(X2bpy)(CO)3Br was synthesised according to a reported method.1,2fac-Mn(X2bpy)(CO)3Br was synthesised according to a reported method with a small difference indicated as follows.15 All procedures for the synthesis of the Mn(I) complexes were performed in a dark room with red light. W(bpy)(CO)4 and fac-W(bpy)(CO)3(MeCN) were synthesised according to a reported method.51,52The following Mn complexes were synthesised by a similar method to that of [Mn(bpy)(CO)3(MeCN)](PF6) except for using the corresponding Br complexes as the starting complexes.
fac-[Mn(4,4′-dibromo-2,2-bipyridine)(CO)3(MeCN)] (PF6). Yield: 0.45 g (95%). 1H NMR (400 MHz, chloroform-d1, ppm): δ = 8.83 (d, 2H, J = 6.8 Hz, bpy-6,6′), 8.42 (d, 2H, J = 2.4 Hz, bpy-3,3′), 7.82 (dd, 2H, J = 2.4, 6.8 Hz, bpy-5,5′), 2.16 (s, 3H, NC–CH3, H). FT-IR (MeCN): v(CO)/cm−1, 2051, 1963. Elemental anal. calcd (%) for C15H9Br2MnN3O3PF6: C, 28.20; H, 1.42; N, 6.58. Found: C, 28.50; H, 1.28; N, 6.69.
fac-[Mn(4,4′-methoxy-2,2-bipyridine)(CO)3(MeCN)](PF6). Yield: 0.26 g (75%). 1H NMR (400 MHz, chloroform-d1, ppm): δ = 8.72 (d, 2H, J = 6.4 Hz, bpy-6,6′), 7.81 (d, 2H, J = 2.6 Hz, bpy-3,3′), 7.82 (dd, 2H, J = 2.6, 6.4 Hz bpy-5,5′), 4.11 (s, 6H, –OCH3) 2.16 (s, 3H, NC–CH3). FT-IR (MeCN): v(CO)/cm−1, 2047, 1953. Elemental anal. calcd (%) for C17H15MnN3O5PF6: C, 37.73; H, 2.79; N, 7.76. Found: C, 37.71; H, 2.72; N, 7.75.
fac-[Re(4,4′-dibromo-2,2-bipyridine)(CO)3(MeCN)](PF6). Yield: 0.44 g (63%). 1H NMR (400 MHz, acetonitrile-d3, ppm): δ = 8.81 (d, 2H, J = 6.0 Hz, bpy-6,6′), 8.72 (d, 2H, J = 2.0 Hz, bpy-3,3′), 7.92 (dd, 2H, J = 2.0, 6.0 Hz, bpy-5,5′), 2.06 (s, 3H, NC–CH3). FT-IR (MeCN): v(CO)/cm−1, 2042, 1941. Elemental anal. calcd (%) for C15H9Br2ReN3O3PF6: C, 23.39; H, 1.18; N, 5.46. Found: C, 23.56; H, 1.10; N, 5.62.
fac-[Re(4,4′-methoxy-2,2-bipyridine)(CO)3(MeCN)](PF6). Yield: 0.44 g (62%). 1H NMR (400 MHz, acetonitrile-d3, ppm): δ = 8.76 (d, 2H, J = 6.0 Hz, bpy-6,6′), 7.92 (d, 2H, J = 2.0 Hz, bpy-3,3′), 7.19 (dd, 2H, J = 2.0, 6.0 Hz, bpy-5,5′), 4.03 (s, 6H, –OCH3), 2.06 (s, 3H, NC–CH3). FT-IR (MeCN): v(CO)/cm−1, 2038, 1932. Elemental anal. calcd (%) for C17H15ReN3O5PF6: C, 30.36; H, 2.25; N, 6.25. Found: C, 30.85; H, 2.24; N, 6.43.
DFT calculations of changes in Gibbs free energy (ΔG0)
The geometry optimisations of chemical species involved in CO2-capturing were carried out using a hybrid density functional with 25% exchange and a 75% Perdew, Burke, and Ernzerhof correlation functional (PBE1PBE)53 using a smaller def2-SVP basis set with an effective core potential for Re and Br atoms. The solvent DMF was modelled as a dielectric continuum using a polarisable continuum model.54 The electronic energies were then obtained as the SCF energy of a single-point calculation on the optimised geometries using a larger basis set of def2-TZVP. The solvent effect of DMF was considered using the SMD method, a parametrised SCRF-based solvation model developed to predict the free energy of solvation.55 The thermal correction terms to evaluate the standard Gibbs energy of formation (Gf) were computed by vibrational frequency analysis of the stationary structures using the same calculation level as for the geometry optimisations. An appropriate scaling factor of 0.9817 was used for the computed zero-point energy.50 Changes in the Gibbs free energy (ΔG0) were calculated as the difference in Gf between the reactants and the products. For the ΔG0 values corresponding to K2 and K3 with the unit of M−1, the calculated Gf values were corrected by −7.9 kJ mol−1 for the change in the reference states from 1 bar to 1 M.56 All DFT calculations were executed using Gaussian 16 packages.57Conclusions
We found that the CO2-capturing reactions of Mn(I) diimine tricarbonyl complexes with a deprotonated TEOA ligand were similar to those of the corresponding Re(I) complexes. The equilibrium constants of both the Mn(I) and Re(I) diimine complexes for the ligand substitution (Process 1) and for CO2 capture (Process 2) in DMF–TEOA solutions were determined. From the DFT calculations, in addition to these equilibrium constants, we systematically and quantitatively clarified the effects of both the metal and the substituents on the bpy ligand. This kind of metal affected both Processes 1 and 2. On the other hand, ligand substituents had a greater influence on Process 1 than Process 2. The DFT calculation can be applied to estimate the ΔG0 of the total reaction containing both the ligand substitution and CO2 capture (Process 3), and the ΔG0 values were in good agreement with those calculated from the experimental data. The CO2-capturing reaction of W(bpy)(CO)3(DMF) in the TEOA–DMF solution did not proceed at all because of the large ΔG0 value for Process 3. These calculation approaches can give a good approximation to judge whether the total CO2-capturing phenomenon (Process 3) proceeds or not with various metal complexes.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by JST CREST Grant number JPMJCR13L1. This work was also partially supported by JSPS KAKENHI Grant number 17H06440 in Scientific Research on Innovative Areas ‘Innovations for Light-Energy Conversion (I4LEC)’.Notes and references
- J. Hawecker, J.-M. Lehn and R. Ziessel, J. Chem. Soc., Chem. Commun., 1983, 536–538 RSC.
- M. Bourrez, F. Molton, S. Chardon-noblat and A. Deronzier, Angew. Chem., Int. Ed., 2011, 50, 9903–9906 CrossRef CAS PubMed.
- H. Ishida, T. Terada, K. Tanaka and T. Tanaka, Inorg. Chem., 1990, 29, 905–911 CrossRef CAS.
- S. Sato, T. Morikawa, T. Kajino and O. Ishitani, Angew. Chem., Int. Ed., 2013, 52, 988–992 CrossRef CAS PubMed.
- V. S. Thoi, N. Kornienko, C. G. Margarit, P. Yang and C. J. Chang, J. Am. Chem. Soc., 2013, 135, 14413–14424 CrossRef CAS PubMed.
- D. Hong, Y. Tsukakoshi, H. Kotani, T. Ishizuka and T. Kojima, J. Am. Chem. Soc., 2017, 139, 6538–6541 CrossRef CAS PubMed.
- L. Chen, Z. Guo, X. G. Wei, C. Gallenkamp, J. Bonin, E. Anxolabéhère-Mallart, K. C. Lau, T. C. Lau and M. Robert, J. Am. Chem. Soc., 2015, 137, 10918–10921 CrossRef CAS PubMed.
- H. Takeda, K. Ohashi, A. Sekine and O. Ishitani, J. Am. Chem. Soc., 2016, 138, 4354–4357 CrossRef CAS PubMed.
- A. Rosas-Hernández, P. G. Alsabeh, E. Barsch, H. Junge, R. Ludwig and M. Beller, Chem. Commun., 2016, 52, 8393–8396 RSC.
- Z. Guo, S. Cheng, C. Cometto, E. Anxolabéhère-Mallart, S.-M. Ng, C.-C. Ko, G. Liu, L. Chen, M. Robert and T.-C. Lau, J. Am. Chem. Soc., 2016, 138, 9413–9416 CrossRef CAS PubMed.
- H. Rao, L. C. Schmidt, J. Bonin and M. Robert, Nature, 2017, 548, 74–77 CrossRef CAS PubMed.
- J. Shen, R. Kortlever, R. Kas, Y. Y. Birdja, O. Diaz-Morales, Y. Kwon, I. Ledezma-Yanez, K. J. P. Schouten, G. Mul and M. T. M. Koper, Nat. Commun., 2015, 6, 1–8 Search PubMed.
- T. Ouyang, H.-H. Huang, J.-W. Wang, D.-C. Zhong and T.-B. Lu, Angew. Chem., Int. Ed., 2017, 56, 738–743 CrossRef CAS PubMed.
- J. Hawecker, J.-M. Lehn and R. Ziessel, J. Chem. Soc., Chem. Commun., 1984, 6, 328–330 RSC.
- H. Takeda, H. Koizumi, K. Okamoto and O. Ishitani, Chem. Commun., 2014, 50, 1491–1493 RSC.
- M. D. Sampson, A. D. Nguyen, K. A. Grice, C. E. Moore, A. L. Rheingold and C. P. Kubiak, J. Am. Chem. Soc., 2014, 136, 5460–5471 CrossRef CAS PubMed.
- J. Agarwal, T. W. Shaw, H. F. Schaefer and A. B. Bocarsly, Inorg. Chem., 2015, 54, 5285–5294 CrossRef CAS PubMed.
- T. Morimoto, T. Nakajima, S. Sawa, R. Nakanishi, D. Imori and O. Ishitani, J. Am. Chem. Soc., 2013, 135, 16825–16828 CrossRef CAS PubMed.
- T. Nakajima, Y. Tamaki, K. Ueno, E. Kato, T. Nishikawa, K. Ohkubo, Y. Yamazaki, T. Morimoto and O. Ishitani, J. Am. Chem. Soc., 2016, 138, 13818–13821 CrossRef CAS PubMed.
- S. K. Mandal, D. M. Ho and M. Orchin, Organometallics, 1993, 12, 1714–1719 CrossRef CAS.
- D. J. Darensbourg, W. Z. Lee, A. L. Phelps and E. Guidry, Organometallics, 2003, 22, 5585–5588 CrossRef CAS.
- R. D. Simpson and R. G. Bergman, Organometallics, 1992, 11, 4306–4315 CrossRef CAS.
- M. K. Mbagu, D. N. Kebulu, A. Winstead, S. K. Pramanik, H. N. Banerjee, M. O. Iwunze, J. M. Wachira, G. E. Greco, G. K. Haynes, A. Sehmer, F. H. Sarkar, D. M. Ho, R. D. Pike and S. K. Mandal, Inorg. Chem. Commun., 2012, 21, 35–38 CrossRef CAS.
- T. Tsuda and T. Saegusa, Inorg. Chem., 1972, 11, 2561–2563 CrossRef CAS.
- S. M. Kupchan and C. Kim, J. Am. Chem. Soc., 1975, 97, 5625–5627 CrossRef.
- A. Immirizi and A. Musco, Inorg. Chim. Acta, 1977, 22, 35–36 CrossRef.
- T. Yamamoto, M. Kubota and A. Yamamoto, Bull. Chem. Soc. Jpn., 1980, 53, 680–685 CrossRef CAS.
- L. J. Newman and R. G. Bergman, J. Am. Chem. Soc., 1985, 107, 5314–5315 CrossRef CAS.
- M. Kato and T. Ito, Inorg. Chem., 1985, 24, 509–514 CrossRef CAS.
- D. J. Darensbourg, K. M. Sanchez, J. H. Reibenspies and A. L. Rheingold, J. Am. Chem. Soc., 1989, 111, 7094–7103 CrossRef CAS.
- D. J. Darensbourg, B. L. Mueller, C. J. Bischoff, S. S. Chojnacki and J. H. Reibenspies, Inorg. Chem., 1991, 30, 2418–2424 CrossRef CAS.
- B. Buffin, A. Arif and T. Richmond, J. Chem. Soc., Chem. Commun., 1993, 18, 1432–1434 RSC.
- M. Ruf and H. Vahrenkamp, Inorg. Chem., 1996, 35, 6571–6578 CrossRef CAS PubMed.
- M. Aresta, A. Dibenedetto and C. Pastore, Inorg. Chem., 2003, 42, 3256–3261 CrossRef CAS PubMed.
- D. R. Moore, M. Cheng, E. B. Lobkovsky and G. W. Coates, J. Am. Chem. Soc., 2003, 125, 11911–11924 CrossRef CAS PubMed.
- M. M. Ibrahim, K. Ichikawa and M. Shiro, Inorg. Chem. Commun., 2003, 6, 1030–1034 CrossRef CAS.
- O. Tardif, D. Hashizume and Z. Hou, J. Am. Chem. Soc., 2004, 126, 8080–8081 CrossRef CAS PubMed.
- H. Brombacher and H. Vahrenkamp, Inorg. Chem., 2004, 43, 6042–6049 CrossRef CAS PubMed.
- D. Cui, M. Nishiura, O. Tardif and Z. Hou, Organometallics, 2008, 27, 2428–2435 CrossRef CAS.
- E. C. Y. Tam, N. C. Johnstone, L. Ferro, P. B. Hitchcock and J. R. Fulton, Inorg. Chem., 2009, 48, 8971–8976 CrossRef CAS PubMed.
- L. A. M. Steele, T. J. Boyle, R. A. Kemp and C. Moore, Polyhedron, 2012, 42, 258–264 CrossRef CAS.
- A. Arunachalampillai, N. Loganathan and O. F. Wendt, Polyhedron, 2012, 32, 24–29 CrossRef CAS.
- B. J. Truscott, D. J. Nelson, A. M. Z. Slawin and S. P. Nolan, Chem. Commun., 2014, 50, 286–288 RSC.
- Y. Arikawa, T. Nakamura, S. Ogushi, K. Eguchi and K. Umakoshi, Dalton Trans., 2015, 44, 5303–5305 RSC.
- F. Parrino, C. Deiana, M. R. Chierotti, G. Martra and L. Palmisano, J. CO2 Util., 2016, 13, 90–94 CrossRef CAS.
- J.-C. Choi, H.-Y. Yuan, N. Fukaya, S. Onozawa, Q. Zhang, S. J. Choi and H. Yasuda, Chem.–Asian J., 2017, 12, 1297–1300 CrossRef CAS PubMed.
- S. V. C. Vummaleti, G. Talarico, S. P. Nolan, L. Cavallo and A. Poater, Eur. J. Inorg. Chem., 2015, 28, 4653–4657 CrossRef.
- T. E. Dorsett and R. A. Walton, J. Chem. Soc., Dalton Trans., 1976, 347–350 RSC.
- G. J. Stor, D. J. Stufkens, P. Vernooijs, E. J. Baerends, J. Fraanje and K. Goubitz, Inorg. Chem., 1995, 34, 1588–1594 CrossRef CAS.
- M. K. Kesharwani, B. Brauer and J. M. L. Martin, J. Phys. Chem. A, 2015, 119, 1701–1714 CrossRef CAS PubMed.
- T. S. A. Hor and S.-M. Chee, J. Organomet. Chem., 1987, 331, 23–28 CrossRef CAS.
- Y. Yamaguchi, H. Nakazawa, T. Itoh and K. Miyoshi, Bull. Chem. Soc. Jpn., 1996, 69, 983–998 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6169 CrossRef CAS.
- J. Tomasi, B. Mennucci and E. Cancès, J. Mol. Struct.: THEOCHEM, 1999, 464, 211–226 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- J. Keith and E. A. Carter, J. Chem. Theory Comput., 2012, 8, 3187–3206 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. Paul, D. Connolly, M. Schulz, M. T. Pryce and J. G. Vos, Inorg. Chem., 2012, 51, 1977–1979 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc04389b |
‡ As shown in Table S1, a similar discussion can be done by using 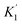 instead of K1. instead of K1. |
| § Unfortunately, we could not use the step-by-step substitution synthesis method in the case of the Mn complexes because dissolving fac-[Mn(bpy)(CO)3(MeCN)]+ into DMF gave not only 1Mn-bpy but also a minor product which we have not been able to identify. As described above, therefore, we dissolved the Mn complexes directly into the DMF–TEOA mixed solution. |
| ¶ In this experiment, we observed other small bands at 2019 cm−1, peaks of which appeared and gradually increased after the addition of TEOA. This species was probably attributed to the formato complex Re(bpy)(CO)3(OCHO), the formate ligand of which was probably supplied from DMF. This decomposition of DMF under basic conditions with TEOA and H2O was reported by Vos and his coworkers.58 It was also reported that this reaction is suppressed under more acidic conditions such as under a CO2 atmosphere. We used well dehydrated TEOA and DMF and minimized the time for measuring the IR spectra of the equilibrated mixtures under an Ar atmosphere after addition of TEOA (typically 120 min) for minimizing formation yields. The formation of the formato complex was less than 3% in all the Re complexes. In the case of Mn(I) complexes, this formation of the formato complex was very slow. |
| || W(bpy)(CO)3(MeCN) was unstable in air probably because of oxidation of the metal centre and decarbonylation. Therefore, W(bpy)(CO)3(MeCN) was used without any purification after the synthesis. |
| This journal is © The Royal Society of Chemistry 2019 |