Open Access Article
Open Access ArticleChemisorption of metallic radionuclides on a monolayer MoS2 nanosheet
Zheng
Zhang
ab,
Qiang
Zhao
 *ab,
Mei
Huang
ab,
Xiaodong
Zhang
ab and
Xiaoping
Ouyang
acd
*ab,
Mei
Huang
ab,
Xiaodong
Zhang
ab and
Xiaoping
Ouyang
acd
aBeijing Key Laboratory of Passive Safety Technology for Nuclear Energy, North China Electric Power University, Beijing 102206, People's Republic of China. E-mail: qzhao@ncepu.edu.cn
bSchool of Nuclear Science and Engineering, North China Electric Power University, Beijing 102206, People's Republic of China
cNorthwest Institute of Nuclear Technology, Xi'an 710024, People's Republic of China
dSchool of Materials Science and Engineering, Xiangtan University, Xiangtan 411105, People's Republic of China
First published on 10th September 2018
Abstract
In the process of developing nuclear energy, removing radioactive waste in the environment is a challenging problem that human beings have to face. The main work of this paper is to investigate the mechanism of the interaction between metallic radionuclides (Cs, Sr, and Ba) and a monolayer MoS2 nanosheet, and the work is completed by using the first principles calculation method. The results show that all of the three kinds of metallic radionuclides can be chemisorbed on the monolayer MoS2 nanosheet. The optimum adsorption site for the metallic radionuclides adsorbed on the monolayer MoS2 is TMo (top of the Mo atom), because the metallic radionuclides can interact with the three nearest S atoms when the metallic radionuclides are at the TMo site. The chemisorption strength of the metallic radionuclides on the monolayer MoS2 is Ba > Sr > Cs. The mechanism of the chemisorption is explored by using the total charge transfer, density of states, and electron density difference. The final analysis shows that the s orbital of S atoms plays an important role in the chemisorption.
1 Introduction
The disposal of radioactive materials has long been a difficult problem for nuclear power development;1 especially, when a serious nuclear accident occurs, large amounts of radioactive waste water are produced in the damaged nuclear power plant. How to remove radionuclides from radioactive waste water quickly and efficiently has become a worldwide challenging problem, such as the Fukushima Daiichi nuclear disaster.2,3 To solve this problem, many radioactive material removal methods, such as sorption, (co)precipitation, ion exchange, solidification, and membrane separation, have been extensively applied to eliminate radionuclides from waste water. Among these methods, the sorption technique has widely been applied in real environmental pollution management because of its simple operation, low cost, and applications on a large scale.4In the past few decades, a considerable number of materials were studied to find out a candidate material for the efficient removal of radionuclides, and the related research on zeolites, molecular sieves, and other materials has achieved great progress. Since graphene was invented, the research on the two-dimensional material has received increasing attention from scientists and engineers, due to its unique band structure, semi-conducting or superconducting properties, excellent mechanical performance, and so on. The two-dimensional material is widely considered for use in electronic devices, catalysis, energy storage, tools used under extreme conditions, and other fields. With the deepening of the research, the two-dimensional material is considered as a new kind of candidate material, which is used in environmental remediation. Through the hard work of Wang's team,5–9 the mechanism of graphene removing radionuclides from the environment has been clarified, and their studies show that oxygen-containing functional groups are crucial for improving the adsorption capacity of graphene for radionuclides. Meanwhile, scientists have found that MoS2 has some adsorption capacity for heavy metal ions10,11 and toxic gas molecules,12–15 and the optical properties of monolayer MoS2 changed when some organic macromolecules were adsorbed on monolayer MoS2.16 Monolayer MoS2 can also be considered as a candidate cathode material for Li-ion batteries.17 Based on the above research, MoS2 is considered as a potential material for environmental restoration.18 Especially, scientists believe that MoS2 is a potential sensor material for toxic gases, such as CO, NO, HS2, NH3, SO2 and so on. Using the first principles calculation method, the electronic and magnetic properties of MoS2 have been investigated,19 and the adsorption energy and charge transfer of different kinds of toxic gas molecules adsorbed on monolayer MoS2 have been reported,20–22 and the result shows that MoS2 can monitor toxic gases in the atmosphere. Based on this research, we think that MoS2 might be a candidate material for radionuclide removal from the environment. As for the preparation of monolayer MoS2, three successful methods have been reported, such as mechanical exfoliation, liquid exfoliation, and chemical vapor deposition (CVD). The successful preparation of the material has provided the possibility for its large-scale application, especially in the field of radioactive environmental restoration.
89Sr, 90Sr, 134Cs, 137Cs, and 140Ba are the common radionuclides in waste water from nuclear plants, and the half-time of 89Sr, 90Sr, 134Cs, 137Cs, and 140Ba is about 50.5 days, 28.6 years, 2.06 years, 30.17 years, and 12.75 days, respectively. 89Sr, 90Sr, and 140Ba are pure beta decay nuclides, and the maximum energy of the β ray is about 1.46 MeV, 0.546 MeV, and 1.0 MeV, respectively. 134Cs and 137Cs are both the gamma source and the beta source, and the characteristic energy of the γ ray from the emission of 137Cs is about 661.66 keV. All of the metallic radionuclides have adverse impacts on the environment, and more importantly, they are harmful to public health. How to remove the three kinds of metallic radionuclides in waste water is very important for the treatment of radioactive waste water. Therefore, we focused on the adsorption of the three kinds of metallic radionuclides on monolayer MoS2. As we know, although the atomic mass of isotopes is different, their chemical properties are basically similar. The chemical properties of metallic radionuclides depend upon the electrons on the outside. The effects of the radioactivity of metallic radionuclides on the adsorption capacity of MoS2 is beyond the scope of this study.
In our previous work,23 we just show that monolayer MoS2 can adsorb metallic radionuclides, and the adsorption belongs to chemisorption according to the adsorption energies of the metallic radionuclides on monolayer MoS2. In this paper, we aim to study why monolayer MoS2 can adsorb metallic radionuclides. The mechanism of monolayer MoS2 adsorbing metallic radionuclides has been explored clearly, which may provide a theoretical basis for relevant experimental research in the future. Based on our previous work, we calculated the charge transfer, electron density difference, total densities of states (TDOS) and partial densities of states (PDOS), to clarify the mechanism of the adsorption. We hope that our work can shed some light on environmental remediation, especially the treatment of radioactive waste water.
2 Computation method and details
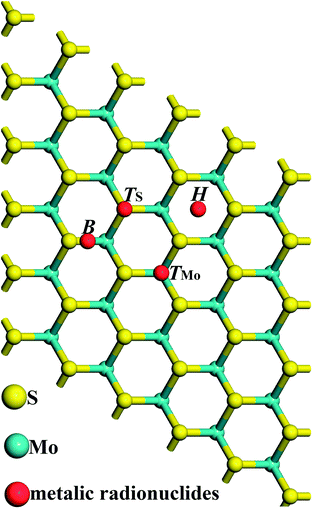
First principles calculations based on density functional theory24,25 are used in this paper and all calculations are conducted in the Cambridge serial total energy package (CASTEP).26 In the crystal periodic potential field, the multi-electron system is expressed by the plane wave function through the three-dimensional periodic boundary condition, and in order to reduce the number of plane wave bases, the CASTEP software package uses the ultrasoft pseudopotential to describe the interaction between ions and electrons. As we know, metallic radionuclides exist in valence forms as metal ions (such as Cs+, Sr2+ and Ba2+) in radioactive waste water, and we set a corresponding charge on these metallic radionuclide atoms. In the reciprocal space, the plane wave cutoff energy is set to 500 eV, and the exchange and correlation functions among electrons are described by the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA).27–29 Structure optimization is conducted using the Broyden–Fletcher–Goldfarb–Shanno minimization, modified to take into account the total energy as well as the gradients. The self-consistent field (SCF) tolerance is set to 1.0 × 10−6 eV per atom. After the convergence test, all the calculations are performed using 3 × 3 × 1 Monkhorst–Pack k points. In order to avoid interlayer interactions, a vacuum layer of 16 Å is used in the c direction. In the process of geometry optimization, all the structures are fully relaxed, and the optimal atomic positions are determined until satisfying the following conditions: (1) the maximal force on them is less than 0.03 eV Å−1; (2) the maximal change of energy per atom is less than 1.0 × 10−5 eV; (3) the maximal displacement is less than 5.0 × 10−4 Å; (4) the maximal stress in the supercell is less than 0.02 GPa.A 5 × 5 × 1 supercell of monolayer MoS2 (containing 25 Mo atoms and 50 S atoms) with a single metallic radionuclide adsorbed onto it is constructed to be the calculation model. Fig. 1 shows the positions of the metallic radionuclides adsorbed on the 5 × 5 × 1 MoS2 supercell, and glaucous and yellow balls represent Mo and S atoms, respectively. For the single metallic radionuclide, there are four possible adsorption sites, TMo (top of the Mo atom), TS (top of the S atom), H (the centre of the hexagon), and B (the bridge of Mo–S).
For the adsorption of the metallic radionuclides, the adsorption energy is calculated using the following relationship:
| Ead = EM+MoS2 − EMoS2 − EM, | (1) |
We calculated the charge transfer Qt based on Mulliken30 and Hirshfeld31 methods. To understand the difference between Mulliken and Hirshfeld methods, here we briefly introduce these two methods of calculating atomic charge. First, the normalization condition of the molecular orbital wave function is considered,
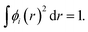 | (2) |
Where, r represents the space coordinates. The molecular orbitals ϕi are expanded by using atomic-centered basis functions χm,
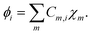 | (3) |
Where, C is the matrix of coefficient, and by substituting eqn (3) into eqn (2), a result can be obtained after integration,
 | (4) |
Where, 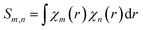 . The first item in eqn (4) is the sum of independent contributions of each basis function to the orbit, and it is called the localized term. The second item is the cross term, and it represents the joint contribution to the orbit due to the coupling between each pair of basis functions. Mulliken defines the composition of the fundamental function m in molecular orbital i as:
. The first item in eqn (4) is the sum of independent contributions of each basis function to the orbit, and it is called the localized term. The second item is the cross term, and it represents the joint contribution to the orbit due to the coupling between each pair of basis functions. Mulliken defines the composition of the fundamental function m in molecular orbital i as:
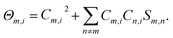 | (5) |
That is to say, the localized term is completely assigned to the corresponding base function, and the cross term is bisected into the corresponding two basis functions. The atomic populations can be obtained by adding up the populations of all the basis functions that belong to the same atom in all the orbitals, and the Mulliken atomic charge is given by the equation,
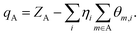 | (6) |
Where, ZA is the nuclear charge number, and η is the orbital population.
The Hirshfeld atomic charge is defined as,
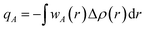 | (7) |
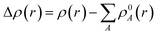 | (8) |
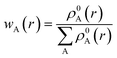 | (9) |
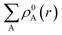 represents the sum of the electron density of all atoms in the free state, also known as the promolecule density. Δρ(r) is called the deformation density, and it stands for the change of electron density in the relaxation process after atoms form molecules. wA(r) is the weight function of atom A, and it defines the entire real space that belongs to atom A. Hirshfeld's division has a clear physical meaning, and Nalewajski and Parr prove from the point of view of information theory that this division is a way to minimize the distance (Kullback–Leibler relative entropy) of information between atoms and molecules when the electron density is allowed to transfer between atoms. Because the results obtained by the Mulliken method depend too much on the basis group, scientists generally believe that the Hirshfeld method is more effective. We also draw a conclusion based on the results obtained by the Hirshfeld method. Nevertheless, the results obtained from the Mulliken method still have a good reference.
represents the sum of the electron density of all atoms in the free state, also known as the promolecule density. Δρ(r) is called the deformation density, and it stands for the change of electron density in the relaxation process after atoms form molecules. wA(r) is the weight function of atom A, and it defines the entire real space that belongs to atom A. Hirshfeld's division has a clear physical meaning, and Nalewajski and Parr prove from the point of view of information theory that this division is a way to minimize the distance (Kullback–Leibler relative entropy) of information between atoms and molecules when the electron density is allowed to transfer between atoms. Because the results obtained by the Mulliken method depend too much on the basis group, scientists generally believe that the Hirshfeld method is more effective. We also draw a conclusion based on the results obtained by the Hirshfeld method. Nevertheless, the results obtained from the Mulliken method still have a good reference.
The atoms have a positive charge when the Mulliken or Hirshfeld charge (e) > 0, and the atom has a negative charge when the Mulliken or Hirshfeld charge (e) < 0. The positive value of Qt shows that the electrons transferred from the metallic radionuclides to monolayer MoS2, while the negative value of Qt indicates that the electrons transferred from monolayer MoS2 to the metallic radionuclides. In order to explore the interaction mechanism between the metallic radionuclides and monolayer MoS2, we calculated the electron density difference, total densities of states (TDOS) and partial densities of states (PDOS).
3 Results and discussion
In order to explain the rationality of the calculation in this paper, we first explore the structure and properties of monolayer MoS2. The lattice constant is 3.166 Å, and the bond length of Mo–S and S–S bonds is 2.409 Å, and 3.137 Å, respectively. Our calculations are in good agreement with the available numerical results.32,33Fig. 2 shows the band structure, TDOS, and PDOS of monolayer MoS2. The band gap of monolayer MoS2 is 1.93 eV, which is in good agreement with other theoretical values (1.80 eV34,35 and 1.70 eV (ref. 36)) and experimental data (1.98 eV37 and 1.90 eV (ref. 38)). Additionally, the bottom of conduction bands and the top of valence bands of the pristine monolayer MoS2 are mainly composed of Mo 4d and S 3p orbitals, which is consistent with previous calculational results.39–41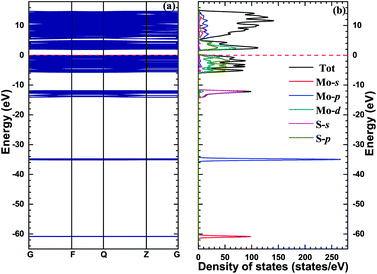 | ||
| Fig. 2 The band structure (a) and density of states (b) of monolayer MoS2, and the red dashed lines stand for the Fermi level. | ||
3.1 Adsorption of Cs on the monolayer MoS2 nanosheet
The adsorption energy, total charge transfer and adsorption height (the height of the radionuclide Cs above the MoS2 surface) of the radionuclide Cs adsorbed on the monolayer MoS2 nanosheet with different configurations are given in Table 1. When the initial configuration of the radionuclide Cs on the monolayer MoS2 nanosheet is B, the radionuclide Cs is repelled from the initial site B and migrates to the first nearest neighbor Mo atom after relaxation, and the radionuclide Cs can interact with the three nearest S atoms. From the adsorption energy, it can be seen that the adsorption energy of the B initial structure is the lowest (−3.259 eV). Therefore, TMo is the energetically favorable site. For the Ni adsorbed on monolayer MoS2,42 TMo is also the energetically favorable site. Fig. 3(a) shows the optimized structure of metallic radionuclide Cs adsorbed on the monolayer MoS2 nanosheet with the B initial configuration. We can find that the height of Cs atoms above the monolayer MoS2 surface is 2.829 Å. The bond length of Mo–S1 and Mo–S2 bonds increased to 2.421 Å and 2.438 Å, while the length of Mo–S3 decreased to 2.405 Å, respectively. The increase of the bond length indicates that the interaction between Mo atoms and S atoms is weakened. The distance between the radionuclide Cs and Mo atom is 4.462 Å, while the distance between the radionuclide Cs and S1, S2, and S3 is 3.459 Å, 3.490 Å, and 3.457 Å, respectively.| Configuration | E ad | Q t-Mulliken | Q t-Hirshfeld | h |
|---|---|---|---|---|
| TMo | −3.258 | 0.99 | 0.59 | 2.821 |
| TS | −3.028 | 0.98 | 0.66 | 3.221 |
| B | −3.259 | 1.00 | 0.59 | 2.829 |
| H | −3.255 | 0.99 | 0.59 | 2.817 |
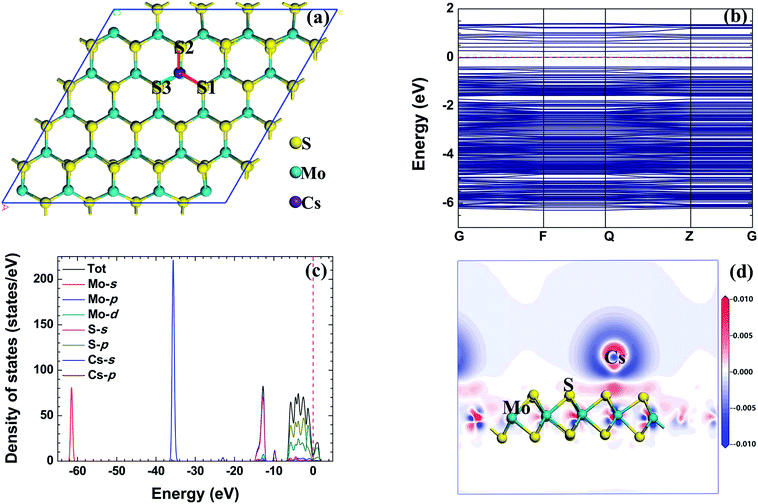 | ||
| Fig. 3 The relaxed configuration, band structure (from −10 eV to 5 eV), density of states, and electron density difference of the radionuclide Cs on monolayer MoS2. | ||
In addition, it can be found that the total charge transfer Qt for different initial structures obtained by the Mulliken and Hirshfeld methods have the same trend. The total charge transfer of the radionuclide Cs adsorbed on the monolayer MoS2 nanosheet with all of the initial configurations is positive, indicating that the radionuclide Cs acts as the electron donor and the monolayer MoS2 nanosheet acts as the electron acceptor. For the adsorption of the radionuclide Cs on monolayer MoS2 with all of the initial structures, the corresponding charge transfer value based on the Mulliken method is higher than that of the Hirshfeld method. And for the adsorption of the radionuclide Cs on monolayer MoS2 with the B initial structure, the corresponding charge transfer obtained by Mulliken and Hirshfeld methods is 1.00 e and 0.59 e, respectively.
Fig. 3(b) shows the band structure of a metallic radionuclide Cs adsorbed on monolayer MoS2. There is no band gap in the band structure, and this phenomenon means that the band gap disappeared in the band structure after a metallic radionuclide Cs was adsorbed on monolayer MoS2.
In order to further explore the interaction mechanism between the radionuclide Cs and monolayer MoS2 nanosheet, we calculated the TDOS, PDOS and electron density difference of the system before and after adsorption. Fig. 3(c) shows the TDOS and PDOS of the Cs atom adsorbed on monolayer MoS2 with the B initial structure. There are four regions in the valence band, including the high energy region (from −6 eV to 0 eV), the second high energy region (near −14 eV), the medium energy region (near −36 eV), and the low energy region (near −62 eV). The high energy region, the medium energy region, and the low energy region consist of Mo d, p, and s orbitals, and the S p orbital also makes a contribution to the high energy region; the second high energy region is composed of the S s orbital. After the radionuclide Cs was adsorbed on monolayer MoS2, two small peaks (near −10 eV and −23 eV) appeared in the valence band. According to the density of states, the adsorption of the radionuclide Cs on monolayer MoS2 was mainly caused by the hybridization between Cs p and S s orbitals.
The electron density difference of radionuclide Cs adsorbed on monolayer MoS2 with the B initial structure is shown in Fig. 3(d). The red and blue regions in the figure indicate the increase and decrease of the electron density, respectively. It can be found that the electron density near the S atom increased obviously and the electron density near the Mo and Cs atoms decreased after the radionuclide Cs was adsorbed on monolayer MoS2, which further confirmed that the radionuclide Cs acts as the electron donor and monolayer MoS2 acts as the electron acceptor; more precisely, the S atoms near the radionuclide Cs act as the electron acceptor.
3.2 Adsorption of Sr on the monolayer MoS2 nanosheet
Table 2 shows the adsorption energy, total charge transfer, and adsorption height of the radionuclide Sr atom adsorbed on the monolayer MoS2 nanosheet with different initial configurations. The result shows that the adsorption energy of the radionuclide Sr atom on the monolayer MoS2 nanosheet is higher than that of the radionuclide Cs; therefore, the interaction between the radionuclide Sr and monolayer MoS2 nanosheet is weaker than that of the radionuclide Cs. When the initial configuration of the radionuclide Sr on monolayer MoS2 is B, the radionuclide Sr migrates to the first nearest neighbor Mo atom (TMo) after relaxation, and TMo is the optimum adsorption site. The adsorption energy of the Sr atom adsorbed on the monolayer MoS2 nanosheet with TMo configuration is −3.863 eV.| Configuration | E ad | Q t-Mulliken | Q t-Hirshfeld | h |
|---|---|---|---|---|
| TMo | −2.822 | 1.27 | 0.73 | 1.845 |
| TS | −2.589 | 1.28 | 0.89 | 2.265 |
| B | −3.863 | 1.24 | 0.72 | 1.836 |
| H | −3.847 | 1.27 | 0.74 | 1.799 |
Fig. 4(a) shows the optimized structure of radionuclide Sr adsorbed on monolayer MoS2 with the B initial configuration. After relaxation, the bond length of Mo–S1, Mo–S2, and Mo–S3 bonds increased to 2.412 Å, 2.466 Å, and 2.424 Å, respectively. Due to the radionuclide Sr adsorbed on monolayer MoS2, the length of Mo–S bonds (near the radionuclide Sr) becomes longer than that in MoS2, and this result means that the interaction between the Mo atom and S atom is weakened by the radionuclide Sr. The distances between the radionuclide Sr and Mo, S1, S2, and S3 are 3.517 Å, 2.776 Å, 2.778 Å, and 2.764 Å, respectively. These values indicate that the interaction between the radionuclide Sr and S atoms is stronger than the interaction between the radionuclide Cs and S atoms.
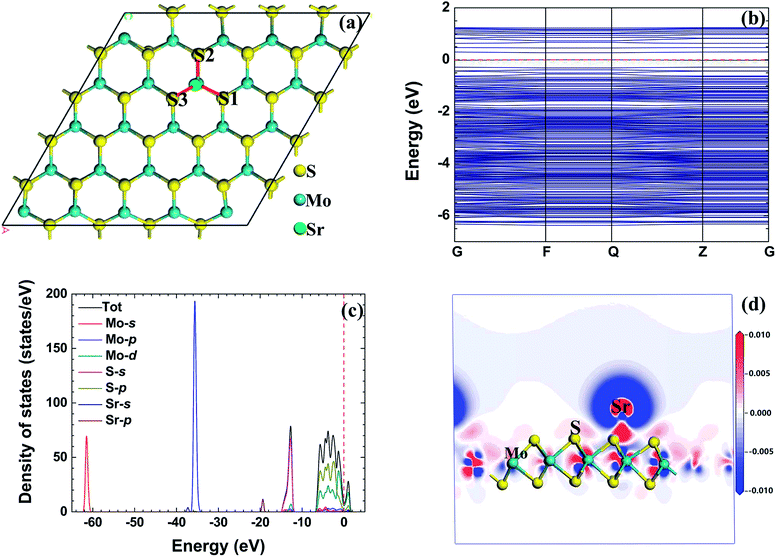 | ||
| Fig. 4 The relaxed configuration, band structure (from −10 eV to 5 eV), density of states, and electron density difference of the radionuclide Sr on monolayer MoS2. | ||
Although the total charge transfer Qt for different initial configurations obtained by the Mulliken and Hirshfeld method is different, they have the same trend. In the interaction process, the Sr atom acts as electron donor and monolayer MoS2 acts as electron acceptor. For the adsorption of Sr on monolayer MoS2 with B initial configuration, the corresponding charge transfer Qt obtained by Mulliken and Hirshfeld method is 1.24 e and 0.72 e, respectively.
Fig. 4(b) shows the band structure of a radionuclide Sr on monolayer MoS2 with the initial configuration B, and the band gap of this configuration is 0.271 eV. The decrease of the band gap is due to the adsorption of the radionuclide Sr. Fig. 4(c) shows the TDOD and PDOS of the radionuclide Sr adsorbed on monolayer MoS2. There is a hybridization exists between the s orbital of the S atom and the p orbital of the Sr atom and the Mo p orbital. When the radionuclide Sr is at the TMo site, there is an interaction between the radionuclide Sr and the three nearest S atoms.
Fig. 4(d) shows the electron density difference of the radionuclide Sr adsorbed on monolayer MoS2 with TMo configuration. The S atoms act as the electron accepter, and the Mo and Sr atoms act as the electron donor. This result is in good agreement with the total charge transfer Qt obtained by Mulliken and Hirshfeld methods.
3.3 Adsorption of Ba on the monolayer MoS2 nanosheet
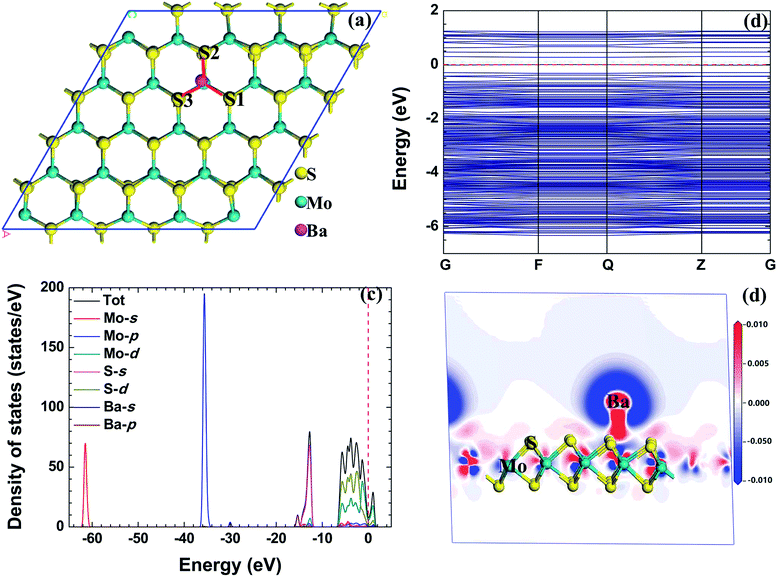
We calculated the adsorption energy, total charge transfer, and adsorption height of the radionuclide Ba adsorbed on the monolayer MoS2 nanosheet, as shown in Table 3. The radionuclide Ba migrates from the initial configuration B to the first nearest neighbor Mo atom after relaxation. The adsorption energy of the radionuclide Ba on monolayer MoS2 is the lowest, followed by the radionuclide Sr, and the adsorption energy of the radionuclide Cs on monolayer MoS2 is the highest. Therefore, the strength of the adsorption of the three kinds of metallic radionuclides on the monolayer MoS2 nanosheet is: Ba > Sr > Cs. For the radionuclide Ba, TMo is the energetically favorable site, and the corresponding adsorption energy is −4.137 eV. According to the magnitude of the adsorption energy, all of the three kinds of metallic radionuclides can be chemisorbed on monolayer MoS2. The adsorption height of the radionuclide Ba on monolayer MoS2 is about 2.1 Å, and the adsorption height of the radionuclide Ba on monolayer MoS2 is higher than that of the radionuclide Sr, while the adsorption height of the radionuclide Ba on monolayer MoS2 is lower that of the radionuclide Cs. The length of the S–Mo bond is longer than that of the pristine Mo–S bond, and the result means that the adsorption of the radionuclide Ba weakens the interaction between S and Mo. The distance between radionuclides Ba and Mo is 3.726 Å, and the value is higher than that of the radionuclide Sr, but the value is lower than that of the radionuclide Cs. The distance between Ba and S1, S2, and S3 is 2.969 eV, 2.921 eV, and 2.922 eV, respectively. The distance between Ba and S and Mo indicates that the interaction between Ba and monolayer MoS2 is weaker than the interaction between Sr and monolayer MoS2, while the interaction between Ba and monolayer MoS2 is stronger than the interaction between radionuclide Cs and monolayer MoS2.| Configuration | E ad | Q t-Mulliken | Q t-Hirshfeld | h |
|---|---|---|---|---|
| TMo | −2.208 | 0.95 | 0.81 | 2.128 |
| TS | −4.108 | 0.95 | 0.80 | 2.185 |
| B | −4.137 | 0.94 | 0.80 | 2.093 |
| H | −4.114 | 0.90 | 0.78 | 2.056 |
When we calculated the total charge transfer, the difference in the total charge transfer obtained by the Mulliken and Hirshfeld methods still exists, but the total charge transfer obtained by the two methods has the same trend. Like Cs and Sr adsorbed on monolayer MoS2, the Ba atom acts as the electron donor and monolayer MoS2 acts as the electron acceptor. For Ba adsorbed on monolayer MoS2 with B initial configuration, the total charge transfer obtained by the Mulliken and Hirshfeld methods is 0.94 e and 0.80 e, respectively. The relationship between charge transfer and adsorption energy is analyzed, but the effect of the charge transfer on the adsorption energy is not obvious.
Fig. 5(b) shows the band structure of the radionuclide Ba adsorbed on monolayer MoS2. When compared with pristine monolayer MoS2, the band gap of monolayer MoS2 has narrowed due to the adsorption of the radionuclide Ba, and all of the three kinds of metallic radionuclides have similar effects on the band structure of monolayer MoS2. Fig. 5(c) shows the TDOS and PDOS of the radionuclide Ba adsorbed on monolayer MoS2, and there is a hybridization between the S s orbital and Ba p orbital, and the main reason for the adsorption of the radionuclide Ba on monolayer MoS2 might be the hybridization.
Fig. 5(d) shows the electron density difference of the radionuclide Ba adsorbed on monolayer MoS2 with the TMo configuration (relaxed from the B initial configuration). The red and blue regions in the figure indicate the increase and decrease of the electron density, respectively. The radionuclide Ba and Mo atoms act as the electron acceptor and the S atoms near the radionuclide Ba act as the electron donor, and the result is in agreement with the total charge transfer Qt obtained by the Mulliken and Hirshfeld methods.
4 Conclusions
In this paper, we investigated the adsorption of three kinds of metallic radionuclides, Cs, Sr, and Ba, on monolayer MoS2 by using the first principles calculation method. The result shows that all of the three kinds of metallic radionuclides can be chemisorbed on the monolayer MoS2 nanosheet, according to the magnitude of the adsorption energy. The adsorption strength of the three kinds of metallic radionuclides on the monolayer MoS2 nanosheet is Ba > Sr > Cs. All of the radionuclides act as the electron donor, while monolayer MoS2 acts as the electron acceptor; more precisely, the S atoms near the radionuclides act as the electron acceptor. For the three kinds of metallic radionuclides, the optimum adsorption site is TMo, because the radionuclides can interact with the three nearest S atoms.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Fundamental Research Funds for the Central Universities under Grant No. 2017MS079 and 2018ZD10 and the National Natural Science Foundation of China under grant No. 11705059.Notes and references
- X. Tan, Q. Fan, X. Wang and B. Grambow, Environ. Sci. Technol., 2009, 43, 3115–3121 CrossRef CAS PubMed.
- N. Shinohara and H. Yoshidaohuchi, Environ. Int., 2018, 114, 107–114 CrossRef CAS PubMed.
- T. Horiguchi, K. Kodama, T. Aramaki, Y. Miyata and S. Nagao, Mar. Environ. Res., 2018, 114, 107–114 Search PubMed.
- J. Florek, F. Chalifour, F. Bilodeau, D. Larivière and F. Kleitz, Adv. Funct. Mater., 2014, 24, 2668–2676 CrossRef CAS.
- G. Zhao, T. Wen, X. Yang, S. Yang, J. Liao, J. Hu, D. Shao and X. Wang, Dalton Trans., 2012, 41, 6182–6188 RSC.
- Y. Sun, X. Wang, W. Song, S. Lu, C. Chen and X. Wang, Environ. Sci.: Nano, 2016, 4, 222–232 RSC.
- X. Liu, X. Wang, J. Li and X. Wang, Sci. China: Chem., 2016, 59, 869–877 CrossRef CAS.
- Y. J. Ai, Y. Liu, W. Y. Lan, J. R. Jin, J. L. Xing, Y. D. Zou, C. F. Zhao and X. K. Wang, Chem. Eng. J., 2018, 343, 460–466 CrossRef CAS.
- X. Liu, X. T. Xu, J. Sun, A. Alsaedi, T. Hayat, J. X. Li and X. K. Wang, Chem. Eng. J., 2018, 343, 217–224 CrossRef CAS.
- F. Jia, X. Zhang and S. Song, Phys. Chem. Chem. Phys., 2017, 19, 3837–3844 RSC.
- Z. Wang and B. Mi, Environ. Sci. Technol., 2017, 51, 8229–8244 CrossRef CAS PubMed.
- B. Zhao, C. Y. Li, L. L. Liu, B. Zhou, Q. K. Zhang, Z. Q. Chen and Z. Tang, Appl. Surf. Sci., 2016, 382, 280–287 CrossRef CAS.
- Y. Qu, Z. Shao, S. Chang and J. Li, Nanoscale Res. Lett., 2013, 8, 425 CrossRef PubMed.
- M. Ganji, N. Sharifi, M. G. Ahangari and A. Khosravi, Phys. E, 2014, 57, 28–34 CrossRef CAS.
- D. Ma, W. Ju, T. Li, X. Zhang, C. He, B. Ma, Z. Lu and Z. Yang, Appl. Surf. Sci., 2016, 383, 98–105 CrossRef CAS.
- Y. Jing, X. Tan, Z. Zhou and P. Shen, J. Mater. Chem. A, 2014, 2, 16892–16897 RSC.
- Y. Li, D. Wu, C. R. Cabrera and Z. Chen, J. Phys. Chem. Lett., 2012, 3, 2221–2227 CrossRef CAS PubMed.
- N. Saha, A. Sarkar, A. B. Ghosh, P. Mondal, J. Satra and B. Adhikary, Ecotoxicol. Environ. Saf., 2018, 160, 290–300 CrossRef CAS PubMed.
- Y. Li, Z. Zhou, S. Zhang and Z. Chen, J. Am. Chem. Soc., 2008, 130, 16739 CrossRef CAS PubMed.
- H. Li, M. Huang and G. Cao, Phys. Chem. Chem. Phys., 2016, 18, 15110–15117 RSC.
- K. Ding, Y. Lin and M. Huang, Vacuum, 2016, 130, 146–153 CrossRef CAS.
- Y. H. Zhang, J. L. Chen, L. J. Yue, H. L. Zhang and F. Li, Comput. Theor. Chem., 2017, 1104, 12–17 CrossRef CAS.
- Q. Zhao, Z. Zhang and X. Ouyang, Mater. Res. Express, 2018, 5, 045506 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800–8802 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- K. Burke, J. P. Perdew and Y. Wang, in Electronic Density Functional Theory, Springer, 1998, pp. 81–111 Search PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- N. Lu, H. Guo, L. Li, J. Dai, L. Wang, W. N. Mei, X. Wu and X. C. Zeng, Nanoscale, 2014, 6, 2879–2886 RSC.
- W. Wang, C. Yang, L. Bai, M. Li and W. Li, Nanomaterials, 2018, 8, 74 CrossRef PubMed.
- T. Boeker, R. Severin, A. Mueller, C. Janowitz, R. Manzke, D. Voss, P. Krueger, A. Mazur and J. Pollmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 235305 CrossRef.
- S. Lebègue and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 5409 Search PubMed.
- J. V. Lauritsen, J. Kibsgaard, S. Helveg, H. Topsoe, B. S. Clausen, E. Laegsgaard and F. Besenbacher, Nat. Nanotechnol., 2007, 2, 53–58 CrossRef CAS PubMed.
- A. Splendiani, L. Sun, Y. Zhang, T. Li, J. Kim, C. Y. Chim, G. Galli and F. Wang, Nano Lett., 2010, 10, 1271–1275 CrossRef CAS PubMed.
- Q. Yue, S. Chang, S. Qin and J. Li, Phys. Lett. A, 2013, 377, 1362–1367 CrossRef CAS.
- C. Ataca and S. Ciraci, J. Phys. Chem. C, 2010, 115, 13303–13311 CrossRef.
- A. Kumar and P. K. Ahluwalia, Eur. Phys. J. B, 2012, 85, 186 CrossRef.
- N. Singh, G. Jabbour and U. Schwingenschlögl, Eur. Phys. J. B, 2012, 85, 392 CrossRef.
- Y. Li, X. Zhang, D. Cheng, X. Song and J. Tang, Appl. Surf. Sci., 2018, 443, 274–279 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |