Directional freeze-cast hybrid-backbone meso-macroporous bodies as micromonolith catalysts for gas-to-liquid processes

Abstract

Materials with spatially organized and multimodal porosities are very attractive in catalysis, as they can reconcile nano-confinement effects in micro- and mesopores with fast molecular transport in wide macropores. However, the associated large pore volumes often result in low overall thermal conductivities, and thus suboptimal heat management in reactions with a high thermal signature, usually with a deleterious impact on the catalytic performance. Here we report the directional freeze-casting assembly of bimodally meso-macroporous micromonolithic bodies with a hybrid backbone composed of intimately bound carbon nanotubes (CNTs) and ZrO_x–Al₂O₃ nanocrystals. A honeycomb-shaped and axially oriented macroporous architecture is achieved through the use of zirconium acetate as an ice growth modulator. (S)TEM and EDX nanospectroscopy show that the nanoscale intimacy between the CNT and oxide backbone components depends on the synthesis route of the mother slurry. As revealed by X-ray tomography, coupled to quantitative image analysis, not only the macrochannel size and wall thickness, but also the extent of axial heterogeneities in macropore diameter and spatial orientation depend on the axial temperature gradient rate during casting. The structured bodies are explored as carriers for cobalt-based catalysts for the Fischer–Tropsch production of synthetic hydrocarbons from syngas, of central significance in intensified X-to-liquid processes. Hybrid CNT-Al₂O₃ backbone micromonolith catalysts show a high selectivity to C_3–8 olefins, owing to the fast evacuation of these primary reaction products from the metal active sites through the directional macropore system. Remarkably, the high olefin selectivity is maintained up to higher operating temperatures compared to reference catalysts based on all-oxide supports, due to a higher effective thermal conductivity which inhibits the development of hotspots under industrially relevant operating conditions.

---

1 Introduction

Materials displaying multimodal porosities, which integrate various pore systems ranging from nanometer to micrometer regimes, hold promise for advanced performances in a wide array of technologies.¹ In the field of catalysis, hierarchically organized porosities are interesting due to the fact that they combine high specific surface areas and nano-confinement effects in micro- and mesopores – which are important to facilitate the activation of reactants and stabilize nanosized active species, e.g. metal nanoparticles – with fast molecular transport in wide macropores. Enhanced molecular transport rates through macropores can be exploited to reduce or eliminate mass transport limitations to and from the active sites, as well as to adjust the overall selectivity of the process, e.g. when the pore residence time for highly reactive or unstable intermediate products determines the extent of undesired secondary reactions.²

Organized multimodal porosities are typically assembled through the use of soft- or hard-templating routes. Removal of the template material, often via dissolution, chemical etching or combustion methods, opens up the (tailored) porosity in the final material. Freeze casting synthesis routes pioneered by Fukasawa et al.³ have gathered a significant deal of attention as a relatively cost-effective, versatile and low-waste approach towards materials with well-defined macroporosity. In this case, the hard-templating of a high-pore-volume macroporous system is achieved via the growth of micron-sized crystals (typically ice) from a slurry precursor. Ice contributes a dual role as both a hard template and an auto-assembly driver, leading to the rejection of the initially suspended solid building units from the freezing front and their entrapment in the inter-crystal spaces.⁴ Finally, non-destructive removal of the template under notably mild conditions, via freeze drying (sublimation), and optionally hardening treatments result in the cast material. Such mild removal of the template, alongside the fact that freeze-casting relies primarily on physical phenomena, makes the method suitable for the assembly of materials in a wide range of chemical compositions, from organic to inorganic, from oxidic to carbonaceous.

Directional freeze casting, i.e. the case where the temperature gradient which triggers crystallization is imposed along a specific direction, has been demonstrated to assemble macroscopic bodies with a spatially oriented macroporosity and anisotropic mechanical properties.⁴ In addition to the growth directionality, the use of additives with tensioactive and/or facet-sensitive adsorption properties⁵ has been studied to modulate the ice growth aspect, which can ultimately be inverse-transferred to the cast macropore system after template removal. The scope of materials ranges from ceramics,⁶ polymers,⁷ to graphene (oxide)⁸ and directionally freeze cast materials find application in areas spanning from structural biology⁹ to energy storage¹⁰ or separation.¹¹ Taking advantage of its high material compatibility, (directional) freeze casting is amenable to synthesize not only single-component materials but also bodies with hybrid backbones. Conceivably, this expands the range of properties through the achievement of synergisms between various structural components, an approach which has been explored to develop e.g. ceramic/polymer bodies uniting high fracture toughness with high ductility¹² or lightweight, ductile and electrically conductive graphene/polymer composites.¹³

Although largely unexplored in the field of catalysis, the open porosity of freeze-cast ceramics provides interesting possibilities for enhanced mass transport and to accommodate carbonaceous (coke) deposits while preserving acceptable pressure drops in high-flow catalytic applications.¹⁴ However, their large porosity results in low overall thermal conductivities, which are undesired for reactions with a high thermal signature, as they may result in temperature gradients and uncontrolled hot-spots or even runaway events under relevant operating conditions. Here we report the synthesis of micromonolith bodies with a hybrid backbone composed of carbon nanotubes (CNTs) and mesoporous alumina as scaffolds for solid catalysts in intensified chemical processes. A honeycomb-shaped and axially oriented macroporous architecture, which resembles closely the structure of conventional macroscopic monolithic catalyst bodies at a micrometer scale, is achieved through the use of zirconium acetate as an ice growth modulator. X-ray tomography is coupled to quantitative image analysis to gain fundamental insights into the process of ice growth, in connection to synthesis settings and the ultimate monolith architecture. The mesoporous Al₂O₃ component in the backbone of the micromonoliths serves as an excellent carrier material to disperse and stabilize active cobalt nanoparticles, while percolating CNT skeletons are expected to contribute low thermal resistance pathways and thus improve the spatial dissipation of heat within the catalyst body. The materials are applied as micromonolithic catalysts for the Fischer–Tropsch (FT) synthesis of hydrocarbons from syngas (H₂ + CO), a process of central significance for gas-to-liquid, and more broadly X-to-liquid, technologies geared at the production of synthetic fuels and platform chemicals from carbon resources alternative to petroleum, e.g. (unconventional) natural gas or (waste) biomass. The reaction is highly exothermic (ΔH⁰_r = −170 kJ (mol CO)⁻¹), whilst both heat management and pore mass transport phenomena are known to be determinant for the selectivity of the process, representing an excellent showcase which would benefit from the engineering of hybrid-backbone multimodally porous micromonolithic catalysts.

2 Results and discussion

2.1 Monolith synthesis and characterization

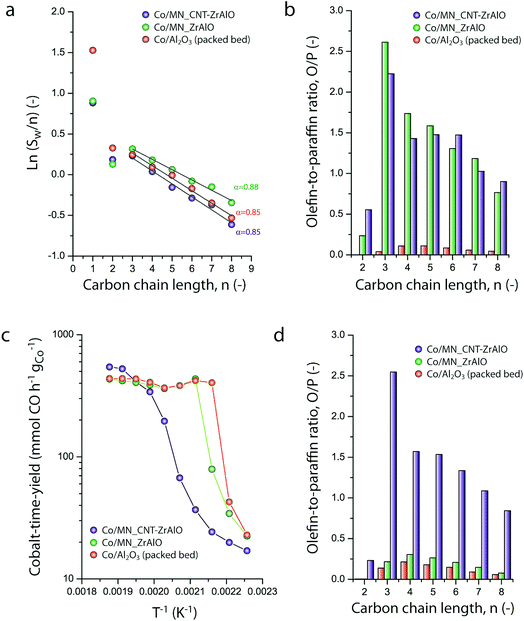
Cylindrical hybrid-backbone micromonoliths were assembled by directional freeze casting through imposing an axial and dynamic temperature gradient to a PVP-stabilized aqueous suspension containing highly graphitic and surface COOH-functionalized multiwall carbon nanotubes (CNTs, Fig. S1†) and water-dispersible pseudo-boehmite (AlO(OH)) solid precursors. The vertical propagation rate of the freezing front was controlled through the adjustment of the cooling rate at the bottom section of the cylindrical monolith mold. Zirconium acetate was dissolved in the mother slurry to act as an ice growth directing agent, given its ability to anchor on the surface of ice crystals through a hydroxy-bridged polymeric structure and thus modify ice growth kinetics and the structure in a way which resembles ice-structuring proteins.^15,16 Four different monolith bodies were cast employing different cooling rates of −10.0, −5.0, −2.0 and −0.5 K min⁻¹, respectively. Fig. 1a shows a picture of a representative body (diameter: 12.5 mm; length: 25 mm) after casting and freeze drying. High-resolution SEM micrographs of a mechanically crushed monolith showed an intimate blend between the oxide and the CNT components in the monolith backbone (Fig. 1b). Cross-sectional SEM imaging revealed a honeycomb-like macroporous structure, aligned along the axial direction of the bodies, regardless of the cooling rate applied during casting (Fig. 1c–f). Monoliths cast through the same protocol, albeit in the absence of zirconium acetate, showed a slit-type macroporous architecture which is conventional for directionally freeze cast materials (Fig. S2†), alongside poorer mechanical stability. These results confirmed the essential role of the zirconium acetate additive to both direct ice growth into hexagonal column crystals, resulting in the honeycomb-like macropore architecture after template removal, as well as a binder, adding to the mechanical compliance of the final monoliths. Despite the fact that the CNT and oxide (hereafter referred to as ZrAlO_x) components were found to be blended in the macropore walls under all synthesis conditions, the route applied to prepare the starting suspension was found to determine the intimacy of both components at the nanoscale. Exemplary, two slurries were prepared by either prolonged wet milling of the solid precursors or high-energy ultrasonication in water using a cell-disruptor (see the Experimental). For the resulting cast bodies, (scanning) transmission electron microscopy ((S)TEM) and energy dispersive X-ray nanospectroscopy (EDX) revealed remarkable differences in the spatial organization of the CNT and oxide building units at the nanoscale. Tightly bound, albeit unblended, patches of the individual components were found in the first case (Fig. S3†). In contrast, ultrasound disruption was found to be essential to achieve a very effective intermixing of the two components at the meso- and nanoscales (Fig. S4 and S5†). Such higher intimacy between the oxide and CNT components eliminates thermally insulating “all-oxide” regions within the skeleton of the monolithic body.

Fig. 1 (a) Picture of a CNT-ZrAlO_x monolith body after freeze-casting and annealing. (b) High-resolution SEM micrograph showing the structure of the channel walls in a CNT-ZrAlO_x monolith. (c–f) Representative cross-sectional SEM micrographs after sectioning CNT-ZrAlO_x monoliths cast at cooling rates of (c) −0.5, (d) −2.0, (e) −5.0 and (f) −10 K min⁻¹ perpendicular to their axial axis.

For reference purposes, all-oxide monolith bodies were assembled from slurries in which the CNT component had been replaced by an equivalent volume amount of Al₂O₃ nanofibers (AONF, Fig. S6†). The textural properties of the individual building units as well as the resulting monoliths were evaluated using N₂ physisorption (Fig. S7†). Both CNTs and AONF nanomaterials showed isotherms with an intermediate character between types III and IV according to the IUPAC classification, with a very narrow hysteresis loop at high relative pressures (P/P₀ > 0.8), indicating the prevalence of very wide mesopores and macropores (not probed by N₂-physisorption) created as interparticle voids within the network of the 1D-shaped primary particles. After annealing, following the same protocol applied to the monolith bodies, the pseudo-boehmite precursor crystallized quantitatively into γ-Al₂O₃, which showed a high specific surface area (320 m² g⁻¹) alongside a type IV isotherm, indicative of an exclusively mesoporous material, for which a total mesopore volume of 0.46 cm³ g⁻¹ and an average mesopore size of 4.5 nm were determined. Monoliths incorporating both γ-Al₂O₃ and either CNTs or AONF, along with ZrO_x species derived from the ice growth modulating agent, displayed specific surface areas – corrected per mass of nanosized inorganic components – in the range of 260 ± 10 m² g_ZrAlOx⁻¹, as well as type IV isotherms with total mesopore volumes of 0.13 ± 0.03 cm³ g_ZrAlOx⁻¹ and average mesopore diameters of 4–5 nm. It is hence inferred that a similar degree of mesoporosity, owed primarily to the high-surface-area γ-Al₂O₃ component, is introduced into the freeze-cast bodies regardless of the nature of the 1D component incorporated as the basis for the material's skeleton. The resulting monoliths display a bimodal meso-macroporosity, ideal to unite a confined stabilization of catalytic metal nanoparticles in mesopores, with fast (non-Knudsen) molecular transport rates within macropores.

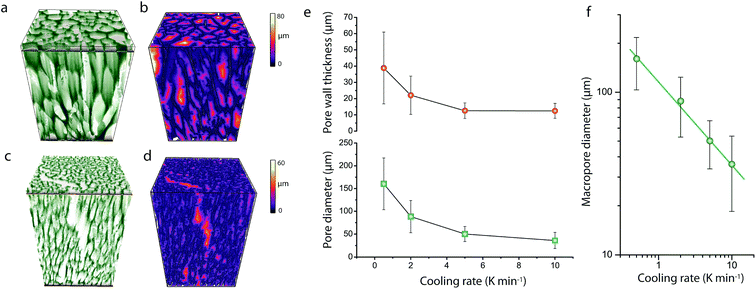
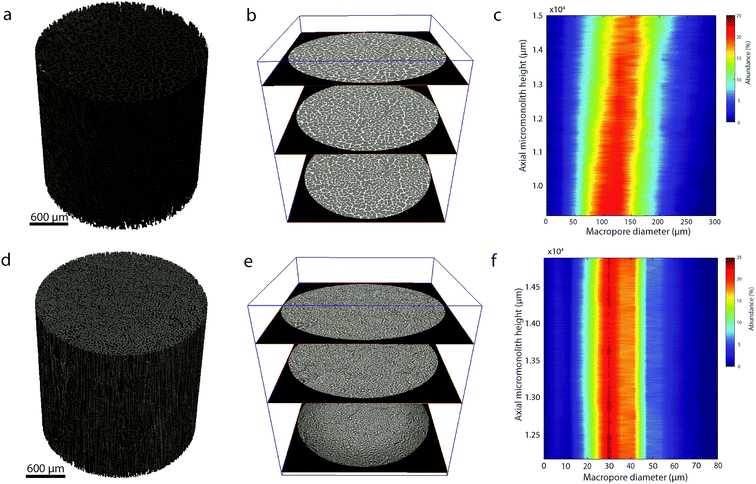
As shown in Fig. 1, cross-sectional SEM imaging after deliberate monolith fracture suggested the axial alignment of the macropores in the monoliths. To gain further insight into the macroporous architecture of these materials – and thus into the growth of ice crystals during directional freeze casting – selected intact monolith bodies were imaged with X-ray tomography. This tomographic (3D) imaging method has been previously applied to image the internal architecture of portions of freeze-cast solids.^17–19 However, very recent advancements, namely the so-called two-stage magnification approaches, have helped disentangle the spatial resolution from the operating distance and opened the way to submicron resolution imaging of unprecedently large bodies in their intact form. Here, we have taken advantage of these advances to image the internal microstructure of CNT-ZrAlO_x monolithic bodies with a resolution down to 0.85 μm (Fig. S8†). Fig. 2 shows the reconstructed tomograms for a representative sub-region of monoliths cast at −0.5 and −10 K min⁻¹, respectively. A local thickness algorithm was applied to analyze the macropore diameter as well as the macropore wall thickness as a function of the cooling rate applied during casting (Fig. 2b and d). As shown in Fig. 2e, both the volume-averaged macropore diameter and the pore wall thickness decreased remarkably upon increasing the cooling rate in the range from −0.5 to −5 K min⁻¹, and then further decreased only to a minor extent upon further increasing the cooling rate to −10 K min⁻¹. The macropore diameter (PD), i.e. the cross-sectional size of the ice crystals developed in situ as hard templates during freeze casting, depended on the cooling rate (σ) according to a power law, PD = kσⁿ, where the exponent n was found to be 0.50 (Fig. 2f). Such dependence can be ascribed to an increase in the magnitude of supercooling ahead of the freezing interface, resulting in higher nucleation rates and narrower ice crystal sizes, upon increasing the propagation rate of the freezing front with increasingly higher cooling rates.⁷

Fig. 2 (a and c) Surface-rendered 3D reconstructed X-ray tomograms and (b and d) local thickness 3D contour maps for the macropore diameter for CNT-ZrAlO_x micromonoliths freeze cast at cooling rates of −0.5 K min⁻¹ (a and b) and −10 K min⁻¹ (c and d). (e) Evolution of the volume-averaged macropore diameter and macropore wall thickness with the cooling rate applied to freeze cast CNT-ZrAlO_x micromonoliths. (f) Relationship between the volume-averaged macropore diameter and the cooling rate applied during freeze casting for CNT-ZrAlO_x micromonoliths. Error bars correspond to the standard deviation of the average.

In addition, quantitative image analysis of the X-ray tomograms reconstructed over mm³-sized volumes revealed structural heterogeneities in the structure of the cast monolith bodies, along their axial direction, as a function of the cooling rate applied during casting. Fig. 3 shows the axial evolution of the macropore size histogram over mm-long distances for CNT-ZrAlO_x micromonoliths cast at −0.5 and −5 K min⁻¹, respectively. For the slowest cooling rate, resulting in a coarser macropore system, a significant right-shift and broadening of the macropore size distribution is observed in the positive z-direction, which indicates the progressive growth of ice crystals as the freezing-front propagates vertically during monolith casting. Analysis of the spatial kinetics of this growth phenomenon was performed according to an equation of the type:

where S denotes the volume-specific surface of the growing ice crystals during casting (as determined from the cross-sectional diameter of the corresponding macropores in the cast body, assuming no significant shrinkage during template removal), z is the axial coordinate along the ice propagation direction, and the growth constant k and the exponent n are two independent fitting parameters. These growth kinetics provided a reasonably good description of the experimental data extracted from the reconstructed tomogram, being the optimal least-square fit to the z-resolved macropore size distributions obtained for n = 1 (k = 2.9 × 10⁻⁷ μm⁻¹), see Fig. S9.† These results indicate that the cross-sectional growth of ice columns, as the ice front propagates during casting, can be adequately described with a conventional solid state sintering model, in which the rate of ice surface decay is approximately proportional to the ice specific surface area. In contrast, no significant variations of the macropore diameter were observed as a function of the axial monolith coordinate for the monolith cast at a 10 times faster cooling rate of −5 K min⁻¹, indicating that the sintering of ice crystals during freeze casting can be inhibited kinetically, by increasing the rate of spatial propagation of the freezing front during casting.

Fig. 3 (a and d) Reconstructed X-ray tomograms; (b and e) selected slices along the reconstructed X-ray tomograms; and (c and f) contour plot showing the evolution of the number-weighted macropore size histogram with the axial length along the monolith as derived from quantitative image analysis of the tomograms for micromonoliths with a CNT-ZrAlO_x backbone freeze-cast employing cooling rates of (a–c) −0.5 and (d–f) −5 K min⁻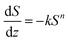¹.

Moreover, image analysis of the reconstructed tomograms revealed cross-sectional shape deformations, as well as trajectories which deviated significantly from the z-axis of the macroscopic cylindrical body, for the macropore channels as they propagate along the axial direction of the monoliths (Fig. S10†). Even though more complex image analysis routines need to be ad hoc developed in the future to get further insight into this phenomenon, this finding suggests that during casting ice crystals grow along minimum-energy microscopic pathways, collectively determined by the population of crystals composing the freezing front, and hence not perfectly aligned with the macroscopic temperature gradient.

In order to assess the impact of the backbone composition on the thermal properties of the micromonolith bodies, the effective thermal conductivity of the macroporous materials was determined using a hot-disk method. A thermal conductivity of 0.0890 ± 0.0003 W m⁻¹ K⁻¹ was determined for the all-oxide ZrAlO_x monolith, which is in the range expected for a highly porous oxide. Remarkably, the effective thermal conductivity was 0.236 ± 0.002 W m⁻¹ K⁻¹ for the CNT-ZrAlO_x counterpart, i.e. a significant 2.5-fold increment, which is comparable in magnitude to those reported previously upon incorporation of MWCNT fillers in composites with microporous zeolite crystals.^20,21 The value obtained for the effective thermal conductivity is far lower than the values of >100 W m⁻¹ K⁻¹ reported for bundles of MWCNTs,²² which reflects the contribution of interfaces and porosity to the overall thermal resistance of the hybrid-backbone monolith composites. Nevertheless, its value is in the range of those reported for highly porous metal foams²³ and thus susceptible to bring about noticeable differences in the thermal response of the multimodally porous bodies in demanding catalytic applications.

2.2 Incorporation of Fischer–Tropsch active species

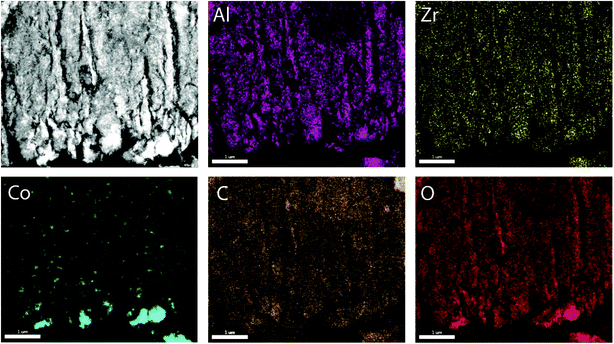
To prove the suitability of the multimodally porous micromonoliths as catalyst supports, Fischer–Tropsch active cobalt species were incorporated on selected bodies (cast at a cooling rate of −5 K min⁻¹) by impregnation of the pre-dried monolith with an aqueous solution of nitrate precursors, followed by controlled drying and metal nitrate thermal decomposition. Ruthenium was added in a Ru/Co atomic ratio of 0.02 as a promoter, to facilitate the reduction of cobalt oxides at lower temperatures.²⁴ Cross-sectional photographs showed a spatially uniform distribution of the metal precursor throughout the monolith body after impregnation, suggesting a successful fixation of the impregnating solution by capillary forces within the mesoporous skeleton (Fig. S11†). After nitrate decomposition, X-ray diffraction (XRD) showed the Co₃O₄ spinel as the only crystalline metal phase (Fig. S12†). Line broadening analysis revealed volume-averaged Co₃O₄ crystallite sizes of 13 and 23 nm for catalysts supported on micromonoliths with an all-oxide ZrAlO_x and a hybrid CNT-ZrAlO_x backbone, respectively. After reductive activation in a hydrogen flow, these metal oxide crystallite sizes translated into specific metal surface areas of 11 and 7 m² g_Co⁻¹, respectively, as quantified by H₂-chemisorption. These results indicate that a slightly lower metal dispersion is achieved on the hybrid-backbone CNT-ZrAlO_x monolith, likely due to a lower chemical interaction of the metal nitrate precursors with the more hydrophobic CNT component, which favors a higher extent of metal agglomeration during impregnation and drying.

The nanoscale spatial distribution of different elements within the structure of the Co/CNT-ZrAlO_x monolithic catalysts was examined with HAADF-STEM and EDX on ultramicrotomed specimens. As observed in Fig. 4, cobalt species were found to be dispersed within the ZrAlO_x-based mesoporous regions which constitute the walls of the axial monolith channels. In addition, a few larger cobalt oxide crystals were also found on the outer surface of these macropore walls, thus not confined to the mesoporosity of the monolith. These unconfined cobalt species appeared not only as relatively large (>100 nm) Co₃O₄ crystals (Fig. 4) but also as clusters of smaller cobalt oxide crystallites stabilized by ZrO_x species which protrude out of the Al₂O₃-rich macropore walls (Fig. S13†). All three populations of cobalt oxide crystals contribute to a volume-averaged Co₃O₄ crystallite size of 23 nm determined for this material by XRD. In all cases, a very high dispersion of ZrO_x species is ascertained, which brings these species into close contact with the FT-active Co species. This is desirable, as mildly Lewis acidic oxides, such as ZrO₂, have been shown to act as activity promoters in the cobalt-catalyzed FT reaction.^25,26 Overall, these characterization results illustrate the incorporation of highly dispersed cobalt nanocrystals within the mesopores of the micromonolith carriers by a simple and scalable impregnation route, coexisting, however, with a few larger extra-mesopore agglomerates located on the outer walls of the monolith microchannels.

Fig. 4 Representative HAADF-STEM micrograph (top-left panel) of an ultramicrotomed cross section (150 nm nominal thickness) of a Co/CNT-ZrAlO_x micromonolithic catalyst and EDX compositional maps of the same region obtained from the corresponding K-spectral lines.

2.3 Catalysis

Micromonolithic bodies like the ones assembled herein could be interesting as solid catalysts in intensified chemical processes. Their reduced dimensions are well suited to their application in miniaturized reactor technologies, while their resemblance to conventional monolith-structured catalysts is ideal for modular upscaling and once-through flow operations with a limited pressure drop. At present, there is rising interest in developing intensified and miniaturized X-to-liquid technologies, e.g. based on the Fischer–Tropsch synthesis of hydrocarbons from (bio)syngas, to valorize a wide array of unconventional and renewable, small-scale and spatially delocalized carbon-based raw materials.²⁷ The catalytic activity of selected cobalt-loaded micromonoliths was assessed under industrially relevant operating conditions. In order to investigate the impact of the monolith backbone composition on the heat management under reaction conditions, experiments were designed to avoid direct temperature feedback from the catalyst body into the heating control loop, by controlling the temperature at the outer side of the reactor wall while ensuring negligible axial temperature gradients. The results are summarized in Fig. 5. At a reaction temperature of 453 K, the lowest at which full product distribution analysis was possible, monolithic Co/CNT-ZrAlO_x and Co/ZrAlO_x catalysts showed a cobalt-time-yield (CTY) of 20 and 34 mmol CO h⁻¹ g_Co⁻¹, respectively, slightly lower than the time-yield of 43 mmol CO h⁻¹ g_Co⁻¹ obtained with a benchmark granular CoRu/Al₂O₃ catalyst tested in a packed bed configuration under otherwise identical operational settings. Differences in activity arose from differences in the available cobalt surface area after catalyst reductive activation, whereas the Turnover Frequencies (TOFs), determined per surface-exposed metal atom, were all in the range of 1.3 ± 0.5 × 10⁻³ s⁻¹ at this temperature. Under mild operating temperatures (<473 K) similar hydrocarbon chain growth probabilities of 0.86 ± 0.02 were obtained for all three catalysts (Fig. 5a). However, the hydrocarbon product patterns differed notably in terms of olefinicity. As shown in Fig. 5b, monolithic catalysts led to over an order of magnitude higher olefin-to-paraffin molar ratio in the hydrocarbon chain length range of C_3–8 compared to the reference CoRu/Al₂O₃ catalyst. 1-Olefins are known to be a primary product of the Fischer–Tropsch reaction.²⁸ However, they can readsorb on the metal sites and undergo pore transport-enhanced secondary chain-reinsertion and hydrogenation reactions into paraffin secondary products, as they diffuse out of the catalyst particle where they formed.²⁹ This secondary processing of primary reaction products typically results in a significant depletion of olefins in the final product hydrocarbon mixture when conventional, e.g. essentially mesoporous, cobalt-based catalysts are applied under industrially relevant operating conditions. These phenomena limit the suitability of highly active cobalt-based FT catalysts to produce liquid (C₅₊) olefins, which are particularly interesting products of the reaction. Fischer–Tropsch olefins have been shown to moderate undesired overcracking in tandem FT-hydrotreating processes geared at the production of wax-free hydrocarbons in a single reactive step.³⁰ Moreover, they serve as precursors for important chemicals such as syngas-derived higher oxygenates, via a subsequent hydroformylation step.³¹ It has been shown that the development of catalysts with hierarchically organized meso-macroporous structures results in shorter effective transport distances for primary products in contact with the metal species, mitigating secondary olefin hydrogenation and resulting in an enhanced olefinicity in the final products over a very wide range of CO conversion levels.^32,33 Hence, we ascribe the very high C₃₊ olefin content in the products obtained with the monolithic catalysts to a very fast evacuation of these primary reaction products from the active sites, by diffusion through the ultrathin mesoporous channel walls (<70 μm thickness, Fig. 2e) followed by convective transport along the wider macropores.

Fig. 5 (a) Anderson–Schulz–Flory hydrocarbon chain-length distribution plots and (b) olefin-to-paraffin molar ratio for hydrocarbon products in the carbon chain length range from C₂ to C₈, for different Co-based Fischer–Tropsch catalysts at 463 K. (c) Evolution of the metal-specific Fischer–Tropsch reaction rate (cobalt-time yield) with the reaction temperature for different Co-based Fischer–Tropsch catalysts. (d) Olefin-to-paraffin molar ratio for hydrocarbon products in the carbon chain length range from C₂ to C₈, for different Co-based Fischer–Tropsch catalysts at 483 K. WHSV = 1.44 g_CO g_Co⁻¹ h⁻¹, P = 20 bar, and H₂/CO = 1.0.

As discussed above, a major challenge faced in highly intensified, e.g. once-through (high conversion per reactor pass) chemical processes based on catalytic reactions with a high thermal signature, is the management of the heat of reaction in order to avoid the development of significant temperature gradients within the solid catalyst, which is often based on a porous oxide as a support and hence intrinsically insulating. The remarkably exothermic Fischer–Tropsch synthesis of hydrocarbons is a relevant showcase. Suboptimal dissipation of the heat of reaction might lead to the development of hotspots within the catalyst body/bed (and even runaway events) with deleterious consequences for the selectivity of the reaction, i.e. an enhanced production of undesired methane and C₄₋ light gases, and catalyst lifetime. Hence, several approaches have been put forward to increase heat dissipation within Fischer–Tropsch catalyst beds. They include the deposition of thin catalyst overlays on conventional macromonoliths with metallic backbones³⁴ or the entrapment of microparticulate catalysts within metallic open foams³⁵ or meshes.³⁶ These strategies add to the temperature uniformity within the catalyst compartment under conditions where convective heat transfer from the circulating gas phase to the conductive component of the catalyst bed/body is expected to be followed by a conductive heat dissipation within the latter. However, these approaches are only compatible with relatively low volumetric catalyst loadings and thus low reaction throughputs. The hybrid backbone micromonoliths developed in this study might represent a suitable alternative, offering higher volumetric catalyst loadings owing to the much higher surface-to-volume ratio of their directional microchannels. In order to assess the influence of the CNT skeleton on the thermal behavior of the micromonolith catalyst, a set of experiments involving the stepwise increase of the reaction temperature at a constant metal-specific syngas space velocity of 9.2 mmol syngas g_Co⁻¹ min⁻¹ were performed. As shown in Fig. 5c, a very steep increase in the catalytic activity was observed when either the reference CoRu/Al₂O₃ microparticulate catalyst or the Co/ZrAlO_x monolith were tested, leading to essentially full CO conversion (plateau in time-yield) and exceedingly high methane selectivities (>43%) at 473 K. Both the steep activity increment with the temperature, actually corresponding to an unrealistically high apparent activation energy of 225–243 kJ mol⁻¹, and the boost in undesired methanation indicate the creation of hotspots within the catalysts already at these relatively mild operating temperatures. This is a general shortcoming of highly active cobalt-based Fischer–Tropsch catalysts based on all-oxide, thermally insulating porous support materials (Al₂O₃ and ZrAlO_x in this study). In marked contrast, the Co/CNT-ZrAlO_x monolithic catalyst displayed a much more progressive increase in the specific catalytic activity over a wider range of operating temperatures 443–523 K (Fig. 5c). In this case, an Arrhenius analysis in the temperature range of 463–503 K resulted in an apparent activation energy of 134 kJ mol⁻¹, significantly better aligned with an intrinsic activation energy of ca. 100 kJ mol⁻¹ known for the FT reaction.³⁷ The inhibition of hotspots is also reflected in the fact that the Co/CNT-ZrAlO_x monolith catalyst retains a very high selectivity to C₃₊ olefin products even upon increasing the temperature. This is for instance illustrated in Fig. 5d at a reaction temperature of 493 K, at which catalysts based on a purely oxidic carrier, either monolithic or granulated, offer a much lower olefin content in the reaction products due to the enhancement of secondary hydrogenation at hotspots developed within their structure. Overall, these results suggest a notably improved heat management, largely inhibiting the development of hotspots owing to the higher effective thermal conductivity of the hybrid CNT-oxide micromonolith backbone.

3 Conclusions

Micromonolith bodies with a hybrid backbone, integrating mesoporous ZrAlO_x oxide species and a carbon nanotube skeleton, have been assembled via directional freeze casting. The materials display a bimodal porosity which unites mesoporous walls with a honeycomb-like system of macropore channels running along the axial direction of the bodies. Quantitative X-ray tomography reveals a complex propagation of the macrochannels, with axially resolved heterogeneities in macropore size and trajectory, likely as a result of deflection and sintering phenomena at play during the directional growth of ice crystals in the casting stage. The mesoporous oxide component in the backbone of the micromonoliths enables the dispersion of ruthenium-promoted cobalt nanoparticles by a simple, capillarity-driven impregnation approach from nitrate precursor solutions, while the incorporation of the CNT skeleton leads to a 2.5-fold increment in the effective thermal conductivity in the composite bodies. The cobalt-loaded structured micromonoliths proved to be effective catalysts for the Fischer–Tropsch synthesis of synthetic hydrocarbons from syngas. Under industrially relevant reaction conditions, higher rates of evacuation of primary reaction products from the metal active sites through a directional macropore system leads to notably enhanced selectivities to liquid (C₅₊) α-olefin products compared to conventional, microgranulated catalysts based on unimodally mesoporous γ-Al₂O₃ support materials. Moreover, the higher effective thermal conductivity associated with the hybrid CNT-ZrAlO_x micromonolith backbone inhibits the development of hotspots within the catalyst body, preventing undesired secondary hydrogenation of primary olefin products and methanation reactions in a wider range of operating temperatures. These findings illustrate the significance of a dual compositional and structural design of multimodally porous bodies by directional freeze casting to produce effective solid catalysts for intensified catalytic processes based on reactions with a high thermal signature.

4 Experimental

4.1 Synthesis of monolithic scaffolds

Hierarchically porous monolithic scaffolds with Al₂O₃/CNT (50–50 wt%) hybrid backbones were synthesized by unidirectional freeze casting. Starting suspensions were prepared by mixing 3.0 g of nanosized pseudo-boehmite (Disperal P2, Sasol), 2.30 g of COOH-functionalized graphitized multi-walled carbon nanotubes (Cheap Tubes Inc.) and 250 mg of polyvynilpyrrolidone PVP (MW 24 000, Sigma Aldrich) in 60 mL deionized water. After mixing, the solid components were dispersed by either mechanical grinding or through the use of an ultrasonic homogenizer (Bandelin Sonopuls HD 2200, 20 kHz) for 3 hours. Next, the water content in the suspension was reduced to 70 wt% by rotary evaporation under reduced pressure and 8.5 mL of a zirconium acetate solution (∼16% Zr, Sigma Aldrich) were added as an ice growth directing agent. Prior to ice casting, the resulting slurry was poured into a cylindrical PTFE mold and de-aired in a vacuum desiccator and tempered in a cold-room (kept at 276 K). Vertically oriented ice casting was performed by applying a dynamic temperature gradient along the axial direction of the cylindrical mold. This was achieved by cooling at the bottom of the PTFE mold using a liquid nitrogen-cooled copper rod, while keeping the temperature of the air in contact with the top surface of the suspension constant at 276 K and preventing radial heat flux via isolation with PTFE. The cooling rate was adjusted in the range of 0.5–10 K min⁻¹ through a thermocouple and a ring heater placed around the copper rod. Once the freezing of the suspension was complete, the samples were freeze dried at 258 K and 0.1 Pa for at least 72 hours, in order to ensure complete removal of the ice template, and further annealed under an Ar flow at 773 K for 10 hours (heating rate of 5 K min⁻¹). Reference all-alumina micromonoliths were synthesized following the same procedure, with the exception of replacing the CNT component for an identical volume of Al₂O₃ nanofibers (Sigma-Aldrich).

4.2 Incorporation of Fischer–Tropsch active species

A stock solution was prepared dissolving 20 g of Co(NO₃)₂·6H₂O (98%, Sigma Aldrich) in the required volume of a 0.25 vol% HNO₃ aqueous solution to obtain 3.4 M concentration. To this solution, 9.8 mL of a ruthenium(III) nitrosyl nitrate solution in diluted nitric acid (Sigma Aldrich, 1.5 wt% Ru) were added. Prior to metal incorporation, the micromonolith was dried at 473 K under dynamic vacuum (3 × 10⁻⁵ bar) for 2 hours. Then, 1 mL of the metal nitrate stock solution was dripped onto the monolith under static vacuum and fixed within the body by capillary forces. The impregnated monolith was transferred to a quartz tube and dried at 343 K for 20 hours under an Ar flow followed by calcination at 623 K (heating rate of 2 K min⁻¹) for 4 hours in an Ar flow in order to decompose the nitrate metal precursors into the corresponding oxide species. The cobalt content was set to 1 mmol Co per monolith in all cases. A reference microparticulate Co–Ru/γ-Al₂O₃ catalyst (22 wt% Co nominal content) was synthesized via repeated incipient wetness impregnation of a commercial alumina support material (Puralox NWa155, Sasol, 0.4–0.6 μm particle size) as described elsewhere,³² applying the same drying and nitrate decomposition thermal treatments after each impregnation step. In this case, the overall cobalt content in the catalyst bed was also set to 1 mmol Co via dilution with the γ-Al₂O₃ microbeads used as the catalyst support.

4.3 Characterization methods

N₂-physisorption. Nitrogen physisorption isotherms were recorded at 77 K using a Micromeritics 3Flex instrument. Prior to the adsorption experiment, the micromonoliths were ground down to particles in the range of 40–80 μm and degassed at 423 K under vacuum for 5 h. Surface areas were derived using the BET method in the relative pressure (P/P₀) regime of 0.05–0.30. Total mesopore volumes were derived from the amount of N₂ adsorbed at a relative pressure P/P₀ = 0.95 and mesopore size distributions were determined by using the BJH formalism applied to the desorption branch of the isotherm.

H₂-chemisorption. H₂-chemisorption followed by temperature-programmed-desorption (H₂-TPD) experiments were performed using a Micromeritics Autochem 2910 device to quantify the surface-exposed metallic surface area of the as-reduced catalysts. About 200 mg of sample (in the case of monolith bodies, ground to discrete particles in the range of 40–80 μm) were initially flushed with an Ar flow (50 cm³ min⁻¹) at 748 K (heating ramp of 5 K min⁻¹) for 15 min, and then cooled down to 323 K. The sample was then reduced under 10 vol% H₂ in Ar at 673 K (heating ramp of 3 K min⁻¹) for 8 h. After reduction, the gas was switched to Ar and the temperature increased up to 723 K (heating ramp of 3 K min⁻¹) for 1 h, to remove any chemisorbed H₂. The sample was then cooled down to a temperature of 493 K, at which the gas was switched to 10 vol% H₂ in Ar and further cooled to 323 K, allowing the chemisorption of H₂ on the cobalt surface. The sample was then flushed with an Ar flow (50 cm³ min⁻¹) for 80 min to remove non-bound H₂, after which the H₂ desorption profile was measured using a thermal conductivity detector (TCD) previously calibrated via the injection of known volumes of hydrogen using a gas syringe by heating the sample from 323 K to 748 K at a rate of 10 K min⁻¹. To determine specific metal surface areas and surface metal sites, a chemisorption stoichiometry of H/Co_s = 1 and a surface site density of 14.6 Co_s nm⁻² were considered.

X-ray diffraction. Powder X-ray diffraction (XRD) patterns were recorded using a STOE Theta/Theta diffractometer operating in reflection mode with Cu Kα radiation which was monochromatized with a secondary graphite monochromator using a step size of 0.02° and an accumulation time of 3 s per step.

Scanning electron microscopy (SEM). Cross-sectional scanning electron micrographs of the monolithic bodies were collected with a Hitachi TM3030 microscope. The monoliths were razor-sectioned perpendicularly to the axial direction, mounted on a pin-stub holder and gently blown with compressed air to remove surface debris generated upon sectioning.

Bulk chemical analysis. The overall (bulk) chemical composition of the materials was determined by means of Energy Dispersive X-ray (EDX) spectroscopy. The samples were finely ground in a mortar and the resulting powder was applied on a pin-stub SEM mount coated with a double-adhesive-face conductive carbon-tab. Areas of 1 mm² were analyzed and the resulting EDX spectra were collected with an Oxford Pentafet 10 mm² detector.

TEM. For scanning transmission electron microscopy and nanoscale energy dispersive X-ray spectroscopy analysis, powder materials, e.g. CNTs and alumina nanofibers, were directly drop-cast on a copper TEM grid (400 mesh) covered with a lacey carbon film. In the case of monolithic bodies, and in order to gain access to extended cross sections of the materials and avoid artifacts arising from uneven specimen thickness, samples (in the case of monolith bodies, ground to discrete particles <200 μm) were first embedded in a low viscosity resin (Spurr) and then nanometer thin slices (nominal thickness of ca. 150 nm) were obtained with a Diatome diamond knife mounted on a Reichert Ultracut ultramicrotome and collected on a copper TEM grid (400 mesh) covered with a lacey carbon film. Bright-field TEM experiments were performed with a Hitachi H7500 microscope operated at 100 kV. High-angle annular dark field (HAADF) micrographs and EDX elemental maps were acquired using a C_s-corrected Hitachi HD-2700 dedicated Scanning Transmission Electron Microscope (STEM) equipped with a cold field-emission gun and two EDAX Octane T Ultra W EDX detectors and operated at 200 kV.

X-ray tomography. X-ray computed tomography (CT)³⁸ as a non-destructive technique for collecting 3D volumetric data of opaque solid objects was applied to analyze the interior structure of the four monolithic scaffolds. A series of projection X-ray radiographs at various viewing angles (achieved by rotating the monoliths and exposing them to the X-ray beam) were collected using a Zeiss Xradia 520 Versa X-ray microscope (Carl Zeiss X-ray Microscopy, Pleasanton, CA, USA). The resulting projection images were subsequently reconstructed by using commercial reconstruction software from Zeiss (Scout and Scan Control System) using a Feldcamp standard filtered back projection algorithm and stored as a stack of tomograms.

All scans within this study were performed with an X-ray energy level of 80 kV and 7 W. First, the four monoliths (cast at cooling rates of −0.5, −2.0, −5.0 and −10.0 K min⁻¹, respectively) were scanned with a field of view of approximately 14 × 14 mm² (0.4× objective lens, the 2 k × 2 k CCD camera binned 2 × 2), resulting in a voxel size of 14 μm. Thus the whole diameter and more than half of the monolith height could be imaged for a first analysis of the rough inner monolith structure. After that, the “Scout & Zoom” technique^39,40 was applied to non-destructively (i.e. without sectioning) image sub-regions inside the monoliths with higher resolution, thus enabling to adequately resolve all details of the inner macropore walls. A 4× objective lens was used to collect a total of 3201 projections from each sample with a voxel size of 0.85 μm (camera binned 2 × 2), resulting in a reconstructed cylindrical volume with approximately 850 μm both in diameter and height.

In addition, for the monoliths cast with the lowest cooling rate of −0.5 K min⁻¹ and the one cast at a 10 times faster cooling rate of −5.0 K min⁻¹, a considerably larger volume of the inner structure was scanned with a still higher resolution. Taking into account the macropore diameter and macropore wall thickness of the different samples, the monolith cast with −0.5 K min⁻¹ (resulting in a coarser macropore system) was scanned with a voxel size of 3 μm, while the sample cast with −5.0 K min⁻¹ (finer macropore system) was scanned with a voxel size of 1.5 μm (camera binning = 1 for both scans). Thus, from 3201 projection images collected for each sample, cylindrical volumes with diameters (and heights) of about 6 and 3 mm, respectively, could be reconstructed.

X-ray tomogram quantitative image analysis. Raw data stacks were slightly filtered using a smoothing filter (Gaussian or anisotropic diffusion filters) and segmented using a single threshold value. Macropore diameter and pore wall thickness analyses were performed in 3D by applying a local thickness algorithm⁴¹ implemented in the Bonej plugin for FIJI on the reconstructed volumes collected with a resolution of 0.85 μm (as shown in Fig. S8†). The algorithm defines the local thickness at each sampling point within the segmented “solid” phase of the tomogram as the diameter of the greatest sphere which fits within the “trabeculae” of the solid phase, delimited in this case by voxels corresponding to the macropore or pore wall phases, respectively, and which contains the said sampling point. The analysis of the evolution of the macropore diameter with the axial length along the axial axis of the micromonoliths was applied on much larger datasets (shown in Fig. 3a and d) and is based on a similar method. An algorithm for calculating the particle size distribution of multiphase electrodes⁴² was used, adapted for the analysis of segmented 2D images. It calculates a distance map based on the Euclidean distance transform, where the value of each pixel corresponds to the distance to the closest pixel outside the pores. Hence, the value at a maximum in the distance map corresponds to the radius of the largest circle that can be placed inside the pores. Based on the individual pore sizes, the average pore size and the pore size distribution are then calculated. By applying this to each of the almost 2000 slices in the axial monolith direction, the evolution of the pore size distribution with respect to the monolith height could be calculated. 3D rendering and visualization were performed in Avizo (Thermo Fisher Scientific) and GeoDict (Math2Market Gmbh).

Effective solid heat conductivity analysis. The effective heat conductivity of the porous monolith bodies was determined at room temperature with a hot disk TPS 2500 S conductimeter equipped with a Kapton sensor 7577 (2 mm diameter). The dried solid materials were placed between two sample holders to achieve a probing depth of 3 mm. Measurements were performed on intact portions of the monoliths, after cross-sectional slicing at the required thickness, and also after disassembly of the bodies by gentle grinding, to ensure an adequate contact to the flat temperature sensor. In both cases, very similar thermal conductivity values (deviating less than 10%) were obtained. Each measurement was repeated three times and the standard deviation took values <0.7% of the average in all cases.

Catalytic tests. Catalytic experiments were performed in a 316 L stainless-steel fixed-bed reactor (12 mm inner diameter). Gas feeds, i.e. H₂ (99.999%, Air Liquide) and a premixed syngas mixture (CO : H₂ : Ar 3 : 6 : 1, Ar as an internal standard for chromatography, from Air Liquide) were fed using calibrated mass flow controllers (Bronkhorst). Upstream of the reactor, the syngas feed stream was purified in a high-pressure metal carbonyl trap operated at 30 bar and room temperature and filled with commercial activated carbon pellets (Norit Darko 12 × 20). For catalytic experiments using micromonoliths, the cylindrical monolithic bodies (diameter = 10.5 mm, height = 25 mm) were embedded in a ceramic embedding medium (Thermokitt Roth 1100 °C, Roth) using a cylindrical mold in order to ensure a tight fit with the inner surface of the stainless-steel reactor. The encased monolith was fit-mounted inside the reactor and a 9 mL bed of SiC granules (350–560 μm, grit 46) was placed upstream of it to achieve turbulent plug-flow conditions at the front section of the monolithic body. Downstream of the micromonolith a second 2 mL layer of SiC granules was placed. The embedded monolith and the two SiC beds were held in place using two quartz wool plugs. The reactor was heated with two finned copper elements, with embedded heating cartridges (180 W), which were tightly attached to the outer surface of the reactor tube. This heater design ensures a high rate of heat dissipation to the atmosphere and prevents axial temperature gradients. In order to test the heat management provided by different (monolithic and conventional particulate) catalysts under industrially relevant reaction conditions, a set of experiments was conducted placing two steering thermocouples (K-type, 2 mm) at the boundary between the outer reactor wall and the inner wall of the heating elements, with axial positions coinciding with the upstream SiC bed and the micromonolith, respectively. This configuration intentionally avoided temperature feedback from the catalytic body into the PID control loop, and thus enabled the evaluation of the thermal management in the catalyst indirectly, through performance parameters which are very sensitive to the presence of hotspots, i.e. the apparent activation energy or the selectivity to methane. Reference experiments were performed with a commercial-like microparticulate CoRu/Al₂O₃ catalyst (400–600 μm macroscopic particle size). In this case, the catalyst was diluted with high-purity γ-Al₂O₃ microbeads to achieve an identical bed length and overall cobalt loading in the reactor as for the tests performed with micromonolithic bodies. Prior to catalysis, cobalt (and ruthenium) species in the catalyst body were reduced at atmospheric pressure under a H₂ flow (200 mL min⁻¹) at 723 K (3 K min⁻¹, 8 h). After reduction, the reactor was cooled to 423 K and the gas flow was switched to syngas. After 5 min, the system was pressurized to a reaction pressure of 20 bar, which was further controlled during the reaction experiments using a membrane dome pressure regulator (GO regulator), and the syngas flow was set to 100 mL min⁻¹, corresponding to a cobalt weight-hourly space-velocity (WHSV) of ca. 1.44 g_CO g_Co⁻¹ h⁻¹. Next, the reactor temperature was slowly increased to the desired reaction temperature (0.1 K min⁻¹ to 683 K) and increased stepwise to higher reaction temperatures up to 733 K (10 K steps, heating ramp 0.2 K min⁻¹). Downstream of the tubular reactor two consecutive cold traps were set at temperatures of 423 and 373 K, respectively, at the reaction pressure, to collect heavy hydrocarbons and part of the water product. The rest of all pipelines downstream of the reactor were kept at a temperature of 443 K to prevent condensation. The lighter fraction of hydrocarbons leaving the traps was depressurized in the dome pressure controller and analyzed online by gas chromatography (GC). The online gas chromatograph (Agilent) was equipped with two sampling loops of which one injects towards a capillary column (RTX-1, 60 m) and a FID detector for the analysis of the hydrocarbons, and the other injects towards two consecutive packed bed columns (HS-Q 80/120 1 and 3 m respectively) and a TCD detector for the analysis of H₂, CO₂ and C₂–C₃. Along this analysis channel, a molecular sieve column is additionally used to separate Ar, CH₄ and CO, which were detected in a second TCD detector. CO, CH₄ and CO₂ were quantified using response factors relative to the Ar internal standard, whereas C₂₊ hydrocarbons were quantified based on their FID signal relative to methane, after calibration with several PIANO analytical standard hydrocarbon mixtures (Sigma-Aldrich).

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

The authors are grateful to Sasol and Dr Patrick Bussian for providing the commercial pseudo-boehmite Al₂O₃ precursor. The authors are grateful to W. Kersten and his team (MPI-KOFO) for their contribution to the assembly of the freeze-casting setup and to P. Malkowski (MPI-CEC) for access to a cold-room and cell-disruption equipment. B. Spliethoff, and A. Schlüter are acknowledged for TEM characterization and F. Winkelmann (MPI-KOFO) and Paul Stannek (ZBT GmbH, Duisburg) for their assistance with the thermal conductivity measurements. This research received funding from the Fonds der Chemischen Industrie of Germany and the Max Planck Institute für Kohlenforschung. The financial support of the Deutsche Forschungsgemeinschaft (DFG) throughout the projects 281041241/GRK2218 (SiMET) and GZ: INST 121384/134-1 FUGB is also highly acknowledged. Open Access funding provided by the Max Planck Society.

References

1. X. Y. Yang, L. H. Chen, Y. Li, J. C. Rooke, C. Sanchez and B. L. Su, Chem. Soc. Rev., 2017, 46, 481–558.
2. C. M. A. Parlett, K. Wilson and A. F. Lee, Chem. Soc. Rev., 2013, 42, 3876–3893.
3. T. Fukasawa, M. Ando, T. Ohji and S. Kanzaki, J. Am. Ceram. Soc., 2001, 84, 230–232.
4. K. Michaela, A. Idris, G. Christian, V. Céline and D. Sylvain, Adv. Eng. Mater., 2012, 14, 1123–1127.
5. M. A. White, J. Conrad, S. N. Ellis and R. Chen, J. Am. Ceram. Soc., 2017, 100, 5066–5074.
6. S. Deville, Adv. Eng. Mater., 2008, 10, 155–169.
7. H. F. Zhang, I. Hussain, M. Brust, M. F. Butler, S. P. Rannard and A. I. Cooper, Nat. Mater., 2005, 4, 787–793.
8. C. Wang, X. Chen, B. Wang, M. Huang, B. Wang, Y. Jiang and R. S. Ruoff, ACS Nano, 2018, 12, 5816–5825.
9. U. G. K. Wegst, H. Bai, E. Saiz, A. P. Tomsia and R. O. Ritchie, Nat. Mater., 2015, 14, 23–36.
10. Y. L. Shao, M. F. El-Kady, C. W. Lin, G. Z. Zhu, K. L. Marsh, J. Y. Hwang, Q. H. Zhang, Y. G. Li, H. Z. Wang and R. B. Kaner, Adv. Mater., 2016, 28, 6719–6726.
11. C. Gaudillere, J. Garcia-Fayos, M. Balaguer and J. M. Serra, Chemsuschem, 2014, 7, 2554–2561.
12. E. Munch, M. E. Launey, D. H. Alsem, E. Saiz, A. P. Tomsia and R. O. Ritchie, Science, 2008, 322, 1516–1520.
13. G. Lian, C. C. Tuan, L. Y. Li, S. L. Jiao, Q. L. Wang, K. S. Moon, D. L. Cui and C. P. Wong, Chem. Mater., 2016, 28, 6096–6104.
14. C. Gaudillere, J. J. González, A. Chica and J. M. Serra, Appl. Catal., A, 2017, 538, 165–173.
15. S. Deville, C. Viazzi and C. Guizard, Langmuir, 2012, 28, 14892–14898.
16. I. K. Voets, Soft Matter, 2017, 13, 4808–4823.
17. A. Bareggi, M. Eric, L. Audrey and D. Sylvain, J. Am. Ceram. Soc., 2011, 94, 3570–3578.
18. E. Papa, V. Medri, P. Benito, A. Vaccari, S. Bugani, J. Jaroszewicz and E. Landi, RSC Adv., 2016, 6, 24635–24644.
19. V. Naglieri, H. A. Bale, B. Gludovatz, A. P. Tomsia and R. O. Ritchie, Acta Mater., 2013, 61, 6948–6957.
20. L. Pino, Y. Aristov, G. Cacciola and G. Restuccia, Adsorption, 1996, 3, 33–40.
21. L. Borchardt, N. L. Michels, T. Nowak, S. Mitchell and J. Perez-Ramirez, Microporous Mesoporous Mater., 2015, 208, 196–202.
22. E. A. Ali, H. L. Marcio, M. S. Edward and H. B. Ray, Nanotechnology, 2010, 21, 035709.
23. T. Fend, O. Reutter, J. Sauerhering, K. S. do Couto Aktay, R. Pitz-Paal and S. Angel, 17th European Conference on Thermophysical Properties, Bratzislava, Slovakia, 2005.
24. A. Y. Khodakov, W. Chu and P. Fongarland, Chem. Rev., 2007, 107, 1692–1744.
25. G. Prieto, M. I. S. De Mello, P. Concepción, R. Murciano, S. B. C. Pergher and A. n. Martínez, ACS Catal., 2015, 5, 3323–3335.
26. G. R. Johnson and A. T. Bell, J. Catal., 2016, 338, 250–264.
27. D. A. Wood, C. Nwaoha and B. F. Towler, J. Nat. Gas Sci. Eng., 2012, 9, 196–208.
28. H. Schulz, Top. Catal., 2003, 26, 73–85.
29. E. Iglesia, Appl. Catal., A, 1997, 161, 59–78.
30. N. Duyckaerts, I.-T. Trotuş, A.-C. Swertz, F. Schüth and G. Prieto, ACS Catal., 2016, 6(7), 4229–4238.
31. R. Franke, D. Selent and A. Börner, Chem. Rev., 2012, 112, 5675–5732.
32. N. Duyckaerts, M. Bartsch, I. T. Trotus, N. Pfander, A. Lorke, F. Schuth and G. Prieto, Angew. Chem., Int. Ed., 2017, 56, 11480–11484.
33. A. Martinez, G. Prieto and J. Rollán, J. Catal., 2009, 263, 292–305.
34. L. C. Almeida, O. González, O. Sanz, A. Paul, M. A. Centeno, J. A. Odriozola and M. Montes, in Studies in Surface Science and Catalysis, ed. F. Bellot Noronha, M. Schmal and E. Falabella Sousa-Aguiar, Elsevier, 2007, vol. 167, pp. 79–84.
35. L. Fratalocchi, C. G. Visconti, G. Groppi, L. Lietti and E. Tronconi, Chem. Eng. J., 2018, 349, 829–837.
36. M. S. Challiwala, B. A. Wilhite, M. M. Ghouri and N. O. Elbashir, AIChE J., 2018, 64, 1723–1731.
37. I. C. Yates and C. N. Satterfield, Energy Fuels, 1991, 5, 168–173.
38. A. P. Merkle and J. Gelb, Microsc. Today, 2013, 21, 10–15.
39. J. Gelb, D. P. Finegan, D. J. L. Brett and P. R. Shearing, J. Power Sources, 2017, 357, 77–86.
40. T. L. Burnett, S. A. McDonald, A. Gholinia, R. Geurts, M. Janus, T. Slater, S. J. Haigh, C. Ornek, F. Almuaili, D. L. Engelberg, G. E. Thompson and P. J. Withers, Sci. Rep., 2014, 4, 4711.
41. R. Dougherty and K. H. Kunzelmann, Microsc. Microanal., 2007, 13, 1678–1679.
42. M. Ender, J. Joos, A. Weber and E. Ivers-Tiffée, J. Power Sources, 2014, 269, 912–919.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ta07512c

‡ These authors contributed equally to this work.

---