Kirigami enhances film adhesion†
Ruike
Zhao
 a,
Shaoting
Lin
a,
Hyunwoo
Yuk
a and
Xuanhe
Zhao
a,
Shaoting
Lin
a,
Hyunwoo
Yuk
a and
Xuanhe
Zhao
 *ab
*ab
aDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: zhaox@mit.edu
bDepartment of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 5th March 2018
Abstract
Structures of thin films bonded on substrates have been used in technologies as diverse as flexible electronics, soft robotics, bio-inspired adhesives, thermal-barrier coatings, medical bandages, wearable devices and living devices. The current paradigm for maintaining adhesion of films on substrates is to make the films thinner, and more compliant and adhesive, but these requirements can compromise the function or fabrication of film–substrate structures. For example, there are limits on how thin, compliant and adhesive epidermal electronic devices can be fabricated and still function reliably. Here we report a new paradigm that enhances adhesion of films on substrates via designing rational kirigami cuts in the films without changing the thickness, rigidity or adhesiveness of the films. We find that the effective enhancement of adhesion by kirigami is due to (i) the shear-lag effect of the film segments; (ii) partial debonding at the film segments’ edges; and (iii) compatibility of kirigami films with inhomogeneous deformation of substrates. While kirigami has been widely used to program thin sheets with desirable shapes and mechanical properties, fabricate electronics with enhanced stretchability and design the assembly of three-dimensional microstructures, this paper gives the first systematic study on kirigami enhancing film adhesion. We further demonstrate novel applications including a kirigami bandage, a kirigami heat pad and printed kirigami electronics.
1. Introduction
Structures of films bonded on substrates are used in diverse technological applications such as flexible electronics,1–5 soft robotics,6–8 bio-inspired adhesives,9–12 thermal-barrier coatings,13 medical bandages,14 wearable devices15–20 and living devices.21,22 While maintaining the adhesion of the films on the substrates is critical in these applications, the films are usually prone to delamination failure when the substrates are highly deformed. For example, the skin on the human elbow, knee, wrist and ankle can be highly stretched during body motions, and films such as bandages and wearable devices attached on these regions may get detached. Fig. 1a illustrates the debonding process of a continuous film bonded on a thick substrate under deformation.23–28 As the substrate is stretched, the film initially deforms with the substrate. However, when the strain in the substrate reaches a critical value, a crack propagates along the interface and the film eventually detaches from the substrate.22,29 In order to maintain the adhesion of films on substrates, thinner and more compliant films and tougher interfaces have been proposed.23,24,28–31 However, in many cases, it is challenging to vary the thickness or rigidity of the films or tune the interfacial toughness. For example, there are limits on how thin, compliant and adhesive epidermal electronic devices can be fabricated and still function reliably.29,32 Therefore, new methods to enhance film adhesion are of critical importance in various technological applications of film–substrate structures.Here we show that rationally designed kirigami cuts in a film on a substrate can greatly enhance the critical strain for overall detachment of the film, especially on substrates undergoing inhomogeneous deformation. We find that the effective enhancement of adhesion by kirigami is due to (i) the shear-lag effect of the film segments; (ii) partial debonding at the film segments’ edges; and (iii) compatibility of kirigami films with inhomogeneous deformation of substrates (Fig. 1b). This new mechanism on enhancing film adhesion by kirigami has been validated by numerical simulation and experiments (Fig. 2–4), and its application has been demonstrated by the example of a kirigami bandage that achieves much enhanced adhesion on skin without changing the thickness or rigidity of the films or film–substrate interfaces (Fig. 4). In particular, we find that the kirigami film can better accommodate the deformation of wavy conductive wires adhered on or embedded in the films without delamination than continuous films32–34 (Fig. 5). We further demonstrated the novel applications of the kirigami-wavy wire structure including a kirigami heat pad and printed kirigami wearable electronics (Fig. 6). While kirigami has been intensively studied for programming thin sheets with desirable shapes and mechanical properties,35–41 fabricating stretchable electronics with enhanced stretchability,42 and designing the assembly of 3D structures;43–46 to our knowledge, this is the first time kirigami has been harnessed to enhance the effective adhesion of films on substrates with broad applications ranging from adhesive bandages to wearable electronics.
2. Numerical simulations
Two-dimensional (2D) finite element models are established to calculate the energy release rates for both initiation and propagation of the film–substrate debonding. The simulations are implemented by commercial software package ABAQUS/Standard with plane-strain element CPE4RH. Both film and substrate are represented by an incompressible neo-Hookean material which has the strain energy density of | (1) |
The energy release rate G is calculated by evaluating the energy released to propagate a crack by a unit length. Thereafter, we divide the energy release rate by μfHf to give a dimensionless value.
For debonding initiation (Fig. 2), the film–substrate structure has width L at the reference state (ESI,† Fig. S1a) and a lateral stretch λ is applied to the substrate (ESI,† Fig. S1b). Next, a case with a prescribed crack length R (ESI,† Fig. S1c) is stretched to the same amount (ESI,† Fig. S1d) and the crack length changes to r at the current state. The energy release rate G is calculated as the energy difference between the crack-free case and the cracked case, then divided by the crack length at the reference state. For debonding propagation (Fig. 3), the initial adherent film segment width is L, and the analyzed adherent film segment widths are LA. Then, the same procedure as described for calculating the energy release rate of debonding initiation is followed (ESI,† Fig. S2).
To compare the simulation results with the experimental results on critical debonding stretch as shown in Fig. 3e and f, the parameters in the numerical model are set to be the same as experimentally measured values. The corresponding energy release rate G is calculated as a function of applied stretch λ. By setting the calculated G equal to interfacial toughness Γ, we calculate the corresponding critical stretches λc for delamination from FEM and compare the critical stretches with the experimental results.
3. Materials and methods
3.1. Fabrication of film–substrate system
In this paper, the fabrications of soft materials for a film–substrate system were conducted using two types of silicone rubbers: PDMS (DowCorning Sylgard 184 Silicone Elastomer Kit) for fabrication of films and Ecoflex (Smooth-On Ecoflex™ 00-30) for fabrication of substrates. PDMS films with different moduli were fabricated by mixing resin and crosslinker in a weight ratio of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 15
1, and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (DowCorning Sylgard 184 Silicone Elastomer Kit), and then curing for 5 h at 90 °C. The corresponding shear moduli are measured to be 27 kPa and 128 kPa, respectively (fitted by neo-Hookean material constitutive law as shown in ESI,† Fig. S5). The Ecoflex substrate was fabricated by mixing the two components of the Ecoflex 00-30 in the weight ratio of 1A
1 (DowCorning Sylgard 184 Silicone Elastomer Kit), and then curing for 5 h at 90 °C. The corresponding shear moduli are measured to be 27 kPa and 128 kPa, respectively (fitted by neo-Hookean material constitutive law as shown in ESI,† Fig. S5). The Ecoflex substrate was fabricated by mixing the two components of the Ecoflex 00-30 in the weight ratio of 1A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1B, and then curing for 2 hours at room temperature. The corresponding shear modulus of the Ecoflex was measured to be 20 kPa. The single layer PDMS film with shear modulus 27 kPa or 128 kPa was attached on the Ecoflex substrate, giving a film–substrate modulus ratio of 1.4 or 6.4, respectively. To make the fabricated PDMS film adhesive, a layer of silicone adhesive (WACKER SiGel 613) was made by mixing resin and crosslinker with 10
1B, and then curing for 2 hours at room temperature. The corresponding shear modulus of the Ecoflex was measured to be 20 kPa. The single layer PDMS film with shear modulus 27 kPa or 128 kPa was attached on the Ecoflex substrate, giving a film–substrate modulus ratio of 1.4 or 6.4, respectively. To make the fabricated PDMS film adhesive, a layer of silicone adhesive (WACKER SiGel 613) was made by mixing resin and crosslinker with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio, spin-coating onto the fabricated PDMS films at the spin speed of 1000 rpm for 30 seconds, and then curing for 5 h at 60 °C. This gave an adhesive PDMS layer with thickness around 100 μm, much thinner than the film thickness (1.5 mm).
1 weight ratio, spin-coating onto the fabricated PDMS films at the spin speed of 1000 rpm for 30 seconds, and then curing for 5 h at 60 °C. This gave an adhesive PDMS layer with thickness around 100 μm, much thinner than the film thickness (1.5 mm).
3.2. Fabrication of the inhomogeneous substrate
To achieve inhomogeneous deformation of a substrate under uniaxial tension, we fabricated an inhomogeneous substrate by bonding three material sections along the loading direction: two rigid PDMS sections on the sides with one compliant Ecoflex section in the middle (Fig. 4a). The PDMS sections were fabricated by mixing resin and crosslinker in the weight ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (DowCorning Sylgard 184 Silicone Elastomer Kit), and then curing for 5 h at 90 °C, which gave the corresponding shear modulus of 245 kPa. The Ecoflex substrate was fabricated by mixing the two components of the Ecoflex 00-30 in the weight ratio of 1A
1 (DowCorning Sylgard 184 Silicone Elastomer Kit), and then curing for 5 h at 90 °C, which gave the corresponding shear modulus of 245 kPa. The Ecoflex substrate was fabricated by mixing the two components of the Ecoflex 00-30 in the weight ratio of 1A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1B, and then curing for 2 hours at room temperature, which gave the corresponding shear modulus of 20 kPa. Thereafter, a thin Ecoflex layer with a thickness of 0.5 mm was cured on top of the inhomogeneous substrate surface to ensure the same surface adhesion on the substrate.
1B, and then curing for 2 hours at room temperature, which gave the corresponding shear modulus of 20 kPa. Thereafter, a thin Ecoflex layer with a thickness of 0.5 mm was cured on top of the inhomogeneous substrate surface to ensure the same surface adhesion on the substrate.
3.3. Fabrication of adhesive PDMS films with kirigami designs
PDMS sheets with designed kirigami cuts were fabricated by pouring the mixed resin and crosslinker in the weight ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (DowCorning Sylgard 184 Silicone Elastomer Kit) into 3D-printed molds. A layer of silicone adhesive (WACKER SiGel 613) was made by mixing resin and crosslinker with 10
1 (DowCorning Sylgard 184 Silicone Elastomer Kit) into 3D-printed molds. A layer of silicone adhesive (WACKER SiGel 613) was made by mixing resin and crosslinker with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio, spin-coating onto the fabricated PDMS films at the spin speed of 1000 rpm for 30 seconds and then curing for 5 h at 60 °C, which gave an adhesive PDMS layer with thickness around 100 μm, much thinner than the film thickness (1.5 mm).
1 weight ratio, spin-coating onto the fabricated PDMS films at the spin speed of 1000 rpm for 30 seconds and then curing for 5 h at 60 °C, which gave an adhesive PDMS layer with thickness around 100 μm, much thinner than the film thickness (1.5 mm).
3.4. Fabrication of a kirigami film with an embedded heating module
The kirigami film was prepared by pouring the two components of the Ecoflex 00-30 in the weight ratio of 1A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1B into a 3D-printed mold. For the heating module, we used a 0.1 mm-diameter AWG38 Nichrome resistance heating wire. The heating wire was then stitched into the Ecoflex kirigami film with designed sinusoidal shape as illustrated in Fig. 5a. Another thin layer of Ecoflex was cured on the kirigami film to fully encapsulate the heating wire. A layer of adhesive (WACKER SiGel 613) was then spin coated onto the prepared film. To heat up the heating wire, a 3 V DC input was introduced by a DC power supply (Agilent). A thermal imaging camera (Seek Thermal CompactPro Imaging Camera for iPhone) was used to monitor the surface temperature of the kirigami film.
1B into a 3D-printed mold. For the heating module, we used a 0.1 mm-diameter AWG38 Nichrome resistance heating wire. The heating wire was then stitched into the Ecoflex kirigami film with designed sinusoidal shape as illustrated in Fig. 5a. Another thin layer of Ecoflex was cured on the kirigami film to fully encapsulate the heating wire. A layer of adhesive (WACKER SiGel 613) was then spin coated onto the prepared film. To heat up the heating wire, a 3 V DC input was introduced by a DC power supply (Agilent). A thermal imaging camera (Seek Thermal CompactPro Imaging Camera for iPhone) was used to monitor the surface temperature of the kirigami film.
3.5. Fabrication of a kirigami film with an embedded stretchable electronic device
The kirigami film was prepared by introducing kirigami cuts into a PDMS sheet with adhesive backing (McMaster) by a laser cutter (EPILOG LASER). The electrical circuit was printed onto the kirigami substrate by a customized 3D printer consisting of an XYZ robotic gantry (Aerotech) and microdispensers (Ultimus V; Nordson EFD). The printing paths for the electrical circuit were generated with G-code. A commercial silver ink (DuPont ME603) was used as a conductive ink and a 200 μm nozzle (Nordson EFD) was used to print the ink. After printing the circuit onto the kirigami substrate, four parallel aligned LEDs were placed onto desired locations and the assembly was cured in the oven for 2 h at 120 °C. To light up the LEDs, a 3 V DC input was introduced by the DC power supply (Agilent).3.6. Measurement of energy release rate for steady-state crack propagation at the film–substrate interface
Many experimental techniques and models have been developed to evaluate the interfacial toughness of thin film adhesives.23,47,48 In our case, we measured the interfacial adhesion energy of the film–substrate system fabricated in Section 3.1 by the 90° peeling test, which gave the adhesion energy of 1 J m−2 (Fig. S3, ESI†). In order to evaluate the critical energy release rate for steady-state crack propagation, we introduced initial cracks at both edges of the film prior to applying the load, as shown in ESI,† Fig. S6. Then, we used a universal test machine (2 kN load cell; Zwick/Roell Z2.5) to stretch the film–substrate system. The critical stretch for steady-state crack propagation was identified when the adherent film segment started to detach, as illustrated in ESI,† Fig. S6 and Movie S7.4. Results and discussion
Consider a film with thickness Hf bonded to a thick stretchable substrate with thickness Hs. Without losing generality, both the film and the substrate are taken as incompressible neo-Hookean materials with initial shear moduli of μf and μs, respectively. The film–substrate structure is assumed to undergo plane-strain deformation with an applied substrate stretch λ, defined as the ratio between the structure's lengths along the stretching direction in the current and undeformed states. The elastic energy stored in the film drives the film's delamination from the substrate, and the adhesion energy between the film and substrate prevents debonding. The energy release rate G is defined as the reduction of the film–substrate structure's elastic energy when the film delaminates by a unit area, and the interfacial toughness Γ as the work required to separate the film from the substrate by a unit area. At a critical stretch λc, when the energy release rate G reaches the interfacial toughness Γ, the film begins to delaminate from the substrate. By dimensional argument, we can express the energy release rate as| G = μfHff, | (2) |
4.1. Design of the kirigami pattern
To focus on kirigami's effect on adhesion of films, we adopt a simple kirigami pattern in the current study. As illustrated in Fig. 1b, a row of cuts with equal length C and equal length of gap between two adjacent cuts D is applied in a film, perpendicular to the stretching direction. In an adjacent parallel row with distance L, the same cuts are repeated but shifted up by (C + D)/2. In this way, a pattern of kirigami is generated by repeating the parallel rows of cuts and keeping the same distance L between adjacent rows. The width of the kirigami cuts is negligible in the current study, i.e., no subtraction of film material during the cut. In addition, the length of the cuts C is much larger than the gap length between adjacent cuts D and the distance between adjacent rows of cuts L, so that each resultant film segment can be approximately taken to undergo plane-strain deformation.4.2. Shear-lag effect in delaying film–substrate debonding
A cross section of the kirigami–film–substrate structure along the stretching direction is illustrated in Fig. 2a. When the substrate is stretched, the edges of each film segment undergo shear deformation prior to delamination, as illustrated in the schematic and experimental images in Fig. 2b, with the experimental image shown in Fig. 2c. The shear lag can reduce the energy release rate of kirigami films compared with the corresponding continuous films under the same applied stretch, and allows the film to bear larger stretch prior to debonding. The shear-lag effect is especially significant when the width of the film segment L is comparable with the film thickness Hf.To quantitatively understand the shear-lag effect of film segments on adhesion, we calculate the energy release rate G for the initiation of delamination in a unit cell of the kirigami film–substrate system using commercial software package ABAQUS/Standard (Fig. S1, ESI†). In the simulation, the substrate is considered to have infinite depth (i.e., Hs ≫ Hf). Therefore, the normalized energy release rate for the initiation of delamination G/Hfμf can be expressed as
 | (3) |
Fig. 2d and e give the simulation results of the normalized energy release rate G/Hfμf as functions of the film segment size L/Hf, applied stretch λ and film–substrate modulus ratio μf/μs. For each fixed value of stretch λ and modulus ratio μf/μs, the normalized energy release rate G/Hfμf indeed increases with film segment size L/Hf and reaches a plateau at very large values of L/Hf (i.e., over 100). The reduction of the energy release rate with decreasing L/Hf is more pronounced for systems with higher stretch λ (Fig. 2d) and higher modulus ratio μf/μs (Fig. 2e).
4.3. Effect of partial delamination of film segments in delaying film–substrate debonding
Although the shear-lag effect can delay the initiation of delamination, the edges of film segments will eventually begin to debond from the substrate under a critical stretch. However, the delamination process will stop before the film segments are fully detached from the substrate, due to the reduction of energy release rate with interfacial crack propagation (Fig. 1b and 3b); and the middle regions of the film segments can still bond on the substrate. Therefore, the kirigami film can maintain overall adhesion on the substrate, despite partial delamination, under applied stretches that would have delaminated the corresponding continuous films.To quantitatively understand the partial delamination's effect on enhancing film adhesion, we calculate the energy release rate G for the propagation of delamination in a unit cell of the kirigami film–substrate system (Fig. S2, ESI†). Fig. 3b illustrates the cross section of partially delaminated film segments on a stretched substrate, with the experimental image shown in Fig. 3c. The width of the adherent region between film segment and substrate in the undeformed reference state is denoted as LA. When the substrate undergoes applied stretch, the width of the adherent film segment is lA at the current state. The energy release rate for propagation of an interfacial crack in the adherent region can then be expressed as
 | (4) |
To focus on partial delamination's effect, we fix the width of the kirigami film segment to be L/Hf = 150 and calculate the energy release rate as a function of the applied stretch λ, the modulus ratio μf/μs, and the width of remaining adherent film segment LA/Hf, as shown in Fig. 3d and e. For various values of modulus ratios μf/μs and applied stretches λ, when the interfacial crack is propagating away from the edges of the film segment (i.e., after crack initiation), the normalized energy release rate G/Hfμf decreases drastically and reaches the value for steady-state propagation G/μfHf = (λ2 + λ−2 − 2)/2. As the interfacial crack further propagates and the adherent width LA reaches a few times the film thicknesses (e.g., 20Hf ∼ 50Hf), the energy release rate decreases from the steady-state value (shown by dashed lines in Fig. 3d and e). Therefore, a higher applied stretch is required to further delaminate the adherent film segments than the critical stretch for steady-state propagation of an interfacial crack in the corresponding continuous film. In addition, the effect of partial delamination (i.e., decreasing LA/Hf) on reducing energy release rate is more pronounced in systems with higher modulus ratio μf/μs as shown in Fig. 3e.
We next experimentally validate the partial delamination's effect on delaying interfacial debonding, by measuring the critical stretches for delamination and comparing the experimental results with simulations. In the experiments, PDMS and Ecoflex are used to fabricate the film and substrate with thicknesses of 1.5 mm and 12.5 mm, respectively. The shear modulus of the substrate is measured to be μs = 20 kPa, and the moduli of the film with different crosslinking densities are measured to be μf = 27 kPa and 128 kPa. The film–substrate interfacial toughness is measured to approximate Γ ≈ 1 J m−2 (Fig. S3, ESI†). The width of the film segment is set to be L = 90 mm, and a number of typical adherent segment widths are chosen in the tests from LA = 4.5 mm to LA = 90 mm. For each modulus ratio and adherent segment width, the Ecoflex substrates are stretched to critical stretches until the crack begins to propagate in the adherent region (Fig. S6, ESI†). The experimentally measured critical stretches λc for various values of μf/μs and LA/Hf have been plotted in Fig. 3f and g. In comparison, we set the values of μf/μs, L/Hf, and LA/Hf in the numerical model to be the same as experimental values, and then calculate the corresponding energy release rate G as a function of applied stretch λ. By setting the calculated G equal to the measured interfacial toughness Γ, we calculate the corresponding critical stretches λc for delamination and compare the experimental and simulation results in Fig. 3f and g. The numerical model can consistently predict the critical stretch for interfacial crack propagation in adherent film segments. In addition, both the experimental and simulation results validate that partial delamination in kirigami film segments can significantly enhance critical stretches for delamination.
4.4. Kirigami film accommodating inhomogeneous deformation of the substrate
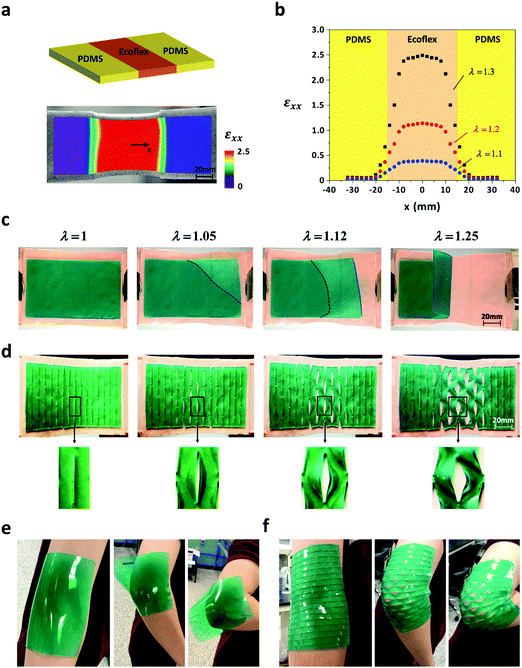
In many applications such as bandages and wearable devices, the deformation of the substrates can be inhomogeneous. For example, the skin right above the joints in the human body can be deformed much more significantly than adjacent regions during rotational movements of the joints. Adherent films usually cover both the joint and adjacent regions. As a result, the part of a continuous film adhered on the joint regions can be highly stretched during body motion to give a high energy release rate for delamination propagation. On the other hand, the part of a kirigami film (Fig. 1b) adhered on joint regions may be partially or fully detached during body motion; however, the part of the kirigami film on adjacent regions can still maintain its adhesion due to low energy release rate for delamination in adjacent regions.We next demonstrate kirigami's effect on adhesion of films on substrates undergoing inhomogeneous deformation. As illustrated in Fig. 4a, an inhomogeneous substrate is fabricated with Ecoflex with shear modulus of 20 kPa in the middle (width 30 mm) and PDMS with shear modulus of 245 kPa on the sides (width 25 mm). A thin layer of Ecoflex is further coated on the surface of the substrate to ensure the same surface adhesion of the inhomogeneous substrate. We next uniaxially stretch the substrate to different levels and use digital image correlation (DIC) to measure the strain distribution in the substrate. Fig. 4b indicates that the designed substrate can effectively give inhomogeneous deformation to approximate the deformation around joint regions in the body. In addition, PDMS with thickness of 1.5 mm and shear modulus of 128 kPa is selected as the continuous film. To fabricate the kirigami film, the periodic cuts illustrated in Fig. 1b are applied on the corresponding continuous film with L = 7.0 mm, C = 19.0 mm and D = 3.0 mm. The continuous or kirigami film is physically attached to the inhomogeneous substrate, which is then subjected to uniaxial tension. As shown in Fig. 4c, the continuous film begins to delaminate from the substrate under relatively low applied stretch (i.e., λ = 1.05), with the black dashed line indicating the boundary of the detached region. Under the same stretch (i.e., λ = 1.05), the kirigami film only shows the initiation of partial debonding at the edges of the film segments (Fig. 4d). As the applied stretch increases to higher values (e.g., λ = 1.25), the continuous film detaches from one side of the substrate. On the contrary, under the same high stretch (λ = 1.25), the kirigami film only partially delaminates from the highly stretched middle region of the substrate, while it maintains good adhesion on the less-stretched side regions (Movie S1, ESI†). Delamination tests are further done on a conventional medical bandage (3M™ Elastic Adhesive Bandage, thickness 0.3 mm) and the same bandage with kirigami cuts (L = 1.8 mm C = 14.0 mm and D = 2.6 mm) on the same inhomogeneous substrate. ESI,† Fig. S4 and Movie S2 demonstrate the significantly enhanced adhesion of the kirigami bandage over the continuous bandage on a substrate undergoing inhomogeneous deformation. Besides the three major factors (film shear lag, partial debonding, and accommodation of inhomogeneous deformation) that explain the mechanism of kirigami film enhancing interface adhesion, there are other potential factors such as buckling, twisting, and in-plane and out of plane rotation of the film segments, which may also affect interfacial debonding.35,37,49
Next we demonstrate that the kirigami film can significantly enhance adhesion on the skin above moving joints of the human body compared with continuous films. We attach the continuous or kirigami film (PDMS with overall dimension of 110.0 mm × 69.0 mm × 1.5 mm, shear modulus of 128 kPa, L = 7.0 mm, C = 19.0 mm and D = 3.0 mm) onto the elbow of an arm in the straight state (i.e., 180° angle). Thereafter, we bend the elbow to states of 90° and 45° angles. From Fig. 4e, f and ESI,† Movie S3, it can be seen that the continuous film delaminates easily from the elbow during bending motion. On the other hand, the kirigami film can maintain overall adhesion on the elbow even under severe bending (45° angle), despite partial delamination right above the joint.
4.5. Kirigami film-wavy wire structure
Wearable electronics in the form of thin films adhered on various parts of the body have been intensively developed over the last decade.3,50,51 However, it is still challenging to maintain reliable adhesion of thin-film wearable electronics on deforming body parts such as joints.52,53 In addition, the delamination and fracture of electronic components on highly stretched thin films still causes serious reliability issues to wearable electronics.54 Here we will demonstrate a new type of wearable devices based on kirigami films that can significantly enhance the effective adhesion and reduce the strains in the kirigami films compared with corresponding continuous films. As a result, the kirigami wearable devices can reliably adhere on moving joints and maintain the bonding of electronic components on them.Rigid metallic and semiconductor materials have been made into wires of wavy (or serpentine) shapes and bonded on compliant films to enhance the stretchability of these rigid materials.2,55–59 When the film–wavy wire structure is stretched, the maximum strain in the rigid wire can be significantly reduced compared with the bulk material under the same stretch. However, the rigid wire still constrains the deformation of the stretched film right beneath it, potentially driving the debonding of the wire from the film.29,32,33 Here we will show that the strain in a kirigami film (and thus mismatch strain between film and wire) can be significantly reduced compared with the corresponding continuous film under the same stretch, delaying delamination of the wire from the kirigami film. The deformation of the continuous film–wavy wire structure will be compared with the corresponding kirigami film–wavy wire structure under the same stretch. Since the rigid wire cannot cross the kirigami cuts, without loss of generality we make the wavy wire follow a sinusoidal shape with wavelength ω = 2L and amplitude A = (C + D)/4, and set the peak and valley points of the sinusoidal wire to overlap with the middle points of the gaps between adjacent cuts in a row, as illustrated in Fig. 5a. For comparison, a rigid wire with the same sinusoidal shape is attached on the corresponding continuous film (Fig. 5b).
Thereafter, we simulate the deformation of the continuous film–wavy wire structure and kirigami film–wavy wire structure in a plane to approximate their deformation on substrates, using ABAQUS. (Note the approximation also accounts for partial delamination of the kirigami film to allow opening of the cuts.) In the simulation, we set the width and height of the rigid wire to be 2 < Hf and Hf, respectively; the wire-film modulus ratio μwire/μf = 105; and the kirigami parameters L = 70Hf, C = 190Hf, and D = 30Hf. Then we uniaxially stretch representative segments (Fig. 5b) of the film–wavy wire structures in the simulation to a typical stretch λ = 1.5. As shown in Fig. 5d, while most of the regions in the continuous film are stretched to a strain over εxx = 0.5 (nominal strain), the rigid wire constrains the deformation of the film around it and causes high mismatch strain at the film–wavy wire interface, potentially driving the delamination of rigid wires.32 On the other hand, the strain in the kirigami film is much reduced (around εxx = 0.07) compared with the continuous film under the same stretch (λ = 1.5), due to the opening of cuts in the kirigami film resulting from its partial delamination (e.g., Fig. 4d and f, experimental figures in the paper showing the opening). As a result, the mismatch strain between kirigami film and rigid wire and thus the driving force for wire debonding have been significantly reduced, which gives more reliable wire adhesion on the kirigami film than on the corresponding continuous film (Fig. 5c).
5. Conclusion
Kirigami has been intensively studied for programming thin sheets with desirable shapes and mechanical properties, enhancing the stretchability of films, and designing the assembly of 3D structures. In this paper, for the first time, we introduce designed kirigami cuts into films to significantly enhance their adhesion on substrates under large inhomogeneous deformation, without the need to change the film's thickness, rigidity or adhesiveness. We show that the mechanisms of kirigami enhancing film adhesion include the shear-lag effect of the film segments, partial debonding at the film segments’ edges, and compatibility of kirigami films with inhomogeneous deformation of substrates. These mechanisms have been systematically explained and validated by combined theory, experiments and numerical simulation. We further propose kirigami film–wavy wire structures as a new strategy for the design of kirigami wearable devices with much enhanced adhesion on body parts undergoing large deformation such as the heart and joints. Based on the new mechanisms and design, we further demonstrate novel and tangible applications including a kirigami bandage, a kirigami heat pad, and printed kirigami wearable electronics. In addition to wearable electronics, the kirigami strategy for enhancing film adhesion is expected to enable novel applications in diverse areas such as soft robotics, bio-inspired adhesives, medical bandages, and living devices, where robust film-substrate structures are critical but it is challenging to vary the film's thickness, rigidity or adhesiveness.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work is supported by Tibet Cheezheng Tibetan Medicine Co. Ltd, National Science Foundation (CMMI-1661627), MIT Institute for Soldier Nanotechnologies.References
- J. A. Rogers, T. Someya and Y. Huang, Science, 2010, 327, 1603–1607 CrossRef CAS PubMed
.
- C. H. Lee, Y. Ma, K.-I. Jang, A. Banks, T. Pan, X. Feng, J. S. Kim, D. Kang, M. S. Raj, B. L. McGrane, B. Morey, X. Wang, R. Ghaffari, Y. Huang and J. A. Rogers, Adv. Funct. Mater., 2015, 25, 3698–3704 CrossRef CAS
.
- D.-H. Kim, N. Lu, R. Ma, Y.-S. Kim, R.-H. Kim, S. Wang, J. Wu, S. M. Won, H. Tao and A. Islam, Science, 2011, 333, 838–843 CrossRef CAS PubMed
.
- M. Kaltenbrunner, T. Sekitani, J. Reeder, T. Yokota, K. Kuribara, T. Tokuhara, M. Drack, R. Schwödiauer, I. Graz and S. Bauer-Gogonea, Nature, 2013, 499, 458 CrossRef CAS PubMed
.
- M. S. White, M. Kaltenbrunner, E. D. Głowacki, K. Gutnichenko, G. Kettlgruber, I. Graz, S. Aazou, C. Ulbricht, D. A. Egbe and M. C. Miron, Nat. Photonics, 2013, 7, 811–816 CrossRef CAS
.
- N. Lu and D.-H. Kim, Soft Robot., 2014, 1, 53–62 CrossRef
.
- C. Majidi, Soft Robot., 2014, 1, 5–11 CrossRef
.
- S. Bauer, S. Bauer-Gogonea, I. Graz, M. Kaltenbrunner, C. Keplinger and R. Schwödiauer, Adv. Mater., 2014, 26, 149–162 CrossRef CAS PubMed
.
- M. P. Murphy, B. Aksak and M. Sitti, Small, 2009, 5, 170–175 CrossRef CAS PubMed
.
- D. M. Drotlef, P. Blumler and A. del Campo, Adv. Mater., 2014, 26, 775–779 CrossRef CAS PubMed
.
- L. F. Boesel, C. Greiner, E. Arzt and A. del Campo, Adv. Mater., 2010, 22, 2125–2137 CrossRef CAS PubMed
.
- T. Zhang, Z. Zhang, K.-S. Kim and H. Gao, J. Adhes. Sci. Technol., 2014, 28, 226–239 CrossRef CAS
.
- W. Zhu, L. Yang, J. W. Guo, Y. C. Zhou and C. Lu, Int. J. Plast., 2015, 64, 76–87 CrossRef
.
- P. Zahedi, I. Rezaeian, S. O. Ranaei-Siadat, S. H. Jafari and P. Supaphol, Polym. Adv. Technol., 2010, 21, 77–95 CAS
.
- Y. Khan, A. E. Ostfeld, C. M. Lochner, A. Pierre and A. C. Arias, Adv. Mater., 2016, 28, 4373–4395 CrossRef CAS PubMed
.
- M. K. Kwak, H. E. Jeong and K. Y. Suh, Adv. Mater., 2011, 23, 3949–3953 CrossRef CAS PubMed
.
- G. Schwartz, B. C. Tee, J. Mei, A. L. Appleton, D. H. Kim, H. Wang and Z. Bao, Nat. Commun., 2013, 4, 1859 CrossRef PubMed
.
- Y. Wang, L. Wang, T. Yang, X. Li, X. Zang, M. Zhu, K. Wang, D. Wu and H. Zhu, Adv. Funct. Mater., 2014, 24, 4666–4670 CrossRef CAS
.
- C. Dagdeviren, B. D. Yang, Y. Su, P. L. Tran, P. Joe, E. Anderson, J. Xia, V. Doraiswamy, B. Dehdashti and X. Feng, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1927–1932 CrossRef CAS PubMed
.
- T. Yamada, Y. Hayamizu, Y. Yamamoto, Y. Yomogida, A. Izadi-Najafabadi, D. N. Futaba and K. Hata, Nat. Nanotechnol., 2011, 6, 296–301 CrossRef CAS PubMed
.
- X. Liu, T.-C. Tang, E. Tham, H. Yuk, S. Lin, T. K. Lu and X. Zhao, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2200–2205 CrossRef CAS PubMed
.
- S. Lin, H. Yuk, T. Zhang, G. A. Parada, H. Koo, C. Yu and X. Zhao, Adv. Mater., 2016, 28, 4497–4505 CrossRef CAS PubMed
.
- J. Tang, J. Li, J. J. Vlassak and Z. Suo, Soft Matter, 2016, 12, 1093–1099 RSC
.
- Q. Wang and X. Zhao, Sci. Rep., 2015, 5, 8887 CrossRef CAS PubMed
.
-
L. B. Freund and S. Suresh, Thin film materials: stress, defect formation and surface evolution, Cambridge University Press, 2004 Search PubMed
.
- H.-H. Yu and J. W. Hutchinson, Int. J. Fract., 2002, 113, 39–55 CrossRef
.
- D. Marshall and A. Evans, J. Appl. Phys., 1984, 56, 2632–2638 CrossRef CAS
.
- H. Yuk, T. Zhang, S. Lin, G. A. Parada and X. Zhao, Nat. Mater., 2016, 15, 190–196 CrossRef CAS PubMed
.
- N. Lu, J. Yoon and Z. Suo, Int. J. Mater. Res., 2007, 98, 717–722 CrossRef CAS
.
- T. Zhang, H. Yuk, S. Lin, G. A. Parada and X. Zhao, Acta Mech. Sin., 2017, 1–12 Search PubMed
.
- H. Yuk, T. Zhang, G. A. Parada, X. Liu and X. Zhao, Nat. Commun., 2016, 7, 12028 CrossRef PubMed
.
- O. van der Sluis, Y. Y. Hsu, P. H. M. Timmermans, M. Gonzalez and J. P. M. Hoefnagels, J. Phys. D: Appl. Phys., 2011, 44, 034008 CrossRef
.
- J. P. M. Hoefnagels, J. Neggers, P. H. M. Timmermans, O. van der Sluis and M. G. D. Geers, Scr. Mater., 2010, 63, 875–878 CrossRef CAS
.
- M. Gonzalez, F. Axisa, M. V. Bulcke, D. Brosteaux, B. Vandevelde and J. Vanfleteren, Microelectron. Reliab., 2008, 48, 825–832 CrossRef
.
- Y. Tang, G. Lin, S. Yang, Y. K. Yi, R. D. Kamien and J. Yin, Adv. Mater., 2017, 29, 1604262 CrossRef PubMed
.
- Y. Tang, G. Lin, L. Han, S. Qiu, S. Yang and J. Yin, Adv. Mater., 2015, 27, 7181–7190 CrossRef CAS PubMed
.
- T. C. Shyu, P. F. Damasceno, P. M. Dodd, A. Lamoureux, L. Xu, M. Shlian, M. Shtein, S. C. Glotzer and N. A. Kotov, Nat. Mater., 2015, 14, 785–789 CrossRef CAS PubMed
.
- Y. Tang and J. Yin, Extreme Mech. Lett., 2017, 12, 77–85 CrossRef
.
- V. Kunin, S. Yang, Y. Cho, P. Deymier and D. J. Srolovitz, Extreme Mech. Lett., 2016, 6, 103–114 CrossRef
.
- Y. Cho, J.-H. Shin, A. Costa, T. A. Kim, V. Kunin, J. Li, S. Y. Lee, S. Yang, H. N. Han and I.-S. Choi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17390–17395 CrossRef CAS PubMed
.
- M. K. Blees, A. W. Barnard, P. A. Rose, S. P. Roberts, K. L. McGill, P. Y. Huang, A. R. Ruyack, J. W. Kevek, B. Kobrin and D. A. Muller, Nature, 2015, 524, 204–207 CrossRef CAS PubMed
.
- Z. Song, X. Wang, C. Lv, Y. An, M. Liang, T. Ma, D. He, Y.-J. Zheng, S.-Q. Huang and H. Yu, Sci. Rep., 2015, 5, 10988 CrossRef CAS PubMed
.
- Y. Zhang, Z. Yan, K. Nan, D. Xiao, Y. Liu, H. Luan, H. Fu, X. Wang, Q. Yang, J. Wang, W. Ren, H. Si, F. Liu, L. Yang, H. Li, J. Wang, X. Guo, H. Luo, L. Wang, Y. Huang and J. A. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11757–11764 CrossRef CAS PubMed
.
- T. Castle, Y. Cho, X. Gong, E. Jung, D. M. Sussman, S. Yang and R. D. Kamien, Phys. Rev. Lett., 2014, 113, 245502 CrossRef PubMed
.
- Z. Yan, F. Zhang, J. Wang, F. Liu, X. Guo, K. Nan, Q. Lin, M. Gao, D. Xiao and Y. Shi, Adv. Funct. Mater., 2016, 26, 2629–2639 CrossRef CAS PubMed
.
- D. M. Sussman, Y. Cho, T. Castle, X. Gong, E. Jung, S. Yang and R. D. Kamien, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7449–7453 CrossRef CAS PubMed
.
- D. A. Dillard, B. Chen, T. Chang and Y.-H. Lai, J. Adhes., 1999, 69, 99–120 CrossRef CAS
.
- Y.-H. Lai, M. D. Rakestraw and D. A. Dillard, Int. J. Solids Struct., 1996, 33, 1725–1743 CrossRef
.
- R. Zhao, T. Zhang, M. Diab, H. Gao and K.-S. Kim, Extreme Mechanics Letters, 2015, 4, 76–82 CrossRef
.
- K. Fukuda, Y. Takeda, Y. Yoshimura, R. Shiwaku, L. T. Tran, T. Sekine, M. Mizukami, D. Kumaki and S. Tokito, Nat. Commun., 2014, 5 Search PubMed
.
- D. Son, J. Lee, S. Qiao, R. Ghaffari, J. Kim, J. E. Lee, C. Song, S. J. Kim, D. J. Lee and S. W. Jun, Nat. Nanotechnol., 2014, 9, 397–404 CrossRef CAS PubMed
.
- M. Amjadi, K. U. Kyung, I. Park and M. Sitti, Adv. Funct. Mater., 2016, 26, 1678–1698 CrossRef CAS
.
- M. Amjadi, Y. J. Yoon and I. Park, Nanotechnology, 2015, 26, 375501 CrossRef PubMed
.
- Y. Ma, M. Pharr, L. Wang, J. Kim, Y. Liu, Y. Xue, R. Ning, X. Wang, H. U. Chung and X. Feng, Small, 2017, 13 Search PubMed
.
- Y. Su, X. Ping, K. J. Yu, J. W. Lee, J. A. Fan, B. Wang, M. Li, R. Li, D. V. Harburg, Y. Huang, C. Yu, S. Mao, J. Shim, Q. Yang, P. Y. Lee, A. Armonas, K. J. Choi, Y. Yang, U. Paik, T. Chang, T. J. Dawidczyk, Y. Huang, S. Wang and J. A. Rogers, Adv. Mater., 2017, 29, 1604989 CrossRef PubMed
.
- D.-H. Kim, J. Song, W. M. Choi, H.-S. Kim, R.-H. Kim, Z. Liu, Y. Y. Huang, K.-C. Hwang, Y.-W. Zhang and J. A. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18675–18680 CrossRef CAS PubMed
.
- D. S. Gray, J. Tien and C. S. Chen, Adv. Mater., 2004, 16, 393–397 CrossRef CAS
.
- A. Mamidanna, Z. Song, C. Lv, C. S. Lefky, H. Jiang and O. J. Hildreth, ACS Appl. Mater. Interfaces, 2016, 8, 12594–12598 CAS
.
- C. Lv, H. Yu and H. Jiang, Extreme Mech. Lett., 2014, 1, 29–34 CrossRef
.
- J.-K. Jiang, J.-H. Chiu and J.-K. Lin, Dis. Colon Rectum, 1999, 42, 1152–1159 CrossRef CAS PubMed
.
- S. A. Mazzuca, M. C. Page, R. D. Meldrum, K. D. Brandt and S. Petty-Saphon, Arthritis Care Res., 2004, 51, 716–721 CrossRef PubMed
.
- W. Zeng, L. Shu, Q. Li, S. Chen, F. Wang and X. M. Tao, Adv. Mater., 2014, 26, 5310–5336 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sm02338c |
| This journal is © The Royal Society of Chemistry 2018 |