Molecular shape as a means to control the incidence of the nanostructured twist bend phase

Abstract

Liquid crystalline phases with a spontaneous twist-bend modulation are most commonly observed for dimers and bimesogens with nonamethylene spacers. In order to redress this balance we devised a simple chemical intermediate that can be used to prepare unsymmetrical bimesogens; as a proof of concept we prepared and studied eleven novel materials with all found to exhibit the twist-bend phase and exhibit a linear relationship between TN-I and TTB-N. A computational study of the conformational landscape reveals the octamethyleneoxy spacer to have a broader distribution of bend-angles than the nonamethylene equivalent, leading to reductions in the thermal stability of the TB phase. This result indicates that a tight distribution of bend-angles should stabilise the TB phase and lead to direct TB-Iso phase transitions, and conversely a broader distribution should destabilise the TB phase which may allow new states of matter that are occluded by the incidence of this phase to be revealed.

---

Introduction

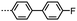
Nematic to nematic transitions are a highly topical area of liquid crystal research, largely due to the discovery of the twist-bend phase.^1–19 The local structure of the twist-bend phase is a helix of short (∼10 nm) pitch.^2,3,20,21 Previously we suggested the phase be described as ‘twist-bend’ rather than ‘twist-bend nematic’ (i.e. TB not N_TB)²² as the local helical structure of this phase is at odds with the definition of a nematic phase as defined by IUPAC, sharing only the lack of positional order of a true nematic phase. The TB phase has to date been observed in liquid crystalline dimesogens,^22–30 oligomers,^31–36 polymers^37,38 and bent-core materials and,³⁹ and as with all mesophases there is an interest in elucidating which (molecular factors if any) lead to the formation of the twist-bend phase.^4,40–44 In dimesogenic liquid crystals the twist-bend phase has been suggested to be a product of the gross bent shape; both theory and experiment^45,46 suggest a link between the gross molecular bend and the stability or incidence of this phase, but this has still not been demonstrated definitively. The experimental observation of a linear relationship between the clearing point and the onset temperature of the twist-bend phase found within homologous series of materials⁴⁷ supports earlier theoretical works suggesting the incidence of this phase is a consequence of steric factors.^48,49 Although several unsymmetrical materials are also known to exhibit this phase,^50,51 symmetrical methylene linked dimers with a nonamethylene spacer remain the most commonly encountered class of materials exhibiting the twist-bend phase.³⁰

Given the ease of preparing ethers from a phenol and alcohol (via the Mitsunobu protocol) we considered that dimers with mixed methylene/ether linking units could easily be constructed if an appropriate precursor was made available. To this end we devised 4-(8-hydroxyoctyloxy)-4′-cyanobiphenyl, prepared in 3 steps (74% yield over 3 steps) from inexpensive commercial precursors. The difference in behaviour between the present materials containing an octamethyleneoxy spacer and those containing nonamethylene spacers is rationalised as being a consequence of the broader distribution of bend-angles.

Experimental

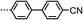
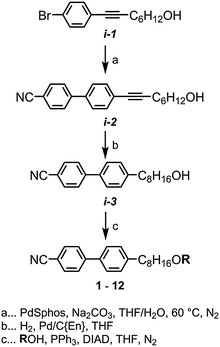
The synthesis of the target materials 1 to 12 is shown in Scheme 1, where ‘R’ is an appropriate mesogenic unit. Chemical intermediates were obtained from commercial suppliers and used without further purification, with the exception of solvents which were dried via percolation over activated alumina prior to use. The intermediate i-1 was prepared in one step (84% yield) from the Pd/Cu mediated Sonogashira coupling of oct-7-yn-1-ol and 1-bromo-4-iodobenzene, and the liquid crystalline material CB8OCB was prepared reported previously.⁴⁵ Suzuki–Miyaura coupling of i-1 with 4-hydroxyphenyl boronic acid afforded i-2 (96% yield); selective hydrogenation of the alkyne with hydrogen and palladium on carbon poisoned with diaminoethane afforded i-3 (92% yield). Subsequently, i-3 was then etherified with appropriate phenols via the Mitsunobu protocol, affording the target compounds 2–12 in high yield and purity (RP-HPLC assay) following chromatographic separation and recrystalisation. Full experimental details are given in the ESI† to this article.

Scheme 1

Results

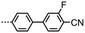
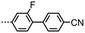
Compounds 2–9 were studied by a combination of polarised optical microscopy (POM), differential scanning calorimetry (DSC) and – for selected examples, small angle X-ray scattering (SAXS). Phase identification was made by POM/SAXS while transition temperatures, presented below in Table 1, are the average of two DSC cycles. Compound 1 was reported previously by us in ref. 45, and we reproduce this data in Table 1.

Table 1 Transition temperatures (T, °C) and associated enthalpies (ΔH, kJ mol⁻¹) for compounds 1–9, values being the average of two runs as measured via DSC at a heat/cool rate of 10 °C min⁻¹

No.	R=		MP	TB-N	N-Iso
1		T	110.6	109.9	153.3
CB8OCB		ΔH	33.9	<0.1	2.3
2		T	130.6	87.5	126.8
		ΔH	42.6	<0.1	1.8
3		T	104.8	97.5	133.0
		ΔH	38.2	<0.1	2.8
4		T	104.9	74.9	107.8
		ΔH	45.1	0.2	1.5
5		T	71.5	59.8	85.8
		ΔH	39.1	0.1	1.3
6		T	97.5	35.7	57.8
		ΔH	41.0	<0.1	0.6
7		T	117.2	31.1	51.9
		ΔH	52.7	<0.1	0.9
8		T	107.1	72.2	105.8
		ΔH	37.8	<0.1	1.5
9		T	111.0	70.8	104.8
		ΔH	41.4	<0.1	1.3

---

In our previous work on compound 1 we identified two nematic phases by SAXS; microscopy demonstrated the upper temperature phase to be a ‘classical’ nematic, the lower temperature was tentatively assigned as being a twist-bend phase and this was confirmed via miscibility studies with CB9CB in ref. 45. A subsequent publication also features this material and also identified the lower temperature mesophase as being a twist-bend phase.²⁶ Microscopy studies reveal compounds 2–9 exhibit both nematic and twist-bend phases (Fig. 1). In all cases, values of T_TB-N and T_N-I are lower in 2–9 than for the parent material 1. Lateral substitution of 1 with fluorine (2, 3) leads to predictable reductions in T_TB-N and T_N-I, mirroring the behaviour of low simple rod-like materials.⁵² Loss of the nitrile group (4) and introduction of additional fluoro substituents (5, 6) leads to further reductions in T_TB-N and T_N-I, as does incorporation of the SF₅ group (7), mirroring the behaviour of phenyl benzoate dimesogens.³² Despite having differing terminal chain lengths the transition temperatures of 8 and 9 are essentially identical.

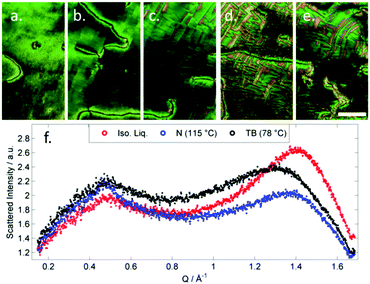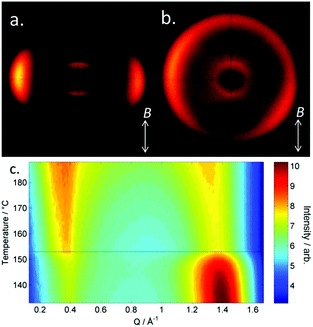
Fig. 1 Photomicrographs (×100 and crossed polarisers, a–e, scale bar in e is 50 μm and all photos are at the same magnification) of the nematic and TB phases of compound 3, each photomicrograph represents adjacent areas of the same slide (see ESI† for full images); (a) 105 °C; (b) 94 °C; (c) 92 °C; (d) 90 °C; (e) 88 °C. Plot of scattered X-ray intensity (arb.) as a function of Q (Å⁻¹) for compound 2 in the isotropic liquid (red) nematic (blue) and TB (black) phases.

The schlieren texture of the nematic phase (Fig. 1a) gives way to the blocky texture in the twist-bend phase (Fig. 2b and c) which becomes more complex as the sample is cooled further (Fig. 2d and e). Further photomicrographs are given in the ESI,† however the optical textures obtained for the TB phase are consistent with previous observations.⁵³ Furthermore, the identity of the TB phase in 1 was confirmed by miscibility with CB9CB as reported in ref. 45. In all cases the nematic to twist-bend transition occurs with a vanishingly small associated enthalpy; however these values are consistent with a nematic to twist-bend phase transition in a dimer.^50,54

Fig. 2 SAXS study compound 10 (EP16): (a) magnetically aligned 2D SAXS pattern obtained in the nematic phase at 180 °C; (b) unaligned 2D SAXS pattern obtained in the twist-bend phase at 140 °C; (c) heatmap plot of the scattered SAXS intensity (intensity arb.) as a function of temperature (°C) and of the scattering vector, Q (Å⁻¹). The dashed line corresponds to the TB-N transition.

SAXS was performed on compound 2 to further elucidate on the nematic-like nature of the lower temperature phase (Fig. 1f). The materials in Table 1 are all monotropic and thus SAXS on members of this series is complicated by crystallisation, in the case of 2 the material can be successfully supercooled to ∼60 °C without crystallisation. Both phases exhibited diffuse scattering at small and wide angles; the lack of Bragg scattering indicates no modulation of electron density associated with lamellar or splay-bend type organisation⁵⁵ and therefore supports the identification as a twist-bend phase. In both phases we find the d-spacing of the small angle peak is 15.1 Å, roughly ½ of the molecular length (29.6 Å at the B3LYP/6-31G(d) level of DFT). We do not observe Bragg scattering associated with the twist-bend periodicity. The intensity of the wide- and small-angle peaks is roughly equal throughout the nematic phase range; however the small-angle intensity decreases marginally at the N-TB transition whereas the intensity of the wide-angle peak almost doubles (see Fig. S6 in ESI†). The reduction of small angle scattering intensity following the N-TB transition has been reported previously,^21,56,57 and we conjecture this is due to a lack of lamellar (cybotactic) fluctuations in the TB phase. Materials which exhibit transitions from the TB phase into smectic phases would be expected to exhibit cybotactic fluctuations; and consequently they do not show this reduction in scattering intensity.⁵⁸

We note that again there is an approximately linear relationship between T_N-I and T_TB-N for this set of materials.⁵⁹

To develop structure–property correlations we prepared materials featuring mesogenic units with differing aspect ratios. Previously we demonstrated that extending the aspect ratio of one or both arms of a liquid crystal dimer can lead to significantly increased clearing points as well as modestly enhanced onset temperatures for the twist-bend phase.⁴¹ We also hypothesized that the increase in aspect ratio leads to the formation of smectic phases,⁶⁰ and therefore for certain materials twist-bend to smectic phase transitions. Compounds 10–12 were studied by a combination of POM, DSC and SAXS; transition temperatures and associated enthalpies are given in Table 2.

Table 2 Transition temperatures (T, °C) and associated enthalpies (ΔH, kJ mol⁻¹) for compounds 1, and 10–12, values being the average of two runs as measured via DSC at a heat/cool rate of 10 °C min⁻¹

No.	R=		MP	TB-N	N-I
1		T	110.6	109.9	153.3
		ΔH	33.9	<0.1	2.3
10		T	121.5	152.9	266.3
		ΔH	45.3	<0.1	3.2
11		T	84.9	101.2	179.6
		ΔH	36.1	<0.1	1.6
12		T	101.5	84.3	181.7
		ΔH	40.9	<0.1	1.5

---

Compound 10 is a mixed biphenyl/terphenyl analogue of 1 and the anticipated increase in transition temperatures although displaying only a modestly higher melt and therefore leading to an enantiotropic twist-bend phase. The use of mesogenic units with large transverse dipole moments affords 11 and 12, although these materials exhibit enhanced clearing points we observed both the melting points and N-TB transition temperatures to be suppressed somewhat.

We subjected 10 to further study by SAXS; the nematic phase exhibited typical diffuse scattering at small- and wide-angles, in the twist-bend phase there is a reduction in the d-spacing of the small angle peak from an average of 17.2 Å in the nematic to just 16.1 Å in the TB phase. Assuming this is the result of the tilting of the molecules away from the heliaxis then this corresponds to a conical angle of ∼21° in the twist-bend phase. The d-spacing of the small angle peak in both phases is on the order of half the molecular length, calculated to be 33 Å at the DFT(B3LYP/6-31G(d)) level. There is a continual decrease in the d-spacing of the wide-angle scattering peak (Fig. S7 in the ESI†) from 4.55 Å to 4.4 Å, with the intensity of the wide-angle peak increasing dramatically with the onset of helical organisation, beginning with the TB-N transition (Fig. 2c). As with SAXS on 2, we observe a significant reduction in the intensity of the small angle peak upon entering the TB phase of 10.

The fact that only a single signal is seen at both small- and wide-angles suggests there is no segregation of the differing mesogenic units into biphenyl or terphenyl rich regions.

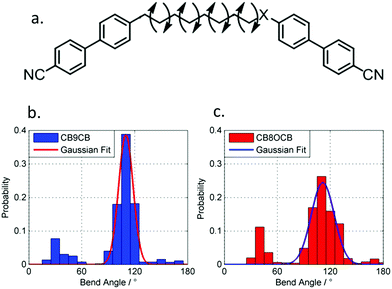
There is some evidence to point to a relationship between the conformational landscape of bimesogens and the twist-bend phase,^45,46 and so we opted perform a comparative study of the conformational landscape of CB8OCB/1 and CB9CB. CB9CB is a well-known standard material, and 1 is structurally analogous to this compound. Using the AM1 method we performed fully relaxed scans about each dihedral angle in the flexible spacers of both materials in Gaussian G09 rev.e01,⁶¹ with each dihedral allowed only a threefold rotation so as to give +gauche/trans/−gauche conformers. From the final Gaussian output files we extracted the final energy of the geometry and Cartesian coordinates using a Matlab script. Conformers that were higher in energy than that of the global energy minima by 20 kJ mol⁻¹ were discarded at this step. For the remaining conformers the angle between the two mesogenic units for each discrete conformer was calculated from the Cartesian coordinates. Using a Boltzmann distribution (temperature 300 K) we obtained the probability for a given bend-angle, as shown in the histogram plot in Fig. 3. Additionally, we obtained probability weighted average bend-angle for both materials. The average bend-angles for the two materials are similar; 1 was determined to be 104° whereas for CB9CB a bend-angle of 102° was found. However, as shown in Fig. 3, there is a broader distribution of bend-angles for compound 1 (CB8OCB) than for CB9CB. We quantified this by measuring the FWHM of a Gaussian fit to the major peak as 19° for CB9CB and 31° for compound 1. For both materials there is a similar probability of conformers with near-linear (>140°) geometries, however 1 has a somewhat higher probability of forming hairpin (<50°) conformers than CB9CB. The fit (and therefore FWHM) display a sensitivity to the number of bins used in the histogram and so the presented FWHM values are best considered qualitatively, however, for every bin size studied we find that materials with methylene linking groups offer a narrower distribution of bend-angles than for the mixed methylene-ether equivalent. The major contribution to the conformational landscape is from the central spacer, although the chemical makeup of the mesogenic unit could also have a small impact.

Fig. 3 (a) The structure of CB9CB (X = –CH₂–) and compound 1/CB8OCB (X = –O–), arrows denote bonds allowed to undergo threefold rotation during the conformational search (3⁸ = 6561 conformers each); histogram plots showing the probability of a given intermesogen angle for CB9CB (b) and 1/CB8OCB (c) along with Gaussian fits (solid lines) to the major peak centred at ∼105°.

As shown in Fig. 4 a linear relationship between T_N-Iso and T_TB-N is observed which is in keeping with the nona- and hepta-methylene systems reported previously.^30,47,62 As with our previous work these plots contains only materials where both mesogenic units contain two cyclic units, materials with differing aspect ratios cannot be compared in this way. While there are no examples of oligomeric materials incorporating the octamethyleneoxy spacer presently employed, we note that oligomeric and polymeric materials exhibiting TB phases obey this linear relationship and so we would expect a similar result for future oligomers employing this spacer. There are significant differences in the two intercept values; the result of this is that for two materials with identical clearing points – one with a nonamethylene spacer and one with octamethyleneoxy – the di-methylene linked material will have a significantly higher nematic to twist-bend transition temperature. Conversely, if these two materials have identical T_TB-N values then the clearing point of the mixed ether/methylene material will be higher. The slopes of the two fits are virtually identical; despite the wide range of mesogenic units employed in both symmetric and unsymmetrical materials (see Table 1 and ref. 30, 62), reinforcing the idea of shape – specifically the gross molecular bend which is a product of the flexibility and length of the central spacer – as a driving force for the incidence of this phase as opposed to specific molecular structural features. It has been shown that for materials with an even parity spacer the transitions for the various phase transitions are randomly distributed,⁶³ making this ongoing observation of the universality of the relationship between T_N-Iso and T_TB-N all the more remarkable.

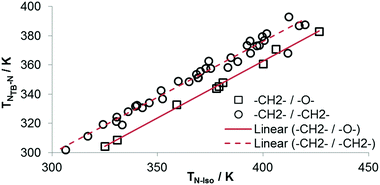Fig. 4 Plot of T_TB-Nversus T_N-Iso for dimers with 2-ring mesogenic units and a nonamethylene spacer (circles)^30,59,62 and an octamethyleneoxy spacer (squares). Linear fits to the data take the form y = 0.766x + 69.67 for octamethyleneoxy (R² > 0.99) and y = 0.7788x + 51.27 for nonamethylene (R² = 0.97) spacers.

As discussed above, the average bend-angles of the two materials are not especially different; however 1 (CB8OCB) exhibits a broader distribution of bend-angles than the all methylene linked CB9CB, and we attribute the reduced intercept value to this broadening of the distribution of bend-angles. The paucity of rigid bent-core materials that exhibit a TB phase implies that some degree of flexibility is critical, given that the bent portion of these compounds tends to be rigid or semi rigid.³⁹ Present results suggest that, if a material having a high value of T_TB-N-N relative to T_N-Iso is desired – or even a twist bend phase forming directly from the isotropic liquid⁶⁴ – then a tight distribution of bend-angles is a key molecular design feature. This hypothesis provides a molecular structure–property relationship that explains the direct isotropic to twist-bend phase transitions that can occur in materials where the bend-angle distribution is especially tight, such as in CB-CN3NC-CB (Fig. 5).⁴⁶ This design rationale can also be applied in reverse; Luckhurst et al. recently suggested that the twist-bend phase may ‘block’ the occurrence of a biaxial nematic phase, from molecular field theory.⁶⁵ By preparing materials in which the bend-angle distribution is broad but a gross bent shape is retained it may be possible to realise thermotropic biaxial nematics without the intervening twist-bend phase.

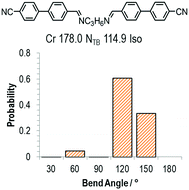Fig. 5 The molecular structure, transition temperatures (°C) and distribution of bend-angles for the dimer CB-CN3NC-CB.⁴⁶

Conclusions

Expanding on the recently reported material CB8OCB we have prepared eleven novel unsymmetrical bimesogenic liquid crystalline materials, all containing a octamethyleneoxy spacer group, all exhibiting the twist-bend phase; once again demonstrating this ubiquity of this liquid-crystalline phase. Dimers and bimesogens with a nonamethylene spacer exhibit a linear relationship between the clearing point (T_N-I) and onset temperature of the twist-bend phase (T_TB-N); not only is such a linear relationship present for materials with mixed ether/methylene linking units but remarkably the slope is virtually identical to that for the purely methylene linked dimers/bimesogens, albeit with a smaller intercept value. This is a further demonstration that the twist-bend phase is driven by gross molecular shape.^30,47,63,66 The relative transition temperatures are insensitive to chemical structure provided a sufficiently flexible bent shape is obtained, although the absolute transition temperatures are of course dependent upon it. A computational study of the conformational landscapes of both CB8OCB and CB9CB shows them to have similar average bend-angles, with the distribution of bend-angles is approximately Gaussian, with a FWHM of 19° for CB9CB and 31° for CB8OCB. It is not only the average bend, but also how the distribution of bend-angles which dictates both the absolute and relative transition temperatures of the resulting material. Given the apparent universality of the TB phase in bent or helical materials across a range of length scales^{21,31–33,36,37,43,44,66–68} we hypothesise that these same structure–property relations will hold true for equivalent oligomeric and polymeric systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

RJM thanks the department of Chemistry for funding EEP. The authors thank the EPSRC for funding the Bruker D8 SAXS equipment via grant EP/K039660/1 and ongoing work via EP/M020584/1.

Notes and references

1. I. Dozov, Europhys. Lett., 2001, 56, 247–253.
2. D. Chen, J. H. Porada, J. B. Hooper, A. Klittnick, Y. Shen, M. R. Tuchband, E. Korblova, D. Bedrov, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15931–15936.
3. V. Borshch, Y. K. Kim, J. Xiang, M. Gao, A. Jakli, V. P. Panov, J. K. Vij, C. T. Imrie, M. G. Tamba, G. H. Mehl and O. D. Lavrentovich, Nat. Commun., 2013, 4, 2635.
4. P. A. Henderson and C. T. Imrie, Liq. Cryst., 2011, 38, 1407–1414.
5. C. Greco, G. R. Luckhurst and A. Ferrarini, Phys. Chem. Chem. Phys., 2013, 15, 14961–14965.
6. C. Meyer, G. R. Luckhurst and I. Dozov, Phys. Rev. Lett., 2013, 111, 067801.
7. P. K. Challa, V. Borshch, O. Parri, C. T. Imrie, S. N. Sprunt, J. T. Gleeson, O. D. Lavrentovich and A. Jakli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 060501.
8. Z. B. Lu, P. A. Henderson, B. J. A. Paterson and C. T. Imrie, Liq. Cryst., 2014, 41, 471–483.
9. N. Sebastian, D. O. Lopez, B. Robles-Hernandez, M. R. de la Fuente, J. Salud, M. A. Perez-Jubindo, D. A. Dunmur, G. R. Luckhurst and D. J. Jackson, Phys. Chem. Chem. Phys., 2014, 16, 21391–21406.
10. G. Barbero, L. R. Evangelista, M. P. Rosseto, R. S. Zola and I. Lelidis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 030501(R).
11. J. P. Jokisaari, G. R. Luckhurst, B. A. Timimi, J. F. Zhu and H. Zimmermann, Liq. Cryst., 2015, 42, 708–721.
12. C. Meyer, G. R. Luckhurst and I. Dozov, J. Mater. Chem. C, 2015, 3, 318–328.
13. B. Robles-Hernández, N. Sebastián, M. R. de la Fuente, D. O. López, S. Diez-Berart, J. Salud, M. B. Ros, D. A. Dunmur, G. R. Luckhurst and B. A. Timimi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 062505.
14. C.-J. Yun, M. R. Vengatesan, J. K. Vij and J.-K. Song, Appl. Phys. Lett., 2015, 106, 173102.
15. J. W. Emsley, M. Lelli, H. Joy, M. G. Tamba and G. H. Mehl, Phys. Chem. Chem. Phys., 2016, 18, 9419–9430.
16. C. Meyer and I. Dozov, Soft Matter, 2016, 12, 574–580.
17. S. Parthasarathi, D. S. Rao, N. B. Palakurthy, C. V. Yelamaggad and S. Krishna Prasad, J. Phys. Chem. B, 2016, 120, 5056–5062.
18. E. Ramou, Z. Ahmed, C. Welch, P. K. Karahaliou and G. H. Mehl, Soft Matter, 2016, 12, 888–899.
19. A. G. Vanakaras and D. J. Photinos, Soft Matter, 2016, 12, 2208–2220.
20. C. Zhu, M. R. Tuchband, A. Young, M. Shuai, A. Scarbrough, D. M. Walba, J. E. Maclennan, C. Wang, A. Hexemer and N. A. Clark, Phys. Rev. Lett., 2016, 116, 147803.
21. M. Cestari, S. Diez-Berart, D. A. Dunmur, A. Ferrarini, M. R. de la Fuente, D. J. Jackson, D. O. Lopez, G. R. Luckhurst, M. A. Perez-Jubindo, R. M. Richardson, J. Salud, B. A. Timimi and H. Zimmermann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031704.
22. R. J. Mandle, E. J. Davis, S. A. Lobato, C. C. A. Vol, S. J. Cowling and J. W. Goodby, Phys. Chem. Chem. Phys., 2014, 16, 6907–6915.
23. R. J. Mandle, E. J. Davis, C. T. Archbold, C. C. A. Voll, J. L. Andrews, S. J. Cowling and J. W. Goodby, Chem. – Eur. J., 2015, 21, 8158–8167.
24. A. N. Scarbrough, M. R. Tuchband, E. D. Korblova, R. F. Shao, Y. Q. Shen, J. E. Maclennan, M. A. Glaser, N. A. Clark and D. M. Walba, Mol. Cryst. Liq. Cryst., 2017, 647, 430–438.
25. V. P. Panov, J. K. Vij and G. H. Mehl, Liq. Cryst., 2017, 44, 147–159.
26. D. A. Paterson, J. P. Abberley, W. T. Harrison, J. M. Storey and C. T. Imrie, Liq. Cryst., 2017, 44, 127–146.
27. J. P. Abberley, S. M. Jansze, R. Walker, D. A. Paterson, P. A. Henderson, A. T. M. Marcelis, J. M. D. Storey and C. T. Imrie, Liq. Cryst., 2017, 44, 68–83.
28. A. A. Dawood, M. C. Grossel, G. R. Luckhurst, R. M. Richardson, B. A. Timimi, N. J. Wells and Y. Z. Yousif, Liq. Cryst., 2017, 44, 106–126.
29. C. T. Archbold, J. L. Andrews, R. J. Mandle, S. J. Cowling and J. W. Goodby, Liq. Cryst., 2017, 44, 84–92.
30. R. J. Mandle, Soft Matter, 2016, 12, 7883–7901.
31. F. P. Simpson, R. J. Mandle, J. N. Moore and J. W. Goodby, J. Mater. Chem. C, 2017, 5, 5102–5110.
32. R. J. Mandle and J. W. Goodby, RSC Adv., 2016, 6, 34885–34893.
33. R. J. Mandle and J. W. Goodby, ChemPhysChem, 2016, 17, 967–970.
34. Y. Wang, G. Singh, D. M. Agra-Kooijman, M. Gao, H. K. Bisoyi, C. M. Xue, M. R. Fisch, S. Kumar and Q. Li, CrystEngComm, 2015, 17, 2778–2782.
35. S. M. Jansze, A. Martinez-Felipe, J. M. Storey, A. T. Marcelis and C. T. Imrie, Angew. Chem., Int. Ed., 2015, 54, 643–646.
36. A. Al-Janabi, R. J. Mandle and J. Goodby, RSC Adv., 2017, 7, 47235–47242.
37. J. An, W. Stevenson, M. Xie, Y. Liu, X. Zeng and G. Ungar, presented in part at the Twist-Bend Nematics and Beyond Conference, University of Southampton, 2016.
38. G. Ungar, J. L. Feijoo, V. Percec and R. Yourd, Abstr. Pap. Am. Chem. Soc., 1991, 201, 212-POLY.
39. D. Chen, M. Nakata, R. Shao, M. R. Tuchband, M. Shuai, U. Baumeister, W. Weissflog, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022506.
40. T. Ivsic, M. Vinkovic, U. Baumeister, A. Mikleusevic and A. Lesac, RSC Adv., 2016, 6, 5000–5007.
41. R. J. Mandle, E. J. Davis, C. C. A. Voll, C. T. Archbold, J. W. Goodby and S. J. Cowling, Liq. Cryst., 2015, 42, 688–703.
42. T. Ivsic, M. Vinkovic, U. Baumeister, A. Mikleusevic and A. Lesac, Soft Matter, 2015, 11, 6716.
43. M. Sepelj, A. Lesac, U. Baumeister, S. Diele, H. L. Nguyen and D. W. Bruce, J. Mater. Chem., 2007, 17, 1154–1165.
44. M. Sepelj, A. Lesac, U. Baumeister, S. Diele, D. W. Bruce and Z. Hamersak, Chem. Mater., 2006, 18, 2050–2058.
45. R. J. Mandle, C. T. Archbold, J. P. Sarju, J. L. Andrews and J. W. Goodby, Sci. Rep., 2016, 6, 36682.
46. C. T. Archbold, R. J. Mandle, J. L. Andrews, S. J. Cowling and J. W. Goodby, Liq. Cryst., 2017, 1–10,  DOI:10.1080/02678292.2017.1360954.
47. R. J. Mandle and J. W. Goodby, Chem. – Eur. J., 2016, 22, 18456–18464.
48. C. Greco, G. R. Luckhurst and A. Ferrarini, Soft Matter, 2014, 10, 9318–9323.
49. N. Vaupotic, S. Curk, M. A. Osipov, M. Cepic, H. Takezoe and E. Gorecka, Phys. Rev. E, 2016, 93, 022704.
50. R. J. Mandle, C. C. A. Voll, D. J. Lewis and J. W. Goodby, Liq. Cryst., 2016, 43, 13–21.
51. Z. Ahmed, C. Welch and G. H. Mehl, RSC Adv., 2015, 5, 93513–93521.
52. J. E. Fearon, G. W. Gray, A. D. Ifill and K. J. Toyne, Mol. Cryst. Liq. Cryst., 1985, 124, 89–103.
53. R. J. Mandle, E. J. Davis, C. T. Archbold, S. J. Cowling and J. W. Goodby, J. Mater. Chem. C, 2014, 2, 556–566.
54. R. J. Mandle and J. W. Goodby, CrystEngComm, 2016, 18, 8794–8802.
55. C. H. Zhu, M. R. Tuchband, A. Young, M. Shuai, A. Scarbrough, D. M. Walba, J. E. Maclennan, C. Wang, A. Hexemer and N. A. Clark, Phys. Rev. Lett., 2016, 116, 147803.
56. D. A. Paterson, M. Gao, Y. K. Kim, A. Jamali, K. L. Finley, B. Robles-Hernandez, S. Diez-Berart, J. Salud, M. R. de la Fuente, B. A. Timimi, H. Zimmermann, C. Greco, A. Ferrarini, J. M. D. Storey, D. O. Lopez, O. D. Lavrentovich, G. R. Luckhurst and C. T. Imrie, Soft Matter, 2016, 12, 6827–6840.
57. N. Sebastian, M. G. Tamba, R. Stannarius, M. R. de la Fuente, M. Salamonczyk, G. Cukrov, J. Gleeson, S. Sprunt, A. Jakli, C. Welch, Z. Ahmed, G. H. Mehl and A. Eremin, Phys. Chem. Chem. Phys., 2016, 18, 19299–19308.
58. R. J. Mandle, S. J. Cowling and J. W. Goodby, Sci. Rep., 2017, 7, 13323.
59. R. J. Mandle and J. W. Goodby, Chemistry, 2016, 22, 18456–18464.
60. R. J. Mandle and J. W. Goodby, Chemistry, 2016, 22, 9366–9374.
61. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, 2009.
62. F. P. Simpson, R. J. Mandle, J. N. Moore and J. W. Goodby, J. Mater. Chem. C, 2017, 5, 5102–5110.
63. J. W. Goodby, Liq. Cryst., 2017, 44, 1755–1763.
64. C. T. Archbold, E. J. Davis, R. J. Mandle, S. J. Cowling and J. W. Goodby, Soft Matter, 2015, 11, 7547–7557.
65. T. B. T. To, T. J. Sluckin and G. R. Luckhurst, Phys. Chem. Chem. Phys., 2017, 19, 29321–29332.
66. R. J. Mandle, Chem. – Eur. J., 2017, 23, 8771–8779.
67. G. Ungar, V. Percec and M. Zuber, Macromolecules, 1992, 25, 75–80.
68. E. Barry, Z. Hensel, Z. Dogic, M. Shribak and R. Oldenbourg, Phys. Rev. Lett., 2006, 96, 018305.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sm02364b

---