 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Porosity of silica Stöber particles determined by spin-echo small angle neutron scattering
S. R.
Parnell
*ab,
A. L.
Washington
cd,
A. J.
Parnell
c,
A.
Walsh
e,
R. M.
Dalgliesh
f,
F.
Li
b,
W. A.
Hamilton
g,
S.
Prevost
h,
J. P. A.
Fairclough
d and
R.
Pynn
bg
aFaculty of Applied Sciences, Delft University of Technology, Mekelweg 15, 2629 JB Delft, The Netherlands. E-mail: S.R.Parnell@tudelft.nl
bCentre for Exploration of Energy and Matter, Indiana University, Bloomington, 47408, USA
cDepartment of Physics and Astronomy, The University of Sheffield, Sheffield, S3 7RH, UK
dDepartment of Mechanical Engineering, The University of Sheffield, Sheffield, S1 3DJ, UK
eDepartment of Chemistry, The University of Sheffield, Sheffield, S3 7HF, UK
fISIS, Rutherford Appleton Laboratory, Chilton, Oxfordshire, OX11 0QX, UK
gNeutron Sciences Directorate, Oak Ridge National Laboratory, Oak Ridge, 37831, USA
hID02 Beamline, European Synchrotron Radiation Facility, F38043, Grenoble, France
First published on 17th March 2016
Abstract
Stöber silica particles are used in a diverse range of applications. Despite their widespread industrial and scientific uses, information on the internal structure of the particles is non-trivial to obtain and is not often reported. In this work we have used spin-echo small angle neutron scattering (SESANS) in conjunction with ultra small angle X-ray scattering (USAXS) and pycnometry to study an aqueous dispersion of Stöber particles. Our results are in agreement with models which propose that Stöber particles have a porous core, with a significant fraction of the pores inaccessible to solvent. For samples prepared from the same master sample in a range of H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O ratio solutions we were able to model the SESANS results for the solution series assuming monodisperse, smooth surfaced spheres of radius 83 nm with an internal open pore volume fraction of 32% and a closed pore fraction of 10%. Our results are consistent with USAXS measurements. The protocol developed and discussed here shows that the SESANS technique is a powerful way to investigate particles much larger than those studied using conventional small angle scattering methods.
D2O ratio solutions we were able to model the SESANS results for the solution series assuming monodisperse, smooth surfaced spheres of radius 83 nm with an internal open pore volume fraction of 32% and a closed pore fraction of 10%. Our results are consistent with USAXS measurements. The protocol developed and discussed here shows that the SESANS technique is a powerful way to investigate particles much larger than those studied using conventional small angle scattering methods.
Introduction
Silica particles have applications in a diverse range of industrial and technological applications. Examples include information and communications technologies, medicine, biology and environmental monitoring.1–3 Since these applications often require control over the particle size and density, significant efforts have been applied to the accurate determination of these parameters.4 Conventional size determination methods such as nanoparticle tracking analysis, transmission electron microscopy (TEM) and dynamic light scattering (DLS) are often used.One of the most common and important methods of forming silica particles uses the process developed by Stöber and co-workers in the 1960's,5 which is known to give superior control over the particle size dispersity-an advantage reflected in over 8000 citations (to date) on the original paper outlining the method. The excellent uniformity which makes Stöber particles so useful also makes them suitable for more detailed structural characterisation and a number of scattering experiments have been performed on these particles – the regularity of the process even allowing small angle X-ray scattering (SAXS) and ultra small angle X-ray scattering (USAXS) measurements to be made during particle formation. These showed that the particles initially nucleate as a ramified fractal structure which then grow by aggregating silica from solution6,7 while becoming more compact as the reaction proceeds. Similar results were found more recently by Pontoni et al.8 showing nucleation from a single small particle to a size of ≈20 nm. Once fully formed, the particles have been studied in greater depth.4,9–11 Proposed particle structures have been presented by several groups with larger silica particles formed by this aggregation and clumping of much smaller particles – with radii of the order 14 nm.12 In smaller Stöber particles (a few tens of nm) however, no core–shell structure is observed, rather a heterogeneous open structure is observed.13 In most cases, the polydispersity of Stöber particles is seen to decrease with increasing reaction time and in microscopy studies this has been associated with development of a pronounced smooth particle surface (see for example ref. 14).
Whilst a significant number of studies have looked at the structure of Stöber silica, very few have looked at the porosity, although this would seem to be a necessary concomitant of the fast nucleation and slower growth model outlined above. In one study9 helium pycnometry was used to measure the Stöber silica densities, finding values initially in the range of 2.04–2.10 g cm−3 for particles in the 80–900 nm size range, approximately a density 80% of that of crystalline quartz (2.65 g cm−3). However, after rigorous washing and drying at 90 °C the measured density decreased to 1.9–1.95 g cm−3. It has been postulated that pycnometry measurements do not measure the porosity of the entire silica particles as the C18 from stearyl alcohol, which is sometimes used in the formation process, can effectively block the pores to the helium probe gas.9
In order to investigate the structure of colloidal Stöber particles we have applied the relatively new technique of spin-echo small angle neutron scattering (SESANS).15–17 Briefly SESANS uses a series of magnetic fields to encode the scattering angle information into the polarisation of a neutron beam, a more detailed description is presented in Appendix A. The structural length scale probed depends upon the applied magnetic field strength and the neutron wavelength squared. On a time of flight neutron source, where a range of wavelengths are used, this allows a corresponding range of length scales (termed spin echo length, z) to be probed simultaneously. This technique has the ability to probe both the inter-particle and intra-particle structure in suspensions of solvents, by measuring the transverse projection of the real-space Debye correlation function G(z), rather than its Fourier transform that is obtained in the more familiar technique of small angle neutron scattering (SANS). At spin echo lengths much greater than the particle radius the spin echo signal depends very simply upon the difference in scattering length density (SLD) between the particle and solution,18 allowing this difference to be determined very accurately. In this study the particles were suspended in either pure H2O or a mixture of H2O and D2O allowing the neutron contrast between the particle and solution to be changed in a predictable way and the particle density to be inferred with similar accuracy with an absolute minimum of structural assumptions or free parameters. It is also important to note that the SESANS technique allows the measurement of the total scattering in absolute terms (eqn (11) in Appendix A) and unlike other neutron techniques the structural signal is not seriously affected by incoherent (non-structural) scattering.
The SESANS technique is capable of examining much larger length scales (up to 10's of microns) than traditional SANS and is comparable in the upper range to the accessible length scales probed by ultra small angle neutron scattering (USANS).19 The approach has a major advantage over the latter technique in that it can be applied to high concentration samples, as multiple neutron scattering effects may be taken into account exactly,20 whereas USANS is a dilute solution measurement. The technique does not change the geometry of the sample, the scan ranges are determined by the applied magnetic fields and since the scattering is encoded in the beam polarisation rather than determined from angular deviations SESANS can also employ rather divergent beams, allowing efficient use of the available polarised neutron flux.
Experimental methods
A sample of monodisperse silica particles was synthesised using the method reported by Stöber and co-workers.5 For the synthesis, ethanol (30.0 g), deionised water (5.0 g, 18 MΩ) and ammonium hydroxide (3.0 g 28–30% NH3) (Aldrich) were added to a round bottom flask and stirred for ten minutes at room temperature followed by the rapid addition of tetraethyl orthosilicate (3.0 g 98% TEOS) (Aldrich). The solution was left to stir at 250 rpm for 24 h at room temperature. Silica particles were purified by centrifugation at 3000 rpm for 1 h 3× into ethanol then 3× into deionised water, (18.2 MΩ) H2O (ELGA Purelab Option-Q) being used exclusively in the preparation. A fraction of the prepared silica was weighed then dried over 24 hours to determine the mass fraction in solution. This was determined to be 15%.A number of different techniques were used to fully characterise the Stöber silica particles in conjunction with our primary SESANS measurements. Dynamic light scattering (DLS) was performed using a Zetasizer NanoZS (Malvern instruments) to give values for the intensity-average and number-average hydrodynamic diameters of the silica particles. Silica dispersions were analysed using disposable cuvette cells and the results were averaged over three consecutive runs. Prior to measurement the silica dispersions were diluted with deionised water (18 MΩ) and filtered through a 0.20 μm filter membrane (to remove any dust). An LM10 particle tracker (Nanosight) was used to measure the size of a large number of single particles via tracking the individual particle tracks, which act as point scatterers and move via Brownian motion. The video footage was analysed using the inbuilt particle tracking analysis software, which gave a particle hydrodynamic radius of 73 nm. DLS measurements were also used to check the polydispersity of the samples, which was measured to be 1%, suitably mono disperse for our sample requirements here (Fig. 1).
Density measurements were made using an AccuPyc 1330 helium pycnometer (Micrometrics) with a 0.1 cm3 sample cell. Our silica particles were dried for 24 h in an oven at 100 °C to produce a dry powder sample suitable for analysis. The gas pycnometer measured a density of 2.32 g cm−3 which is only 12.5 percent lower than the value for crystalline SiO2 (2.65 g cm−3) indicating Stöber particles of good quality. SANS investigations have returned a range of density values depending on sample conditions and preparation and an accepted value of good colloidal silica particles is in the region of 2.26 g cm−3.21
The SESANS measurements were performed on the Offspec instrument22 at the ISIS pulsed neutron and Muon source (Oxfordshire, UK). Once dried the samples were then dispersed into H2O and further diluted with D2O as detailed below to make the different solution volume fractions. The data was normalised to the instrumental polarisation using a blank (pure solvent) sample of the same thickness. Similar measurements were obtained on the instrument SESAME at the Low Energy Neutron Source LENS (Indiana, USA)23,24 and are detailed in Parnell et al.25 In order to conclusively check for systematic differences in the solvent scattering, a series of H2O and D2O solvent blanks were run on the SESAME instrument in SESANS mode to check for changes in instrumental polarisation. No changes were observed between pure D2O and pure H2O for blanks of 5 mm path length, confirming that, as expected, the incoherent background which normally arises from using H2O in conventional neutron scattering measurements does not affect these SESANS measurements. Here the G(z) for the samples was determined from a comparison of the spin echo signal with and without the sample (for details see Appendix A)
USAXS measurements were performed on the beamline ID02 at ESRF and SANS measurements were performed at the LENS SANS instrument. For the dilute samples necessary for USAXS measurements a sample in H2O was diluted in concentration down to a volume fraction of ≈1%. For the SANS measurements the H2O sample was dried and redispersed into D2O to reduce incoherent scattering. The redispersed sample was sonicated for 2 hours and checks were made visually to observe that the sample was fully re-dispersed.
Results
A series of SESANS measurements were performed for various different combinations of concentration and solvent scattering length density (SLD). They are shown in Fig. 2 and the data were fitted using the theory presented in the appendices with the appropriate form and structure factors for uniform density spheres as given in Pedersen.26 In the process of fitting the data two facts become immediately apparent. The first is that when simulating the undiluted sample it has a larger radius than that determined by our DLS measurement. Secondly simulations of the shape of the curves cannot model the shape of the dip observed at z = 150 nm due to the excluded volumes, which are more pronounced in the higher silica concentration sample. Attempts to simulate the data to the measured mass fraction (0.15) and radius (73 nm) determined from the DLS were unsuccessful. Good agreement was found for a volume fraction of 0.1 rather than the 0.06 value which would be expected from the measured mass fraction with the silica of the density measured by pycnometry. In order to accurately simulate the asymptotic value at long spin echo length the porous structure model described in the appendix was used with two additional parameters for the volume fractions for the accessible and inaccessible voids in the silica particles, these are VOpen and VClosed respectively. Good agreement was found with values of VOpen = 0.32 and VClosed = 0.10 and the resulting fits are shown in Fig. 2.While very accurate for measurements of overall scattering power SESANS is somewhat less sensitive to small changes in particle radius compared to other techniques such as traditional scattering methods and hence our best estimate of the Stöber particle radius is from the dilute sample measured on ID02 at the ESRF. The measured USAXS data is shown in Fig. 3 with a simulation to a hard sphere model with a radius of 83 ± 1 nm. This value was used in the SESANS modelling, although fits of similar accuracy can be obtained for R ≈ 82.5 ± 2.5 nm, however these do change the total porosity and porous fractions due to Σt being dependent on R viaeqn (4) and (11).
Finally in order to achieve information on the surface of the particles SANS was measured at LENS from a dilute (volume fraction 1.2%) sample of the same particles in D2O (Fig. 4). Fitting to the observed Porod surface scattering region at this higher Q is shown falling off into the incoherent background signal (4). The structural scattering intensity in this data falls of as the scattering vector to the power −3.90 ± 0.03, very close to the −4 expected from a perfectly smooth sharp particle surface.
 | ||
| Fig. 4 SANS data for a low concentration solution of Stöber silica particles in D2O. Line is fit to Porod scattering with a fractal index (n) of 3.90 ± 0.03. | ||
Discussion
Our model fits show clearly in Fig. 2 that the Stöber nano-particles can be well described as porous with both open and closed pores. The agreement between the particle radius derived from SESANS and USAXS is consistent, however both scattering methods return values significantly higher than that determined by our DLS measurements.The inaccessible void structure is similar to that recently deduced from gas adsorption measurements by Li et al.10 The predicted value from SESANS of 10% inaccessible pores is close to that predicted by pycnometry of 13%. While in an earlier SESANS investigation27 no porosity changes were observed and the SLD used for the particles was in good agreement with that obtained with bulk measurements. However in this case the silica particles were also covered by a sterically stabilizing layer of polyisobutene, 4 ± 5 nm thick. This disagreement with our results could be due to differences in the method used for particle formation or the hydrophobic coating blocking the pores and resulting in only closed pores, which appears more likely.
We observed scattering from smooth surfaces, which is consistent with earlier electron microscopy14 and measured fractal indexes of Stöber particles with a long reaction time,7 unlike fractal surface previously observed by others,11,28 albeit for larger particles.
Conclusions
The work shown in this communication highlights the applicability of the SESANS technique to both the study of colloids in solution and also porous media. The relatively trivial model used here allows for the extraction of both the inaccessible and accessible void volume fractions. The advantages of this technique arise from the unambiguous determination of the total scattering as given by the normalised spin-echo signal which is obtained at long spin-echo lengths. Also due to the insensitivity of the technique to incoherent scattering, a series of samples can be prepared in H2O and D2O from the same master sample, allowing the volume fractions to be determined as a ratio from one data set to another. This approach avoids the problem of separately determining the volume fraction and the contrast which often plagues conventional SANS.The technique can also be applied to larger Stöber particles and also to look at changes in internal pore sizes where calcination is used to seal surface pores, however the consequence of this upon the internal pore structure has yet to be investigated.29
We have also shown that SESANS can easily be used to work with hydrogenous samples without the additional complications of incoherent scattering, unlike traditional SANS experiments. Furthermore, by analysis of the asymptotic value for the polarisation at long spin echo length, we are able to easily interpret the results without complex calibration and corrections as would be required for the analysis using traditional small angle and ultra small angle techniques.
Appendix A: spin-echo small angle neutron scattering
The SESANS theory has now been described in a number of publications.18,30 We briefly summarise the salient points. The accessible spin-echo length for a neutron of wavelength λ for our setup utilising a series of magnets is given by;z = cBLλ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cot cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (1) |
The SESANS method encodes the scattering angle in the polarisation of the neutron beam and the resulting change in polarisation from the scattering (P(z)) is given by;
| P(z) = exp(Σt[G(z) − 1]) | (2) |
 | (3) |
 | (4) |
For a sample which scatters isotropically, G(z) is related to the neutron scattering cross section per unit volume of sample (dσ/dΩ), as measured in a conventional SANS experiment by;30
 | (5) |
 | (6) |
 | (7) |
 | (8) |
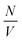 is the particle number density and S(q) and F(q) are the structure and form factors respectively. We use the equations for hard spheres, these are reproduced for clarity from ref. 26 as suggested by the referees. For a hard sphere system, S(q) is calculated with the Percus–Yevick closure relation.
is the particle number density and S(q) and F(q) are the structure and form factors respectively. We use the equations for hard spheres, these are reproduced for clarity from ref. 26 as suggested by the referees. For a hard sphere system, S(q) is calculated with the Percus–Yevick closure relation. | (9) |
 | (10) |
G(A) = α(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A − A A − A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A)/A2 + β(2A A)/A2 + β(2A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A + (2 − A2)cos A + (2 − A2)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A − 2)/A3 + γ[ −a4 A − 2)/A3 + γ[ −a4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A + 4((3A2 − 6)cos A + 4((3A2 − 6)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A + (A3 − 6A)sin A + (A3 − 6A)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A + 6)]/A5 A + 6)]/A5 |
| α = (1 + 2ϕ)2/(1 − ϕ)4 |
| β = −6ϕ(1 + ϕ/2)2/(1 − ϕ)2 |
| γ = ϕα/2 |
Finally the total (single) scattering probability (Σt) for a sample of thickness t is given by;
 | (11) |
Appendix B: model of an isotropic porous particle
In order to correctly model the silica Stöber particles we developed the following model, which is valid for any homogeneous particle with open and closed pores. Assuming that the volume fraction of accessible and inaccessible voids is VOpen and VClosed respectively and that the overall particle volume is VP. The number of particles per unit volume of sample is N we can write the mass fraction (MF) of the particles. | (12) |
The density of the particles determined from the gas pycnometer measurements is given by.
 | (13) |
The contrast difference defined in eqn (7) can be written in terms of the scattering length densities of the particle (ρp) and the liquid (ρl) given as;
| ρp − ρl = (1 −VOpen −VClosed)ρS − (1 − VOpen)ρl | (14) |
Acknowledgements
Construction of LENS was supported by the National Science Foundation grants DMR-0220560 and DMR-0320627, the 21st Century Science and Technology fund of Indiana, Indiana University, and the Department of Defence. One of us, Steven Parnell acknowledges funding from Oak Ridge National Laboratory. We thank the ISIS facility (STFC) in the UK for the award of beam time.References
- B. Karmakar, G. De and D. Ganguli, J. Non-Cryst. Solids, 2000, 272, 119 CrossRef CAS.
- F. Vollmer, D. Braun, A. Libchaber, M. Khoshsima, I. Teraoka and S. Arnold, Appl. Phys. Lett., 2002, 80, 4057 CrossRef CAS.
- I. M. White, N. M. Hanumegowda and X. Fan, Opt. Lett., 2005, 30, 3189 CrossRef CAS PubMed.
- N. C. Bell, C. Minelli, J. Tompkins, M. M. Stevens and A. G. Shard, Langmuir, 2012, 28, 10860 CrossRef CAS PubMed.
- W. Stöber, A. Fink and E. Bohn, J. Colloid Interface Sci., 1968, 26, 62 CrossRef.
- H. Boukari, J. Lin and M. Harris, J. Colloid Interface Sci., 1997, 194, 311 CrossRef CAS PubMed.
- H. Boukari, G. Long and M. Harris, J. Colloid Interface Sci., 2000, 229, 129 CrossRef CAS PubMed.
- D. Pontoni, T. Narayanan and A. R. Rennie, Langmuir, 2002, 18, 56 CrossRef CAS.
- G. H. Bogush, M. A. Tracy and C. F. Zukoski IV, J. Non-Cryst. Solids, 1988, 104, 95 CrossRef CAS.
- S. Li, Q. Wan, Z. Qin, Y. Fu and Y. Gu, Langmuir, 2014, 31, 824, DOI:10.1021/la5042103.
- V. M. Masalov, E. A. Kudrenko, N. A. Grigoryeva, K. V. Ezdakova, V. V. Roddatis, N. S. Sukhinia, M. V. Arefev, A. A. Mistonov, S. V. Grigoriev and G. A. Emelchenko, Nano, 2013, 08, 1350036 CrossRef.
- V. M. Masalov, N. S. Sukhinina, E. A. Kudrenko and G. A. Emelchenko, Nanotechnology, 2011, 22, 275718 CrossRef CAS PubMed.
- C. A. P. Leite, E. F. d. Souza and F. Galembeck, J. Braz. Chem. Soc., 2001, 12, 519 CrossRef CAS.
- I. A. Karpov, É. N. Samarov, V. M. Masalov, S. I. Bozhko and G. A. Emel'chenko, Phys. Solid State, 2005, 47, 347 CrossRef CAS.
- R. Pynn, Neutron Spin Echo, ed. F. Mezei, Lecture Notes in Physics, Springer, Heidelberg, 1980, vol. 128, pp. 159–177 Search PubMed.
- T. Keller, R. Gähler, H. Kunze and R. Golub, Neutron News, 1995, 6, 16 CrossRef.
- M. T. Rekveldt, Nucl. Instrum. Methods Phys. Res., Sect. B, 1996, 114, 366 CrossRef CAS.
- A. L. Washington, X. Li, A. B. Schofield, K. Hong, M. R. Fitzsimmons, R. Dalgliesh and R. Pynn, Soft Matter, 2014, 10, 3016 RSC.
- C. Rehm, J. Barker, W. G. Bouwman and R. Pynn, J. Appl. Crystallogr., 2013, 46, 354 CrossRef CAS.
- M. T. Rekveldt, J. Plomp, W. G. Bouwman, W. H. Kraan, S. Grigoriev and M. Blaauw, Rev. Sci. Instrum., 2005, 76, 033901 CrossRef.
- W. A. Hamilton, 2004, communicated by Wei-Ren Chen at NIST SANS Workshop.
- J. Plomp, V. O. de Haan, R. M. Dalgliesh, S. Langridge and A. A. van Well, Thin Solid Films, 2007, 515, 5732 CrossRef CAS.
- C. M. Lavelle, D. V. Baxter, A. Bogdanov, V. P. Derenchuk, H. Kaiser, M. B. Leuschner, M. A. Lone, W. Lozowski, H. Nann, B. v. Przewoski, N. Remmes, T. Rinckel, Y. Shin, W. M. Snow and P. E. Sokol, Nucl. Instrum. Methods Phys. Res., Sect. A, 2008, 587, 324 CrossRef CAS.
- D. V. Baxter, J. M. Cameron, V. P. Derenchuk, C. M. Lavelle, M. B. Leuschner, M. A. Lone, H. O. Meyer, T. Rinckel and W. M. Snow, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 241, 209 CrossRef CAS.
- S. R. Parnell, A. L. Washington, K. Li, H. Yan, P. Stonaha, F. Li, T. Wang, A. Walsh, W. C. Chen, A. J. Parnell, J. P. A. Fairclough, D. V. Baxter, W. M. Snow and R. Pynn, Rev. Sci. Instrum., 2015, 86, 023902 CrossRef CAS PubMed.
- J. S. Pedersen, Adv. Colloid Interface Sci., 1997, 70, 171 CrossRef CAS.
- T. Krouglov, W. G. Bouwman, J. Plomp, M. T. Rekveldt, G. J. Vroege, A. V. Petukhov and D. M. E. Thies-Weesie, J. Appl. Crystallogr., 2003, 36, 1417 CrossRef CAS.
- M. Szekeres, J. Tóth and I. Dékány, Langmuir, 2002, 18, 2678 CrossRef CAS.
- N. Plumeré, A. Ruff, B. Speiser, V. Feldmann and H. A. Mayer, J. Colloid Interface Sci., 2012, 368, 208 CrossRef PubMed.
- R. Andersson, L. F. Van Heijkamp, I. M. De Schepper and W. G. Bouwman, J. Appl. Crystallogr., 2008, 41, 868 CrossRef CAS.
- J. Plomp, V. de Haan, R. Dalgliesh, S. Langridge and A. van Well, Phys. B, 2011, 406, 2354 CrossRef CAS.
- L. A. Feigin and D. I. Svergun, Structure Analysis by Small Angle X-ray and Neutron Scattering, Pelnum, New York, 1987 Search PubMed.
| This journal is © The Royal Society of Chemistry 2016 |



