Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the onset of oscillatory swimming in microchannels†
Joost
de Graaf
*a,
Arnold J. T. M.
Mathijssen
b,
Marc
Fabritius
a,
Henri
Menke
a,
Christian
Holm
a and
Tyler N.
Shendruk
b
aInstitute for Computational Physics, University of Stuttgart, Allmandring 3, 70569 Stuttgart, Germany. E-mail: jgraaf@icp.uni-stuttgart.de
bThe Rudolf Peierls Centre for Theoretical Physics, 1 Keble Road, Oxford, OX1 3NP, UK
First published on 10th May 2016
Abstract
Self-propelled colloids (swimmers) in confining geometries follow trajectories determined by hydrodynamic interactions with the bounding surfaces. However, typically these interactions are ignored or truncated to the lowest order. We demonstrate that higher-order hydrodynamic moments cause rod-like swimmers to follow oscillatory trajectories in quiescent fluid between two parallel plates, using a combination of lattice-Boltzmann simulations and far-field calculations. This behavior occurs even far from the confining walls and does not require lubrication results. We show that a swimmer's hydrodynamic quadrupole moment is crucial to the onset of the oscillatory trajectories. This insight allows us to develop a simple model for the dynamics near the channel center based on these higher hydrodynamic moments, and suggests opportunities for trajectory-based experimental characterization of swimmers' hydrodynamic properties.
The locomotion of self-propelled particles (swimmers) typically occurs at boundaries or under confinement. Accurately describing the effect of confinement on swimmers is therefore of significant interest to understanding the behavior of microorganisms and artificial swimmers. In modelling these systems, hydrodynamic interactions (HIs) are often ignored, which is a valid approximation in some cases, such as when microbial swimmers' run-and-tumble dynamics dominate.1 However, HIs can play an important role, e.g., see ref. 2–6, and therefore cannot be a priori ignored in modelling. Recent experiments on self-phoretic colloidal swimmers have shown that their orientation is strongly influenced by HIs due to the presence of a wall.7 However, there is ongoing debate on the importance of near-wall effects and the level at which to truncate the hydrodynamic moment expansion.8
A specific example of this are the helical and oscillatory trajectories of single swimmers in confining geometries as observed experimentally by Jana et al.5 and in simulations9–11. Such oscillatory trajectories appear to be commonplace, having been reproduced by many models, and independent of the specific swimmer type. However, a physical understanding of these oscillations remains wanting. It is indisputable that the oscillations do not arise simply from the lowest order hydrodynamics, which result in direct attraction to surfaces,12 while the inclusion of higher-order modes can lead to more complex behavior.8,13 Although observed in confined quiescent fluids, these oscillatory trajectories are reminiscent of those observed in the rheotaxis of swimmers subjected to external flows,14 which result primarily from the interplay between the flow and persistent particle motion due to self-propulsion. Zöttl and Stark indicate that near-field lubrication theory can be used when there is no externally applied flow to describe such trajectories.15,16 Yet, the observations of Zhu et al. demonstrate that oscillatory trajectories arise in a channel that is three times as wide as the self-propelled particle. Additionally, the trajectories of squirmers close to single walls in quiescent fluid show oscillations,17 which have been explained by the competition between far-field HIs and short-ranged wall-swimmer potentials.18 Thus, there is a clear need to establish to what extent the observation of oscillatory trajectories in systems with confinement originates from near- or far-effects and, in conjunction, to assess the importance of higher-order hydrodynamic modes.
In this manuscript, we demonstrate that the onset of time-varying oscillatory trajectories in systems confined within a channel and without external flow can be well-understood using far-field theory.19 We investigate the specific case of two parallel infinite plates that enclose the fluid and a single rod-shaped swimmer, using our lattice-Boltzmann (LB) ‘raspberry’ force/counter-force formalism20 (Fig. 1; insets). We have previously shown that the rod-shaped LB swimmers have well-defined higher-order hydrodynamic moments;20 see Table 1 for representations of the first five moments. These simulations conclusively show that a puller-type rod that starts far from the wall but off-center follows a damped oscillatory trajectory towards the middle of the channel, whereas a pusher-type rod moves between the walls along a sinusoidal path with increasing amplitude. Surprisingly, the oscillations are observable even for plate separations as large as ten times the length of the rod. We explain these observations within the framework of our far-field hydrodynamic theory: the dipole and octupole moments induce hydrodynamic forces towards the center (puller) or towards the walls (pusher), while the quadrupole moment causes pure oscillatory motion. The oscillatory trajectories within plate confinement thus provide an indirect means to characterize the hydrodynamic properties of swimmers, which would grant access to moments beyond those that can be obtained from lattice swimming21 or tracer paths.20
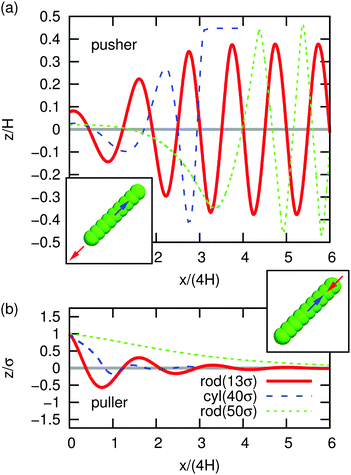 | ||
| Fig. 1 The trajectory of swimmers between two parallel plates with separation H. The horizontal displacement x and vertical position z are given for a swimmer that is initially oriented parallel to the walls and at z = 1σ, with σ the MD unit of length (LB lattice size) and z = 0 the center of the channel. (a) The results for pushers: rod for H = 13σ (red, solid), cylinder for H = 40σ (blue, dashed), and rod for H = 50σ (green, dots). The inset shows a schematic representation of the raspberry rod-swimmer (scaled for H = 13σ), the force is indicated in red and counter force in blue. (b) The results for pullers otherwise the systems are the same. The ESI† contains a companion figure showing the evolution of the angle ϕ for these swimmers. | ||
We consider two raspberry swimmers (rod and cylinder) in the main text to study the movement of shape-anisotropic swimmers under confinement using our ESPResSo LB implementation.20,22 Their construction and characterization in terms of hydrodynamic moments, as well as the fluid and coupling parameters, are introduced in ref. 20 and 23 and detailed in the ESI.† Our swimming model's essential aspect is that a force is applied to the body, consisting of many fluid-particle coupling points, and the system is made force free by applying an equal and opposite force to the fluid, see the insets in Fig. 1. This coupling gives rise to a series of hydrodynamic modes for anisotropic particles.20
These raspberry particles are placed in an LB fluid between two parallel (no-slip) bounce-back plates, with normals in the ẑ direction, separated by a distance H. The fluid domain is periodic in the other two (xy) directions. The vertical position of the swimmer's center of mass (CM) is indicated using z ∈ [−H/2,H/2], with z = 0 the middle of the channel. Lateral displacement is given by x and measured from the swimmer's initial position (x = 0)—our trajectories are straight in the xy-plane. Finally, the angle of the swimmer's director ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) (which points along the main axis) with the plate normal ẑ is given by ϕ ∈ [−π/2,π/2], with ϕ = 0 swimming parallel to the plates. To prevent the swimmers from penetrating the wall, we imposed a short-ranged (almost hard) Weeks–Chandler–Anderson (WCA) interaction between the raspberry swimmers and the walls (ESI†). This wall–swimmer interaction is necessary as our LB algorithm does not explicitly account for near-wall lubrication corrections.23 All of the results shown in the main text employ a WCA diameter d = σ, with σ the LB lattice size. We limit the swimming speed to ensure the low Reynolds number regime, Re < 0.01.
(which points along the main axis) with the plate normal ẑ is given by ϕ ∈ [−π/2,π/2], with ϕ = 0 swimming parallel to the plates. To prevent the swimmers from penetrating the wall, we imposed a short-ranged (almost hard) Weeks–Chandler–Anderson (WCA) interaction between the raspberry swimmers and the walls (ESI†). This wall–swimmer interaction is necessary as our LB algorithm does not explicitly account for near-wall lubrication corrections.23 All of the results shown in the main text employ a WCA diameter d = σ, with σ the LB lattice size. We limit the swimming speed to ensure the low Reynolds number regime, Re < 0.01.
Fig. 1 and the supplemental movies (ESI†) demonstrate the onset of oscillatory trajectories. These are representative sample swimmer trajectories, where the swimmers start off-center and oriented parallel to the plates. Both the rod and cylinder models of pushers and pullers display time-varying oscillatory behavior. In the specific case of our rods, the wavelength of the oscillations is λ ≈ 4H. All pushers move towards the wall and the pullers move towards the center of the plates. After only a few periods, these pullers move along the centreline of the channel and these pushers have arrived in the near-wall region, where swimmer specific details and lubrication corrections would be required to accurately predict dynamics. Oscillations are observed for all cylinder and rod swimmers in plate separations that we could simulate (5σ ≤ H ≤ 50σ). The rod is ∼5σ in length, thus the oscillatory trajectories arise in systems with a channel height to particle size ratio up to at least 10.
To verify the generality of the initial oscillations, we considered several initial positions z and orientations ϕ for rod pusher and puller swimmers. We found that depending on the type of swimmer and its initial position/orientation, several oscillations in the physical regime can be observed, before near-wall effects cannot be ignored. We further showed that oscillations for rod-like swimmers appear for a large range in rod aspect ratios (ESI†). At long times the LB pusher rods display a limit cycle, whereas the pusher cylinder does not. To what extent such a limit cycle (Fig. 1a; solid red curve) or sliding dynamics (Fig. 1a; dashed blue curve) might be physical is not considered here, as algorithmic artifacts close to the walls impact the near-wall dynamics. The ESI† provides a discussion of these limitations and this work does not confirm their physical nature.11 However, our results establish that the initial oscillations before the rod comes close to the wall (a proximity of ∼2σ) are physical. It is this onset of oscillatory trajectories that we concern ourselves with here and subject to theoretical analysis in the following.
We model the raspberry swimmers theoretically as ellipsoids with aspect ratio γ, position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and orientation
and orientation ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = (cos
= (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, 0, sin
ϕ, 0, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ). Due to its motion, the swimmer generates a flow field
ϕ). Due to its motion, the swimmer generates a flow field ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) , which we define in terms of a multipole expansion of the Stokeslet flow solution. Spagnolie et al. argue that far-field HIs give surprisingly accurate results, when compared to theory that includes a finite-size correction to more accurately account for near-field effects, even for small swimmer–wall separations.8 Hence, the flow at the position
, which we define in terms of a multipole expansion of the Stokeslet flow solution. Spagnolie et al. argue that far-field HIs give surprisingly accurate results, when compared to theory that includes a finite-size correction to more accurately account for near-field effects, even for small swimmer–wall separations.8 Hence, the flow at the position ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) generated by the force-free and torque-free swimmer is
generated by the force-free and torque-free swimmer is
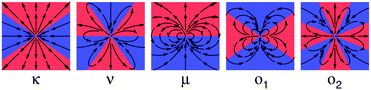
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) ( (![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) , ,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , ,![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ) = κ ) = κ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) D + ν D + ν![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) Q + μ Q + μ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) SD + o1 SD + o1![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) O1 + o2 O1 + o2![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) O2 +… O2 +… | (1) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) D is the Stokes dipole that models the force balance between propulsion and drag,
D is the Stokes dipole that models the force balance between propulsion and drag, ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) Q is the quadrupole that represents the fore–aft asymmetry of the propulsion mechanism,
Q is the quadrupole that represents the fore–aft asymmetry of the propulsion mechanism, ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) SD is the quadrupolar source doublet that is associated with the finite size of the swimmer, and
SD is the quadrupolar source doublet that is associated with the finite size of the swimmer, and ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) O1 and
O1 and ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) O2 are the two octupolar terms (ESI†). The shape of these moments in bulk is shown in Table 1. Note that this is a point-based expansion, which should not be confused with the squirmer expansion for finite-sized spheres; in the far-field these expansions can be mapped onto each other.
O2 are the two octupolar terms (ESI†). The shape of these moments in bulk is shown in Table 1. Note that this is a point-based expansion, which should not be confused with the squirmer expansion for finite-sized spheres; in the far-field these expansions can be mapped onto each other.
The effect of the confining walls (two parallel no-slip plates) is now accounted for by the method of images, where we truncate the approximation after four image systems on each side of the microchannel. Subsequently, the wall-induced flow advects and reorients the swimmer according to the Faxén relations, resulting in the translational and angular velocities ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) HI and
HI and 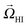 (ESI†). In ref. 19 details are given of the procedure by which these velocities in terms of the multipole coefficients can be obtained. The swimmer's equations of motion are given by
(ESI†). In ref. 19 details are given of the procedure by which these velocities in terms of the multipole coefficients can be obtained. The swimmer's equations of motion are given by
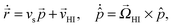 | (2) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) HI and
HI and 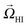 are functions of the multipole coefficients.
are functions of the multipole coefficients.
To predict the swimmer dynamics of Fig. 1 theoretically, we integrate the equations of motion (2). Here, we use the same swimming speed and initial conditions as in the LB simulations, but we allow the multipole coefficients to vary about their measured values. We thus fit the multipole coefficients via a least-squares method. To obtain the best agreement with the measured trajectory, we used the four initial oscillations (ESI†). The 3rd and 5th columns of Table 1 show the multipole coefficients found in this manner for swimmers of the rod and cylinder types, respectively. Using only a single oscillation leads to a change in the fitted values of ∼20%, showing our method to be robust and requiring only fragments of a trajectory to be effective. In addition, we verified that the result of the fitting was independent of the height H of the channel, eliminating the possibility of boundary artifacts. In our previous work,20 we obtained the multipole coefficients directly from the flow field of the swimmers in our LB simulations by means of projection via the Legendre–Fourier decomposition. These values are listed in the 2nd and 4th columns of Table 1, respectively. The projection was carried out in the absence of confinement, using a large simulation box under periodic boundary conditions, for which the finite-size effects differ strongly from those of the confining geometry. There is excellent correspondence between the two measurements of the hydrodynamic moments for both swimmer shapes. This demonstrates the applicability of far-field theory to describe the onset of the observed oscillatory trajectories. The far-field result is accurate until the swimmer–wall distance becomes too small.
Let us now focus on the general features of the theoretical model and analyze the impact of the various hydrodynamic moments on the motion of the swimmer. Firstly, our calculations confirm that the pusher swimmer (κ > 0) undergoes oscillatory trajectories that move away from the center of the channel, and pullers (κ < 0) converge towards the centerline. However, oscillations about the center only occur if the quadrupolar terms are included, and the oscillation wavelength decreases with the associated quadrupolar coefficients ν and μ. A spherical swimmer with ν = μ = 020 does not display such oscillations. The octupolar contributions further control the damping and growth of the trajectories, where the positive signs of o1 and o2 correspond to motion towards the boundaries. The aspect ratio γ leads only to a second-order correction in the theory. That is, the hydrodynamic moments dominate the dynamics of the swimmer; therefore rods with different aspect ratios still show similar oscillations (ESI†).
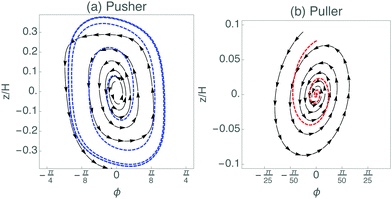
The dynamical system can be understood further by considering the motion of the swimmer in phase space. Due to the translational invariance in the x and y coordinates, the equations of motion can be reduced to two coupled first-order PDEs in (ϕ,z) space, next to the uncoupled equation for the x coordinate. Fig. 2 shows the LB swimmer trajectories in phase space, superimposed with the theoretical model, where the fitted multipole moments in Table 1 have been used. The dipolar term leads to a star-type fixed point (curves radiating from a point) at the origin that is stable for pullers and unstable for pushers. The oscillatory motion due to the quadrupolar contributions corresponds to a circle-type phase-space trajectory (closed loops around a point) centered at the origin. Together the dipole and quadrupole produce a spiral. For pushers, the trajectories spiral outwards (Fig. 2a), and inwards for pullers (Fig. 2b). The theoretical predictions do not show a limit cycle in Fig. 2. Both the far-field framework and the LB method are unable to adequately capture the hydrodynamic interactions in the near-wall region and further study of this region, where both lubrication corrections15 and short-ranged potentials18 can play a role, is required.
Our result shows that movement of a swimmer under confinement can in principle be used to quantitatively determine the hydrodynamic moments, even up to the octupolar moment as shown here. Specifically, about one period is the minimum path length required to fit these modes to within 20%. This suggests that our method has applicability to experimental systems where thermal noise and tumbling can affect the trajectory. The presence of these sources of noise would require ensemble averaging trajectories in (ϕ,z) space, which can then be fitted using our procedure. Noise also implies that parts of the trajectory will occur many times during measurements, meaning that the near-wall dynamics in which we observed a limit cycle does not play an important role. One simply averages many different trajectories away from the wall to improve the fitting statistics.
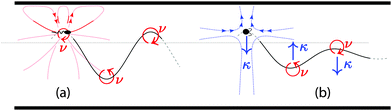
A physical intuition for the onset of oscillatory swimming can be distilled from the LB simulations and far-field hydrodynamic description by considering the trajectory of a swimmer initially set at z0 near the centerline and oriented parallel to the walls (Fig. 3). Since our raspberry swimmers have large quadrupolar moments (ν ∼ 10−1), we first consider only the flow fields generated by the positive quadrupole. This flow serves to rotate the swimmer away from the nearest wall, as shown schematically in Fig. 3a. The continual rotation away from the nearest wall establishes the oscillations. By linearly expanding the equations of motion (2) about the centerline, the micro-swimmer dynamics can be captured by a linear system of coupled differential equations (ESI†). Whenever there is only a quadrupolar flow field, the trajectory is approximated to be simple oscillatory motion z(t) ≈ z0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) with angular frequency ω = 4(3νvs/H5)1/2 and wavelength λ ≈ 2πvs/ω. Although μ = 0 in this study, a source dipole moment also leads to simple oscillations (ESI†). This also theoretically explains the observations of persistent oscillations for neutral squirmers made by Zhu et al.,9 even though there are differences in the confining geometry. Next we add the dipolar term to the expansion
cos(ωt) with angular frequency ω = 4(3νvs/H5)1/2 and wavelength λ ≈ 2πvs/ω. Although μ = 0 in this study, a source dipole moment also leads to simple oscillations (ESI†). This also theoretically explains the observations of persistent oscillations for neutral squirmers made by Zhu et al.,9 even though there are differences in the confining geometry. Next we add the dipolar term to the expansion
| z(t) ≈ z0eαtcos(ωt) | (3) |
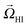 , but this effect is negligible if ν ≫ 81κ2/(48Hvs), which is the case here. A pusher also obeys eqn (3) but with α > 0 and exponentially growing amplitudes, which leads to a rapid breakdown of the near-centerline assumption. The sensitivity of oscillations to channel height is unmistakable in the exp(H−3)-dependence of (3) reflecting the fact that the essential hydrodynamic moments are high order. Whereas higher order moments are required to predict the oscillation wavelength and damping factor quantitatively, the dipolar and quadrupolar moments can be fit from the dynamics using (3) with an error margin of ∼40% compared to the LB-measured values. Hence, (1)–(3) allow for characterization of the swimmer's hydrodynamic properties based on experimental trajectories and can be readily transferred to the observations made by Zhu et al.9 Likewise, LB raspberry simulations can be extended to more complex 3D geometries such as square channels and round tubes, in which we observed helical motion (ESI†).
, but this effect is negligible if ν ≫ 81κ2/(48Hvs), which is the case here. A pusher also obeys eqn (3) but with α > 0 and exponentially growing amplitudes, which leads to a rapid breakdown of the near-centerline assumption. The sensitivity of oscillations to channel height is unmistakable in the exp(H−3)-dependence of (3) reflecting the fact that the essential hydrodynamic moments are high order. Whereas higher order moments are required to predict the oscillation wavelength and damping factor quantitatively, the dipolar and quadrupolar moments can be fit from the dynamics using (3) with an error margin of ∼40% compared to the LB-measured values. Hence, (1)–(3) allow for characterization of the swimmer's hydrodynamic properties based on experimental trajectories and can be readily transferred to the observations made by Zhu et al.9 Likewise, LB raspberry simulations can be extended to more complex 3D geometries such as square channels and round tubes, in which we observed helical motion (ESI†).
In conclusion, we have studied the onset of oscillatory motion of swimmers in microchannels without externally applied flow and in an otherwise quiescent medium using both LB simulations and hydrodynamic theory. The pusher-type swimmers follow a sinusoidal trajectory with increasing amplitude, whereas pullers perform a damped oscillation towards the center of the channel. Our results and previous observations of such phenomena9 can be explained by our theoretical model, which uses far-field hydrodynamics only. We conclude that the onset of oscillations can be described without taking into account near-wall lubrication effects as has been previously presumed15 provided that a quadrupole moment (or source-dipole) is accounted for in addition to the primary dipole moment. To fully characterize particle trajectories in relatively wide channels, many hydrodynamic moments are required, as high as the octupole in our case. However, the excellent match of our trajectory-fitted moments to those measured in bulk suggests that similar experimental measurements can be used to determine the hydrodynamic moment decomposition of microorganisms or artificial swimmers. Our work stresses the relevance of far-field hydrodynamics in confining geometries and thus opens the way for new studies that aim to exploit these insights into microfluidic environments. Future work will focus on the analysis of more complex force/counter-force swimmers to model the richness in shape and hydrodynamic moments of experimentally available swimmers.
Acknowledgements
AJTMM and TNS gratefully acknowledge funding from the ERC Advanced Grant (291234 MiCE) and EMBO (ALTF181-2013); JdG from an NWO Rubicon Grant (#680501210) and a Marie Skłodowska-Curie Intra European Fellowship (G. A. No. 654916) within Horizon 2020. JdG and CH further thank the DFG for funding through the SPP 1726 “Microswimmers–From Single Particle Motion to Collective Behaviour”. We would also like to thank A. Zöttl, A. Doostmohammadi, and A. T. Brown for useful discussions.References
- A. J. T. M. Mathijssen, A. Doostmohammadi, J. M. Yeomans and T. N. Shendruk, J. R. Soc., Interface, 2016, 13, 20150936 CrossRef PubMed.
- E. Lauga, W. DiLuzio, G. Whitesides and H. Stone, Biophys. J., 2006, 90, 400 CrossRef CAS PubMed.
- K. Drescher, J. Dunkel, L. Cisneros, S. Ganguly and R. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940 CrossRef CAS PubMed.
- R. Di Leonardo, D. Dell'Arciprete, L. Angelani and V. Iebba, Phys. Rev. Lett., 2011, 106, 038101 CrossRef CAS PubMed.
- S. Jana, S. Um and S. Jung, Phys. Fluids, 2012, 24, 041901 Search PubMed.
- E. Lushi, H. Wioland and R. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 9733 CrossRef CAS PubMed.
- S. Das, A. Garg, A. Campbell, J. Howse, A. Sen, D. Velegol, R. Golestanian and S. Ebbens, Nat. Commun., 2016, 6, 8999 CrossRef PubMed.
- S. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105 CrossRef.
- L. Zhu, E. Lauga and L. Brandt, J. Fluid Mech., 2013, 726, 285 CrossRef.
- H. Wu, M. Thiébaud, W.-F. Hu, A. Farutin, S. Rafa, M.-C. Lai, P. Peyla and C. Misbah, Phys. Rev. E, 2015, 92, 050701 CrossRef PubMed.
- H. Shum and E. Gaffney, Phys. Rev. E, 2015, 91, 033012 CrossRef PubMed.
- A. Berke, L. Turner, H. Berg and E. Lauga, Phys. Rev. Lett., 2008, 101, 038102 CrossRef PubMed.
- K. Ishimoto and E. Gaffney, Phys. Rev. E, 2013, 88, 062702 CrossRef PubMed.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2012, 108, 218104 CrossRef PubMed.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef PubMed.
- R. Rusconi, J. Guasto and R. Stocker, Nat. Phys., 2014, 10, 212–217 CrossRef CAS.
- G.-J. Li and A. Ardekani, Phys. Rev. E, 2014, 90, 013010 CrossRef PubMed.
- J. Lintuvuori, A. Brown, K. Stratford, D. Marenduzzo, 2015, arxiv:1508.04255, 1.
- A. Mathijssen, A. Doostmohammadi, J. Yeomans and T. Shendruk, 2016, arxiv:1511.01859.
- J. de Graaf, H. Menke, A. Mathijssen, M. Fabritius, C. Holm and T. Shendruk, J. Chem. Phys., 2016, 144, 134106 CrossRef PubMed.
- A. Brown, I. Vladescu, A. Dawson, T. Vissers, J. Schwarz-Linek, J. Lintuvuori and W. Poon, Soft Matter, 2016, 12, 131 RSC.
- A. Arnold, O. Lenz, S. Kesselheim, R. Weeber, F. Fahrenberger, D. Roehm, P. Košovan and C. Holm, Meshfree Methods for Partial Differential Equations VI, 2013, p. 1 Search PubMed.
- L. Fischer, T. Peter, C. Holm and J. de Graaf, J. Chem. Phys., 2015, 143, 084107 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details of the calculations and supporting figures, as well as two movies of the oscillatory swimming of self-propelled rods in microchannels. See DOI: 10.1039/c6sm00939e |
| This journal is © The Royal Society of Chemistry 2016 |