A systematic study of DNA conformation in slitlike confinement†
Liang
Dai
a,
Jeremy J.
Jones
b,
Johan R. C.
van der Maarel
ac and
Patrick S.
Doyle
*ab
aBioSystems and Micromechanics (BioSyM) IRG, Singapore-MIT Alliance for Research and Technology (SMART) Centre, 3 Science Drive 2, Republic of Singapore 117543. E-mail: pdoyle@mit.edu
bDepartment of Chemical Engineering, Massachusetts Institute of Technology (MIT), Cambridge, MA 02139, USA
cDepartment of Physics, National University of Singapore, 2 Science Drive 3, Republic of Singapore 117542
First published on 2nd February 2012
Abstract
DNA conformation in slitlike confinement is studied using Monte Carlo simulation and scaling theory. We focus on analysing the in-plane DNA extension as a function of slit height and DNA properties, such as contour length, persistence length and width. Similar to tube confinement, we identify an extended de Gennes regime which is prevalent in many experimental studies. However, unlike previous studies in tubes, we find two highly confined regimes (so called Odijk regimes) that depend on chain crossing. Our results support the majority of experiments which display a gradual transition into the Odijk regime and give new insight into the importance of chain width for DNA in nanoslits.
1. Introduction
Advancements in nanofabrication techniques have given rise to a new generation of micro and nanodevices for use in biological assays.1–4 A subset of these devices, used in DNA separation and genome analysis, are predicated on confinement-induced changes in molecular structure. In pursuit to better control molecular conformation, researchers have carried out a wide range of single molecule studies focused on understanding biopolymers in confined environments.5 Experimentally, many studies measure a mean size or extension of DNA in the unconfined dimensions.6–11 As such, here we will focus on the static, equilibrium properties of DNA. In this correspondence, we examine and elaborate on subtleties of theory and simulations for DNA confined in a slit (confined between two infinite parallel plates). We seek to show that the current understanding of uniaxial confinement is more complex than previously described. Moreover, we show that subtle deviations from existing theories may account for apparent disagreements in the existing literature.Statistical properties of DNA confined to nanofluidic channels deviate from their free solution or bulk values and depend on the degree of confinement and confinement geometry. New fabrication techniques provide an attractive route to develop a number of complex channel geometries.12–17 Nevertheless, slits and tubes act as canonical examples of uniaxial and biaxial confinement, respectively. Furthermore, more complex geometries can be understood as combinations of tubes and slits.15,16 Therefore, tubes and slits have received the majority of attention. DNA conformation in confinement has typically been viewed as being dependent on a competition between three length scales: the three-dimensional bulk radius of gyration Rg, bulk, the persistence length Lp, and the characteristic size of the channel confining dimension H. For slits, the confining dimension is the channel height. In weak confinement where H ∼ 3Rg, bulk, the DNA coil is only slightly perturbed by the presence of the confining walls. In moderate confinement (also known as the de Gennes regime) Lp ≪ H < Rg, bulk and the polymer is viewed as a series of self-avoiding isometric blobs of diameter H, which leads to scaling predictions for static and dynamic properties of the polymer.18–20 The blob description of the DNA breaks down once H approaches Lp because the orientational and translational degrees of freedom become restricted at the length scale of a statistical segment. Thus, Odijk21–23 proposed a deflection chain model in which the entire polymer contour consists of a series of segments that deflect off of the channel walls.
To date, tubes have been the most widely studied geometry, and, as a result, the theories describing polymer conformation in tube confinement are well in hand. However, sufficient controversy still exists for polymers confined to slits. Much progress has been made experimentally in understanding slit confined polymer configuration in the de Gennes regime.24–27 Consistent, accurate predictions of polymer equilibrium size versus chain contour length and channel height in experiments provide compelling evidence that the framework of blob theory provides an acceptable description of polymer conformation in moderate slit confinement.
In contrast to our understanding of DNA conformation in moderate confinement, remarkable disagreement exists among the experimental studies in nanoslits trying to probe the transition from de Gennes to Odijk regime. Several studies have suggested that the transition from de Gennes to Odijk regime is gradual and broad. Balducci et al.28 measured the diffusivity of DNA in nanoslits over a range of heights spanning from weak to strong (Odijk) confinement. They did not see any significant changes in scaling for diffusivity as channel height H approached DNA persistence length Lp. Studies by Strychalski et al.16,29 also support a gradual transition. They extended the measurements of DNA diffusivity into more shallow slits well below the DNA persistence length without any apparent signature of transitioning into the Odijk regime. They instead observed a single power law scaling for diffusivity for channels heights from 541 nm to 28 nm. More recently Tang et al.26 reported power law scalings for dynamics and static properties of DNA, which extend into the Odijk regime. Contrary to the aforementioned results, Bonthuis et al.25 measured the in plane radius of gyration R∥ scaling as a function of the slit height H and found a sharp change at H ≈ 100 nm. For H smaller than this value, R∥ did not vary. A similar plateau in nanoslits was observed by Lin et al.,30 albeit this transition occurred at heights below the persistence length.
We now turn our attention to the current simulation literature of polymers confined in slits. There is consensus among coarse-grained simulations of DNA in weak and moderate confinement. In weak confinement, the 3D radius of gyration of a polymer shows an initial dip and then increases when decreasing the channel height,31–33 in accord with the theoretical prediction.34,35 This nonmonotonic behaviour of 3D polymer size is due to a competition between compression in the z-direction and swelling in the x–y plane.26 However, the in-plane 2D polymer size (projection on the confining planes) increases monotonically with decreasing channel height.26,33,36 In moderate confinement, simulations of equilibrium in-plane radius of gyration for DNA have consistently shown the expected power law scaling derived from blob theory.24,37 However, the transition from the de Gennes to Odijk regime of slit-like confinement has not been studied extensively. Cifra et al.37 performed worm-like chain simulations of short chains confined to slits. A small change in the scaling for the end-to-end distance was observed. These simulations consist of relatively short chains, and it is not evident how this changes with chain length. A variety of other researchers have probed the Odijk regime by means of worm-like chain models to explore the physics in strong confinement.38,39 However, these prior studies do not extend into the de Gennes regime.38,39
In this paper, we aim to obtain a comprehensive understanding of DNA conformation in slitlike confinement. An issue with the simulations in the existing literature is that they do not span across all relevant length scales. Weak and moderate confinement simulations require significant coarse graining which approximates multiple statistical segments as single entities. Traditional semi-flexible chain models are too computationally expensive and therefore cannot be used to simulate large polymers. Inspired by Wang et al.,40 we find a middle ground to simulate DNA in slits that allows us to probe all regimes of confinement. In doing so, we shed new light on the existing experimental data and also demonstrate the existence of another regime under strong confinement.
2. Theory and computer simulation
2.1 de Gennes regime and extended de Gennes regime
The free energy of DNA in a nanotube was derived by Jun et al.41 using Flory theory.20,42 Later, it was applied to analyse the simulation results of DNA in a square channel by Wang et al.40 In the current study, we use similar free energy arguments to derive scaling laws for DNA in slit confinement. In the de Gennes regime, a DNA chain confined in a slit can be considered as a series of self-avoiding isometric blobs in two-dimensions, as shown in Fig. 1. The free energy is expressed as: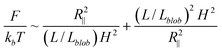 | (1) |
| Lblob ∼ H5/3w−1/3L−1/3p. | (2) |
| 〈R∥〉 ∼ L3/4H−1/4w1/4L1/4p | (3) |
| H** ≅ L2p/w. | (4) |
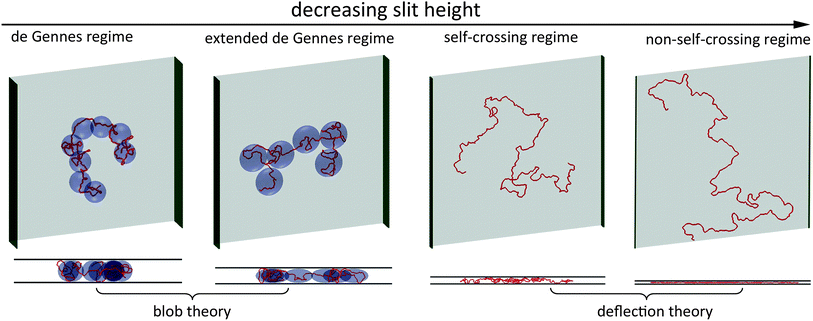 | ||
| Fig. 1 Top and side views of representative simulation snapshots of DNA in four regimes. The red line curves represent 3D DNA conformation. The width of the green sidewall in each scheme indicates the slit height. The light blue blobs in the de Gennes regime represent spheres with a diameter equal to the slit height. The light blue blobs in the extended de Gennes regime represent discoids with an in-plane diameter larger than the slit height. In the first two regimes, DNA conformation can be described by blob theory. In the last two regimes, DNA conformation in the direction perpendicular to the slit wall can be described by deflection theory. | ||
The contour length L** of the sub-chain inside a blob of size H** is:
| L** ≅ L3p/w2 | (5) |
If H becomes less than H**, DNA will enter the so-called “extended“ de Gennes regime,23 which is illustrated in Fig. 1. In this regime, the contour length contained in each spherical blob becomes so short that the excluded volume interaction between segments inside a blob becomes less than kbT.40 Therefore, the sub-chain behaves like an ideal chain, and the scaling law becomes Lblob ∼ H1/2. The blob needs to be enlarged from a sphere to a discoid, such that the chain is now at the crossover between real and ideal chain behaviour. The discoid has a height H and in-plane radius B. The contour length of the sub-chain inside this discoid is L*. The value of B needs to satisfy two conditions.40
| B ∼ L1/2*L1/2p ∼ (L2*w/H)1/2 | (6) |
The middle expression assumes ideal chain behaviour inside a blob. The last term corresponds to the situation that the excluded volume interaction inside a discoid L2*w/(HB2) equals 1 (in units of kbT). Then, L* and B are determined to be:
| L* ∼ LpH/w | (7) |
| B ∼ LpH1/2/w1/2 | (8) |
The free energy in the extended de Gennes regime can be obtained from blob theory by replacing the spherical blob by a discoid. Accordingly, the free energy reads:
 | (9) |
Substituting eqn (7) and eqn (8) into eqn (9), the free energy is expressed as:
 | (10) |
Minimizing eqn (10), we obtain the same expression of the DNA extension as eqn (3). This means that the scaling law relating R∥ to H is the same in the extended de Gennes regime and the de Gennes regime, even though the free energy expressions are different. A similar result was also derived by Wang et al.40 for DNA in a nanotube.
2.2 Odijk regime
To analyse the relationship between R∥ and H in the Odijk regime, we consider a virtual in-plane chain corresponding to the projection of the DNA chain onto a slit wall. Then, R∥ is the radius of gyration for this virtual in-plane chain. This virtual in-plane chain has a projected contour length L∥, an apparent persistence length Lp,∥ and a chain width w. Before calculating R∥, we need to know how L∥ and Lp,∥ are related to H.The scaling law for L∥ was previously derived by Odijk:21
| 〈L∥〉 = L[1 − α(H/Lp)2/3] | (11) |
The prefactor α has been determined to be 0.09137 ± 0.00007 by Burkhardt et al.38,39 Regarding the relationship between Lp,∥and H, we obtained an empirical expression by fitting simulation results (details are given in the results section):
| Lp,∥/Lp ≈ 1.29 × 0.48H/Lp + 0.71 | (12) |
Next, we derive R∥ from L∥, Lp,∥ and w using Flory theory by considering a 2D self-avoiding walk. Free energy of DNA in the Odijk regime also consists of elastic entropy and excluded volume interactions. The excluded area between two DNA segments in a plane is calculated based on the assumption of random orientations (see supplementary materials for the derivation):
| Aev ∼ (Lp,∥ + 1.3w)2 | (13) |
As a result, the total free energy is written as:
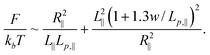 | (14) |
Minimizing the above equation with respect to R∥, we obtain:
| 〈R∥〉 ∼ L3/4∥L1/4p,∥(1 + 1.3w/Lp,∥)1/2. | (15) |
To eliminate the unknown prefactor in eqn (15), we normalize R∥by R∥,plane. R∥,plane corresponds to DNA confined to a plane. In that case, L∥ = L and Lp,‖ = 2Lp.45
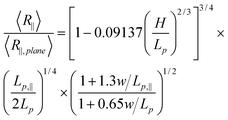 | (16) |
In eqn (16), 〈R∥〉/〈R∥,plane〉 is independent of the contour length, which is confirmed in our simulations of DNA in strong confinement.
Note that the derivation of eqn (13) is based on a 2D self-avoiding walk. It assumes the DNA projection on a slit wall cannot cross itself. This assumption is valid when H ≤ w. We refer to this as Odijk regime I, or “non-self-crossing” regime, as shown in Fig. 1. When w < H < 2Lp, DNA can cross itself. We refer to this as Odijk regime II, or “self-crossing” regime, as shown in Fig. 1. Because of the self-crossing conformation of DNA, the excluded volume interaction term becomes different from eqn (13). In the self-crossing regime, we consider the DNA as a series of deflection segments and write the free energy as:
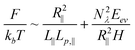 | (17) |
2.3 Monte Carlo simulation of DNA in slits
We use Monte Carlo simulation method to study DNA in a slit, following a similar approach as Wang et al. with slight modifications.40DNA is modelled as a chain of Nbead beads connected by Nbead − 1 inextensible bonds of length lB, corresponding to a contour length L = (Nbead − 1)lB. Different from the approach of Wang et al.,40 pairwise interaction between beads in our simulation is pure hard-core repulsion, which leads to a faster simulation. When the distance between two beads is less than the chain width w, the interaction potential is infinitely large, and the configuration is rejected in the simulation. The hard-core repulsion does not significantly change the simulation results, compared with other short-range interaction potentials. The interaction between a bead and a slit wall is also a hard-core repulsion. If the centre of a bead is beyond a slit wall, the potential will be infinitely large, and the configuration is rejected in Monte Carlo moves. Note that Wang et al.40 judge whether a bead hits the channel wall according to the surface of the bead rather than the centre of the bead. So they subtract the bead diameter from the slit height to obtain an effective slit height. This effective slit height should be used when applying eqn (11). Besides hard-core and hard-wall repulsion, the only interaction in the simulation system is the bending energy between two adjacent bonds. The total bending energy for a wormlike chain is | (18) |
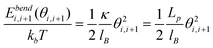 | (19) |
During Monte Carlo simulation, we perform two types of trial moves, crankshaft and reptation.46,47 In each Monte Carlo cycle, we perform one crankshaft move and one reptation move. The simulation starts from a random configuration and usually reaches equilibrium after about 107 steps. In the production run, we perform 1010 steps and record the configuration every 105 steps for data analysis. For each DNA configuration, we calculate R2∥ from the in-plane coordinate xi and yi of each bead using:
 | (20) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) and ȳ are the averages of xi and yi over all beads in a given DNA configuration. We record R2∥ for each configuration and then, we average R2∥ over stored configurations to calculate the square root to obtain R∥. The estimated error of ensemble averaged R∥ is within the size of the symbols in the figures.
and ȳ are the averages of xi and yi over all beads in a given DNA configuration. We record R2∥ for each configuration and then, we average R2∥ over stored configurations to calculate the square root to obtain R∥. The estimated error of ensemble averaged R∥ is within the size of the symbols in the figures.
There are five parameters in the simulation: persistence length Lp, contour length L, chain width w, slit height H and bond length lB. Table 1 shows the parameter sets used in the current study.
| Index | DNA parameter | H = ∞ or H = 0 | H range for different regimes (nm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| L p (nm) | l B (nm) | w (nm) | L (nm) | R ∥,bulk | R ∥,plane | non-self-cross | self-cross | extended de Gennes | de Gennes | weak confine | |
| a 1st column is the index for a set of simulations using the same parameters of DNA and varying the slit height H. 2nd to 5th columns are DNA parameters, persistence length Lp, bond length lB, chain width w and contour length L. 6th to 7th columns are the in-plane radius of gyration of DNA obtained from simulations for two extreme cases H = ∞ and H = 0. 8th to 12th columns are the slit height ranges for different regimes. The last two rows show DNA parameters corresponding to the experimental conditions used in previous research. λ-DNA1 and λ-DNA2 refer to the DNA molecules used in ref. 26 and ref. 25, respectively. | |||||||||||
| 1 | 50 | 40 | 40 | 4 | 285 | 546 | [0, 40] | [40, 100] | skipped | [100, 143] | [143, ∞] |
| 2 | 50 | 40 | 40 | 8 | 432 | 916 | [0, 40] | [40, 100] | skipped | [100, 216] | [216, ∞] |
| 3 | 50 | 40 | 40 | 12 | 549 | 1239 | [0, 40] | [40, 100] | skipped | [100, 275] | [275, ∞] |
| 4 | 50 | 40 | 40 | 16 | 652 | 1537 | [0, 40] | [40, 100] | skipped | [100, 326] | [326, ∞] |
| 5 | 50 | 5 | 10 | 8 | 339 | 846 | [0, 10] | [10, 100] | [100, 170] | skipped | [170, ∞] |
| 6 | 50 | 5 | 15 | 8 | 354 | 855 | [0, 15] | [15, 100] | [100, 167] | [167, 177] | [177, ∞] |
| 7 | 50 | 5 | 20 | 8 | 372 | 863 | [0, 20] | [20, 100] | [100, 125] | [125, 186] | [186, ∞] |
| 8 | 50 | 10 | 10 | 22 | 607 | 1802 | [0, 10] | [10, 100] | [100, 170] | [170, 304] | [304, ∞] |
| 9 | 50 | 20 | 20 | 22 | 675 | 1834 | [0, 20] | [20, 100] | [100, 125] | [125, 338] | [338, ∞] |
| 10 | 50 | 40 | 40 | 22 | 786 | 1950 | [0, 40] | [40, 100] | skipped | [100, 393] | [393, ∞] |
| λ-DNA1 | 54 | 6.6 | 22 | 520 | [0, 13] | [13, 108] | [108, 260] | skipped | [260, ∞] | ||
| λ-DNA2 | 66 | 6.6 | 20 | 840 | [0, 13] | [13, 132] | [132, 420] | skipped | [420, ∞] | ||
3. Results and discussions
3.1 de Gennes regime
First, we present the simulation results for the de Gennes regime. Fig. 2(a) and 2(b) show the normalized R∥ − H curve for different L. We set w to a large value of 40 nm, so that DNA can easily enter the de Gennes regime. We apply two types of normalization for R∥ and H. In the weak confinement regime, DNA conformation is close to that found in bulk and hence we normalize both R∥ and H by R∥,bulk, as shown in Fig. 2(a). After normalization, four curves with different contour lengths collapse in the weak and moderate confinement regimes. It can also be proved from the scaling theory that the normalized R∥ − H curve is independent of L. From Flory theory, R∥,bulk ∼ L3/5L1/5pw1/5. Then, the scaling for R∥ in de Gennes regime, eqn (3), can be rewritten as: | (21) |
 | ||
| Fig. 2 Relative in-plane radius of gyration as a function of the inverse of relative slit height. Four symbols (or colors) correspond to different contour lengths of chains in simulations. They correspond to the simulations #1, #2, #3 and #4 in Table 1. The dashed lines are the best power law fits to the simulation data points in the de Gennes regime. (a) and (b) use different normalizations. The values in parentheses, e.g. (±0.023), refer to the uncertainties of the exponents from the fits. The uncertainties for the prefactors are 1.22 ± 0.02, 1.20 ± 0.01, 1.19 ± 0.01, 1.19 ± 0.01, 1.00 ± 0.03, 1.01 ± 0.01, 1.01 ± 0.01, 1.01 ± 0.01. R∥,bulk is the in-plane radius of gyration of DNA in bulk. R∥,plane is the in-plane radius of gyration of DNA confined to a plane. The chain width w equals 40nm. The insets in (a) and (b) show the fitting residues. The vertical line in (a) corresponds to R∥,bulk/H = 2, which is used as the lower bound of R∥,bulk/H for the de Gennes regime. The vertical line in (b) corresponds to w/H = 0.4 or H = 2Lp = 100 nm, which is used as the upper bound of w/H for the de Gennes regime. | ||
Consistent with theory, the log-log plot of R∥ − H curve exhibits a linear behaviour in the moderate confinement regime, which corresponds to the scaling law in de Gennes regime. Irrespective of L, the best power fit to the simulation data in de Gennes regime gives an exponent of about 1/4, which agrees with the theoretical prediction. In addition to the scaling exponent, our simulation results also provide the prefactor for the scaling relationship. This prefactor is very important for the quantitative comparison between simulations and experiments. The prefactor of the best power law fit to our simulation results is approximately 1.2.
Fig. 2(b) shows the same simulation data as Fig. 2(a), but using different normalization. In the strong confinement regime, DNA conformation is close to the case of DNA on a plane. Thus, we normalize R∥ by the in-plane radius of gyration of DNA on a plane R∥,plane. From the Flory theory, R∥,plane ∼ L3/4L1/4p. Then, we obtain
 | (22) |
As a result, we normalize H by w so that the normalized R∥ − H curve is independent of both L and w from the theory. Using this normalization, the four curves with different contour lengths collapse not only in the moderate confinement regime but also in the strong confinement regime. Considering that the right side of eqn (22) is independent of L and R∥,plane is scaled as L3/4, we can conclude that R∥ is always proportional to L3/4 from the strong confinement to moderate confinement regime. The exponent 3/4 is due to the nature of 2D self-avoiding walk. This exponent has been confirmed experimentally in quasi-2D confinement48 as well as the de Gennes regime.49 Changing normalization does not affect the scaling exponent, but affects the prefactor. Surprisingly, the prefactor of the best power-law fit is very close to unity. It is probably because the prefactor of R∥ in eqn (3) is cancelled by the prefactor of R∥,plane.
It is worth noting that the best power law fit to the simulation data depends on the H range where the fit is applied. The two bounds of the de Gennes regime are not well defined. In the current study, we set the H range for the de Gennes regime as H ∈ [2Lp, R∥,bulk/2] so that the simulation data points do not deviate much from the line of best fit in this range, as shown in the insets of Fig. 2(a) and 2(b). The lower bound of H ≅ 2Lp has also been suggested by Wang et al.40 for the simulation of DNA in a square channel. When H > R∥,bulk/2, DNA does not contain sufficient number of blobs to make the blob theory applicable, and so it enters weak confinement regime. In Fig. 2, the scaling exponents appear to be maximized in the range of H ∈ [2Lp, R∥,bulk/2]. Therefore, if the fit is applied in a range broader than H ∈ [2Lp, R∥,bulk/2], the fitted exponent will decrease. However, when w is much less than Lp, the scaling exponent does not show the maximum in the de Gennes regime. This will be shown later.
After investigating the effect of changing L on the R∥ − H curve, we proceed to the effect of changing w. Fig. 3 shows the normalized R∥ − H curve for different w and a fixed L = 8 μm. When we reduce w in the simulation, the extended de Gennes regime will emerge between the de Gennes regime (moderate confinement) and the Odijk regime (strong confinement). Recall that the scaling exponent relating R∥ to H remains unchanged from the extended de Gennes regime to de Gennes regime based on the scaling analysis. This is also confirmed by our simulation. When w = 10 nm (blue squares in Fig. 3), the de Gennes regime is skipped (refer to Table 1). The best power law fit (dashed blue line) to the data points in the extended de Gennes regime (filled blue squares) gives an exponent of 0.251 ± 0.025, which agrees with the theoretical prediction. Although the scaling exponent is not affected by changing w, the prefactor changes with w. Fig. 3 reveals that reducing w will slightly shift down the middle part of the curve, which means the relative DNA extension R∥/R∥,plane is smaller at the same confinement strength R∥,bulk/H. When w = 10 nm, the best power law fit (dashed blue line in Fig. 3) follows y = 1.11x0.251. When w = 40 nm, the best power law fit (dashed black line in Fig. 2(a)) follows y = 1.20x0.250. The prefactor of the power law increases slightly as w increases. However, the normalized R∥ − H curve in de Gennes regime should be independent of w, based on eqn (21). One possible reason for the deviation between theory and simulation is that the scaling law R∥,bulk ∼ L3/5L1/5pw1/5 breaks down when w is small. We recall that when w is small enough to make excluded volume interactions unimportant, DNA behaves like an ideal chain with R∥,bulk ∼ L1/2L1/2p. The transition from ideal chain behaviour (R ∼ L1/2) to real chain behaviour (R ∼ L3/5) has been observed in the simulations by Wang et al.40 Assuming the ideal chain behaviour, eqn (21) becomes
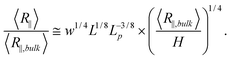 | (23) |
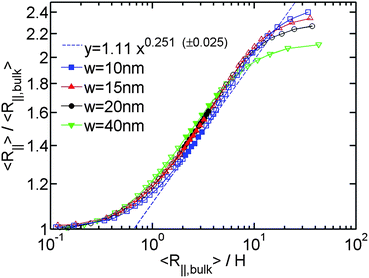 | ||
| Fig. 3 Relative in-plane radius of gyration as a function of the inverse of relative slit height for the simulation #5,#6,#7,#2 in Table 1. The filled symbols are the data points in both extended de Gennes and de Gennes regimes. The open symbols are the data points in other regimes. The blue dashed line is a best power law fit to the filled blue squares. (±0.025) refers to the uncertainty of the exponent from the fits. The uncertainty for the prefactor is 1.11 ± 0.03. | ||
Then, the prefactor of the best power law fit corresponds to L1/8w1/4L−3/8p. This may be the reason why the prefactor of the best power law fit increases with w. Since the transition from a real chain to an ideal chain is gradual when w decreases, the prefactor changes slowly.
3.2 Odijk regime
After investigating the DNA extension in the de Gennes regime (moderate confinement), we proceed to the Odijk regime (strong confinement). The theory for DNA in strong slit confinement is lacking. Before presenting the simulation results in this regime, we introduce our theoretical approach to analyse the DNA extension in strong slit confinement.For the analysis of R∥ in strong confinement, it is convenient to imagine a virtual in-plane chain corresponding to the DNA projection on a slit wall. This virtual in-plane chain looks like the chains shown in the last two images of Fig. 1. In this way, the quasi-2D problem of DNA in strong slit confinement becomes a rescaled 2D problem of a chain in a plane. This virtual chain has its own contour length L∥, an apparent persistence length Lp,∥ and a chain width w. In order to derive R∥ from L∥, Lp,∥ and w, we need to know the expressions of L∥ and Lp,∥. The expression of L∥ is given by eqn (11). Note that eqn (11) is derived when H ≪ Lp. The range of applicability of the equation is not a prior clear. As a result, we plot L∥/L as a function of H/Lp for the simulations using different w in Fig. 4. The simulation results roughly agree with eqn (11) when H ∈ [0,2Lp], irrespective of w. It suggests that the deflection model, which is assumed by eqn (11), can be applied to describe the projected contour length until H ∼ 2Lp.
 | ||
| Fig. 4 Projected contour length as a function of the relative slit height. The symbols with different colors correspond to the simulations using different chain widths. The solid line is calculated from eqn (11). | ||
Regarding Lp,∥, we extract its relationship with H from simulations. In simulations, the persistence length can be calculated from the correlation of bond orientation through the definition of the persistence length u(0)·u(s) = exp(−s/Lp), where s is the separation in arc length along the contour, and u(s) is the local tangent vector to the chain at position s. For the case of the virtual in-plane chain, the equation becomes u∥(0)·u∥(s∥) = exp(−s∥/Lp,∥). This approach to calculate the persistence length only works for a wormlike chain without excluded volume interactions, since excluded volume interactions will break down the exponential decay of orientational correlation. Thus we perform simulations without excluded volume interaction to extract Lp,∥.
Fig. 5(a) shows the correlation of u∥(0)·u∥(s∥) as a function of s∥ for different slit heights. The straight lines in Fig. 5(a) demonstrate the exponential decay of orientational correlation still holds for the virtual in-plane chain. Fig. 5(b) shows Lp,∥/Lp as a function of H/Lp. When H = 0, corresponding to DNA in a plane,45 we obtain the theoretically expected result Lp,∥/Lp = 2. When H/Lp = ∞, corresponding to DNA in bulk, we obtain the value of Lp,∥/Lp around 0.71. The value of Lp,∥/Lp − 0.71 monotonically decays from 1.29 to 0, when H increases from 0 to large values. We then empirically fit the data to the equation Lp,∥/Lp − 0.71 = 1.29*aH/Lp. Here, a is a fitting parameter, which is determined to be 0.48 ± 0.02.
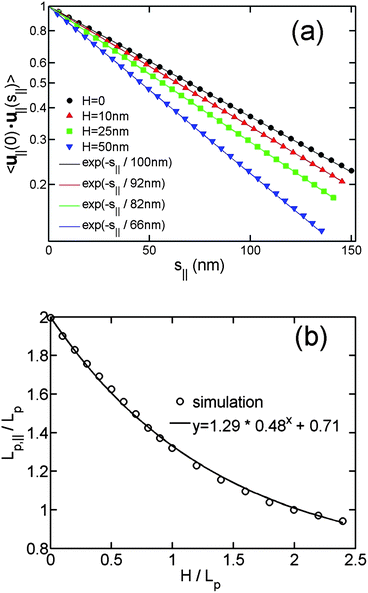 | ||
| Fig. 5 (a) In-plane orientation correlation as a function of the in-plane separation of contour length for the simulations without excluded volume interaction and using different slit heights. The symbols are simulation results, and the solid lines are the best exponential fits to the simulation data using a single fitting parameter Lp,∥. The contour lengths are 4 μm and bond lengths are 5 nm in the simulations. (b) The in-plane persistence length Lp,∥ as a function of the relative slit height. | ||
After obtaining expressions for L∥and Lp,∥, we derive the relationship between R∥ and H by considering a 2D self-avoiding walk, as shown in eqn (16). Then, we can compare the simulation results in the Odijk regime with the theoretical predictions. Similar to the de Gennes regime, the R∥ − H curve in the Odijk regime is also determined by L and w in the simulations. It has been shown by the theory and our simulation that R∥ is scaled as L3/4from strong confinement to moderate confinement. When we normalize R∥ by R∥,plane, the L dependence of R∥ will be eliminated. So we only need to investigate the effect of changing w. Fig. 6(a) and 6(b) shows the normalized R∥ − H curve for the simulation using different chain width. Fig. 6(a) normalizes H by Lp, because L∥ and Lp,∥ are determined by H/Lp. The theoretical predictions (solid lines in Fig. 6(a)) agree with the simulation results in the non-self-crossing regime H ∈ [0,w] (filled squares) and deviate in the self-crossing regime H ∈ [w,2Lp] (open inverse triangles). The simulation results using larger w deviate from the theoretical prediction at larger H. In Fig. 6(b), we normalize H by w. Using this normalization, the three curves corresponding to different w collapse onto a master curve from the strong to moderate confinement regime, except for some deviation at the crossover. Comparing Fig. 6(a) and 6(b), we can see R∥/R∥,plane is more related to the ratio H/w than H/Lp.
 | ||
| Fig. 6 (a)Relative in-plane radius of gyration as a function of the relative slit height. The symbols with different colours correspond to the simulations using different chain widths, listed as #5, #6 and #7 in Table 1. The filled squares, inverse triangles, triangles correspond to the data points in non-self-crossing, self-crossing and weak confinement regimes, respectively. The filled circles correspond to the data points in both the de Gennes and extended de Gennes regime. The solid lines correspond to theoretical prediction from eqn (16). The dashed lines correspond to the best power-law fits to the data points in both the de Gennes and extended de Gennes regimes. The values in parentheses, e.g. (±0.005), refer to the uncertainties of the exponents from the fits. The uncertainties for the prefactors are 0.84 ± 0.05, 0.79 ± 0.01 and 0.72 ± 0.02, respectively. (b) same data with (a) but H is normalized by w. | ||
Combining the results in Fig. 4, 5 and 6, we can understand what is changed and what is unchanged from non-self-crossing to self-crossing regime. The expressions of L∥ and Lp,∥ keep unchanged in these two regimes, which suggests the elastic entropy (first term in eqn (17)) follow the same rule in these two regimes. The change of R∥ behaviour is purely caused by the excluded volume interaction (second term in eqn (17)). As H increases, the excluded area between two DNA segments in a plane decreases. However, in the self-crossing regime, decrease in the excluded area is enhanced, relative to the non-self-crossing regime, due to the onset of segment overlap. As a result, R∥ from the simulation is smaller than the prediction from eqn (16) in the self-crossing regime.
Fig. 6(a) also includes the best power-law fits to the data points in de Gennes regime and extended de Gennes regime, indicated by the dashed lines. The combination of the dashed line and the solid line almost covers the R∥ − H curves from de Gennes regime to Odijk regime, except the slight deviation in the crossover. A significant part of the R∥ − H curve in self-crossing regime almost follows the same scaling law as the de Gennes regime. As discussed in Sec. 2.2, it is because the excluded volume interaction in self-crossing regime becomes similar to the extended de Gennes regime when H approaches 2Lp. If we consider there is a transition from de Gennes regime to Odijk regime, the transition point is roughly determined by the cross point of the dashed line and the solid line. This transition point strongly depends on the chain width. Usually, the chain width is less than the persistence length, so the transition occurs at a slit height less than persistence length.
3.3 Comparison with previous simulation and experimental results
Monte Carlo simulation of DNA extension in slitlike confinement has been performed by Cifra et al.37 However, the DNA contour length in their simulation is only ten times the persistence length, and so DNA does not enter the de Gennes regime. Nevertheless, they observed a gradual transition from moderate confinement to strong confinement. In addition, Brownian dynamics simulations have been performed for the DNA chain in slitlike confinement.24,26 However, only moderate confinement was investigated in these simulations, because the DNA model in these studies is coarse-grained on a length scale larger than the DNA persistence length. These simulations also give the same scaling law with blob theory in the de Gennes regime.Next, we compare our simulation results with two previous experimental results.25,26 They represent two typical but controversial observations of R∥ − H curve. Table 1 includes the parameters for the DNA molecules used in ref. 26 and ref. 25. The DNA molecules used in the experiments are intercalated with YOYO-1 dye. The dye intercalation will change the contour length, the persistence length and the effective chain width.50–52 The staining ratios of YOYO-1 to DNA base pair are 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and 1
4 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 in ref. 26 and ref. 25, respectively, corresponding to the contour lengths of 22 and 20 μm.50 The effect of YOYO-1 intercalation on DNA persistence length is controversial. Several studies found Lp becomes shorter after YOYO-1 intercalation,51,52 while Murade et al. found Lp is rather independent of staining ratio.50 Considering the ionic strengths in both experiments are around 60 mM, the persistence length of unstained DNA is about 54 nm, based on the calculation in ref. 53. However, Bonthuis et al.25 used Lp of 66 nm based on ref. 54. Table 1 shows the value of Lp copied from the original publication. The effective width of unstained DNA is 6.6 nm, considering the ionic strengths in two studies are around 60 mM.53 The positively charged YOYO-1 will reduce the electrostatic repulsion between DNA molecules and affects the effective chain width. Since the quantitative effect is unclear, we put 6.6 nm in Table 2 as an estimation.
6 in ref. 26 and ref. 25, respectively, corresponding to the contour lengths of 22 and 20 μm.50 The effect of YOYO-1 intercalation on DNA persistence length is controversial. Several studies found Lp becomes shorter after YOYO-1 intercalation,51,52 while Murade et al. found Lp is rather independent of staining ratio.50 Considering the ionic strengths in both experiments are around 60 mM, the persistence length of unstained DNA is about 54 nm, based on the calculation in ref. 53. However, Bonthuis et al.25 used Lp of 66 nm based on ref. 54. Table 1 shows the value of Lp copied from the original publication. The effective width of unstained DNA is 6.6 nm, considering the ionic strengths in two studies are around 60 mM.53 The positively charged YOYO-1 will reduce the electrostatic repulsion between DNA molecules and affects the effective chain width. Since the quantitative effect is unclear, we put 6.6 nm in Table 2 as an estimation.
| Regime | H range | L min | Scaling laws | ||
|---|---|---|---|---|---|
| R ∥ vs. H | R ∥ vs. L | L ∥ vs. H | |||
| a 1st column is the regime name. Odijk regime is divided to two sub-regimes according to whether the DNA projection on a slit wall can cross itself or not. 2nd column is the slit height range corresponding to a certain regime. R∥,bulk is the in-plane radius of gyration in bulk. 3rd column is the minimum contour length to enter a certain regime. The last three columns are the scaling laws relating the quantities, the in-plane radius of gyration R∥, the projected contour length L∥, the 3D contour length L and the slit height H. | |||||
| Odijk I (non-self-crossing) | H < w | H 2/3 L 1/3 p | eqn (16) | L 3/4 | eqn (11) |
| Odijk II (self-crossing) | w < H < 2Lp | L p | L 3/4 | eqn (11) | |
| extended de Gennes | 2Lp < H < L2p/w | L p H/w | H −1/4 | L 3/4 | |
| de Gennes | L 2 p /w < H < R∥,bulk/2 | L 3 p /w2 | H −1/4 | L 3/4 | |
After describing L, Lp and w in the experiments, we move to the slit height H. Recall that the slit height in our simulation corresponds to an effective slit height that is accessible for the centreline of the DNA chain. For the comparison with experiments, the slit height in simulations should add the thickness δ of the repulsion layer between DNA and the negatively charged slit walls in the experiments. The thickness δ is mainly determined by the Debye length λD, which is about 1.24 nm when the ionic strength is 60 mM. Since δ is quite small and its precise value is unknown, we ignore it.
Besides the differences in the experimental conditions, the methods to determine DNA extension are also different in different experiments. One direct method is to measure DNA extension in the fluorescence microscopy image, which is used by Bonthuis et al.25 Because DNA in the image is convolved with the point spread function of the microscopy, DNA extension is overestimated and then R∥/R∥,bulk is underestimated. Another way is to measure DNA diffusivity and then infer DNA extension from diffusivity, which is used by Tang et al.26 The difference in measurement method is probably the major reason why R∥,bulk in the experiment by Bonthuis et al. is larger than that by Tang et al., as shown in Table 1. In addition, R∥/R∥,bulk in the experiment by Bonthuis et al. is for the most part smaller than in the experiment by Tang et al., as shown in Fig. 7. We recall that Tang et al. measured DNA extension using two methods (microscopy imaging and diffusivity measurement). In the current study, we only use the data from the diffusivity measurement since Tang et al. argued that this is the more accurate data set.
 | ||
| Fig. 7 (a) Relative in-plane radius of gyration as a function of the inverse relative slit height. Three lines with open symbols correspond to the simulations #8, #9 and #10 in Table 1. Red squares are the data of Tang et al.26 Blue triangles are the data of Bonthuis et al.25 (b)Relative in-plane radius of gyration as a function of the slit height. | ||
Based on the parameters of two experimental studies in Table 1, we can determine the H ranges corresponding to different regimes. The experimental conditions in both studies skip the de Gennes regime, but we recall that R∥ scales with H in the same way in the extended de Gennes and the de Gennes regimes.
Limited by the computational power, we are incapable to perform the simulation using the same values of Lp, L and w with experiments. Instead, we attempt to fix the contour length as 22 μm and observe the trend of the R∥ − H curve when changing the chain width in simulations, as shown in Fig. 7(a). Since the scaling exponent of the de Gennes regime is always about 1/4 in our simulations and two experimental studies, the differences are in the terms of the H range and the prefactor of the middle linear range of the R∥ − H curve. Regarding the H range of the power law, the middle linear region also becomes broader as w decreases. This is because the transition from de Gennes regime to Odijk regime is delayed for smaller w. Regarding the prefactor of the power law, the middle region of the R∥ − H curve shifts down as w decreases, which is in agreement with Fig. 3. The best power law fits to the experimental data by Tang et al. and Bonthuis et al. are y = (1.07 ± 0.06)x0.237±0.036 and y = (0.81 ± 0.02)x0.230±0.015, respectively. It has been shown in the Sec. 3.1 that the prefactor is reduced from 1.20 to 1.11 when w is reduced from 40 nm to 10 nm. Based on the trends in the H range and the prefactor, it can be expected that if we further reduce the chain width in the simulation to a certain value, the curve will significantly match the experimental data by Tang et al.26
The effective chain width of DNA in the experiment by Tang et al. can be estimated from the value of R∥,bulk. If we fit our simulation results of R∥,bulk when w = 10, 20, 40 nm, we obtain an equation R∥,bulk ≈ 392 × w0.19. From this equation, R∥,bulk = 520 nm corresponds to w = 4.4 nm. Recall that we use Lp = 50 nm in the simulations. If actual Lp in experiments is different from 50 nm, say 66 nm, we need to rescale every length parameter in our simulations by a factor of 66/50. (Note that multiplying Lp, w, L and H by a common factor will change R∥,bulk and R∥ by the same factor, and thus the normalized R∥ − H curve remains unchanged.) This factor can change the estimated chain width. This chain width inferred from R∥,bulk = 520 nm is less than the value of 6.6 nm estimated from the theory for DNA without YOYO-1 intercalation under the ionic strength of 60 mM. The difference may be caused by YOYO-1 intercalation.
In addition to the difference in w, the deviation between the simulation results and experimental data by Tang et al. might be also caused by experimental error in R∥,bulk, because R∥,bulk is used to normalize H and changing R∥,bulk will shift the normalized R∥ − H curve. Thus, we make another plot in Fig. 7(b) without normalization of H. We still normalize R∥ by R∥,bulk, because the possible experimental error in R∥ would also affect R∥,bulk. The normalization may eliminate this type of error. In Fig. 7(b), the experimental data by Tang et al. is still below the simulation results. It suggests the deviation between our simulations and the experiment may be not caused by the possible experimental error in R∥,bulk.
Both our simulation results and the experimental results from Tang et al. show large differences with the experimental result from Bonthuis et al.25 The abrupt transition in their result might correspond to the onset of non-self-crossing regime in our simulation, as shown in Fig. 6(a). However, the plateau of R∥ in our simulation starts from the slit height H ∼ w instead of 2Lp. Recently Ren et al.55,56 reported that the abrupt transition point depends on the ionic strength and shifts towards the larger slit heights when reducing the ionic strength. Ren et al. attribute the trend to the fact that lower ionic strength enhances the electrostatic repulsion between DNA and slit wall and hence reduces the effective slit height. Our simulation indicates that the transition point, i.e. the onset of self-crossing regime, depends on the effective chain width and hence depends on the ionic strength. It is also a possible reason for their observation. We do not plot their data in Fig. 7(a) and 7(b) since they recently retracted the article.56
4. Conclusions
Using both scaling theory and Monte Carlo simulations, we systematically investigate the static property of DNA in slitlike confinement. The scaling laws for different regimes are summarized in Table 2. In moderate confinement, blob theory works well, analogous to what was previously shown for a tube. In the strong confinement (Odijk regime), deflection theory is applicable, but it only gives the projected contour length instead of the in-plane DNA extension when H < 2Lp. The in-plane DNA extension is derived by assuming a 2D self-avoiding walk when H < w. This assumption breaks down when H > w, because DNA can cross itself. The chain crossing conformation in a slit (excluded volume) is analogous to the hairpin conformation in a tube (bending energy cost). As a result, the chain width is a crucial parameter to determine the static property of DNA in strong confinement. Since the chain width of DNA can be controlled by ionic strength, changing ionic strength is an effective way to manipulate DNA in a nanoslit, especially, in strong confinement.Our simulation results show that in the log-log plot of R∥versus H, the de Gennes regime, extended de Gennes regime and part of the self-crossing regime follow a power law with an exponent of about 1/4, although the physics in these regimes are different. The deviation from this power law occurs at a certain slit height that depends on the chain width.
We do admit that the simulation system differs from the experiment in some aspects. First, the electrostatic interaction between DNA segments is softer than a hard sphere interaction. As a result, even when H < w, the DNA chain still has a finite probability to cross itself. Second, we ignore electrostatic interactions with the channel walls. However, these limitations are not expected to fundamentally change the result. In the current study, we focus on the static properties of DNA in slits. Future work can build off these results to consider chain dynamics, though the subtle points of hydrodynamic coupling/screening will need to be properly treated, which are lacking in our simulations.
Acknowledgements
This work is supported by the Singapore-MIT Alliance for Research and Technology (SMART) and National Science Foundation (NSF) grant CBET-0852235. The authors thank the center for computational science and engineering in National University of Singapore for providing the computational resource. L.D. is grateful for the fruitful communication with K.D. Dorfman, T.W. Burkhardt and P. Cifra about the scaling law of DNA in strong confinement.References
- J. O. Tegenfeldt, C. Prinz, H. Cao, S. Chou, W. W. Reisner, R. Riehn, Y. M. Wang, E. C. Cox, J. C. Sturm, P. Silberzan and R. H. Austin, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 10979–10983 CrossRef CAS.
- D. Stein, F. H. van der Heyden, W. J. Koopmans and C. Dekker, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15853–15858 CrossRef CAS.
- K. Jo, D. M. Dhingra, T. Odijk, J. J. de Pablo, M. D. Graham, R. Runnheim, D. Forrest and D. C. Schwartz, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2673–2678 CrossRef CAS.
- W. Reisner, N. B. Larsen, H. Flyvbjerg, J. O. Tegenfeldt and A. Kristensen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 79–84 CrossRef CAS.
- C. C. Hsieh and P. S. Doyle, Korea-Aust. Rheol. J., 2008, 20, 127–142 Search PubMed.
- W. Reisner, K. J. Morton, R. Riehn, Y. M. Wang, Z. Yu, M. Rosen, J. C. Sturm, S. Y. Chou, E. Frey and R. H. Austin, Phys. Rev. Lett., 2005, 94, 196101 CrossRef.
- M. Krishnan, I. Monch and P. Schwille, Nano Lett., 2007, 7, 1270–1275 CrossRef CAS.
- C. Zhang, F. Zhang, J. A. van Kan and J. R. C. van der Maarel, J. Chem. Phys., 2008, 128, 225109 CrossRef.
- C. Zhang, P. G. Shao, J. A. van Kan and J. R. C. van der Maarel, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16651–16656 CrossRef CAS.
- Y. Kim, K. S. Kim, K. L. Kounovsky, R. Chang, G. Y. Jung, J. J. dePablo, K. Jo and D. C. Schwartz, Lab Chip, 2011, 11, 1721–1729 RSC.
- T. X. Su, S. K. Das, M. Xiao and P. K. Purohit, PLoS One, 2011, 6, e16890 CAS.
- L. H. Thamdrup, A. Klukowska and A. Kristensen, Nanotechnology, 2008, 19, 125301 CrossRef.
- F. Persson, P. Utko, W. Reisner, N. B. Larsen and A. Kristensen, Nano Lett., 2009, 9, 1382–1385 CrossRef CAS.
- H. Cao, J. O. Tegenfeldt, R. H. Austin and S. Y. Chou, Appl. Phys. Lett., 2002, 81, 3058–3060 CrossRef CAS.
- S. M. Stavis, E. A. Strychalski and M. Gaitan, Nanotechnology, 2009, 20 Search PubMed.
- E. A. Strychalski, S. M. Stavis and H. G. Craighead, Nanotechnology, 2008, 19 Search PubMed.
- S. R. Leslie, A. P. Fields and A. E. Cohen, Anal. Chem., 2010, 82, 6224–6229 CrossRef CAS.
- F. Brochard and P. G. de Gennes, J. Chem. Phys., 1977, 67, 52–56 CrossRef CAS.
- M. Daoud and P. G. de Gennes, J. Phys., 1977, 38, 85 CAS.
- P. G. de Gennes, Scaling concepts in polymer physics, Cornell University Press, Ithaca, NY, 1979 Search PubMed.
- T. Odijk, Macromolecules, 1983, 16, 1340–1344 CrossRef CAS.
- T. Odijk, J. Chem. Phys., 2006, 125, 204904 CrossRef.
- T. Odijk, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 060901 CrossRef.
- Y.-L. Chen, M. D. Graham, J. J. de Pablo, G. C. Randall and P. S. Doyle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 060901 CrossRef.
- D. J. Bonthuis, C. Meyer, D. Stein and C. Dekker, Phys. Rev. Lett., 2008, 101, 108303 CrossRef.
- J. Tang, S. L. Levy, D. W. Trahan, J. J. Jones, H. G. Craighead and P. S. Doyle, Macromolecules, 2010, 43, 7368–7377 CrossRef CAS.
- P. K. Lin, J.-F. Chang, C.-H. Wei, P. H. Tsao, W. S. Fann and Y.-L. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031917 CrossRef.
- A. Balducci, P. Mao, J. Y. Han and P. S. Doyle, Macromolecules, 2006, 39, 6273–6281 CrossRef CAS.
- E. A. Strychalski, S. L. Levy and H. G. Craighead, Macromolecules, 2008, 41, 7716–7721 CrossRef CAS.
- P. K. Lin, K. H. Lin, C. C. Fu, K. C. Lee, P. K. Wei, W. W. Pai, P. H. Tsao, Y. L. Chen and W. S. Fann, Macromolecules, 2009, 42, 1770–1774 CrossRef CAS.
- J. H. van Vliet and G. ten Brinke, J. Chem. Phys., 1990, 93, 1436 CrossRef CAS.
- J. H. van Vliet, M. C. Luyten and G. ten Brinke, Macromolecules, 1992, 25, 3802–3806 CrossRef CAS.
- P. Cifra and T. Bleha, Macromol. Theory Simul., 1999, 8, 603 CrossRef CAS.
- C. E. Cordeiro, M. Molisana and D. Thirumalai, J. Phys. II, 1997, 7, 433 CrossRef CAS.
- D. Chaudhuri and B. Mulder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 031803 CrossRef.
- H. P. Hsu and P. Grassberger, J. Chem. Phys., 2004, 120, 2034 CrossRef CAS.
- P. Cifra, Z. Benkova and T. Bleha, Faraday Discuss., 2008, 139, 377–392 RSC.
- Y. Z. Yang, T. W. Burkhardt and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011804 CrossRef.
- T. W. Burkhardt, Y. Z. Yang and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041801 CrossRef.
- Y. Wang, D. R. Tree and K. D. Dorfman, Macromolecules, 2011, 44, 6594–6604 CrossRef CAS.
- S. Jun, D. Thirumalai and B. Y. Ha, Phys. Rev. Lett., 2008, 101, 138101 CrossRef.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51 CrossRef CAS.
- D. W. Schaefer, J. F. Joanny and P. Pincus, Macromolecules, 1980, 13, 1280 CrossRef CAS.
- B. Li, N. Madras and A. J. Sokal, J. Stat. Phys., 1995, 80, 661–754 CrossRef.
- P. A. Wiggins, T. van der Heijden, F. Moreno-Herrero, A. Spakowitz, R. Phillips, J. Widom, C. Dekker and P. C. Nelson, Nat. Nanotechnol., 2006, 1, 137–141 CrossRef CAS.
- S. K. Kumar, M. Vacatello and D. Y. Yoon, J. Chem. Phys., 1988, 89, 5206–5215 CrossRef CAS.
- A. V. Vologodskii, S. D. Levene, K. V. Klenin, M. Frank-Kamenetskii and N. R. Cozzarelli, J. Mol. Biol., 1992, 227, 1224 CrossRef CAS.
- B. Maier and J. O. Radler, Phys. Rev. Lett., 1999, 82, 1911–1914 CrossRef CAS.
- P. K. Lin, C. C. Fu, Y. L. Chen, Y. R. Chen, P. K. Wei, C. H. Kuan and W. S. Fann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011806 CrossRef.
- C. U. Murade, V. Subramaniam, C. Otto and M. L. Bennink, Nucleic Acids Res., 2010, 38, 3423–3431 CrossRef CAS.
- K. Gunther, M. Mertig and R. Seidel, Nucleic Acids Res., 2010, 38, 6526–6532 CrossRef.
- A. Sischka, K. Toensing, R. Eckel, S. D. Wilking, N. Sewald, R. Ros and D. Anselmetti, Biophys. J., 2005, 88, 404–411 CrossRef CAS.
- C. C. Hsieh, A. Balducci and P. S. Doyle, Nano Lett., 2008, 8, 1683–1688 CrossRef CAS.
- S. R. Quake, H. Babcock and S. Chu, Nature, 1997, 388, 151–154 CrossRef CAS.
- Y. Q. Ren and D. Stein, Phys. Rev. Lett., 2011, 106, 068302 CrossRef.
- D. Stein, Phys. Rev. Lett., 2011, 107, 049901 CrossRef (E).
Footnote |
| † Electronic Supplementary Information (ESI) available: bench marking the simulations using long bond lengths as well as the derivation of excluded volume interaction of DNA confined to a plane. See DOI: 10.1039/c2sm07322f/ |
| This journal is © The Royal Society of Chemistry 2012 |
