Exploring the nonlinear conductive properties of polymer/graphene composites at the molecular level: a machine learning approach

Abstract

Polymer/graphene (Py/GN) composites under the influence of external electric fields often exhibit unique nonlinear conducting behaviors. However, the underlying mechanism of this field effect at the molecular level is still obscure until now. Herein, the evolution of electrical properties of Py/GN composites induced by electric fields has been explored by combining high-throughput first-principles calculations with machine learning models. The results show that the polymer valence band maximum (PVBM) and polymer conduction band minimum (PCBM) of Py/GN composites under different electric fields can be accurately predicted by the XGBoost regression algorithm. The band arrangement of polymers in Py/GN composites can be easily altered with applied electric fields, where charges accumulate around the graphene layer and depleted around the polymer layer. Moreover, the electrons at the pyrrole/GN interface may overcome the Schottky barrier height, leading to a transition from a Schottky contact to an ohmic contact under a critical field (E_b), which can be effectively predicted with an R² value of 0.854. Then, two types of novel Py/GN composites with lower or higher E_b values were screened by reverse engineering the ML model, offering valuable guidance for the application of Py/GN composites in different electric field conditions. This work can provide new insights into the nonlinear electrical response of Py/GN composites under electric fields, which has significant implications for practical applications.

---

1 Introduction

Polymer/graphene (Py/GN) composites hold significant scientific and technological importance as advanced functional materials. Carbon-based nanofillers, such as graphene, carbon nanotubes, and carbon fibers, have been widely utilized to improve the thermal, electrical, and mechanical properties of polymer-based composites.^1–4 Graphene, in particular, possessing semi-metallic characteristics, when blended with polymers, can exhibit percolation behavior at extremely low loading fractions.^5–9 This unique low-loading electronic transport effect help prevent mechanical property degradation seen in high-loading concentration systems. Recent studies have revealed that Py/GN composites display distinctive nonlinear current density–electric field (J–E) characteristics under high electric fields.¹⁰ This nonlinear conducting behavior positions these composites as smart materials capable of real-time electrical resistance modulation through external electric field control. These materials exhibit high resistance at low electric fields, but once a specific threshold is surpassed, their carrier mobility increases exponentially, causing rapid switching between high-resistance and low-resistance states.¹¹ The nonlinear electrical response of Py/GN composites allows for adaptive impedance matching of the material, which is particularly promising for next-generation electromagnetic shielding applications.¹² Wang et al. found that polydimethylsiloxane (PDMS) composites filled with graphene showed significant nonlinear conductive properties with the addition of only 3 vol% of filler.¹³

The nonlinear conductive behavior of polymer/graphene composites is due to the electric field-induced effect, which significantly impacts the electronic structure of the interface region between graphene and polymer matrix, leading to the rearrangement of interfacial charges. The microstructure of Py/GN composites plays a crucial role in determining the complex interactions between polymer molecules and graphene surfaces. However, there is a lack of studies investigating the influence of electric fields on the microstructure of these composites. Specifically, establishing a connection between the microstructure and the unique nonlinear electrical properties of Py/GN composites is challenging due to the electrical insulating nature of polymer materials. Gaining a thorough knowledge of how electric fields affect the microstructure of Py/GN composites could lead to a better comprehension of their nonlinear conduction behavior. First-principles characterization design serves as the initial step towards gaining a deeper understanding of the transport properties of Py/GN composites.^14,15 Therefore, to better understand the source of the power-law nonlinear transport behavior in Py/GN composites, we use an ab initio calculation framework to simulate nanocomposites at the molecular level and accurately characterize quantum effects.

Machine learning approaches have become increasingly popular in the field of research pertaining to the prediction,^16–24 discovery and design,^25–29 and structural testing^30–32 of polymer-based composites. Shi et al. developed a machine learning model to predict the electromagnetic interference shielding capabilities of carbon-based filler nanocomposites.³³ Finite element analysis, in conjunction with neural networks, was proposed by Lu et al. to simulate the nonlinear conductive behavior of Py/GN composites.³⁴ The investigation of the breakdown of polymer-based nanocomposites was explored by combining high-throughput random breakdown simulation and machine learning techniques.^35,36 Moreover, machine learning approaches have been successfully applied to the field of molecular simulation. Willhelm et al.³⁷ combined machine learning and DFT to predict the electronic and structural properties of bilayer materials. Shayeganfar³⁸ employed neural networks to explore the correlation between van der Waals pressures and interfacial characteristics in polymer/graphene interfaces, thus speeding up the identification of novel materials. While machine learning algorithms provide strong support for predicting the electric field response properties of Py/GN composites, molecular-level machine learning methods still face significant challenges in materials informatics. These include data limitations, complexity in feature representation, and the requirement for multi-scale correlation. The lack of first-principles simulation datasets severely limits the ability of model generalization. Effective descriptors are critical for accurately capturing the microscopic structure–property mapping and predicting the electric field response properties of graphene/polymer interfaces. In addition, we have summarized key experimental and theoretical studies on the electrical and band structure properties of Py/GN hybrids in Tables S1 and S2† (see ESI†). These findings highlight that the multi-scale correlation of “structure–property–mechanism” presents a challenge in bridging the gap between atomic predictions and macroscopic composite behavior.

In this manuscript, the electrical properties of Py/GN composites under different electric fields were investigated via a combination of first-principles calculations and machine learning techniques. Based on high-throughput first-principles calculations results, the correlation of five interfacial properties, including the polymer valence band maximum (PVBM) and polymer conduction band minimum (PCBM), adsorption energy (E_ads), graphene gap (E_g), and dielectric constant (ε) was discussed under electric field induction. The evolution of PVBM and PCBM in Py/GN composites under different electric fields was successfully predicted using the ML algorithm. By analyzing the projected density of state (PDOS) and charge density difference of pyrrole/GN, it was observed that there is a transition from Schottky contact to ohmic contact at a certain critical field, causing a sharp shift in electrical properties. Furthermore, the critical field (E_b) at which this transition occurs can be efficiently predicted by machine learning algorithms. The novel Py/GN composites with lower or higher E_b values were screened by reverse engineering of the ML model. The ML framework functions as a robust design tool for efficiently screening Py/GN field-responsive composites. It establishes a vital bridge between DFT-level theoretical simulations and the performance of experimental composite materials.

2 Computational methodology

2.1 First-principles calculations

In this study, geometric and electronic calculations utilizing DFT were performed using the VASP code.^39,40 The Perdew–Burke–Ernzerhof (PBE) functional of the generalized gradient approximation (GGA)⁴¹ was employed to address the exchange and correlation effects, which is a commonly utilized approach for material simulations. The 7 × 7 × 1 k-point grid were sampled in the Brillouin Zone (BZ) for performing the structures optimization. The vacuum space was adjusted to 20 Å to prevent any unnecessary interaction between the slabs. The van der Waals (vdW) correction factor was taken into account at the vdW-DF level.^42,43 All geometries were fully relaxed until the total energy reached convergence at 10⁻⁵ eV and the maximum force was set to 0.001 eV Å⁻¹. The cutoff energy was set to 500 eV, and the electronic energy convergence threshold was set to 1 × 10⁻⁵ eV, with the atomic force convergence threshold at 0.02 eV Å⁻¹. The electronic band structure was calculated along the high-symmetry k path of Γ–K–M–Γ. To address the issue of image interactions resulting from the implementation of periodic boundary conditions in the plane-wave DFT calculations, a dipole correction was implemented to the total energy in the Z-direction perpendicular to the plane. The PDOS was calculated by employing a 14 × 14 × 1 k-point grid. Moreover, considering the unavoidable issue of band gap narrowing with the standard PBE functional, the hybrid functional of HSE06 is utilized for precise electronic structure calculations. The adsorption energy is defined as E_ads = E_sum – (E_Py + E_GN), where E_sum is the total energy of Py/GN composites, E_Py is the energy of the polymer monomer, and E_GN is the energy of the graphene substrate.

2.2 Machine learning process

A flowchart illustrating the workflow is depicted in Fig. 1, which includes data preparation, construction of a machine learning model, and analysis and prediction of critical fields.

Fig. 1 Flowchart of a simulation to investigate the effect of electric fields on the interfacial properties of Py/GN composites by machine learning process and first-principles calculations.

2.2.1 Data preparation. Data sets are the basic resource for building machine learning models.⁴⁴ Initially, the single-chain polymer utilized in our study was acquired from the PubChem database⁴⁵ (https://pubchem.ncbi.nlm.nih.gov/), which offers an extensive collection of polymer small molecule structures and their corresponding properties. Subsequently, a total of 186 kinds of polymers were chosen to construct Py/GN composites. Regarding the consideration of the graphene layer, experimental data demonstrate that multilayer graphene (2–4 layers) maintains stable mobility around 3000 cm² V⁻¹ s⁻¹, whereas monolayer graphene exhibits significantly superior mobility at room temperature up to 8200 cm² V⁻¹ s⁻¹.⁴⁶ The exceptional performance of monolayer graphene originates from its distinctive Dirac cone band structure and weak phonon scattering properties.⁴⁷ Existing theoretical models primarily focus on monolayer systems for graphene-based composites. For example, the first-principles studies have examined the electronic properties and Schottky barriers in graphene/MoSeS,⁴⁸ SnS,⁴⁹ MoSe₂ (ref. 50) heterojunctions under electric fields. Therefore, in this study, a composite configuration of polymer monomers adsorbed on monolayer graphene was constructed, and an electric field was applied perpendicularly to the Py/GN interface. By utilizing high-throughput first-principles calculations, the atomic positions of the bilayer components were optimized, enabling the calculation of the related electronic properties. Eventually, the initial data were obtained for studying of the effect of electric field on the interfacial properties of Py/GN composites.

2.2.2 Feature generation. It has been previously observed that electric fields have the ability to alter the structural deformation, dielectric properties, and electronic properties of Py/GN composites.⁵¹ To investigate this, high-throughput first-principles calculations were used to calculate the PVBM, PCBM, graphene bandgap (E_g), adsorption energy (E_ads) and dielectric constant (ε) of Py/GN composites under different electric fields. The results indicated that the PVBM and PCBM energies exhibit greater responsiveness to electric field modulation. Subsequently, machine learning techniques were used to predict the alterations in PVBM and PCBM when an electric field is applied. Building on Pereira et al.‘s work, the relationship between properties and electron orbital energies was established using machine learning algorithms.⁵² This enabled accurate prediction of the alterations of PVBM and PCBM influenced by the electric field, utilizing physicochemical properties of the polymers obtained from PubChem and the electric field as feature labels. Initially, we collected 30 original input features from the PubChem database (Table S3†), carried out machine learning pre-training, and then chose the top 7 features as descriptors based on their importance ranking, as listed in Table 1. Furthermore, the existing molecular descriptor feature set was modified by excluding the CID feature and combined with the intrinsic bandgap of polymers. This was done to predict the critical field E_b for the transition from Schottky contact to ohmic contact in Py/GN composites.

Table 1 7 input features acquired from the PubChem database for machine learning training of Py/GN composites

Label	Features
MW	Molecular weight
TPSA	Topological polar surface area
QX	XStericQuadrupole3D
QY	YStericQuadrupole3D
QZ	ZStericQuadrupole3D
CID	Chemical identifiers
XLogP	Octanol-water partition coefficient

---

2.2.3 Machine learning model construction. Two machine learning models of Py/GN composites have been developed: one to predict the evolution of the PCBM and PVBM under an electric field, and the other to predict the critical field, i.e., the transition from a Schottky contact to an ohmic contact. The process of machine learning consists of model selection, model training, and model evaluation. For model selection, five different machine learning algorithms, namely AdaBoost regression (AdaBoost),⁵³ bagging regression (Bagging),⁵⁴ random forest regression (RFR),⁵⁵ XGBoost regression (XGB),⁵⁶ and gradient boosting regression (GBR)⁵⁷ algorithms, were chosen for training. These five algorithms, all of which are improved integrated algorithms, are more powerful and have achieved great success in many algorithmic competitions. They are particularly popular due to their outstanding accuracy and efficiency on small sample sizes. The machine learning models were trained using a dataset comprising 80% of the samples, and the performance was evaluated on the remaining 20%. The optimal hyperparameters for all models were determined using Bayesian optimization. To minimize random error, multiple trials with 100 iterations were conducted in parallel, and the final evaluation metrics were the average values of all the trials. To measure the fitting performance of the models, common machine learning metrics such as the determination coefficient (R²), root mean square error (RMSE), and mean absolute error (MAE) were employed. The parameters are derived from the following equations:where N is the number of samples in the dataset, y_true and y_pred are the true and predicted values, respectively, y_avg is the average of the true values of all the samples.

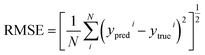3 Results and discussion

3.1 Correlation analysis of the interfacial properties of Py/GN composites

Firstly, in order to acquire a comprehensive understanding of the relationship between the interfacial properties of Py/GN composites under the influence of an electric field, the correlation matrix for the interfacial properties of Py/GN composites was derived (Fig. 2). The Pearson correlation coefficient α, as labeled in Fig. 2, was used to quantify the degree of the correlation between interface properties, using the following formula:where x and y are an array of two variables, with m_x and m_y being the means of x and y respectively. In order to obtain a more precise correlation coefficient, the correlation matrix of each Py/GN composite is calculated separately, and then all values are averaged as the final result. The study findings indicate that, except for E_g, which exhibits a negative correlation with the electric fields, the other interfacial properties (PCBM, PVBM, E_ads, ε) demonstrate a positive correlation with the electric field. Specifically, the PVBM and PCBM of the composites show a strong positive correlation with the applied electric fields, with correlation coefficients of 0.49 and 0.57, respectively. This indicates that the band structures of polymers in Py/GN composites become more sensitive to vertical electric field tuning. The correlation coefficient of 0.32 between ε and the applied electric field indicates that ε increases with the electric field, as has been previously reported.⁵⁸ The effect of the electric field on E_ads and E_g is much smaller than that on ε, PVBM, and PCBM. Additionally, the ε showed a positive correlation with PVBM and PCBM with correlation coefficients of 0.34 and 0.22 respectively, which was higher than that of E_ads with PVBM and PCBM (0.076 and 0.19 respectively). This indicates that the evolution of band structures of polymers in Py/GN composites might have a stronger correlation with ε than with E_ads. It was observed that the correlation between ε and E_ads was 0.17, implying that a stronger adsorption between the polymer and graphene might reduce the dielectric constant. Overall, the matrix analysis suggests that the interaction between interfacial properties should be taken into account in the design of Py/GN composites to achieve an excellent electrical response to electric fields.

Fig. 2 Correlation matrix of five interfacial properties and applied electric fields. The corresponding Pearson correlation coefficient α was labeled. A higher absolute value signifies a greater degree of correlation. Histograms of interfacial properties are displayed along the matrix diagonal.

3.2 Prediction and evaluation of PVBM and PCBM models

The predictive models for the evolution of PVBM and PCBM under different electric fields were developed using machine learning algorithms. To evaluate the performance of five algorithms on PVBM and PCBM, the metrics of R², RMSE, and MAE were used and the results of this assessment are shown in Table 2. The R² value is close to 1, indicating a better fit of the machine learning model. The smaller the MAE and RMSE, the higher the accuracy of the estimation. The findings indicated that all five machine learning algorithms were able to effectively capture the correlation between PVBM and PCBM with the applied electric fields. It is evident from the results that the XGBoost algorithm shows superior performance in terms of R², achieving 91.3% for PVBM and 91.6% for PCBM. Other algorithms also exhibit satisfactory levels of accuracy, such as GBR algorithm (89.9% and 83.3%), RFR algorithm (86.6% and 78.0%), and Bagging algorithm (84.7% and 88.6%). In contrast, the AdaBoost algorithm (75.9% and 73.6%) shows relatively lower accuracy. Consequently, the XGBoost machine learning algorithm was chosen as the ultimate prediction model for PVBM and PCBM in this study. Simultaneously, Fig. 3 visually illustrates the difference between the values obtained from the DFT simulation and those predicted by the XGBoost regression algorithm. The results show that each point of the PVBM and PCBM models is distributed near the dashed line, indicating that the prediction results have better accuracy.

Table 2 Evaluation of the five algorithms for PVBM and PCBM models of Py/GN composites under the applied electric fields on the testing set

Model	PVBM (eV)			PCBM (eV)
	R^2	MAE	RMSE	R^2	MAE	RMSE
XGBoost	0.913	0.185	0.240	0.916	0.102	0.135
RFR	0.866	0.219	0.262	0.780	0.161	0.237
GBR	0.899	0.193	0.265	0.833	0.136	0.191
AdaBoost	0.759	0.316	0.388	0.736	0.242	0.312
Bagging	0.847	0.248	0.294	0.886	0.162	0.206

---

Fig. 3 Scatter plots between the predicted and the calculated values of (a) PVBM (b) and PCBM models of Py/GN composites under the action of electric fields on the testing sets using the XGBoost algorithm. The dashed line is the ideal prediction line, and the nearer a scatter is to it, the better the prediction result.

The seven input features of the polymer, which were selected from the PubChem database, are presented in Table 2. The addition of the electric field variable and the polymer descriptors to the feature set has been shown to be effective in predicting PVBM and PCBM. To enhance the credibility of the electric field regulation of polymer PVBM and PCBM models, the XGBoost algorithm was employed to calculate the feature importance ranking of each feature. As depicted in Fig. 4, it can be seen that the electric field feature holds the highest rank among the features, indicating that the electric field has a significant impact on the evolution of polymer band arrangement. Feature ranking analysis verifies the validity of the PVBM and PCBM models, which are regulated by electric fields.

Fig. 4 Features importance ranking of the (a) PVBM and (b) PCBM prediction models for Py/GN composites.

3.3 Mechanism analysis of electric fields effect on electronic structures

To better understand the underlying mechanism of the impacts of electric fields on the electronic characteristics of Py/GN composites, pyrrole/GN composite was taken as representative example. The PDOSs of the pyrrole/GN interfaces under varying electric fields were analyzed and are presented in Fig. 5(a–c). The results demonstrate that with the increase of the electric fields, the PVBM of pyrrole obviously shifts closer to the Fermi level. Specifically, at +1.0 V Å⁻¹, the PVBM crosses above the Fermi level, and the Schottky barrier heights (SBH) of the interface decrease to zero. This E_ads to a transition from a p-type Schottky contact to an ohmic contact. In contrast to the evolution of the PVBM, the PCBM of pyrrole exhibits a substantial deviation from the Fermi level. These findings indicate that the differential work function of graphene and pyrrole creates a built-in electric field near the interface.⁵⁹ The positions of the valence and conduction bands at the pyrrole/GN interface are influenced by the internal electric field, resulting in alterations in their energy levels. The aforementioned transition has a significant impact on the energy barrier associated with the transport of electrons and holes, consequently influencing the electrical properties of the composites. The SBH acts as a barrier to prevent electron tunneling across the interface layer. A decrease in SBH will result in a reduction in the resistivity of the Py/GN composites. Therefore, the variation of potential barrier heights provides valuable insights into the nonlinear conducting characteristics of dielectric composites. Although the application of electric fields can be utilized to regulate the charge transfer and the Schottky barrier between the polymer and graphene, its impact on the intrinsic bandgap of both layers is minimal.

Fig. 5 PDOSs for pyrrole/GN composites under electric fields of (a) +0 V Å⁻¹, (b) +0.5 V Å⁻¹, (c) +1.0 V Å⁻¹. The charge difference is plotted under electric fields of (d) +0.3 V Å⁻¹, (e) +0.5 V Å⁻¹, (f) +1.0 V Å⁻¹. The yellow and cyan regions indicate electron accumulation and depletion, respectively.

The charge density difference at the interface between the polymer and graphene under various electric fields is illustrated in Fig. 5(d–f). The charge density difference (ρ_diff) was defined as ρ_diff = ρ_ele – ρ_noele, where ρ_ele is the charge density under electric fields and ρ_noele is the charge density without electric fields. The yellow and cyan regions illustrate the presence of electron accumulation and depletion, respectively, at the isosurface of 3 × 10⁻⁴ e Å⁻³. The yellow color indicates an excess of electron charge compared to the pristine pyrrole/GN composites. The results indicate that a notable redistribution of charges takes place in the vicinity of the van der Waals interface of the Py/GN composites. With the increase in electric field strength, a significant charge dissipation region appears above the pyrrole layer, corresponding to the migration of π electrons from the polymer molecular orbitals to the interface. Meanwhile, the range of the charge accumulation region below the graphene layer is extended, confirming the directional enrichment of electrons in the graphene layer. This enhances carrier mobility and reduces interfacial contact resistance. Thus, the electric field promotes the transfer of additional negative charge from the pyrrole layer to the graphene layer. The presence of a charge depletion layer leads to a change in the Fermi energy level, which further reduces the SBH at the interface. The change in Fermi energy level and the reduction of SBH jointly affect the electron transport properties, which in turn affects the electrical properties of GN/pyrrole composites.

3.4 The critical fields E_b prediction model of Py/GN composites

According to our simulations using DFT, we have found that the applied electric field can effectively transform the Schottky contact to an ohmic contact in Py/GN composites by adjusting the wide bandgap of the polymer. The critical field E_b was proposed as an effective description to evaluate the difficulty of transition in electrical conductive performance of Py/GN composites by analysing the charge conduction mechanism under electric fields. The E_b was calculated based on the behavior of the PVBM passing through the Fermi levels for Py/GN composites. The E_b of 186 polymer monomers obtained from the PubChem database is listed in Table S4.†

After successfully predicting the PVBM and PCBM sets, we found that the bandgap of the polymer is important for the field-effect regulation of Py/GN composites. Therefore, we incorporated the bandgap data of the polymer into the molecular descriptor sets, forming a new feature set for Py/GN composites as shown in Fig. 1. Subsequently, a prediction model for critical fields E_b was developed based on this updated feature set. The same parameters of the machine learning algorithms consisting of XGBooxt, GBR, RFR, AdaBoost, and Bagging which were mentioned above, were still used. To enhance the accuracy and effectiveness of the prediction results, we carried out 100 iterations and determined the mean value as the final predictive outcome. The performance evaluation of the five algorithms for the E_b model is shown in Table 3. From the results shown above, it could be seen that the XGBoost algorithm achieved the best performance for the E_b prediction model (R²: 0.854, MAE: 0.056, RMSE: 0.103) for Py/GN composites. Fig. 6(a) illustrates the comparisons between the machine learning predicted and DFT calculated values for the E_b prediction model. It is evident that the XGBoost machine learning model fits each point closely distributed near the diagonal. In Fig. 6(b), the visual representation demonstrates the strong agreement between the predicted values and the true values on the test set of the E_b prediction model. These results indicate that the model exhibits high prediction accuracy for the critical electric field of composites.

Table 3 Evaluation of the five algorithms for E_b models of Py/GN composites under the applied electric fields on the testing set

Model	Eb (eV)
	R^2	MAE	RMSE
XGBoost	0.854	0.056	0.103
RFR	0.814	0.078	0.132
GBR	0.816	0.067	0.125
AdaBoost	0.808	0.098	0.120
Bagging	0.759	0.129	0.164

---

Fig. 6 (a) Scatter plots between the machine learning and the DFT values of E_b of Py/GN composites using the XGBoost algorithm. (b) The comparisons between machine learning and DFT values of test sets of E_b prediction model.

Our final and most crucial objective in this study is to prove that our prediction model is capable of directing researchers towards interesting discoveries. Once the E_b ML model is established, it can be reverse-engineered to facilitate the discovery of new Py/GN composites with favorable performance. The 33 375 polymer monomers were chosen from the Pubchem database as potential binders to graphene. The above optimized E_b model was then used to predict the E_b of 33 375 potential combinations under the action of an electric field. From the predicted results, we chose the top 10 polymer monomers with low E_b values and the bottom 10 polymer monomers with high E_b values. These findings are detailed in Table S5.† From the predicted results, we selected two different polymer monomers: benzene and 1,2-diamine (CID 7243) with lower E_b values and carbonyl chloride fluoride (CID 9622) with higher E_b values.

The PDOSs of two composites under different electric fields are depicted in Fig. 8. The benzene-1,2-diamine/GN composite showed a transition from Schottky contact to ohmic contact at 0.1 V Å⁻¹, while the carbonyl chloride fluoride/GN composite reached a critical field value close to 2.0 V Å⁻¹. This validates the effectiveness of the machine learning prediction model. This serves as a useful guide for the future utilization of nonlinear conductivity in polymer/graphene composites, whether in low or high electric field environments. In this reverse material design, the goal is to identify promising materials without the need to evaluate every single candidate. By doing so, this method effectively minimizes computational costs and overcomes the constraints imposed by combinatorial complexity.

The importance ranking of each feature is listed in Fig. 7, and the analysis demonstrates that the bandgap of the polymer plays a more significant role in predicting the E_b of Py/GN composites. Moreover, to illustrate the significance of features and assess the relationship between E_b and features, scatter plots between 7 input features and E_b are depicted in Fig. S1.† From Fig. S1,† it is clear that polymer gap features exhibit a positive correlation and have distinct impacts on E_b. This aligns with the findings of feature importance. It was additionally found that E_b shows a negative correlation with other features, such as the fact that E_b might decrease with increasing molecular weight. This study leverages the computational power of machine learning algorithms to provide additional insights that can improve our comprehension of the relationship between the characteristics of Py/GN composites and the critical fields.

Fig. 7 Features importance ranking for the E_b prediction model of Py/GN composites.

Fig. 8 PDOSs for benzene-1,2-diamine/GN composites under electric fields of (a) 0 V Å⁻¹ (b) 0.1 V Å⁻¹ (c) 0.5 V Å⁻¹ and carbonyl chloride fluoride/GN composites under electric fields of (d) 0 V Å⁻¹ (e) 1.0 V Å⁻¹ (f) 2.0 V Å⁻¹.

4 Conclusions

In summary, the evolution of electrical properties of Py/GN composites under the applied electric fields was examined to explore the nonlinear conductive properties of these composites at the molecular level. The correlation matrix of interfacial properties (PVBM, PCBM, E_g, E_ads, and ε) with the electric field was initially constructed by averaging the correlation coefficients between variables of each Py/GN composite from high-throughput simulation results. The results demonstrate that the applied electric field has a particularly notable effect on the variations of PVBM and PCBM. Additionally, ε exhibits a higher positive correlation with both PVBM and PCBM. The evolution of PVBM and PCBM under varying electric fields was accurately predicted using the XGBoost algorithm, which was superior to other machine learning algorithms, achieving the highest R² of 0.913 and 0.916 respectively. Meanwhile, the effectiveness of electric field modulation was verified by feature importance ranking. Further analysis was carried out on the PDOS and charge density difference of the pyrrole/GN interface under different electric fields to observe that the Fermi level substantially shifts towards the VBM of the polymer with increasing electric field. In particular, at a critical field E_b, the SBH reduces to 0, achieving a transition from a Schottky contact to an ohmic contact. The E_b of Py/GN composites can be successfully predicted with the best R² of 0.854 through 100 iterations using the XGBoost algorithm. A total of 33 375 potential combinations were predicted, leading to the identification of Py/GN composites with the lowest or highest E_b values. This information can effectively guide the application of Py/GN composites in various electric field conditions. This work delves into the molecular-level exploration of the electric field-induced nonlinear electrical properties of Py/GN composites, providing a fresh perspective for future research in this area.

Data availability

The data supporting this article have been included as part of the ESI.† The polymer structures in this research article can be obtained from PubChem database at https://pubchem.ncbi.nlm.nih.gov/.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China, [No. 52077220].

References

1. Z. Spitalsky, D. Tasis, K. Papagelis and C. Galiotis, Prog. Polym. Sci., 2010, 35, 357–401.
2. Q. Li, M. R. Siddaramaiah, N. H. Kim, G.-H. Yoo and J. H. Lee, Composites, Part B, 2009, 40, 218–224.
3. W. Li, A. B. Dichiara and J. Bai, Compos. Sci. Technol., 2013, 74, 221–227.
4. G. G. Tibbetts, M. L. Lake, K. L. Strong and B. P. Rice, Compos. Sci. Technol., 2007, 67, 1709–1718.
5. S. J. A. Woltornist, J. M. Y. Carrillo, T. O. Xu, A. V. Dobrynin and D. H. Adamson, Macromolecules, 2015, 48, 687–693.
6. M. Shtein, R. Nadiv, M. Buzaglo, K. Kahil and O. Regev, Chem. Mater., 2015, 27, 2100–2106.
7. H. Zhao and J. Bai, ACS Appl. Mater. Interfaces, 2015, 7, 9652–9659.
8. T. Wang, G. Liang, L. Yuan and A. Gu, Carbon, 2014, 77, 920–932.
9. H. Pang, T. Chen, G. Zhang, B. Zeng and Z.-M. Li, Mater. Lett., 2010, 64, 2226–2229.
10. X. Lu, J. Yvonnet, F. Detrez and J. Bai, J. Comput. Phys., 2017, 337, 116–131.
11. X. Yang, J. Hu, S. Wang, P. Meng, X. Zhao, S. Peng, Z. Yuan, C. Yuan, Q. Li and J. He, Nano Lett., 2022, 22, 5167–5174.
12. X. Liu, Y. Li, X. Sun, W. Tang, G. Deng, Y. Liu, Z. Song, Y. Yu, R. Yu, L. Dai and J. Shui, Matter, 2021, 4, 1735–1747.
13. Z. Wang, J. K. Nelson, H. Hillborg, S. Zhao and L. S. Schadler, Adv. Mater., 2012, 24, 3134–3137.
14. P. N. Samanta and K. K. Das, J. Phys. Chem. C, 2019, 123, 5447–5459.
15. Y. Duan, J. Liu, Y. Zhang and T. Wang, RSC Adv., 2016, 6, 73915–73923.
16. M. A. Matos, S. T. Pinho and V. L. Tagarielli, Carbon, 2019, 146, 265–275.
17. H. Wei, S. Zhao, Q. Rong and H. Bao, Int. J. Heat Mass Transfer, 2018, 127, 908–916.
18. Z. Yang, X. Gu, X. Liang and L. Ling, Mater. Des., 2010, 31, 1042–1049.
19. A. Alzghoul, A. Alhalaweh, D. Mahlin and C. A. S. Bergström, J. Chem. Inf. Model., 2014, 54, 3396–3403.
20. S. Venkatram, R. Batra, L. Chen, C. Kim, M. Shelton and R. Ramprasad, J. Phys. Chem. B, 2020, 124, 6046–6054.
21. M. Yuan, H. Zhao, Y. Xie, H. Ren, L. Tian, Z. Wang, B. Zhang and J. A. Chen, Compos. Sci. Technol., 2022, 218.
22. Y. Yan, T. Mattisson, P. Moldenhauer, E. J. Anthony and P. T. Clough, Chem. Eng. J., 2020, 387, 124072.
23. H. T. Nguyen, K. T. Nguyen, T. C. Le, L. Soufeiani and A. P. Mouritz, Compos. Sci. Technol., 2021, 215, 109007.
24. A. Rahman, P. Deshpande, M. S. Radue, G. M. Odegard, S. Gowtham, S. Ghosh and A. D. Spear, Compos. Sci. Technol., 2021, 207, 108627.
25. F. Chen, J. Wang, Z. Guo, F. Jiang, R. Ouyang and P. Ding, ACS Appl. Mater. Interfaces, 2021, 13, 53425–53438.
26. M. Fetanat, M. Keshtiara, R. Keyikoglu, A. Khataee, R. Daiyan and A. Razmjou, Sep. Purif. Technol., 2021, 270, 118383.
27. X. Zhu, Z. Wan, D. C. Tsang, M. He, D. Hou, Z. Su and J. Shang, Chem. Eng. J., 2021, 406, 126782.
28. A. Sharma, T. Mukhopadhyay, S. M. Rangappa, S. Siengchin and V. Kushvaha, Arch. Comput. Methods Eng., 2022, 29, 3341–3385.
29. Y. Tang, H. Chen, J. Wang and X. Niu, Phys. Chem. Chem. Phys., 2023, 25, 18086–18094.
30. H. Guo, J. Zhao, J. Yin and L. Yao, Polym. Test., 2018, 70, 30–38.
31. A. Jac Fredo, R. Abilash, R. Femi, A. Mythili and C. S. Kumar, Composites, Part B, 2019, 168, 77–86.
32. C. Tao, C. Zhang, H. Ji and J. Qiu, Composites, Part B, 2021, 216, 108816.
33. M. Shi, C.-P. Feng, J. Li and S.-Y. Guo, Compos. Sci. Technol., 2022, 223, 109414.
34. X. Lu, D. G. Giovanis, J. Yvonnet, V. Papadopoulos, F. Detrez and J. Bai, Comput. Mech., 2019, 64, 307–321.
35. D. Yue, Y. Feng, X.-X. Liu, J.-H. Yin, W.-C. Zhang, H. Guo, B. Su and Q.-Q. Lei, Adv. Sci., 2022, 9, 2105773.
36. Z.-H. Shen, J.-J. Wang, J.-Y. Jiang, S. X. Huang, Y.-H. Lin, C.-W. Nan, L.-Q. Chen and Y. Shen, Nat. Commun., 2019, 10, 1843.
37. D. Willhelm, N. Wilson, R. Arroyave, X. Qian, T. Cagin, R. Pachter and X. Qian, ACS Appl. Mater. Interfaces, 2022, 14, 25907–25919.
38. F. Shayeganfar and R. Shahsavari, Sci. Rep., 2021, 11, 15111.
39. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
40. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
42. G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102.
43. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
44. L. Himanen, A. Geurts, A. S. Foster and P. Rinke, Adv. Sci., 2019, 6, 1900808.
45. S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen, B. Yu, L. Zaslavsky, J. Zhang and E. E. Bolton, Nucleic Acids Res., 2018, 47, D1102–D1109.
46. K. Nagashio, T. Nishimura, K. Kita and A. Toriumi, Appl. Phys. Express, 2009, 2, 025003.
47. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
48. K. D. Pham, N. N. Hieu, H. Phuc, V. B. D. Hoi, V. V. Ilysov, B. Amin and C. V. Nguyen, Comput. Mater. Sci., 2018, 153, 438–444.
49. W. Xiong, C. Xia, X. Zhao, T. Wang and Y. Jia, Carbon, 2016, 109, 737–746.
50. W. Zhang, G. Hao, R. Zhang, J. Xu, X. Ye and H. Li, J. Phys. Chem. Solids, 2021, 157, 110189.
51. H. Li, Z. Qu, Y. Chen, L. Zhou and Y. Wang, Polymers, 2022, 14, 2949.
52. F. Pereira, K. Xiao, D. A. R. S. Latino, C. Wu, Q. Zhang and J. Aires-de Sousa, J. Chem. Inf. Model., 2017, 57, 11–21.
53. W. Hu, W. Hu and S. Maybank, IEEE Trans. Syst. Man Cybern., 2008, 38, 577–583.
54. L. Breiman, Mach. Learn., 1996, 24, 123–140.
55. G. Biau and E. Scornet, TEST, 2016, 25, 264–268.
56. T. Chen and C. Guestrin, KDD'16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 1601 Broadway, 10th Floor, New York, NY, United States, 2016, pp. 785–794.
57. J. Friedman, Ann. Math. Stat., 2001, 29, 1189–1232.
58. Y. Sun, S. Ma and S. A. Boggs, IEEE Trans. Dielectr. Electr. Insul., 2015, 22, 1719–1722.
59. F. Xu, K. Meng, B. Cheng, S. Wang, J. Xu and J. Yu, Nat. Commun., 2020, 11, 4613.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra00705d

---