Computational insights on dynamic disorder in molecular crystals – from electron structure over phonons to thermodynamics

Abstract

Quantum-chemical nature of molecular interactions and atomic vibrations imparts a ubiquitous internal dynamics even to solid molecular materials that appear as very rigid from the macroscopic point of view. Existence of flat potential energy basins related to dynamic degrees of freedom in molecular crystals usually gives birth to large-amplitude motions of molecular segments or entire molecules that is commonly recognized as dynamic disorder. Computational chemistry offers suitable approaches for sampling these potential energy surfaces, subsequently enabling to model atomic displacements related to disorder and contributions of this internal dynamics to macroscopic material properties such as entropy, volatility, solubility, plasticity or conductivity. This highlight article presents a mosaic of recent research results which were achieved thanks to the computational methods playing a perfectly complementary role to experimental approaches. Observed material properties and the either beneficial or detrimental impact of dynamic disorder thereon can be then interpreted at the atomic level which naturally contributes to a better understanding of the underlying phenomena and enables to rationalize future material design. This highlight article illustrates the impact of dynamic disorder in the fields of barocaloric materials for heat management, active pharmaceutical ingredients and organic molecular semiconductors. Such a scope enables to account for how the dynamic disorder manifests itself in modelling thermodynamic or spectroscopic properties, phase behavior, electron structure and charge transport in molecular crystals.

---

1. Introduction

Computational chemistry has tremendously benefited from the concept of a perfect crystal, having all its atoms located at their equilibrium positions in the crystal structure. Over the last decades, such a simplified view has enabled development of quantum-chemical approaches to model and predict structural,^1–3 electronic,⁴ cohesive,^5–9 spectroscopic^10–12 and thermodynamic properties^13–15 of molecular crystals. The crude static computational model of molecular crystals has been gradually complemented with its dynamic counterpart, allowing individual atoms to vibrate around their equilibrium positions in the crystal lattice.¹⁶ First-principles treatment of these dynamic degrees of freedom, i.e. phonons, has allowed computational models to advance from the absolute zero to finite temperatures, and to mimic real behavior of molecular crystals appreciably more closely.^17–22 Still, the realm of molecular crystals is a way more rich so that one is always forced to extend existing computational approaches.

Experimental crystallographers have known for a century that a long-range order of a crystal structure may be violated at a local level, and still, leaving such a material with distinct sharp signals in its X-ray diffractograms.²³ The concept of local disorder had to be admitted to the realm of molecular crystals. Thanks to extensive experimental efforts, numerous platforms of plastic crystals, liquid crystals and other mesophases, all representing a stage on the path from the fully ordered perfect crystal to a completely disordered amorphous liquid, have been gradually introduced and characterized.^23,24

Disordered crystals are known to appear typically as a high-temperature phase below the melting temperature of a given material. Frequently, such structures belong to high-symmetry space groups although a single spatial configuration of its molecules may not be able to accommodate such a high symmetry.²⁴ That becomes possible only thanks to time- or space-averaging of distinct local configurations, also referred to as archetypes.²⁵ Over time, several pre-requisites for the disorder occurrence have been formulated, including aspects such as energetic, structural, and charge-distribution proximity of individual disorder components or comparable numbers and intensities of the main cohesive features in all disorder components.²⁶

Should these configurations be separated by large enough energy barriers (compared to the mean thermal energy RT), one can consider the disorder as static, i.e. frozen in at creation of the crystalline sample. On the other hand, low energy barriers (or large enough thermal energy) then enable individual disordered moieties to transit from one configuration to another with a relative ease, leading to the dynamic disorder.²⁶ Disorder governed by orientation of molecules and their functional groups or conformational degrees of freedom is referred to as orientational disorder.^27,28 A subgroup of disordered crystals has gained a label of plastic crystals thanks to their mechanical softness and even ability to flow which is governed by a large orientation flexibility of molecules around their equilibrium lattice positions.²⁹

Local disorder and existence of plastic crystals have finally gained their deserved attention as around 20% of known molecular crystals are currently estimated to be disordered.²⁶ Furthermore, this type of molecular materials offer very interesting properties, such as controllable conductivity or optoelectronic switching in the solid organic semi-conductors,²⁴ larger solubility of metastable disordered active pharmaceutical ingredients,³⁰ or barocaloric properties for cooling or excess heat management applications,³¹ etc. Although in silico modeling plays an important role also in the design of inorganic semiconductors,³² the scope of this article remains focused primarily on organic materials.

Despite this broad application potential and experimental evidences thereof, disordered molecular crystals have remained out of scope of most computational solid-state chemists for long. Disordered nature of a simulated crystal can complicate the computation already in the structural optimization stage as the average structure may not correspond to a true minimum of the potential. Treatment of the static disorder then inevitably consists in modelling more than one single configuration of the perfect crystal structure. Numerous perturbed supercells, mimicking individual disorder components and corresponding to various local energetic minima, need to be considered, largely increasing computational complexity and related human-labor requirements of such modelling.³³ In the case of dynamic disorder, atomic amplitudes and extent of the anharmonicity related to the dynamic degrees of freedom of the crystalline material need to be assessed. Only over the last two decades, the area of computational modelling of structure and properties of disordered molecular crystals has undergone a rapid growth. Viable computational approaches treating both the static and dynamic disorder cases have been developed, allowing various quantum-chemical theories to be used to describe the associated energetics.^26,34–36

This highlight article does not aim at providing an exhaustive review of the field, but its goal is to present a mosaic of interesting research results based on an important computational contribution that were achieved during the last half-decade. The principal phenomenon covered in this article is the dynamic disorder in molecular crystals and its technological implications. Its characteristic time scales are that short that existing spectroscopic methods cannot typically distinguish individual configurations of the disordered molecules or segments, but provide an averaged image over their configuration space.^37,38 Computational chemistry then offers unique ways how to investigate potential energy surfaces of such disorder-related atomic movements and to assess the extent of their anharmonicity,^35,39 how to interpret the experimentally observed time-averaged signals at the atomic scale, and to decipher contributions of the dynamic disorder and its components to material properties.

Primary material scopes of this article are threefold: i) crystals of caged molecules exhibiting rotational disorder with a potential for barocaloric heat management; ii) crystals of active pharmaceutical ingredients (API) with varying extents of segmental dynamics that is closely related to triggering polymorphism; and iii) crystals of organic semi-conductors (OSC) and their dynamic disorder affecting charge-carrier mobility. The rest of this article is organized in a way that each of the subsequent sections is devoted to one of these areas, the common aspects of which are finally emphasized in the discussion.

2. Barocaloric caged molecules

Caged molecules, containing a three-dimensional enclosed carbon skeleton, represent a very efficient platform for designing crystalline materials that exhibit local disorder or plastic behavior. Representatives of this class of compounds, such as derivatives of adamantane,^40–43 cubane,^44,45 diamantane,⁴⁶ or fullerene,^47,48 all contain carbon scaffolds with manifold rotational axes, belonging thus to high-symmetry point groups. This molecular symmetry, given by nearly cylindrical or even spherical molecular shapes, predetermines these materials also to crystallize in highly symmetric space groups.²⁹

Molecules in such crystal structures can experience a rather uniform interaction field of their neighbors, leading not only to relatively isotropic characteristics of the crystals, but it also imparts unique shapes of the potential energy surface. Focusing on the dynamic degrees of freedom that correspond to intermolecular libration modes, the potential energy surface may consist of relatively wide and flat basins separated by relatively low energy barriers.^35,49 Provided that sufficient thermal energy is available, hindered molecular rotations can be then triggered on in such disordered crystals. Since the discrete structure of available energy levels of a hindered rotor is quite different from that of a harmonic oscillator,⁵⁰ it ceases to be appropriate to model thermodynamic properties of these materials merely with the harmonic phonon model. Significant anharmonicity of this kind should be expected to impart large amplitudes of the vibrating molecules, but also appreciable additional entropy contributions due to this dynamic disorder originating from the phonon anharmonicity.

In our recent study,³⁵ we developed a computational approach incorporating the one-dimensional hindered model⁵⁰ in the quasi-harmonic modeling of thermodynamic properties of dynamically disordered molecular crystals at finite temperatures. We focused on a set of caged hydrocarbons, scanning their potential energy profiles associated with molecular libration modes in their crystals. Fig. 1 showcases a representative example from that study,³⁵ diamantane molecule belonging itself to the D_3d point group and crystallizing in a cubic space group (Fig. 1a). When diamantane molecule is viewed along its three-fold rotational axis, a nearly perfect rotational symmetry of the molecule becomes obvious (Fig. 1b and c).

Fig. 1 First-principles thermodynamic modelling of dynamic disorder in crystalline diamantane: a) structure of diamantane monomer and the cubic unit cell of its crystal; b) diamantane molecule in its equilibrium orientation in the crystal structure; c) diamantane molecule rotated in the crystal with respect to its molecular C₃ axis; d) calculated potential energy profiles E_rot corresponding to rotation of a molecule within the crystal structure; e) calculated contributions to entropy S and heat capacity C_p of the crystal from a single mode treated either as a harmonic oscillator (HO) at the periodic PBE-D3/PAW level of theory, or as an anharmonic hindered-rotation (AHR) with the MP2C-F12 potential energy profile depicted in d); f) blue diamonds represent calculated ratios of sublimation pressures for selected caged hydrocarbons obtained by models treating the libation mode either as harmonic oscillator (p^HO_sub) or one-dimensional hindered rotor (p^AHR_sub) and the red line shows a tentatively interpolated trend among the calculated data points. Adapted from ref. 35, Copyright 2023 the Authors, published by American Chemical Society under the terms of the Creative Commons Attribution 4.0 International License.

Quantum chemical calculations then confirmed that rotation of a single diamantane molecule from its equilibrium orientation within the crystal structure leads only to minor energy penalties ranging from 4 to 8 kJ mol⁻¹, depending on the actual level of theory (Fig. 1d).³⁵ Such an energy barrier is already comparable with the thermal energy available at ambient conditions (≈2.5 kJ mol⁻¹), which justifies the initiative to adopt an explicitly anharmonic model for description of this degree of freedom.

Note that periodic DFT calculations, commonly performed over the last decade at the dispersion-corrected^51–53 PBE level of theory,^{18–20,54–56} enable efficient optimizations of the crystal structures and even searching for the transition states⁵⁷ at the respective potential energy surfaces, but the periodic boundary conditions may naturally impart artifacts related to periodicity of molecular rotations in the crystal unless very large and costly supercells are constructed.

On the other hand, fragment-based ab initio calculations⁴ can mitigate this artificial periodicity of defects. This approach consists in constructing the electronic energy of a molecular solid in a form of a many-body expansion of monomer energies, pair interaction energies, a correction for long-range interactions, and optionally higher-order terms^6,58–61 that are relevant for a particular crystal structure. Treatment of small clusters instead of the whole crystal enables to use high-level ab initio wavefunction methods to calculate their energies, not limiting the computational affordability to DFT methods only. Using such complex electron structure methods also enables to improve the accuracy of modeling the energies of individual geometries (of crystal structures with displaced or rotated molecules), in general allowing for a systematic convergence to the sub-chemical accuracy in terms of lattice energies,^6,18 sublimation enthalpies,⁵⁹ or even free energies of crystal polymorphs with uncertainties below 1 kJ mol⁻¹.¹³

Since searches for transition-state geometries or geometry optimization of a large number of disorder components is generally limited to low-tier DFT functionals that suffer from delocalization errors,⁶² frequently leading to overestimation of torsional barrier within molecules, there is a clear motivation to employ more sophisticate electron-structure theories to refine the potential-energy profiles due to libration of molecules in their crystal structures.

A computationally efficient protocol then relies on performing single-point refinements of the energy with ab initio many-body expansion methods for DFT-optimized geometries of a supercell along the libration phonon mode (Fig. 1d).³⁵

Having plugged such rotational potential energy profiles along with molecular moments of inertia to a one-dimensional Schrödinger equation for the rotation mode,⁵⁰ we could access its energy levels and construct the respective partition function. Resulting contributions of the given hindered-rotation mode (with the potential energy refined with the fragment-based MP2C-F12 model) to thermodynamic functions of the crystal, such as its entropy or isobaric heat capacity obviously differ from those obtained with the harmonic oscillator model (based on periodic PBE-D3/PAW calculations) as shown in Fig. 1e. For such low-barrier hindered rotations, the difference of the anharmonic and harmonic entropy terms was found to exceed 10 J K⁻¹ mol⁻¹ at ambient conditions.³⁵

Note that hindered rotations mimic harmonic oscillations at low temperatures (or for high torsional barriers) which are generally hard to excite, resulting in relatively few eigenstates that are thermally accessible at ambient conditions, and thus also in a relatively low entropy. At high temperatures (or for low barriers), hindered rotor modes converge to a free rotor, which is appreciably easier to excite. Entropy of a free rotor is thus generally larger than that of a harmonic oscillator at temperatures relevant for the stability of organic molecular crystals. Hindered rotor modes with torsion barriers ranging to higher units or lower tens of kJ mol⁻¹ that are typical for organic molecules then range between the two limiting cases at ambient conditions, with their entropy somewhat exceeding the harmonic oscillator model.⁶³ Recall also that typical hindered rotor modes in organic molecules exhibit a gradual decline of the heat capacity contribution from values near 1·R temperatures at (near-)ambient temperatures to the high-temperature (free-rotor) limit at ½·R.⁶⁴

Such an additional entropy value (compared to the harmonic oscillator) is large enough to significantly impact sublimation of such disordered molecular crystals. Although the hindered-rotor anharmonicity leads also to a slight increase of the enthalpy of such a disordered crystal (compared to the harmonic model), the entropic effect prevails and it propagates to appreciable decrease of the volatility of the dynamically disordered crystals. Fig. 1f illustrates this predicted trend indicating that the lower the predicted barrier height within the AHR model, the more the sublimation pressure decreases due to the explicit treatment of the rotational disorder.

Furthermore, existence of distinct minima on the potential energy surface, separated by reasonable high energy barriers, imparts orientational disorder with molecules undergoing sudden changes in their orientation at their equilibrium lattice site. Discontinuity of those orientational molecular transitions has been confirmed experimentally for various caged-molecular materials,⁴² indicating that the molecules occupy only the potential energy basins in the context of Fig. 1d. Both the large vibrational amplitudes and orientational flexibility contribute then to the plastic character of high-temperature crystalline phases of caged molecules.²⁴

Concurrently, crystals of caged molecules are known to undergo first-order solid–solid phase transitions from a low-temperature ordered phase to a high-temperature disordered phase.⁴⁰ This phase transition is typically accompanied with a large density increase (routinely 5–10%),^42,65 a large entropy increase and a massive sensitivity of the phase transition temperature to external pressure.⁶⁶ As a consequence, caged materials possess a very large (original literature says colossal^42,65,66) potential to exhibit the barocaloric effect.

An archetypal caged hydrocarbon, adamantane,⁴² and its hydroxylated⁶⁶ and halogenated⁶⁵ derivatives have been proved experimentally to exhibit strong barocaloric effects at (sub-)ambient temperatures. Another caged molecular platform relying on substituted boron three-dimensional frameworks, such as lithium monocarba-closo-dodecaborate salt (LiCB₁₁H₁₂) has been demonstrated only recently to exhibit colossal barocaloric effects as well.³¹

Clearly, understanding the entropy associated to the order–disorder phase transition is the keystone for design of efficient media for barocaloric applications. In addition to high-pressure calorimetry and inelastic neutron scattering, molecular-dynamics simulations of dynamic degrees of freedom of relevant crystal structures serve to identify individual important entropic contributions associated to the order–disorder phase transition. Zeng et al. have performed both classical and ab initio molecular-dynamics simulations to compare the dynamic degrees of freedom of low-temperature and high-temperature phases of LiCB₁₁H₁₂.³¹ Fig. 2a reprints their illustration of the ordered and disordered polymorphs sketching molecular rotations in the latter.

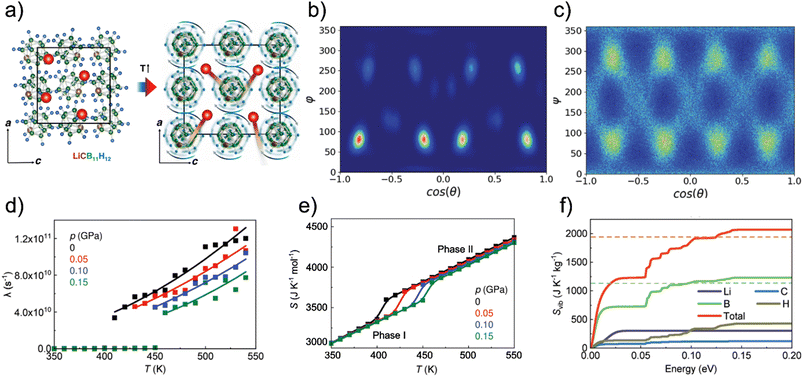Fig. 2 Order–disorder solid–solid transition in lithium monocarba-closo-dodecaborate imparting a colossal barocaloric effect: a) ball-stick representation of the low-temperature ordered (left) and high-temperature disordered (right) phases; b and c) angular probability density function estimated for the molecular [CB₁₁H₁₂⁻] anions calculated in the ordered (350 K, b)) and disordered (550 K, c)) phases at zero pressure, expressed as a function of the polar (θ) and azimuthal (ϕ) angles, dark and bright areas represent low and high probability regions, respectively; d) anionic reorientational frequency (λ), solid lines correspond to Arrhenius law fits; e) calculated total entropy curves expressed as a function of pressure and temperature; f) cumulative function of the vibrational entropy as a function of the phonon energy separated to contributions from individual atomic species calculated for the disordered phase at 412 K and zero pressure, dashed lines indicate analogous asymptotic values reached in the ordered phase. Adapted with permission from ref. 31, Copyright 2024 the Authors, published by Wiley-VCH GmbH under the terms of the Creative Commons Attribution 4.0 International License.

Fig. 2b and c further show the simulated angular distribution of molecular orientations in both LiCB₁₁H₁₂ polymorphs. While there is only one dominating orientation in the low-temperature phase, two significant orientations emerge in the high-temperature phase with rates of rearrangements of the molecular orientations following an Arrhenius trend in the latter phase (Fig. 2d).³¹ Analyzing the velocity auto-correlation functions, Zeng et al. calculated absolute entropies of both polymorphs which differ by as much as 34 J K⁻¹ mol⁻¹ and this offset is nearly constant over a broad temperature and pressure range (Fig. 2e).³¹ Since that value largely exceeds the configurational entropy of a two state system, R ln(2), there have to be additional factors imparting such a large solid–solid transition entropy.

Zeng et al. finally separated contributions to the total entropy from vibrations related to individual atom types and compared such results for both polymorphs.³¹ Fig. 2f shows that it is above all the phonon modes including displacements of the boron atoms that contribute to significantly higher vibrational entropy of the disordered LiCB₁₁H₁₂ polymorph when compared to its low-temperature structure. These vibrational entropy differences between the polymorphs can be traced to an appreciable softening of the lattice modes upon the phase transition from the ordered to the disordered phase.³¹

In a similar context, Meijer et al. performed a computational analysis of the low-frequency phonon modes of the ordered and disordered polymorphs of adamantane, having focused on determining translational and rotational character of individual phonon modes.⁴² In agreement with the above mentioned mode softening for LiCB₁₁H₁₂, Meijer et al. found that a phonon pattern, being conventional for molecular crystals, can be seen for the ordered adamantane phase – the acoustic modes exhibit a translational character whereas the rotational (librational) character prevails only for optical modes with wavenumbers above 40 cm⁻¹ (≈5 meV) as illustrated in Fig. 3.⁴² Adamantane molecules are interlocked in the low-temperature phase, rendering the rotational modes more energy demanding. On the other hand, the high-temperature phase resembles closely packed spheres allowing for more rotational flexibility. That imparts significant rotational character already for its acoustic phonon modes which then resemble molecular rolling with an appreciable red-shift of the respective frequencies.

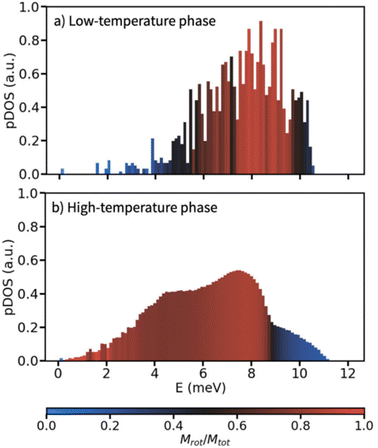Fig. 3 Phonon density of states calculated on the basis of an atomistic force field for a) the high-temperature polymorph, and b) the low-temperature polymorph of adamantane. Each bar in the histograms is coloured by the average rotational character M_rot/M_tot of the modes in that bin. Reproduced with permission from ref. 42, Copyright 2023 the Royal Society of Chemistry under the terms of the Creative Commons Attribution 3.0 Unported License.

Both studies conclude that the orientational disorder in such high-temperature polymorphs accounts for less than a half of the total solid–solid transition entropy change and that the phonon softening represents the dominant entropy contribution.^31,42 Still, occurrence of the disordered high-temperature phases is essential for the barocaloric effect to occur. Meijer et al. presented also a warning that the configurational disorder reduced the phonon lifetime, and thus also the thermal conductivity of such materials, which may be an adverse side-effect of the disorder in plastic crystals.^31,42

A common feature of the studies highlighted in this section is an explicitly anharmonic treatment of at least some of the phonon modes which is naturally costly, and as such, frequently avoided or bypassed upon modelling of molecular crystals. Further development of straightforward computational protocols for modeling anharmonic contributions to the thermodynamic properties for molecular crystals, including an initial versatile assessment of the anharmonicity of individual phonon modes also for crystals with large and complex unit cells, is thus desirable. Protocols that would enable to model largely disordered plastic polymorphs from the first principles with a computational ease similar to what the quasi-harmonic approximation offers are also demanded.

3. Active pharmaceutical ingredients

API molecules frequently constitute from multiple rigid segments that are interlinked with flexible bridges that enable significant torsional motions, and thus various molecular conformations that can be packed on a crystal lattice. At the same time, polymorphism is a very important phenomenon that needs to be addressed during the development of every solid-form API.⁶⁷ Conformational polymorphism has been demonstrated to concur with very rich polymorph landscapes, leading to a long-term coexistence of multiple polymorphs exhibiting very distinct properties.⁶⁸ Facile conformational variation of individual segments of API molecules may, however, also lead to disorder of their crystal structures.²³

In the pharmaceutical context, increasing the solubility of hydrophobic API molecules has been an emerging field of research.⁶⁹ For example, mechanochemical impulses invoke orientational disorder in originally ordered crystalline API.³⁰ Provided that the disorder in such a disordered bulk API phase has a static frozen in character, it may resist to recrystallize over interesting periods of time. Such bulk phases disordered by force then correspond to a thermodynamically metastable state, being on a path of partial amorphisation towards glassy API formulations that inherently exhibit higher solubility.^70,71

On the other hand, presence of the dynamic disorder in API crystals has been considered as a risk factor,⁷² frequently imparting crystallizability issues,⁶⁷ or adverse changes of mechanical properties or physico-chemical stability of the desired metastable phases^23,73 complicating further development and characterization of novel API candidates.⁷⁴

Recent advent of NMR crystallography techniques and complementary computational approaches has enabled to detect subtle variations in molecular dynamics that occur upon order–disorder transitions of bulk API systems.^72,75–79 An illustrative example of this phenomenon can be provided with a study of the relationship of polymorphism and disorder of teriflunomide, being depicted in Fig. 4a, which is a moderately sized API approved for treatment of various brain diseases.⁸⁰ Its ordered low-temperature polymorph has been reported to be triclinic with Z′ = 2 and to contain four molecules in the unit cell.⁸⁰ This ordered polymorph undergoes a very weakly endothermic phase transition at around 234 K, being still deep below the melting temperature, which can be revealed only after a detailed inspection of experimental thermograms from differential scanning calorimetry (DSC) in Fig. 4b.⁸⁰ The weak thermal effect accompanying this solid–solid transition accounts for only a minor structural rearrangement of the structure. Combined efforts of X-ray diffraction and solid-state NMR experiments revealed that the unit cell of the high-temperature phase retains the triclinic symmetry, but its size is halved, containing only two molecules and having Z′ = 1 (Fig. 4c).

Fig. 4 Disorder-induced polymorphism of teriflunomide: a) molecular structure; b) DSC plot of a crystalline sample heated at a rate 5 K min⁻¹ up to the melting point, inset plot zooms on the endothermic order–disorder phase transition; c) asymmetric unit cell of the high-temperature disordered polymorph; d) ¹H → ¹³C CP MAS NMR spectra of the high-temperature (top) and the low-temperature (bottom) polymorphs; e) superposition of clusters of 15 molecules from the low-temperature ordered (blue) and high-temperature disordered (green) structures determined within the COMPACK algorithm;⁸¹ f) potential energy related to the C4−NH−C5−C6 torsion mode within the high-temperature polymorph calculated at the PBE-MBD level of theory. Adapted with permission from ref. 80, Copyright 2021 the Authors, published by American Chemical Society under the terms of the Creative Commons Attribution 4.0 International License.

This lowering of Z′ occurring upon the phase transition can be evidenced by analysing ¹H → ¹³C CP MAS NMR spectra of both polymorphs. While the spectrum of the low-temperature form contains most NMR signals as doublets (Fig. 4d), clearly indicating the presence of two static conformations, the high-temperature phase exhibits only singlet NMR signals, confirming that the conformational dynamics in the high-temperature phase is fast and distribution of the conformers can be averaged out to a single structure with a smaller unit cell.⁸⁰ Fig. 4c reprints a plot of the asymmetric part of the high-temperature unit cell with indication of atomic thermal ellipsoids which suggest very fast rotational movements of the trifluoromethyl moiety in the crystal and admit also large amplitudes of the atoms forming the six-membered aromatic core of teriflunomide. A structural similarity check between both polymorphs confirm that both structures are indeed very similar, differing predominantly only in the torsional orientation of the aromatic core and the degree of mobility of the terminal trifluoromethyl moiety (Fig. 4e).⁸⁰

From the computational perspective, Pawlak et al. performed also in sillico crystal structure prediction,⁸⁰ where they used the CrystalPredictor II tool⁸² to generate structures with Z′ = 1–2. Subsequently, a preliminary ranking of the generated structures was performed in terms of the static lattice energies at the force-field level, followed by a quantum-chemical reoptimization of the most promising structures at the PBE-MBD/PAW level of theory.⁸³ This computational analysis correctly yielded the triclinic Z′ = 2 structure, corresponding to the true low-temperature phase, as the most stable in terms of its lattice energy. Furthermore, a Z′ = 1 structure closely resembling the averaged configuration of the disordered high-temperature polymorphs was found only 1.4 kJ mol⁻¹ above the global minimum structure, being accompanied with a handful of other structures exhibiting very similar packing motifs.⁸⁰ Although this CSP ranking stage omits calculations of any phonon-based contributions to the free energy, this predicted energy proximity of both real polymorphs agrees well with the observed minor latent thermal effect accompanying the phase transition. Furthermore, the presence of multiple similar predicted structures in such a narrow energy window indicates a somewhat glassy polymorph landscape. Following this idea, Pawlak et al. computed scans of the potential energy related to the torsional motion of the teriflunomide aromatic core in the periodic environment at the PBE-MBD level of theory.⁸⁰ Fig. 4f shows the extraordinary flatness of the potential energy surface which allows to easily vary the particular torsion angle over an interval spanning over 45° with an energy penalty that is lower than 3 kJ mol⁻¹.⁸⁰ Altogether, Pawlak et al. assembled unambiguous clues for a dynamic disorder occurring in the high-temperature phase of teriflunomide and for its solid–solid phase transition to exhibit the order–disorder character.⁸⁰

Another API example with even more peculiar order–disorder polymorphic transitions represents simvastatin, a drug routinely used for hypercholesterolemia treatment. Calorimetry and X-ray diffraction experiments undeniably revealed its trimorphic behavior upon temperature variation,⁸⁴ with both solid–solid transitions being reversible and accompanied with minor latent heat effects. Only recently, Brus et al. performed a detailed NMR crystallographic study addressing segmental dynamics of simvastatin molecules in its crystals and mapped important changes of the dynamics character to individual phase transitions.⁷⁵

Simvastatin molecule, being depicted in Fig. 5a, contains two rigid units with a flexible linker and a relatively mobile ester side chain. Expectedly, the low-temperature phase III of simvastatin is ordered exhibiting low-to-negligible segmental dynamics which can be deduced from a distinct splitting of its ¹³C CP/MAS NMR signals corresponding to a Z′ = 2 structure again (Fig. 5b), and from a minimum temperature dependence of the order parameter S² related to individual carbon atomic sites (Fig. 5c).⁷⁵ The ester segment that is particularly prone to disorder is held rigid with a strong hydrogen bond to the hydroxyl moiety of the lactone segment of another simavastatine molecule in the phase III.

Fig. 5 Polymorphism and disorder in simvastatin crystals: a) molecular structure with individual segments distinguished; b) variation of ¹³C NMR shifts of carbon atoms at the ester tails with respect to temperature; c) temperature trends of the order parameter S²; d) unit cell of the transient phase II with marked ester-hydroxyl hydrogen bonds; e and f) 2D fingerprint plots associated to Hirshfeld surfaces in the simvastatin phases III and I, respectively. Reprinted with permission from ref. 75, Copyright 2022 the Authors, published by MDPI under the terms of the Creative Commons Attribution 4.0 International License.

Performing quantum-chemical calculations of NMR shielding tensors and ¹³C chemical shifts at the PBE/GIPAW level of theory helped to map the measured solid-state NMR signals to individual simvastatin atomic sites and to decipher temperature-induced signal splitting.⁷⁵ Upon heating above the calorimetrically detected temperature of the III → II phase transition at around 232 K, the splitting width of NMR signals due to carbon atoms at the ester side chain starts to diminish and the order parameter S² for the ester carbon atoms obtains a strong decreasing tendency (Fig. 5b and c).⁷⁵ Such a triggering of large-amplitude dynamics has to be caused by spatial or temporary weakening of the ester-hydroxyl hydrogen bond in phase II (Fig. 5d). Interestingly, the temperature at which the NMR signal splitting vanishes and both signal lines unify, being at around 250 K, does not correspond to any phase transition temperature observed via calorimetry. Analyzing the temperature trends of the relaxation times of various ¹³C simvastatin sites, Brus et al. interpret this behavior as if the III → II phase transition unlocked hindered-rotation degrees of freedom for the ester tail in the crystal lattice.⁷⁵ The temperatures at which the split NMR signals unify is given by simvastatin molecules reaching sufficient thermal energy to surpass the hindered-rotation barriers imposed by the crystal environment, rendering those motions fast enough so that individual populations cease to be distinguishable via solid-state NMR. After the ultimate II → I phase transition, temperature trends of the signal positions disappear and the order parameters of ester-tail carbon sites converge to remain stationary at very low values, indicating a nearly free rotation of the ester tail occurring in the high-temperature dynamically-disordered phase with Z′ = 1.⁷⁵ Calculations of Hirshfeld surfaces of the low- and high-temperature phases and construction of related 2D fingerprint plots confirm that the ester-hydrogen bond is significantly weaker (O⋯H distance longer by 0.2 Å) in phase I than in phase III, and that the distribution of the closest atomic contacts is somewhat broader in phase I,⁷⁵ as illustrated in Fig. 5e and f.

Importantly, Brus et al. conclude that such enantiotropic solid–solid phase transitions that should occur practically instantaneously within a very narrow temperature range according to thermodynamics may be quite gradual in terms of local and segmental dynamics of molecules in the crystal lattice. The middle-temperature phase II exhibits a transient dynamics-modulated character, which is a result of hindered molecular rotations taking place therein propagating in large variations of its spectral and dynamic properties with respect to temperature.⁷⁵

In a similar context, polymorphism of spironolactone, being an API approved for treatments of heart failures, was recently investigated.⁷⁶ Spironolactone is a pentacyclic molecule with three segments (lactone ring, thioester chain, and a six-membered ring bearing a carbonyl oxygen atom) being particularly prone to large-amplitude dynamics. Golz and Krawczuk described its dynamic disorder in the high-temperature orthorhombic Z′ = 1 phase II where all the three mentioned segments are subject to dynamic disorder.⁷⁶ Upon cooling, a gradual freezing in of this disorder takes place. Dynamic disorder is reported to be turned off for individual segments in a row of decreasing temperature: thioester > carbonyl > lactone.

Somewhat confusingly, crystals structures observed below 150 K are still referred to as phase II even though a clear change of the lattice system to monoclinic occurred. Only at 100 K, where all the three mentioned spirolactone segments are frozen to their equilibrium sites, a proper low-temperature ordered monoclinic Z′ = 2 phase III with unit-cell parameters distinct from phase II was finally recognized.⁷⁶ Golz and Krawczuk justify not distinguishing the two varieties of phase II as polymorphs following an earlier literature precedent,⁸⁵ arguing that the structural changes upon all the observed transitions are extremely small and relate exclusively to subtle conformational variations.⁷⁶ Unfortunately, calorimetric investigations that could reveal any thermal effects related to additional solid–solid phase transitions, and thus to distinguish the reported low-and high-temperature varieties of phase II as individual polymorphs, have not been performed to my knowledge. To conclude, considering the existence of the mentioned transient dynamics-modulated simvastatin polymorph, a similar explanation might work well also for the yet unresolved ambiguities related to the polymorphism of spironolactone.

The selected cases of order–disorder polymorphic API illustrate how important it is to combine various experimental and computational approaches, spanning calorimetry, NMR crystallography, in silico crystal structure prediction and first-principles potential energy surface scans to be able to decipher and understand the stories about unlocking dynamic degrees of freedom of individual molecular segments that in fact govern such peculiar solid–solid transitions.

4. Organic semi-conductors

Semi-conductive materials based on organic molecular platforms have garnered significant scientific attention ever since first discoveries of non-insulating properties of carbon based materials in 1950s.^86,87 The organic platform imparts numerous beneficial characteristics to this class of materials, obviously including lightweight, low-temperature solution processability, structural customizability, and optionally also optical transparency.⁸⁸ Unfortunately, all these properties come at a high price of relatively low conductivity, which significantly lowers the performance and efficiency of potential devices based on the OSC platform, in turn impeding broader use of OSC in real-life applications.⁸⁹

Since OSC belong to the vast family of molecular crystals, a delicate interplay of dispersion, electrostatic, induction and exchange interactions governs their bulk cohesion.^60,90–92 At one hand, the non-covalent character of OSC imparts a massive structural variability, polymorphism and tunability.^4,88 On the other hand, the weaker magnitude of these non-covalent cohesive interactions gives birth to various large-amplitude dynamic degrees of freedom,^93–95 important electron–phonon coupling,^{86,87,94,96,97} and a predominantly adverse variation of the charge-transfer integrals (i. e. electronic coupling) among neighboring molecules in the bulk.^95,98–100 Building upon the first formulation of how the structural disorder traps the charge carriers half a century ago,¹⁰¹ state-of-the art computational methods were extensively used to investigate the impact of dynamic disorder on the overall charge-carrier mobility within OSC over the last two decades.^{86,87,93,94,96,100,102–106}

Still, material development in this field has advanced to an extent that state-of-the-art OSC reach charge-carrier mobilities ranging to orders of magnitude 10⁰–10¹ cm² V⁻¹ s⁻¹, which makes OSC already competitive with amorphous silicon as a typical representative of the conventional inorganic semi-conductor platform.^87,94,96 Further research initiatives related to OSC are naturally oriented at further improvements of their charge-carrier mobilities which still lag 2–3 orders of magnitude behind those observed in crystalline silicon.^88,107 Importantly, material design of better performing OSC is closely linked to understanding disorder in their bulk structures.

Shape of the potential energy surface of a typical molecular material, including also bulk OSC, imparts low frequencies of the intermolecular (lattice) phonon modes, commonly located below 250 cm⁻¹.^{19,87,94,95,108} Relatively shallow potential wells then also enable individual molecules to reach amplitudes around 0.1 Å from their equilibrium positions during those lattice phonon modes at ambient conditions.^93,95 This phenomenon of large amplitudes can be further amplified when the lattice phonon modes exhibit large anharmonicity, leading to broad basins of low potential energy around the equilibrium configuration instead of steep localized potential wells.^35,94

Since these molecular vibrations are faster than the typical rate at which charge carriers travel in OSC, models of dynamic disorder can be associated to explain the impact of electron–phonon coupling in this context.^86,109 In case of high-mobility OSC, charge transport is explained via a Boltzmann band-type mechanism of delocalized electrons with the conductivity being a decreasing function of temperature.¹¹⁰ Large phonon amplitudes distort the Hamiltonian structure, break its symmetry, and finally result in temporary localization of electronic states.⁸⁷ Ab initio sampling of the potential energy surface related to the dynamic degrees of freedom is the key ingredient for assessing the extent of disorder-induced fluctuations of transfer integrals that govern the charge transport rate.⁹⁵ However, not all phonon lattice modes necessarily possess potential to trap the charge carriers and to exhibit that detrimental impact on the charge-carrier mobility.^103,107

Multiple spectroscopic and computational studies have thus focused on identification of particular phonon modes that exhibit the most unfavorable electron–phonon coupling.⁹³ Schweicher et al. introduced a term killer phonon modes for such degrees of freedom that are detrimental for charge transport.⁹⁴ Identification of these killer phonon modes and understanding of their occurrence is a prerequisite for development of chemical and chemical-engineering strategies for design and fine-tuning molecular and bulk structures, preventing novel OSC from exhibiting such killer phonon modes.

Focusing on the killer phonon modes in high-mobility OSC, such as polyaromatic thienoacenes or rubrene, Schweicher et al. established a rigorous computational protocol, based on density functional theory and explicit sampling of the anharmonicity of the potential energy surface.⁹⁴ Killer modes were mapped based on a bi-criterial procedure, considering phonon amplitudes and electron–phonon couplings of individual phonon modes. Product of these parameters then serves for a final assessment and selection of the most detrimental phonon modes.

Results presented for a crystal phase of a particular isomer of dinaphtho-thieno-thiophene (DNTT) reprinted in Fig. 6 clearly indicate that not every low-frequency phonon mode has a detrimental potential for charge transport unless it concurrently exhibits also large electron–phonon coupling. Fig. 6a illustrates a systematic decrease of the vibrational amplitudes σ_q for higher-frequency modes, leading to insignificant electron–phonon coupling for modes above 200 cm⁻¹.⁹⁴ On the other hand, the electron–phonon coupling constants β_c in Fig. 1b are rather scattered, without any obvious dependence on the phonon frequency. Product of these two parameters (having properly accounted for the anisotropy of transfer integrals) then clearly indicate the phonon modes that are able to trap the charge carriers (Fig. 6c). A low-frequency sliding mode at 23 cm⁻¹ that corresponds to long-axis relative displacements of neighboring DNTT molecules in opposite directions (atomic displacements for that mode in Fig. 6d) appears as the largest contributor (45%) towards the dynamic disorder and the most significant dampener of the charge transport in bulk DNTT.⁹⁴ Fig. 6c reveals that there are at least two additional important phonon modes contributing to the adverse impact of the dynamic disorder.

Fig. 6 Electron–phonon coupling maps and identification of phonon modes that are the most detrimental for charge transport in crystalline modes of dinaphtho-thieno-thiophene (DNTT): (a) amplitudes σ_q of zone center phonon modes calculated at the PBE-D3/6–311G(2d,2p) level of theory as a function of phonon wave number ω; (b) mode-resolved non-local electron–phonon coupling constants β_c calculated at the PBE0/def2-SVP basis level of theory; (c) corresponding mode-resolved fluctuation of the transfer integrals σ_c = σ_q β_c; (d) eigenvectors of the most important phonon modes. Adapted from ref. 94, Copyright 2019 the Authors, published by Wiley-VCH GmbH under the terms of the Creative Commons Attribution 4.0 International License.

Note that adopting a multi-potential approach is a common practice in modeling properties of molecular crystals. A cheaper model (here PBE functional) is usually used to optimize the crystal geometry and to model the phonons, whereas a more sophisticate model (here hybrid PBE0 functional) is then used on such optimized geometries to refine other electron-structure properties.^4,13,58 Performing the phonon calculations with a more sophisticate hybrid DFT functional (such as PBE0) would be extremely costly, most likely not imparting that massive accuracy improvements.¹¹¹ On the other hand, subtle features of the electron structure or molecular interactions are highly sensitive on the quality of the underlying DFT functional with low-tier generalized-gradient approximation (GGA) functionals exhibiting severe flaws,⁶² so it is worth the effort to model those as accurately as possible.

Equipped with such a predictive protocol, further studies formulating strategies how to suppress such killer phonon modes have emerged. Schweicher et al. contributed to this initiative with a detailed discussion of the impact of extended alkylation of the active molecular core on charge transport properties.⁹⁴ Presence of long alkyl chains itself augments the number of phonon modes, which are nevertheless relatively harmless to most charge-transfer integrals, often also blue-shifting the frequencies of important sliding modes. Still, the total extent of the dynamic disorder imparted by alkylation is so large that it cancels out a significant portion of the possible charge-carrier mobility gain due to beneficial constellations of charge-transfer integrals in alkylated species.⁹⁴

Schweicher et al. then conclude that mutual intermolecular shifts in a bulk material at equilibrium determine both the set of relevant charge-transfer integrals and their dependence on the long-axis sliding coordinate. Subtle chemical-engineering of the side chains, its branching, substitution and incorporation of additional active sites will affect mutual orientation of molecules in the bulk, including also their mutual tilt angle, all impacting the resulting charge transport characteristics.⁹⁴

Following the same motivation to improve the charge-carrier mobility via suppressing the dynamic disorder in crystalline OSC, Sosorev et al. aimed at enforcing a more beneficial packing motif of several families of molecular crystals. A series of recent studies exploiting Raman spectroscopy and first-principles modelling presents Raman spectra and electron–phonon coupling in crystalline benzothieno-benzothiophenes (BTBT),¹⁰⁵ bisphenyl-bisthiophenes (PTTP)¹⁰⁸ or naphthalene diimides.¹¹²

Fig. 7a reprints a schematic tutorial of relationships between the dynamic disorder and signals in Raman spectra of selected solid OSC in the low-frequency region.¹⁰⁵ Unsubstituted PTTP exhibits a rather uniform distribution of the electrostatic potential with only vague maxima at its phenyl termini (Fig. 7b).¹⁰⁸ That favors a layered herringbone packing motif of PTTP crystals dominated by weak dispersion interactions, where each molecule has a long face-to-edge contact with its closest neighbor, but minimum contact areas with other proximate molecules in the remaining directions (Fig. 7c). Both theory and experiment proved that this arrangement imparts a low-frequency phonon at 30 cm⁻¹ with a massive Raman intensity,¹⁰⁸ which corresponds to a libration mode around the short molecular axis of PTTP as depicted in Fig. 7d. Sosorev et al. performed subsequent quantum-chemical calculations of the electron–phonon coupling which revealed a similar character of that particular libration mode to the above mentioned killer modes.¹⁰⁸

Fig. 7 Schematic illustration of the dynamic disorder assessed via Raman spectroscopy in the low-frequency region: a) room-temperature Raman spectrum for a representative of benzothieno-benzothiophenes (BTBT), reproduced with permission from ref. 105, Copyright 2021 Royal Society of Chemistry; b) molecular electrostatic potentials around a representative of bisphenyl-bisthiophene core (PTTP, left) and its bismethoxy derivative (MeO-PTTP-MeO, right);¹⁰⁸ c) unit cells of crystalline PTTP and MeO-PTTP-MeO exhibiting layered and brickwall motifs, respectively;¹⁰⁸ d) Raman intensities of low-frequency phonon modes calculated for crystalline PTTP and MeO-PTTP-MeO at the PBE-D3/6-31G** level of theory with an inset representation of the most intense libration mode of PTTP.¹⁰⁸ Parts b–d) adapted with permission from ref. 108, Copyright 2023 American Chemical Society.

Incorporation of electron-withdrawing or electron-donating moieties in the molecules active as OSC surely alters the map of molecular electrostatic potentials. Fig. 7b depicts how presence of methoxy moieties imparts important minima and maxima of molecular electrostatic potential of substituted MeO-PTTP-MeO.¹⁰⁸ That largely fortifies the capability of such molecule for stronger electrostatic interactions and enables a brickwall packing motif of MeO-PTTP-MeO crystals. Sosorev et al. found that the importance of the packing change is twofold. Unlike unsubstituted PTTP, each MeO-PTTP-MeO molecule experiences sufficiently large contact areas with its multiple neighbors in the crystal lattice, which opens a two-dimensional network for charge transport. In addition, stronger interactions of MeO-PTTP-MeO blue-shift frequencies of their lattice modes which propagates to a generally lower extent of dynamic disorder.¹⁰⁸

Sosorev et al. conclude that in addition to the sliding phonon modes, there can be also other dynamic degrees of freedom with detrimental potential for charge transport, such as large-amplitude low-frequency libration modes when molecules are packed in layers.¹⁰⁸ Adverse effects of these librations can be erased by a suitable chemical substitution that alters the electrostatic potential map, fortifies molecular interactions in the crystal lattice, enforces a different crystal packing, and finally reduces dynamic disorder of such crystals. There are also additional reports justifying the multidimensional charge-transport topology in brick-wall packed crystals more resistant to detrimental disorder effects.⁹⁸

In order not to draw overgeneralized conclusions, the complexity of dynamic disorder and its impact on OSC performance can be illustrated with a recent very detailed study by Vong et al.,¹¹³ addressing the hole mobility in crystalline OSC with state-of-the-art experimental and computational methods. Since vibrational optical spectroscopies including Raman and infrared are inherently limited by the optical selection rules to observe some phonon modes, furthermore being capable to detect Γ-point phonons only, inelastic neutron scattering is a superior approach to detect phonon dispersion over the entire Brillouin zone. Since the low-frequency lattice phonon modes are typically prone to large dispersion effects, sampling the entire Brillouin zone can have an important impact on modeling the dynamic disorder in bulk OSC as well.¹¹³ Concurrently, performing cheaper and more straightforward phonon calculations at the Γ-point only can lead to significant loss of information, and thus, to distorting the actual extent of the dynamic disorder, as argued by Vong et al.¹¹³

Having performed extensive inelastic neutron scattering experiments and expensive periodic DFT calculations of phonon dispersion for a set of archetypal OSC, Vong et al. were able to establish a benchmark of the accuracy of the electron–phonon coupling and thence resulting hole mobilities that rely either on Γ-point phonons only, or explicitly assume the phonon dispersion.¹¹³ Based on a set of six archetypal OSC, the non-local disorder coefficient σ was shown to differ by 12% when the full phonon dispersion was accounted for (with a predominant increase of the total disorder).¹¹³ That propagates to a prevailing decrease of the hole mobility when the phonon dispersion is included. Also, with the exception of rubrene, assuming the full phonon dispersion leads to more accurate hole mobilities.¹¹³

Fig. 8 reprints the computational results on hole mobilities in crystalline BTBT.¹¹³ Such a detailed investigation accounting properly for the phonon dispersion reveals that there is not only a single phonon killer mode in BTBT systems, but multiple translation, flexing and twisting modes contribute to a similar extent to the total disorder coefficient. Eigenvectors of these detrimental phonon modes depicted in Fig. 8a also indicate that the presence of heteroatoms, such as sulphur in BTBT, does not necessarily lead to beneficial electron–phonon coupling. Due to the relative weakness of the covalent C–S bonds, sulphur atoms can exhibit large vibration amplitudes in BTBT crystals.¹¹³ On the other, hand Vong et al. confirm that suitable substitution (here alkylation) leads to a more rigid locking of the active molecular cores, to blue shifts of the respective phonon modes, and thus to lower amplitudes of the sulphur atoms (Fig. 8b). An analysis of the spectral density of electron–phonon coupling, rigorously obtained assuming the phonon dispersion, amplitudes of individual phonon modes, and electronic structure of the solid enables to identify all the possible adverse phonon modes (Fig. 8c).¹¹³

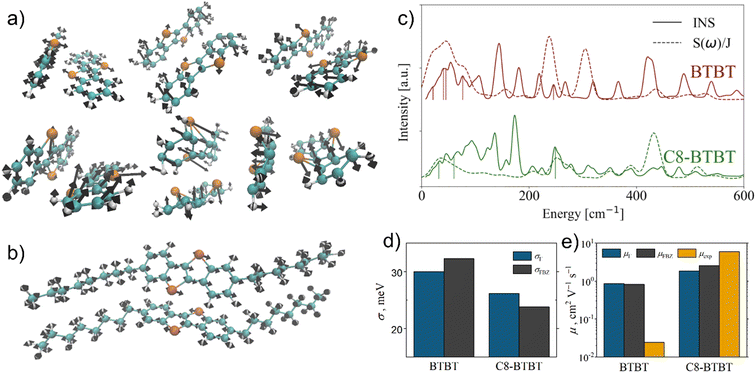Fig. 8 Overview of charge transport in crystalline benzothieno-benzothiophene (BTBT):¹¹³ a) phonon modes identified to be the most detrimental in unsubstituted BTBT, eigenvectors shown on the two molecules included in the primitive unit cell; b) the lowest-frequency phonon mode with large contribution to disorder in alkylated C8-BTBT; c) normalized spectral density of electron–phonon coupling S(ω)/J overlaid with respective inelastic neutron scattering spectrum (INS) for BTBT and C8-BTBT, vertical lines indicate selected detrimental phonon modes shown in a and b); d) non-local dynamic disorder calculated in ref. 113 using Γ-point phonons only (σ_Γ) or phonon dispersion over the entire Brillouin zone (σ_FBZ); e) comparison of hole mobilities calculated ref. 113 using the two phonon models (μ_Γ and μ_FBZ) with experimental values.¹¹³ Parts a–c) adapted with permission from ref. 113, Copyright 2022 American Chemical Society.

Finally, Fig. 8d shows that assuming the full phonon dispersion leads to a more significant drop of the total disorder in alkylated C8-BTBT than in unsubstituted BTBT, which in turn propagates to more accurate predictions of hole mobilities when the full dispersion model is used (Fig. 8e). Note that the reported experimental hole mobility for BTBT is distorted by its too large contact resistance.¹¹³ Without that knowledge, using this experimental value as a proper reference could result in severe misinterpretations of the computational performance, which also illustrates the need for using low-uncertainty reference data for benchmarking of first-principles computational methodologies.

Vong et al. conclude that it is important not only to develop rapid methods for screening of OSC properties and of the performance of novel theoretical materials. One should also pay attention to subtle phenomena, such as phonon dispersion that may appear at the first sight as minor corrections to the overall disorder, but their real significance becomes obvious only after careful extensive benchmarking and adoption of state-of-the-art methods.¹¹³

Furthermore, there is another very recent study adopting finite-displacement Boltzmann transport theory to reveal also multiple high-frequency intramolecular ring-breathing phonon modes in tetracene as the most detrimental factors reducing charge-carrier mobility.¹¹⁴ Omitting the high-frequency region thus can cause severe misinterpretations of charge transport phenomena in some cases.

Interestingly, such an adverse impact of the dynamic disorder on charge-carrier mobility is not ubiquitous in OSC. In low-mobility OSC, such as merocyanine derivatives with larger band gaps, charge transport has to rely on a hopping mechanism.¹⁰⁰ Holes or electrons then transit between states localized at neighboring molecules in the bulk structure with a certain limited rate. Merocyanine crystals adopt either a columnar packing motif predominantly limiting the hole hopping to one-dimensional intracolumnar channels, or brick-wall packing which allows for a multi-dimensional charge-transfer topologies.¹¹⁵

Existence of suitable phonon modes in such low-mobility OSC may significantly improve this hopping rate, and thus also the charge-carrier mobility.⁹⁵ Gildemeister et al. investigated the impact of dynamic disorder on charge transport in multiple materials based on the merocyanine platform.¹⁰⁰ Fig. 9a and b shows molecular and crystal structure of a merocyanine species, containing an indole-based donor unit and a cyanated thiazole acceptor unit, packed in displaced π–π stacked layers forming columnar dimers that enable the most efficient hole hopping (Fig. 9c).¹⁰⁰

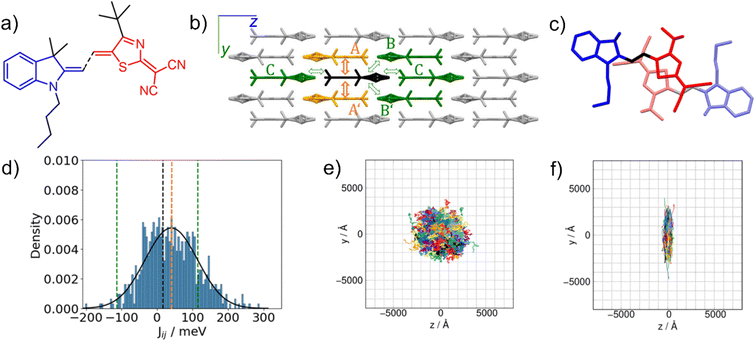Fig. 9 Modelling the hopping rate of holes in a merocyanine derivative composed of a butylated donor unit and tert-butylated acceptor unit denoted nbu,tbu-D2A1: a) molecular structure; b) schematic view of the crystal structure with the most significant hole transport channels; c) an intracolumnar dimer labelled A; d) thermalized distribution of the transfer integral J_ij relevant for hole hopping within the dimer A; e) hole trajectories in a three-dimensional hopping topology simulated in 1000 kinetic Monte Carlo simulations neglecting the disorder; f) hole trajectories simulated assuming the dynamic disorder related to dimer A. Adapted with permission from ref. 100, Copyright 2024 the Authors, published by Royal Society of Chemistry under the terms of the Creative Commons Attribution 3.0 Unported License.

Assuming a static crystal structure, Gildemeister et al. quantified the transfer integral J_ij relevant for hole hopping within the most important columnar dimer to be only 16 meV using the ωB97X-D/6-311G** level of theory.¹⁰⁰ However, performing a classical molecular-dynamics simulation to sample the thermal motion of molecules in the crystal, and subsequent quantum-chemical calculations using the ZINDO/S method revealed the width of J_ij distribution due to thermal motion. Fig. 9d reprints the results of Gildemeister et al. showing that the mean value of thermalized J_ij is more than doubled when compared to the static crystal model.¹⁰⁰ Such an increase largely augments (by a factor of 12) also the simulated hole hopping rate in the intracolumnar direction defined by the respective merocyanine dimer. It is not surprising then that when such a beneficial impact of the dynamic disorder on hole hopping is assumed in only one direction, the charge-transport will respond in changing from the nearly isotropic three-dimensional (disorder neglected) to strictly one-dimensionally oriented, as illustrated in Fig. 9e and f by hole trajectories obtained from kinetic Monte Carlo simulations.¹⁰⁰

In addition to the dynamic disorder, there is also an option of the nuclear motions being appreciably slower than those of the charge carriers, leading to a static character of the disorder.⁸⁶ Variations of local electrostatic and induction interactions also shift energy levels of the charge carriers in OSC which affect the site energy distribution that impacts in turn the charge-carrier mobility. The static energetic disorder generally has a detrimental impact on the charge transport in organic semiconductors,^87,100,106 especially when manufactured in thin layers.⁹⁶

5. Discussion

Note that in the context of OSC, mere thermal oscillations of atoms around their equilibrium positions in the bulk structure are considered as a disorder source due to the high sensitivity of any electronic properties to subtle crystal-structure variations. Concerning API or other types of molecular crystals, however, existence of distinct configurations of the unit cell, or crystal archetypes that can continuously and rapidly transit one to another is required to label a general molecular crystal to be dynamically disordered.

There is, however, a clear link interconnecting the highlighted efforts in all three application fields. The ability to assess the atomic amplitudes due to individual phonon modes and to sample related potential energy surfaces is crucial to understand material properties, either thermodynamic or optoelectronic. Performing first-principles calculations of phonon dispersion is very expensive for complex crystals of large molecules, but it can prove worth the effort when polymorphism, massive anisotropy of the crystal and its inner dynamics occur. In those cases, relying only on the cheaper calculations of Γ-point phonon frequencies (or equivalently too small supercells) may correspond to discarding important pieces of information about the inner dynamics within the material, which can in turn lead to computational misinterpretations. Provided that material behavior is governed not only by its lattice phonon modes, but also by stiffer intramolecular modes related to conformations of cyclic molecular segments, one should pay attention to significantly broader ranges of phonon spectra.

All these considerations should obviously turn one's attention to the questions of feasibility and applicability limits of the underlying fist-principles calculations. For an efficient computational protocol, a multi-potential approach seems as a reasonable or even inevitable choice. Cheaper methods (semi-empiric DFTB or low-tier DFT) suitable for optimizing geometries and calculating phonons of large numbers of crystal archetypes or disorder components can be combined with more accurate methods (hybrid DFT or ab initio wavefunction theories) focusing on refinements of the electron structure, molecular interactions or other specific related properties that can be derived from modeling smaller clusters of molecules extracted from the periodic crystal structure.

6. Conclusion

Current article highlighted the significance of dynamic disorder in molecular crystals across various application areas. Computational strategies and their recent achievements were pointed out in the context of barocaloric materials for heat management, active pharmaceutical ingredients and organic semiconductors. While the dynamic disorder can be actively sought and promoted by research for certain applications (barocalorics), it can present additional risk factors in development and approval process (API), or even be a completely detrimental phenomenon that needs to be largely suppressed (high-conductivity OSC). Computational methods addressing phonons and conformational dynamics in the solid state, relying either on classical molecular-dynamics, or on quantum-chemical DFTB or even DFT theories, have matured to a state that their results nicely complement experimental findings. Computations then usually enable to focus and interpret potential energy surfaces related to internal dynamic degrees of freedom, to assess related atomic amplitudes, and to separate contribution from individual functional group and molecular segments to the total dynamic disorder in molecular crystals at finite temperatures. Such a state of the art indeed renders computational chemistry extremely important in material design in various fields. Despite this optimistic perspective, future development of computational methods needs to focus on extending the computational affordability and feasibility of first-principles modelling of the dynamics to significantly larger systems that frequently arise in real API or OSC applications. Finally, an interdisciplinary approach, including diverse computational, crystallographic, spectroscopic and calorimetric techniques is important to tackle polymorphism and dynamic disorder, especially when gradual order–disorder phase transitions take place, as a complete understanding of these phenomena may require observations at various time-scales and spatial resolutions.

Data availability

No primary research results, software or code have been included and no new data were generated or analyzed as part of this review.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

C. Č. acknowledges financial support from the Czech Science Foundation (GACR No. 23-05476M).

References

1. L. M. Hunnisett, N. Francia, J. Nyman, N. S. Abraham, S. Aitipamula, T. Alkhidir, M. Almehairbi, A. Anelli, D. M. Anstine, J. E. Anthony, J. E. Arnold, F. Bahrami, M. A. Bellucci, G. J. O. Beran, R. M. Bhardwaj, R. Bianco, J. A. Bis, A. D. Boese, J. Bramley, D. E. Braun, P. W. V. Butler, J. Cadden, S. Carino, C. Cervinka, E. J. Chan, C. Chang, S. M. Clarke, S. J. Coles, C. J. Cook, R. I. Cooper, T. Darden, G. M. Day, W. Deng, H. Dietrich, A. DiPasquale, B. Dhokale, B. P. van Eijck, M. R. J. Elsegood, D. Firaha, W. Fu, K. Fukuzawa, N. Galanakis, H. Goto, C. Greenwell, R. Guo, J. Harter, J. Helfferich, J. Hoja, J. Hone, R. Hong, M. Husak, Y. Ikabata, O. Isayev, O. Ishaque, V. Jain, Y. Jin, A. Jing, E. R. Johnson, I. Jones, K. V. J. Jose, E. A. Kabova, A. Keates, P. F. Kelly, J. Klimes, V. Kostkova, H. Li, X. Lin, A. List, C. Liu, Y. M. Liu, Z. Liu, I. Loncaric, J. W. Lubach, J. Ludik, N. Marom, H. Matsui, A. Mattei, R. A. Mayo, J. W. Melkumov, B. Mladineo, S. Mohamed, Z. Momenzadeh Abardeh, H. S. Muddana, N. Nakayama, K. S. Nayal, M. A. Neumann, R. Nikhar, S. Obata, D. O'Connor, A. R. Oganov, K. Okuwaki, A. Otero-de-la-Roza, S. Parkin, A. Parunov, R. Podeszwa, A. J. A. Price, L. S. Price, S. L. Price, M. R. Probert, A. Pulido, G. R. Ramteke, A. U. Rehman, S. M. Reutzel-Edens, J. Rogal, M. J. Ross, A. F. Rumson, G. Sadiq, Z. M. Saeed, A. Salimi, K. Sasikumar, S. Sekharan, K. Shankland, B. Shi, X. Shi, K. Shinohara, A. G. Skillman, H. Song, N. Strasser, J. van de Streek, I. J. Sugden, G. Sun, K. Szalewicz, L. Tan, K. Tang, F. Tarczynski, C. R. Taylor, A. Tkatchenko, R. Tom, P. Tous, M. E. Tuckerman, P. A. Unzueta, Y. Utsumi, L. Vogt-Maranto, J. Weatherston, L. J. Wilkinson, R. D. Willacy, L. Wojtas, G. R. Woollam, Y. Yang, Z. Yang, E. Yonemochi, X. Yue, Q. Zeng, T. Zhou, Y. Zhou, R. Zubatyuk and J. C. Cole, Acta Crystallogr., Sect. B: Struct. Sci., 2024, 80, 548–574.
2. L. M. Hunnisett, J. Nyman, N. Francia, N. S. Abraham, C. S. Adjiman, S. Aitipamula, T. Alkhidir, M. Almehairbi, A. Anelli, D. M. Anstine, J. E. Anthony, J. E. Arnold, F. Bahrami, M. A. Bellucci, R. M. Bhardwaj, I. Bier, J. A. Bis, A. D. Boese, D. H. Bowskill, J. Bramley, J. G. Brandenburg, D. E. Braun, P. W. V. Butler, J. Cadden, S. Carino, E. J. Chan, C. Chang, B. Cheng, S. M. Clarke, S. J. Coles, R. I. Cooper, R. Couch, R. Cuadrado, T. Darden, G. M. Day, H. Dietrich, Y. Ding, A. DiPasquale, B. Dhokale, B. P. van Eijck, M. R. J. Elsegood, D. Firaha, W. Fu, K. Fukuzawa, J. Glover, H. Goto, C. Greenwell, R. Guo, J. Harter, J. Helfferich, D. W. M. Hofmann, J. Hoja, J. Hone, R. Hong, G. Hutchison, Y. Ikabata, O. Isayev, O. Ishaque, V. Jain, Y. Jin, A. Jing, E. R. Johnson, I. Jones, K. V. J. Jose, E. A. Kabova, A. Keates, P. F. Kelly, D. Khakimov, S. Konstantinopoulos, L. N. Kuleshova, H. Li, X. Lin, A. List, C. Liu, Y. M. Liu, Z. Liu, Z.-P. Liu, J. W. Lubach, N. Marom, A. A. Maryewski, H. Matsui, A. Mattei, R. A. Mayo, J. W. Melkumov, S. Mohamed, Z. Momenzadeh Abardeh, H. S. Muddana, N. Nakayama, K. S. Nayal, M. A. Neumann, R. Nikhar, S. Obata, D. O'Connor, A. R. Oganov, K. Okuwaki, A. Otero-de-la-Roza, C. C. Pantelides, S. Parkin, C. J. Pickard, L. Pilia, T. Pivina, R. Podeszwa, A. J. A. Price, L. S. Price, S. L. Price, M. R. Probert, A. Pulido, G. R. Ramteke, A. U. Rehman, S. M. Reutzel-Edens, J. Rogal, M. J. Ross, A. F. Rumson, G. Sadiq, Z. M. Saeed, A. Salimi, M. Salvalaglio, L. Sanders de Almada, K. Sasikumar, S. Sekharan, C. Shang, K. Shankland, K. Shinohara, B. Shi, X. Shi, A. G. Skillman, H. Song, N. Strasser, J. van de Streek, I. J. Sugden, G. Sun, K. Szalewicz, B. I. Tan, L. Tan, F. Tarczynski, C. R. Taylor, A. Tkatchenko, R. Tom, M. E. Tuckerman, Y. Utsumi, L. Vogt-Maranto, J. Weatherston, L. J. Wilkinson, R. D. Willacy, L. Wojtas, G. R. Woollam, Z. Yang, E. Yonemochi, X. Yue, Q. Zeng, Y. Zhang, T. Zhou, Y. Zhou, R. Zubatyuk and J. C. Cole, Acta Crystallogr., Sect. B: Struct. Sci., 2024, 80, 517–547.
3. G. J. O. Beran, Chem. Sci., 2023, 14, 13290–13312.
4. G. J. O. Beran, Chem. Rev., 2016, 116, 5567–5613.
5. C. Červinka, M. Fulem and K. Růžička, J. Chem. Phys., 2016, 144, 064505.
6. J. Yang, W. Hu, D. Usvyat, D. Matthews, M. Schütz and G. K.-L. Chan, Science, 2014, 345, 640–643.
7. J. Klimeš, J. Chem. Phys., 2016, 145, 094506.
8. J. Moellmann and S. Grimme, J. Phys. Chem. C, 2014, 118, 7615–7621.
9. K. N. Pham, M. Modrzejewski and J. Klimeš, J. Chem. Phys., 2023, 158, 144119.
10. J. D. Hartman, G. M. Day and G. J. O. Beran, Cryst. Growth Des., 2016, 16, 6479–6493.
11. S. Hirata, K. Gilliard, X. He, J. Li and O. Sode, Acc. Chem. Res., 2014, 47, 2721–2730.
12. C. Cook and G. J. O. Beran, J. Chem. Phys., 2020, 153, 224105.
13. C. Červinka and G. J. O. Beran, Chem. Sci., 2018, 9, 4622–4629.
14. J. L. McKinley and G. J. O. Beran, Faraday Discuss., 2018, 211, 181–207.
15. J. Hoja, A. M. Reilly and A. Tkatchenko, WIREs Comput. Mol. Sci., 2017, 7, e1294.
16. R. P. Stoffel, C. Wessel, M.-W. Lumey and R. Dronskowski, Angew. Chem., Int. Ed., 2010, 49, 5242–5266.
17. A. M. Reilly and A. Tkatchenko, J. Chem. Phys., 2013, 139, 024705.
18. G. A. Dolgonos, J. Hoja and A. D. Boese, Phys. Chem. Chem. Phys., 2019, 21, 24333–24344.
19. C. Červinka, M. Fulem, R. P. Stoffel and R. Dronskowski, J. Chem. Phys., 2016, 120, 2022–2034.
20. J. Ludík, V. Kostková, Š. Kocian, P. Touš, V. Štejfa and C. Červinka, J. Chem. Theory Comput., 2024, 20, 2858–2870.
21. J. George, V. L. Deringer, A. Wang, P. Müller, U. Englert and R. Dronskowski, J. Chem. Phys., 2016, 145, 234512.
22. J. Nyman and G. M. Day, Phys. Chem. Chem. Phys., 2016, 18, 31132–31143.
23. E. Shalaev, K. Wu, S. Shamblin, J. F. Krzyzaniak and M. Descamps, Adv. Drug Delivery Rev., 2016, 100, 194–211.
24. S. Das, A. Mondal and C. M. Reddy, Chem. Soc. Rev., 2020, 49, 8878–8896.
25. B. Dittrich, L. E. Connor, F. P. A. Fabbiani and P. Piechon, IUCrJ, 2024, 11, 347–358.
26. B. Dittrich, IUCrJ, 2021, 8, 305–318.
27. W. Press and A. Huller, Acta Crystallogr., Sect. A, 1973, 29, 252–256.
28. J. Hulliger, K. Brahimi, M. Burgener and G. Dulcevscaia, J. Mol. Struct., 2014, 1078, 20–25.
29. J. Timmermans, J. Phys. Chem. Solids, 1961, 18, 1–8.
30. J. Iyer, M. Brunsteiner, D. Modhave and A. Paudel, J. Pharm. Sci., 2023, 112, 1539–1565.
31. M. Zeng, C. Escorihuela-Sayalero, T. Ikeshoji, S. Takagi, S. Kim, S. I. Orimo, M. Barrio, J. L. Tamarit, P. Lloveras, C. Cazorla and K. Sau, Adv. Sci., 2024, 11, 2306488.
32. J. C. M. Madrid and K. K. Ghuman, Adv. Phys.: X, 2021, 6, 1848458.
33. P. R. Spackman, IUCrJ, 2024, 11, 275–276.
34. M. Habgood, R. Grau-Crespo and S. L. Price, Phys. Chem. Chem. Phys., 2011, 13, 9590–9600.
35. P. Touš and C. Červinka, Cryst. Growth Des., 2023, 23, 4082–4097.
36. C. Červinka, V. Štejfa, V. Pokorný, P. Touš and K. Růžička, Cryst. Growth Des., 2023, 23, 9011–9024.
37. P. Hodgkinson, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 118–119, 10–53.
38. E. Chaloupecká, V. Tyrpekl, K. Bártová, Y. Nishiyama and M. Dračínský, Solid State Nucl. Magn. Reson., 2024, 130, 101921.
39. Q. Li, A. D. Bond, T. M. Korter and J. A. Zeitler, Mol. Pharmaceutics, 2022, 19, 227–234.
40. A. B. Bazyleva, A. V. Blolchin, G. J. Kabo, A. G. Kabo and Y. U. Paulechka, J. Chem. Thermodyn., 2005, 37, 643–657.
41. E. O. R. Beake, M. G. Tucker, M. T. Dove and A. E. Phillips, ChemPhysChem, 2017, 18, 459–464.
42. B. E. Meijer, R. J. C. Dixey, F. Demmel, R. Perry, H. C. Walker and A. E. Phillips, Phys. Chem. Chem. Phys., 2023, 25, 9282–9293.
43. D. Szewczyk, J. F. Gebbia, A. Jezowski, A. I. Krivchikov, T. Guidi, C. Cazorla and J. L. Tamarit, Sci. Rep., 2021, 11, 18640.
44. M. A. White, R. E. Wasylishen, P. E. Eaton, Y. H. Xiong, K. Pramod and N. Nodari, J. Phys. Chem., 1992, 96, 421–425.
45. T. Yildirim, P. M. Gehring, D. A. Neumann, P. E. Eaton and T. Emrick, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 314–321.
46. R. Sandrock and G. M. Schneider, Ber. Bunsenges. Phys. Chem., 1983, 87, 197–201.
47. S. Pekker, É. Kováts, G. Oszlányi, G. Bényei, G. Klupp, G. Bortel, I. Jalsovszky, E. Jakab, F. Borondics, K. Kamarás, M. Bokor, G. Kriza, K. Tompa and G. Faigel, Nat. Mater., 2005, 4, 764–767.
48. J. Ye, M. Barrio, R. Céolin, N. Qureshi, P. Negrier, I. B. Rietveld and J. L. Tamarit, CrystEngComm, 2019, 21, 1180–1185.
49. N. A. Murugan, J. Phys. Chem. B, 2005, 109, 23955–23962.
50. J. Pfaendtner, X. Yu and L. J. Broadbelt, Theor. Chem. Acc., 2007, 118, 881–898.
51. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122.
52. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
53. E. R. Johnson, in Non-Covalent Interactions in Quantum Chemistry and Physics, ed. A. Otero de la Roza and G. A. DiLabio, Elsevier, 2017, pp. 169–194,  DOI:10.1016/B978-0-12-809835-6.00006-2.
54. J. G. Brandenburg, J. Potticary, H. A. Sparkes, S. L. Price and S. R. Hall, J. Phys. Chem. Lett., 2017, 8, 4319–4324.
55. M. T. Ruggiero, J. A. Zeitler and A. Erba, Chem. Commun., 2017, 53, 3781–3784.
56. E. J. Blancas, Á. Lobato, F. Izquierdo-Ruiz, A. M. Márquez, J. M. Recio, P. Nath, J. J. Plata and A. Otero-de-la-Roza, npj Comput. Mater., 2024, 10, 267.
57. A. Heyden, A. T. Bell and F. J. Keil, J. Chem. Phys., 2005, 123, 224101.
58. J. Hoja, A. List and A. D. Boese, J. Chem. Theory Comput., 2024, 20, 357–367.
59. C. Červinka and M. Fulem, J. Chem. Theory Comput., 2017, 13, 2840–2850.
60. V. Pokorný, P. Touš, V. Štejfa, K. Růžička, J. Rohlíček, J. Czernek, J. Brus and C. Červinka, Phys. Chem. Chem. Phys., 2022, 24, 25904–25917.
61. G. J. O. Beran, J. D. Hartman and Y. N. Heit, Acc. Chem. Res., 2016, 49, 2501–2508.
62. K. R. Bryenton, A. A. Adeleke, S. G. Dale and E. R. Johnson, WIREs Comput. Mol. Sci., 2023, 13, e1631.
63. C. Červinka, M. Fulem and K. Růžička, J. Chem. Eng. Data, 2013, 58, 1382–1390.
64. K. Irikura and D. J. Frurip, Computational Thermochemistry: Prediction and Estimation of Molecular Thermodynamics, American Chemical Society, Washington, DC, 1998.
65. A. Aznar, P. Negrier, A. Planes, L. Mañosa, E. Stern-Taulats, X. Moya, M. Barrio, J.-L. Tamarit and P. Lloveras, Appl. Mater. Today, 2021, 23, 101023.
66. A. Salvatori, P. Negrier, A. Aznar, M. Barrio, J. L. Tamarit and P. Lloveras, APL Mater., 2022, 10, 111117.
67. P. M. J. Szell, S. P. Brown, L. P. Hughes, H. Blade and S. O. N. Lill, Chem. Commun., 2020, 56, 14039–14042.
68. G. J. O. Beran, I. J. Sugden, C. Greenwell, D. H. Bowskill, C. C. Pantelides and C. S. Adjiman, Chem. Sci., 2022, 13, 1288–1297.
69. M. Dhaval, K. Dudhat, M. Soniwala, A. Dudhrejiya, S. Shah and B. Prajapati, Mater. Today Commun., 2023, 37, 107411.
70. J. Iyer, M. Barbosa, J. F. Pinto and A. Paudel, J. Pharm. Sci., 2025, 114, 599–616.
71. P. Kanaujia, P. Poovizhi, W. K. Ng and R. B. H. Tan, Powder Technol., 2015, 285, 2–15.
72. V. Erastova, I. R. Evans, W. N. Glossop, S. Guryel, P. Hodgkinson, H. E. Kerr, V. S. Oganesyan, L. K. Softley, H. M. Wickins and M. R. Wilson, J. Am. Chem. Soc., 2024, 18360–18369,  DOI:10.1021/jacs.4c03246.
73. S. Yoshioka and Y. Aso, J. Pharm. Sci., 2007, 96, 960–981.
74. P. M. J. Szell, J. R. Lewandowski, H. Blade, L. P. Hughes, S. O. Nilsson Lill and S. P. Brown, CrystEngComm, 2021, 23, 6859–6870.
75. J. Brus, J. Czernek, M. Urbanova and C. Červinka, Molecules, 2022, 27, 679.
76. C. Golz and A. Krawczuk, Cryst. Growth Des., 2023, 23, 7504–7516.
77. P. M. J. Szell, Z. Rehman, B. Tatman, L. P. Hughes, H. Blade and S. P. Brown, ChemPhysChem, 2023, 24, e202200558.
78. L. Szeleszczuk, K. Bethanis, E. Christoforides and D. M. Pisklak, CrystEngComm, 2024, 27, 433–446.
79. A. J. Al-Ani, P. M. J. Szell, Z. Rehman, H. Blade, H. P. Wheatcroft, L. P. Hughes, S. P. Brown and C. C. Wilson, Cryst. Growth Des., 2022, 22, 4696–4707.
80. T. Pawlak, I. Sudgen, G. Bujacz, D. Iuga, S. P. Brown and M. J. Potrzebowski, Cryst. Growth Des., 2021, 21, 3328–3343.
81. J. A. Chisholm and S. Motherwell, J. Appl. Crystallogr., 2005, 38, 228–231.
82. M. Habgood, I. J. Sugden, A. V. Kazantsev, C. S. Adjiman and C. C. Pantelides, J. Chem. Theory Comput., 2015, 11, 1957–1969.
83. A. Ambrosetti, A. M. Reilly, R. A. DiStasio Jr. and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508.
84. R. G. Simões, C. E. S. Bernardes, A. Joseph, M. F. M. Piedade, W. Kraus, F. Emmerling, H. P. Diogo and M. E. Minas da Piedade, Mol. Pharmaceutics, 2018, 15, 5349–5360.
85. J. Granifo, M. Westermeyer, M. Riquelme, R. Gavino, S. Suarez, E. B. Halac and R. Baggio, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 805–813.
86. D. P. McMahon and A. Troisi, ChemPhysChem, 2010, 11, 2067–2074.
87. H. Ishii, N. Kobayashi and K. Hirose, Jpn. J. Appl. Phys., 2019, 58, 110501.
88. G. Schweicher, G. Garbay, R. Jouclas, F. Vibert, F. Devaux and Y. H. Geerts, Adv. Mater., 2020, 32, 1905909.
89. C. Wang, H. Dong, W. Hu, Y. Liu and D. Zhu, Chem. Rev., 2012, 112, 2208–2267.
90. L. M. LeBlanc, J. A. Weatherby, A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Theory Comput., 2018, 14, 5715–5724.
91. G. Saleh, C. Gatti, L. Lo Presti and J. Contreras-García, Chem. – Eur. J., 2012, 18, 15523–15536.
92. G. J. O. Beran, Y. N. Heit and J. D. Hartman, in Non-Covalent Interactions in Quantum Chemistry and Physics, ed. A. Otero de la Roza and G. A. DiLabio, Elsevier, 2017, pp. 303–331,  DOI:10.1016/B978-0-12-809835-6.00012-8.
93. S. Illig, A. S. Eggeman, A. Troisi, L. Jiang, C. Warwick, M. Nikolka, G. Schweicher, S. G. Yeates, Y. H. Geerts, J. E. Anthony and H. Sirringhaus, Nat. Commun., 2016, 7, 10736.
94. G. Schweicher, G. D'Avino, M. T. Ruggiero, D. J. Harkin, K. Broch, D. Venkateshvaran, G. M. Liu, A. Richard, C. Ruzié, J. Armstrong, A. R. Kennedy, K. Shankland, K. Takimiya, Y. H. Geerts, J. A. Zeitler, S. Fratini and H. Sirringhaus, Adv. Mater., 2019, 31, 1902407.
95. Z. J. Knepp and L. A. Fredin, J. Phys. Chem. A, 2022, 126, 3265–3272.
96. T. Vehoff, B. Baumeier, A. Troisi and D. Andrienko, J. Am. Chem. Soc., 2010, 132, 11702–11708.
97. L. A. Agapito and M. Bernardi, Phys. Rev. B, 2018, 97, 235146.
98. L. J. Wang, Q. K. Li, Z. G. Shuai, L. P. Chen and Q. Shi, Phys. Chem. Chem. Phys., 2010, 12, 3309–3314.
99. S. Fratini, D. Mayou and S. Ciuchi, Adv. Funct. Mater., 2016, 26, 2292–2315.
100. N. Gildemeister, S. Geller, R. Herzhoff, F. Negri, K. Meerholz and D. Fazzi, Mater. Adv., 2024, 5, 8475–8489.
101. J. Sworakowski, Mol. Cryst. Liq. Cryst., 1976, 33, 83–89.
102. S. W. Birch and K. P. Pipe, J. Appl. Phys., 2022, 131, 135104.
103. T. Nematiaram and A. Troisi, Mater. Horiz., 2020, 7, 2922–2928.
104. P. Reiser, M. Konrad, A. Fediai, S. Léon, W. Wenzel and P. Friederich, J. Chem. Theory Comput., 2021, 17, 3750–3759.
105. A. Y. Sosorev, O. D. Parashchuk, N. V. Tukachev, D. R. Maslennikov, D. I. Dominskiy, O. V. Borshchev, M. S. Polinskaya, M. S. Skorotetcky, O. G. Kharlanov and D. Y. Paraschuk, Phys. Chem. Chem. Phys., 2021, 23, 15485–15491.
106. F. Suzuki, S. Kubo, T. Fukushima and H. Kaji, Sci. Rep., 2018, 8, 5203.
107. F. H. A. Nasir and K. L. Woon, Synth. Met., 2024, 307, 117661.
108. A. Y. Sosorev, M. V. Vener, O. G. Kharlanov, E. V. Feldman, O. V. Borshchev, N. I. Sorokina, T. V. Rybalova, S. A. Ponomarenko and D. Y. Paraschuk, J. Phys. Chem. C, 2023, 127, 17948–17957.
109. A. Troisi and D. L. Cheung, J. Chem. Phys., 2009, 131, 014703.
110. N.-E. Lee, J.-J. Zhou, L. A. Agapito and M. Bernardi, Phys. Rev. B, 2018, 97, 115203.
111. C. Červinka, J. Comput. Chem., 2022, 43, 448–456.
112. M. V. Vener, O. G. Kharlanov and A. Y. Sosorev, Int. J. Mol. Sci., 2022, 23, 13305.
113. D. Vong, T. Nematiaram, M. A. Dettmann, T. L. Murrey, L. S. R. Cavalcante, S. M. Gurses, D. Radhakrishnan, L. L. Daemen, J. E. Anthony, K. J. Koski, C. X. Kronawitter, A. Troisi and A. J. Moulé, J. Phys. Chem. Lett., 2022, 13, 5530–5537.
114. Z. J. Knepp and L. A. Fredin, Phys. Rev. B, 2024, 109, 094307.
115. A. Liess, L. Huang, A. Arjona-Esteban, A. Lv, M. Gsänger, V. Stepanenko, M. Stolte and F. Würthner, Adv. Funct. Mater., 2015, 25, 44–57.

---