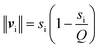Inclusion and intercalation compounds of arsenic(III) oxide polymorphs

Abstract

Arsenic(III) oxycompounds exhibit rich structural chemistry due to the presence of stereoactive lone electron pairs on arsenic and secondary As⋯O bonds that stabilize variable conformations of chains and rings in the case of oxyanions and layers or molecules in the case of oxide. These two features are also responsible for the fact that arsenic(III) oxide forms inclusion and intercalation compounds. In this Highlight article, the discovery and characterization of molecular arsenic(III) oxide inclusion compounds with hydrogen and helium are presented. Also, structural studies of As₂O₃ intercalation compounds with alkali metal halides and pseudohalides are thoroughly described. Finally, future research avenues in the field are presented, which have become more appealing due to the recent literature reports of extraordinary optical properties of arsenic(III) oxide intercalates.

---

Piotr A. Guńka

Dr. Piotr A. Guńka graduated from Warsaw University of Technology in 2010. He received his Ph. D. degree in 2016 and his D. Sc. degree in 2022. He completed a postdoctoral internship with Dr. Timothy A. Strobel at Earth & Planets Laboratory, Carnegie Institution for Science. He is currently employed as an associate professor at the Faculty of Chemistry, Warsaw University of Technology, where he teaches courses on general and inorganic chemistry as well as crystallography. His research interests include arsenic(III) structural chemistry, high-pressure structural chemistry, and chemical crystallography.

---

Introduction

The main building block of arsenic(III) oxide is a ψ-tetrahedron AsO₃ (see Fig. 1). The arsenic atomic core is surrounded by a stereoactive lone electron pair (LEP) and three oxide ligands which are shared with neighboring arsenic atomic cores so that As₂O₃ stoichiometry is achieved. As a consequence, arsenic(III) oxide forms a wide range of both crystalline and glassy polymorphs. They encompass layered forms comprising infinite (As₂O₃)_∞ sheets with varied degrees of corrugation and a molecular polymorph, arsenolite, with As₄O₆ molecules that exhibit symmetry of the 43̄m point group and are isostructural to the well-known P₄O₆ molecules.^1–7

Fig. 1 AsO₃ ψ-tetrahedron (a); an As₄O₆ molecule (b); two As₄O₆ molecules from arsenolite crystal structure oriented in a face-to-face fashion with As⋯O interactions depicted with brown dashed lines (c);^1,8 claudetite I and II crystal structures (d) and (e), respectively;^2,3 polymeric (As₂O₃)_∞ layers in claudetite I and II (f) and (g), respectively; schematic representation of (As₂O₃)_∞ layers in claudetite I and II (h) and (i), respectively, with ψ-tetrahedra depicted as triangles and the orientation of stereoactive LEPs on arsenic atomic cores directed toward opposite sides of the sheet indicated with white and grey. As and O atoms are depicted as green and red spheres, respectively. Reprinted from author's PhD thesis.

However, the crystal structure of arsenolite is completely different from that of P₄O₆ due to directional As⋯O interactions that are often dubbed secondary bonds.^6,7,9 They are located trans with respect to primary bonds and, similarly as hydrogen bonds in ice, cause arsenolite to be less densely packed than phosphorus(V) oxide.¹⁰ Consequently, there are small voids in the crystal structure of arsenolite which, as will be presented in the article, leads to the propensity of arsenolite to form inclusion compounds with hydrogen and helium.

In the same vein, the crystal structures of layered As₂O₃ polymorphs, naturally occurring claudetite I and synthetic claudetite II, are governed by the intra- and interlayer As⋯O interactions as well as mutual orientations of LEPs on neighboring arsenic atoms. The interlayer As⋯O interactions can be replaced with different interactions, which is the reason why As₂O₃ forms numerous intercalation compounds in which charged layers of cations and anions are sandwiched between As₂O₃ sheets.

The Highlight article is divided into two sections. The first one deals with arsenolite inclusion compounds with hydrogen and helium. Their discovery, as well as detailed investigations, are concisely presented. The second part concerns As₂O₃ intercalates and starts with a historical introduction to their research. Then, the latest results in the field are presented. Instead of conclusions, future research avenues are proposed.

Discovery and studies of arsenolite inclusion compounds with helium and hydrogen

During our high-pressure structural study of the crystal structure of arsenolite, helium was used as a pressure-transmitting medium (PTM).¹¹ It was found that arsenolite does not undergo polymorphic phase transitions up to at least 30 GPa. Also, surprising deformations of As₄O₆ molecules were observed. The distance of arsenic atomic cores from the As₄O₆ cages' center of gravity increased, and, simultaneously, the distance of oxygen atomic cores from the cages' center decreased (see the bottom of Fig. 2).

Fig. 2 The molecular structure of As₄O₆ presented in the wireframe model and symmetry coordinates of molecular deformations: scaling ξ (top) and distortion η (bottom). Arsenic and oxygen atoms denoted green and red, respectively.

The most exciting result of the research was an accidental observation that, starting from 3 GPa, there was a very weak reflection on the lower-2θ side in the vicinity of every reflection coming from an arsenolite single-crystal. After ruling out all possible instrumental reasons for the appearance of the weak reflections, a bold hypothesis was made that helium, which is usually treated as an inert PTM, can permeate the non-porous arsenolite structure and diffuse into small voids which are smaller than helium atoms. Consequently, the introduction of helium causes unit-cell expansion, and reflections stemming from the formed inclusion compound are located at lower values of diffraction angles than the corresponding arsenolite reflections. The intensity of the weak reflections coming from the inclusion compound, which we called clathrate at that time, was integrated, and its crystal structure was determined and refined (see Fig. 3). To our surprise, it was possible to find helium atoms in electron density difference maps and to determine the stoichiometry of the obtained compound to be As₄O₆·2He.

Fig. 3 Crystal structure of arsenolite inclusion compounds with helium and hydrogen, As₄O₆·2He and As₄O₆·2H₂. As₄O₆ molecules are presented in the wireframe model with As and O atoms denoted green and red, respectively. Helium atoms are presented as grey transparent spheres, whereas hydrogen molecules are shown in blue in the ball-and-stick model. Helium atoms and dihydrogen molecules are located at the 0, 0, 0 position. The most likely orientation of H₂ molecules along 〈111〉 crystallographic direction is shown. Adapted from P. A. Guńka, L. Zhu, T. A. Strobel and J. Zachara, J. Chem. Phys., 2020, 153, 054501,¹² with the permission of AIP Publishing.

This result was confirmed via quantum-mechanical computations within the density functional theory (DFT) framework with periodic boundary conditions. Equation of state (EoS), which is the unit cell volume dependence of the obtained inclusion compound on pressure, obtained from DFT calculations was in excellent agreement with the experimental EoS. In addition to that, the discovery was confirmed independently by a group of Spanish researchers who subjected powdered arsenolite to pressure in various PTM and observed the formation of the As₄O₆·2He compound.¹³

The co-existence of the weak reflections coming from the arsenolite-helium inclusion compound with the reflections stemming from arsenolite was interpreted such that helium permeated only the surface layer of the studied single crystal, and there were two compounds present in the diamond anvil cell (DAC) during the experiment.¹¹ Subsequently, studies to elucidate the mechanism of helium permeation into non-porous arsenolite, to check whether it is possible to transform arsenolite into the inclusion compound with helium completely, and to reveal the thermodynamic driving force of the As₄O₆·2He compound formation were undertaken. With this in view, a series of X-ray diffraction experiments were carried out on arsenolite single crystals under high pressure in helium and neon as PTM. They allowed for a conclusion that the mechanism of helium diffusion is two-fold. The first one consists most likely in the slow diffusion of helium atoms along temporary channels appearing in the arsenolite crystal due to crystal lattice vibrations (phonons).¹⁴ The second mechanism dominates for low-quality crystals and consists in much faster helium diffusion along the borders of mosaic domains which real crystals are built of. The two postulated processes explain the fact that the complete transformation of an arsenolite crystal into the inclusion compound crystal lasts for 24 h under 5 GPa, causes crystal quality deterioration, and proceeds in such a way that two single-crystalline phases exist before the process is completed. However, decreasing pressure below 3 GPa causes practically instant reformation of arsenolite, and subsequent pressure increase causes the virtually instantaneous reformation of the inclusion compound.¹⁵

The thermodynamic driving force for the following reaction was revealed via DFT computations:

As₄O_6(s) + 2He_(x) = As₄O₆·2He_(s) (1)

The idea behind the approach was to determine theoretically the free energy of all reagents at various pressures and to calculate the enthalpy of the above reaction by taking into account the pV term. Reaction enthalpy calculated in such a way equals Gibbs free energy at 0 K which is the thermodynamic potential at isobaric and isothermal conditions. In the above reaction equation, the phase of helium is denoted x because of a simplification that was made. The reaction takes place around 2–3 GPa, and helium is in a liquid phase at these pressures. It was assumed arbitrarily, though, that helium exists in a solid phase at all pressures, so periodic boundary conditions could be applied in all computations. Despite this approximation, the pressure above which the reaction of As₄O₆·2He formation should be spontaneous is 1.8 GPa, according to the computations. It is in remarkable agreement with the experiment considering the above approximation and the fact that kinetic barriers were not taken into account. After modeling crystal structures of arsenolite and its inclusion compound with helium at numerous pressures, it was noticed that the introduction of helium atoms into arsenolite causes a decrease of As₄O₆ molecular deformations at each pressure point which, as it turned out in further studies, leads to the reduction of conformational energy of the molecules. This observation inspired a decomposition of the enthalpy of reaction (1) into the following terms: pΔV, E_def, and ΔE_inter, which denote pressure-volume work, deformation energy of molecules due to the introduction of helium atoms into arsenolite structure, and the difference in the intermolecular interactions' energy in product and the sum of intermolecular interactions' energies in the substrates, respectively. This analysis concluded that the main driving force of reaction (1) is the pΔV term, and the second most significant factor is the deformation energy (see Fig. 4). It can be understood as the energetic gain arising from the change in As₄O₆ molecular conformation due to repulsive interactions with helium atoms.¹⁵

Fig. 4 Enthalpy, pΔV term, and difference in energy of intermolecular interactions (ΔE_inter) for the As₄O₆·2He formation reaction at 0 K together with As₄O₆ deformation energy (E_def) plotted as a function of pressure. pΔV_exp and pΔV_comp denote the pΔV term calculated using EoS fitted to the values of pressure and volume from the experiment and DFT computations, respectively. All energies are given per mole of As₄O₆ molecules. Reprinted from P. A. Guńka, M. Hapka, M. Hanfland, M. Dranka, G. Chałasiński and J. Zachara, ChemPhysChem, 2018, 19, 857–864,¹⁵ with the permission of John Wiley and Sons. Copyright 2018, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.

A Spanish group of scientists led by Sans, who obtained the As₄O₆·2He inclusion compound independently of us, concluded that there are specific As⋯He interactions in its structure. They even claimed that they are localized bonds.¹³ Such assertions seemed to be entirely untrustworthy from a chemical point of view to us, but, not to rely on chemical intuition alone, quantum-mechanical computations within the framework of symmetry-adapted perturbation theory (SAPT) were carried out. They showed beyond reasonable doubt that, at the He⋯As₄O₆ distances observed in the structure of the inclusion compound, the He⋯As₄O₆ interaction is repulsive and results mainly from the Pauli exclusion principle.¹⁵

The apparent contradiction that there is no net attraction between He atoms and As₄O₆ molecules as suggested by SAPT analysis dominated by Pauli repulsion and the fact that As₄O₆·2He is thermodynamically stable above 2 GPa shows an interesting principle that is currently the subject of scientific discussion. Namely, repulsive two-body contributions do not necessarily prevent the creation of new compounds or the stabilization of new phases as other contributions to Gibbs free energy may prevail over the local repulsions (see Fig. 4), e.g. pV term and long-range interactions in ε-glycine.¹⁶ Another contribution to Gibbs free energy that may favor the creation of new compounds is Madelung energy which was proven to drive the formation of inclusion compounds of helium with salts that have different stoichiometry from 1 : 1.¹⁷ Introduction of helium atoms into such crystal structures alleviates the Coulomb repulsions of the majority ions that have the same charge. It was also shown rigorously that the same effect is the energetic driving force for the formation of Na₂He compound which is an electride with localized pairs of electrons.^17,18

Obtaining the arsenolite inclusion compound with helium allowed one to suppose hydrogen should also form an analogous compound. Synchrotron X-ray diffraction experiments revealed that hydrogen forms, indeed, an analogous inclusion compound already at pressure ∼1.5 GPa. In this case, its crystal structure determination was trickier than in the case of the inclusion compound with helium. The difficulties were caused, on the one hand, by the lower quality of diffraction data and, on the other hand, by the fact that a dihydrogen molecule has more degrees of freedom than a helium atom. At this research stage, stoichiometry As₄O₆·2H₂ and a crystal structure in which H₂ molecules occupy analogous sites as helium atoms and are aligned along crystallographic 〈111〉 direction were proposed based on DFT computations (see Fig. 3). The assumptions on the same stoichiometry and quasiisostructurality of the arsenolite inclusion compounds with helium and hydrogen were made based on the observation that both compounds are formed at the pressure at which the ratio of hydrogen or helium molar volumes to the difference in molar volumes of arsenolite and its inclusion compound reaches the same value (see Fig. 5).¹⁹

Fig. 5 The ratio of hydrogen or helium molar volumes to the difference between molar volumes of arsenolite and its inclusion compound with hydrogen or helium plotted as a function of pressure. X = H₂, He. Reprinted with permission from P. A. Guńka, M. Hapka, M. Hanfland, G. Chałasiński and J. Zachara, J. Phys. Chem. C, 2019, 123, 16868–16872.¹⁹ Copyright 2019 American Chemical Society.

Raman spectra of the compound As₄O₆·2H₂ were also recorded. A strong redshift of dihydrogen vibron (the band corresponding to rotational–vibrational transitions of H₂ molecule) was observed, and it split into three components below 5 GPa, and two at higher pressures. This showed that the H–H bond is significantly weakened in the inclusion compound. DFT computations with periodic boundary conditions and subsequent analysis of crystal orbital Hamilton populations (COHP) and crystal orbital overlap populations (COOP) in the theoretically calculated electron density distribution revealed that the H–H bond becomes weaker and more polarized due to the interactions with arsenic lone electron pair (LEP).¹⁹

The observation of dihydrogen vibron splitting was surprising and puzzling because the diffraction data and DFT computations suggested the presence of an H₂ molecule in one symmetry-independent position only. To understand this phenomenon, more Raman measurements on polycrystalline arsenolite samples in protium and deuterium under high pressure, both at room temperature and low temperatures down to 80 K, were carried out (see Fig. 6). These studies showed that the dihydrogen vibron is split into three components in the whole investigated pressure range (up to 20 GPa), and two out of the three vibrons stem from the ortho and para dihydrogen spin isomers which result from hydrogen nuclear spin. Unfortunately, the explanation of the cause of the third vibron was not possible based on these experiments.¹² The working hypotheses assuming a different inclusion compound stoichiometry or disorder in its structure consisting in some dihydrogen molecules occupying a different site in the crystal were ruled out with high likelihood via molecular dynamics modeling. The third vibron might result from more complex many-body interactions, and more research is necessary to elucidate its origin. The analysis of hydrogen rotons' shape, which are bands coming from hydrogen molecules being excited to higher rotational states, showed that the earlier hypothesis of total or, at least, partial suppression of H₂ molecule rotations and its alignment along the 〈111〉 direction is most likely valid, especially at low temperatures.¹²

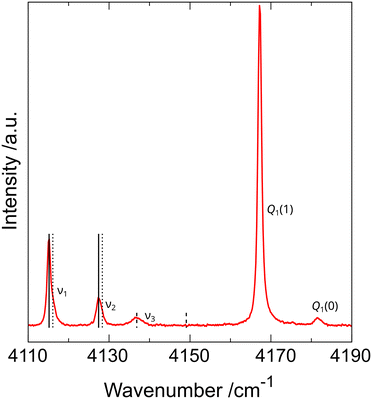Fig. 6 Raman spectrum of As₄O₆·2H₂ inclusion compound in the wavenumber range corresponding to hydrogen vibrons recorded at 85(2) K and 1.29(5) GPa. Q₁(1) and Q₁(0) denote vibrons of free hydrogen, which was used as PTM, whereas ν₁, ν₂, and ν₃ denote vibrons of H₂ molecules present in the inclusion compound. Vertical lines represent pairs coming from ortho and para spin isomers of dihydrogen. Solid and dotted lines correspond to vibrons in which adjacent hydrogen molecules vibrate in and out of phase, respectively. Dashed lines indicate that the ν₃ vibron does not occur as a pair coming from two spin isomers, and its cause is different. Reprinted from P. A. Guńka, L. Zhu, T. A. Strobel and J. Zachara, J. Chem. Phys., 2020, 153, 054501,¹² with the permission of AIP Publishing.

Last but not least, the kinetics of hydrogen permeation into arsenolite single crystals have been determined using Fourier transform infrared (IR) spectroscopy at the SOLEIL synchrotron. Micrometer-thick As₄O₆ single crystals have been obtained via spatial confinement by decomposing ammonium arsenite between glass slides.^20,21 The thin plates of arsenolite were placed in diamond anvil cells together with hydrogen, and pressure was increased to ca. 1.5 GPa. It was assumed that hydrogen would enter the crystals only through the top large face (see Fig. 7). The thickness of the arsenolite hydrogen inclusion compound layer was determined from the absorbance of its bands observed in the IR spectra recorded as a function of time. It was found that the growth of the As₄O₆·2H₂ inclusion compound was linear, indicating the process was not diffusion-limited, but the reactions taking place at phase boundaries were rate-limiting (see Fig. 7).²¹ While only one region of linear growth was found at 1.47(5) GPa, two domains of linear growth with different slopes were observed at 1.37(5) GPa. The origin of this induction effect was not fully understood, but it was proposed that it may stem from the fact that, initially, islands of the inclusion compound are formed on the surface of arsenolite single crystal, and only after they have merged together does the layer of inclusion compound start to grow in thickness.²¹

Fig. 7 Schematic drawing of the applied experimental setup; note that proportions between different parts in the drawing are not maintained (a). The peak area of inclusion compound As₄O₆·2H₂ plotted as a function of time for the peak around 250 cm⁻¹. Measurements were carried out at 1.47 (5) and 1.37 (5) GPa (b and c, respectively). Figure adapted from P. A. Guńka, K. F. Dziubek and F. Capitani, J. Phys. Chem. C, 2023, 127, 15871–15875.²¹

Studies of arsenic(III) oxide intercalates

As mentioned earlier, arsenic(III) oxide forms three ambient-pressure crystalline polymorphs. One of them, arsenolite, is a molecular solid, while the other two, claudetites I and II, are made of infinite As₂O₃ layers. It was found a long time ago, much earlier than it was realized, that He atoms and H₂ molecules can be inserted between As₄O₆ molecules, that alkali metal halides can be introduced, i.e. intercalated, between the As₂O₃ layers. According to the International Union of Pure and Applied Chemistry (IUPAC), intercalation compounds are substances formed due to reversible inclusion, without the formation of covalent bonds, of one kind of molecules into the solid matrix of a different compound with a layered structure.²²

Arsenic(III) oxide intercalates are not typical examples of intercalation compounds as the introduction of ions between As₂O₃ layers changes their conformation and involves breaking and re-formation of As–O covalent bonds. Several of them occur in nature as minerals.^23–26 Synthetic intercalates with potassium, ammonium, and sodium halides of a general formula nMX·mAs₂O₃ were obtained for the first time in the 19th century, although their structure was unknown at that time, and they were not considered intercalation compounds.^27–30 The crystal structure of the intercalates with the general formula MX·2As₂O₃ was determined by Pertlik in the 1980s, though he used a different notation for their sum formula.³¹ The compounds are built of As₂O₃ sheets that separate alternating charged layers of cations and anions (see Fig. 8). The intercalates containing potassium and ammonium cations crystallize in the hexagonal P6/mmm space group and are isotypic. Hexagonal (As₂O₃)_n layers are flat, and all LEPs are pending on one side of the layers; the one which is adjacent to anions. The oxygen ligands are situated on the other side of the As₂O₃ sheet coordinating cations (Fig. 8). The intercalates with such crystal structure will be denoted P_MX hereafter, where P denotes the crystal structure type determined by Pertlik and MX is the salt that intercalates arsenic(III) oxide. Contrary to other ammonium halides, ammonium chloride only forms a hydrated intercalate with a formula NH₄Cl·As₂O₃·½H₂O, which also exhibits hexagonal symmetry and an analogous conformation of As₂O₃ sheets.³² A different structure has been observed for the intercalate with sodium bromide, which crystallizes in the orthorhombic crystal system, space group Pmcn. The As₂O₃ sheet is slightly more corrugated, and there are two kinds of AsO₂ stripes within it: one with LEPs on all arsenic atoms pending to one side of the layers and another one with alternating LEPs (see Fig. 8).

Fig. 8 Crystal structures of As₂O₃ intercalates with potassium and sodium bromide. KBr·2As₂O₃ (P_KBr) crystal structure viewed down [102] and [001] directions (a) and (b), respectively;³¹ NaBr·2As₂O₃ structure viewed along [100] direction (c).³³ Schematic and ball-and-stick representations of polymeric (As₂O₃)_∞ layers in NaBr·2As₂O₃ (d) and (e), respectively. The two kinds of AsO₂ stripes mentioned in the text run horizontally. ψ-Tetrahedra are depicted as triangles, and the orientation of stereoactive LEPs on arsenic atomic cores directed toward opposite sides of the sheet indicated with white and grey. As, O, K, Na and Br atomic cores are depicted as green, red, violet, blue and brown spheres, respectively. Reprinted from author's PhD thesis.

Our studies of arsenic(III) oxide intercalates with potassium chloride have led to the crystallization of two new intercalates in addition to the known KCl·2As₂O₃ (P_KCl): KCl·As₂O₃·3H₂O (X_KCl) and KCl·As₂O₃·½H₂O (Y_KCl). Intercalate X_KCl undergoes slow decomposition at room temperature to compound Y_KCl. The decomposition can be completed at 120 °C within half an hour. Heating intercalate Y_KCl to ∼250 °C leads to intercalate P_KCl and free KCl. The crystal structures of both hydrated compounds have been determined, and it was found that they crystallize in the hexagonal crystal system and contain disordered water molecules (see Fig. 9). The crystal structure determination of intercalate Y_KCl was particularly interesting. Initially, the presence of water was overlooked. Thermogravimetric analysis coupled with mass spectrometry (TG-MS) and differential scanning calorimetry (DSC) allowed us to conclude that there is a mass loss of 3.19(5)% associated with an endothermic effect of 174 J g⁻¹ and the presence of water in gas in temperature range 150–180 °C. The presence of water was also confirmed by attenuated total reflection Fourier transform infrared (ATR-FTIR) spectroscopy and ¹H NMR in the solid state. Interestingly, upon cooling from 200 °C, the intercalate re-absorbs moisture from the air, which results in the fact that powder diffraction patterns and ATR-FTIR spectra before and after heating are identical.³⁴ Analysis of unit cell parameters of compound Y_KCl and of compound NH₄Cl·As₂O₃·½H₂O, whose structure was determined in the 1950s, together with the fact that other potassium–halide and ammonium–halide intercalates are isostructural allowed for a conclusion that the two compounds are also isostructural.³⁴ Consequently, a corrected crystal structure model of compound NH₄Cl·As₂O₃·½H₂O was proposed and confirmed using X-ray diffraction and solid-state NMR studies.³⁵

Fig. 9 Crystal structure of compounds P_KCl (a and d), Y_KCl (b and e), and X_KCl (c and f). Structures are presented in the ball-and-stick model along crystallographic [001] direction (a–c) and with thermal ellipsoids drawn at the 50% probability level along [120] direction (d–f). As, O, K, and Cl atoms are colored dark green, red, blue, and light green, respectively. The yellow color denotes the position of disordered potassium cations and water molecules. Hydrogen atoms were not refined in the structural models. Figure reprinted from M. A. Domański, K. Kraszewski, P. Paluch and P. A. Guńka, Cryst. Growth Des., 2021, 21, 5215–5222.³⁵

Subsequently, the first crystal structures of arsenic(III) oxide intercalates with rubidium cations were determined. A series of quasihydrothermal crystallizations of As₂O₃ mixed with RbCl in molar ratios of 2 : 1, 1 : 1, and 1 : 2 in a solution having acidic, neutral, and alkaline pH were performed. Intercalate RbCl·2As₂O₃ (P_RbCl) isostructural with compound KCl·2As₂O₃ (P_KCl) crystallized from acidic solutions. In contrast, compound RbCl·As₂O₃·½H₂O (Y′_RbCl) with a very similar structure to that of compound KCl·As₂O₃·½H₂O (Y_KCl) precipitated from alkaline solutions. The only difference between the structures of these compounds occurs in the disordered layers. It is most likely related to the differences in ionic radii and, possibly, the acidity of K⁺ and Rb⁺ cations (see Fig. 10). Importantly, this difference also results in the existence of superstructure in compound Y′_RbCl, which was described using a supercell with a volume three times as large as that of the basic unit cell. Reflections indicating the presence of superstructure were only observed in the diffraction pattern stemming from a large single crystal of intercalate Y′_RbCl. Intercalates P_RbCl and Y′_RbCl were also characterized by ¹H and ⁸⁷Rb solid-state NMR spectroscopy. Comparing the intercalates' spectra allowed for assigning signals in the ⁸⁷Rb NMR spectrum of compound Y′_RbCl to rubidium cations occupying particular sites in its crystal structure.

Fig. 10 ATR-FTIR spectra of intercalates Y′_RbCl (solid black line) and Y_KCl (red dashed line). Inset above the legend shows the disordered layers located at z = ½. The bottom right unit cells show the coordinates of the Wyckoff sites 3g and 6m in Y_KCl and Y′_RbCl, respectively, depicted with yellow spheres. In other unit cells possible random arrangement of cations and H₂O molecules is shown, taking into account their occupancies. As, O, K, Rb, and Cl atoms are depicted in dark green, red, dark blue, light blue, and light green, respectively. Figure reproduced from P. Michalak, P. Paluch and P. A. Guńka, Cryst. Growth Des., 2022, 22, 711–717.³⁶

Then, analysis of interlayer interaction energies in intercalate P_RbCl and isostructural intercalates with potassium halides P_KX was performed, and formation energies of these compounds from respective alkali-metal halides and arsenolite were computed. This allowed us to conclude that the stability of intercalates with potassium halides increases with the increase of halide anion ionic radius. Similarly, the computations revealed intercalate P_RbCl is more stable than compound P_KCl.³⁶

Last but not least, a comprehensive study of the anhydrous intercalates of potassium, rubidium, cesium, and ammonium halides (P_MX) was carried out. For this purpose, the intercalates P_RbBr, P_RbI, P_CsCl, P_CsBr, and P_CsI were synthesized for the first time. It was demonstrated that As⋯X interactions, where X is a halogen, are present in the intercalates, and they are analogous to the As⋯O secondary bonds that govern the structures of As₂O₃ polymorphs and other As(III) oxycompounds. The As⋯X interactions are, therefore, also secondary bonds.⁹ The analysis of As⋯X interactions was carried out using the analysis of arsenic LEP stereoactivity that was gauged using the bond-valence vector model proposed by Zachara.³⁷ The idea of this model is to assign a bond-valence vector to every bond formed by a coordination center that is parallel to the bond, directed from the coordination center to the ligand, and whose length is given by the following equation:

where v_i and s_i denote bond-valence vector and valence of ith bond, respectively, whereas Q denotes coordination-center atomic core charge. For coordination spheres where no strain is present, the net bond-valence vector resulting from the summation of all bond-valence vectors should be a zero vector. If there is strain in a coordination sphere, the magnitude of the resultant vector is a measure of the strain magnitude. For example, if there is a stereoactive lone electron pair, i.e., there is electronic strain, the net bond valence vector is large, and its length is a measure of lone-electron-pair stereoactivity. For a fully stereoactive LEP a valence s_LEP of 2 would be assigned and ||v_i|| = 2(1 − 2/5) = 1.2 v.u.³⁷

The strength of As⋯X interactions was assessed using the first-order valence entropy coordination number (¹VECN).³⁸ Coordination number is one of the many terms used in chemistry that are very intuitive and broadly used but difficult to define precisely. For instance, in arsenic(III) oxycompounds, arsenic atomic cores form three strong, so-called primary bonds with oxygen atomic cores and, additionally, up to three weaker, so-called secondary bonds localized trans with respect to the primary bonds. In such cases, the arsenic coordination number is described as 3 + n, where n = 1, 2, or 3. Such a description is not precise enough to compare subtle differences in the arsenic coordination sphere caused by secondary interactions or increasing pressure, among others. Bond-valence-based definitions of coordination numbers are ideally suited to such applications.³⁸ Here, only the definition of valence-entropy coordination number of order n (ⁿVECN) will be presented so that readers can follow the analysis of the significance of As⋯X interactions. An interested reader is referred to ref. 38 to get acquainted with the definition of valence-diversity coordination number (VDCN). ⁿVECN is defined by the following equation:

where s_i denotes valency of the ith bond, k_VECN,n stands for valence entropy coordination number of order n and N is the number of bonds between coordination center and ligand which are taken into account. Relatively simple, but tedious, algebraic transformations allow one to get the following formula for the natural logarithm of ⁿVECN:
where .

The application of these tools allowed for the analysis of the correlation between LEP stereoactivity and arsenic coordination number in the studied intercalates incorporating As⋯X interactions. The correlation overlain on the analogous correlation for As⋯O secondary bonds is presented in Fig. 11. The characteristic decrease in LEP stereoactivity correlated with an increase in ¹VECN together with the fact that As⋯X interactions are located trans with respect to the primary As–O bonds testifies to the fact that As⋯X interactions are indeed secondary bonds.

Fig. 11 Arsenic first-order valence entropy coordination number (¹VECN_As) and arsenic net bond valence vector length (||v_As||), which equals the length of bond valence vector of arsenic lone electron pair, plotted as a function of the anion type present in the intercalates (a and b, respectively). ¹VECN_As plotted as a function of ||v_As|| for arsenic(III) oxycompounds (denoted with grey x markers) and for anhydrous hexagonal P_AX intercalates denoted with colored circles (c). Data for arsenic(III) oxycompounds taken from ref. 38. Figure reprinted from M. Dąbrowski, W. Wrześniewska, A. Prystupiuk, J. Zachara and P. A. Guńka, Cryst. Growth Des., 2023, 23, 6081–6085.³⁹

It is noteworthy that recently, an article appeared online that describes the first anhydrous polar As₂O₃ intercalate CsBr·As₂O₃ (N_CsBr, where N indicates that the crystal structure of the intercalate is non-centrosymmetric) that exhibits a very strong second harmonic generation (SHG) response, which is 20.5 higher than that of KH₂PO₄. The intercalate P_CsBr studied in the same article exhibited very high birefringence (0.26), which was only slightly larger than that of N_CsBr (0.24).⁴⁰ Zeng and co-workers attribute the strong SHG effect to the fact that the polar AsO₃ ψ-tetrahedra are polymerized into (As₂O₃)_∞ layers and are all aligned in the same direction in N_CsBr. Actually, they designed the intercalates to attain such extraordinary optical properties.⁴⁰

Last but not least, two intercalates with non-spherical pseudohalide azide anions have been obtained and structurally characterized: KN₃·2As₂O₃ (P_KN3) and NH₄N₃·2As₂O₃ (P_NH4N3). Their structure is analogous to other P_MX intercalates where the linear azide anions replace halide anions and are oriented perpendicularly to As₂O₃ sheets.⁴¹ Detailed computational analysis of interlayer interaction energies between ions and arsenic(III) oxide layers, structural similarity of cations surroundings between As₆O₁₂ rings to cations coordination by crown ether (see Fig. 12), structural similarity of potassium and ammonium cations, our earlier structural studies of ammonium oxoarsenates(III),⁴² and the fact that intercalate with NaBr exhibits different conformation of As₂O₃ layers allowed for a conclusion that alkali metal and ammonium cations template the conformation of As₂O₃ layers and enforce their hexagonal symmetry described by the P6mm layer group.^41,42 Interestingly, comparative crystal structure analysis of the anhydrous intercalates P_MX revealed that the size of halide anions exerts a more significant influence on intercalate structural parameters, such as unit-cell parameters, As–O bond lengths, As⋯X distances, and O–As–O and As–O–As valence angles, even though cations serve as templates for the As₂O₃ layers and determine their conformation in the intercalates.^39,41

Fig. 12 Comparison of potassium complex with 18-crown-6 and potassium neighborhood in P_KX intercalates where X stands for halide or pseudohalide anions. As, O, K, C, and H depicted as green, red, violet, grey, and white spheres, respectively.

Conclusions

The great structural diversity of arsenic(III) oxycompounds is well represented in the inclusion and intercalation compounds of arsenic(III) oxide. It is caused by the fact that As(III) forms primary and secondary bonds. These weaker interactions not only stabilize various conformations in the As₂O₃ polymorphs but are also responsible for the interactions with hydrogen, helium, and salts that co-form inclusates and intercalates with arsenic(III) oxide. There are still a lot of open questions concerning these compounds. For instance, the exact stoichiometry and structural model of the inclusion compound with hydrogen are questionable, and the reason for the third component of H₂ Raman vibron is unclear. These issues could be resolved using neutron diffraction or inelastic neutron scattering experiments. Also, it remains an open question whether arsenic(III) oxide forms intercalates with other salts of sodium, lithium, and other cations, particularly ones with higher electric charge. I am convinced that pursuing these research questions will lead to new exciting results, and the recent paper by Zeng et al. describing the extraordinary optical properties of As₂O₃ intercalates opens up a new perspective on the application potential of this class of compounds.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this highlight article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Stimulating discussions and fruitful collaboration with Maciej Dranka and Kamil F. Dziubek when carrying out the research summarized in this Highlight article as well as financial support from the Polish National Science Centre, grant no. 2020/39/D/ST4/00128, are gratefully acknowledged. An anonymous Reviewer is acknowledged for their constructive remarks that helped to improve the manuscript significantly. Last but not least, the valuable cooperation with Dr. Michael Hanfland is sincerely appreciated, as he kindly carried out numerous measurements during his in-house beamtime at the ESRF.

References

1. F. Pertlik, Czech. J. Phys., 1978, 28, 170–176.
2. F. Pertlik, Monatsh. Chem., 1978, 109, 277–282.
3. F. Pertlik, Monatsh. Chem., 1975, 106, 755–762.
4. K. S. Andrikopoulos, D. Christofilos, G. A. Kourouklis and S. N. Yannopoulos, High Pressure Res., 2006, 26, 401–406.
5. P. A. Guńka, M. Dranka, M. Hanfland, K. F. Dziubek, A. Katrusiak and J. Zachara, Cryst. Growth Des., 2015, 15, 3950–3954.
6. M. Jansen and M. Moebs, Inorg. Chem., 1984, 23, 4486–4488.
7. M. Jansen, M. Voss and H.-J. Deiseroth, Angew. Chem., 1981, 93, 1023–1024.
8. P. Ballirano and A. Maras, Z. Kristallogr. – New Cryst. Struct., 2002, 217, 177–178.
9. N. W. Alcock, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeléus and A. G. Sharpe, Academic Press, 1972, vol. 15, pp. 1–58.
10. F. Pertlik, Monatsh. Chem., 1979, 110, 387–392.
11. P. A. Guńka, K. F. Dziubek, A. Gładysiak, M. Dranka, J. Piechota, M. Hanfland, A. Katrusiak and J. Zachara, Cryst. Growth Des., 2015, 15, 3740–3745.
12. P. A. Guńka, L. Zhu, T. A. Strobel and J. Zachara, J. Chem. Phys., 2020, 153, 054501.
13. J. A. Sans, F. J. Manjón, C. Popescu, V. P. Cuenca-Gotor, O. Gomis, A. Muñoz, P. Rodríguez-Hernández, J. Contreras-García, J. Pellicer-Porres, A. L. J. Pereira, D. Santamaría-Pérez and A. Segura, Phys. Rev. B, 2016, 93, 054102.
14. L. J. Barbour, Chem. Commun., 2006, 1163–1168.
15. P. A. Guńka, M. Hapka, M. Hanfland, M. Dranka, G. Chałasiński and J. Zachara, ChemPhysChem, 2018, 19, 857–864.
16. S. A. Moggach, W. G. Marshall, D. M. Rogers and S. Parsons, CrystEngComm, 2015, 17, 5315–5328.
17. Z. Liu, J. Botana, A. Hermann, S. Valdez, E. Zurek, D. Yan, H. Lin and M. Miao, Nat. Commun., 2018, 9, 951.
18. X. Dong, A. R. Oganov, A. F. Goncharov, E. Stavrou, S. Lobanov, G. Saleh, G.-R. Qian, Q. Zhu, C. Gatti, V. L. Deringer, R. Dronskowski, X.-F. Zhou, V. B. Prakapenka, Z. Konôpková, I. A. Popov, A. I. Boldyrev and H.-T. Wang, Nat. Chem., 2017, 9, 440–445.
19. P. A. Guńka, M. Hapka, M. Hanfland, G. Chałasiński and J. Zachara, J. Phys. Chem. C, 2019, 123, 16868–16872.
20. P. A. Guńka, M. Dranka, J. Piechota, G. Z. Żukowska, A. Zalewska and J. Zachara, Cryst. Growth Des., 2012, 12, 5663–5670.
21. P. A. Guńka, K. F. Dziubek and F. Capitani, J. Phys. Chem. C, 2023, 127, 15871–15875.
22. IUPAC Compendium of Chemical Terminology: Gold Book, ed. M. Nič, J. Jirát, B. Košata, A. Jenkins and A. McNaught, IUPAC, Research Triangle Park, NC, 3.0.1., 2009.
23. A. R. Kampf, B. P. Nash, M. Dini and A. A. M. Donoso, Mineral. Mag., 2014, 78, 747–755.
24. A. R. Kampf, B. P. Nash, M. Dini and A. A. M. Donoso, Mineral. Mag., 2016, 80, 1265–1272.
25. A. Garavelli, D. Mitolo, D. Pinto and F. Vurro, Am. Mineral., 2013, 98, 470–477.
26. U. Hålenius, F. Hatert, M. Pasero and S. J. Mills, Mineral. Mag., 2016, 80, 407–413.
27. H. Schiff and R. Sestini, Justus Liebigs Ann. Chem., 1885, 228, 72–91.
28. H. L. Wheeler, Am. J. Sci., 1893, 46(3), 88–98.
29. F. Rüdorff, Ber. Dtsch. Chem. Ges., 1888, 21, 3051–3053.
30. F. Rüdorff, Ber. Dtsch. Chem. Ges., 1886, 19, 2668–2679.
31. F. Pertlik, Monatsh. Chem., 1988, 119, 451–456.
32. M. Edstrand and G. Blomqvist, Ark. Kemi, 1955, 8, 245–256.
33. F. Pertlik, J. Solid State Chem., 1987, 70, 225–228.
34. M. A. Domański, K. Kraszewski, P. Paluch and P. A. Guńka, Cryst. Growth Des., 2021, 21, 5215–5222.
35. W. Wrześniewska, P. Paluch and P. A. Guńka, Acta Crystallogr., Sect. B, 2023, 79, 207–212.
36. P. Michalak, P. Paluch and P. A. Guńka, Cryst. Growth Des., 2022, 22, 711–717.
37. J. Zachara, Inorg. Chem., 2007, 46, 9760–9767.
38. P. A. Guńka and J. Zachara, Acta Crystallogr., Sect. B, 2019, 75, 86–96.
39. M. Dąbrowski, W. Wrześniewska, A. Prystupiuk, J. Zachara and P. A. Guńka, Cryst. Growth Des., 2023, 23, 6081–6085.
40. W. Zeng, Y. Tian, H. Zeng, Z. Lin and G. Zou, Angew. Chem., Int. Ed., 2025, e202422818.
41. P. A. Guńka, K. Kraszewski, Y.-S. Chen and J. Zachara, Dalton Trans., 2014, 43, 12776–12783.
42. P. A. Guńka, M. Dranka and J. Zachara, CrystEngComm, 2011, 13, 6163–6170.

---

Footnote

† Dedicated to the memory of Prof. Janusz Zachara (1955–2024) for his mentoring of the Author and contributions to the structural chemistry of arsenic.

---