Strength of fluid-filled soft composites across the elastofracture length†
Christopher W.
Barney
 ab,
Megan T.
Valentine
ab,
Megan T.
Valentine
 *b and
Matthew E.
Helgeson
*b and
Matthew E.
Helgeson
 *a
*a
aDepartment of Chemical Engineering, University of California Santa Barbara, Santa Barbara, CA 93106, USA. E-mail: helgeson@ucsb.edu
bDepartment of Mechanical Engineering, University of California Santa Barbara, Santa Barbara, CA 93106, USA. E-mail: valentine@engineering.ucsb.edu
First published on 10th June 2022
Abstract
Materials that utilize heterogeneous microstructures to control macroscopic mechanical response are ubiquitous in nature. Yet, translating nature's lessons to create synthetic soft solids has remained challenging. This is largely due to the limited synthetic routes available for creating soft composites, particularly with submicron features, as well as uncertainty surrounding the role of such a microstructured secondary phase in determining material behavior. This work leverages recent advances in the development of photocrosslinkable thermogelling nanoemulsions to produce composite hydrogels with a secondary phase assembled at well controlled length scales ranging from tens of nm to tens of μm. Through analysis of the mechanical response of these fluid-filled composite hydrogels, it is found that the size scale of the secondary phase has a profound impact on the strength when at or above the elastofracture length. Moreover, this work shows that mechanical integrity of fluid–filled soft solids can be sensitive to the size scale of the secondary phase.
The exploitation of heterogeneous microstructure to tune mechanical response is abundant in nature. Specifically, the diversity of natural systems that control mechanics through multiphase microstructures (e.g. mussel adhesive plaques,1 brain tissue,2 trabecular bone,3etc.) highlights the potential of leveraging both local properties and geometry to influence material behavior. Despite these potential advantages, translating the strategy of tailoring mechanical response through complex microstructure to soft synthetic materials has been challenging, both in terms of developing systematic synthetic processing routes for creating multiphase materials and understanding how length scales of structure impact the failure of soft solids.
To meet the first challenge, multiple processing routes have been developed including block copolymer assembly,4 solvent exchange-induced phase separation,5 3D printing,6–8 and colloidal assembly.9–15 Block copolymer assembly offers precise control of the size scale of the secondary phase, yet is limited in range to the molecular size scale of the polymers (typically <100 nm).16 While solvent exchange-induced phase separation offers greater flexibility in size scale, it fails to provide control of the polymer volume fraction in the primary phase and there is an inherent distribution of shrinkage stresses arising from the strain mismatch at the interface between phases, which can undermine material strength.5 3D printing is promising yet often requires post-processing steps and is typically limited to larger size scales.6–8 By contrast, recent developments in colloidal assembly provide a promising alternative that addresses the limitations of the three previous techniques. Among such materials, thermogelling nanoemulsions have recently emerged as an assembling colloidal material with particular advantages: it is possible to alter the length scale(s) of the secondary phase from tens of nm to tens of μm while also controlling the polymer volume fraction and avoiding the development of shrinkage stresses at the interface between phases.13,14 These nanoemulsions can also be used to template hydrogels with controlled porosity,13,17–19 which has commercial advantage, for example in developing cellular scaffolds with porosity-defined mechanical and transport properties for use as soft tissue replacements.20–22 These developments in the processing of nanoemulsion-based materials lay the foundation for probing the mechanics of multiphase soft composites to understand the roles of local composition and geometry on macroscopic behavior, which has yet to be studied in the case of emulsion-templated soft composites.
Incorporating a secondary phase into a soft solid at different size scales should influence its deformation response in the elastic (linear and weakly nonlinear) and failure (fully nonlinear) regimes. The impact of secondary phases on the former has been well-documented.23 By comparison, a precise understanding of the influence of a secondary phase on the failure strength of soft solids is lagging. Many soft solids owe their strength to a crosslinked polymer network structure, which is generally viewed as insensitive to flaws on the size scale of material defects, typically on the order of tens to hundreds of nm.24,25 This flaw insensitivity arises from the fact that polymer networks, such as those found in rubbers or hydrogels, are often characterized by an elastofracture length of macroscopic dimensions (0.1–10 mm).26 The elastofracture length is a physical size scale, set by the ratio of the fracture energy Gc to the elastic modulus E, below which the onset of nonlinear failure processes are insensitive to the initial size scale of a material defect.26 This suggests that the strength of a polymer network should only be impacted by incorporating a secondary phase at size scales greater than or equal to 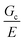 , where it would act as a critical flaw.
, where it would act as a critical flaw.
For most polymer networks, the elastofracture length (typically 0.1–10 mm) is much larger than the inherent size scale of heterogeneity (typically ∼100 nm), and so the nonlinear mechanics are insensitive to such heterogeneities.24,26 However, it is possible to crosslink a network to the point where it should become sensitive to material defects. This can occur because increasing the crosslinking density simultaneously increases E while decreasing Gc. For example, taking a value of E = 1 MPa and Gc = 100 N m−1 gives a value of 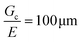 . According to the affine deformation model for elasticity27,28 and Lake–Thomas theory,29
. According to the affine deformation model for elasticity27,28 and Lake–Thomas theory,29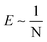 and
and 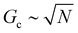 , giving that
, giving that 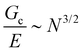 where N is the number of Kuhn segments between crosslinking junctions. This argument suggests that as E increases to 10 MPa and 100 MPa,
where N is the number of Kuhn segments between crosslinking junctions. This argument suggests that as E increases to 10 MPa and 100 MPa, 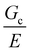 decreases to 3.2 μm and 100 nm, respectively. This inherent tradeoff between stiffness and toughness explains why simply crosslinked networks lose mechanical integrity and often crumble when the stiffness approaches approximately 10 MPa.
decreases to 3.2 μm and 100 nm, respectively. This inherent tradeoff between stiffness and toughness explains why simply crosslinked networks lose mechanical integrity and often crumble when the stiffness approaches approximately 10 MPa.
Building on these ideas, we explore the possibility that a secondary phase introduced into a soft solid will act as a critical flaw and reduce material strength as its size scale becomes greater than 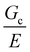 . If true, this hypothesis would expand the current understanding of strength in multiphase soft composites. The work to follow is divided into several parts. First, we present the thermogelling nanoemulsion materials used to systematically create hydrogels with a secondary phase at different size scales. The puncture method used to quantify material strength is then described and, finally, the role of damage nucleation during the puncture process is considered. These results have strong implications for designing multiphase soft materials with templated porosity that maintain mechanical integrity, and provide guidelines for the use of such materials in structural applications such as scaffolds for tissue engineering or in high-pressure separations technologies.20–22
. If true, this hypothesis would expand the current understanding of strength in multiphase soft composites. The work to follow is divided into several parts. First, we present the thermogelling nanoemulsion materials used to systematically create hydrogels with a secondary phase at different size scales. The puncture method used to quantify material strength is then described and, finally, the role of damage nucleation during the puncture process is considered. These results have strong implications for designing multiphase soft materials with templated porosity that maintain mechanical integrity, and provide guidelines for the use of such materials in structural applications such as scaffolds for tissue engineering or in high-pressure separations technologies.20–22
1 Experimental
1.1 Materials
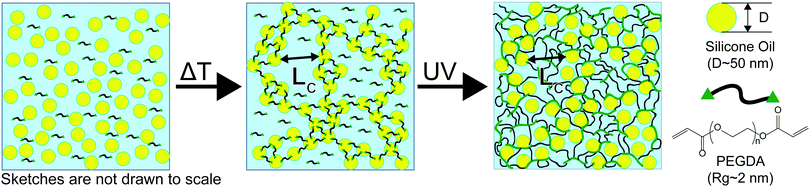
As the assembly process is driven by colloidal “bonds” formed through physical interactions and not chemical changes, these colloidal gels are thermoreversible and can be kinetically trapped at different size scales of assembly (0.1–10 μm)17–19 due to a process of coarsening and arrest of spinodal phase separation.19 Once a colloidal network is formed, its structure is made permanent by photocuring the acrylate end group of PEGDA through free radical polymerization, initiated by incorporation of 100 μL of 2-hydroxy-2-methyl-propiophenone for every 40 mL of nanoemulsion. In previous work, it has been demonstrated that the length scale of heterogeneity imparted by arrested phase separation within the colloidal gel is not significantly affected by the crosslinking process.13,17,18
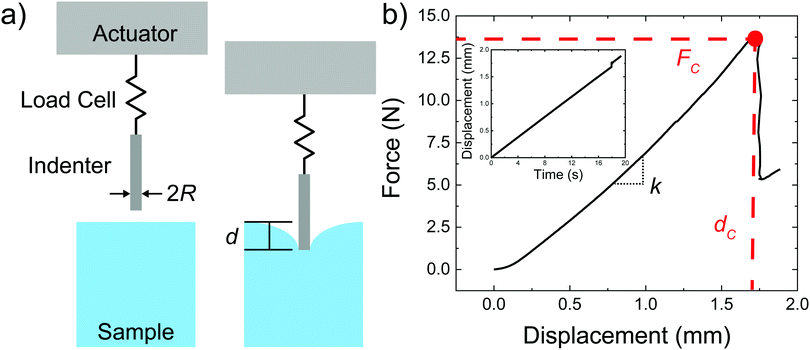
Images of the sample geometry used to prepare puncture samples are shown in ESI,† Fig. S2. Samples for puncture were made with 3 mL of material in a 5 mL vial with a conical base and an internal diameter of 14.5 mm. The height of the sample filled above the bottom cone was ∼17.5 mm while the height of the cone was ∼5 mm. Samples were punctured with a 2 mm diameter flat steel cylinder. Dimensions of the sample and probe were kept constant so as not to convolute changes in material behavior with finite sample size effects, for which no quantitative guidelines have been developed for puncture tests. Samples for optical microscopy were produced by adding a nanoemulsion solution to a container constructed of two 100 μm thick glass coverslips separated by 1 mm thick cut glass slides that were super glued to one of the coverslips. Samples were aged in an oven (Isotemp Incubator Model 6858 from Fisher Scientific) with a passive heat block under different temperature ramps. Temperature profiles during thermal treatment were monitored via thermocouple (6802 II Dual Channel Digital Thermometer). UV curing was performed by exposing the samples at 365 nm from the bottom of the vial for 5 minutes with an Analytikjena UVGL-15 4 watt UV lamp. The samples were further exposed to UV irradiation for an additional 5 minutes with the lamp positioned above the samples to ensure a homogeneous cure throughout the material.
Drawing on the functionality of these photocrosslinkable thermogelling nanoemulsions, composite hydrogels with an interpenetrated hydrophobic network assembled at different size scales were produced at values of Lc close to the underlying material heterogeneity ∼50 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 as well as around and above
25 as well as around and above 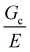 of the hydrogel phase. The shear modulus of the hydrogel phase was measured via rheological characterization, described in the ESI,† and multiplied by a factor of 3 to get a value of E = 3.6 MPa for Young's modulus. Note that this high value of the modulus suggests that these networks are densely, not lightly, crosslinked. Following the scaling argument presented in the introduction,
of the hydrogel phase. The shear modulus of the hydrogel phase was measured via rheological characterization, described in the ESI,† and multiplied by a factor of 3 to get a value of E = 3.6 MPa for Young's modulus. Note that this high value of the modulus suggests that these networks are densely, not lightly, crosslinked. Following the scaling argument presented in the introduction, 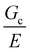 can be estimated as being on the order of 14.6 μm. This is within a factor of 3 to the value of
can be estimated as being on the order of 14.6 μm. This is within a factor of 3 to the value of 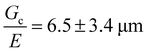 measured experimentally using notch tests that are described fully in the ESI.† The agreement of these measurements suggests that
measured experimentally using notch tests that are described fully in the ESI.† The agreement of these measurements suggests that 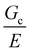 can be estimated in such cases where direct measurement is difficult or not possible.
can be estimated in such cases where direct measurement is difficult or not possible.
While the experiments presented in this work focus on the elastofracture length, it is also possible for the elastocapillary length (defined as the ratio of the interfacial tension γ to E) to drive the mechanical response of soft gels. Here these effects are not considered based on the high stiffness of these gels. Estimating the interfacial tension between the hydrogel and silicone oil droplets as γ = 40 mN m−1 and E = 3.6 MPa gives 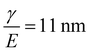 . This value is a factor of two smaller than the smallest droplet radius employed in this work. Moreover, the droplets in these nanoemulsions are stabilized by surfactant, which makes a value of 40 mN m−1 likely to be a significant overestimate of the interfacial tension. However, we note the possibility that the system under study could be used to to examine elastocapillary effects for much softer hydrogel systems.
. This value is a factor of two smaller than the smallest droplet radius employed in this work. Moreover, the droplets in these nanoemulsions are stabilized by surfactant, which makes a value of 40 mN m−1 likely to be a significant overestimate of the interfacial tension. However, we note the possibility that the system under study could be used to to examine elastocapillary effects for much softer hydrogel systems.
The size distribution of the droplets after multiple cycles/pulses was monitored using dynamic light scattering (DLS) with a BI-200SM Goniometer System with a TurboCorr correlator (Brookhaven Instruments) and a Cobolt Samba 500 mW laser operating at 532 nm (Hübner Photonics). DLS measurements were carried out at a 90° scattering angle with 200 correlation channels ranging from 100 ns to 100 ms and sampling rates of 100 ns, 5 ms, and 50 ms, depending on the channel delay. 100 μL of nanoemulsion was diluted with 3 mL of deionized (18.3 MΩ) water in a borosilicate glass test tube. The sample was then loaded into an index-matched recirculating bath at 20 °C and with a 2 minute measurement time. The measurements were used to infer the Z-average hydrodynamic droplet sizes. For samples containing assembled droplets, the target Z-average diameter was 50 nm. For samples containing dispersed droplets, target Z-average diameters ranged from 25–75 nm, regardless of the emulsification method employed. Dispersity values, defined as the square of the ratio of the standard error σ of the particle size distribution normalized by the average particle diameter 2b (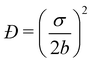 ), were calculated from the second-order cumulant of the autocorrelation function and were approximately 0.3 for all samples.
), were calculated from the second-order cumulant of the autocorrelation function and were approximately 0.3 for all samples.
1.2 Methods
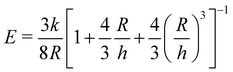 | (1) |
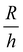 is a geometric constant that corrects the analysis for the influence of finite sample thickness, and does not represent a stretch ratio. The failure during puncture is quantified by the critical puncture force Fc and displacement dc. There is a slight nonlinearity observed in the force displacement curve at high displacements. As discussed fully in the ESI,† the extensional strains on the surface at puncture are small enough (1–3%) that the material should display linear elastic behavior. This suggests that the apparent nonlinearity is likely associated with the development of hydrostatic stress below the indenter and not the material accessing a high strain nonlinear elastic response. Summary of the data gathered is available in ESI,† Table S1.
is a geometric constant that corrects the analysis for the influence of finite sample thickness, and does not represent a stretch ratio. The failure during puncture is quantified by the critical puncture force Fc and displacement dc. There is a slight nonlinearity observed in the force displacement curve at high displacements. As discussed fully in the ESI,† the extensional strains on the surface at puncture are small enough (1–3%) that the material should display linear elastic behavior. This suggests that the apparent nonlinearity is likely associated with the development of hydrostatic stress below the indenter and not the material accessing a high strain nonlinear elastic response. Summary of the data gathered is available in ESI,† Table S1.
Further, the microstructure of the assembled nanoemulsion droplets under the precise conditions used in this work has been extensively characterized previously by a combination of small angle neutron scattering, cryo-TEM and optical microscopy.19,39 It was found that the structure of the assembled nanoemulsions could be accurately described using a model involving a bicontinuous phase separated network consisting of droplet-dense and droplet-dilute phases, in which the droplet-dense phase is arranged in a dense fractal structure with an associated mass fractal dimension of ∼2.7. This fractal dimension is consistent with that for random close packing of spheres, and so any interstitial space between droplets is on the order of the mesh size of the surrounding PEGDA matrix. This picture of the structure of the nanoemulsion phase was supported by cryo-TEM images. Because of this, it is reasonable to expect that individual droplets in the assembled droplet networks do not themselves act as defects for crack propagation (although they would in the unassembled state due to their isolated nature). Rather, it is the larger phase separated domains that likely act as defects when the droplets are assembled. In the previous studies, a sharp scattering peak in the micron size range was observed, whose shape was consistent with a narrow distribution of domain sizes arising from late-stage spinodal decomposition.
2 Deep indentation and puncture of composite hydrogels
Plots of the raw metrics extracted from deep indentation and puncture of the composite hydrogels for samples with varying Lc are shown in Fig. 4. When the temperature at which the sample is exposed to UV irradiation is less than the colloidal gelation temperature, TUV < TGel, the secondary phase is composed of distributed nanodroplets at size scales similar to the underlying heterogeneity of the hydrogel phase (∼50 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13,25). When TUV > TGel, the secondary phase consists of an assembled droplet-rich phase at size scales around and above
13,25). When TUV > TGel, the secondary phase consists of an assembled droplet-rich phase at size scales around and above 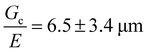 determined for the non-composite hydrogel. E appears to be fairly independent of Lc and varies from 2.5 ± 0.3 MPa in the dispersed droplet samples down to 1.7 ± 0.3 MPa in the assembled droplet samples. The modulus of the continuous hydrogel phase was measured to be 3.6 MPa. Replacing
determined for the non-composite hydrogel. E appears to be fairly independent of Lc and varies from 2.5 ± 0.3 MPa in the dispersed droplet samples down to 1.7 ± 0.3 MPa in the assembled droplet samples. The modulus of the continuous hydrogel phase was measured to be 3.6 MPa. Replacing 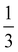 of the load bearing network with oil droplets would result in a predicted value of
of the load bearing network with oil droplets would result in a predicted value of 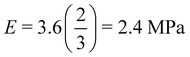 which appears consistent with the value measured in the dispersed droplet samples. The further reduction in modulus in assembled droplet samples is likely due to a composite stiffness effect. The modulus of the assembled phase is estimated using a similar load bearing network argument as that above while assuming that the droplet-rich phase has a silicone volume fraction of 0.64 consistent with random-packed non-deformable spheres (E = 3.6(1 − 0.64) = 1.296 MPa). Calculating a rule of mixtures estimate with the droplet and hydrogel phases loaded in parallel and series gives estimates of E = 2.5 MPa and E = 1.9 MPa, respectively, and the experimental value appears to be reasonably consistent with the lower bound theoretical estimate. The slight overestimation of this value from theory may be attributed to error in either estimating the density of silicone in the assembled phase or in using the load bearing network argument to estimate E in the assembled phase.
which appears consistent with the value measured in the dispersed droplet samples. The further reduction in modulus in assembled droplet samples is likely due to a composite stiffness effect. The modulus of the assembled phase is estimated using a similar load bearing network argument as that above while assuming that the droplet-rich phase has a silicone volume fraction of 0.64 consistent with random-packed non-deformable spheres (E = 3.6(1 − 0.64) = 1.296 MPa). Calculating a rule of mixtures estimate with the droplet and hydrogel phases loaded in parallel and series gives estimates of E = 2.5 MPa and E = 1.9 MPa, respectively, and the experimental value appears to be reasonably consistent with the lower bound theoretical estimate. The slight overestimation of this value from theory may be attributed to error in either estimating the density of silicone in the assembled phase or in using the load bearing network argument to estimate E in the assembled phase.
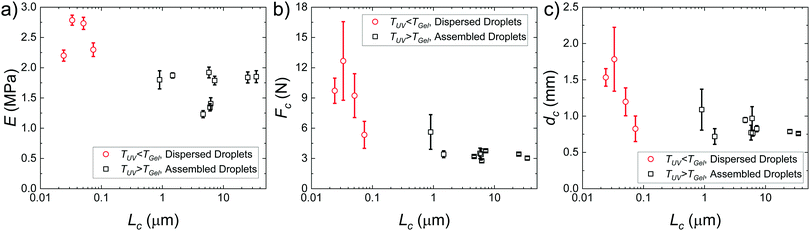 | ||
| Fig. 4 Plots showing the (a) elastic modulus, (b) critical puncture force, and (c) critical puncture displacement with respect to characteristic size scale of the secondary phase. | ||
Two distinct behaviors are observed when comparing Fc to Lc (Fig. 4b). When TUV < TGel, the puncture force appears to be inversely proportional to Lc and is larger than in the assembled droplet samples. When TUV > TGel, Fc appears to be largely independent of Lc and smaller than in the dispersed droplet samples. A similar inverse dependence of dc with Lc is observed in the dispersed droplet samples; however, the values of dc do not appear to be sensitive to Lc in the assembled droplet case. The strength of a material during puncture is defined by the nominal stress that the material can support before failure. Since the geometry of the indenter and samples remains constant, the reduction in Fc indicates that assembly of the droplets into network structure with size scales around 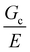 decreases the puncture strength of a material.
decreases the puncture strength of a material.
If a critical flaw size argument holds, the strength of a material should relate to the critical stress intensity factor K1c and the critical flaw size a.40
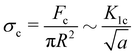 | (2) |
Assuming that linear elastic fracture mechanics (LEFM) are valid gives 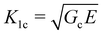 ,40 which can be substituted into eqn (2) and rearranged to relate the strength to
,40 which can be substituted into eqn (2) and rearranged to relate the strength to 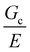 and a.
and a.
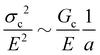 | (3) |
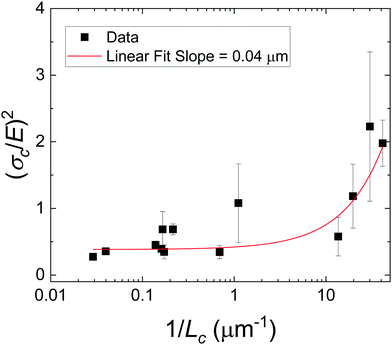
As there is no initial pre-notch or macroscopic defect introduced into the material before puncture, the critical flaw size is likely determined by structural size scales such as Lc. A plot showing (σc/E) 2 for varying 1/Lc (Fig. 5) produces a linear slope, which represents 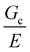 multiplied by a geometric constant that should not vary between samples. This slope is expected to alter for the dispersed droplet samples, where LEFM is expected to be invalid because the size scale of the defects are well below the elastofracture length.40 While the puncture strength is reduced when the droplets are arranged into a secondary structure, a single slope of 0.04 μm (with a y-intercept of 0.38) appears to fit all of the samples measured. This is counter to the expectation that distinct slopes would be observed in each regime with the dispersed droplet samples being largely independent given that
multiplied by a geometric constant that should not vary between samples. This slope is expected to alter for the dispersed droplet samples, where LEFM is expected to be invalid because the size scale of the defects are well below the elastofracture length.40 While the puncture strength is reduced when the droplets are arranged into a secondary structure, a single slope of 0.04 μm (with a y-intercept of 0.38) appears to fit all of the samples measured. This is counter to the expectation that distinct slopes would be observed in each regime with the dispersed droplet samples being largely independent given that 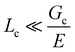 . These results likely indicate that the assumption that a = Lc for the samples containing dispersed droplets does not hold. This means that the critical flaw size argument laid out above does not hold for failure of these materials. This is attributed to a failure of the critical flaw size argument and not a breakdown of LEFM because the slight nonlinearity observed in Fig. 2b is likely associated with hydrostatic compression below the probe which would not drive failure. This suggests that the failure is more complicated than a simple crack propagation process and likely initiates through a complex damage nucleation process. This nucleation process is critical for understanding the failure strength of a material, and will set design limits in many applications. The observation that Fc reduces in the assembled droplet samples suggests that the size scale of the secondary phase influences this damage nucleation process in an “on/off” manner between the assembled and dispersed droplet cases.
. These results likely indicate that the assumption that a = Lc for the samples containing dispersed droplets does not hold. This means that the critical flaw size argument laid out above does not hold for failure of these materials. This is attributed to a failure of the critical flaw size argument and not a breakdown of LEFM because the slight nonlinearity observed in Fig. 2b is likely associated with hydrostatic compression below the probe which would not drive failure. This suggests that the failure is more complicated than a simple crack propagation process and likely initiates through a complex damage nucleation process. This nucleation process is critical for understanding the failure strength of a material, and will set design limits in many applications. The observation that Fc reduces in the assembled droplet samples suggests that the size scale of the secondary phase influences this damage nucleation process in an “on/off” manner between the assembled and dispersed droplet cases.
Overall, the results of these experiments reveal that the mechanics of a composite gel can be sensitive to the size scale of the secondary phase, though not through a critical flaw size argument. E was shown to be consistent with a simple chain density argument when the secondary phase was uniformly dispersed, and alternatively with a conventional composite theory when the droplets were assembled into a bicontinuous microstructure. The puncture strength of a composite gel was shown to decrease once the size scale of the secondary phase approaches the elastofracture length of the primary gel phase. Values of 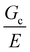 were readily estimated for different systems using scalings from classical theory in combination with typical values of Gc and E. Together these results highlight the importance of controlling the size scale of the secondary phase when developing composite soft solids with controlled porosity for structural applications, such as load-bearing scaffolds for tissue engineering or high-pressure separations technologies, where mechanical integrity is critical.
were readily estimated for different systems using scalings from classical theory in combination with typical values of Gc and E. Together these results highlight the importance of controlling the size scale of the secondary phase when developing composite soft solids with controlled porosity for structural applications, such as load-bearing scaffolds for tissue engineering or high-pressure separations technologies, where mechanical integrity is critical.
These results demonstrate that the strength of a composite soft solid can be sensitive to the size scale of the secondary phase, though not in a manner consistent with a critical flaw size argument. However, our findings are subject to certain limitations. First, the observation that failure initiates through a damage nucleation process is a consequence of the puncture technique used to quantify material strength. No initial notch is introduced into the material and thus the failure strength includes the energy required to nucleate a crack.32 This technique was employed as the materials were too brittle to manipulate into a notch test geometry. Performing notch tests on a similar composite that is less brittle is of interest in the future as it would enable the quantification of the fracture energy without a contribution from the nucleation process. We note that selecting a less brittle material will increase 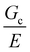 , requiring a significant increase in the size scale of the secondary phase in order to cover the same range of
, requiring a significant increase in the size scale of the secondary phase in order to cover the same range of 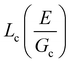 , likely into the range of Lc ∼ 0.1–1 mm, which would not be accessible with the current material system. Second, our analysis assumes that Lc in the case of dispersed droplets can be represented as the radius of the droplets. For this to be true, the droplets would need to be uniformly dispersed throughout the material; however, it is possible that the random motions of the droplets form larger structures below TGel that persist over short timescales and may be stabilized during the photopolymerization process.19,30
, likely into the range of Lc ∼ 0.1–1 mm, which would not be accessible with the current material system. Second, our analysis assumes that Lc in the case of dispersed droplets can be represented as the radius of the droplets. For this to be true, the droplets would need to be uniformly dispersed throughout the material; however, it is possible that the random motions of the droplets form larger structures below TGel that persist over short timescales and may be stabilized during the photopolymerization process.19,30
3 Conclusions
Photocrosslinkable thermogelling nanoemulsions were used to create composite hydrogels where the size scale of the secondary phase was altered. This control over composite structure was employed to examine how the length scale of the secondary phase can be used to alter the linear and nonlinear mechanical properties of such soft composite materials. Deep indentation and puncture measurements revealed that the elastic modulus of these systems agreed with conventional theories for two-phase composites. It was also found that the strength reduces once the size scale of the secondary phases becomes close to the elastofracture length. These results demonstrate that the strength of a fluid–filled composite is sensitive to the assembly size scale of the secondary phase.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Professor Robert M. McMeeking for helpful discussions on the estimation of the surface strains at puncture. This work was supported by the Materials Research Science and Engineering Center (MRSEC) Program of the National Science Foundation under Award No. DMR 1720256 (IRG-3). This work was performed within the research facilities within the California NanoSystems Institute, supported by the University of California, Santa Barbara and the University of California, Office of the President, and leveraged resources supported by the National Science Foundation under Award No. DMR-1933487.References
- N. Cohen, J. H. Waite, R. M. McMeeking and M. T. Valentine, Philos. Trans. R. Soc., B, 2019, 374, 1–7 Search PubMed.
- S. Budday, T. C. Ovaert, G. A. Holzapfel, P. Steinmann and E. Kuhl, Arch. Comput. Methods Eng., 2020, 27, 1187–1230 CrossRef.
- J. Norman, J. G. Shapter, K. Short, L. J. Smith and N. L. Fazzalari, J. Biomed. Mater. Res., Part A, 2008, 87, 196–202 CrossRef PubMed.
- F. S. Bates, M. F. Schulz, A. K. Khandpur, S. Forster and J. H. Rosedale, Faraday Discuss., 1994, 98, 7–18 RSC.
- J. Cui, M. A. Lackey, G. N. Tew and A. J. Crosby, Macromolecules, 2012, 45, 6104–6110 CrossRef CAS.
- A. E. Jakus, N. R. Geisendorfer, P. L. Lewis and R. N. Shah, Acta Biomater., 2018, 72, 94–109 CrossRef CAS PubMed.
- L. C. Hwa, S. Rajoo, A. M. Noor, N. Ahmad and M. B. Uday, Curr. Opin. Solid State Mater. Sci., 2017, 21, 323–347 CrossRef CAS.
- P. Bedarf, A. Dutto, M. Zanini and B. Dillenburger, Autom. Constr., 2021, 130, 103861 CrossRef.
- Y. J. Lee and P. V. Braun, Adv. Mater., 2003, 15, 563–566 CrossRef CAS.
- Y. J. Lee, S. A. Pruzinsky and P. V. Braun, Langmuir, 2004, 20, 3096–3106 CrossRef CAS PubMed.
- B. Hatton, L. Mishchenko, S. Davis, K. H. Sandhage and J. Aizenberg, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 10354–10359 CrossRef CAS PubMed.
- M. N. Lee and A. Mohraz, Adv. Mater., 2010, 22, 4836–4841 CrossRef CAS PubMed.
- M. E. Helgeson, S. E. Moran, H. Z. An and P. S. Doyle, Nat. Mater., 2012, 11, 344–352 CrossRef CAS PubMed.
- M. E. Helgeson, Curr. Opin. Colloid Interface Sci., 2016, 25, 39–50 CrossRef CAS.
- Y. S. Zhang, C. Zhu and Y. Xia, Adv. Mater., 2017, 29, 1–25 Search PubMed.
- M. E. Seitz, W. R. Burghardt, K. T. Faber and K. R. Shull, Macromolecules, 2007, 40, 1218–1226 CrossRef CAS.
- L. C. Hsiao and P. S. Doyle, Soft Matter, 2015, 11, 8426–8431 RSC.
- L. C. Hsiao, A. Z. Badruddoza, L.-C. Cheng and P. S. Doyle, Soft Matter, 2017, 13, 921–929 RSC.
- Y. Gao, J. Kim and M. E. Helgeson, Soft Matter, 2015, 11, 6360–6370 RSC.
- S. Yang, K. Leong, Z. Du and C. Chua, Tissue Eng., 2001, 7, 679–689 CrossRef CAS PubMed.
- S. Yang, K. F. Leong, Z. Du and C. K. Chua, Tissue Eng., 2002, 8, 1–11 CrossRef CAS PubMed.
- I. M. El-Sherbiny and M. H. Yacoub, Glob. Cardiol. Sci. Pract., 2013, 2013, 38 CrossRef PubMed.
- C. T. Herakovich, Mech. Res. Commun., 2012, 41, 1–20 CrossRef.
- X. Zhao, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8138–8140 CrossRef CAS PubMed.
- P. Malo De Molina, S. Lad and M. E. Helgeson, Macromolecules, 2015, 48, 5402–5411 CrossRef CAS.
- C. Creton and M. Ciccotti, Rep. Prog. Phys., 2016, 79, 046601 CrossRef PubMed.
- P. J. Flory, Chem. Rev., 1944, 35, 51–75 CrossRef CAS.
- P. Flory, Polymer, 1985, 17, 1–12 CAS.
- G. J. Lake and A. G. Thomas, Proc. R. Soc. London, Ser. A, 1967, 300, 108–119 CAS.
- J. Kim, Y. Gao, C. Hebebrand, E. Peirtsegaele and M. E. Helgeson, Soft Matter, 2013, 9, 6897–6910 RSC.
- A. Gupta, H. B. Eral, T. A. Hatton and P. S. Doyle, Soft Matter, 2016, 12, 2826–2841 RSC.
- S. Fakhouri, S. B. Hutchens and A. J. Crosby, Soft Matter, 2015, 11, 4723–4730 RSC.
- S. Rattan and A. J. Crosby, Extreme Mech. Lett., 2018, 24, 14–20 CrossRef.
- S. Rattan, L. Li, H. K. Lau, A. J. Crosby and K. L. Kiick, Soft Matter, 2018, 14, 3478–3489 RSC.
- S. Rattan and A. J. Crosby, ACS Macro Lett., 2019, 8, 492–498 CrossRef CAS PubMed.
- C. W. Barney, C. Chen and A. J. Crosby, Soft Matter, 2021, 17, 5574–5580 RSC.
- K. R. Shull, D. Ahn, W.-L. Chen, C. M. Flanigan and A. J. Crosby, Macromol. Chem. Phys., 1998, 199, 489–511 CrossRef CAS.
- Y. Gao and M. E. Helgeson, Opt. Express, 2014, 22, 10046 CrossRef CAS PubMed.
- M. E. Helgeson, Y. Gao, S. E. Moran, J. Lee, M. Godfrin, A. Tripathi, A. Bose and P. S. Doyle, Soft Matter, 2014, 10, 3122–3133 RSC.
- J. G. Williams, Polym. Eng. Sci., 1977, 17, 144–149 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00177b |
| This journal is © The Royal Society of Chemistry 2022 |