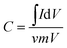Study on the relation between pore size and supercapacitance in mesoporous carbon electrodes with silica-supported carbon nanomembranes

Abstract

Electrochemical capacitors (ECs) have traditionally been considered as standing at the opposite end against batteries in energy–power diagram. They charge and discharge faster than batteries but are limited by much lower energy density. By optimizing the pore structure of porous electrode materials, the performance of ECs could overcome this limitation. However to date, no study has addressed the complex relationship between the texture parameters of the electrode materials and the supercapacitance of ECs. Using silica-supported carbon nanomembranes, four electrode materials with similar pore geometry are generated. The electrodes with a pore size of 4.14 nm shows the highest capacitance of 305 F g⁻¹ in aqueous electrolytes. A new model is developed to simulate the accommodation of the solvated ions at the electrode surface. The simulation reveals that the optimal capacitance of ECs can be achieved using porous carbon electrode materials with open pores of 3.0–5.0 nm.

---

1. Introduction

Electrochemical capacitors are the essential components of high-rate electric devices used in the development of portable systems, electric vehicles and hybrid electric vehicles. Such capacitors are based on electrochemical charge accommodation at the electrical double layer (EDL) (in the case of EDL capacitors, EDLCs) and/or the occurrence of Faradaic reactions (in the case of pseudocapacitors).^1–3 In recent years, the development of electrode materials for high-performance EDLCs has attracted considerable research interest, and porous carbon materials are regarded as the first-candidate electrode materials for EDLCs owing to their high surface areas, tunable structures, and good conductivities.⁴ Therefore, various porous carbon materials have been lately developed for EDLC applications.^5–13 The pore structures of these carbon nanomaterials can be microporous, mesoporous, or hierarchical, and specific surface areas (SSA) are up to several thousand square meters per gram. The specific capacitances of these electrode materials, however, are typically below 200 F g⁻¹, significantly lower than the theoretical values.² Unfortunately, the effect of the texture parameters of porous electrode materials on the EDL capacitance still remains unexplained, rendering the improvement of capacitances of electrode materials to be a great challenge.

The capacitance (C) of a planar EDLC can be expressed by the Helmholtz equation as follows:

where S is the electrode surface area accessible to electrolyte ions, ε_r is the relative static permittivity, ε₀ is the electric constant (8.854 × 10⁻¹² F m⁻¹), and d is the separation between the electrolyte ions and electrode. Given the small d values (0.2–1.0 nm),² the theoretical specific EDL capacitance would be in the range of 40–200 μF cm⁻². However, the specific capacitance of porous carbon drops to only several microfarads per square centimetre, when SSA reaches over 1500 m² g⁻¹ because most of the micropores are inaccessible to solvated ions owing to closed pores or narrow bottlenecks. Recently, Gogotsi et al. discovered the ‘anomalous increase’ of supercapacitance in microporous region by using carbons derived from metal carbide (CDCs) electrodes.^11–13 Therefore, many theoretical and experimental efforts had been devoted to understand the relation between the nanoporous structure of carbon electrodes and their electrochemical performance.^14–20 It is now well acknowledged that pores with diameters comparable to the sizes of the solvated ions are optimal for high specific capacitance. However, for pulse power applications, the extremely narrow pores may present certain adverse effects as the ion transport is severely restricted in pores because of their sizes similar to those of the ions during the supercapacitor charge–discharge. The increase of the pore size in the mesoporous region might be beneficial for both the high energy and power outputs of supercapacitors. However, the pore size effect on supercapacitance in this region is still not considerably explored.

Carbon nanomembranes (CNMs) are conductive membranes with a thickness of approximately one nanometre. They are fabricated by the crosslinking of surface bound self-assembled monolayers of carbon-rich compounds.^21–24 We recently developed a kind of three-dimensional (3D) CNMs, namely silica-supported carbon nanomembranes (SS-CNMs) on the surfaces (both internal and external) of mesoporous silica SBA-15 through Bergman cyclization of an enediyne monolayer grafted onto the surface of mesoporous silica followed by carbonization.²⁵ Because electrochemical charge accommodation in EDLCs takes place exclusively at the surface, these SS-CNMs are expected to similarly act towards ordered mesoporous carbon (OMC) electrode materials. However, the pore structure variability of the SS-CNMs is considerably higher than that of conventional OMCs owing to the rapid development of mesoporous silicas.²⁶ Moreover, these SS-CNMs are free from pore structure complication that typically occurs in the preparation of OMCs, making them the ideal candidates for studying the relation between pore size and EDL capacitance in mesoporous region. Thus, we fabricated four SS-CNMs with similar geometry but different mesopore sizes as supercapacitor electrode materials and found that SS-CNMs with medium pore size exhibited the highest capacitance.

2. Experimental section

Materials

The SBA-15-supported carbon nanomembrane (denoted SS-CNM-2) was prepared according to our recently published procedure.²³ SS-CNM-1, SS-CNM-3 and SS-CNM-4 were prepared according to the similar procedure with MCM-41 (ref. 27) and pore-expanded SBA-15s^28,29 as templates, respectively.

Characterizations

The morphology of the samples was investigated using a transmission electron microscope (TEM, JEOL, JEM-2010) operated at 200 kV. X-ray diffraction (XRD) patterns were obtained on a RIGAKU D/MAX 2550 VB/PC X-ray diffractometer (Cu Kα radiation generated at 40 kV and 450 mA). Thermogravimetric analyses (TGA) were conducted on a TG/WRT-2P in air. Nitrogen adsorption–desorption isotherms were measured with an adsorption apparatus on an ASAP2010 instrument. The surface areas of the samples were determined from the Brunauer–Emmett–Teller (BET) equation and pore volumes from the desorption branches of the isotherms were measured using the Barrett–Joyner–Halenda (BJH) method.

Electrochemical tests

Electrochemical measurements were performed in a three-electrode cell with an electrochemical analyser (CHI660D workstation). In an aqueous solution, a carbon paper coated with SS-CNM (2–3 mg), platinum gauze (99.9%), and a Hg/HgO electrode were used as working, counter, and reference electrodes, respectively. In organic solution, silver wire was used, instead of the Hg/HgO electrode, and the cell was carefully sealed under vacuum. To evaluate electrochemical capacitor characteristics, cyclic voltammetry (CV) and chronopotentiometry were carried out either in 6 M KOH or deionized water. The mass specific capacitance of electrode can be calculated according to the following equation:³⁰
where C is the specific capacitance based on the mass of electroactive materials (F g⁻¹), I is the response current density (A g⁻¹), V is the potential window (V), ν is the potential scan rate (V s⁻¹), and m is the mass of the SS-CNM materials in the electrodes (g).

3. Results and discussion

Mesoporous silicas of the same space group (p6mm) but different pore size (MCM-41, SBA-15, and two pore-expanded SBA-15s)^27–29,31 were used as supports to fabricate SS-CNMs with small (SS-CNM-1) to large (SS-CNM-4) mesopores by following our recently published procedure (Fig. 1).²⁵ Fig. 2a–d shows the transmission electron microscopy (TEM) images of the SS-CNMs. The straight lattice edge indicates that SS-CNMs exhibit well-ordered arrays of mesopores after the introduction of the CNMs. Previous work carried out by our group confirmed that the CNMs were uniformly coated on the channel surface of the silica. Even after etching off the silica framework, the mesoporous channels originating from the carbon remained intact.²³ The spacings between the lattice fringes of these SS-CNMs were determined with TEM to be 4.2 nm, 8.2 nm, 8.5 nm and 10.0 nm, respectively, indicating that the values for the mesoporous silica supports were retained.

Fig. 1 Schematic illustration of the conversion of mesoporous silicas to silica-supported carbon nanomembranes. (1) Formation of self-assembled monolayer of enediyne compounds on the surface of mesoporous silicas (where PE is an abbreviation of ‘pore-expanded’). (2) Bergman cyclization under elevated temperature. (3) Carbonization in an inert atmosphere under high temperature to create a thin and strong carbon nanomembrane on the surface of mesoporous silicas.

Fig. 2 TEM images of (a) SS-CNM-1, (b) SS-CNM-2, (c) SS-CNM-3 and (d) SS-CNM-4; scale bar: 20 nm.

Small-angle X-ray diffraction patterns (Fig. 3) of the SS-CNMs show well-resolved peaks that are indexable as (100), (110), and (200) reflections, associated with p6mm hexagonal symmetry. The intense (100) peaks reveal d spacings of 4.4, 8.5, 8.7 and 9.7 nm, respectively, consistent with that obtained from TEM. The contents of carbon in these SS-CNMs were determined by TGA performed under air (Fig. 4). The SS-CNM-1 has higher carbon content (16.02%) than SS-CNM-2 (12.33%), SS-CNM-3 (8.76%) and SS-CNM-4 (6.00%) due to the higher SSA of the MCM-41 support.

Fig. 3 Small angle X-ray diffraction patterns of SS-CNM-1 (red), SS-CNM-2 (green), SS-CNM-3 (blue) and SS-CNM-4 (purple).

Fig. 4 TGA curves of SS-CNM-1 (red), SS-CNM-2 (green), SS-CNM-3 (blue) and SS-CNM-4 (purple).

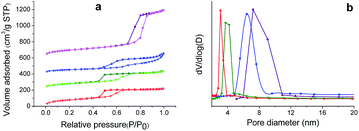
The nitrogen adsorption–desorption isotherms for SS-CNMs are shown in Fig. 5a, where obvious hysteresis loops are observed in the pressure range of 0.4–0.8p/p₀, indicating the presence of mesoporosity in all the samples. The Brunauer–Emmett–Teller (BET) surface areas, pore sizes, and total pore volumes are listed in Table 1. As expected, these values are less than those of mesoporous silica supports, indicating the role of the CNMs in the channels. Fig. 5b shows the mesopore size distribution curves of the four SS-CNMs calculated with the Barrett–Joyner–Halenda (BJH) method. The narrow pore size distributions of the four samples indicate that the pores of these materials are uniform, and the highly ordered structures of the mesoporous silica supports are preserved despite the decrease of mesopore size. The SSA of all these SS-CNMs are predominantly contributed by mesopores, which is possibly due to the micropores in the supports being covered during the formation of the enediyne monolayers and carbonization, making SS-CNMs an ideal candidates for studying the relationship between mesopore size and EDLC performance.

Fig. 5 (a) Nitrogen sorption isotherms and (b) normalized pore size distribution curves of SS-CNM-1 (red), SS-CNM-2 (green), SS-CNM-3 (blue) and SS-CNM-4 (purple). In nitrogen sorption isotherms, lighter colours were used in all the adsorption branches and the curves of SS-CNM-2, SS-CNM-3 and SS-CNM-4 were moved up along the vertical axis for clarity.

Table 1 Texture parameters of the SS-CNMs

Sample	BET surface area (m^2 g^−1)	Pore size (nm)	Pore volume (cm^3 g^−1)
SS-CNM-1	450	3.05	0.41
SS-CNM-2	280	4.14	0.37
SS-CNM-3	190	6.68	0.40
SS-CNM-4	350	8.02	0.92

---

Electrochemical measurements were performed in aqueous (6 M KOH) electrolytes with cyclic voltammetry (CV) techniques for measuring capacitance. The CV curves (Fig. 6a) of all the samples are quasi-rectangular in shape along the current–potential axis, indicating that the samples display ideal capacitive behaviour.³² The galvanostatic charge–discharge curves of the three SS-CNMs are linear and symmetrical (Fig. 6b), which is a typical characteristic of an ideal EDL capacitor. No obvious IR drop is observed for any of the curves, indicating a low internal resistance. Electrochemical impedance spectroscopy (Fig. 6d) revealed low equivalent series resistances (<0.5 Ω) and short relaxation time constants (τ₀), ensuring a high rate response. It is notable that high specific capacitance of 305 F g⁻¹ is obtained for SS-CNM-2 at 10 mV s⁻¹, which is superior to 68, 173, and 75 F g⁻¹ for SS-CNM-1, SS-CNM-3 and SS-CNM-4 composites, respectively. With an increase in the pore size from 3.66 to 10.47 nm, the specific capacitance initially increases and then decreases. This curved capacitance trend in the small-mesopore region is attributed to the trade-off between the increase of the hosting capacity of mesopores for solvated ions and the decrease of the SSA.

Fig. 6 Electrochemical evaluation of SS-CNM electrode materials (SS-CNM-1, red; SS-CNM-2, green; SS-CNM-3, blue; SS-CNM-4, purple) using an aqueous electrolyte of 6.0 M potassium hydroxide (KOH) dissolved in deionized water. (a) CV curves of four SS-CNM electrode materials at a scan rate of 0.05 V s⁻¹, showing a considerably larger CV area of SS-CNM-2 than the other three SS-CNMs. (b) Galvanostatic charge–discharge curves of SS-CNM electrode materials when operated at a current density of 5 A g⁻¹, showing a near symmetric triangular shapes for all the electrode materials and a considerably longer charging/discharging time of SS-CNM-2 than the other three SS-CNMs at the same current density. (c) Stack capacitance values calculated from CV curves as a function of the scan rate. (d) Impedance Nyquist plots of the SS-CNMs, showing a considerable steeper plot for SS-CNM-2 than the other three SS-CNMs.

Many recent studies have attempted to clarify the relation between pore size and EDL capacitance.^4,18–20 A conceptual limitation of these studies is the assumption of pores being slits or tunnels in the walls of infinite thickness representing porous electrode materials, which actually possess complex geometries. The pore size and SSA cannot vary without changing each other and/or the wall structure of the porous materials, in particular, when the pore size and wall thickness are of nanometre scale. A general model to explain the complex relationship between the texture parameter and capacitance has been lacking, and the pore size effect on capacitance remains unexplained.

The fractal dimension was suggested by many studies to describe the complex geometry of porous carbon materials.³³ Fig. 7 shows our simulation (see ESI†) on the theoretical capacitance versus the ratio of the pore and solvated ion diameters (R/r) in a porous electrode with a fractal dimension D of 2.5. In region I, when the pore size is close to the diameter of the solvated ion, the specific capacitance increases with a decrease in pore size, similar to the trend reported by Gogotsi et al. in the CDC system.^11–13 The hosting capacity of a cylinder channel does not considerably change in this region; however, the SSA constantly increases with a decrease in pore size. In addition, the solvated shell may become highly distorted to squeeze through the narrow pore¹² and further boost the capacitance. In region II, the SSA slowly decreases with an increase in pore size; however, the solvated-ion hosting capacity of mesopores sharply increases around R/r = 2, resulting in a rapid increase in specific capacitance. In region III, the SSA steadily decreases with an increase in pore size for porous materials with D > 2, whereas the solvated-ion hosting capacity of pores is close to its maximum. The combined effect of these two factors is that the specific capacitance slowly decreases with increasing pore size. Considering the diameters of solvated ions (0.7–1.5 nm),³⁴ the best electrode materials for EDLC are those which use porous electrode materials with open pores of 2.0–6.0 nm, optimally of 3.0–5.0 nm, which according to the International Union of Pure and Applied Chemistry (IUPAC) classification are the mesoporous materials.

Fig. 7 (A) Fitting the specific capacitances of the SS-CNMs with the model plot. (B) Drawings of solvated ions residing in pores with R/r values of 1.5 (top left), 2 (top right), and 4 (bottom).

The higher performance of SS-CNM-2 over the other SS-CNMs (vide supra) consolidates the pore size effect on the EDLC electrode materials by assuming the diameter of the solvated ions to be 1.0 nm. These findings would provide insight for the future electrode material design as follows: either using purely microporous electrode materials with pore size close to the diameter of ‘naked’ ions, sacrificing the rate response, for high-energy-density supercapacitors, or more preferably, using mesoporous electrode materials with pore sizes in the range of 3.0–5.0 nm to accomplish the demand of both high energy density and high power density.

4. Conclusions

A series of SS-CNMs were synthesized by the formation of self-assembled monolayers of enediyne compounds on silica support, with different pore diameters. The SS-CNMs were used as the electrode materials for EDLCs to study the pore size effect in mesoporous regions. SS-CNM-2 with a pore size of 5.24 nm exhibited a high capacitance of 305 F g⁻¹, much higher than that of other SS-CNMs with smaller or larger pores. Theoretical modelling validated this curved dependence of supercapacitance on the pore size of mesoporous electrode materials. A rational design of electrode materials (Fig. S4†) based on these results may allow the fabrication of supercapacitors with energy density comparable to that of a Li-ion battery.

Acknowledgements

The support of National Natural Science Foundation of China (91023008), Ph.D. Programs Foundation of Ministry of Education of China (20100074110002), the Fundamental Research Funds for the Central Universities, and Shanghai Leading Academic Discipline Project (B502) is gratefully acknowledged. AH thanks the “Eastern Scholar Professorship” support from Shanghai local government and Prof. Baohang Han for providing valuable comments.

Notes and references

1. B. E. Conway, Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications, Plenum Publishers, New York, 1999.
2. G. Wang, L. Zhang and J. Zhang, Chem. Soc. Rev., 2012, 41, 797–828.
3. R. Kötz and M. Carlen, Electrochim. Acta, 2000, 45, 2483–2498.
4. P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854.
5. K. Hata, A. Izadi-Najafabadi, D. N. Futaba and S. Iijima, J. Am. Chem. Soc., 2010, 132, 18017–18019.
6. Y. W. Zhu, S. Murali, M. D. Stoller, K. J. Ganesh, W. W. Cai, P. J. Ferreira, A. Pirkle, R. M. Wallace, K. A. Cychosz, M. Thommes, D. Su, E. A. Stach and R. S. Ruoff, Science, 2011, 332, 1537–1541.
7. M. F. El-Kady, V. Strong, S. Dubin and R. B. Kaner, Science, 2012, 335, 1326–1330.
8. W. Gao, Y. Wan, Y. Dou and D. Zhao, Adv. Energy Mater., 2011, 1, 115–123.
9. H. Nishihara, H. Itai, T. Kogure and T. Kyotani, J. Am. Chem. Soc., 2011, 133, 1165–1167.
10. D. Hulicova-Jurcakova, A. M. Puziy, O. I. Poddubnaya, F. Suarez-Garcia, J. M. D. Tascon and G. Q. Lu, J. Am. Chem. Soc., 2009, 131, 5026–5027.
11. C. Largeot, C. Portet, J. Chmiola, P.-L. Taberna, Y. Gogotsi and P. Simon, J. Am. Chem. Soc., 2008, 130, 2730–2731.
12. J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Science, 2006, 313, 1760–1763.
13. J. Chmiola, C. Largeot, P. L. Taberna, P. Simon and Y. Gogotsi, Science, 2010, 328, 480–483.
14. H. N. Wang and L. Pilon, J. Power Sources, 2013, 221, 252–260.
15. F. Stoeckli and T. A. Centeno, J. Mater. Chem. A, 2013, 1, 6865–6873.
16. C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, Nat. Mater., 2012, 11, 306–310.
17. G. W. Sun, W. H. Song, X. J. Liu, D. H. Long, W. M. Qiao and L. C. Ling, Electrochim. Acta, 2011, 56, 9248–9256.
18. G. Feng and P. T. Cummings, J. Phys. Chem. Lett., 2011, 2, 2859–2864.
19. J. S. Huang, B. G. Sumpter and V. Meunier, Chem.–Eur. J., 2008, 14, 6614–6626.
20. D. E. Jiang, Z. H. Jin and J. Z. Wu, Nano Lett., 2011, 11, 5373–5377.
21. A. Turchanin, A. Beyer, C. T. Nottbohm, X. H. Zhang, R. Stosch, A. Sologubenko, J. Mayer, P. Hinze, T. Weimann and A. Golzhauser, Adv. Mater., 2009, 21, 1233–1237.
22. W. Eck, A. Küller, M. Grunze, B. Völkel and A. Gölzhäuser, Adv. Mater., 2005, 17, 2583–2587.
23. X. Yang, Z. Li, J. Zhi, J. Ma and A. Hu, Langmuir, 2010, 26, 11244–11248.
24. Z. Li, D. Song, J. Zhi and A. Hu, J. Phys. Chem. C, 2011, 115, 15829–15833.
25. J. Zhi, D. Song, Z. Li, X. Lei and A. Hu, Chem. Commun., 2011, 47, 10707–10709.
26. G. J. d. A. A. Soler-Illia, C. Sanchez, B. Lebeau and J. Patarin, Chem. Rev., 2002, 102, 4093–4138.
27. Q. Cai, Z.-S. Luo, W.-Q. Pang, Y.-W. Fan, X.-H. Chen and F.-Z. Cui, Chem. Mater., 2001, 13, 258–263.
28. H. Q. Ru, W. Wang, W. J. Shan and N. Wu, J. Mater. Chem., 2011, 21, 12059–12067.
29. P. F. Fulvio, S. Pikus and M. Jaroniec, J. Mater. Chem., 2005, 15, 5049–5053.
30. J. Yan, T. Wei, B. Shao, F. Ma, Z. Fan, M. Zhang, C. Zheng, Y. Shang, W. Qian and F. Wei, Carbon, 2010, 48, 1731–1737.
31. D. Zhao, J. Feng, Q. Huo, N. Melosh, G. H. Fredrickson, B. F. Chmelka and G. D. Stucky, Science, 1998, 279, 548–552.
32. S. Numao, K. Judai, J. Nishijo, K. Mizuuchi and N. Nishi, Carbon, 2009, 47, 306–312.
33. D. Avnir and M. Jaroniec, Langmuir, 1989, 5, 1431–1433.
34. C. M. Yang, Y. J. Kim, M. Endo, H. Kanoh, M. Yudasaka, S. Iijima and K. Kaneko, J. Am. Chem. Soc., 2007, 129, 20–21.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed theoretical calculation and cycling stability data of SS-CNM-2, proposed structure for electrode material of EDLC. See DOI: 10.1039/c4ra06260d

---