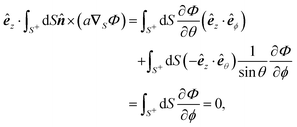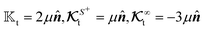DOI:
10.1039/D4SM00360H
(Paper)
Soft Matter, 2024,
20, 6907-6919
Phoresis kernel theory for passive and active spheres with nonuniform phoretic mobility†
Received
27th March 2024
, Accepted 8th July 2024
First published on 27th August 2024
Abstract
By introducing geometry-based phoresis kernels, we establish a direct connection between the translational and rotational velocities of a phoretic sphere and the distributions of the driving fields or fluxes. The kernels quantify the local contribution of the field or flux to the particle dynamics. The field kernels for both passive and active particles share the same functional form, depending on the position-dependent surface phoretic mobility. For uniform phoretic mobility, the translational field kernel is proportional to the surface normal vector, while the rotational field kernel is zero; thus, a phoretic sphere with uniform phoretic mobility does not rotate. As case studies, we discuss examples of a self-phoretic axisymmetric particle influenced by a globally-driven field gradient, a general scenario for axisymmetric self-phoretic particle and two of its special cases, and a non-axisymmetric active particle.
1. Introduction
Phoresis encompasses a group of phenomena where particles move under the influence of a gradient in a physical property of their medium or a field within the fluid.1–4 Such phenomena include diffusiophoresis,5–9 prompted by the concentration gradient of a solute; electrophoresis,10–16 resulting from the spatial variation of electric potential; and thermophoresis,17–21 driven by temperature gradients. These phoretic movements play a vital role in various scientific and industrial processes, such as particle separation in mixtures, purification, pollution control, drug delivery system design, surface coatings, and the rapidly growing fields of microswimmers, active colloids and microrobotics.22–29
Designing particles for specific purposes that undergo phoresis phenomena under a driving field or controlling their behavior requires a deep understanding of the particle–field interactions and the phoresis phenomena. In the linear regime, the majority of the interactions between particle and the surrounding field gradient occurs in the interaction layer, which is a region in the vicinity of the particle surface. In the regime where the length scale of the interaction layer is much smaller than the particle size, the effect of the phenomena inside the interaction layer is usually lumped into a quantity known as slip velocity. This is the fluid velocity at the outer surface of the interaction layer. Models then use the slip velocity as a boundary condition to solve for the fluid flow to study the velocity of a single particle system1,10,11,13,30–34 or particle–particle35–40 and particle–boundary41 interactions.
In this paper, our focus is on the dynamics of an individual particle in an unbounded domain. The traditional approach to determining the velocity of a phoretic particle with a given surface composition involves calculating the driving field and obtaining the slip velocity over the particle surface, from which we calculate the translational and rotational velocities of the particle using the reciprocal theorem.4,42 To solve the inverse problem of finding a surface composition that leads to the desired dynamics, we typically engage in a series of trial-and-error designs, supported by intuition and experience, to determine the surface composition and corresponding slip velocities. From these, we derive the particle velocities, potentially converging to a surface composition that achieves the desired dynamics. With the calculation of slip velocity as an intermediate step, this trial-and-error process seems inevitable.
Since we typically have more direct control, albeit still not very precise, over flux than over slip velocity, to overcome this challenge or at least reduce the complications, we will bypass the need for calculating slip velocity. Our goal is to establish a direct connection between the field distribution or its flux with particle velocity through integral kernels. These kernels encompass the effects of geometry as well as the surface phoretic mobility, which is a measure of the interaction of the particle with the field, irrespective of the field's distribution. Thus, phoresis kernels provide deeper insight into how geometry and surface composition can influence phoresis phenomena. This knowledge can then be used to design phoretic particles for specific purposes or to optimize and fine-tune their properties.
Particles undergoing phoresis are typically categorized into two classes: passive and active. Passive particles alter the distribution of the field around them but do not contribute to the creation of the field. For instance, a silica sphere in the presence of an external electric field undergoes electrophoresis; it influences the electric potential around it but does not create the field gradient that drives the phoresis phenomenon. Conversely, active particles interact with their environment in a way that leads to the creation of a local gradient of the driving field. An example is a platinum–gold bimetallic micro-rod43 in a hydrogen peroxide solution, which interacts to generate a self-produced gradient of electric potential, resulting in self-electrophoresis.11–13
Since active particles move under their self-generated field gradient, they are also referred to as self-phoretic or auto-phoretic particles. However, this does not preclude them from being driven by external fields, similar to passive particles. For example, a platinum–gold bimetallic micro-rod, while performing self-electrophoresis due to the local gradient of hydronium ions, may be subjected to a global concentration gradient of non-ionic molecules and undergo diffusiophoresis. Therefore, rather than focusing on the active or passive properties of the particle, we concentrate on the length scale of the field gradient.
We describe a phoresis process as globally-driven when the length scale of the field variation is of system size, much larger than the particle size. Conversely, we refer to a phoresis process as locally-driven when the length scale of the field gradient is on the order of the particle size. Within this framework, an active particle can be simultaneously locally-driven by its self-generated field gradient and globally-driven by another externally imposed field gradient. In general, a particle's phoretic motion may result from the superposition of multiple phoresis processes driven by distinct fields.
In both locally-driven and globally-driven phoresis processes, even though the particle velocity is a vectorial quantity for the entire particle, the driving field on the particle surface is distributed and varies locally across the particle surface. To bridge the dynamics and the field distribution within the phoresis kernel theory, we quantify the local contribution of the field to the particle velocity using integral kernels. These kernels depend on the geometry and surface properties of the particle and remain independent of the field's distribution. Thus, for both active and passive particles, the functional forms of the field kernels should be identical. However, the flux of the driving field in locally-driven processes is distributed over the particle's surface, whereas, for globally-driven processes, its far-field value is known. As a result, their respective flux kernels are different, and the surface integration of the normal component of the flux, weighted by these kernels, holds distinct interpretations for locally-driven and globally-driven phoresis phenomena.
In what follows, we begin by formulating the phoresis of a sphere in the linear regime of a thin interaction layer. We base our approach on Fair and Anderson's expressions for the rotational and translational velocities of a phoretic sphere, which rely on slip velocity.10 However, we replace the integration involving slip velocity with the integration of the field, weighted by position-dependent field kernels, over the particle surface. Using expressions for fields over the particle surface for locally-driven and globally-driven phoresis processes, we derive the corresponding flux kernels. We then apply this formalism to study examples including the self-phoresis of axisymmetric particles with uniform phoretic mobility influenced by a globally-driven field gradient, the translational velocity of an axisymmetric self-phoretic swimmer with a distribution of phoretic mobility, and a non-axisymmetric active particle. The details of the derivations and calculations are provided in the ESI.†
2. Formulation of the problem
A. Driving field for phoresis
For a sphere situated within a fluid to undergo phoretic motion, the particle is subjected to at least one driving field Ψ corresponding to a phoresis process. In the limit of a thin interaction layer, we approximate the outer surface of the interaction layer, denoted by S+, as a sphere of radius a. For brevity, we refer to S+ as the particle surface henceforth. The flux of the field is proportional to the gradient of the field,| | 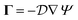 | (1) |
where the proportionality constant 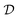 is a diffusion coefficient associated with the phoresis process.
is a diffusion coefficient associated with the phoresis process.
The gradient of the field, and thus its flux, drives the phoresis process. The flux can be imposed globally or generated locally. Typically, a passive particle is driven by a global gradient, while an active particle can self-generate a local gradient even as it undergoes another phoresis process imposed by a global gradient. In this paper, we focus on phoresis processes which obey the following surface and far-field boundary conditions,
| | 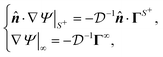 | (2) |
where
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif)
is the unit normal to the particle surface. For the locally-generated flux
ΓS+, the distribution of the normal component of the flux over
S+ may vary. Conversely, the far-field flux
Γ∞, which pertains to the globally-driven aspect of the phoresis process, is typically uniform. The boundary condition
(2) includes both local and global gradients of the driving field. Common special cases include self-phoresis (
ΓS+ ≠ 0) in the absence of global flux (
Γ∞ = 0),
3,4 and globally-driven phoresis (
Γ∞ ≠ 0) of a passive particle in the absence of surface flux (
ΓS+ = 0).
10
B. Translational and rotational velocities
The interaction of the particle with the field Ψ near the particle surface, and the resulting flow within the interaction layer, can be lumped into a slip velocity,tangent to the outer surface S+ of the interaction layer. The phoretic mobility μ depends on the local thermodynamic conditions of the interface. Using the identity matrix 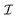 , the expression
, the expression 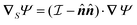 is tangent to S+, providing the surface gradient of the field over the particle surface.
is tangent to S+, providing the surface gradient of the field over the particle surface.
In scenarios where more than one phoresis process occurs, the slip velocity over the particle surface is the sum of these phoresis-specific slip velocities,
| | 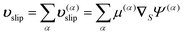 | (4) |
where
α sums over different phoresis processes involved and the validity of this summation stems from the linearity of the governing equations.
The flow field around a particle moving with translational velocity U and rotational velocity Ω in a Newtonian fluid of viscosity η follows the Stokes and continuity equations,
respectively, subject to surface (
xS ∈
S+) and far-field boundary conditions,
| | | u(xS) = U + Ω × xS + υslip, | (6a) |
The translational and rotational velocities of the phoretic sphere are given by Fair and Anderson,10
| | 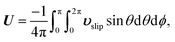 | (7a) |
| | 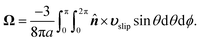 | (7b) |
Similar expressions were presented by Stone and Samuel44 for the propulsion of microorganisms by surface distortions. The eqn (7) are surface integrations of integrands related to the slip velocity and, thus, to the surface gradient of the fields. In the next section, we discuss how we can eliminate the slip velocity from these equations, thereby relating the velocities U and Ω directly to the driving field Ψ and fluxes ΓS+ and Γ∞ using phoresis kernels.
C. Phoresis kernel theory
Exploiting the linearity of the governing equations, the standard practice for obtaining the translational and rotational velocities for a phoresis process can be summarized in three steps:| |  | (8) |
First, we obtain the field Ψ from fluxes ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·ΓS+ and Γ∞ using eqn (17); second, calculate the surface gradient of the field, and obtain the slip velocity (3); and third, use the slip velocity in integrals (7) to yield the velocities.
·ΓS+ and Γ∞ using eqn (17); second, calculate the surface gradient of the field, and obtain the slip velocity (3); and third, use the slip velocity in integrals (7) to yield the velocities.
In this paper, our goal is to provide a direct connection between the field Ψ and the fluxes ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·ΓS+ and Γ∞ to the translational U and rotational Ω velocities using integral kernels. For this purpose, we need to circumvent the calculation of slip velocity, specifically step II, in the steps (8). In the next section, Background, we review earlier efforts to derive geometrical kernel in order to connect the surface flux to self-phoretic velocities for particles with uniform phoretic mobility. Subsequently, in the following section, we introduce the concepts of field-kernels and flux-kernels for spheres for more general scenarios where the particle can be passive or active and the phoretic mobility can be non-uniform.
·ΓS+ and Γ∞ to the translational U and rotational Ω velocities using integral kernels. For this purpose, we need to circumvent the calculation of slip velocity, specifically step II, in the steps (8). In the next section, Background, we review earlier efforts to derive geometrical kernel in order to connect the surface flux to self-phoretic velocities for particles with uniform phoretic mobility. Subsequently, in the following section, we introduce the concepts of field-kernels and flux-kernels for spheres for more general scenarios where the particle can be passive or active and the phoretic mobility can be non-uniform.
1. Background.
Nourhani and Lammert3 introduced a kernel-based integral equation for the translational self-phoretic velocity of an axisymmetric spheroidal swimmer, ranging from discotics to spheres to rod-like geometries, with uniform surface phoretic mobility, moving along its symmetry axis. The integral kernel weighs the local contribution of the surface flux to the particle's velocity. They showed that in rod-like geometries, the flux value near the particle's equator is almost zero, making the contribution of surface flux in this region to the velocity negligible. Therefore, in rod-like geometries, the major contribution of the surface flux to motion comes from the poles. From a design principle perspective, we can place the expensive active surface near the poles and a less expensive passive conductive region near the equator. As the aspect ratio decreases towards discotic geometries, the flux over a larger portion of the particle's surface contributes to the velocity. Schnitzer and Yariv34 obtained an approximate expression for osmotic self-propulsion of slender particles with uniform phoretic mobility in terms of weighted integral of the surface flux. Lammert, Crespi, and Nourhani in a subsequent publication4 extended the flux-based geometrical kernel formalism to include translational and rotational velocities for particles of arbitrary geometry with uniform phoretic mobility. They recovered the earlier results3,34 as special cases.
The assumption of uniform phoretic mobility is the zeroth-order approximation for the surface properties of the swimmer. However, this approximation may not be suitable for scenarios where the surface properties of different materials on various parts of the swimmer's surface differ significantly, and we need to address the presence of a non-uniform distribution of phoretic mobility over the particle surface. The techniques and theorems introduced in ref. 3 and 4 are suitable for uniform phoretic mobility. To address the scenario of non-uniform phoretic mobility in this paper, we introduce two identities (12) for integration over a sphere's surface and employ them to derive a kernel-based formalism for the self-phoretic translational and rotational velocities of a sphere with a surface distribution of phoretic mobility.
2. Field and flux kernels for spheres.
This paper focuses on the phoretic dynamics of a single sphere. The extension to other geometries and the interactions of the particle with other particles or boundaries will be the scope of future studies. We are interested in extending the scope of the velocity expressions in ref. 3 and 4, which are based on local flux ΓS+ and uniform phoretic mobility, to additionally include phoresis by the global flux Γ∞ and non-uniform phoretic mobility. Moreover, beyond flux kernels, we will provide field kernels that connect the velocities to the values of the field over the particle surface S+.
For this purpose, using eqn (3) for slip velocity, we first rewrite the expressions for the translational and rotational velocities (7) in terms of surface integrals involving the surface gradients of the field,
| | 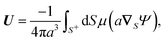 | (9a) |
| | 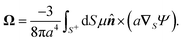 | (9b) |
and use them as the basis for obtaining the kernels. For a given phoresis phenomenon, we define translational
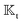
and rotational
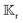
field kernels that quantify the local contribution of the field over the particle surface to the translational and rotational velocities, respectively. For flux kernels we will have distinct local flux kernel
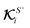
and global flux kernel
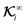
for translational (
i =
t) and rotational (
i =
r) velocities, using integrations equivalent to the integrations in
eqn (9),
| | 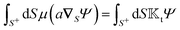 | (10a) |
| | 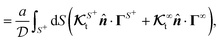 | (10b) |
| | 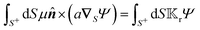 | (10c) |
| | 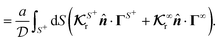 | (10d) |
Within these definitions, the kernels possess dimensions of phoretic mobility. As we will see shortly, in cases of non-uniform phoretic mobility, the kernels are functionals of the surface distribution of phoretic mobility.
Both locally-driven and globally-driven field gradients, manifested in ΓS+ and Γ∞ respectively, as specified in eqn (2), contribute to the surface distribution of the field Ψ(xS) around the particle. The field kernels 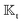 and
and 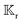 , which deal directly with the field, are independent of the origin of the field gradient, whether locally ΓS+ or globally Γ∞. The field kernels for both locally-driven and globally-driven aspects of phoresis processes are conceptually the same.
, which deal directly with the field, are independent of the origin of the field gradient, whether locally ΓS+ or globally Γ∞. The field kernels for both locally-driven and globally-driven aspects of phoresis processes are conceptually the same.
On the other hand, in the case of flux kernels, we deal with two conceptually distinct types of fluxes: one distributed over the particle surface ΓS+ and the other a uniform far-field Γ∞. Therefore, the integrations of the normal component of these fluxes over the particle surface in eqn (10b) and (10d), weighted by the associated local flux kernels 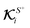 and global flux kernels
and global flux kernels 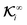 , have distinct interpretations, as we elaborate below. The integration involving local flux kernels
, have distinct interpretations, as we elaborate below. The integration involving local flux kernels 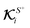 and the normal component of the locally-driven flux ΓS+ has the same intuitive interpretation as the integration involving field kernels and the field; the local flux kernels
and the normal component of the locally-driven flux ΓS+ has the same intuitive interpretation as the integration involving field kernels and the field; the local flux kernels 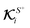 define the local contribution of the surface flux ΓS+ to the particle's translational and rotational velocities.
define the local contribution of the surface flux ΓS+ to the particle's translational and rotational velocities.
However, in the integrals involving the global flux kernels 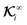 , although the integration is over the particle surface S+, the value of the flux is far-field. Therefore, the term
, although the integration is over the particle surface S+, the value of the flux is far-field. Therefore, the term ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·Γ∞ in the integration
·Γ∞ in the integration 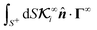 in eqn (10b) and (10d), while integrated over the particle surface, does not represent the surface flux of the field over the particle surface. For example, in the case of globally driven phoresis of an impermeable, non-polarizable passive particle, the surface flux of the field
in eqn (10b) and (10d), while integrated over the particle surface, does not represent the surface flux of the field over the particle surface. For example, in the case of globally driven phoresis of an impermeable, non-polarizable passive particle, the surface flux of the field 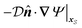 is zero and different from
is zero and different from ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·Γ∞. To visualize the scenario and develop an intuition about the integral
·Γ∞. To visualize the scenario and develop an intuition about the integral 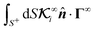 , imagine a uniform field gradient with a flux value Γ∞ throughout the entire space. Then, we place an imaginary sphere in this field gradient without distorting the field gradient, and integrate
, imagine a uniform field gradient with a flux value Γ∞ throughout the entire space. Then, we place an imaginary sphere in this field gradient without distorting the field gradient, and integrate ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·Γ∞ over the surface of the imaginary particle weighted by the kernel
·Γ∞ over the surface of the imaginary particle weighted by the kernel 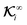 . Therefore, while the flux Γ∞ is a far-field value, we use the same value for integration over the surface of the sphere in the velocity expressions (19) as if the presence of the sphere has not distorted the uniform distribution of the far-field flux over the particle surface.
. Therefore, while the flux Γ∞ is a far-field value, we use the same value for integration over the surface of the sphere in the velocity expressions (19) as if the presence of the sphere has not distorted the uniform distribution of the far-field flux over the particle surface.
Another interpretation is as follows. Writing the uniform far-field in the form Γ∞ = Γ∞ê, where ê is a unit vector defining the direction of the global field gradient, the integral 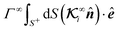 is effectively proportional to the weighted integration of the projection of the direction of the far-field flux on the normal surface vector, that is,
is effectively proportional to the weighted integration of the projection of the direction of the far-field flux on the normal surface vector, that is, ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·ê. This expression shows how the particle dynamics result from the coupling of the direction ê of the far-field flux to the surface characteristics and orientation of the particle, quantified by the second-rank tensor
·ê. This expression shows how the particle dynamics result from the coupling of the direction ê of the far-field flux to the surface characteristics and orientation of the particle, quantified by the second-rank tensor 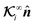 .
.
3. Field kernels
For the field kernels 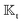 and
and 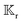 , we combine eqn (9), (10a) and (10c) and reformulate the velocities in terms of weighted surface integrals of the fields such that
, we combine eqn (9), (10a) and (10c) and reformulate the velocities in terms of weighted surface integrals of the fields such that| | 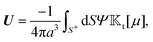 | (11a) |
| | 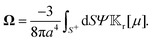 | (11b) |
where the position-dependent field kernels 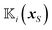 for i = t, r are functionals of the surface distribution of the phoretic mobility μ(xS).
for i = t, r are functionals of the surface distribution of the phoretic mobility μ(xS).
In case more than one phoresis process was involved similar to the slip velocity (4) the resulting velocities are the linear sum of the velocities (11) corresponding to the distinct phoresis processes. Keeping in mind the functional dependence of the kernels on phoretic mobility is critical, especially when more than one phoresis process is involved. For example, consider a particle that performs self-electrophoresis while also being subjected to a global concentration gradient of non-electrolyte solutes, thus undergoing diffusiophoresis simultaneously. Each phenomenon has its own field, Ψ(self-elec) and Ψ(diff), and phoretic mobility, μ(self-elec) and μ(diff), respectively, along with their corresponding kernels and phoretic velocities. The particle's velocities will be the sum of the velocities resulting from each phoresis process. Fortunately, while the position dependence of the phoretic mobility for each phoresis process may differ depending on the distribution of the surface composition of the sphere, the functional dependence of the kernels is independent of the phoretic mobility distribution, as will be discussed soon and shown in eqn (13).
To obtain the field kernels 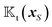 and
and 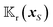 over the particle surface in the velocity expressions (11), we exploit the following two identities, the proofs of which are provided in Appendix A. For a function Φ(xS) over the surface of a sphere, we have
over the particle surface in the velocity expressions (11), we exploit the following two identities, the proofs of which are provided in Appendix A. For a function Φ(xS) over the surface of a sphere, we have
| | 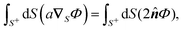 | (12a) |
| | 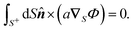 | (12b) |
By setting
Φ =
μΨ in the above identities, using
μ(
a∇SΨ) =
a∇S(
μΨ) −
Ψ(
a∇Sμ), and comparing the results with the integral expressions
(10a) and (10c), we obtain the translational and rotational field kernels,
| | 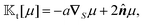 | (13a) |
| | 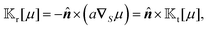 | (13b) |
respectively, as functionals of phoretic mobility distribution. For a constant field (
Ψ = cte) over the surface of a particle, the slip velocity
(3) is zero, and we expect no phoretic motion. This necessitates that the surface integral of the field kernels over the particle surface be zero,
| | 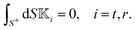 | (14) |
which can be mathematically demonstrated by setting a constant field
Ψ(
xS) = 1 in the integral expressions
(10a) and (10c).
A glance at the field kernels (13) immediately offers some physical insights. A particle with uniform phoretic mobility, for which ∇Sμ = 0, has a zero rotational field kernel, 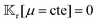 , meaning the particle does not rotate. Therefore, a heterogeneous distribution of the field over a sphere's surface does not induce rotation for a sphere if the phoretic mobility is uniform. Furthermore, in the scenario of uniform phoretic mobility, the translational field kernel simplifies to a radial vector field over the sphere surface,
, meaning the particle does not rotate. Therefore, a heterogeneous distribution of the field over a sphere's surface does not induce rotation for a sphere if the phoretic mobility is uniform. Furthermore, in the scenario of uniform phoretic mobility, the translational field kernel simplifies to a radial vector field over the sphere surface, 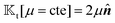 . Consequently, the calculation of the translational velocity is reduced to the surface integration of the field, weighted by the surface normal vector and phoretic mobility.
. Consequently, the calculation of the translational velocity is reduced to the surface integration of the field, weighted by the surface normal vector and phoretic mobility.
Therefore, for a spherical particle undergoing a phoresis processe with uniform phoretic mobility, the particle does not rotate, and its velocities are
| | 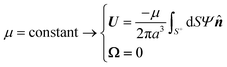 | (15) |
In an axisymmetric scenario of constant phoretic mobility with the symmetry axis along
êz, the field is independent of the
ϕ coordinate. Thus, the translational kernel
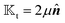
effectively reduces to
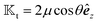
, as shown in
Fig. 1. Here, the field kernel provides us with another physical insight: in an axisymmetric scenario with uniform phoretic mobility, the field at the equator does not contribute to the motion, and the majority of the contribution comes from the poles.
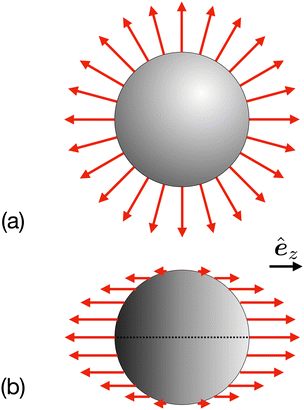 |
| | Fig. 1 For uniform phoretic mobility, the translational field kernel and flux kernels are (a) proportional to the normal ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) of the surface, of the surface, 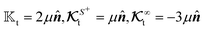 , and (b) for the special case of an axisymmetric distribution of the field or flux, the , and (b) for the special case of an axisymmetric distribution of the field or flux, the ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) term in kernels can be reduced to cos term in kernels can be reduced to cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θêz, where êz is the symmetry axis. In this scenario, each kernel has a negligible value around the equator and maximum magnitude at the poles. θêz, where êz is the symmetry axis. In this scenario, each kernel has a negligible value around the equator and maximum magnitude at the poles. | |
The field kernels are solely functionals of phoretic mobilities and are independent of whether the distribution of the field over the particle surface is due to locally-driven or globally-driven field gradients. In the next section, we discuss how to quantify the local effect of geometry to the overall particle motion through flux kernels and their dependance on the origin of the flux.
4. Flux kernels
To obtain the flux kernels in terms of field kernels using eqn (10), we need to use the relationship between the fluxes ΓS+ and Γ∞ in the boundary conditions (2) and the driving field Ψ. In the limit of the thin interaction layer, the driving field outside the interaction layer is often harmonic3,4,11 and satisfies the Laplace equation. Therefore, in what follows, we first provide the expression for the harmonic field and use it to find the flux kernels.
A. Harmonic driving field
For our analysis we use the spherical coordinate system, where the position vector x = (r,θ,ϕ) is identified by a radial coordinate r and two angular coordinates. Utilizing the orthogonality of spherical harmonics Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,m(θ,ϕ), the solution to the Laplace equation,subject to boundary conditions (2) yields the field,
,m(θ,ϕ), the solution to the Laplace equation,subject to boundary conditions (2) yields the field,| | 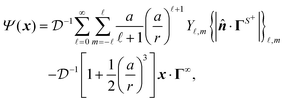 | (17) |
where we have employed the banana-curly-bracket notation {|·|}![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,m for the expansion coefficients in terms of spherical harmonics. That is, for a function Φ(θ,ϕ) defined over the surface of a sphere, we have
,m for the expansion coefficients in terms of spherical harmonics. That is, for a function Φ(θ,ϕ) defined over the surface of a sphere, we have| | 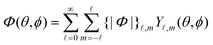 | (18a) |
| | 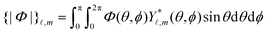 | (18b) |
Since the gradient of the fields drives motion, constant terms in the fields do not contribute to the translational and rotational velocities, and we have ignored them in the solution (17).
B. Local and global flux kernels
To formulate the velocity expressions in terms of the local flux kernels 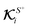 and global flux kernels
and global flux kernels 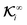 , we combine eqn (9), (10b) and (10d) and recast the velocities in the form,
, we combine eqn (9), (10b) and (10d) and recast the velocities in the form,| | 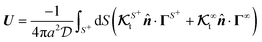 | (19a) |
| | 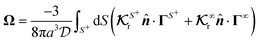 | (19b) |
in terms of weighted surface integrals of the normal components of the surface flux ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·ΓS+ and far-field global flux
·ΓS+ and far-field global flux ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·Γ∞. As discussed following eqn (10), the integrands in these expressions have distinct interpretations. To obtain the local flux kernel, we consider a scenario where ΓS+ ≠ 0 and Γ∞ = 0. For the global flux kernel, we study a situation where ΓS+ = 0 and Γ∞ ≠ 0. The combination of these two scenarios leads to the boundary conditions (2).
·Γ∞. As discussed following eqn (10), the integrands in these expressions have distinct interpretations. To obtain the local flux kernel, we consider a scenario where ΓS+ ≠ 0 and Γ∞ = 0. For the global flux kernel, we study a situation where ΓS+ = 0 and Γ∞ ≠ 0. The combination of these two scenarios leads to the boundary conditions (2).
In the first scenario, where phoresis is driven solely by a locally generated field gradient, by plugging the field expression (17) over the particle surface,
| | 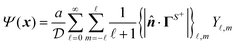 | (20) |
into the kernel-based integral expressions
(10) and performing some rearrangements, we obtain the flux kernels in terms of the field kernels for translational (
i =
t) and rotational (
i =
r) velocities,
| | 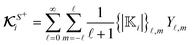 | (21) |
which differs from the spherical harmonic expansion
(18) of the field kernel
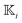
by the factor 1/(
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
+ 1) for each term.
The zero surface integral of the field kernel (14), Y0,0(θ,ϕ) = 1, and the definition (18b) yield 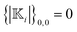 . Additionally, the orthogonality of the spherical harmonics results in
. Additionally, the orthogonality of the spherical harmonics results in 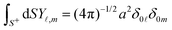 . Together with eqn (21), this leads to a zero surface integral of the flux kernels,
. Together with eqn (21), this leads to a zero surface integral of the flux kernels,
| | 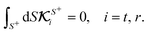 | (22) |
This confirms that a uniform distribution of activity does not lead to motility within the regime of our study.
In the second scenario, where the phoresis process is driven by a global gradient of the field in the absence of surface flux, ΓS+ = 0, the field (17) over the particle surface reduces to
| | 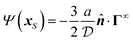 | (23) |
while the uniform flux
Γ∞ is far-field. By plugging this expression into the kernel-based integral expressions
(10), we obtain the flux kernel to be proportional to the field kernel for a uniform global flux,
| | 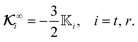 | (24) |
The zero surface integral of the field kernel (14) and the linearity of eqn (24) necessitate
| |  | (25) |
Although the flux Γ∞ is uniform over the particle surface, what we integrate in eqn (19) is its normal component ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·Γ∞, which is not uniform over the particle surface.
·Γ∞, which is not uniform over the particle surface.
C. Discussion of the kernels
The field kernels (13) are functionals of phoretic mobility and are independent of the origin of the field gradient, provided the slip velocity follows the expression (3) for the involved phoresis processes. On the other hand, the flux kernels for locally-generated field gradients (21) and globally-generated field gradients (24) differ, and the integrated normal fluxes offer two distinct concepts.
In the uniform phoretic mobility scenario, ∇Sμ = 0, the rotational flux kernels 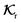 , which are linearly proportional to the rotational field kernel
, which are linearly proportional to the rotational field kernel 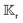 , are also zero. Therefore, for an active particle, heterogeneity in surface activity alone is not sufficient to induce rotation; heterogeneity in the surface distribution of phoretic mobility is necessary. Additionally, the translational flux kernels are proportional to the normal vector
, are also zero. Therefore, for an active particle, heterogeneity in surface activity alone is not sufficient to induce rotation; heterogeneity in the surface distribution of phoretic mobility is necessary. Additionally, the translational flux kernels are proportional to the normal vector ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) , thus,
, thus,
| | 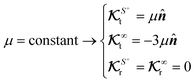 | (26) |
Therefore, for each phoresis process, the translational velocity is proportional to the surface integral of fluxes weighted by the unit normal. Similar to the scenario for the axisymmetric field, as shown in Fig. 1, in the case of axisymmetric normal flux, the ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) term in kernels (26) can be reduced to cos
term in kernels (26) can be reduced to cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θêz, where êz is the symmetry axis. Again, we learn that in the axisymmetric scenario with constant phoretic mobility, the majority of the flux contribution to motion comes from the poles, and the flux around the equator has a negligible contribution.
θêz, where êz is the symmetry axis. Again, we learn that in the axisymmetric scenario with constant phoretic mobility, the majority of the flux contribution to motion comes from the poles, and the flux around the equator has a negligible contribution.
In the next section, we study some examples to demonstrate the utility of the phoresis kernel theory. We start with a simple axisymmetric problem involving uniform phoretic mobility for a self-phoretic particle subjected to an additional globally-driven phoresis process, considering two scenarios: active-passive and sink–source surface configurations. Afterward, we tackle the general problem of an axisymmetric self-phoretic particle with multiple regions of distinct phoretic mobilities and also address two special cases. Finally, to present an example for the rotational kernel, we solve an analytically addressable problem for a non-axisymmetric scenario that contains both translational and rotational dynamics.
5. Examples with analytical solutions
A. Axisymmetric self-phoretic particle under global field gradient
In this example, we deal with axisymmetric Janus particles, each half covered with distinct materials and having uniform phoretic mobilities. The particles perform self-phoresis while simultaneously undergoing an additional globally-driven phoresis process. This latter process involves uniform phoretic mobility μ(glb) and is exposed to a globally-generated uniform flux in the êz direction, that is, Γ∞ = Γ(glb)êz with field diffusivity 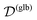 .
.
The director ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) of the Janus particle points from one face to the other, defining the particle's orientation in space. Positioned along the symmetry axis, the direction of the director is arbitrary, yet it determines how we refer to the Janus particle based on its rear-front composition. For instance, in Fig. 2(a), the Janus particle is termed
of the Janus particle points from one face to the other, defining the particle's orientation in space. Positioned along the symmetry axis, the direction of the director is arbitrary, yet it determines how we refer to the Janus particle based on its rear-front composition. For instance, in Fig. 2(a), the Janus particle is termed ![[a with combining low line]](https://www.rsc.org/images/entities/char_0061_0332.gif) ctive–
ctive–![[p with combining low line]](https://www.rsc.org/images/entities/char_0070_0332.gif) assive (a.p.), reflecting the orientation of its director: the normal component of the surface flux on the passive side is zero, while on the active side, it can be either negative or positive. Alternatively, in Fig. 2(b), both sides are active, and the Janus particle is described as s
assive (a.p.), reflecting the orientation of its director: the normal component of the surface flux on the passive side is zero, while on the active side, it can be either negative or positive. Alternatively, in Fig. 2(b), both sides are active, and the Janus particle is described as s![[i with combining low line]](https://www.rsc.org/images/entities/char_0069_0332.gif) nk–s
nk–s![[o with combining low line]](https://www.rsc.org/images/entities/char_006f_0332.gif) urce (i.o.): the surface flux at the sink is negative, and at the source, it is positive.
urce (i.o.): the surface flux at the sink is negative, and at the source, it is positive.
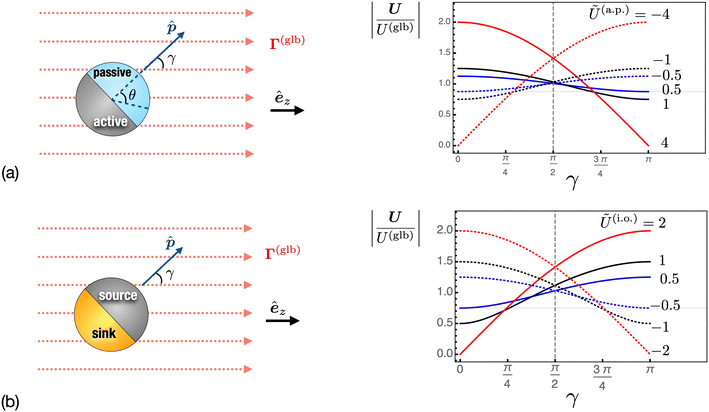 |
| | Fig. 2 Two self-phoretic Janus models of (a) active–passive (a.p.) and (b) sink–source (i.o.) composition are undergoing globally-driven phoresis by the far-field flux Γ(glb). The angle γ defines the orientation of the Janus director ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) with respect to Γ(glb). Solid lines represent positive values of Ũ(α), while dashed lines represent negative values. with respect to Γ(glb). Solid lines represent positive values of Ũ(α), while dashed lines represent negative values. | |
The normal component of the surface flux in these two scenarios are represented by,
| | 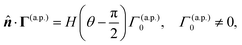 | (27a) |
| | 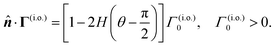 | (27b) |
where
H(
θ) is the Heaviside step function. As shown in
Fig. 2(a), the angle
θ is the polar angle with respect to the Janus director
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif)
. The globally-generated uniform flux
Γ(glb) forms an angle
γ with the Janus director
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif)
, such that
êz·
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif)
= cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ
γ.
For globally-driven phoresis, using the kernel for uniform phoretic mobility (26), the velocity expression (19a), and the identity 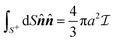 , we obtain the phoretic velocity,
, we obtain the phoretic velocity,
| | 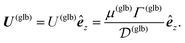 | (28) |
For self-phoresis phenomena α = a.p., i.o., we define the ratio of velocity scales as
| | 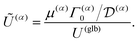 | (29) |
Using the surface flux models (27), the translational velocity expression (19a), and the kernel for uniform phoretic mobility (26), we obtain the particle velocity for the two scenarios:
| | 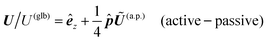 | (30) |
| | 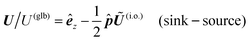 | (31) |
The particles have uniform phoretic mobilities, and thus their angular velocities are zero according to eqn (15). Therefore, there is no deterministic change in orientation, γ, over time, and the globally-driven phoresis modulates the self-phoretic velocities, as shown in the curve of Fig. 2.
The scenario of an axisymmetric particle with uniform phoretic mobility does not take advantage of the terms in the translational and rotational kernels (13) that stem from the surface gradient of phoretic mobility. In the next two sections, we will take these terms into account to solve for problems with non-uniform phoretic mobility.
B. Axisymmetric self-phoretic particle with multiple surface regions
We start with a general scenario, shown in Fig. 3(a), where the surface of the sphere is partitioned into k axisymmetric regions such that the distribution of phoretic mobility over the sphere surface is described by| | 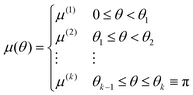 | (32) |
where θi's defines the boundaries of the regions. The motion is along the symmetry axis êz, and using eqn (13a) and (21), the corresponding field and flux kernels are| | 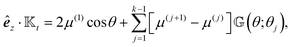 | (33a) |
| | 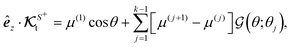 | (33b) |
respectively, where the dimensionless functions are| | 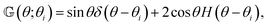 | (34a) |
| | 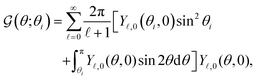 | (34b) |
and the Dirac delta function δ(θ − θi) is the derivative of the Heaviside function H(θ − θi).
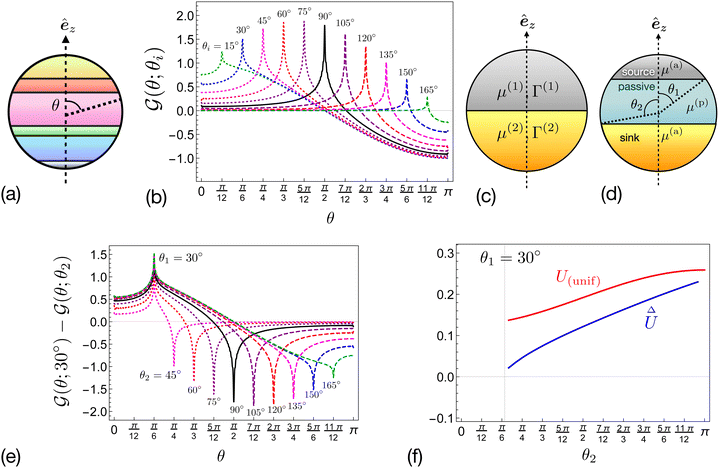 |
| | Fig. 3 (a) General axisymmetric scenario of a self-phoretic particle with multiple distinct regions. (b) The θ-dependent function 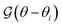 locally quantifying the disparity of the phoretic mobilities in the flux kernel (33b). (c) Self-phoretic particle with two active surfaces. (d) A source–sink self-phoretic particle with a passive region in the middle, and (e) the corresponding dimensionless component of the flux kernel due to the difference in the phoretic mobility of passive and active regions. (f) Dimensionless velocities for the model swimmer presented in Fig. 3(d). locally quantifying the disparity of the phoretic mobilities in the flux kernel (33b). (c) Self-phoretic particle with two active surfaces. (d) A source–sink self-phoretic particle with a passive region in the middle, and (e) the corresponding dimensionless component of the flux kernel due to the difference in the phoretic mobility of passive and active regions. (f) Dimensionless velocities for the model swimmer presented in Fig. 3(d). | |
Fig. 3(b) shows the plot of 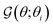 for different values of θi. The function shows a peak at the boundary θ = θi. Therefore, we can expect k − 1 peaks in the flux kernel (33b) at the boundaries of the regions, and the strength of the peaks depends on the differences in phoretic mobilities of the neighboring regions forming the boundaries.
for different values of θi. The function shows a peak at the boundary θ = θi. Therefore, we can expect k − 1 peaks in the flux kernel (33b) at the boundaries of the regions, and the strength of the peaks depends on the differences in phoretic mobilities of the neighboring regions forming the boundaries.
To demonstrate the utility of the formalism, we revisit a model Janus particle presented by Golestanian et al.31 and shown in Fig. 3(c). The model is fairly general and is not limited to a source–sink scenario. For example, both sides can be sources consisting of distinct materials with different surface fluxes, thus leading to an asymmetry condition. The distribution of surface flux and phoretic mobility over the surface is given by
| | 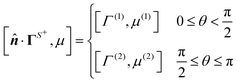 | (35) |
The corresponding flux kernel
(33b) along the symmetry axis direction for this problem takes the form
| | 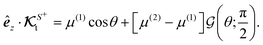 | (36) |
Using the expression
(19a) for translational velocity and
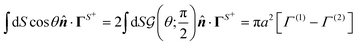
we reobtain
eqn (9) in ref.
31,
| | 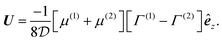 | (37) |
An important outcome of this equation is that in a scenario where μ(1) = −μ(2), despite asymmetry in the structure and composition resulting in distinct surface fluxes, the active particle does not move.
In another scenario, shown in Fig. 3(d), we address a source–sink problem with a conductive passive region in the middle. This configuration could represent a classic platinum–gold pair with a chemically passive region in the middle that supports the electrochemical electron current from source to sink. Therefore, in the phoretic mobility model (32), we can approximate the source and sink to have the same phoretic mobility, μ(a) := μ(1) = μ(3), which is distinct from the phoretic mobility of the passive part in the middle, μ(p) := μ(2). Consequently, the translational flux kernel (33b) reduces to
| | 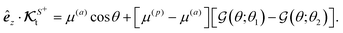 | (38) |
The source–sink surface flux model, satisfying the steady-state condition 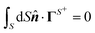 , is
, is
| | 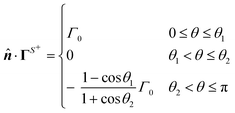 | (39) |
Using the flux-based velocity expression
(19a) for this scenario gives the translational velocity along the symmetry axis,
| | 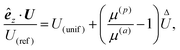 | (40) |
where the dimensionless terms are
| | 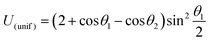 | (41a) |
| | 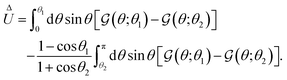 | (41b) |
The reference velocity scale in eqn (40),
| | 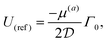 | (42) |
used for non-dimensionalization, corresponds to a scenario where the particle is half-coated by source and sink surfaces with no passive surface in the middle, that is,
θ1 =
θ2 = π/2.
As an example, for a source region identified by the angle θ1 = 30°, Fig. 3(e) shows the dependence of  in the flux kernel (38) for different sizes of the sink region, identified by θ2. The curves show two peaks at the boundaries, θ1 and θ2, of the regions. Fig. 3(f) shows the corresponding dimensionless velocities (41), both of which increase monotonically with an increase in θ2.
in the flux kernel (38) for different sizes of the sink region, identified by θ2. The curves show two peaks at the boundaries, θ1 and θ2, of the regions. Fig. 3(f) shows the corresponding dimensionless velocities (41), both of which increase monotonically with an increase in θ2.
C. Non-axisymmetric self-phoretic particle
In this section, we discuss the scenario of a non-axisymmetric self-phoretic particle shown in Fig. 4(a). A passive particle with surface phoretic mobility μ(p) is covered by two active surfaces, each with approximately the same phoretic mobility μ(a). Within the spherical coordinate system, the polar angle with respect to the z-axis is denoted by θ, and as shown in Fig. 4(b), the angle θ0 defines the active cap region. Half of the cap (i.e., y > 0) acts as the source with surface flux Γ0 > 0, and the other half serves as the sink with surface flux −Γ0. The surface flux Γ is symmetric about the yz plane, but antisymmetric about the xz plane.
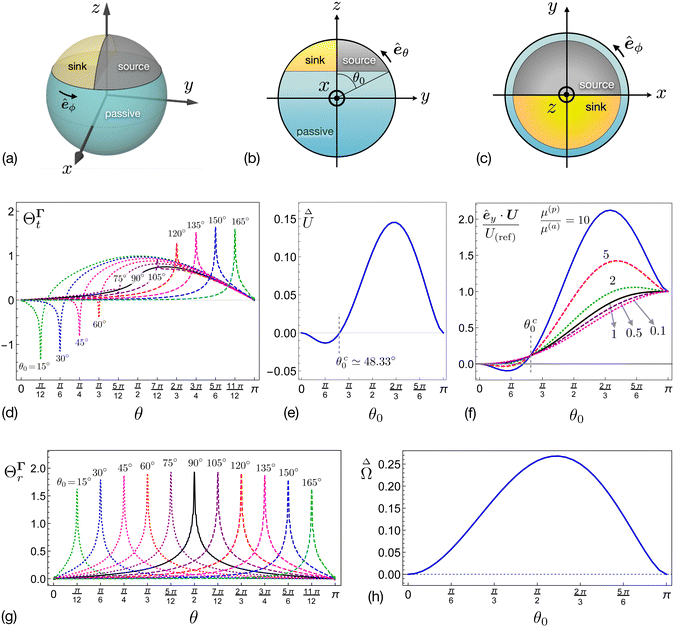 |
| | Fig. 4 Non-axisymmetric self-phoretic particle with rotational and translational dynamics. (a) The microswimmer is a passive particle covered by an active cap consisting of source and sink regions of equal area. (b) The size of the cap is quantified by θ0. (c) Top view. (d) The dimensionless function ΘΓt(θ;θ0) in the translational flux kernel (48) shows a peak at θ = θ0. (e) The dimensionless function 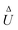 in the translational velocity expression (49) determines the contribution of the difference in phoretic mobilities to motion. (f) The scaled velocity êy·U/U(ref) for difference ratios of phoretic mobilities. (g) The θ-dependent function ΘΓr(θ;θ0) of the rotational flux-kernel (52b) shows peak at θ = θ0. (h) The dimensionless function in the translational velocity expression (49) determines the contribution of the difference in phoretic mobilities to motion. (f) The scaled velocity êy·U/U(ref) for difference ratios of phoretic mobilities. (g) The θ-dependent function ΘΓr(θ;θ0) of the rotational flux-kernel (52b) shows peak at θ = θ0. (h) The dimensionless function 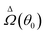 shows the behavior of the magnitude of the angular velocity. shows the behavior of the magnitude of the angular velocity. | |
Thus, the position-dependent phoretic mobility μ(θ) is
| | | μ(θ) = μ(a) + [μ(p) − μ(a)]H(θ − θ0), | (43) |
and the normal component of the flux
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif)
·
ΓS+ over the surface of the sphere is given by
| | ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·ΓS+(θ,ϕ) = [1 − H(θ − θ0)][1 − 2H(ϕ − π)]Γ0. ·ΓS+(θ,ϕ) = [1 − H(θ − θ0)][1 − 2H(ϕ − π)]Γ0. | (44) |
We aim to obtain the translational
U and rotational
Ω velocities of the self-phoretic particle.
1. Translational velocity.
We start with the translational velocity, U. As shown in Fig. 4(b), the yz-plane is the symmetry plane, and thus the particle has no preference to move in the êx or −êx direction. Therefore, there is no translation along the x direction, andTo show that there is no motion in the z direction, we first write the translational field kernel (13a) for our problem. Since 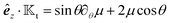 has no ϕ-dependence, the expansion coefficients
has no ϕ-dependence, the expansion coefficients  for the flux kernel (21) are non-zero only when m = 0. Therefore, the z-component of the flux kernel,
for the flux kernel (21) are non-zero only when m = 0. Therefore, the z-component of the flux kernel, 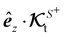 , has no ϕ-dependence. On the other hand,
, has no ϕ-dependence. On the other hand, 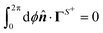 . Hence,
. Hence,| | 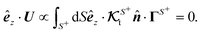 | (46) |
Hence, the particle only moves along the y-direction, and using eqn (13a) the field kernel is given by
| | 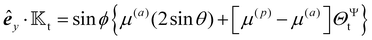 | (47a) |
| | ΘΨt(θ;θ0) = 2H(θ − θ0)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − cos θ − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θδ(θ − θ0) θδ(θ − θ0) | (47b) |
The dependence of the field kernel (47a) on sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ necessitates that the flux kernel coefficients
ϕ necessitates that the flux kernel coefficients 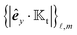 can be non-zero only when m = ±1. Thus, using the expression (21) for the flux kernel of self-phoresis and plugging in the field kernel (47), we obtain the y-component of the flux kernel,
can be non-zero only when m = ±1. Thus, using the expression (21) for the flux kernel of self-phoresis and plugging in the field kernel (47), we obtain the y-component of the flux kernel,
| | 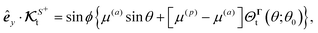 | (48a) |
| | 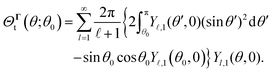 | (48b) |
The θ-dependent part ΘΓt of the translational flux kernel determines the significance of the difference between the phoretic mobilities of active and passive surfaces and is plotted for different values of θ0 in Fig. 4(d). The function ΘΓt has a peak at θ = θ0.
As reference speed, similar to the axisymmetric scenario, we use that for θ0 = π (a swimmer fully and symmetrically covered by two active surfaces), namely eqn (42). By plugging the flux kernel (48) and the model surface flux (44) into the velocity expression (19a), we obtain the scaled translational velocity along the y direction, similar to eqn (40),
| | 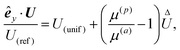 | (49) |
with the dimensionless functions
| | 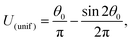 | (50a) |
| | 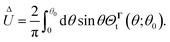 | (50b) |
The function
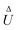
, plotted in
Fig. 4(e), quantifies the effect of the disparity in phoretic mobilities between passive and active surfaces on the translational velocity.
We can see that the function 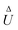 must go to zero at θ0 = π by definition of U(ref), and at θ0 = 0 because μ(p) is meaningless there, so that the prefactor of
must go to zero at θ0 = π by definition of U(ref), and at θ0 = 0 because μ(p) is meaningless there, so that the prefactor of 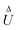 is effectively arbitrary. Apart from that, there is a critical value θc0 ≈ 48.33°, such that the function is negative for smaller, and positive for larger values of θ0. Interestingly, at θ0 = θc0, the velocity is independent of μ(p), even though the passive area is larger than the active area.
is effectively arbitrary. Apart from that, there is a critical value θc0 ≈ 48.33°, such that the function is negative for smaller, and positive for larger values of θ0. Interestingly, at θ0 = θc0, the velocity is independent of μ(p), even though the passive area is larger than the active area.
Fig. 4(f) shows the scaled velocity (49) of the microswimmer for different ratios of the phoretic mobility of the passive surface to that of the active surface. All curves intersect at the same point at the critical θc0, where êy·U/U(ref) ≈ 0.11. Furthermore, for some ratios of μ(p)/μ(a), we observe maximum values for the scaled velocity at θmax0 < π, suggesting that a particle with smaller active surface coverage can move faster than a particle with a fully covered active surface.
2. Rotational velocity.
The analysis of the microswimmer's rotational dynamics requires less calculations compared to translational velocity. The constant term in the expression (43) for phoretic mobility does not contribute to the rotation of a phoretic sphere. As a result, the rotational velocity is essentially proportional to the difference in phoretic mobility between the passive and active surfaces. The following symmetry considerations indicate that the angular velocity is purely along êx. Reflecting the particle about the antisymmetric xz plane effectively swaps the source and sink regions, leading to the transformation Γ0 → −Γ0. This transformation, along with eqn (19b), results in the inversion of the z component of the angular velocity, êz·Ω → −êz·Ω. However, this reflection is equivalent to rotating the sphere around êz by an angle of π, which does not change the sign of êy·Ω; consequently, êz·Ω must be zero. Furthermore, reflecting the particle about the symmetry yz plane preserves the direction of êy·Ω, while it should reverse its direction. This requires êy·Ω to be zero as well.
Using the general expression (13b) for the rotational field kernel and the example phoretic mobility (43), we can derive the rotational field kernel  . Subsequently, using the general expression for self-phoresis flux-kernel (21), we obtain the rotational flux kernel
. Subsequently, using the general expression for self-phoresis flux-kernel (21), we obtain the rotational flux kernel  as follows
as follows
| | 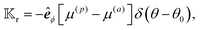 | (51a) |
| | 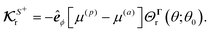 | (51b) |
Expanding the θ-dependence in terms of spherical harmonics with zero azimuthal angle (ϕ = 0),
| | 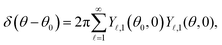 | (52a) |
| | 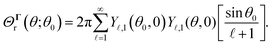 | (52b) |
shows that the differentiation between the field kernel and the flux kernel lies in the expansion coefficient within the square brackets for each
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
. The dimensionless function
ΘΓr(
θ;
θ0), plotted in
Fig. 4(g) for different values of
θ0, shows a peak at
θ0.
Since a fully covered particle (half source/half sink) does not rotate, defining the characteristic angular velocity scale is not as straightforward as in the case of translational motion. We define the angular velocity scale as
representing the angular velocity of a sphere moving at a linear speed
U(ref), defined in
eqn (42), along a circular trajectory of radius
a. Thus, using the flux kernel
(52b), the surface flux model
(44), and the angular velocity expression
(19b), we derive the scaled angular velocity as
| | 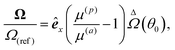 | (54) |
where the dimensionless function
| | 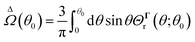 | (55) |
is illustrated in
Fig. 4(h) and is non-negative. Hence, the direction of rotation is primarily determined by the ratio of phoretic mobilities. As expected, the angular velocities are zero at the poles (
θ0 = 0, no active surface) and (
θ0 = π, full active surface) due to the lack of chiral asymmetry in the structure. The maximum angular velocity occurs at a coverage of
θ0 = 103.32°, where the active area exceeds half the surface area of the sphere.
6. Conclusion
The kernel-based approach discussed in this work provides an analytical framework that simplifies the analysis of phoresis phenomena by breaking it down into elementary problems. This allows for individual solutions that can be compounded to address the main problem. Integral kernels enhance understanding of the impact of geometry and phoretic mobility variations on translational and rotational velocities. This necessitates a fundamental understanding of material composition and surface properties, especially when phoretic mobility is non-uniform across the particle surface. The connection between the driving field, its flux distribution, and particle velocities is established through integral kernels. These kernels quantify local contributions of the field or flux to velocities, amalgamating the effects of geometry and surface composition into a position-dependent weight function for integration. This framework offers insights into phoretic particle behavior and the fine-tuning of their properties based on geometrical considerations. Our formalism for studying the phoresis of particles, compliant with the boundary condition (2), paves the way for future studies on non-spherical particles.
Data availability
This article is a theory paper, has no data other than plotting the equations in the draft.
Conflicts of interest
There are no conflicts to declare.
Appendix
Appendix A: Proofs of identities
We establish the validity of identities (12). Given the geometric isotropy of a sphere, which lacks a preferred direction, we can demonstrate each identity along any arbitrarily chosen fixed direction, such as êz. Consider the expression:| | 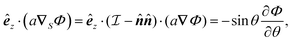 | (A1) |
we have| | 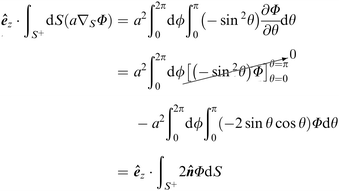 | (A2) |
where the first step utilizes integration by parts. In the last step, we apply dS = a2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdθdϕ and êz·
θdθdϕ and êz·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) = cos
= cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. As êz is an arbitrary constant unit vector, it can be eliminated from both sides, thus proving identity (12a).
θ. As êz is an arbitrary constant unit vector, it can be eliminated from both sides, thus proving identity (12a).
The proof of the second identity is more straightforward. Given that êz·êϕ = 0 and êz·êθ = −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, we find:
θ, we find:
| | 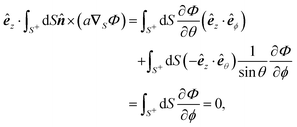 | (A3) |
where in the last step we used the periodic property
Φ(
θ,0) =
Φ(
θ,2π).
Acknowledgements
I extend my sincere gratitude to Paul E. Lammert for his insightful discussions and valuable comments. I also thank Mohammad Nabil for insightful comments. I wish to acknowledge the support from the National Science Foundation CAREER award, grant number CBET-2238915.
References
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef.
- H. Brenner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 066317 CrossRef PubMed.
- A. Nourhani and P. E. Lammert, Phys. Rev. Lett., 2016, 116, 178302 CrossRef PubMed.
- P. E. Lammert, V. H. Crespi and A. Nourhani, J. Fluid Mech., 2016, 802, 294 CrossRef CAS.
- J. L. Anderson and D. C. Prieve, Sep. Purif. Methods, 1984, 13, 67–103 CrossRef CAS.
- D. Velegol, A. Garg, R. Guha, A. Kar and M. Kumar, Soft Matter, 2016, 12, 4686–4703 RSC.
- S. Ebbens, M.-H. Tu, J. R. Howse and R. Golestanian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 020401 CrossRef PubMed.
- A. Gupta, S. Shim and H. A. Stone, Soft Matter, 2020, 16, 6975–6984 RSC.
- S. Michelin and E. Lauga, Sci. Rep., 2017, 7, 42264 CrossRef CAS.
- M. C. Fair and J. L. Anderson, J. Colloid Interface Sci., 1989, 127, 388–400 CrossRef CAS.
- E. Yariv, Proc. R. Soc. A, 2011, 467, 1645–1664 CrossRef.
- A. Nourhani, V. H. Crespi and P. E. Lammert, Phys. Rev. E, 2015, 91, 062303 CrossRef.
- A. Nourhani, P. E. Lammert, V. H. Crespi and A. Borhan, Phys. Fluids, 2015, 27, 092002 CrossRef.
- E. Yariv, J. Fluid Mech., 2010, 655, 105–121 CrossRef CAS.
- B. Sabass and U. Seifert, J. Chem. Phys., 2012, 136, 214507 CrossRef.
- E. Yariv and H. Brenner, SIAM J. Appl. Math., 2004, 64, 423–441 CrossRef.
- H. Brenner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 036325 CrossRef PubMed.
- R. Piazza and A. Parola, J. Phys.: Condens. Matter, 2008, 20, 153102 CrossRef.
- H. Brenner and J. R. Bielenberg, Phys. A, 2005, 355, 251–273 CrossRef.
- H. Brenner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 061201 CrossRef.
- A. Mohan and H. Brenner, SIAM J. Appl. Math., 2006, 66, 787–801 CrossRef.
- F. Soto, E. Karshalev, F. Zhang, B. Esteban Fernandez de Avila, A. Nourhani and J. Wang, Chem. Rev., 2021, 122, 5365–5403 CrossRef PubMed.
- A. Doostmohammadi, R. Stocker and A. M. Ardekani, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 3856–3861 CrossRef CAS PubMed.
- G. Li, E. Lauga and A. M. Ardekani, J. Non-Newtonian Fluid Mech., 2021, 297, 104655 CrossRef CAS.
- C. Chen, S. Ding and J. Wang, Nat. Rev. Mater., 2024, 1–14 Search PubMed.
- F. Katzmeier and F. C. Simmel, Nat. Commun., 2023, 14, 6247 CrossRef CAS PubMed.
- K. J. Bishop, S. L. Biswal and B. Bharti, Annu. Rev. Chem. Biomol. Eng., 2023, 14, 1–30 CrossRef CAS.
- M. Urso, M. Ussia and M. Pumera, Nat. Rev. Bioeng., 2023, 1, 236–251 CrossRef PubMed.
- U. Córdova-Figueroa, J. Brady and S. Shklyaev, Soft Matter, 2013, 9, 6382–6390 RSC.
- G. Rückner and R. Kapral, Phys. Rev. Lett., 2007, 98, 150603 CrossRef.
- T. Liverpool and A. Ajdari, New J. Phys., 2007, 9, 126 CrossRef.
- L. F. Valadares, Y.-G. Tao, N. S. Zacharia, V. Kitaev, F. Galembeck, R. Kapral and G. A. Ozin, Small, 2010, 6, 565–572 CrossRef CAS.
- R. Kapral, J. Chem. Phys., 2013, 138, 020901 CrossRef.
- O. Schnitzer and E. Yariv, Phys. Fluids, 2015, 27, 031701 CrossRef.
- R. Singh and R. Adhikari, J. Phys. Commun., 2018, 2, 025025 CrossRef.
- R. Singh, R. Adhikari and M. Cates, J. Chem. Phys., 2019, 151, 044901 CrossRef.
- B. Nasouri and R. Golestanian, Phys. Rev. Lett., 2020, 124, 168003 CrossRef CAS PubMed.
- B. Nasouri and R. Golestanian, J. Fluid Mech., 2020, 905, A13 CrossRef CAS.
- J. Zhang, A. Laskar, J. Song, O. E. Shklyaev, F. Mou, J. Guan, A. C. Balazs and A. Sen, ACS Nano, 2022, 17, 251–262 CrossRef.
- S. Thakur and R. Kapral, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 026121 CrossRef PubMed.
-
G. Turk, R. Adhikari and R. Singh, arXiv, 2023, preprint, arXiv:2310.01572 DOI:10.48550/arXiv.2310.01572.
- H. Masoud and H. A. Stone, J. Fluid Mech., 2019, 879, P1 CrossRef.
- W. F. Paxton, K. C. Kistler, C. C. Olmeda, A. Sen, S. K. St. Angelo, Y. Cao, T. E. Mallouk, P. E. Lammert and V. H. Crespi, J. Am. Chem. Soc., 2004, 126, 13424–13431 CrossRef CAS PubMed.
- H. A. Stone and A. D. Samuel, Phys. Rev. Lett., 1996, 77, 4102 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article abc
abc
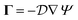
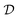 is a diffusion coefficient associated with the phoresis process.
is a diffusion coefficient associated with the phoresis process.
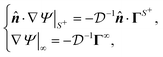
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) is the unit normal to the particle surface. For the locally-generated flux ΓS+, the distribution of the normal component of the flux over S+ may vary. Conversely, the far-field flux Γ∞, which pertains to the globally-driven aspect of the phoresis process, is typically uniform. The boundary condition (2) includes both local and global gradients of the driving field. Common special cases include self-phoresis (ΓS+ ≠ 0) in the absence of global flux (Γ∞ = 0),3,4 and globally-driven phoresis (Γ∞ ≠ 0) of a passive particle in the absence of surface flux (ΓS+ = 0).10
is the unit normal to the particle surface. For the locally-generated flux ΓS+, the distribution of the normal component of the flux over S+ may vary. Conversely, the far-field flux Γ∞, which pertains to the globally-driven aspect of the phoresis process, is typically uniform. The boundary condition (2) includes both local and global gradients of the driving field. Common special cases include self-phoresis (ΓS+ ≠ 0) in the absence of global flux (Γ∞ = 0),3,4 and globally-driven phoresis (Γ∞ ≠ 0) of a passive particle in the absence of surface flux (ΓS+ = 0).10
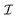 , the expression
, the expression 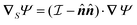 is tangent to S+, providing the surface gradient of the field over the particle surface.
is tangent to S+, providing the surface gradient of the field over the particle surface.
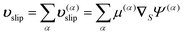
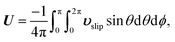
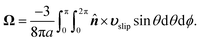

![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·ΓS+ and Γ∞ using eqn (17); second, calculate the surface gradient of the field, and obtain the slip velocity (3); and third, use the slip velocity in integrals (7) to yield the velocities.
·ΓS+ and Γ∞ using eqn (17); second, calculate the surface gradient of the field, and obtain the slip velocity (3); and third, use the slip velocity in integrals (7) to yield the velocities.
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·ΓS+ and Γ∞ to the translational U and rotational Ω velocities using integral kernels. For this purpose, we need to circumvent the calculation of slip velocity, specifically step II, in the steps (8). In the next section, Background, we review earlier efforts to derive geometrical kernel in order to connect the surface flux to self-phoretic velocities for particles with uniform phoretic mobility. Subsequently, in the following section, we introduce the concepts of field-kernels and flux-kernels for spheres for more general scenarios where the particle can be passive or active and the phoretic mobility can be non-uniform.
·ΓS+ and Γ∞ to the translational U and rotational Ω velocities using integral kernels. For this purpose, we need to circumvent the calculation of slip velocity, specifically step II, in the steps (8). In the next section, Background, we review earlier efforts to derive geometrical kernel in order to connect the surface flux to self-phoretic velocities for particles with uniform phoretic mobility. Subsequently, in the following section, we introduce the concepts of field-kernels and flux-kernels for spheres for more general scenarios where the particle can be passive or active and the phoretic mobility can be non-uniform.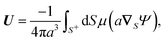
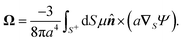
 and rotational
and rotational  field kernels that quantify the local contribution of the field over the particle surface to the translational and rotational velocities, respectively. For flux kernels we will have distinct local flux kernel
field kernels that quantify the local contribution of the field over the particle surface to the translational and rotational velocities, respectively. For flux kernels we will have distinct local flux kernel 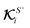 and global flux kernel
and global flux kernel 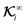 for translational (i = t) and rotational (i = r) velocities, using integrations equivalent to the integrations in eqn (9),
for translational (i = t) and rotational (i = r) velocities, using integrations equivalent to the integrations in eqn (9),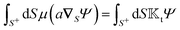
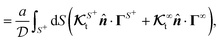
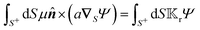
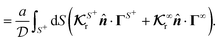
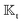 and
and  , which deal directly with the field, are independent of the origin of the field gradient, whether locally ΓS+ or globally Γ∞. The field kernels for both locally-driven and globally-driven aspects of phoresis processes are conceptually the same.
, which deal directly with the field, are independent of the origin of the field gradient, whether locally ΓS+ or globally Γ∞. The field kernels for both locally-driven and globally-driven aspects of phoresis processes are conceptually the same.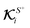 and global flux kernels
and global flux kernels 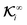 , have distinct interpretations, as we elaborate below. The integration involving local flux kernels
, have distinct interpretations, as we elaborate below. The integration involving local flux kernels 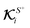 and the normal component of the locally-driven flux ΓS+ has the same intuitive interpretation as the integration involving field kernels and the field; the local flux kernels
and the normal component of the locally-driven flux ΓS+ has the same intuitive interpretation as the integration involving field kernels and the field; the local flux kernels 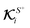 define the local contribution of the surface flux ΓS+ to the particle's translational and rotational velocities.
define the local contribution of the surface flux ΓS+ to the particle's translational and rotational velocities.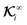 , although the integration is over the particle surface S+, the value of the flux is far-field. Therefore, the term
, although the integration is over the particle surface S+, the value of the flux is far-field. Therefore, the term ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·Γ∞ in the integration
·Γ∞ in the integration 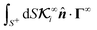 in eqn (10b) and (10d), while integrated over the particle surface, does not represent the surface flux of the field over the particle surface. For example, in the case of globally driven phoresis of an impermeable, non-polarizable passive particle, the surface flux of the field
in eqn (10b) and (10d), while integrated over the particle surface, does not represent the surface flux of the field over the particle surface. For example, in the case of globally driven phoresis of an impermeable, non-polarizable passive particle, the surface flux of the field 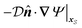 is zero and different from
is zero and different from ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·Γ∞. To visualize the scenario and develop an intuition about the integral
·Γ∞. To visualize the scenario and develop an intuition about the integral 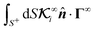 , imagine a uniform field gradient with a flux value Γ∞ throughout the entire space. Then, we place an imaginary sphere in this field gradient without distorting the field gradient, and integrate
, imagine a uniform field gradient with a flux value Γ∞ throughout the entire space. Then, we place an imaginary sphere in this field gradient without distorting the field gradient, and integrate ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·Γ∞ over the surface of the imaginary particle weighted by the kernel
·Γ∞ over the surface of the imaginary particle weighted by the kernel 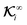 . Therefore, while the flux Γ∞ is a far-field value, we use the same value for integration over the surface of the sphere in the velocity expressions (19) as if the presence of the sphere has not distorted the uniform distribution of the far-field flux over the particle surface.
. Therefore, while the flux Γ∞ is a far-field value, we use the same value for integration over the surface of the sphere in the velocity expressions (19) as if the presence of the sphere has not distorted the uniform distribution of the far-field flux over the particle surface.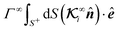 is effectively proportional to the weighted integration of the projection of the direction of the far-field flux on the normal surface vector, that is,
is effectively proportional to the weighted integration of the projection of the direction of the far-field flux on the normal surface vector, that is, ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·ê. This expression shows how the particle dynamics result from the coupling of the direction ê of the far-field flux to the surface characteristics and orientation of the particle, quantified by the second-rank tensor
·ê. This expression shows how the particle dynamics result from the coupling of the direction ê of the far-field flux to the surface characteristics and orientation of the particle, quantified by the second-rank tensor 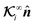 .
.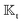 and
and 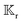 , we combine eqn (9), (10a) and (10c) and reformulate the velocities in terms of weighted surface integrals of the fields such that
, we combine eqn (9), (10a) and (10c) and reformulate the velocities in terms of weighted surface integrals of the fields such that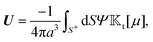
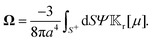
 for i = t, r are functionals of the surface distribution of the phoretic mobility μ(xS).
for i = t, r are functionals of the surface distribution of the phoretic mobility μ(xS).
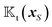 and
and 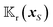 over the particle surface in the velocity expressions (11), we exploit the following two identities, the proofs of which are provided in Appendix A. For a function Φ(xS) over the surface of a sphere, we have
over the particle surface in the velocity expressions (11), we exploit the following two identities, the proofs of which are provided in Appendix A. For a function Φ(xS) over the surface of a sphere, we have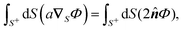
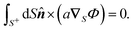
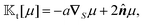
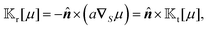
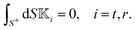
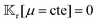 , meaning the particle does not rotate. Therefore, a heterogeneous distribution of the field over a sphere's surface does not induce rotation for a sphere if the phoretic mobility is uniform. Furthermore, in the scenario of uniform phoretic mobility, the translational field kernel simplifies to a radial vector field over the sphere surface,
, meaning the particle does not rotate. Therefore, a heterogeneous distribution of the field over a sphere's surface does not induce rotation for a sphere if the phoretic mobility is uniform. Furthermore, in the scenario of uniform phoretic mobility, the translational field kernel simplifies to a radial vector field over the sphere surface, 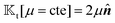 . Consequently, the calculation of the translational velocity is reduced to the surface integration of the field, weighted by the surface normal vector and phoretic mobility.
. Consequently, the calculation of the translational velocity is reduced to the surface integration of the field, weighted by the surface normal vector and phoretic mobility.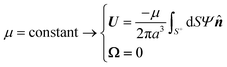
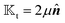 effectively reduces to
effectively reduces to 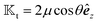 , as shown in Fig. 1. Here, the field kernel provides us with another physical insight: in an axisymmetric scenario with uniform phoretic mobility, the field at the equator does not contribute to the motion, and the majority of the contribution comes from the poles.
, as shown in Fig. 1. Here, the field kernel provides us with another physical insight: in an axisymmetric scenario with uniform phoretic mobility, the field at the equator does not contribute to the motion, and the majority of the contribution comes from the poles.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,m(θ,ϕ), the solution to the Laplace equation,
,m(θ,ϕ), the solution to the Laplace equation,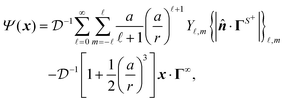
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,m for the expansion coefficients in terms of spherical harmonics. That is, for a function Φ(θ,ϕ) defined over the surface of a sphere, we have
,m for the expansion coefficients in terms of spherical harmonics. That is, for a function Φ(θ,ϕ) defined over the surface of a sphere, we have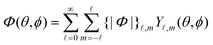
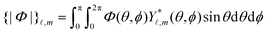
 and global flux kernels
and global flux kernels 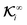 , we combine eqn (9), (10b) and (10d) and recast the velocities in the form,
, we combine eqn (9), (10b) and (10d) and recast the velocities in the form,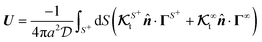
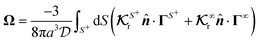
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·ΓS+ and far-field global flux
·ΓS+ and far-field global flux ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·Γ∞. As discussed following eqn (10), the integrands in these expressions have distinct interpretations. To obtain the local flux kernel, we consider a scenario where ΓS+ ≠ 0 and Γ∞ = 0. For the global flux kernel, we study a situation where ΓS+ = 0 and Γ∞ ≠ 0. The combination of these two scenarios leads to the boundary conditions (2).
·Γ∞. As discussed following eqn (10), the integrands in these expressions have distinct interpretations. To obtain the local flux kernel, we consider a scenario where ΓS+ ≠ 0 and Γ∞ = 0. For the global flux kernel, we study a situation where ΓS+ = 0 and Γ∞ ≠ 0. The combination of these two scenarios leads to the boundary conditions (2).
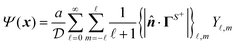
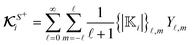
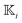 by the factor 1/(
by the factor 1/(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1) for each term.
+ 1) for each term.
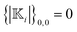 . Additionally, the orthogonality of the spherical harmonics results in
. Additionally, the orthogonality of the spherical harmonics results in 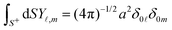 . Together with eqn (21), this leads to a zero surface integral of the flux kernels,
. Together with eqn (21), this leads to a zero surface integral of the flux kernels,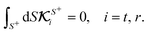
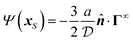
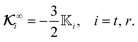

![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·Γ∞, which is not uniform over the particle surface.
·Γ∞, which is not uniform over the particle surface. , which are linearly proportional to the rotational field kernel
, which are linearly proportional to the rotational field kernel 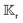 , are also zero. Therefore, for an active particle, heterogeneity in surface activity alone is not sufficient to induce rotation; heterogeneity in the surface distribution of phoretic mobility is necessary. Additionally, the translational flux kernels are proportional to the normal vector
, are also zero. Therefore, for an active particle, heterogeneity in surface activity alone is not sufficient to induce rotation; heterogeneity in the surface distribution of phoretic mobility is necessary. Additionally, the translational flux kernels are proportional to the normal vector ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) , thus,
, thus,
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) term in kernels (26) can be reduced to cos
term in kernels (26) can be reduced to cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θêz, where êz is the symmetry axis. Again, we learn that in the axisymmetric scenario with constant phoretic mobility, the majority of the flux contribution to motion comes from the poles, and the flux around the equator has a negligible contribution.
θêz, where êz is the symmetry axis. Again, we learn that in the axisymmetric scenario with constant phoretic mobility, the majority of the flux contribution to motion comes from the poles, and the flux around the equator has a negligible contribution. .
.
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) of the Janus particle points from one face to the other, defining the particle's orientation in space. Positioned along the symmetry axis, the direction of the director is arbitrary, yet it determines how we refer to the Janus particle based on its rear-front composition. For instance, in Fig. 2(a), the Janus particle is termed
of the Janus particle points from one face to the other, defining the particle's orientation in space. Positioned along the symmetry axis, the direction of the director is arbitrary, yet it determines how we refer to the Janus particle based on its rear-front composition. For instance, in Fig. 2(a), the Janus particle is termed ![[a with combining low line]](https://www.rsc.org/images/entities/char_0061_0332.gif) ctive–
ctive–![[p with combining low line]](https://www.rsc.org/images/entities/char_0070_0332.gif) assive (a.p.), reflecting the orientation of its director: the normal component of the surface flux on the passive side is zero, while on the active side, it can be either negative or positive. Alternatively, in Fig. 2(b), both sides are active, and the Janus particle is described as s
assive (a.p.), reflecting the orientation of its director: the normal component of the surface flux on the passive side is zero, while on the active side, it can be either negative or positive. Alternatively, in Fig. 2(b), both sides are active, and the Janus particle is described as s![[i with combining low line]](https://www.rsc.org/images/entities/char_0069_0332.gif) nk–s
nk–s![[o with combining low line]](https://www.rsc.org/images/entities/char_006f_0332.gif) urce (i.o.): the surface flux at the sink is negative, and at the source, it is positive.
urce (i.o.): the surface flux at the sink is negative, and at the source, it is positive.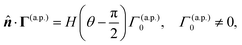
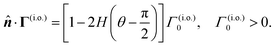
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) . The globally-generated uniform flux Γ(glb) forms an angle γ with the Janus director
. The globally-generated uniform flux Γ(glb) forms an angle γ with the Janus director ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) , such that êz·
, such that êz·![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) = cos
= cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ.
γ.
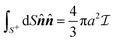 , we obtain the phoretic velocity,
, we obtain the phoretic velocity,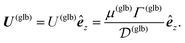
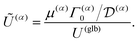
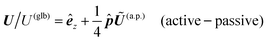
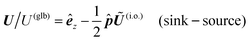
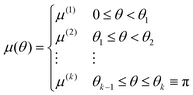
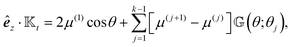
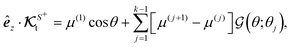
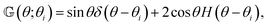
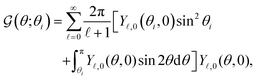

 locally quantifying the disparity of the phoretic mobilities in the flux kernel (33b). (c) Self-phoretic particle with two active surfaces. (d) A source–sink self-phoretic particle with a passive region in the middle, and (e) the corresponding dimensionless component of the flux kernel due to the difference in the phoretic mobility of passive and active regions. (f) Dimensionless velocities for the model swimmer presented in Fig. 3(d).
locally quantifying the disparity of the phoretic mobilities in the flux kernel (33b). (c) Self-phoretic particle with two active surfaces. (d) A source–sink self-phoretic particle with a passive region in the middle, and (e) the corresponding dimensionless component of the flux kernel due to the difference in the phoretic mobility of passive and active regions. (f) Dimensionless velocities for the model swimmer presented in Fig. 3(d). for different values of θi. The function shows a peak at the boundary θ = θi. Therefore, we can expect k − 1 peaks in the flux kernel (33b) at the boundaries of the regions, and the strength of the peaks depends on the differences in phoretic mobilities of the neighboring regions forming the boundaries.
for different values of θi. The function shows a peak at the boundary θ = θi. Therefore, we can expect k − 1 peaks in the flux kernel (33b) at the boundaries of the regions, and the strength of the peaks depends on the differences in phoretic mobilities of the neighboring regions forming the boundaries.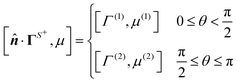
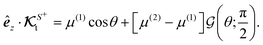
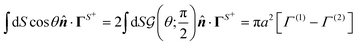 we reobtain eqn (9) in ref. 31,
we reobtain eqn (9) in ref. 31,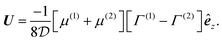
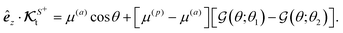
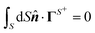 , is
, is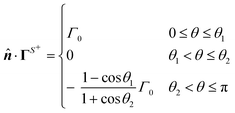
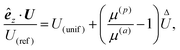
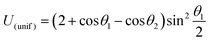
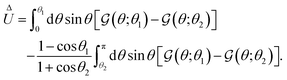
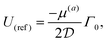
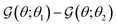 in the flux kernel (38) for different sizes of the sink region, identified by θ2. The curves show two peaks at the boundaries, θ1 and θ2, of the regions. Fig. 3(f) shows the corresponding dimensionless velocities (41), both of which increase monotonically with an increase in θ2.
in the flux kernel (38) for different sizes of the sink region, identified by θ2. The curves show two peaks at the boundaries, θ1 and θ2, of the regions. Fig. 3(f) shows the corresponding dimensionless velocities (41), both of which increase monotonically with an increase in θ2.
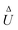 in the translational velocity expression (49) determines the contribution of the difference in phoretic mobilities to motion. (f) The scaled velocity êy·U/U(ref) for difference ratios of phoretic mobilities. (g) The θ-dependent function ΘΓr(θ;θ0) of the rotational flux-kernel (52b) shows peak at θ = θ0. (h) The dimensionless function
in the translational velocity expression (49) determines the contribution of the difference in phoretic mobilities to motion. (f) The scaled velocity êy·U/U(ref) for difference ratios of phoretic mobilities. (g) The θ-dependent function ΘΓr(θ;θ0) of the rotational flux-kernel (52b) shows peak at θ = θ0. (h) The dimensionless function 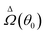 shows the behavior of the magnitude of the angular velocity.
shows the behavior of the magnitude of the angular velocity.![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·ΓS+ over the surface of the sphere is given by
·ΓS+ over the surface of the sphere is given by![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ·ΓS+(θ,ϕ) = [1 − H(θ − θ0)][1 − 2H(ϕ − π)]Γ0.
·ΓS+(θ,ϕ) = [1 − H(θ − θ0)][1 − 2H(ϕ − π)]Γ0.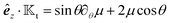 has no ϕ-dependence, the expansion coefficients
has no ϕ-dependence, the expansion coefficients 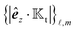 for the flux kernel (21) are non-zero only when m = 0. Therefore, the z-component of the flux kernel,
for the flux kernel (21) are non-zero only when m = 0. Therefore, the z-component of the flux kernel, 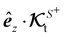 , has no ϕ-dependence. On the other hand,
, has no ϕ-dependence. On the other hand, 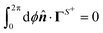 . Hence,
. Hence,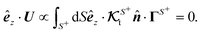
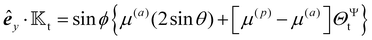
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − cos
θ − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θδ(θ − θ0)
θδ(θ − θ0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ necessitates that the flux kernel coefficients
ϕ necessitates that the flux kernel coefficients 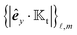 can be non-zero only when m = ±1. Thus, using the expression (21) for the flux kernel of self-phoresis and plugging in the field kernel (47), we obtain the y-component of the flux kernel,
can be non-zero only when m = ±1. Thus, using the expression (21) for the flux kernel of self-phoresis and plugging in the field kernel (47), we obtain the y-component of the flux kernel,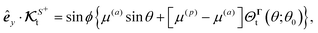
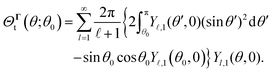
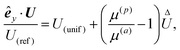
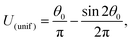
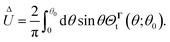
 , plotted in Fig. 4(e), quantifies the effect of the disparity in phoretic mobilities between passive and active surfaces on the translational velocity.
, plotted in Fig. 4(e), quantifies the effect of the disparity in phoretic mobilities between passive and active surfaces on the translational velocity.
 must go to zero at θ0 = π by definition of U(ref), and at θ0 = 0 because μ(p) is meaningless there, so that the prefactor of
must go to zero at θ0 = π by definition of U(ref), and at θ0 = 0 because μ(p) is meaningless there, so that the prefactor of 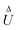 is effectively arbitrary. Apart from that, there is a critical value θc0 ≈ 48.33°, such that the function is negative for smaller, and positive for larger values of θ0. Interestingly, at θ0 = θc0, the velocity is independent of μ(p), even though the passive area is larger than the active area.
is effectively arbitrary. Apart from that, there is a critical value θc0 ≈ 48.33°, such that the function is negative for smaller, and positive for larger values of θ0. Interestingly, at θ0 = θc0, the velocity is independent of μ(p), even though the passive area is larger than the active area.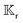 . Subsequently, using the general expression for self-phoresis flux-kernel (21), we obtain the rotational flux kernel
. Subsequently, using the general expression for self-phoresis flux-kernel (21), we obtain the rotational flux kernel 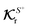 as follows
as follows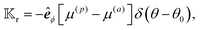
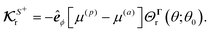
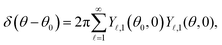
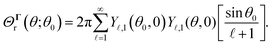
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . The dimensionless function ΘΓr(θ;θ0), plotted in Fig. 4(g) for different values of θ0, shows a peak at θ0.
. The dimensionless function ΘΓr(θ;θ0), plotted in Fig. 4(g) for different values of θ0, shows a peak at θ0.
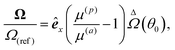
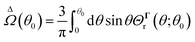
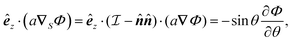
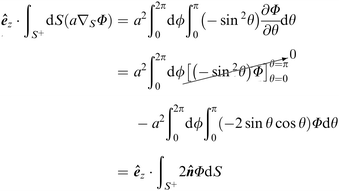
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdθdϕ and êz·
θdθdϕ and êz·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) = cos
= cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. As êz is an arbitrary constant unit vector, it can be eliminated from both sides, thus proving identity (12a).
θ. As êz is an arbitrary constant unit vector, it can be eliminated from both sides, thus proving identity (12a).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, we find:
θ, we find: