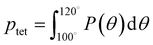Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computation of Overhauser dynamic nuclear polarization processes reveals fundamental correlation between water dynamics, structure, and solvent restructuring entropy†
Dennis C.
Robinson Brown
 a,
Thomas R.
Webber
a,
Thomas R.
Webber
 a,
Thomas M.
Casey
b,
John
Franck
c,
M. Scott
Shell
a and
Songi
Han
*abd
a,
Thomas M.
Casey
b,
John
Franck
c,
M. Scott
Shell
a and
Songi
Han
*abd
aDepartment of Chemical Engineering, University of California, Santa Barbara, California 93106, USA
bDepartment of Chemistry and Biochemistry, University of California, Santa Barbara, California 93106, USA
cDepartment of Chemistry, Syracuse University, Syracuse, NY, USA
dDepartment of Chemistry, Northwestern University, Evanston, Illinois 60208, USA. E-mail: songi.han@northwestern.edu
First published on 4th April 2024
Abstract
Hydration water dynamics, structure, and thermodynamics are crucially important to understand and predict water-mediated properties at molecular interfaces. Yet experimentally and directly quantifying water behavior locally near interfaces at the sub-nanometer scale is challenging, especially at interfaces submerged in biological solutions. Overhauser dynamic nuclear polarization (ODNP) experiments measure equilibrium hydration water dynamics within 8–15 angstroms of a nitroxide spin probe on instantaneous timescales (10 picoseconds to nanoseconds), making ODNP a powerful tool for probing local water dynamics in the vicinity of the spin probe. As with other spectroscopic techniques, concurrent computational analysis is necessary to gain access to detailed molecular level information about the dynamic, structural, and thermodynamic properties of water from experimental ODNP data. We chose a model system that can systematically tune the dynamics of water, a water–glycerol mixture with compositions ranging from 0 to 0.3 mole fraction glycerol. We demonstrate the ability of molecular dynamics (MD) simulations to compute ODNP spectroscopic quantities, and show that translational, rotational, and hydrogen bonding dynamics of hydration water align strongly with spectroscopic ODNP parameters. Moreover, MD simulations show tight correlations between the dynamic properties of water that ODNP captures and the structural and thermodynamic behavior of water. Hence, experimental ODNP readouts of varying water dynamics suggest changes in local structural and thermodynamic hydration water properties.
Introduction
Local hydropathies near molecular interfaces to water (e.g., proteins and polymers) modulate the surface activity for solute binding,1–5 among many other properties.2,6–19 Locally hydrophobic regions of proteins are key to facilitating folding and inter-protein interactions, and are often characteristic of active sites.1,16,17,20 In reality, hydropathy or hydrophobicity is not truly a property of the protein itself, but rather a statement of how water in the vicinity responds to the presence of particular protein side chains. Experimentally characterizing the structural, dynamical, and thermodynamic properties of water in fully hydrated environments at the molecular scale is challenging. Several experimental methods can probe the behavior of hydration layer waters,6,16,19,21,22 but experimental measurements are often limited to detecting average water properties of the entire ensemble.23–25 There is extensive literature on molecular dynamics (MD) simulation studies that probe hydration dynamics of different solution systems with heterogeneous water–protein interfaces,7–9,11,16,17,21,26–34 but relatively few directly compare and validate with experimental techniques,16,17,21,22 in part, due to the difficulty of resolving local water dynamics experimentally. Undoubtedly, it is critical to leverage atomistic MD simulations synergistically with experiments to comprehensively and robustly characterize the heterogeneous hydration environments on soft material and biomolecular surfaces1,3,4,9,17,20Advanced techniques such as quasi-elastic neutron scattering (QENS),17,35,36 Overhauser dynamic nuclear polarization (ODNP),16,21,37 terahertz (THz) spectroscopy38–41 and pump–probe infrared (IR) spectroscopy42 can directly yield surface-specific water properties. Among those, only ODNP is sensitive to translational hydration water properties around localized sites or surfaces that are fully surrounded by bulk water in biological or synthetic solution-state environments. Fundamentally, ODNP is a magnetic resonance technique that quantifies electron-1H cross-relaxation by measuring (1) the enhancement of 1H NMR signals induced by dynamic nuclear polarization (DNP) via the transfer of polarization from an unpaired electron of a nitroxide spin probe to the 1H nucleus of water, and (2) the longitudinal spin lattice relaxation time, T1, that reports on all 1H relaxation mechanisms induced by the dipolar coupling between the 1H nuclear spin and the electron spin of the nearby spin probe. The electron-1H cross-relaxivity at a magnetic field of 0.35 Tesla and electron Larmor frequency of 9.8 GHz is sensitive to translational movement of hydration waters near the electron spin probe on instantaneous timescales ranging from about 10 picoseconds to nanoseconds and within 8 to 15 angstroms of nitroxide-based spin probes that can be tethered to specific surface sites.
ODNP responds sensitively to the chemically or topologically distinct local environments that are generated by highly heterogeneous surfaces immersed in bulk water. It thus demonstrates a diversity of local water dynamics and structure that reflects the diversity in these local environments. A recent synergistic ODNP-MD simulation study of sites with varying hydropathy on a CheY protein surface displayed a positive correlation between site-specific hydrophobicity and translational water dynamics.16,43 This study demonstrated a connection between the ODNP spectroscopic quantities and computed thermodynamic properties of water by demonstrating a correlation between the two. However, no study has directedly computed ODNP parameters for the purpose of deriving hydration water dynamical information and coupling to molecular dynamical, structural, and thermodynamic properties of hydration water near surfaces or solutes.
In the present work, we compute ODNP spectroscopic parameters—specifically, the coupling factor and electron-1H cross-relaxation rates—and use molecular dynamics simulations to characterize the dynamical, structural, and thermodynamic properties of water in water–glycerol mixtures with increasing glycerol content [Fig. 1]. Water–glycerol mixtures allow us to probe the complex interrelationship between water properties at the molecular scale while varying solution viscosity by a known amount. Moreover, glycerol is of fundamental interest due to its ubiquity in biological studies for its role in cryopreservation of proteins and has been recently shown to alter not only the dynamical, but also structural and thermodynamic properties of water.44 Regardless of the system, the study of molecular determinants of surface hydration requires dual experimental and computational insight. Experimental techniques like ODNP offer valuable, but incomplete, insight on the molecular scale properties of hydration waters. On the other hand, without experimental validation, simulations can be subject to doubts, especially when it comes to variations in the structure and dynamics of water near interfaces. Synergistic fully-atomistic simulations can aide in elucidating the molecular details that are often inaccessible to experimental methods.
In this study, we perform atomistic MD simulations of glycerol–water to test the ability of MD simulations to reproduce ODNP spectroscopic quantities and to connect ODNP spectroscopic and MD-derived translational, rotational, and hydrogen bonding dynamical quantities. We furthermore exploit the atomistic information content of MD simulations to quantify the relationship between hydration water dynamics, structure, and thermodynamics in glycerol–water mixtures across a wide range of compositions.
Methods
Overhauser dynamic nuclear polarization
We perform experimental ODNP measurements with samples containing mixtures of water (Milli-Q purity, Milli-Q UV Plus system, Millipore Inc., Bedford, MA, USA), glycerol (d8, 99%, DLM-558, Cambridge Isotope Laboratory, Tewksbury, MA, USA) and 4-hydroxy-TEMPO (176141, Sigma Aldrich) at a constant concentration of 318 μM. We transfer 4 μL samples into round quartz capillaries of 0.6 mm ID × 0.84 mm OD (Vitrocom, New Jersey, USA), sealed with Critoseal on one end and melted beeswax on the other end. We perform ODNP experiments using the X-channel of a a Bruker EMXPlus spectrometer and a Bruker Avance III NMR console (Bruker, Massachusetts, USA) that utilizes specialized automation (AU) programs to interact with the ODNP microwave hardware. We install the capillaries in a home-built NMR probe with a U-shaped coil centered in a high sensitivity microwave cavity (Bruker ER 4119HS-LC).45 ODNP measurements rely on the saturation of the electron paramagnetic resonance (EPR) of 4-hydroxy-TEMPO at 9.8 GHz (X-band) frequency at a center field of 3484 G, which coincides with the center resonance of the nitroxide EPR spectrum. Dry air at 9.44 L min−1 streams through the cavity across the probe and capillary to maintain a temperature of 18 °C. Theory and experimental details are outlined in previous publications.16,22,37,46Molecular dynamics simulations
We perform molecular dynamics simulations using the OPC 4-site water model,47 the Blieck–Chelli (BC) model for glycerol48–50 and a 4-hydroxy-TEMPO nitroxide spin probe. Both the OPC water model and the BC model for glycerol accurately reproduce the diffusivities of pure water47 and pure glycerol48,50 under ambient conditions (298.15 K and 1-bar). For the spin probe, its partial charges are obtained using the AMBER18 Antechamber package51 informed by quantum chemical calculations using the Gaussian 16 software.52 Specifically, we apply the B3LYP functional and the 6-311++G(d,p) to perform geometry optimization of 4-hydroxy-TEMPO. All other inter- and intramolecular parameters derive from the second-generation generalized Amber forcefield (GAFF2).53,54 The results of this parametrization scheme yield similar parameters to those obtained in previous publications.55 All Coulombic interactions are modeled with the particle–mesh Ewald summation scheme (PME).56We simulate glycerol–water–spin probe systems with glycerol mole fractions (xglyc) of 0, 0.01, 0.033, 0.05, 0.075, 0.1, 0.15, 0.2 and 0.3 using the GPU-optimized OpenMM molecular simulation software.57 At each of these concentrations, we include a single 4-OH-TEMPO molecule in the simulation box. Hence, the spin probe concentration varies depending on glycerol concentration (from 27 mM in pure water to 10 mM for xglyc = 0.3). We first energy minimize each system, then equilibrate in the NPT ensemble using a Langevin thermostat57 paired with a Monte Carlo barostat57 at 290 K and 1 atm. Following equilibration, the NPT run continues for 250 ns with system configurations saved every 10 ns. Each saved configuration serves as the starting point for an independent 1 nanosecond NVE simulation for dynamic properties, with system coordinates saved every 0.1 ps. To calculate hydration water dynamics timescales and ODNP spectroscopic quantities, we compute 95% confidence intervals by bootstrapping the results obtained from 20 independent MD simulations.
We characterize the effect of glycerol on solvation thermodynamics via the solvation free energy ΔGsolv of methane—an ideal small hydrophobic solute—in glycerol–water. To estimate ΔGsolv for this series of mixtures, we implement an expanded ensemble simulation procedure in which we gradually scale intermolecular interaction parameters between the methane molecule and the glycerol–water mixture. We smoothly scale Lennard Jones (LJ) and coulombic interaction parameters via a scalar parameter λ from λ = 0 (non-interacting, or ideal gas molecule) [panels (1) and (3) in Fig. 6(a)] to 1 (fully interacting methane) [panels (2) and (4) in Fig. 6(a)]. To estimate the Gibbs free energy of solvation ΔGsolv [Fig. 6(b)], we then apply the multistate Bennett acceptance ratio (MBAR) method distributed via the pymbar58 Python library.
Theory
Computing spectroscopic quantities
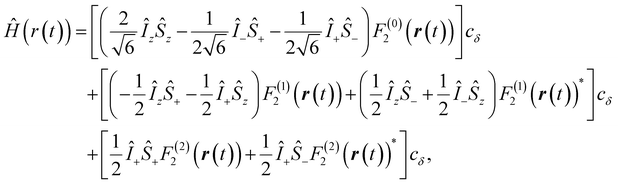 | (1) |
 ,
,  , and γS = γI/1.52 × 10−3 are the vacuum permeability, gyromagnetic ratio of the proton spin, and the gyromagnetic ratio of the electron spin, respectively.
, and γS = γI/1.52 × 10−3 are the vacuum permeability, gyromagnetic ratio of the proton spin, and the gyromagnetic ratio of the electron spin, respectively.
Using this semi-classical framework, we compute the equilibrium translational diffusion of water molecules by constructing the time-autocorrelation functions (ACFs), C(m)ODNP(t), that depend purely on the relative positions of water hydrogen and the unpaired electron of a spin probe via the classical spherical harmonic functions included in eqn (1)
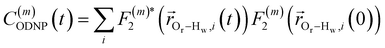 | (2) |
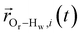 is the displacement vector between the water hydrogen i and the oxygen radical of the spin probe and m = 0, 1, 2 the order, which correspond, respectively, to the flip–flop, single spin flip, and double spin flip transitions of the coupled I–S spin system. The C(m)ODNP(t) functions decay with time as water molecules diffuse from their initial position relative to the spin probe, just as the dipolar coupling between the proton and electron spin weakens with increased spatial separation. The C(m)ODNP(t) functions are complex-valued, but the complex part is negligible for isotropic systems59 and thus ignored in this study [more detailed description in ESI,† Section D]. Further, the system isotropy ensures that C(m)ODNP(t) = C(n)ODNP(t) for all n and m. Hence, we refer to only a single ACF for computing ODNP properties, CODNP(t), for the remainder of the discussion. For the present work, we find that all measured CODNP(t) are well-described by a tri-exponential fit:
is the displacement vector between the water hydrogen i and the oxygen radical of the spin probe and m = 0, 1, 2 the order, which correspond, respectively, to the flip–flop, single spin flip, and double spin flip transitions of the coupled I–S spin system. The C(m)ODNP(t) functions decay with time as water molecules diffuse from their initial position relative to the spin probe, just as the dipolar coupling between the proton and electron spin weakens with increased spatial separation. The C(m)ODNP(t) functions are complex-valued, but the complex part is negligible for isotropic systems59 and thus ignored in this study [more detailed description in ESI,† Section D]. Further, the system isotropy ensures that C(m)ODNP(t) = C(n)ODNP(t) for all n and m. Hence, we refer to only a single ACF for computing ODNP properties, CODNP(t), for the remainder of the discussion. For the present work, we find that all measured CODNP(t) are well-described by a tri-exponential fit:| CODNP,fit(t) = a1e−t/τ1 + a2e−t/τ2 + a3e−t/τ3 | (3) |
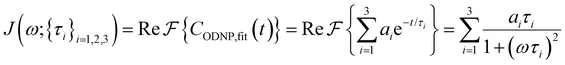 | (4) |
Fig. 2(a) illustrates the dynamic spin–spin dipolar interaction between the unpaired electron of 4-OH-TEMPO and water protons underpinning the calculation of CODNP,fit(t). In Fig. 2(b), we depict CODNP(t) for a representative model system, a water–glycerol mixture with xglyc = 0.1. We find that CODNP(t) and its model fit, CODNP,fit(t), are nearly indistinguishable with R2 = 0.99. In Table S1 (ESI†), we summarize the tri-exponential fitting parameters for each glycerol–water mixture. In Fig. 2(c), we apply eqn (4) to compute the spectral density function J(ω) from CODNP(t) for the same mixture with xglyc = 0.1. Here, the amplitude of the spectral density values at frequencies ωI and ωS [J(ωI = 14.8 MHz) and J(ωS = 9.8 GHz)] are sensitive to translational dynamics on nanosecond and picosecond timescales, respectively.
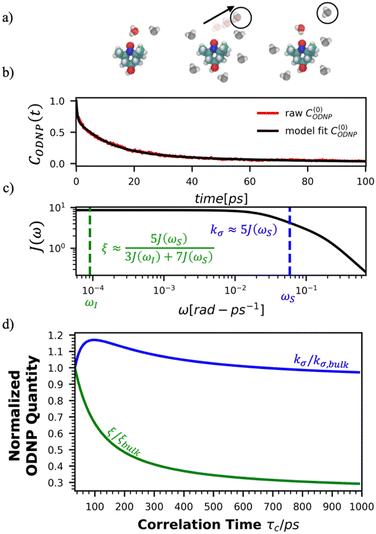 | ||
| Fig. 2 Schematic of ODNP spectroscopic quantities calculation from classical MD trajectories. (a) The snapshot shows 4-OH-TEMPO in a 0.1 mole fraction glycerol mixture at 290 K with bulk water represented in VMD as a medium and the hydration waters within 3.5 angstroms of the spin probe in VDW sphere representation. Glycerol molecules are omitted for clarity. The diagram to the right of the snapshot illustrates the ODNP mechanism for the nearest water molecule to the spin probe at some time t. (b) The ODNP time autocorrelation function CODNP(t) at a glycerol mole fraction of 0.1 (red line) is fit to a tri-exponential model [eqn (3)] (black line) as described in the text. (c) The real part of the Fourier transforms of CODNP,fit(t) gives spectral density function J(ω). Subsequently, J(ω) values at radical electron J(ωS) and proton Larmor frequencies J(ωI) are identified on the plot by the blue and green vertical lines, respectively. Approximate functional forms of ODNP spectroscopic quantities kσ and ξ are in blue and green text, respectively. (d) Based on the force-free hard sphere model,60 we depict the expected trends in kσ/kσ,bulk (blue line) and ξ/ξbulk (green line). Here, kσ,bulk and ξbulk are the expected bulk values of kσ and ξ in pure STP water as defined by Franck et al.22 | ||
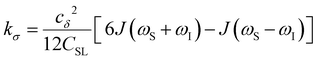 | (5) |
To provide an illustration, we depict the theoretical FFHS-derived cross-relaxivity, kFFHSσ, at B0 = 0.35 T as a function of the correlation time in Fig. 2(d). The kFFHSσ values exhibit non-monotonic behavior with increasing translational correlation time, τc, of hydration waters. Specifically, kFFHSσ increases with correlation times up to τc ≈ 100 ps. Upon further retardation of translational dynamics, kFFHSσ decreases monotonically with increasing τc. Notably, this maximum in kFFHSσ is found at τc that is 3 times greater than the expected correlation time, τc ≈ 33 ps, for pure water at standard temperature (298.15 K) and pressure (1 bar) conditions (STP).22 The precise location of the peak in kFFHSσ strongly depends on the Larmor precession frequencies by way of the applied magnetic field strength, B0.
Under the present B0, hydration waters with translational diffusion coefficients smaller than 1/3 of the diffusivity of pure water under ambient conditions (T = 25 °C and P = 1 bar), 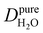 , yield kσ values that linearly decrease with the diffusivity of hydration waters, DH2O,local. In systems with
, yield kσ values that linearly decrease with the diffusivity of hydration waters, DH2O,local. In systems with 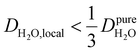 , such as waters hydrating catalyst support surfaces, hydrophilic materials interfaces,42 or protein surfaces and interiors,16kσ decreases upon retardation of hydration water translational dynamics. However, under the conditions considered in the present work, kσ begins to decrease when
, such as waters hydrating catalyst support surfaces, hydrophilic materials interfaces,42 or protein surfaces and interiors,16kσ decreases upon retardation of hydration water translational dynamics. However, under the conditions considered in the present work, kσ begins to decrease when 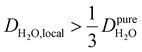 . Here, we demonstrate the non-monotonicity of kσ by spanning water translational dynamics from those of pure water to those of water–glycerol mixtures with
. Here, we demonstrate the non-monotonicity of kσ by spanning water translational dynamics from those of pure water to those of water–glycerol mixtures with 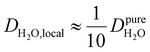 .
.
Another ODNP spectroscopic quantity of interest is the proton self-relaxivity kρ—the rate at which water proton polarization returns to thermal equilibrium modulated by the electron spin dipolar coupled to the proton nuclear spin, as follows:
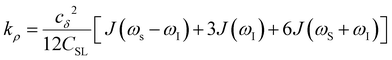 | (6) |
 the coupling factor that is defined by the ratio of kσ and kρ eliminates the dependence on CSL.
the coupling factor that is defined by the ratio of kσ and kρ eliminates the dependence on CSL.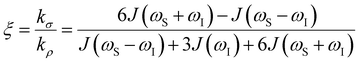 | (7) |
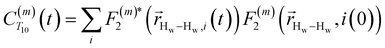 . The right-hand-side of the equation is nearly identical to eqn (2), but with the proton–proton displacement vector
. The right-hand-side of the equation is nearly identical to eqn (2), but with the proton–proton displacement vector 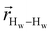 replacing
replacing 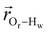 . To efficiently compute
. To efficiently compute 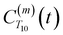 , we only consider displacement vectors
, we only consider displacement vectors 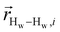 between a randomly chosen “probe” water proton and all other nearby water protons that the probe water proton encounters. Just as with CODNP(t), the
between a randomly chosen “probe” water proton and all other nearby water protons that the probe water proton encounters. Just as with CODNP(t), the 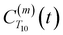 decays monotonically as water protons diffuse away from the “probe” proton. As in eqn (4), we fit eqn (6) to a multiexponential model and analytically Fourier transform the multiexponential
decays monotonically as water protons diffuse away from the “probe” proton. As in eqn (4), we fit eqn (6) to a multiexponential model and analytically Fourier transform the multiexponential 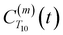 functions to obtain the spectral density functions, as follows:
functions to obtain the spectral density functions, as follows: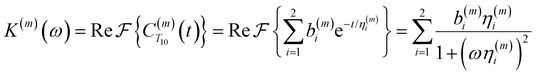 | (8) |
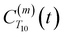 decays much faster than CODNP(t), allowing us to fit
decays much faster than CODNP(t), allowing us to fit 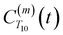 with R2 > 0.95 for the entire range of glycerol concentrations with only two exponentials, as shown in Table S2 (ESI†). Given these analytical spectral densities, we directly compute the longitudinal relaxation time using a formula from Bloembergen and coworkers65
with R2 > 0.95 for the entire range of glycerol concentrations with only two exponentials, as shown in Table S2 (ESI†). Given these analytical spectral densities, we directly compute the longitudinal relaxation time using a formula from Bloembergen and coworkers65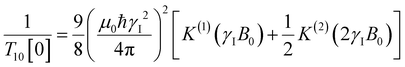 | (9) |
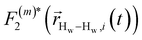 strictly depend on the displacement between water protons on separate water molecules, and not the re-orientation of the displacement vector between protons on the same water molecules. As such,
strictly depend on the displacement between water protons on separate water molecules, and not the re-orientation of the displacement vector between protons on the same water molecules. As such, 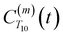 reduces to the same functional form as CODNP(t) with water protons acting as probes (such as the electron in a nitroxide spin probe) for the surrounding water protons. Because water protons are indistinguishable from each other, the resulting correlation functions are manifestly system-average properties of water. The corresponding intermolecular relaxation rate, (T10−1[0])inter, calculated from eqn (8) and (9) is hence sensitive to the system-average translational dynamics of water.
reduces to the same functional form as CODNP(t) with water protons acting as probes (such as the electron in a nitroxide spin probe) for the surrounding water protons. Because water protons are indistinguishable from each other, the resulting correlation functions are manifestly system-average properties of water. The corresponding intermolecular relaxation rate, (T10−1[0])inter, calculated from eqn (8) and (9) is hence sensitive to the system-average translational dynamics of water.
Computational probes of water dynamics
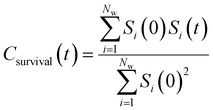 | (10) |
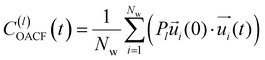 | (11) |
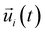 is the unit vector of water dipole i. For this present work, we only consider the second order OACF C(2)OACF due to its relevance to longitudinal spin-relaxation rates.
is the unit vector of water dipole i. For this present work, we only consider the second order OACF C(2)OACF due to its relevance to longitudinal spin-relaxation rates.
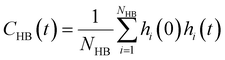 | (12) |
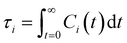 | (13) |
Results
Direct comparison of ODNP and MD-derived spectroscopic quantities
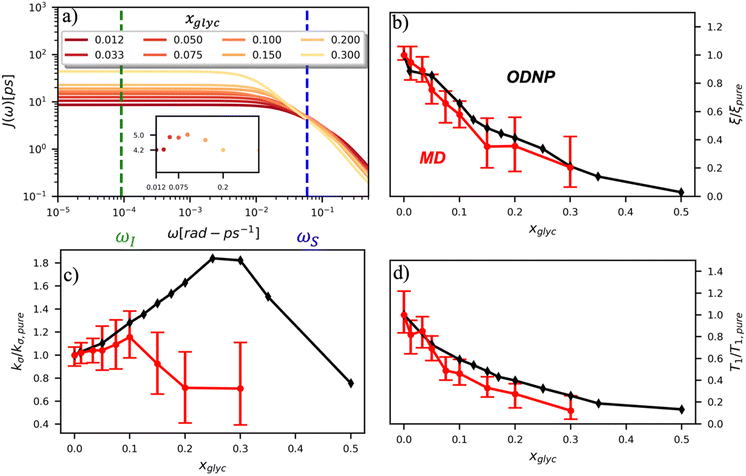
To directly probe the effect of hydration water retardation on the ODNP parameters (including T10[0]), we systematically increase the solution viscosity by adding glycerol to water at mole percentages ranging from xglyc = 0 to 0.3. In Fig. 3(a), we highlight the composition-dependent amplitude of the spectral density, J(ω), at the Larmor precession frequencies of protons (ωI = γIB0 ≈ 14.8 MHz) and unpaired electrons (ωS = γSB0 ≈ 9.8 GHz) at B0 = 0.35 T. The increase in J(ωI) from pure water to xglyc = 0.3 reflects on the increase in the relaxation rate of the proton spins, which according to eqn (7), leads to a monotonic decay of the coupling factor, as depicted in Fig. 3(b). The inset of Fig. 3(a) shows the approximate spectral density contribution to the cross-relaxation rate of 5J(ωS). The approximation stems from the limit of ωS ≫ ωI and hence—by eqn (5)—kσ goes as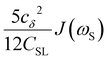 . 5J(ωS) shows the same trend as the direct computation of kσ [Fig. 3(c)], increasing up to a glycerol concentration of xglyc = 0.1 and decreasing at xglyc > 0.1.
. 5J(ωS) shows the same trend as the direct computation of kσ [Fig. 3(c)], increasing up to a glycerol concentration of xglyc = 0.1 and decreasing at xglyc > 0.1.
The MD simulation-derived relative coupling factor ξr = ξ/ξpure exhibits a similar monotonic decrease as the experimental coupling factor with increasing glycerol concentration throughout the whole range of the glycerol–water mixture [Fig. 3(b)]. Here, we normalize ξ by the coupling factor of pure water to better compare directly to the experimental results. Though simulation systematically underestimates the experimental ξr values by 5 to 60%, we observe qualitative agreement between both measures of ξr for xglyc < 0.30. Notably, the 95% confidence interval (CI) broadens with increasing glycerol concentration. At xglyc = 0.3, MD simulations underestimate ξr by 60%, with the experimental value lying outside the 95% confidence interval (CI) of the MD-computed value. While ODNP measurements measure e–n dipolar correlations averaged over 1014 spin probes, our simulated systems contain a single spin probe molecule. Hence, we observe inherent fluctuations in CODNP(t) due to limited sampling of the dipolar interactions between the spin probe and the water nuclei. Increasing the concentration of glycerol exacerbates this sampling limitation due a systematic decrease in the average number of hydration waters. Increasing the NVE simulation length computes CODNP(t) with improved resolution, which we assess by performing 20 additional independent 3-ns long (versus the original 1-ns) simulations at xglyc = 0.30. For xglyc > 0.3, the difficulty of sampling water–TEMPO interactions combined with slowing translational dynamics makes accurate calculation of ODNP quantities intractable. While increasing NVE simulation time slightly decreases the width of the 95% CI on ξr (approximately by 6%), the simulations continue to systematically underestimate ξr at xglyc = 0.3. This suggests that the disagreement between experiment and simulation ξr does not solely stem from under sampling of long timescale collective water motions.
Instead, the quantitative disagreement between the experimental and simulation results may stem in large part from the use of classical, fixed-charge molecular models. For instance, such MD models can only approximate interactions between water and a fixed position atomic position of 4-OH-TEMPO. In reality, the electron spin is delocalized between the N and O of the nitroxide radical. Additionally, the water hydrogen may polarize differently near the spine probe compared to bulk water, yielding different O–H bond length and H–O–H angle. Further, OPC is a rigid water model and hence does not contain bonded (O–H) or angular (∠H–O–H) interaction terms. In particular, the inability to capture O–H vibrations with rigid water molecules likely affects the measurement of proton–nitroxide pair distances and thus the resulting spectroscopic quantities. Applying flexible,68,69 or even polarizable,70,71 water models may rectify some of the discrepancy between ODNP experiment and MD simulations.
Additionally, ξr is sensitive to the motion of bound waters—such as those buried within soft materials—on longer timescales (100-ps to 10-ns). While we do not expect these longer timescale dynamics to dramatically impact hydration water dynamics in glycerol–water mixtures, the magnitude of the slow time constant τ1 exceeds 100-ps for xglyc = 0.3. As the timescales for diffusive and viscous relaxation approach the nanosecond regime, accurately quantifying spectroscopic quantities becomes more difficult for simulations. For glycerol–water, we find that precise quantification of τ1 becomes challenging for xglyc > 0.15 [Fig. S7, ESI†].
In the inset of Fig. 3(a), we highlight the spectral density J(ωS) at the Larmor precession frequency of the electron spin (ωS = γSB0 ≈ 9.8 GHz) with increasing glycerol concentration. Notably, J(ωS) is non-monotonic, increasing up to a glycerol concentration of xglyc = 0.1, then decreasing at higher concentrations [Fig. 3(a) inset]. Accordingly, the computed kσ values in Fig. 3(c) exhibit the same non-monotonic trend as J(ωS) with increasing glycerol concentration. Notably, both the experimental and computed values of the relative cross-relaxivity kσ,r = kσ/kσ,pure exhibit the non-monotonic trends with increasing viscosity, with kσ,r values initially increasing up to a critical glycerol concentration (xglyc ≈ 0.10) and then decreasing thereafter [Fig. 3(c)]. In the glycerol–water system with compositions from xglyc = 0 to 0.1, the experimental and MD-derived kσ,r are in near quantitative agreement. Here, simulation underestimates kσ,r, but the 95% CI of the MD-derived kσ,r values bracket the experimental results. For glycerol concentrations beyond xglyc = 0.1, simulations again underestimate the kσ,r, values, with the experimental kσ,r consistently lying above the 95%-CI of the simulation-derived values. We further note a dramatic increase in the relative error in computing kσ,r at high concentrations.
We attribute the underestimation of kσ,r to the inability of classical MD simulations to reproduce spectral density amplitudes at high frequency (ω ≫ ωI). We also note that the agreement between ODNP and MD results is much improved for ξr. We believe that this improved agreement results from the dominant influence of spectral density amplitudes at the lower frequencies [e.g., J(ωI) ≫ J(ωS)] in the denominator of ξ [eqn (5)]. The agreement of MD-derived values of both ξr and kσ,r with experiments for concentrations between xglyc = 0 and 0.1 demonstrates that atomistic MD simulations accurately model trends in the translational dynamics of hydration waters on timescales of tens to hundreds of picoseconds.
We also verify the ability of MD simulations to reproduce spectroscopic measures of glycerol–water bulk dynamics via computation of T10[0]. The relative proton longitudinal relaxation time, (T10[0])r = T10[0]/T10[0]pure, exhibits a similar monotonic decrease as ξr with increasing glycerol content [Fig. 3(d)]. Further, we observe a striking, near-quantitative agreement between experimental and MD-derived (T10[0])r for xglyc < 0.10. The MD-derived (T10[0])r data systematically underestimate the experimental value for xglyc > 0.075 with the experimental data falling outside of the 95% CI of the MD-calculated values. For xglyc ≥ 0.1, the computed values underestimate the experimental results by between 20 and 50%. In combination with the ξr and kσ,r results, the (T10[0])r results suggest that classical atomistic MD simulations can reliably capture the low-frequency contributions to spectroscopic quantities, but less well the high-frequency contribution from instantaneous motion reflected in quantities such as kσ.
Connecting other hydration water dynamics probes to ODNP measurements
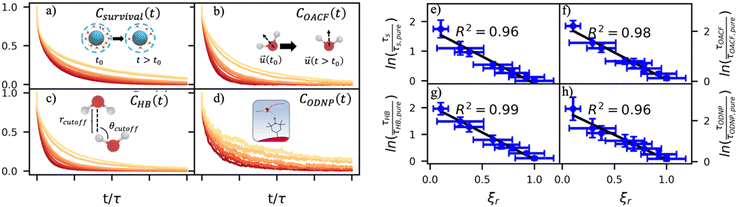
By effectively modeling spectroscopic quantities, we can directly connect ODNP measurements to the microscopic dynamics and structural properties of water. MD simulations also enable computation of other modes of hydration water dynamics that cannot be measured experimentally. For instance, the coupling of these various modes of water dynamics have been studied extensively in liquid water.32,72–74 One such example is the extended jump model of Laage and Hynes,27,28 describing the process of water reorientation as dependent simultaneously on the breaking/forming of hydrogen bonds precipitated by large rotational jumps while being rate-limited by translational motion. In this work, we measure characteristic time scales for hydration water translation, rotation, and hydrogen bonding in the glycerol–water mixtures, as summarized in Table S3 (ESI†), using computed autocorrelation functions (ACFs): C(0)ODNP(t), Csurvival(t), C(2)OACF(t) and CHB(t). Further, we explicitly characterize hydration water dynamics via the different relaxation time constants for ODNP-derived diffusion (τODNP), translational diffusion underlying survival probability (τsurvival), rotational diffusion (τOACF), and hydrogen bonding (τHB).To complement ODNP-derived measurements of water dynamics, we probe the translational mobility of hydration waters local to the spin probe via the survival probability ACF, Csurvival(t) [see Theory Section]. Fig. 4(a) depicts slower decay of Csurvival(t) as glycerol concentration increases, indicating the retardation of translational dynamics near the spin probe. We quantify this translational retardation via a characteristic time constant of translational diffusion τsurvival by fitting Csurvival(t) to a bi-exponential model c1e−t/α1 + (1 − c1)e−t/α2 and integrating over time. Here, c1, α1, and α2 are the fitting parameters with α1 > α1. In agreement with the visible shift in the decay rate of Csurvival(t), τsurvival monotonically increases with glycerol concentration [Fig. 4(e)]. There, we illustrate the simultaneous increase in τsurvival and decrease in ξr with glycerol concentration. This strong correlation [R2 = 0.96] suggests a correspondence between the ODNP coupling factor and measures of the instantaneous translation dynamics of hydration water.
In addition to the translational mobility, we also examine the hydration water orientational dynamics via the orientational autocorrelation functions (OACFs) [see Theory section]. While we anticipate strong coupling between the translational and rotational mobility of water molecules in dilute solutions, the degree of translation–rotation coupling in crowded glycerol–water mixtures is less intuitive given that the breakdown of orientational–translational coupling has been previously observed for water under confinement.73 As seen in Fig. 4(b), C(2)OACF decays more slowly with increasing glycerol content, signifying the retardation of rotational motion of hydration waters. This systematic slowdown of rotational dynamics is further illustrated by the monotonic increase in the characteristic time constants for rotational diffusion τOACF. As with τsurvivial we derive τOACF by fitting C(2)OACF to a bi-exponential model. The simultaneous increase in characteristic timescales τsurvivial and τOACF [Fig. 4(e) and (f)] across the whole range of glycerol concentrations establishes that, even in highly crowded glycerol–water mixtures, translational and rotational water diffusion remain strongly coupled. The persistent connection between rotational and translational dynamics suggests that—in contrast to water under geometric confinement (i.e., micelles)—the effect of glycerol on water stems from a distinct physical mechanism such as the development of a collective glycerol–water hydrogen bond network.
Glycerol is often assumed to simply decrease water translational dynamics due to increased mixture viscosity, but the effect of glycerol on water structural dynamics is typically not considered nor well understood. To investigate the relevance of such considerations, we probe the dynamics of hydrogen bonding of spin probe hydration waters via the hydrogen bond survival probability CHB(t). Like Csurvival(t) and C(2)OACF(t), we report slower decay of CHB(t) with rising glycerol content [Fig. 4(c)]. As with τsurvival and τOACF, we compute water–water hydrogen bond lifetimes τHB by integrating a bi-exponential fit to CHB(t). The resultant τHB values monotonically increase with increasing glycerol concentration, again in a manner strongly correlated with the ODNP results. The simultaneous increase in τOACF and τHB suggests that glycerol enhances the lifetime of orientationally-coordinated and hydrogen bonded microstructures. Such an enhancement water structure with increasing glycerol content was demonstrated in our recently published study.75 In this work, we found that increased glycerol concentration not only slows the water diffusivity, but also enhances water orientational structure by increasing the tetrahedrality of water.76 We expand this analysis in the following sub-section, discussing connections between water tetrahedrality and various characteristic time constants in glycerol–water.
With these analyses, we elucidate the as-of-yet unknown persistent coupling between metrics for water translational, rotational, and hydrogen bonding dynamics in glycerol–water, including ODNP-derived and computational translational water diffusivity. We support this finding in Fig. S9 (ESI†) by depicting the connections between the hydration water dynamics relaxation times τsurvival, τHB, τOACF, and τODNP with spectroscopic quantities kσ, ξ, and T10[0]. Apart from kσ, we observe strong correlation between each of these quantities and the others (R2 > 0.9). The persistent connection between the characteristic time constants of hydration water dynamics suggests that glycerol, even in significant quantities, does not decouple the translational and rotational modes of water motion, in contrast to dynamic decoupling reported for water under nanoscale confinement73 and in supercooled conditions.72,74,77 In the context of nanoconfinement between silica planar surfaces, Romero-Vargas Castrillón et al. find that water rotational diffusion is bulk-like near the center of the nanochannel while translational diffusion is suppressed relative to bulk.73 The authors attribute this rotation–translation decoupling to the strong inverse dependences of translational diffusion on density (above bulk near the center channel) and the water–water hydrogen bond network (same as the bulk near the center channel). In contrast, increasing glycerol concentration yields simultaneous increases in mixture density and water–water network hydrogen bond lifetimes (increasing τHB), as well as water structuring as measured by tetrahedrality, relative to pure water.
Due to the non-monotonic behavior of kσ [Fig. 3(c)] with composition, it correlates less well (R2 < 0.9) with the monotonically varying relaxation times and spectroscopic quantities. Traditionally, glycerol is thought to act as a classical viscogen without specifically considering its effect on water's molecular structure. With our simulation studies, we observe an increase in the rotational time constant τOACF and hydrogen bond lifetimes τHB that suggest tetrahedral enhancement with increasing glycerol concentration. To directly quantify tetrahedrality, we require a more direct structural metric, which we pursue next.
Glycerol enhances the population of tetrahedral waters
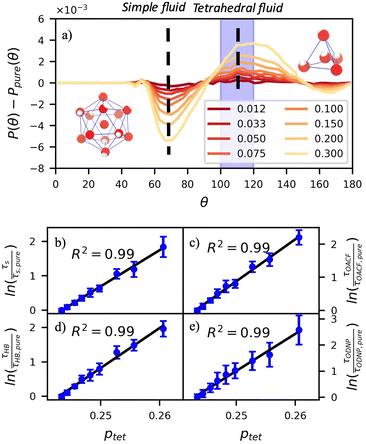
A number of order parameters have been used to assess the tetrahedrality of water in simulation studies.78–80 Many such parameters are influenced by the fact that water is undercoordinated near surfaces and in confined environments due to geometrical constraints.23,78,79,81 For example, the tetrahedral order parameter, q, from Errington and Debenedetti80 effectively characterizes water's tetrahedrality in many contexts, but in particular in dilute aqueous mixtures. However, the interpretation of q is more challenging when the average spatial separation between water molecules increases (e.g., concentrated glycerol–water mixtures) because it relies on four nearest water neighbors, which in such cases can populate non-first shell distances such that they adopt less correlated orientational order (decreased tetrahedrality).As an alternative to q, three-body angle distributions avoid this geometric bias by consider only nearest neighboring water molecules within a distance cutoff of each central water molecule and computing the distribution of neighbor–central–neighbor triplet angles78,79 averaged over all simulation time steps. We can characterize the population of tetrahedrally coordinated waters, ptet, by integrating P(θ) over the tetrahedral region of the distribution 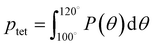 . In addition to readily accommodating cases when water is under-coordinated, three-body angle distributions have been shown to aptly capture changes in water structure in response to shifts in thermodynamic properties78,79 and solute chemistry.81 Furthermore, shifts in three-body angle distribution have also proved to be predictive of solvation thermodynamics for a wide range of colloidal particle sizes.78
. In addition to readily accommodating cases when water is under-coordinated, three-body angle distributions have been shown to aptly capture changes in water structure in response to shifts in thermodynamic properties78,79 and solute chemistry.81 Furthermore, shifts in three-body angle distribution have also proved to be predictive of solvation thermodynamics for a wide range of colloidal particle sizes.78
In Fig. 5(a), we illustrate shifts in the populations of waters in tetrahedral and icosahedral (simple fluid) environments at 109.5 degrees and 64 degrees, respectively, that report on water's structural orientational environment. In Fig. 5(a), we show that the increase in glycerol concentration from xglyc = 0.01 to 0.3 is accompanied by an increase of 2% in the overall ptet and an equivalent decrease in the population of icosahedrally-coordinated waters. Curiously, prior work by Monroe and Shell demonstrated that increasing pure water density tended to decrease tetrahedrality as measured by the three body angle distribution,78 while glycerol–water behaves in the opposite manner: as mixture density increases (increasing xglyc), ptet increases. This finding further supports that glycerol, rather than acting as a simple viscogen, enhances water's structural environment through enhanced water–glycerol hydrogen bonding. Work by Sharp, Vanderkooi, and coworkers supports this finding, using infrared spectroscopy and MD simulation to show that glycerol mimics enhanced hydrogen bonding structures commonly seen in ice.25
Remarkably, the enhancement of water tetrahedrality strongly correlates with the retardation of hydration water dynamics probes. In Fig. 5(b)–(e), we discover nearly linear relationships (R2 > 0.96) between ptet and several probes of water dynamics, including logarithms of characteristic time constants for translational diffusion τsurvival, rotational diffusion τOACF, hydrogen bonding lifetimes τHB, and the ODNP correlation time τODNP. The near mono-exponential relationship between ptet and these time constants demonstrates that structural enhancements—driven by the addition of glycerol—impose systematic retardation of water dynamics. Moreover, the remarkably strong correlation between τODNP and the structural metric ptet suggests that ODNP measurements indirectly reports on the effect of mixture properties on tetrahedrality of water in bulk solution. The strong correspondence between equilibrium water dynamics and water's molecular structure in glycerol–water is consistent with a previous work by Shell and coworkers.76 In this prior work, we find correlation between the system-average water self-diffusivity and several structural metrics such as ptet, the water–water coordination numbers, water specific volumes, and q among others. Further, we discovered that the system-average water self-diffusivity is accurately predicted by only two structural metrics—including ptet. In the present work, we expand upon this observation finding strong relationships between not only the system-average translational dynamics of water, but local dynamics for water rotation and water–water hydrogen bonding.
Impact of glycerol on solvation thermodynamics
We apply this understanding of water dynamics and structure to contextualize glycerol–water thermodynamics by characterizing the tendency for a model small hydrophobic molecule (methane) to transfer from an ideal gas to a glycerol–water solution phase in the infinite dilution limit. We directly quantify this by computing the excess free energy of solvation ΔGexsolv as discussed in the Methods section. ΔGexsolv < 0 suggests favorable solvation of a solute relative to ideal gas phase while the opposite is true for ΔGexsolv > 0. In Fig. S10(b) (ESI†), we observe a monotonically increasing and positive ΔGexsolv with increasing xglyc for xglyc < 0.1. This increase in ΔGexsolv is in part explained by the enhancement of water structure [Fig. 5] that presumably generates an increase in the entropic penalty for restructuring water–glycerol. However, for xglyc > 0.1, ΔGexsolv begins to plateau to a constant ΔGexsolv ≈ 4.25kBT. Notably, none of the structural or dynamic metrics above exhibit such a plateau.To better understand the trend depicted in Fig. S10(b) (ESI†), we apply a free energy decomposition ΔGexsolv = Usw + Sres previously described by Monroe and Shell.78 Here, Usw is the mean interaction energy between methane and glycerol–water in the solvated state (2) and the restructuring entropy Sres is strictly positive and largely gives the entropic penalty to create a void large enough to accommodate the solvation of methane from the gas phase (1) into the solution phase (2). We quantify Usw by directly calculating the interaction energy between methane and glycerol–water Usw while Sres follows from Sres = ΔGexsolv − Usw. We observe a monotonic decrease in Usw with increased glycerol concentration [Fig. 6(a)], indicating a more favorable enthalpy of solvation for methane in glycerol–water. On the other hand, we demonstrate that Sres increases monotonically with glycerol concentration [Fig. 6(b)], which indicates an increase in restructuring penalty to methane solvation. The entropic penalty (Sres > 0) and enthalpic gain (Usw < 0) for methane solvation in glycerol–water are consistent with the long-known hydration behavior of small hydrophobic molecules in aqueous environments.82,83 As ΔGexsolv becomes less favorable (more positive) for xglyc < 0.1, Usw decreases such that further increases in Sres yield constant ΔGexsolv for xglyc > 0.1.
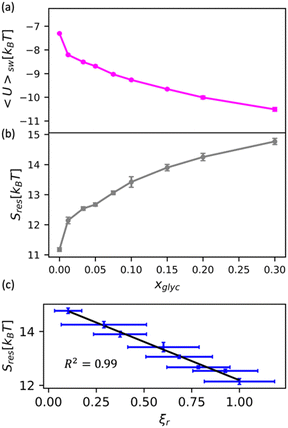 | ||
| Fig. 6 Decomposition of the solvation free energy of methane into glycerol–water mixtures. We calculate the solvation free energy for a methane molecule via expanded ensemble calculations, decomposing the resultant solvation free energy [Fig. S10(b), ESI†] into (a) enthalpic contribution via the direct energy term Usw and (b) entropy of solution restructuring Sres. (a) Usw decreases as more glycerol is added to the mixture. (b) Sres increases as more glycerol is added to the mixture. (c) We observe a strong correlation (R2 = 0.99) between the MD-computed ODNP coupling factor ξr and Sres. | ||
While the excess solvation free energy, ΔGexsolv, does not show a simple correlation with dynamic or structural metrics, the entropic and energetic contributions display striking connections to dynamic metrics. Specifically, we note that the increasing penalty for restructuring glycerol–water Sres displays a strong negative correlation with the MD-computed relative coupling factor ξr [R2 = 0.99; Fig. 6(c)]. Given that increases in Sres are driven by an enhancement in the underlying glycerol–water solution structure, the connection between Sres and ξr again suggests a persistent structure–dynamics connection in glycerol–water. Beyond reiterating the structure–dynamics connections depicted in Fig. 5, the Sres − ξr relationship is reminiscent of entropic theories for microscopic dynamics like the viscosity–entropy relationship proposed by Adam and Gibbs.84
Adam–Gibbs theory proposes that retardation of liquid dynamics (such as liquid viscosity, η, or self-diffusivity, D) stems from a decrease in the number of available configurational states of a liquid via the configurational entropy Sconf. Notably, a recent study by Handle and Sciorno85 demonstrated that a persistent ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D − (TSconf)−1 connection—per Adam–Gibbs theory—in simulations of pure TIP4P/2005 water. The observed correlation between the probe of water dynamics (ξr) and restructuring entropy hints at a theoretical analog to Adam–Gibbs relating equilibrium water dynamics to solvation thermodynamics. If such a Sres-dynamics relationship persists for contexts beyond glycerol–water, it may be possible to forecast the solvation thermodynamics of small molecules in aqueous mixtures without computationally laborious free energy calculations. Probing dynamics–structure–thermodynamics correspondence at heterogeneous surfaces would be fascinating extensions of the present analysis. For instance, one could specifically interrogate how water–glycerol's molecular scale structure and dynamics mediate hydration free energies at protein–water interfaces to elucidate the cosolvent-mediated mechanisms of protein cryoprotection.86–89
D − (TSconf)−1 connection—per Adam–Gibbs theory—in simulations of pure TIP4P/2005 water. The observed correlation between the probe of water dynamics (ξr) and restructuring entropy hints at a theoretical analog to Adam–Gibbs relating equilibrium water dynamics to solvation thermodynamics. If such a Sres-dynamics relationship persists for contexts beyond glycerol–water, it may be possible to forecast the solvation thermodynamics of small molecules in aqueous mixtures without computationally laborious free energy calculations. Probing dynamics–structure–thermodynamics correspondence at heterogeneous surfaces would be fascinating extensions of the present analysis. For instance, one could specifically interrogate how water–glycerol's molecular scale structure and dynamics mediate hydration free energies at protein–water interfaces to elucidate the cosolvent-mediated mechanisms of protein cryoprotection.86–89
Conclusions
In the present study, we reproduce critical ODNP spectroscopic measures of translational hydration water dynamics using classical atomistic molecular simulations to model equilibrium dynamics in glycerol–water mixtures with semi-quantitative agreement. Further, using the molecular scale detail revealed through MD simulations, we discover strong correlations between ODNP-measured coupling factors and computational probes of translational, rotational, and hydrogen bonding dynamics. The strong relationships found between MD-derived measures of water structure and dynamics are exciting for the potential of ODNP to serve as a surrogate probe of underlying solution structure. Finally, the clear connection between water tetrahedrality, water dynamics, and solvent restructuring entropy suggests a novel framework to describe and quantify the molecular scale mechanisms underlying hydrophobic hydration.Though the existing literature on local water properties and water-mediated behavior is extensive, our analyses are unique because we directly link simulation to experiment and develop a dynamics–structure–thermodynamics connection. The use of ODNP as a tool to inspect ambient local water environments will greatly complement alternative NMR approaches to studying confined and interfacial water.90–92 The generality of the experimental and computational methods discussed here will enable further investigations of other systems of broad interest such as water–alcohol and multicomponent mixtures used for protein stabilization (e.g., water–glycerol–DMSO). Further, the dynamics–structure–thermodynamics framework will aide further understanding of the molecular scale mechanisms (e.g., water tetrahedrality and diffusivity) underlying hydration properties in a wide range of chemically and topologically heterogeneous interfaces such as at protein–water interfaces.
Author contributions
Dennis Robinson Brown (conceptualization, MD simulations and methodology, data analysis and analytical modelling, writing – original draft); Thomas R. Webber (conceptualization, ODNP experiments and methodology, data analysis, writing – original draft); Thomas M. Casey (conceptualization, ODNP experiments and methodology, data analysis, writing – review & editing); John Franck (conceptualization, analytical modelling, writing – review & editing); M. Scott Shell (conceptualization, writing – review & editing, supervision, funding acquisition); Songi Han (conceptualization, writing – review & editing, supervision, funding acquisition).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported as part of the Center for Materials for Water and Energy Systems (M-WET), an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award #DE-SC0019272. Use was made of computational facilities purchased with funds from the National Science Foundation (CNS-1725797) and administered by the Center for Scientific Computing (CSC). The CSC is supported by the California NanoSystems Institute and the Materials Research Science and Engineering Center (MRSEC; NSF DMR 1720256) at UC Santa Barbara. Support for ODNP method development comes from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy EXC2033 390677874 RESOLV. Support for surface hydration structure and dynamics is supported by the NIH MIRA grant R35GM136411 awarded to SH.References
- N. B. Rego, E. Xi and A. J. Patel, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2018234118 CrossRef CAS PubMed.
- S. N. Jamadagni, R. Godawat and S. Garde, Langmuir, 2009, 25, 13092–13099 CrossRef CAS PubMed.
- R. Godawat, S. N. Jamadagni and S. Garde, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15119–15124 CrossRef CAS PubMed.
- J. I. Monroe, S. Jiao, R. J. Davis, D. Robinson Brown, L. E. Katz and M. S. Shell, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2020205118 CrossRef CAS PubMed.
- T. Young, R. Abel, B. Kim, B. J. Berne and R. A. Friesner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 808–813 CrossRef CAS PubMed.
- H. Wirtz, S. Schäfer, C. Hoberg and M. Havenith, J. Infrared Milli Terahz Waves, 2018, 39, 816–827 CrossRef CAS.
- I. Moskowitz, M. A. Snyder and J. Mittal, J. Chem. Phys., 2014, 141, 18C532 CrossRef PubMed.
- D. Laage, G. Stirnemann and J. T. Hynes, J. Phys. Chem. B, 2009, 113, 2428–2435 CrossRef CAS PubMed.
- J. I. Monroe and M. S. Shell, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8093–8098 CrossRef CAS PubMed.
- K. Lum, D. Chandler and J. D. Weeks, J. Phys. Chem. B, 1999, 103, 4570–4577 CrossRef CAS.
- J. Mittal and G. Hummer, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20130–20135 CrossRef CAS PubMed.
- S. Garde, G. Hummer, A. E. García, L. R. Pratt and M. E. Paulaitis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1996, 53, R4310–R4313 CrossRef CAS PubMed.
- H. Acharya, S. Vembanur, S. N. Jamadagni and S. Garde, Faraday Discuss., 2010, 146, 353–365 RSC.
- E. Xi, V. Venkateshwaran, L. Li, N. Rego, A. J. Patel and S. Garde, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13345–13350 CrossRef CAS PubMed.
- N. Giovambattista, P. G. Debenedetti and P. J. Rossky, J. Phys. Chem. C, 2007, 111, 1323–1332 CrossRef CAS.
- R. Barnes, S. Sun, Y. Fichou, F. W. Dahlquist, M. Heyden and S. Han, J. Am. Chem. Soc., 2017, 139, 17890–17901 CrossRef CAS PubMed.
- G. Schirò, Y. Fichou, F.-X. Gallat, K. Wood, F. Gabel, M. Moulin, M. Härtlein, M. Heyden, J.-P. Colletier, A. Orecchini, A. Paciaroni, J. Wuttke, D. J. Tobias and M. Weik, Nat. Commun., 2015, 6, 6490 CrossRef PubMed.
- J. G. Davis, K. P. Gierszal, P. Wang and D. Ben-Amotz, Nature, 2012, 491, 582–585 CrossRef CAS PubMed.
- F. Böhm, G. Schwaab and M. Havenith, Angew. Chem., Int. Ed., 2017, 56, 9981–9985 CrossRef PubMed.
- N. B. Rego, E. Xi and A. J. Patel, J. Am. Chem. Soc., 2019, 141, 2080–2086 CrossRef CAS PubMed.
- A. M. Schrader, J. I. Monroe, R. Sheil, H. A. Dobbs, T. J. Keller, Y. Li, S. Jain, M. S. Shell, J. N. Israelachvili and S. Han, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2890–2895 CrossRef CAS PubMed.
- J. M. Franck, Y. Ding, K. Stone, P. Z. Qin and S. Han, J. Am. Chem. Soc., 2015, 137, 12013–12023 CrossRef CAS PubMed.
- J. Monroe, M. Barry, A. DeStefano, P. Aydogan Gokturk, S. Jiao, D. Robinson-Brown, T. Webber, E. J. Crumlin, S. Han and M. S. Shell, Ann. Rev. Chem. Biomol. Eng., 2020, 11, 523–557 CrossRef CAS PubMed.
- J. M. Franck and S. Han, in Methods in Enzymology, ed. A. J. Wand, Academic Press, 2019, vol. 615, pp. 131–175 Search PubMed.
- J. L. Dashnau, N. V. Nucci, K. A. Sharp and J. M. Vanderkooi, J. Phys. Chem. B, 2006, 110, 13670–13677 CrossRef CAS PubMed.
- M. Heyden, J. Chem. Phys., 2019, 150, 094701 CrossRef PubMed.
- D. Laage, Science, 2006, 311, 832–835 CrossRef CAS PubMed.
- D. Laage and J. T. Hynes, J. Phys. Chem. B, 2008, 112, 14230–14242 CrossRef CAS PubMed.
- S. Xiao, F. Figge, G. Stirnemann, D. Laage and J. A. McGuire, J. Am. Chem. Soc., 2016, 138, 5551–5560 CrossRef CAS PubMed.
- H. F. M. C. Martiniano and N. Galamba, J. Phys. Chem. B, 2013, 117, 16188–16195 CrossRef CAS PubMed.
- G. Stirnemann, S. R.-V. Castrillón, J. T. Hynes, P. J. Rossky, P. G. Debenedetti and D. Laage, Phys. Chem. Chem. Phys., 2011, 13, 19911 RSC.
- P. Tan, J. Huang, E. Mamontov, V. García Sakai, F. Merzel, Z. Liu, Y. Ye and L. Hong, Phys. Chem. Chem. Phys., 2020, 22, 18132–18140 RSC.
- B. Qiao, F. Jiménez-Ángeles, T. D. Nguyen and M. Olvera de la Cruz, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 19274–19281 CrossRef CAS PubMed.
- J. N. Dahanayake and K. R. Mitchell-Koch, Phys. Chem. Chem. Phys., 2018, 20, 14765–14777 RSC.
- S.-H. Chen, P. Gallo, F. Sciortino and P. Tartaglia, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1997, 56, 4231–4243 CrossRef CAS.
- J.-C. Perrin, S. Lyonnard and F. Volino, J. Phys. Chem. C, 2007, 111, 3393–3404 CrossRef CAS.
- B. D. Armstrong and S. Han, J. Am. Chem. Soc., 2009, 131, 4641–4647 CrossRef CAS PubMed.
- Y. Xu and M. Havenith, J. Chem. Phys., 2015, 143, 170901 CrossRef PubMed.
- J. Zhang, J. Phys. Chem. B, 2019, 123, 2971–2977 CrossRef CAS PubMed.
- H. Hoshina, Y. Iwasaki, E. Katahira, M. Okamoto and C. Otani, Polymer, 2018, 148, 49–60 CrossRef CAS.
- S. J. Kim, B. Born, M. Havenith and M. Gruebele, Angew. Chem., Int. Ed., 2008, 47, 6486–6489 CrossRef CAS PubMed.
- C. P. Lawrence and J. L. Skinner, J. Chem. Phys., 2003, 118, 264–272 CrossRef CAS.
- H. Moon, R. P. Collanton, J. I. Monroe, T. M. Casey, M. S. Shell, S. Han and S. L. Scott, J. Am. Chem. Soc., 2022, 144, 1766–1777 CrossRef CAS PubMed.
- D. D. Mahanta, D. R. Brown, S. Pezzotti, S. Han, G. Schwaab, M. S. Shell and M. Havenith, Chem. Sci., 2023, 14, 7381 RSC.
- I. Kaminker, R. Barnes and S. Han, in Methods in Enzymology, ed. P. Z. Qin and K. Warncke, Academic Press, 2015, vol. 564, pp. 457–483 Search PubMed.
- J. M. Franck, A. Pavlova, J. A. Scott and S. Han, Prog. Nucl. Magn. Reson. Spectrosc., 2013, 74, 33–56 CrossRef CAS PubMed.
- S. Izadi, R. Anandakrishnan and A. V. Onufriev, J. Phys. Chem. Lett., 2014, 5, 3863–3871 CrossRef CAS PubMed.
- J. Blieck, F. Affouard, P. Bordat, A. Lerbret and M. Descamps, Chem. Phys., 2005, 317, 253–257 CrossRef CAS.
- R. Chelli, P. Procacci, G. Cardini and S. Califano, Phys. Chem. Chem. Phys., 1999, 1, 879–885 RSC.
- D. A. Jahn, F. O. Akinkunmi and N. Giovambattista, J. Phys. Chem. B, 2014, 118, 11284–11294 CrossRef CAS PubMed.
- D. A. Case, 2018.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, 2016 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- Development of the Second Generation of the General AMBER Force Field, https://www.researchgate.net/project/Development-of-the-Second-Generation-of-the-General-AMBER-Force-Field, (accessed June 17, 2020).
- D. Sezer, J. H. Freed and B. Roux, J. Phys. Chem. B, 2008, 112, 5755–5767 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- P. Eastman and V. Pande, Comput. Sci. Eng., 2010, 12, 34–39 CAS.
- M. R. Shirts and J. D. Chodera, J. Chem. Phys., 2008, 129, 124105 CrossRef PubMed.
- D. Sezer, M. Gafurov, M. J. Prandolini, V. P. Denysenkov and T. F. Prisner, Phys. Chem. Chem. Phys., 2009, 11, 6638 RSC.
- L.-P. Hwang and J. H. Freed, J. Chem. Phys., 1975, 63, 4017 CrossRef CAS.
- J. H. Ortony, B. Qiao, C. J. Newcomb, T. J. Keller, L. C. Palmer, E. Deiss-Yehiely, M. Olvera de la Cruz, S. Han and S. I. Stupp, J. Am. Chem. Soc., 2017, 139, 8915–8921 CrossRef CAS PubMed.
- D. Sezer, M. J. Prandolini and T. F. Prisner, Phys. Chem. Chem. Phys., 2009, 11, 6626 RSC.
- B. D. Armstrong, P. Soto, J.-E. Shea and S. Han, J. Magn. Reson., 2009, 200, 137–141 CrossRef CAS PubMed.
- B. D. Armstrong and S. Han, J. Chem. Phys., 2007, 127, 104508 CrossRef PubMed.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- S. Shin and A. P. Willard, J. Chem. Theory Comput., 2018, 14, 461–465 CrossRef CAS PubMed.
- A. Luzar and D. Chandler, J. Chem. Phys., 1993, 98, 8160–8173 CrossRef CAS.
- Y. Wu, H. L. Tepper and G. A. Voth, J. Chem. Phys., 2006, 124, 024503 CrossRef PubMed.
- M. A. González and J. L. F. Abascal, J. Chem. Phys., 2011, 135, 224516 CrossRef PubMed.
- T. E. Gartner, K. M. Hunter, E. Lambros, A. Caruso, M. Riera, G. R. Medders, A. Z. Panagiotopoulos, P. G. Debenedetti and F. Paesani, J. Phys. Chem. Lett., 2022, 13, 3652–3658 CrossRef PubMed.
- V. Babin, C. Leforestier and F. Paesani, J. Chem. Theory Comput., 2013, 9, 5395–5403 CrossRef CAS PubMed.
- S. Dueby, V. Dubey and S. Daschakraborty, J. Phys. Chem. B, 2019, 123(33), 7178–7189 CrossRef CAS PubMed.
- S. Romero-Vargas Castrillón, N. Giovambattista, I. A. Aksay and P. G. Debenedetti, J. Phys. Chem. B, 2009, 113, 1438–1446 CrossRef PubMed.
- V. Dubey, S. Erimban, S. Indra and S. Daschakraborty, J. Phys. Chem. B, 2019, 123, 10089–10099 CrossRef CAS PubMed.
- D. C. Robinson Brown, T. R. Webber, S. Jiao, D. M. Rivera Mirabal, S. Han and M. S. Shell, J. Phys. Chem. B, 2023, 127(20), 4577–4594 CrossRef CAS PubMed.
- D. C. Robinson Brown, T. R. Webber, S. Jiao, D. M. Rivera Mirabal, S. Han and M. S. Shell, J. Phys. Chem. B, 2023, 127, 4577–4594 CrossRef CAS PubMed.
- P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259–267 CrossRef CAS PubMed.
- J. I. Monroe and M. S. Shell, J. Chem. Phys., 2019, 151, 094501 CrossRef PubMed.
- A. Chaimovich and M. S. Shell, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81(6), 060104 CrossRef PubMed.
- J. R. Errington and P. G. Debenedetti, Nature, 2001, 409, 318–321 CrossRef CAS PubMed.
- P. Stock, J. I. Monroe, T. Utzig, D. J. Smith, M. S. Shell and M. Valtiner, ACS Nano, 2017, 11, 2586–2597 CrossRef CAS PubMed.
- E. Gallicchio, M. M. Kubo and R. M. Levy, J. Phys. Chem. B, 2000, 104, 6271–6285 CrossRef CAS.
- H. S. Frank and M. W. Evans, J. Chem. Phys., 1945, 13, 507–532 CrossRef CAS.
- G. Adam and J. H. Gibbs, J. Chem. Phys., 1965, 43, 139–146 CrossRef CAS.
- P. H. Handle and F. Sciortino, Mol. Phys., 2018, 116, 3366–3371 CrossRef CAS PubMed.
- J. J. Towey, A. K. Soper and L. Dougan, Faraday Discuss., 2013, 167, 159 RSC.
- L. Weng, C. Chen, J. Zuo and W. Li, J. Phys. Chem. A, 2011, 115, 4729–4737 CrossRef CAS PubMed.
- L. Weng, S. L. Stott and M. Toner, Annu. Rev. Biomed. Eng., 2019, 21, 1–31 CrossRef CAS PubMed.
- J. J. Towey, A. K. Soper and L. Dougan, J. Phys. Chem. B, 2012, 116, 13898–13904 CrossRef CAS PubMed.
- F. Persson, P. Söderhjelm and B. Halle, J. Chem. Phys., 2018, 148, 215103 CrossRef PubMed.
- N. V. Nucci, M. S. Pometun and A. J. Wand, Nat. Struct. Mol. Biol., 2011, 18, 245–249 CrossRef CAS PubMed.
- C. Mattea, J. Qvist and B. Halle, Biophys. J., 2008, 95, 2951–2963 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00030g |
| This journal is © the Owner Societies 2024 |