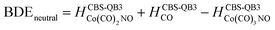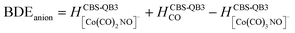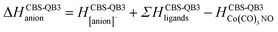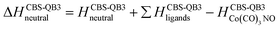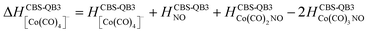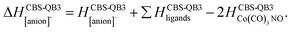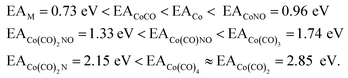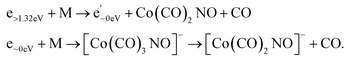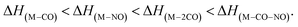Formation of negative ions from cobalt tricarbonyl nitrosyl Co(CO)3NO clusters†
Dušan
Mészáros
,
Štefan
Matejčík
 and
Peter
Papp
and
Peter
Papp
 *
*
Department of Experimental Physics, Faculty of Mathematics, Physics and Informatics, Comenius University in Bratislava, Mlynská dolina F2, 842 48 Bratislava, Slovakia. E-mail: peter.papp@uniba.sk
First published on 1st February 2024
Abstract
Electron attachment and corresponding dissociative electron attachment (DEA) to cobalt tricarbonyl nitrosyl (Co(CO)3NO) clusters have been studied by co-expansion with Ar gas into a high vacuum. A monochromatic electron beam was utilized to generate negative ions and the resulting reaction products were identified using mass spectrometry. The ion fragments corresponding to Co(CO)3NO monomers closely resemble results from earlier gas phase experiments and studies conducted on Co(CO)3NO in He nanodroplets. However, contrary to the gas phase or He nanodroplet ion yields, a resonance structure comprising several peaks at energies above ∼4 eV was observed both in the case of molecular clusters [Co(CO)3NO]n− (with n = 1, 2, 3) and clusters comprising DEA fragments. Additionally, the ion yields of numerous other clusters such as ions without nitrosyl ([Co(CO)4]−, [Co2(CO)5]−), clusters consisting of two fragments such as ([Co2(CO)NO]−, [Co2(CO)(NO)2]−, [Co2(CO)2NO]−, [Co2(CO)2(NO)2]−, [Co3(CO)(NO)3]−, [Co3(CO)8(NO)3]−, [Co3(CO)(NO)2]−, [Co3(CO)3(NO)2]−, and [Co3(CO)5(NO)2]−) were recorded. Moreover, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond dissociation was confirmed with the [Co(CO)2N]−ion and with N- or O-retaining cluster ions, such as [Co2(CO)(NO)N]−, [Co2(CO)2(NO)N]−, [Co3(CO)2(NO)N]−, [Co3(CO)3(NO)N]− and [Co3(CO)(NO)2N]−, or [Co2(CO)2O]−, [Co2(CO)3O]−, [Co3(CO)3O]−, [Co3(CO)4O]−and [Co3(CO)2(NO)O]− respectively.
O bond dissociation was confirmed with the [Co(CO)2N]−ion and with N- or O-retaining cluster ions, such as [Co2(CO)(NO)N]−, [Co2(CO)2(NO)N]−, [Co3(CO)2(NO)N]−, [Co3(CO)3(NO)N]− and [Co3(CO)(NO)2N]−, or [Co2(CO)2O]−, [Co2(CO)3O]−, [Co3(CO)3O]−, [Co3(CO)4O]−and [Co3(CO)2(NO)O]− respectively.
Introduction
The Focused Electron Beam-Induced Deposition (FEBID) method1–4 is increasingly employed to deposit various layers and 3D structures at the nanoscale.5–9 In FEBID, a high-energy electron beam is used to induce the decomposition of precursor gases, leading to the deposition of the metal component from the precursor onto the surface.1,2,4 Various types of precursors have been utilized in FEBID, including W(CO)6, Et4Pb, Fe(CO)5, Fe2(CO)9, Co2(CO)8, HCo3Fe(CO)12, AgO2Me2Bu and many others.2,3,6,8 Cobalt tricarbonyl nitrosyl (Co(CO)3NO) has been used as an alternative to dicobalt octacarbonyl (Co2(CO)8)10,11 for cobalt deposition using FEBID.12–14 Co(CO)3NO has got a high vapor pressure (100 torr at 25 °C)15 and relatively high thermal stability due to its high decomposition temperature (130–140 °C).14 Metallic cobalt has ferromagnetic properties, making it a good choice of a material for creating deposits with magnetic properties.12,14,16The crucial role of low-energy electrons has been the focus of numerous experimental studies17–21 and theoretical investigations.22–26 The primary electron beam is of extremely narrow width,2,27 compared to the diameter of the deposited structures. These high-energetic electrons from the focused beam can penetrate the substrate, generating a non-negligible flux of secondary low-energy electrons or backscattered electrons. Therefore, elastic and inelastic scattering reactions occurring via substrate irradiation make a significant contribution to the processes present in FEBID. The kinetic energy of secondary electrons typically ranges between 0 and 50 eV, with a maximum flux around 15 eV.2,19,27 These electrons carry the energy which is sufficient for the dissociation of precursor molecules, leading to potential issues regarding the purity of the created structure and causing structural broadening.18,27 Partial dissociation of metal–ligand complexes may take place, instead of the complete decomposition to the metal atom, which is a source of unwanted impurities deposited on the surface. They also contribute to the broadening of the deposited structures as they are active in a much larger area above the surface than the focus of the primary beam.28 Despite the primary beam diameter being much narrower than that of the deposited structure, the role of low-energy electrons originating from the surface material and back scattering processes reduces this advantage of the FEBID method.
A recently introduced alternative technique for electron-induced deposition is known as electron beam-induced surface activation (EBISA).29,30 This method involves using a high-energy electron beam to activate the surface before the deposition process, thereby preventing the interaction of secondary electrons and backscattered electrons with the precursor molecules. This approach has been applied using Co(CO)3NO in recent studies,31,32 opening a new area of further challenging investigations of the activated surface constituents with low-energy electrons. These studies aim to provide a reasonable explanation of the chemistry occurring between the activated surface and introduced precursors.
The interactions of electrons with Co(CO)3NO in the gas phase, including various processes, have been extensively documented. This involves a detailed description of electron-induced ionization,24,33,34 as well as dissociative electron attachment.17,19 These studies have revealed the complete decomposition of the molecule into charged Co atoms (either positive or negative ions), demonstrating sequential losses of CO ligands, as well as CO and NO ligands simultaneously. However, the investigations of Co(CO)3NO clusters are less common, with prior studies limited to the DEA study conducted in liquid He nanodroplets by Postler et al.21 In our study, we aim to present results obtained through an alternative method to the He clusters’ experiments. In particular, we employ the co-expansion of Co(CO)3NO and argon gas into a high-vacuum environment (CLUSTER-ILN experiment). Our focus is on providing comparisons between the recent CLUSTER-ILN results and the known gas-phase DEA products,17,19 the molecular ion, its dimer, trimer, and several DEA fragments within clusters containing Co(CO)3NO molecules, as reported by Postler et al.21 Furthermore, our study will discuss the ion yields of several new cluster ions. These ions originate from a combination of neutral dissociation and DEA products, as well as through bond breakage in the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ligand.
O ligand.
Material and methods
The CLUSTER-ILN experiment
The current experiments were conducted using a crossed electron and cluster beams setup (CLUSTER-ILN).35–39 Molecular cluster formation was a result of a supersonic expansion into a vacuum through an approximately 80 μm nozzle, creating a pressure difference of roughly 7 orders of magnitude on either side of the nozzle. These molecular clusters were then skimmed to generate a cluster beam that collided with an electron beam in a separate reaction chamber, characterized by another 1–2 orders of magnitude lower pressure.The electron beam was generated by a trochoidal electron monochromator perpendicular to the cluster beam. The electron energy could be adjusted within the range of 0–40 eV, with an energy resolution of about 200 meV, determined by the full width at half maximum of the SF6− resonance.40,41 The resulting ions were analysed based on their mass/charge ratio (m/z) using the quadrupole mass analyser (Pfeiffer QMA400). This analysis involved:
(a) recording a standard mass spectrum at a fixed electron energy (corresponding to the energy of resonance forming negative ion(s)), and
(b) recording the partial cross-sections for the ionic products with a fixed m/z value and varied electron energy.
A mixture of Co(CO)3NO (purchased from Strem Chemicals Inc., CAS #14096-82-3, 99% purity) with Ar gas was prepared in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 ratio (33 mbar of Co(CO)3NO mixed with 10 bar of Ar), and the expansion into a high vacuum was carried out at a stagnation pressure of approximately 2 bar.
300 ratio (33 mbar of Co(CO)3NO mixed with 10 bar of Ar), and the expansion into a high vacuum was carried out at a stagnation pressure of approximately 2 bar.
For some ion yields, an increase of signal above ∼11.5 eV was observed, which does not stem from the ionization of the sample being measured. At these energy levels, the potential formation of metastable Ar atoms becomes plausible, where the excitation energy is at 11.548 eV and higher.42 These metastable Ar atoms subsequently de-excite by striking the material of the deflector wires located behind the QMA and emitting electrons from the deflector wires in close proximity to the entrance of the channeltron signal multiplier. This signal increase can be detected across the entire mass range of the QMA, independent of the masses associated with the DEA products of Co(CO)3NO clusters under investigation. Additionally, this signal vanishes upon altering the acceleration voltage polarity at the channeltron entrance to its opposite. This effect is observable solely in the background spectrum or in the case of ions with extremely weak signals near 11.5 eV. Despite the possibility that a substantial number of incident monochromatic electrons possessing energies above ∼11.5 eV might lose their kinetic energy through inelastic scattering on Ar atoms, and subsequently induce DEA channels within the measured sample as low-energy electrons (∼0 eV and above), this behaviour remains undetectable in the experiment.
Theory
The GAUSSIAN 16 programme package43 was used to model the ground state energies of the neutral and anionic Co(CO)3NO molecule (M and [M]−) and its fragments, corresponding to the experimental observations. The CBS-QB344,45 method was used to obtain thermochemical data, electron affinities (EAs), bond dissociation energies (BDEs), enthalpies of formation (ΔfH° (298.15 K) in the ESI† file), as well as reaction enthalpies (ΔH at 298.15 K) leading to various neutral or ionized products. This composite method uses the B3LYP46,47 density functional method to obtain the optimal geometries and frequencies, followed by single point ab initio calculations (MP2,48–52 MP453,54 and CCSD(T)55,56), all together combined with different basis sets to perform a complete basis set extrapolation57–60 within the CBS-QB3 model. The same method was used in similar studies of DEA to Co(CO)3NO clusters in He nanodroplets reported by Postler et al.,21 showing the 0 K CBS-QB3 BDEs for CO, NO, 2CO and CO+NO ligand dissociations from [Co(CO)3NO]−, which agreed well with their experimental expectations.The CBS-QB3 method offers one of the lowest computational costs compared with other composite approaches in GAUSSIAN developed to achieve very accurate energies, such as G3,61 G3MP2,62 G4,63 CBS-APNO,64 and W1BD.65 Thus, the CBS-QB3 method can be several units, tens or even hundreds times faster when applied to different organic compounds66,67 and can be used for transition metal complexes contrary to some of the other composite methods mentioned above. However, saving the computer time decreases the accuracy of the method compared to other composite approaches. Benchmark studies predicted for the calculated enthalpies of formation exhibit the averaged mean unsigned deviations of ∼1.5 kcal mol−1 (estimated for several tens of CxHyOz molecules66) or even up to ∼3 kcal mol−1 (estimated for several tens of chlorinated/brominated compounds67) with respect to experimental values. With considerably lower computational costs, the CBS-QB3 enthalpies of formation are comparable with the most accurate ones derived from the G4 approach.67 However, poorer accuracy of CBS-QB3 is declared for relative energies such as BDEs calculated for organic brominated and chlorinated compounds, with an averaged mean unsigned deviation above 6 kcal mol−1,67 or reaction barrier heights (of 26 pericyclic reactions) with a mean absolute deviation of 2.1 kcal mol−1 (contrary to 0.6 kcal mol−1 of G4, or 0.2 kcal mol−1 of most accurate CCSD(T)/CBS(MPn) approaches used68). Heats of formation calculated for transition metal complexes can be achieved with the best accuracy by Wilson's ccCA-TM composite method developed for transition metals,69,70 with a mean absolute deviation of ∼3 kcal mol−1, including MP2/cc-pVxZ CBS extrapolation followed by high level CCSD(T). Thus, it offers comparable accuracy and less computational costs than the highly accurate DK-CCSD(T).69 Careful T1/D1 diagnostics has to be considered to exclude any multireference behaviour of modelled transition metals treated with single reference methods in ccCA.70 Alternatively, several density functional approximations can be used as well to reach comparable accuracy for heats of formation, bonding energies of clusters with mean absolute deviations varying from ∼1 kcal mol−1 (DSD-PBEP86,71 ωB97M-V,72 ωB97X-V,73 MN15,74 B97M-rV75) up to ∼10 kcal mol−1, depending on the model system and functional used.76–79
Considering all this benchmark data, we should expect that the CBS-QB3 reaction energies and bond dissociation energies for the Co(CO)3NO transition metal complex will not be as accurate as those obtained using computationally more expensive approaches listed above. However, the choice of this approach offered fast calculations with a reasonable accuracy (averaging around ∼6 kcal mol−1, or ∼0.3 eV), used to interpret the CLUSTER-ILN DEA experiment (as Postler et al. did for Co(CO)3NO with CBS-QB321) and to determine the positions of resonances for some ion clusters and their potential ion + neutral pair constituents.
Results and discussion
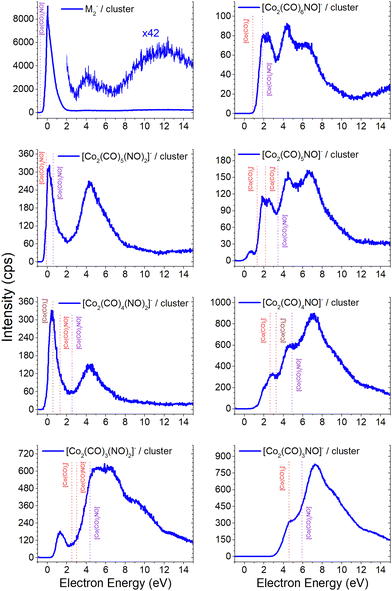
Electron attachment to clusters of Co(CO)3NO formed via co-expansion with Ar atoms at room temperature resulted in several types of products in this experiment:(a) the proposed gas-phase products17,19 were identified in the cluster measurements as isolated products (Fig. 1) or in the cluster with one Co(CO)3NO molecule (Fig. 2);
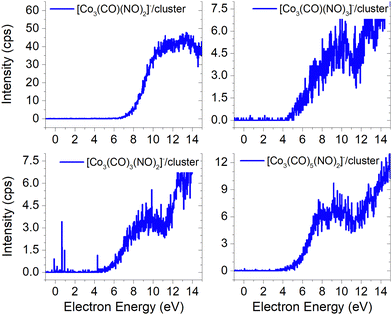
(b) the molecular dimer [M2]− (Fig. 2) and its clusters with DEA products (Fig. 3), such as [Co3(CO)6(NO)2]−, [Co3(CO)7(NO)2]−, [Co3(CO)8(NO)2]−, [Co3(CO)8(NO)3]− and the molecular trimer [M3]−;
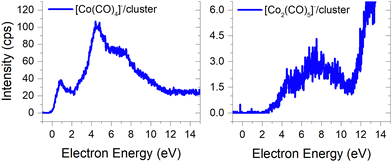
(c) products associated with electron scavenging reactions,35 where the neutral dissociation is followed by DEA to a neighbouring molecule, including ions [Co(CO)4]− and [Co2(CO)5]− (Fig. 4), [Co2(CO)NO]−, [Co2(CO)(NO)2]−, [Co2(CO)2NO]−, [Co2(CO)2(NO)2]− in (Fig. 5), [Co3(CO)(NO)2]−, [Co3(CO)3(NO)2]−, [Co3(CO)5(NO)2]− and [Co3(CO)(NO)3]− in (Fig. 6);
(d) products associated with N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond break (Fig. 7); [Co(CO)2N]− and clusters like [Co2(CO)(NO)N]−, [Co2(CO)2(NO)N]−, [Co3(CO)2(NO)N]−, [Co3(CO)3(NO)N]−, and [Co3(CO)(NO)2N]−; or alternatively oxygen retaining products with the same m/z, such as [Co2(CO)2O]−, [Co2(CO)3O]−, [Co3(CO)3O]−, [Co3(CO)4O]−, and [Co3(CO)2(NO)O]−.
O bond break (Fig. 7); [Co(CO)2N]− and clusters like [Co2(CO)(NO)N]−, [Co2(CO)2(NO)N]−, [Co3(CO)2(NO)N]−, [Co3(CO)3(NO)N]−, and [Co3(CO)(NO)2N]−; or alternatively oxygen retaining products with the same m/z, such as [Co2(CO)2O]−, [Co2(CO)3O]−, [Co3(CO)3O]−, [Co3(CO)4O]−, and [Co3(CO)2(NO)O]−.
The following thermochemical data were evaluated using the CBS-QB3 method and providing the interpretation of the experiment:
(a) for the electron affinities of the Co(CO)3NO molecule, and of its Co(CO)2NO, Co(CO)2, Co(CO)NO, Co(CO), Co(NO), and Co fragments (Table 1);
(b) for the bond dissociation energies in the neutral Co(CO)3NO molecule as:
summarized in (Table 1);
(c) for the theoretical thresholds (ΔH) of Co(CO)3NO reactions with an electron, resulting in the formation of experimentally identified anionic fragments and the corresponding dissociated neutral ligands, as:
summarized in (Table 2);
(d) additionally, for the interaction of two Co(CO)3NO molecules resulting in the production of [Co(CO)4]− (Table 2):
All optimised CBS-QB3 structures can be found in the ESI† file, together with more reactions than those listed in the discussion.
Molecular ion and its fragments, clusters vs. gas-phase
The results from the CLUSTER-ILN regarding DEA to Co(CO)3NO clusters are in good agreement with the proposed gas-phase ion yields of specific products previously reported by Engmann et al.17,19 With only minor deviations, the findings also correspond to the He cluster experiment conducted by Postler et al.21 Thus, the sequential loss of CO ligand(s), with or without NO ligand, observed in recent cluster measurements (represented by blue lines in Fig. 1), is not unexpected. This loss was previously anticipated based on the gas-phase experiments,17,19 depicted by ions shown in red lines in Fig. 1. Notably, the ion yields of small fragments such as Co−, [CoNO]− and [CoCO]− do not exhibit differences, and the recent CLUSTER-ILN data closely align with the gas-phase reference.17,19 Additionally, the He cluster measurements21 are included for comparison, plotted in grey along with the corresponding scaling factors relative to the intensities of Engmann's work.17,19 For ion fragments with at least two ligands, several higher-energy resonances are observed, in contrary to the gas-phase17,19 or He clusters.21 In the case of the [Co(CO)NO]− ion and electron energies above ∼4 eV, the primary resonance peaking at 2 eV vanishes completely in the gas-phase spectrum above 4 eV energies. However, in the cluster spectrum, its decline occurs gradually up to ∼7 eV, which may be associated with the ∼4.5 eV resonance that is clearly visible in the spectrum of [Co(CO)3NO]− or [Co(CO)2NO]−. Furthermore, beyond ∼7 eV, there is a notable rise in signal resulting in the formation of the [Co(CO)NO]− ion, in contrast to previous works,17,19,21 consisting of at least 2 resonances peaking at ∼10 and ∼13 eV. This may be the result of core-excited process; however, at these energies, there is no absorption data in the literature according to our knowledge. The rise in signal above 7 eV can also be identified in the Postler's21 measurements, for [Co(CO)3NO]−, [Co(CO)2NO]−, [Co(CO)3]− and [Co(CO)NO]−, although as a monotonically increasing signal instead of a resonant shape. For the [Co(CO)2NO]− ion, they provided explanation for these higher-energy signals via dipolar dissociation coupled with DEA of the molecular dimer. In the spectra of [Co(CO)2]− and [Co(CO)3]− ions, higher-energy resonances are evident with peaks around ∼7 eV and ∼10 eV, but their intensities are considerably lower than those observed in fragments containing nitrosyl.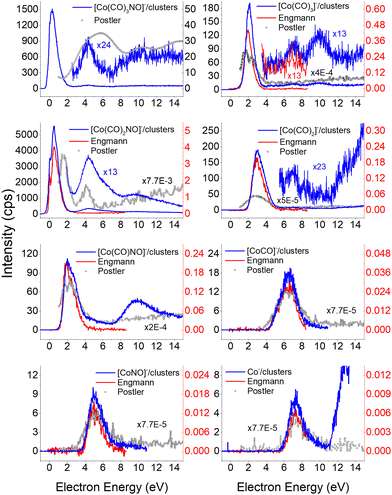 | ||
| Fig. 1 The DEA products of Co(CO)3NO obtained from CLUSTER-ILN measurements (blue lines) compared with previously published experiments: gas-phase date17,19 (red lines), He clusters data21 (grey circles). The y-axis on the left represents the intensities of CLUSTER-ILN data, while the intensities from previous works17,19 (with scaling factors) are on the right. | ||
In the spectrum of the most intense DEA product [Co(CO)2NO]−, a new channel emerges with a maximum at ∼4.5 eV, while the previously mentioned higher-energy channels remain active as well. The [Co(CO)2NO]− ion yield from He cluster results21 anticipated this channel above 4 eV, contrary to the gas-phase ion yield.17,19 Generally, the dissociation processes initiated either with photons or electrons can take place via an initial excitation mechanism.17 Contrary to the higher-energy core-excited resonances discussed above, for these energies around the ∼4.5 eV resonance, the UV/VIS absorption spectrum80 of Co(CO)3NO indicates two broad bands centred at 380 nm (≈3.3 eV) and 210 nm (≈5.1 eV), respectively. Photodissociation studies81 conducted with excitation wavelengths at 355 nm (≈3.5 eV) resulted in the loss of NO and/or one CO ligand, and at 266 nm (≈4.7 eV) in the formation of Co(CO)2 and NO-retaining products. Thus, low-lying excited states can be accessible for the core-excited process via electron attachment,17 followed, similar to the photodissociation process, by one or sequential ligand losses. Moreover, a repulsive character of the excited state, or with a shallow minimum only, leads preferably to the dissociation channels. However, if there is a possibility of redistributing the excess energy in the cluster, the DEA to the core-excited channel may be quenched21 and the excited ionic monomer can be detected, contrary to the gas-phase where the DEA takes place.17 Quenching of the 4.3 eV channel of [CoNO]− was discussed in He cluster studies, leading to the formation of the [Co(CO)2NO]− ion at energies above 4 eV. The same behaviour is seen in the recent CLUSTER-ILN ion yield of the [Co(CO)2NO]− ion shown in Fig. 1 at energies above 3 eV followed by the higher-energy resonances above 7 eV and 10 eV. However, no data for electron energies below 1 eV are reported in He clusters studies,21 preventing a comparison of the dominant single-particle shape-resonance of this ion below 1 eV, as well as with other ions in this study or in the gas-phase results.17,19
Similarly, a distinct resonance dominates the ion yield of [Co(CO)3NO]− as a consequence of low-energy electron capture below 1 eV. This ion is also formed in the He clusters;21 however, at very low abundances and only for higher electron energies at ∼4 and ∼10 eV, the present data only partially align. According to the CBS-QB3 calculations21 at 0 K, the EA of Co(CO)3NO is 0.75 eV, while the energy required for –CO ligand loss is 0.65 eV. In Table 1, we present our theoretical results evaluated at room temperature based on the CBS-QB3 enthalpies. The EA for Co(CO)3NO is calculated at 0.73 eV, and the BDE of the –CO ligand increases to 0.72 eV compared to the 0 K value.21 Consequently, it becomes evident that electron attachment to isolated Co(CO)3NO in the gas-phase can immediately access the dissociation channel [Co(CO)2NO]− + CO without any additional energy costs. However in clusters, similar to the quenching of DEA to [CoNO]− at 4.3 eV and favouring the formation of the [Co(CO)2NO]− ion, the transient negative ion [Co(CO)3NO]#− formed via electron capture to M can also distribute the excess energy in the cluster and the monomer remains viable throughout the flight time in the QMA (≥10 μs). Therefore, the molecular ion [M]− can only be observed in cluster experiments; isolated molecules in the gas-phase conditions do not form this ion, and no signal was reported in Engmann's work.17,19
| EA/eV | BDE(neut)/eV | BDE(anion)/eV | |||
|---|---|---|---|---|---|
| –CO | –NO | –CO | –NO | ||
| Co(CO)3NO | 0.73 | 1.32 | 2.58 | 0.72 | 1.57 |
| Co(CO)2NO | 1.33 | 1.94 | 2.85 | 1.69 | 1.33 |
| Co(CO)NO | 1.58 | 1.84 | 2.35 | 2.47 | 3.14 |
| CoNO | 0.96 | — | 1.53 | — | 1.62 |
| Co(CO)3 | 1.74 | 1.59 | — | 0.47 | — |
| Co(CO)2 | 2.85 | 1.44 | — | 3.51 | — |
| CoCO | 0.79 | 1.02 | — | 0.95 | — |
| Co | 0.87 | — | — | — | — |
| Co(CO)4 | 2.84 | 1.60 | — | 2.70 | — |
| Co(CO)2N | 2.15 | — | — | — | — |
The values presented in Table 1 summarize the calculated electron affinities and bond dissociation energies related to sequential –CO or –NO ligand losses in both neutral and anionic molecules. This enables the theoretical evaluation of the EA sequence among the possible fragments, starting with the Co(CO)3NO molecule labelled as M:
This does not entirely agree with the estimates provided by Engmann et al.,17 which were derived using an average BDE(Co–CO) = 1.42 eV,82 evaluated from Co(CO)4, and BDE(Co–NO) = 1.89 eV evaluated from Co+ appearance energy.34 They predicted the lowest EA for Co(CO)2 and the highest for Co(CO)2NO within the elementary fragments. The calculated average BDECBS-QB3(Co–CO) in Co(CO)4 is 1.41 eV, which agrees perfectly with the Connor's estimate82 used in Engmann's work. However, the BDECBS-QB3(Co–NO) is 1.53 eV, indicating a weaker bond than estimated by Opitz et al.34 The values presented in Table 1 represent the theoretical estimates of BDEs in Co(CO)3NO and [Co(CO)3NO]−, derived from individual CBS-QB3 calculations conducted in this study, for the optimal ground state energies and geometries of each element listed in the table, neutral or anionic, without utilizing any averaged values. The CBS-QB3 method utilized in this study has a notable limitation, and it struggles to handle molecular fragments exhibiting multireference character, which may be a possibility for certain fragments identified in this research. The S2 eigenvalue in CCSD(T) and later computational steps of CBS-QB3 of some neutral/anionic fragments (Co(CO)2, Co(CO), [CoCO]− and [CoNO]−) did not align with the initial spin state of the wave function, which could in fact reveal a multireference behaviour of the model treated with the single reference method. Seeking the T1/D1 diagnostic would help to confirm such behaviour, however it is not a part of the CBS-QB3 protocol. This would require more extensive and detailed theoretical investigations, which are beyond the intended scope of this combined experimental and theoretical work.
In Table 2, the theoretical threshold energies ΔH for various possible reactions are detailed, separately for neutral dissociations and interactions of incident electrons with neutral Co(CO)3NO leading to DEA products alongside neutral ligand fragments. A similar data set covering only the initial four reactions, originating from anionic [Co(CO)3NO]−, can be found in the study by Postler et al.21 Although we do not present the 0 K CBS-QB3 results for comparison, we confirm that these were completely replicated. The recent CBS-QB3 data, located in the right column of Table 2, serve as a basis for comparing with the experimental thresholds corresponding to specific DEA products evident from the ion yields depicted in Fig. 1. Based on these theoretical data, we anticipate the following order of ion formations: [Co(CO)2NO]− at 0 eV, [Co(CO)3]− at 0.85 eV, [Co(CO)2]− at 1.32 eV, [Co(CO)NO]− at 1.68 eV, [CoNO]− at 4.14 eV, [CoCO]− at 4.82 eV and Co− at 6.13 eV. Later, we will use these data to identify the possible [ion + neutral] pairs corresponding to the resonances measured for several DEA cluster products.
| ΔH/eV | ||
|---|---|---|
| [Neut. frag.] | [Anion frag.] | |
| Co(CO)3NO | ||
| → [Co(CO)2NO] + CO | 1.32 | -0.01 |
| → [Co(CO)3] + NO | 2.58 | 0.85 |
| → [Co(CO)2] + CO + NO | 4.17 | 1.32 |
| → [Co(CO)NO] + 2CO | 3.26 | 1.68 |
| → [CoCO] + 2CO + NO | 5.61 | 4.82 |
| → [CoNO] + 3CO | 5.10 | 4.14 |
| → [Co] + 3CO + NO | 6.63 | 5.77 |
| → [Co(CO)2N] + CO + O | 8.06 | 6.13 |
| 2Co(CO)3NO | ||
| → [Co(CO)4] + Co(CO)2NO + NO | 2.30 | −0.53 |
Clusters composed of a single Co(CO)3NO molecule along with DEA fragments, and the [M2]− ion
Based on the previous discussion, it is now evident that the gas phase measurements conducted by Engmann et al.17,19 revealed the absence of the molecular ion and some of the core-excited resonances, the dominant one at ∼4.5 eV and also at higher energies. This is in contrast to the clusters formed via electron attachment and DEA, for which the dominant product is the molecular ion in its dimer form [M2]−, and the core-excited resonant channels become more abundant for the [M·(DEA fragment)]− or alternative [ion + neutral] pair cluster products (refer to Fig. 2 and a comparative analysis with the He cluster data21 is available in the ESI†). A prevalent channel emerges consistently at 4–4.5 eV for all ions which plays a pivotal role in [M2]− and its fragments.The [M2]− ion, together with [Co2(CO)5NO2]−, which is in fact a [M·Co(CO)2NO]− cluster, exhibits similar ion yield characteristics as depicted in Fig. 1, excluding the high-energy resonances above 8 eV. The low-energy single-particle shape-resonance leading to [M2]− formation is the most abundant channel in all of the recent measurements. It indicates that the dimer form is more stable than the monomer (or even the trimer shown in this article later) and it could be considered as a magic number, typical for atomic83–85 or molecular clusters.86–90 However, we lack any theoretical confirmation of the stability of the dimer structure as the CBS-QB3 did not converge, and the experimental confirmation of magic numbers for larger [Mn]− clusters goes beyond the range of detection of our QMS.
The thermochemical data in Table 2 already indicate that both attachment ([M]−) and DEA channels ([Co(CO)2NO]−) are exothermic and accessible for electron energies around ∼0 eV. Some of the products shown in Fig. 2 exhibit recognizable DEA resonances from Fig. 1, such as:
– in [Co2(CO)6NO]−, the dominant ∼2 eV and the weaker ∼6 eV resonances of [Co(CO)3]−,
– in [Co2(CO)5NO]−, the weak ∼6 eV resonance of [Co(CO)2]−,
– in [Co2(CO)4NO]−, the ∼6 eV resonance of [Co(CO)]−,
– in [Co2(CO)3(NO)2]−, the ∼5 eV resonance of [CoNO]−, and
– in [Co2(CO)3NO]−, the ∼7 eV resonance of Co−.
However, determining the exact thresholds is challenging. The ion yields shown in Fig. 2 present convoluted resonances, making it difficult to determine precise values of thresholds for the peaks at higher energies. Nevertheless, beyond the reported absorption bands at 3.3 and 5.1 eV, for resonance at higher energies, it is crucial to consider the potential role of two-step reactions in clusters.35 If the initial step involves neutral dissociation initiated by an electron e through inelastic scattering on a cluster constituent, resulting electron e′ exits the reaction with reduced kinetic energy subsequently inducing the attachment or DEA reaction on a neighbouring Co(CO)3NO molecule.
There are several possible reactions which can be derived from the EAs and BDEs in Table 1, as well as from the reaction enthalpies ΔH for various reactions in Table 2. Based on the calculated ΔH of dissociative reactions in the neutral Co(CO)3NO molecule (Table 2), it is reasonable to anticipate that up to the kinetic energies of ∼4.5 eV, the following energetic order of ligand losses can be assumed:
The CBS-QB3 reaction enthalpies ΔH of two Co(CO)3NO molecules producing various ion clusters ([ion + neutral] pairs) such as [Co2(CO)3(NO)2]−, [Co2(CO)4(NO)2]−, [Co2(CO)5(NO)2]−, [Co2(CO)6(NO)2]− are given in Table 3 and those producing [Co2(CO)3NO]−, [Co2(CO)4NO]−, [Co2(CO)5NO]−, and [Co2(CO)6NO]− are given in Table 4. The suggested reactions are those for which the ΔH could potentially elucidate the thresholds observed in Fig. 2 and many other reactions potentially contributing to the ion yields at energies above the thresholds are presented in Tables in the ESI† file. Thus, for the [ion + neutral] pair considered to form the cluster with a given m/z value, we derived the reaction enthalpies using the following three schemes:
| [Ion + neutral pair] + neutral fragments | ΔH/eV |
|---|---|
| 2Co(CO)3NO + e → [Co2(CO)6(NO)2]− | |
| (3.1) → [M + M−] | −0.73 |
| 2Co(CO)3NO + e → [Co2(CO)5(NO)2]− + CO | |
| (3.2) → [M + Co(CO)2NO−] + CO | −0.11 |
| 2Co(CO)3NO + e → [Co2(CO)4(NO)2]− + 2CO | |
| (3.3) → [Co(NO)2 + Co(CO)4−] + 2CO | 0.57 |
| (3.4) → [Co(CO)2NO + Co(CO)2NO−] + 2CO | 1.31 |
| 2 Co(CO)3NO + e → [Co2(CO)3(NO)2]− + 3 CO | |
| (3.5) → [Co(CO)(NO)2 + Co(CO)2−] + 3CO | 2.53 |
| (3.6) → [Co(CO)2NO + Co(CO)NO−] + 3CO | 3.00 |
| [Ion + neutral pair] + neutral fragments | ΔH/eV |
|---|---|
| 2Co(CO)3NO + e → [Co2(CO)6NO]− + NO | |
| (4.1) → [M + Co(CO)3−] + NO | 0.85 |
| (4.2) → [Co(CO)3 + M−] + NO | 1.85 |
| 2Co(CO)3NO + e → [Co2(CO)5NO]− + CO + NO | |
| (4.3) → [M + Co(CO)2−] + CO + NO | 1.32 |
| (4.4) → [Co(CO)2NO + Co(CO)3−] + CO + NO | 2.17 |
| (4.5) → [Co(CO)NO + Co(CO)4−] + CO + NO | 1.41 |
| 2Co(CO)3NO + e → [Co2(CO)4NO]− + 2 CO + NO | |
| (4.6) → [Co(CO)2NO + Co(CO)2−] + 2CO + NO | 2.64 |
| (4.7) → [CoNO + Co(CO)4−] + 2CO + NO | 3.25 |
| 2Co(CO)3NO + e → [Co2(CO)3NO]− + 3 CO + NO | |
| (4.8) → [Co(CO)NO + Co(CO)2−] + 3CO + NO | 4.58 |
i. M and one DEA fragment according to Fig. 1:
ii. neutral fragment (M–ligand) and [M]−:
iii. or the combination of two, (M–ligand) and DEA fragment:
In Tables 3 and 4 for the proposed [ion + neutral] pairs of products forming the given ion with the measured m/z, we report only the sum of the individual CBS-QB3 enthalpies for the neutral and ionic constituents, rather than the actual dimer energy. Considering the estimated binding energy of neutral M2 around 1 eV,21 and potentially higher in an [ion + neutral] pair, all values in Tables 3 and 4 overestimate the theoretical thresholds when an actual [ion + neutral] cluster is formed. By reducing these values by 1 eV, we can come to a reasonable estimate for the threshold energies of resonances as shown in Fig. 2.
The [Co2(CO)4(NO)2]− ion shares a similar profile with [Co2(CO)5(NO)2]−, lacking evident characteristic of the [Co(CO)NO]− signal in this cluster, resulting from the reaction path (i) for the [[M + Co(CO)NO]−] pair. Therefore, the dimer ion of [Co(CO)2(NO)]2− is one of the potential candidates for the low-energy resonance, with a calculated ΔH = 1.31 eV summing the CBS-QB3 enthalpies (reaction 3.4 in Table 3) of individual constituents in the [Co(CO)2NO + Co(CO)2NO−] pair according to reaction path (iii). Considering the similar path but with rearrangement of the ligands in the dimer (reaction 3.3 in Table 3), the calculated reaction threshold lowers to ΔH = 0.57 eV for the [Co(NO)2 + Co(CO)4−] pair. Regarding the [Co2(CO)3(NO)2]− ion, the [Co(CO)2NO + Co(CO)NO−] pair would need a stronger binding than only 1 eV, given the calculated ΔH = 3.0 eV (reaction 3.6 in Table 3), which is >2 eV higher than the threshold of the first resonance. The rearrangement of ligands within the dimer to [Co(CO)(NO)2 + Co(CO)2−] (reaction 3.5 in Table 3) lowers the calculated threshold to 2.53 eV and it gets closer to the ∼1 eV estimate of the binding energy in the dimer structure.21
The first resonance for the [Co2(CO)6NO]− ion can be described using reactions (4.1) and (4.2) in Table 4 (reaction schemes (i) and (ii), respectively), forming the [Co(CO)3]− ion in pair with molecular monomer M, or with the opposite combination of the molecular [M]− ion and Co(CO)3 neutral in pair. The overall ion yield of this ion is formed with comparably intensive higher-energy core-excited resonances at ∼4.5 eV and ∼7 eV, already discussed above. The [Co2(CO)5NO]− ion has a resonance below 1 eV, which can be directly explained with the [M + Co(CO)2−] pair (reaction 4.3) or with the rearrangement product [Co(CO)NO + Co(CO)4−], with calculated ΔH values of 1.32 eV and 1.41 eV, respectively. The [Co(CO)3]− peak can be identified in the second peak of the [Co2(CO)5NO]− ion resulting from the [Co(CO)2NO + Co(CO)3−] pair with a calculated threshold of 2.17 eV (reaction 4.4). Similarly, the first peak of the [Co2(CO)4NO]− ion could be explained via the formation of [Co(CO)2NO + Co(CO)2−] or [CoNO + Co(CO)4−] pairs, as detailed in reactions 4.6 and 4.7 in Table 4. The first threshold of the [Co2(CO)3NO]− ion might be elucidated through the [Co(CO)NO + Co(CO)2−] pair, while the dominant peak at higher energies is from the Co− with M in the cluster.
Clusters composed of a M2 dimer along with DEA fragments, and the [M3]− ion
Due to the limitation of our QMA, the largest cluster we could detect is the molecular trimer [M3]−. Its ion yield at low energies is very similar to that of the monomer and dimer; however the efficiency of trimer formation is weaker. Furthermore, this cluster is associated with the formation of ions through the loss of one –CO ligand, with a similar spectrum as the [Co(CO)2NO]− monomer and the [M + Co(CO)2NO−] ion. However, the intensity of this ion is weak due to the low sensitivity of our QMA at higher masses. Postler et al.21 were able to detect even larger clusters, such as [M2·Co2(CO)2NO]− and [M3·Co2(CO)2NO]− ions at energies above 10 eV, but none of the ions reported in Fig. 3.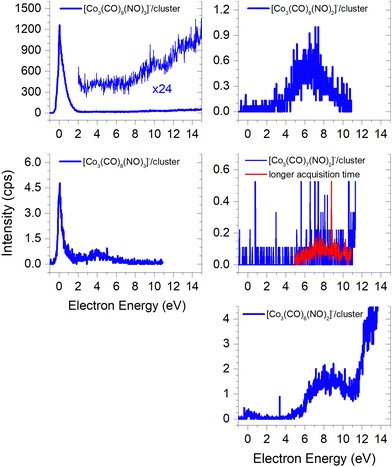 | ||
| Fig. 3 The molecular trimer [M3]− and the associated clusters of two molecules (M2) with the DEA products [Co(CO)2NO]−, [Co(CO)2]−, [CoCO]− and Co−. | ||
The core-excited resonance might be accessible for [M2·Co(CO)2]−, [M2·CoCO]− and [M2·Co]− ions as well. We do not support the larger clusters with CBS-QB3 calculations which could help to identify the cluster constituents (as we did in the case of fragments from the dimer) more exactly based on the comparison of theoretical and experimental thresholds. Therefore, we can only guess that the neutral dissociations of Co(CO)3NO to Co(CO)2 or Co(CO), at 4.17 eV and 5.61 eV, respectively, as well as the decomposition to Co atoms via all ligand losses (costs 6.63 eV, see Table 2), are in fact accessible neutral dissociation channels followed by electron attachment to M2, both producing the [M2·fragment]− cluster.
Ions formed via electron self-scavenging reactions
Unlike the gas-phase, where various cobalt carbonyl ions are commonly detected, their presence in clusters is unusual. In this study, all reported cluster ions contain at least one nitrosyl group, except for two ions with their ion yields depicted in Fig. 4. Regarding [Co(CO)4]−, we determined the CBS-QB3 reaction threshold by considering the interaction of two Co(CO)3NO molecules with an electron, forming the [Co(CO)4]− ion and neutral Co(CO)2NO and NO fragments. The reaction is exothermic (ΔH = −0.53 eV in Table 2), and although the maximum of the low-energy peak lies above 0 eV, the threshold aligns with the calculated energy. Both [Co(CO)4]− and [Co2(CO)5]− ions are formed with core-excited resonances of the M− above 4 and 7 eV. The importance of [Co(CO)4]− was already shown above, this ion could potentially be a resultant product in several cluster ions with m/z values ranging between the monomer and dimer, enabling access to low-energy channels which cannot be accessible via simple [M·(DEA fragment)]− formation.In Fig. 5 and 6, the ion yields of various cluster ions containing nitrosyl that can solely originate from electron self-scavenging reactions are shown. However, given the considerable complexity of the product ions and the limitation of the CBS-QB3 energies evaluated only for isolated molecules and their fragments, we lack the theoretical support to provide an explanation for the positioning of the resonances in this context. In Fig. 5, we observe four cluster ions composed of 2 Co atoms and 2, 3 or 4 ligands. The low energy resonance of the [Co2(CO)NO]− ion cannot be attributed to [Co(CO)2]− or [Co(CO)4]− as it was for several previous dimer clusters, leaving it unexplained. We speculate that the dominant yield might correspond to the [Co(CO)NO·Co]− cluster. For the [Co2(CO)(NO)2]− ion, we recognize a potential convolution of the [CoNO]− resonance and the higher-energy resonance of [Co(CO)NO]−, suggesting the formation of the ion [Co(CO)NO·CoNO]−. Regarding the [Co2(CO)2NO]− ion, we consider [CoNO·Co(CO)2−] to be the product [ion + neutral] pair. However, plausible candidates like [Co(CO)2NO·Co]− and [Co(CO)2NO·CoNO]− cannot be ruled out. The ion yield of the [Co2(CO)2(NO)2]− ion has a similar shape compared to the main resonance of [Co2(CO)3(NO)2]−, which can be described with the [Co(CO)NO]2− dimer or similarly as for the [Co2(CO)3(NO)2]− ion with a rearrangement product of [Co(NO)2·Co(CO)2−] (see reactions 2.13 and 2.14 in Table ESI2, ESI†).
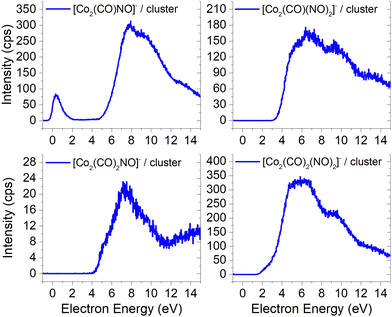 | ||
| Fig. 5 The cluster ions formed from a neutral fragment and DEA ion pair containing the nitrosyl group. | ||
The ion yields of similar products of this type, comprised of three Co atoms and varying numbers of CO and NO ligands, are depicted in Fig. 6. All four cluster ions reported are exclusively formed only through the core-excited channel. This exclusive formation allows the production of ions such as [Co3(CO)(NO)3]−, along with the sequence of ions including [Co3(CO)(NO)2]−, [Co3(CO)3(NO)2]− and [Co3(CO)5(NO)2]−. This sequence is complete with the inclusion of ions [Co3(CO)6(NO)2]− and [Co3(CO)8(NO)2]−, which were previously reported, and their ion yields are shown in Fig. 3.
Ions containing one nitrogen or oxygen atom originating from N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) O ligand bond break
O ligand bond break
In FEBID, the presence of impurities in the deposited structures is a well-documented phenomenon. Deposition of nanowires derived from Co(CO)3NO under different conditions (such as primary beam energy and temperature) has revealed varying deposition rates of Co atoms onto the surface, along with the incorporation of O, N, and C atoms as well.12,14 In most conditions, the ratio of impurities favours O atoms; however, the concentration of N is typically higher than that of C. While the deposition of CoO has been confirmed,14 the possibility of CoN formation cannot be excluded either.21Fig. 7 illustrates the measured ion yields of six distinct ion clusters with m/z ratios that cannot be attributed to the sum of Co, CO, and NO masses.
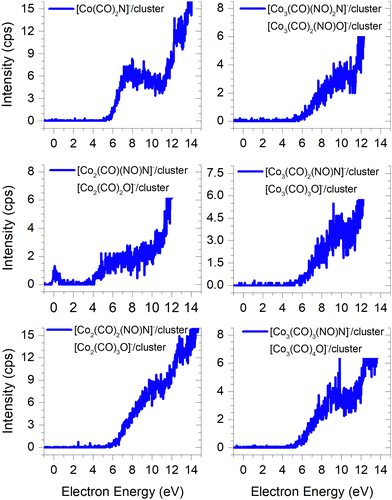 | ||
Fig. 7 The cluster ions where the dissociation of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ligand needs to be considered, the resulting ion products contain either a nitrogen or oxygen atoms. O ligand needs to be considered, the resulting ion products contain either a nitrogen or oxygen atoms. | ||
The low-energy electrons, at core-excited energies of the Co(CO)3NO molecule, can initiate reactions accompanied with a bond break in a ligand. With a calculated CBS-QB3 reaction enthalpy of 6.13 eV (Table 2), [Co(CO)2N]− emerges as a potential candidate for one of the ions as shown in Fig. 7. The [Co(CO)(NO)C]− variation of this ion exhibits a calculated threshold almost 2.75 eV higher (Table ESI1, ESI†), thus making it a non-exclusive candidate. Furthermore, even the gas-phase DEA study19 did not confirm the formation of [CoC]− ions, and only the electron ionisation study24 observed weak intensities for [CoC]+, [CoN]+ and [CoO]+. With the exception of the [Co3(CO)3(NO)N]− ion, none of the measured cluster ions appear to consist of a Co(CO)3NO and ion fragment. A sequence of ions such as [Co2(CO)(NO)N]−, [Co2(CO)2(NO)N]−, [Co3(CO)2(NO)N]−, and [Co3(CO)3(NO)N]− has been observed, together with the [Co3(CO)(NO)2N]− ion. However, considering the confirmed CoO deposit,14 it is possible to consider that the remaining five ion clusters shown in Fig. 7 (except [Co(CO)2N]−) could potentially be identified as [Co2(CO)2O]−, [Co2(CO)3O]−, [Co3(CO)3O]−, [Co3(CO)4O]− and [Co3(CO)2(NO)O]−.
Conclusions
This study is focused on the dissociative electron attachment to Co(CO)3NO clusters formed in an argon environment. Our findings reveal that the ion yields of DEA products from clusters align closely with both gas-phase results and cluster investigations conducted in helium nanodroplets. Additionally, recent cluster experiments revealed several core-excited resonances peaking above 4 eV, 6 eV, and approximately 10 eV, previously unreported in similar studies.The exclusive formation of the molecular ion from clusters was confirmed, indicating its relaxation caused by the cluster environment competing with the CO ligand loss in [Co(CO)3NO]− at energies around ∼0 eV. The Co ligand loss has been validated as an exothermic process using CBS-QB3 calculations and the preference of this reaction instead of the molecular ion formation was shown in gas-phase results. Additionally, the resonances observed for most of the ion cluster products in the energy range above 3–5 eV correlate with the previously observed absorption and photodissociation data associated with Co(CO)3NO. We reported new resonances for various ions known from the similar studies, including [Co(CO)2NO]− above 4 eV, [Co(CO)NO]− close to 10 eV, [Co(CO)3]− at 7 and 10 eV, and [Co(CO)2]− at 7 eV. Using CBS-QB3, we evaluated the electron affinities of Co(CO)3NO and its fragments along with bond dissociation energies in neutral Co(CO)3NO and anionic [Co(CO)3NO]−. This dataset enabled us to predict [ion + neutral] fragment pairs contributing to resonance structures observed in dimer-like clusters, such as [Co(CO)3NO]2− with sequential CO ligand losses up to [Co2(CO)3(NO)2]−, or with simultaneous CO and NO ligand losses, such as [Co2(CO)6NO]− up to [Co2(CO)3NO]−. Our CBS-QB3 calculated thresholds aligned well with experimentally observed thresholds of these smaller cluster ions as well as of the individual DEA products. Notably, our theoretical predictions suggest the formation of the [Co(CO)2NO]2− dimer instead of the [Co(CO)3NO + Co(CO)NO]− pair, predicted experimentally along with the ion yield of [Co2(CO)4(NO)2]− similar to the yield of the [Co(CO)2NO]− ion than that of the [Co(CO)NO]− ion.
We offered theoretical explanations for resonances occurring at energies lower than the expected threshold of the potential DEA fragment in the small ion clusters [Co(CO)3NO + DEA fragment]−, involving the [Co(CO)2]− or even [Co(CO)4]− ion constituents for [Co2(CO)6NO]−, [Co2(CO)5NO]−, [Co2(CO)4NO]− and [Co2(CO)3NO]− clusters. The [Co(CO)4]− ion was confirmed in this study as the product of DEA to Co(CO)3NO clusters, alongside the [Co2(CO)5]− variation. Due to the stoichiometry of the [Co(CO)4]− ion, as well as of various dimer-like clusters reported in this study, [Co2(CO)NO]−, [Co2(CO)2NO]−, [Co2(CO)2NO]− and [Co2(CO)2(NO)2]−, the formation of the potential products was explained only through electron self-scavenging reactions. The inelastic electron scattering initiates neutral dissociation in one constituent followed by DEA to the neighbouring molecule, or even more with the rearrangement of the ligands to [Co(NO)2 + Co(CO)4−] or [Co(CO)(NO)2 + Co(CO)2−] within the dimer like structures of the [ion + neutral] pairs.
The sequential CO and/or NO ligand losses from the trimer [Co(CO)3NO]3− ion were measured as well, producing ions such as [Co3(CO)8(NO)3]−, [Co3(CO)8(NO)2]− up to [Co3(CO)5(NO)2]−, and also forming smaller fragments such as [Co3(CO)3(NO)2]−, [Co3(CO)(NO)2]− or [Co3(CO)(NO)3]−. We confirmed experimentally that the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond dissociation may occur during low-energy electron interactions at core-excited energy levels. The formation of [Co(CO)2N]− was confirmed in this experiment, calculated as an exothermic reaction of Co(CO)3NO with electrons. The N
O bond dissociation may occur during low-energy electron interactions at core-excited energy levels. The formation of [Co(CO)2N]− was confirmed in this experiment, calculated as an exothermic reaction of Co(CO)3NO with electrons. The N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond break was observed within their respective clusters, such as [Co2(CO)(NO)N]−, [Co2(CO)2(NO)N]−, [Co3(CO)2(NO)N]−, [Co3(CO)3(NO)N]− and [Co3(CO)(NO)2N]− or their alternative forms such as [Co2(CO)2O]−, [Co2(CO)3O]−, [Co3(CO)3O]−, [Co3(CO)4O]− and [Co3(CO)2(NO)O]−.
O bond break was observed within their respective clusters, such as [Co2(CO)(NO)N]−, [Co2(CO)2(NO)N]−, [Co3(CO)2(NO)N]−, [Co3(CO)3(NO)N]− and [Co3(CO)(NO)2N]− or their alternative forms such as [Co2(CO)2O]−, [Co2(CO)3O]−, [Co3(CO)3O]−, [Co3(CO)4O]− and [Co3(CO)2(NO)O]−.
Author contributions
DM performed the CLUSTER-ILN experiments, PP performed computational modelling, both together worked on data analysis and the preparation of figures. PP and ŠM provided the scientific advice, supervised the research projects and financing. All co-authors contributed to the discussions and writing of the manuscript equally.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
This work was supported by the Slovak Research and Development Agency under the Contract no. APVV-19-0386 and the Slovak Grant Agency for Science (contract no. VEGA 1/0553/22). This work was supported in part through the Comenius University in Bratislava CLARA@UNIBA.SK high-performance computing facilities, services and staff expertise of Centre for Information Technology (https://uniba.sk/en/HPC-Clara). PP would like to express gratitude to Professor Pavel Mach from Comenius University in Bratislava for his valuable discussions regarding the CBS-QB3 calculations. We express our gratitude to Professor Petra Swiderek from the University of Bremen, who initiated the DEA study of Co(CO)3NO clusters in our laboratories as part of the Celina COST Action and Elena ITN projects. This publication is based on the work from COST Action CA18212 – Molecular Dynamics in the GAS phase (MD-GAS).References
- W. F. Van Dorp and C. W. Hagen, J. Appl. Phys., 2008, 104, 081301 CrossRef.
- I. Utke, P. Hoffmann and J. Melngailis, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 2008, 26, 1197 CrossRef CAS.
- M. Huth, F. Porrati and O. V. Dobrovolskiy, Microelectron. Eng., 2018, 185–186, 9–28 CrossRef CAS.
- M. Huth, F. Porrati, C. Schwalb, M. Winhold, R. Sachser, M. Dukic, J. Adams and G. Fantner, Beilstein J. Nanotechnol., 2012, 3, 597–619 CrossRef CAS PubMed.
- P. Orús, F. Sigloch, S. Sangiao and J. M. De Teresa, Nanomaterials, 2022, 12, 1–29 CrossRef PubMed.
- I. Utke, P. Swiderek, K. Höflich, K. Madajska, J. Jurczyk, P. Martinović and I. B. Szymańska, Coord. Chem. Rev., 2022, 458, 213851 CrossRef CAS.
- F. Jungwirth, F. Porrati, D. Knez, M. Sistani, H. Plank, M. Huth and S. Barth, ACS Appl. Nano Mater., 2022, 5, 14759–14770 CrossRef CAS.
- S. Barth, M. Huth and F. Jungwirth, J. Mater. Chem. C, 2020, 8, 15884–15919 RSC.
- R. Winkler, M. Brugger-Hatzl, F. Porrati, D. Kuhness, T. Mairhofer, L. M. Seewald, G. Kothleitner, M. Huth, H. Plank and S. Barth, Nanomaterials, 2023, 13, 2907 CrossRef CAS PubMed.
- L. M. Belova, E. D. Dahlberg, A. Riazanova, J. J. L. Mulders, C. Christophersen and J. Eckert, Nanotechnology, 2011, 22, 145305 CrossRef CAS PubMed.
- A. Fernández-Pacheco, J. M. De Teresa, R. Córdoba and M. R. Ibarra, J. Phys. D: Appl. Phys., 2009, 42, 055005 CrossRef.
- G. C. Gazzadi, J. J. L. Mulders, P. Trompenaars, A. Ghirri, A. Rota, M. Affronte and S. Frabboni, Microelectron. Eng., 2011, 88, 1955–1958 CrossRef CAS.
- F. Vollnhals, M. Drost, F. Tu, E. Carrasco, A. Späth, R. H. Fink, H. P. Steinrück and H. Marbach, Beilstein J. Nanotechnol., 2014, 5, 1175–1185 CrossRef PubMed.
- G. C. Gazzadi, H. Mulders, P. Trompenaars, A. Ghirri, M. Affronte, V. Grillo and S. Frabboni, J. Phys. Chem. C, 2011, 115, 19606–19611 CrossRef CAS.
- A. R. Ivanova, G. Nuesca, X. Chen, C. Goldberg, A. E. Kaloyeros, B. Arkles and J. J. Sullivan, J. Electrochem. Soc., 1999, 146, 2139–2145 CrossRef CAS.
- I. Utke, P. Hoffmann, R. Berger and L. Scandella, Appl. Phys. Lett., 2002, 80, 4792–4794 CrossRef CAS.
- S. Engmann, M. Stano, Š. Matejčík and O. Ingólfsson, Angew. Chem., Int. Ed., 2011, 50, 9475–9477 CrossRef CAS PubMed.
- R. M. Thorman, T. P. Ragesh Kumar, D. Howard Fairbrother and O. Ingólfsson, Beilstein J. Nanotechnol., 2015, 6, 1904–1926 CrossRef CAS PubMed.
- S. Engmann, M. Stano, P. Papp, M. J. Brunger, Š. Matejčík and O. Ingólfsson, J. Chem. Phys., 2013, 138, 044305 CrossRef PubMed.
- P. Y. Shih, M. Cipriani, C. F. Hermanns, J. Oster, K. Edinger, A. Gölzhäuser and O. Ingólfsson, Beilstein J. Nanotechnol., 2022, 13, 182–191 CrossRef CAS PubMed.
- J. Postler, M. Renzler, A. Kaiser, S. E. Huber, M. Probst, P. Scheier and A. M. Ellis, J. Phys. Chem. C, 2015, 119, 20917–20922 CrossRef CAS PubMed.
- M. Lacko, P. Papp, K. Wnorowski and Š. Matejčík, Eur. Phys. J. D, 2015, 69, 84 CrossRef.
- M. Allan, M. Lacko, P. Papp, Š. Matejčík, M. Zlatar, I. I. Fabrikant, J. Kočišek and J. Fedor, Phys. Chem. Chem. Phys., 2018, 20, 11692–11701 RSC.
- P. Papp, S. Engmann, M. Kučera, M. Stano, Š. Matejčík and O. Ingólfsson, Int. J. Mass Spectrom., 2013, 356, 24–32 CrossRef CAS.
- M. Lacko, P. Papp, I. B. Szymańska, E. Szłyk and Š. Matejčík, Beilstein J. Nanotechnol., 2018, 9, 384–398 CrossRef PubMed.
- A. Prosvetov, A. V. Verkhovtsev, G. Sushko and A. V. Solov’yov, Eur. Phys. J. D, 2023, 77, 15 CrossRef CAS.
- N. Silvis-Cividjian, C. W. Hagen and P. Kruit, J. Appl. Phys., 2005, 98, 084905 CrossRef.
- T. P. Ragesh Kumar, S. Hari, K. K. Damodaran, O. Ingólfsson and C. W. Hagen, Beilstein J. Nanotechnol., 2017, 8, 2376–2388 CrossRef CAS PubMed.
- M. M. Walz, M. Schirmer, F. Vollnhals, T. Lukasczyk, H. P. Steinrück and H. Marbach, Angew. Chem., Int. Ed., 2010, 49, 4669–4673 CrossRef CAS PubMed.
- H. Marbach, Appl. Phys. A: Mater. Sci. Process., 2014, 117, 987–995 CrossRef CAS.
- M. Drost, F. Tu, L. Berger, C. Preischl, W. Zhou, H. Gliemann, C. Wöll and H. Marbach, ACS Nano, 2018, 12, 3825–3835 CrossRef CAS PubMed.
- K. Ahlenhoff, C. Preischl, P. Swiderek and H. Marbach, J. Phys. Chem. C, 2018, 122, 26658–26670 CrossRef CAS.
- B. Sztáray and T. Baer, J. Phys. Chem. A, 2002, 106, 8046–8053 CrossRef.
- J. Opitz, Int. J. Mass Spectrom., 2003, 225, 115–126 CrossRef CAS.
- J. Lengyel, P. Papp, Š. Matejčík, J. Kočišek, M. Fárník and J. Fedor, Beilstein J. Nanotechnol., 2017, 8, 2200–2207 CrossRef CAS PubMed.
- D. Mészáros, P. Papp and Š. Matejčík, Eur. Phys. J. D, 2023, 77, 62 CrossRef.
- E. Illenberger, Chem. Rev., 1992, 92, 1589–1609 CrossRef CAS.
- A. Kühn and E. Illenberger, J. Chem. Phys., 1990, 93, 357–364 CrossRef.
- J. Lotter and E. Illenberger, J. Phys. Chem., 1990, 94, 8951–8956 CrossRef CAS.
- E. C. M. Chen, L. R. Shuie, E. D. D'sa, C. F. Batten and W. E. Wentworth, J. Chem. Phys., 1988, 88, 4711–4719 CrossRef CAS.
- L. G. Christophorou and J. K. Olthoff, J. Phys. Chem. Ref. Data, 2000, 29, 267–330 CrossRef CAS.
- A. Kramida, Yu Ralchenko and J. Reader, NIST Atomic Spectra Database (ver. 5.10) 2023, November 6, https://physics.nist.gov/asd.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. C. 01, 2016 Search PubMed.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822–2827 CrossRef CAS.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532–6542 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275–280 CrossRef CAS.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 281–289 CrossRef CAS.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
- S. Sæbø and J. Almlöf, Chem. Phys. Lett., 1989, 154, 83–89 CrossRef.
- M. Head-Gordon and T. Head-Gordon, Chem. Phys. Lett., 1994, 220, 122–128 CrossRef CAS.
- K. Raghavachari and J. A. Pople, Int. J. Quantum Chem., 1978, 14, 91–100 CrossRef.
- K. Raghavachari, M. J. Frisch and J. A. Pople, J. Chem. Phys., 1980, 72, 4244–4245 CrossRef.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975 CrossRef CAS.
- M. R. Nyden and G. A. Petersson, J. Chem. Phys., 1981, 75, 1843–1862 CrossRef CAS.
- G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090 CrossRef CAS.
- G. A. Petersson, T. G. Tensfeldt and J. A. Montgomery, J. Chem. Phys., 1991, 94, 6091–6101 CrossRef CAS.
- J. A. Montgomery, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1994, 101, 5900–5909 CrossRef CAS.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov and J. A. Pople, J. Chem. Phys., 1998, 109, 7764–7776 CrossRef CAS.
- L. A. Curtiss, K. Raghavachari and J. A. Pople, J. Chem. Phys., 1993, 98, 1293–1298 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108 CrossRef PubMed.
- J. W. Ochterski, G. A. Petersson and J. A. Montgomery, J. Chem. Phys., 1996, 104, 2598–2619 CrossRef CAS.
- E. C. Barnes, G. A. Petersson, J. A. Montgomery, M. J. Frisch and J. M. L. Martin, J. Chem. Theory Comput., 2009, 5, 2687–2693 CrossRef CAS PubMed.
- J. M. Simmie and K. P. Somers, J. Phys. Chem. A, 2015, 119, 7235–7246 CrossRef CAS PubMed.
- S. Xu, Q. De Wang, M. M. Sun, G. Yin and J. Liang, RSC Adv., 2021, 11, 29690–29701 RSC.
- A. Karton and L. Goerigk, J. Comput. Chem., 2015, 36, 622–632 CrossRef CAS PubMed.
- N. J. DeYonker, K. A. Peterson, G. Steyl, A. K. Wilson and T. R. Cundari, J. Phys. Chem. A, 2007, 111, 11269–11277 CrossRef CAS PubMed.
- W. Jiang, N. J. Deyonker, J. J. Determan and A. K. Wilson, J. Phys. Chem. A, 2012, 116, 870–885 CrossRef CAS PubMed.
- S. Kozuch and J. M. L. Martin, J. Comput. Chem., 2013, 34, 2327–2344 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904 RSC.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- N. Mardirossian, L. Ruiz Pestana, J. C. Womack, C. K. Skylaris, T. Head-Gordon and M. Head-Gordon, J. Phys. Chem. Lett., 2017, 8, 35–40 CrossRef CAS PubMed.
- B. Chan, J. Phys. Chem. A, 2019, 123, 5781–5788 CrossRef CAS PubMed.
- B. Chan, P. M. W. Gill and M. Kimura, J. Chem. Theory Comput., 2019, 15, 3610–3622 CrossRef CAS PubMed.
- B. Chan, Int. J. Quantum Chem., 2021, 121, e26453 CrossRef CAS.
- B. Chan, J. Phys. Chem. A, 2022, 126, 4981–4990 CrossRef CAS PubMed.
- S. Georgiou and C. A. Wight, J. Chem. Phys., 1989, 90, 1694–1700 CrossRef CAS.
- W. Wang, F. Chen, J. Lin and Y. She, J. Chem. Soc., Faraday Trans., 1995, 91, 847–853 RSC.
- J. A. Connor, Inorganic Chemistry Metal Carbonyl Chemistry, Springer-Verlag, Berlin/Heidelberg, 2006, pp. 71–110 Search PubMed.
- M. Renzler, M. Kuhn, A. Mauracher, A. Lindinger, P. Scheier and A. M. Ellis, Phys. Rev. Lett., 2016, 117, 1–4 CrossRef PubMed.
- A. W. Castleman, in Clustering Phenomena in Atoms and Nuclei. Springer Series in Nuclear and Particle Physics, ed. M. Brenner, T. Lönnroth and F. B. Malik, Springer, Berlin, Heidelberg, 1992, pp. 99–109 Search PubMed.
- M. Gatchell, P. Martini, L. Kranabetter, B. Rasul and P. Scheier, Phys. Rev. A, 2018, 98, 1–4 CrossRef.
- S. Kollotzek, O. V. Lushchikova, L. Tiefenthaler, F. Zappa and P. Scheier, Int. J. Mol. Sci., 2022, 23, 3613 CrossRef CAS PubMed.
- C. Leidlmair, P. Bartl, H. Schöbel, S. Denifl, S. Yang, A. M. Ellis and P. Scheier, ChemPhysChem, 2012, 13, 469–476 CrossRef CAS PubMed.
- K. Hansen, M. J. Ryding and E. Uggerud, Int. J. Mass Spectrom., 2019, 440, 14–19 CrossRef CAS.
- L. Kranabetter, P. Martini, N. Gitzl, M. Kuhn, F. Saleem, B. Rasul, M. Mahmoodi Darian, E. Jabbour Al Maalouf, I. Sukuba, A. Kaiser, M. Goulart, D. K. Böhme and P. Scheier, Phys. Chem. Chem. Phys., 2018, 20, 21573–21579 RSC.
- H. M. Lee, S. B. Suh, P. Tarakeshwar and K. S. Kim, J. Chem. Phys., 2005, 122, 044309 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Optimal CBS-QB3 geometries and reaction enthalpies. See DOI: https://doi.org/10.1039/d3cp05601e |
| This journal is © the Owner Societies 2024 |