Density functional theory study of high-energy metal (Al, Mg, Ti, and Zr)/CuO composites

Abstract

We investigated the geometric and electronic structures and stability of high-energy metal metastable intermolecular composites (Al, Mg, Ti, and Zr)/CuO(111) between metal layers and a CuO(111) substrate by density functional theory. Structural relaxation primarily occurs on the M–O_suf and M–Cu bonds. This indicates that ionic and metallic bonding play a major role in the interfaces. The interactions between metal adlayers and substrates are strong and the interface has an ionic/metallic character. The Zr/CuO(111) composite has the highest adsorption energy, while the Al/CuO (111) has the lowest deformation energy. The electron density differences of the four composites suggest that electron activity mainly occurs at the interface but not at the substrate. Comprehensively considering these factors, it is evident that the Al/CuO (111) composite is the most stable system.

---

1. Introduction

Metastable intermolecular composites (MICs), kinds of nanoenergetic materials (nEMs), are generally composed of fuel and oxidizers and can release thermal energy rapidly when they are ignited. When the MICs are triggered by external energy via an electrical heat coil, laser beam, or flame, there occur so-called self-sustaining exothermic reactions in them. Therefore, the MICs with strenuous exothermic properties can be utilized in numerous applications, such as explosives, propulsion fuels, and pyrotechnics.^1–3

Among several types of reactive MICs, nanosized metal/copper oxide (commonly cupric oxide (CuO) and cuprous oxide (Cu₂O)) composites have attracted much attention due to their significant applications in industry and the military.^4,5 Recently, nano-CuO, such as wires, belts, rods, and tubes, has been utilized to serve as nEMs when incorporating with nano-Al, Mg, Ti, or Zr etc. due to high energy release according to eqn (1).

M + CuO → MO + Cu + ΔH (1)

where M are Al, Mg, Ti, or Zr etc. and ΔH represented the heat released. The formation energy of CuO (−157.3 kJ mol⁻¹) is much lower than that of Al₂O₃ (−1676 kJ mol⁻¹), MgO (−601 kJ mol⁻¹), TiO₂ (−944 kJ mol⁻¹), or ZrO₂ (−1097 kJ mol⁻¹).^6–10 Different approaches have been realized to synthesize high-energy metal/CuO (M/CuO, M = Al, Mg, Ti, or Zr etc.) systems, of which Al/CuO nanolaminate has a relatively higher energy density (21 kJ cm⁻³) than trinitrotoluene (TNT, 7.6 kJ cm⁻³), a standard high-energy explosive. Therefore, many experimental and theoretical studies have been paying attention to the M/CuO nanofoils in the past decade.^11–16 Hu et al.¹⁷ used density functional theory (DFT) to study the effects of electronic properties of molecule adsorption on several CuO surfaces and nanowires. Lanthony et al.¹³ calculated the initial steps of CuO deposition onto Al(111) surface and of Al deposition onto CuO(11−1) surface to study the basic mechanisms responsible for the growth of Al/CuO interface using DFT. Combining experiments and first-principle calculations, Oison et al.¹⁸ presented a detailed study of the O₃ detection mechanism on the CuO(111) surface. However, the knowledge on the electronic effects and stability of MICs based CuO(111) combined with different metals is lacking.

In this work, we performed periodic DFT calculations to study the geometric and electronic structures and stability of M/CuO(111) (M = Al, Mg, Ti, or Zr) composites. Our main purpose is to uncover how different metals affect the interface properties of CuO-based MICs.

2. Computational methodology

We perform spin-polarized DFT^19,20 as implemented in the Vienna Simulation Package (VASP).^21–23 The Kohn–Sham equations are used with a plane-wave basis set and periodic boundary conditions. Electron exchange and correlation are described using the Perdew–Burke–Ernzerhof (PBE) version²⁴ of the generalized gradient approximation (GGA). The ion cores are described by projector-augmented wave (PAW) potentials²⁵ as implemented by Kresse and Joubert.²⁶ The on-site Coulomb repulsion (Hubbard U) is applied to Cu d state, where U = 7.5 eV and J = 0.98 eV are adopted from ref. 27. For the k-point sampling of the Brillouin zone, we use the Monkhorst–Pack scheme.²⁸

We used an energy cutoff of 400 eV in the plane-wave basis set expansion for all calculations. The total energies of the M/CuO(111) systems were converged up to 10⁻⁴ eV per atom using Gaussian smearing with a smearing width of 0.1 eV and a 3 × 3 × 1 Monkhorst–Pack k-point mesh for the sampling of Brillouin zones. Vertically there is at least 12 Å of empty space. We relaxed all atomic positions (no constraints) according to their forces using a conjugate gradient algorithm, and the relaxation is stopped when the forces on each atom were below 0.03 eV Å⁻¹. Also, we relaxed several structures until the forces were less than 0.01 eV Å⁻¹. The results indicated that this did not lead to significant differences in total energies or structures.

Upon our calculations, the adsorption energy (E_ads) of metal on CuO is defined as²⁹

E_ads = [E_metal/CuO − (E_CuO + E_metal)]/n (2)

where E_metal/CuO, E_CuO, and E_metal are the energies of the total system, isolated CuO support, and isolated metal layers, respectively. The number of atoms in a single plane is represented by n.

The adsorption of different metal layers can lead to the deformation of CuO(111) substrate which can affect the stability of interface formed. The deformation energy (E_def) can be quantified by³⁰

E_def = (E_relaxed/CuO − E_def/CuO)/n (3)

where E_relaxed/CuO and E_def/CuO are the energies of the isolated CuO support after metal layer modification and the clean CuO support without surface modification, respectively.

Electron density difference Δρ(r) maps are obtained by

Δρ(r) = ρ^metal/CuO(r) − ρ^metal(r) − ρ^CuO(r) (4)

where ρ^metal/CuO(r) is the electron density of the total system and ρ^metal(r) and ρ^CuO(r) are the unperturbed electron densities of metal layer and CuO support, respectively.

2.1 Bulk CuO

The bulk CuO crystallizes in a monoclinic lattice with C2/c (number 15) space group.³¹ The lattice constants are calculated by relaxing both ions and cell volume and shape simultaneously. A Monkhorst–Pack k-point grid of 11 × 11 × 11 was employed for the sampling of the Brillouin zones. Full geometry relaxation was carried out until energy minimization and the forces on each ion were less than 0.001 eV Å⁻¹. The unit cell parameters determined from this approach is listed in Table S1 of the ESI† in comparison with experiment values. These values fit fairly well to the experimental lattice parameters^31,32 with deviation of −0.3 to −1.7% and other calculations(Table S1†).^18,33

CuO is a p-type semiconductor with an experimentally determined band-gap of 1.2–1.9 eV. We calculated this band-gap to be 1.1 eV, indicating the usual underestimation of band-gaps by DFT and agreeing with calculated results by other studies.^17,18,33

2.2 CuO(111) surface

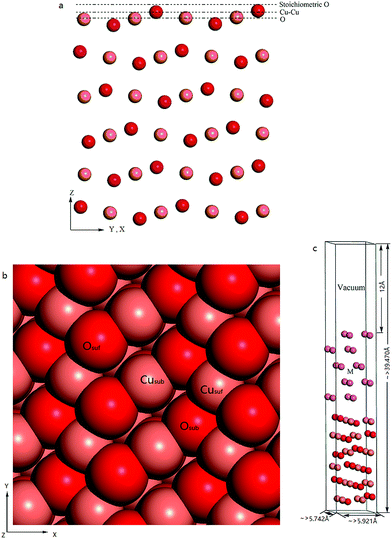
CuO(111) surface is demonstrated to be the most often observed one under experimental conditions and previous works have shown that the CuO(111) surface is more stable than the others.^12,16–18 There are three probable terminations for (111) CuO slabs: stoichiometric O termination, Cu–Cu termination (two top Cu layers), and non-stoichiometric O termination as shown in Fig. 1a. Theoretical calculations predicted that the stoichiometric surface is the most stable one, terminated by O layer. This type of surface is also demonstrated to be the most often observed under experimental conditions. Therefore, only the CuO surface with the stoichiometric O termination was used in this work. The CuO slab consists of six stoichiometric layers (O_suf–Cu_sub–O_sub–Cu_suf), as shown in Fig. 1b. This is thick enough to describe the surface structure. Cu_suf is the outer-most copper atom of the surface and Cu_sub is the subsurface copper atom. O_suf is the outer-most oxygen atom and O_sub is the subsurface oxygen atom.

Fig. 1 (a) Possible surface terminations of CuO(111) (side view). Red and salmon pink spheres stand for copper and oxygen atoms, respectively. (b) Different positions in the inner layer of adsorbed metals (top view); each metal layer has four atoms. (c) Schematic picture of triclinic unit cell.

2.3 Metal/CuO(111) composites

A few of metal layers were placed on the top of the CuO(111) slab to construct a metal/CuO composite. The metals can be absorbed in different positions over the substrate. Theoretical study indicated that the Al atoms preferentially deposits onto the O atoms of the CuO substrate.¹² Therefore, all simulation models are constructed with the metal atoms firstly placed on the top O atoms of the substrate with a interlayer spacing about 3 Å.

To determine how many layers of metals must be included in the composites, several Al/CuO models with different numbers of Al layers were built and their adsorption energies were calculated. As presented in Table S2 of the ESI,† the energy converges well as the layer increases. Four or more Al layers may represent the real characteristic of the composites. Here we used five metal layers to build different metal/CuO(111) composites. A schematic diagram of the interface model is shown in Fig. 1c.

3. Results and discussion

3.1 Atomic structure of metal/CuO(111) composites

The optimized geometry structures for the M/CuO(111) systems are displayed in Fig. 2. Among the geometric structures, the CuO(111) surface undergoes some changes as the absorbed metal atoms are regularly arranged upon it.

Fig. 2 Optimized geometries of M/CuO(111) interfaces with side (left) and top (right) views, where M = Al, Mg, Ti, and Zr, respectively.

To investigate the effect of the substrate on the adsorbed metal layers, the interlayer relaxations Δ_ij = (d_ij − d₀)/d₀ with the bulk interlayer distance were calculated and listed in Table 1. The first-second interlayer contractions (Table 1) adjacent to the substrate are about 2.1%, 5.4%, 8.6%, and 2.3%, for the Al, Mg, Ti, and Zr layers, respectively. This indicate that the inside metal layers remain their bulk structures. At the interface of the M/CuO(111) systems, the M–O_suf bond length formed between the O_suf atom of the CuO(111) slab and the metal atom in the outmost layer of the slab increases in the order of Al, Mg, Ti, and Zr with 1.79, 1.91, 2.00, and 2.13 Å, respectively. The whole metal layers are close to the CuO(111) surface in comparison with the initial distance of 3 Å. This indicates that there formed metal oxides between the M/CuO interfaces, consistent with the experimental and other theoretical results.^12,34–37

Table 1 Calculated metal interlayer relaxation Δ_ij (in percent) and distances of the M–Cu and M–O_suf for four M/CuO(111) composites along with some experimental and theoretical results

	Δ12 (%)	M–Cusuf (Å)	M–Cusub (Å)	M–Osuf (Å)	M–O ref. (Å)
Al	−2.1	2.69	3.19	1.79	1.86 12, 1.79 34
Mg	−5.4	2.78	2.99	1.91	1.97 35
Ti	−8.6	2.72	2.81	2.00	2.09 36
Zr	−2.3	2.98	3.24	2.13	2.28 37

---

It is interesting to note that the Mg atoms (top view) are situated in the middle of the two O_suf atoms, different from the others. The Zr–O_sub bond length between the substrate O_sub and the adlayer Zr atoms (2.21 Å) is slightly larger than the Zr–O_suf one. In contrast, the M–Cu_suf distances for Al, Mg, Ti, and Zr are 2.69, 2.78, 2.72, and 2.98 Å, respectively. There is an abnormal case appearing in the Ti–Cu_suf bond length. This is not in agreement with the variation order of their M–O_suf bond lengths. The bond lengths for the Ti–Cu_sub and Ti–Cu_suf are 2.81 and 2.72 Å, respectively. This indicates that the Ti layers predominately present close contacts with the Cu atoms compared to other metal layers. Therefore, Ti layers may produce the most important role on the surface and substrate Cu atoms of the CuO(111) among the four interfaces.

For the CuO(111) substrate, the relaxations of the surface O_sub and O_suf atoms experience more significant variations than those of the Cu_sub and Cu_suf atoms. Especially, the top-most oxygen atoms in the Zr/CuO(111) composite migrate inward about ∼0.6 Å, while the subsurface ones are extracted about ∼0.6 Å in comparison with the clean CuO(111) system. Such atom migration alters the surface termination and results in the Zr adlayers to be close contact with the substrate. This is distinctly different from to other three composites. Overall, the majority of structural relaxations takes place at the M–O_suf and M–Cu_suf bonds, indicating that ionic and metallic bonding play a leading role in the interface between the metal layers and the CuO(111) substrate.

3.2 Adsorption energies of metal/CuO composites and deformation energy of CuO(111)

To study the stability of the metals adsorbed on the CuO(111), the adsorption energy of the M/CuO(111) composite and deformation energy of the substrate due to the adsorption of the metal layers were calculated and presented in Table 2. It is seen that the adsorption energies of the M/CuO(111) interfaces are −1.21, −1.89, −2.63, and −3.75 eV for Al, Mg, Ti, and Zr adlayers, respectively. The adsorption energy of the Ti/CuO(111) interface is twice more than that of the Al/CuO(111) one and 0.74 eV higher than that of the Mg/CuO(111) one. The Zr/CuO(111) interface was triple and twice more than the Al/CuO(111) and Mg/CuO(111) ones, respectively. The above energies indicate that the interaction between the metal adlayers and the substrate is strong and the interface has an ionic/metallic character, compared with the other metal/oxide systems.³⁸ The stability of the interface increases in the sequence of Al, Mg, Ti, and Zr. The Zr/CuO(111) composite presents the strongest adsorption energy. This large energy differences with other metal interfaces are mainly due to the O_sub atoms bonded to the Zr metals. The Ti–Cu_suf bond length is slight difference from the Al–Cu_suf and Mg–Cu_suf ones. The Ti–Cu_sub bond length is much smaller than other M–Cu_sub ones, especially the Zr–Cu_sub bond length. In addition, some Ti–Cu bond lengths of the Ti/CuO(111) interface are shorter than the Mg–Cu and Zr–Cu bond lengths and this results in high adsorption energy. This energy difference from the Zr/CuO system indicates that the metallic bond (Ti–Cu) is weaker than the ionic bond (Zr–O_sub). Therefore, it may be concluded that stable metallic atom adsorption occurs atop the surface O atom.

Table 2 Adsorption energies of M/CuO(111) composites and deformation energies of CuO(111) substrates in different interfaces

M	Eads (eV)	Edef (eV)
Al	−1.21	−0.06
Mg	−1.89	−0.37
Ti	−2.63	−0.58
Zr	−3.75	−1.05

---

The presence of metal layers strongly modifies the surface construction. Thus, the deformation energies of the modified CuO surface were calculated and listed in Table 2. It is found that the variation order of the deformation energy of the CuO substrate is in good agreement with that of the adsorption energy of the interface. The CuO substrate adsorbed with Al metal layers has the lowest deformation energy of 0.06 eV, indicating that it experiences the least deformation among the four interfaces. On the contrary, the substrate covered with Zr adlayers presents the most significant deformation. Such results are consistent with the above configuration analysis that the substrate with Zr adlayers appears to be the largest immigration outward and inward for the O_sub and O_suf atoms, respectively. Indeed, the interfaces with the least structural change are supposed to be most stable. As the CuO substrate with Al adlayers deforms the least, the Al layers adsorb on it most stably.

3.3 Electronic structure of metal/CuO(111) interfaces

To reveal the electronic pictures of the interfaces, total density of states (TDOS) and atom-projected partial DOS (PDOS) of the four interfaces are plotted in Fig. S1 of the ESI.† The PDOS profiles involve interfacial metal atoms (Al, Mg, Ti, and Zr) bonded to the interfacial O atoms, the metal (Al, Mg, Ti, and Zr) at the center of the absorbed metal layers (denoted as “bulk”), and interfacial O atoms at the on-top site, respectively.

It is seen in Fig. S1(a)† that the TDOS curves of the Al/CuO and Mg/CuO systems are notably different from those of the Ti/CuO and Zr/CuO. This is mostly because the d bands of transition metals Ti and Zr presents different characters with those of alkaline-earth metals Al and Mg. Despite all this, there are some subtle differences between the TDOS of Ti/CuO and Zr/CuO. Mostly this is since the Ti–Cu metallic bonding formed in the interface of the Ti/CuO system while the Zr–O_sub bond comes into being in the Zr/CuO interface.

Apparently, it is seen in Fig. S1(b)† that the PDOS shapes of the interfacial metal atoms are different from those of the atoms in bulk. This indicates that there are interactions occurred between the interfacial metal atoms and CuO. For the Ti and Zr atoms, the PDOSs at the interface are altered very distinctly from those of the bulk ones. There are the strong interactions between the Ti-3d/Zr-4d orbitals and the O-2p orbitals. Thus, there are significant charge transfers during the interface formation compared with the Al and Mg atoms in the bulks. In addition, the PDOS curves of the interfacial O atoms for the four interfaces are displayed in Fig. S1(c).† Obviously, the PDOS shapes of the interfacial O atoms appear to be distinctly different each other with little comparability. This is because different metal adlayers produce different effects on the interfacial O atoms.

To further investigate the intrinsic electronic character at the interface, Fig. 3 displays the electron density difference with isosurface values of 0.05 e Å⁻³ (yellow) and −0.05 e Å⁻³ (light blue) of the four interfaces, where the electron gain and loss are represented in yellow and light blue, respectively.

Fig. 3 Electron density difference plots of Ml/CuO(111) interfaces, where metal = Al, Mg, Ti and Zr, respectively, electron gain (yellow) and loss (light blue), and isosurface contour values between 0.05 e Å⁻³ (yellow) and −0.05 e Å⁻³ (light blue). This image was produced using Vesta software.³⁹

It is found that the electron density differences of the Zr/CuO(111) are completely different from those for the Al/CuO(111), Mg/CuO(111), and Ti/CuO(111) interfaces. It may be due to the strong interactions between Zr metal layers and O atoms. In addition, there are the interactions between the Ti metal layers and interfacial Cu atoms along with the strong interactions between the Ti and O atoms. This is consistent with the geometry structure analysis. There is a distinct region of electron gain and loss at the interface between the metal layers and CuO(111) substrate owing to the delocalized electrons of the metal layer and CuO surface. This suggests that electron activity mainly occurs at the interface but not at the substrate. Obviously, the electrons in the Al and Ti metal layers transfer from the Al and Ti atoms to Cu atoms upon equilibration, leading the metal layers to lose electrons toward the interfacial Cu atoms. Therefore, the interfaces are predominantly composed of ionic M–O_suf bond and metallic M–Cu bond.

4. Conclusions

DFT calculations has been performed to study the geometric and electronic structures and stability of high-energy metastable intermolecular composites M/CuO(111) (M = Al, Mg, Ti, or Zr). It is found that the interfaces are composed of the surface O and Cu atoms in CuO(111) and M atoms by the ionic M–O_suf and metallic M–Cu bonds. Structural relaxation primarily occurs in the M–O_suf and M–Cu bonds, indicating that the ionic and metallic bonding plays a major role in the interfaces. The interactions between the metal adlayers and substrate are strong and the interface has an ionic/metallic character. The Zr/CuO(111) composite presents the highest adsorption energy, while the Al/CuO(111) one has the lowest deformation energy. This indicates that the Al/CuO(111) composite is the most stable system. The delocalized electrons of the metal layers and CuO surface suggest that electron activity mainly occurs at the interface but not at the substrate.

Acknowledgements

This work was supported by A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.

References

1. C. Rossi, K. Zhang, D. Estève, P. Alphonse, P. Tailhades and C. Vahlas, J. Microelectromech. Syst., 2007, 16, 919–931.
2. K. Zhang, C. Rossi, G. A. A. Rodriguez, C. Tenailleau and P. Alphonse, Appl. Phys. Lett., 2007, 91, 113117.
3. D. G. Piercey and T. M. Klapötke, Cent. Eur. J. Energ. Mater., 2010, 7, 115–129.
4. J. C. Park, J. Kim, H. Kwon and H. Song, Adv. Mater., 2009, 21, 803–807.
5. J. T. Zhang, J. F. Liu, Q. Peng, X. Wang and Y. D. Li, Chem. Mater., 2006, 18, 867–871.
6. R. Shende, S. Subramanian, S. Hasan, S. Apperson, R. Thiruvengadathan, K. Gangopadhyay, S. Gangopadhyay, P. Redner, D. Kapoor, S. Nicolich and W. Balas, Propellants, Explos., Pyrotech., 2008, 33, 122–130.
7. X. Zhou, R. Shen, Y. Ye, P. Zhu, Y. Hu and L. Wu, J. Appl. Phys., 2011, 110, 094505.
8. X. Zhou, D. Xu, Q. Zhang, J. Lu and K. Zhang, ACS Appl. Mater. Interfaces, 2013, 5, 7641–7646.
9. P. Zhu, R. Shen, N. N. Fiadosenka, Y. Ye and Y. Hu, J. Appl. Phys., 2011, 109, 084523.
10. E. J. Mily, A. Oni, J. M. LeBeau, Y. Liu, H. J. Brown-Shaklee, J. F. Ihlefeld and J. P. Maria, Thin Solid Films, 2014, 562, 405–410.
11. C. Lanthony, M. Guiltat, J. M. Ducéré, A. Verdier, A. Hémeryck, M. Djafari-Rouhani, C. Rossi, Y. J. Chabal and A. Estève, ACS Appl. Mater. Interfaces, 2014, 111, 15086–15097.
12. J. Kwon, J. M. Ducéré, P. Alphonse, M. Bahrami, M. Petrantoni, J.-F. Veyan, C. Tenailleau, A. Estève, C. Rossi and Y. J. Chabal, ACS Appl. Mater. Interfaces, 2013, 5, 605–613.
13. C. Lanthony, J. M. Ducéré, A. Estève, C. Rossi and M. Djafari-Rouhani, Thin Solid Films, 2012, 520, 4768–4771.
14. F. Séverac, P. Alphonse, A. Estève, A. Bancaud and C. Rossi, Adv. Funct. Mater., 2012, 22, 323–329.
15. G. Jian, N. W. Piekiel and M. R. Zachariah, J. Phys. Chem. C, 2012, 116(51), 26881–26887.
16. L. Marín, C. E. Nanayakkara, J.-F. Veyan, B. Warot-Fonrose, S. Joulie, A. Estève, C. Tenailleau, Y. J. Chabal and C. Rossi, ACS Appl. Mater. Interfaces, 2015, 7(22), 11713–11718.
17. J. Hu, D. Li, J. G. Lu and R. Wu, J. Phys. Chem. C, 2010, 114, 17120–17126.
18. V. Oison, H. Ouadi, C. Lambert-Mauriat and M. Freyss, Surf. Sci., 2014, 622, 44–50.
19. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev. [Sect.] A, 1964, 136, B864.
20. W. Kohn and L. J. Sham, Phys. Rev. [Sect.] A, 1965, 140, A1133.
21. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115.
22. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
23. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
24. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
25. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
26. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
27. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
28. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
29. B. Hinnemann and E. A. Carter, J. Phys. Chem. C, 2007, 111, 7105–7126.
30. A. Jiang, N. Awasthi, A. Kolmogorov, W. Setyawan, A. Börjesson, K. Bolton, A. Harutyunyan and S. Curtarolo, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 205426.
31. S. Asbrink and L. J. Norrby, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 8–15.
32. F. Marabelli, G. B. Parravicini and F. Salghetti-Drioli, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 1433–1436.
33. D. Wu and Q. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235206–235212.
34. L. I. Johansson and J. Stöhr, Phys. Rev. Lett., 1979, 43(25), 1882.
35. A. O. Yazaydın, R. Q. Snurr, T. H. Park, K. Koh, J. Liu, M. D. LeVan, A. I. Benin, P. Jakubczak, M. Lanuza, D. B. Galloway, J. J. Low and R. R. Willis, J. Am. Chem. Soc., 2009, 131(51), 18198–18199.
36. L. Li, F. Meng, H. Tian, X. Hu, W. Zheng and C. Q. Sun, Phys. Chem. Chem. Phys., 2015, 17(15), 9867–9872.
37. Y. M. Wang, Y. S. Li and A. R. Mitchell, Surf. Sci., 1995, 342(1), 272–280.
38. K. Wong, Q. H. Zeng and A. B. Yu, J. Phys. Chem. C, 2011, 115, 4656–4663.
39. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra18326c

---