 Open Access Article
Open Access ArticleEssential aspects of the CFD software modelling of biomass gasification processes in downdraft reactors
ZiTeng Yuab,
ZiXing Wangab,
HuiXiong Zhongab and
KeKe Cheng *ab
*ab
aGuangdong Provincial Key Laboratory of Distributed Energy Systems, Dongguan University of Technology, Dongguan 523808, China. E-mail: chengkeke@dgut.edu.cn
bChina-Latin America Joint Laboratory for Clean Energy and Climate Change, School of Chemical Engineering and Energy Technology, Dongguan University of Technology, 523808, China
First published on 10th September 2024
Abstract
Mathematical modelling and simulation of gasification processes are increasingly used in the scientific field. This review explores the application of computational fluid dynamics (CFD) in modeling biomass gasification processes in downdraft gasifiers. It discusses the different types of gasification agents used, the composition of syngas, and key operational parameters influencing the process. The review then delves into the aspects of CFD modeling, focusing on the implementation of sub-models within ANSYS fluent software. The limitations of the existing literature are addressed, and strategies for enhancing downdraft gasifier performance are proposed to facilitate successful commercialization.
1. Introduction
Biomass refers to any organic material generated as forest residues or residual by-products of agricultural activities, including solid-state or pulp waste derived from pruning ornamental trees in urban environments, or remains from crop cleaning to prevent pests and forest fires.1,2 As agricultural production continues to expand, the volume of residual by-products also increases, often leading to environmental concerns.3 However, these wastes can be converted into thermal or heat energy through thermochemical processes such as direct combustion, pyrolysis, and gasification.4 In particular, gasification is a promising technique for converting biomass into clean energy.5,6 Among the different types of gasifiers, downdraft gasifiers are simple and economically designed, and their application in biomass gasification has become widespread.7The global scientific community continues to evaluate and offer possible solutions to the problems that affect the gasification process to expand the use of this technology in both developed and developing countries. The main challenges include understanding and predicting the parameters that provide insights into the functionality of the gasification process.8,9
Various methods are employed to predict the behavior and functionality of the gasification process, which can be concrete (direct measurements in pilot plants) or virtual (mathematical equations used to describe the physical or chemical properties of the process). By employing these methods, variables are analyzed and factors affecting the process are investigated. The method is selected based on the purpose of fuel. Mathematical modelling is essential for understanding and predicting possible changes or alterations during the gasification process.10 The advantage of mathematical modelling lies in avoiding the high costs of experimentation and enabling the study of different situations at varying levels of complexity solely through computational means.9
The use of mathematical modelling and simulation has increased as a means to study and predict changes in the parameters that affect the biomass gasification process.10,11 These include thermodynamic models and kinetic models. Thermodynamic models represent equilibrium via perfect mixing and infinite reaction time, offering flexibility as they are time-invariant and unaffected by dynamics. Kinetic models predict non-equilibrium product distribution, system changes, and residence times in chemical reactors.12 Computational fluid dynamics (CFD) modelling has shown particular promise, and commercial software programs such as ANSYS Fluent and OpenFOAM are widely utilized.13,14
OpenFOAM and ANSYS Fluent are used for chemical engineering fluid dynamics, including reactors. They offer rapid data generation, user-friendly interfaces, documentation, and simplified biomass gasification simulation.15 It is easier for researchers to use these software programs for simulating biomass gasification processes. A one-dimensional volume particle model is coupled with ANSYS Fluent's dense discrete phase model (DDPM) through user-defined functions to achieve a multi-scale modeling approach. It exhibits good consistency with experimental data within a feasible computational time frame and allows for in-depth analysis of processes inside the reactor. This enables tracking of individual reaction particles while resolving gradients within the particles.16
The review will meticulously examine the application of Computational Fluid Dynamics (CFD) in optimizing downdraft gasifiers for biomass gasification, encompassing peer-reviewed journal articles and conference papers published within the last decade. The primary objective is to systematically analyze the interplay between gasification agents, reactor types, and operational parameters on syngas composition, heating value, and gasification efficiency. Inclusion criteria for studies will be meticulously defined, prioritizing those employing CFD as a core analytical methodology and ensuring the availability of detailed data regarding model setup, parameters, and results. The analysis will follow a structured and systematic approach, focusing on key parameters and categorizing studies based on the CFD model employed.
2. Gasification processes
During biomass gasification, water content, temperature, lignocellulosic structure, and particle size are key factors that affect the efficiency of gasification and the composition of the syngas. When the water content in biomass increases from 20% to 40%, the gasification efficiency decreases by about 10%. Furthermore, an excessively high water content can lead to a reduction in the hydrogen content of the syngas, as water reacts with hydrocarbons to produce water vapor.1 Temperature also has a significant impact on the efficiency of gasification and the composition of the syngas. When the temperature rises from 700 °C to 900 °C, the gasification efficiency increases by about 20%, while the hydrogen content in the syngas decreases from 25% to 20%.3 The lignocellulosic structure refers to the pore structure within the biomass, and its size and distribution can affect the diffusion and transfer of gases, thereby influencing the efficiency of gasification and the composition of the syngas. The larger the lignocellulosic structure, the easier it is for gases to diffuse and transfer, which is conducive to improving gasification efficiency and the hydrogen content of the syngas.4 Particle size also has a significant impact on the efficiency of gasification and the composition of the syngas. When the particle size decreases from 1 mm to 0.5 mm, the gasification efficiency increases by about 20%, and the hydrogen content in the syngas also increases accordingly. Therefore, during the gasification process, appropriate operating parameters should be selected based on specific circumstances to enhance the gasification efficiency and the hydrogen content of the syngas.5Gasification is a process in which incomplete combustion of the fuel or, using different terminologies, partial oxidation, occurs due to the insufficiency of a gasification agent.17–19 The partial oxidation of the fuel provides energy for various processes that occur during gasification such as drying, devolatilization, and reduction. The gaseous products of devolatilization consist of CO, CO2, H2, CH4, H2O, steam, and light hydrocarbons.20,21 Sometimes, tars and char are also present. Tars, as organic byproducts, exist in the form of steam at the gasification temperature (above 400 °C) and are in a liquid state at ambient temperature, whereas at high temperatures, they can decompose and form light gases such as CO, CO2, and H2.2,22 Char is a solid residue that undergoes oxidation via heterogeneous reactions, producing CO and CO2 in proportions that depend on the operating temperature, gasifier, oxygen availability, and ash content of the biomass.
3. Classification of gasifiers
The study of the gasification process has spanned over two centuries, resulting in various gasifier configurations ranging from small-scale laboratory (pilot plants) to industrial scale. A comparative classification of the reactors can be made as shown in Fig. 1.23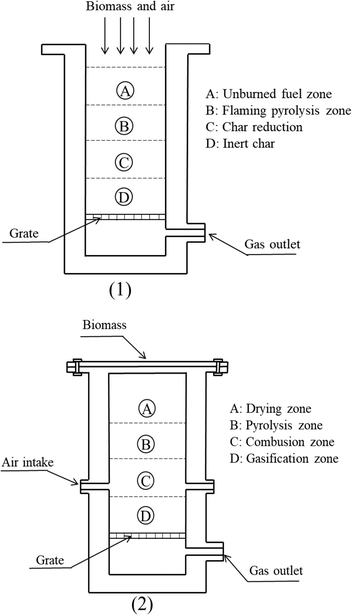 | ||
| Fig. 1 Different designs of downdraft gasifiers: a gasifier with open top (1) and a gasifier with closed top (2). | ||
While this review primarily focuses on downdraft gasifiers, it is crucial to acknowledge the existence and relevance of other gasifier types. A brief overview of these alternatives is provided below to contextualize downdraft gasifiers within the broader spectrum of gasification technologies.
All reactors differ in four main parameters: the medium (gasification agent), the pressure applied, the heat source, and the overall design. There are three design configurations, each with several subcategories. For the purposes of this current review, below we provide a brief comparative analysis of fluidized bed design and fixed bed design, focusing on downdraft and updraft reactor types.
3.1 Fluidized gasifiers
In fluidized bed gasifiers, air is introduced through a bed of pre-treated solid particles at a velocity enough to keep the particles in a suspended state and behave like a fluid.24 This velocity is known as the fluidization rate and is crucial for these types of gasifiers.25,26 The fundamental purpose of fluidized bed gasifier technology is to obtain syngas with a higher percentage of hydrogen, which is a product of the biomass gasification process.27 These gasifiers have a lower temperature at the exit of the process, leading to an increase in tar content because the reactor temperatures do not reach the level necessary for the tar to disintegrate into other chemical species.25,26,283.2 Entrained gasifiers
Entrained flow gasifiers use oxygen as the gasification agent, operating at temperatures around 1200–1500 °C. This enables the handling of a wider range of coal types and offers high efficiency.29,30 However, the high temperatures and use of microscopic fuel particles lead to increased energy consumption and material costs, limiting their applicability for biomass gasification.31–353.3 Updraft gasifiers
In updraft gasifiers, the gasification agent enters through the bottom of the bed and moves upwards, while the fuel or biomass moves from top to bottom.36 Similar to fluidized bed gasifiers, updraft gasifiers also have lower temperatures at the exit of the process, resulting in an increased tar content due to the same reasons mentioned earlier.37–413.4 Downdraft gasifiers
As shown in Fig. 1, downdraft gasifiers have two reactor design configurations: open and closed.42,43 The open design is widely used today. Biomass is added from the top, simultaneously drawing in primary air, ensuring no hot spots at the reactor inlet and reducing inefficiencies in the thermochemical process.A downdraft is formed by a straight cylinder of thermo-resistant material or an interior cylinder with a reduction called a throat or nozzle. The latter is widely used for the gasification of poly-dispersed materials such as small, low-density grain shells. The nozzle design is one of the most studied configurations for downdraft gasifiers.44 Air enters the throat area through several nozzles distributed radially in the center of the gasifier. These nozzles are the conduits for secondary air, where biomass oxidation begins and heat transfer increases the temperature in the reactor bed. Due to the heating of the bed, drying zones appear and devolatilization starts. The synthesis gas and biomass moved downward.45 In the absence of oxygen, gasification reactions occur at high temperatures, thus the tar concentration is low because temperatures reach the level at which tar disintegrates into other chemical species.46–48 The disadvantage of downdraft gasifiers is that the high temperature of the gases at the process outlet leads to heat loss, resulting in the formation of alkaline vapors and particles.49 Therefore, it is essential that the gas product of gasification be cleaned for future use.50,51
3.5 Gaps in the existing literature
While extensive research exists on various gasifier types, comprehensive reviews specifically focusing on downdraft gasifiers and their CFD modelling are limited. This review aims to fill this gap by providing a detailed analysis of downdraft gasifier design, operational parameters, syngas composition, and CFD modelling approaches. By consolidating existing knowledge and highlighting potential areas for further investigation, this review aims to contribute to the advancement of downdraft gasifier technology and its successful commercialization.4. Parameters of studies in gasification modelling
To address the question of key parameters in gasification modeling, this section focuses on factors that significantly influence simulation efficiency and accuracy. These parameters, as identified through a review of various studies, include moisture content, reactor temperature,52 equivalence ratio, and particle size.53 The moisture content impacts combustion, temperature distribution, and steam content. The reactor temperature influences reaction rates and syngas composition, affecting LHV. The equivalence ratio controls temperature and product yields, while the particle size affects gasification rates and temperature profiles. Optimizing these parameters enhances simulation reliability and gasifier performance.The integration of feedstock properties in biomass gasification models involves considerations of moisture content, particle size, and composition.54,55 The moisture content impacts combustion time and matrix temperature, affecting the reaction efficiency and steam content. The particle size affects the reaction kinetics and product distribution, with smaller particles enhancing H2 and CO production.52,56 Chemical compositions including elemental ratios influence gas formation.57 Thermodynamic and non-stoichiometric equilibrium models are used to incorporate these parameters.58 Thermodynamic models account for biomass type and composition but require significant computational resources, while non-stoichiometric models are simpler but have limitations.59,60 Overall, these parameter optimizations can enhance the gasification efficiency and economics.
Model validation and calibration in biomass gasification rely on a combination of experimental data, sensitivity analysis, and comparison with established models. Experimental validation involves comparing model predictions with experimental data to adjust parameters until the model accurately captures the process behavior.61 Sensitivity analysis identifies influential parameters, ensuring their accurate representation and assessing model robustness.23 Benchmarking with existing models and employing machine learning algorithms for pattern identification and predictive modeling further enhances reliability.62 Careful parameter selection, continuous refinement, and utilization of validated models are essential for maintaining model accuracy and reliability.
4.1 Moisture content of the feedstock
A direct relationship has been demonstrated between the moisture content in the biomass and the final composition of the gas obtained in the gasification simulation process.63 Amit Kumar Biswas et al.64 observed that an increase in the moisture content of the biomass leads to a prolonged combustion time of the biomass pellets and an increase in the temperature of the matrix. It is expected that the increase in the moisture content of the biomass will decrease the temperature value in the drying zone due to the relative heating of the feedstock upon entering the gasification zone. The moisture content greatly affects the reactor temperature, causing an increase in steam content, which favors other reactions that are less efficient in energy conversion.65,66Andrés Melgar et al.67 demonstrated in their study that when the ratio of air/fuel is higher, the moisture content of the biomass is lower. Higher efficiency of cold gas is obtained in the gasification process. Based on the variation in the preheating temperature of the feed gas and the steam/air ratio (S/A), Yueshi Wu et al.68 developed a 2D CFD model in ANSYS Fluent of a downdraft gasifier with an HTAG-type technology. The behavior of the temperature profile within the gasifier and the composition of the synthesis gas were analyzed. The authors demonstrate that with the increase in bed temperature, the residence time of the biomass decreases, causing an increase in combustible gases (H2 and CO) and a decrease in tars. This phenomenon does not occur with the decrease in temperature inside the reactor, which would lead to a decrease in the LVH of the gas and the appearance of condensed tars, which would be detrimental to the gasification process. C. Dejtrakulwong et al.69 conducted a parametric study focusing on the effects of the humidity of biomass and the air/biomass ratio on the height of the fundamental zone of a downdraft gasifier. The authors show an increase in the height of the pyrolysis zone and a decrease in the reduction zone with the decrease in moisture of the material to be gasified. For the air/biomass ratio, there is a decrease in the main areas of the downdraft gasifier when this ratio increases. Shweta Sharma et al.70 reported a decrease in the efficiency of the gasification process when the moisture content in the biomass is higher; this behavior is similar in the study.71 Vladimirs Kirsanovs et al.72 focused their study on a real downdraft gasification facility with a nominal capacity of 400 kW. The investigation shows that biomass moisture, fuel supply, and the ratio of secondary/primary air flows have a significant effect on the gasification process. The researchers established that the decrease in the moisture content of the fuel from 21.1 to 10.9% causes an increase in the efficiency of the hot gas by 17% and the decrease in fuel flow causes a decrease in the thermal capacity of the plant and the efficiency by more than 5.0%.
4.2 Effect of temperature on the gasification process
The reactor temperature significantly impacts the gasification process, influencing reaction kinetics, equilibrium, tar formation, and overall efficiency.73–76Studies have shown that increasing the temperature promotes endothermic reactions such as steam gasification and the Boudouard reaction, leading to higher CO and H2 production.77–79 This results in a decrease in CO2 and H2O concentrations and an increase in the lower heating value (LHV) of the syngas.78
This has been confirmed by studies in which biomass gasification with a steam/air mixture is evaluated as a gasification agent.70,80,81 Additionally, higher temperatures can reduce the tar content by promoting tar cracking and decomposition.20
4.3 Equivalence ratio (ER)
The equivalence ratio (ER), which compares the actual fuel-to-air ratio with the stoichiometric ratio, plays a critical role in the gasification process, affecting the reactor temperature, syngas composition, efficiency, and tar formation.82–84 An optimal ER is essential for achieving the highest lower heating value (LHV) and minimizing energy losses.23 Studies by Rukshan Jayathilake et al.85 and Pratik N. Sheth et al.86 highlight that while a higher ER can increase the temperature and promote complete combustion, it may also lead to increased tar production; conversely, a lower ER can result in incomplete combustion and reduced tar, but with a trade-off in LHV and efficiency. Junxi Jia et al.87 analyzed the effect of the equivalence ratio (ER), the biomass feed flow, and the steam/biomass ratio in a downdraft gasifier; it is demonstrated that a warming of the gasification zone increases the formation of combustible species and causes an increase in the LHV of the gas. Chao Gai et al.79 used air as a gasification agent in a downdraft gasifier to evaluate the operation parameters. The temperature profile of the reactor and the composition of the synthesis gas produced by the process are studied. The author evaluated an ER ranging between 0.18 and 0.41, demonstrating that the main characteristics of the gasifier are affected. The ER values between 0.28 and 0.32 result in an LHV, optimal with this value at 5.39 MJ N−1 m−3, and an increase in cold gas yield of 73.61%. However, ER values outside this range lead to a reduction in the previous parameters. The CH4/H2 ratio experiences little or almost zero ER variation. This is because the two species decrease in the same way, although the fraction of H2 is much larger in relation to the small variations of CH4.88,89Pratik N. Sheth et al.86 studied the impact of the variation in the ER parameter in a downdraft gasifier fueled with wood and using air as the gasification agent on the composition of the gas at the exit of the process. Their study reported that the trends in the growth and reduction of CO and H2 fractions were consistently opposite to those of N2 and CO2. The CO/CO2 and H2/CO2 ratios initially showed an increasing trend with the increase in ER within the range of 0.18–0.32 but decreased for higher ER values.90,91 Controlling the ER is therefore a balancing act to ensure the desired syngas quality and process performance.
4.4 Particle size
The particle size has a profound effect on gasification processes, influencing both reaction kinetics and product distribution. Smaller particle sizes expedite the reaction process by increasing the surface area available for reactions to occur, leading to faster conversion of biomass to syngas and a greater emphasis on the production of hydrogen (H2) and carbon monoxide (CO).92,93 Conversely, larger particle sizes lead to slower reaction rates, limiting the exposure of biomass to the reaction environment and resulting in lower syngas production.94 The size of the particles also dictates the distribution of the products in the syngas. Smaller particles, with their greater surface area, facilitate the endothermic steam gasification and Boudouard reactions, leading to higher H2 and CO yields. Larger particles, however, tend to favor the exothermic water–gas shift reaction, resulting in increased production of carbon dioxide (CO2) and water (H2O).93,95,964.5 Composition of the syngas obtained from different studies
The gasification process is a series of thermochemical transformations that convert biomass or solid organic materials into combustible gases under high-temperature conditions (800–1000 °C) and in the presence of gasification agents such as air, oxygen, and steam.97–100 Depending on the gasification agent and the origin of the biomass, various compositions and qualities of process gases can be obtained.101In the works of Z. A. Zainal et al.102 and P. P. Dutta et al.,103 the focus is on downdraft gasifiers where the gasification agent is air. Air as a gasification agent is the most widely implemented technology today because the gasification process is simple and economically feasible.104,105 V. M. Jaganathan et al.106 used an O2–CO2 mixture for the thermochemical conversion of three types of biomasses (agricultural waste, coconut shell, and wood pellets) to enhance the low heating value (LHV) of the syngas. In the study by Daniele Antolini et al.,107 a mixture of air and CO2 was used as the gasification agent. The injection of CO2 led to an increased consumption of coal, favoring the Boudouard reaction, resulting in a higher CO conversion compared to air alone. The study showed a 20–30% reduction in the rate of biomass consumption compared to air gasification alone.
The final composition of the gas obtained during the gasification process depends on multiple factors including the biomass and the gasifier, as well as the operational conditions (temperature, pressure, and gasification agent),108–110 as illustrated in Table 1.
| Composition (vol%) | |||||||
|---|---|---|---|---|---|---|---|
| Gasification agent | H2 | CO | CO2 | CH4 | N2 | HV (MJ m−3) | Reference |
| Air (downdraft) | 21.06 | 19.61 | 12.01 | 0.64 | 46.68 | 4.72 | 111 |
| Air (downdraft) | 7.12 | 17.56 | 13.74 | 1.01 | 60.57 | — | 112 |
| Air (downdraft) | 18.25 | 25.85 | 7.84 | 2.9 | 45.16 | — | 113 |
| Air (downdraft) | 15.62 | 15.62 | 14.37 | 1.95 | 52.42 | 15.45 | 114 |
| Air (updraft) | 11 | 24 | 9 | 3 | 53 | 5.5 | 115 |
| O2 (downdraft) | 32 | 48 | 15 | 2 | 3 | 10.4 | 116 |
| Air (BFB) | 14.1 | 18.7 | 14.7 | 3.5 | 47.7 | n.d. | 117 |
| Steam (CFB) | 34.2 | 27.2 | 22.7 | 11.1 | 4.8 | n.d. | 118 |
| Steam (BFB) | 52 | 23 | 18 | 7 | n.d. | n.d. | 26 |
| Air (BFBD) | 19.24 | 18.2 | 10.89 | 0.57 | 40.23 | 4.57 | 118 |
| Steam (CFB) | 43.6 | 33.2 | 11.7 | 11.5 | — | 1.3 | 119 |
| Air (BFB) | 5.0–16.3 | 9.9–22.4 | 9.0–19.4 | 2.2–6.2 | 41.6–61.6 | 3.7–8.4 | 120 |
| Steam (BFB) | 38–56 | 17–32 | 13–17 | 7–12 | 0 | 12.2–13.8 | 120 |
| Oxygen (open top) | 30–34 | 30–37 | 25–29 | 4–6 | — | 10–15 | 121 |
| Steam/CO2 (open top) | 24–50 | 30–45 | 10–19 | 5–12 | — | 12–20 | 121 |
| Oxy/steam (downdraft) | 45–51 | 13–25 | 15–20 | 1–4 | — | 7–10 | 122 |
All review articles report that the gas composition after conversion depends on the gasifier and the gasifying agent used in the process. As can be seen from Table 1, different gasifying agents result in a range of heating values (HV) for the obtained process gases. Using air as a gasifying agent is the most common method because it is economic and easy to operate. However, since air contains a large amount of nitrogen, it dilutes the combustible gases in the output gas, leading to a relatively low heating value of the syngas. Additionally, air gasification typically produces more CO and less H2. Steam gasification or CO2 gasification can produce syngas with higher heating values, especially at high temperatures. These methods can produce hydrogen-rich syngas because they promote the water–gas shift reaction and the methane reforming reaction. These methods are usually more complex and costly, but they are very attractive for producing high-heating-value gases or hydrogen for specific chemical reactions. Using oxygen as a gasifying agent can increase the heating value of the output gas and significantly increase the production of hydrogen. This is because oxygen gasification produces more CO and H2, thereby increasing the energy density of the syngas. However, using pure oxygen as a gasifying agent is costly and requires a more complex system to supply and operate the oxygen.
In summary, the choice of different gasifying agents has a significant impact on the effectiveness of biomass gasification, requiring a trade-off between cost, technical complexity, and the quality of the output gas.
4.6 Optimizing gasification efficiency
The optimization of gasification processes is significantly influenced by the interplay between temperature, particle size, and equivalence ratio. Higher temperatures accelerate reaction rates and shift reaction equilibria, promoting the formation of hydrogen (H2) and carbon monoxide (CO).79,123 Smaller particle sizes enhance the kinetics and favor H2 and CO production, while larger particles tend to favor CO2 and H2O formation.92,93 The equivalence ratio (ER) controls the balance of chemical reactions, influencing syngas composition, efficiency, and tar formation.85,86These interactions are complex and must be carefully managed to achieve optimal process performance. The ideal conditions depend on the specific biomass type and desired syngas product mix. By carefully controlling and optimizing these parameters, researchers can enhance the kinetics of the gasification process, tailor the product distribution to meet specific process requirements, and maximize the lower heating value (LHV) and efficiency of the syngas produced.85,86
In conclusion, the interactions between the temperature, particle size, and equivalence ratio are pivotal for gasification process optimization. These parameters must be carefully controlled and balanced to achieve the desired syngas composition, maximize LHV, and minimize tar formation.
5 Numerical modelling
Over the years, various types of numerical and non-numerical modelling have been developed, ranging from the simplest, such as zero-dimensional modelling, to the most complex, three-dimensional modelling.61,124–127 The models most commonly described in the scientific literature include thermodynamic equilibrium modelling, kinetic modelling, computational fluid dynamics (CFD) modelling, and artificial neural network (ANN) modelling.128–130 A good model provides assistance and identifies the sensitivity of gasification performance to variations in different operating and design parameters.131The mathematical description of the biomass gasification process is generally based on the laws of heat and mass transfer, energy laws, and the principle of momentum conservation. More complex models are employed to analyze the fluid dynamics and chemical reactions. The simplest models consider material and energy balances throughout the reactor to predict the composition of the gas produced, without taking into account chemical processes and reactions. These models include global mass and heat balances throughout the reactor and are referred to as equilibrium modelling.
Many researchers have analyzed the processes of mathematical modelling and simulation, which has made them faster and less expensive to perform. The modelling and simulation of the gasification process is a complex phenomenon, involving the transformation of organic matter based on its carbonaceous structure. The simulations achieved during the research provide invaluable information for understanding the physicochemical processes occurring within the reactor, thus facilitating future design, construction, and optimization of gasification equipment.
5.1 Thermodynamic equilibrium modelling
The Gibbs free energy minimization principle serves as the foundation of thermodynamic equilibrium modelling, often referred to as zero-dimensional modelling.132,133 When the gasifier achieves chemical equilibrium, its composition is deemed the most stable, at which point entropy increases and the Gibbs free energy is minimized. Thermodynamic equilibrium modelling can serve as a useful tool for predicting the possible composition of the syngas at the reactor outlet and for studying the effects of different process parameters on the gas obtained at the outlet of the gasifier. However, thermodynamic equilibrium modelling cannot assess the effects of fluid dynamic or geometric parameters, fluidization velocities of fluidized beds, or the height of the gasifier, among other design variables. There are two ways to establish chemical equilibrium: using equilibrium constants (stoichiometric methods) and by directly minimizing Gibbs free energy (non-stoichiometric methods).134,135The stoichiometric model requires clearly defined reaction mechanisms, where chemical reactions and the species involved in the process are incorporated. The main objective of this modelling is to evaluate the equilibrium constants of a set of reactions that can be associated with Gibbs free energy. It is necessary to establish the specifications of the chemical reactions and the species involved in the process. The non-stoichiometric model focuses on the direct minimization of Gibbs free energy in the system, without the need to propose possible reactions that could be carried out.
In equilibrium modelling, only the elementary composition of the biomass expressed in the form of separate chemical species is required, such as C, H, O, N, and S if the biomass contains it.136 This is why thermodynamic or thermochemical equilibrium modelling is particularly suitable for cases where all possible reactions that may occur in the gasification process are not required. It should be noted that researchers who describe these two models in detail use the Lagrange method as an optimization method to perform the minimization of Gibbs free energy.55,65 Other optimization methods could also be used to achieve the same goal. Conducting a comparative study of different methods of minimization, as well as their results, could be a topic for future research.
5.2 Kinetic modelling
Kinetic modelling can explore a wide range of factors that equilibrium models cannot. The models are founded on kinetic principles, which elucidate the chemical reactions occurring throughout the biomass gasification process, and they are indispensable for the development, evaluation, and enhancement of gasifiers.137 For instance, residence time, gasifier design, fuel feeding rate, and reactor hydraulics can all be predicted using these models. The kinetic model can also accurately describe the conversion mechanisms throughout the length of the gasifier.138 Kinetic mechanisms involve parameters such as the hydrodynamics of the reactor, the residence time of biomass particles, the length of the reactor, reaction rates, and the formation of chemical species.Equilibrium modelling calculates the maximum yield that can be obtained under equilibrium conditions, which may differ significantly from the actual yield achieved within the gasifier. Although these models are convenient choices for embedding in flowsheet calculations for system-wide analysis, their output reliability is lower. Kinetic modelling may be more suitable if a more precise model is required, as it requires knowledge of reactor hydrodynamics, energy, and mass balances to obtain the gas yield at a specific operating state.139
In summary, kinetic modelling includes not only reaction and transport dynamics but also a distribution and transformation model of biomass particles within the reactor, analyzing discrete phases in different gasification zones. These models provide a set of parameters for investigating the behavior of the biomass gasification process via simulation, although they require more programming and computational time for simulation.140 Many authors have conducted significant work aimed at analyzing kinetic modelling, as can be seen in studies.138,141–144 These studies address issues related to kinetic modelling and present different solutions to these arising issues.
5.3 CFD modelling
Kinetic models rely on detailed chemical reactions that are not dependent on the reactor geometry.47 The limitations of kinetic models are addressed through CFD modelling, which involves the combined solution of mass, momentum, energy, turbulence, and fluid dynamics of flow. It provides a better understanding of the interactions between different phases and reactions inside the gasifier. The results can then be used to optimize the operation of downdraft gasifiers, leading to the production of higher-value syngas. Meanwhile, the increasing popularity of downdraft gasifiers and the applicability of the gas obtained from the gasification process have prompted us to conduct this literature review, aiming to unify and explain the various methods, models, and sub-models used in CFD, and to provide a reliable research path for new researchers while guiding research in the commercial CFD software.In the literature review, it is observed that authors propose the use of different analytical models, methods, and forms. Maria Puig-Arnavat et al.145 conducted a review with the objective of comparing and analyzing various biomasses used in the gasification process. In their study, they mention gasification models proposed by different authors and briefly describe the properties of different types of gasifiers. The research does not mention CFD modelling but refers to Aspen Plus as a robust software program. It also analyzes different gasification agents and briefly introduces Artificial Neural Network (ANN) optimization processes.
Tigabwa Y. Ahmed et al.146 refer to mathematical modelling techniques that focus on the formation of chemical species, particularly hydrogen. For a better understanding, they categorize the models into two broad categories: mathematical modelling (equilibrium, kinetic modelling) and modelling and simulation (CFD). They do not refer to the so-called ‘black box testing software’ such as Aspen Plus or DWSIM as modelling or simulation tools. The research by Dipal Baruah et al.139 is entirely based on the biomass gasification process in fluidized bed-type gasifiers. Focusing on chemical and kinetic equilibrium modelling, they briefly mention CFD modelling and some techniques used in them. Similarly, ANN techniques are proposed without going into any depth. In the work of Tapas Kumar Patra et al.,140 various models of the downdraft-type gasification process were analyzed, including thermodynamic numerical modelling, balance modelling, kinetic, CFD, ANN, and Aspen Plus. Patra performed a critical analysis of the effects of some gasification process parameters and presented the advantages and disadvantages of each modelling technique. The article refers to many processes but does not analyze them in depth; it serves as an informative basis for what was achieved in research in 2015. M. La Villetta et al.23 presented a vision of different models, namely: thermodynamic, kinetic equilibrium, and Artificial Neural Network (ANN). The scope seems fairly restrictive as CFD modelling is not discussed, and other models mentioned are described very generally. The article studies some parameters that affect the gasification process and their influence on the composition of the gas obtained in the process. However, it does not propose any techniques such as ANN to optimize the gasification process. Jürgen Karl et al.147 in their work provided a layout and sizing of the so-called dual fluidized bed (DFB) gasifiers and studied the characteristics and operation of these types of gasifiers working with steam as a gasification agent. The article also reviews the interaction properties of the biomass and the bed, the efficiency of the gas obtained and its quality in the DFB gasifiers. However, this work does not mention CFD modelling or any optimization methods. The work of Ana Ramos et al.53 studied different modelling techniques of biomass gasification and co-gasification processes. The article is based on the dynamic modelling of fluids, kinetic, thermodynamic, and computational modelling. The review introduces the topic in general, without emphasizing ANN and only mentioning some of the programs that utilize the CFD methods without going into any specifics. Sahar Safarian et al.148 in their study investigated different gasification models, focusing on fluidized bed gasifiers. The study showcases a number of published articles on gasification process modelling. These articles are selected to serve the author's purpose, so the vast majority are models applied exclusively in fluidized bed gasifiers. The authors emphasize thermodynamic, kinetic, and kinetic/equilibrium modelling, stating that thermodynamic equilibrium modelling is the most widely used. Although a brief description of CFD and ANN modelling is provided, the study diminishes the importance of these modelling algorithms, despite the fact that their use has been increasing in the scientific community worldwide.
The study of biomass gasification attempts to explore alternative approaches to facilitate a deeper understanding of this thermochemical process. As biomass gasification research becomes increasingly complex, the computational methods involved have also become extremely intricate, with iterative processes consuming a significant amount of time. These programs employ computational fluid dynamics (CFD) modelling systems, typically denoted by the acronym CFD in English.149 CFD is a computationally intensive program used globally to achieve simulations and models that closely resemble the reality of a given process, thereby reducing the use of material resources and lowering the costs of new projects.150 Computational fluid dynamics has been utilized as a crucial design tool in various industrial sectors, and CFD techniques have demonstrated the capability to provide accurate predictions for certain chemical processes.151,152 Unlike previous models, CFD modelling offers a visual and more comprehensive representation of the biomass gasification process. It provides quantitative and qualitative solutions to the physical and chemical processes in biomass gasification plants; it allows for simulations using different operational parameters of a reactor in a more cost-effective manner.
Computational Fluid Dynamics (CFD) can be instrumental in the process modelling that takes place inside biomass reactors, including various types of downdraft gasifiers. It serves as an advanced tool that assists in the analysis and comprehension of the gasification process, providing temperature profiles and the potential formation of distinct chemical species, as well as parameter profiles specified by researchers in their solutions.149,153
This computational method is based on the numerical solution of the Navier–Stokes momentum equations and the transfer and conservation of mass. Some studies have been conducted on the numerical solution of flow equations for typical fluids, whether in differential or vectorial form.26,154,155 CFD modelling is based on simulating patterns (such as velocity profiles, temperature, pressure, chemical species, or flow variables) within a given geometry, which involves solving a set of equations that govern the modelling. This starts with the fragmentation of the geometry (control volume) into small geometric segments (volume or finite elements), creating a computational mesh where the variables of interest are solved.
Some guidelines for the proper use of solution-adaptive refinement and grid-independent are guided as follows:
• The surface mesh must be fine enough to adequately represent the important features of the geometry.
• The initial mesh should contain enough cells to capture the essential features of the flow field. Subsequent gradient adaptation can be used to sharpen the shock and establish a grid-independent solution.
• A reasonably well-converged solution should be obtained before you perform an adaptation. If you adapt to an incorrect solution, cells will be added in the wrong region of the flow. However, you must use careful judgment in deciding how well to converge the solution before adopting, because there is a trade-off between adapting too early to an unconverged solution and wasting time by continuing to iterate when the solution is not changing significantly. Note that this does not directly apply to dynamic adaptation, as here the solution is adapted either at every iteration or at every time step, depending on the solver being used.
• When performing gradient adaptation, you must select suitable variables. For some flows, the choice is clear. For instance, adapting to gradients of pressure is a good criterion for refining in the region of shock waves. In most incompressible flows, however, it makes little sense to refine pressure gradients. A more suitable parameter in an incompressible flow might be mean velocity gradients. If the flow feature of interest is a turbulent shear flow, it will be important to resolve the gradients of turbulent kinetic energy and turbulent energy dissipation, so these might be appropriate refinement variables. In reacting flows, the temperature or concentration (or mole or mass fraction) of reacting species might be appropriate.
• Poor adaptation practices can have adverse effects. One of the most common mistakes is to over-refine a particular region of the solution domain, causing very large gradients in cell volume. This can adversely affect the accuracy of the solution.
The discretization (in space and time) of the differential equations results in a system of algebraic equations; their numerical solution yields the unknowns of the problem in each element of the mesh, which are the distributions of the velocity and temperature components.149,153 This approach to solving the Navier–Stokes equations in either 1D, 2D, or 3D has been created with commercial software programs such as ANSYS Fluent, CFX, CFD2000, CFD, and Phoenics, mentioned in the course of this review. This software has been utilized in many of the latest research projects because it offers the option to simulate various configurations and process operations for this gasification. Table 2 presents a set of articles where different models are used according to the gasifier and other parameters that influence the choice of an appropriate modelling strategy.
| References | Software | Oxidizer | Type of gasifier | Type of feedstock | Studied parameters | Started models |
|---|---|---|---|---|---|---|
| Luc Gerun et al.156 | 2D axisymmetric CFD | Air/Steam | Downdraft | Wood chips | The nozzle surface area | Model RNG k-epsilon |
| Air injection velocity | Eddy dissipation concept | |||||
| Experimental number | ||||||
| A. Rogel-Ramírez157 | 2D CFD PHOENICS algorithm IPSA | Air | Downdraft | Rice husk | Air to feed | Conservation equations |
| Biomass to feed | Eulerian model/k-epsilon model | |||||
| Gas composition | Numerical/validated with bibliography | |||||
| Cleiton B. da Porciúncula et al.158 | ANSYS® CFX 11.0, CFD, 3D | Air | Downdraft | Wastes, leather industries | Syngas composition | Turbulence model k–w (frequency)) |
| Numerical | ||||||
| I. Janajreh et al.159 | ANSYS fluent, CFD | Air | Downdraft | Wood chips | The temperature along the gasifier equivalent ratio | Turbulence model standard k-epsilon |
| 2D axisymmetric | Composition of adiabatic and non-adiabatic outflow gases | The discrete solid particle phase solved in a Lagrange frame of reference (DPM) | ||||
| Experimental and numerical | ||||||
| Keran D. Patel et al.160 | Fluent 6.2.16 2D | Air | Downdraft | Lignite | Temperature flow pattern formation | Turbulence model standard k-epsilon |
| Turbulence and product gas composition | Eddy dissipation combustion model | |||||
| Probability density function (PDF) | ||||||
| Non-Premixed combustion model | ||||||
| Second-order discretization numerical | ||||||
| Xijia Lu et al.161 | ANSYS fluent | Oxygen | Entrained | Coal | Different radiations in a gasifier model | Focus Euler–Lagrange discrete |
| Transfer Radiation model (DTRM) | ||||||
| Radiation model, P-1, Rosseland | ||||||
| Surface-to-surface (S2S), and discrete | ||||||
| Ordinates (DO) turbulence model | ||||||
| Standard k-epsilon numerical | ||||||
| H. Liu162 | ANSYS fluent and programming language C, 2Dy3D | Air | Circulating fluidized bed | Biomass | Equivalence ratio | Turbulence model RNG k-epsilon |
| Char combustion distribution coefficient | Eulerian–Eulerian gas–solid drag model | |||||
| Gidaspow's model | ||||||
| Radiation model P-1 | ||||||
| Numerical | ||||||
| Rahul Gupta et al.163 | ANSYS fluent, 2D | Air | Downdraft | Sobabul wood | Airflow, the number of air intake points | Turbulence model standard k-epsilon |
| Radiation model P-1 | ||||||
| Discrete phase | ||||||
| Species transport | ||||||
| Experimental and numerical | ||||||
| Xiaoke Ku et al.164 | OpenFOAM (CFD-DEM)/3D | Steam | Fluidized bed | Pinewood | Steam/biomass ratio reactor temperature | Eulerian–Lagrange multi-phase model |
| Biomass retention time | Numerical | |||||
| Biomass injection in different positions | ||||||
| Pubet Meenaroch et al.165 | CFD fluent 2D axisymmetric | Air | Downdraft | Wood chips | Gasifier inlet airflow | Euler–Lagrange multiphase model |
| Syngas composition | Turbulence model standard k-epsilon | |||||
| Reactor temperature | Numerical | |||||
| M. anil et al.153 | ANSYS Fluent/2D | Air/steam | Bubbling fluidized bed | Sawdust | Equivalent ratio | Multi-phase model Eulerian–Eulerian |
| Steam/biomass ratio | Numerical | |||||
| Airflow | ||||||
| Steam temperature | ||||||
| Aytekin Gel et al.166 | MFIX/3D | Steam/oxygen | Bubbling FB | Coal | Coal flow | Multi-phase model Eulerian–Eulerian |
| Coal particle diameter | Experimental and numerical | |||||
| Steam/oxygen ratio | ||||||
| Hui Liu et al.167 | Barracuda reactor virtual/3D | Steam/oxygen | Dual fluidized-bed | Almond prunings | Reactor temperature | The gas phase is described by the large Eddy simulation (LES) |
| Steam/biomass ratio | MP-PIC (multiphase particle-in-cell) | |||||
| Combustion air supply | Experimental and numerical | |||||
| S. Rupesh et al.165 | ASPEN plus | Air/steam | R Gibbs- | Sawdust | Gasifier temperature | Non-stoichiometric quasi-steady state model |
| Effects of CaO addition | Equivalence ratio (ER) | Total Gibbs free energy of the system is minimum | ||||
| Steam/biomass ratio | Numerical | |||||
| Linbo Yan et al.168 | OpenFOAM/3D | Steam | Dual fluidized bed (DFB) | Biomass | Fluidization rate | MP-PIC |
| Biomass feed cup | DEM | |||||
| The diameter of biomass particles | Eulerian model | |||||
| Bed temperature | Numerical | |||||
| R. Esquivel et al.169 | ANSYS Fluent/3D | Air | Downdraft | Sawdust pellets | Inlet airflow to the gasifier | Multi-phase model Eulerian–Eulerian |
| Syngas chemical composition | Turbulence model standard k-epsilon | |||||
| Experimental and numerical | ||||||
| Chen Juhui et al.149 | ANSYS 16.0 with the self-programming code 2D | Steam/air | Internal circulating fluidized bed (ICFB) | Coal/Biomass | Circulation time | Euler multifluid model with the kinetic theory of granular mixing (KTGM) |
| Ratio of equivalences | Experimental and numerical | |||||
| Steam/biomass ratio | ||||||
| Biomass feed flow | ||||||
| Xiaoyan Gao et al.170 | ANSYS Fluent/2D | Air | Entrained flow | Rice husk | Gasification temperature particle diameter | Turbulence model standard k-epsilon |
| Air/CO2 | Equivalent ratio | Euler–Lagrange model | ||||
| CO2/biomass ratio | Eddy-dissipation | |||||
| Experimental and numerical | ||||||
| Mikael Risberg et al.171 | ANSYS CFX | Air | Cyclonic | Wood dust | Mass fuel flow | Euler–Lagrange model |
| Mass airflow | Turbulence model standard k-epsilon | |||||
| Equivalence ratio (ER) | Experimental and numerical | |||||
| Xiaoyan Gao et al.172 | ANSYS Fluent/2D | Air | Entrained flow | Coal | Turbulence | Euler–Lagrange model |
| Syngas composition | Turbulence model standard k-epsilon | |||||
| Product equivalent ratio | UDF | |||||
| Eddy dissipation | ||||||
| P-1 radiation model | ||||||
| Numerical | ||||||
| Tamer M. Ismail et al.89 | COMMENT-code/2D | Air | Fluidized bed | Coffee husks | Equivalent ratio | Eulerian multifluid model |
| The moisture content of biomass | Turbulence model standard k-epsilon | |||||
| Experimental and numerical | ||||||
| Phuet Prasertcharoensuk et al.20 | ANSYS Fluent/3D | Air | Downdraft | Wood | Throat diameter | Eulerian–Eulerian model |
| Throat diameter ratios gasifier area | Turbulence model standard k-epsilon | |||||
| Quantity positions air intake nozzles | Numerical | |||||
| Yueshi Wu et al.68 | ANSYS Fluent/2D | Steam/air | Downdraft | Wood pellets | Steam/air ratio | Eulerian–Eulerian model |
| The preheating temperature of the gasification agent | Model eddy dissipation | |||||
| Biomass flow | Turbulence model standard k-epsilon | |||||
| Inlet airflow | Numerical |
Simulation in commercial CFD solution software such as CFX Fluent, STAR-CD, STAR-CCM, OpenFOAM, and COMSOL MULTI FACE, among others, has been employed in numerous scientific research projects, both for dynamic modelling and for simulating various types of gasification processes now in practice. J. Ward et al.173 developed a model using ASPEN PLUS to maximize the yield of products obtained during pyrolysis, such as bio-oils, biochar, and syngas; their study utilized four types of biomass (green waste, pine chips, wood, and birch). The formation of chemical species in the syngas was analyzed based on the temperature, operating conditions, and biomass characteristics. The authors noted and demonstrated that crushed green waste is more efficient in producing bio-oil, as it has a higher cellulose content and lower moisture. Bhargav Manek et al.174 conducted research on the gasification of coal in an updraft gasifier, using a steam/air mixture as the gasification agent. ANSYS Fluent was used for the simulation and numerical modelling of the gasifier. In this work, the authors employed various parameters, such as the equivalence ratio (ER) ranging from 0.24 to 0.36. To simulate the coal gasification process, an Euler–Lagrange-type discrete phase approach was adopted. The software yielded temperature profiles along the reactor and syngas compositions that varied with the operating parameters proposed by the researcher. The authors stated that increasing the steam/air ratio promotes the formation of H2 in the gas produced by gasification. All results were compared with a real gasifier of the same type and parameters, showing consistency between the data obtained from numerical simulations and experimental simulations. The importance of validating numerical simulation results against experimentally obtained data is worth emphasizing. In this case, the authors validated their numerical simulation against a commercial plant used by the ceramics industry in Morbi (India). Keran D. Patel et al.160 utilized fluid dynamics in the Fluent solver to simulate the gasification process in a downdraft scheme. The authors used coal as the raw material and air as the gasification agent. This article constructs and meshes the control volume in GAMBIT; this software only allows for the construction, meshing, and marking of boundary conditions; the simulation was carried out by Fluent in this case. Keran D. Patel et al.160 evaluated various parameters to study the efficiency of the gasifier, the temperature profile along the reactor, the turbulence, and the formation of chemical species throughout the entire control volume. The authors compared the simulation results with those available in the literature. Thus, it can be seen that many authors successfully use the CFD software for their research, with some of the work reviewed in this article.175,176
Computational Fluid Dynamics (CFD) has been applied to the modelling of numerous biomass gasification processes, although all of these processes share a common feature: the Navier–Stokes equations, which describe the conservation of mass, energy, and momentum in all possible dimensions. According to the literature consulted, a large number of articles have authors who use commercial software for modelling to predict the composition of the syngas product of the biomass transformation process.177 Other studies focus on the impact of ER (equivalence ratio) on species formation and the temperature profile of the model. All of these studies are validated through models proposed by the researchers.
The study is based on the regulation and simulation of downdraft gasification, aiming to assess the possibility of using waste from the leather industry in Rio Grande do Sul, Brazil, to produce energy. The simulation is carried out in a commercial CFD simulation package within the CFX 11.0 software. The researchers simulated the four main zones of downdraft gasifiers (drying, devolatilization, reduction, and combustion), and the temperature profile within the gasifier. Christian Maier et al.178 in their article described a two-phase flow model within a fixed carbon bed gasifier. The comparison of the simulation results with the data shown in the literature yields a good approximation. Additionally, optimal operating parameters are predicted to achieve the highest efficiency.179
Rahul Gupta et al.163 used CFD to analyze the performance of a 10 kW downdraft gasifier. The model was simulated in ANSYS Fluent, using a transport model of species with volumetric reactions and particle surfaces to calculate the temperature of the syngas at the exit of the simulation and the mass fraction of each element that composes it.
Umesh Kumar et al.78 developed a two-dimensional multiphase numerical model (2D) to simulate the gasification process of rubberwood, specifically the discrete phase model (DPM), focusing on the Euler–Lagrange equations. The model was used to determine the relationship between the gas composition at the exit of the process and different equivalence ratio (ER) values. The ER values within the range of 0.35 to 0.6 were studied, which indicates that as the ER value increases, the temperature in the oxidation zone increases due to the increased concentration of O2 in the oxidation zone.
Pichet Ninduangdee et al.180 studied two models of a pressurized circulating fluidized bed carbon enhanced with CO2, to predict the composition of the syngas at the exit of the gasification process.154,181 These two simulation models were developed in commercial software ANSYS Fluent and CPFD Barracuda. Model generation and simulation provided an approximation of the process development and the composition of the gases at the exit, which were compared with an experimental plant. The authors verified that the temperature distribution obtained in the overall simulation in both programs was consistent with that shown experimentally, although in Fluent, the temperature and appearance of chemical species were better approximated compared to the CPFD model. It was also confirmed that enrichment with CO2 as a gasification agent could increase the concentration of CO per unit of fuel in the syngas and thus improve the efficiency of the process.
Rahul Gupta et al.163 presented an innovative model for the combustion of packed biomass bedding, considering an Euler–Granular model for the hydrodynamics of the multiphase flow of particle-gas and a thermally thin particle model. The new fixed-bed model has the advantage of considering the profiles of species and energy formation of the combustion bed close to reality and allows us to consider the physical and chemical properties of the fuel particles, as well as the influence of the primary air intake on the efficiency of the process. Ravi Kumar Rachamala et al.182 used ANSYS CFX 11.0 to analyze the temperature distribution throughout the gasifier chamber and analyze the airflow in the process. They adjust the nozzle angles in the reduction chamber from 0° to 30° with four nozzles in circles. A reduction in the airflow rate in the central region was observed when the angle was 0°, not so when the angle of the nozzle increased to 30°. The comparison of all cases in the article shows that the best design is a throttle nozzle with an angle of 30° and four inclined nozzles with the same angle, achieving almost complete gasification with maximum temperatures of 1483 K.
The validation and calibration of CFD models for biomass gasifiers involve comparing model predictions with experimental data, sensitivity analysis, benchmarking, mesh independence studies, and statistical analysis. These techniques ensure the model's accuracy by aligning predictions with physical observations, reducing errors, and enhancing predictive capabilities. Key references include Wang et al.183 for experimental validation, Bilbao et al.184 for sensitivity analysis, Kumar and Shankar185 for benchmarking, Yu et al.186 for mesh independence, and Pan et al.187 for statistical analysis.
The challenges in CFD modeling of biomass gasifiers involve complex reaction mechanisms, turbulent flow, heat and mass transfer, and biomass heterogeneity. Addressing these includes detailed reaction mechanisms, advanced turbulence models, enhanced heat and mass transfer models, and accounting for biomass heterogeneity. The validation of high-quality data is crucial. These challenges can be addressed through a multidisciplinary approach, combining expertise in chemical engineering, fluid dynamics, and computational methods.
6 Conclusion and outlook
This comprehensive review elucidated the pivotal role of Computational Fluid Dynamics (CFD) in modeling the complex process of biomass gasification within downdraft gasifiers. The study systematically analyzed the results of various investigations, categorizing them based on critical parameters such as gasification agents, reactor types, and operational conditions. This approach reveals the interplay between these factors and their impact on syngas composition, heating value, and gasification efficiency.The findings emphasize the versatility of CFD in predicting the performance of downdraft gasifiers under diverse operating scenarios. By simulating fluid dynamics, heat transfer, and chemical reactions, CFD models offer valuable insights into potential challenges such as tar/char formation and temperature distribution. This information is crucial for optimizing gasifier design, guiding parameter selection for maximum efficiency and environmental friendliness, and facilitating virtual testing to expedite product development.
Looking ahead, several avenues for future research beckon. Investigating the influence of various feedstocks on gasification efficiency and syngas composition remains essential. Exploring the integration of CFD with optimization techniques such as Artificial Neural Networks (ANN) could further enhance the prediction accuracy and design optimization. Additionally, studying the long-term behavior and durability of gasifiers under different operating conditions is vital for their successful commercialization and widespread adoption.
This review underscores the transformative potential of CFD in advancing the field of biomass gasification within downdraft gasifiers. The insights gained contribute to a deeper understanding of the complex processes involved and pave the way for the development of more efficient and sustainable gasification technologies. As research continues to refine CFD models and explore new optimization techniques, the full potential of biomass gasification as a viable energy source for a sustainable future draws nearer.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Author contributions
ZiTeng Yu, writing the original manuscript and data collation. ZiXing Wang, writing the original manuscript and data collation. HuiXiong Zhong, data collation; KeKe Cheng, supervision, investigation, conceptualisation, project management and funding acquisition.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the Guangdong Basic and Applied Basic Research Foundation (No. 2021B1515140041), and Guangdong Provincial Key Laboratory of Distributed Energy Systems (No. 2020B1212060075).Notes and references
- R. Hermawan, A. Suryosatyo, Y. T. Tosuli and H. Dafiqurrohman, Case Stud. Therm. Eng., 2024, 56, 104182 CrossRef.
- N. Yesilova, O. Tezer, A. Ongen and A. Ayol, Int. J. Hydrogen Energy, 2024, 76, 290–303 CrossRef CAS.
- Ö. Tezer, N. Karabağ, A. Öngen and A. Ayol, Int. J. Hydrogen Energy, 2023, 48(60), 22909–22920 CrossRef.
- B. I. Ali and D. G. Gunjo, Int. J. Thermofluids, 2024, 22, 100608 CrossRef CAS.
- Y. Zhang, A. Zhou, Z. Li, H. Zhang, Y. Xiong, R. Xiao, Z. Hu and X. Wang, J. Energy Inst., 2024, 114, 101596 CrossRef CAS.
- R. Aguado, A. Baccioli, A. Liponi and D. Vera, Energy Convers. Manage., 2023, 289, 117149 CrossRef CAS.
- S. Khan, I. Adeyemi, K. Moustakas and I. Janajreh, Environ. Res., 2024, 252, 118597 CrossRef CAS.
- C. Rodriguez Correa, T. Otto and A. Kruse, Biomass Bioenergy, 2017, 97, 53–64 CrossRef CAS.
- S. Ferreira, E. Monteiro, P. Brito and C. Vilarinho, Energies, 2019, 12(1), 160 CrossRef CAS.
- K. Rabea, S. Michailos, M. Akram, K. J. Hughes, D. Ingham and M. Pourkashanian, Energy Convers. Manage., 2022, 258, 115495 CrossRef CAS.
- K. W. Kuttin, H. Yu, M. Yang, L. Ding, X. Chen, G. Yu and F. Wang, Green Carbon, 2024, 2, 176–196 CrossRef.
- C. A. Díaz González, D. C. de Oliveira, D. M. Yepes, L. E. Pacheco and E. E. Silva, Energy Convers. Manage., 2023, 296, 117570 CrossRef.
- M. Hassan, I. Ahmad, M. Anwar, S. A. Muhammed Ali, Y. Subramanian and A. K. Azad, Mater. Today Proc., 2023 DOI:10.1016/j.matpr.2023.07.085.
- F. Patuzzi, D. Basso, S. Vakalis, D. Antolini, S. Piazzi, V. Benedetti, E. Cordioli and M. Baratieri, Energy, 2021, 223, 120039 CrossRef CAS.
- J. Pérez, D. Borge and J. Agudelo, Rev. Fac. Ing., Univ. Antioquia, 2010, 52(52), 95–107 Search PubMed.
- L. von Berg, A. Anca-Couce, C. Hochenauer and R. Scharler, Fuel, Part B, 2022, 324, 124677 CrossRef CAS.
- Q. Eri, W. Wu and X. Zhao, Energies, 2017, 10(12), 2163–2182 CrossRef.
- P. Prasertcharoensuk, D. A. Hernandez, S. J. Bull and A. N. Phan, Biomass Bioenergy, 2018, 116, 216–226 CrossRef CAS.
- B. I. Ali and D. G. Gunjo, Res. Eng., 2023, 20, 101642 CAS.
- U. Kumar and M. C. Paul, Chem. Eng. Sci., 2019, 195, 413–422 CrossRef CAS.
- M. La Villetta, M. Costa and N. Massarotti, Renewable Sustainable Energy Rev., 2017, 74, 71–88 CrossRef CAS.
- S. Du, J. Wang, Y. Yu and Q. Zhou, Renewable Energy, 2023, 202, 483–498 CrossRef CAS.
- P. Ninduangdee and V. I. Kuprianov, Bioresour. Technol., 2015, 182, 272–281 CrossRef CAS.
- N. Pichet and K. Vladimir, Appl. Energy, 2016, 176, 34–48 CrossRef.
- W. Fu, Y. Zhang, L. Cui, H. Liu and T. Maqsood, Bioresour. Technol., 2023, 369, 128378 CrossRef CAS.
- P. Ninduangdee and K. Vladimir, Biomass Bioenergy, 2018, 112, 73–84 CrossRef CAS.
- M. Dammann, M. Mancini, T. Kolb and R. Weber, Therm. Sci. Eng. Prog., 2023, 42, 101772 CrossRef.
- Q. Guo, R. Li, G. Yang, Y. Liu, Q. Deng and Z. He, Energy Rep., 2023, 9, 4298–4305 CrossRef.
- M. Haas, M. Dammann, S. Fleck and T. Kolb, Fuel, 2023, 334, 126572 CrossRef CAS.
- J. Gao, W. Su, X. Wang, X. Song, J. Wang, J. Yang and G. Yu, J. Mater. Res. Technol., 2023, 24, 8754–8765 CrossRef CAS.
- T. Xu, Y. Wu and S. Bhattacharya, Int. J. Min. Sci. Technol., 2021, 31(3), 473–481 CrossRef CAS.
- A. Y. Ilyushechkin, D. G. Roberts and D. J. Harris, Fuel Process. Technol., 2014, 118, 98–109 CrossRef CAS.
- N. Samani, R. Khalil, M. Seljeskog, J. Bakken, R. K. Thapa and M. S. Eikeland, Fuel, 2024, 362, 130713 CrossRef CAS.
- J. Qi, Y. Wang, M. Hu, P. Xu, H. Yuan and Y. Chen, Energy, 2023, 268, 126642 CrossRef CAS.
- M. Ismail T and M. A. El-Salam, Renewable Energy, 2015, 78, 484–497 CrossRef.
- A. Salah, L. Hanel, M. Beirow and G. Scheffknecht, Comput.-Aided Chem. Eng., 2016, 38, 19–24 CAS.
- N. Fernando and M. Narayana, Renewable Energy, 2016, 99, 698–710 CrossRef CAS.
- C. Diblasi, C. Branca, A. Galgano, D. Meier, I. Brodzinski and O. Malmros, Biomass Bioenergy, 2007, 31(11–12), 802–811 CAS.
- L. Ding, K. Yoshikawa, T. M. Ismail and M. Abd El-Salam, Energy Procedia, 2017, 142, 166–171 CrossRef.
- K. M. N. Ravi, B. K. Suresh and K. A. Venkata Vishnu, Int. J. Adv. Eng. Res. Develop., 2016, 3(1), 58–64 Search PubMed.
- J. D. Martínez, K. Mahkamov, R. V. Andrade and E. E. Silva Lora, Renewable Energy, 2012, 38(1), 1–9 CrossRef.
- X. Shang, J. Xie, J. Chen and Y. Gu, ACS Omega, 2024, 9(18), 20378–20387 CrossRef CAS PubMed.
- A. Zachl, M. Buchmayr, J. Gruber, A. Anca-Couce, R. Scharler and C. Hochenauer, Renewable Energy, 2024, 226, 120407 CrossRef CAS.
- A. Kumar, Fuel, 2024, 361, 130708 CAS.
- A. M. Salem and M. C. Paul, Biomass Bioenergy, 2023, 168, 106656 CrossRef CAS.
- D. Awasthi, A. Datta and N. Gakkhar, Mater. Today Proc., 2023 DOI:10.1016/j.matpr.2023.05.625.
- P. Kumar, P. M. V. Subbarao, L. D. Kala and V. K. Vijay, Chem. Eng. J. Adv., 2023, 13, 100431 CrossRef CAS.
- M. Siedlecki and W. de Jong, Biomass Bioenergy, 2011, 35, S40–S62 CrossRef CAS.
- P. J. Woolcock and R. C. Brown, Biomass Bioenergy, 2013, 52, 54–84 CrossRef CAS.
- R. Saini, S. M Mahajani, S. Deb Barma and D. Srinivas Rao, J. Cleaner Prod., 2024, 434, 139955 CrossRef CAS.
- A. Ramos, E. Monteiro and A. Rouboa, Renewable Sustainable Energy Rev., 2019, 110, 188–206 CrossRef CAS.
- H. Beohara, B. Gupta, V. K. Sethib and M. Pandeyb, Int. J. Therm. Technol., 2012, 2(1), 134–140 Search PubMed.
- N. Ramzan, A. Ashraf, S. Naveed and A. Malik, Biomass and Bioenergy, 2011, 35(9), 3962–3969 CrossRef CAS.
- D. Gündüz Han, K. Erdem and A. Midilli, Int. J. Hydrogen Energy, 2023, 48(99), 39315–39329 CrossRef.
- V. Shirke, S. V. Ranade and R. Bansal, Mater. Today: Proc., 2018, 5(11), 22983–22992 CAS.
- S. Tomasek, Á. Bárkányi, A. Egedy and N. Miskolczi, Chem. Eng. J. Adv., 2024, 17, 100586 CrossRef CAS.
- R. Mouselmani, A. Hachem, A. Alaaeddine, E. Métay and M. Lemaire, Org. Biomol. Chem., 2018, 16(35), 6600–6605 RSC.
- S. Hwa Lee, K. Young Kwon, B. Kil Choi and H. Deog Yoo, J. Electroanal. Chem., 2022, 924, 116828 CrossRef CAS.
- L. Moretti, F. Arpino, G. Cortellessa, S. Di Fraia, M. Di Palma and L. Vanoli, Energies, 2022, 15(1), 61 CrossRef CAS.
- A. Atikah Ahmad, N. Abdullah Zawawi, F. Hafiz Kasim, A. Inayat and A. Khasri, Renewable and Sustainable Energy Reviews, 2016, 53, 1333–1347A CrossRef.
- A. K. Biswas, M. Rudolfsson, M. Broström and K. Umeki, Appl. Energy, 2014, 119, 79–84 CrossRef.
- S. Rupesh, C. Muraleedharan and P. Arun, Resour., Conserv. Recycl., 2016, 2(2), 94–103 Search PubMed.
- E. Monteiro, T. M. Ismail, A. Ramos, M. Abd El-Salam, P. Brito and A. Rouboa, Energy, 2018, 142, 862–877 CrossRef CAS.
- A. Melgar, J. F. Pérez, H. Laget and A. Horillo, Energy Convers. Manage., 2007, 48(1), 59–67 CrossRef CAS.
- Y. Wu, Q. Zhang, W. Yang and W. Blasiak, Energy Fuels, 2013, 27(6), 3274–3282 CrossRef CAS.
- C. Dejtrakulwong and S. Patumsawad, Energy Procedia, 2014, 52, 142–149 CrossRef CAS.
- S. Sharma and P. N. Sheth, Energy Convers. Manage., 2016, 110, 307–318 CrossRef CAS.
- V. Kirsanovs, D. V. Blumberga, I. Rochas, C. Vigant and E. Vigants, Energy Procedia, 2017, 128, 332–338 CrossRef CAS.
- V. Kirsanovs, D. Blumberga, I. Veidenbergs, C. Rochas, E. Vigants and G. Vigants, Energy Procedia, 2017, 128, 332–338 CrossRef CAS.
- A. Okati, M. R. Khani, B. Shokri, E. Monteiro and A. Rouboa, J. Energy Inst., 2023, 107, 101173 CrossRef CAS.
- R. Mandal and T. Maity, J. Process Control, 2023, 129, 103031 CrossRef CAS.
- K. Erdem, D. Gündüz Han and A. Midilli, Int. J. Hydrogen Energy, 2024, 52, 1434–1444 CrossRef CAS.
- A. Pitkäoja and J. Ritvanen, Energy, 2022, 244, 123201 CrossRef.
- S. Rapagnà and A. Latif, Biomass Bioenergy, 1997, 12(4), 281–288 CrossRef.
- U. Kumar, A. M. Salem and M. C. Paul, Energy Procedia, 2017, 142, 822–828 CrossRef CAS.
- C. Gai and Y. Dong, Int. J. Hydrogen Energy, 2012, 37(6), 4935–4944 CrossRef CAS.
- S. Rapagnà and A. Latif, Biomass Bioenergy, 1997, 12(4), 281–288 CrossRef.
- S. N. Sazali, K. A. Al-attab and Z. A. Zainal, Energy, 2019, 186, 115901 CrossRef CAS.
- T. Sathish, S. Karthikeyan, R. sathyamurthy, A. Kumar, K. Rajaram, S. S. Kumar, A. A. Al-Kahtani, B. Pandit, M. Gupta, N. Senthilkumar, N. Malik and M. Ubaidullah, Int. J. Hydrogen Energy, 2024 DOI:10.1016/j.ijhydene.2024.01.323.
- S. Sarker and H. K. Nielsen, Energy Convers. Manage., 2015, 103, 801–813 CrossRef CAS.
- H. Liu, R. J. Cattolica and R. Seiser, Chem. Eng. Sci., 2017, 169, 235–245 CrossRef CAS.
- R. Jayathilake and S. Rudra, Energies, 2017, 10(8), 1232 CrossRef.
- P. N. Sheth and B. V. Babu, Int. J. Hydrogen Energy, 2010, 35(19), 10803–10810 CrossRef CAS.
- J. Jia, L. Xu, A. Abudula and B. Sun, Energy Convers. Manage., 2018, 155, 138–146 CrossRef CAS.
- N. D. Couto, V. B. Silva, E. Monteiro and A. Rouboa, Energy, 2015, 93, 864–873 CrossRef CAS.
- T. M. Ismail, M. Abd El-Salam, E. Monteiro and A. Rouboa, Appl. Therm. Eng., 2016, 106, 1391–1402 CrossRef.
- D. K. Singh and J. V. Tirkey, Int. J. Hydrogen Energy, 2021, 46(36), 18816–18831 CrossRef CAS.
- A. Okati, M. Reza Khani, B. Shokri, E. Monteiro and A. Rouboa, Fuel, 2023, 331, 125952 CrossRef CAS.
- H. Rezk, A. Inayat, M. A. Abdelkareem, A. G. Olabi and A. M. Nassef, Energy, 2022, 239, 122072 CrossRef CAS.
- M. Simone, F. Barontini, C. Nicolella and L. Tognotti, Bioresour. Technol., 2012, 116, 403–412 CrossRef CAS PubMed.
- D. Lu, K. Yoshikawa, T. M. Ismail and M. Abd El-Salam, Appl. Energy, 2018, 220, 70–86 CAS.
- V. R. Patel, D. S. Upadhyay and R. N. Patel, Energy, 2014, 78, 323–332 CrossRef CAS.
- S. J. Yoon, Y.-I. Son, Y.-K. Kim and J.-G. Lee, Renewable Energy, 2012, 42, 163–167 CrossRef CAS.
- S. Hashem Samadi, B. Ghobadian, M. Nosrati and M. Rezaei, Fuel, 2023, 333, 126249 CrossRef CAS.
- Ö. Tezer, N. Karabağ, A. Öngen and A. Ayol, Sustain. Energy Technol. Assess., 2023, 56, 103042 Search PubMed.
- A. Singh, A. M. Shivapuji and S. Dasappa, Appl. Therm. Eng., 2023, 234, 121247 CrossRef CAS.
- M. HajiHashemi, S. Mazhkoo, H. Dadfar, E. Livani, A. Naseri Varnosefaderani, O. Pourali, S. Najafi Nobar and A. Dutta, Energy, 2023, 276, 127506 CrossRef CAS.
- R. Raj, J. V. Tirkey, D. K. Singh and P. Jena, J. Energy Inst., 2023, 109, 101271 CrossRef CAS.
- Z. A. Zainal, R. Ali, C. H. Lean and K. N. Seetharamu, Energy Convers. Manage., 2001, 42(12), 1499–1515 CrossRef CAS.
- P. P. Dutta, V. Pandey, A. R. Das, S. Sen and D. C. Baruah, Energy Procedia, 2014, 54, 21–34 CrossRef CAS.
- P. Milčák, M. Baláš, M. Lisý, H. Lisá, P. Kracík and J. Lachman, Fuel Process. Technol., 2024, 258, 108091 CrossRef.
- M. Cortazar, L. Santamaria, G. Lopez, J. Alvarez, L. Zhang, R. Wang, X. Bi and M. Olazar, Energy Convers. Manage., 2023, 276, 116496 CrossRef CAS.
- V. M. Jaganathan and S. Varunkumar, Fuel, 2019, 244, 545–558 CrossRef CAS.
- D. Antolini, S. S. Ail, F. Patuzzi, M. Grigiante and M. Baratieri, Fuel, 2019, 253, 1473–1481 CrossRef CAS.
- J. Makwana, A. D. Dhass, P. V. Ramana, D. Sapariya and D. Patel, Int. J. Thermofluids, 2023, 20, 100492 CrossRef CAS.
- K. Rabea, S. Michailos, K. J. Hughes, D. Ingham and M. Pourkashanian, Energy Convers. Manage., 2023, 298, 117812 CrossRef CAS.
- C. Freda, E. Catizzone, A. Villone and G. Cornacchia, Res. Eng., 2024, 21, 101763 CAS.
- Z. Zainal, R. Ali, C. Lean and K. Seetharamu, Energy Convers. Manage., 2001, 42(12), 1499–1515 CrossRef CAS.
- M. A. Masmoudi, K. Halouani and M. Sahraoui, Energy Convers. Manage., 2017, 144, 34–52 CrossRef CAS.
- O. Yucel and M. A. Hastaoglu, Fuel Process. Technol., 2016, 144, 145–154 CrossRef CAS.
- K. Arun, M. Venkata Ramanan and S. Sai Ganesh, Energy Fuels, 2016, 30(9), 7435–7442 CrossRef CAS.
- A. Bridgwater, Fuel, 1995, 74(5), 631–653 CrossRef CAS.
- H. Olgun, S. Ozdogan and G. Yinesor, Biomass Bioenergy, 2011, 35(1), 572–580 CrossRef CAS.
- S. Vakalis and K. Moustakas, Appl. Energy, 2019, 242, 526–533 CrossRef CAS.
- K. T. Wu and R. Y. Chein, Energy Procedia, 2015, 75, 214–219 CrossRef CAS.
- S. Rapagnà, N. Jand, A. Kiennemann and P. U. Foscolo, Biomass Bioenergy, 2000, 19(3), 187–197 CrossRef.
- J. Gil, J. Corella, M. a. P. Aznar and M. A. Caballero, Biomass Bioenergy, 1999, 17(5), 389–403 CrossRef CAS.
- D. Prando, S. Shivananda Ail, D. Chiaramonti, M. Baratieri and S. Dasappa, Fuel, 2016, 181, 566–572 CrossRef.
- K. N. Dhanavath, K. Shah, S. K. Bhargava, S. Bankupalli and R. Parthasarathy, J. Environ. Chem. Eng., 2018, 6(2), 3061–3069 CrossRef CAS.
- A. V. Bridgwater, Fuel, 1995, 74(5), 631–653 CrossRef CAS.
- A. Hashemisohi, L. Wang and A. Shahbazi, Chem. Eng. Res. Des., 2024, 206, 1–11 CrossRef CAS.
- M. Y. Arshad, H. Jaffer, M. W. Tahir, A. Mehmood and A. Saeed, J. Taiwan Inst. Chem. Eng., 2024, 156, 105365 CrossRef CAS.
- H. Zuo, K. Zeng, D. Zhong, J. Li, H. Xu, Y. Lu, Y. Yu, H. Yang and H. Chen, Fuel, 2024, 367, 131174 CrossRef CAS.
- F. Njuguna, H. Ndiritu, B. Gathitu, M. Hawi and J. Munyalo, Bioresour. Technol. Rep., 2023, 22, 101477 CrossRef CAS.
- Y. Liu, D. Bi, M. Yin, K. Zhang, H. Liu and S. Liu, Therm. Sci. Eng. Prog., 2024, 50, 102584 CrossRef CAS.
- O. Yucel and E. S. Aydin, J. Indian Chem. Soc., 2023, 100(1), 100854 CrossRef CAS.
- K. W. Kuttin, A. Leghari, H. Yu, Z. Xia, L. Ding and G. Yu, Chem. Eng. Sci., 2024, 287, 119716 CrossRef CAS.
- H. O. Kargbo, J. Zhang and A. N. Phan, Int. J. Hydrogen Energy, 2023, 48(29), 10812–10828 CrossRef CAS.
- M. Costa, V. Rocco, C. Caputo, D. Cirillo, G. Di Blasio, M. La Villetta, G. Martoriello and R. Tuccillo, Appl. Therm. Eng., 2019, 160, 114083 CrossRef.
- M. Mohamadi-Baghmolaei, P. Zahedizadeh, M. Khajeh, S. Zendehboudi and N. M. C. Saady, Energy Convers. Manage., 2024, 307, 118302 CrossRef CAS.
- J. Brito, F. Pinto, A. Ferreira, M. A. Soria and L. M. Madeira, Fuel Process. Technol., 2023, 250, 107859 CrossRef CAS.
- Y. Zhao, J. Yao, G. Chen, J. Liu, Z. Cheng, L. Wang, W. Yi and S. Xu, Energy Convers. Manage., 2023, 295, 117623 CrossRef CAS.
- S. Yao, Y. Zhang, J. Xia, T. Xie, Z. Zhang, H. Li and J. Hu, Case Stud. Therm. Eng., 2023, 52, 103680 CrossRef.
- A. De Padova, E. Giglio and M. Santarelli, Renewable Energy, 2024, 223, 120071 CrossRef CAS.
- J. Yu and J. D. Smith, Chem. Eng. Process., 2018, 125, 214–226 CAS.
- D. Baruah and D. C. Baruah, Renewable Sustainable Energy Rev., 2014, 39, 806–815 CrossRef CAS.
- T. K. Patra and P. N. Sheth, Renewable Sustainable Energy Rev., 2015, 50, 583–593 CrossRef CAS.
- A. M. Salem and M. C. Paul, Biomass Bioenergy, 2018, 109, 172–181 CrossRef CAS.
- L. Yan, Y. Cao and B. He, Chem. Eng. J., 2018, 331, 435–442 CrossRef CAS.
- A. Saravanakumar, M. J. Hagge, T. M. Haridasan and K. M. Bryden, Biomass Bioenergy, 2011, 35(10), 4248–4260 CrossRef CAS.
- I. G. Donskoy, A. V. Keiko, A. N. Kozlov, V. A. Shamansky and D. A. Svishchev, Renew. Bioresour., 2016, 4(1), 1–4 CrossRef.
- M. Puig-Arnavat, J. C. Bruno and A. Coronas, Renewable Sustainable Energy Rev., 2010, 14(9), 2841–2851 CrossRef CAS.
- T. Y. Ahmed, M. M. Ahmad, S. Yusup, A. Inayat and Z. Khan, Renewable Sustainable Energy Rev., 2012, 16(4), 2304–2315 CrossRef CAS.
- J. Karl and T. Pröll, Renewable Sustainable Energy Rev., 2018, 98, 64–78 CrossRef CAS.
- S. Safarian, R. Unnpórsson and C. Richter, Renewable Sustainable Energy Rev., 2019, 110, 378–391 CrossRef CAS.
- J. Chen, W. Yin, S. Wang, G. Yu, J. Li, T. Hu and F. Lin, Energy Convers. Manage., 2017, 148, 506–516 CrossRef CAS.
- L. von Berg, A. Anca-Couce, C. Hochenauer and R. Scharler, Energy Convers. Manage., 2023, 286, 117070 CrossRef CAS.
- J. Chen, S. Zhong, D. Li, C. Zhao, C. Han, G. Yu and M. Song, Int. J. Hydrogen Energy, 2022, 47(53), 22328–22339 CrossRef CAS.
- M. Yang, J. Zhang, S. Zhong, T. Li, T. Løvås, H. Fatehi and X.-S. Bai, Combust. Flame, 2022, 236, 111744 CrossRef CAS.
- M. Anil, R. S, M. C and A. P, Energy Procedia, 2016, 90, 154–162 CrossRef CAS.
- L. P. R. Pala, Q. Wang, G. Kolb and V. Hessel, Renewable Energy, 2017, 101, 484–492 CrossRef CAS.
- S. Kraft, F. Kirnbauer and H. Hofbauer, Appl. Energy, 2017, 190, 408–420 CrossRef CAS.
- L. Gerun, M. Paraschiv, R. Vîjeu, J. Bellettre, M. Tazerout, B. Gøbel and U. Henriksen, Fuel, 2008, 87(7), 1383–1393 CrossRef CAS.
- A. Rogel-Ramírez, Ing., Invest. Tecnol., 2008, 9, 329–338 Search PubMed.
- C. B. da Porciúncula, N. R. Marcilio, M. Godinho and A. R. Secchi, in Computer Aided Chemical Engineering, ed. R. M. de Brito Alves, C. A. O. do Nascimento and E. C. Biscaia, Elsevier, 2009, vol. 27, pp. 1071–1076 Search PubMed.
- I. Janajreh and M. Al Shrah, Energy Convers. Manage., 2013, 65, 783–792 CrossRef CAS.
- K. D. Patel, N. K. Shah and R. N. Patel, Procedia Eng., 2013, 51, 764–769 CrossRef CAS.
- X. Lu and T. Wang, Int. J. Heat Mass Transfer, 2013, 67, 377–392 CrossRef CAS.
- H. Liu, Waterloo, 2014 Search PubMed.
- R. Gupta, P. Jain and S. Vyas, Int. J. Curr. Eng. Technol., 2017, 7, 4 Search PubMed.
- X. Ku, T. Li and T. Løvås, Chem. Eng. Sci., 2015, 122, 270–283 CrossRef CAS.
- P. Meenaroch, S. Kerdsuwan and K. Laohalidanond, Energy Procedia, 2015, 79, 278–283 CrossRef CAS.
- A. Gel, M. Shahnam, J. Musser, A. K. Subramaniyan and J.-F. Dietiker, Ind. Eng. Chem. Res., 2016, 55(48), 12477–12490 CrossRef CAS.
- H. Liu, R. J. Cattolica and R. Seiser, Int. J. Hydrogen Energy, 2016, 41(28), 11974–11989 CrossRef CAS.
- S. Rupesh, C. Muraleedharan and P. Arun, Resour.-Effic. Technol., 2016, 2(2), 94–103 Search PubMed.
- L. Yan, C. J. Lim, G. Yue, B. He and J. R. Grace, Bioresour. Technol., 2016, 221, 625–635 CrossRef CAS PubMed.
- R. Esquivel, P. C. Treto and K. S. Ramírez, Comput. Eng., 2018, 20, 16–26 Search PubMed.
- X. Gao, F. Xu, F. Bao, C. Tu, Y. Zhang, Y. Wang, Y. Yang and B. Li, Renewable Energy, 2019, 139, 611–620 CrossRef CAS.
- X. Gao, Y. Zhang, B. Li and X. Yu, Energy Convers. Manage., 2016, 108, 120–131 CrossRef CAS.
- J. Ward, M. G. Rasul and M. M. K. Bhuiya, Procedia Eng., 2014, 90, 669–674 CrossRef CAS.
- B. Manek, M. S. Javia, A. Harichandan and H. Ramani, Therm. Sci. Eng. Prog., 2019, 9, 11–20 CrossRef.
- N. Abani and A. F. Ghoniem, Fuel, 2013, 104, 664–680 CrossRef CAS.
- A. Chaurasia, Energy, 2016, 116, 1065–1076 CrossRef CAS.
- C. Maier, C. Jordan, M. Harasek, C. Feilmayr and C. Thaler, Chem. Eng. Transac., 2012, 29, 925–930 Search PubMed.
- M. Risberg, P. Carlsson and R. Gebart, Appl. Therm. Eng., 2015, 90, 694–702 CrossRef CAS.
- M. K. Cohce, I. Dincer and M. A. Rosen, Int. J. Hydrogen Energy, 2010, 35(10), 4970–4980 CrossRef CAS.
- P. Ninduangdee and V. I. Kuprianov, Biomass Bioenergy, 2018, 112, 73–84 CrossRef CAS.
- D. Vera, B. de Mena, F. Jurado and G. Schories, Appl. Therm. Eng., 2013, 51(1–2), 119–129 CrossRef CAS.
- R. K. Rachamala, M. Baba, K. Kumar and A. Vishnu, Int. J. Adv. Eng. Res. Dev., 2016, 3, 3–134 Search PubMed.
- S. I. Serdyukov, M. I. Kniazeva, I. A. Sizova, Y. V. Zubavichus, P. V. Dorovatovskii and A. L. Maximov, Mol. Catal., 2021, 502, 111357 CrossRef CAS.
- I. Wysocka, J. Karczewski, A. Gołąbiewska, M. Łapiński, B. M. Cieślik, M. Maciejewski, B. Kościelska and A. Rogala, Int. J. Hydrogen Energy, 2023, 48(29), 10922–10940 CrossRef CAS.
- H. Pei, G. Liu, R. Guo, N. Liu and Z. Mo, Int. J. Hydrogen Energy, 2022, 47(83), 35227–35240 CrossRef CAS.
- Z. Wang, N. Ze, S. Jun, L. Peng, N. Yan, Z. Wei and W. Xian, Fuel Process. Technol., 2019, 185, 31–38 CrossRef.
- J. Bi, Z. Hao, C. Di, G. Peng, L. Xing and G. Aggidis, Energy Convers. Manage., 2018, 165, 856–865 Search PubMed.
- A. Kumar and P. Shankar, Renewable Sustainable Energy Rev., 2017, 76, 1378–1390 Search PubMed.
- X. Yu, C. Xi, T. Kienpin, E. Marwa and A. Rizwan, Renewable Energy, 2016, 95, 423–433 Search PubMed.
- W. Pan, L. Ming, Z. Xu, Y. Kai, M. Yue and Y. Jun, Energy Convers. Manage., 2015, 89, 832–839 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |
