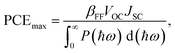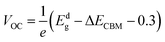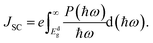DOI:
10.1039/D2TC05268G
(Paper)
J. Mater. Chem. C, 2023,
11, 3875-3884
Two-dimensional borocarbonitrides for photocatalysis and photovoltaics†
Received
10th December 2022
, Accepted 15th February 2023
First published on 8th March 2023
Abstract
We have designed two-dimensional borocarbonitrides (poly-butadiene-cyclooctatetraene framework BC2N) with hexagonal unit cells, which are stable according to the cohesive energy, phonon dispersion, ab initio molecular dynamics, and elastic modulus results. They are n-type semiconductors with strain-tunable direct band gaps (1.45–2.20 eV), an ultrahigh electron mobility (5.2 × 104 cm2 V−1 s−1 for β-BC2N), and strong absorption (an absorption coefficient of up to 105 cm−1). The intrinsic electric field due to the Janus geometry of α-BC2N reduces the recombination of photo-generated carriers. The band edge positions of α-BC2N and β-BC2N are suitable for photocatalytic hydrogen production, achieving high solar-to-hydrogen efficiencies of 17% and 12%, respectively, in excess of the typical target value of 10% for industrial application. Both γ-BC2N and δ-BC2N can be used as electron donors in type-II heterostructures with two-dimensional transition metal dichalcogenides, and the power conversion efficiency of a solar cell based on these heterostructures can be as high as 21%, approaching the performance of perovskite-based solar cells.
1. Introduction
Increasingly serious environmental pollution, climate abnormalities, and growing energy shortage call for a transition from the current fossil-fuel economy to a low-carbon (or even zero-carbon) economy1 with a large share of green energy resources such as wind, solar, and hydrogen.2 Being one of the most promising resources, great scientific efforts have been directed toward the development of environmentally friendly and efficient materials for converting solar energy.3 Two-dimensional (2D) materials have emerged as outstanding candidates in this endeavor.4,5
Photocatalytic water splitting aims at the production of hydrogen and oxygen. The solar-to-hydrogen (STH) efficiency of a photocatalyst is determined jointly from the efficiency of light harvesting and separation of the photogenerated carriers. For many photocatalysts the STH efficiency falls short of the aspired 10%6 due to low absorbance and carrier recombination. 2D materials, on the other hand, can provide strong absorption of solar radiation and can generate high electrical currents beyond the reach of bulk materials.7 In addition, their atomic thickness is suitable for photocatalysis, because the distance that the photogenerated carriers have to overcome to participate in chemical reactions (on the surface) is much shorter than in bulk materials. Due to efficient light harvesting and carrier utilization, high STH efficiencies are reported for 2D materials, for example, 10.0% and 6.7% for the ferroelectric and paraelectric phases of AgBiP2Se6, respectively.8 The 2D Janus materials B2P6, Pd4S3Se3, Pd4S3Te3, and Pd4Se3Te3 even achieve STH efficiencies of 28.2–38.6%.9,10
Conversion of solar to electrical energy is another efficient technology for solar energy harvesting. The power conversion efficiency (PCE) achieved by state-of-the-art silicon solar cells is as high as ∼30% and that of perovskite solar cells is as high as ∼26%.11 Excitonic thin-film solar cells based on 2D van der Waals heterostructures hold the promise of high efficiency due to high carrier mobility and strong absorption of visible light.12,13 Examples include MoS2/p-Si (PCE = 5.23%),14 graphene/GaAs (PCE = 18.5%),15 and CdS/GeSe (PCE = 1.48%)16 solar cells. Theoretical studies show PCEs as high as 20.1% in δ-CS/MoTe217 and 20% in 2D fullerene/CBN18 solar cells.
Borocarbonitrides, recently added members of the family of 2D materials, are of interest for application in a variety of cutting-edge technologies due to appealing sizes of the provided band gaps.19–21 Based on the first-principles calculations, we therefore designed new 2D borocarbonitrides, namely, poly-butadiene-cyclooctatetraene framework BC2N (PBCF-BC2N), employing elemental mutation of poly-butadiene-cyclooctatetraene framework-graphene (PBCF-graphene)22 and then systematically investigated their stability, electronic structure, and optical properties. Excellent stability is inferred from the obtained cohesive energies, phonon dispersions, and elastic moduli as well as from ab initio molecular dynamics simulations. The materials are found to be direct band gap semiconductors with band edge positions suitable for photocatalytic water splitting. We also study the application potential of heterostructures formed from PBCF-BC2N and transition metal dichalcogenides.
2. Methods
First-principles calculations are performed using the plane-wave Vienna ab initio simulation package with projector-augmented wave pseudopotentials.23 The Perdew–Burke–Ernzerhof (PBE) functional is used for both the structure optimization and calculation of the material properties. The Heyd–Scuseria–Ernzerhof (HSE06) functional with a mixing parameter of 0.25 and a screening parameter of 0.2 Å−1 for the Hartree–Fock exchange is adopted to rectify the band gap sizes and band edge positions, because both GW24 and self-interaction-corrected25 calculations are computationally much too expensive. The optical absorption spectrum is calculated by means of the random phase approximation method. The plane-wave cutoff energy is set to 500 eV and 9 × 9 × 1 Monkhorst–Pack meshes are utilized for Brillouin zone integrations. Vacuum slabs of 25 Å thickness are applied to generate 2D models. A total energy convergence of 1 × 10−8 eV per atom and an atomic force convergence of 0.001 eV Å−1 are achieved. The phonon spectra are calculated using density functional perturbation theory (Phonopy26 and Vienna ab initio simulation package) and a 3 × 3 × 1 supercell. Ab initio molecular dynamics simulations at 1000 K are carried out for 10 ps (time step 1 fs) using a 3 × 3 × 1 supercell and a canonical ensemble.27
3. Results and discussion
3.1 Structure and stability
Starting from the structure of PBCF-graphene,22 we design four ternary structures of PBCF-BC2N by replacing half of the C–C pairs with B–N pairs, see the optimized structures in Fig. 1 and structural details in Table 1. In each case, the primitive hexagonal unit cell contains six B, twelve C, and six N atoms. It turns out that α-BC2N, β-BC2N, γ-BC2N, and δ-BC2N have space groups P6mm (no. 183), P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (no. 164), P
m1 (no. 164), P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) 2m (no. 189), and P
2m (no. 189), and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1m (no. 162), respectively, with optimized lattice constants of 6.99, 7.05, 7.14, and 7.13 Å. The orthorhombic lattice constants are 6.99 Å (armchair direction) and 12.11 Å (zigzag direction) for α-BC2N, 7.05 Å and 12.21 Å for β-BC2N, 7.14 Å and 12.37 Å for γ-BC2N, and 7.13 Å and 12.35 Å for δ-BC2N. The sandwich-like structures are 2.47 to 2.53 Å thick. The top and bottom layers of α-BC2N and β-BC2N are connected by B–N bonds while those of γ-BC2N and δ-BC2N are connected by C
1m (no. 162), respectively, with optimized lattice constants of 6.99, 7.05, 7.14, and 7.13 Å. The orthorhombic lattice constants are 6.99 Å (armchair direction) and 12.11 Å (zigzag direction) for α-BC2N, 7.05 Å and 12.21 Å for β-BC2N, 7.14 Å and 12.37 Å for γ-BC2N, and 7.13 Å and 12.35 Å for δ-BC2N. The sandwich-like structures are 2.47 to 2.53 Å thick. The top and bottom layers of α-BC2N and β-BC2N are connected by B–N bonds while those of γ-BC2N and δ-BC2N are connected by C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds. α-BC2N realizes a pronounced Janus geometry. In each case, the hexagonal unit cell comprises six C–C, six B–N, twelve C–B, and twelve C–N bonds. The C
C bonds. α-BC2N realizes a pronounced Janus geometry. In each case, the hexagonal unit cell comprises six C–C, six B–N, twelve C–B, and twelve C–N bonds. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths of 1.36 to 1.39 Å are slightly shorter than those in graphene (1.42 Å), whereas the B–N bond lengths of 1.44 to 1.46 Å closely resemble the value for h-BN (1.45 Å). The relatively short C
C bond lengths of 1.36 to 1.39 Å are slightly shorter than those in graphene (1.42 Å), whereas the B–N bond lengths of 1.44 to 1.46 Å closely resemble the value for h-BN (1.45 Å). The relatively short C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and B–N bond lengths represent strong covalent bonds. The C–B and C–N bond lengths range from 1.53 to 1.60 Å and from 1.45 to 1.48 Å, respectively.
C and B–N bond lengths represent strong covalent bonds. The C–B and C–N bond lengths range from 1.53 to 1.60 Å and from 1.45 to 1.48 Å, respectively.
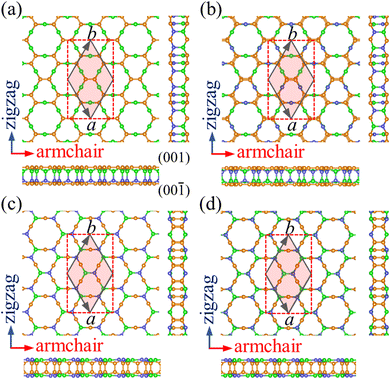 |
| | Fig. 1 Top and side views of the atomic structures of (a) α-BC2N, (b) β-BC2N, (c) γ-BC2N, and (d) δ-BC2N. The primitive hexagonal unit cell is shown by gray solid lines and the orthorhombic unit cell is shown by red dashed lines. The orange, green, and blue spheres represent C, B, and N atoms, respectively. | |
Table 1 Space groups, lattice constants (a), thickness (h), bond lengths (lC−N, lC−B, and lB−N), cohesive energy (Ecoh), and band gaps (EPBEg and EHSE06g)
|
|
Space group |
a (Å) |
h (Å) |
l
C–C (Å) |
l
C–N (Å) |
l
C–B (Å) |
l
B–N (Å) |
E
coh (eV per atom) |
E
PBEg (eV) |
E
HSE06g (eV) |
| α-BC2N |
P6mm |
6.99 |
2.53 |
1.36/1.39 |
1.48 |
1.53 |
1.46 |
6.25 |
0.75 |
1.97 |
| β-BC2N |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 m1 |
7.05 |
2.51 |
1.37 |
1.45 |
1.59 |
1.44 |
6.31 |
1.10 |
2.20 |
| γ-BC2N |
P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) 2m 2m |
7.14 |
2.53 |
1.36 |
1.46 |
1.60 |
1.44 |
6.33 |
0.46 |
1.45 |
| δ-BC2N |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1m 1m |
7.13 |
2.47 |
1.36 |
1.46 |
1.59 |
1.44 |
6.31 |
0.66 |
1.68 |
To analyze the chemical bonding in PBCF-BC2N, we calculate the electron localization function, as plotted in Fig. 2. Localized electrons between the atoms represent covalent C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, B–N, C–B, and C–N bonds. The obtained Bader charges agree with the electronegativities of the involved atoms: for α-BC2N the C and B atoms on the (001) side show values of +1.29 and −1.96 e, respectively, while the C and N atoms on the (00
C, B–N, C–B, and C–N bonds. The obtained Bader charges agree with the electronegativities of the involved atoms: for α-BC2N the C and B atoms on the (001) side show values of +1.29 and −1.96 e, respectively, while the C and N atoms on the (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) side show values of −0.64 and +1.31 e. For β-BC2N, γ-BC2N, and δ-BC2N, respectively, we obtain Bader charges of −1.90, −1.94, and −1.96 e for the B atoms, +0.25, +0.28, and +0.28 e for the C atoms, and +1.40, +1.38, and +1.40 e for the N atoms. Hence, the chemical bonding in PBCF-BC2N is governed by strongly polarized covalent bonds.
) side show values of −0.64 and +1.31 e. For β-BC2N, γ-BC2N, and δ-BC2N, respectively, we obtain Bader charges of −1.90, −1.94, and −1.96 e for the B atoms, +0.25, +0.28, and +0.28 e for the C atoms, and +1.40, +1.38, and +1.40 e for the N atoms. Hence, the chemical bonding in PBCF-BC2N is governed by strongly polarized covalent bonds.
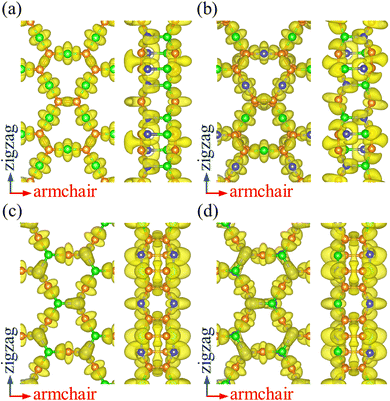 |
| | Fig. 2 Electron localization function (isosurface value 0.8) of (a) α-BC2N, (b) β-BC2N, (c) γ-BC2N, and (d) δ-BC2N. | |
The cohesive energy per atom, Ecoh = [xE(B) + yE(C) + zE(N) − xE(BxCyNz)]/(x + y + z), where E(B), E(C), E(N), and E(BxCyNz) are the total energies of a B atom, a C atom, a N atom, and a unit cell of PBCF-BC2N, respectively, follows the trend γ-BC2N (6.33 eV) > β-BC2N (6.31 eV) = δ-BC2N (6.31 eV) > α-BC2N (6.25 eV). It is lower than in the cases of graphene (7.85 eV) and h-BN (7.07 eV) but higher than in the cases of (experimentally existing) N-graphdiyne (6.02 eV),28B-graphdiyne (5.85 eV),29 and g-C3N4 (5.71 eV),30 demonstrating pronounced stability. The obtained phonon spectra and densities of states in Fig. 3 demonstrate dynamical stability. The maximal phonon frequencies turn out to be 46.6, 44.4, 45.2, and 44.9 THz for α-BC2N, β-BC2N, γ-BC2N, and δ-BC2N, respectively. The high-frequency phonons are due to the presence of sp2-hybridized C atoms, whereas the B and N atoms contribute below 40 THz. Our ab initio molecular dynamics simulations, see Fig. 3 for the potential energy as a function of the time and the final atomic structure, demonstrate the absence of bond breaking.
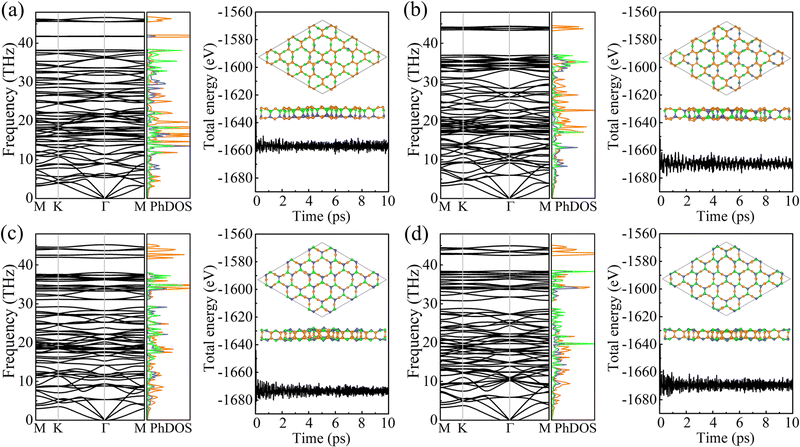 |
| | Fig. 3 Phonon spectra and densities of states (left; colors correspond to the atomic species) as well as results of ab initio molecular dynamics simulations (right; at 1000 K) of (a) α-BC2N, (b) β-BC2N, (c) γ-BC2N, and (d) δ-BC2N. | |
The mechanical properties of PBCF-BC2N are investigated by calculating the in-plane elastic constants, Young's modulus, Poisson's ratio, and the strain–stress relationship. The hexagonal lattice results in isotropic in-plane elasticity and the elastic energy accumulated under strain εij can be expressed as
| | 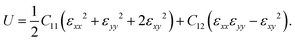 | (1) |
Perfect parabolic dependencies under uniaxial and biaxial strain (Fig. S1, ESI†) demonstrate reliability of the employed calculation method. Fulfilling the relations C11 = C22 and 2C44 = C11 − C12 we obtain the elastic constant C11, C12, and C44 values of 236, 100, and 68 N m−1 for α-BC2N; 230, 84, and 73 N m−1 for β-BC2N; 237, 73, and 82 N m−1 for γ-BC2N; and 223, 62 and 80 N m−1 for δ-BC2N, respectively. Therefore, the Born criteria (C44 > 0 and C11C22 − C122 > 0)31 of mechanical stability are satisfied. The in-plane Young's modulus Y = (C112 − C122)/C11 and Poisson's ratio v = C12/C11 amount to 194 N m−1 and 0.42 for α-BC2N; 199 N m−1 and 0.37 for β-BC2N; 215 N m−1 and 0.31 for γ-BC2N; and 206 N m−1 and 0.28 for δ-BC2N. The Young's modulus is thus lower than that in graphene (344 N m−1)32 but much higher than those in MoS2 (123 N m−1)33 and black phosphorene (83 N m−1),34 indicating mechanical robustness.
Strain–stress curves under biaxial strain are shown in Fig. 4(a). When the strain increases, the stress is found to increase first linearly and afterwards nonlinearly. The fracture strength and strain turn out to be 23.6 N m−1 and 16% for α-BC2N; 18.7 N m−1 and 18.5% for β-BC2N; 18.1 N m−1 and 16.5% for γ-BC2N; and 15.6 N m−1 and 13% for δ-BC2N. In contrast to α-BC2N, β-BC2N, and γ-BC2N, we find for δ-BC2N, a sudden drop in stress under high strain (between 13.5% and 14%). Comparison of the electron localization functions of δ-BC2N under 13.5% and 14% strain in Fig. 4(b) and (c) points to the strengthening of the inter-layer B–N bonds at the cost of intra-layer bonds, resulting in structural collapse. The calculated phonon spectra of α-BC2N, β-BC2N, γ-BC2N, and δ-BC2N (Fig. S2, ESI†), on the other hand, show no imaginary frequencies under 8%, 18%, 16%, and 12% strain, respectively (while showing imaginary frequencies under 8.5%, 18.5%, 16.5%, and 12.5% strain), which correspond to fracture strengths of 18.3 N m−1, 18.7 N m−1, 18.1 N m−1, and 15.5 N m−1, respectively.
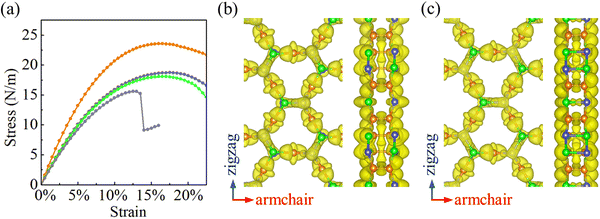 |
| | Fig. 4 (a) Strain–stress curves under biaxial strain (orange = α-BC2N; blue = β-BC2N, green = γ-BC2N, and gray = δ-BC2N). Electron localization function (isosurface value = 0.8) of δ-BC2N under (b) 13.5% and (c) 14% biaxial strain. | |
3.2 Electronic properties
Fig. 5 shows the electronic band structures and partial densities of states of PBCF-BC2N obtained using the PBE and HSE06 functionals. In each case we find a direct band gap with the conduction band minimum (CBM) and valence band maximum (VBM) located at the center of the Brillouin zone (Γ point). The size of the band gap of α-BC2N, β-BC2N, γ-BC2N, and δ-BC2N is found to be 1.97 (0.84), 2.20 (1.13), 1.45 (0.54), and 1.68 (0.70) eV using the PBE (HSE06) functional, respectively. The CBM of α-BC2N (β-BC2N) is dominated by the C (B) atoms and the VBM is dominated by the B (N) and C atoms. The CBM of both γ-BC2N and δ-BC2N is dominated by B atoms (with contributions of the N atoms) and the VBM by the C atoms.
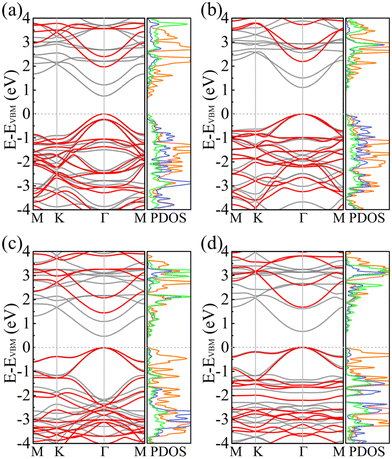 |
| | Fig. 5 Electronic band structures (black = PBE and red = HSE06) and partial densities of states (PBE; in units of 1/eV; orange = C; green = B; blue = N) of (a) α-BC2N, (b) β-BC2N, (c) γ-BC2N, and (d) δ-BC2N. | |
For the HSE06 functional, the effect of biaxial strain on the size of the band gap is shown in Fig. 6(a) (see Fig. S3, ESI† for the electronic band structures). With the exception of α-BC2N, the strain tunes the size of the band gap effectively. For the PBE functional, the carrier effective mass is obtained by fitting the electronic band structure at the respective band edge as m* = ℏ2/(∂2E/∂k2)−1; see the results in Fig. 6(b) and (c). The electron (hole) effective masses of PBCF-BC2N turn out to be isotropic with values of 0.37 (0.49), 0.44 (0.80), 0.47 (0.77), and 0.60 (1.04) m0 for α-BC2N, β-BC2N, γ-BC2N, and δ-BC2N in the absence of strain, respectively. The electron effective masses increase slowly under strain, while the hole effective masses show a more complex behavior.
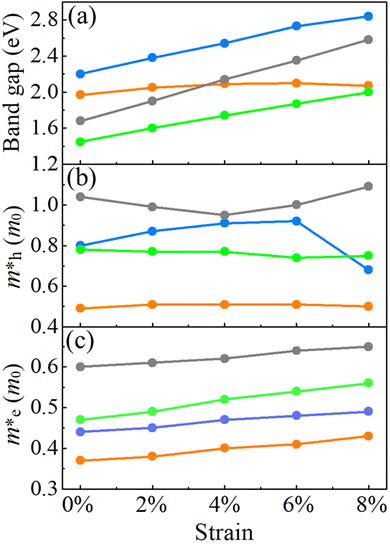 |
| | Fig. 6 (a) Band gaps, (b) hole effective masses and (c) electron effective masses of PBCF-BC2N under biaxial strain (orange = α-BC2N; blue = β-BC2N, green = γ-BC2N, and gray = δ-BC2N). | |
The carrier mobility is calculated using the Bardeen–Shockley deformation potential theory as
| | 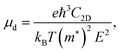 | (2) |
where
C2D denotes the in-plane elastic constant and
E denotes the (direction-dependent) deformation potential constant. The results should be understood as upper limits, since the carrier mobility tends to be overestimated. The band edge positions under strain along the armchair and zigzag directions are shown in
Fig. 7.
Table 2 summarizes the obtained in-plane elastic constants, deformation potential constants, and carrier mobilities at 300 K. We find virtually no anisotropy for electron mobilities and only a minor anisotropy for hole mobilities. All the materials show significantly larger electron mobilities than hole mobilities, where the particularly high electron mobility of β-BC
2N is a consequence of a small deformational potential constant. The hole mobilities of α-BC
2N and β-BC
2N exceed those of 2D MoS
2 (armchair direction: 2.0 × 10
2 cm
2 V
−1 s
−1 and zigzag direction: 1.5 × 10
2 cm
2 V
−1 s
−1)
35 by more than a factor of two and all the electron mobilities exceed those of 2D MoS
2 (armchair direction: 7.2 × 10
1 cm
2 V
−1 s
−1 and zigzag direction: 6.2 × 10
1 cm
2 V
−1 s
−1 in the)
36 by about two orders of magnitude, resembling few-layer black phosphorus.
36 The electron mobility of β-BC
2N is even comparable to that of 2D Ca
3Sn
2S
7 (6.7 × 10
4 cm
2 V
−1 s
−1),
37 suggesting its great potential for application in nano-electronic devices.
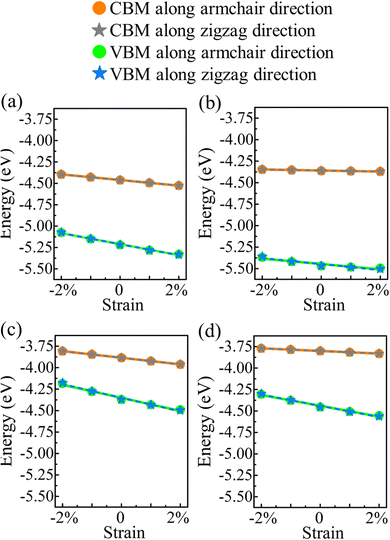 |
| | Fig. 7 Valence and conduction band edges of (a) α-BC2N, (b) β-BC2N, (c) γ-BC2N, and (d) δ-BC2N under biaxial strain. | |
Table 2 Carrier effective mass (m*), in-plane elastic constants (C2D), deformation potential constants (Earmchair and Ezigzag), and carrier mobilities at 300 K (μarmchair and μzigzag)
|
|
Carrier type |
m* (m0) |
C
2D (N m−1) |
E
armchair (eV) |
E
zigzag (eV) |
μ
armchair (cm2 V−1 s−1) |
μ
zigzag (cm2 V−1 s−1) |
| α-BC2N |
Electron |
0.37 |
236 |
3.28 |
3.29 |
4.8 × 103 |
4.8 × 103 |
| β-BC2N |
0.44 |
230 |
0.82 |
0.83 |
5.2 × 104 |
5.2 × 104 |
| γ-BC2N |
0.47 |
237 |
3.86 |
3.86 |
2.1 × 103 |
2.1 × 103 |
| δ-BC2N |
0.60 |
223 |
1.54 |
1.54 |
7.8 × 103 |
7.8 × 103 |
| α-BC2N |
Hole |
0.49 |
236 |
6.39 |
6.51 |
7.2 × 102 |
6.9 × 102 |
| β-BC2N |
0.80 |
230 |
5.02 |
5.21 |
4.2 × 102 |
3.9 × 102 |
| γ-BC2N |
0.78 |
237 |
7.62 |
7.93 |
2.1 × 102 |
1.9 × 102 |
| δ-BC2N |
1.04 |
223 |
6.28 |
6.57 |
1.5 × 102 |
1.4 × 102 |
3.3 Photocatalytic properties
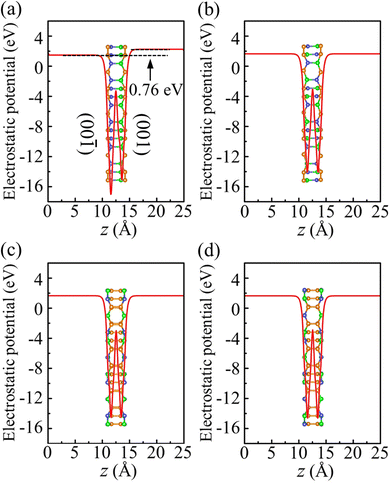
To investigate the photocatalytic potential for water splitting, we determined the positions of the band edges with respect to the vacuum level using the HSE06 functional. One of the fundamental requirements of a photocatalytic semiconductor is band edges (CBM and VBM) enclosing the redox potentials of water, i.e., the CBM must exceed the reduction potential of H+/H2 (−4.44 eV at pH = 0 and −4.03 eV at pH = 7) and the VBM must not exceed the oxidation potential of O2/H2O (−5.67 eV at pH = 0 and −5.26 eV at pH = 7).38 To determine the positions of the band edges, we have shown the electrostatic potential in Fig. 8. Due to its Janus geometry, the value is different for the two sides of α-BC2N (specifically: 0.76 eV higher for the (001) side than the (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) side).
) side).
 |
| | Fig. 8 Electrostatic potential of (a) α-BC2N, (b) β-BC2N, (c) γ-BC2N, and (d) δ-BC2N. | |
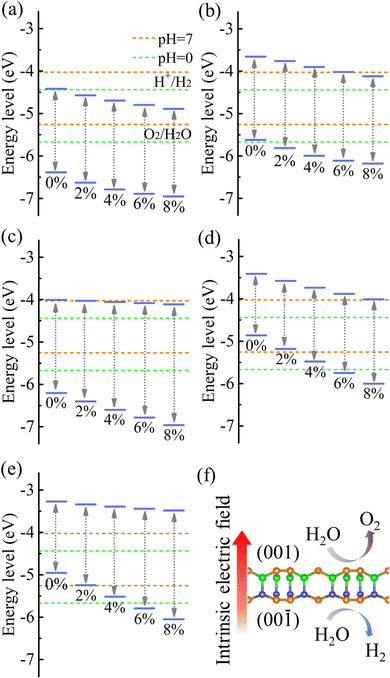
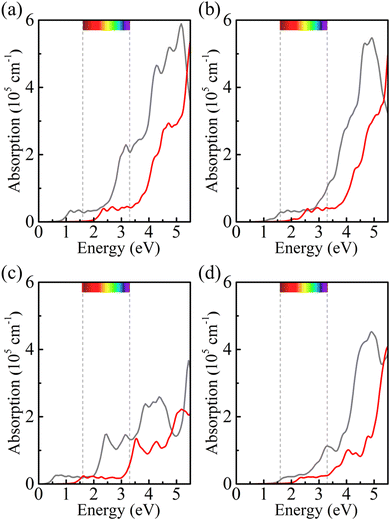
Strain engineering is an effective approach to modulate the electronic properties of materials,39–41 and the effect of strain on the positions of the band edges is shown in Fig. 9(a)–(e). For α-BC2N we find that the (001) side is suitable only for the oxygen evolution reaction and the (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) side is suitable only for the hydrogen evolution reaction, see Fig. 9(f). Photocatalytic water splitting is possible for β-BC2N (from pH = 0 to pH = 7), while for γ-BC2N and δ-BC2N it is possible only under at least 6% strain. Strong optical absorption from the visible to ultraviolet spectral range is another key requirement of a high-efficiency photocatalytic semiconductor. The optical spectra in Fig. 10, calculated by random approximation (RPA) with the polarization being parallel to the 2D material, show that PBCF-BC2N fulfills this requirement even though the RPA does not include excitonic effects42,43 (renormalization of the peak intensities, redshifting of the spectra due to electron–hole interaction, etc.) and these effects can be significant in 2D materials.
) side is suitable only for the hydrogen evolution reaction, see Fig. 9(f). Photocatalytic water splitting is possible for β-BC2N (from pH = 0 to pH = 7), while for γ-BC2N and δ-BC2N it is possible only under at least 6% strain. Strong optical absorption from the visible to ultraviolet spectral range is another key requirement of a high-efficiency photocatalytic semiconductor. The optical spectra in Fig. 10, calculated by random approximation (RPA) with the polarization being parallel to the 2D material, show that PBCF-BC2N fulfills this requirement even though the RPA does not include excitonic effects42,43 (renormalization of the peak intensities, redshifting of the spectra due to electron–hole interaction, etc.) and these effects can be significant in 2D materials.
 |
| | Fig. 9 Positions of the band edges relative to the vacuum level of (a) (001) side of α-BC2N, (b) (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) side of α-BC2N, (c) β-BC2N, (d) γ-BC2N, and (e) δ-BC2N under biaxial strain. (f) Intrinsic electric field of α-BC2N. ) side of α-BC2N, (c) β-BC2N, (d) γ-BC2N, and (e) δ-BC2N under biaxial strain. (f) Intrinsic electric field of α-BC2N. | |
 |
| | Fig. 10 Optical spectra of (a) α-BC2N, (b) β-BC2N, (c) γ-BC2N, and (d) δ-BC2N (gray = PBE + RPA; red = HSE06 + RPA; polarization parallel to the 2D material). | |
We next quantify the photocatalytic performance. The STH efficiency is estimated from ηsth = ηab × ηcu, where ηab is the efficiency of absorption and ηcu is the efficiency of carrier utilization. We have
| | 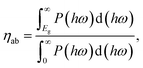 | (3) |
where
Eg is the optical gap (1.97 eV for α-BC
2N and 2.20 eV for β-BC
2N) and
P(
ℏω) is the AM1.5 solar energy flux at photon energy
ℏω, resulting in
ηab = 37.7% for α-BC
2N and 28.2% for β-BC
2N. Furthermore, we have
| | 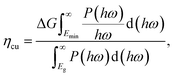 | (4) |
where Δ
G = 1.23 eV for water and
Emin (minimum energy of the photons that can be utilized for the redox reactions) can be determined as
| | 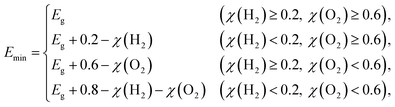 | (5) |
where
χ(H
2) and
χ(O
2) represent the overpotentials of the hydrogen and oxygen evolution reactions, respectively. Considering that the intrinsic electric field of a Janus material reduces the recombination of the photo-generated carriers, the STH efficiency is corrected as
| | 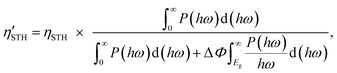 | (6) |
where Δ
Φ is the electrostatic potential difference between the two sides of the materials. We find
χ(H
2) = 0.78 eV,
χ(O
2) = 0.72 eV,
Emin = 1.97 eV, Δ
Φ = 0.76 eV, and
ηcu = 49.4% for α-BC
2N and
χ(H
2) = 0.43 eV,
χ(O
2) = 0.53 eV,
Emin = 2.27 eV, and
ηcu = 40.8% for β-BC
2N. Thus, the STH efficiency and corrected STH efficiency of α-BC
2N turn out to be 19% and 17%, respectively, approaching the conventional theoretical limit (∼18%). The STH efficiency of β-BC
2N turns out to be 12%, which is comparable to the values reported for GeN
3 (12.6%)
44 and AgBiP
2Se
6 (10.2%),
26 exceeding the target value for industrial application (10%).
19 Both α-BC
2N and β-BC
2N therefore emerge as economically viable photocatalysts for water splitting.
3.4 Photovoltaic properties
Due to their moderate direct band gaps of 1.45 and 1.68 eV, respectively, and excellent absorption of solar radiation, γ-BC2N and δ-BC2N are potential candidates for heterostructure solar cell materials. We study heterostructures with hexagonal 2D MX2 (M = Mo and W; X = S, Se, and Te), which also show direct band gaps and strong absorption.45–47Table 3 summarizes the structural and electronic parameters of 2D MX2 (M = Mo and W; X = S, Se, and Te) obtained using the HSE06 hybrid functional with spin–orbital coupling (SOC) being included (see Fig. S4, ESI† for the electronic band structures). The positions of the valence and conduction band edges relative to the vacuum level are illustrated in Fig. 11(a). The band edges of γ-BC2N and δ-BC2N enclose those of WTe2, leading to type-I band alignment, while they are interlaced with those of MoS2, MoSe2, MoTe2, WS2, and WSe2, leading to type-II band alignment. Due to the lower electron affinity as compared to 2D MX2 (M = Mo and W; X = S, Se, and Te), both γ-BC2N and δ-BC2N act as electron donors in the heterostructure. For γ-BC2N (δ-BC2N), we obtain conduction band offsets of 0.84 (0.98), 0.48 (0.62), 0.31 (0.45), 0.43 (0.57), 0.12 (0.26), and 0.14 (0.28) eV relative to MoS2, MoSe2, MoTe2, WS2, WSe2, and WTe2, respectively.
Table 3 Lattice constants (a; space group P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2), thickness (h), bond lengths (lM–X), positions of the band edges with respect to the vacuum level (EHSE06+SOCVBM and EHSE06+SOCCBM), band gaps (EHSE06+SOCg), and spin–orbit splitting in the valence band (ΔHSE06+SOC)
m2), thickness (h), bond lengths (lM–X), positions of the band edges with respect to the vacuum level (EHSE06+SOCVBM and EHSE06+SOCCBM), band gaps (EHSE06+SOCg), and spin–orbit splitting in the valence band (ΔHSE06+SOC)
|
|
a (Å) |
h (Å) |
l
M–X (Å) |
E
HSE06+SOCVBM (eV) |
E
HSE06+SOCCBM (eV) |
E
HSE06+SOCg (eV) |
ΔHSE06+SOC (eV) |
| MoS2 |
3.18 |
3.13 |
2.41 |
−6.27 |
−4.25 |
2.02 |
0.21 |
| MoSe2 |
3.32 |
3.34 |
2.54 |
−5.60 |
−3.89 |
1.71 |
0.28 |
| MoTe2 |
3.55 |
3.61 |
2.73 |
−4.99 |
−3.72 |
1.27 |
0.35 |
| WS2 |
3.18 |
3.14 |
2.42 |
−5.83 |
−3.84 |
1.99 |
0.55 |
| WSe2 |
3.32 |
3.35 |
2.55 |
−5.17 |
−3.53 |
1.64 |
0.62 |
| WTe2 |
3.55 |
3.62 |
2.74 |
−4.59 |
−3.55 |
1.04 |
0.68 |
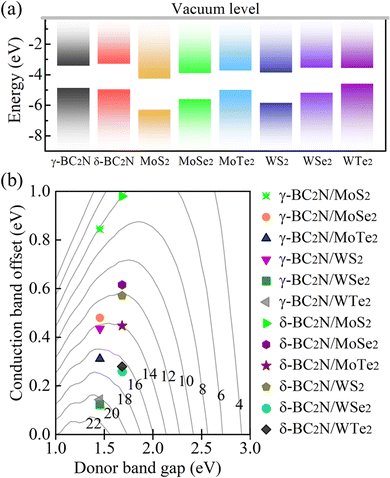 |
| | Fig. 11 (a) Band alignments and (b) PCE (in %). | |
The maximum PCE of a solar cell is given using the following expression
| | 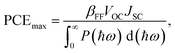 | (7) |
where we assume a fill factor of
βFF = 0.65. The open circuit voltage
| | 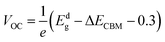 | (8) |
can be obtained from the optical gap of the donor (
Edg ∼ 1.45 eV for γ-BC
2N and 1.68 eV for δ-BC
2N) and conduction band offset (Δ
ECBM) considering an empirical loss of 0.3 eV. The short circuit current (limit of external quantum efficiency) is given using the following expression
| | 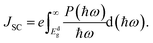 | (9) |
As shown in Fig. 11(b), PCEmax values in excess of 20% are achieved by the γ-BC2N/WSe2 and γ-BC2N/WTe2 heterostructures, which are comparable to those of organic solar cells (18.2%)11 and the δ-CS/MoTe2 heterostructure (20.1%).17 They approach the performances of state-of-the-art perovskites (25.5%), silicon (27.6%), and GaAs (30.5%) solar cells,11 pointing toward their great application potential.
4. Conclusion
Using comprehensive first-principles calculations, we have proposed 2D hexagonal borocarbonitrides (α-BC2N, β-BC2N, γ-BC2N, and δ-BC2N) with cohesive energies of 6.25–6.33 eV per atom combined with dynamical, mechanical, and thermal (at 1000 K) stability. High fracture strengths and strains are interesting for nano-mechanical applications. Moderate direct band gaps of 1.45–2.20 eV (HSE06) and isotropic small carrier effective masses are found. It also turns out that the size of the band gap can be effectively tuned using strain. Electronic applications can benefit from the discovered ultrahigh electron mobilities. Both α-BC2N and β-BC2N show potential in photocatalytic water splitting with excellent absorption of solar radiation. In particular, the intrinsic electric field induced by the Janus geometry of α-BC2N separates the photo-generated electrons and holes, therefore minimizing their recombination. The electrons and holes migrate to opposite sides of the two-dimensional material to take part in the redox reactions for water splitting. The high efficiency of carrier utilization (49.4%) resulting from the intrinsic electric field leads to an outstanding solar-to-hydrogen efficiency of 17%. According to the band alignments, γ-BC2N and δ-BC2N act as electron donors in heterostructures with 2D MX2 (M = Mo and W; X = S, Se, and Te). It turns out that such heterostructures can show a PCE of up to 21%.
Author contributions
W. Zhang, M. Sun, and U. Schwingenschlögl conceived the study. C. Chai and M. Sun performed the calculations and analyzed the data. W. Zhang and Q. Fan wrote the manuscript guided by M. Sun, M. Palummo, and U. Schwingenschlögl. C. Chai and Y. Yang provided equipment support.
Conflicts of interest
The authors declare no competing interests.
Acknowledgements
The authors acknowledge financial support from the National Natural Science Foundation of China (no. 61974116 and no. 61804120), the China Postdoctoral Science Foundation (no. 2019TQ0243 and no. 2019M663646), and the Key Scientific Research Project of Education Department of Shannxi-Key Laboratory Project (no. 20JS066). M. P. acknowledges CN1 (Spoke6) - Centro Nazionale di Ricerca (High-Performance Computing Big Data and Quantum Computing and TIME2QUEST-INFN projects). Xidian University provided computational resources and support. The research reported in this publication was supported by funding from King Abdullah University of Science and Technology (KAUST).
References
- S. Carley and D. M. Konisky, The justice and equity implications of the clean energy transition, Nat. Energy, 2020, 5, 569–577 CrossRef CAS.
- R. Fouquet, Historical energy transitions: Speed, prices and system transformation, Energy Res. Soc. Sci., 2016, 22, 7–12 CrossRef.
- F. Creutzig, P. Agoston, J. C. Goldschmidt, G. Luderer, G. Nemet and R. C. Pietzcker, The underestimated potential of solar energy to mitigate climate change, Nat. Energy, 2017, 2, 17140 CrossRef.
- P. Miró, M. Audiffred and T. Heine, An atlas of two-dimensional materials, Chem. Soc. Rev., 2014, 43, 6537–6554 RSC.
- M. Buscema, J. O. Island, D. J. Groenendijk, S. I. Blanter, G. A. Steele, H. S. J. van der Zant and A. Castellanos-Gomez, Photocurrent generation with two-dimensional van der Waals semiconductors, Chem. Soc. Rev., 2015, 44, 3691–3718 RSC.
- C. R. Cox, J. Z. Lee, D. G. Nocera and T. Buonassisi, Ten-percent solar-to-fuel conversion with nonprecious materials, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14057–14061 CrossRef CAS PubMed.
- M. Bernardi, M. Palummo and J. C. Grossman, Extraordinary sunlight absorption and one nanometer thick photovoltaics using two-dimensional monolayer materials, Nano Lett., 2013, 13, 3664–3670 CrossRef CAS PubMed.
- L. Ju, J. Shang, X. Tang and L. Kou, Tunable photocatalytic water splitting by the ferroelectric switch in a 2D AgBiP2Se6 monolayer, J. Am. Chem. Soc., 2019, 142, 1492–1500 CrossRef PubMed.
- M. Sun and U. Schwingenschlögl, B2P6: A two-dimensional anisotropic Janus material with potential in potocatalytic water splitting and metal-ion batteries, Chem. Mater., 2020, 32, 4795–4800 CrossRef CAS.
- Y. Luo, M. Sun, J. Yu and U. Schwingenschlögl, Pd4S3Se3, Pd4S3Te3, and Pd4Se3Te3: Candidate two-dimensional Janus materials for photocatalytic water splitting, Chem. Mater., 2021, 33, 4128–4134 CrossRef CAS.
- M. A. Green, E. D. Dunlop, J. Hohl-Ebinger, M. Yoshita, N. Kopidakis and X. Hao, Applications, Solar cell efficiency tables (Version 58), Prog. Phot. Res. Appl., 2021, 29, 657–667 CrossRef.
- M. Bernardi, M. Palummo and J. C. Grossman, Semiconducting monolayer materials as a tunable platform for excitonic solar cells, ACS Nano, 2012, 6, 10082–10089 CrossRef CAS PubMed.
- M. M. Furchi, A. Pospischil, F. Libisch, J. Burgdörfer and T. Mueller, Photovoltaic effect in an electrically tunable van der Waals heterojunction, Nano Lett., 2014, 14, 4785–4791 CrossRef CAS PubMed.
- M. L. Tsai, S. H. Su, J. K. Chang, D. S. Tsai, C. H. Chen, C. I. Wu, L. J. Li, L. J. Chen and J. H. He, Monolayer MoS2 heterojunction solar cells, ACS Nano, 2014, 8, 8317–8322 CrossRef CAS PubMed.
- X. Li, W. Chen, S. Zhang, Z. Wu, P. Wang, Z. Xu, H. Chen, W. Yin, H. Zhong and S. Lin, 18.5% efficient graphene/GaAs van der Waals heterostructure solar cell, Nano Energy, 2015, 16, 310–319 CrossRef CAS.
- D. J. Xue, S. C. Liu, C. M. Dai, S. Chen, C. He, L. Zhao, J. S. Hu and L. J. Wan, GeSe thin-film solar cells fabricated by self-regulated rapid thermal sublimation, J. Am. Chem. Soc., 2017, 139, 958–965 CrossRef CAS PubMed.
- M. Sun and U. Schwingenschlögl, δ-CS: A direct-band-gap semiconductor combining auxeticity, ferroelasticity, and potential for high-efficiency solar cells, Phys. Rev. Appl., 2020, 14, 044015 CrossRef CAS.
- M. Bernardi, M. Palummo and J. C. Grossman, Semiconducting monolayer materials as a tunable platform for excitonic solar cells, ACS Nano, 2012, 6, 10082–10089 CrossRef CAS PubMed.
- M. Chhetri, S. Maitra, H. Chakraborty, U. V. Waghmare and C. N. R. Rao, Superior performance of borocarbonitrides, BxCyNz, as stable, low-cost metal-free electrocatalysts for the hydrogen evolution reaction, Energy Environ. Sci., 2016, 9, 95–101 RSC.
- J. Wang, J. Hao, D. Liu, S. Qin, D. Portehault, Y. Li, Y. Chen and W. Lei, Porous boron carbon nitride nanosheets as efficient metal-free catalysts for the oxygen reduction reaction in both alkaline and acidic solutions, ACS Energy Lett., 2017, 2, 306–312 CrossRef CAS.
- L. Cheng, J. Meng, X. Pan, Y. Lu, X. Zhang, M. Gao, Z. Yin, D. Wang, Y. Wang, J. You, J. Zhang and E. Xie, Two-dimensional hexagonal boron-carbon-nitrogen atomic layers, Nanoscale, 2019, 11, 10454–10462 RSC.
- W. Zhang, C. Chai, Q. Fan, Y. Song and Y. Yang, PBCF-graphene: A 2D sp2 hybridized honeycomb carbon allotrope with a direct band gap, ChemNanoMat, 2020, 6, 139–147 CrossRef CAS.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- R. J. Hunt, B. Monserrat, V. Zólyomi and N. D. Drummond, Diffusion quantum Monte Carlo and GW study of the electronic properties of monolayer and bulk hexagonal boron nitride, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 101, 205115 CrossRef CAS.
- R. Shinde, S. S. R. K. C. Yamijala and B. M. Wong, Improved band gaps and structural properties from Wannier-Fermi-Löwdin self-interaction corrections for periodic systems, J. Phys.: Condens. Matter, 2021, 33, 115501 CrossRef CAS PubMed.
- X. Gonze and J. P. Vigneron, Density-functional approach to nonlinear-response coefficients of solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 13120–13128 CrossRef PubMed.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- X. Kan, Y. Ban, C. Wu, Q. Pan, H. Liu, J. Song, Z. Zuo, Z. Li and Y. Zhao, Interfacial synthesis of conjugated two-dimensional N-graphdiyne, ACS Appl. Mater. Interfaces, 2018, 10, 53–58 CrossRef CAS PubMed.
- N. Wang, X. Li, Z. Tu, F. Zhao, J. He, Z. Guan, C. Huang, Y. Yi and Y. Li, Synthesis and electronic structure of boron-graphdiyne with an sp-hybridized carbon skeleton and its application in sodium storage, Angew. Chem., Int. Ed., 2018, 130, 4032–4037 CrossRef.
- A. Thomas, A. Fischer, F. Goettmann, M. Antonietti, J.-O. Müller, R. Schlögl and J. M. Carlsson, Graphitic carbon nitride materials: Variation of structure and morphology and their use as metal-free catalysts, J. Mater. Chem. A, 2008, 18, 4893–4908 RSC.
- F. Mouhat and F. X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- E. Cadelano, P. L. Palla, S. Giordano and L. Colombo, Elastic properties of hydrogenated graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 235414 CrossRef.
- K. Liu, Q. Yan, M. Chen, W. Fan, Y. Sun, J. Suh, D. Fu, S. Lee, J. Zhou, S. Tongay, J. Ji, J. B. Neaton and J. Wu, Elastic properties of chemical-vapor-deposited monolayer MoS2, WS2, and their bilayer heterostructures, Nano Lett., 2014, 14, 5097–5103 CrossRef CAS PubMed.
- Q. Wei and X. Peng, Superior mechanical flexibility of phosphorene and few-layer black phosphorus, Appl. Phys. Lett., 2014, 104, 251915 CrossRef.
- Y. Cai, G. Zhang and Y. W. Zhang, Polarity-reversed robust carrier mobility in monolayer MoS2 nanoribbons, J. Am. Chem. Soc., 2014, 136, 6269–6275 CrossRef CAS PubMed.
- J. Qiao, X. Kong, Z.-X. Hu, F. Yang and W. Ji, High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus, Nat. Commun., 2014, 5, 4475 CrossRef CAS PubMed.
- J. Du and J. Shi, 2D Ca3Sn2S7 chalcogenide perovskite: A graphene-like semiconductor with direct bandgap 0.5 eV and ultrahigh carrier mobility 6.7 × 104 cm2 V−1 s−1, Adv. Mater., 2019, 31, 1905643 CrossRef CAS PubMed.
- V. Chakrapani, J. C. Angus, A. B. Anderson, S. D. Wolter, B. R. Stoner and G. U. Sumanasekera, Charge transfer equilibria between diamond and an aqueous oxygen electrochemical redox couple, Science, 2007, 318, 1424–1430 CrossRef CAS PubMed.
- R. Nechache, C. Harnagea, A. Ruediger, F. Rosei and A. Pignolet, Effect of epitaxial strain on the structural and ferroelectric properties of Bi2FeCrO6 thin films, Funct. Mater. Lett., 2010, 3, 83–88 CrossRef CAS.
- S. Wang, M. S. Ukhtary and R. Saito, Strain effect on circularly polarized electroluminescence in transition metal dichalcogenides, Phys. Rev. Res., 2020, 2, 033340 CrossRef CAS.
- L. Du, C. Ren, L. Cui, W. Lu, H. Tian and S. Wang, Robust valley filter induced by quantum constructive interference in graphene with line defect and strain, Phys. Scr., 2022, 97, 125825 CrossRef.
- M. Rohlfing and S. G. Louie, Electron–hole excitations in semiconductors and insulators, Phys. Rev. Lett., 1998, 81, 2312–2315 CrossRef CAS.
- G. Onida, L. Reining and A. Rubio, Electronic excitations: Density-functional versus many-body Green's-function approaches, Rev. Mod. Phys., 2002, 74, 601–659 CrossRef CAS.
- J. Liu, Y. Shen, X. Gao, L. Lv, Y. Ma, S. Wu, X. Wang and Z. Zhou, GeN3 monolayer: A promising 2D high-efficiency photo-hydrolytic catalyst with High carrier mobility transport anisotropy, Appl. Catal., B, 2020, 279, 119368 CrossRef CAS.
- T. Georgiou, R. Jalil, B. D. Belle, L. Britnell, R. V. Gorbachev, S. V. Morozov, Y. J. Kim, A. Gholinia, S. J. Haigh, O. Makarovsky, L. Eaves, L. A. Ponomarenko, A. K. Geim, K. S. Novoselov and A. Mishchenko, Vertical field-effect transistor based on graphene-WS2 heterostructures for flexible and transparent electronics, Nat. Nanotechnol., 2013, 8, 100–103 CrossRef CAS PubMed.
- M. Palummo, M. Bernardi and J. C. Grossman, Exciton radiative lifetimes in two-dimensional transition metal dichalcogenides, Nano Lett., 2015, 15, 2794–2800 CrossRef CAS PubMed.
- S. Memaran, N. R. Pradhan, Z. Lu, D. Rhodes, J. Ludwig, Q. Zhou, O. Ogunsolu, P. M. Ajayan, D. Smirnov, A. Fernandez, F. J. García-Vidal and L. Balicas, Pronounced photovoltaic response from multilayered transition-metal dichalcogenides pn-junctions, Nano Lett., 2015, 15, 7532–7538 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Elastic energies under uniaxial and biaxial strain, phonon spectra under extreme biaxial tensile strain, electronic band structures under biaxial tensile strain, and electronic band structures of 2D transition metal dichalcogenides. POSCAR files. See DOI: https://doi.org/10.1039/d2tc05268g |
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Changchun
Chai
a,
Qingyang
Fan
c,
Yintang
Yang
a,
Minglei
Sun
*ab,
Changchun
Chai
a,
Qingyang
Fan
c,
Yintang
Yang
a,
Minglei
Sun
 *d,
Maurizia
Palummo
*d,
Maurizia
Palummo
 e and
Udo
Schwingenschlögl
e and
Udo
Schwingenschlögl
 *d
*d
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (no. 164), P
m1 (no. 164), P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) 2m (no. 189), and P
2m (no. 189), and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1m (no. 162), respectively, with optimized lattice constants of 6.99, 7.05, 7.14, and 7.13 Å. The orthorhombic lattice constants are 6.99 Å (armchair direction) and 12.11 Å (zigzag direction) for α-BC2N, 7.05 Å and 12.21 Å for β-BC2N, 7.14 Å and 12.37 Å for γ-BC2N, and 7.13 Å and 12.35 Å for δ-BC2N. The sandwich-like structures are 2.47 to 2.53 Å thick. The top and bottom layers of α-BC2N and β-BC2N are connected by B–N bonds while those of γ-BC2N and δ-BC2N are connected by C
1m (no. 162), respectively, with optimized lattice constants of 6.99, 7.05, 7.14, and 7.13 Å. The orthorhombic lattice constants are 6.99 Å (armchair direction) and 12.11 Å (zigzag direction) for α-BC2N, 7.05 Å and 12.21 Å for β-BC2N, 7.14 Å and 12.37 Å for γ-BC2N, and 7.13 Å and 12.35 Å for δ-BC2N. The sandwich-like structures are 2.47 to 2.53 Å thick. The top and bottom layers of α-BC2N and β-BC2N are connected by B–N bonds while those of γ-BC2N and δ-BC2N are connected by C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds. α-BC2N realizes a pronounced Janus geometry. In each case, the hexagonal unit cell comprises six C–C, six B–N, twelve C–B, and twelve C–N bonds. The C
C bonds. α-BC2N realizes a pronounced Janus geometry. In each case, the hexagonal unit cell comprises six C–C, six B–N, twelve C–B, and twelve C–N bonds. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths of 1.36 to 1.39 Å are slightly shorter than those in graphene (1.42 Å), whereas the B–N bond lengths of 1.44 to 1.46 Å closely resemble the value for h-BN (1.45 Å). The relatively short C
C bond lengths of 1.36 to 1.39 Å are slightly shorter than those in graphene (1.42 Å), whereas the B–N bond lengths of 1.44 to 1.46 Å closely resemble the value for h-BN (1.45 Å). The relatively short C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and B–N bond lengths represent strong covalent bonds. The C–B and C–N bond lengths range from 1.53 to 1.60 Å and from 1.45 to 1.48 Å, respectively.
C and B–N bond lengths represent strong covalent bonds. The C–B and C–N bond lengths range from 1.53 to 1.60 Å and from 1.45 to 1.48 Å, respectively.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1
m1![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) 2m
2m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1m
1m![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, B–N, C–B, and C–N bonds. The obtained Bader charges agree with the electronegativities of the involved atoms: for α-BC2N the C and B atoms on the (001) side show values of +1.29 and −1.96 e, respectively, while the C and N atoms on the (00
C, B–N, C–B, and C–N bonds. The obtained Bader charges agree with the electronegativities of the involved atoms: for α-BC2N the C and B atoms on the (001) side show values of +1.29 and −1.96 e, respectively, while the C and N atoms on the (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) side show values of −0.64 and +1.31 e. For β-BC2N, γ-BC2N, and δ-BC2N, respectively, we obtain Bader charges of −1.90, −1.94, and −1.96 e for the B atoms, +0.25, +0.28, and +0.28 e for the C atoms, and +1.40, +1.38, and +1.40 e for the N atoms. Hence, the chemical bonding in PBCF-BC2N is governed by strongly polarized covalent bonds.
) side show values of −0.64 and +1.31 e. For β-BC2N, γ-BC2N, and δ-BC2N, respectively, we obtain Bader charges of −1.90, −1.94, and −1.96 e for the B atoms, +0.25, +0.28, and +0.28 e for the C atoms, and +1.40, +1.38, and +1.40 e for the N atoms. Hence, the chemical bonding in PBCF-BC2N is governed by strongly polarized covalent bonds.
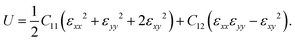

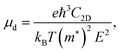

![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) side).
) side).
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) side is suitable only for the hydrogen evolution reaction, see Fig. 9(f). Photocatalytic water splitting is possible for β-BC2N (from pH = 0 to pH = 7), while for γ-BC2N and δ-BC2N it is possible only under at least 6% strain. Strong optical absorption from the visible to ultraviolet spectral range is another key requirement of a high-efficiency photocatalytic semiconductor. The optical spectra in Fig. 10, calculated by random approximation (RPA) with the polarization being parallel to the 2D material, show that PBCF-BC2N fulfills this requirement even though the RPA does not include excitonic effects42,43 (renormalization of the peak intensities, redshifting of the spectra due to electron–hole interaction, etc.) and these effects can be significant in 2D materials.
) side is suitable only for the hydrogen evolution reaction, see Fig. 9(f). Photocatalytic water splitting is possible for β-BC2N (from pH = 0 to pH = 7), while for γ-BC2N and δ-BC2N it is possible only under at least 6% strain. Strong optical absorption from the visible to ultraviolet spectral range is another key requirement of a high-efficiency photocatalytic semiconductor. The optical spectra in Fig. 10, calculated by random approximation (RPA) with the polarization being parallel to the 2D material, show that PBCF-BC2N fulfills this requirement even though the RPA does not include excitonic effects42,43 (renormalization of the peak intensities, redshifting of the spectra due to electron–hole interaction, etc.) and these effects can be significant in 2D materials.
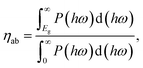
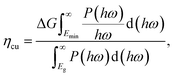
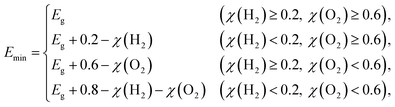
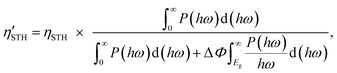
![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2), thickness (h), bond lengths (lM–X), positions of the band edges with respect to the vacuum level (EHSE06+SOCVBM and EHSE06+SOCCBM), band gaps (EHSE06+SOCg), and spin–orbit splitting in the valence band (ΔHSE06+SOC)
m2), thickness (h), bond lengths (lM–X), positions of the band edges with respect to the vacuum level (EHSE06+SOCVBM and EHSE06+SOCCBM), band gaps (EHSE06+SOCg), and spin–orbit splitting in the valence band (ΔHSE06+SOC)