Temperature- and strain-dependent transient microstructure and rheological responses of endblock-associated triblock gels of different block lengths in a midblock selective solvent†
Rosa Maria
Badani Prado
a,
Satish
Mishra
a,
Humayun
Ahmed
a,
Wesley R.
Burghardt
b and
Santanu
Kundu
 *a
*a
aDave C. Swalm School of Chemical Engineering, 323 Presidents Circle, Mississippi State University, Mississippi State, MS 39762, USA. E-mail: santanukundu@che.msstate.edu
bDepartment of Chemical Engineering, Northwestern University, Evanston, IL, USA
First published on 16th August 2022
Abstract
Endblock associative ABA gels in midblock selective solvents are attractive due to their easily tunable mechanical properties. Here, we present the effects of A- and B-block lengths on the rheological properties and microstructure of ABA gels by considering three low and one high polymer concentrations. The triblock polymer considered is poly(methyl methacrylate)–poly(n-butyl acrylate)–poly(methyl methacrylate) [PMMA–PnBA–PMMA] and the midblock solvent is 2-ethyl-1-hexanol. The gelation temperature has been found to be strongly dependent on the B-block (PnBA) length, as longer B-blocks facilitate network formation resulting in higher gelation temperature even with lower polymer chain density. Longer A-blocks (PMMA chains) make the endblock association stronger and significantly increase the relaxation time of gels. Temperature-dependent microstructure evolution for the gels with high polymer concentration reveals that the gel microstructure does not change significantly after the gel formation takes place. The dynamic change of microstructure in an applied strain cycle was captured using RheoSAXS experiments. The microstructure orients with the applied strain and the process is reversible in nature, indicating no significant A-block pullout. Our results provide new understandings regarding the temperature and strain-dependent microstructural change of ABA gels in midblock selective solvents.
1 Introduction
ABA triblock copolymer gels are a class of physically assembled gels that have been studied widely due to their tunable mechanical properties.1–23 These gels consist of ABA triblock copolymers dissolved in B-block selective solvents. The gelation in these gels originates from a strong temperature-dependent solubility of A-blocks in a chosen solvent, while the solubility of B-blocks is relatively insensitive to the temperature.6,16 Upon dissolving the polymer in the solvent at a high temperature, a clear polymer solution is obtained, signifying a good solubility of both blocks. With decreasing temperature, the A-block solubility decreases drastically, and many of theses blocks physically associate to form aggregates of the size of a few nanometers.16,24 These aggregates act like crosslinks as these are connected by the B-blocks, which remain soluble in the solvent. Here, the B-blocks act as the load-bearing or elastically active chains.6–8 In combination, a three-dimensional swollen crosslinked network or gel is obtained.Due to the temperature-driven associations, these gels are thermoreversible. Also, the triblock polymers considered are mostly thermoplastics; therefore, these gels are often referred to as thermoplastic elastomeric gels. The thermo-mechanical properties of these gels have been shown to be tuned by temperature,6,15,18,19,23,25 polymer concentration,6,21,23,26,27 length of A- and B-blocks,7,28,29 choice of solvent,16 inclusion of homopolymer,9 and nanoparticles.15 Because of the tunability of properties in such a diverse way, these gels have potential applications in ballistics,25 tissue surrogates,30 comfort and healthcare products like shoe soles and prosthetics,31,32 gelcasting,33 and soft robotics.34,35 In many of these applications, the gels can be subjected to large strain mechanical deformation and temperature change. Therefore, a fundamental understanding of microstructural development with temperature and the corresponding mechanical properties is useful to engineer gels for targeted applications. The structure–property relationship for these gels can be applied to other gels consisting of solubility-triggered aggregates.35,36
From the numerous studies on these gels over the last few decades for the various combinations of A-blocks, B-blocks, and solvents, significant understanding regarding the self-assembled structure and the corresponding mechanical properties has been achieved.4–6,17,22,23,26,37 A few common characteristics of these gels are (1) higher gelation temperature for the gels with higher polymer concentration,22,23 and longer A- and B-blocks,7,19 (2) micellar microstructure (spherical A-aggregates) at low-to-moderate polymer concentration evolving into cylindrical micelles at higher polymer concentration,4,6,16–19,23 (3) higher elastic moduli at higher polymer concentration,6,7,21,23 also for longer A-blocks,5,7,15,16 (4) strain-rate dependent moduli for the gels with B-block entanglements,18,19,23,28,29 and (5) longer relaxation times for the gels with higher polymer concentrations and at lower temperatures.6,17,22,23,26
Interestingly, a few other characteristics, such as strain stiffening behavior10,14 and stress relaxation mechanism, are not similar for all different types of ABA gels. For example, poly(methyl methacrylate)–poly(n-butyl acrylate)–poly(methyl methacrylate) [PMMA–PnBA–PMMA] gels in midblock-selective solvents display strain-stiffening behavior subjected to shear-strain;10,14 however, such a feature has not been captured for the poly(styrene)–rubber–poly(styrene) [PS–rubber–PS] gels in midblock selective solvents.23,25 Here, the rubber block is generally poly(isoprene) [PI] or (ethylene-co-butylene) [PEB]. Note that the strain-stiffening behavior is not very common in synthetic gels but is typical to biomaterials and biopolymer gels, such as alginate gels.23,38–41 The strain-stiffening responses of PMMA–PnBA–PMMA gels make these attractive for tissue-surrogate or ballistic applications.25,30 Furthermore, the stress relaxation behavior of PMMA–PnBA–PMMA gels follows a similar trend over a range of temperatures and can be superimposed in forming a master curve.12 In contrast, the temperature-dependent stress relaxation responses for PS–PI–PS gels can not be superimposed.18 However, a reasonable superimposition has been demonstrated for the concentration-dependent stress relaxation responses at a given temperature.18 Different mechanical responses in PMMA–PnBA–PMMA gels compared to the PS–PI–PS gels can be attributed to the difference in interactions of the A- (PMMA, PS) and B-blocks (PnBA, PI) with the chosen solvents. A small change in such interactions can lead to a difference in properties. For example, in the case of the PMMA–PnBA–PMMA gel, changing the solvent from 2-ethyl-1-hexanol to 1-butanol leads to a decrease in gelation temperature by ≈3 to 5 °C and a decrease of modulus depending on the polymer concentration. This was attributed to the more favorable phase separation of PMMA in 2-ethyl-1-hexanol than in 1-butanol.16
Real-time microstructure characterization of polymer gels as a function of mechanical loading provides additional understanding regarding the structure–property relationships necessary for their practical applications. This can be achieved by using simultaneous rheology and scattering experiments, such as RheoSAXS and RheoSANS.42–44 With that goal, recently, the microstructure of PS–PI–PS gels in mineral oil as a function of temperature and oscillation strain has been studied using the RheoSAXS technique.45 It was found that during an oscillatory strain cycle at a high strain amplitude, the gel microstructure splits into both oriented and non-oriented ones. It has been hypothesized that not all PI-blocks participate as the load-bearing chains.45
Although PMMA–PnBA–PMMA gels have been investigated for their gelation mechanism and mechanical properties,6,8,46 the microstructural change in real-time as a function of mechanical deformation for these has not been reported in the literature. This is further important as the mechanical responses of PS–PI–PS and PMMA–PnBA–PMMA are not exactly similar, especially at large deformation. Since we could capture the strain-stiffening responses of PMMA–PnBA–PMMA gels only at low polymer concentrations, investigations were conducted for low polymer concentrations in the present study. The effect of polymer concentrations was also investigated by considering a high polymer concentration for a polymer. The three triblock copolymers considered have different PMMA- and PnBA-block lengths; therefore, the effects of block lengths on the mechanical properties and microstructural changes in gels have also been elucidated utilizing shear-rheometry and RheoSAXS. For RheoSAXS experiments, we focused on investigating the change in microstructure as a function of temperature and oscillatory strain. This technique allowed us to capture the microstructural change with a very short exposure time and in the 1–2 plane. Such a microstructural change has also been related to the rheological responses obtained using shear-rheometry.
2 Experiments
2.1 Materials and sample preparation
Three different triblock copolymers (ABA) that were kindly provided by Kuraray America Inc. and having the commercial designations of LA2550, LA2330, and LA2140E have been considered here. In these polymers, the A-block is poly(methyl methacrylate) [PMMA], and the B-block is poly(n-butyl acrylate) [PnBA]. As summarized in Table 1, the molecular weights of these polymers are different, i.e., they have different A- and B-block lengths. Note that the subscripts for A and B-blocks indicate their respective molecular weights. For example, A25 indicates PMMA with a molecular weight of ≈25 kg mol−1. To prepare the gel samples, an estimated amount of a polymer was added to the midblock selective solvent, 2-ethyl-1-hexanol (Sigma-Aldrich). A clear solution was obtained as the mixture was placed overnight in an oven maintained at 80 °C. The gel was obtained upon cooling the solution to room temperature. In our case, all polymers and solvents were used as received.| Polymer | ϕ (v/v) | Gel nomenclature | Chain density (m3) | ϕ* (v/v) |
|---|---|---|---|---|
| LA2550 | 0.03 | A25B104A25-L | 1.29 × 1023 | ≈0.025 |
| LA2330 | 0.04 | A12B96A12-L | 2.21 × 1023 | ≈0.035 |
| 0.30 | A12B96A12-H | 16.5 × 1023 | ||
| LA2140E | 0.05 | A8B54A8-L | 4.60 × 1023 | ≈0.045 |
2.2 Shear-rheometry
For the shear-rheometry experiments, a Discovery HR-2 hybrid rheometer (TA Instruments) fitted with a Peltier system was used. A 25 mm parallel plate geometry was utilized. The warm polymer solution was poured onto the bottom plate maintained at 80 °C, and subsequently, the gap between the two plates was adjusted to 1 mm. Temperature sweep experiments were performed using a strain amplitude (γ0) of 0.01 and frequency (ω) of 1 rad s−1 over a temperature range of 60 to 18 °C. A temperature step of 2 °C min−1 with an equilibration time of 180 s was used. Other than temperature sweep experiments, all rheometry experiments were conducted at ≈27 °C (room temperature at Argonne National Laboratory, where scattering experiments were conducted). Frequency sweep experiments were conducted using γ0 = 0.01 over the ω range of 1–30 rad s−1. Amplitude sweep experiments were performed over the γ0 range of 10−4 to 200, with ω = 1 rad s−1. The stress-relaxation experiments were performed by applying a step strain of 0.01 in 0.01 s, after which the samples were allowed to relax for 1800 s.2.3 RheoSAXS experiments
The RheoSAXS experiments were performed using a custom-built shear stage attached to the DND-CAT small X-ray scattering (SAXS) setup at the Advanced Photon Source, Argonne National Laboratory. The shear stage was equipped with an annular cone and plate geometry with the cone angle of 5°, and the outer and inner diameters of the plates were 50 and 30 mm, respectively. A schematic of the setup is presented in Fig. 1. Here, the X-ray beam with a wavelength of 0.7293 Å passed through a pinhole located at the bottom plate of the geometry and then through the sample. The two-dimensional scattering data were captured by a CCD detector. This setup allowed obtaining scattering data at the 1–2 plane. More information about the setup can be found in previous studies.42,44,45 IgorPro software and Nika macros were used to reduce the data from 2D to 1D.47,48 NCNR macro was used to create and fit the data with polydispersed spheres form factor and hard-sphere structure factor models.49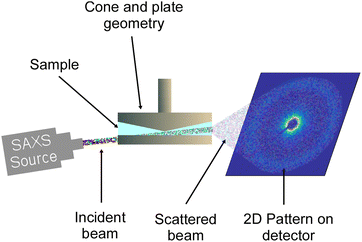 | ||
| Fig. 1 Schematic of the RheoSAXS setup where X-ray the beam passed through a hole at the bottom plate at a 5° angle and then through the sample capturing the scattering data in the 1–2 plane. | ||
For the low-ϕ gels, the samples in the sol-form were loaded at 55, 45, and 35 °C for the A25B104A25-L, A12B96A12-L, and A8B54A8-L gels, respectively. The high-ϕ gel (A12B96A12-H) was loaded at 85 °C. These temperatures were decided based on shear-rheometry experiments to ensure that the samples were in the sol-form while loading. The setup was then allowed to cool down to room temperature (≈27 °C) via natural convection, and no strain was applied during this process. After thermal equilibrium was reached, oscillatory shear experiments were conducted. Three cycles with γ0 = 1 (for A25B104A25-L, A12B96A12-L, and A8B54A8-L) or γ0 = 0.5 (for A12B96A12-H) at ω = 1 rad s−1 were applied. The beam-exposure time was 0.03 s, and the interval between the data collection was 0.157 s. To capture the temperature-dependent microstructural change of A12B96A12-H, scattering data were recorded during the natural cooling process with an exposure time of 0.03 s. The corresponding instrument temperature as a function of time was noted.
Multiple experiments were conducted on each sample. However, after each experiment, the samples were heated to sol-state to erase the deformation history. The samples were then cooled down to room temperature via natural convection. To ensure thermal equilibrium, ≈15 min wait time was used before starting an experiment.
3 Results and discussion
Four gels, three with low polymer volume fractions (low-ϕ gels) of LA2550, LA2330, and LA2140E and one with high polymer volume fraction of LA2330 were considered here (see Table 1). LA2550 and LA2330 have similar B-block (PnBA) lengths, but slightly different A-block (PMMA) length. LA2140E has the shortest A- and B-block lengths; however, the A-block length is not so different than that of LA2330. For low-ϕ gels, we have considered ϕ (v/v) ≈ 0.03, 0.04, and 0.05 of LA2550, LA2330, and LA2140E polymers, respectively. These gels have been designated as A25B104A25-L, A12B96A12-L, and A8B54A8-L, respectively (see Table 1). The polymer chain density was the lowest in A25B104A25-L due to the highest polymer molecular weight and the lowest ϕ considered here. Furthermore, the chain density was ≈1.71 and 3.56 times lower than that for A12B96A12-L and A8B54A8-L, respectively. To ensure that the stable gels were obtained for the polymer volume fractions considered here, we have determined the critical micelle volume fractions (ϕ*) for the three polymers using the vial inversion test (Fig. S1, ESI†). Four solutions of each polymer were considered, with the lowest ϕ value of 0.02 lower than that used in the present study and three additional solutions with a ϕ increment of 0.005. As observed in Fig. S1 (ESI†), the approximate ϕ* was considered the volume fraction at which the vial inversion tests provided the stable non-flowing gels. ϕ* has been found to be 0.005 less than ϕ considered here. Therefore, we have considered that ϕ*s for A25B104A25, A12B96A12, and A8B54A8 polymers were ≈0.025, 0.035, and 0.045, respectively. Although the low-ϕ gels were close to their critical micelle concentrations, they were still stable gels.We have also considered a high polymer volume fraction gel of LA2330 with ϕ ≈ 0.3 and is designated as A12B96A12-H. Due to high polymer concentration, and with the PnBA-block molecular weight (MB) higher than the entanglement molecular weight of PnBA in the melt phase (Me–B ≈ 22 kg mol−1),50 the possibility of PnBA-block entanglements was evaluated. Theoretically, the average number of entanglements per PnBA chain can be estimated as ne ≈ ϕ5/4 (MB/Me–B).18,19,28,29,50 We estimated ne ≈ 0.97 < 1 indicating that there were no significant PnBA entanglements in A12B96A12-H.
3.1 Shear-rheometry on low-ϕ gels
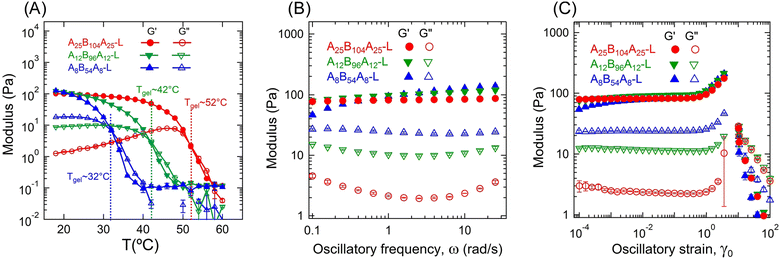
The gelation temperature for all low-ϕ gels was identified using temperature sweep experiments. Fig. 2A shows the evolution of storage (G′) and loss (G″) moduli over a temperature range of 18 to 60 °C for all three low-ϕ gels obtained from these experiments. Fig. 2A is also presented in the high-to-low temperature scale in Fig. S2A (ESI†) to visualize the moduli increase with decreasing temperature. Data at high temperatures were not very reliable, as the measured torque values were near to the instrument limit. However, with decreasing temperature once the torque was in the measurable range, G″ was higher than G′, signifying the liquid-like behavior of the samples. Further decrease in temperature caused an increase in both moduli leading to a crossover of G′ and G″. The crossover temperature has been considered as the gelation temperature (Tgel). The Tgel for A25B104A25-L, A12B96A12-L, and A8B54A8-L were 52 °C, 42 °C, and 32 °C, respectively. At T < Tgel, G′ > G″ signifying the solid-like behavior of the samples. With decreasing temperature, the solubility of the A-block drastically decreased, but the solubility of the B-block mostly remained unchanged.16 To minimize the unfavorable interaction with 2-ethyl-1-hexanol, A-blocks collapsed to form aggregates by associating with other A-blocks. As these aggregates were connected by the B-block, a three-dimensional polymer gel network evolved with the decrease in temperature.The Tgel is dictated by the lengths of A- and B-blocks and chain density. The longer B-blocks facilitate the connectivity between the aggregates of A-blocks by reducing the entropic penalty caused by the stretching of B-blocks. The A-block length governs the strength of aggregates; therefore, the energy required to pullout the longer A-blocks from the aggregates is relatively higher than the shorter A-blocks. This is due to the friction that the A-blocks need to overcome during the pullout process.18 The importance of the above-mentioned factors manifested in the highest Tgel for A25B104A25-L despite the lowest polymer chain density, as A25B104A25 has the longest A- and B-blocks. The smallest A- and B-blocks resulted in the lowest Tgel in A8B54A8-L. Away from Tgel, at room temperature, all three gels displayed similar G′ values, although the polymer concentrations were slightly different. In contrast, the G″ values for three gels did not reach to a similar value over the temperature range investigated here. For T ≤ Tgel, G″ was the lowest for A25B104A25-L, followed by A12B96A12-L, and A8B54A8-L. This can be attributed to the different dissipation behavior in these gels, further discussed below.
It has been shown earlier that the Tgel of the triblock copolymer gels can depend on the applied frequency.22,23 We have not made any attempt to determine the absolute gelation temperature using the Winter–Chambon criterion;51–54 however, physically assembled ABA gels in B-selective solvents have shown not to follow this criterion.22,23
To understand the change in gel moduli subjected to deformation over different time scales, frequency sweep experiments were conducted. In Fig. 2B, G′ and G″ are plotted as a function of ω for three low-ϕ gels. Over the ω-range considered here (0.1–30 rad s−1), G′ did not change significantly, particularly for A25B104A25-L and A12B96A12-L. For A8B54A8-L, a slight increase in G′ with ω was observed. However, as observed in the temperature sweep experiments (Fig. 2A), all these gels displayed similar G′ values, particularly, G′ ≈ 100 Pa at 1 rad s−1. Also, over the frequency range investigated, G″ was the lowest for the A25B104A25-L, followed by A12B96A12-L, and A8B54A8-L. G″ displayed a weak minimum at ω ≈ 3 rad s−1 for all three gels, and this minimum was more prominent for the gels with longer B-blocks.19,55
The pullout of A-blocks can cause energy dissipation, however, that likely was not the case in temperature and frequency sweep experiments since the time scale for the A-block reassociation has been reported to be significantly higher than the time scale associated with the applied strain cycle for the frequencies considered here.56 Therefore, the dissipation here can likely be attributed to the lower bridging fraction caused by poor network connectivity with a higher number of loops and dangling chains rather than elastically active connecting chains of B-blocks.6,8,23,29 Here, a loop refers to a polymer chain for which both A-blocks are connected to the same aggregate. For a chain with only one A-block connected to an aggregate is referred to as a dangling chain. Both loops and dangling chains do not participate in network formation and are often viewed as defects.5,18 The applied mechanical load can lead to increased interactions of loops, dangling chains, and bridges of B-blocks among themselves or with the solvent, mostly in the form of friction, leading to energy dissipation. As a result, the higher fractions of loops and dangling chains dissipate more energy, as energy cannot be stored and transmitted like in the bridging chains.
A8B54A8-L, with the shortest B-blocks, displayed the highest G″ values. At low polymer concentrations, to avoid high stretching of B-blocks, it was entropically favorable to form loops and dangling chains instead of bridging two aggregates. Therefore, a higher polymer concentration was required in this gel in comparison to the other two gels with longer B-blocks to achieve similar G′ values. Although the lengths of B-blocks in A25B104A25-L and A12B96A12-L were comparable and the chain density was higher in A12B96A12-L, a lower dissipation in A25B104A25-L suggests that a stronger association of A-blocks also deterred the energy dissipation in gels. The minima in G″ observed can be attributed to the relaxation behavior of longer B-blocks. A similar trend of minima in G″ was also reported for the cases of other ABA triblock copolymer gels, especially with longer B-blocks.5,19,55,57
The effect of applied shear-strain on these gels was investigated next using amplitude sweep experiments. Fig. 2C displays G′ and G″ plotted as a function of γ0 over a range of 10−4 to 200. Below γ0 ≈ 0.6, G′ almost remained constant at ∼100 Pa for all three gels. However, the ratio of G′ and G″ varied from ≈5 to 50. At γ0 ≥ 0.6, G′ increased with γ0 for all three gels, displaying a strain-stiffening behavior. Interestingly, the maximum strain amplitude that the gels could sustain was similar despite different lengths of A- and B-blocks. Beyond γ0 ≈ 3.6, a drastic decrease of G′ for all three samples was observed along with the phase angle >90°. A video has been presented in the ESI† (VideoRheology.mp4), capturing the oscillatory cycle at which the sample failed and a cycle prior to it with a lower γ0 value for comparison. At failure strain, the gel was ejected out of the rheometer geometry. Therefore, the data for γ0 > 3.6 was not reliable.
The failure of the gel samples in our case has similarities to the edge-fracture typically observed in highly elastic polymer melts.58 The underlying principle leading to such failure behavior in our case needs further investigation, as strain-stiffening behavior has been hypothesized earlier to be related to the finite extensibility of the B-blocks.10,14,15 This is a plausible explanation only for A8B54A8-L, as the length of B-blocks in A8B54A8-L is the shortest and γ0 ≈ 3.6 corresponds to the finite extensibility of B-blocks.14 With an increase in B-block length, the finite extensibility of gel was also expected to increase, as shown previously for the compression tests,7 but not observed for the simple-shear mode considered here.
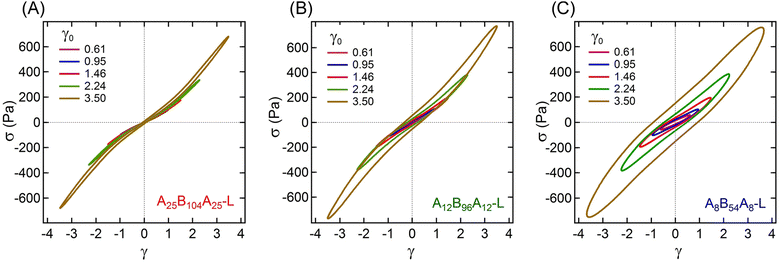
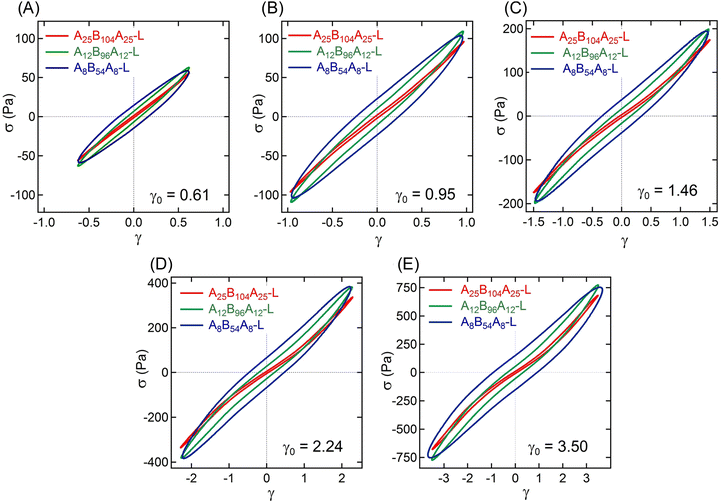
The non-linear rheological responses at high strain amplitude can further be investigated from the intracycle strain responses. Fig. 3A–C display the shear stress–strain (σ–γ) responses, i.e., Lissajous plots, for A25B104A25-L, A12B96A12-L, and A8B54A8-L obtained at γ0 ≈ 0.61, 0.95, 1.46, 2.24, and 3.50. For more clarity, the σ–γ responses of all three gels for a particular γ0 values are shown in Fig. 4. At γ0 = 0.61, the Lissajous plots have been found to be elliptical for all three gels, a typical response in the linear viscoelastic regime (Fig. 2C). The Lissajous plot became non-elliptical for γ0 > 0.6, capturing the non-linear responses.
Decomposing the stress into Fourier series does not provide a clear understanding of the non-linear behavior of a sample;59,60 therefore, we utilized the MITlaos framework. In this framework, the σ–γ response for a particular strain amplitude value is fitted with the Chebyshev polynomial series of the first kind, which is mathematically represented as59
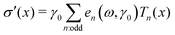 | (1) |
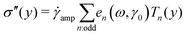 | (2) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) /
/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) amp, Tn represent the nth-order Chebyshev polynomial with en as elastic, and νn as viscous coefficients. Using this framework, we have estimated e1 and e3 from the σ–γ responses, where the e3 values provide an estimate of non-linearity. In the linear viscoelastic regime, e1 ≫ e3 and ν1 ≫ ν3 leading to e1 ≈ G′ and ν1 ≈ G″/ω.59 The higher order harmonics, e5 and e7, were really small in comparison to e1 and are not reported here.
amp, Tn represent the nth-order Chebyshev polynomial with en as elastic, and νn as viscous coefficients. Using this framework, we have estimated e1 and e3 from the σ–γ responses, where the e3 values provide an estimate of non-linearity. In the linear viscoelastic regime, e1 ≫ e3 and ν1 ≫ ν3 leading to e1 ≈ G′ and ν1 ≈ G″/ω.59 The higher order harmonics, e5 and e7, were really small in comparison to e1 and are not reported here.
Fig. 5A represents the e3/e1 as a function of γ0 for all three gels. The e3 values for different γ0 values are also shown in the ESI† (see Table S1). Positive values of e3 at higher γ0 for all gels suggest a strain-stiffening behavior, which increased with γ0. A25B104A25-L and A12B96A12-L displayed a linear increase of e3 with γ0, however, as γ → 2.24, e3 for A8B54A8-L deviated from linearity.
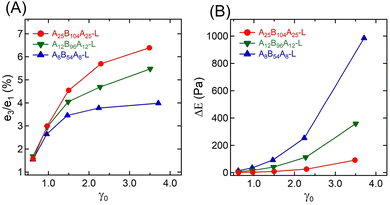 | ||
| Fig. 5 (A) Ratio of Chebyshev elastic coefficients (e3/e1), and (B) energy dissipated (ΔE) over a strain cycle for A25B104A25-L, A12B96A12-L, and A8B54A8-L as a function of γ0 = 0.61–3.50. | ||
The strain-stiffening behavior has been further evaluated by estimating the strain-stiffening ratio, S ≈ 4e3/(e1 + e3).61 As shown in Table S1 in the ESI,† the S value increased with γ0, except for A8B54A8-L, where at the highest γ0, it almost reached a plateau. Over the range investigated here, A25B104A25-L displayed the highest strain-stiffening ratio. The stiffening in these gels has been hypothesized to be related to the non-linear stretchability of B-blocks near their maximum stretchability limit attained before those are pulled out from the aggregates.6,10,14 A higher strain-stiffening ratio in A25B104A25-L, where the maximum extensibility was reached, most likely resulted from the higher fraction of elastically active chains and lower dissipation.
The dissipation in a strain-cycle, representing loading and unloading, can be obtained by estimating the area (ΔE) of the corresponding σ–γ curve. ΔE for γ0 = 0.61–3.50 for three gels are shown in Fig. 5B, providing a quantitative estimate of dissipation (also see the Table S1, ESI†). As observed in Fig. 3 and 4, for a particular strain-cycle, A8B54A8-L displayed the highest area, i.e., the highest dissipation. This was also true for all strain values, whereas, for all cases, A25B104A25-L displayed the lowest dissipation. As discussed above, the frictional interactions of loops, dangling chains within themselves, and with the solvent likely caused the dissipation.
To compare and quantify the stress-relaxation (dissipative) behavior of gels, stress relaxation experiments were conducted. The results are shown in Fig. 6, where the time-dependent shear modulus (G(t)) as a function of time (t) for the three gels is plotted. In order to quantify the stress relaxation behavior, data were fitted with the stretched-exponential model, mathematically represented as:6,12,15,18,19,56
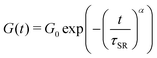 | (3) |
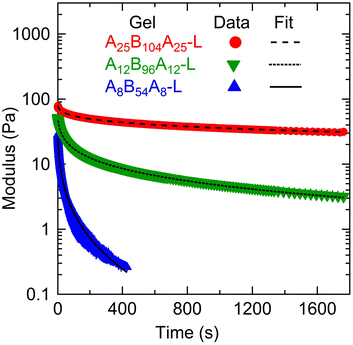 | ||
| Fig. 6 Shear modulus (G(t)) as a function of time (t) for A25B104A25-L, A12B96A12-L, and A8B54A8-L obtained from stress-relaxation experiments for a step-strain of γ0 = 0.01 at ≈27 °C. The lines represent the fitting of the stretched-exponential model (eqn (3)). | ||
| Gel | G 0 (Pa) | τ SR (s) | α |
|---|---|---|---|
| A25B104A25-L | 104 ± 2 | 756 ± 57 | 0.22 ± 0.01 |
| A12B96A12-L | 135 ± 6 | 3.4 ± 0.6 | 0.21 ± 0.00 |
| A8B54A8-L | 120 ± 0 | 0.63 ± 0.05 | 0.28 ± 0.00 |
The stress relaxation in these gels can take place in different manners such as (i) the exchange of A-blocks among the aggregates,6,12,15,18,19 (ii) viscous dissipation resulting from loops and dangling chains as discussed above, and (iii) the relaxation of entangled B-block,5,19 which was not important here. The difference in τSR values signifies that the relaxation time of gels captured using the stress-relaxation experiments was governed by both A- and B-block lengths since the ϕ was not very different. Here, a significant difference in τSR values for A25B104A25-L and A12B96A12-L suggests that the effect of A-block length was more prominent than that of the B-block length. The shorter A-blocks facilitate faster chain exchange among the aggregates leading to faster relaxation, as evident from the response of A8B54A8-L. In addition, higher fractions of loops and dangling chains in A8B54A8-L increased the viscous dissipation and expedited the relaxation behavior.
3.2 Room temperature microstructure of low-ϕ gels
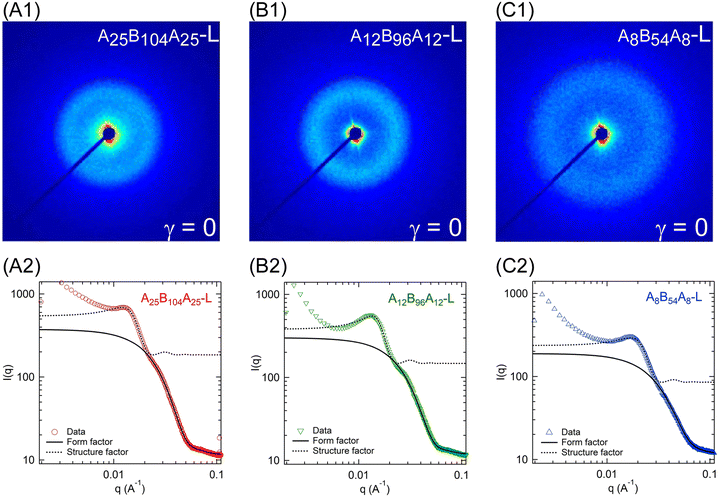
The microstructure of the gels without any applied strain was probed using SAXS experiments and Fig. 7A1–C1 displays the 2D-scattering patterns for A25B104A25-L, A12B96A12-L, and A8B54A8-L at room temperature. Circular scattering patterns in all three samples indicate the isotropic microstructure. For further analysis, the circular averaged intensity (I(q)) as a function of scattering angle (q) was estimated and is shown in Fig. 7A2–C2. The nature of these curves is typical of that of other triblock gels.2,6,9,16,18,19,23 We observed a distinct peak at q ≈ 0.013 Å−1 for A25B104A25-L and A12B96A12-L (Fig. 7A2–C2, and Fig. S3, ESI†). For A8B54A8-L, the peak slightly shifted to higher q at q ≈ 0.017 Å−1. This peak corresponds to the structure factor peak, representing the inter-aggregate scattering. The form factor shoulder, related to the aggregates’ shape and size, was observed at q ≈ 0.028 Å−1 for A25B104A25-L, whereas for A12B96A12-L and A8B54A8-L, the form factor shoulder shifted towards the high q and was located at q ≈ 0.030 Å−1 and q ≈ 0.038 Å−1, respectively (see Fig. S4, ESI†). Data beyond q ≥ 0.06 Å−1 can be related to the secondary reflections or from the local structure of the solvent.16 Compared to the other gels, for A12B96A12-L, the structure factor peak was narrower and the form-factor peak was more prominent.Although not significantly different, the scattering intensities were not equal for all three gels, particularly for the structure factor peak and q-range below that. The intensity of the structure-factor peak was the highest for A25B104A25-L, and the lowest for A8B54A8-L. We have attributed the higher intensity to the less solvated state of aggregates. The scattering data were collected at the laboratory temperature of 27 °C, and this temperature was the farthest from the Tgel of A25B104A25-L but closest to that of A8B54A8-L. It was likely that the distance from Tgel led to slightly different solvation states of the aggregates in three gels. It has been shown earlier that the aggregates expel solvent with decreasing temperature farther from Tgel and the aggregates become glassy.24 As discussed in the later section for temperature-dependent microstructure evolution of A12B96A12-H, the structure factor peak increased with decreasing temperature and then became constant. It was likely that most of the solvent was expelled at that point. This can also be linked to the plateau of G′ observed in the temperature sweep experiments. Once the G′ attains a plateau, the microstructural parameters do not vary significantly.6,45
Note that the experimental temperature of 27 °C was very close to Tgel of 32 °C for A8B54A8-L. However, the temperature sweep data in Fig. 2A indicate that G′ almost reached a plateau at 27 °C. Furthermore, frequency and amplitude sweep experiments were also conducted at 22 °C, and the results were compared with the data obtained at 22 °C (Fig. S5, ESI†). The results at those temperatures were not very different. Therefore, we considered that the data at 27 °C could capture most of the microstructural information for A8B54A8-L.
As shown in Fig. S3 (ESI†), for q ≤ 0.01 Å−1, I(q) ∼ q−3.1–3.3, representing the mass fractal nature of the aggregate clusters. The scattering data of triblock copolymer gels have traditionally been fitted with a polydispersed core hard-sphere model with Percus–Yevick closure.6,16,18,19,23,45,62 This model approximates the gel microstructure consists of spherical aggregates of A-blocks connected by B-blocks. Mathematically, this model is expressed as I(q) ∝ P(q) × S(q), where P(q) is the form factor representing the spherical aggregates with a mean radius rc, and polydispersity of κ/rc. Here, κ is the standard deviation. S(q) is the structure factor capturing the hard-spheres concentric with the aggregates, having a thickness of s and occupying a volume fraction of ψ. With the combined polydispersed core hard-sphere model, a good fit could not be obtained, especially for the gels with low ϕ and for the high q region. This was likely due to weak form factor shoulders for all low-ϕ gels. Therefore, we have fitted the form factor and structure factor models separately. The polydispersed spheres’ form factor model was fitted over 0.022 ≤ q ≤ 0.1 Å−1 to capture the form factor shoulder and the structure factor model was fitted over 0.01 ≤ q ≤ 0.022 Å−1 capturing the peak.
Fig. 7A2–C2 display the fitting and the fitted parameters shown in Table 3. It was estimated that the A25B104A25-L aggregates were the largest and that the A8B54A8-L aggregates were the smallest. The aggregation number, i.e., the average number of A-blocks contributing to form an aggregate can be estimated as (8πρϕNav(rc + s)3)/(3ψM). Here, ρ, Nav, and M represent the polymer density, Avogadro constant, and polymer molecular weight, respectively.6 We estimated aggregation numbers as ≈31, 45, and 41 for A25B104A25-L, A12B96A12-L, and A8B54A8-L, respectively. Clearly, longer A-blocks were responsible for the higher core radius in A25B104A25-L and A12B96A12-L. The inter-aggregate distance (rc + s) for A12B96A12 and A25B104A25-L were similar (≈18.6 nm); however, it was ≈13.2 nm for A8B54A8-L. This estimate followed the B-block length.
| Gel | Sector | γ | β (°) | r c (nm) | s (nm) | ψ |
|---|---|---|---|---|---|---|
| A25B104A25-L | Circle | 0 | 0 | 6.9 | 11.7 | 0.22 |
| Minor-axis | +1 | 35 | 6.9 | 12.3 | 0.22 | |
| Major-axis | +1 | 125 | 6.9 | 12.0 | 0.16 | |
| A12B96A12-L | Circle | 0 | 0 | 6.4 | 12.1 | 0.26 |
| Minor-axis | +1 | 35 | 6.4 | 13.1 | 0.27 | |
| Major-axis | +1 | 125 | 6.4 | 13.1 | 0.25 | |
| A8B54A8-L | Circle | 0 | 0 | 4.0 | 9.2 | 0.21 |
| Minor-axis | +1 | 35 | 4.0 | 9.9 | 0.24 | |
| Major-axis | +1 | 125 | 4.0 | 9.7 | 0.18 |
The end-to-end distance of B-blocks in the gels can be estimated as D − 2rc. Here, inter-aggregate distance, D = [4π (r0 + s)3/(3ψ)]1/3, represents an average center to center distance of the aggregates.6,45 We estimate that D − 2rc ≈ 36.0, 34.0, and 27.6 for A25B104A25-L, A12B96A12-L, and A8B54A8-L, respectively. We can compare D − 2rc values to the B-block end-to-end distance in θ-solvent (Rθ,e–e) to determine whether the chains were in compressed or extended states. The number of Kuhn segments (NB) in each polymer was estimated by considering the Kuhn molecular weight of PnBA-blocks as 0.844 kg mol−1.63 With the Kuhn length of B-block (b ≈ 1.71 nm),63 the end-to-end distance of B-blocks 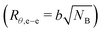 in θ-solvent was estimated as 18.9, 18.1, and 13.6 nm for A25B104A25-L, A12B96A12-L, and A8B54A8-L, respectively. The stretch ratios of B-blocks in the gel can then be estimated as (D − 2rc)/Rθ,e–e ≈ 1.9, 1.9, and 2.0 for A25B104A25-L, A12B96A12-L, and A8B54A8-L, respectively (see Table S2, ESI†). Interestingly, the stretch ratios were similar for all gels despite different B-block lengths. Although 2-ethyl-1-hexanol was considered a θ-solvent, it was most likely a good solvent for the B-blocks. Therefore, the B-blocks were not so highly stretched but were stretched to some extent in the as-prepared gels.
in θ-solvent was estimated as 18.9, 18.1, and 13.6 nm for A25B104A25-L, A12B96A12-L, and A8B54A8-L, respectively. The stretch ratios of B-blocks in the gel can then be estimated as (D − 2rc)/Rθ,e–e ≈ 1.9, 1.9, and 2.0 for A25B104A25-L, A12B96A12-L, and A8B54A8-L, respectively (see Table S2, ESI†). Interestingly, the stretch ratios were similar for all gels despite different B-block lengths. Although 2-ethyl-1-hexanol was considered a θ-solvent, it was most likely a good solvent for the B-blocks. Therefore, the B-blocks were not so highly stretched but were stretched to some extent in the as-prepared gels.
3.3 Evolution of high-ϕ gel microstructure with temperature
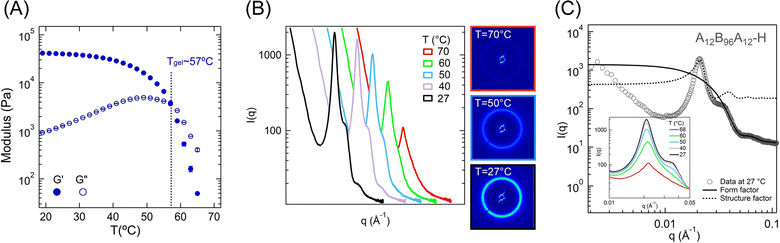
Next, we investigate the microstructure of high-ϕ gel, A12B96A12-H, which displayed a significantly clear scattering pattern in comparison to low-ϕ gels. Fig. 8A displays the evolution of G′ and G″ over a temperature range of 65 °C to 20 °C obtained from shear-rheometry experiments using the same protocol as for low-ϕ gels (see Fig. S2B for high-to-low temperature scale, ESI†). Tgel was identified as ≈57 °C, as increasing the volume fraction from 0.04 to 0.3 led to an increase in gelation temperature by ≈15 °C. Although the strength of PMMA associations is temperature-dependent, an increase in polymer concentration resulted in higher chain density facilitating the network formation. Therefore, the higher polymer volume fraction led to increased gelation temperature, similar to that observed for other types of triblock gels.5,6,15,23 At room temperature, the G′ ≈ 39.4 kPa, which was significantly higher than that obtained for A12B96A12-L. Also, G′ was two orders of magnitude higher than the G″, indicating the elastic nature of the gel.To elucidate the evolution of gel microstructure with temperature, the scattering data were captured during the natural cooling of the polymer solution from ≈70 °C to ≈27 °C, at every ≈5 °C of temperature change. In Fig. 8B, I(q) − q data are plotted for 70, 60, 50, 40, and 27 °C (see Fig. S2C for high-to-low temperature scale, ESI†) and the 2D scattering patterns corresponding to 70, 50, and 27 °C are also shown. In these 2D images, the circular pattern emerged, and the intensity increased with decreasing temperature indicating the formation of an isotropic microstructure, similar to low-ϕ gels discussed above.6,16 The microstructure formation was further evident from the corresponding I(q) − q plots, particularly, the evolution of the structure factor peak at q ≈ 0.02 Å−1 and the development of a form-factor shoulder at q ≈ 0.03 Å−1 (Fig. 8C inset).
Fig. 8C displays I(q) against q at room temperature fitted with polydispersed spheres form factor and hard-sphere structure factor models over the range of 0.02 ≤ q ≤ 0.1 Å−1, similar to low-ϕ gels. For q < 0.01 Å−1, I(q) ∼ q−3.3 captured a rough surface originating from the fractal nature of the polymer network in the gel when observed at large length scales. The hard-sphere structure factor was fitted over the 0.02 ≤ q ≤ 0.03 Å−1, and the polydispersed spheres form factor over 0.035 ≤ q ≤ 0.1 Å−1. Similar to low-ϕ gels, this framework allowed us to reasonably fit the data for all temperatures. A fit for the data at 27 °C is presented in Fig. 8C, and the fitted parameters for all temperatures are provided in Table 4.
| T (°C) | 70 | 65 | 60 | 55 | 50 | 45 | 40 | 35 | 30 | 27 |
|---|---|---|---|---|---|---|---|---|---|---|
| r c (nm) | 3.4 | 4.7 | 4.9 | 5.3 | 7.7 | 7.7 | 8.3 | 8.3 | 8.3 | 8.3 |
| s (nm) | 10.4 | 9.7 | 9.4 | 9.0 | 7.7 | 7.7 | 6.7 | 6.7 | 6.7 | 6.7 |
| ψ | 0.41 | 0.44 | 0.42 | 0.39 | 0.46 | 0.46 | 0.44 | 0.44 | 0.44 | 0.44 |
| κ/rc | 0.5 | 0.5 | 0.5 | 0.47 | 0.21 | 0.21 | 0.16 | 0.16 | 0.16 | 0.16 |
The appearance of an inter-aggregate peak at T > Tgel suggests the presence of already formed aggregates. This indicates that the gelation in these systems takes place over a temperature range and that is likely the reason the Winter–Chambon criterion is not applicable for this system.22,23 Above Tgel, the aggregates were loosely associated and swollen with solvent.6,8,16 With the decrease in T from 70 to 40 °C, rc increased from 3.4 nm to 8.3 nm, indicating that more A-blocks were associated, forming bigger aggregates. Consequentially, a decrease in s can be observed from 10.4 nm to 6.7 nm and ψ slightly increased from 0.41 to 0.44. The polydispersity (κ/rc) also changed from 0.50 to 0.16, signifying a narrower distribution in aggregate radius with decreasing temperature. For T < 40 °C, the fitted parameters did not change significantly (rc ≈ 8.3 nm, s ≈ 6.7 nm, and ψ ≈ 0.44). Therefore, below 40 °C, gel structure remained mostly unchanged up to the room temperature, also manifested by a plateau in G′, as indicated above.
Over 70–27 °C, the end-to-end length of B-block (D0 − 2rc) decreased from 23.2 to 15.3 nm. With Rθ,e–e ≈ 18.1 nm, it was estimated that (D0 − 2rc)/Rθ,e–e ≈ 0.85 < 1; therefore, the B-blocks were slightly compressed in A12B96A12-H, in comparison to slightly stretched chains in low-ϕ gels. In A12B96A12-H, the longer B-blocks and high aggregate density resulted in a compressed state of B-blocks.
3.4 Effect of oscillatory strain on gel microstructure
The change in the gel microstructure with applied strain was investigated using RheoSAXS experiments. Fig. 9A represents the G′ and G″ evolution as a function of γ0. Over the γ0 range studied here, no significant changes in G′ and G″ were observed. Beyond γ0 > 1, the failure of gels takes place similar to that observed for low-ϕ gels. However, strain-stiffening behavior could not be captured here. Also, the failure took place at a much lower strain than low-ϕ gels, further indicating that gel failure in our case was not completely related to the midblock length and their finite extensibility.To ensure that the data collection time was lower than the gel relaxation time, the stress relaxation experiment was also conducted on this gel (Fig. S6, ESI†). By fitting eqn (3), we obtained G0 = 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231 Pa, τSR = 5328 s, and α = 0.26. The scattering data collection time (≈0.03 s) was much shorter than the stress relaxation time; therefore, the scattering data were mostly unaffected by the stress relaxation process.
231 Pa, τSR = 5328 s, and α = 0.26. The scattering data collection time (≈0.03 s) was much shorter than the stress relaxation time; therefore, the scattering data were mostly unaffected by the stress relaxation process.
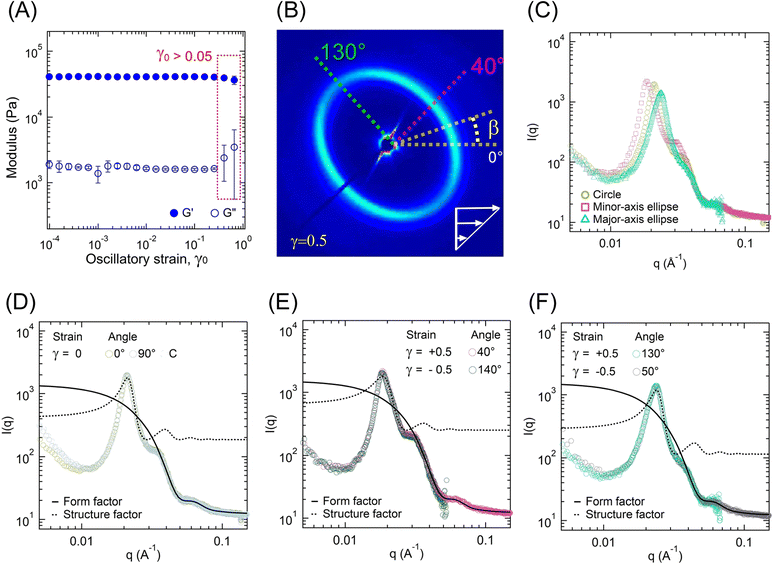
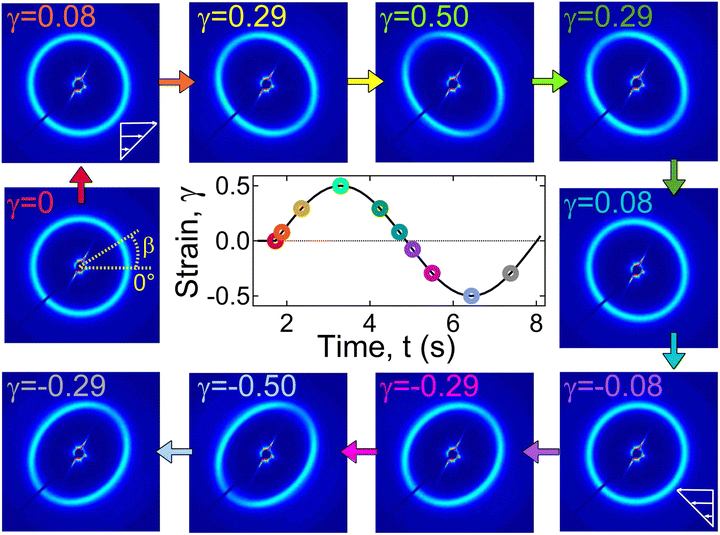
Fig. 10 displays the 2D scattering patterns within a strain cycle for γ0 = 0.5 applied at a frequency of 1 rad s−1 for different intracycle-strain (γ) values. For γ = 0, the 2D pattern was circular. With an increase in γ from 0 to 0.5, the circular pattern transformed into an elliptical one. The major axis of the ellipse was along the β-angle of 130°, whereas the minor axis was along β ≈ 40°. The pattern returned to the isotropic structure as γ decreased from 0.5 to 0. During the negative half-cycle of strain (0 ≤ γ ≤ |−0.5|), the 2D pattern displayed the same qualitative behavior. It was elongated along the β ≈ 50° (major-axis), and the minor-axis was along β ≈ 140°. Because of the unique configuration of our system, the 2D scattering profiles captured data along the 1–2 plane, where “1” is the stretch direction, and “2” is the direction orthogonal to that. Therefore, the observed transition from a circular to an elongated pattern captured the change in orientation of the microstructure with applied strain.
The oriented 2D scattering profiles, an example of one presented in Fig. 9B for γ = +0.5, were investigated further for various azimuthal angles. We used a sector β ± 5° to estimate an average I(q) vs. q for that β-angle (see Fig. 9C). The circular average of I(q) − q data for γ = 0 was compared with those at |γ| = 0.5 along the major- and minor axes (Fig. 9C). For the isotropic pattern at γ = 0, a sector average at any angle and the circularly averaged data mostly overlapped (Fig. 9D). As shown in Fig. 9E, for γ = ±0.5, the sectors along minor-axis of the ellipse (βγ=0.5 ≈ 40°, βγ=−0.5 ≈ 140°) also overlapped. Similarly, Fig. 9F displays the overlapped curves along the major-axis (βγ=+0.5 ≈ 130°, βγ=−0.5 ≈ 50°).
The overlap of I(q) − q data suggests that the extent of change in microstructure was independent of the strain direction and solely dependent on the strain amplitude (|γ|). The structure factor peak corresponding to the circular pattern (γ = 0) was at q ≈ 0.021 Å−1, which for |γ| = 0.5 shifted to 0.024 Å−1 with slightly lower intensity for the major-axis, and to 0.018 Å−1 with slightly higher intensity for the minor-axis (Fig. 9C). For each case, data were collected for three strain cycles, and the 2D patterns were found to be similar for each cycle. This suggests that the structural changes during the strain cycles were completely reversible.
The polydispersed spheres’ form factor and hard-sphere structure factor models were fitted individually over 0.035 ≤ q ≤ 0.1 Å−1 and 0.01 ≤ q ≤ 0.03 Å−1, respectively (Fig. 9D–F). The fitted parameters are shown in Table 5. The parameters for γ = 0 were similar to those estimated from the temperature sweep data at 27 °C (Table 4). Within a strain-cycle, the rc value did not change significantly, indicating that the aggregates remained intact and no significant pullout events of A-blocks occurred that could potentially reduce the rc. The hard-sphere thickness increased along the minor axis and decreased along the minor axis in comparison to the radius of the circle at γ = 0. This suggests that the aggregates became oriented along the applied strain direction, manifested by the formation of a minor axis. To conserve the volume, compression took place in the orthogonal direction, manifested by the elongation along the major axis. A schematic of this process is displayed in Fig. S7 (ESI†).
| Direction | γ | β (°) | r c (nm) | s (nm) | ψ |
|---|---|---|---|---|---|
| Circle | 0 | 0 | 8.3 | 6.7 | 0.44 |
| Minor-axis | +0.5 | 40 | 8.3 | 5.4 | 0.45 |
| Major-axis | +0.5 | 130 | 8.5 | 8.2 | 0.42 |
The inter-aggregate distances along the minor- and major axes were estimated as Dm = 36.0 and DM = 28.8 nm, respectively, representing the stretching and compression of chains between the aggregates. Consecutively, the stretch and compression ratios have been calculated as Dm/D0 and DM/D0, equal to 1.12 and 0.90, respectively. These ratios can be compared with the applied deformation by converting γ to the elongation ratio (λ) as γ = λ − λ−1.64 Using the affine deformation model, for γ = 0.5, we obtain λ = 1.25 and −0.75, for the stretching and compression, respectively. The affine model predicts a slightly higher extension ratio in comparison to the experimental data. This can be attributed to the inhomogeneities in the gel microstructure leading to an uneven distribution of strain within the gel.
For the low-ϕ gels, we also attempted to capture the microstructural evolution within a strain cycle. Fig. S8A1–C1 (ESI†) displays the 2D-scattering patterns for A25B104A25-L, A12B96A12-L, and A8B54A8-L at γ = +1 (maximum inrtracycle strain for γ0 = 1) applied at ω = 1 rad s−1. Instead of a clear elliptical pattern observed for A12B96A12-H, mostly a circular pattern was observed here. We have estimated I(q) − q along β ≈ 125° and along β ≈ 35° with a sector dβ = ±5° (Fig. S8A1, ESI†), similar to the protocol applied for A12B96A12-H. Both those profiles were not very different from the circular averaged plot for γ = 0 (see Fig. S9A–C, ESI†) over the 0.01 ≤ q ≤ 0.08 Å−1, therefore, RheoSAXS experiments could not capture deformed microstructure very well, although we observed distinct strain-induced rheological signals. In addition, Fig. S10 (ESI†) represents the normalized intensity (I(β)) plotted as a function of azimuthal angle (β) over the q range of 0.01–0.05 Å−1 for the cases of γ = 0 and γ = 1. Again, these curves were not significantly different. To investigate closely, I(q) − q curves were also fitted with polydispersed spheres form factor and hard-sphere structure factor (see Fig. S8, ESI†). The fitted parameters for with and without applied strain were very similar (Table 3). No apparent difference in strain-induced microstructure could be a result of low polymer concentration and corresponding weaker signal. The signal intensities could have been improved by increasing the data collection time. However, that may not be practical for collecting data within a strain cycle.
As the microstructure became elliptical (anisotropic) during the application of strain, we can estimate microstructure anisotropic factor (Ω) and angle (χ) from the 2D-scattering patterns for better understanding. We have considered the region 0.015 ≤ q ≤ 0.025 Å−1 encompassing the structure factor peak shift with applied γ (see Fig. 9C). Averaging the intensity over this q range provides I(β) as a function β.42,45 For the unoriented or slightly oriented microstructure, the I(β) − β curve would generally be flat while axis-symmetric peaks were reported for the oriented microstructure.43,45Ω captures the degree of orientation in the microstructure, whereas χ represents the orientation direction with respect to the applied strain direction. Mathematically,42,44
| Ω = [(〈qx2〉 − 〈qy2〉)2 + 4〈qxqy〉2]1/2 | (4) |
| χ = 0.5 tan−1(2〈qxqy〉/(〈qx2〉 − 〈qy2〉)). | (5) |
Here, ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) =
= ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) x + iqy corresponds to a point in the azimuthal plot of intensity I(β) making an angle β from the qx axis. The average values can be estimated as42,44,45
x + iqy corresponds to a point in the azimuthal plot of intensity I(β) making an angle β from the qx axis. The average values can be estimated as42,44,45
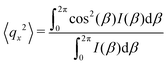 | (6) |
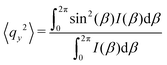 | (7) |
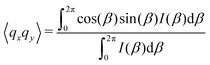 | (8) |
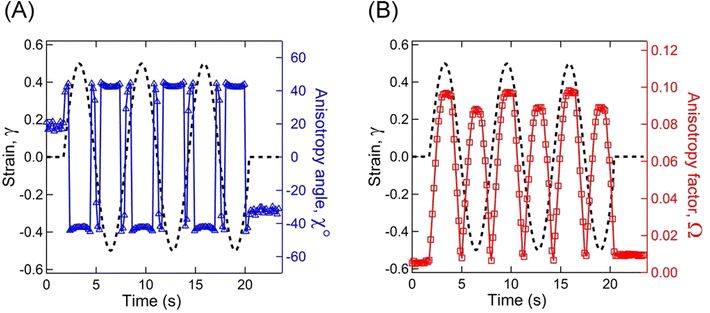
Fig. 11A represents the γ and χ as a function of time displaying a microstructure orientation along the stretch direction at ≈40° as soon as γ was applied for A12B96A12-H. Similarly, Fig. 11B displays γ and Ω as a function of time. With an increase in |γ|, a smooth increase in Ω can be observed from ≈0.01 to ≈0.10, which returned to the initial value as γ approaches 0.
The results for high-ϕ gel can be compared with our previous study of PS–PI–PS gels,45 where not all the PI-blocks stretched in high intracycle strain values. In that study, a fraction of aggregates oriented along the strain direction while the rest returned to their original position in a strain cycle, resulting in a combination of circular and elliptical patterns in the scattering profiles. On the contrary, in the present case, all the B-block bridges appeared to participate in load-bearing since only an elliptical pattern was observed at a high strain value. The difference can likely be attributed to the long and flexible PI-blocks (662 Kuhn segments), in comparison to shorter PnBA-blocks here (123 Kuhn segments in A25B104A25),50 likely leading to higher inhomogeneity in the microstructure of PS–PI–PS gels. One more factor could be the higher segregation energy of PMMA-blocks in 2-ethyl-1-hexanol (≈550 kJ mol−1)6,26 in comparison to that of PS in mineral oil (≈220 kJ mol−1),19 which led to a stronger association of PMMA endblocks in the gels investigated here. This can be further investigated for PMMA–PnBA–PMMA or other triblock gels in the future, where the solvent quality for the blocks will be varied systematically, and the corresponding strain-dependent microstructure will be investigated.
4 Conclusions
The gelation, rheological properties, and microstructure for three PMMA–PnBA–PMMA triblock copolymers (denoted as ABA) viz., A25B104A25, A12B96A12, and A8B54A8 in a B-block selective solvent, 2-ethyl-1-hexanol, have been investigated. At a lower polymer concentration, the polymer volume fractions for each polymer were tweaked such that their low-strain shear modulus remained similar. The longer B-blocks facilitated the formation of a connected network leading to an increase in Tgel, even with a lower density of polymer chains. The A-block lengths were responsible for the aggregation strength; therefore, with an increase in their length, the stress relaxation time increased significantly. Despite differences in their B-block length, all gels displayed similar strain for the onset of non-linearity and failure. A gel with a polymer concentration of 30% (v/v), A12B96A12-H, was investigated for microstructural change as a function of temperature and intracycle strain, as the scattering patterns were distinct due to a higher number of aggregates. Our investigation indicates that the microstructural change with temperature became negligible once the system reached room temperature, away from Tgel. In an applied strain cycle, the microstructure is oriented with the applied strain and returned to its original state when the intracycle strain value was zero. The oriented microstructure resulted in an elliptical scattering pattern. The aggregates became oriented at an angle of 40° with the direction of applied strain while attaining an anisotropic factor value of 0.1. In summary, we captured the microstructure and its evolution with the change in temperature and applied strain for PMMA–PnBA–PMMA gels at different volume fractions and molecular weights. The results have some similarities to those obtained for the PS–PI–PI gels, but the microstructural response in an applied strain cycle was different. The underlying factors causing the differences in microstructural responses need further investigation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation [DMR-2004501, DMR-1352572]. and RheoSAXS experiments were performed at the DuPont–Northwestern–Dow Collaborative Access Team (DND-CAT) located at Sector 5 of the Advanced Photon Source (APS). DND-CAT is supported by Northwestern University, The Dow Chemical Company, and DuPont de Nemours, Inc. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract no. DE-AC02-06CH11357. Data were collected using an instrument funded by the National Science Foundation under Award Number 0960140. We acknowledge Dr Steven Weigand for assisting in the RheoSAXS experiments.References
- J. L. Adams, W. W. Graessley and R. A. Register, Macromolecules, 1994, 27, 6026–6032 CrossRef CAS.
- J. H. Laurer, J. F. Mulling, S. A. Khan, R. J. Spontak and R. Bukovnik, J. Polym. Sci., Part B: Polym. Phys., 1998, 36, 2379–2391 CrossRef CAS.
- J. H. Laurer, J. F. Mulling, S. A. Khan, R. J. Spontak, J. S. Lin and R. Bukovnik, J. Polym. Sci., Part B: Polym. Phys., 1998, 36, 2513–2523 CrossRef CAS.
- J. H. Laurer, S. A. Khan, R. J. Spontak, M. M. Satkowski, J. T. Grothaus, S. D. Smith and J. S. Lin, Langmuir, 1999, 15, 7947–7955 CrossRef CAS.
- D. A. Vega, J. M. Sebastian, Y. L. Loo and R. A. Register, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 2183–2197 CrossRef CAS.
- M. E. Seitz, W. R. Burghardt, K. T. Faber and K. R. Shull, Macromolecules, 2007, 40, 1218–1226 CrossRef CAS.
- M. E. Seitz, D. Martina, T. Baumberger, V. R. Krishnan, C.-Y. Hui and K. R. Shull, Soft Matter, 2009, 5, 447–456 RSC.
- R. E. Bras and K. R. Shull, Macromolecules, 2009, 42, 8513–8520 CrossRef CAS.
- M. E. Seitz, R. L. Rottsolk and K. R. Shull, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 1395–1408 CrossRef CAS.
- K. A. Erk, K. J. Henderson and K. R. Shull, Biomacromolecules, 2010, 11, 1358–1363 CrossRef CAS PubMed.
- K. A. Erk and K. R. Shull, Macromolecules, 2011, 44, 932–939 CrossRef CAS.
- K. A. Erk and J. F. Douglas, MRS Proc., 2012, 1418, Mrsf11-1418-ll01-02 CrossRef.
- K. A. Erk, J. D. Martin, Y. T. Hu and K. R. Shull, Langmuir, 2012, 28, 4472–4478 CrossRef CAS.
- S. Hashemnejad and S. Kundu, Soft Matter, 2015, 11, 4315–4325 RSC.
- M. Zabet, S. Mishra and S. Kundu, RSC Adv., 2015, 5, 83936–83944 RSC.
- M. Zabet, S. Mishra, R. Boy, K. B. Walters, A. K. Naskar and S. Kundu, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 877–887 CrossRef CAS.
- A. J. Peters and T. P. Lodge, Macromolecules, 2016, 49, 7340–7349 CrossRef CAS.
- S. Mishra, R. M. Badani Prado, T. E. Lacy and S. Kundu, Soft Matter, 2018, 14, 7958–7969 RSC.
- S. Mishra, R. M. Badani Prado, S. Zhang, T. E. Lacy, X. Gu and S. Kundu, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 1014–1026 CrossRef CAS.
- S. Rattan and A. J. Crosby, Extreme Mech. Lett., 2018, 24, 14–20 CrossRef.
- S. Rattan and A. J. Crosby, ACS Macro Lett., 2019, 492–498 CrossRef CAS PubMed.
- Y. N. Ye, K. Cui, T. Indei, T. Nakajima, D. Hourdet, T. Kurokawa and J. P. Gong, Macromolecules, 2019, 52, 8651–8661 CrossRef CAS.
- S. Mishra, R. M. Badani Prado and S. Kundu, ACS Appl. Polym. Mater., 2020, 53, 5388–5397, DOI:10.1021/acsapm.0c00583.
- P. L. Drzal and K. R. Shull, Macromolecules, 2003, 36, 2000–2008 CrossRef CAS.
- R. A. Mrozek, B. Leighliter, C. S. Gold, I. R. Beringer, J. H. Yu, M. R. VanLandingham, P. Moy, M. H. Foster and J. L. Lenhart, J. Mech. Behav. Biomed. Mater., 2015, 44, 109–120 CrossRef CAS.
- K. Inomata, D. Nakanishi, A. Banno, E. Nakanishi, Y. Abe, R. Kurihara, K. Fujimoto and T. Nose, Polymer, 2003, 44, 5303–5310 CrossRef CAS.
- L. A. Rankin, B. Lee and K. P. Mineart, J. Polym. Sci., 2021, 59, 34–42 CrossRef CAS.
- T. L. Chantawansri, T. W. Sirk and Y. R. Sliozberg, J. Chem. Phys., 2013, 138, 1–11 CrossRef PubMed.
- T. L. Chantawansri, T. W. Sirk, R. A. Mrozek, J. L. Lenhart, M. Kröger and Y. R. Sliozberg, Chem. Phys. Lett., 2014, 612, 157–161 CrossRef CAS.
- Z. I. Kalcioglu, M. Qu, K. E. Strawhecker, T. Shazly, E. Edelman, M. R. Vanlandingham, J. F. Smith and K. J. Van Vliet, Philos. Mag., 2011, 91, 1339–1355 CrossRef CAS.
- J. Y. Chen, Tear Resistant Gels, Composites, and Cushion Articles, US Pat., 7222380, 2007 Search PubMed.
- J. Ford and T. Wesbey, Gel-filled Shoe Sole Inserts, US Pat., US D612,139 S, 2010.
- M. E. Seitz, PhD thesis, Northwestern University, 2009.
- D. Trivedi, C. D. Rahn, W. M. Kier and I. D. Walker, Appl. Bionics. Biomech., 2008, 5, 99–117 CrossRef.
- R. M. Badani Prado, S. Mishra, B. Morgan, R. Wijayapala, S. M. Hashemnejad and S. Kundu, ACS Appl. Mater. Interfaces, 2020, 12, 40719–40727 CrossRef PubMed.
- J. Chen, Y. Ao, T. Lin, X. Yang, J. Peng, W. Huang, J. Li and M. Zhai, Polymer, 2016, 87, 73–80 CrossRef CAS.
- L. Peng, T. Liu, S. Liu, Y. Han, X. Li, N. Guang and W. Sheng, J. Polym. Res., 2015, 22, 1–12 CrossRef CAS.
- P. A. Janmey, M. E. McCormick, S. Rammensee, J. L. Leight, P. C. Georges and F. C. MacKintosh, Nat. Mater., 2007, 6, 48–51 CrossRef CAS PubMed.
- J.-M. Y. Carrillo, F. C. MacKintosh and A. V. Dobrynin, Macromolecules, 2013, 46, 3679–3692 CrossRef CAS.
- S. Hashemnejad and S. Kundu, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 1767–1775 CrossRef CAS.
- S. M. Hashemnejad and S. Kundu, Soft Matter, 2019, 15, 7852–7862 RSC.
- F. E. Caputo and W. R. Burghardt, Macromolecules, 2001, 34, 6684–6694 CrossRef CAS.
- K. M. Weigandt, L. Porcar and D. C. Pozzo, Soft Matter, 2011, 7, 9992 RSC.
- M. K. Sing, M. J. Glassman, X. T. Vronay-Ruggles, W. R. Burghardt and B. D. Olsen, Soft Matter, 2017, 13, 8511–8524 RSC.
- R. M. B. Prado, S. Mishra, H. Ahmad, W. R. Burghardt and S. Kundu, Macromolecules, 2021, 54, 8946–8959 CrossRef CAS.
- M. E. Seitz, W. R. Burghardt and K. R. Shull, Macromolecules, 2009, 42, 9133–9140 CrossRef CAS.
- F. Zhang, J. Ilavsky, G. G. Long, J. P. Quintana, A. J. Allen and P. R. Jemian, Metall. Mater. Trans. A, 2010, 41, 1151–1158 CrossRef.
- J. Ilavsky, J. Appl. Crystallogr., 2012, 45, 324–328 CrossRef CAS.
- S. R. Kline, J. Appl. Crystallogr., 2006, 39, 895–900 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer Physics, 2003 Search PubMed.
- H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367–382 CrossRef CAS.
- J. M. Yu, P. Dubois, P. Teyssié, R. Jérôme, S. Blacher, F. Brouers and G. L'Homme, Macromolecules, 1996, 29, 5384–5391 CrossRef CAS.
- H. Soenen, H. Berghmans, H. Winter and N. Overbergh, Polymer, 1997, 38, 5653–5660 CrossRef CAS.
- T. Sato, H. Watanabe and K. Osaki, Macromolecules, 2000, 33, 1686–1691 CrossRef CAS.
- A. Noro, Y. Matsushita and T. P. Lodge, Macromolecules, 2008, 41, 5839–5844 CrossRef CAS.
- T. L. Thornell, B. A. Helfrecht, S. A. Mullen, A. Bawiskar and K. A. Erk, ACS Macro Lett., 2014, 3, 1069–1073 CrossRef CAS.
- Y. Lei and T. P. Lodge, Soft Matter, 2012, 8, 2110–2120 RSC.
- C. Macosko, R. Larson and K. (Firm), Rheology: Principles, Measurements, and Applications, VCH, 1994 Search PubMed.
- R. H. Ewoldt, PhD thesis, Massachusetts Institute of Technology, 2009.
- K. Hyun, M. Wilhelm, C. O. Klein, K. S. Cho, J. G. Nam, K. H. Ahn, S. J. Lee, R. H. Ewoldt and G. H. McKinley, Prog. Polym. Sci., 2011, 36, 1697–1753 CrossRef CAS.
- R. H. Ewoldt, A. E. Hosoi and G. H. McKinley, J. Rheol., 2008, 52, 1427 CrossRef CAS.
- N. Mischenko, K. Reynders, M. H. J. Koch, K. Mortensen, J. S. Pedersen, F. Fontaine, R. Graulus and H. Reynaers, Macromolecules, 1995, 28, 2054–2062 CrossRef CAS.
- Z. Huo, S. J. Skala, L. Falck, J. E. Laaser and A. Statt, 2021, DOI:10.48550/arXiv.2110.12070.
- L. R. Treloar, The Physics of Rubber Elasticity, Oxford University Press, USA, 1975 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The vial inversion test for the determination of critical micelle volume fractions; temperature sweep and SAXS curves with a high-to-low temperature axis; comparison of amplitude and frequency sweep data at 22 and 27 °C; I(q) − q data for low-ϕ gels; I(q) − q data for low-ϕ gels shifted along the y-axis; I(q) − q data for high-ϕ gels fitted with the polydispersed core hard-sphere model; stress relaxation of high-ϕ gels; schematic of the microstructural change with applied strain; scattering plots and I(q) − q data for low-ϕ gels subjected to strain and the corresponding model fit; I(q) − q plots for low-ϕ displaying overlapping of scattering data; normalized I(β) − β plots for low-ϕ gels; table displaying nonlinear rheology parameters for low-ϕ gels; table displaying details regarding the polymers and estimated parameters obtained by fitting low-ϕ gels scattering data; and a video capturing gel fracture subjected to oscillation strain. See DOI: https://doi.org/10.1039/d2sm00567k |
| This journal is © The Royal Society of Chemistry 2022 |