Shrinking rates of polymer gels composed of star-shaped polymers of N-isopropylacrylamide and dimethylacrylamide copolymers: the effect of dimethylacrylamide on the crosslinking network†
Yuka
Hiei
a,
Ikuya
Ohshima
a,
Mitsuo
Hara
 a,
Takahiro
Seki
a,
Taiki
Hoshino
a,
Takahiro
Seki
a,
Taiki
Hoshino
 b and
Yukikazu
Takeoka
*a
b and
Yukikazu
Takeoka
*a
aGraduate School of Engineering Nagoya University, Furo-cho, Chikusaku, Nagoya 464-8603, Japan. E-mail: ytakeoka@chembio.nagoya-u.ac.jp; Fax: +81-52-789-4669; Tel: +81-52-789-4670
bRIKEN SPring-8 Center, Sayo, Hyogo 679-51982, Japan
First published on 13th June 2022
Abstract
Thermoresponsive polymer gels can be applied as culture beds for cell sheets, drug release agents for drug delivery, and sensing materials. In general, the shrinkage behavior of thermoresponsive polymer gels is complex, and they may require much longer times than swelling to reach thermodynamically stable shrinkage states. This slow volume change during shrinkage is often a drawback in using reversible changes in polymer gel volumes with changing temperature for applications such as those described above, and attempts have been made to improve the shrinkage rates of polymer gels. However, using the conventional method results in a low density of the three-dimensional crosslinked network comprising the polymer gel, which weakens the mechanical properties of the polymer gel. In this study, we investigated the effects of monomer arrangement and composition for star-shaped polymers composed of N-isopropylacrylamide and N,N-dimethylacrylamide on the shrinkage behavior of gels comprising star-shaped polymers with the aim of increasing their shrinkage rates without reducing the network densities of the temperature-responsive polymer gels. Based on selective network decomposition by methanolysis and SAXS measurements, the network structures of the obtained spherical gels were found to be more homogeneous than those of polymer gels obtained by conventional free radical polymerization. These gels exhibited reversible volume changes in water, with low-temperature swelling and high-temperature shrinkage. The rates of volume changes from a high temperature shrunken state to a low temperature swollen one were almost the same for all gels. However, the rates of volume changes from low-temperature swollen states to high-temperature shrunken states varied greatly depending on the compositions and sequences of monomers that made up the polymer networks. We confirmed that the introduction of more than 20% DMA as a block copolymer in the network suppressed phase separation and formation of a skin layer and the water inside the polymer gel drained smoothly to the outside, which resulted in an increase in the shrinkage speed.
1. Introduction
Thermoresponsive polymer gels reversibly and significantly change their volume at a certain temperature in aqueous solution and exhibit significant changes in physicochemical properties such as solvent retention capacity and surface hydrophilicity/hydrophobicity.1–3 Application of the temperature responsiveness of these polymer gels as culture beds for cell sheets,4 drug release agents for drug delivery,5 and sensing materials6–8 has been investigated. The swelling behavior of a temperature-responsive polymer gel, which increases its volume in solution, can be explained to some extent by the collective diffusion equation described by the Tanaka–Filmore theory,9 which shows a relatively smooth change. On the other hand, shrinkage of a temperature-responsive polymer gel is complex: spinodal decomposition and phase separation with nucleation inside the polymer gel, skin phase formation on the surface of the polymer gel, and bubble pattern formation can occur during shrinkage.10,11 Therefore, a much longer time may be required for the polymer gel to reach a thermodynamically stable collapsed state compared to that required for reaching the swollen state. This slow volume change occurring during shrinkage is often a disadvantage when using temperature-induced reversible changes of polymer gel volumes for applications such as those described above, and attempts have been made to improve the shrinkage rates of polymer gels. Attempts have been made to prepare polymer gels in a phase-separated state,12 to apply pores to polymer gels13,14 and to introduce dangling chains with one end unbound to the polymer gel,15–17 all of which reduce the three-dimensional crosslinked network density that constitutes the polymer gel. As a result, the mechanical properties of the polymer gel are weakened. If the polymer gel that exhibits reversible changes in volume is mechanically weak, repeated use can lead to destruction of the polymer gel. Therefore, it is necessary to increase the response speed of the temperature-responsive polymer gel while avoiding degradation of its mechanical performance.In addition, based on the mechanism for forming crosslinked networks of polymer gels by conventional free radical polymerization, the network structures can include dangling chains in which one end is not connected to the crosslinking point, looped chains in which both ends are connected to one crosslinking point and hang down, and network chains that are not resolved by the constraint of the crosslinking point entanglements.18,19 Furthermore, there is also spatial sparsity in the network structure, and the actual network structure is extremely heterogeneous compared to the ideal homogeneous network structure used in classical theory. Therefore, it is not easy to discuss the behavior of crosslinked networks in polymer gels with respect to mechanical properties and temperature changes due to structural changes of the networks occurring at the molecular level. If we can construct a crosslinked network with the smallest polymer unit for which the structure is controlled at the molecular level, we may be able to explain macroscopic changes in polymer gels with respect to the behavior of polymer chains.17,20–25
In previous studies, we reported that star-shaped polymers obtained from living radical polymerization, which enables precise syntheses of polymers, can be combined under conditions appropriate for obtaining polymer gels with more homogeneous network structures than polymer networks obtained by conventional free radical polymerization.26–28 Using living radical polymerization, star-shaped polymers consisting of block copolymers as well as random copolymers consisting of multiple monomers can be synthesized. In particular, polymer gels composed of block copolymers containing a temperature-responsive polymer (PNIPA) of N-isopropylacrylamide (NIPA) and a water-soluble polymer (PDMA) of N,N-dimethylacrylamide (DMA), as well as polymer gels comprising star-shaped random copolymers of these monomers as building blocks, can be prepared.28
In this study, we investigated the effects of monomer arrangement and composition of star-shaped polymers composed of NIPA and DMA on the shrinkage behaviors of thermoresponsive polymer gels, with the aim of accelerating shrinkage rates without reducing the network densities. These polymer gels were processed into spherical shapes to facilitate evaluations of their kinetics.11 All of the obtained spherical gels showed behaviors that can be explained by the Tanaka–Filmore theory, including swelling changes brought about by abrupt conversion from a high-temperature shrunken state to a low-temperature swollen state. The collective diffusion coefficients of those polymer networks were 2.0–2.5 × 10−6 cm2 s−1 and were not significantly affected by composition or arrangements of the monomers constituting the crosslinked network. On the other hand, shrinkage of spherical polymer gels from the low-temperature swelling state to the high-temperature shrinkage state was brought about by an abrupt temperature change, and this behavior was significantly affected by composition and arrangements of the monomers constituting the crosslinked network. Among the block copolymers forming the spherical gels studied in this study, a greater PDMA proportion was more likely to generate more isotropic shrinkage and less likely to generate a phase-separated state. As a result, polymer gels composed of block copolymers containing 20% and 30% DMA based on the number of monomers were always transparent to the naked eye during shrinkage, and the volume changes during shrinkage were rapid. We succeeded in producing polymer gels exhibiting rapid shrinkage without reducing the density of the 3D polymer network.
2. Experiments
Chemicals
N-Isopropylacrylamide (NIPA) and N,N-dimethylacrylamide (DMA) were provided by Kohjin, and the ligand tris(2-dimethylaminoethyl)amine (Me6TREN) was provided by Mitsubishi Chemical. DMA and Me6TREN were purified by vacuum distillation before use. The catalyst CuCl was purchased from Kishida Chemical. Purification methods for NIPA and CuCl are described in the ESI.† Pentaerythritol tetra(2-chloropropionate) (PETCP), a tetrabranched initiator, was purchased from Tokyo Chemical Industry Co. Ammonium persulfate (APS) was commercially obtained from ICN Biomedicals Inc. Silicone fluids (KF-96 L-2cs, KF-96-20cs, KF-96-50cs, KF-96-100cs) were provided by Shin-Etsu Chemical, and surfactant DOWSIL™ RSN-0749 Resin12 was provided by Dow Toray Industries, Inc. HCl (12 N), N,N-dimethylformamide (DMF), and toluene were purchased from Kanto Chemical, and hexane, methanol, diethyl ether, and tetrahydrofuran (THF) were purchased from Kishida Chemical. Na2CO3 and methanol were purchased from Kishida Chemical. DMF was purified by vacuum distillation before use. The water used was ultrapure water (specific resistance: 18.2 MΩ cm) purified with a Millipore Direct-Q system (Merck), and ion-exchanged water was obtained by passing tap water through a G-5C cartridge purchased from Organo.Measurements
Preparation of spherical gels with tetrabranched star-shaped polymers as building blocks
The syntheses of tetrabranched star-shaped polymers utilized the method described in our previous paper and also in the ESI† (Fig. 1a).26,28 Among the tetrabranched star-shaped polymers, we synthesized a NIPA homopolymer (tetrabranched PNIPA), a block copolymer of NIPA and DMA (tetrabranched PNIPA1−x-b-PDMAx), and a random copolymer of NIPA and DMA (tetrabranched PNIPA1−x-r-PDMAx). Herein, the subscript x is the number of monomer units contained in the star-shaped polymer; e.g., x = 0.1, if the star-shaped polymer consists of 10% DMA. The gels consisting of these star-shaped polymers were PNIPA gel, PNIPA1−x-b-PDMAx gel, and PNIPA1−x-r-PDMAx gel (Fig. 1b). The method used for preparing polymer gels with tetrabranched star-shaped polymers as building blocks was previously described (Fig. 1a).26,28In this study, spherical polymer gels with isotropic shapes were prepared to measure the volume changes of polymer gels occurring with temperature jumps quantitatively. A pregel solution of a tetrabranched star-shaped polymer plus a crosslinker was dripped using a Pasteur pipette into a silicone oil (KF-96 L-2cs) solution (DOWSIL™ RSN-0749 Resin12 prepared to 3 wt%) (hereafter referred to as the oil phase) under an argon atmosphere, cooled to 4 °C, and stirred at approximately 1000 rpm for 1 hour (Fig. 2). The details of the synthesis of spherical polymer gels are described in the ESI.† The resulting gel particles were measured using a VHX-500K digital microscope (KEYENCE), and average particle diameters were calculated. The gel particles were washed with hexane, methanol, and water to obtain a spherical gel that was swollen and dispersed with water. Washing of the gel particles was performed by repeating a series of operations in which the spherical gel in a test tube was allowed to settle spontaneously, the supernatant was removed, and a new washing solution was added. The preparation methods for spherical gels with different compositions are detailed in the ESI.†
Decomposition of gel network by methanolysis
The polymer gels prepared in this study, which consisted of star-shaped polymers, utilized an initiator with the ester groups, so ester exchange reactions occurred when the gels were immersed in methanol containing dissolved sodium carbonate. As a result, the polymer gels were converted into star-shaped polymers whose polymer chains were crosslinked by N,N'-methylenebisacrylamide (MBAA), a crosslinking agent, and those that were not crosslinked by MBAA (Fig. 3). By examining these fractions, the fraction of star-shaped polymers that were crosslinked by MBAA was determined. | ||
| Fig. 3 Chemical structures of initiators (left) and crosslinkers (right), (b) illustration of gel decomposition by methanolysis. | ||
After syntheses, the PNIPA gels and PNIPA1−x-b-PDMAx (x = 0.1, 0.2, 0.3) gels in the oil phase were washed with hexane and methanol, respectively. Each gel was placed in a pressure-resistant test tube, 4.5 mg of NaCO3 and 4.5 mL of methanol were added, and the gel was refluxed at 80 °C for 24 hours using a Chemi-Station (Personal Synthesizer PPS-CTRL1, EYELA) connected to a cooling water circulation system (CCA-1111, EYELA). After the reaction, the solution was neutralized with 1 N HCl, placed in dialysis tubes (fractional molecular weight = 3500), dialyzed with ion-exchanged water for 3 days, and lyophilized. The resulting purified product was dissolved in the SEC eluent to a concentration of 2 wt% and filtered through a Millex-LCR SLCRX13NL 13 mm membrane filter (pore size 0.45 µm) before SEC measurement.
Small-angle X-ray scattering (SAXS) measurements of spherical gels
Small-angle X-ray scattering (SAXS) measurements were used to analyze network structures. PNIPA gel, PNIPA0.9-b-PDMA0.1 gel, PNIPA0.8-b-PDMA0.2 gel, and PNIPA gel made by free radical polymerization in the dispersed state in water were each placed in 2.0 mm quartz-glass capillaries (Mark-tubes, Hilgenberg GmbH) and irradiated with X-rays with a wavelength of 0.12 mm. The SAXS measurements were performed at the BL38B1 beamline SPring-8 (Hyogo, Japan). The scattered X-rays were detected using a PILATUS3X 2 M detector (DECTRIS Ltd.) with a sample-to-detector distance of ∼2.6 m. The temperature of the sample area was ca. 20 °C.Equilibrium swelling measurements
The diameters (d) of the prepared spherical gels were measured when they reached equilibrium at each temperature. The spherical gels were placed in the experimental apparatus as shown in Fig. S22 (ESI†), and their diameters were measured using an inverted optical microscope (OLYMPUS: CKX41), while the temperatures were controlled by a circulating thermostatic bath RE104 (Lauda). Approximately 300 spherical gels were measured, and their mean values and distributions were determined. The experimental results are shown in Fig. 6. | ||
| Fig. 4 SEC curve obtained after methanolysis decomposition of (a) PNIPA gel, (b)PNIPA0.9-b-PDMA0.1 gel, (c) PNIPA0.8-b-PDMA0.2 gel and (d) PNIPA0.7-b-PDMA0.3 gel. | ||
Temperature jump tests
The spherical gels were placed in the experimental apparatus as shown in Fig. S22 (ESI†) and connected to two circulating constant-temperature water baths RE 104 (Lauda) set at two different temperatures, and the circuit is shown in Fig. S23 (ESI†). The temperatures around the gel particles were switched by circulating water from one of the two circulating thermostatic baths set at different temperatures to bring the gel particles to swelling equilibrium and then reconnecting them to the other different thermostatic bath in the circuit as shown in Fig. S23 (ESI†). The morphological and diameter changes of the gel particles after the temperature jumps were observed using an inverted optical microscope (OLYMPUS: CKX41), and the temperatures were measured by a thermometer connected to a thermocouple near the gel particle. In each measurement, at least three gels were observed, and the average value was taken.3. Results and discussion
The methods for syntheses of star-shaped polymers and spherical gels are described in the ESI.† Here, the results for preparation and the properties of spherical gels are described.Particle sizes of spherical gels
The synthesized PNIPA gels, PNIPA1−x-b-PDMAx (x = 0.1, 0.2, 0.3) gels, PNIPA0.8-r-PDMA0.2 gels, and conventional gels made by free radical polymerization all had sizes of several hundred micrometers and the coefficient of variation (CV values) of 20–50% (Fig. S11–S16, ESI†).Decomposition of gel networks by methanolysis
The network structures of the synthesized gels were selectively degraded by methanol containing base (methanolysis) because of the presence of ester groups in the initiator moiety. Therefore, if the network structure was homogeneous with the same molecular weights between crosslinking points and the same number of branches at crosslinking points, the network structure was degraded by methanolysis to one type of star-shaped polymer derived from the crosslinking agent. However, if crosslinking was insufficient, in addition to the star-shaped polymer derived from the crosslinking agent, there may be arm polymers obtained by degradation of tetrabranched polymers at the initiator site (Fig. 3). Therefore, it is possible to analyze the homogeneity of the network structure in the original gel with a SEC measurement of the polymer solution obtained from the degradation of the gel and estimate the peaks and molecular weight distributions of arm polymers and star-shaped polymers.SEC measurements on degradation products of the polymer network obtained by methanolysis are shown in Fig. 4(a)–(d) SEC results for the degradation products obtained from PNIPA gel, PNIPA0.9-b-PDMA0.1 gel, PNIPA0.8-b-PDMA0.2 gel, and PNIPA0.7-b-PDMA0.3 gel, respectively. Two peaks at two different positions were observed in all SEC curves. The peak on the low molecular weight side was for the arm polymer of the uncrosslinked tetrabranched polymer, and the peak on the high molecular weight side was for the star-shaped polymer derived from the crosslinking agent. These results show that the gels had high crosslinking ratios (>80%) for the network structures. As the percentage of DMA was increased, the peak for the arm polymers increased, and the crosslinking rate decreased. Rademacher et al. reported that in atom transfer radical polymerization (ATRP) of DMA, the bromine-terminated PDMA chain passed through a cyclic intermediate, which was hydrolyzed and became hydroxyl-terminated (Fig. S21, ESI†).29 This is because the cyclic intermediate was more easily hydrolyzed than the bromine-terminated PDMA chain. The initiator used in this study had a chlorine terminus, and in this polymerization system in which a large amount of water was present, the chlorine terminus may be replaced by a hydroxyl group, as in the case of the bromine terminus, and polymerization may be stopped. As a result, we believed that increasing the percentage of DMA resulted in a larger percentage of arm polymers that were not crosslinked. However, the crosslinking rate was sufficiently high compared to those of conventional polymer networks with low network densities that exhibited rapid shrinkage. Based on the average molecular weights of the star-shaped polymers derived from the crosslinker and the uncrosslinked arm polymers, we estimated the number of branches at the crosslinking points to be 13–14 branches for the PNIPA gel, 13 branches for the PNIPA0.9-b-PDMA0.1 gel, 15–16 branches for the PNIPA0.8-b-PDMA0.2 gel, and 21–22 branches for the PNIPA0.7-b-PDMA0.3 gel.
Small-angle X-ray scattering measurement of spherical gels
SAXS profiles of spherical gels exhibiting equilibrium swelling in pure water at 20 °C are shown in Fig. 5. From the top of the figure, the results are for gels made by free radical polymerization of NIPA, PNIPA gels, PNIPA0.9-b-PDMA0.1 gel, PNIPA0.7-b-PDMA0.3 gel and PNIPA0.8-r-PDMA0.2 gel, respectively. In all five gels, the monomer loading concentration during star polymer synthesis was 0.5 M. This concentration was sufficiently higher than the overlapping concentrations of the star-shaped polymers obtained in this study (0.3 M in the case of the PNIPA system). In addition, the solvent and temperature used in the reaction constituted conditions under which these star-shaped polymers do not tangle even at concentrations higher than the overlapping concentration. In other words, it is highly likely that the star-shaped polymers were crosslinked under conditions similar to bond percolation conditions.The SAXS profile of the PNIPA gel synthesized by free radical polymerization was almost linear. On the other hand, the SAXS profiles of PNIPA gel, PNIPA0.9-b-PDMA0.1 gel, PNIPA0.7-b-PDMA0.3 gel, and PNIPA0.8-r-PDMA0.2 gel with controlled network structures showed shoulders at q = 0.1–0.5 nm−1, which were not observed for the gels made by free radical polymerization. This may indicate that the four gels had narrower distributions of correlation lengths and more homogeneous network structures than the PNIPA gels synthesized by free radical polymerization. To quantitatively discuss the network structures of these gels, the scattering profiles were fitted and analyzed with the following equations:
| I(q) = I0PS(q)SHS(q) + IOZ(q) + Cq−d | (1) |
 | (2) |
| Sample | r c (nm) | R HS (nm) | ξ OZ (nm) | d |
|---|---|---|---|---|
| PNIPA | 1.58 | 8.04 | 8.16 | 3.01 |
| PNIPA0.9-b-PDMA0.1 | 1.65 | 7.37 | 9.49 | 4.20 |
| PNIPA0.7-b-PDMA0.3 | 1.67 | 8.74 | 5.56 | 2.86 |
| PNIPA0.8-r-PDMA0.2 | 2.03 | 7.96 | 3.95 | 4.31 |
The value of ξOZ corresponds to the correlation length of the liquid-like structural parts in the gel, which is smaller in PNIPA0.8-r-PDMA0.2 than in the other gels. This may be related to the random polymerization of NIPA and DMA. The value of d is 2.8–4.2, which implies the existence of a two-phase structure that has a sharp boundary characterized by the so-called Porod law (I(q) ∼ q−4).31 For PNIPA0.8-r-PDMA0.2, the contribution of Cq−d was small and not significant.
Swelling curve (spherical gel)
The diameters of the spherical gels exhibiting equilibrium swelling state in water at 20 °C to 60 °C are shown in Fig. 6. All spherical gels showed volume changes indicating the swollen state at lower temperatures and collapsed state at higher temperatures. From the derivative curves of the experimental values obtained, we estimated the temperatures at which the volume changes were greatest: for PNIPA gel, PNIPA0.9-b-PDMA0.1 gel, PNIPA0.8-b-PDMA0.2 gel, PNIPA0.7-b-PDMA0.3 gel, and PNIPA0.8-r-PDMA0.2 gel, these temperatures were 33 °C, 33.5 °C, 34.5 °C, 37 °C, and 37 °C, respectively. The temperature at which the volume changed increased with increases in the amount of DMA added. The volume changes also tended to become more gradual as more DMA was introduced. However, we also found that for the introduction of the same amount of DMA, the volume changes were more gradual for systems with random sequences. The volume at thermodynamic equilibrium of a polymer gel consisting of nonionic polymer chains is determined by the osmotic pressure due to mixing of the polymer chains and solvent, which also takes into account the conformational changes of the polymer chains and the osmotic pressure due to rubber elasticity caused by crosslinking.1 It is known that PNIPA chains exhibit sharp coiled globule transitions of the chains due to the collective effects of hydration.32–35 Introduction of DMA is thought to affect the coil-globule transitions of the polymer chains that occur with temperature changes. In addition, as is clear from the results shown in Fig. 4, for the system into which DMA was introduced as a block copolymer, higher amounts of DMA led to lower crosslink densities, suggesting that osmotic pressure due to rubber elasticity also affects the equilibrium degree of swelling. As a result of these influences, the volume changes of the polymer gels were more gradual due to the introduction of DMA.36 However, it was found that the monomers and their arrangements had significant effects on the volume changes of polymer gels.Evaluation of the swelling behavior seen for spherical gels as a result of temperature drop jumps
The swelling behavior of each spherical gel was observed when the temperature was decreased from 60 °C to 20 °C. Changes in diameter and temperature over time for spherical gels are shown in Fig. 7a, which uses the PNIPA gel as an example. It can be seen that the temperature change was sufficiently fast relative to the gel diameter change. Therefore, based on this experiment, the kinetics of volume changes were investigated for spherical gel particles. Fig. 7b shows the observed times for the swelling of the PNIPA gels when the temperature was decreased from 60 °C to 20 °C. At 34 seconds after the temperature jump, the gel separated into two layers: a swollen phase on the surface and a shrunken layer in the interior. A clear boundary surface was formed between these two layers, and this boundary moved to the interior with the passage of time, i.e., swelling occurred and disappeared after 66 seconds. This behavior was also observed for the swelling of conventional PNIPA gels.11,37 When the temperature jumped from high to low, only the surface of the shrunken gel was in contact with a lot of water. Therefore, the gel expands from the surface and the interior remains contracted, and the gel was considered to be separated into two layers, as shown in the photograph.In the PNIPA0.9-b-PDMA0.1 gel, the gel also separated into two layers, a swollen phase on the surface and an internal shrinkage layer, obtained within 16 s after the temperature jump (Fig. 7c). The boundary between these two layers moved inward with time, with swelling, as in the PNIPA gel, and this boundary disappeared after 66 seconds.
On the other hand, in the cases of PNIPA0.8-b-PDMA0.2 gel (Fig. 7d), PNIPA0.7-b-PDMA0.3 gel (Fig. 7e), and PNIPA0.8-r-PDMA0.2 gel (Fig. 7f), in which the amounts of DMA introduced were further increased, the swelling changes with temperature jumps were not observed on the surfaces, and the boundaries separating the interior were not observed with the naked eye. Because these spherical gels had higher water contents than spherical gels composed mainly of NIPA due to the presence of hydrophilic DMA, even in the shrunken state at 60 °C, the refractive indexes of the gels during shrinkage were not significantly different from those of the swollen gels at lower temperatures. As a result, the presence of a clear boundary surface between the shrinking and swelling layers could not be observed by the naked eye.
Evaluation of the shrinkage behavior of spherical gels with temperature jumps
Shrinkage of each spherical gel was observed when the temperature was increased from 20 °C to 60 °C. Changes in diameter and temperature over time for a spherical gel are shown in Fig. 8a, in which the PNIPA gel was used as an example. The temperature change was sufficiently fast relative to the change in gel diameter, even in the experiment with a temperature increase. Therefore, based on this experiment, the kinetics for volume changes of the spherical gel particles were investigated.Fig. 8b shows the shrinkage of the PNIPA gel over time during a temperature jump from 20 °C to 60 °C. The PNIPA gel was observed to form bubbles and it became cloudy during shrinkage.10,11,38,39 The sudden temperature change resulted in dehydration from the gel surface, resulting in contraction from the gel surface and formation of a skin phase.40 This skin phase prevented the gel from releasing the internal water; pressure was exerted from the inside of the gel, and this internal pressure led to the formation of bubbles. In addition, as the gel had unstable regions during the process of contraction, the phases separated, dense and sparse portions of the network were formed, and the gel became cloudy. At a much longer time (approximately 1800 seconds) after the spherical gel particles exhibited almost constant sizes (several hundred seconds), the white turbidity finally disappeared, and a thermodynamically stable state of contraction was achieved.
The PNIPA0.9-b-PDMA0.1 gel also shrank with bubble formation and cloudiness, as did the PNIPA gel (Fig. 8c). However, the degree of cloudiness was lower than that of the PNIPA gel, suggesting that the regular presence of hydrophilic, temperature-resistant PDMA reduced the effects of phase separation due to the aggregation of crosslinked networks.
On the other hand, PNIPA0.8-b-PDMA0.2 and PNIPA0.7-b-PDMA0.3 gels did not show bubble formation or cloudiness and remained transparent and isotropically contracted (Fig. 8d, 8e). It is thought that the hydrophilic, temperature-resistant PDMA, which was regularly distributed within the network structure, acted as a water pathway and suppressed the formation of an aggregated network skin phase on the gel surface, thus preventing the generation of pressure inside the gel and precluding bubble formation. In addition, the regular distribution of PDMA prevented the aggregation of PNIPA blocks, which may have suppressed phase separation and resulted in shrinkage and transparency without cloudiness. These gels reached a thermodynamically stable contracted state within 300 s after the temperature jump.
However, the PNIPA0.8-r-PDMA0.2 gel, despite containing 20% DMA, shrank while exhibiting bubble formation and cloudiness (Fig. 8f). The sizes and volumes of the bubbles were smaller than those of the PNIPA and PNIPA0.9-b-PDMA0.1 gels, but the degree of cloudiness was greater than those of the latter gels. When the temperature was changed rapidly, the PDMA, which was randomly distributed within the network structure, may have prevented the confinement of water in the gels to some extent, which may have resulted in less bubble formation. However, the phase separation associated with sudden shrinkage was found to be more pronounced when the gel consisted of polymer chains exhibiting a random sequence of NIPA and DMA. The behavior was significantly different from that of the PNIPA0.8-b-PDMA0.2 gel, a copolymer gel incorporating the same amount of PDMA, which indicated that the monomer sequence in the polymer chain had a significant effect on the shrinkage behavior of the polymer gel.
Calculation of the collective diffusion coefficient (swelling)
Based on the results of Fig. 7 and Fig. 8, to discuss the kinetics of gel swelling and contraction, the collective diffusion coefficient of the polymer network comprising each gel was calculated in the following way. With the diameter d(t) at a certain time t, the diameter di in the initial state, and the diameter d(t∞) in the equilibrium swollen state after a temperature jump, the change in the diameter of the gel can be approximated with the following equation:10,38 | (3) |
Experimentally, the following equation, which was obtained by taking the logarithms of both sides, is used:
 | (4) |
By plotting the values of the left-hand side of this equation against time t and obtaining the relaxation time τ from the slope at a time when the intercept was fixed at ln(6/π2), a linear approximation can be applied. As a result, the collective diffusion coefficient D can be obtained for a spherical gel and expressed by the following equation:9,37
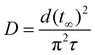 | (5) |
We first observed swelling of the spherical gels by fixing the temperature at 20 °C and conducting temperature jump tests with descending temperatures by varying the initial temperature in various ways and then determined the collective diffusion coefficient D based on the above ideas. The relationship between initial temperature and the collective diffusion coefficient for each spherical gel was investigated.
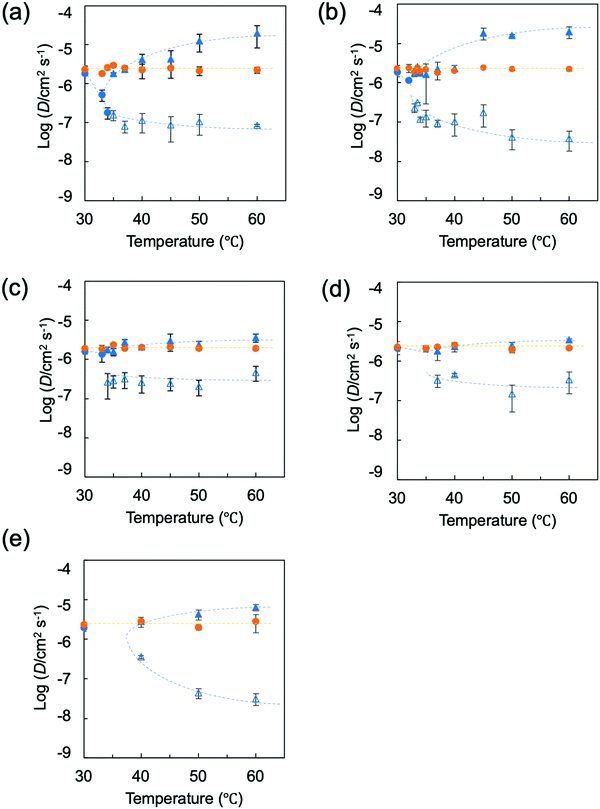
The results for a spherical gel composed of PNIPA are shown in Fig. 9a. The results obtained by substituting the diameter change with time into eqn (4) when the initial temperature was 60 °C are shown in Fig. S46 (ESI†). The relaxation time τ was obtained from the slope of this line. Using the value of τ, the collective diffusion coefficient was calculated from eqn (5). The initial temperature was varied from 30 °C to 60 °C, and the collective diffusion coefficients were calculated in the same way for each temperature (orange solid circles in Fig. 9a and Fig. S47, ESI†). The collective diffusion coefficients were approximately 2.0–2.5 × 10−6 cm2 s−1 at all initial temperatures and were almost constant regardless of the initial temperature. For PNIPA0.9-b-PDMA0.1 gel, PNIPA0.8-b-PDMA0.2 gel, PNIPA0.7-b-PDMA0.3 gel, and PNIPA0.8-r-PDMA0.2 gel, the collective diffusion coefficients of the polymer gels were calculated under similar conditions with temperature jumps descending from various temperatures to 20 °C. It was found that the collective diffusion coefficients of the polymer gels were approximately 2.0–2.5 × 10−6 cm2 s−1 for any initial temperature in all systems and that the collective coefficients of the polymer gels with temperature jumps descending to a temperature of 20 °C were constant regardless of the compositions and sequences of monomers forming the polymer gel (Fig. 9a–e).
Calculation of the collective diffusion coefficient (contraction)
The collective diffusion coefficient of the shrinkage process can be calculated in the same way as in the swelling process if there is no phase separation (blue solid circles in Fig. 9). However, when phase separation is involved, the behavior is completely different from that of the swelling process, and the collective diffusion coefficient cannot be calculated in the same way. In the case of shrinkage with phase separation, a straight line with a different slope was obtained at a certain point, and two stages of shrinkage were observed. These two stages were defined as stage 1 and stage 2, respectively; the time when stages 1 and 2 switch was t1, and the complete shrinkage time in stage 2 was t∞.38,39 The diameter change in stage 1 was defined by the following equation, where the initial diameter is di and the relaxation time is τ1. | (6) |
Taking the logarithm of both sides yielded the following equation:
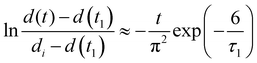 | (7) |
 | (8) |
Similarly, the diameter change in stage 2 was defined by the following equation, where d(t∞) is the fully shrunk diameter after the temperature jump and τ2 is the relaxation time.
 | (9) |
τ 2 was obtained from the slope of the straight line obtained, when the values on the left side of this equation were plotted against time. From this, the collective diffusion coefficient D2 at stage 2 was calculated by using the following formula:
 | (10) |
In this study, shrinkage behavior was observed by fixing the initial temperature at 20 °C and performing temperature jump tests by varying the final temperature.
First, we will discuss the results obtained for spherical gels composed of PNIPA. The final temperatures were set between 30 °C and 60 °C. The results for substituting the diameter change with time into the swelling equation at the final temperature of 30 °C are shown in Fig. S56 (ESI†). Because 30 °C is lower than the temperature at which the volume of this gel changes significantly, the swelling change was not accompanied by phase separation, and the plot was a straight line. The same results were obtained at temperatures of 32 °C and 33 °C. From this, the collective diffusion coefficients for 30 °C, 32 °C, and 33 °C were calculated by using eqn (3)–(5). At a final temperature of 30 °C, the value of the collective diffusion coefficient was almost identical to the value of the collective diffusion coefficient seen for swelling. However, the collective diffusion coefficients decreased as the final temperatures were increased. It is known that polymer gels with ionic groups introduced into the chains of PNIPA show discontinuous volume changes in response to temperature changes. Near the critical point, the collective diffusion coefficient decreases, and swelling and contraction become infinitely slow due to critical slowing. In nonionic PNIPA gels as well, although there is no critical point at which swelling and contraction become infinitely slow, the collective diffusion coefficient tends to decrease as the transition point is approached.
The results obtained by substituting diameter changes over time into the swelling equation when the temperature jump is 60 °C are shown in Fig. S57 (ESI†). From the plot, a straight line with a different slope was obtained after a certain point (t1,d(t1)), and two stages of shrinkage, stage 1 and stage 2, were observed. Similarly, two-stage contraction was observed when the temperature jump reached 33.5 °C or higher. From the above equations, the collective diffusion coefficients D1 and D2 were calculated for stage 1 and stage 2, respectively. Fig. 9a shows stage 1 values with ▲ and stage 2 values with Δ. The collective diffusion coefficients increased as the attained temperature was increased in stage 1. This may be because the driving force increased as the attained temperature was increased, which accelerated the shrinkage rate.
Because the stage 1 shrinkage was accompanied by bubble formation, it is thought that a skin phase was formed in the early stages of shrinkage, and the rapid shrinkage in stage 1 can be attributed to skin phase formation. On the other hand, the collective diffusion coefficient in stage 2 is one to two orders of magnitude smaller than that in stage 1. This slow behavior is considered to be due to the skin phase formed in stage 1 and relaxation of the phase-separated structure.
The PNIPA0.9-b-PDMA0.1 gel showed the same behavior as the PNIPA gel (Fig. 9b). Stage 2 behavior was found to change even more slowly than it did for the PNIPA gel.
In the PNIPA0.8-b-PDMA0.2 gel containing 20% DMA, the shrinkage change due to the temperature jump was similar to those of the two systems described above; it showed a two-step shrinkage change when the temperature reached was above the temperature at which the volume changed rapidly. However, the collective diffusion coefficient for stage 1 was almost identical to the collective diffusion coefficient at swelling, although the collective diffusion coefficient tended to increase as the attained temperature was increased. In other words, based on the fact that the PNIPA0.8-b-PDMA0.2 gel shrank isotropically without bubble formation, formation of a skin layer was suppressed in the initial stages of shrinkage. In addition, the collective diffusion coefficient in stage 2 was larger than those of the PNIPA gel and the PNIPA0.9-b-PDMA0.1 gel. Suppression of skin layer formation in the PNIPA0.8-b-PDMA0.2 gel suggested that the shrinkage in stage 2 was due to relaxation associated with the shrinkage. For PNIPA gels prepared by conventional free radical polymerizations, there are two mechanisms: nucleation (metastable region) and spinodal decomposition (unstable region) caused by a temperature jump through an unstable or metastable region. Suzuki et al. point out that the phase separation mechanism differs depending on the region through which the temperature jump occurs, and the time required for the phase transition also differs significantly.41 These phase separation mechanisms are thought to prevail even for PNIPA gels and PNIPA0.9-b-PDMA0.1 gels, which have more homogeneous network structures than conventional systems. On the other hand, in the PNIPA0.8-b-PDMA0.2 gel, the regular distribution of PDMA into the network prevented nucleation and spinodal decomposition, which may have resulted in a phase separation mechanism different from those of the PNIPA and PNIPA0.9-b-PDMA0.1 gels. In the PNIPA0.7-b-PDMA0.3 gel, the shrinkage behavior was found to be similar to that of the PNIPA0.8-b-PDMA0.2 gel (Fig. 9d).
For the PNIPA0.8-r-PDMA0.2 gel, results are shown for final temperatures of 30 °C, 40 °C, 50 °C, and 60 °C (Fig. 9e). The results of substituting diameter changes with time into the swelling equation for a final temperature of 30 °C are shown in Fig. S69 (ESI†). At a temperature of 30 °C, the relationship constituted a straight line, and as with the swelling process, a single collective diffusion coefficient was obtained (Fig. S70, ESI†). However, two stages of shrinkage were observed at final temperatures of 40 °C, 50 °C, and 60 °C (Fig. S69, ESI†). In stage 1, although the collective diffusion coefficient tended to increase as the attained temperature was increased, the rate of increase was smaller than those for PNIPA and PNIPA0.9-b-PDMA0.1 gels. The value of the collective diffusion coefficient in stage 1 was almost consistent with the value for swelling. Considering that the PNIPA0.8-r-PDMA0.2 gel shrank without bubble formation, it is likely that the formation of a skin layer was suppressed in the initial stage of shrinkage, as seen for the PNIPA0.8-b-PDMA0.2 and PNIPA0.7-b-PDMA0.3 gels. On the other hand, the collective diffusion coefficient for stage 2 was close to those for the PNIPA gel and the PNIPA0.9-b-PDMA0.1 gel. Suppression of skin layer formation suggested that the slow behavior in stage 2 was due to the formation of a phase-separated structure inside the gel and subsequent relaxation. From the above, it is thought that the gel with DMA randomly incorporated into the network structure prevented the formation of a skin layer but did not suppress phase separation.
4. Conclusions
In this study, living radical polymerization was used to synthesize tetrabranched polymers with homogeneous arm lengths and various monomer compositions and sequences, and spherical gels were synthesized by using them as building blocks. The resulting spherical gels were several hundred micrometers in size, and selective reticulation by methanolysis and SAXS measurements showed that the reticular structure was more homogeneous than those of polymer gels obtained by conventional free radical polymerization. These gels exhibited reversible volume changes in water, i.e., low-temperature swelling and high-temperature shrinkage, but when the volume changes associated with rapid temperature changes (temperature jumps) were examined, the rates for changes from a shrunken state at high temperature to a swollen state at low temperature were almost the same for all gels. However, the rates for changes from the low-temperature swollen state to the high-temperature shrunken state varied greatly depending on the compositions and sequences of the monomers that made up the polymer networks. It was confirmed that regular introduction of more than 20% of a DMA block copolymer into a network structure consisting of PNIPA inhibited phase separation and skin layer formation resulted in smooth discharge of the water inside the polymer gel and thus improved the shrinkage rate.Conflicts of interest
There are no conflicts to declare.References
- T. Tanaka, Sci. Am., 1981, 244, 126–136 CrossRef PubMed.
- S. P. O. Danielsen, H. K. Beech, S. Wang, B. M. El-Zaatari, X. D. Wang, L. Sapir, T. Ouchi, Z. Wang, P. N. Johnson, Y. X. Hu, D. J. Lundberg, G. Stoychev, S. L. Craig, J. A. Johnson, J. A. Kalow, B. D. Olsen and M. Rubinstein, Chem. Rev., 2021, 121, 5042–5092 CrossRef CAS PubMed.
- X. H. Zhao, X. Y. Chen, H. Yuk, S. T. Lin, X. Y. Liu and G. Parada, Chem. Rev., 2021, 121, 4309–4372 CrossRef CAS PubMed.
- M. Yamato and T. Okano, Mater. Today, 2004, 7, 42–47 CrossRef CAS.
- A. Matsumoto, N. Sato, T. Sakata, R. Yoshida, K. Kataoka and Y. Miyahara, Adv. Mater., 2009, 21, 4372–4378 CrossRef CAS PubMed.
- A. V. Goponenko and S. A. Asher, J. Am. Chem. Soc., 2005, 127, 10753–10759 CrossRef CAS PubMed.
- D. Nakayama, Y. Takeoka, M. Watanabe and K. Kataoka, Angew. Chem., Int. Ed., 2003, 42, 4197–4200 CrossRef CAS PubMed.
- H. Saito, Y. Takeoka and M. Watanabe, Chem. Commun., 2003, 2126–2127, 10.1039/b304306a.
- T. Tanaka, L. O. Hocker and G. B. Benedek, J. Chem. Phys., 1973, 59, 5151–5159 CrossRef CAS.
- S. Takata, K. Suzuki, T. Norisuye and M. Shibayama, Polymer, 2002, 43, 3101–3107 CrossRef CAS.
- Y. Li and T. Tanaka, J. Chem. Phys., 1990, 92, 1365–1371 CrossRef CAS.
- T. Chung, I. K. Han, J. Han, K. Ahn and Y. S. Kim, Gels, 2021, 7, gels7010018 CrossRef PubMed 1-10.
- Y. Takeoka and M. Watanabe, Langmuir, 2002, 18, 5977–5980 CrossRef CAS.
- T. Serizawa, K. Wakita and M. Akashi, Macromolecules, 2002, 35, 10–12 CrossRef CAS.
- R. Yoshida, K. Uchida, Y. Kaneko, K. Sakai, A. Kikuchi, Y. Sakurai and T. Okano, Nature, 1995, 374, 240–242 CrossRef CAS.
- Y. Kaneko, K. Sakai, A. Kikuchi, R. Yoshida, Y. Sakurai and T. Okano, Macromolecules, 1995, 28, 7717–7723 CrossRef CAS.
- A. Yasumoto, H. Gotoh, Y. Gotoh, A. Bin Imran, M. Hara, T. Seki, Y. Sakai, K. Ito and Y. Takeoka, Macromolecules, 2017, 50, 364–374 CrossRef CAS.
- S. Seiffert, Polym. Chem., 2017, 8, 4472–4487 RSC.
- S. Johnsen, Sci. Am., 2000, 282, 80–89 CrossRef CAS PubMed.
- T. Sakai, T. Matsunaga, Y. Yamamoto, C. Ito, R. Yoshida, S. Suzuki, N. Sasaki, M. Shibayama and U. I. Chung, Macromolecules, 2008, 41, 5379–5384 CrossRef CAS.
- Y. Okumura and K. Ito, Adv. Mater., 2001, 13, 485–487 CrossRef CAS.
- S. Ida, S. Toda, M. Oyama, H. Takeshita and S. Kanaoka, Macromol. Rapid Commun., 2021, 42(8), 2000558 CrossRef CAS PubMed.
- X. Li, S. Nakagawa, Y. Tsuji, N. Watanabe and M. Shibayama, Sci. Adv., 2019, 5, eaax8647 CrossRef CAS PubMed 1-7.
- S. Nakagawa and N. Yoshie, Polym. Chem., 2022, 13, 2074–2107 RSC.
- D. E. Apostolides, C. S. Patrickios, T. Sakai, M. Guerre, G. Lopez, B. Ameduri, V. Ladmiral, M. Simon, M. Gradzielski, D. Clemens, C. Krumm, J. C. Tiller, B. Ernould and J. F. Gohy, Macromolecules, 2018, 51, 2476–2488 CrossRef CAS.
- Y. Jochi, T. Seki, T. Soejima, K. Satoh, M. Kamigaito and Y. Takeoka, NPG Asia Mater., 2018, 10, 840–848 CrossRef CAS.
- Y. Okaya, Y. Jochi, T. Seki, K. Satoh, M. Kamigaito, T. Hoshino, T. Nakatani, S. Fujinami, M. Takata and Y. Takeoka, Macromolecules, 2020, 53, 374–386 CrossRef CAS.
- D. Kwon, Y. Jochi, Y. Okaya, T. Seki, K. Satoh, M. Kamigaito, T. Hoshino, K. Urayama and Y. Takeoka, Macromolecules, 2021, 54, 5750–5764 CrossRef CAS.
- J. T. Rademacher, R. Baum, M. E. Pallack, W. J. Brittain and W. J. Simonsick, Macromolecules, 2000, 33, 284–288 CrossRef CAS.
- M. Vamvakaki, C. S. Patrickios, P. Lindner and M. Gradzielski, Langmuir, 2007, 23, 10433–10437 CrossRef CAS PubMed.
- T. Matsunaga, T. Sakai, Y. Akagi, U. Chung and M. Shibayama, Macromolecules, 2009, 42, 1344–1351 CrossRef CAS.
- X. H. Wang and C. Wu, Macromolecules, 1999, 32, 4299–4301 CrossRef CAS.
- R. Walter, J. Ricka, C. Quellet, R. Nyffenegger and T. Binkert, Macromolecules, 1996, 29, 4019–4028 CrossRef CAS.
- F. Tanaka, T. Koga, H. Kojima and F. A. Winnik, Macromolecules, 2009, 42, 1321–1330 CrossRef CAS.
- E. I. Tiktopulo, V. E. Bychkova, J. Ricka and O. B. Ptitsyn, Macromolecules, 1994, 27, 2879–2882 CrossRef CAS.
- S. Ida, Polym. J., 2019, 51, 803–812 CrossRef CAS.
- T. Tanaka and D. J. Fillmore, J. Chem. Phys., 1979, 70, 1214–1218 CrossRef CAS.
- K. Takahashi, T. Takigawa and T. Masuda, J. Chem. Phys., 2004, 120, 2972–2979 CrossRef CAS PubMed.
- T. Okajima, I. Harada, K. Nishio and S. Hirotsu, J. Chem. Phys., 2002, 116, 9068–9077 CrossRef CAS.
- T. Tanaka, E. Sato, Y. Hirokawa, S. Hirotsu and J. Peetermans, Phys. Rev. Lett., 1985, 55, 2455–2458 CrossRef CAS PubMed.
- A. Suzuki and S. Yoshikawa, Jpn. J. Appl. Phys., Part 1, 2000, 39, 5195–5201 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00402j |
| This journal is © The Royal Society of Chemistry 2022 |