Photoelectron spectroscopy in molecular physical chemistry

Abstract

Photoelectron spectroscopy has long been a powerful method in the toolbox of experimental physical chemistry and molecular physics. Recent improvements in coincidence methods, charged-particle imaging, and electron energy resolution have greatly expanded the variety of environments in which photoelectron spectroscopy can be applied, as well as the range of questions that can now be addressed. In this Perspectives Article, we focus on selected recent studies that highlight these advances and research areas. The topics include reactive intermediates and new thermochemical data, high-resolution comparisons of experiment and theory using methods based on pulsed-field ionisation (PFI), and the application of photoelectron spectroscopy as an analytical tool to monitor chemical reactions in complex environments, like model flames, catalytic or high-temperature reactors.

---

Introduction

In this Perspective, we will highlight recent developments that demonstrate the power of photoelectron spectroscopy (PES) to address current questions in gas-phase physical chemistry and related fields. To motivate the selection of topics included in the article, we start with a brief historical overview. Photoelectron spectroscopy (PES) can be traced back to the photoelectric effect,^1–3 explained in 1905 by Einstein.⁴ Early on it was realised that the threshold frequency required to remove an electron from a metal, the work function, was a characteristic property of the material. The application of these concepts to gas-phase molecules proved to be difficult, however, because the energy required to remove a valence electron from these species (that is, the ionisation energy, IE) typically corresponds to a photon energy in the vacuum ultraviolet (VUV) region.

Siegbahn and coworkers began developing X-ray photoelectron spectroscopy for studying the inner shells of atoms and molecules in 1957.⁵ Ultimately, this approach was developed into an analytical tool, electron spectroscopy for chemical analysis, or ESCA, for which Siegbahn was awarded the 1981 Nobel Prize in Physics.⁶ In contrast, the development of valence-shell photoelectron spectroscopy took somewhat longer. The first such spectra of gas-phase molecules were reported by Vilesov et al. in 1961.⁷ These experiments were performed using a continuum source and a monochromator, resulting in relatively low photon intensities. In 1962, Al Jobory and Turner developed a high-intensity He(I) discharge lamp that emitted light at 21.2 eV, and used it to record the photoelectron spectra and ionisation energies of a series of molecules by analyzing the kinetic energy of the photoelectrons based on their retardation in an electric field.^8,9 This development launched valence-shell photoelectron spectroscopy as a novel tool for physical chemistry.¹⁰

Well before the development of photoelectron spectroscopy, Koopmans¹¹ showed that in the frozen-core Hartree–Fock limit, the first ionisation energy of the molecule corresponds to the negative of the energy of the corresponding highest occupied molecular orbital (HOMO) of the neutral molecule. More generally, the energies of bands in a photoelectron spectrum can be approximated by the energy of the molecular orbital (MO) from which the electron is ejected, IE ≈ −E(MO). This realisation allowed the association of an experimental observable with the otherwise abstract concept of an MO and contributed to the widespread acceptance of MO theory.^12,13 Since then, photoelectron spectroscopy has become an important tool to elucidate the electronic structure of molecules, to characterise their MO's experimentally, and to determine the structure of molecular ions. The sensitivity of PES to the character of electronic states is employed today in femtosecond spectroscopy to monitor time-dependent changes of electronic states.^14–16

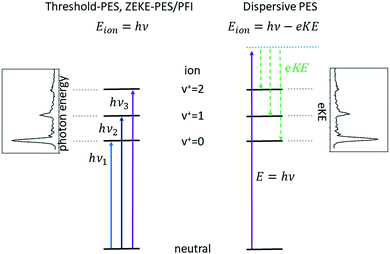
Subsequent developments of PES followed the original approach of using a fixed photon energy and recording the photoelectron signal as a function of the electron kinetic energy eKE (or momentum), see right-hand side of Fig. 1. In 1967, however, Villarejo et al. demonstrated an alternative approach to PES in which only near-zero energy electrons, or threshold electrons, were detected as the photon energy was continuously scanned.¹⁷ Soon thereafter, Baer, Peatman, and Schlag introduced a threshold electron detector with considerably improved collection efficiency and resolution.^18,19

Fig. 1 Comparison between threshold photoelectron spectroscopy (TPES) and its variants, which employ tunable radiation (left-hand side) with dispersive photoelectron spectroscopy using fixed-frequency light (right). In TPES, as the photon energy is scanned through each ionisation threshold, a peak is observed in the spectrum, while in dispersive PES the photoelectron signal is recorded at a fixed-photon energy as a function of the electron kinetic energy, eKE, and peaks are observed at energies corresponding to the population of the energetically accessible rovibronic states of the ion.

This approach to photoelectron spectroscopy is illustrated schematically on the left-hand side of Fig. 1 and compared to conventional dispersive PES. As the photon energy is scanned through each ionisation threshold, a peak is observed in the threshold photoelectron spectrum (TPES). Subsequent variations on TPES include pulsed-field ionisation-zero-electron-kinetic-energy PES (PFI-ZEKE-PES),^20–22 mass-analysed threshold ionisation (MATI)^23,24 and slow-PES (SPES).²⁵ Note that in PFI-ZEKE and MATI spectroscopy, the electrons and ions are produced by excitation and delayed pulsed field ionisation of Rydberg states lying just below the ionisation threshold, rather than by direct photoionisation into an open continuum (see below). Up to a point, the principal limitation to the resolution of these approaches is the photon bandwidth, and with laser sources, even sub-cm⁻¹ energy resolution becomes possible.

Each of the two basic types of PES has its own set of strengths and weaknesses. Dispersive PES (right-hand side of Fig. 1) reveals what states of the ion are populated at a given photon energy and provides a map of the electronic structure of the cation. If the photon energy is tuned to a continuum resonance (for example, an Rydberg state based on a higher lying state of the cation,²⁶ or a shape resonance in which the continuum electron is temporarily trapped by a centrifugal barrier in the molecule²⁷), the spectrum shows how that resonance decays. Vibrational intensity distributions in the open continuum often follow Franck–Condon distributions, providing insight into the geometry change of the ion state relative to the neutral, and electronic band intensities can provide insight into the energy ordering of the relevant molecular orbitals. Furthermore, measurements of the angular distributions of the photoelectrons can provide insight into the continuum wave function and photoionisation dynamics.²⁸ The principal challenge of dispersive PES is that it is difficult to measure electron kinetic energies with high resolution across a wide range of electron energies, particularly without sacrificing considerable electron signal. Nevertheless, dispersive analysers with exceptionally high resolution (∼10–40 cm⁻¹) have been developed,^29,30 and magnetic-bottle^31,32 and imaging spectrometers³³ have largely solved the issue of collection efficiency.

Threshold photoelectron spectroscopy has the advantage that it is relatively straightforward to develop a very high-resolution detector of near-zero energy electrons, and as mentioned above the resolution of the technique is then at least in principle limited only by the photon bandwidth. By scanning the photon source, TPES peaks are observed whenever the photon energy is coincident with an ionisation threshold. PFI-ZEKE PES with laser sources typically can provide resolution significantly better than 1 cm⁻¹, sufficient to resolve rotational structure in many molecular systems.³⁴ The approach thus allows detailed spectroscopic studies of molecular cations, along with the characterisation of spin–orbit, vibronic, and non-covalent interactions in a wide range of systems. The downside of TPES is that the measurement is not made at a single photon energy. As the photon energy is scanned, the photoionisation matrix element can change both in magnitude and in composition with respect to the relevant electron partial waves (in other words, one is accessing a different state of the electron–ion system at each photon energy). Because the relative intensities of rotational peaks, vibrational bands, and even electronic bands can be affected by the changing photon energy, the interpretation of these intensities and the photoionisation dynamics that they reflect can be difficult. Note, however, that these intensity perturbations can also be a feature, as they can allow the population of ionic states that lie in the “Franck–Condon gap” that is not accessible by direct ionisation processes, i.e., final states that would not be populated in dispersive PES due to small Franck–Condon factors. The vibrational enhancement has been explained by interaction with resonantly excited autoionising states.³⁵ A second drawback of TPES is that angular distribution measurements on near-zero energy electrons (or electrons produced by field ionisation) are generally not very informative.

Recording the full PES as a function of photon energy results in a 2D map of the photoelectron signal vs. photon energy (x-axis) and electron kinetic energy (y-axis).²⁵Fig. 2 shows data obtained for HBBH as an example.^36,37 A horizontal slice through this map generates the photoelectron signal at a constant electron energy, and for zero (threshold) kinetic energy, this slice corresponds to the TPE spectrum. (Ref. 25 provides an excellent illustration of this approach.) A vertical slice at a fixed photon energy corresponds to the PES at that energy. For a given final state of the ion, the electron energy will increase linearly with the photon energy, so that a diagonal slice of the 2D map correspond to the spectrum for producing that specific state, which is known as the constant ionic state (CIS) spectrum. The 2D map can be rotated to align the CIS spectra in the vertical direction.²⁵ A horizontal slice through the rotated spectrum gives the final state distribution at a specific electron energy, with the TPES spectrum still corresponding to the slice at zero kinetic energy. Because the signal for each final state is lined up along the vertical, the horizontal slices can be summed to provide better statistics without significantly affecting the overall resolution. The spectrum obtained by summing over kinetic energies near threshold (typically from zero to 50–100 meV) is known as the slow photoelectron spectrum (SPES).²⁵ SPES and TPES have similar advantages/issues relative to PES, but because the SPES signal is integrated over a larger range of electron kinetic energies, the resulting signal-to-noise ratio can be significantly higher than with TPES, without significant degradation of resolution.

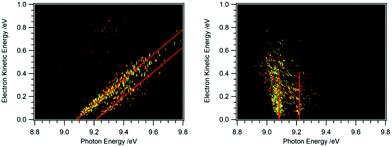Fig. 2 2D map of the full photoelectron spectrum of HBBH with the vibrational bands indicated by the red diagonals (left-hand side).^36,37 A horizontal slice at 0 eV eKE corresponds to a TPE spectrum, a vertical slice at a given photon energy to the PES. After rotation of the matrix the 2D map on the right-hand side is obtained. Summing up horizontal slices yields a slow photoelectron spectrum, SPES, which often provides a better signal/noise ratio.

As a result of these considerations, both techniques find considerable use in modern gas-phase chemical physics. Indeed, with the development of velocity map imaging techniques for photoelectrons, high-quality threshold and dispersive photoelectron spectra can be obtained simultaneously, although the data acquisition is typically optimised for the relevant information desired in a particular experiment. In the context of physical chemistry, perhaps the most important development in recent years has been the blossoming of photoelectron–photoion coincidence (PEPICO) techniques in all their glory.^38,39 These techniques allow the correlation of the ion mass and angular distribution with the corresponding photoelectron energy and angular distributions. For example, ion mass-selected (threshold) photoelectron spectra, ms-(T)PES, for different species can be extracted from the full data set. These techniques are therefore extremely valuable for studying photoelectron spectra of minor species in complex mixtures, such as those used to produce radicals, clusters, and other ephemeral species.

Numerous textbooks and monographs review the history of photoelectron spectroscopy^26,40–43 and its applications, and several recent reviews provide up-to-date surveys of selected aspects of the field.^38,44,45 Here, we will focus on recent developments and applications in which the PES of neutral molecules is applied to current problems in physical chemistry. We will not discuss photoelectron (photodetachment) studies of negative ions. Furthermore, although many important applications of PES involve inner-valence- and core-ionisation processes, we will focus on photoionisation from the outer-valence orbitals below about 20 eV, where the molecular orbital approximation is generally valid.

Contributions covering other areas of photoelectron spectroscopy are planned for submission and these subjects will not be discussed here; they include the following areas: photoelectron spectroscopy as an element of key diagnostics in attosecond spectroscopy; photoelectron angular distributions, particularly in the molecular frame, which provide insight into the dynamics of electron–ion interactions and can be used to characterise alignment and orientation in chemical reactants and products; time-resolved photoelectron spectroscopy, which provides insight into how both electronic and heavy-particle structures change with time, as well as into the paths that reactants follow to products; and finally, applications of photoelectron spectroscopy to complex media, which address the energetics, dynamics, and kinetics of clusters, aerosols, microdroplets, and liquid jets. Most of the work discussed in these other perspectives involves dispersive photoelectron spectroscopy, and to balance this somewhat, the present Perspective focuses primarily on threshold photoelectron spectroscopy and its variants as well as methods based on pulsed field ionisation (PFI). Nevertheless, recent advances in coincidence measurements using dispersive photoelectron spectroscopy have considerable potential for elucidating the dynamics and kinetics of chemical reactions, and these are touched on in the present discussion.

Photoelectron spectroscopy has many applications in molecular physical chemistry. The method can provide accurate IEs of both stable molecules and reactive species such as molecular radicals. These ionisation energies can be used in thermochemical cycles to provide thermochemical information, such as accurate bond energies and heats of formation. In its very high-resolution forms, PES allows the detailed characterisation of electronic, vibrational, and even rotational energy levels, and is thus an excellent method to yield structural information on both neutrals and cations. In PEPICO measurements, photoelectron spectroscopy can be performed on mass-selected samples, and because the technique is based on monitoring charged-particles, it can provide high detection sensitivity. Thus, threshold-PEPICO (TPEPICO) measurements provide the means to produce state-selected ions for spectroscopy and the study of unimolecular and bimolecular reactions. Finally, the combination of structural information and mass selectivity provided by PEPICO makes it suitable for the analysis of mixtures and characterisation of the products of chemical reactions in a wide range of reacting environments. In what follows, each of these applications is illustrated by using recent examples from the literature.

Tools

Photoion–photoelectron threshold/coincidence spectroscopy

In PEPICO experiments, the photoelectron and photoion from each photoionisation event are correlated and detected in coincidence.^38,46,47 In this manner, mass-specific photoelectron spectra and angular distributions can be recorded. While PEPICO methods have been employed since the 1970s, technological improvements on the last two decades have dramatically increased the range of their application. As discussed by Baer and Tuckett,³⁸ the use of velocity map imaging detectors for both electrons and ions,^48,49 the implementation of multistart–multistop detectors for electrons and ions,⁵⁰ and the incorporation of novel ion deflection and imaging techniques to minimise false coincidences^49,51 have all greatly enhanced the utility and power of the method. Several excellent recent discussions of these advances are available.^38,52,53 The photoelectron spectrum in PEPICO measurements can be generated by scanning the photon energy and detecting only threshold photoelectrons (TPEPICO), or by fixing the photon energy and recording the full photoelectron spectrum on the imaging detector. As discussed above the latter approach does not provide resolution as high as in the TPES approach, but isomeric identification has been demonstrated,⁵⁴ and the method can be considerably faster than scanning the photon energy.⁵⁵ Furthermore, it is possible that the corresponding photoelectron angular distributions, which are also provided by this approach, may also help distinguish among multiple isomers.

Despite the recent improvements, PEPICO requires relatively low count rates per photon pulse and is thus typically combined with a continuous or high-repetition-rate photon source. For many applications, synchrotron radiation (SR) is employed.⁵⁶ SR is emitted from bunches of electrons that circulate in a storage ring at velocities close to the speed of light, producing broadly tunable light pulses with a repetition rate of ∼100 MHz, which make it highly suitable for coincidence measurements. In a typical facility, dedicated beamlines exist that use dispersive optics to offer radiation that is tunable over a wide energy range. In this manuscript, we will focus on work performed at VUV/XUV beamlines that provide tunable light between roughly 5 and 50 eV. In comparison to lasers, SR has a significantly broader tuning range and a higher repetition rate. In contrast, VUV/XUV sources based on pulsed lasers can provide higher resolution as well as a higher peak power, and can also be performed in-house, rather than at an external research facility.

Franck–Condon simulations

In several examples shown below, the vibrational structure of photoelectron spectra was modelled using Franck–Condon simulations. The Franck–Condon approximation follows from the separability of the wavefunction into electronic and vibrational components (Born–Oppenheimer approximation) in the neutral state and the continuum, and then writing the bound-continuum matrix element as a product of electronic transition matrix element and a vibrational overlap integral. If it is assumed that the electronic matrix element is independent of electron kinetic energy, the intensities of the vibrational bands are determined by the squares of the vibrational overlap integrals, i.e., the Franck–Condon factors. Typically, the Franck–Condon factors (FCF) for the various vibrational transitions are calculated based on geometries and force constants obtained from ab initio computations. Easy-to-use programs are now available that allow the experimentalist to model photoelectron spectra.^57–59 Starting from a computed IE, the simulated spectrum is usually shifted somewhat to provide the best fit to the experimental spectrum. Computed IEs can be accurate to within 0.1 eV when coupled-cluster theory (CCSD(T)) or composite methods like CBS-QB3 are used, but the IEs obtained by methods like MP2 or density functional theory (DFT) can deviate from the experimental value by several tenths of an eV.⁶⁰ Assignment of a novel photoelectron spectrum to a given structure is thus based on two factors: a determination of the IE, which must be reasonably close to the computed value, and an appropriate description of the vibrational structure. As an example, the slow photoelectron spectrum of BH₂, a textbook example for molecular orbital theory, is given in the upper trace of Fig. 3, with a Franck–Condon simulation shown in blue in the lower trace.⁶¹ In its X ²A₁ ground electronic state BH₂ is a bent, near prolate asymmetric top (C_2v) with bond angle ∼129°, while the cationic state is a linear (D_∞h) singlet (¹Σ_g⁺). Therefore, a large change in the bending angle is expected and the long progression can be assigned as a 2ⁿ₀ progression of the bending mode. In addition, combination bands with the symmetric stretch are visible, 1¹₀2ⁿ₀. However, when the geometry change is large, the first band in the spectrum needs not to coincide with the IE, because the origin band is weak due to the small overlap between two significantly displaced vibrational wave functions. In fact, the simulation shows negligible intensity for the origin transition, and the best match of relative intensities is achieved when the first recognisable peak in the experimental spectrum at 8.24 eV is assigned to the 2¹₀ fundamental rather than the 0⁰₀ transition. Based on the simulations, an IE of 8.12 ± 0.02 eV was determined for ¹¹BH₂.⁶¹ Note that a value of 8.21 eV was computed in this work by the CBS-QB3 method, and without the FC simulation the ionisation threshold might have been assigned incorrectly.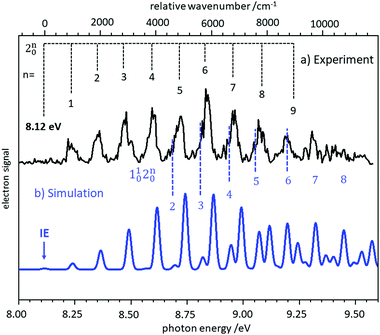

Fig. 3 Slow photoelectron spectrum of BH₂ (upper trace) compared with a Franck–Condon simulation. The IE was derived from the best agreement between experiment and simulation. Figure taken from ref. 61 by permission of the RSC.

The example shows the importance of spectral simulation for a reliable assignment. Using high-level computations, the photoelectron spectra of rather complicated systems can be described. Examples are cyclobutadiene, which is characterised by a pseudo-Jahn–Teller effect in the neutral and a E ⊗ β Jahn–Teller effect in the cation,⁶² and the ethane cation with its three strongly mixed electronic states.⁶³

Applications

IEs of reactive molecules and thermochemistry

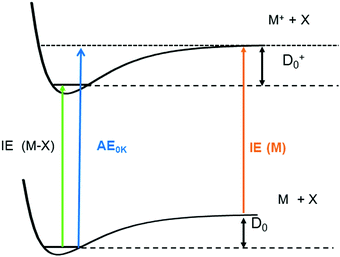
One significant application for data obtained from photoionisation experiments is the determination of bond dissociation energies (BDE), which, at 0 K, become equivalent to the dissociation energy, D₀.⁶⁴ This is accomplished via the thermochemical cycle depicted in Fig. 4.⁶⁵ When a suitable anchor is available, standard heats of formation, Δ_fH° can be derived. Data bases like the Active Thermochemical Tables (ATcT) systematically use new spectroscopic data to improve the accuracy of thermochemical information.⁶⁶ To determine the BDE for the M–X bond in a molecule, two properties must be known, the 0 K appearance energy for the fragment ion M⁺, AE_0K(M–X, M⁺), given as a blue arrow and the ionisation energy of the radical M˙ (orange arrow). If the dissociation process is barrierless, D₀ can be calculated from these two quantities via(1):

D₀ = AE_0K(MX, M⁺) − IE(M) (1)

Alternatively, a combination of the AE with the IE of the molecule MX (green arrow) yields the dissociation energy D₀⁺ of the ion MX⁺. By choosing a photon energy and detecting threshold electrons in coincidence with the ion, the internal energy of the ion is determined (assuming the ionisation energy of the molecule is known). The fragmentation onset can then be characterised in detail. Accurate AEs are available from PEPICO experiments by monitoring the relative ratio of the parent ion MX⁺ and the fragment ion M⁺ in conjunction with threshold electrons, which yields a so-called breakdown diagram, see below. The approach is described in detail in recent review articles.^38,46,67

Fig. 4 Dissociation energies, D₀, can be determined by combining the appearance energy AE_0K(MX, M⁺) of a molecule with the ionisation energy of the radical M, IE (M). Combination of the AE with the IE of the molecule IE (MX) yields D₀⁺ in the ion.

While IEs of stable molecules are readily obtained and can be determined with very high precision when required (see section on “Structural information by high-resolution photoelectron spectroscopy” below), obtaining IEs of radicals and other reactive molecules, is more challenging, as has been pointed out previously.^44,68 First of all, radicals must be generated with a number density sufficient to perform gas-phase experiments. Second, in addition to the species of interest, reactions of this species and further fragmentation of the precursor are often unavoidable, and can produce undesired signals in conventional PES. Thus, mass information is beneficial for a reliable assignment. Finally, excited electronic states of reactive species are not always well-characterised and often found to be short-lived.⁶⁹ Therefore, resonant ionisation techniques may not be applicable, and one-photon ionisation with tunable VUV radiation is required. Progress in coincidence spectroscopy, which allows the generation of ion mass-selected (threshold) photoelectron spectra, ms-(T)PES, from the full PEPICO data set (see above) has to a large extent solved this problem. As a result, there is a large body of recent work on unstable and reactive molecules that have been studied using VUV synchrotron radiation. Note, however, that in some instances it can still be difficult to distinguish ions produced by photoionisation of neutral molecules from ions of the same mass produced by dissociative ionisation.⁷⁰ Here, analysis of the ion kinetic energy available from the image is valuable, because fragments from dissociative photoionisation are associated with a considerable momentum distribution and can thus be distinguished from photoionised neutrals.^71,72

The most commonly used approaches for the generation of reactive molecules are illustrated in Fig. 5. Each of them has specific advantages and disadvantages. In pyrolysis sources, Fig. 5a), radicals are generated thermally from suitable precursors.⁷⁴ An electrically heated silicon carbide tube with a length of 10–20 mm and a diameter of 1 mm is mounted onto a molecular beam source with an orifice of 0.6–0.8 mm. Originally, this approach was used to study excited electronic states of radicals, and to record dispersive photoelectron spectra.^68,75–77 Allyl (C₃H₅) was the first ms-TPE spectrum recorded using SR.⁷⁸ A variety of radicals and carbenes have been generated in high number densities and successfully studied by using this method. These species include (but are not limited to) CH₃,^79–81 CF₃,⁸² C₂H₃,^83,84 C₆H₄ (ortho-benzyne),^85,86 C₇H₆,⁸⁷ C₇H₅,⁸⁷ various isomers of C₃H₂,^88,89 C₉H₇,⁹⁰ C₄H₇,⁹¹ C₄H₅,⁹¹ C₈H₉, and C₈H₈,⁹² as well as nitrogen-containing radicals like pyrrolyl⁹³ and picolyl.⁹⁴ In all these cases IEs were determined and vibrational structure was observed, despite the comparatively high temperatures of around 500 K. The major challenge in pyrolysis is often the identification and synthesis of a suitable precursor, thus chemical expertise is required. Recent examples are the TPE spectra of cyclopropenylidene, obtained from a quadricyclane⁹⁵ and of cyclobutadiene, which was produced from the Pettit-complex Fe(C₄H₄)(CO)₃.⁶²

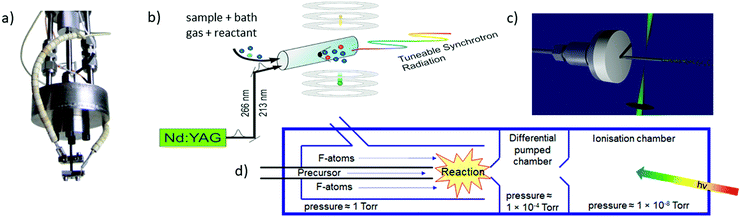Fig. 5 The most frequently used radical sources combined with photoelectron spectroscopy are (a) pyrolysis, (b) photolysis in a side sampled flow reactor (with SR) or in (c) a quartz reactor (very high-resolution experiments) and (d) reactions in a fluorine atom discharge. Figures (a) and (b) taken from ref. 73 by permission of Wiley.

Perhaps the most common method to produce radicals is photolysis. In SR experiments, side-sampled flow reactors are used (Fig. 5b).⁹⁶ The reactor consists of a quartz tube with a ≈0.2 mm hole. A mixture of reactants (often bromides or iodides) and rare gas flows through this tube and is irradiated by laser light, which propagates collinearly down the reactor. It generates radicals that effuse through the small hole directly into the ionisation region of the spectrometer. Reactions of photolysis products with O₂ is a convenient approach to generate oxy- or peroxy-species and thus often used to study species of interest to atmospheric chemistry. For example, MS-TPE spectra of CH₃OO,⁹⁷ IO,⁹⁸ and NCl₂⁹⁹ were reported. A further advantage of a flow reactor is the possibility to investigate the kinetics of chemical reactions, see below. In high-resolution experiments with ns-lasers a simpler approach is often chosen, Fig. 5(c). Here, a quartz tube is mounted onto a molecular beam source and irradiated with a Nd:YAG or excimer laser.^100–103

Another common method for radical generation employs a microwave discharge, which can be used to produce radicals directly¹⁰⁴ or, as in Fig. 5d, to generate fluorine atoms (and other reactive species) that produce radicals through secondary reactions.¹⁰⁵ The F-atoms then abstract H atoms from a sample molecule, see (2) and (3). The formation of HF is the thermodynamic driving force in this process, i.e.:

F₂ → 2F˙ (2)

F˙ + R–H → HF + R˙. (3)

The high reactivity of F permits the synthesis of species that are difficult to produce by any other means. In particular, Dyke and coworkers recorded a large number of photoelectron spectra of reactive molecules generated in a fluorine discharge using mostly dispersive PES,⁴⁴ but in several cases also (non-mass selected) TPES, e.g. IF and CF₂.^44,106 However, H-abstraction is generally not very selective. When inequivalent E–H bonds (E = element) are present in a precursor, several different species are often produced. In this situation, coincidence detection again comes to the rescue, greatly expanding the variety of species that can be studied. Recent examples of TPES or SPES include OH,⁴⁹ NH,¹⁰⁷ NH₂,¹⁰⁸ C₂,¹⁰⁹ C₂H₃,¹¹⁰ C₂H₅,⁷⁰ C₃H_x,¹¹¹ C₂H,¹¹² isomers of C₄H₅,¹¹³ and CH₂NC,¹¹⁴ but also methoxy¹¹⁵ and peroxy radicals,^116–119 including the Criegee-Intermediate CH₂OO,¹¹⁴ as well as fundamental boron-containing species like HBBH³⁶ and BH₂.⁶¹ In all cases, vibrational progressions were well resolved.

As an example of a BDE determination, consider the homolytic dissociation of the first Me₂Bi–CH₃ bond in BiMe₃, which is crucial to the radical chemistry of this compound and related species. From the breakdown diagram in the upper trace of Fig. 6, an AE_0K(Bi(CH₃)₃, Bi(CH₃)₂⁺) = 9.445 eV has been determined.¹²⁰ Combined with the IE = 7.27 eV of Bi(CH₃)₂ (lower trace), which has been generated by pyrolysis from Bi(CH₃)₃, a Me₂Bi–CH₃ homolytic bond dissociation energy of 210 ± 7 kJ mol⁻¹ was revealed, in agreement with computations.¹²¹ This measurement led to a revision of the previously reported value by more than +15% (+28 kJ mol⁻¹). Note that the simulation in the lower trace of Fig. 6 is based on computations that only include scalar relativistic effects and might therefore underestimate the change in the Bi–C bond length upon ionisation.

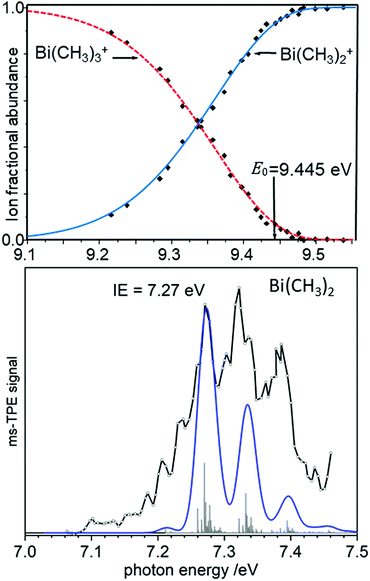Fig. 6 The appearance energy AE_0K(Bi(CH₃)₃, Bi(CH₃)₂⁺) has been determined from a breakdown diagram (upper trace, here labelled E₀). Combined with the IE of Bi(CH₃)₂ (lower trace) a Bi-CH₃ bond dissociation energy is obtained. Upper trace: Redrawn with permission from ref. 120, Copyright 2009, American Chemical Society. Lower trace: Reproduced from ref. 121 with permission of the Royal Society of Chemistry.

Ionisation energies are in principle also accessible from simple ion yield spectra. Indeed, the precise determination of accurate IEs from PES, TPES, ZEKE and in particular PIMS remains a challenging task, and the optimum approach depends on the system of interest. However, for many molecules several isomers exist, which are often difficult to separate in the ion signal, but more readily distinguished in the photoelectron spectrum. As an example, the three isomers of the (pyrolytically generated) picolyl radical are given in Fig. 7. IEs of 7.70 eV, 7.59 eV and 8.01 eV were determined for 2-, 3- and 4-picolyl, respectively.⁹⁴ The vibrational structure is due to an in-plane deformation mode of the aromatic ring, similar to the related benzyl radical.¹²² The radicals were generated by pyrolysis from aminomethylpyridine precursors via deamination.

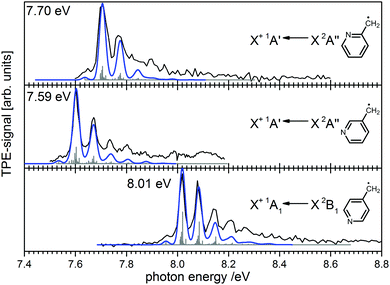Fig. 7 Photoelectron spectroscopy allows the clear distinction of three isomers of the picolyl radical. (Figure taken from ref. 82 by permission of Wiley-VCH.)

Structural information by high-resolution photoelectron spectroscopy

While ms-TPES is sufficiently accurate for many applications, higher resolution of around one cm⁻¹ or less is sometimes required. For example, this situation arises when experimental data are compared to very sophisticated calculations on small molecules, as well as for weakly bound systems (van der Waals clusters), where even small errors in the IE can produce significant errors in the description of the system. Here, pulsed-field ionisation-zero kinetic energy photoelectron spectroscopy (PFI-ZEKE-PES) with tunable laser-based light sources shows its value.^40,45,123 In this method, molecules are excited into very high-lying Rydberg-states within a few cm⁻¹ of the ionisation limit, and are subsequently ionised by a time-delayed electric field pulse. Because the highly excited Rydberg electron only weakly perturbs the molecular ion core, the rovibronic structure of the ion can be characterised in great detail. The method has two principal advantages over threshold photoelectron spectroscopy with conventional or synchrotron-based light sources. First, the ultimate resolution of narrow-band lasers is considerably higher than that achieved with monochromators and, in principle, allows considerably higher resolution in the photoelectron spectrum. Second, while many PFI-ZEKE experiments are performed using single-photon ionisation with VUV laser sources, resonance-enhanced ionisation schemes allow selective excitation and ionisation of not only particular species within a sample, but also specific rovibronic states of that species, providing significantly more detail in the experiments. Efforts to push the resolution and precision of PFI-ZEKE have been reviewed previously, as have numerous applications of the method.⁴⁵ Here, we briefly describe a few recent examples of the latter to provide a perspective on the range of current applications.

The high resolution of PFI-ZEKE has made it a powerful tool for determining ionisation thresholds and characterising the rovibronic structure of ions.^40,45 One of the key testing grounds of PFI-ZEKE methods has been the determination of the ionisation energy of molecular hydrogen, H₂, which can be used in a thermodynamic cycle to determine the dissociation energy of H₂. As discussed by Merkt et al.,⁴⁵ over the years PFI-ZEKE spectroscopy has led to significant advances in the determination of ionisation thresholds, but for H₂, new PFI-ZEKE measurements combining mm-wave spectroscopy of Rydberg states¹²⁴ and modelling based on multichannel quantum defect theory now provide the most accurate determination of this value.¹²⁵ For larger systems, PFI-ZEKE continues to produce impressive new information on the spectroscopy and rovibronic structure of molecular cations. For example, partially rotationally resolved PFI-ZEKE spectra of diacetylene allowed the experimental characterisation of the spin–orbit interaction in the ²Π_g ground state cation, and steps toward unravelling the Renner–Teller interactions in this system.¹²⁶ PFI-ZEKE has also provided the key experimental data required for understanding the classic Jahn–Teller interactions in the ground state of the methane cation.¹²⁷

Because the ionisation process projects the lower state wavefunction onto the ionic state surface, PFI-ZEKE can also provide considerable information on the rovibronic structure of the lower state. As an example, Wright and coworkers^128,129 have recently used PFI-ZEKE, along with complementary techniques such as two-dimensional laser-induced fluorescence, to characterise the vibrational structure in the S₁ state of a series of para-substituted benzene molecules.^129–131 The goal of this work was to elucidate the effects that promoted intramolecular vibrational redistribution (IVR). The PFI-ZEKE studies allowed the characterisation of interactions among vibrational and torsional modes, and the determination of the roles of symmetry, density of states, and “serendipitous” near-degeneracies of vibrational/torsional levels in IVR.

Although not technically photoelectron spectroscopy, mass-analyzed threshold ionisation (MATI) spectroscopy^23,132,133 is closely related to PFI-ZEKE spectroscopy. In MATI, however, the ion produced by the pulsed-field ionisation of neutral Rydberg molecules is mass analyzed and detected instead of the electron; nevertheless, the resulting spectra are similar to the corresponding PFI-ZEKE spectra. The advantage of MATI is that it simplifies the identification of the absorbing species by providing its mass, a feature of considerable utility in complex reaction mixtures. However, efficiently extracting the ions after the delayed pulse is more difficult than extracting the electrons, and typically results in reduced signal or requires a larger field pulse, which in turn results in lower signal-to-noise or reduced resolution. New methods continue to be developed to address these difficulties.¹³³ MATI is closely related to threshold photoelectron photoion coincidence (TPEPICO) discussed above. In MATI, however, the coincident threshold/zero-energy photoelectron is implied rather than actually detected.

As an example, in a recent series of papers, Kwon and coworkers have performed a systematic series of MATI studies to characterise the conformer structure and strain in a series of saturated cyclic ethers: oxetane,¹³⁴ tetrahydrofuran,¹³⁵ and tetrahdropyran¹³⁶ (C₃H₆O, C₄H₈O, and C₅H₁₀O, respectively). The experiments were performed using single-photon VUV ionisation, and provided information on both the ground state neutral and ground state cation, thus providing insight into how the potential surfaces and structures change with the removal of an electron from the lone-pair HOMO on the oxygen atom. In this work, the comparison of experiment with quantum chemical calculations was particularly helpful in assigning the vibronic structure, and low-dimensional potentials describing the torsional motions allowed simulations that reproduced the experimental data quite satisfactorily.

The work of Yang and coworkers provides an instructional example of the utility of MATI in the context of bond activation in hydrocarbons and amines.^137,138 For example, they studied the gas-phase reactions of La atoms with two C₅H₈ isomers, 1,4 pentadiene and 1-pentyne, and used a combination of MATI and electronic structure calculations to identify radical complexes present in the reaction mixtures.¹³⁹ They found a common La(C₅H₆) radical produced by dehydrogenation of both reagent hydrocarbons, and they used the comparison of the MATI spectrum with the calculations to determine the structure of the La(C₅H₆) species. Furthermore, both hydrocarbons also produced the La(C₃H₄) radical resulting from C–C bond cleavage and the elimination of C₂H₄. The resulting MATI spectra for both reagents were quite similar, and calculations showed that this common spectrum resulted from two different La(C₃H₄) isomers. Such measurements of the energies and structures of short-lived gas-phase species can provide considerable insight into catalytic mechanisms for bond activation at metal centers.

Recently, both PFI-ZEKE and MATI spectroscopy have been demonstrated for the positively charged atomic and molecular ions Mg⁺ and MgAr⁺.^140,141 This work, using positive ions as samples rather than neutrals, represents a significant extension of the types of species that can be characterised with these methods. An analysis of the line shapes and electric-field shifts for cations has also been presented, and the field-induced thresholds shifts were found to scale with the atomic number, Z, as Z^1/2. In the cation experiments, neutral Mg atoms were produced by laser ablation, and the MgAr molecules were formed in the subsequent supersonic expansion used to form a molecular beam. The target ions were then prepared by either resonant two-photon ionisation (Mg) or ionisation from a metastable electronic state populated in the formation process (MgAr). The resulting singly charged ions were excited to high Rydberg states via resonant two- or three-color processes, and pulse-field-ionised to produce the observed spectra.

The ultimate resolution of PFI-ZEKE and MATI for cations is not expected to be quite as high as for neutral molecules, but an experimental resolution of ∼2 cm⁻¹ was demonstrated. This resolution is particularly useful for characterising thermodynamically stable molecules such as MgAr²⁺. In particular, the resonant excitation process for MgAr⁺ allowed the modification of the rotational (and vibrational) distributions of the high Rydberg states and the resulting MgAr²⁺, and the resolution was sufficient to observe changes in the positions and rotational band contours in the PFI-ZEKE and MATI spectra.¹⁴² An accurate potential energy curve for MgAr²⁺ was derived from the data, giving insight into the underlying intermolecular interactions. The latter spectra also allowed the separation of the spectra for the ²⁴MgAr⁺ and ²⁶MgAr⁺ isotopes, which in turn allowed the assignment of the absolute vibrational quantum numbers in the doubly charged cation.

While the PFI-ZEKE and MATI spectra of MgAr⁺ were an experimental tour de force, rapid developments in VUV laser technology will likely soon allow the application of this approach to the study of a much wider range of molecular cations. Many doubly charged cations have a relatively high number of low-lying electronic states and unravelling the assignment using experiments can be challenging. PFI-ZEKE spectroscopy of cations suggests the possibility of recording spectra from multiple electronic states of the singly charged cation, which could provide insight into the assignment of such states.

State-selected ions for spectroscopy, dynamics, and kinetics

Since its original development, one of the principal applications of threshold PES and TPEPICO techniques has been for state-selected unimolecular and bimolecular reactions of ions. With the development of PFI-ZEKE and PFI-PEPICO techniques, the selectivity of the ion-preparation was considerably enhanced, as has been reviewed by Ng.⁴⁷ In 1994, Mackenzie and Softley¹⁴³ demonstrated the ability to study ion–molecule reactions of rotationally (and vibrationally) state-selected H₂⁺ prepared by ZEKE-PES. That work was recently advanced when Höveler et al.¹⁴⁴ developed a related approach to investigate ion–molecule reactions at extremely low temperatures (0–30 K) with high precision by studying the reactions of H₂ molecules in very high Rydberg states. Here, the Rydberg electron hardly perturbs the reaction dynamics, but minimises negative effects such as heating of ions by stray electric fields.

The reactions of spin–orbit- and electronic-state-selected ions can also be studied. For example, using PFI techniques, Chang et al.¹⁴⁵ have recently demonstrated resonance excitation schemes to produce J-selected V⁺a (⁵D_J=0–4), a (⁵F_J=1–5), and a (³F_J=2–4) ions. Subsequently, Xu et al.¹⁴⁶ have used these schemes to study the state-selected reactions of V⁺ with water. While the V⁺ + H₂O cross sections do not appear to depend significantly on the total J within any of the spin–orbit states of V⁺, the reaction of H₂O with V⁺a (³F_J) ions had a substantially larger cross section than with V⁺a (⁵D_J) and a (⁵F_J) ions. These studies thus contribute to the long-term effort to use reactant state-selection to control the outcome (or cross section) of chemical reactions. TPES and PFI techniques can also be used to study the spectroscopy of state-selected ions. For example, Jacovella et al.¹⁴⁷ combined single-photon ionisation with MATI to produce rotational and spin–orbit-state-selected acetylene ions, and then recorded the infrared spectrum by using the large increase in reactivity of the vibrationally excited ions with H₂. In particular, the reaction: C₂H₂⁺(v₃⁺, J⁺) + H₂ → C₂H₃⁺ + H is much faster for v₃⁺ = 1 than 0, so infrared absorption from the ground vibrational level to v₃⁺ = 1 leads to a significant signal at the C₂H₃⁺ mass. This approach had been demonstrated previously by cooling C₂H₂⁺(v₃⁺ = 0, J⁺) to very low temperatures in an ion trap.¹⁴⁸ Note, however, that the approach based on PFI allows the study of J⁺-selected samples of C₂H₂⁺.

Characterisation of reaction products

More recently, there has been a shift toward using PEPICO techniques, in particular ms-TPES, to examine more complex reacting environments, particularly those in which isomeric specificity is required to unravel reaction mechanisms. Consequently, PEPICO has evolved into an analytical tool to probe elusive intermediates and reaction products in reactive environments. This includes kinetics experiments, catalytic reactors, model flames, shock tubes, and jet-stirred reactors. All these environments are characterised by the presence of a vast number of species – reactants, intermediates, and products. Even in a single-fuel flame, hundreds of different species can be present. Therefore, a method is required that can detect numerous species in parallel with high detection sensitivity, and also provide structural information. Due to the high sensitivity of charged-particle detection and the multiplexing-capability of photoionisation mass spectrometry, PIMS has been employed for online-monitoring of reaction intermediates using synchrotron radiation.^149,150 Compounds were identified based on their IEs, which are derived from steps in the photoion yield signal (see upper trace of Fig. 8 as an example). Although multiplexed PIMS can be used to distinguish isomers, that approach becomes challenging to use when there are multiple isomers of minor species in multi-component systems. The photoelectron kinetic energy in PEPICO experiments adds an additional dimension to the data that considerably enhances the information content of the measurement because different isomers have different photoelectron spectra.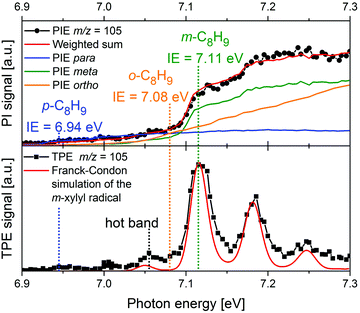

Fig. 8 In a m-xylene flame, m/z 105 was identified, corresponding to xylyl radicals. The photoion signal (upper trace) does not permit identification of the product isomer. The TPE spectrum in the lower trace, on the other hand shows that meta-xylyl is the dominant product isomer and the band around 7.05 eV assigned to a hot band. The Figure was published in ref. 151, Copyright Elsevier, 2017.

As mentioned above, flame chemistry is highly complex, and even simple aromatic molecules and radicals exist in numerous isomeric forms that have comparable IEs. The picolyl radicals given in Fig. 7, which are possible intermediates in the combustion of N-containing biofuels, provide an example of this structural complexity. This is particularly relevant for research that aims to unravel the mechanisms that form PAH and soot in flames, still one of the major topics in combustion research. Here, structurally sensitive detection of the various aromatic molecules formed is required. Detection of ions alone does not always provide sufficient information to assign the photoion yield at a given mass to one structure. Photoelectron detection, on the other hand, is more sensitive to the molecular structure and often allows different isomers to be distinguished.

An example is given in Fig. 8. Due to complexity of combustion processes, reactions are often carried out under controlled conditions. A fuel-rich meta-xylene (m/z 106) model flame was coupled to a molecular beam/mass spectrometry setup, with the aim of detecting polycyclic aromatic hydrocarbons (PAH).¹⁵¹ The primary reaction step in the combustion of most hydrocarbons is loss of a H-atom and formation of a radical. The upper trace shows the xylyl photoion yield at m/z 105 as a function of photon energy. There is a pronounced step in the photoion signal around 7.1 eV, but signal is already present below 7 eV. It is impossible to tell whether this signal is due to the para-isomer or to hot bands. In addition, the IEs of ortho- and meta-xylyl differ by only 30 meV. However, from the ms-TPE-spectrum given in the lower trace and the simulation (red line), meta-xylyl can be unambiguously identified as the dominant product isomer and the signal at 7.05 eV assigned to a hot band.

Such assignments rely on the existence of isomer-specific data for elusive molecules. The increasing importance of photoionisation and photoelectron spectroscopy as analytical tools thus motivates experiments targeted at specific reactive intermediates and provides an important motivation for the experiments given in the Sections IEs of reactive molecules and thermochemistry and structural information by high-resolution photoelectron spectroscopy.

High-temperature reactions of radicals have also been studied in pyrolysis sources, which can be viewed as tubular microreactors.¹⁵² Here, bimolecular reactions can be enhanced by increasing the precursor (and thus radical) concentration, the pressure, and the length of the heated region. It was found that PAH formation can be rather selective for certain radicals. In additions to IR/UV spectroscopy¹⁵³ and PIMS,¹⁵⁴ ms-TPES turned out to be an efficient tool for a structure-sensitive detection of PAH isomers. For ortho-benzyne, produced by pyrolysis from benzocyclobutendione, it was found that a series of 1,4-cycloaddition (Diels–Alder) reactions with benzyne led to a rapid growth of PAH up to triphenylene.^155,156 The mechanism was derived from a combination of IR/UV and ms-TPE-spectroscopy that yielded complementary data. In the reaction of ortho-benzyne with allyl, indene was found to be the dominant reaction product by TPES.¹⁵⁷

In a jet stirred reactor (JSR), several jets of fuel are fed into a mixing chamber maintained at combustion-like temperatures. In most cases their reaction with O₂ is studied. A big advantage of these JSR is the spatial homogeneity of the reaction mixture, which is ensured by rapid mixing due to the turbulent jets. Recently such a JSR was coupled to a PEPICO spectrometer and the products of the reaction of n-pentane with O₂ were analysed by ms-TPES.¹⁵⁸ The authors reported product branching ratios for numerous isomeric products. For illustration, the ms-TPE spectrum recorded at m/z 42 is given in Fig. 9. A product branching ratio of ketene (IE = 9.62 eV, blue dashed line)/propene (IE = 9.73 eV, green dotted line) of 2 : 1 was determined from the TPE-spectra. The determination of this branching ratio by using PIMS alone requires high mass resolution to distinguish the isobaric ions, an approach has also been effectively used in recent years.^159–161

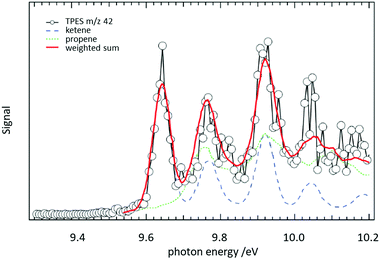Fig. 9 The reaction of n-pentane with O₂ was studied in a jet-stirred reactor. From a fit to the ms-TPE spectra recorded at m/z 42, it was possible to extract a ketene/propene product branching ratio of 2 : 1. Reproduced from ref. 158 with permission from the Royal Society of Chemistry.

As another example of elucidating chemistry in a complex environment, a PEPICO spectrometer was recently coupled to a novel high-repetition rate shock tube system to study the high-temperature pyrolysis of ethanol.¹⁶² Although the experimental repetition rate was high for a shock tube (∼1 Hz vs. the usual once every 10–30 minutes), it was still quite low for coincidence measurements. Fortunately, the reproducibility of the shock waves was high, allowing signal averaging to improve statistics. The low duty cycle of the experiments impedes scanning and, as a result, the full photoelectron spectra were obtained from the imaging detector at selected wavelengths. These spectra were then used to distinguish among the isomers present in the reaction mixture. For example, with a suitable choice of photon energy, the photoelectron spectrum for the species at mass 40 (C₃H₄⁺) confirmed that both propyne and allene were produced in the pyrolysis and subsequent reactions. The large changes in pressure over the time of the shock waves introduced significant challenges for quantitative measurements, but there are known approaches to deal with this issue. The example shows that dispersive PES has its place as a tool to analyse chemical reactions.

Radical reactions of interest to atmospheric chemistry are often studied using flow reactor setups similar to the one depicted in Fig. 5b). A particular highlight has been the generation of the carbonyl oxides (Criegee-intermediates) RCHOO (R = H, CH₃) from RCHI₂ and O₂, using photolysis at 248 nm.¹⁶³ The reaction with SO₂ and with NO₂ proved unexpectedly rapid and implied a greater role of carbonyl oxides in tropospheric chemistry than previously anticipated. In that experiment, reactants and products were detected by analysing the photoion yield only. Recently a similar flow tube was coupled to a PEPICO spectrometer. It was employed to investigate the reaction of allyl and the isomers of methylallyl (C₄H₇) with oxygen.^164,165E- and Z-1-methylallyl were distinguished by their TPE spectra and rates for the two isomers were determined. Within the experimental accuracy they were found to be identical. In contrast, conformer-dependent reactivity has been observed for reactions of the syn- and anti-isomers of CH₃CHOO.¹⁶⁶ In PIMS studies it was found that anti-CH₃CHOO is substantially more reactive toward water and SO₂ than the syn-isomer.

Another recent application of PEPICO is to “operando” studies to characterise catalytic reaction mechanisms in situ.¹⁶⁷ In these experiments, reactants flowed through a SiC “microreactor” coated with the catalyst of interest, CrPO₄. The temperature of the reactor could be controlled, and the length of the reactor and flow speed determined the exposure time to the catalyst. The effluent from the reactor was formed into a molecular beam, which passed through a skimmer and into the interaction region of the PEPICO spectrometer. Reactant, products, and reactive intermediates (e.g., radicals, etc.) could all be observed. TPEPICO was used to record the ms-TPES spectra for the species of interest, allowing the identification of specific isomers. For example, in the oxybromination of propane, employed to generate feedstock chemicals from hydrocarbons, the reaction mechanism was found to include a gas-phase reaction involving C₃H₇ radical intermediates, and the TPES spectra demonstrated that these radicals were essentially all 2-C₃H₇ rather than 1-C₃H₇ (see upper trace of Fig. 10).¹⁶⁸ The C₃H₅ signal (lower trace) was assigned to allyl rather than cyclopropyl. Further analysis of the data demonstrated that while the oxybromination mechanism proceeded through gas-phase reactions of Br₂ and Br radicals generated in surface reactions, the oxychlorination mechanism involved surface reactions on the catalyst. Additional studies provided insight into the conditions leading to the generation of larger hydrocarbons relevant to coking at larger scales. The flexibility and generality of this experimental approach should make it a significant resource for researchers in catalysis.

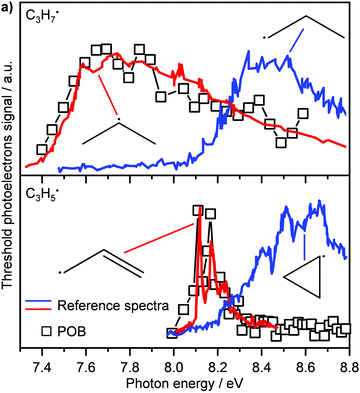Fig. 10 In the oxybromination of propane (POB) over CrPO₄, C₃H₇ and C₃H₅ radicals were detected by ms-TPEs (symbols) spectra in operando PEPICO. The colored lines in panel (a) denote reference ms-TPE spectra of the different isomers of C₃H₇ and C₃H₅, the structures are given as insets. As visible, 2-propyl rather than 1-propyl and allyl rather than cyclopropyl are formed. Reprinted with permission from ref. 149. Copyright 2020, American Chemical Society.

Outlook

As outlined in the previous section, one recent development in photoelectron spectroscopy is its application as an analytical tool for monitoring chemical reactions. With the increasing complexity of the chemical environments of interest, there is an increasing desire for multidimensional characterisation techniques, and photoelectron spectroscopy is being incorporated into a growing number of these. The one-to-one correspondence between electrons and ions provided by the PEPICO approach, which yields ion-mass selected (or ion-momentum selected) photoelectron spectra, allows the extraction of unprecedented details on the reaction mechanisms of processes in complex environments. We therefore expect the number of such studies to grow significantly in the near future.

Concurrent theoretical studies are now an integral part of most photoelectron spectroscopy studies, particularly those performed with the highest energy resolution. As mentioned above, the highest precision measurement of the ionisation and dissociation energies of H₂ incorporate results from multichannel quantum defect theory in the analysis of the results.^124,125 Similarly, in larger systems, detailed calculations of the rovibronic structure of the cations is essential for the assignment of the spectra.^62,127,169 Often, these calculations point to the need for higher resolution or better signal-to-noise ratio to provide a more direct comparison with theory.⁴⁵ A significant part of this feature dealt with TPES (and SPS) of radicals and other reactive intermediates. Rotationally resolved studies of such species using ZEKE and MATI can provide additional insight and more accurate data. Roughly 20 years ago, a review summarised high-resolution work on radicals, but at the time mostly (but not exclusively) di- or triatomic ones were addressed.¹⁷⁰ Several species have been addressed since, like CH₃,^76,171 C₃H₃,^101,172 C₃H₅,¹⁷³ NH₂,^174,175 or C₅H₅,¹⁷⁶ but the reported number of rotationally resolved photoelectron spectra of open-shell species is still limited. For example, improvements in the ms-TPES of cyclobutadiene⁶² would allow an even better comparison with the theoretically predicted structure. Such improved resolution would likely require a shift from synchrotron- to laser-based light sources, and it may also require improved methods to generate intense cold beams of radicals and reactive species. Finally, it is worth mentioning that the calculation of ionisation energies and photoionisation cross sections, particularly for isomeric systems, can be invaluable in sorting out the relative isomer concentrations and the composition of complex mixtures. Theory will continue to be essential to the advancement of photoelectron spectroscopy.

Novel new applications are already on the horizon. For example, plug flow reactors provide another approach to study chemistry at high temperatures in a continuous flowing system. Such reactors have already been coupled to synchrotron radiation using ion detection,¹⁷⁷ and the application of PEPICO for product analysis will likely soon follow. Note that similar flow reactors are used in many other areas of chemistry, including the production of pharmaceuticals,¹⁷⁸ so the potential range of applications is large.

At the other temperature extreme, the CRESU technique (Cinétique de Réaction en Ecoulement Supersonique Uniforme or Reaction Kinetics in Uniform Supersonic Flow) allows the study of gas-phase kinetics at very low temperatures down to 20 K.^179,180 Such studies are particularly relevant for astrochemistry, due to the low temperatures in large parts of interstellar space.¹⁸¹ Very recently, a CRESU setup was coupled with a PEPICO spectrometer and tested using the reaction of ethynyl radicals with acetylene:¹⁸²

C₂H + C₂H₂ → C₄H₂ + H

Ethynyl was produced by photolysis of acetylene at 193 nm and a diacetylene ion signal was observed. Photoelectron spectra have not yet been reported, but they are anticipated.

To date, the application of PEPICO to chemical reactors relies on access to synchrotron radiation as a high-repetition rate source of VUV and soft X-ray radiation, which imposes severe boundary conditions, like limited beam times. The availability of high-repetition rate laboratory XUV sources would thus greatly expand the scope of PEPICO as an analytical tool. In fact, such systems are now becoming commercially available,¹⁸³ and their application in photoionisation studies of chemical reactivity¹⁸⁴ is expected to grow rapidly in the near future.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are indebted to a large number of coworkers and colleagues for contributing to the work discussed in this feature article. IF acknowledges continuous funding by the Deutsche Forschungsgemeinschaft (DFG). The contribution of STP is based on work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences under contract No. DE-AC02-06CH11357.

Notes and references

1. W. Hallwachs, Philos. Mag., 1888, 26, 78–80.
2. W. Hallwachs, Wied. Ann., 1888, 33, 301–312.
3. H. Hertz, Wied. Ann, 1887, 983–1000,  DOI:10.1002/andp.18872670827.
4. A. Einstein, Ann. Phys., 1905, 322, 132–148.
5. C. Nordling, E. Sokolowski and K. Siegbahn, Phys. Rev., 1957, 105, 1676–1677.
6. K. Siegbahn, Rev. Mod. Phys., 1982, 54, 709–728.
7. F. I. Vilesov, B. L. Kurbatov and A. N. Terenin, Dokl. Akad. Nauk SSSR, 1961, 138, 1329–1332.
8. M. I. Al-Joboury and D. W. Turner, J. Chem. Soc., 1963, 5141–5147,  10.1039/JR9630005141.
9. D. W. Turner and M. I. Al Jobory, J. Chem. Phys., 1962, 37, 3007.
10. D. W. Turner, Annu. Rev. Phys. Chem., 1970, 21, 107–128.
11. T. Koopmans, Physica, 1934, 1, 104–113.
12. T. A. Carlson, Annu. Rev. Phys. Chem., 1975, 26, 211–234.
13. R. E. Ballard, Photoelectron Spectroscopy and Molecular Orbital Theory, John Wiley & Sons, New York, 1978.
14. V. Blanchet, S. Lochbrunner, M. Schmitt, J. P. Shaffer, J. J. Larsen, M. Z. Zgierski, T. Seideman and A. Stolow, Faraday Discuss., 2000, 115, 33.
15. A. Stolow, A. E. Bragg and D. M. Neumark, Chem. Rev., 2004, 104, 1719–1758.
16. A. Stolow and J. G. Underwood, in Adv. Chem. Phys., ed. S. A. Rice, 2008, vol. 139, pp. 497–583.
17. D. Villarejo, R. R. Herm and M. G. Inghram, J. Chem. Phys., 1967, 46, 4995–4996.
18. T. Baer, W. B. Peatman and E. W. Schlag, Chem. Phys. Lett., 1969, 4, 243–247.
19. W. B. Peatman, T. B. Borne and E. W. Schlag, Chem. Phys. Lett., 1969, 3, 492–497.
20. K. Müller-Dethlefs, M. Sander and E. W. Schlag, Z. Naturforsch., 1984, 39a, 1089–1091.
21. K. Müller-Dethlefs and E. W. Schlag, Annu. Rev. Phys. Chem., 1991, 42, 109–136.
22. G. Reiser, W. Habenicht, K. Müller-Dethlefs and E. W. Schlag, Chem. Phys. Lett., 1988, 152, 119–123.
23. P. M. Johnson and L. Zhu, Int. J. Mass Spectrom. Ion Proc., 1994, 131, 193–209.
24. L. Zhu and P. Johnson, J. Chem. Phys., 1991, 94, 5769–5771.
25. J. C. Poully, J. P. Schermann, N. Nieuwjaer, F. Lecomte, G. Grégoire, C. Desfrançois, G. A. Garcia, L. Nahon, D. Nandi, L. Poisson and M. Hochlaf, Phys. Chem. Chem. Phys., 2010, 12, 3566–3572.
26. J. Berkowitz, Photoabsorption, Photoionization, and Photoelectron Spectroscopy, Academic Press, New York, 1979.
27. J. Stöhr, NEXAFS Spectroscopy, 2nd edn, Springer, New York, 1996.
28. K. L. Reid, Mol. Phys., 2012, 110, 131–147.
29. P. Baltzer, B. Wannberg and M. Carlsson Göthe, Rev. Sci. Instrum., 1991, 62, 643–654.
30. P. Baltzer, L. Karlsson and B. Wannberg, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 315–317.
31. P. Kruit and F. H. Read, J. Phys. E: Sci. Instrum., 1983, 16, 313–324.
32. A. M. Rijs, E. H. G. Backus, C. A. de Lange, N. P. C. Westwood and M. H. M. Janssen, J. Electron Spectrosc. Relat. Phenom., 2000, 112, 151–162.
33. A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477.
34. R. Lindner, K. Müller-Dethlefs, E. Wedum, K. Haber and E. R. Grant, Science, 1996, 271, 1698–1702.
35. P. T. Murray and T. Baer, Int. J. Mass Spectrom. Ion Phys., 1979, 30, 165–174.
36. D. Schleier, A. Humeniuk, E. Reusch, F. Holzmeier, D. Nunez-Reyes, C. Alcaraz, G. A. Garcia, J. C. Loison, I. Fischer and R. Mitric, J. Phys. Chem. Lett., 2018, 9, 5921–5925.
37. D. Schleier, Dr rer. nat., Julius-Maximilians-Universität Würzburg, 2021.
38. T. Baer and R. P. Tuckett, Phys. Chem. Chem. Phys., 2017, 19, 9698–9723.
39. T. Arion and U. Hergenhahn, J. Electron Spectrosc. Relat. Phenom., 2015, 200, 222–231.
40. E. W. Schlag, ZEKE Spectroscopy, Cambridge University Press, Cambridge, 1998.
41. T. Baer and P.-M. Guyon, in High Resolution Laser Photoionisation and Photoelectron Studies, ed. C. Y. Ng, T. Baer and I. Powis, Wiley, New York, 1995.
42. V. Schmidt, Electron Spectrometry of Atoms using Synchrotron Radiation, Cambridge University Press, Cambridge, UK, 1997.
43. J. H. D. Eland, Photoelectron Spectroscopy, Butterworths, London, 2nd edn, 1984.
44. J. M. Dyke, Phys. Chem. Chem. Phys., 2019, 21, 9106–9136.
45. F. Merkt, S. Willitsch and U. Hollenstein, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, West Sussex, UK, 2011, vol. 3, pp. 1617–1654.
46. T. Baer, Int. J. Mass Spectrom., 2000, 200, 443–457.
47. C. Y. Ng, Int. J. Mass Spectrom., 2000, 200, 357–386.
48. T. Baer and Y. Li, Int. J. Mass Spectrom., 2002, 219, 381–389.
49. G. A. Garcia, X. Tang, J.-F. Gil, L. Nahon, M. Ward, S. Batut, C. Fittschen, C. A. Taatjes, D. L. Osborn and J.-C. Loison, J. Chem. Phys., 2015, 142, 164201.
50. A. Bodi, B. Sztaray, T. Baer, M. Johnson and T. Gerber, Rev. Sci. Instrum., 2007, 78, 084102.
51. D. L. Osborn, C. C. Hayden, P. Hemberger, A. Bodi, K. Voronova and B. Sztaray, J. Chem. Phys., 2016, 145, 164202.
52. P. Hemberger, A. Bodi, T. Bierkandt, M. Köhler, D. Kaczmarek and T. Kasper, Energy Fuels, 2021, 35, 16265–16302.
53. B. Sztáray, K. Voronova, K. G. Torma, K. J. Covert, A. Bodi, P. Hemberger, T. Gerber and D. L. Osborn, J. Chem. Phys., 2017, 147, 013944.
54. A. Bodi, P. Hemberger, D. L. Osborn and B. Sztáray, J. Phys. Chem. Lett., 2013, 4, 2948–2952.
55. D. Felsmann, A. Lucassen, J. Krüger, C. Hemken, L.-S. Tran, J. Pieper, G. A. Garcia, A. Brockhinke, L. Nahon and K. Kohse-Höinghaus, Z. Phys. Chem., 2016, 230, 31.
56. G. Margaritondo, J. Synchrotron Rad., 1995, 2, 148–154.
57. R. Brause, M. Schmitt, D. Krügler and K. Kleinermanns, Mol. Phys., 2004, 102, 1615–1623.
58. S. Gozem, P. Wojcik, V. Mozhayskiy and A. Krylov, ezSpectrum, http://iopenshell.usc.edu/downloads.
59. S. Gozem and A. I. Krylov, Wiley Interdiscip. Rev.: Comput. Mol. Sci. DOI:10.1002/wcms.1546.
60. M. Isegawa, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2016, 12, 2272–2284.
61. D. P. Mukhopadhyay, D. Schleier, I. Fischer, J. C. Loison, C. Alcaraz and G. A. Garcia, Phys. Chem. Chem. Phys., 2020, 22, 1027–1034.
62. L. Bosse, B. P. Mant, D. Schleier, M. Gerlach, I. Fischer, A. Krueger, P. Hemberger and G. Worth, J. Phys. Chem. Lett., 2021, 12, 6901–6906.
63. U. Jacovella, C. J. Stein, M. Grutter, L. Freitag, C. Lauzin, M. Reiher and F. Merkt, Phys. Chem. Chem. Phys., 2018, 20, 1072–1081.
64. P. Chen, in Advances in Carbene Chemistry, ed. U. H. Brinker, JAI, New York, 1998, vol. 2.
65. J. Berkowitz, G. B. Ellison and D. Gutman, J. Phys. Chem., 1994, 98, 2744–2765.
66. B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszevski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108, 9979–9997.
67. B. Sztaray, A. Bodi and T. Baer, J. Mass Spectrom., 2010, 45, 1233–1245.
68. P. Chen, in Unimolecular and Bimolecular Reaction Dynamics, ed. C. Y. Ng, T. Baer and I. Powis, Wiley, New York, 1994, pp. 371–425.
69. A. Röder, J. Petersen, K. Issler, I. Fischer, R. Mitric and L. Poisson, J. Phys. Chem. A, 2019, 123, 10643–10662.
70. B. Gans, G. A. Garcia, S. Boyé-Péronne, J.-C. Loison, S. Douin, F. Gaie-Levrel and D. Gauyacq, J. Phys. Chem. A, 2011, 115, 5387–5396.
71. A. Bodi, P. Hemberger, T. Gerber and B. Sztaray, Rev. Sci. Instrum., 2012, 83, 083105.
72. X. Tang, G. A. Garcia and L. Nahon, J. Phys. Chem. A, 2017, 121, 5763–5772.
73. C. Alcaraz, D. Schröder and I. Fischer, in Encyclopedia of Radicals in Chemistry, Biology and Materials, ed. C. Chatgilialoglu and A. Studer, John Wiley & Sons, Chichester, 2012, vol. 1, pp. 477–502.
74. D. W. Kohn, H. Clauberg and P. Chen, Rev. Sci. Instrum., 1992, 63, 4003–4005.
75. J. A. Blush, D. W. Minsek and P. Chen, J. Phys. Chem., 1992, 96, 10150.
76. P. Chen, S. D. Colson and W. A. Chupka, Chem. Phys. Lett., 1988, 147, 466–470.
77. P. Chen, S. D. Colson, W. A. Chupka and J. A. Berson, J. Phys. Chem., 1986, 90, 2319.
78. T. Schüßler, H.-J. Deyerl, S. Dümmler, I. Fischer, C. Alcaraz and M. Elhanine, J. Chem. Phys., 2003, 118, 9077–9080.
79. B. K. Cunha de Miranda, C. Alcaraz, M. Elhanine, B. Noller, P. Hemberger, I. Fischer, G. Garcia, H. Soldi-Lose, B. Gans, L. A. Viera Mendez, S. Boye-Peronne, S. Douin, J. Zabka and P. Botschwina, J. Phys. Chem. A, 2010, 114, 4818–4830.
80. Y. P. Zhu, X. K. Wu, X. F. Tang, Z. Y. Wen, F. Y. Liu, X. G. Zhou and W. J. Zhang, Chem. Phys. Lett., 2016, 664, 237–241.
81. J. A. Blush, P. Chen, R. T. Wiedmann and M. G. White, J. Chem. Phys., 1993, 98, 3557–3559.
82. H. Dossmann, G. A. Garcia, L. Nahon, B. K. C. de Miranda and C. Alcaraz, J. Chem. Phys., 2012, 136, 204304.
83. J. A. Blush and P. Chen, J. Phys. Chem., 1992, 96, 4138–4140.
84. X. K. Wu, X. G. Zhou, P. Hemberger and A. Bodi, Phys. Chem. Chem. Phys., 2019, 21, 22238–22247.
85. X. Zhang and P. Chen, J. Am. Chem. Soc., 1992, 114, 3147–3148.
86. D. Kaiser, E. Reusch, P. Hemberger, A. Bodi, E. Welz, B. Engels and I. Fischer, Phys. Chem. Chem. Phys., 2018, 20, 3988–3996.
87. M. Steinbauer, P. Hemberger, I. Fischer and A. Bodi, ChemPhysChem, 2011, 12, 1795–1797.
88. H. Clauberg, D. W. Minsek and P. Chen, J. Am. Chem. Soc., 1992, 114, 99–107.
89. P. Hemberger, B. Noller, M. Steinbauer, I. Fischer, C. Alcaraz, B. K. Cunha de Miranda, G. A. Garcia and H. Soldi-Lose, J. Phys. Chem. A, 2010, 114, 11269–11276.
90. P. Hemberger, M. Steinbauer, M. Schneider, I. Fischer, M. Johnson, A. Bodi and T. Gerber, J. Phys. Chem. A, 2009, 114, 4698–4703.
91. M. Lang, F. Holzmeier, P. Hemberger and I. Fischer, J. Phys. Chem. A, 2015, 119, 3995–4000.
92. P. Hemberger, A. J. Trevitt, E. Ross and G. da Silva, J. Phys. Chem. Lett., 2013, 4, 2546–2550.
93. F. Holzmeier, I. Wagner, I. Fischer, A. Bodi and P. Hemberger, J. Phys. Chem. A, 2016, 120, 4702–4710.
94. E. Reusch, F. Holzmeier, P. Constantinidis, P. Hemberger and I. Fischer, Angew. Chem., Int. Ed., 2017, 56, 8000–8003.
95. F. Holzmeier, I. Fischer, B. Kiendl, A. Krueger, A. Bodi and P. Hemberger, Phys. Chem. Chem. Phys., 2016, 18, 9240–9247.
96. D. L. Osborn, P. Zou, H. Johnsen, C. C. Hayden, C. A. Taatjes, V. D. Knyazev, S. W. North, D. S. Peterka, M. Ahmed and S. R. Leone, Rev. Sci. Instrum., 2008, 79, 104103.
97. K. Voronova, K. M. Ervin, K. G. Torma, P. Hemberger, A. Bodi, T. Gerber, D. L. Osborn and B. Sztáray, J. Phys. Chem. Lett., 2018, 9, 534–539.
98. D. Schleier, E. Reusch, L. Lummel, P. Hemberger and I. Fischer, ChemPhysChem, 2019, 20, 2413–2416.
99. M. Gerlach, S. Monninger, D. Schleier, P. Hemberger, J. T. Goettel, H. Braunschweig and I. Fischer, ChemPhysChem, 2021, 22, 2164–2167.
100. M. Gasser, A. M. Schulenburg, P. M. Dietiker, A. Bach, F. Merkt and P. Chen, J. Chem. Phys., 2009, 131, 014304.
101. U. Jacovella, B. Gans and F. Merkt, J. Chem. Phys., 2013, 139, 084308.
102. A. M. Schulenburg, C. Alcaraz, G. Grassi and F. Merkt, J. Chem. Phys., 2006, 125, 104310.
103. B. S. Willitsch, J. M. Dyke and F. Merkt, Helv. Chim. Acta, 2003, 86, 1152–1166.
104. J. D. Barr, L. Beeching, A. De Fanis, J. M. Dyke, S. D. Gamblin, N. Hooper, A. Morris, S. Stranges, J. B. West, A. E. Wright and T. G. Wright, J. Electron Spectrosc. Relat. Phenom., 2000, 108, 15.
105. J. M. Dyke, N. Jonathan and A. Morris, Int. Rev. Phys. Chem., 1982, 2, 3–42.
106. F. Innocenti, M. Eypper, E. P. F. Lee, S. Stranges, D. K. W. Mok, F.-T. Chau, G. C. King and J. M. Dyke, Chem. – Eur. J., 2008, 14, 11452–11460.
107. G. A. Garcia, B. Gans, X. Tang, M. Ward, S. Batut, L. Nahon, C. Fittschen and J.-C. Loison, J. Electron Spectrosc. Relet. Phenom., 2015, 203, 25–30.
108. F. Holzmeier, M. Lang, I. Fischer, P. Hemberger, G. A. Garcia, X. Tang and J. C. Loison, Phys. Chem. Chem. Phys., 2015, 17, 19507–19514.
109. O. J. Harper, S. Boyé-Péronne, G. A. Garcia, H. R. Hrodmarsson, J.-C. Loison and B. Gans, J. Chem. Phys., 2020, 152, 041105.
110. G. A. Garcia, J.-C. Loison, F. Holzmeier, B. Gans, C. Alcaraz, L. Nahon, X. Wu, X. Zhou, A. Bodi and P. Hemberger, Mol. Phys., 2021, 119, e1825851.
111. G. A. Garcia, B. Gans, J. Krüger, F. Holzmeier, A. Röder, A. Lopes, C. Fittschen, C. Alcaraz and J. C. Loison, Phys. Chem. Chem. Phys., 2018, 20, 8707–8718.
112. B. Gans, G. A. Garcia, F. Holzmeier, J. Kruger, A. Roder, A. Lopes, C. Fittschen, J. C. Loison and C. Alcaraz, J. Chem. Phys., 2017, 146, 011101.
113. S. Hartweg, J. C. Loison, S. Boye-Peronne, B. Gans, D. M. P. Holland, G. A. Garcia, L. Nahon and S. T. Pratt, J. Phys. Chem. A, 2020, 124, 6050–6060.
114. B. Gans, S. Hartweg, G. A. Garcia, S. Boye-Peronne, O. J. Harper, J. C. Guillemin and J. C. Loison, Phys. Chem. Chem. Phys., 2020, 22, 12496–12501.
115. X. F. Tang, X. X. Lin, G. A. Garcia, J. C. Loison, C. Fittschen, X. J. Gu, W. J. Zhang and L. Nahon, J. Chem. Phys., 2020, 153, 031101.
116. X. F. Tang, X. X. Lin, G. A. Garcia, J. C. Loison, C. Fittschen, A. Roder, D. Schleier, X. J. Gu, W. J. Zhang and L. Nahon, J. Chem. Phys., 2020, 153, 124306.
117. X. F. Tang, X. X. Lin, G. A. Garcia, J. C. Loison, Z. Gouid, H. H. Abdallah, C. Fittschen, M. Hochlaf, X. J. Gu, W. J. Zhang and L. Nahon, Chem. Commun., 2020, 56, 15525–15528.
118. X. Tang, X. Gu, X. Lin, W. Zhang, G. A. Garcia, C. Fittschen, J.-C. Loison, K. Voronova, B. Sztáray and L. Nahon, J. Chem. Phys., 2020, 152, 104301.
119. D. V. Chicharro, S. M. Poullain, L. Bañares, H. R. Hrodmarsson, G. A. García and J.-C. Loison, Phys. Chem. Chem. Phys., 2019, 21, 12763–12766.
120. B. Hornung, A. Bodi, C. I. Pongor, Z. Gengeliczki, T. Baer and B. Sztáray, J. Phys. Chem. A, 2009, 113, 8091–8098.
121. D. P. Mukhopadhyay, D. Schleier, S. Wirsing, J. Ramler, D. Kaiser, E. Reusch, P. Hemberger, T. Preitschopf, I. Krummenacher, B. Engels, I. Fischer and C. Lichtenberg, Chem. Sci., 2020, 11, 7562–7568.
122. J. D. Savee, J. Zador, P. Hemberger, B. Sztaray, A. Bodi and D. L. Osborn, Mol. Phys., 2015, 113, 2217–2227.
123. K. Müller-Dethlefs and S. Riese, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, West Sussex, UK, 2011, vol. 3, pp. 1713–1740.
124. F. Merkt and A. Osterwalder, Int. Rev. Phys. Chem., 2002, 21, 385–403.
125. N. Hölsch, M. Beyer, E. J. Salumbides, K. S. E. Eikema, W. Ubachs, C. Jungen and F. Merkt, Phys. Rev. Lett., 2019, 122, 103002.
126. U. Jacovella and F. Merkt, Phys. Chem. Chem. Phys., 2017, 19, 23524–23531.
127. U. Jacovella, H. J. Wörner and F. Merkt, J. Mol. Spectrosc., 2018, 343, 62–75.
128. D. J. Kemp, W. D. Tuttle, A. M. Gardner, L. E. Whalley and T. G. Wright, J. Chem. Phys., 2019, 151, 064308.
129. W. D. Tuttle, A. M. Gardner, L. E. Whalley, D. J. Kemp and T. G. Wright, Phys. Chem. Chem. Phys., 2019, 21, 14133–14152.
130. A. M. Gardner, W. D. Tuttle, L. E. Whalley and T. G. Wright, Chem. Sci., 2018, 9, 2270–2283.
131. C. J. Hammond, V. L. Ayles, D. E. Bergeron, K. L. Reid and T. G. Wright, J. Chem. Phys., 2006, 125, 124308.
132. D. P. Taylor, J. G. Goode, J. E. LeClaire and P. M. Johnson, J. Chem. Phys., 1995, 103, 6293.
133. F. Michels, F. Mazzoni, M. Becucci and K. Müller-Dethlefs, Chem. Phys. Lett., 2017, 685, 477–481.
134. D. W. Kang, S. M. Park, C. B. Park, B. J. Sung, H. L. Kim and C. H. Kwon, J. Chem. Phys., 2021, 154, 054308.
135. S. M. Park, Y. R. Lee, D. W. Kang, H. L. Kim and C. H. Kwon, Phys. Chem. Chem. Phys., 2017, 19, 30362–30369.
136. S. Y. Eom, D. W. Kang and C. H. Kwon, Phys. Chem. Chem. Phys., 2021, 23, 1414–1423.
137. S. Nyambo, Y. C. Zhang and D. S. Yang, J. Chem. Phys., 2020, 153, 064304.
138. Y. C. Zhang, W. J. Cao and D. S. Yang, J. Chem. Phys., 2019, 151, 124307.
139. W. J. Cao, Y. C. Zhang and D. S. Yang, J. Organomet. Chem., 2019, 880, 187–195.
140. D. Wehrli, M. Génévriez, C. Kreis, J. A. Agner and F. Merkt, J. Phys. Chem. A, 2020, 124, 379–385.
141. M. Genevriez, D. Wehrli, J. A. Agner and F. Merkt, Int. J. Mass Spectrom. Ion Processes, 2019, 435, 209–216.
142. D. Wehrli, M. Genevriez and F. Merkt, Phys. Chem. Chem. Phys., 2021, 23, 10978–10987.
143. S. R. Mackenzie and T. P. Softley, J. Chem. Phys., 1994, 101, 10609–10617.
144. K. Höveler, J. Deiglmayr, J. A. Agner, H. Schmutz and F. Merkt, Phys. Chem. Chem. Phys., 2021, 23, 2676–2685.
145. Y. C. Chang, B. Xiong, Y. Xu and C.-Y. Ng, J. Phys. Chem. A, 2019, 123, 2310–2319.
146. Y. Xu, Y.-C. Chang, M. Parziale, A. Wannenmacher and C.-Y. Ng, J. Phys. Chem. A, 2020, 124, 8884–8896.
147. U. Jacovella, J. A. Agner, H. Schmutz, J. Deiglmayr and F. Merkt, J. Chem. Phys., 2016, 145, 014301.
148. S. Schlemmer, E. Lescop, J. Von Richthofen, D. Gerlich and M. A. Smith, J. Chem. Phys., 2002, 117, 2068–2075.
149. C. A. Taatjes, N. Hansen, D. L. Osborn, K. Kohse-Höinghaus, T. A. Cool and P. R. Westmoreland, Phys. Chem. Chem. Phys., 2008, 10, 20–34.
150. T. A. Cool, K. Nakajima, T. A. Mostefaoui, F. Qi, A. McIlroy, P. R. Westmoreland, M. E. Law, L. Poisson, D. S. Peterka and M. Ahmed, J. Chem. Phys., 2003, 119, 8356–8365.
151. T. Bierkandt, P. Hemberger, P. Oßwald, M. Köhler and T. Kasper, Proc. Combust. Inst., 2017, 36, 1223–1232.
152. Q. Guan, K. N. Urness, T. K. Ormond, D. E. David, G. B. Ellison and J. W. Daily, Int. Rev. Phys. Chem., 2014, 33, 447–487.
153. K. H. Fischer, J. Herterich, I. Fischer, S. Jaeqx and A. M. Rijs, J. Phys. Chem. A, 2012, 116, 8515–8522.
154. D. S. N. Parker, R. I. Kaiser, B. Bandyopadhyay, O. Kostko, T. P. Troy and M. Ahmed, Angew. Chem., Int. Ed., 2015, 54, 5421–5424.
155. F. Hirsch, E. Reusch, P. Constantinidis, I. Fischer, S. Bakels, A. M. Rijs and P. Hemberger, J. Phys. Chem. A, 2018, 122, 9563–9571.
156. A. Comandini, S. Abid and N. Chaumeix, J. Phys. Chem. A, 2017, 121, 5921–5931.
157. M. N. McCabe, P. Hemberger, E. Reusch, A. Bodi and J. Bouwman, J. Phys. Chem. Lett., 2020, 11, 2859–2863.
158. J. Bourgalais, Z. Gouid, O. Herbinet, G. A. Garcia, P. Arnoux, Z. Wang, L.-S. Tran, G. Vanhove, M. Hochlaf, L. Nahon and F. Battin-Leclerc, Phys. Chem. Chem. Phys., 2020, 22, 1222–1241.
159. L. G. Dodson, L. Shen, J. D. Savee, N. C. Eddingsaas, O. Welz, C. A. Taatjes, D. L. Osborn, S. P. Sander and M. Okumura, J. Phys. Chem. A, 2015, 119, 1279–1291.
160. J. D. Savee, O. Welz, C. A. Taatjes and D. L. Osborn, Phys. Chem. Chem. Phys., 2012, 14, 10410.
161. M. Braun-Unkhoff, N. Hansen, M. Dietrich, T. Methling, K. Moshammer and B. Yang, Proc. Combust. Inst., 2021, 38, 2387–2395.
162. S. Nagaraju, R. S. Tranter, F. E. C. Ardila, S. Abid, P. T. Lynch, G. A. Garcia, J. F. Gil, L. Nahon, N. Chaumeix and A. Comandini, Combust. Flame, 2021, 226, 53–68.
163. O. Welz, J. D. Savee, D. L. Osborn, S. S. Vasu, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Science, 2012, 335, 204–207.
164. D. Schleier, P. Constantinidis, N. Faßheber, I. Fischer, G. Friedrichs, P. Hemberger, E. Reusch, B. Sztaray and K. Voronova, Phys. Chem. Chem. Phys., 2018, 20, 10721–10731.
165. D. Schleier, E. Reusch, M. Gerlach, T. Preitschopf, D. P. Mukhopadhyay, N. Fassheber, G. Friedrichs, P. Hemberger and I. Fischer, Phys. Chem. Chem. Phys., 2021, 23, 1539–1549.
166. C. A. Taatjes, O. Welz, A. J. Eskola, J. D. Savee, A. M. Scheer, D. E. Shallcross, B. Rotavera, E. P. F. Lee, J. M. Dyke, D. K. W. Mok, D. L. Osborn and C. J. Percival, Science, 2013, 340, 177–180.
167. P. Hemberger, V. B. F. Custodis, A. Bodi, T. Gerber and J. A. van Bokhoven, Nat. Commun., 2017, 8, 15946.
168. G. Zichittella, P. Hemberger, F. Holzmeier, A. Bodi and J. Pérez-Ramírez, J. Phys. Chem. Lett., 2020, 11, 856–863.
169. U. Jacovella, C. J. Stein, M. Grutter, L. Freitag, C. Lauzin, M. Reiher and F. Merkt, Phys. Chem. Chem. Phys., 2018, 20, 1072–1081.
170. I. Fischer, Int. J. Mass Spectrom. Ion Processes, 2002, 216, 131–153.
171. A. M. Schulenburg, C. Alcaraz, G. Grassi and F. Merkt, J. Chem. Phys., 2006, 125, 104310.
172. H. Gao, Y. Xu, L. Yang, C.-S. Lam, H. Wang, J. Zhou and C. Y. Ng, J. Chem. Phys., 2011, 135, 224304.
173. M. Gasser, A. M. Schulenburg, P. M. Dietiker, A. Bach, F. Merkt and P. Chen, J. Chem. Phys., 2009, 131, 014304.
174. S. Willitsch, C. Jungen and F. Merkt, J. Chem. Phys., 2006, 124, 204312.
175. S. Willitsch, J. M. Dyke and F. Merkt, Mol. Phys., 2004, 102, 1543–1553.
176. H. J. Worner and F. Merkt, Angew. Chem., Int. Ed., 2006, 45, 293–296.
177. F. Qi, Proc. Combust. Inst., 2013, 34, 33–63.
178. R. M. Lindeque and J. M. Woodley, Catalysts, 2019, 9, 262.
179. I. R. Cooke and I. R. Sims, ACS Earth Space Chem., 2019, 3, 1109–1134.
180. I. R. Sims and I. W. M. Smith, Annu. Rev. Phys. Chem., 1995, 46, 109–137.
181. E. Herbst, Chem. Soc. Rev., 2001, 30, 168.
182. O. Durif, M. Capron, J. P. Messinger, A. Benidar, L. Biennier, J. Bourgalais, A. Canosa, J. Courbe, G. A. Garcia, J. F. Gil, L. Nahon, M. Okumura, L. Rutkowski, I. R. Sims, J. Thievin and S. D. Le Picard, Rev. Sci. Instrum., 2021, 92, 014102.
183. D. E. Couch, D. D. Hickstein, D. G. Winters, S. J. Backus, M. S. Kirchner, S. R. Domingue, J. J. Ramirez, C. G. Durfee, M. M. Murnane and H. C. Kapteyn, Optica, 2020, 7, 832–837.
184. D. E. Couch, Q. L. D. Nguyen, A. Liu, D. D. Hickstein, H. C. Kapteyn, M. M. Murnane and N. J. Labbe, Proc. Combust. Inst., 2021, 38, 1737–1744.

---