Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A rationale for non-linear responses to strong electric fields in molecular dynamics simulations
Paolo
Marracino
 *a,
Alessandra
Paffi
*a,
Alessandra
Paffi
 bc and
Guglielmo
d’Inzeo
bc
bc and
Guglielmo
d’Inzeo
bc
aRise Technology S. R. L., L. Re Paolo Toscanelli 170, 00121 Rome, Italy. E-mail: paolo.marracino@risetechnology.com
bUniversity of Rome “La Sapienza”, DIET, Rome, Italy
cCentre on the Interactions between Electromagnetic Fields and Biosystems (ICEmB), University of Genoa, Genoa, Italy
First published on 10th May 2022
Abstract
Many approaches for calculation of the field-dependent electric properties of water solutions rely on the Onsager and Kirkwood theories of polar dielectrics. Such basic theories implicitly consider the electric field intensity to fulfill the so-called ‘weak field conditions’, i.e. to produce a linear response in the system. In this work we made use of molecular dynamics simulations to investigate possible non-linear effects induced by high intensity electric fields, specifically continuous wave bursts with nanosecond duration, comparing them with the ones predicted by the theory. We found that field intensities above 0.15 V nm−1 produce remarkable nonlinear responses in the whole 100 MHz-100 GHz frequency window considered, with the onset of higher order polarization signals, which are the clear fingerprint of harmonic distorsions. That non-linear response turned out to depend on the considered frequency. We finally show that MD outcomes are consistent with a modelization based on an extended formulation of the Langevin function including a frequency-dependent parameter.
Introduction
One of the fundamentals of bioelectromagnetic research is the theoretical treatments of dielectric properties developed by Lorentz, Clausius and Mossotti1 in the 19th century, essentially focused on the effects of electric stimuli on biological targets composed of many polarizable objects. Some further refinements of this treatment were made by Onsager and Kirkwood2,3 who finally resolved the macroscopic/microscopic link of polarizable systems with the introduction of the strong correlation factor between nearby dipoles, which provides a theoretical description of dielectric systems in good agreement with experiments.4If we assume that such a classical theory should at least have a qualitative usefulness, what can we say about the expected occurrence of dielectric nonlinearity?
Chiabrera and co-workers theoretically investigated the behaviour of electric dipoles in the presence of very intense, non-uniform electric fields,5 which can be found near molecular crevices, molecular filters and biological macromolecules. Such endogenous perturbations can reach values exceeding 0.1 V/nm near transmembrane proteins,6 falling into the range of electric field intensities predicted to saturate the dipolar polarization response as given by the Langevin function.7 The theoretical model developed by Chiabrera found dielectric saturation effects for electric fields higher than 0.1 V nm−1, the same intensities obtained by Apol et al.8 with a different approach, based on molecular dynamics (MD) simulations.
MD simulations can provide a powerful tool for obtaining insights into behaviours at an atomic level, and unravelling microscopic information on the structure and dynamics of biological polarizable targets in presence of electromagnetic stimuli.9–12
As specific example, Amadei and Marracino13 obtained the thermodynamic link between the free energy of a dielectric system and an applied external (homogeneous) electric field. Authors explicitly calculated the chemical potential change due to a static external field on water–protein solutions in the limit of solute infinite dilution and in the so-called weak field conditions, i.e. by considering the thermodynamic dipole linear in the field.
Interestingly, there is very few literature focussing on the effects of electric fields above the weak field condition threshold and the possible impacts in terms of system's dipolar response.9
This is even more interesting at present, due to the increasing number of significant applications involving electric pulses with intensities above 0.01 V nm−1,14 with the concrete possibility to exceed 0.1 V nm−1 in the near future with proper applicators.15–18 In particular, it has been established that nanosecond pulsed electric field (nsPEFs)19–22 can modulate intracellular structures and functions and directly interact with the genetic material.14 The study of the interaction mechanisms between nsPEFs and the biological targets, due to the nanoscopic time-spatial resolution involved, took advantage of a numerical characterization at molecular level. The same could apply to our case, in order to unveil the basic interaction mechanisms leading to dielectric nonlinearity.
In this work we try to identify the characteristics of the applied electric field, namely amplitude and frequency, able to exceed the threshold of the linear response. The investigation will be carried out via MD simulations on a rather simple biological system: a myoglobin protein in aqueous environment, well characterized in previous works23 in terms of polarization response to both static and pulsed electric stimuli. Here we go a step further with a broad interpretation of the dipolar response of the protein-water system by using a set of continuous wave signals with nanosecond duration, which allow both a rigorous analysis of protein response in the frequency domain and a direct comparison with the theoretical predictions on (time) dispersive biological media.
Methods
General relations
If one considers a local electric field E acting on a dipole, the interaction energy U is: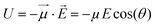 | (1) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) and
and ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) that determines the extent of the interaction.
that determines the extent of the interaction.
In accordance with the Boltzmann distribution, the probability of finding a dipole aligned within a solid angle dθ is proportional to 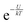 , with a mean value equal to:
, with a mean value equal to:
〈![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) 〉 = μ 〉 = μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 〈cos 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (θ)〉 (θ)〉 | (2) |
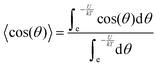 | (3) |
By substituting 〈cos(θ)〉 expression in eqn (2) and by integrating on the whole solid angle, the mean dipole results:
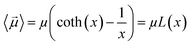 | (4) |
Langevin function is linear for small x values, hence its Taylor series with x ≪ 1 (μE ≪ kT) can be truncated to the first order, providing a dipole approximation:
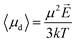 | (5) |
By increasing x value, Langevin function starts to experiment saturation, i.e. it cannot be linearly approximated and higher order terms have to be considered:
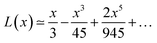 | (6) |
Some interesting implications on system dipolar response to the external field frequency, besides its amplitude, can be inferred considering a continuous wave (CW) signal ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) CW =
CW = ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt). In fact, if one introduces the term x = E
cos(ωt). In fact, if one introduces the term x = E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt)/kT in eqn (6) and in eqn (4), using some elementary trigonometric transformations, the mean dipole moment results:
cos(ωt)/kT in eqn (6) and in eqn (4), using some elementary trigonometric transformations, the mean dipole moment results:
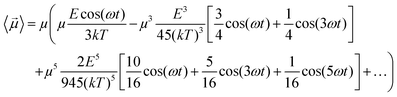 | (7) |
MD simulations
We carried out MD simulations of myoglobin in water using the GROMACS package.24 The simulated system consisted of a rectangular box (around 6 nm side), where we placed a single myoglobin protein and 16339 single point charge (SPC)25 water molecules resulting in a typical density of 1000 kg m−1.3 Note that, to properly describe myoglobin physiological behaviour, it was necessary to simulate a box of water molecules large enough to reproduce both the first hydration shells and a significant amount of bulk water. The myoglobin is made of 153 residues and the heme group (the overall charge of the system is zero). Following an energy minimization and subsequent solvent relaxation, the system was gradually heated from 50 to 300 K using short (typically 60 ps) MD simulations. A first trajectory was propagated up to 50 ns in the NVT ensemble using an integration step of 2 fs and removing the myoglobin center of mass translation, but with no constraints on its related rotation. The temperature was kept constant at 300 K by the Berendsen thermostat26 with the relaxation time (τ) equal to the simulation time step, hence virtually equivalent to the isothermal coupling27 which provides consistent statistical mechanical behaviour. All bond lengths were constrained using LINCS algorithm.28 Long-range electrostatics were computed by the particle mesh Ewald method29 with 34 wave vectors in each dimension and a fourth-order cubic interpolation. The ffG43a1 force field30 parameters were adopted. Once an exhaustive equilibrated-unexposed trajectory was obtained, we choose to investigate the effects of high intensity (ranging from 0.002 up to 0.2 V nm−1) CW electric fields, with frequencies ranging from 100 MHz up to 100 GHz and a duration of 50 ns, for a total of 54 simulations.MD physical observables
The main observable, here considered, is the system dipole M and its coupling with the time-varying electric perturbation. According to the general theory introduced in the previous sections, the macroscopic properties of the system (i.e. M or ε) can be obtained from the microscopic dipoles and the Langevin function via: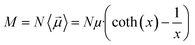 | (8) |
| M = MW + MP | (9) |
In order to detect the presence of different harmonic components in our simulation outputs, as predicted by eqn (7), we performed a transformation of the dipole moment (time) signal in the frequency domain by applying the Welch algorithm over five segments weighted with the Hanning windowing, except for the case of 100 MHz, where the required spectral resolution prevented us from doing averaging operations.31
Note that the sample rate used in our MD simulations sets the upper limit of the observable frequency to 250 GHz, as results from the calculation of the Nyquist frequency (half of the sampling rate of our discrete signal, that is 2 ps).
Results and discussion
Simulation outcomes
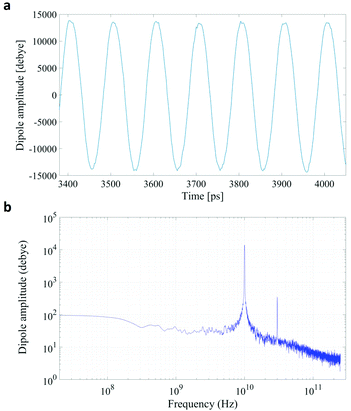
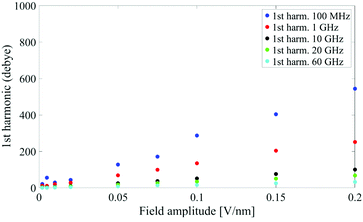
In Fig. 1 we present the polarization response in the time domain of the whole system to the highest intensity considered in this work, i.e. 0.2 V nm−1, and a frequency of 10 GHz. Panel A of the figure highlights the presence of the original signal's carrier frequency (note that the time-interval between two consecutive positive peaks is 100 ps) coupled to clear oscillations in amplitude, possibly due to the presence of higher order harmonics arising from a non-linear response. To confirm such an assumption, in panel B of the same figure we show the amplitude spectrum of the dipolar response obtained as the square root of the power spectrum integrated over the resolution bandwidth (note that the unit is Debye, equal to that of the signal in time domain). Fig. 1b evidences the presence of two harmonics: the first and the third at 10 and 30 GHz; the third harmonic, clearly evident on a vertical logarithmic scale, has an amplitude approximately equal to one fiftieth of the first one.A similar behaviour is observable even for the other considered frequencies, when a certain E-field threshold is overcome, approximately equal to 0.1 V nm−1 for the present molecular system. In Fig. 2, the amplitudes of the fundamental (M1) and the third harmonics (M3) are extracted from the complete simulation set, except for the case of 100 GHz, where the third harmonic falls outside our observation window. For all considered frequencies, below the field intensity of 0.1 V nm−1 no high order harmonics are visible, indicating that a possible higher order harmonic is below the intrinsic standard deviation of our spectral analysis; thus the linear response is considered a very good approximation. Interestingly, a reduction of dipolar response while increasing frequency is obtained, as predicted by the general theory of dipolar relaxation. From Fig. 2 we can see that, as suggested by eqn (7), the third harmonic increases in a non-linear fashion as the E-field increases; for values from 0.1 V nm−1 (when non linearity emerges) to 0.2 V nm−1, the total harmonic distortion ranges between 0 and 4%, depending on the frequency considered.
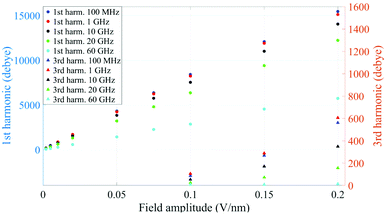 | ||
| Fig. 2 Spectrum peaks of the fundamental and third harmonics associated to the overall system dipole; note the different scales for the first and third harmonics on the vertical axis. | ||
As an example, at 1 GHz and 0.2 V nm−1 of field amplitude, the total harmonic distortion results THDM = M3/M1 = 0.04, i.e. a significant percentage of interaction energy defined in eqn (1) is associated to a frequency different from the fundamental one. Moreover, eqn (7) suggests that the phase of M3 is shifted of +π with respect the fundamental term M1, hence the impact of the harmonic distortions on the overall system dipole is such that M = M1 − M3.
In Table 1 we compare the mean system dipole obtained from the spectral analysis, indicated with M(ω), with the ones directly obtained by time-varying system dipole, indicated with M(t). Data show a very good match (mean values within two standard deviations) between the M values calculated via the two approaches, confirming that the spectral analysis can capture all the essential features of the polarization process, adding further quantitative information on the characteristics of the non-linear terms as above discussed.
| Frequency [GHz] | 0.1 | 1 | 10 | 20 | 60 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Amplitude [V nm−1] | M (t) | M (ω) | M (t) | M (ω) | M (t) | M (ω) | M (t) | M (ω) | M (t) | M (ω) |
| 0.2 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 501 ± 247 501 ± 247 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 899 ± 80 899 ± 80 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768 ± 167 768 ± 167 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 506 ± 38 506 ± 38 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685 ± 277 685 ± 277 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 701 ± 38 701 ± 38 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 358 ± 289 358 ± 289 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 064 ± 19 064 ± 19 |
6123 ± 339 | 6074 ± 18 |
| 0.15 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 454 ± 227 454 ± 227 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 819 ± 96 819 ± 96 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 ± 203 030 ± 203 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 ± 44 621 ± 44 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 ± 279 797 ± 279 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 847 ± 29 847 ± 29 |
9258 ± 307 | 9333 ± 32 | 4581 ± 352 | 4532 ± 11 |
| 0.1 | 9091 ± 246 | 8324 ± 19 | 8546 ± 182 | 8133 ± 31 | 7528 ± 334 | 7486 ± 72 | 6349 ± 332 | 6344 ± 37 | 3010 ± 333 | 2849 ± 14 |
| 0.075 | 7070 ± 235 | 6372 ± 31 | 6610 ± 224 | 6251 ± 32 | 5716 ± 265 | 5758 ± 12 | 4926 ± 330 | 4803 ± 27 | 2270 ± 349 | 2250 ± 15 |
| 0.05 | 5011 ± 223 | 4331 ± 58 | 4845 ± 205 | 4236 ± 47 | 4000 ± 330 | 3840 ± 44 | 3506 ± 318 | 3208 ± 16 | 1680 ± 362 | 1418 ± 9 |
| 0.02 | 2543 ± 217 | 1692 ± 36 | 2276 ± 253 | 1704 ± 43 | 1675 ± 331 | 1547 ± 24 | 1552 ± 301 | 1300 ± 19 | 566 ± 309 | 567 ± 14 |
| 0.01 | 1796 ± 150 | 838 ± 80 | 1603 ± 200 | 863 ± 38 | 1014 ± 257 | 773 ± 16 | 942 ± 333 | 643 ± 16 | 342 ± 345 | 282 ± 9 |
| 0.005 | 1267 ± 259 | 466 ± 80 | 1264 ± 181 | 421 ± 38 | 732 ± 306 | 398 ± 16 | 553 ± 308 | 327 ± 16 | 240 ± 345 | 141 ± 9 |
Analogously to the first harmonic shown in Fig. 2, even the total dipole moment, calculated both in time and frequency domain, increases with the E-field amplitude and decreases with the frequency.
It is worth noting that both M(t) and M(ω) terms describe the polarization response of the whole system: an interesting point is whether the identified non-linear coupling mechanism refers to all the dipoles inside the simulation box or just to specific chemical species. In our case, the system is composed of a single protein dipole surrounded by thousands of small water dipoles. To this end, we repeated the analysis by separating protein and water dipoles, as explained in eqn (9). The calculated protein polarization response is approximately 20-fold lower than the whole system and reveals a complete lack of higher order harmonics, indicative of a fully linear protein response even in presence of extremely high intense electric fields. Fig. 3 shows the magnitudes of the protein's polarization, also evidencing the relaxation process of the protein dipole known to start in the 1–10 MHz frequency range32,33 and reaching saturation (our simulations data) after 1 GHz.
A model to link simulation outcomes and theoretical predictions.
The relationship between the polarization response given by simulation data and the mean dipole introduced in eqn (7) is not straightforward, since the appropriate values of E and μ to use in the aforementioned equation may dramatically differ between the theoretical and the numerical approaches.First of all, the electric field considered in eqn (7) is the local electric field, which, in general, may differ from the macroscopic external electric field E0 used in numerical simulations, since the latter induces a net system polarization which brings out a depolarization term. Nonetheless, here we can consider no depolarizing field present, i.e. the charge density at the boundary of the infinite periodic replicas is removed. In fact, MD simulations with the presence of an applied homogeneous field necessarily correspond to a needle-like macroscopic ellipsoidal system with the major axis oriented along the field and hence E = E0.
The second point relates to the proper values for the N elementary dipoles μ inside MD simulations. If one considers that the simulation system consists in a single myoglobin protein surrounded by thousands of water molecules, then the problem can be conveniently treated by considering the separate contributions of three terms: (i) the protein dipole alone; (ii) a given number NW,hyd of water molecules belonging to the protein's hydration shell; (iii) a given number NW,bulkof bulk-like water molecules (ad hoc post elaboration routines have been developed to calculate dipole moments of the different groups aforementioned).
Myoglobin's dipole contributes to eqn (7) with a single term MP, which is linear in the field (as above discussed) and obviously dependent on the applied field frequency.32
The role of hydration water has been evaluated in several experimental and numerical studies33–36 which demonstrated that the presence of a surface and interfaces interrupt the extensive H-bond network of bulk water, resulting in many exotic features, which are not seen in the bulk, including orientational effects and modified water dipole–dipole interactions. Del Galdo et al.37 evaluated the geometrical extent of Myoglobin's hydration shell, finding out that about 500 water molecules (about the 3% of the total number of water molecules considered within our simulations) belong to such a region. In view of the difference between the two populations of water, i.e. bound and bulk, for the sake of simplicity, in the following discussion we’ll consider the polarization response of the whole water content within our simulation box, and hence:
| MW = μW,BULKNW,BULK + μW,HYDNW,HYD = μWNW | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639 and μW is water elementary dipole. It is worth noting that the dipole moment of an isolated water monomer38 is 1.855 D, whereas the corresponding value in the condensed phase increases from 2.4 to 2.6 D as a result of polarization by the environment.39
639 and μW is water elementary dipole. It is worth noting that the dipole moment of an isolated water monomer38 is 1.855 D, whereas the corresponding value in the condensed phase increases from 2.4 to 2.6 D as a result of polarization by the environment.39
Eqn (7), in its standard form, considers the dipole μ to correspond to the isolated water monomer. However, in order to compare theoretical predictions with the actual simulation data, two general remarks should be made: (i) water models in molecular mechanics simulation use pairwise additive potentials generally requiring monomer dipoles of 2.3 to 2.4 D to reproduce experimental data.40,41 As an example, in the used SPC water model the intrinsic dipole is μW = μSPC = 2.27 D; (ii) the common practice of dielectric constant calculation in MD simulation relies on the calculation of the fluctuations of the total system dipole M which is linked to the orientational order of the N elementary dipoles μ measured with the distance-dependent Kirkwwod factor GR(r). Such a function allows a good estimation of dielectric properties of water solutions.42 In a similar way, we shall introduce in our model a dipolar correlation function P(ω), which will take into account both the mutual interaction of dipoles (i.e. due to the large polarization caused by the electric field induced by surrounding dipoles43 with each other and the expected dependence of such an interaction with the frequency of the external electric signal. In fact, Fig. 2 unveiled how the system's polarization response is highly dependent on the CW signal frequency, in a way that a dipolar relaxation process is expected.
In the light of the above, the model linking the theoretical predictions in eqn (7) and the simulation outcomes presented in Fig. 2 becomes:
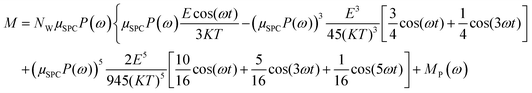 | (11) |
Fig. 4 indicates that the total system dipole (M(ω)) MD data almost perfectly follows the analytical function given by eqn (11), with coefficients of determination always close to unity. The most relevant differences between actual dipolar data and the fitting equations seem to be limited to the lower frequency range (from 100 MHz up to 10 GHz) and the highest amplitude of the local field (0.2 V nm−1): in such cases the fitting curves seem to overestimate the total dipole M(ω) or, from a different viewpoint, to underestimate the third harmonic contribution as apparent from eqn (11). To confirm such an assumption, we calculated the total harmonic distortions estimable by eqn (11) and compared it to the one obtained from our MD data. Interestingly, the electric field to be used in eqn (11) to match the third harmonic distortion from MD data is as high as 0.5 V nm−1, indicating that the saturation of the Langevin function (see eqn (4)) seems more relevant in MD simulations than in the theoretical predictions.
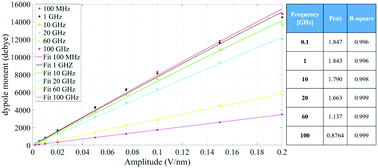 | ||
| Fig. 4 Simulation data fitted with the model given in eqn (11). The table provides the frequency dependence of the parameter P(ω) used in our model. | ||
As corollary of the findings shown in Fig. 4, in Fig. 5 we present the frequency profile of the P(ω) parameter, which perfectly follows a Debye relaxation model with a relaxation frequency in the range of 30–40 GHz. It is worth noting that this result is in very good accordance with the expected SPC water dipolar relaxation value.25
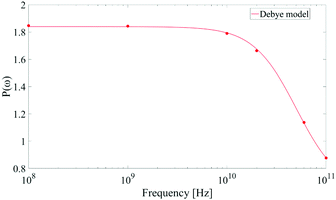 | ||
| Fig. 5 Frequency profile of the dipolar correlation parameter P(ω) introduced in eqn (11). Data are consistent with a Debye-like relaxation process. | ||
Limitations
(1) Recent works by Matyushov and Richert44–46 made big steps in the field of non-linear dielectrics about the analysis and interpretation of the field dependent dielectric function ε(E), and its expected saturation,47 involving both dipolar correlations and less trivial, and harder to calculate, three and four particle orientational correlations. Fulton48 argued that, while the connection between the multi-dipole auto-correlation function and the dielectric function is highly dependent on the sample shape, the use and interpretation of multi-dipole auto-correlation functions in the calculation of the dielectric functions requires care. The starting point of this work was to perform MD simulations around the “weak field condition intensity range” (i.e. about 0.005–0.2 V nm−1 in the present simulation conditions), keeping the electric field intensity low enough to avoid significant saturation effects (see for example ref. 13 where saturation effects were identified for the same simulation protocol). Accordingly, the present approach only considers dipolar correlation for the description of both field intensity and frequency effects on polarizable targets.(2) In the highest frequency range (10–100 GHz) probed in the simulations, dissipation effects cannot be ignored. It could be possible to evaluate them from simulated data, by calculating the phase shift between the applied field and the system response. However, in the frequency domain, the computed phases were affected by noisy fluctuations that have not allowed an accurate estimate of the imaginary part of the susceptibility. Nonetheless, once the parameter P(ω) is inferred (Fig. 5), the imaginary part can be obtained using the Kramers–Kronig relationship, under the assumption of system causality.
Conclusions
In conclusion, the investigation here reported showed that the interaction mechanisms between CW electric signals and protein-water systems, as unveiled by molecular dynamics simulations, can be corroborated by theoretical predictions in the framework of the classical Onsager-Kirkwood theory on polar dielectrics. In particular, our main findings can be summarized as follows:(1) the amplitude of the applied CW signal plays a key role in creating significant harmonic distortions in the system polarization response. In our MD simulations, such an effect is far more relevant for the lowest frequencies considered (for the 100 MHz signal the total harmonic distortion reaches a value of 4% for the highest field here considered), while it becomes almost irrelevant for frequencies exceeding the dipolar relaxation frequency. The theory, while predicting such harmonic distortions, set a higher value for the field amplitude needed to obtain similar THDM values, specifically around 2.5-fold the electric field used in MD simulations.
(2) Harmonic distortions are completely ascribed to the CW field interaction with water molecules, as appeared studying separately protein and water polarization responses. In fact, protein molecule exhibits a fully linear response even in presence of extremely high intense electric fields.
(3) Simulation data (a total of 54 simulations, 50 ns each, with field amplitude ranging from 0.002 up to 0.2 V nm−1 and frequency ranging from 100 MHz up to 100 GHz) perfectly follow a Langevin-like polarization response, fingerprint of the expected occurrence of the dielectric nonlinearity. Unavoidable differences between MD data and theoretical prediction are essentially due to (i) a mismatch between the amplitude of the electric field used in MD simulations and the one to be inserted in the Langevin equation; (ii) a mismatch between the theoretical dipole to be used in the Langevin equation and the actual dipole of the water model used within MD simulations; (iii) the lack, in the theoretical prediction, of the dipolar relaxation process, well captured in MD simulations.
(4) By modifying the Langevin function according to the previous points, we were able to construct a robust model for the dipolar interaction mechanism, which allows us to predict the system polarization response with coefficients of determination always close to unity. Such a model also considers the frequency dependence of the dipolar response via a correlation function P(ω), which takes into account both the mutual interaction of molecules dipoles with each other and the expected dependence of such interaction with the frequency of the external electric signal. Remarkably, the P(ω) profile exhibits an expected Debye-like relaxation process, with a time constant for the water model adopted in line with literature predictions.
The general approach presented in this paper, an interweaving of MD data and theoretical assumptions, aims to provide a simple model for the basic mechanisms of interaction between exogenous electric fields and complex polarizable molecular systems. The results is a complete description of both intensity and frequency effects on polarizable targets, describable with a limited number of parameters.
Author contributions
Paolo Marracino: conceptualization, methodology, software, data curation, writing – original draft preparation. Alessandra Paffi: data curation, methodology, visualization. Guglielmo d’Inzeo: supervision, validation, writing – reviewing and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the project “MIRABILIS-Multilevel methodologies to investigate interactions between radiofrequencies and biological systems” funded by MIUR Progetti di Ricerca di Rilevante Interesse Nazionale (PRIN) Grant 2017SAKZ78.Notes and references
- J. Frenkel, Kinetic theory of liquids, New York, NY, 1955.
- L. Onsager, J. Am. Chem. Soc., 1936, 58, 1486 CrossRef CAS.
- M. Mandel, Physica, 1972, 57(1), 141–151 CrossRef.
- C. J. F. Böttcher, Theory of electric polarization, Elsevier Press, Amsterdam, 1952 Search PubMed.
- A. Chiabrera, A. Morro and M. Parodi, Water concentration and dielectric permittivity near molecular crevices, Il Nuovo Cimento D, 1989, 11, 981–992 CrossRef.
- A. Philippsen, W. Im, A. Engel, T. Schirmer, B. Roux and D. J. Mu, Biophys. J., 2002, 82, 1667–1676 CrossRef CAS PubMed.
- E. T. Jaynes, Non linear dielectric materials, Proc. IRE, 1995, 43, 12 Search PubMed.
- M. E. F. Apol, A. Amadei and A. Di Nola, J. Chem. Phys., 2002, 116, 11 CrossRef.
- N. J. English and C. J. Waldron, Phys. Chem. Chem. Phys., 2015, 17, 12407 RSC.
- L. Zanetti-Polzi, P. Marracino, M. Aschi, I. Daidone, A. Fontana, F. Apollonio, M. Liberti, G. D’Inzeo and A. Amadei, Theor. Chem. Acc., 2013, 132, 1393 Search PubMed.
- M. Bernardi, P. Marracino, M. R. Ghaani, M. Liberti, F. Del Signore, C. J. Burnham, J. A. Gárate, F. Apollonio and N. J. English, J. Chem. Phys., 2018, 149(24), 245102 CrossRef PubMed.
- E. della Valle, P. Marracino, O. Pakhomova, M. Liberti and F. Apollonio, PLoS One, 2019, 14(8), e0221685 CrossRef CAS PubMed.
- A. Amadei and P. Marracino, RSC Adv., 2015, 5(117), 96551–96561 RSC.
- S. J. Beebe and K. H. Schoenbach, J. Biomed. Biotechnol., 2005, 4, 297–300 CrossRef PubMed.
- C. Merla, S. El Amari, M. Kenaan, M. Liberti, F. Apollonio, D. Arnaud-Cormos, V. Couderc and P. Leveque, IEEE Trans. Microwave Theory Tech., 2010, 58, 4079 Search PubMed.
- C. Merla, A. Denzi, A. Paffi, M. Casciola, G. D’Inzeo, F. Apollonio and M. Liberti, IEEE Trans. Biomed. Eng., 2012, 59, 2302 CAS.
- M. Balucani, P. Nenzi, R. Crescenzi, P. Marracino, F. Apollonio, M. Liberti, A. Denzi and C. Colizzi, Electronic Components and Technology Conference (ECTC), 2011, pp. 1319-1324.
- P. Nenzi, A. Denzi, K. Kholostov, R. Crescenzi, F. Apollonio, M. Liberti, P. Marracino, A. Ongaro, R. Cadossi and M. Balucani, Electronic Components and Technology Conference (ECTC), 2013, pp. 486–493.
- B. L. Ibey, S. Xiao, K. H. Schoenbach, M. R. Murphy and A. G. Pakhomov, Bioelectromagnetics, 2009, 30, 92–99 CrossRef PubMed.
- C. Yao, Y. Mi, X. Hu, C. Li, C. Sun, J. Tang and X. Wu, 30th Annual International IEEE EMBS Conference, 2008, pp. 20–24.
- S. J. Beebe, Y. J. Chen, N. M. Sain, K. H. Schoenbach and S. Xiao, PLoS One, 2012, 7, e51349 CrossRef CAS PubMed.
- L. Chopinet and M. P. Rols, Bioelectromagnetics, 2015, 103, 2–6 CAS.
- P. Marracino, F. Apollonio, M. Liberti, G. d’Inzeo and A. Amadei, J. Phys. Chem. B, 2013, 117(8), 2273–2279 CrossRef CAS PubMed.
- D. van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26(16), 1701–1718 CrossRef CAS PubMed.
- D. van der Spoel, P. J. van Maaren and H. J. C. Berendsen, J. Chem. Phys., 1998, 108, 10220 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and A. Di Nola, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- D. J. Evans and G. P. Morriss, Statistical Mechanics of Nonequilibrium Liquids, Academic press, London, 1990 Search PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Frajie, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- T. A. Darden, D. M. York and L. G. Pedersen, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS.
- W. F. Van Gunsteren, S. R. Billeter, A. A. Eising, P. H. Hunemberger,P. Kruger, A. E. Mark, V. R. P. Scott and I. G. Tironi, Biomolecular Simulation: The GROMOS96 Manual and User Guide, Hochschlverlag AG an der ETH: Zurich, 1996 Search PubMed.
- A. V. Oppenheim, R. W. Schafer and J. R. Buck, Discrete-Time Signal Processing, Prentice Hall, Englewood Cliffs, NJ, 2nd edn, 1998 Search PubMed.
- C. Cametti, S. Marchetti, C. M. C. Gambi and G. Onori, J. Phys. Chem. B, 2011, 115(21), 7144–7153 CrossRef CAS PubMed.
- U. Kaatze, J. Mol. Liq., 2011, 162(3), 105–112 CrossRef CAS.
- R. Biswas and B. Bagchi, J. Phys.: Condens. Matter, 2018, 30(1), 013001 CrossRef PubMed.
- Y. Yang, A. H. A. Abdallah and M. A. Lill, Methods Mol. Biol., 2018, 1762, 389–402 CrossRef CAS PubMed.
- A. Charkhesht, C. K. Regmi, K. R. Mitchell-Koch, S. Cheng and N. Q. Vinh, J. Phys. Chem. B, 2018, 122, 6341–6350 CrossRef CAS PubMed.
- S. Del Galdo, P. Marracino, M. D'Abramo and A. Amadei, Phys. Chem. Chem. Phys., 2015, 17(46), 31270–31277 RSC.
- F. J. Lovas, J. Phys. Chem. Ref. Data, 1998, 7, 1445 CrossRef.
- C. A. Coulson and D. Eisenburg, Proc. R. Soc. London, Ser. A, 1966, 291, 454 CAS.
- J. Caldwell, X. D. Liem and P. A. Kollman, J. Am. Chem. Soc., 1990, 112, 9144 CrossRef CAS.
- K. Laasonen, M. Sprik, M. Parrinello and R. Car, J. Chem. Phys., 1993, 99, 9080 CrossRef CAS.
- C. Zhang, J. Hutter and M. Sprik, J. Phys. Chem. Lett., 2016, 7, 2696–2701 CrossRef CAS PubMed.
- J. K. Gregory, D. C. Clary, K. Liu, M. G. Brown and R. J. Saykally, Science, 1997, 275(5301), 814–817 CrossRef CAS PubMed.
- D. V. Matyushov, J. Chem. Phys., 2015, 142, 244502 CrossRef PubMed.
- R. Richert, J. Phys.: Condens. Matter, 2017, 29, 363001 CrossRef PubMed.
- R. Richert and D. V. Matyushov, J. Phys.: Condens. Matter, 2021, 33, 385101 CrossRef CAS PubMed.
- A. Piekara and S. Kielich, J. Chem. Phys., 1958, 29, 1297 CrossRef CAS.
- R. L. Fulton, J. Chem. Phys., 2016, 144, 087101 CrossRef PubMed.
| This journal is © the Owner Societies 2022 |