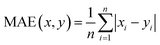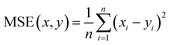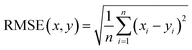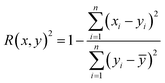Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The application of machine learning for predicting the methane uptake and working capacity of MOFs
Mikhail
Suyetin

Institute of Nanotechnology, Karlsruhe Institute of Technology, P. O. Box 3640, 76021 Karlsruhe, Germany. E-mail: msuyetin@gmail.com
First published on 9th April 2021
Abstract
Multiple linear regression analysis, as a part of machine learning, is employed to develop equations for the quick and accurate prediction of the methane uptake and working capacity of metal–organic frameworks (MOFs). Only three crystal characteristics of MOFs (geometric descriptors) are employed for developing the equations: surface area, pore volume and density of the crystal structure. The values of the geometric descriptors can be obtained much more cheaply in terms of time and other resources compared to running calculations of gas sorption or performing experimental work. Within this work sets of equations are provided for the different cases studied: a series of MOFs with NbO topology, a set of benchmark MOFs with outstanding methane storage and working capacities, and the whole CoRE MOF database (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures).
000 structures).
Introduction
Methane, as a major component of natural gas, is considered to be an alternative fuel to oil. Natural gas is much cleaner than gasoline or diesel.1 Methane is a gas at room temperature and pressure and has a very low energy density. To overcome this problem, there are two forms of stored natural gas in automobiles – liquified for trucks and compressed for personal cars. MOFs have been studied for years as promising adsorbents for automobile applications. MOFs are promising materials for different applications: gas storage2–6 and separation,7–9 catalysis,10–12 sensing,13 electrochemical energy storage,14–16 memory devices,17 biomedical imaging,18,19 biomolecule encapsulation and drug delivery.20–23 The US Department of Energy (DoE) has established targets of 50 wt% and 263 cm(STP)3 cm−3 for methane storage methods suitable for such employment. On the one hand, recent results show that it is almost impossible to simultaneously get both the gravimetric and volumetric methane working capacities at room temperature.24 On the other hand, there have been some recent improvements showing the great potential of MOFs for effective methane storage.25Computational approaches have played a great role in studying MOFs and other porous materials for gas storage: grand canonical Monte Carlo methods (GCMC) for revealing adsorption isotherms, classical molecular dynamics (MD) for studying gas diffusion in MOFs, density functional theory for obtaining favourable binding sites and crystal structure change, etc. Material simulations have been predicting novel advanced not yet synthesized MOFs since 2004,26 when the design of new IRMOF materials was proposed for methane storage using computer simulations. The large-scale screening of hypothetical MOFs has been performed computationally by creating porous structures from chemical databases of building blocks, which are based on known MOFs.27 More than 300 MOFs have been identified with outstanding methane storage capacities and structure–property relationships were also revealed. A total of 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 835 MOFs have been designed computationally to reveal both the total methane uptake and working capacity as a function of the void fraction, volumetric surface area and heat of adsorption, identifying a maximal working capacity at room temperature.28
835 MOFs have been designed computationally to reveal both the total methane uptake and working capacity as a function of the void fraction, volumetric surface area and heat of adsorption, identifying a maximal working capacity at room temperature.28
A lot of effort has been put into creating a database of structures for computational screening, which are free from solvents, disorders, etc. The Computation-Ready, Experimental Metal–Organic Framework Database (CoRE MOF Database) contains over 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 porous, three-dimensional MOFs.29 It is very convenient for potential users that pore analytics and physical property data are included as well.29 Another database is a subset of the Cambridge Structural Database (CSD), where 69
000 porous, three-dimensional MOFs.29 It is very convenient for potential users that pore analytics and physical property data are included as well.29 Another database is a subset of the Cambridge Structural Database (CSD), where 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 666 MOF materials were identified by the Cambridge Crystallographic Data Centre (CCDC).30 A total of 13
666 MOF materials were identified by the Cambridge Crystallographic Data Centre (CCDC).30 A total of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512 MOFs with 41 different edge-transitive topologies were generated using the ToBaCCo code, which employed a reverse topological approach.31 The structure files of MOFs obtained experimentally and published can contain some disorders, solvent molecules, etc. which are not suitable for computational work.
512 MOFs with 41 different edge-transitive topologies were generated using the ToBaCCo code, which employed a reverse topological approach.31 The structure files of MOFs obtained experimentally and published can contain some disorders, solvent molecules, etc. which are not suitable for computational work.
Recently, machine learning (ML) has become an important tool in designing new materials, leading materials chemistry towards more rational design.32 The World Economic Forum identified the union of big data and artificial intelligence as the Fourth Industrial Revolution, which can dramatically improve the research process.33 The high-throughput screening (HTC) of databases employing MD or GCMC is computationally very intensive and demanding. On the one hand, the employment of ML methods can significantly decrease the complexity of computational screening, and at the same time provides results with high accuracy, and on the other hand, the existing results of the HTC of databases are an outstanding opportunity for employing ML methods to reveal desired properties. ML has been employed to perform an analysis of the chemical diversity of MOFs.34 ML methods are significantly developed nowadays, but in the case of MOFs there is still a lot of work that needs to be done. ML is very promising approach in discovering new MOFs, revealing structure–property relationships. Predictive algorithms are employed to help and sometimes replace simulations. There are some nice examples of employing ML for discovering the properties of porous materials: an artificial neural network has been used to identify the performance limits of methane storage in zeolites, and revealed good agreement in the methane working capacity of the top structures between the zeolites and the structures generated by the neural network.35 A MOF generation approach based on ML was discovered in ref. 36 by devising and constructing the supramolecular variational autoencoder (SmVAE). SmVAE is employed for the ‘‘inverse design”, where MOFs with the best performance are identified and generated. A generative adversarial artificial neural network has been created to produce 121 crystalline porous materials, employing inputs in the form of energy and material dimensions.37 Finally, there has been a nice overview of ML algorithms for the chemical sciences.38
Experimental and/or computational work needs to be done to reveal the desired property of a structure. In case of identifying the sorption properties of experimentally obtained MOFs, computer simulations need to be done or specific equipment should be employed. This is acceptable for studying several crystals, but in the case of revealing the properties of a big family of structures conventional approaches are too costly in terms of time, money, workforce, etc. ML can help a lot for revealing the properties of MOFs, saving both experimental and computational efforts. In spite of the wide employment of ML techniques, they have been used very rarely for developing equations describing the sorption properties (including the working capacity) of MOFs.
Linear regression is a supervised ML algorithm. Simple linear regression employs the slope–intercept form, where x is the input data (independent variable), f(x) is the prediction (dependent variable), k is the slope coefficient for the x variable and b is the y intercept, which are adjusted via learning to give the accurate prediction: f(x) = kx + b. Multiple linear regression is the most popular form of linear regression. Multiple linear regression is employed to show the relationship between one dependent variable and two or more independent variables: f(x, y, z) = ix + jy + kz + b, where x, y and z are the independent variables, f(x, y, z) are the dependent variables and i, j, k and b are the adjustable parameters.
The main goal of this work is to show that multiple linear regression analysis is an outstanding tool for revealing the structure–property relationships of MOFs. More importantly, by employing multiple linear regression analysis analytical equations can be developed, showing that the methane total and working capacity values at different thermodynamic conditions can be calculated from three variables based on the crystal characteristics of MOFs (geometric descriptors): surface area, pore volume and density. The values of the descriptors can be obtained routinely and very quickly in comparison to GCMC simulations or experimental work by well known and highly efficient simulation packages such as Poreblazer,39,40 Zeo++,41etc.
Therefore, if an experimentalist or theoretician has a file with a crystal structure, or a bunch of files, she/he can easily obtain the methane total and working capacities by simply employing the equations. The performance of the model designed can be measured by several characteristics: the mean absolute error (MAE), mean square error (MSE), root-mean-square error (RMSE) and the coefficient of determination,R2, as described below, where xi is obtained from experiments or GCMC simulations, yi is the value predicted by multiple linear regression and ȳ is the average of the predicted values.
It should be noted that a higher value of R2 and lower values of MAE, MSE and RMSE show the better accuracy of the ML model used. R2 is in the range beween 0 and 1, where 1 shows that the prediction is performed without any error from the set of geometrical descriptors and 0 means that the prediction cannot be performed by any of the geometrical descriptors.
Results and discussion
Application of multiple linear regression analysis for developing equations from a set of MOFs with one topology (NbO)
The application of multiple linear regression analysis has shown very exciting results for developing equations of the methane total uptake and working capacity of a family of MOFs with the same topology. Multiple regression analysis has been applied to reveal structure–property relationships, employing data obtained for MOFs with NbO topology studied by different groups, pioneered by Chen et al.,42 and then Schröder et al.43–45 and Bai et al.4The following parameters (descriptors) of the crystal structures of MOFs of different sizes are used to develop the equations for predicting the gravimetric total uptake and working capacity of methane sorption obtained at a pressure range of 65–5 bar at a temperature of 298 K: surface area (Sa), density of a crystal (Dc) and pore volume (PV). The data of the crystal structure parameters, as well as the values of the total uptake (at a pressure of 65 bar) and working capacity (at a pressure range of 65–5 bar) at a temperature of 298 K are summarized in Table 1.
| MOFs | Sa, m2 g−1 | Pv, cm3 g−1 | Dc, g cm−3 | Total uptake, cm3 g−1 | Working capacity, cm3 g−1 | Ref. |
|---|---|---|---|---|---|---|
| ZJU-5a | 2829 | 1.08 | 0.679 | 367 | 277 | 46 |
| UTSA-75a | 2836 | 1.06 | 0.698 | 360 | 275 | 46 |
| UTSA-76a | 2820 | 1.09 | 0.699 | 368 | 282 | 46 |
| UTSA-77a | 2807 | 1.08 | 0.690 | 361 | 272 | 46 |
| UTSA-78a | 2840 | 1.09 | 0.694 | 363 | 275 | 46 |
| UTSA-79a | 2877 | 1.08 | 0.697 | 366 | 277 | 46 |
| NOTT-101a | 2805 | 1.08 | 0.688 | 344 | 263 | 46 |
| UTSA-111a | 3252 | 1.229 | 0.590 | 397 | 309 | 25 |
| UTSA-20a | 1620 | 0.66 | 0.909 | 278 | 206 | 47 |
| UTSA-88a | 1771 | 0.685 | 0.860 | 288 | 215 | 48 |
| UTSA-80a | 2280 | 1.03 | 0.694 | 336 | 251 | 49 |
| PCN-14 | 2000 | 0.85 | 0.829 | 334 | 228 | 47 |
| NOTT-100a | 1661 | 0.677 | 0.927 | 248 | 150 | 50 |
| NOTT-102a | 3342 | 1.268 | 0.587 | 404 | 327 | 50 |
| NOTT-103a | 2958 | 1.157 | 0.643 | 367 | 285 | 50 |
| NOTT-109a | 2110 | 0.850 | 0.790 | 306 | 215 | 50 |
| NJU-Bai 41 | 2370 | 0.92 | 0.741 | 331 | 232 | 4 |
| NJU-Bai 42 | 2830 | 1.07 | 0.693 | 356 | 278 | 4 |
| NJU-Bai 43 | 3090 | 1.22 | 0.639 | 397 | 310 | 4 |
The equations developed are shown below:
| Total_uptake = 181.726 + 0.02 × Sa + 138.777 × Pv − 38.763 × Dc |
| Working_capacity = 266.409 + 0.038 × Sa + 23.013 × Pv − 176.169 × Dc |
The results obtained with multiple linear regression analysis show that for the family of MOFs with the same topology (NbO) R2 = 0.931 for the total uptake and R2 = 0.913 for the working capacity. Delightfully, the MAE is very small: 7.59 cm3 g−1 and 9.33 cm3 g−1 for the total uptake and working capacity, respectively. The RMSE shows moderate values: 10.56 cm3 g−1 and 12.31 cm3 g−1 for the total uptake and working capacity, respectively.
The main conclusion from this part is that from using only the crystal structure parameters of a series of MOFs with NbO topology anyone can calculate the methane working capacity and total uptake, using the equations developed, very easily and extremely fast with a high precision. This is extremely useful for discovering new structures and screening MOFs with the same topology. For example, a user can draw and optimize a MOF in Material Studio (or employing other programs), reveal the values of the geometrical descriptors using the simulation packages Poreblazer or Zeo++, or tools in Material Studio, then use the equations to get the accurate values of the methane total uptake and working capacity. Of course, the same approach can be expanded for other MOFs with other topologies. Once equations are developed, there is no need to run simulations and/or perform experimental work.
Application of multiple linear regression analysis for developing equations from the set of benchmark MOFs
Another case to have a look at is the set of benchmark MOFs, obtained by different groups around the globe: NiMOF-74, UTSA-20, MOF-505, PCN-14, HKUST-1, NOTT-109, NU-135, UTSA-80, NOTT-101, UTSA-76, NOTT-103, NOTT-102, NOTT-122a/NU-125, NU-800, ZJU-36, NU-140, NU-111 and Al-soc-MOF-1. These frameworks have outstanding methane total uptakes and working capacities, and this data is considered for applying multiple linear regression analysis for developing equations. It should be noted that there has been a nice attempt to develop an empirical equation for the prediction of methane storage capacity at 65 bar and 270 K for the set of benchmark MOFs.51 The average deviation was found to be below 4%, which shows good applicability. The empirical equation can be used for predicting the methane storage of MOFs, employing the following parameters: density of the crystal and pore volume. The set of benchmark MOFs is always of interest to compare with new MOFs obtained experimentally or theoretically.24,52,53 The following geometrical descriptors are employed to develop the equations for predicting the gravimetric total uptake and working capacity: Sa, Dc, Pv. The data of the crystal structure parameters, as well as the values of the total uptake (at a pressure of 65 bar) and working capacity at temperatures of 240 K, 270 K and 298 K (at a pressure range of 65–5 bar), are shown in Table 2.| MOFs | Total uptake, cm3 g−1 | Working capacity, cm3 g−1 | Ref. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sa, m2 g−1 | Pv, cm3 g−1 | Dc, g cm−3 | 240 K | 270 K | 298 K | 240 K | 270 K | 298 K | ||
| NiMOF-74 | 1350 | 0.56 | 1.195 | 251 | 232 | 210 | 67 | 89 | 108 | 47 |
| UTSA-20 | 1620 | 0.66 | 0.909 | 319 | 297 | 253 | 129 | 182 | 187 | 47 |
| MOF-505 | 1661 | 0.68 | 0.927 | 300 | 270 | 248 | 97 | 121 | 150 | 50 |
| PCN-14 | 2000 | 0.85 | 0.829 | 362 | 326 | 277 | 145 | 185 | 189 | 47 |
| HKUST-1 | 1850 | 0.78 | 0.883 | 369 | 341 | 302 | 120 | 190 | 215 | 47 |
| NOTT-109 | 2110 | 0.85 | 0.790 | 362 | 341 | 306 | 138 | 199 | 215 | 50 |
| NU-135 | 2530 | 1.02 | 0.751 | 387 | 357 | 306 | 188 | 232 | 226 | 54 |
| UTSA-80 | 2280 | 1.03 | 0.694 | 442 | 390 | 336 | 207 | 258 | 251 | 49 |
| NOTT-101 | 2805 | 1.08 | 0.684 | 472 | 414 | 346 | 231 | 276 | 265 | 50 |
| UTSA-76 | 2820 | 1.09 | 0.699 | 491 | 431 | 368 | 240 | 293 | 282 | 55 |
| NOTT-103 | 2958 | 1.16 | 0.643 | 496 | 440 | 367 | 252 | 306 | 285 | 50 |
| NOTT-102 | 3342 | 1.27 | 0.587 | 532 | 477 | 404 | 310 | 354 | 327 | 50 |
| NOTT-122a/NU-125 | 3120 | 1.29 | 0.578 | 519 | 469 | 401 | 296 | 334 | 317 | 56 and 57 |
| NU-800 | 3149 | 1.34 | 0.546 | 559 | 452 | 359 | 410 | 370 | 310 | 58 |
| ZJU-36 | 4014 | 1.60 | 0.496 | 617 | 514 | 409 | 458 | 425 | 353 | 59 |
| NU-140 | 4300 | 1.97 | 0.43 | 728 | 591 | 465 | 551 | 484 | 395 | 60 |
| NU-111 | 4930 | 2.09 | 0.409 | 856 | 694 | 504 | 653 | 584 | 438 | 47 |
| Al-soc-MOF-1 | 5585 | 2.30 | 0.34 | 882 | 712 | 579 | 697 | 632 | 518 | 24 |
In contrast to the previous case considered, several equations are developed for the set of benchmark MOFs, which have different topologies, metals in nodes, etc., therefore the values of R2, MAE and RMSE are expected to be more moderate. The equations are developed for the quick and accurate prediction of the methane uptake and working capacity employing only three crystal characteristics of MOF (descriptors): surface area, pore volume and density of the MOFs. The equations are shown below:
At 298 K
| Total_uptake = 233.476 + 0.062 × Sa + 2.595 × Pv − 87.024 × Dc |
| Working_capacity = 189.033 + 0.061 × Sa + 4.318 × Pv − 135.846 × Dc |
At 270 K
| Total_uptake = 200.152 + 0.057 × Sa + 99.547 × Pv − 78.894 × Dc |
| Working_capacity = 53.433 + 0.059 × Sa + 121.325 × Pv − 94.025 × Dc |
At 240 K
| Total_uptake = 106.071 + 0.040 × Sa + 249.422 × Pv − 35.399 × Dc |
| Working_capacity = −224.435 + 0.007 × Sa + 379.715 × Pv + 50.945 × Dc |
The equations developed in this section will be an opportunity to estimate the methane total uptake and working capacity of newly designed MOFs. The values of R2, MAE and RMSE show the robustness of the models obtained. The coefficients of determination for the working capacity are: R2 = 0.979 at T = 298 K, R2 = 0.987 at T = 273 K and R2 = 0.990 at T = 240 K. The coefficients of determination for the total uptake are: R2 = 0.965 at T = 298 K, R2 = 0.980 at T = 273 K and R2 = 0.984 at T = 240 K. An interesting trend is observed: the lower the temperature, the higher the R2.
Application of multiple linear regression for developing equations from the CoRE MOF database
Multiple linear regression analysis has been employed to develop equations to describe methane working capacities at 35–5.8 bar considering the database obtained from high-throughput GCMC calculations61 of the CoRE MOF database (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOFs). The details of the methane sorption simulation via GCMC simulations are presented in that work. The CoRE MOF database considered contains a wide range of different kinds of MOFs with different topologies, forms of linkers, metals in nodes, etc., and it is obvious that the values of R2, MAE and RMSE will be a bit smaller than in case of studying MOFs with one topology. The equation developed based on only three geometrical descriptors – surface area, pore volume and density of the MOFs – is shown below:
000 MOFs). The details of the methane sorption simulation via GCMC simulations are presented in that work. The CoRE MOF database considered contains a wide range of different kinds of MOFs with different topologies, forms of linkers, metals in nodes, etc., and it is obvious that the values of R2, MAE and RMSE will be a bit smaller than in case of studying MOFs with one topology. The equation developed based on only three geometrical descriptors – surface area, pore volume and density of the MOFs – is shown below:| Working_capacity (35–5.8 bar) = 39.989 + 0.026 × Sa + 12.789 × Pv − 14.862 × Dc |
A much smaller set of MOFs can be studied for the comparison of the models’ performances. The following equation is developed by employing 500 randomly chosen MOFs for training from the CoRE MOF database:
| Working_capacity_500 MOFs (35–5.8 bar) = 51.567 + 0.022 × Sa + 13.989 × Pv − 20.526 × Dc |
The employment of 500 MOFs for training shows that the R2 is almost the as that when employing 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOFs. The MAE and RMSE are a little bit bigger.
000 MOFs. The MAE and RMSE are a little bit bigger.
Also, the equation developed via training with 500 MOFs can be applied to the rest of the CoRE MOF database, treating it as a test set. The following values of the model’s characteristics are obtained:
| R2 = 0.895; MAE = 9.69 cm3 g−1; MSE = 165.29; RMSE = 12.86 cm3 g−1. |
These results show that the model’s characteristics are very close to those obtained via the employment of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOFs: the R2 is a bit smaller, while the MAE, MSE and RMSE are a little bit bigger.
000 MOFs: the R2 is a bit smaller, while the MAE, MSE and RMSE are a little bit bigger.
The accuracy of the prediction may be further enhanced by implementing in the equation some more geometrical descriptors:61 void fraction, LCD (largest cavity diameter) and PLD (pore limiting diameter)
| Working_capacity (35–5.8 bar) = 36.191 + 0.023 × Sa − 3.405 × Pv − 14.153 × Dc + 35.154 × Vf + 0.689 × LCD − 0.695 × PLD |
Interestingly, no increase in the accuracy of the model is observed by employing the equation with six descriptors: the R2 values are the same and the MAE, MSE and RMSE are almost the same. In the case of the equations with three descriptors, these characteristics are even a little bit better.
Conclusions
This work aimed to show that multiple linear regression analysis is a fast and highly efficient approach for revealing the methane total uptake and working capacity of MOFs. Only three variables – geometric descriptors obtained from the crystal structure information: surface area, pore volume and density of the MOFs – need to be employed to develop the equations for the methane total uptake and working capacity values. The analytical equations obtained can predict the methane total and working capacity values with high accuracy employing only these three descriptors. The values of the descriptors can be obtained much faster than the actual GCMC simulations or experimental work for revealing sorption isotherms, employing simulation packages such as Poreblazer or Zeo++, or tools in Material Studio.A set of equations is developed for predicting the methane total uptake and working capacity for MOFs with the same topology (NbO, in the case studied). The model exhibits very high accuracy. Several equations are developed for the set of benchmark MOFs, which have different topologies, metals in nodes, etc. The values of R2, MAE and RMSE show the robustness of the models obtained, for example for the working capacity: R2 = 0.979 at 298 K, R2 = 0.987 at 273 K and R2 = 0.990 at 240 K. The GCMC results from the CoRE MOF database are considered for developing equations for predicting the methane working capacity which take into account only three parameters. The R2 = 0.899, MAE = 9.23 cm3 g−1 and RMSE = 12.60 cm3 g−1. The further enhancement of the model by employing more descriptors does not lead to increase in the accuracy of the model. This is very convenient for both experimentalists or theoreticians to easily obtain the methane total and working capacities via employing equations and just having a file of a crystal structure(s) and the values of the three descriptors.
Conflicts of interest
The author declares that there are no conflicts of interest.References
- M. E. Casco, M. Martínez-Escandell, E. Gadea-Ramos, K. Kaneko, J. Silvestre-Albero and F. Rodríguez-Reinoso, Chem. Mater., 2015, 27, 959–964 CrossRef CAS.
- N. H. Alsmail, M. Suyetin, Y. Yan, R. Cabot, C. P. Krap, J. Lü, T. L. Easun, E. Bichoutskaia, W. Lewis, A. J. Blake and M. Schröder, Chem. - Eur. J., 2014, 20, 7317–7324 CrossRef CAS PubMed.
- H. Wu, W. Zhou and T. Yildirim, J. Am. Chem. Soc., 2009, 131, 4995–5000 CrossRef CAS.
- M. Zhang, W. Zhou, T. Pham, K. A. Forrest, W. Liu, Y. He, H. Wu, T. Yildirim, B. Chen, B. Space, Y. Pan, M. J. Zaworotko and J. Bai, Angew. Chem., Int. Ed., 2017, 56, 11426–11430 CrossRef CAS PubMed.
- S. Yang, X. Lin, W. Lewis, M. Suyetin, E. Bichoutskaia, J. E. Parker, C. C. Tang, D. R. Allan, P. J. Rizkallah, P. Hubberstey, N. R. Champness, K. Mark Thomas, A. J. Blake and M. Schröder, Nat. Mater., 2012, 11, 710–716 CrossRef CAS PubMed.
- O. K. Farha, A. Özgür Yazaydın, I. Eryazici, C. D. Malliakas, B. G. Hauser, M. G. Kanatzidis, S. T. Nguyen, R. Q. Snurr and J. T. Hupp, Nat. Chem., 2010, 2, 944–948 CrossRef CAS PubMed.
- P. Nugent, Y. Belmabkhout, S. D. Burd, A. J. Cairns, R. Luebke, K. Forrest, T. Pham, S. Ma, B. Space, L. Wojtas, M. Eddaoudi and M. J. Zaworotko, Nature, 2013, 495, 80–84 CrossRef CAS PubMed.
- D. Antypov, A. Shkurenko, P. M. Bhatt, Y. Belmabkhout, K. Adil, A. Cadiau, M. Suyetin, M. Eddaoudi, M. J. Rosseinsky and M. S. Dyer, Nat. Commun., 2020, 11, 6099 CrossRef CAS PubMed.
- K.-J. Chen, D. G. Madden, S. Mukherjee, T. Pham, K. A. Forrest, A. Kumar, B. Space, J. Kong, Q.-Y. Zhang and M. J. Zaworotko, Science, 2019, 366, 241–246 CrossRef CAS PubMed.
- B. Han, H. Wang, C. Wang, H. Wu, W. Zhou, B. Chen and J. Jiang, J. Am. Chem. Soc., 2019, 141, 8737–8740 CrossRef CAS PubMed.
- P. Deria, D. A. Gómez-Gualdrón, I. Hod, R. Q. Snurr, J. T. Hupp and O. K. Farha, J. Am. Chem. Soc., 2016, 138, 14449–14457 CrossRef CAS PubMed.
- A. Pustovarenko, A. Dikhtiarenko, A. Bavykina, L. Gevers, A. Ramírez, A. Russkikh, S. Telalovic, A. Aguilar, J.-L. Hazemann, S. Ould-Chikh and J. Gascon, ACS Catal., 2020, 10, 5064–5076 CrossRef CAS.
- Z. Hu, B. J. Deibert and J. Li, Chem. Soc. Rev., 2014, 43, 5815–5840 RSC.
- K. Zhang, K. O. Kirlikovali, Q. V. Le, Z. Jin, R. S. Varma, H. W. Jang, O. K. Farha and M. Shokouhimehr, ACS Appl. Nano Mater., 2020, 3, 3964–3990 CrossRef CAS.
- K. Jayaramulu, M. Horn, A. Schneemann, H. Saini, A. Bakandritsos, V. Ranc, M. Petr, V. Stavila, C. Narayana, B. Scheibe, Š. Kment, M. Otyepka, N. Motta, D. Dubal, R. Zbořil and R. A. Fischer, Adv. Mater., 2020, 2004560 Search PubMed.
- L. Wang, Y. Zhu, C. Du, X. Ma and C. Cao, J. Mater. Chem. A, 2020, 8, 24895–24919 RSC.
- M. Suyetin and T. Heine, J. Mater. Chem. C, 2020, 8, 1567–1570 RSC.
- P. Horcajada, T. Chalati, C. Serre, B. Gillet, C. Sebrie, T. Baati, J. F. Eubank, D. Heurtaux, P. Clayette, C. Kreuz, J.-S. Chang, Y. K. Hwang, V. Marsaud, P.-N. Bories, L. Cynober, S. Gil, G. Férey, P. Couvreur and R. Gref, Nat. Mater., 2010, 9, 172–178 CrossRef CAS.
- J. Della Rocca, D. Liu and W. Lin, Acc. Chem. Res., 2011, 44, 957–968 CrossRef CAS PubMed.
- L. Wang, M. Zheng and Z. Xie, J. Mater. Chem. B, 2018, 6, 707–717 RSC.
- M.-X. Wu and Y.-W. Yang, Adv. Mater., 2017, 29, 1606134 CrossRef PubMed.
- M. H. Teplensky, M. Fantham, P. Li, T. C. Wang, J. P. Mehta, L. J. Young, P. Z. Moghadam, J. T. Hupp, O. K. Farha, C. F. Kaminski and D. Fairen-Jimenez, J. Am. Chem. Soc., 2017, 139, 7522–7532 CrossRef CAS PubMed.
- I. Abánades Lázaro, S. Haddad, S. Sacca, C. Orellana-Tavra, D. Fairen-Jimenez and R. S. Forgan, Chem, 2017, 2, 561–578 Search PubMed.
- D. Alezi, Y. Belmabkhout, M. Suyetin, P. M. Bhatt, Ł. J. Weseliński, V. Solovyeva, K. Adil, I. Spanopoulos, P. N. Trikalitis, A.-H. Emwas and M. Eddaoudi, J. Am. Chem. Soc., 2015, 137, 13308–13318 CrossRef CAS PubMed.
- H.-M. Wen, K. Shao, W. Zhou, B. Li and B. Chen, Chem. Commun., 2020, 56, 13117–13120 RSC.
- T. Düren, L. Sarkisov, O. M. Yaghi and R. Q. Snurr, Langmuir, 2004, 20, 2683–2689 CrossRef.
- C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2012, 4, 83–89 CrossRef CAS PubMed.
- D. A. Gómez-Gualdrón, C. E. Wilmer, O. K. Farha, J. T. Hupp and R. Q. Snurr, J. Phys. Chem. C, 2014, 118, 6941–6951 CrossRef.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling, J. S. Camp, B. Slater, J. I. Siepmann, D. S. Sholl and R. Q. Snurr, J. Chem. Eng. Data, 2019, 64, 5985–5998 CrossRef CAS.
- P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. P. Maloney, P. A. Wood, S. C. Ward and D. Fairen-Jimenez, Chem. Mater., 2017, 29, 2618–2625 CrossRef CAS.
- Y. J. Colón, D. A. Gómez-Gualdrón and R. Q. Snurr, Cryst. Growth Des., 2017, 17, 5801–5810 CrossRef.
- S. M. Moosavi, K. M. Jablonka and B. Smit, J. Am. Chem. Soc., 2020, 142, 20273–20287 CrossRef CAS PubMed.
- Y. Gil, M. Greaves, J. Hendler and H. Hirsh, Science, 2014, 346, 171–172 CrossRef CAS PubMed.
- S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Nat. Commun., 2020, 11, 4068 CrossRef CAS PubMed.
- S. Lee, B. Kim and J. Kim, J. Mater. Chem. A, 2019, 7, 2709–2716 RSC.
- Y. Zhenpeng, S.-L. Benjamin, B. N. Scott, B. J. Benjamin, K. Sai Govind Hari, C. P. Sean, B. Thomas, W. K. Tom, F. Omar, S. Q. Randall and A.-G. Alan, Nature Machine Intelligence, 2021, 3, 76–86 CrossRef.
- B. Kim, S. Lee and J. Kim, Sci. Adv., 2020, 6, eaax9324 CrossRef CAS PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- L. Sarkisov, R. Bueno-Perez, M. Sutharson and D. Fairen-Jimenez, Chem. Mater., 2020, 32, 9849–9867 CrossRef CAS.
- L. Sarkisov and A. Harrison, Mol. Simul., 2011, 37, 1248–1257 CrossRef CAS.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- B. Chen, N. W. Ockwig, A. R. Millward, D. S. Contreras and O. M. Yaghi, Angew. Chem., Int. Ed., 2005, 44, 4745–4749 CrossRef CAS PubMed.
- X. Lin, J. Jia, X. Zhao, K. M. Thomas, A. J. Blake, G. S. Walker, N. R. Champness, P. Hubberstey and M. Schröder, Angew. Chem., Int. Ed., 2006, 45, 7358–7364 CrossRef CAS PubMed.
- X. Lin, I. Telepeni, A. J. Blake, A. Dailly, C. M. Brown, J. M. Simmons, M. Zoppi, G. S. Walker, K. M. Thomas, T. J. Mays, P. Hubberstey, N. R. Champness and M. Schröder, J. Am. Chem. Soc., 2009, 131, 2159–2171 CrossRef CAS PubMed.
- S. Yang, X. Lin, A. Dailly, A. J. Blake, P. Hubberstey, N. R. Champness and M. Schröder, Chem. - Eur. J., 2009, 15, 4829–4835 CrossRef CAS PubMed.
- B. Li, H.-M. Wen, H. Wang, H. Wu, T. Yildirim, W. Zhou and B. Chen, Energy Environ. Sci., 2015, 8, 2504–2511 RSC.
- Y. Peng, V. Krungleviciute, I. Eryazici, J. T. Hupp, O. K. Farha and T. Yildirim, J. Am. Chem. Soc., 2013, 135, 11887–11894 CrossRef CAS PubMed.
- G. Chang, B. Li, H. Wang, Z. Bao, T. Yildirim, Z. Yao, S. Xiang, W. Zhou and B. Chen, Chem. Commun., 2015, 51, 14789–14792 RSC.
- H.-M. Wen, B. Li, D. Yuan, H. Wang, T. Yildirim, W. Zhou and B. Chen, J. Mater. Chem. A, 2014, 2, 11516–11522 RSC.
- Y. He, W. Zhou, T. Yildirim and B. Chen, Energy Environ. Sci., 2013, 6, 2735–2744 RSC.
- B. Li, H.-M. Wen, W. Zhou, J. Q. Xu and B. Chen, Chem, 2016, 1, 557–580 CAS.
- M. Suyetin, M. V. Peskov and U. Schwingenschlögl, Chem. Eng. J., 2020, 384, 123296 CrossRef CAS.
- M. Suyetin, M. V. Peskov and U. Schwingenschlögl, ACS Appl. Energy Mater., 2019, 2, 222–231 CrossRef CAS.
- R. D. Kennedy, V. Krungleviciute, D. J. Clingerman, J. E. Mondloch, Y. Peng, C. E. Wilmer, A. A. Sarjeant, R. Q. Snurr, J. T. Hupp, T. Yildirim, O. K. Farha and C. A. Mirkin, Chem. Mater., 2013, 25, 3539–3543 CrossRef CAS.
- B. Li, H.-M. Wen, H. Wang, H. Wu, M. Tyagi, T. Yildirim, W. Zhou and B. Chen, J. Am. Chem. Soc., 2014, 136, 6207–6210 CrossRef CAS PubMed.
- C. E. Wilmer, O. K. Farha, T. Yildirim, I. Eryazici, V. Krungleviciute, A. A. Sarjeant, R. Q. Snurr and J. T. Hupp, Energy Environ. Sci., 2013, 6, 1158–1163 RSC.
- Y. Yan, M. Suyetin, E. Bichoutskaia, A. J. Blake, D. R. Allan, S. A. Barnett and M. Schröder, Chem. Sci., 2013, 4, 1731–1736 RSC.
- D. A. Gomez-Gualdron, O. V. Gutov, V. Krungleviciute, B. Borah, J. E. Mondloch, J. T. Hupp, T. Yildirim, O. K. Farha and R. Q. Snurr, Chem. Mater., 2014, 26, 5632–5639 CrossRef CAS.
- G.-Q. Kong, Z.-D. Han, Y. He, S. Ou, W. Zhou, T. Yildirim, R. Krishna, C. Zou, B. Chen and C.-D. Wu, Chem. - Eur. J., 2013, 19, 14886–14894 CrossRef CAS PubMed.
- G. Barin, V. Krungleviciute, D. A. Gomez-Gualdron, A. A. Sarjeant, R. Q. Snurr, J. T. Hupp, T. Yildirim and O. K. Farha, Chem. Mater., 2014, 26, 1912–1917 CrossRef CAS.
- R. Wang, Y. Zhong, L. Bi, M. Yang and D. Xu, ACS Appl. Mater. Interfaces, 2020, 12, 52797–52807 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |