Atomistic explorations of mechanisms dictating the shear thinning behavior and 3D printability of graphene flake infused epoxy inks†
Received
25th May 2021
, Accepted 25th October 2021
First published on 28th October 2021
Abstract
Nanofiller-based epoxy inks have found extensive use in fabricating 3D printed nanocomposites for applications in aerospace, automobile, and marine systems. In this paper, we employ an all-atom molecular dynamic (MD) simulation to atomistically explore the mechanisms dictating the shear-thinning behavior of the graphene flake-infused (GFI) epoxy inks. We compare our findings with those for pure epoxy inks: non-equilibrium MD (NEMD) simulations reveal that both the GFI epoxy ink and pure epoxy ink demonstrate shear thinning behavior, i.e., their viscosities decrease with an increase in the shear rate. However, interestingly, the viscosity of the GFI epoxy ink is larger than that of pure epoxy for smaller shear rates, while for higher shear rates, the viscosities of these two materials are similar. This indicates a much more favorable viscosity profile for the GFI epoxy inks in the context of 3D printing. From the context of exploring the nanoscale mechanism, we identify the tendency of the bisphenol F molecules (the key constituent of the epoxy inks) and the graphene flakes (for the case of GFI epoxy inks) to align along the shear planes (in the presence of a shear flow) allowing the dissipation of viscous force among them ensuring shear-thinning behavior for both pure epoxy and GFI epoxy inks. In this context, we also identify that the bisphenol F chains prefer to localize along a given shear plane to reduce the effect of tension forces: such an alignment ensures that the radius of gyration for the bisphenol F molecules (for both pure epoxy and GFI epoxy inks) is larger for the case of finite shear and has a non-monotonic variation with the shear rate. Finally, the equilibrium MD (EMD) simulations establish that the presence of the graphene flakes significantly slows down the rotational dynamics of the bisphenol F molecules that are adsorbed to these graphene flakes and, as a result, causes the zero-shear viscosity of the GFI epoxy to be three orders of magnitude larger than that of the pure epoxy. This difference provides a qualitative justification of the viscosity of the GFI epoxy being larger than that of pure epoxy at smaller shear rate values.

Siddhartha Das
| Siddhartha Das is currently an Associate Professor in the Department of Mechanical Engineering, University of Maryland, College Park. Siddhartha received his PhD from the Indian Institute of Technology Kharagpur (IITKGP) in 2010 and postdoctoral training from the University of Twente (2009–2011) and as a Banting Fellow from the University of Alberta (2011–2013). Siddhartha's research interests are in soft materials, nanomaterials, nanofluidics, and additive manufacturing. As recognition to his work, Siddhartha has received several awards and fellowships such as the Fellowship of the Royal Society of Chemistry, Fellowship of the Institute of Physics, IITKGP Young alumni Award, etc. |
Introduction
Epoxy nanocomposites have been found to be useful in aeronautic and aerospace applications,1 the automobile industry,2 marine systems,3 and high-voltage applications4 due to their excellent mechanical, electrical, thermal, and anti-corrosive characteristics.5 Over the last few years, direct-ink writing (DIW) or 3D-printing of epoxy nanocomposites has gained significant attention owing to the flexibility that 3D printing offers in achieving complex structures with controlled composition, shape, and function.6–12 The rheology of the nanofiller-infused epoxy inks (i.e., liquid epoxy resin mixed with nanofillers) plays an important role in their printability. Ideally, such 3D-printable nanofiller-epoxy inks, like other direct writable inks, should possess a large zero-shear viscosity to maintain the printed shape and must also exhibit a strong shear-thinning behavior to facilitate extrusion through fine nozzles.6,7,12 To achieve such properties, rheology modifying fillers such as fumed silica,7,8,11 nano-clay,6,10–12 and graphene flakes9 were added as nanofillers to epoxy-based inks in previous studies. Among these fillers, the graphene filler infused epoxy composites, due to their excellent mechanical and thermal properties,13–21 have been extensively studied through experiments and molecular dynamics (MD) simulations. Specifically, the MD simulation studies have enabled a thorough understanding of the effect of graphene nanofillers on the thermo-mechanical properties of cross-linked epoxy composites at an atomistic-scale resolution. Hadden et al.13 studied the effect of graphene nanoplatelet (GNP) volume fraction and dispersion on the mechanical properties of GNP/carbon fiber/epoxy hybrid composites by employing multiscale modeling, involving MD simulations and micromechanical modeling. Aluko et al.14 employed MD simulations for studying the effect of different strain rates on the elastic behavior of GNP/carbon fiber/epoxy hybrid composites. Mortazavi et al.15 used MD simulations and finite element methods to calculate the effective thermal conductivity of graphene epoxy nanocomposites. Finally, Shiu et al.16 employed MD simulations for investigating the effect of graphene dispersion on the polymer density distribution, Young's modulus, glass transition temperature, and coefficient of thermal expansion of graphene/epoxy nanocomposites.
In spite of the existence of many MD simulation studies on graphene reinforced epoxy composites, most of the previous works mainly explored the mechanical and thermal characteristics of cross-linked graphene–epoxy composites.13–17 However, to the best of the authors’ knowledge, there is a lack of extensive study on the effects of graphene filler on the rheology of un-crosslinked (and hence in liquid state) graphene-infused epoxy inks at the nanoscale. In this study, we employ equilibrium MD (EMD) and non-equilibrium MD (NEMD) simulations to investigate the polymer rotational dynamics, viscosity, and shear-thinning behavior of un-crosslinked pure epoxy inks and un-crosslinked graphene-flake-infused (GFI) epoxy inks. Through the NEMD simulations, we calculate the shear viscosity, polymer radius of gyration (Rg), and graphene orientation distribution for different shear rates, which help us explain the shear thinning behavior in the GFI epoxy inks. In addition, our findings reveal that GFI epoxy inks demonstrate a viscosity larger (similar) than (to) that of the pure epoxy inks for smaller (larger) shear rate values: more desirable in the context of 3D printability is that the addition of graphene flakes leads to an enhanced low-shear viscosity and therefore a greater retention of printed shape prior to curing. On the other hand, we use the data obtained from the EMD simulations to compute the re-orientational correlation function of end-to-end vectors of polymer molecules in pure epoxy and GFI epoxy inks to understand the effect of graphene flakes on the rotational dynamics of surrounding epoxy molecules. Furthermore, we obtain the rotational relaxation times of the polymer molecules in pure epoxy and GFI epoxy inks enabling us to predict (using the Debye–Stokes–Einstein relationship22,23) the zero-shear viscosity of the GFI epoxy inks to be several orders of magnitude larger than that of pure epoxy inks: such a finding also explains (qualitatively) the enhanced viscosity (a key component dictating a preferable viscosity profile in the context of 3D printability) of the GFI epoxy, as compared to pure epoxy inks, for the case of smaller shear rate values.
The rest of the paper is organized as follows: following this Introduction section, we first provide a detailed description of the MD simulation methods employed for this study. Next, in the Results and discussions section, we shall provide the NEMD simulation results quantifying the viscosity of pure epoxy and GFI epoxy as a function of the applied shear rate. The following subsection in the Results and discussions section will provide the zero-shear viscosity ratio between pure and GFI epoxy. This ratio will be obtained from the corresponding values of the rotational relaxation time of bisphenol-F molecules in pure epoxy and graphene-bound bisphenol-F molecules in GFI epoxy. The third subsection of the Results and discussions section will use the MD simulation findings (quantifying the diagonal elements of the radius of gyration tensor, the mean-squared radius of gyration, and the alignment of the graphene sheets with respect to the shear planes in GFI epoxy) for providing a physical basis for the more pronounced shear-thinning behavior of the GFI epoxy ink as compared to the pure epoxy ink. In the final subsection of the Results and discussions section, some of our MD simulation findings will be compared against existing experimental data. Finally, we end the paper with a Conclusions section, where the main findings of the paper are summarized.
Simulation details
We used the LAMMPS24 parallel MD package to perform all the simulations. The epoxy ink was modelled using an un-crosslinked mixture of diglycidyl ether of bisphenol F (DGEBF, EPON 862) and diethyltoluenediamine (DETDA, EPIKURE W), which was used in previous experimental studies involving 3D-printing of epoxy composites.7 We used 200 bisphenol F molecules and 100 DETDA molecules to form a stoichiometric mixture. For simulations involving GFI epoxy, we used graphene fillers with a size of approximately 30 Å × 30 Å, and their edge atoms are saturated by hydrogen groups. Each graphene flake consisted of 400 carbon atoms and 56 hydrogen atoms. The atomistic models of DGEBF, DETDA, and the graphene flakes used in this study are illustrated in Fig. 1. We have employed PCFF25 (Polymer Consistent Force Field), which uses the class II functional form, to model all the bonded and non-bonded interactions. PCFF parameters were derived using ab initio data25 and were developed to accurately model several polymers and other organic materials.26 These force field parameters have been previously used and validated by several other works to study the thermal and mechanical properties of graphene infused epoxy composites.27–30 The graphene flakes were modeled to be flexible with the bond, angle, dihedral, and improper parameters obtained from the PCFF. The inner atoms of the graphene flakes were considered as uncharged Lennard Jones spheres while the edge carbon (hydrogen) atoms had a charge of −0.1268 e (0.1268 e) obtained from the PCFF parameter set as a sum of bond increments.25 The non-bonded interaction parameters used to capture the intermolecular interactions are listed in Table S1 and Fig. S4 of the ESI.† The sixth power combining rules were used to obtain the pairwise LJ interaction parameters between atoms of different species. Simulations with 6 wt% graphene filler have one graphene sheet, and the ones with 12 wt% graphene have two. Periodic boundary conditions were used in all three directions. For both the Lennard Jones (LJ) and coulombic interactions, a cutoff distance of 12 Å was used. We used the PPPM31 solver to compute the long-range electrostatic interactions with an accuracy of 0.0001. A timestep of 0.5 fs was used in all the simulations, and all the data was outputted every 500 time steps. The choice of a relatively small-time step (0.5 fs) is based on the fact that all-atom simulation of polymeric fluids involves a large number of high-frequency motions caused by the presence of many bonded interactions between the atoms of a polymer molecule. If a large time step is used to integrate the equations of motion, the bonds between the atoms could be stretched too far resulting in unphysical stresses in the system, which would eventually cause the simulation to become unstable and crash. To avoid such crashes and to maintain proper energy conservation, we have chosen a timestep of 0.5 fs. The systems were initially equilibrated in the isothermal–isobaric (NPT) ensemble for 5 ns followed by a 10 ns run in the canonical (NVT) ensemble. The last 5 ns of these equilibrium simulations were used for data analysis. In all the equilibrium simulations, the temperature is maintained at 300 K using a Nosé–Hoover thermostat32,33 with a damping constant of 100 timesteps. A Nosé–Hoover barostat, with a damping constant of 1000 timesteps, was used during the NPT equilibration at 1 atm pressure. The equilibrated system configurations from the equilibrium MD simulations were used as initial configurations for the NEMD simulations. During the NEMD simulations, shear rates ranging from 0.1 to 100 ns−1 were applied in the x-direction with velocity gradient in the y-direction, using a “box deformation” coupled with SLLOD equations of motion in LAMMPS. This technique is equivalent to the Lees–Edwards boundary condition.34,35 The thermal velocities (excluding the streaming velocity) of the atoms were used to thermostat the system at 300 K using a Nosé–Hoover thermostat to maintain a steady state.36 These simulations lasted for 2–10 ns, with the larger shear rates having shorter runs. All the simulation snapshots were generated using OVITO.37
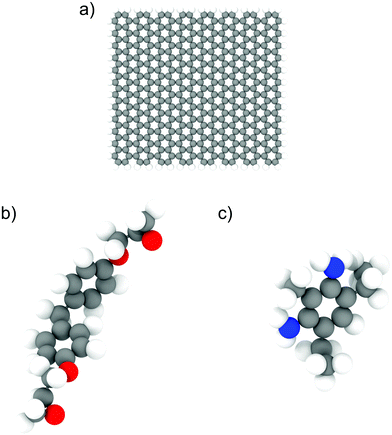 |
| | Fig. 1 Illustration of atomistic models for (a) graphene flakes, (b) DGEBF (bisphenol F) molecules, and (c) DETDA molecules. The color code for the atoms is as follows; carbon-grey, nitrogen-blue, oxygen-red and hydrogen-white. | |
Results and discussions
A. NEMD simulations for studying the viscosity of graphene-flake-infused (GFI) epoxy ink
We have performed NEMD simulations of pure and graphene-flake-infused (GFI) epoxy resin (EPON 862) for studying the effect of graphene flakes on the rheology of the epoxy-based 3D printable inks. Fig. 2 shows the simulation snapshots of graphene-filled epoxy both in the absence and in the presence of shear (under a shear rate of 1 ns−1 and 80 ns−1). For simulations with GFI epoxy, we have considered two different systems with graphene weight percentages of 6 wt% and 12 wt%, respectively. These values are close to the weight percentages of rheology modifiers used in previous experimental studies involving 3D printable epoxy resin inks.6,7,11 For the NEMD simulations, we have considered shear rates ranging from 0.1 ns−1 to 100 ns−1. These values are much larger than the actual shear rates, which can be only as high as 10−7 ns−1 (or 100 s−1), to which the 3D printable epoxy resins are subjected in actual experiments.6,7,11 However, the problems corresponding to shear strain rates lower than 0.1 ns−1 are practically unfeasible to study using NEMD due to the low signal-to-noise ratio. In this regard, the results reported in this section act as direct evidence of the qualitative effect of graphene flakes on the viscosity of GFI epoxy resin ink with respect to pure epoxy ink.
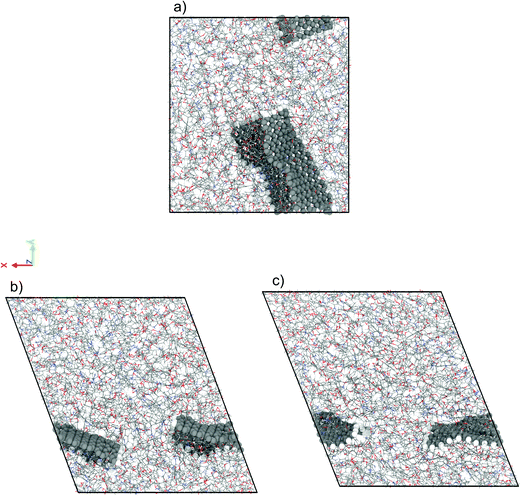 |
| | Fig. 2 Simulation snapshots of 6 wt% graphene infused epoxy ink (a) in the absence of shear rate (EMD) and in the presence of a shear rate (NEMD) of (b) 1 ns−1 and (c) 80 ns−1. | |
Fig. 3 shows the shear viscosity as a function of the shear rate for all the three systems (i.e., pure epoxy, GFI epoxy with 6 wt% of graphene flakes, and GFI epoxy with 12 wt% of graphene flakes). All three systems exhibit shear-thinning behavior, i.e., the viscosity decreases with an increase in the shear rate. Also, for all the shear rates, the viscosities of the GFI epoxy systems are higher than that of pure epoxy, and the viscosities of the GFI epoxy inks increase with an increase in the graphene weight percentages. This qualitative trend indicates that graphene flakes are capable of enhancing the viscosity of the epoxy resin. Equally importantly, this difference in viscosities significantly reduces for larger shear rates. This implies that for a given range of shear rate values, the viscosities for the GFI epoxy inks show a much larger variation, as compared to that exhibited by the pure epoxy inks. In other words, while the flowability (dictated by low viscosities at large shear rates) is not significantly compromised by the addition of the graphene flakes to the epoxy resin, the zero-shear viscosity for the GFI epoxy is significantly enhanced, which in turn, will significantly retard the deposited drop from flowing (and thereby enabling it to retain its shape) after printing. This makes the GFI epoxy inks much “better candidates” as 3D printable inks as compared to pure epoxy inks. The rest of the paper will provide a detailed mechanistic understanding of the following two critical facets associated with the GFI epoxy inks: (1) a larger zero-shear viscosity as compared to pure epoxy inks and (2) shear-thinning behavior with little change in viscosity (as compared to pure epoxy inks) at large shear rate values.
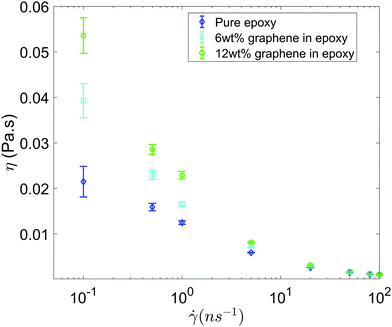 |
| | Fig. 3 Viscosity as a function shear rate for all the three systems considered in this study. Error bars are estimated using the block averaging method. Block sizes are chosen as the value beyond which the standard error plateaus out. | |
B. Equilibrium MD simulations for predicting the relative zero-shear viscosity of the GFI epoxy ink with respect to pure epoxy
In order to predict the zero-shear viscosity of the GFI epoxy inks, we first need to study the effect of graphene flakes on the surrounding epoxy molecules. The zero-shear viscosity (η0) of a liquid is linearly related to its molecular rotational relaxation time (τr) through the Debye–Stokes–Einstein (DSE) relationship, i.e.,22,23| | 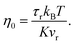 | (1) |
Here, T is the temperature, kB is the Boltzmann constant, vr is the free space volume per rotating molecule, and K is a constant that depends on the molecule shape and the hydrodynamic boundary condition. For our simulations, in order to obtain the rotational relaxation time of the epoxy resin without and with the infused graphene flakes, we first calculated the re-orientational correlation function (C(t)) of the end-to-end vectors of (a) bisphenol F molecules in pure epoxy and (b) bisphenol F molecules that are adsorbed to the graphene surface in GFI epoxy systems. C(t) can be expressed as:38Here, u is the end-to-end unit vector of a bisphenol F molecule.
Once C(t) has been obtained, it can be used to calculate the rotational relaxation time as:38
| | 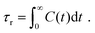 | (3) |
For case (b) (
i.e., GFI epoxy system), we have considered those bisphenol F molecules whose centers of mass are present in the first parallel layer of molecules adsorbed to the graphene surface. To identify the molecules in the first parallel layer surrounding the graphene sheet, we have followed the method given in Bačová
et al.39 We have generated a histogram distribution of the shortest distance between a polymer atom and the graphene surface as shown in Fig. S1 in the ESI.
† The distance corresponding to the first minimum of the histogram is considered as the thickness of the first polymer layer surrounding the graphene sheet. Using this analysis, we have found that the first layer lies below a distance of 6 Å from the graphene surface.
Fig. 4 shows the re-orientational correlation function of the end-to-end vectors of bisphenol F molecules in pure epoxy and of the bisphenol F molecules adsorbed to the graphene surface in GFI systems. From these results, we can see that the re-orientational correlation function of the graphene-bound bisphenol F molecules decays much slower than the bisphenol F molecules present in pure epoxy. This confirms the slow rotational dynamics [or larger rotational relaxation time τr, see eqn (3)] of the bisphenol F molecules adsorbed on the graphene surfaces for the GFI epoxy systems. One can explain such behavior by noting that the graphene flakes themselves have slow rotational dynamics, thereby slowing the rotational dynamics of these adsorbed bisphenol F molecules. Also, depending on their proximity to the graphene surface, even the non-adsorbed bisphenol F molecules demonstrate a rotational relaxation time larger than that of bisphenol F molecules in pure (graphene-free) epoxy resin inks. Therefore, we embark on a scenario where the GFI epoxy resin ink behaves as a “multicomponent” system by virtue of the fact that the bisphenol F molecules, depending on their adsorbed state on the graphene molecules and their proximity to the graphene molecules (in case they are non-adsorbed), demonstrate a wide spectrum of rotational relaxation times. The longest of these different rotational relaxation times is associated with those bisphenol F molecules that are adsorbed on the graphene flakes. In Fig. S3 in the ESI,† for the case of 6 wt% graphene infused epoxy, we have compared the re-orientational correlation function of the end-to-end vectors of bisphenol F molecules that are graphene bound with those that are far away from the graphene surface. One can clearly see that the re-orientational correlation function decays much faster for molecules far from the graphene sheet as compared to the ones close to the sheet. In previous studies, for multicomponent systems, the DSE relationship [see eqn (1)] has been used to obtain the viscosity of the system by relating it to the longest rotational relaxation time (i.e., the rotational relaxation time of the slowest component).40,41 As explained above, for our case this longest rotational relaxation time corresponds to those bisphenol F molecules that are adsorbed on the graphene flakes. Therefore, we can use this particular relaxation time to obtain the relative characteristic viscosity for the GFI epoxy ink systems with respect to pure epoxy inks.
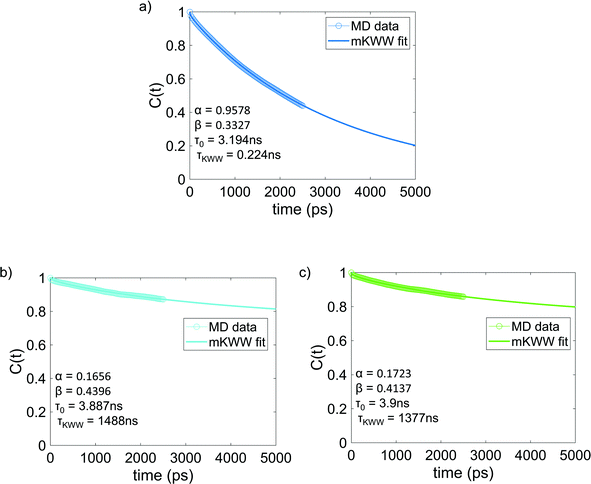 |
| | Fig. 4 Reorientational correlation function of the end-to-end vectors of (a) bisphenol F molecules in pure epoxy and the graphene bound bisphenol F molecules in (b) 6 wt% graphene infused epoxy and (c) 12 wt% graphene infused epoxy. The solid lines indicate the mKWW fits [see eqn (5)] for all three cases. The parameters governing the fits for the different cases have been provided in each of the figures. | |
While the previous paragraph outlines a framework to connect the zero-shear viscosity with the rotational relaxation time for the GFI epoxy inks, it is essential to note that a direct calculation of the zero-shear viscosity, via equilibrium MD simulations, becomes impractical for highly viscous fluids due to the high computational cost involved. Typically, such direct calculation of the viscosity is performed by employing the Green–Kubo formalism, where the viscosity is obtained by integrating the autocorrelation function of the off-diagonal elements of the stress tensor.38 For a highly viscous fluid, this autocorrelation function decays very slowly, enforcing running the simulations for a very long time. For such liquids, it is often necessary to run the simulations for a time that is at least a hundred times larger than the longest relaxation time of the liquid molecules.40,42,43 For example, consider the case of pure epoxy resin. We computed the rotational relaxation time for the bisphenol F molecules of the pure epoxy resin as ∼3 ns. Therefore, to calculate the zero-shear viscosity, we would be expected to run the simulations for nearly 300 ns. Next, consider the case of GFI epoxy resin inks. For these, the relaxation time itself is in the order of microseconds. Therefore, one would need to run the equilibrium MD simulations for hundreds of microseconds if one desires to obtain a direct calculation of the zero-shear viscosity of the GFI epoxy resin inks. This is not feasible from the standpoint of the computational cost involved. Therefore, we have adopted an indirect method40 to predict the relative viscosity of GFI epoxy inks with respect to pure epoxy. In this method, which is based on the DSE relationship [please see eqn (1)], we assume that the ratio of the zero-shear viscosity (between the graphene-bound bisphenol F molecules and pure epoxy bisphenol F molecules) is equal to the ratio of their rotational relaxation times. This assumption was justified by noting that the parameters kBT, K, and vr remain identical for the graphene-bound bisphenol F molecules and pure epoxy bisphenol F molecules. Under such circumstances, we can write:
| | 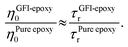 | (4) |
The rotational relaxation times were obtained by first fitting the re-orientational correlation function (see
Fig. 4) to a modified Kohlrausch–Williams–Watts (mKWW)
40,41,44,45 function using nonlinear regression [see
eqn (5)], and subsequently integrating this fitting function [see
eqn (6)]. Therefore, we can write:
| | 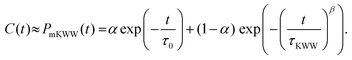 | (5) |
| | 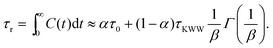 | (6) |
Here,
τ0 and
τKWW represent the characteristic times of the initial exponential decay and the stretched exponential decay, respectively, of the re-orientational correlation function. The weights
α and (1 −
α) represent the contributions from the initial exponential decay and the stretched exponential decay. The parameter
β describes the width of the stretched exponential decay. This extrapolation/fitting method has been widely used by many previous studies to estimate the rotational relaxation time of molecules with slow relaxations (
τr in the order of 10
3 ns).
40,41,46,47 Given that the rotational relaxation time of graphene-bound epoxy molecules is estimated to be in the order of thousands of nanoseconds, it is practically not possible for the classical MD simulation to capture the full rotational relaxation time. Due to this reason, the mKWW function is a useful tool for extrapolating the re-orientational correlation data to longer time scales. Also, considering that we are not using direct methods such as the Green–Kubo formulation or numerical integration of re-orientational correlation data, there is no need for the simulation to capture the full rotational relaxation time. Due to these reasons, it is both impractical and unnecessary to capture the full rotational relaxation time, which is in the order of microseconds for graphene-bound epoxy molecules.
Fig. 5 shows the rotational relaxation time of bisphenol F molecules in pure epoxy and graphene-bound bisphenol F molecules in GFI epoxy systems. We can see that the rotational relaxation time of graphene-bound bisphenol F molecules is three orders of magnitude higher than that of the pure epoxy molecules. Based on eqn (4), therefore, at a constant temperature, the zero-shear viscosity of the GFI epoxy (considering only the graphene-bound bisphenol F molecules of the GFI for analysis) will be three orders of magnitude higher than that of pure epoxy. Such an improvement in viscosity is consistent with the values reported in previous experimental studies.9,48 Also, the zero-shear viscosity increases with an increase in the fraction of molecules with longer relaxation times.49 Since the fraction of graphene-adsorbed bisphenol F molecules increases with an increase in the graphene content (i.e., the fraction of bisphenol F molecules with longer relaxation times increases), we expect the zero-shear viscosity to increase when the graphene content increases. Further, it is worth pointing out that we do not see a significant difference in the rotational relaxation time between the cases of GFI epoxy with 6 wt% and 12 wt% of infused graphene flakes. The rotational dynamics of an adsorbed bisphenol-F molecule primarily depend on the dynamics of the single graphene flake to which the bisphenol-F molecule has adhered. In our simulations, we have one graphene flake in the 6 wt% graphene infused epoxy, and two identical graphene flakes in the 12 wt% graphene infused epoxy. In both the systems, we have used identical graphene flakes with the same size and shape (i.e., identical graphene flake molecular weight). Unless there is a significant slowdown of the rotational dynamics of the two individual graphene flakes in 12 wt% graphene–epoxy, compared to the single graphene flake in 6 wt% graphene–epoxy, one cannot expect the rotational relaxation time of adsorbed molecules to increase. For the graphene weight percentages considered in this study, the flakes are distributed sparsely enough so that the rotational dynamics of the individual flakes is similar in 6 wt% and 12 wt% graphene infused epoxy; as a consequence, one obtains similar rotational relaxation times of the graphene-bound bisphenol f molecules in 6 wt%, and 12 wt% graphene infused epoxy (please see Fig. 5).
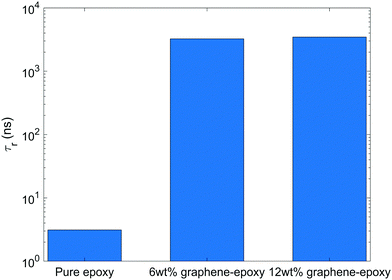 |
| | Fig. 5 Rotational relaxation time of bisphenol F molecules in pure epoxy and graphene-bound bisphenol F molecules in GFI epoxy systems. | |
The above discussions provide a qualitative mechanistic understanding of why one sees, using MD simulations, (1) a significantly larger viscosity in GFI epoxy inks as compared to that of pure epoxy for smaller shear rate values (see Fig. 3) and (2) the viscosity at smaller shear rates is larger for the GFI epoxy resin inks with a larger weight percentage of graphene. However, please note that we do not aim to provide a quantitative understanding of the situation. This stems from the fact that the above discussion relates the viscosities of the GFI epoxy and pure epoxy at zero-shear conditions, while the “small” shear rate values studied by our NEMD simulations is a significantly large shear rate (of ∼0.1 ns−1) as compared to zero shear (or even the largest experimentally realizable shear rates). This discrepancy occurs due to the fact that NEMD simulations invariably require the consideration of the application of a very large shear rate so as to nullify the condition of poor signal-to-noise ratio.
C. Shear thinning mechanism of GFI epoxy inks
For the GFI epoxy ink to be 3D printable via direct ink writing, it must possess a strong shear thinning behavior. Fig. 3 confirms such shear-thinning nature of both the pure epoxy ink and the GFI epoxy ink corresponding to shear rate values ranging from 0.1 ns−1 to 100 ns−1. Also, while discussing Fig. 3, we point out that the GFI epoxy shows a more “3D-printable-behavior” in this range of shear rate values since their viscosities are much higher than that of pure epoxy for smaller shear rates but become similar to that of pure epoxy for larger shear rates. In this section, we aim to understand the detailed nanoscopic mechanism responsible for such favored shear thinning behavior of the GFI epoxy ink. First, to understand the shear rate dependent size and conformation of bisphenol F molecules in various settings considered in this study, we have calculated the corresponding radius of gyration tensor (G) and the mean-squared radius of gyration (Rg2), defined as| | 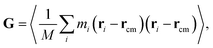 | (7) |
andHere, mi and ri are the mass and position of the ith atom of a bisphenol F molecule, M is the total mass of a bisphenol F molecule, and rcm is its center of mass position. The three diagonal elements of G indicate the average polymer size along the three Cartesian components x, y, and z. In the presence of shear rate, these quantities inform us about alignment and elongation/shrinking along each direction.
Fig. 6 shows the mean squared radius of gyration (Rg2) and the diagonal elements of the radius of gyration tensor (Gxx, Gyy, and Gzz) of the bisphenol F molecules in pure epoxy and 6 wt% GFI epoxy systems in the absence and presence of shear flow. Two key results emerge from Fig. 6(a). First, we find that for both pure epoxy and GFI epoxy, Rg2 of the bisphenol F molecules is larger for the case with shear compared to that with zero shear. Second, in the studied range of the shear rate variation, we find that for both the cases of pure epoxy and GFI epoxy, Rg2 for the bisphenol F molecules initially increases and then decreases with the shear rate. A similar trend, where the radius of gyration of long molecules first increases and then decreases with an applied shear, was observed in previous studies involving alkanes.50,51 Padilla and Toxvaerd51 explained such a behavior to be caused by the tendency of a decane chain to minimize the presence of its different parts in multiple shear planes simultaneously. The mechanism of polymer elongation/shrinkage in the presence of shear rate can be understood in further detail by studying the deformation of bisphenol F molecules in the flow direction (which is parallel to the x-axis in this study), and in the direction perpendicular to the shear planes (which is along the y-axis). From Fig. 6(b), we can see that Gxx increases monotonically with the shear rate, which indicates that the bisphenol F molecules align and elongate in the flow direction. The elongation is also evident from the increase in Rg2, in the presence of shear rate, compared to the equilibrium values [please see Fig. 6(a)]. On the other hand, as shown in Fig. 6(c and d), Gyy and Gzz decrease monotonically as the shear rate increases, with Gyy dropping more rapidly among the two. Such a rapid drop in Gyy indicates that the bisphenol F molecules shrink in the direction perpendicular to the shear plane. This observation aligns with previous theories that the polymer molecules tend to minimize their simultaneous presence in multiple shear planes with an increase in shear rate.51 When the different parts of a chain molecule are present in different shear planes, these parts get subjected to different velocities, and therefore, the chain experiences large deforming tension forces. The chains try to avoid such a scenario; thus, they tend to localize in a given shear plane and undergo shrinkage in the direction perpendicular to the shear planes. For smaller shear rates, elongation along the flow direction is the dominant effect resulting in an overall increase of polymer size (as evident from the initial increase in Rg2). Whereas for larger shear rates, the elongation in the flow direction slows down [see Fig. 6(b)] due to the increase in tension forces along that direction. This results in a scenario where the shrinkage in the direction normal to the shear plane becomes dominant over the total elongation in the shear plane (i.e., −ΔGyy > ΔGxx + ΔGzz), resulting in a decreasing trend of Rg2 at higher shear rates. These nanoscale mechanisms explain why the Rg2 for the Bisphenol F molecules (in both pure epoxy and GFI epoxy inks) is (1) larger for the case of finite shear as compared to the case with zero shear and (2) first increases and then decreases with the shear rate. Also, such localization of molecules in individual shear planes (resulting from the molecule shrinkage in the direction perpendicular to the shear planes) allows the dissipation of viscous force among them, resulting in the shear-thinning behavior,52 as observed in Fig. 3, for both pure epoxy and GFI epoxy inks.
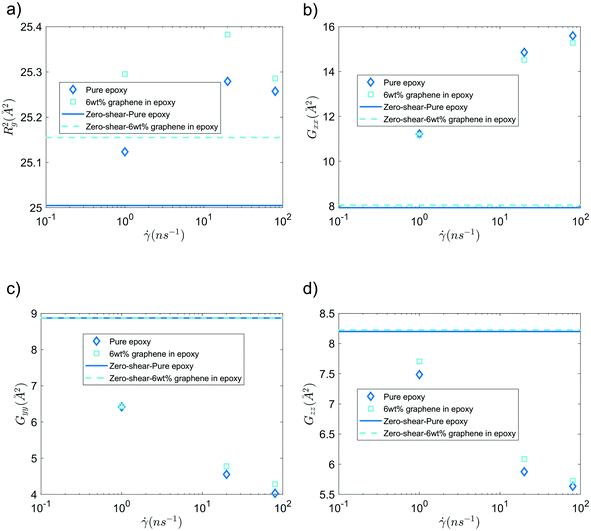 |
| | Fig. 6 (a) Mean-squared radius of gyration, (b) Gxx, (c) Gyy and (d) Gzz of bisphenol F molecules, in pure epoxy and GFI epoxy, in the presence and in the absence of shear slow. | |
Finally, we have analyzed the alignment of the graphene sheet with respect to the shear planes in the NEMD simulations [see Fig. 7(a) for the schematic description] in the presence and absence of shear flow. This alignment is quantified by studying the probability distribution of angle θ between the y-axis (which is the normal vector to the shear planes in NEMD simulations) and the vector normal to the graphene surface [see Fig. 7(a)]. The normal vector is obtained by calculating the eigenvector, corresponding to the largest eigenvalue of the graphene inertia tensor. Also, these probability distributions for θ are provided for the case of 6 wt% GFI epoxy system in the presence and in the absence of shear flow [see Fig. 7(b–d)]. In the absence of shear flow, we see the angles arbitrarily distributed between 105–115° [see Fig. 7(b)]. On the other hand, in the presence of shear flow, the angles between the graphene normal vector and the shear plane normal vector are distributed around 20° and 160°, indicating that the graphene flakes tend to align parallel to the shear planes [see Fig. 7(c and d)]. At very high shear rates, we see small probabilities distributed over a wide range of angles [see Fig. 7(d)]. This stems from the graphene sheet occasionally making complete rotations at very high shear rates, followed by realignment along the shear direction. Thus, in addition to the epoxy molecules, graphene flakes also align along the shear planes resulting in a more prominent shear thinning behavior of the GFI epoxy inks.
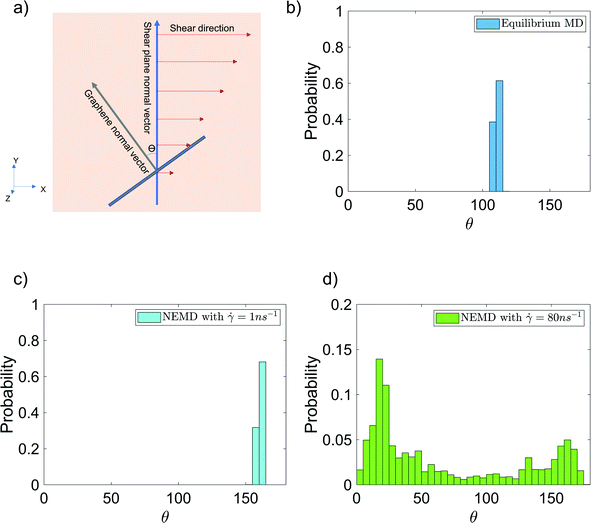 |
| | Fig. 7 Probability distribution of the angle [shown schematically in (a)] between the graphene normal vector and the y-axis (normal vector to the shear planes in NEMD simulations) in the (b) absence and (c and d) presence of shear flow for the case of 6 wt% graphene infused epoxy system. | |
D. Comparison of the findings from the MD simulations with the experimental data
To compare findings from our MD simulations with the existing data from previous experimental studies, we first fit the high shear rate viscosity data (obtained from the NEMD simulations of the pure epoxy resin) to a standard Ostwald and de Waele power-law model (known to capture the shear-thinning behavior of polymer liquids53,54), expressed as:| | η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = A ) = A![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n. n. | (9) |
Here, η is the shear rate dependent viscosity, A is the proportionality constant, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate, and n is the flow behavior index. The high shear rate viscosity data regression is shown in Fig. S2 in the ESI,† where n equals −0.4787. From this plot, we see a linear variation of the log
is the shear rate, and n is the flow behavior index. The high shear rate viscosity data regression is shown in Fig. S2 in the ESI,† where n equals −0.4787. From this plot, we see a linear variation of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η as a function of log
η as a function of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for the entire range of shear rates considered in this study (0.1 to 100 ns−1). Also, we do not see any plateauing of the viscosity at these shear rates (please see Fig. 3). Such plateauing occurs when the liquid starts to demonstrate Newtonian behavior. Given that all the data points obtained from the NEMD simulations are within the shear-thinning regime and there is no evidence of plateau characterizing a transition to the Newtonian regime, we assume that the standard power-law model is suitable to extrapolate the low shear rate viscosity values.53 However, one cannot directly extrapolate zero-shear rate viscosities using the power law as the viscosity goes to infinity as the shear rate tends towards zero. To overcome this issue, the extrapolation should only be performed until a specific shear rate below which the shear-thinning regime ends, and the Newtonian regime starts. This shear rate is generally known as the critical shear rate. Previous experimental works have reported the critical shear rate for pure epoxy (Epon 862 with EpiCure curing agent W) as 2700 s−1.55 Our fit to the power-law model predicts a viscosity of 4.7 Pa s at this shear rate, which is close to the corresponding experimental value of 3.93 Pa s.
for the entire range of shear rates considered in this study (0.1 to 100 ns−1). Also, we do not see any plateauing of the viscosity at these shear rates (please see Fig. 3). Such plateauing occurs when the liquid starts to demonstrate Newtonian behavior. Given that all the data points obtained from the NEMD simulations are within the shear-thinning regime and there is no evidence of plateau characterizing a transition to the Newtonian regime, we assume that the standard power-law model is suitable to extrapolate the low shear rate viscosity values.53 However, one cannot directly extrapolate zero-shear rate viscosities using the power law as the viscosity goes to infinity as the shear rate tends towards zero. To overcome this issue, the extrapolation should only be performed until a specific shear rate below which the shear-thinning regime ends, and the Newtonian regime starts. This shear rate is generally known as the critical shear rate. Previous experimental works have reported the critical shear rate for pure epoxy (Epon 862 with EpiCure curing agent W) as 2700 s−1.55 Our fit to the power-law model predicts a viscosity of 4.7 Pa s at this shear rate, which is close to the corresponding experimental value of 3.93 Pa s.
In addition, we have also compared the experimentally measured changes in viscosity, due to the addition of graphene, with the change predicted from our simulations. Previous experimental studies have reported an increase, in viscosity (relative to pure epoxy), of 2 to 3 orders of magnitude (depending on the graphene wt%)9,48 due to graphene addition. Our MD simulation results predict a viscosity increase of 3 orders of magnitude due to graphene addition. Therefore, the findings from our MD simulations are in line with the results from experimental studies. Here, we would like to point out that our predictions report a characteristic change in viscosity due to graphene addition and do not consider the effect of graphene weight percentage.
Conclusions
The results presented in this study give us a detailed mechanistic understanding of the effect of graphene flakes on the viscosity, shear-thinning behavior, and the resulting 3D printability of GFI epoxy inks. First, the presence of the graphene flakes significantly slows down the rotational dynamics of the surrounding bisphenol F molecules that are adsorbed to the graphene surface resulting in much larger rotational relaxation times compared to the bisphenol F molecules in pure epoxy inks. Consequently, the zero-shear viscosity of the GFI epoxy ink is predicted to be approximately three orders of magnitude larger than pure epoxy ink. Second, in the presence of the shear flow, a bisphenol F molecule tends to localize itself in a single shear plane, and the graphene flakes tend to align parallel to the shear planes resulting in a shear-thinning behavior. These two properties play an essential role in the 3D printability of epoxy-based ink. Also, by following the methodology presented in this study, it is possible to in silico design 3D printable epoxy-based inks by predicting the zero-shear viscosity and shear thinning behavior of various types of nanofiller-infused epoxy-based inks.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors gratefully acknowledge NAVAL Air Command for supporting this research. We also gratefully acknowledge the high-performance computing cluster Deepthought2 of the University of Maryland that enabled us to perform the MD simulations and the analyses.
References
- A. Toldy, B. Szolnoki and G. Marosi, Flame retardancy of fibre-reinforced epoxy resin composites for aerospace applications, Polym. Degrad. Stab., 2011, 96(3), 371–376 CrossRef CAS.
-
E. Ghassemieh, Materials in automotive application, state of the art and prospects, New trends and developments in automotive industry, 2011, vol. 20, pp. 364–394 Search PubMed.
- W. Tian, L. Liu, F. Meng, Y. Liu, Y. Li and F. Wang, The failure behaviour of an epoxy glass flake coating/steel system under marine alternating hydrostatic pressure, Corros. Sci., 2014, 86, 81–92 CrossRef CAS.
- G. Iyer, R. S. Gorur, R. Richert, A. Krivda and L. E. Schmidt, Dielectric properties of epoxy based nanocomposites for high voltage insulation, IEEE Trans. Dielectr. Electr. Insul., 2011, 18(3), 659–666 CAS.
- H. Gu, C. Ma, J. Gu, J. Guo, X. Yan, J. Huang and Z. Guo, An overview of multifunctional epoxy nanocomposites, J. Mater. Chem. C, 2016, 4(25), 5890–5906 RSC.
- B. G. Compton and J. A. Lewis, 3D-printing of lightweight cellular composites, Adv. Mater., 2014, 26(34), 5930–5935 CrossRef CAS PubMed.
- J. P. Lewicki, J. N. Rodriguez, C. Zhu, M. A. Worsley, A. S. Wu, Y. Kanarska and M. J. King, 3D-printing of meso-structurally ordered carbon fiber/polymer composites with unprecedented orthotropic physical properties, Sci. Rep., 2017, 7(1), 1–14 CrossRef PubMed.
- R. R. Collino, T. R. Ray, R. C. Fleming, J. D. Cornell, B. G. Compton and M. R. Begley, Deposition of ordered two-phase materials using microfluidic print nozzles with acoustic focusing, Extreme Mech. Lett., 2016, 8, 96–106 CrossRef.
- B. G. Compton, N. S. Hmeidat, R. C. Pack, M. F. Heres and J. R. Sangoro, Electrical and mechanical properties of 3D-printed graphene-reinforced epoxy, JOM, 2018, 70(3), 292–297 CrossRef CAS.
- S. Malek, J. R. Raney, J. A. Lewis and L. J. Gibson, Lightweight 3D cellular composites inspired by balsa, Bioinspiration Biomimetics, 2017, 12(2), 026014 CrossRef PubMed.
- J. R. Raney, B. G. Compton, J. Mueller, T. J. Ober, K. Shea and J. A. Lewis, Rotational 3D printing of damage-tolerant composites with programmable mechanics, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(6), 1198–1203 CrossRef CAS PubMed.
- N. S. Hmeidat, J. W. Kemp and B. G. Compton, High-strength epoxy nanocomposites for 3D printing, Compos. Sci. Technol., 2018, 160, 9–20 CrossRef CAS.
- C. M. Hadden, D. R. Klimek-McDonald, E. J. Pineda, J. A. King, A. M. Reichanadter, I. Miskioglu and G. M. Odegard, Mechanical properties of graphene nanoplatelet/carbon fiber/epoxy hybrid composites: Multiscale modeling and experiments, Carbon, 2015, 95, 100–112 CrossRef CAS.
- O. Aluko, S. Gowtham and G. M. Odegard, Multiscale modeling and analysis of graphene nanoplatelet/carbon fiber/epoxy hybrid composite, Composites, Part B, 2017, 131, 82–90 CrossRef CAS.
- B. Mortazavi, O. Benzerara, H. Meyer, J. Bardon and S. Ahzi, Combined molecular dynamics-finite element multiscale modeling of thermal conduction in graphene epoxy nanocomposites, Carbon, 2013, 60, 356–365 CrossRef CAS.
- S. C. Shiu and J. L. Tsai, Characterizing thermal and mechanical properties of graphene/epoxy nanocomposites, Composites, Part B, 2014, 56, 691–697 CrossRef CAS.
- R. Rahman and A. Haque, Molecular modeling of crosslinked graphene–epoxy nanocomposites for characterization of elastic constants and interfacial properties, Composites, Part B, 2013, 54, 353–364 CrossRef CAS.
- K. M. Shahil and A. A. Balandin, Graphene–multilayer graphene nanocomposites as highly efficient thermal interface materials, Nano Lett., 2012, 12(2), 861–867 CrossRef CAS PubMed.
- L. C. Tang, Y. J. Wan, D. Yan, Y. B. Pei, L. Zhao, Y. B. Li and G. Q. Lai, The effect of graphene dispersion on the mechanical properties of graphene/epoxy composites, Carbon, 2013, 60, 16–27 CrossRef CAS.
- M. G. Prolongo, C. Salom, C. Arribas, M. Sánchez-Cabezudo, R. M. Masegosa and S. G. Prolongo, Influence of graphene nanoplatelets on curing and mechanical properties of graphene/epoxy nanocomposites, J. Therm. Anal. Calorim., 2016, 125(2), 629–636 CrossRef CAS.
- X. J. Shen, Y. Liu, H. M. Xiao, Q. P. Feng, Z. Z. Yu and S. Y. Fu, The reinforcing effect of graphene nanosheets on the cryogenic mechanical properties of epoxy resins, Compos. Sci. Technol., 2012, 72(13), 1581–1587 CrossRef CAS.
- P. A. Gordon, Characterizing Isoparaffin Transport Properties with Stokes–Einstein Relationships, Ind. Eng. Chem. Res., 2003, 42(26), 7025–7036 CrossRef CAS.
- J. L. Dote, D. Kivelson and R. N. Schwartz, A molecular quasi-hydrodynamic free-space model for molecular rotational relaxation in liquids, J. Phys. Chem., 1981, 85(15), 2169–2180 CrossRef CAS.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117(1), 1–19 CrossRef CAS.
- H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, An ab initio CFF93 all-atom force field for polycarbonates, J. Am. Chem. Soc., 1994, 116(7), 2978–2987 CrossRef CAS.
- H. B. Fan and M. M. Yuen, Material properties of the cross-linked epoxy resin compound predicted by molecular dynamics simulation, Polymer, 2007, 48(7), 2174–2178 CrossRef CAS.
- M. Li, H. Zhou, Y. Zhang, Y. Liao and H. Zhou, The effect of defects on the interfacial mechanical properties of graphene/epoxy composites, RSC Adv., 2017, 7(73), 46101–46108 RSC.
- A. A. Sahraei, A. H. Mokarizadeh, D. George, D. Rodrigue, M. Baniassadi and M. Foroutan, Insights into interphase thickness characterization for graphene/epoxy nanocomposites: a molecular dynamics simulation, Phys. Chem. Chem. Phys., 2019, 21(36), 19890–19903 RSC.
- Y. Sun, L. Chen, L. Cui, Y. Zhang and X. Du, Molecular dynamics simulation of cross-linked epoxy resin and its interaction energy with graphene under two typical force fields, Comput. Mater. Sci., 2018, 143, 240–247 CrossRef CAS.
- R. Rahman, The role of graphene in enhancing the stiffness of polymeric material: A molecular modeling approach, J. Appl. Phys., 2013, 113(24), 243503 CrossRef.
-
R. W. Hockney and J. W. Eastwood, Computer Simulations Using Particles, McGraw-Hill International Book Co., New York, 1981 Search PubMed.
- W. G. Hoover, Canonical Dynamics: Equilibrium Phase-Space Distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31(3), 1695–1697 CrossRef PubMed.
- S. Nosé, A Unified Formulation of the Constant Temperature Molecular Dynamics Methods, J. Chem. Phys., 1984, 81(1), 511–519 CrossRef.
- Y. Chen, Z. Li, S. Wen, Q. Yang, L. Zhang, C. Zhong and L. Liu, Molecular simulation study of role of polymer–particle interactions in the strain-dependent viscoelasticity of elastomers (Payne effect), J. Chem. Phys., 2014, 141(10), 104901 CrossRef PubMed.
- P. Xu, J. Lin, L. Wang and L. Zhang, Shear flow behaviors of rod-coil diblock copolymers in solution: A nonequilibrium dissipative particle dynamics simulation, J. Chem. Phys., 2017, 146(18), 184903 CrossRef.
- M. E. Tuckerman, C. J. Mundy, S. Balasubramanian and M. L. Klein, Modified nonequilibrium molecular dynamics for fluid flows with energy conservation, J. Chem. Phys., 1997, 106(13), 5615–5621 CrossRef CAS.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2009, 18(1), 015012 CrossRef.
-
J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, Amsterdam, 3rd edn, 2006 Search PubMed.
- P. Bačová, A. N. Rissanou and V. Harmandaris, Edge-functionalized graphene as a nanofiller: molecular dynamics simulation study, Macromolecules, 2015, 48(24), 9024–9038 CrossRef.
- L. Zhang and M. L. Greenfield, Relaxation time, diffusion, and viscosity analysis of model asphalt systems using molecular simulation, J. Chem. Phys., 2007, 127(19), 194502 CrossRef PubMed.
- D. D. Li and M. L. Greenfield, Viscosity, relaxation time, and dynamics within a model asphalt of larger molecules, J. Chem. Phys., 2014, 140(3), 034507 CrossRef PubMed.
- M. Mondello and G. S. Grest, Viscosity calculations of n-alkanes by equilibrium molecular dynamics, J. Chem. Phys., 1997, 106(22), 9327–9336 CrossRef CAS.
- P. A. Gordon, Influence of simulation details on thermodynamic and transport properties in molecular dynamics of fully flexible molecular models, Mol. Simul., 2003, 29(8), 479–487 CrossRef CAS.
- G. Williams and D. C. Watts, Non-symmetrical dielectric relaxation behaviour arising from a simple empirical decay function, Trans. Faraday Soc., 1970, 66, 80–85 RSC.
- G. Williams, D. C. Watts, S. B. Dev and A. M. North, Further considerations of non symmetrical dielectric relaxation behaviour arising from a simple empirical decay function, Trans. Faraday Soc., 1971, 67, 1323–1335 RSC.
- L. Zhang and M. L. Greenfield, Rotational relaxation times of individual compounds within simulations of molecular asphalt models, J. Chem. Phys., 2010, 132(18), 184502 CrossRef.
- K. Sonibare, G. Rucker and L. Zhang, Molecular dynamics simulation on vegetable oil modified model asphalt, Constr. Build. Mater., 2021, 270, 121687 CrossRef CAS.
-
C. N. Fayed, Rheology of Graphene Based Composites for Printing Applications, 2018. http://purl.flvc.org/fsu/fd/FSU_libsubv1_scholarship_submission_1524503606_a559be15.
- L. I. Kioupis and E. J. Maginn, Rheology, dynamics, and structure of hydrocarbon blends: a molecular dynamics study of n-hexane/n-hexadecane mixtures, Chem. Eng. J., 1999, 74(1-2), 129–146 CrossRef CAS.
- J. D. Moore, S. T. Cui, H. D. Cochran and P. T. Cummings, Rheology of lubricant basestocks: A molecular dynamics study of C 30 isomers, J. Chem. Phys., 2000, 113(19), 8833–8840 CrossRef CAS.
- P. Padilla and S. R. Toxvaerd, Fluid n-decane undergoing planar Couette flow, J. Chem. Phys., 1992, 97(10), 7687–7694 CrossRef CAS.
- S. T. Cui, P. T. Cummings, H. D. Cochran, J. D. Moore and S. A. Gupta, Nonequilibrium molecular dynamics simulation of the rheology of linear and branched alkanes, Int. J. Thermophys., 1998, 19(2), 449–459 CrossRef CAS.
-
C. W. Macosko, Rheology principles, measurements, and applications, VCH Publ. Inc., New York, 1994 Search PubMed.
- H. C. Tseng, J. S. Wu and R. Y. Chang, Shear thinning and shear dilatancy of liquid n-hexadecane via equilibrium and nonequilibrium molecular dynamics simulations: Temperature, pressure, and density effects, J. Chem. Phys., 2008, 129(1), 014502 CrossRef PubMed.
- J. Zhu, S. Wei, J. Ryu, L. Sun, Z. Luo and Z. Guo, Magnetic epoxy resin nanocomposites reinforced with core− shell structured Fe@ FeO nanoparticles: fabrication and property analysis, ACS Appl. Mater. Interfaces, 2010, 2(7), 2100–2107 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02321g |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a
*a

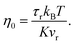
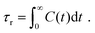


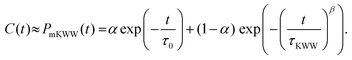
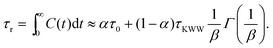

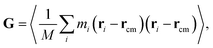

![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = A
) = A![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n.
n.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate, and n is the flow behavior index. The high shear rate viscosity data regression is shown in Fig. S2 in the ESI,† where n equals −0.4787. From this plot, we see a linear variation of the log
is the shear rate, and n is the flow behavior index. The high shear rate viscosity data regression is shown in Fig. S2 in the ESI,† where n equals −0.4787. From this plot, we see a linear variation of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η as a function of log
η as a function of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for the entire range of shear rates considered in this study (0.1 to 100 ns−1). Also, we do not see any plateauing of the viscosity at these shear rates (please see Fig. 3). Such plateauing occurs when the liquid starts to demonstrate Newtonian behavior. Given that all the data points obtained from the NEMD simulations are within the shear-thinning regime and there is no evidence of plateau characterizing a transition to the Newtonian regime, we assume that the standard power-law model is suitable to extrapolate the low shear rate viscosity values.53 However, one cannot directly extrapolate zero-shear rate viscosities using the power law as the viscosity goes to infinity as the shear rate tends towards zero. To overcome this issue, the extrapolation should only be performed until a specific shear rate below which the shear-thinning regime ends, and the Newtonian regime starts. This shear rate is generally known as the critical shear rate. Previous experimental works have reported the critical shear rate for pure epoxy (Epon 862 with EpiCure curing agent W) as 2700 s−1.55 Our fit to the power-law model predicts a viscosity of 4.7 Pa s at this shear rate, which is close to the corresponding experimental value of 3.93 Pa s.
for the entire range of shear rates considered in this study (0.1 to 100 ns−1). Also, we do not see any plateauing of the viscosity at these shear rates (please see Fig. 3). Such plateauing occurs when the liquid starts to demonstrate Newtonian behavior. Given that all the data points obtained from the NEMD simulations are within the shear-thinning regime and there is no evidence of plateau characterizing a transition to the Newtonian regime, we assume that the standard power-law model is suitable to extrapolate the low shear rate viscosity values.53 However, one cannot directly extrapolate zero-shear rate viscosities using the power law as the viscosity goes to infinity as the shear rate tends towards zero. To overcome this issue, the extrapolation should only be performed until a specific shear rate below which the shear-thinning regime ends, and the Newtonian regime starts. This shear rate is generally known as the critical shear rate. Previous experimental works have reported the critical shear rate for pure epoxy (Epon 862 with EpiCure curing agent W) as 2700 s−1.55 Our fit to the power-law model predicts a viscosity of 4.7 Pa s at this shear rate, which is close to the corresponding experimental value of 3.93 Pa s.




