A computational study of the influence of methyl substituents on competitive ring closure to α- and β-lactones

Abstract

Ring-closure of substituted 2-chlorosuccinates to α- or β-lactones has been studied by means of MP2/6-311+G(d,p)//MP2/6-31+G(d) calculations in water treated as a polarised continuum (PCM) and in vacuum. Optimised geometries have been obtained for 2-chlorosuccinate and its 2-methyl, 3,3-dimethyl, and 2,3,3-trimethyl derivatives, along with the transition structures and products for intramolecular nucleophilic displacement leading to the 3- or 4-membered rings. Relative enthalpies and Gibbs free energies of activation and reaction are presented, along with key geometrical parameters, and changes in electrostatic-potential-derived atomic charges. The difference in free-energy barriers for α- and β-lactone formation from the 2-methyl substrate at 298 K is less than 1 kJ mol⁻¹. Primary ¹⁴C kinetic isotope effects calculated for substitution at C2 are significantly smaller for α-lactone formation than for β, suggesting a possible way to distinguish between the competing pathways of reaction. The B3LYP method without dispersion corrections predicts the wrong relative stability order for methyl-substituted succinate dianions in PCM water.

---

Introduction

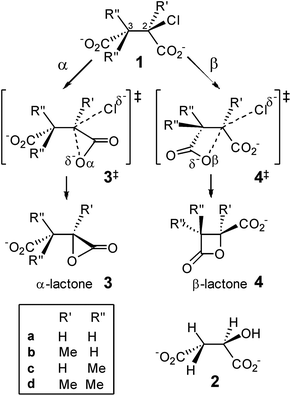
Strained small-ring lactones are of considerable topical interest. The β-lactone moieties of salinosporamide A (Marizomib) and tetrahydrolipstatin (Orlistat) allow for irreversible covalent modification of the proteasome and pancreatic lipase, respectively, as potential anti-cancer or actual anti-obesity drugs, via reaction with nucleophilic serine or threonine residues,^1,2 and a β-lactone synthase has recently been reported.³

Over a century ago, Holmberg⁴ demonstrated the intermediacy of a β-lactone 4a in the Walden cycle⁵ for stereochemical interconversion of chlorosuccinic acid 1a and malic acid 2 which, given the intermediacy of α-lactone in hydrolysis of 2-bromopropionate with stereochemical retention at low hydroxide concentration,^6,7 begged the question: why is α-lactone 3a not involved in the similar intramolecular nucleophilic substitution of halosuccinate?

The very high strain energy (179 kJ mol⁻¹, see ESI†) of the α-lactone 3-membered ring (3MR) vs. the β-lactone 4MR (94 kJ mol⁻¹) does not provide the answer, as the 3MR species is an intermediate in room-temperature bromination of 2,3-dimethylmaleate and fumarate in water.⁸ DFT calculations (B3LYP/6-31+G* in PCM water) showed collapse of cyclic bromonium structures derived from these alkene dicarboxylates directly to α-lactones; β-lactones were formed only by subsequent intramolecular nucleophilic substitution of the second carboxylate upon the first-formed α-lactone.⁹ Similarly, cyclic halonium ions derived from acrylate are transition structures (TSs) for degenerate rearrangement of equivalent α-lactones;¹⁰ β-lactone may be formed by dyotropic rearrangement involving a significant barrier but not by direct intramolecular nucleophilic substitution at the distal carbon of the halonium ring.¹¹ Attack at the proximal carbon of the acrylate chloronium (yielding α-lactone) involves an OC_αCl angle (∼112°) that is larger than the OC_βCl angle (∼91°) required for attack at the distal carbon.

Conversely, DFT calculations with the same method for competitive α- vs. β-lactone formation by intramolecular nucleophilic substitution in chlorosuccinate dianion 1a predict a lower barrier for attack by the distal carboxylate (O_βC2Cl angle ∼174° in 4a^‡) than by the proximal carboxylate (O_αC2Cl angle ∼139° in 3a^‡), in accord with β-lactone as the preferred intermediate in the double displacement mechanism that explains overall retention of configuration in Walden's classic Ag₂O/H₂O-promoted hydrolysis of chlorosuccinic acid.¹² However, solvation energy plays a crucial role in determining this outcome: α-lactone formation is favoured in vacuum.¹²

It is well known that geminal dialkyl substitution¹³ promotes ring formation,¹⁴ and this effect is widely used in synthesis,¹⁵ although its origin is hotly disputed.^16,17 In particular, Kostal and Jorgensen have argued, on the basis of computations in the gas phase and in aqueous solution, that the enhanced rate of epoxide-forming ring-closure accompanying increasing methylation at C1 in 2-chloroethoxide is due mostly to a solvent effect.¹⁸ It is timely, therefore, to investigate computationally how methylation at C2 and C3 in 2-chlorosuccinate affects the competition between α- and β-lactone formation, including consideration of the influence of solvation and the role of dispersion in assessing the relative reactivity of such sterically crowded molecules (Scheme 1).

Scheme 1 Ring-closure of substituted 2-chlorosuccinates to α- or β-lactones. The three-membered α-lactones are designated as structures 3a–d based on substitution at C₂ and/or C₃. The four-membered β-lactones follow the same rule.

Computational methods

The Gaussian09 program (revision D.01)¹⁹ was used to perform electronic structure calculations. Optimised geometries for reactant structures (RSs) and product structures were obtained by standard methods, and transition structures (TSs) were located with the Berny algorithm and confirmed through frequency analyses. Second-order Møller–Plesset perturbation theory (frozen-core MP2) and the density functional B3LYP were used for geometry optimisations with the 6-31+G(d) basis set. Dispersion-corrected B3LYP optimisations incorporating Grimme's D3 correction with Becke–Johnson damping (keyword empiricaldispersion = gd3bj) were carried out on the RSs. Implicit solvation by means of the integral-equation-formalism polarised continuum model (IEFPCM) with the universal force field (UFF) cavity model also involved re-optimisation of all geometries. Atomic charges were computed using the electrostatic potential fitting (ESP) model. Single-point energies were evaluated with the larger 6-311+G(d,p) basis for all structures at their 6-31+G(d) optimised geometries. Zero-point and thermal energy contributions to enthalpies and entropic contributions to Gibbs free energies (298 K, 1 atm) were evaluated with the 6-31+G(d) basis. Kinetic isotope effects (KIEs) were determined by means of our SULISO software²⁰ within the standard rigid-rotor harmonic-oscillator approximation for semi-classical contributions; the quantum-tunnelling factor was estimated by means of the one-dimensional Bell model.

Results and discussion

Table 1 contains activation enthalpies ΔH^‡ and Gibbs free energies ΔG^‡ for intramolecular nucleophilic displacement reactions of substituted 2-chlorosuccinate dianionic RSs 1a–1d, by means of TSs 3a^‡–3d^‡ and 4a^‡–4d^‡, along with the respective enthalpies ΔH_rxn and Gibbs free energies ΔG_rxn of reaction for formation of α-lactones 3a–3d and β-lactones 4a–4d. These values are computed at the MP2/6-311+G(d,p) level for structures optimised with MP2/6-31+G(d) in both vacuum and PCM water.

Table 1 MP2/6-311+G(d,p) enthalpy and Gibbs free-energy changes (kJ mol⁻¹) of activation and reaction for α-lactone formation (3) and β-lactone formation (4) of each of the substituted chlorosuccinates a–d determined from MP2/6-31+G(d) optimised structures (298 K, 1 atm)

	ΔH^‡		ΔG^‡		ΔHrxn		ΔGrxn
	3	4	3	4	3	4	3	4
PCM water
a	101.5	95.6	107.6	100.8	52.2	−18.6	56.1	−17.5
b	97.4	97.3	102.6	102.2	40.4	−32.8	43.5	−31.6
c	99.3	86.6	105.2	90.9	41.2	−39.5	44.3	−39.8
d	82.5	82.6	88.0	86.6	5.3	−68.6	8.1	−68.5
Vacuum
a	52.3	75.1	58.3	80.1	−200.5	−265.2	−196.8	−264.7
b	65.5	85.1	70.3	89.3	−197.9	−267.2	−195.3	−266.7
c	53.9	66.7	58.9	71.0	−206.9	−277.2	−204.8	−278.6
d	75.5	74.1	79.3	77.1	−225.7	−289.2	−224.7	−291.4

---

Thermodynamics

It is evident that both ΔH_rxn and ΔG_rxn have very large negative values for formation of either α- or β-lactone (plus a free chloride anion) from any of the compounds in vacuum (Table 1). This arises from reduction of the very large coulombic repulsion between the two negative charges in 1 as the chloride anion departs and single-charged lactone carboxylates 3 or 4 are formed. The free-energy changes are more negative than the enthalpy changes because there is an increase in entropy for the dissociated products of each reaction. The corresponding values of ΔH_rxn and ΔG_rxn for reaction in PCM water are all less negative by ≈236 kJ mol⁻¹ because the negative charges are strongly stabilised by the continuum solvation method. The entropic contribution to ΔG_rxn ought to be corrected for the change of standard state from 1 atm to 1 mol dm⁻³, but this would be of no consequence for the present discussion, which focuses upon direct comparison between 3- and 4MR-formation in aqueous solution.

Clearly, formation of β-lactone is always more energetically favourable than formation of α-lactone (Table 1). This is consistent with the known difference in ring-strain energy between 3MRs and 4MRs.²¹ A question of interest is how the position and degree of methyl substitution affects the relative energies for formation of α- and β-lactones. Formation of 4a is 74 kJ mol⁻¹ more exothermic than 3a, but formation of 4c is 84 kJ mol⁻¹ more exothermic than 3c. It seems that dimethyl substitution at C3 favours formation of 4c over 3c (4MR vs. 3MR) by an additional 10 kJ mol⁻¹: this is a thermodynamic gem-dimethyl¹³ or Thorpe–Ingold¹⁴ effect. However, methylation at C2 alone, or at both C2 and C3, favours 4MR by only a small amount (1 to 3 kJ mol⁻¹): it seems that the thermodynamic effects are not additive.

Kinetics

The values calculated for ΔH^‡ and ΔG^‡ do not differ very significantly (Table 1); this discussion considers only the free energies of activation, as these are more directly related to reaction rate constants that could be measured experimentally.

The free-energy barriers for 3MR formation via3a^‡–3d^‡ are consistently higher than those for 4MR formation via4a^‡–4d^‡ in competing intramolecular reactions in PCM water, in accord with expectation.²¹ However, this behaviour is not predicted for reactions in vacuum, for which substitutions a, b and c have lower barriers for α-lactone formation, in line with our previous report for 3a^‡vs. 4a^‡ at the B3LYP/6-31+G(d) level.¹² Clearly, the influence of solvation is very important. Previously the lower barrier for β-lactone formation was attributed to a much more-favourable angle θ_O–C–Cl between the making and breaking bonds at C2 in 4a^‡ than in 3a^‡;¹² now it may be noted that the average value of θ_O–C–Cl in the four TSs 4a^‡–4d^‡ is 30° larger (172°) than in the four TSs 3a^‡–3d^‡ (142°) in PCM water.

In PCM water, methylation at C2 alone raises the value of ΔG^‡ for β-lactone formation by only 1 kJ mol⁻¹; a less-favourable angle θ_O–C–Cl between the making and breaking bonds at C2 (168° in 4b^‡vs. 173° in 4a^‡) is largely offset by increased partial positive charge at this atom in the TS (0.41|e| vs. 0.26|e|). gem-Dimethylation at C3 reduces ΔG^‡ for β-lactone formation by about 10 kJ mol⁻¹ in PCM water: this is a kinetic gem-dimethyl¹³ or Thorpe–Ingold¹⁴ effect. The corresponding reduction in ΔG^‡ in vacuum is similar (9 kJ mol⁻¹), implying that, in this case, solvation has little influence on the gem-dimethyl effect. This result is contrary to the findings of Kostal and Jorgensen, for the gem-dimethyl effect upon 3MR-formation in 1,1-dimethyl-2-chloroethoxide vs. 2-chloroethoxide, which was greatly enhanced by solvation, treated both by the PCM method and by means of Monte Carlo calculations with explicit water molecules. A possible reason for the difference in behaviour may be the presence of a second negatively charged group in the chlorosuccinate substrates. However, substitution at both C2 and C3 reduces the barrier by a further 4 kJ mol⁻¹ in PCM water but raises it by 6 kJ mol⁻¹ in vacuum, implying a significant influence of solvation. While an explicit treatment of solvation would be desirable (not least) as a check for possible error in the present PCM treatment, it may be noted that the explicit and implicit treatments of Kostal and Jorgensen yielded the same qualitative results for their system.

Methylation at C2 lowers the value of ΔG^‡ for α-lactone formation in PCM water by 5 kJ mol⁻¹; although the θ_O–C–Cl angle is even less-favourable (142° in 3b^‡vs. 147° in 3a^‡), the charge at C2 is more positive in the TS (0.78|e| vs. 0.50|e|). It is noteworthy that the barrier for α-lactone formation is only about 0.4 kJ mol⁻¹ higher than that for β-lactone formation, which corresponds to relative rates of 1: ∼1.2 for α vs. β at 298 K. gem-Dimethylation at C3 has only a small effect, reducing the free-energy barrier by 2 kJ mol⁻¹, since this substitution is exocyclic to the forming 3MR: the Thorpe–Ingold effect disfavours α-lactone formation by 14 kJ mol⁻¹ in competition with β-lactone formation. However, methylation at both C2 and C3 significantly reduces ΔG^‡ by 20 kJ mol⁻¹, so that the barrier for α-lactone formation is again only slightly higher than that for β-lactone formation.

Origin of the gem-dimethyl effect at C3 on β-lactone formation

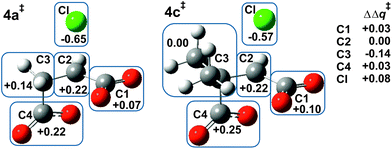
Fig. 1 shows the MP2/6-31+G(d) optimised structures of TSs 4a^‡ and 4c^‡ in PCM water, which are remarkably similar apart from the two methyl substituents at C3 in the latter. The respective lengths (in Å) for the making and breaking bonds are: C⋯O = 1.991 and 1.990, C⋯Cl = 2.352 and 2.358; the respective θ_O–C–Cl angles are 173° and 177°. The Pauling bond orders for the making and breaking bonds are n_O–C = 0.40 and n_C–Cl = 0.39 for both 4a^‡ and 4c^‡, suggesting relatively loose but balanced TSs. The blue boxes in Fig. 1 enclose groups of atoms whose electrostatic-potential-derived charges have been summed together; the values displayed are the changes Δq in those sums from 1a to 4a^‡ and from 1c to 4c^‡, respectively, in units of electron charge (|e|). The Table within Fig. 1 provides values of the differential changes within each boxed group of atoms between the two TSs shown. The most significant change is centred on C3, which undergoes a positive shift from 1a to 4a^‡ but essentially no change from 1c to 4c^‡ with dimethyl substitution. Formation of the TS for both reactions involves separation of group charges, but the magnitude of the separation is smaller for the dimethyl-substituted compound, as evidenced by the smaller differential charge change on the leaving-group Cl. The 10 kJ mol⁻¹ reduction in ΔG^‡ in PCM water for β-lactone formation due to dimethylation at C3 seems to arise from more-favourable changes in electrostatic interactions between the RS and the TS involving the site of nucleophilic displacement.

Fig. 1 Changes in MP2-PCM/6-311+G(d,p) ESP atomic charges (Δq^‡/|e|) summed over the atoms within each boxed group, from chlorosuccinate 1a or 1c to TS 4a^‡ or 4c^‡, respectively, together with differential changes (ΔΔq^‡).

Origin of the methylation effect at C2 on α-lactone formation

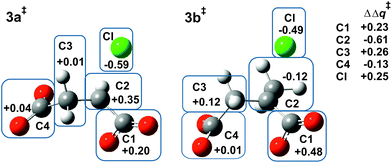
Fig. 2 shows the MP2/6-31+G(d) optimised structures of TSs 3a^‡ and 3b^‡ in PCM water. The respective lengths (in Å) for the making and breaking bonds are: C⋯O = 1.905 and 1.965, C⋯Cl = 2.516 and 2.613; the respective θ_O–C–Cl angles are 147° and 142°. The Pauling bond orders are n_O–C = 0.46 and 0.42, n_C–Cl = 0.30 and 0.25, respectively, suggesting relatively less bond-making and more bond-breaking in a more “exploded S_N2-like” TS²² for reaction of the 2-methyl substrate. As before, the blue boxes in Fig. 2 enclose groups of atoms whose electrostatic-potential-derived charges have been summed together; the values displayed are the changes Δq in those sums from 1a to 3a^‡ and from 1b to 3b^‡, respectively, in units of electron charge (|e|). The Table within Fig. 2 provides values of the differential changes within each boxed group of atoms between the two TSs shown. The most significant change is centred on C2, which undergoes a positive shift from 1a to 3a^‡ but a negative shift from 1b to 3b^‡. Once again, formation of the TS for both reactions involves separation of group charges, but the magnitude of the separation is much smaller for the methyl-substituted compound. The 5 kJ mol⁻¹ reduction in ΔG^‡ in PCM water for α-lactone formation due to methylation at C2 arises again from less-unfavourable changes in electrostatic interactions between the RS and the TS.

Fig. 2 Changes in MP2-PCM/6-311+G(d,p) ESP atomic charges (Δq^‡/|e|) summed over the atoms within each boxed group, from chlorosuccinate 1a or 1b to TS 3a^‡ or 3b^‡, respectively, together with differential changes (ΔΔq^‡).

Relative stabilities of substituted chlorosuccinate dianions

The isodesmic eqn (1)–(3) provide a means to estimate the stabilities of the methyl-substituted RSs 1b, 1c and 1d relative to 1a; an equal number of C(sp³) and H atoms on both sides of each formal equilibrium is achieved by balancing numbers of ethane and methane molecules. The electronic-energy differences ΔE computed for each isodesmic relation using different methods are presented in Table 2.

1a + C₂H₆ → 1b + CH₄ (1)

1a + 2C₂H₆ → 1c + 2CH₄ (2)

1a + 3C₂H₆ → 1d + 3CH₄ (3)

Table 2 Stabilities (kJ mol⁻¹) of substituted chlorosuccinate dianions 1b, 1c and 1d relative to 1a, estimated by means of isodesmic eqn (1)–(3). For each method the energies are evaluated with the 6-311+G(d,p) basis using geometries optimised with the 6-31+G(d) basis

	MP2 PCM water	MP2 vacuum	B3LYP PCM water	B3LYP+GD3BJ PCM water
1b	−21.4	−33.7	0.9	−45.1
1c	−26.6	−36.0	16.4	−74.6
1d	−30.9	−54.0	38.5	−101.9

---

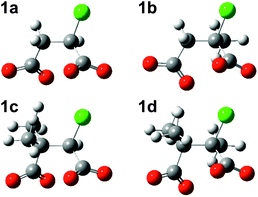
Successive methylation at C2, at C3, and at both C2 and C3 gives rise to increasingly negative ΔE values calculated with the MP2 method in PCM water, meaning that the substituted chlorosuccinate dianionic RSs 1b, 1c and 1d become more stable relative to 1a. The optimised geometries of these four structures (Fig. 3) all display the same conformation in regard to the relative disposition of the two carboxylate groups and the chloride. Although methyl substituents are usually considered to be electron-donating groups, in this case each methyl group in the substituted chlorosuccinate dianions acquires a net negative charge, with the result that unfavourable interelectronic repulsions are reduced as charge is spread more evenly around the molecule. Thus the single methyl substituent at C2 in 1b and 1d possesses a net charge of −0.19 and −0.31, respectively, and the two at C3 in 1c and 1d have combined net charges of −0.62 and −0.65.

Fig. 3 MP2/6-31+G(d) optimised structures for chlorosuccinate dianions 1a–1d in PCM water.

The relative stabilities at the MP2 level in vacuum are larger in magnitude but follow the same trend. However, Table 2 shows that the B3LYP method in PCM water predicts the opposite trend; this is because this density functional method does not correctly describe dispersion interactions between the various groups within these molecules.²³ Inclusion of the GD3BJ correction for dispersion recovers the same trend as MP2. Our previous study¹² of the relative energies for 3a^‡vs. 4a^‡ employed the B3LYP method with the same 6-31+G(d) basis as used in this work but gave a very similar result to that obtained with MP2. It is now evident that the agreement was fortuitous: apparently the contribution of dispersion interactions to the relative barriers for α- and β-lactone formation from unsubstituted chlorosuccinate 1a is very small.

Note that alternative isodesmic schemes could be employed. For example, ethane and methane in eqn (1)–(3) could be replaced by propane and ethane, respectively, to reduce the so-called “end effect”: this would increase the values of the stabilisation energies by about 10 kJ mol⁻¹ per methyl group for MP2 in PCM water, but would not change the relative stability order. The purpose of these calculations is simply to demonstrate the inadequacy of B3LYP without corrections for dispersion, as this method gives a completely wrong order of relative stabilities. In the MP2 method these interactions are captured by the perturbative treatment of electron correlation. However, it should also be noted that this deficiency of B3LYP is not evident for reactions of the unsubstituted compound 1a in which intramolecular dispersion effects are not very important. The results of the earlier study of the relative barriers for α- and β-lactone formation from 1a (summarised in the Introduction) remain valid (see the ESI† for further analysis).

Kinetic isotope effects

Isotopic substitution with ¹⁴C at position 2 gives rise to MP2-PCM/6-31+G(d) calculated primary KIEs ¹²k/¹⁴k for β-lactone formation with magnitudes (Table 3, 298 K) entirely in accord with expectation for (intermolecular) reactions following the S_N2 mechanism.²⁴ The values are all >1.1 but diminish with increasing methylation of the chlorosuccinate substrate. The degree of diminution does not simply follow the increase in mass but depends upon the position of the methylation. Methyl substitution at C2 gives rise to smaller contributions to the KIE from both the semi-classical factor (SC, as mirrored by the magnitude of the vibrational frequency for symmetric C⋯O/C⋯Cl stretching of the making and breaking bonds for the ¹²C2 TSs) and the much-smaller quantum-tunnelling factor (QC, which correlates with the magnitude of the imaginary frequency for asymmetric C⋯O/C⋯Cl stretching). The semi-classical contribution to these primary KIEs reflects the symmetry of the TSs: near maximal values arise when there are approximately equal contributions from both the making and breaking bonds in the symmetric stretching mode, which then involves almost no motion of the isotopically-labelled C atom. The essentially equal Pauling bond orders n_O–C and n_C–Cl in the TSs for β-lactone formation were already noted above.

Table 3 MP2/6-31+G(d) kinetic isotope effects ¹²k/¹⁴k (298 K) for intramolecular nucleophilic displacements reactions in PCM water of substituted chlorosuccinate dianions labelled at C2 leading to α-lactones via TSs 3a^‡–3d^‡ and to β-lactones via TSs 4a^‡–4d^‡. Natural logarithms of the semi-classical (SC) and quantum-tunnelling (QC) factors are presented together with vibrational frequencies (cm⁻¹) for symmetric (sym) and asymmetric (asym) stretching of the making C⋯O and breaking C⋯Cl bonds

	3					4
	^12 k/^14k	ln(SC)	sym	ln(QC)	asym	^12 k/^14k	ln(SC)	sym	ln(QC)	asym
a	1.094	0.0806	236	0.0090	433i	1.127	0.0917	235	0.0276	625i
b	1.071	0.0619	181	0.0064	371i	1.106	0.0782	186	0.0225	572i
c	1.065	0.0584	211	0.0044	365i	1.119	0.0862	230	0.0266	604i
d	1.049	0.0437	185	0.0037	335i	1.104	0.0776	164	0.0217	548i

---

The same ¹⁴C substitution at C2 gives rise to MP2-PCM/6-31+G(d) calculated primary KIEs ¹²k/¹⁴k for α-lactone formation with considerably lower magnitudes, all <1.1 (Table 3, 298 K). This reflects the less symmetric nature of the respective TSs, as also shown by the unequal Pauling bond orders for the making and breaking bonds (n_O–C > n_C–Cl). Variation in the semi-classical contribution to the KIE is not followed by the value of the symmetric stretching frequency. The tunnelling factor is an order of magnitude smaller but does correlate with the imaginary frequency for asymmetric stretching.

Concluding remarks

α-Lactones are Cinderella species, whose existence is often overlooked. Despite producing experimental evidence for its involvement as a key reaction intermediate in hydrolysis of α-bromopropionate at low hydroxide concentration, Ingold did not name it as an α-lactone.^6,25 Owing to their high reactivity, these are indeed elusive species, but it has been demonstrated that they are involved as the first-formed intermediate in bromination of the dianions of 2,3-dimethylmaleic and 2,3-dimethylfumaric acids in water at room temperature, but then undergo rearrangement to more-stable β-lactone products.⁹ A motivation for the present study was to determine if appropriate alkyl substitution might affect the relative barriers for competitive formation of α- or β-lactones by nucleophilic displacement at sp³ carbon rather than sp². The computational results presented here do suggest that the difference between the free energies of activation for 3MR and 4MR formation from 2-chloro-2-methylsuccinate is very small. Perhaps substituents larger than methyl might swing the balance in favour of α-lactone formation. The potential significance for synthetic chemistry is the possibility that trapping of α-lactone might lead to a different and useful product. The clear difference in magnitude of the ¹⁴C KIE at the site of nucleophilic displacement suggests a possible experimental test to discriminate between α- or β-lactone-formation as being rate-determining in competitive intramolecular reactions.

More detailed mechanistic insight for these competing reactions under simulated experimental conditions, with different values of pH, would require explicit treatment of solvation and consideration of alternative protonation states beyond the remit of the present study, the purpose of which is to consider intramolecular competition that exists only for the doubly ionised succinates. An important finding is that the standard B3LYP method without dispersion corrections does not provide reliable estimates of the relative stabilities of the methyl-substituted dianions, in contrast to the MP2 method which captures intramolecular dispersion interactions by means of its perturbative treatment of electron correlation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

EPSRC is thanked for a DTA Studentship (PBW) and the University of Bath for access to its High-Performance Computing Facility. Professor J. Grant Buchanan (1926–2012) suggested the idea for this study to IHW on the evening before he died; we dedicate this paper to his memory.

Notes and references

1. R. Bauer, Drug Discovery Today, 2015, 20, 1061–1073.
2. K. Camara, S. S. Kamat, C. C. Lasota, B. F. Cravatt and A. R. Howell, Bioorg. Med. Chem. Lett., 2015, 25, 317–321.
3. J. K. Christenson, J. E. Richman, M. R. Jensen, J. Y. Neufeld, C. M. Wilmot and L. P. Wackett, Biochemistry, 2017, 56, 348–351.
4. B. Holmberg, Ber. Dtsch. Chem. Ges., 1912, 45, 1713–1715.
5. P. Walden, Ber. Dtsch. Chem. Ges., 1896, 29, 133–138.
6. W. A. Cowdrey, E. D. Hughes, C. K. Ingold, S. Masterman and A. D. Scott, J. Chem. Soc., 1937, 1252–1271.
7. S. Winstein, J. Am. Chem. Soc., 1939, 61, 1635–1640.
8. J. J. Robinson, J. G. Buchanan, M. H. Charlton, R. G. Kinsman, M. F. Mahon and I. H. Williams, Chem. Commun., 2001, 485–486.
9. N. Pirinççioğlu, J. J. Robinson, M. F. Mahon, J. G. Buchanan and I. H. Williams, Org. Biomol. Chem., 2007, 5, 4001–4009.
10. G. D. Ruggiero and I. H. Williams, Chem. Commun., 2002, 732–733.
11. J. G. Buchanan, G. D. Ruggiero and I. H. Williams, Org. Biomol. Chem., 2008, 6, 66–72.
12. J. G. Buchanan, R. A. Diggle, G. D. Ruggiero and I. H. Williams, Chem. Commun., 2006, 1106–1108.
13. M. E. Jung and G. Piizzi, Chem. Rev., 2005, 105, 1735–1766.
14. R. M. Beesley, C. K. Ingold and J. F. Thorpe, J. Chem. Soc., Dalton Trans., 1915, 1080–1106.
15. Z. Yongpeng and X. Jiaxi, Prog. Chem., 2014, 26, 1471–1491.
16. A. L. Ringer and D. H. Magers, J. Org. Chem., 2007, 72, 2533–2537.
17. S. M. Bachrach, J. Org. Chem., 2008, 73, 2466–2468.
18. J. Kostal and W. L. Jorgensen, J. Am. Chem. Soc., 2010, 132, 8766–8773.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian Inc., Wallingford, CT, 2009.
20. I. H. Williams and P. B. Wilson, SoftwareX, 2017, 6, 1–6.
21. C. Galli and L. Mandolini, Eur. J. Org. Chem., 2000, 3117–3125.
22. (a) G. A. Craze, A. J. Kirby and R. Osborne, J. Chem. Soc., Perkin Trans. 2, 1978, 357–368; (b) B. L. Knier and W. P. Jencks, J. Am. Chem. Soc., 1980, 102, 6789–6798.
23. (a) M. D. Wodrich, C. Corminboeuf and P. v. R. Schleyer, Org. Lett., 2006, 8, 3631–3634; (b) H. Kruse, L. Goerigk and S. Grimme, J. Org. Chem., 2012, 77, 10824–10834; (c) P. R. Schreiner and J. P. Wagner, Angew. Chem., Intl. Ed., 2015, 54, 12274–12296.
24. K. C. Westaway, Adv. Phys. Org. Chem., 2006, 41, 217–273.
25. C. K. Ingold, Structure and Mechanism in Organic Chemistry, Cornell University Press, Ithaca, 1953.

---

Footnote

† Electronic supplementary information (ESI) available: Including geometrical coordinates and energies for all optimised structures. See DOI: 10.1039/c7ob01653k

---