Formation of amorphous calcium carbonate and its transformation into mesostructured calcite†
Carlos
Rodriguez-Navarro
*a,
Krzysztof
Kudłacz
b,
Özlem
Cizer
c and
Encarnacion
Ruiz-Agudo
a
aUniversity of Granada, Department of Mineralogy and Petrology, Granada, Spain. E-mail: carlosrn@ugr.es
bInstitute of Metallurgy and Materials Science, Polish Academy of Sciences, Reymonta 25, 30-059 Kraków, Poland
cKU Leuven, Department of Civil Engineering, Leuven, Belgium
First published on 28th October 2014
Abstract
Amorphous calcium carbonate (ACC) is a key precursor of crystalline CaCO3 biominerals and biomimetic materials. Despite recent extensive research, its formation and amorphous-to-crystalline transformation are not, however, fully understood. Here we show that hydrated ACC nanoparticles form after spinodal liquid–liquid phase separation and transform via dissolution/(re)precipitation into poorly hydrated and anhydrous ACC nanoparticles that aggregate, forming a range of 1D, 2D and 3D structures. The formation of these structures appears to be achieved by oriented attachment (OA), facilitated by the calcite medium-range order of ACC nanoparticles. Both electron irradiation processes in the TEM and under humid air exposure at room temperature of the latter ACC structures result in pseudomorphs of single crystalline mesostructured calcite. While the high-vacuum/e-beam heating leads to solid-state transformation, the transformation in air occurs via an interface-coupled dissolution/precipitation mechanism. Our results differ significantly from the currently accepted model, which considers that the low T ACC-to-calcite transformation in air and during biomineralization is a solid-state process. These results may help to better understand how calcite biominerals form after ACC and offer the possibility of biomimetically preparing single crystalline calcite structures after ACC by tuning pH2O at room temperature.
Introduction
Questions persist on the mechanism(s) of crystallization of calcium carbonate, the most abundant biomineral and a key chemical, industrial and technological (bio)material.1,2 Growing evidence shows that it follows non-classical nucleation3,4 and growth pathways,1 where amorphous precursor phase(s) play a critical role.5,6 It has been suggested that amorphous calcium carbonate (ACC) forms after binodal7 or spinodal8,9 separation of a (dense) liquid phase.10 This liquid phase may develop after the formation of stable prenucleation clusters (PNC)3,11 that eventually aggregate, forming ACC nanoparticles.4 The formation of such a dense liquid phase preceding ACC can be favored (or stabilized) by organics (i.e., polymer-induced liquid precursor or PILP).6 The resulting biogenic or synthetic ACCs display differences in water content and stability (hydrated vs. anhydrous ACC),12,13 as well as in short- to medium-range order (the so-called polyamorphism)14 that appears to be inherited by or imprinted in the final crystalline polymorph (i.e., calcite, vaterite or aragonite).11 Upon amorphous-to-crystalline phase transition, growth by oriented attachment (OA) of nanocrystal units can take place,15,16 in some cases resulting in CaCO3 crystals composed of mutually oriented nanoparticle units, the so-called mesocrystals.17,18 Formation of ACC during biomineralization facilitates the temporal storage of calcium and carbonate ions by organisms, circumvents the slow ion diffusion characteristic of classical crystal growth, and enables the development of complex, hierarchical crystalline structures not bounded by crystal faces.12,13 Mimicking this advantageous biomineralization strategy, and with the aid of organic (bio)macromolecules, material chemists have achieved oriented calcite thin films,1,19 micropatterned bi-dimensional (2D)20 and three-dimensional (3D)21 porous single crystalline calcite, and nacre-like multilayer organic–inorganic (calcite) hybrid structures with physical-mechanical properties that transcend those of the individual components.22 Despite recent progress, the formation and transformation of ACC is still poorly understood. It is not well known how short- or medium-range order ACC develops and is transferred to the final anhydrous polymorph, and what the exact mechanism(s) of ACC-to-crystalline phase transition is, i.e., dissolution/(re)precipitation vs. solid-state transformation, involving a possible secondary nucleation.23–28 It is also unknown whether OA of amorphous precursor nanoparticles can take place prior to the transformation of the aggregate into a single crystal (or mesocrystal). Although this is a possibility not contemplated in current OA models, it has been recently suggested that particles with little or no long-range order may adopt favorable configurations prior to the attachment step.29 Overall, this lack of fundamental knowledge not only precludes a better understanding of biomineralization processes, but it is also an important handicap for the bottom-up development of novel biomimetic functional materials and structures using ACC precursors, a long-pursued objective in material chemistry. In order to gain a basic understanding of how ACC forms and transforms, it is necessary to study simple systems that lack (bio)macro-molecules1,6,12 or other additives (e.g., silica,30 magnesium,31 or phosphates32), which affect the precipitation and stability of ACC and add an additional level of complexity.Here we study the formation, aggregation, and transformation of ACC into crystalline CaCO3 (calcite) in saturated Ca(OH)2 solutions subjected to carbonation at room temperature according to the overall reaction Ca(OH)2 + CO2 = CaCO3 + H2O.33 This reaction enables the study of CaCO3 precipitation in an additive-free aqueous system without interference from background electrolytes, and following CO2 diffusion/dissolution, which commonly occurs during in vitro and in vivo ACC formation.34 Our in situ and ex situ analysis of precipitates, in combination with the study of the solution chemistry evolution (see Experimental section), enable us to get a complete and detailed picture of the different stages of formation and transformation(s) of ACC, both in solution and in air (as well as under high vacuum), to finally produce crystalline CaCO3. Based on the results of this study, we propose a model for the formation, aggregation and transformation of ACC into calcite, which may have important implications in understanding calcium carbonate biomineralization and in the biomimetic synthesis of novel calcite functional materials.
Experimental section
Solutions and crystallization of CaCO3
Saturated solutions (20 mM) were prepared at room temperature by dissolving Ca(OH)2 crystals in Milli-Q water (resistivity >18 mΩ) under vigorous stirring for 24 h in a sealed plastic bottle with no head space. Carbonation tests were performed by placing solution droplets (5 to 200 μl) on different supports (see below) and exposing them to atmospheric CO2 at room temperature. The use of such small solution volumes enabled the in situ analysis of precipitation/dissolution events using the range of analytical techniques described below. Droplets subjected to different carbonation times were quenched in ethanol26 or freeze-dried35 (plunge freezing in liquid N2 and subsequent vacuum drying at −50 °C using a Telstar Cryodos equipment) prior to analysis using TEM (see below). Note that such quenching procedures, which are routinely used during the study of ACC, reportedly produce no detectable artifact or drying-induced textural/structural transformations.26,35,36 Ion-selective microelectrodes (ISE) were used for on-line measurement of pH (micro combination electrode model PHR-146B, Lazar Laboratories) and free calcium concentration, [Ca] (micro-ISE model LIS-146CACM with a microdouble junction reference electrode model DDM-146, Lazar laboratories) during carbonation in 200 μl droplets. Microelectrodes were calibrated using standard pH buffered solutions and CaCl2 solutions of known concentration (0.1 to 100 mM). Prior to testing, the electrodes (including the Ca reference electrode) were immersed in Ca(OH)2 saturated solutions for at least 30 min in order to obtain constant readings. The concentration of total dissolved CO2 was measured using a CO2-selective electrode (Thermo Scientific, model 9502BNWP). Because this latter measurement required a minimum solution volume of 5 ml, carbonation of several 200 μl droplets was performed simultaneously, quenching each droplet at predetermined time intervals by adding 5 ml of Milli-Q water and measuring dissolved CO2 immediately after quenching and acidification to a final pH of 5.2 (achieved by adding 0.5 ml of carbon dioxide buffer, i.e., aqueous solution of trisodium citrate, citric acid and sodium chloride, Thermo Fisher Scientific). A minimum of three replicas of each measurement/test were performed.Additional carbonation experiments were performed using a batch reactor (7 cm internal diameter batches, filled with 150 ml of Ca(OH)2 saturated solution). Carbonation took place upon air exposure at 20 °C under continuous stirring (magnetic stirrer set at 150 rpm). Measurements of pH and [Ca], as well as total dissolved CO2, were performed as in the case of droplets. Following precipitation, suspension aliquots (ca. 5 ml) were collected at different reaction times and vacuum filtered or freeze-dried (as described above) prior to storage under dry conditions. Batch reactor tests enabled us to collect sufficient amounts of precipitate for ex situ analyses (see below). Note, however, that the surface/volume ratio in batch reactors was considerably smaller (0.25 cm−1) than that in droplets (13 and 44 cm−1 for 200 and 5 μl droplets, respectively), thus resulting in slower precipitation and evaporation kinetics.
In situ micro-Raman and polarized light microscopy analyses
10 μl droplets of Ca(OH)2 saturated solution were deposited on an ultraclean [100]-oriented silicon wafer (Virginia Semiconductor Inc.) and exposed to air at room temperature inside the chamber of a Jasco NRS-5100 micro-Raman spectrometer equipped with a CCD detector (DV420-OE, Peltier-cooled, 1024 × 255 pixel UV–NIR range), an integrated Olympus optical microscope and a high-resolution built-in CMOS camera. Microscopic observations were performed simultaneously with micro-Raman spectra acquisition (excitation with a 4 mW power diode laser operated at 532 nm or 785 nm; frequency range 100–3900 cm−1; spectral resolution of 4 cm−1). Averaged values of five spectra (10 s acquisition time) for each analyzed spot are reported here. Calibration was performed using the 520.5 cm−1 band of the silicon wafer.Polarized light microscopy (Olympus BX60 equipped with a digital camera) was used to study the crystallinity and morphology of solid phases, as well as their evolution during carbonation. Sample and carbonation conditions were similar to those prevailing in micro-Raman experiments, with the difference that in the former case solution droplets were placed either on Si wafers (observed under reflected light) or on glass slides (observed under transmitted light).
In situ XRD
The time evolution of precipitate formation was analyzed in situ by XRD. Droplets of Ca(OH)2 saturated solution (200 μl) were placed onto a zero-background silicon sample holder, which was subsequently placed inside the chamber of a Philips X'Pert Pro X-ray diffractometer. Carbonation took place at the solution/air interface following exposure to air, at room temperature and pCO2 ~ 10−3.5 atm. Real-time precipitation of calcium carbonate was monitored with continuous acquisition of XRD patterns with Cu Kα radiation (λ = 1.5405 Å), a 2θ range of 10 to 50° and a scanning rate of 0.11° 2θ s−1. This scanning speed (~6 min per diffractogram) was validated to be reliable for the detection of the crystalline phases of calcium carbonate. The variation in the amount of calcite and ACC vs. time was determined by measuring the integral intensity of the main 104 Bragg peak of calcite and the broad humps corresponding to the amorphous phase after background subtraction (including the water contribution to the broad peaks at 2θ = 25–35° and 2θ = 40–45°).In situ ESEM analysis
A FEI Quanta 400 ESEM equipped with a Peltier cooling stage was used to investigate the microstructural features of calcium carbonate phases precipitated after partial carbonation of 5–10 μl droplets of Ca(OH)2 saturated solution exposed to air for 2 to 7 min, after ambient air was progressively replaced by water vapor in the ESEM chamber (pH2O = 6.5 Torr at 3 °C). To simulate the evolution of the system during continuous evaporation of solution droplets (i.e., as it occurs in air during in situ optical microscopy, XRD and micro-Raman experiments), water was allowed to evaporate from the sample by lowering pH2O to 2.5 Torr at 3 °C.Ex situ TG/DSC, XRD, FTIR and FESEM analyses
Solids collected at different time intervals during batch reactor carbonation experiments were subjected to simultaneous thermogravimetry (TG) and differential scanning calorimetry (DSC) analysis on a Mettler Toledo model TGA/DSC1. About 10–20 mg of sample mass was deposited on Pt crucibles and analyzed under flowing air (100 ml min−1) at 10 °C min−1 heating rate, from 25 to 950 °C (TG) or 25 to 400 °C (DSC). Additionally, solids were deposited on zero-background Si sample holders and analyzed on a Philips X'Pert Pro X-ray diffractometer equipped with Cu Kα radiation (λ = 1.5405 Å) at 2θ range between 3 and 70° and at a scanning rate of 0.002° 2θ s−1. Precipitates were also analyzed on a JASCO 6200 FTIR (frequency range 400–4000 cm−1; 4 cm−1 spectral resolution) equipped with an attenuated total reflectance (ATR) device for spectra collection without sample preparation (i.e., minimizing artifacts such as dehydration of ACC). Finally, solids were observed at high magnification using a scanning electron microscope equipped with a field emission gun (FESEM; Zeiss SUPRA40VP). Samples were carbon-coated prior to FESEM observation.TEM-SAED analysis
Analysis of the morphology, size, and proto-structure of ACC precursor phases was performed by means of transmission electron microscopy (TEM) using a Philips CM20, operated at 200 kV and a FEI Titan, operated at 300 kV. Prior to TEM observations, 25 μl droplets of saturated Ca(OH)2 solution were deposited on PVC crystallization dishes and exposed to air at room temperature. Following 5 s to 30 min air exposure, calcium carbonate precipitation was quenched by addition of ethanol. Alcohol dispersions were deposited on carbon/Formvar® film-coated copper or nickel grids. Additional tests were performed by quenching Ca(OH)2 solutions at different carbonation times by plunge-freezing in liquid N2 and vacuum-drying. Afterwards, solids were collected, dispersed in ethanol and deposited on carbon/Formvar® film-coated copper or nickel grids. No significant textural or microstructural differences were observed in ACC phases when comparing the samples prepared following ethanol quenching vs. freeze-drying. TEM observations were performed using a 40 μm (CM20) or a 30 μm (Titan) objective aperture. SAED patterns were collected using a 10 μm aperture, which allowed collection of diffraction data from a circular area ca. 0.2 μm in diameter. In situ decomposition of ACC due to focused electron beam irradiation was also observed in the TEM. In the case of the CM20 equipment, the electron flux was maximized using a large (200 μm) condenser aperture and a focused beam spot size of ~200 nm, thus providing an estimated electron flux of ca. 50–70 A cm−2. Under these conditions, full conversion was achieved after ~90 s exposure. In the case of the Titan equipment and due to the higher acceleration voltage (300 kV), decomposition was achieved following ~30 s focused beam exposure.Simulation of electron scattering patterns of ACC
In order to gain insights into the characteristics of the structural short-to-medium range order of ACC phases, the intensity of pixels in the corresponding SAED patterns was radially integrated (using in-house SAEDP software). This operation allows one to plot the electron scattering intensity as a function of the scattering vector length, k (i.e., the distance in Å−1 from (000) to any point in the reciprocal lattice), and can be considered as an equivalent of the electron powder diffraction pattern (EDP). To these experimental plots, a series of three Pearson VII functions were fitted, including a polynomial function representing the background baseline, in order to estimate the peak profile (i.e., its center – k, and full width at half maximum (FWHM)) and the extent of the short-to-medium range order (~FWHM−1). The estimated FWHM of the first EDP peak for fully hydrated ACC (precipitated during Stage I, see following section) and less hydrated (or anhydrous) ACC (formed during Stage II) corresponded to a size of ~10 Å, which can be interpreted as a cluster size. Cluster sizes ranging from 6 to 16 Å were used in simulations. In agreement with the FWHM results, the best fitting results were obtained using a cluster size of 10 Å during simulations. The shape of the clusters was assumed to be a sphere. Four different arrangements of atoms within the cluster volume were considered during EDP simulation. They corresponded to vaterite, aragonite, calcite and monohydrocalcite. Two sets of simulations were performed, corresponding to the case of randomly oriented clusters and to the case where a possible preferred orientation was developed (i.e., in this latter case the clusters were assumed to possess a particular short- or medium-range order and were aligned along a specific [hkl] direction).The first set of data simulation was performed using the Debye function:37
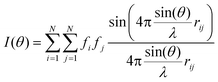 | (1) |
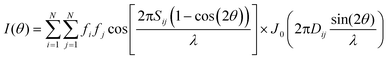 | (2) |
In order to perform the simulation for any arbitrary orientation of the clusters with respect to the electron beam, a change in coordinates has to be performed. The orientation between two Cartesian coordinate systems can be described using Euler angles (φ1, ϕ, φ2). In order to transform one coordinate system into another, it is necessary to perform a set of orientation transformations corresponding to each of the Euler angles according to the equation:
| (x′, y′, z′) = O(φ1, ϕ, φ2) (x, y, z) | (3) |
There are a few different conventions regarding the sequence and the direction of the rotations. Here, one of the most common was used, which involves the consecutive rotation of a set of angles φ1, ϕ, φ2 around the z, x and z axes of the coordinate system subjected to rotation:
| O(φ1, ϕ, φ2) = O(z, φ2)O(x, ϕ)O(z, φ1) | (4) |
As mentioned earlier, different types of cluster internal structures were considered. In order to calculate the different orientations of the cluster according to eqn (4), its lattice (which is non-Cartesian in each case) has to be associated with a Cartesian coordinate system. The applied relationship between the lattice vectors (a, b, c) of the structure considered and the Cartesian axes (x, y, z) is the following: (i) vaterite: a//x and c//z, (ii) aragonite a//x, b//y and c//z, (iii) calcite: a//x and c//z, (iv) monohydrocalcite: a//x and c//z.
The first rotation (i.e., O(z, φ1)) does not change the Sij and Dij values (used in eqn (2)) when the z-axis of the cluster is parallel to the electron beam. Therefore, selection of the initial orientation of the cluster with its z-axis parallel to the electron beam limits the EDP calculation to the two consecutive rotations around the x- and z-axis of the cluster at angles ϕ and φ2, respectively. Therefore the simulation of EDP according to eqn (2) is performed for all orientations described by the equation:
| (x′, y′, z′) = O(z, β)O(x, α)(x, y, z) | (5) |
The procedure for EDP simulation was the following. Initially, the structure (i.e., vaterite, aragonite, calcite or monohydrocalcite) was oriented with its z-axis parallel to the electron beam. Subsequently, the structure was oriented in space according to eqn (5), where α and β were changed every 5°. Finally, the cluster shape (sphere with 6 to 16 Å diameter) was “cut” from the oriented structure and the EDP was simulated according to eqn (2). Ultimately, the agreement between simulated and experimental EDPs was determined by:
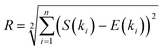 | (6) |
Conversion of ACC into calcite in humid air
ACC solids prepared according to the procedures described above and stored under dry conditions were exposed to humid air in a closed plastic container at 20 °C for 48 h. A relative humidity (RH) of 85% was achieved by placing inside the container a crystallization dish filled with a KCl saturated solution.Calculation of the solubility product (ksp) of anhydrous ACC
Calcium carbonate crystallization typically occurs via the initial formation of metastable phases of higher solubility and lower stability (i.e., with a higher negative value of dissolution enthalpy), which would eventually dissolve when the solution supersaturation drops to their solubility product, and then below this value when the nuclei of another less soluble stable (or metastable) phase reach the critical size and grow at the expense of the dissolving precursor phase.39 Successive transformations occur according to Ostwald's rule of stages until the most stable phase is formed.35 It has been observed that the enthalpy of dissolution, ΔHdiss, of a range of phases shows a linear dependence on the natural logarithm of their solubility (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ksp).40 We plotted published values of ΔHdissvs. ln
ksp).40 We plotted published values of ΔHdissvs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ksp (ESI† Table S1) for the different phases in the CaCO3–H2O system13,32,35,41–43 and observed a good linear correlation (R2 > 0.98) (Fig. S5†). This enabled us to estimate a ksp value of 9.92 × 10−8 for anhydrous ACC using the dissolution enthalpy values measured by Radha et al.13 All values refer to standard temperature and pressure (STP).
ksp (ESI† Table S1) for the different phases in the CaCO3–H2O system13,32,35,41–43 and observed a good linear correlation (R2 > 0.98) (Fig. S5†). This enabled us to estimate a ksp value of 9.92 × 10−8 for anhydrous ACC using the dissolution enthalpy values measured by Radha et al.13 All values refer to standard temperature and pressure (STP).
Note that the synthesis conditions of hydrated ACC used by Rahda et al.13 were highly alkaline, as it is also the case in our system where the formation of hydrated ACC occurred at a high pH (10–12.4) (see below). Therefore, any potential effect that a high OH− concentration could have on the ΔHdiss value of synthetic hydrated ACC reported by Rahda et al.13 would likely be similar in our system. In the case of anhydrous ACC, the dissolution enthalpy does not seem to be affected by the synthesis conditions (i.e., Rahda et al.13 reported similar ΔHdiss values for both abiotic and biogenic anhydrous ACC).
Regarding the ksp value for hydrated ACC, we choose to use the one reported by Clarkson et al.32 (9.1 × 10−7), due to the good agreement with the value independently reported by Ogino et al.,35 and the fact that we obtained a better correlation coefficient when using this value for plotting ΔHdissvs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ksp than when using the often quoted ksp value by Brečević and Nielsen44 (4.0 × 10−7) or those reported by Gebauer et al.4 (3.1 × 10−8 for ACCI and 3.8 × 10−8 for ACCII). Note that the discrepancies in the reported values for ACC solubility are a matter of current discussion and are probably due to compositional and/or structural differences in ACC (polyamorphism) associated with the different precipitation conditions in each study.45
ksp than when using the often quoted ksp value by Brečević and Nielsen44 (4.0 × 10−7) or those reported by Gebauer et al.4 (3.1 × 10−8 for ACCI and 3.8 × 10−8 for ACCII). Note that the discrepancies in the reported values for ACC solubility are a matter of current discussion and are probably due to compositional and/or structural differences in ACC (polyamorphism) associated with the different precipitation conditions in each study.45
Calculation of the saturation index using the PHREEQC computer code
The time evolution of the saturation index, SI (SI = log(IAP/ksp), where IAP and ksp are the ion activity product and the solubility product of a relevant phase, respectively) with respect to the crystalline anhydrous CaCO3 polymorphs observed in our experiments (vaterite and calcite), as well as the hydrated and anhydrous ACC was calculated using PHREEQC,46 for the different values of pH, [Ca], and [CO2] determined experimentally. All calculations were performed considering STP conditions. Note that for the calculation of [CO32−] from the experimentally measured total dissolved CO2, the speciation of all carbonate species at the measured pH values was calculated. However, the calculated [CO32−] used for SI calculation at a particular point in time during calcium carbonate precipitation typically yielded charge unbalance (i.e., overestimation of [CO32−] due to dissolution and hydration of CO2 during the interval between sampling and analysis of total dissolved CO2). Thus, charge balance was forced during SI calculation using PHREEQC. For the calculation of SI, we used published ksp values of calcite, vaterite and hydrated ACC (see Table S1 in the ESI†). In the case of anhydrous ACC, we used the ksp value calculated according to the procedure described above.Results and discussion
In situ analysis of ACC formation and transformation
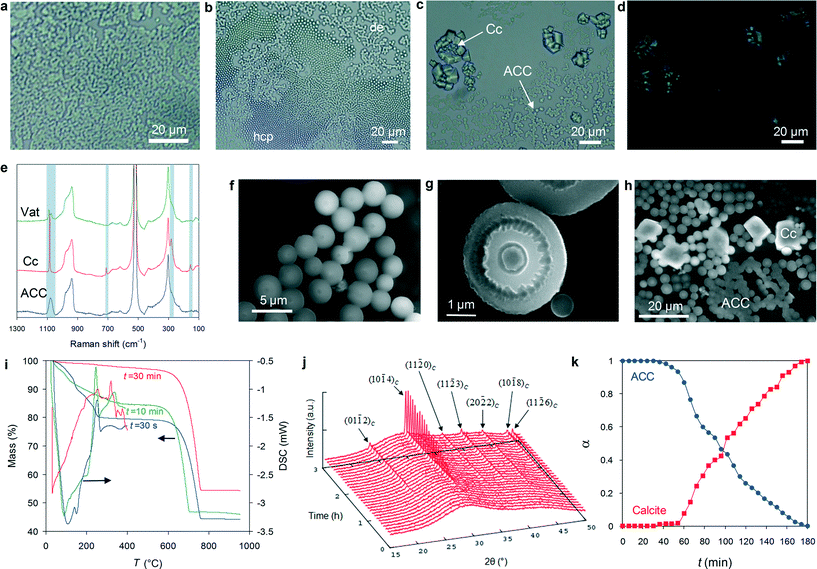
In situ time-lapse polarized light microscopy (PLM) reveals that exposure to atmospheric CO2 of Ca(OH)2 solution droplets (5 to 200 μl) deposited on Si wafers or glass slides results in the nearly instantaneous (<3 s) formation of convoluted structures at the air/solution interface (Fig. 1a). They display the characteristic channel-like bicontinuous patterns of structures formed following liquid–liquid spinodal phase separation in a homogeneous system, in contrast to the structures resulting from binodal demixing or homogeneous nucleation characterized by separate nuclei surrounded by a continuous phase.11 A prerequisite for spinodal liquid–liquid separation is that the system must reach a supersaturation high enough to bypass the binodal.5,8 Our system fulfils this prerequisite as it is highly supersaturated with respect to all CaCO3 phases at the initial stages of precipitation (see the section on Evolution of solution chemistry, below). Subsequently, micrometer sized non-birefringent hemispheres with micro-Raman spectra consistent with ACC form at the air–solution interface at the expense of the dense liquid precursor and rapidly self-assemble, forming either dendritic or hexagonal close-packed aggregates (colloidal crystals) (Fig. 1b and e).After ca. 30–50 min (depending on droplet size), massive dissolution of ACC particles leads to the precipitation at the air–solution interface of abundant calcite rhombohedra and trace amounts of vaterite (Fig. 1c–e). A similar mechanism involving the dissolution of ACC particles preceding the formation of calcite was first observed in situ at high magnification by Rieger et al. using X-ray microscopy.47
At the edge of the drying droplets, iridescent (non-birefringent) ACC films are observed on the substrate (Fig. S1a†). Under the FESEM, such films show a hexagonal closed packed structure made up of ACC spheres (confirmed by Raman spectroscopy; Fig. S1b†) ca. 50–150 nm in size (Fig. S1c and d†), a structure similar to that previously reported for ACC thin films.48 Because these films only appear at the droplet edge, their self-assembly is related to convective transport and capillary attraction between ACC nanoparticles induced by the receding meniscus of the drying liquid film.49 In some areas of the ACC film, calcite rhombohedra are observed, surrounded by precipitate-free circular halos (Fig. S1a†). This observation shows that calcite formed after ACC via a dissolution/precipitation mechanism.50
In situ environmental scanning electron microscopy (ESEM) shows high magnification details of the early (5–15 min carbonation time) development and aggregation of micrometer-sized ACC hemispheres (Fig. 1f–h), very similar to “ACC microlens arrays”,51 as well as some spheres formed in the bulk solution (Fig. S2†). After ca. 20–30 min, the non-homogeneous dissolution of ACC hemispheres discloses their onion-like internal structure (Fig. 1g and S3†). This structure is associated with sequential (discontinuous) precipitation events, that is, the growth of successive layers surrounding an initial core takes place at elapsed time intervals (most likely when the supersaturation in the system rises again after each precipitation event, as it occurs during the development of Liesegang patterns).52 The fact that the core dissolves faster than the outer shell(s) suggests that the solubility of ACC decreases from the core to the surface and may help to explain how hollow-shell ACC spheres (Fig. S3d†), as well as “doughnut-like” ACC structures (see TEM results below) resulting from the partial dissolution of ACC hemispheres, form during this dissolution stage.53 This is interpreted as a time-dependent change in the structure and hydration of ACC,36 consistent with TG/DSC analyses showing a progressive decrease in the water content of ACC from ~1.4 to ~0.4 mol H2O per formula unit at 30 s and 30 min carbonation time, respectively (Fig. 1i). The less hydrated and more stable ACC13 precipitates in solution either as an overgrowth on pre-existing ACC hemispheres and spheres (ESEM results) or as more ordered new 1D and 2D structures, as shown by TEM analyses (see below). This interpretation is consistent with recent polarized Raman spectroscopy analysis showing that the rim of hemispherical ACC microlens includes oriented carbonate groups, which are absent in the fully amorphous core.51 It is also consistent with recent results showing that ACC undergoes a continuous transition from more hydrated (ca. 20 wt% H2O) to less hydrated (nearly anhydrous) phases in solution at room temperature.54 Based on time-resolved wide angle X-ray scattering (WAXS), Bots et al.36 suggested that such dehydration involved an increase in the local order of ACC and was driven by an increase in enthalpy of ACC. However, the actual mechanism responsible for ACC “dehydration” in solution at room temperature was not clarified. By analogy with thermally activated ACC dehydration in air, it has been assumed to be a solid-state transformation.54 This mechanism, however, requires very high activation energies (80–245 kJ mol−1)54 to operate, making dehydration of ACC in solution at room temperature via a solid-state process highly unlikely. Based on our experimental observations (including the evolution of solution chemistry, see below), we conclude that in our system the formation of less hydrated and anhydrous ACC after hydrated ACC in solution at room temperature is a dissolution/(re)precipitation process.
ESEM analyses also show that ACC particles finally transform into rhombohedral calcite via a dissolution/(re)precipitation mechanism.20,35,50 This is clearly shown by Fig. 1h, where partially dissolved ACC spheres are in contact with newly formed calcite rhombohedra, as well as by the above mentioned optical microscopy observations showing calcite rhombohedra surrounded by an ACC-free halo (Fig. S1a†). Such a dissolution/(re)precipitation mechanism is consistent with time-resolved XRD patterns collected in situ during carbonation of 200 μl droplets. They initially display two broadened maxima at ~20–35° 2θ and 40–45° 2θ (Fig. 1j), corresponding to the sum of the scattering intensity of water and ACC phase(s), and eventually show the emergence (after ~40–50 min) of calcite 104 Bragg peak. As the amount of calcite increases, a clear decrease in the amount of ACC is observed, as calculated by the integral intensity of calcite Bragg peaks and ACC scattering patterns after subtraction of the scattering contribution of water (Fig. 1k). Note that despite the fact that evaporation was taking place during in situ XRD data collection, an effect that could lead to supersaturation with respect to Ca(OH)2, no Bragg peaks corresponding to this phase were observed. Its absence is consistent with the fast kinetics of ACC precipitation (and the resulting pH drop, see below), which do not enable portlandite crystallization.
Evolution of solution chemistry
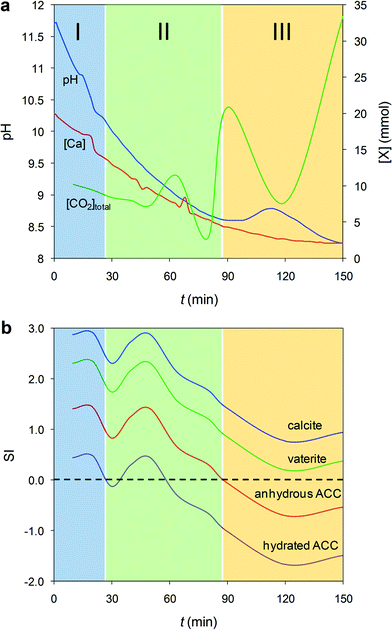
In parallel to the previous in situ experiments, we recorded the time-dependent variation of pH and [Ca2+], as well as total dissolved CO2, during precipitation in 200 μl droplets (Fig. 2a) and in batch reactors, where a similar precipitation trend is observed (Fig. S4†). This enabled us to calculate the evolution of the saturation index, SI, with respect to calcite, vaterite, hydrated ACC and anhydrous ACC phases (see Experimental section for details of the calculation of SI, ksp of anhydrous ACC – see also Fig. S5† − and PHREEQC computer simulation). Three stages in SI evolution are observed regardless of solution volume/geometry (Fig. 2b). During Stage I, the system is highly supersaturated with respect to all phases considered. As a consequence, formation of (hydrated) ACC is very rapid and proceeds via the reactions: Ca2+ + CO2 + H2O → Ca2+ + H2CO3 → Ca2+ + H+ + HCO3− → Ca2+ +2H+ + CO32− → 2H+ + CaCO3(nH2O),51 which reduce both pH and [Ca] (Fig. 2a). Note that due to the very high IAP, prior to the formation of ACC during Stage I, a dense liquid precursor phase forms (spinodal decomposition), as shown in Fig. 1a. The IAP of this liquid phase is unknown, so it is not possible to yield the actual SI of ACC with respect to such a dense liquid phase. In fact, it has been pointed out that there is no constant solubility product describing the liquid–liquid coexistence line in binodal separation or spinodal decomposition.11 Thus, values in Fig. 2b represent the SI of calcium carbonate phases with respect to the bulk solution. Note also that the maxima and minima of the SI shown in Fig. 2b do not necessarily match the maxima and minima of the plot in Fig. 2a. This is due to the fact that the SI with respect to the different phases not only depends on the activity of Ca2+, but also on the activity of CO32−, whose speciation is strongly pH-dependent. During Stage II, the system reaches undersaturation with respect to hydrated ACC, while it is still supersaturated with respect to anhydrous ACC (Fig. 2b). This facilitates the precipitation of less hydrated and anhydrous ACC at the expense of the dissolution of hydrated ACC via the reaction CaCO3·nH2O + CO2 = Ca2+ +2HCO3− + nH2O, in agreement with the time evolution of: (i) the observed fluctuations in pH, [Ca] and total dissolved CO2 (Fig. 2a). The latter, in particular, shows a significant concentration increase associated with hydrated ACC dissolution, followed by a decrease due to the precipitation of less hydrated and/or anhydrous ACC; (ii) TG results showing the formation of less hydrated ACC phases over time (Fig. 1i); and (iii) the preferential dissolution of the core vs. the shell layers of ACC particles observed using ESEM (Fig. 1g). Finally, during Stage III the system is undersaturated with respect to all ACC phases but supersaturated with respect to the crystalline polymorphs (Fig. 2b). This is due to the precipitation of calcite (and minor vaterite) that triggers the dissolution of the remaining ACC. This is reflected in the pH increase and subsequent decrease, as well as the initial increase of total dissolved CO2 (i.e., ACC dissolution) and its subsequent decrease (i.e., massive precipitation of calcite and minor vaterite), as shown in Fig. 2a. Finally, the system approaches equilibrium (i.e., towards the solubility of the most stable phase, calcite), but still the total dissolved CO2 keeps increasing due to further dissolution of atmospheric CO2. Overall, these results confirm that the formation of calcium carbonate in concentrated aqueous solutions is dominated by kinetic effects and follows the Ostwald's rule of stages,35 but for the first time we show that the precipitation of less hydrated and thermodynamically more stable intermediate ACC phase(s)13,36 is associated with the dissolution of more hydrated (more soluble, and therefore less stable) ACC.Unveiling the nanostructure and medium-range order of ACC using TEM-SAED
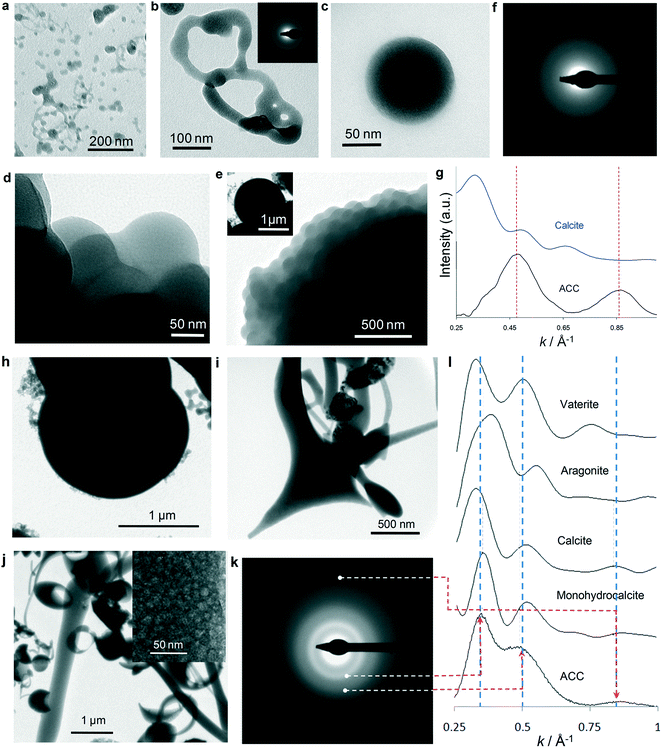
To gain an insight into the (nano)structural features of the different precipitates formed, droplets (5–25 μl) and aliquots collected from batch reactor tests (150 ml) subjected to carbonation for different periods of time were quenched in ethanol or freeze-dried and analyzed using TEM and selected area electron diffraction (SAED) (Fig. 3). Fig. 3a and b show the initial precipitates (<5 s CO2 exposure time), which display shapeless structures resembling a “solidified” dense liquid (emulsion-like) precursor phase.9 Scattered ACC spheres, ca. 5–10 nm in size, are also visible (Fig. 3a). Our TEM observations are consistent with the formation of a dense liquid phase after spinodal decomposition (i.e., optical microscopy results) followed by the formation of ACC particles. It is however unclear how the dense liquid-to-ACC transition takes place. Two plausible mechanism can be envisioned: (i) breaking up into droplets (as in the case of emulsions) followed by partial dehydration to form ACC,9 or (ii) nucleation of ACC within the dense liquid phase. Interestingly, in some areas particles with darker contrast and a better defined spherical morphology are observed (Fig. 3a), which are connected with a less dense (lighter contrast) shapeless lath- or neck-like structure. A similar structure was observed by Rieger et al.9 using cryo-TEM. The authors indicate that after an initial emulsion–liquid or liquid–liquid structure, a less dense and less structured phase connecting ACC particles developed, and concluded that this proved that the dense liquid-to-ACC transformation occurred by densification via expulsion of water, in agreement with recent experimental and computational studies.5 Such a model for the formation of ACC after a dense liquid phase is consistent with our TEM observations. However, we cannot rule out the possibility of ACC nucleation within the liquid phase. The latter process could also result in the formation of ACC particles surrounded/connected by a residual liquid precursor if the transformation is quenched before completion. Droplets quenched after 5 min carbonation show abundant spherical ACC particles (20–100 nm in diameter) (Fig. 3c). Over time (up to 10–20 min carbonation time) these latter nanoparticles aggregate into larger micro-meter-sized structures (Fig. 3d and e) with an overall spherical (or hemispherical) geometry (inset in Fig. 3e). SAED patterns confirm that all structures formed up to this point are ACC (inset in Fig. 3b and f).To check whether ACC precipitates possess a specific crystalline protostructure (that is, short- to medium-range order), SAED analyses and simulations were performed on the scattering function of non-oriented and oriented nanostructured ACC with short- to medium-range order corresponding to the different CaCO3 crystalline polymorphs (see Experimental section for details). The radially integrated electron diffraction patterns (EDPs) of initial ACC precipitates (e.g., ACC particle in Fig. 3c) show poor matching with the calculated scattering patterns of (non-oriented and oriented) crystalline phases (compare Fig. 3g and l). This shows that the hydrated ACC formed at this early stage (Stage I) lacks any short-range order. Irradiation of these particles with the focused electron beam for 30 s systematically results in their shrinking and transformation into an aggregate of randomly oriented CaO nanocrystals (Fig. S6 and S7†). Note that in no case (more than 30 particles were irradiated) a crystalline calcium carbonate phase forms prior to the formation of the oxide. This demonstrates that the early precipitates formed during Stage I are highly unstable hydrated ACC with no short- or medium-range order that could enable the formation of crystalline CaCO3 upon irradiation. This is in full agreement with recent WAXS studies of the early stages of ACC formation.36
In contrast, precipitates collected during Stage II show aggregates of larger (up to 2 μm) spherical ACC particles (Fig. 3h) and abundant ACC structures (see SAED in Fig. 3k) with fibrous or planar shapes (Fig. 3i), as well as “doughnut-like” structures that correspond to partially dissolved ACC hemispheres (Fig. 3j). Interestingly, all of them are made up of an aggregate of nanoparticles 2 to 25 nm in size (inset in Fig. 3j). This observation confirms that these structures do not form via an ion-addition mechanism according to the classic crystallization theory: they form via a non-classical nanoparticle aggregation-based growth mechanism. The important morphological differences between ACC particles collected during Stages I and II indicate that a significant amount of ACC particles formed in Stage I has dissolved (in some cases only partially: i.e., “doughnut-shaped” particles), and those with 1D and 2D morphologies have directly precipitated from solution during Stage II. Such 1D and 2D particles were especially abundant in samples collected (quenched) at pH 9. Note that while these 1D and 2D ACC structures may be considered unusual, they are not unique to our system: for instance, similar 2D structures were obtained by mixing calcium carbamate and calcium acetate,55 while 1D ACC structures were obtained upon mixing calcium chloride with sodium carbonate in the presence of casein.56
The experimental and fitted EDPs of the ACC structures formed during Stage II systematically show a good matching with the calculated EDP of an oriented aggregate of calcite (and monohydrocalcite) with ~1 nm domain size (Fig. 3l). In the case of the ACC particle, whose SAED is shown in Fig. 3k, the best matching (i.e., lowest R values) is observed for calcite with 10 Å domains oriented with the [![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif)
![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1] zone axis parallel to the electron beam. A poor matching (i.e., very low R values) is systematically observed in the case of calculated EDPs of non-oriented crystalline phases (Fig. S8†). Gebauer et al.4,57 have reported that ACC can display different protostructures (short-range order) depending on the synthesis conditions: at pH ~9, ACC with a protocalcite structure develops, while at a higher pH of ~10, ACC with a protovaterite structure forms. It could be argued that because in our system the pH was initially very high (12.4), the formation of ACC with a protovaterite structure should be favored. However, it is important to point out that the protocalcite structure we have identified is present in ACC particles which formed during Stage II, and in particular, those collected at pH 9. Interestingly, such a pH matches that which according to Gebauer et al. favors the formation of ACC with a protocalcite structure.4,57
1] zone axis parallel to the electron beam. A poor matching (i.e., very low R values) is systematically observed in the case of calculated EDPs of non-oriented crystalline phases (Fig. S8†). Gebauer et al.4,57 have reported that ACC can display different protostructures (short-range order) depending on the synthesis conditions: at pH ~9, ACC with a protocalcite structure develops, while at a higher pH of ~10, ACC with a protovaterite structure forms. It could be argued that because in our system the pH was initially very high (12.4), the formation of ACC with a protovaterite structure should be favored. However, it is important to point out that the protocalcite structure we have identified is present in ACC particles which formed during Stage II, and in particular, those collected at pH 9. Interestingly, such a pH matches that which according to Gebauer et al. favors the formation of ACC with a protocalcite structure.4,57
Irradiation of these ACC structures with the focused e-beam for 30 s consistently results in their transformation into single crystalline oriented calcite (more than 20 particles were irradiated). Fig. 4 shows that focused e-beam irradiation of an elongated ACC particle triggers the wake of a crystallization front that results in single crystalline calcite. Interestingly, no shrinking or porosity develops after the transformation, thus confirming that the precursor particle is anhydrous ACC. In other cases, the elongated structures transform into single crystalline calcite after focused e-beam irradiation, but the crystallization front is constrained to the irradiated area (Fig. 5a–d). This is because ACC is partially hydrated (as shown by the expansion associated with trapped water vapor released during e-beam irradiation), thereby not allowing the propagation of the reaction front all along the particle as continuity is lost. Most interestingly, irradiation of this type of elongated ACC structure in different spots results in single crystalline calcite sharing a common orientation (Fig. 5e–g), despite the fact that the irradiated areas are still separated by an amorphous phase, which upon further irradiation transforms into equally oriented single crystalline calcite (Fig. S9†). Such a behavior is observed in several elongated ACC structures formed during Stage II. These results show that there is a “crystallographic” continuity all along the ACC structure, which is “inherited” by the newly formed calcite, regardless of its position within the elongated particle. Otherwise, it would be very unlikely that the resulting calcite in such distant spots would systematically share the same crystallographic orientation. It could be argued that such a “crystallographic” continuity is an artifact resulting from the interaction of the electron beam with the ACC structure (prior to the transformation into the crystalline CaCO3) and leading to a co-alignment of ACC domains all along the different nanoparticles making the 1D, 2D and 3D structures. This is ruled out here because such an effect should also operate in the case of ACC formed during Stage I, and our TEM results show that this is not the case. Furthermore, a similar electron beam-induced transformation of amorphous into single crystalline calcite crystals has been reported both for the case of biotic58 and abiotic59 ACC. In the latter case, the transformation of ACC particles into single crystalline calcite was observed using a cryo-TEM, but only in the case of ACC particles with size >50 nm. Smaller particles yielded randomly oriented calcite following e-beam exposure. Pichon et al.59 suggested that the difference in ease of transformation may be related to the existence of different types of ACC with different degrees of short-range order. These cryo-TEM results support the fact that the medium-range order responsible for the transformation of ACC into single crystalline calcite is not an artifact of our sample preparation procedure involving quenching in ethanol or in liquid N2/freeze-drying. They also show that ACC with differences in short- and medium-range order produce different crystalline CaCO3 structures upon irradiation. There is also the question why our ACC structures that transform into oriented calcite display a 1D and/or 2D morphology (which cannot be ascribed to a sample preparation artifact). This critical point is discussed below.
Oriented attachment (OA) of ACC nanoparticles
The above results suggest that primary ACC nanoparticles (2–25 nm in size) forming the micrometer-sized (less hydrated or anhydrous) ACC structures developed during Stage II underwent OA.15,16,60 Note that recent computational studies have shown that the lower the degree of hydration of ACC, the higher would be its structural order,61 in agreement with our EDP simulation. The medium-range order (calcite protostructure) of this “amorphous” precursor may facilitate OA, a process that most likely involves dipole–dipole interactions during nanoparticle collisions in solution.16 For this to occur, ACC nanoparticles have to be anisotropic. Structural anisotropy is imparted by the oriented protocalcite structure detected by EDP simulation. It could be argued that calcite being centrosymmetric would not readily favor the formation of a dipole. However, there is experimental evidence showing that defects, which presumably are very abundant in ACC (i.e., FWHM−1 of 10 Å−1, see Experimental section), and size-related surface effects can lead to dipole formation even in cubic nanoparticles.62 OA may help to explain why 1D or 2D ACC structures form (i.e., directional aggregation/growth). In the absence of OA, spherical (or hemispherical) structures should form, as observed in the case of hydrated ACC formed during Stage I, which lacks short-range order. OA may offer a straightforward explanation regarding how oriented single crystalline CaCO3 structures develop after ACC.20,21 It could be argued that despite the medium-range order, an amorphous structure should not undergo OA. However, it has been recently indicated that even for poorly crystalline or even amorphous nanoparticles dispersed in an aqueous medium there will be a field that may promote particles to adopt favorable configurations prior to the attachment step.29 In any case, further experimental evidence, for instance using in situ TEM equipped with a fluid cell,63 is needed to confirm or refute the hypothesis presented here regarding the possibility of OA of ACC nanoparticles with medium-range order.The mechanism(s) of ACC-to-calcite transformation
Recent computational modelling shows that anhydrous ACC, considered as an intermediate between hydrated ACC and calcite, displays distorted CaO64− octahedra aligned as in calcite, but rotated at random angles around their longest axis.64 This is consistent with our EDP simulation showing medium-range order and preferential orientation of calcitic domains in less hydrated and anhydrous ACC. By concerted rotation of the distorted octahedra and shortening of the Ca–O bonds along their longest axis, the calcite structure should result. This kind of solid-state transformation is what we observe in Fig. 4 and 5 (as well as in Fig. S9 and S10†). This way, the structural information in ACC (medium-range order) is imprinted/transferred to the final crystalline polymorph (calcite). However, an activation energy (Ea) barrier of up to ca. 245 kJ mol−1 has to be surpassed for this solid-state transformation to take place.54 This can be achieved by e-beam heating or thermal treatment (e.g., the exothermal crystallization event at ca. 330 °C in DSC; see Fig. 1i), but is unlikely to occur at low T during biomineralization or biomimetic synthesis under mild conditions. Importantly, our ACC precipitates remain untransformed for more than 3 months when kept in a dry environment (closed container with silica gel) at 20 °C. This shows that a solid-state transformation at low T does not occur in our system.Interestingly, TEM-SAED analyses show that ACC structures formed during Stage II and exposed for 48 h to humid air (85% RH) at 20 °C pseudomorphically transform into a porous aggregate of crystallographically oriented calcite nanoparticles that diffract as a mesocrystal (Fig. 6 and Fig. S11†).17 This is systematically observed in more than 20 particles analyzed. Under such RH conditions, a water layer of ~2 nm is adsorbed onto CaCO3,65 which, as exemplified in the case of calcite, is enough to promote dissolution and (re)precipitation phenomena.66 Our TEM observations appear to be consistent with an interface-coupled dissolution–precipitation mechanism,67,68 whereby ACC dissolution into such an adsorbed water nanolayer can result in the coupled epitaxial precipitation of calcite onto the remaining ACC, an effect that could be facilitated by the calcite protostructure of ACC. Afterwards, the process may propagate throughout the whole ACC structure, preserving the orientation originally imprinted in ACC. Because the molar volume of ACC (54.1 cm3 mol−1) (CaCO3·H2O; density, ρ = 2.18 g cm−3)69 is higher than that of calcite (36.9 cm3 mol−1), up to 31.8% porosity can be generated to preserve the external shape of the replaced structure, thus producing a pseudomorph (strictly speaking, porosity can be also generated due to solubility differences between parent and product phases).67,68 The porosity should approach zero when ACC is anhydrous, as it is the case depicted in Fig. 4. Such porosity generation should facilitate the progress of the coupled dissolution/precipitation reaction towards the core of the parent phase, thereby enabling a full pseudomorphic replacement. The progress of such a process could also be facilitated by the release of water included in poorly hydrated ACC as well as in anhydrous ACC. Note that anhydrous ACC might in fact not be fully anhydrous: it typically includes a residual amount of H2O (i.e., 3 wt%),13 which seems to be crucial for its lack of long-range order.70
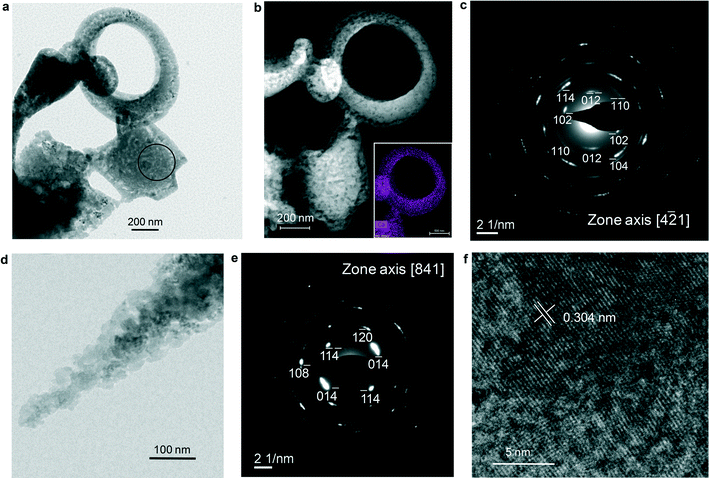 | ||
Fig. 6 ACC structures formed during Stage II and exposed to humid air. TEM (a) and annular dark-field STEM (b) images of porous 2D and 3D structures similar to those depicted in Fig. 3–5. The inset in (b) shows the Ca map of the doughnut-shaped structure. The non-uniform Ca distribution underlines the high porosity of the structure. c) Calcite [4![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1] zone axis SAED pattern of the central structure in (a) (the e-diffraction area is marked with a circle). The angular spreading (<10°) of diffraction spots indicates that there is a slight misorientation among calcite domains formed after ACC, consistent with a mesocrystal structure. d) Detail of ACC transformed into a porous pseudomorph; e) calcite [841] zone axis SAED pattern of the structure in (d); f) HRTEM image of the structure in (d) showing lattice continuity beyond the size of constituent ACC nanoparticles (≤25 nm). 1] zone axis SAED pattern of the central structure in (a) (the e-diffraction area is marked with a circle). The angular spreading (<10°) of diffraction spots indicates that there is a slight misorientation among calcite domains formed after ACC, consistent with a mesocrystal structure. d) Detail of ACC transformed into a porous pseudomorph; e) calcite [841] zone axis SAED pattern of the structure in (d); f) HRTEM image of the structure in (d) showing lattice continuity beyond the size of constituent ACC nanoparticles (≤25 nm). | ||
It could be argued that such an ACC-to-calcite transformation in (humid) air at room temperature could also occur by nucleation of a crystalline phase and subsequent propagation of the crystallization front by solid-state epitaxial secondary crystallization,25,28,54,71 regardless of whether or not the ACC structure is made up of an OA of ACC nanoparticles with a particular medium-range order. However, this is ruled out here for the following main reasons: (i) such a process will not enable the observed polymorph selection, as vaterite or calcite (or even aragonite) could equally crystallize, thus precluding any transfer of the structural information imprinted in ACC; (ii) nucleation of the first seed(s) of crystalline CaCO3 will require the prior dissolution of ACC54 and such a nucleation event would likely occur on different areas simultaneously, thereby generating crystallization fronts with different orientations, either forming randomly oriented mosaic crystals6,48 or spherulitic precipitates (radial aggregates),23 as observed here upon transformation in air at 85% RH of (fully amorphous) hydrated ACC formed in Stage I (Fig. S12†); (iii) solid-state secondary (epitaxial) crystallization is not consistent with our observation that water (adsorbed nm-thick film) is necessary for the ACC-to-calcite transformation. Note that such a solid-state transformation should also occur under dry conditions; (iv) interface-coupled dissolution–precipitation replacement processes are relatively fast as they involve ion diffusion in solution, whereas solid-state mineral replacement mechanisms are impractically slow at low T as they rely on solid-state ion diffusion.72 We extrapolated to room temperature the published values of the self-diffusion coefficient D for Ca ions in solid CaCO3 (calcite) at high T73,74 (Fig. S13†), and obtained log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values of −32.25 to −32.96 m2 s−1 (i.e., D values some 23 orders of magnitude smaller than that corresponding to Ca ion self-diffusion in an aqueous solution).75 Assuming that calcite gives a good approximation for solid state Ca ion self-diffusion in ACC, and that there is no drastic change in the mechanism for lattice diffusion at low T, it is estimated (considering that the one-dimensional diffusion length is ≈ 2√Dt)76 that it would take ca. 25
D values of −32.25 to −32.96 m2 s−1 (i.e., D values some 23 orders of magnitude smaller than that corresponding to Ca ion self-diffusion in an aqueous solution).75 Assuming that calcite gives a good approximation for solid state Ca ion self-diffusion in ACC, and that there is no drastic change in the mechanism for lattice diffusion at low T, it is estimated (considering that the one-dimensional diffusion length is ≈ 2√Dt)76 that it would take ca. 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 years for Ca to diffuse over a distance of just ~1 Å. Although this is a rough estimate, it shows that a solid state mechanism for ACC-to-calcite transformation at room temperature will not be of relevance in biomineralization or in biomimetic synthesis of calcite materials after ACC at low T.
000 years for Ca to diffuse over a distance of just ~1 Å. Although this is a rough estimate, it shows that a solid state mechanism for ACC-to-calcite transformation at room temperature will not be of relevance in biomineralization or in biomimetic synthesis of calcite materials after ACC at low T.
Conclusions
We show that in our system, precipitation of ACC is preceded by the formation of a dense liquid precursor phase. The initially formed ACC is highly hydrated (up to 1.4H2O per formula unit) and due to its relatively high solubility, readily dissolves when less hydrated, or even anhydrous ACC with higher stability (lower negative value of enthalpy of solution) and lower solubility precipitates. The formation of ACC with decreasing degree of hydration preceding calcite crystallization thus follows an energetically downhill pathway consistent with recent theoretical and experimental studies.13,54 In agreement with Nielsen et al.,63 our results also suggest that the different ACC phases we have identified (from the liquid precursor to the hydrated ACC and finally to the less hydrated and anhydrous ACC) should not be considered as fundamentally distinct phases, but rather they should be considered as points on a continuum. Interestingly, the poorly hydrated and anhydrous ACC phases show medium-range order (calcite protostructure), which is absent in the more hydrated ACC, thereby corroborating that a decrease in the amount of structural H2O favors ordering in ACC.61 We argue that this medium-range order could have enabled the OA of ACC nanoparticles which form unusual linear and planar structures. Our result also show that while in the bulk solution ACC transforms into calcite (and vaterite) via a dissolution/(re)precipitation mechanism (so that any structural information in ACC is lost), in the absence of a solution reservoir, transformation of poorly hydrated or anhydrous ACC with a protocalcite structure at pH2O <1 atm and at low T (20 °C) is not a solid-state process, but rather it appears to be an interface-coupled dissolution–precipitation process triggered and facilitated by an adsorbed water layer.We believe that the better mechanistic understanding of formation and transformation of ACC gained through this study can be applied in the rational design of novel materials with complex shapes assembled from precursor amorphous structures depending on the desired function. For instance, anhydrous or poorly hydrated ACC can be prepared (e.g., either by direct precipitation at a relatively low SI, or following thermal dehydration of hydrated ACC) and dispersed in a liquid medium (e.g., an aqueous solution saturated with respect to ACC) to enable OA during casting of a biomimetic material with a specific shape or function (with or without the use of organic additives). Then its transition to single crystalline (mesostructured) calcite functional materials could be achieved at room temperature by controlling pH2O. Ultimately, we believe that this gained knowledge may also have implications in the better understanding of calcium carbonate biomineralization via an ACC precursor phase.
Acknowledgements
This work was financially supported by the Belgium Research Foundation - Flanders (FWO), the Spanish Government (grants MAT2012-37584-ERDF and CGL2012-35992) and the Junta de Andalucía (Research Group RNM-179 and Project P11-RNM-7550). E.R.-A. acknowledges a Ramón y Cajal grant. We thank the Centro de Instrumentación Científica (CIC; University of Granada) for assistance with micro-Raman, ESEM, FESEM, FTIR, TG-DSC, and TEM analyses.Notes and references
- F. C. Meldrum and H. Cölfen, Chem. Rev., 2008, 108, 4332 CrossRef CAS PubMed.
- C. Rodriguez-Navarro and E. Ruiz-Agudo, EMU Notes Miner., 2013, 14, 337 Search PubMed.
- E. M. Pouget, P. H. H. Bomans, J. Goos, P. M. Frederik, G. de With and N. Sommerdijk, Science, 2009, 323, 1455 CrossRef CAS PubMed.
- D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322, 1819 CrossRef CAS PubMed.
- A. F. Wallace, L. O. Hedges, A. Fernandez-Martinez, P. Raiteri, J. D. Gale, G. A. Waychunas, S. Whitelam, J. F. Banfield and J. J. De Yoreo, Science, 2013, 341, 885 CrossRef CAS PubMed.
- L. B. Gower, Chem. Rev., 2008, 108, 4551 CrossRef CAS PubMed.
- R. Q. Song, H. Cölfen, A. W. Xu, J. Hartmann and M. Antonietti, ACS Nano, 2009, 3, 1966 CrossRef CAS PubMed.
- M. Faatz, F. Gröhn and G. Wegner, Adv. Mater., 2004, 16, 996 CrossRef CAS.
- J. Rieger, T. Frechen, G. Cox, W. Heckmann, C. Schmidt and J. Thieme, Faraday Discuss., 2007, 136, 265 RSC.
- M. A. Bewernitz, D. Gebauer, J. Long, H. Cölfen and L. B. Gower, Faraday Discuss., 2012, 159, 291 RSC.
- D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergström and H. Cölfen, Chem. Soc. Rev., 2014, 43, 2348 RSC.
- L. Addadi, S. Raz and S. Weiner, Adv. Mater., 2003, 15, 959 CrossRef CAS.
- A. V. Radha, T. Z. Forbes, C. E. Killian, P. U. P. A. Gilbert and A. Navrotsky, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16438 CrossRef CAS PubMed.
- J. H. E. Cartwright, A. G. Checa, J. D. Gale, D. Gebauer and C. I. Sainz-Díaz, Angew. Chem., Int. Ed., 2012, 51, 11960 CrossRef CAS PubMed.
- R. L. Penn and J. F. Banfield, Science, 1998, 281, 969 CrossRef CAS.
- D. Li, M. H. Nielsen, J. R. I. Lee, C. Frandsen, J. F. Banfield and J. J. De Yoreo, Science, 2012, 336, 1014 CrossRef CAS PubMed.
- H. Cölfen and M. Antonietti, Angew. Chem., Int. Ed., 2005, 44, 5576 CrossRef PubMed.
- L. Zhou and P. O'Brien, Small, 2008, 4, 1566 CrossRef CAS PubMed.
- A. Sugawara, T. Nishimura, Y. Yamamoto, H. Inoue, H. Nagasawa and T. Kato, Angew. Chem., Int. Ed., 2006, 45, 2876 CrossRef PubMed.
- J. Aizenberg, D. A. Muller, J. L. Grazul and D. R. Hamann, Science, 2003, 299, 1205 CrossRef CAS PubMed.
- C. Li and L. M. Qi, Angew. Chem., Int. Ed., 2008, 47, 2388 CrossRef CAS PubMed.
- A. Finnemore, P. Cuhna, T. Shean, S. Vignolini, S. Guldin, M. Oyen and U. Steiner, Nat. Commun., 2012, 3, 966 CrossRef PubMed.
- X. Xu, J. T. Han, D. H. Kim and K. Cho, J. Phys. Chem. B, 2006, 110, 2764 CrossRef CAS PubMed.
- Y. Politi, R. A. Metzler, M. Abretch, B. Gilbert, F. H. Wilt, I. Sagi, L. Addadi, S. Weiner and P. U. P. A. Gilbert, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17362 CrossRef CAS PubMed.
- C. E. Killian, R. A. Metzler, Y. U. T. Gong, I. C. Olson, J. Aizenberg, Y. Politi, F. H. Wilt, A. Scholl, A. Young, A. Doran, M. Kunz, N. Tamura, S. N. Coppersmith and P. U. P. A. Gilbert, J. Am. Chem. Soc., 2009, 131, 18404 CrossRef CAS PubMed.
- J. D. Rodriguez-Blanco, S. Shaw and L. G. Benning, Nanoscale, 2011, 3, 265 RSC.
- S. Weiner and L. Addadi, Annu. Rev. Mater. Res., 2011, 41, 21 CrossRef CAS.
- A. Gal, W. Habraken, D. Gur, P. Fratzl, S. Weiner and L. Addadi, Angew. Chem., Int. Ed., 2013, 52, 4867 CrossRef PubMed.
- H. Zhang, J. J. De Yoreo and J. F. Banfield, ACS Nano, 2014, 8, 6526 CrossRef CAS PubMed.
- A. Gal, S. Weiner and L. Addadi, J. Am. Chem. Soc., 2010, 132, 13206 CrossRef PubMed.
- E. Loste, R. M. Wilson, R. Seshadri and F. C. Meldrum, J. Cryst. Growth, 2003, 254, 206 CrossRef CAS.
- J. R. Clarkson, C. T. Price and J. J. Adams, J. Chem. Soc., Faraday Trans., 1992, 88, 243 RSC.
- O. Cizer, C. Rodriguez-Navarro, E. Ruiz-Agudo, J. Elsen, D. Van Gemert and K. Van Balen, J. Mater. Sci., 2012, 47, 6151 CrossRef CAS.
- J. Ihli, P. Bots, A. Kulak, L. G. Benning and F. C. Meldrum, Adv. Funct. Mater., 2013, 23, 1965 CrossRef CAS.
- T. Ogino, T. Suzuki and K. Sawada, Geochim. Cosmochim. Acta, 1987, 51, 2757 CrossRef CAS.
- P. Bots, L. G. Benning, J. D. Rodriguez-Blanco, T. Roncal-Herrero and S. Shaw, Cryst. Growth Des., 2012, 12, 3806 CAS.
- P. Debye, Ann. Phys., 1915, 46, 809 CrossRef CAS.
- C. R. Berry, Phys. Rev., 1952, 88, 596 CrossRef CAS.
- P. T. Cardew and R. J. Davey, Proc. R. Soc. London, Ser. A, 1985, 398, 415 CrossRef CAS.
- K. Sangwal, J. Cryst. Growth, 1989, 97, 393 CrossRef.
- L. N. Plummer and E. Busenberg, Geochim. Cosmochim. Acta, 1982, 46, 1011 CrossRef.
- G. Wolf, E. Konigsberger, H. G. Schmidt, L. C. Konigsberger and H. Gamsjager, J. Therm. Anal. Calorim., 2000, 60, 463 CrossRef CAS.
- G. Wolf, J. Lerchner, H. Schmidt, H. Gamsjäger, E. Königsberger and P. Schmidt, J. Therm. Anal., 1996, 46, 353 CrossRef CAS.
- L. Brečević and A. E. Nielsen, J. Cryst. Growth, 1989, 98, 504 CrossRef.
- M. Kellermeier, A. Picker, A. Kempter, H. Cölfen and D. Gebauer, Adv. Mater., 2014, 26, 752 CrossRef CAS PubMed.
- D. L. Parkhurst and C. A. J. Appelo, User guide to PHREEQC (version 2) – a computer program for speciation, batch reaction, one-dimensional transport, and inverse geochemical calculations, U.S. Geological Survey Water-Resources Investigation Report 99-4259, 1999 Search PubMed.
- J. Rieger, J. Thieme and C. Schmidt, Langmuir, 2000, 16, 8300 CrossRef.
- X. Xu, J. T. Tark and K. Cho, Chem. Mater., 2004, 16, 1740–1746 CrossRef CAS.
- N. D. Denkov, O. D. Velev, P. A. Kraichevsky, I. B. Ivanov, H. Yoshimura and K. Nagayama, Nature, 1993, 361, 26 CrossRef.
- J. R. I. Lee, T. Y. J. Han, T. M. Willey, D. Wang, R. W. Meulenberg, J. Nilsson, P. M. Dove, L. J. Terminello, T. vanBuuren and J. J. DeYoreo, J. Am. Chem. Soc., 2007, 129, 10370 CrossRef CAS PubMed.
- K. Lee, W. Wagermaier, A. Masic, K. P. Kommareddy, M. Bennet, I. Manjubala, S. W. Lee, S. B. Park, H. Cölfen and P. Fratzl, Nat. Commun., 2012, 3, 725 CrossRef PubMed.
- C. Rodriguez-Navarro, O. Cazalla, K. Elert and E. Sebastian, Proc. R. Soc. London, Ser. A, 2002, 458, 2261 CrossRef CAS.
- A. W. Xu, Q. Yu, W. F. Dong, M. Antonietti and H. Cölfen, Adv. Mater., 2005, 17, 2217 CrossRef CAS.
- J. Ihli, W. C. Wong, E. H. Noel, Y. Y. Kim, A. N. Kulak, H. K. Christenson, M. J. Duer and F. C. Meldrum, Nat. Commun., 2014, 5, 3169 Search PubMed.
- J. Prah, J. Maček and G. Dražič, J. Cryst. Growth, 2011, 324, 229 CrossRef CAS PubMed.
- Y. Liu, Y. Cui and R. Guo, Langmuir, 2012, 28, 6097 CrossRef CAS PubMed.
- D. Gebauer, P. N. Gunawidjaja, J. Y. P. Ko, Z. Bacsik, B. Aziz, L. Liu, Y. Hu, L. Bergström, C. W. Tai, T. K. Sham, M. Edén and N. Hedin, Angew. Chem. Ind. Ed., 2010, 49, 8889 CrossRef PubMed.
- Y. Politi, T. Arad, E. Klein, S. Weiner and L. Addadi, Science, 2004, 306, 1161 CrossRef CAS PubMed.
- B. P. Pichon, P. H. H. Bomans, P. M. Frederik and N. A. J. M. Sommerdijk, J. Am. Chem. Soc., 2008, 130, 4034 CrossRef PubMed.
- R. L. Penn and J. A. Soltis, CrystEngComm, 2014, 16, 1409 RSC.
- M. Saharay, A. O. Yazaydin and R. J. Kirkpatrick, J. Phys. Chem. B, 2013, 117, 3328 CrossRef CAS PubMed.
- K. Yasui and K. Kato, J. Phys. Chem. C, 2012, 116, 319 CAS.
- M. H. Nielsen, S. Aloni and J. J. De Yoreo, Science, 2014, 345, 1158 CrossRef CAS PubMed.
- P. Rez and A. Blackwell, J. Phys. Chem. B, 2011, 115, 11193 CrossRef CAS PubMed.
- R. P. Chiarello, R. A. Wogelius and N. C. Sturchio, Geochim. Cosmochim. Acta, 1993, 57, 4103 CrossRef CAS.
- J. Baltrusaitis and V. H. Grassian, Surf. Sci., 2009, 603, L99 CrossRef CAS PubMed.
- A. Putnis, Rev. Mineral. Geochem., 2009, 70, 87 CrossRef CAS.
- E. Ruiz-Agudo, K. Kudłacz, C. V. Putnis, A. Putnis and C. Rodriguez-Navarro, Environ. Sci. Technol., 2013, 47, 11342 CrossRef CAS PubMed.
- A. Fernandez-Martinez, B. Kalkan, S. M. Clark and G. A. Waychunas, Angew. Chem., 2013, 125, 8512 CrossRef.
- P. Rez, S. Sinha and A. Gal, J. Appl. Crystallogr., 2014, 47, 1651 CrossRef CAS.
- J. Seto, Y. Ma, S. A. Davis, F. Meldrum, A. Gourrier, Y. Kim, U. Schilde, M. Sztucki, M. Burghammer, S. Maltsev, C. Jäger and H. Cölfen, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 3699 CrossRef CAS PubMed.
- A. Putnis, Science, 2014, 343, 1441 CrossRef PubMed.
- D. K. Fisler and R. T. Cygan, Am. Mineral., 1999, 84, 1392 CAS.
- J. R. Farver and R. A. Yund, Contrib. Mineral. Petrol., 1996, 123, 77 CrossRef CAS.
- T. H. Li and S. Gregory, Geochim. Cosmochim. Acta, 1974, 38, 703 CrossRef.
- R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport Phenomena, Wiley, New York, 1976 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Solubility and dissolution enthalpy of calcium carbonate phases (Table S1); additional optical microscopy, Raman, ESEM, FESEM, XRD, FTIR results (Fig. S1–S4); calculation of the solubility product (ksp) of anhydrous ACC (Fig. S5); TEM-SAED images of hydrated ACC decomposition following focused e-beam irradiation (Fig. S6–S7); EDPs of ACC and simulated EDPs of crystalline phases with randomly oriented domains (Fig. S8); focused e-beam transformation of an ACC particle formed during Stage II (Fig. S9–S10); TEM-SAED analysis of ACC structures formed during Stage II and exposed to humid air (85% RH, 20 °C) for 48 h (Fig. S11); transformation of hydrated ACC formed during Stage I into calcite upon exposure to humid air (85% RH; 20 °C) for 48 h (Fig. S12); self-diffusion coefficient, D, of Ca ions in water and in solid CaCO3 (Fig. S13). See DOI: 10.1039/c4ce01562b |
| This journal is © The Royal Society of Chemistry 2015 |

![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]).
0]).
