The surface phase diagram of Fe₃O₄(001) revisited

Abstract

Understanding how the physical and electronic structures of metal-oxide surfaces evolve under varying conditions is crucial for optimizing their performance in applications such as catalysis. In this study, we compute the surface phase diagram of the Fe₃O₄(001) facet using density functional theory (DFT)-based calculations, with an emphasis on understanding the terminations observed in surface science experiments. Our results reveal two stable terminations in addition to the subsurface cation vacancy (SCV) structure, which dominates under oxidizing conditions. The commonly reported octahedral Fe pair, also known as the Fe-dimer termination, is stable within an oxygen chemical potential range of −3.1 eV < μ_O < −2.3 eV. We identify the lowest-energy structure of this surface as the one proposed by J. R. Rustad, E. Wasserman and A. R. Felmy, A Molecular Dynamics Investigation of Surface Reconstruction on Magnetite (001), Surf. Sci., 1999, 432, 1–2, where a tetrahedrally coordinated Fe_A atom is replaced by two octahedrally coordinated Fe_B atoms in the surface layer. This transformation serves as a precursor to the emergence of an FeO-like termination under highly reducing conditions. A key insight from our study is the importance of thoroughly sampling different charge-order configurations to identify the global minima across varying stoichiometries.

---

Introduction

Iron, one of the most abundant elements in the Earth's crust, undergoes oxidation in the ambient atmosphere to form various oxides and hydroxides.¹ Hematite (α-Fe₂O₃), the most stable oxide phase under oxidizing conditions, has a corundum structure with Fe³⁺ cations located in octahedral interstitial sites of a hexagonal close-packed (hcp) O²⁻ lattice. Wüstite (Fe_1−xO) forms under reducing conditions; this material takes the rocksalt structure with Fe²⁺ cations occupying octahedrally coordinated sites in the face-centered cubic (fcc) O sublattice. Magnetite (Fe₃O₄) crystallizes in an inverse spinel structure (AB₂O₄), where Fe³⁺ cations occupy tetrahedral sites (A sites) and a 1 : 1 mixture of Fe²⁺ and Fe³⁺ cations reside in octahedral sites (B sites),² as seen in Fig. 1. The Fe_A and Fe_B cations have antiparallel spin orientations, making Fe₃O₄ a ferrimagnet. Above the Verwey transition temperature of 125 K, the Fe_B atoms become equivalent and have a nominal Fe^2.5+ charge state.³ This results in room-temperature half-metallicity,⁴ which is potentially useful for spintronics applications.^5,6 The redox properties of iron oxides⁷ make their surfaces important in geochemistry¹ and there is a long-standing interest in understanding how the transformation between phases begins at the surface and propagates through the material. Finally, iron oxides are important in catalysis,^1,8–11 both as a reducible support for precious metals and as the active phase for reactions such as the high-temperature water-gas shift reaction.^12,13

Fig. 1 The bulk structure of Fe₃O₄ at low temperature is based on an fcc arrangement of O²⁻ cations (red), where Fe³⁺ cations occupy tetrahedral sites (Fe_A, cyan), and a 1 : 1 mixture of Fe²⁺ and Fe³⁺ cations resides in octahedral sites (Fe_B, dark blue). The experimental lattice parameter at room temperature is 8.397 Å.

Over recent years, the Fe₃O₄(001) surface has emerged as an ideal model system to study fundamental processes occurring at Fe oxide surfaces. In contrast to other much-studied facets such as Fe₃O₄(111) and α-Fe₂O₃(0001),^14–16 a monophase termination is straightforward to prepare on Fe₃O₄(001) under ultrahigh vacuum conditions (UHV). The most commonly observed surface has a periodicity based on an array of subsurface cation vacancies and interstitials. This “subsurface cation vacancy” (SCV) structure was determined using a combination of scanning tunneling microscopy (STM),¹⁷ quantitative low-energy electron diffraction (LEED),¹⁷ surface X-ray diffraction (SXRD)¹⁸ and density functional theory (DFT).¹⁷ Angle-resolved XPS measurements confirm it to be oxidized with respect to the bulk spinel structure.¹⁷ When Fe₃O₄(001) samples are reduced, STM images reveal an alternative termination featuring pairs of protrusions with a periodicity. This is known as the octahedral Fe pair termination (hereafter Fe_oct pair termination), or the Fe-dimer termination.^19–25 The Fe_oct pair termination was experimentally observed by many groups, on single crystals subjected to many sputter/anneal cycles, after Fe deposition on Fe₃O₄(001) bulk crystal,^25,26 or on epitaxial thin films containing an excess of Fe.^20,27 Several models have been proposed,^20,26,28 which differ in stoichiometry and how the Fe atoms are positioned with respect to the subsurface.

In this study, we use first-principles calculations based on DFT to revisit the surface phase diagram of Fe₃O₄(001). We demonstrate that the model originally proposed by Rustad et al.²⁸ represents the most stable variant of the Fe-octahedral (Fe_oct) pair termination. Compared to the B-terminated truncated bulk, this structure replaces one Fe_A atom with two octahedrally coordinated Fe atoms in each reconstructed unit cell. It is stoichiometric, charge-neutral, and satisfies polarity compensation requirements within a purely ionic framework. Under extremely reducing conditions, an FeO-like termination emerges, effectively propagating Rustad's mechanism across the surface. Furthermore, our calculations reveal that the spin orientation and the charge ordering between Fe²⁺-like and Fe³⁺-like ions, particularly in the topmost surface layer, play a crucial role in determining surface stability.

Computational details

The Vienna ab initio simulation package (VASP)²⁹ was used for all calculations, with the near-core regions described by the projector-augmented-wave method.^30,31 Γ-Centered k-meshes of 5 × 5 × 5 and 3 × 3 × 1 were used for the bulk optimization (Fd3̄m) and all surface slabs, respectively, and the plane-wave basis set cutoff was set to 550 eV. Calculations were performed using the regularized-restored strongly constrained and appropriately normed meta-generalized gradient approximation (r²SCAN)³² with an on-site Coulomb repulsion term³³ U_eff = 3.10 eV for the 3d electrons of the Fe atoms,³⁴ where the magnitude of U is determined from experimental oxidation energies. In accordance with the experimental conditions, the bulk lattice constant was optimized for the room-temperature phase (Fe^2.5+) by enforcing Fd3̄m symmetry of the charge density. All other calculations were conducted using the electronic ordering of the low-temperature phase, as there was no straightforward method to stabilize the room-temperature phase and prevent charge disproportionation into Fe²⁺ and Fe³⁺ on an arbitrary surface with broken symmetry. In addition to the r²SCAN calculations, we also adopted the generalized gradient approximation method with the Perdew–Burke–Ernzerhof (PBE) functional,³⁵ with an effective on-site Coulomb repulsion term U_eff = 3.61 eV.^36,37 The PBE-optimized bulk overestimates the lattice constant by ≈1%. The r²SCAN performs better by only overestimating it by ∼0.2%. The calculations were also performed with the experimental magnetite lattice parameter (a = 8.397 Å),³⁸ which may provide increased accuracy with PBE+U in some cases.³⁹ The relative surface energies exhibited minor changes, but these did not significantly alter the conclusions regarding the surface phase diagram of Fe₃O₄(001). A symmetric slab was built with 17 planes (9 planes with octahedral Fe and 8 with tetrahedral Fe; only one Fe atom in the middle layer is fixed, and the rest relaxed) and 14 Å vacuum. The convergence criterion was an electronic energy step of 10⁻⁶ eV and forces acting on ions smaller than 0.02 eV Å⁻¹. Simulated scanning tunneling microscopy (STM) images were generated using the Tersoff–Hamann approximation in constant-height mode, allowing visualization of local electronic density at specific energy levels for a sample bias voltage of +2.5 V.⁴⁰ Surface phase diagrams were derived following the approach described by Reuter and Scheffler.⁴¹ We note that the symmetry of the surface slab is broken; therefore the bulk energy reference of Fe₃O₄ was calculated without enforcing cubic symmetry (resulting in the P/2c-like low-temperature phase).⁴²
Here, γ is the surface energy, and 2A is the surface area of the slab (two sides). E^slab is the total energy of the surface structure obtained from DFT calculations. is the energy for one formula unit of the bulk (P/2c), and , where μ_O2 is the chemical potential of oxygen in the gas phase. E_O2 is the total energy of an isolated O₂ molecule in a spin-polarized calculation at T = 0 K. N_Fe and N_O are the numbers of Fe and O atoms in the surface slab, respectively. The chemical potential of oxygen in the gas phase provides the temperature and pressure dependence in the phase diagram and can be calculated as
where p⁰ is a reference pressure and μ_O2(T, p⁰) = H(T, p⁰) − TS(T, p⁰) can be calculated from tabulated data.⁴³

To check for possible errors in computing the energy of O₂ by DFT, we have calculated the formation energy of bulk Fe₃O₄ using the r²SCAN functional, using O₂ and metallic Fe bulk (BCC) as a reference. Since metallic Fe cannot be correctly described by DFT+U, this was done with U = 0. Our calculated formation energy is −11.70 eV, compared to an experimental value of −11.55 eV at 0 K.⁴³ This results in an estimated error of −0.04 eV per O atom. Previous studies have reported somewhat larger discrepancies. Almeida et al. found an error of −0.23 eV per O atom for the SCAN functional,⁴⁴ while Hütner et al. estimated a comparable error of −0.20 eV per O atom for r²SCAN.⁴⁵ In any case, it is important to note that the O₂ binding energy error causes a minor shift in the μ_O axis of the phase diagrams, but it does not alter the relative ordering of the compared phases.

To selectively control the charge ordering of Fe²⁺ and Fe³⁺ ions on the surface layer, we used the occupation matrix control tool,⁴⁶ which consists of an initial constrained calculation (with an input occupation matrix kept fixed during the calculation) followed by an unconstrained calculation. In what follows, Fe²⁺-like and Fe³⁺-like cations are identified by the calculated Bader charges⁴⁷ (Tables S1–S7†) of 1.30–1.45 e and 1.70–1.80 e, respectively, and the local magnetic moments. Magnetic orientation also plays a crucial role in surface stability. Therefore, we also explore the magnetic ordering and the charge ordering of various Fe₃O₄(001) terminations in reducing conditions.

Results

I. Surface phase diagram

Fig. 2 presents our surface energy diagram of Fe₃O₄(001). To the best of our knowledge, this is the most comprehensive diagram of this type for Fe₃O₄(001) published since the discovery of the SCV reconstruction.^2,17 In particular, we focus on understanding the structures observed experimentally in surface science investigations under reducing conditions. We note that Fe₃O₄(100), Fe₃O₄(010) and Fe₃O₄(001) are equivalent above the Verwey transition. However, the DFT calculations were performed at 0 K, which is below the Verwey transition, where the phase becomes monoclinic due to the charge ordering between Fe²⁺ and Fe³⁺ ions. As a result, the (110), (010), and (001) faces are no longer equivalent. However, this difference is minimal, and we therefore expect similar results for the Fe₃O₄(100) and Fe₃O₄(010). This diagram was calculated at the r²SCAN+U level (Fig. S8† shows an alternative diagram based on PBE+U calculations) and derived from the framework of ab initio atomistic thermodynamics.⁴¹ The upper x-axes show the corresponding oxygen partial pressures at three different temperatures: 300 K (room temperature), 500 K (the minimum temperature at which the Fe diffusion occurs⁴⁸), and 900 K (the typical annealing temperature in UHV experiments). Three surface structures were identified as stable across the considered oxygen chemical potential range: (1) the SCV termination,¹⁷ (2) the Fe-octahedral (Fe_oct) pair termination, and (3) a reduced FeO-like termination. In what follows, we discuss the various structures, including those that do not appear in the convex hull, starting with the SCV termination. This choice is partly motivated by experiments where Fe was systematically deposited on the SCV termination and the resulting structures imaged with STM.^19,26

Fig. 2 Surface phase diagram of Fe₃O₄(001) comparing the surface energies of various terminations as a function of oxygen chemical potential (μ_O); derived from r²SCAN+U calculations. The top axes indicate the corresponding oxygen partial pressures at 300 K, 500 K, and 900 K.⁴³ The light orange, light yellow, and light green regions indicate the range of UHV experiments (10⁻¹² mbar < p_O < 10⁻⁶ mbar) corresponding to each temperature: 300 K, 500 K, and 900 K respectively. Dashed vertical lines show the calculated Fe₂O₃(hematite)–Fe₃O₄(magnetite) and Fe₃O₄(magnetite)–FeO(wüstite) phase equilibrium. The convex hull formed by the three stable terminations is highlighted in dark gray.

II. Oxidized surfaces

We begin with the non-stoichiometric subsurface cation vacancy (SCV) termination (Fig. 3a), which has been described extensively in the past.^17,18 Compared to a bulk truncation at the Fe_B–O plane (Fig. 3b), two Fe_B cations from the third layer are removed and one Fe_A cation is added in the second layer. The Fe interstitial (labelled Fe_int in Fig. 3a) has a Bader charge of 1.75 e, and is thus Fe³⁺-like, like all the other tetrahedrally coordinated Fe atoms. The Bader charges indicate that all Fe atoms in the outermost four layers are Fe³⁺ (Table S1†), which is explicable since the surface is oxidized with respect to bulk Fe₃O₄ (2 Fe atoms missing per unit cell, compared with a stoichiometric termination). We compute the SCV termination to be the most favorable surface for O₂ chemical potentials greater than −2.30 eV (black line in Fig. 2).

Fig. 3 Non-stoichiometric (oxidized) terminations of the Fe₃O₄(001) surface (top view). Iron is large and blue or cyan, and oxygen is small and red. Dark blue (spin up) and cyan (spin down) indicate the spin orientation in Fe atoms, which coincide with the Fe_B and Fe_A sublattices, respectively. The cell is indicated with a black dashed square. (a) SCV termination, (b) distorted B termination (DBT), (c) Fe_A adatom on SCV, and (d) V_O in SCV, where the oxygen vacancy is shown as a red dashed circle. With respect to a stoichiometric termination, SCV, DBT, Fe_A on SCV, and V_O in SCV terminations have a deficiency of 2, 1, 1, and 1.25 Fe atoms per cell, respectively. The highlighted green square indicates that (a) is one of the three stable terminations in the surface phase diagram of the Fe₃O₄(001).

Introducing one additional Fe atom to the SCV structure leads to two possible surface terminations: the distorted bulk truncation (DBT) (alternatively named the distorted Fe_B–O termination) originally proposed by Pentcheva and coworkers⁴⁹ (Fig. 3b), and a surface with an Fe adatom on the SCV-reconstructed surface (Fe_A on SCV) (Fig. 3c). The DBT exhibits a periodicity due to a Jahn–Teller effect, in which a lattice distortion is coupled to subsurface charge order.^49–51 This structure was further discussed in terms of a surface Verwey transition,⁵² and proposed to explain the undulation of the surface Fe_B rows observed in STM images.^53,54 However, this model ultimately failed to explain some properties of the experimentally observed surface, most notably the preference for metal adatoms to bind at one particular site in the unit cell.^55–57 In the DBT model, when ignoring the small distortions, there are two equivalent adsorption sites per unit cell; these sites correspond to the tetrahedral positions of the next layer when continuing the bulk lattice. In the SCV model, one of these sites is blocked by the Fe_int, thus there is only one site for metal adatoms without a tetrahedral Fe_A below.

When an Fe adatom is placed on the SCV termination (Fig. 3c), it binds to the two oxygen atoms that do not have a subsurface Fe_A neighbor. The optimized structure obtained by r²SCAN+U reveals the surface Fe adatom relaxes downward from the tetrahedral bulk-continuation Fe_A site due to its low (twofold) coordination with oxygen. Whereas a bulk-like Fe_A atom is Fe³⁺, the surface Fe_A adatom has a Bader charge of 1.34 e and is thus Fe²⁺. Previous STM studies have identified Fe_A adatoms as a defect on the as-prepared SCV surface,⁴⁸ but a complete monophase 0.5 ML Fe_A termination was never observed. These experimental results are in line with our calculations, which determine that neither DBT nor Fe_A on SCV is favored in the surface phase diagram at any O chemical potential.

Since reduction can also occur through an oxygen vacancy (V_O), we also computed the presence of oxygen vacancies in the surface layer (Fig. 3d). The oxygen atoms that can be removed at the lowest cost are those binding to the Fe_int in the SCV termination. In the optimized structure, the Fe_int from the SCV reconstructed surface moves downward to occupy one of the third-layer Fe_B vacancy sites (cyan dashed arrow and cycle in Fig. 3d). This Fe atom prefers the site opposite to the oxygen vacancy rather than directly beneath it. The oxygen vacancy in SCV (V_O in SCV) structure is more stable than the DBT and Fe_A on SCV terminations for oxygen chemical potentials greater than −2.66 eV (Fig. 2). Nevertheless, this structure is not on the convex hull and, thus, not present at the surface under equilibrium conditions.

III. Stoichiometric surfaces

Next, we explore the stoichiometric surface terminations of Fe₃O₄(001), featuring two additional Fe atoms with respect to the SCV structure in a periodicity. One possible structure model with this composition involves an Fe adatom on a surface truncated at the Fe_B–O plane (Fig. 4a). Previous authors have referred to this as the 0.5 ML Fe_A termination,^23,25,58 because one of the two equivalent Fe_A bulk continuation sites is occupied. In contrast to Fe_A sites of the bulk, this Fe_A atom does not have tetrahedral but only twofold coordination. Upon relaxation, our DFT calculations reveal that the Fe_A does not remain centered at the 2-fold coordinated site, but increases its oxygen coordination by a horizontal shift, which puts it close to an octahedral site. Since it resides rather far (1.11 Å) from the tetrahedral site, we name it Fe_A*. The relaxation is limited by repulsion between the Fe_A* and one of the Fe_A atoms in the first subsurface layer (at a distance of only 2.53 Å). The energy gain of this relaxation is 4.62 meV Å⁻² (Fig. S1†). Therefore, we call this the “0.5 ML Fe_A*” termination. Pentcheva and coworkers observed similar behavior of 0.5 ML and 1 ML of Co adatoms on the Co₃O₄(001) surface.⁵⁹ We consider this structure an initial state, transitioning to the more favorable the Fe_oct pair termination proposed by Rustad et al.²⁸

Fig. 4 Stoichiometric terminations of the Fe₃O₄(001) surface (top view). These structures contain 2 additional Fe atoms per unit cell with respect to the SCV surface. Iron is large and dark blue (spin up) or cyan (spin down), and oxygen is small and red. Fe atoms are labelled with their charge state inferred from the Bader charges (≈1.77 e and 1.40 e for 3+ and 2+, respectively). The cell is indicated with a black dashed square. (a) 0.5 ML of Fe_A* on DBT, and (b) Fe_oct pair termination originally proposed by Rustad.²⁸ The black dashed oval indicates the octahedral pair. The brown arrows and dotted cyan circles show that 0.5 ML Fe_A* surface can be converted into the Fe_oct pair by moving two tetrahedral Fe atoms. The green square indicates that the structure in panel (b) is one of the three stable terminations in the surface phase diagram.

Rustad's Fe_oct pair termination²⁸ (Fig. 4b) is not only energetically superior to the 0.5 ML Fe_A* on DBT by 11.62 meV Å⁻² (equivalent to 0.82 eV per surface cell), but it is also the most preferred structure for a stoichiometric surface. Furthermore, the termination also lies on the convex hull in the phase diagram (Fig. 2). The stability range of this structure is −3.10 eV < μ_O < −2.30 eV. We have also tried an additional stoichiometric termination, an Fe_oct pair on the SCV termination; this is substantially worse in energy. Rustad's Fe_oct pair structure was proposed based on molecular dynamics simulations, which showed that the surface Fe_A adatom moved laterally and downward to occupy an octahedrally coordinated site (Fe_B*) in the surface Fe_B–O plane. Fe–Fe repulsion then caused a subsurface Fe_A atom to move laterally away and upwards (brown arrow in Fig. 4b), and this atom ultimately occupied a similar site with five-fold coordination to oxygen. We will argue here that this is the Fe_oct pair termination (or Fe dimer), frequently observed in STM investigations.^19–25 Moreover, we analyse the magnetic orientation and charge order of the Fe_oct pair termination. Our r²SCAN+U calculations reveal that the spins of the Fe_oct pair couple antiparallel to the Fe_B atoms in the surface layer. In this sense, it constitutes a first step towards the wüstite structure of FeO, in which the (001) planes consist of rows with antiparallel spin. In the Fe_oct pair termination, two of the oxygen atoms in the surface layer have no Fe neighbor in the layer below, resulting in a 4-fold planar coordination and causing the surface to buckle slightly. In the optimal configuration (Fig. 4b), the Fe_oct pair has a Bader charge of 1.77 e, which corresponds to Fe³⁺. However, four Fe_B atoms in the surface layer are reduced from Fe³⁺ to Fe²⁺ (Bader charges around 1.40 e). All four Fe_B atoms in the first subsurface layer are Fe³⁺, based on Bader charge analysis and the local magnetic moment of Fe atoms. We note that the r²SCAN+U and PBE+U calculations can get stuck in local minima (Fig. S3c†) where the Fe_oct pair is Fe²⁺ and four Fe_B atoms in the surface layer are mixed between Fe²⁺ and Fe³⁺ ions. This is 7.23 meV Å⁻² (0.51 eV per 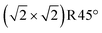surface cell) less stable than the electronic ground state (Fig. 4b) at the r²SCAN+U level. Different possibilities for the charge order in the surface layer are shown in Fig. S3,† together with their relative energy differences with respect to the optimal electronic configuration. We also tested the hybrid functional HSE06; also with this functional the resulting configurations remained trapped in local minima. To counteract this, we initiated the different initial charge configurations using the occupation matrix tool, which controls the charge order of the Fe atoms in the surface layer. Rustad and co-workers treated the Fe ions as a nominal charge state of +2.5 in their molecular dynamics simulations;²⁸ thus, these calculations were not affected by the problem of the charge order.

IV. Reduced surfaces

Now switching to Fe-rich, non-stoichiometric terminations, Fig. 5a shows the Fe_oct pair termination proposed by Novotny et al.,²⁶ which requires the addition of three Fe atoms per unit cell to the SCV termination (one to lift the SCV reconstruction and restore a bulk truncated surface, and the other two for the additional Fe_oct pair itself). This corresponds to one Fe atom per cell more than the stoichiometric terminations of Fig. 4. The surface energy diagram indicates that this termination (dotted green line in Fig. 2) is energetically less favorable compared to the other terminations proposed here across the entire range of oxygen chemical potential. This is because the added Fe_B* atoms and Fe_A atoms below are in close proximity, with Fe–Fe distances of only 2.5 Å. The other two terminations with the same, reduced stoichiometry are 1 ML Fe_A* (as previously reported by many groups,^26,49,52,60 Fig. 5b) and Fe_oct-only (Fig. 5c).

Fig. 5 Non-stoichiometric (reduced) terminations of the Fe₃O₄(001) surface, which contain 3 additional Fe atoms per cell with respect to the SCV surface, one more than the stoichiometric termination (top view). Iron is large and dark blue (spin up) or cyan (spin down), and oxygen is small and red. Black dashed ovals indicate the positions of Fe_oct pairs. A cell is indicated with a black dashed square. (a) 0.5 ML Fe_oct pair on DBT proposed by Novotny et al.²⁶ (b) 1 ML of Fe_A* on DBT, and (c) 1 layer FeO-like on DBT. The brown arrows and dotted cyan circles indicate the Fe_A atoms that have relaxed outward from a 2-fold coordination with the oxygen atoms.

When adding two Fe_A adatoms to the DBT structure, Fig. 5b shows that these two adatoms again relax from their twofold high-symmetry positions, increasing their oxygen coordination but putting them close to the Fe_A atoms in the subsurface (≈2.5 Å). Since the adatoms leave the tetrahedral site, we name them Fe_A*. In principle, there are two possibilities for such a relaxation, the two Fe_A* adatoms of the cell can relax in either the same direction or opposite directions (Fig. S2†); the latter is more favorable. This observation is in line with previous work from Spiridis and coworkers, which suggested that the shifting of Fe_A adatoms towards each other might be responsible for the Fe “dimer” surface observed in STM experiments.^20,61

In Fig. 5c, the two Fe_A atoms in the immediate subsurface layer are removed and, together with the Fe_A* atoms, from two surface Fe_oct pairs. This termination utilizes the mechanism proposed by Rustad²⁸ twice in the 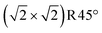unit cell. This structure can alternatively be seen as one layer of FeO(001) supported on Fe₃O₄(001) terminated at the Fe_B–O plane (apart from the slight distortions, the DBT surface of Fig. 3b). In the relaxed structure, the four oxygen atoms in the 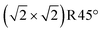unit cell that have no Fe neighbor in the subsurface layer relax upward from the surface by around 0.4 Å above the Fe_B–O surface plane (perspective view in Fig. S5i†). Apart from the vertical buckling, the rows of O atoms also exhibit slight in-plane displacements, which can be also seen in Fig. S5i.† We note that the in-plane displacements of O atoms are due to the orbital interaction between the p-orbitals of the O atoms and the t_2g orbitals of the Fe²⁺ ions (see Fig. S7d†).

In the phase diagram (Fig. 2), neither of these reduced terminations is on the convex hull. Concerning the relative stability, r²SCAN+U predicts the FeO monolayer (two Fe_oct pairs) in Fig. 5C to be lower in energy by 3.31 meV Å⁻², whereas the 1 ML Fe_A* on DBT of Fig. 5b is preferred in a PBE+U calculation. Tests with different charges for the Fe atoms show that this difference between the r²SCAN+U and PBE+U is not due to a local energy minimum but indeed caused by the functional. In this respect, it is noteworthy that r²SCAN+U predicts a larger energy advantage for the Fe_oct pair than PBE+U also for the stoichiometric termination. In any case, charge order plays a significant role in the surface stability of the 1 layer FeO-like termination (Fig. S4†). The surface becomes increasingly stable as the number of Fe²⁺ ions in the surface increases (which increases the number of Fe³⁺ in the first subsurface octahedral layer; this layer converts to fully Fe³⁺ at the favorable charge order of Fig. 5c). Our calculations at the r²SCAN+U level reveal that the maximum number of Fe²⁺ ions in the surface layer is that of Fig. 5c, seven Fe_B atoms within the 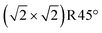unit cell.

Finally, we examine the surface terminations resulting from the deposition of five additional Fe atoms onto the SCV termination. Previous experiments indicate that an FeO(001)-like surface layer is formed in extremely reducing conditions.^26,62 In Fig. 6, we propose two possible FeO-like surface terminations: (a) adding 4 Fe_oct atoms to the DBT surface without removal of the tetrahedral atoms, and (b) 2 layers FeO-like on the DBT surface with the tetrahedral Fe removed. The latter structure is equivalent to adding one layer of FeO on the all-octahedral surface of Fig. 5c. This can also be viewed as the reduction mechanism proposed by Rustad²⁸ occurring four times in the unit cell, in both the surface and the first subsurface Fe_oct layer. Fig. 2 shows that the structure in Fig. 6b is more stable than that in Fig. 6a in r²SCAN+U calculations, while the two structures are almost degenerate in PBE+U calculations (Fig. S8†). The structure of Fig. 6a was previously proposed by Novotny et al.²⁶ Similar to the structure of Fig. 5a it suffers from repulsion between the tetrahedral Fe atoms and the added Fe atoms (Fe_B*), with a distance of only ≈2.6 Å. Thus, the row of additional Fe_B* atoms, shown in cyan (spin down), is not coplanar with the other Fe_oct atoms of the surface but 0.5 Å above the Fe_B atoms of the bulk truncated surface (see the perspective view in Fig. S5j†). The other model with the same stoichiometry (Fig. 6b) is an FeO-like termination obtained by adding two FeO layers to the DBT surface of Fig. 3b. This results in the outermost three layers of the slab made from Fe with octahedral coordination. Since Fig. 5c has a surplus of one Fe atom with respect to a stoichiometric surface and the added layer has a surplus of 2 Fe atoms (Fe₈O₈ vs. the stoichiometric Fe₆O₈) per cell, this structure also corresponds to an Fe excess of 3 atoms. In the relaxed structure, the surface Fe atoms are coplanar. The DFT calculations show only Fe²⁺ in the first layer. In spite of its FeO-like structure, the second layer contains both Fe²⁺ and Fe³⁺. The calculated Bader charges are reported in Table S7.† As all the other structures, this termination has antiparallel spins between neighboring Fe rows. Within a (001) layer, this is the same as expected for FeO(001). Concerning the spin arrangement of adjacent layers, the subsurface layer in Fig. 6b has the spin-down rows running parallel to those in the first layer. This configuration is the same as the bulk spin order of FeO, where the spins are parallel within {111} planes, but adjacent {111} planes have opposite spin. There is also an alternative configuration in which the spin-down rows of the surface and subsurface layers are oriented at a 90° angle. This configuration has surface energy that is almost degenerate with the one where spin-down rows run parallel to those in the first layer. As mentioned above, the subsurface layer of the termination in Fig. 6(b) is not purely Fe²⁺, thus it differs from bulk FeO.

Fig. 6 Non-stoichiometric (reduced) terminations of the Fe₃O₄(001) surface, which contain 5 additional Fe atoms per cell with respect to the SCV surface, three more than the stoichiometric surface (top view). Iron is large and dark blue (spin up) or cyan (spin down), and oxygen is small and red. The cell is indicated with a black dashed square. In both structures, all surface iron atoms are Fe²⁺ according to the Bader charges (between 1.34–1.36 e). (a) 1 ML Fe_oct pair on DBT, and (b) 2 layers FeO-like on DBT. With respect to a stoichiometric termination, these two terminations each contain three additional Fe atoms per cell. The highlighted green square indicates that this is one of the three stable terminations in the surface phase diagram of the Fe₃O₄(001).

Similar to the 1 layer FeO-like termination, surface rumpling of oxygen is also observed for 2 layers FeO but is less pronounced (see Fig. S5k†). In the current case, all oxygen atoms in the surface layer are 5-fold coordinated to Fe_B atoms, with one bond to an Fe_B directly beneath. The rumping is the result of the repulsion between the oxygens atoms and the differently oriented t_2g orbitals of the Fe²⁺ ions in the subsurface layer. Furthermore, the interaction between the t_2g orbitals of the Fe²⁺ atoms in the surface layer and the p-orbitals of the oxygen atoms leads to in-plane displacements, as shown in Fig. S7.†

Discussion

Our updated phase diagram for the Fe₃O₄(001) surface (Fig. 2) predicts two stable surfaces in addition to the SCV termination at the r²SCAN+U level. Starting from the well-characterized oxygen-rich SCV termination,^17,18 the next stable structure as the conditions become more reducing is the stoichiometric Fe_oct pair (or Fe-dimer) termination. This surface is already well known for STM experiments with varying explanations, but here we show that the lowest-energy structure is that proposed by Rustad et al.²⁸ The Fe coverage of this structure (2 Fe atoms per cell in addition to the SCV structure) is consistent with recent experiments;¹⁹ also the simulated STM image (Fig. S6†) agrees well with the experimental STM data.^19,20,26,27 It is interesting to note that this model was not considered in more recent attempts to establish the surface phase diagram of Fe₃O₄(001).^26,49,52,60 Although this structure is stoichiometric, it also makes sense as a first step towards reducing the surface region towards FeO, which contains only octahedrally coordinated Fe²⁺. Essentially, Rustad's Fe_oct-pair structure replaces one subsurface Fe_A³⁺ of the bulk-truncated magnetite surface with two octahedral Fe atoms. Interestingly, the new cations in the Fe_oct pair are both Fe³⁺, and the nearby Fe_B atoms are reduced to Fe²⁺. This can be rationalized because all surface Fe atoms have the same 5-fold oxygen coordination and four Fe neighbors in the first coordination shell, but next-nearest Fe are different: the Fe_B atoms have an Fe_A neighbor in the first subsurface layer at a distance of ≈3.35 Å, while the atoms of the Fe_oct pair have a much larger distance to the Fe_A (4.6 Å). The average charge of the surface layer differs from the nominal 2.5+ of octahedral layers in magnetite. The same is true for the competing 0.5 ML Fe_A* model (Table S4†). We consider it likely that it is more favorable to have the Fe²⁺ with its occupied minority-spin t_2g orbital in the surface layer, where the repulsive overlap of this orbital and the neighboring oxygen atoms is lower than in a fully oxygen-coordinated bulklike site of the subsurface Fe_B layer.

As expected for superexchange favoring antiferromagnetic alignment of Fe atoms coupled via common oxygen neighbors, the surface Fe_B rows from the Fe₃O₄ and the new surface Fe_oct cations have antiparallel spin (the same is true for all the similar structures, also with more Fe-rich stoichiometry). The substitution of one Fe_A with two Fe_B comes at the expense of some surface strain, however: converting Fe₃O₄ into FeO would require a 2.1% lattice expansion according to the r²SCAN+U-calculated lattice constants. Thus, the surface Fe_B cations relax by 0.08 Å away from the Fe_oct pair to accommodate it in the surface. Moreover, two O atoms neighboring the Fe_oct pair move up, which also helps to relieve stress. This upward buckling may be also related to the fact that oxygen usually does not prefer a planar 4-fold geometry.

The relative stability of Rustad's Fe_oct pair termination can also be rationalized in terms of electronic and structural effects. In a purely ionic model, Fe₃O₄(001) is a polar surface with alternating planes of ±6 e per 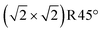cell in the 〈001〉 directions (Fig. S10†). In principle, compensation of the macroscopic dipole of the B-termination (DBT) or a 1 ML Fe_A termination requires that the surface region has a net charge of +3 or −3 e, respectively. Indeed, this is why the 0.5 ML Fe_A model was originally proposed; terminating the DBT surface with a single Fe_A atom per unit cell would provide the necessary +3 charge.^63,64 However, utilizing integer charges as in a truncated bulk is overly simplistic in a half-metallic, multivalent oxide with delocalized charges, and our calculations suggest that a hypothetical twofold coordinated surface Fe_A would be actually Fe²⁺-like (not Fe³⁺ as Fe_A in the bulk) and also the Fe_B surface layer would not retain its average 2.5+ state (Fig. S2a†); the additional charge is localized in the subsurface Fe_B atoms. The Fe_oct pair proposed by Rustad has the same overall stoichiometry, but is more favorable because it avoids highly undercoordinated metal atoms.⁴⁵ All Fe in the surface layer is fivefold coordinated, and the Fe_oct-pair atoms bind down to the subsurface O atoms that have lost an Fe_A bonding partner, ensuring these remain fourfold coordinated.

As we move to reducing conditions, the next surface to consider has one excess Fe atom per 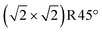cell with respect to the stoichiometric surface. Different functionals predict different lowest-energy terminations, but neither of them is on the convex hull and therefore expected to occur near equilibrium. One structure with this stoichiometry is the 1-layer FeO termination (Fig. 5c). This surface features two Fe_oct pairs instead of the Fe_A atoms present in a truncated bulk. It can be also considered a single layer of FeO added to a truncated bulk, and, therefore, a first step toward the FeO-like termination. Another structure with this stoichiometry has a lower energy in PBE calculations; it has two Fe_A* adatoms near octahedral sites on a truncated-bulk substrate (Fig. 5b). In contrast to the FeO monolayer, this structure can avoid the problem of ≈2% lattice mismatch between an FeO layer and the underlying Fe₃O₄ substrate by slight lateral undulation of the Fe_B rows; it also avoids fourfold planar coordination of oxygen. This comes at the cost of repulsive interactions of the Fe_A* surface atoms with a subsurface Fe_A (2.5 Å distance).

In extremely reducing conditions, the last stable surface predicted in this study is terminated by three fully octahedral FeO(001)-like layers (Fig. 6b). This structure can be considered the result of adding one FeO layer to the 1-layer FeO of Fig. 5c. In this structure, all of the Fe in the topmost surface layer is Fe²⁺, and the antiferromagnetic alignment is as expected for FeO(001). In principle, this process can occur deeper and deeper into the bulk, and it likely underlines the overall transformation from Fe₃O₄ to FeO. A defective and rumpled version of the FeO termination has been observed previously by scanning tunneling microscopy.²⁶

For most structures, the spin orientations of the Fe atoms can be predicted because superexchange via the O anions leads to antiferromagnetic coupling of neighboring Fe rows. Therefore, it is clear that the Fe atoms within Rustad's Fe_oct pair surface must be antiparallel to the Fe_B in the bulk truncated surface and the Fe_B in the layer below. For comparison, we find that the Fe_oct pair termination with the same Fe spin direction as the neighboring Fe_B in the surface layer is less stable by 4.40 meV Å⁻² (Table S8†). We also note that the charge order of Fe²⁺-like and Fe³⁺-like ions in the surface layer has a substantial influence on the energy (Fig. S3 and S4†); the influence of the charge states of the Fe_oct in the subsurface layers is less pronounced. As a general point, our work demonstrates that structural relaxation in DFT+U calculations does not guarantee obtaining the electronic ground state solution in a mixed-valency system.

The conditions required to form the reduced surface structures appear to be unrealistically reducing at the typical temperatures used in experiments (see the top x axes of Fig. 2). However, experimentally, the FeO termination was observed under non-equilibrium conditions, either through sputtering with Ar⁺ ions (a procedure that preferentially removes surface O atoms) or by deposition of metallic Fe. In the case of experiments involving thin films, reduced terminations were reported when the Fe₃O₄(001) film was deposited on an Fe buffer layer.^{20,22,24,27,58,62,65} This excess Fe would diffuse into the film at the growth conditions or upon annealing; the presence of metallic Fe is again incompatible with the assumption of thermodynamic equilibrium of the oxide with the O₂ gas phase and indicates that the conditions are more reducing than what one would expect from the O₂ pressure in the experiment.

While the SCV and 2-layer FeO structures are at the convex hull of the surface phase diagram, their stability ranges do not overlap with the bulk stability range of Fe₃O₄ in the calculated phase diagram (Fig. 2). Taking the phase diagram at face value, this means that the conditions required to from the SCV would be also sufficiently oxidizing to convert the bulk into Fe₂O₃, and the conditions required for forming the 2-layer FeO termination would also convert the bulk into FeO when kinetic limitations are absent. In practice, this is not a limitation for experiments, since the typical temperatures and time scales in surface science experiments are usually far from those required for a bulk phase transition. It must be also noted that the exact conditions for phase transitions are not only determined by the DFT energies at T = 0, as Fig. 2 would suggest. At finite temperatures, vibrational energy and entropy as well as other terms (e.g. entropy from different charge configurations with similar energy, vacancies, defects) have to be considered and may change the relative stabilities of the structures, especially if the energy differences are small and the competing phases differ strongly in their properties.

In spite of these limitations, our revised surface phase diagram of Fe₃O₄(001) provides valuable insights into the structural evolution and stability of iron oxide surfaces under reducing conditions. The agreement between computational results and experimental observations in the literature underlines the reliability of the proposed surface models, paving the way for further exploration of Fe₃O₄(001) surfaces under reducing conditions in diverse applications.

Conclusion

Our revised surface energy phase diagram of the Fe₃O₄(001) shows that the model originally proposed by Rustad et al. is the most stable stoichiometric structure. Rustad's model represents a first step toward the wüstite structure of FeO, because it replaces tetrahedrally coordinated Fe_A atoms with octahedrally coordinated Fe atoms. Additionally, we found that the charge states of the Fe_B atoms in the surface layers play a crucial role in determining surface stability. More broadly, our calculations indicate that the mere structural relaxation in DFT+U calculations does not necessarily ensure convergence to the electronic ground state for Fe₃O₄(001) surfaces.

Data availability

All computational structures and relevant data generated in this study are available in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement No. [864628], Consolidator Research Grant ‘E-SAC’). This research was funded in part by the Austrian Science Fund (FWF) under doi https://doi.org/10.55776/F8100, Taming Complexity in Materials Modeling (TACO) and the Cluster of Excellence MECS, under doi https://doi.org/10.55776/COE5. ME acknowledges funding from the EU Marie Skłodowska-Curie Actions of Horizon-MSCA-2022-PF-01 (Project 101103731-SCI-PHI). MM gratefully acknowledges financial support from the Austrian Science Fund (FWF) through project number (https://doi.org/10.55776/PAT2176923), which partially enabled this research. The computational results have been achieved using the Vienna Scientific Cluster (VSC). For the purpose of open access, the authors have applied a CC BY public copyright license to any Author Accepted Manuscript version arising from this submission.

References

1. R. M. Cornell and U. Schwertmann, The Iron Oxides: Structure, Properties, Reactions, Occurrences and Uses, Wiley-VCH, New York, 2003.
2. G. S. Parkinson, Iron Oxide Surfaces, Surf. Sci. Rep., 2016, 71(1), 272–365,  DOI:10.1016/j.surfrep.2016.02.001.
3. M. S. Senn, J. P. Wright and J. P. Attfield, Charge Order and Three-Site Distortions in the Verwey Structure of Magnetite, Nature, 2012, 481(7380), 173–176,  DOI:10.1038/nature10704.
4. W. Wang, J. M. Mariot, M. C. Richter, O. Heckmann, W. Ndiaye, P. De Padova, A. Taleb-Ibrahimi, P. Le Fèvre, F. Bertran, F. Bondino, E. Magnano, J. Krempaský, P. Blaha, C. Cacho, F. Parmigiani and K. Hricovini, Fe t_2g Band Dispersion and Spin Polarization in Thin Films of Fe₃O₄(001)/MgO(001): Half-Metallicity of Magnetite Revisited, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(8), 1–7,  DOI:10.1103/PhysRevB.87.085118.
5. M. Ziese, Extrinsic Magnetotransport Phenomena in Ferromagnetic Oxides, Rep. Prog. Phys., 2002, 65(2), 143–249,  DOI:10.1088/0034-4885/65/2/202.
6. J. M. D. Coey and C. L. Chien, Half-Metallic Ferromagnetic Oxides, MRS Bull., 2003, 28, 720–724,  DOI:10.1557/mrs2003.212.
7. M. Müllner, M. Riva, F. Kraushofer, M. Schmid, G. S. Parkinson, S. F. L. Mertens and U. Diebold, Stability and Catalytic Performance of Reconstructed Fe₃O₄(001) and Fe₃O₄(110) Surfaces during Oxygen Evolution Reaction, J. Phys. Chem. C, 2019, 123(13), 8304–8311,  DOI:10.1021/acs.jpcc.8b08733.
8. W. Weiss and W. Ranke, Surface Chemistry and Catalysis on Well-Defined Epitaxial Iron-Oxide Layers, Prog. Surf. Sci., 2002, 70(1–3), 1–151,  DOI:10.1016/S0079-6816(01)00056-9.
9. P. Tartaj, M. P. Morales, T. Gonzalez-Carreño, S. Veintemillas-Verdaguer and C. J. Serna, The Iron Oxides Strike Back: From Biomedical Applications to Energy Storage Devices and Photoelectrochemical Water Splitting, Adv. Mater., 2011, 23(44), 5243–5249,  DOI:10.1002/adma.201101368.
10. H. Firouzabadi, N. Iranpoor, M. Gholinejad and J. Hoseini, Magnetite (Fe₃O₄) Nanoparticles-Catalyzed Sonogashira-Hagihara Reactions in Ethylene Glycol under Ligand-Free Conditions, Adv. Synth. Catal., 2011, 353(1), 125–132,  DOI:10.1002/adsc.201000390.
11. Q. Zhang, X. Yang and J. Guan, Applications of Magnetic Nanomaterials in Heterogeneous Catalysis, ACS Appl. Nano Mater., 2019, 2(8), 4681–4697,  DOI:10.1021/acsanm.9b00976.
12. X. Liu, Z. Ma, Y. Meng, Y. j. Ma and X. d. Wen, First-Principles Study on the Mechanism of Water-Gas Shift Reaction on the Fe₃O₄(111)-Fe_tet1, Mol. Catal., 2021, 516, 111998,  DOI:10.1016/j.mcat.2021.111998.
13. M. Zhu and I. E. Wachs, Iron-Based Catalysts for the High-Temperature Water-Gas Shift (HT-WGS) Reaction: A Review, ACS Catal., 2016, 6(2), 722–732,  DOI:10.1021/acscatal.5b02594.
14. F. Kraushofer, M. Meier, Z. Jakub, J. Hütner, J. Balajka, J. Hulva, M. Schmid, C. Franchini, U. Diebold and G. S. Parkinson, Oxygen-Terminated (1 × 1) Reconstruction of Reduced Magnetite Fe₃O₄(111), J. Phys. Chem. Lett., 2023, 14(13), 3258–3265,  DOI:10.1021/acs.jpclett.3c00281.
15. J. Redondo, J. Michalička, F. Kraushofer, G. Franceschi, B. Šmid, N. Kumar, O. Man, M. Blatnik, D. Wrana, B. Mallada, M. Švec, G. S. Parkinson, M. Setvin, M. Riva, U. Diebold and J. Čechal, Hematite α-Fe₂O₃(0001) in Top and Side View: Resolving Long-Standing Controversies about Its Surface Structure, Adv. Mater. Interfaces, 2023, 10(32), 1–9,  DOI:10.1002/admi.202300602.
16. G. Ketteler, W. Weiss, W. Ranke and R. Schlögl, Bulk and Surface Phases of Iron Oxides in an Oxygen and Water Atmosphere at Low Pressure, Phys. Chem. Chem. Phys., 2001, 3(6), 1114–1122,  10.1039/b009288f.
17. R. Bliem, E. McDermott, P. Ferstl, M. Setvin, O. Gamba, J. Pavelec, M. A. Schneider, M. Schmid, U. Diebold, P. Blaha, L. Hammer and G. S. Parkinson, Subsurface Cation Vacancy Stabilization of the Magnetite (001) Surface, Science, 2014, 346(6214), 1215–1218,  DOI:10.1126/science.1260556.
18. B. Arndt, R. Bliem, O. Gamba, J. E. S. Van Der Hoeven, H. Noei, U. Diebold, G. S. Parkinson and A. Stierle, Atomic Structure and Stability of Magnetite Fe₃O₄(001): An X-Ray View, Surf. Sci., 2016, 653, 76–81,  DOI:10.1016/j.susc.2016.06.002.
19. O. Gamba, M. Eder, M. Poglitsch, J. Pavelec, P. Sombut, M. Meier, U. Diebold, M. Schmid and G. Parkinson, Formation and Stability of Fe-Rich Terminations of the Fe₃O₄(001), Surface, Mater. Res. Express, 2023, 4(001) DOI:10.1088/2053-1591/ad0ac5.
20. N. Spiridis, J. Barbasz, Z. Łodziana and J. Korecki, Fe₃O₄(001) Films on Fe(001): Termination and Reconstruction of Iron-Rich Surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(15), 1–5,  DOI:10.1103/PhysRevB.74.155423.
21. S. F. Ceballos, G. Mariotto, K. Jordan, S. Murphy, C. Seoighe and I. V. Shvets, An Atomic Scale STM Study of the Fe₃O₄(001) Surface, Surf. Sci., 2004, 548(1–3), 106–116,  DOI:10.1016/j.susc.2003.10.041.
22. J. M. Gaines, J. T. Kohlhepp, J. T. W. M. van Eemeren, R. J. G. Elfrink, F. Roozeboom and W. J. M. de Jonge, (001) Surface of Fe₃O₄ Grown Epitaxially on MgO and Characterized by Scanning Tunneling Microscopy, Mater. Res. Soc. Symp. Proc., 1997, 477(001), 191–198,  DOI:10.1557/proc-474-191.
23. G. Tarrach, D. Bürgler, T. Schaub, R. Wiesendanger and H. J. Güntherodt, Atomic Surface Structure of Fe₃O₄(001) in Different Preparation Stages Studied by Scanning Tunneling Microscopy, Surf. Sci., 1993, 285(1–2), 1–14,  DOI:10.1016/0039-6028(93)90908-3.
24. J. M. Gaines, P. J. H. Bloemen, J. T. Kohlhepp, C. W. T. Bulle-Lieuwma, R. M. Wolf, A. Reinders, R. M. Jungblut, P. A. A. Van Der Heijden, J. T. W. M. Van Eemeren, J. Aan De Stegge and W. J. M. De Jonge, An STM Study of Fe₃O₄(100) Grown by Molecular Beam Epitaxy, Surf. Sci., 1997, 373(1), 85–94,  DOI:10.1016/S0039-6028(96)01145-4.
25. G. S. Parkinson, Z. Novotný, P. Jacobson, M. Schmid and U. Diebold, A Metastable Fe(A) Termination at the Fe₃O₄(001) Surface, Surf. Sci., 2011, 605(15–16), 1–4,  DOI:10.1016/j.susc.2011.05.018.
26. Z. Novotny, N. Mulakaluri, Z. Edes, M. Schmid, R. Pentcheva, U. Diebold and G. S. Parkinson, Probing the Surface Phase Diagram of Fe₃O₄(001) towards the Fe-Rich Limit: Evidence for Progressive Reduction of the Surface, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(19), 1–8,  DOI:10.1103/PhysRevB.87.195410.
27. E. M. Davis, K. Zhang, Y. Cui, H. Kuhlenbeck, S. Shaikhutdinov and H. J. Freund, Growth of Fe₃O₄(001) Thin Films on Pt(100): Tuning Surface Termination with an Fe Buffer Layer, Surf. Sci., 2015, 636, 42–46,  DOI:10.1016/j.susc.2015.02.004.
28. J. R. Rustad, E. Wasserman and A. R. Felmy, A Molecular Dynamics Investigation of Surface Reconstruction on Magnetite (001), Surf. Sci., 1999, 432(1–2) DOI:10.1016/S0039-6028(99)00581-6.
29. G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50,  DOI:10.1016/0927-0256(96)00008-0.
30. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979,  DOI:10.1103/PhysRevB.50.17953.
31. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775,  DOI:10.1103/PhysRevB.59.1758.
32. J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, Accurate and Numerically Efficient r²SCAN Meta-Generalized Gradient Approximation, J. Phys. Chem. Lett., 2020, 11(19), 8208–8215,  DOI:10.1021/acs.jpclett.0c02405.
33. S. Dudarev and G. Botton, Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57(3), 1505–1509,  DOI:10.1103/PhysRevB.57.1505.
34. G. Sai Gautam and E. A. Carter, Evaluating Transition Metal Oxides within DFT-SCAN and SCAN+U Frameworks for Solar Thermochemical Applications, Phys. Rev. Mater., 2018, 2(9), 1–14,  DOI:10.1103/PhysRevMaterials.2.095401.
35. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
36. A. Kiejna, T. Ossowski and T. Pabisiak, Surface Properties of the Clean and Au/Pd Covered Fe₃O₄(111): DFT and DFT+U Study, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(12), 1–11,  DOI:10.1103/PhysRevB.85.125414.
37. I. Bernal-Villamil and S. Gallego, Charge Order at Magnetite Fe₃O₄(001): Surface and Verwey Phase Transitions, J. Phys.:Condens. Matter, 2015, 27(1) DOI:10.1088/0953-8984/27/1/012001.
38. S. Gates-Rector and T. Blanton, The Powder Diffraction File: A Quality Materials Characterization Database, Powder Diffr., 2019, 34(4), 352–360,  DOI:10.1017/S0885715619000812.
39. M. Meier, Z. Jakub, J. Balajka, J. Hulva, R. Bliem, P. K. Thakur, T. L. Lee, C. Franchini, M. Schmid, U. Diebold, F. Allegretti, D. A. Duncan and G. S. Parkinson, Probing the Geometry of Copper and Silver Adatoms on Magnetite: Quantitative Experiment: Versus Theory, Nanoscale, 2018, 10(5), 2226–2230,  10.1039/c7nr07319d.
40. J. Tersoff and D. R. Hamann, Theory of the Scanning Tunneling Microscope, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31(2), 805–813,  DOI:10.1103/PhysRevB.31.805.
41. K. Reuter and M. Scheffler, Composition, Structure, and Stability of RuO₂(110) as a Function of Oxygen Pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65(3), 1–11,  DOI:10.1103/PhysRevB.65.035406.
42. J. P. Wright, J. P. Attfield and P. G. Radaelli, Long Range Charge Ordering in Magnetite below the Verwey Transition, Phys. Rev. Lett., 2001, 87(26), 2664011–2664014,  DOI:10.1103/PhysRevLett.87.266401.
43. M. W. Chase, NIST-JANAF Thermochemical Tables, J. Phys. Chem. Ref. Data, Monogr., American Chemical Society, American Institute of Physics for the National Institute of Standards and Technology, Washington, D.C., Woodbury, N.Y., 1998, vol. 9.
44. M. O. Almeida, M. J. Kolb, M. R. V. Lanza, F. Illas and F. Calle-Vallejo, Gas-Phase Errors Affect DFT-Based Electrocatalysis Models of Oxygen Reduction to Hydrogen Peroxide, ChemElectroChem, 2022, 9(12), 1–7,  DOI:10.1002/celc.202200210.
45. J. I. Hütner, A. Conti, D. Kugler, F. Mittendorfer, G. Kresse, M. Schmid and J. B. Ulrike Diebold, Stoichiometric Reconstruction of the Al₂O₃(0001) Surface, Science, 2024, 385(6714), 1241–1244,  DOI:10.1126/science.adq4744.
46. J. P. Allen and G. W. Watson, Occupation Matrix Control of d- and f-Electron Localisations Using DFT + U, Phys. Chem. Chem. Phys., 2014, 16(39), 21016–21031,  10.1039/c4cp01083c.
47. G. Henkelman, A. Arnaldsson and H. Jónsson, A Fast and Robust Algorithm for Bader Decomposition of Charge Density, Comput. Mater. Sci., 2006, 36(3), 354–360,  DOI:10.1016/j.commatsci.2005.04.010.
48. O. Gamba, J. Hulva, J. Pavelec, R. Bliem, M. Schmid, U. Diebold and G. S. Parkinson, The Role of Surface Defects in the Adsorption of Methanol on Fe₃O₄(001), Top. Catal., 2017, 60(6–7), 420–430,  DOI:10.1007/s11244-016-0713-9.
49. R. Pentcheva, F. Wendler, H. L. Meyerheim, W. Moritz, N. Jedrecy and M. Scheffler, Jahn-Teller Stabilization of a “Polar” Metal Oxide Surface: Fe₃O₄(001), Phys. Rev. Lett., 2005, 94(12), 3–6,  DOI:10.1103/PhysRevLett.94.126101.
50. R. Pentcheva, W. Moritz, J. Rundgren, S. Frank, D. Schrupp and M. Scheffler, A Combined DFT/LEED-Approach for Complex Oxide Surface Structure Determination: Fe₃O₄(001), Surf. Sci., 2008, 602(7), 1299–1305,  DOI:10.1016/j.susc.2008.01.006.
51. N. Mulakaluri, R. Pentcheva, M. Wieland, W. Moritz and M. Scheffler, Partial Dissociation of Water on Fe₃O₄(001): Adsorbate Induced Charge and Orbital Order, Phys. Rev. Lett., 2009, 103(17), 1–4,  DOI:10.1103/PhysRevLett.103.176102.
52. Z. Łodziana, Surface Verwey Transition in Magnetite, Phys. Rev. Lett., 2007, 99(20), 1–4,  DOI:10.1103/PhysRevLett.99.206402.
53. B. Stanka, W. Hebenstreit, U. Diebold and S. A. Chambers, Surface Reconstruction of Fe₃O₄(001), Surf. Sci., 2000, 448(1), 49–63,  DOI:10.1016/S0039-6028(99)01182-6.
54. R. Wiesendanger, I. V. Shvets, D. Bürgler, G. Tarrach, H. J. Güntherodt, J. M. Coey and S Gräser, Topographic and Magnetic-Sensitive Scanning Tunelling Microscope Study of Magnetite, Science, 1992, 255(5044), 583–586,  DOI:10.1126/science.255.5044.583.
55. R. Bliem, J. Pavelec, O. Gamba, E. McDermott, Z. Wang, S. Gerhold, M. Wagner, J. Osiecki, K. Schulte, M. Schmid, P. Blaha, U. Diebold and G. S. Parkinson, Adsorption and Incorporation of Transition Metals at the Magnetite Fe₃O₄(001) Surface, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(7), 1–9,  DOI:10.1103/PhysRevB.92.075440.
56. J. Hulva, M. Meier, R. Bliem, Z. Jakub, F. Kraushofer, M. Schmid, U. Diebold, C. Franchini and G. S. Parkinson, Unraveling CO Adsorption on Model Single-Atom Catalysts, Science, 2021, 371(6527), 375–379,  DOI:10.1126/science.abe5757.
57. Z. Novotný, G. Argentero, Z. Wang, M. Schmid, U. Diebold and G. S. Parkinson, Ordered Array of Single Adatoms with Remarkable Thermal Stability: Au/Fe₃O₄(001), Phys. Rev. Lett., 2012, 108(21), 1–5,  DOI:10.1103/PhysRevLett.108.216103.
58. S. A. Chambers and S. A. Joyce, Surface Termination, Composition and Reconstruction of Fe₃O₄(001) and γ-Fe₂O₃(001), Surf. Sci., 1999, 420(2–3), 111–122,  DOI:10.1016/S0039-6028(98)00657-8.
59. Y. Peng, H. Hajiyani and R. Pentcheva, Influence of Fe and Ni Doping on the OER Performance at the Co₃O₄(001) Surface: Insights from DFT+U Calculations, ACS Catal., 2021, 11(9), 5601–5613,  DOI:10.1021/acscatal.1c00214.
60. C. Cheng, Structure and Magnetic Properties of the Fe₃O₄(001) Surface: Ab Initio Studies, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(5), 1–4,  DOI:10.1103/PhysRevB.71.052401.
61. N. Spiridis and E. Madej, Adsorption of Gold on an Iron-Rich Fe₃O₄(001) Surface, J. Phys. Chem. C, 2017, 4(001), 2011–2017,  DOI:10.1021/jp4102866.
62. M. Capra, A. Lodesani, A. Brambilla, M. Finazzi, L. Duò, F. Ciccacci and A. Picone, Reversible Metamorphosis from Fe₃O₄ to FeO of Epitaxial Iron Oxide Films Grown on the Fe-p(1 × 1)O Surface, RSC Adv., 2021, 11(19), 11513–11518,  10.1039/d0ra10650j.
63. C. Noguera, Polar Oxide Surfaces, J. Phys.:Condens. Matter, 2000, 12(31) DOI:10.1088/0953-8984/12/31/201.
64. J. Goniakowski, F. Finocchi and C. Noguera, Polarity of Oxide Surfaces and Nanostructures, Rep. Prog. Phys., 2008, 71(1) DOI:10.1088/0034-4885/71/1/016501.
65. N. Spiridis, B. Handke, T. Slezak, J. Barbasz, M. Zajac, J. Haber and J. Korecki, Surface Structure of Epitaxial Magnetite Fe₃O₄(001) Films: In Situ STM and GEMS Studies, J. Phys. Chem. B, 2004, 108(38), 14356–14361,  DOI:10.1021/jp049935i.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5lf00022j

---