Open Access Article
Open Access ArticleTemperature-dependent stress–strain behavior of amorphous and crystalline P3HT†
Kehinde H.
Fagbohungbe
 ,
Connor P.
Callaway
and
Chad
Risko
,
Connor P.
Callaway
and
Chad
Risko
 *
*
Department of Chemistry & Center for Applied Energy Research (CAER) University of Kentucky Lexington, Kentucky 40506, USA. E-mail: chad.risko@uky.edu
First published on 9th October 2024
Abstract
The scalable commercialization of organic electronics wherein π-conjugated polymers serve as the semiconductors hinges on precise control of the material electronic, redox, optical, and mechanical properties, which are each highly influenced by local and long-range morphology. Here, we undertake atomistic molecular dynamics (MD) simulations at three temperatures (150 K, 300 K, and 400 K) to assess the morphological and mechanical response of bulk poly(3-hexylthiophene) (P3HT), a representative homopolymer of interest as an organic semiconductor (OS). As P3HT is a semicrystalline polymer, we characterize mechanical properties for both amorphous and crystalline P3HT models to derive insights into structure–property relationships, including Young's modulus (E) and Poisson's ratio (ν). Mechanical behaviors that arise as a consequence of kinetically induced molecular reorientations/transitions are described, including the determination of entanglement properties over the course of polymer deformation. Specifically, we analyze stress–strain curves to (1) elucidate how, and the extent to which, the rather tangled amorphous domains retain their ductility over temperature ranges that span known phase transitions, and (2) uncover the strength and mechanism of inter-chain mechanical coupling across lamellar stackings as a function of temperature. Generally, this work provides a molecular-level understanding of the thermomechanical behavior of π-conjugated polymers at regions where order or disorder dominates local packing, and prompts a more comprehensive description of the mechanical properties of these systems while recognizing their often inherently semicrystalline nature.
Introduction
Mechanical deformability offers an avenue to expand the range of applications of electronic devices.1–7 Applications such as in nonplanar surfaces acting as electroactive mediums and in portable, sustainable, and recyclable electronic devices with variable form factors necessitate a precise understanding of the deformation of the materials used in these technologies.6,8–10 Organic semiconductors (OS), and OS derived from π-conjugated polymers in particular, boast unique combinations of desirable features due to the ability to chemically fine-tune the electronic, redox, and optical response and deformability, the latter of which arises from the combination of rotatable moieties along the π-conjugated backbones, pendant side chains, and the ability of polymer chain segments to both slip and entangle. While OS are recognized as promising candidate materials in field-effect transistors, light-emitting diodes, energy transforming and storing devices, and biological or environmental sensors, translating these materials into viable commercial applications still requires a deeper understanding of their quantitative structure–property relationships.3,11–15The molecular-scale structure of π-conjugated polymers is generally characterized by long chains of π-conjugated monomers and alkyl, ether, or aromatic (or some combination thereof)-based side chains. Such polymers can form an array of microstructures, ranging from (semi)crystalline to amorphous, with the semiconductor electronic, redox, and optical properties each being highly influenced by the semiconductor percent crystallinity. In general, locally planar (non-planar) structures are often linked with extended (localized) π wave functions and more ordered/crystalline (disordered/amorphous) morphologies. The chemistries of the polymer backbones and the side chains, in combination with the processing conditions used to develop the OS, influence the chain conformations and packings and the relative strengths of the noncovalent intermolecular interactions,5,16,17 which in turn regulate the thermal and mechanical response.
The quest for a precise formulation of how microstructural anisotropy and order regulate the properties and function of polymer-based OS motivates an atomistic consideration of how these characteristics can be harnessed to control device performance in various operating conditions.18,19 This understanding is especially critical given that the environmental conditions a device may experience from fabrication until the end of its lifetime are increasingly variable and, in some cases, can be detrimental to device performance.8,20 Materials characteristics can vary significantly between the amorphous and crystalline phases. Further, regions identified as the rigid (RAF) and mobile (MAF) amorphous fractions exist in many polymer-based semiconductors; these regions characterize the network of tie chains that extends through the amorphous regions, both looping back into the same crystallite repeatedly and connecting different crystallites.21–24 This microstructural sophistication further frustrates the development of a complete understanding of the thermomechanical behavior of polymer-based OS.25–27
Here, we use atomistic molecular dynamics (MD) simulations to model the temperature-dependent stress–strain behavior of the crystalline and amorphous regions of regioregular poly(3-hexylthiophene) (P3HT), a prototypical, paracrystalline semiconducting π-conjugated polymer. While coexistence of the amorphous (MAF and RAF) and crystalline regions are generally to be expected in P3HT, we opt to simplify the problem through a baseline characterization of fully amorphous (aP3HT) and fully crystalline (cP3HT) systems in isolation, an approach that finds previous application in the literature.28 Through simulations at temperatures both above and below the glass transition temperature (Tg), we explore mechanical and structural properties relevant to performance during the processing, packaging, and operational lifetimes of P3HT. By considering three crystalline slabs of varying size, we evaluate the dependencies of performance-relevant properties on the degree of polymerization through models approaching experimental length scales. Finally, we analyze the chain entanglement characteristics of the amorphous domains as functions of strain and temperature to deduce the influence of these topological constraints on the observed mechanical response (such as a strain hardening-like increase in post-yield stress). By connecting the crystalline and amorphous polymer microstructural morphologies to their mechanical response, we offer insights that pave the way to a more complete understanding of the thermomechanical properties of π-conjugated polymer morphology.
Computational methods
All MD simulations were performed using the GROMACS software suite version 2019.5.29,30 The visual molecular dynamics (VMD) program was used to visualize the resulting trajectories.31 All bonded and non-bonded interactions, including modifications to inter-monomer dihedral torsion potentials, were based on the parameterization of P3HT as developed by Huang et al.32 using the OPLS-AA force field.33 Structure and topology files containing the atomic coordinates, bond connectivity, etc., were prepared for P3HT chains using an in-house script that supports the automated construction of polymers by using generalized repeat-unit templates.A template for regioregular P3HT – the molecular structure of which is shown in Fig. 1(a) – was created based on the parameterization by Huang et al.32 Partial atomic charges were taken as those reported by Huang et al. for neutral chain-end and chain-interior monomers.32 Force field parameterization data is available online as part of the ESI† and in Fig. S1 (ESI†). Fully outstretched P3HT chains of three different molecular weights – 6.25 kDa (38 monomers), 12.5 kDa (75 monomers), and 25 kDa (150 monomers) – were prepared using this template. The larger molecular weight was chosen to correspond to chain lengths used in experiments and other computational works, while the smaller molecular weights were chosen to yield insights into the relationship between chain length and mechanical properties in the crystalline systems.34–37 Based on prior literature,36,37 molecular weights of 6.25 kDa and 12.5 kDa are not expected to result in significant chain entanglement; thus, to conserve computational resources, all amorphous systems studied and reported used a molecular weight of 25 kDa.
To prepare the amorphous systems, 180 fully outstretched P3HT chains (about 60 nm per chain and approximately 6.8 × 105 atoms total) were inserted into an empty cubic simulation box of dimensions 75 × 75 × 75 nm3 at random positions with random orientations while ensuring no overlap of atomic van der Waals radii. Periodic boundary conditions (PBC) were applied along each axis. After an energy minimization step performed via steepest descent with a force convergence threshold of 10 kJ mol−1, atomic velocities were randomly generated according to a Maxwell distribution at 300 K. The system was then relaxed via a nineteen-step procedure (Table S1, ESI†) comprising rapid cycles of compression, annealing, and low-temperature relaxation. The kinetic perturbation procedure, originally developed by Hofmann et al.38 and by Karayiannis et al.,39 then refined by Larsen et. al.40 was adapted from our previous simulations of conjugated polymers.41,42 The approach resulted in a condensed, amorphous P3HT system with an average density of 1.04 g cm−3 at 300 K and 1 bar, a value consistent with experiment and previous computational works.28,37
To model a neat crystalline system, we followed a slab approach previously used to rationalize the thermal behavior of OS.43,44 An orthorhombic slab comprising 90 copies of the isolated 25 kDa chain (approximately 3.4 × 105 atoms total) was constructed within a periodic simulation box. The π-stacking direction (i.e., stacking along the thiophene plane-normal direction) contains 18 chains while the lamellar stacking direction (stacking along the alkyl side chain direction) contains five “sheets” (of 18 chains each). Based on a study of low-energy P3HT polymorphism by Zhugayevych et al.,16 alternate P3HT chains in our crystalline slabs are flipped. Table S2 (ESI†) shows the experimentally derived crystal structure data at 230 K that guided the construction of the crystalline system.28,45
All systems began with equilibration to achieve a stabilized system temperature and density. The amorphous system was equilibrated for 20 ns at 300 K and 1 bar. The crystalline system was first equilibrated for 5 ns at 230 K with the system volume fixed, then equilibrated further for 15 ns at the same temperature with a constant pressure of 1 bar. All MD simulations then used the GROMACS leapfrog-based MD integrator setting with a time step of 2 fs. The linear constraint solver (LINCS) was used to constrain hydrogen bonds to their equilibrium lengths. Long-range interactions were modeled using particle mesh Ewald summation, while the short-range van der Waals and Coulombic electrostatic interactions were described using a Lennard-Jones potential with a cut-off range of 1.4 nm. NVT (constant number, N, volume, V, temperature, T) equilibration steps were performed using the velocity-rescale thermostat46 with τT = 0.1 ps. In addition to this thermostat, NPT (constant number, N, pressure, P, temperature, T) equilibration steps were performed using a Berendsen barostat47 with τP = 1.0 ps. By contrast, all production steps were performed within an NPT ensemble using a Nosé–Hoover thermostat48,49 with τT = 0.4 ps and a Parrinello–Rahman barostat50 with τP = 4.0 ps. Unless noted otherwise, all subsequent NVT and NPT steps were performed using these conditions, with all NPT steps using a pressure of 1 bar.
Following equilibration at their respective initial temperatures, the amorphous and crystalline systems were cooled to 150 K, going well below the reported P3HT glass transition temperature.51–55 At this point, preparation of the 12.5 kDa and 6.25 kDa variations of the crystalline system involved truncating chains in the equilibrated 25 kDa slab at 150 K, replacing terminal carbon atoms with hydrogen atoms. The in-house script was used to prepare structure and topology files for the 12.5 kDa and 6.25 kDa chains. Fig. S2 (ESI†) displays snapshots of the crystalline and amorphous systems at various stages of construction. Fig. 1(b) and (c) show a snapshot of the equilibrated amorphous system at 150 K with and without PBC, respectively. Fig. 1(d) and (e) show end views (alkyl-stacking and π-stacking axes) of the equilibrated 25 kDa per chain crystalline slab at 150 K. Fig. 1(f), (g), and (h) show side views (alkyl-stacking and backbone axes) of the 6.25 kDa per chain, 12.5 kDa per chain, and 25 kDa per chain slabs, respectively. While we recognize that the chain lengths and numbers of chains used in the crystalline simulations may be larger than expected in a semicrystalline polymer, we used these model sizes to ensure that the systems were large enough to provide enough physical contacts in these relatively small (compared to experiment) volumes to describe the thermal and mechanical properties.
To study phase transitions arising during heating, the amorphous system was then further cooled to 50 K at a constant rate of 10 K ns−1. After the cooling step, the amorphous system underwent 5 ns of NVT equilibration, followed by 15 ns of NPT production MD to ensure equilibration. The system was then heated to 530 K at a rate of 10 K ns−1. We performed the pre-annealing steps – i.e., cooling and subsequent equilibration – to widen the range of temperatures across which to track thermal transitions during the annealing step. Although the crystalline system also underwent a heating procedure (see Fig. S42, ESI†), the system remained ordered well beyond the melting temperature due to a superheating effect that has been widely reported in literature for crystalline slabs, related to the lack of high-free-energy internal surfaces at which melting can initiate.43,44
To characterize the temperature-dependent stress–strain behavior in the amorphous and crystalline systems, individual snapshots at 300 K and 400 K were extracted from the heating step for comparison with the corresponding system at 150 K. These higher temperature frames were chosen to probe the mechanical properties across a range of operating temperatures relevant to OS devices, with 150 K being well below (and 400 K well above) the experimentally reported glass transition temperature of regioregular P3HT (Tg ≈ 285–295 K).51–53 All extracted frames underwent at least 70 ns of additional NVT and NPT equilibrations, with the first 2 ns being NVT, until their temperatures and densities were stabilized. The bulk density of each system, taken as the average from the final 5 ns of production MD performed following equilibration, is reported in Table 1.
| Temperature (K) | Amorphous P3HT | Crystalline P3HT | ||
|---|---|---|---|---|
| 25 kDa per chain | 25 kDa per chain | 12.5 kDa per chain | 6.25 kDa per chain | |
| 150 | 1.12 ± 0.02 | 1.13 ± 0.00 | 1.11 ± 0.00 | 1.08 ± 0.00 |
| 300 | 1.07 ± 0.00 | 1.05 ± 0.00 | 1.04 ± 0.00 | 1.01 ± 0.00 |
| 400 | 1.03 ± 0.00 | 0.95 ± 0.00 | 0.93 ± 0.00 | 0.92 ± 0.00 (original) |
| 1.05 ± 0.00 (adjusted) | ||||
After convergence, the deform keyword in GROMACS was used to produce stress–strain simulations of each of the six groups of systems – i.e., the crystalline and amorphous systems at 150 K, 300 K, and 400 K each. Uniaxial deformation in GROMACS using the deform keyword requires semi-isotropic pressure coupling and elongates the system along the z-axis at a constant rate. For each system, two copies of the undeformed system were rotated to allow deformation along each of the other two axes as well (except for the crystalline system backbone axis). We note that, for all systems studied, only one simulation was performed for the respective thermal and stress–strain evaluations; the combination of relatively large system sizes and simulation times, plus experimental validation where possible, provide statistical confidence in results presented.
Each system was simulated using at least one of two deformation rates. The faster rate (ȧfast = daz/dt = 5 × 10−3 nm ps−1) was used to model the stress–strain response up to 500% strain, whereas simulations using the slower rate (ȧslow = 5 × 10−4 nm ps−1) extended only to 200% strain (150% for cP3HT). In this work, strain refers to the engineering strain ε, calculated for the uniaxial strain along the z-axis as;
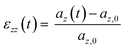 | (1) |
| σzz(t) = −Pzz(t) | (2) |
The estimated values of Young's modulus (E) and Poisson's ratio (ν) were computed from the linear elastic region of the stress–strain curves (up to approximately 2% strain), wherein σzz is linear in εzz. Young's modulus was calculated as the slope of a linear regression of σzz on εzz within the elastic region. Similarly, Poisson's ratio was determined from the negative slope of a linear regression of εxx on εzz (or, equivalently, of εyy on εzz) within the elastic region. We determined ν only for the amorphous systems, as for the highly anisotropic crystalline systems the theoretical limit of 0.5 is not applicable. To examine the effect of the upper bound of the fitting window, the approximate value of dσ/dε was also determined as a function of strain via the finite difference method across a window of Δε = (ε + 0.5w) − (ε − 0.5w) in the elastic region. Plots of dσ/dε as a function of ε for different values of w are shown for the amorphous systems in Fig. S6–S14 and for the crystalline systems in Fig. S15–S32, available in the ESI.†
Finally, to quantify the entanglement properties in the amorphous systems, we applied the Z1+ package developed by Kröger and co-workers.60–62 At each of the three temperatures for which we performed stress–strain simulations (150 K, 300 K, and 400 K), we took snapshots from the system trajectory at every 1% strain; to examine the isotropy of the entanglement characteristics, we repeated this for each of the three uniaxial deformation axes. This resulted in a total of 1800 snapshots across all deformation axes and temperatures.
For each snapshot, we applied a coarse-graining procedure to the polymer chains to simplify the atomic connectivity so that the primitive paths could be determined. A full entanglement analysis was repeated for each of the two coarse-graining approaches illustrated in ESI† Fig. S33. Results in the main text correspond to the first coarse-graining method, which reduces each thiophene unit to a single bead located at the average (x, y, z) coordinate of the five atoms in the thiophene ring. The second method calculates the position of the bead as the closest point between the vectors defined by the bonds connecting the thiophene unit to the two neighboring units; results for this method, including the primitive path lengths, are available in Fig. S34 (ESI†).
We also analyzed the effect of system size on the entanglement characteristics by preparing “doubled” and “tripled” slabs. To produce these doubled and tripled slabs for each snapshot, we used the dimensions (max, may, maz) of the original “single” box (with m = 1) and produced two other boxes using m = 2 and m = 3. For each of these models, a total of c = m3 copies of the original system are placed at each of the translation vectors tc in the set {tc} = [nxax, nyay, nzaz], where ni = {0, 1, …, m−1}. Visual representations of these three slab sizes are shown in Fig. S35 (ESI†). Results in the main text correspond to the tripled slabs to minimize the effects of system size, but a comparison of the entanglement characteristics for different system sizes are available in the ESI† as Fig. S36–S40.
Results and discussion
Thermomechanical behavior of amorphous P3HT
We begin our discussion of the amorphous systems with the heating step from 50 K to 530 K, performed to determine the temperatures at which thermal transitions in the system take place. By plotting the system density as a function of temperature, as shown in Fig. 2, we observe two transitions, one centered at ≈220–230 K and the other centered at ≈370–380 K. These transitions can be identified by changes in the slope (dρ/dT). To examine the range of temperatures over which the thermal transitions take place, the approximate value of dρ/dT was determined for each temperature via the finite difference method across a window of ΔT = (T + 0.5w) − (T − 0.5w) = w. Plots of dρ/dT as a function of T for different values of w are shown in Fig. S41 (ESI†). The discrepancy between the backbone Tg of 285-295 K reported in prior literature51–55 and the thermal transitions reported herein may be a result of the continuous heating rate. Although 10 K ns−1 is a relatively slow heating rate for simulation, it is nonetheless much faster than heating rates in experimental systems. Further, the simulated heating rate is expected to affect the value of Tg; for instance, faster cooling rates are known to lead to artificially elevated transition temperatures.41 Nonetheless, we observe that the amorphous system has clearly undergone one thermal transition between 150 K and 300 K and another between 300 K and 400 K. It is thus of interest to examine how the stress–strain curves, Young's moduli, Poisson's ratios, and entanglement characteristics vary in these three temperature ranges.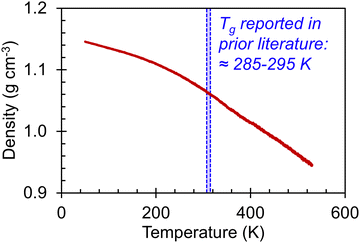 | ||
| Fig. 2 (red line) Amorphous P3HT system density as a function of temperature during continuous heating from 50 K to 530 K at a rate of 10 K ns−1. (blue shaded region) A range of Tg values previously reported in literature for P3HT.51–55 | ||
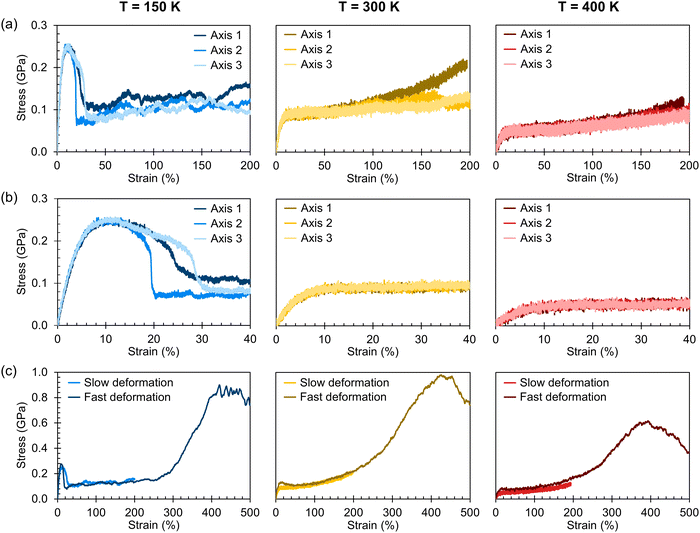
Stress–strain curves showing the uniaxial tensile response of each axis of the amorphous system at 150 K, 300 K, and 400 K are shown in Fig. 3. Young's modulus and Poisson's ratio were determined from the elastic region of each system, which is emphasized in Fig. 3(b); values of these properties, which agree well with prior atomistic modeling at 300 K,37 albeit at different molecular weights, are reported in Table 2. As expected, Young's modulus is significantly higher at 150 K compared to both other temperatures, with a pronounced upper yield point. This upper yield point disappears at 300 K and 400 K, likely corresponding to the thermal transition observed at 220–230 K. However, the thermal transition occurring at 370–380 K does not appear to qualitatively affect the stress–strain curves – the only noteworthy difference between the two temperatures is the lower overall stress at 400 K.
| Temperature (K) | Axis 1 | Axis 2 | Axis 3 | |||
|---|---|---|---|---|---|---|
| E (GPa) | ν | E (GPa) | ν | E (GPa) | ν | |
| 150 | 5.22 | 0.33 | 5.32 | 0.32 | 5.21 | 0.32 |
| 300 | 1.80 | 0.38 | 1.76 | 0.38 | 1.62 | 0.39 |
| 400 | 0.80 | 0.39 | 0.81 | 0.41 | 0.86 | 0.40 |
At all three temperatures, the mechanical response (including Young's modulus and Poisson's ratio) remains essentially isotropic up to about 10% strain; the stress becomes anisotropic at this point at 150 K, whereas it remains isotropic until about 50% at 300 K and about 100% at 400 K. The greater isotropy in the higher-temperature systems is likely due to the chains being more mobile at the elevated temperatures; at 150 K, we hypothesize that chains face more difficulty in coming free of entanglements due to the lower thermal energy. The lack of mobility at 150 K can also explain the ruggedness of the stress–strain curves at 150 K compared to those at higher temperatures. Whereas pulling the chains taut between entanglements requires relatively little stress, once the chains are taut, the entanglements become significant obstacles to further deformation until the chains are pulled free, which requires higher stress. At higher temperatures, however, pulling chains free of entanglements becomes easier, leading to a more consistent stress response.
The effect of deformation rate is illustrated in Fig. 3(c) for Axis 1. As the fast deformation rate is 10× faster than the slow rate, each system has less time to respond to the increasing box size. Because the chains cannot respond quickly enough to the deformation, the stress response in the elastic region is higher than in the systems deformed at the slower rate. The fast deformation rate also results in the appearance of upper yield points at 300 K and 400 K, features that are not present in the more slowly deformed systems.
It is noteworthy that, for the slowly deformed systems, Axis 1 appears to be tougher than Axes 2 and 3; beyond the onset of anisotropy at each temperature, the stress–strain curve for Axis 1 is higher than those for the other two axes. The anisotropy of the amorphous systems at higher strain poses a question: Is there a texturing effect present in the amorphous systems prior to deformation that results in the different stress responses along each axis? To examine this question, a series of plots representing the system texture were prepared by first determining two orientation vectors (OVs) for each thiophene unit in the system. The first vector,  , illustrated at the bottom left of Fig. 4, is calculated from the positions of the two carbon atoms neighboring the sulfur atom; this OV roughly corresponds to the tangent vector of the backbone.
, illustrated at the bottom left of Fig. 4, is calculated from the positions of the two carbon atoms neighboring the sulfur atom; this OV roughly corresponds to the tangent vector of the backbone.  , illustrated at the bottom right of Fig. 4, is the normal vector of each thiophene unit, calculated as the cross product of
, illustrated at the bottom right of Fig. 4, is the normal vector of each thiophene unit, calculated as the cross product of  and a proxy vector (defined as starting at the carbon in
and a proxy vector (defined as starting at the carbon in  and ending at its neighboring carbon). All OVs are normalized and plotted with their tails at the origin. The resulting texture plots are shown for Axis 1 at all three temperatures in Fig. 4. Plots showing all three axes at the same temperature are presented in the ESI† as Fig. S43–S45.
and ending at its neighboring carbon). All OVs are normalized and plotted with their tails at the origin. The resulting texture plots are shown for Axis 1 at all three temperatures in Fig. 4. Plots showing all three axes at the same temperature are presented in the ESI† as Fig. S43–S45. 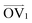 and
and  are each represented by a different color for each chain (with all thiophene units in a given chain using the same color).
are each represented by a different color for each chain (with all thiophene units in a given chain using the same color).
 | ||
| Fig. 4 Texture maps showing the alignment of the backbone direction (yellow to cyan circles) and thiophene plane normal directions (red to purple circles) at each temperature for deformation axis 1. | ||
The first feature evident from the texture plots in Fig. 4 and Fig. S43–S45 (ESI†) is that the amorphous systems are untextured; as evidenced by the plots at 0% strain, the distributions of  and
and 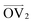 are essentially random. With increasing strain,
are essentially random. With increasing strain,  becomes more highly oriented along the axis of deformation (z), indicating that the backbone is more elongated and linear. By contrast, the values of
becomes more highly oriented along the axis of deformation (z), indicating that the backbone is more elongated and linear. By contrast, the values of  become more focused in a ring wherein the z-component is closer to 0. However, the radial symmetry of the
become more focused in a ring wherein the z-component is closer to 0. However, the radial symmetry of the  distribution suggests that the thiophene units are not locally planar, instead remaining roughly randomly oriented. We also note that the texture increases not only as a function of strain, but also as a function of temperature – for example, the systems with 50% strain at 400 K appear to be similarly textured as the systems with 100–150% strain at 150 K.
distribution suggests that the thiophene units are not locally planar, instead remaining roughly randomly oriented. We also note that the texture increases not only as a function of strain, but also as a function of temperature – for example, the systems with 50% strain at 400 K appear to be similarly textured as the systems with 100–150% strain at 150 K.
Finally, the entanglement properties of each system are shown in Fig. 5. To aid in making comparisons, the stress–strain data is presented again in Fig. 5(a), this time grouped by deformation axis. Fig. 5(b) shows the average number of entanglements per chain, 〈Z〉. As stated previously, these plots correspond to the “tripled” slabs to reduce the intensity of finite-size effects; as shown in Fig. S36–S40 in the ESI,† the differences in the entanglement properties determined for the three slab sizes are relatively minimal.
The variation of 〈Z〉 as the system is strained is not straightforward to parse. On the one hand, for deformation along Axes 1 and 3 at 300 K and at 400 K, the values of 〈Z〉 and stress appear to increase together beyond approximately 100% strain, a feature that may suggest that an increase in chain entanglement plays a role in producing the strain hardening effect observed at higher strain. However, this trend is not consistent with deformation along Axis 2 and the relationship between stress and 〈Z〉 at 150 K is unclear. We suggest that increasing strain modulates the rates of entanglement creation and destruction, as well as the effective entanglement lifetime, all three of which in turn influence the stress response of the bulk material.
 | ||
| Fig. 5 (a) Stress–strain curves shown in Fig. 3(a) grouped instead by deformation axis and with a moving average of width 1.5 ns applied. (b) Average number of entanglements per chain, 〈Z〉, as a function of strain for each of the stress–strain curves in (a), also with a moving average of 1.5 ns applied. | ||
Thermomechanical behavior of crystalline P3HT
While there are previous efforts to understand the anisotropic charge-carrier transport behavior along the π-stacking and alkyl-stacking axes in organic semiconductors,17,18,63–66 the thermal dependence of mechanical properties remain less clear. In Fig. 6, we report axis-dependent stress–strain curves at 150 K, 300 K, and 400 K for crystalline P3HT slabs composed of the three molecular weights: 25 kDa (the same chain size as the amorphous systems), 12.5 kDa, and 6.25 kDa. To highlight the effect of chain molecular weight (MW), a zoomed-in view of the elastic regions of the same stress–strain curves is presented in Fig. 7 grouped by temperature. | ||
| Fig. 7 Zoomed view of the elastic region of the simulated stress–strain curves shown in Fig. 6. To highlight the effect of chain MW on the Young's modulus, the three MW are compared at temperatures of (a) 150 K, (b) 300 K, and (c) 400 K. | ||
Broadly, it is evident that systems deformed along the π-stacking axis resist fracture to a greater extent than those deformed along the alkyl-stacking axis, irrespective of chain MW. In the π-stacking deformation series, a sharp elastic region is followed by a yield peak, a lower yield plateau, and then stress values gradually increasing toward an ultimate tensile strength. However, in the case of the 6.25 kDa system at 150 K, there are two characteristic yield peaks, beyond which the system more closely mirrors the other π-stacking deformation systems. At 300 K, the slab yields at a lower stress, and the yield peak itself is significantly less pronounced, while at 400 K, the yield peak has nearly disappeared. The Young's modulus appears relatively insensitive to chain size in these idealized slabs: For most subplots in Fig. 7, both in the π-stacking and the alkyl-stacking series, the slope of the elastic region is not significantly affected by the chain MW. The values of the Young's moduli for both chain-stacking series are shown in Table 3.
| Temperature (K) | E (GPa), π-stacking axis | E (GPa), alkyl-stacking axis | ||||
|---|---|---|---|---|---|---|
| 25 kDa per chain | 12.5 kDa per chain | 6.25 kDa per chain | 25 kDa per chain | 12.5 kDa per chain | 6.25 kDa per chain | |
| a After noticing misalignment in the slab, we adjusted the alignment and repeated the deformation with the updated slab orientation. b Due to noise within the elastic region, directly applying a least-squares model up to 2% strain to this system results in a negative slope. To better explore the effect of the fitting window on the estimated value of Young's modulus, we applied a finite-difference method with a moving window to the stress–strain data. Plots of dσ/dε are presented as Fig. S6–S32 in the ESI (see S32). | ||||||
| 150 | 3.64 | 3.48 | 2.94 | 5.53 | 5.45 | 4.79 |
| 300 | 1.62 | 1.38 | 1.19 | 1.03 | 1.25 | 1.01 |
| 400 | 0.77 | 0.64 | 0.30a (original) | 0.16 | −0.03b | —a (original) |
| 0.90a (adjusted) | 0.23a (adjusted) | |||||
Notably, the π-stack series resists fracture up to 150% strain regardless of temperature or chain MW. Upon examination of the morphology, we find that the strong cohesion between π-stacked P3HT fragments leads the morphology to buckle rather than fracture, resulting in a zigzag morphology with high ductility. Snapshots of the amorphous and crystalline systems at a range of values of strain are presented in the ESI† as Fig S46–S48 and Tables S3–S5. It is also interesting to note that the stress–strain curves for the π-stacked series of smaller chain MW are more rugged. We hypothesize that this phenomenon is due to the smaller chains diffusing more easily, while the strong interlayer cohesion helps to prevent delamination.
In the alkyl-stacking deformation series (the columns on the right in Fig. 6 and 7), the elastic region is characterized by a steep slope, with the yield strength being high compared to deformation along the π-stacking axis. The slabs still show a pronounced yield peak at higher temperatures, unlike in the π-stacking series, but the yield stress itself greatly decreases. After yielding, the stress does not increase toward an ultimate tensile strength, but rather proceeds monotonically toward failure from the initial yielding regime. Deformation along the alkyl-stacking axis resulted in fracture within the strain window explored, with only one exception (MW = 6.25 kDa, T = 400 K). Overall, for the alkyl-stacking series, higher chain MW delays the onset of fracture, with fracture occurring within 150% strain at 150 K for the system with 25 kDa chains (Fig. 6a), compared to 100% and 25% strain for the systems with chain MW of 12.5 kDa (Fig. 6b) and 6.25 kDa (Fig. 6c), respectively.
As noted, the system with 6.25 kDa chains at 400 K is an exception to the trends discussed above. During the equilibration process of this system, the slab became misaligned with the strain axes. To make comparisons between results for the π-stacking and alkyl-stacking axes more consistent, we realigned the equilibrated slab, correcting the misalignment but resulting in a parallelepiped slab shape. Further discussion of this system on its own is available in Section 8 of the ESI,† including comparisons between the stress–strain curves for both the original (equilibrated) slab and the reoriented slab.
Conclusions
In this work, we report the stress–strain curves and associated mechanical characteristics of fully amorphous and fully crystalline P3HT systems obtained via atomistic MD simulations at three temperatures (150 K, 300 K, and 400 K). As expected, the amorphous systems show high isotropy in their mechanical response: Independent stress–strain simulations along each of the three coordinate axes result in nearly identical elastic regions, with no significant differences among the three deformation axes until approximately 100% strain. The amorphous systems show high ductility, extending to at least 400% at all temperatures before reaching the ultimate tensile point. We hypothesize that this result is due to chain entanglement, although due to the relatively short chains (25 kDa per chain) compared to experimental MW, we did not observe concrete trends in the chain entanglement data as a function of strain.In the crystalline slabs, which were designed to have no chain entanglement, the observed ductility is significantly lower, although the Young's moduli along the π-stacking and alkyl-stacking axes are still quite high. Stress–strain simulations, including systems with shorter chains (6.25 kDa per chain and 12.5 kDa per chain, compared to 25 kDa per chain) reveal that a slip-facilitated chain buckling mode along the π-stacking axis enables relatively high ductility in these systems (above 150% strain at all temperatures and for all chain MW). By contrast, deformation along the alkyl-stacking axis results in a “chain-unzipping” failure within 150% strain for all systems, with one exception (discussed above and in ESI†).
On its own, this work offers insights into the deformation response and failure mode of P3HT in the fully amorphous and fully crystalline phases. More broadly, through this work, we establish a foothold for characterization of the RAF and MAF in P3HT. These regions in semiconducting polymers are influential to the optical, electronic, mechanical, and thermal properties, as well as the bulk morphology, and require further investigation to realize their full impact.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. K. H. F., C. P. C., and C. R. conceived the research. K. H. F. and C. P. C. carried out the simulations and analyses. C. R. supervised the research, established funding for the research, and provided contributions to interpreting the results and drafting the manuscript.Data availability
The data supporting this article are included as part of the ESI.† Information pertaining to the force field parameters and structure file are provided as additional files.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the Office of Naval Research (ONR) through award number N00014-22-1-2179 (for simulations and data analyses) and the National Science Foundation (NSF) under cooperative agreement number 1849213 (force field development). Supercomputing resources were provided by the Department of Defense (DoD) through the DoD High Performance Computing Modernization Program (HPCMP; Project No. ONRDC40433481) and by the University of Kentucky Information Technology Department and Center for Computational Sciences (CCS).References
- B. V. Khau, A. D. Scholz and E. Reichmanis, Advances and opportunities in development of deformable organic electrochemical transistors, J. Mater. Chem. C, 2020, 8, 15067–15078, 10.1039/D0TC03118F.
- J. A. Rogers, T. Someya and Y. Huang, Materials and Mechanics for Stretchable Electronics, Science, 2010, 327, 1603–1607, DOI:10.1126/science.1182383.
- L. Portilla, K. Loganathan, H. Faber, A. Eid, J. G. D. Hester, M. M. Tentzeris, M. Fattori, E. Cantatore, C. Jiang, A. Nathan, G. Fiori, T. Ibn-Mohammed, T. D. Anthopoulos and V. Pecunia, Wirelessly powered large-area electronics for the Internet of Things, Nat. Electron., 2023, 6, 10–17, DOI:10.1038/s41928-023-00927-x.
- B. Wang and A. Facchetti, Mechanically Flexible Conductors for Stretchable and Wearable E-Skin and E-Textile Devices, Adv. Mater., 2019, 31, 1901408, DOI:10.1002/adma.201901408.
- L. Ding, Z.-D. Yu, X.-Y. Wang, Z.-F. Yao, Y. Lu, C.-Y. Yang, J.-Y. Wang and J. Pei, Polymer Semiconductors: Synthesis, Processing, and Applications, Chem. Rev., 2023, 123(12), 7421–7497, DOI:10.1021/acs.chemrev.2c00696.
- D. W. Kim, S. W. Kim, G. Lee, J. Yoon, S. Kim, J.-H. Hong, S.-C. Jo and U. Jeong, Fabrication of practical deformable displays: advances and challenges, Light: Sci. Appl., 2023, 12, 61, DOI:10.1038/s41377-023-01089-3.
- O. Ostroverkhova, Organic Optoelectronic Materials: Mechanisms and Applications, Chem. Rev., 2016, 116(22), 13279–13412, DOI:10.1021/acs.chemrev.6b00127.
- J.-H. Kim, I. Lee, T.-S. Kim, N. Rolston, B. L. Watson and R. H. Dauskardt, Understanding mechanical behavior and reliability of organic electronic materials, MRS Bull., 2017, 42(2), 115–123, DOI:10.1557/mrs.2017.3.
- H. Ling, S. Liu, Z. Zheng and F. Yan, Organic Flexible Electronics, Small Methods, 2018, 2, 1800070, DOI:10.1002/smtd.201800070.
- D. J. Lipomi and Z. Bao, Stretchable and ultraflexible organic electronics, MRS Bull., 2017, 42(2), 93–97, DOI:10.1557/mrs.2016.325.
- R. Xie, R. H. Colby and E. D. Gomez, Connecting the Mechanical and Conductive Properties of Conjugated Polymers, Adv. Electron. Mater., 2018, 4, 1700356, DOI:10.1002/aelm.201700356.
- A. D. Printz and D. J. Lipomi, Competition between deformability and charge transport in semiconducting polymers for flexible and stretchable electronics, Appl. Phys. Rev., 2016, 3(2), 021302, DOI:10.1063/1.4947428.
- N. Balar, Y. Xiong, L. Ye, S. Li, D. Nevola, D. B. Dougherty, J. Hou, H. Ade and B. T. O’Connor, Role of Polymer Segregation on the Mechanical Behavior of All-Polymer Solar Cell Active Layers, ACS Appl. Mater. Interfaces, 2017, 9(50), 43886–43892, DOI:10.1021/acsami.7b13719.
- V. Bhat, C. P. Callaway and C. Risko, Computational Approaches for Organic Semiconductors: From Chemical and Physical Understanding to Predicting New Materials, Chem. Rev., 2023, 123(12), 7498–7547, DOI:10.1021/acs.chemrev.2c00704.
- H. M. Luong, S. Chae, A. Yi, K. Ding, J. Huang, B. M. Kim, C. Welton, J. Chen, H. Wakidi, Z. Du, H. J. Kim, Harald Ade, G. N. M. Reddy and T.-Q. Nguyen, Impact of Thermal Stress on Device Physics and Morphology in Organic Photodetectors, ACS Energy Lett., 2023, 8(5), 2130–2140, DOI:10.1021/acsenergylett.3c00272.
- A. Zhugayevych, O. Mazaleva, A. Naumov and S. Tretiak, Lowest-Energy Crystalline Polymorphs of P3HT, J. Phys. Chem. C, 2018, 122(16), 9141–9151, DOI:10.1021/acs.jpcc.7b11271.
- C. Sutton, C. Risko and J.-L. Brédas, Noncovalent Intermolecular Interactions in Organic Electronic Materials: Implications for the Molecular Packing vs Electronic Properties of Acenes, Chem. Mater., 2016, 28(1), 3–16, DOI:10.1021/acs.chemmater.5b03266.
- B. O’Connor, E. P. Chan, C. Chan, B. R. Conrad, L. J. Richter, R. J. Kline, M. Heeney, I. McCulloch, C. L. Soles and D. M. DeLongchamp, Correlations between Mechanical and Electrical Properties of Polythiophenes, ACS Nano, 2010, 4(12), 7538–7544, DOI:10.1021/nn1018768.
- S. Marina, E. Gutierrez-Fernandez, J. Gutierrez, M. Gobbi, N. Ramos, E. Solano, J. Rech, W. You, L. Hueso, A. Tercjak, H. Ade and J. Martin, Semi-paracrystallinity in semi-conducting polymers, Mater. Horiz., 2022, 9(4), 1196–1206, 10.1039/D1MH01349A.
- E. K. Lee, M. Y. Lee, C. H. Park, H. R. Lee and J. H. Oh, Toward Environmentally Robust Organic Electronics: Approaches and Applications, Adv. Mater., 2017, 29, 1703638, DOI:10.1002/adma.201703638.
- J. Menczel and B. Wunderlich, Heat capacity hysteresis of semicrystalline macromolecular glasses, J. Polym. Sci., Polym. Lett. Ed., 1981, 19(5), 261–264, DOI:10.1002/pol.1981.130190506.
- B. Wunderlich, Reversible crystallization and the rigid–amorphous phase in semicrystalline macromolecules, Prog. Polym. Sci., 2003, 28(3), 383–450, DOI:10.1016/S0079-6700(02)00085-0.
- R. Remy, S. Wei, L. M. Campos and M. E. Mackay, Three-Phase Morphology of Semicrystalline Polymer Semiconductors: A Quantitative Analysis, ACS Macro Lett., 2015, 4(9), 1051–1055, DOI:10.1021/acsmacrolett.5b00481.
- J. Martín, N. Stingelin and D. Cangialosi, Direct Calorimetric Observation of the Rigid Amorphous Fraction in a Semiconducting Polymer, J. Phys. Chem. Lett., 2018, 9, 990–995, DOI:10.1021/acs.jpclett.7b03110.
- R. Noriega, J. Rivnay, K. Vandewal, F. P. Koch, N. Stingelin, P. Smith, M. F. Toney and A. Salleo, A general relationship between disorder, aggregation and charge transport in conjugated polymers, Nat. Mater., 2013, 12(11), 1038–1044, DOI:10.1038/nmat3722.
- I. Botiz, M. M. Durbin and N. Stingelin, Providing a Window into the Phase Behavior of Semiconducting Polymers, Macromolecules, 2021, 54(12), 5304–5320, DOI:10.1021/acs.macromol.1c00296.
- T. Qu, G. Nan, Y. Ouyang, B. Bieketuerxun, X. Yan, Y. Qi and Y. Zhang, Structure–Property Relationship, Glass Transition, and Crystallization Behaviors of Conjugated Polymers, Polymers, 2023, 15(21), 4268, DOI:10.3390/polym15214268.
- C. S. Lee and M. D. Dadmun, Important thermodynamic characteristics of poly(3-hexyl thiophene), Polymer, 2014, 55(1), 4–7, DOI:10.1016/j.polymer.2013.11.033.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1, 19–25, DOI:10.1016/j.softx.2015.06.001.
- E. Lindhal, M. J. Abraham, B. Hess and D. van der Spoel, GROMACS 2019.5 Source code, Zenodo, 2019, DOI:10.5281/zenodo.7852175, https://zenodo.org/records/3577986.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38, DOI:10.1016/0263-7855(96)00018-5.
- D. M. Huang, R. Faller, K. Do and A. J. Moulé, Coarse-Grained Computer Simulations of Polymer/Fullerene Bulk Heterojunctions for Organic Photovoltaic Applications, J. Chem. Theory Comput., 2010, 6(2), 526–537, DOI:10.1021/ct900496t.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 1996, 118(45), 11225–11236, DOI:10.1021/ja9621760.
- F. P. V. Koch, J. Rivnay, S. Foster, C. Müller, J. M. Downing, E. Buchaca-Domingo, P. Westacott, L. Yu, M. Yuan, M. Baklar, Z. Fei, C. Luscombe, M. A. McLachlan, M. Heeney, G. Rumbles, C. Silva, A. Salleo, J. Nelson, P. Smith and N. Stingelin, The impact of molecular weight on microstructure and charge transport in semicrystalline polymer semiconductors–poly(3-hexylthiophene), a model study, Prog. Polym. Sci., 2013, 38(12), 1978–1989, DOI:10.1016/j.progpolymsci.2013.07.009.
- A. M. Ballantyne, L. Chen, J. Dane, T. Hammant, F. M. Braun, M. Heeney, W. Duffy, I. McCulloch, D. D. C. Bradley and J. Nelson, The Effect of Poly(3-hexylthiophene) Molecular Weight on Charge Transport and the Performance of Polymer:Fullerene Solar Cells, Adv. Funct. Mater., 2008, 18(16), 2373–2380, DOI:10.1002/adfm.200800145.
- A. G. Dixon, R. Visvanathan, N. A. Clark, N. Stingelin, N. Kopidakis and S. E. Shaheen, Molecular weight dependence of carrier mobility and recombination rate in neat P3HT films, J. Polym. Sci., Part B: Polym. Phys., 2018, 56(1), 31–35, DOI:10.1002/polb.24531.
- N. R. Tummala, C. Risko, C. Bruner, R. H. Dauskardt and J. L. Brédas, Entanglements in P3HT and their influence on thin-film mechanical properties: Insights from molecular dynamics simulations, J. Polym. Sci., Part B: Polym. Phys., 2015, 53(13), 934–942, DOI:10.1002/polb.23722.
- D. Hofmann, L. Fritz, J. Ulbrich, C. Schepers and M. Böhning, Detailed-atomistic molecular modeling of small molecule diffusion and solution processes in polymeric membrane materials, Macromol. Theory Simul., 2000, 9(6), 293–327, DOI:10.1002/1521-3919(20000701)9:6<293::AID-MATS293>3.0.CO;2-1.
- N. C. Karayiannis, V. G. Mavrantzas and D. N. Theodorou, Detailed Atomistic Simulation of the Segmental Dynamics and Barrier Properties of Amorphous Poly(ethylene terephthalate) and Poly(ethylene isophthalate), Macromolecules, 2004, 37(8), 2978–2995, DOI:10.1021/ma0352577.
- G. S. Larsen, P. Lin, K. E. Hart and C. M. Colina, Molecular Simulations of PIM-1-like Polymers of Intrinsic Microporosity, Macromolecules, 2011, 44(17), 6944–6951, DOI:10.1021/ma200345v.
- C. P. Callaway, J. H. Bombile, W. Mask, S. M. Ryno and C. Risko, Thermomechanical enhancement of DPP-4T through purposeful π-conjugation disruption, J. Polym. Sci., 2022, 60(3), 559–568, DOI:10.1002/pol.20210494.
- S. M. Ryno and C. Risko, Deconstructing the behavior of donor–acceptor copolymers in solution & the melt: the case of PTB7, Phys. Chem. Chem. Phys., 2019, 21(15), 7802–7813, 10.1039/C9CP00777F.
- S. Li, S. M. Ryno and C. Risko, Exploring thermal transitions in anthradithiophene-based organic semiconductors to reveal structure-packing relationships, J. Mater. Chem. C, 2018, 6(40), 10924–10934, 10.1039/C8TC03976C.
- Q. Chen, E. B. Sirota, M. Zhang, T. C. M. Chung and S. T. Milner, Free Surfaces Overcome Superheating in Simulated Melting of Isotactic Polypropylene, Macromolecules, 2015, 48(24), 8885–8896, DOI:10.1021/acs.macromol.5b02030.
- Z. Cao, L. Galuska, Z. Qian, S. Zhang, L. Huang, N. Prine, T. Li, Y. He, K. Hong and X. Gu, The effect of side-chain branch position on the thermal properties of poly(3-alkylthiophenes), Polym. Chem., 2020, 11(2), 517–526, 10.1039/C9PY01026B.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 014101, DOI:10.1063/1.2408420.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690, DOI:10.1063/1.448118.
- S. Nosé, A molecular dynamics method for simulations in the canonical ensemble, Mol. Phys., 1984, 52(2), 255–268, DOI:10.1080/00268978400101201.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31(3), 1695, DOI:10.1103/PhysRevA.31.1695.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190, DOI:10.1063/1.328693.
- R. Xie, Y. Lee, M. P. Aplan, N. J. Caggiano, C. Müller, R. H. Colby and E. D. Gomez, Glass Transition Temperature of Conjugated Polymers by Oscillatory Shear Rheometry, Macromolecules, 2017, 50(13), 5146–5154, DOI:10.1021/acs.macromol.7b00712.
- J. Zhao, A. Swinnen, G. Van Assche, J. Manca, D. Vanderzande and B. V. Mele, Phase Diagram of P3HT/PCBM Blends and Its Implication for the Stability of Morphology, J. Phys. Chem. B, 2009, 113(6), 1587–1591, DOI:10.1021/jp804151a.
- Z. Qian, L. Galuska, W. W. McNutt, M. U. Ocheje, Y. He, Z. Cao, S. Zhang, J. Xu, K. Hong, R. B. Goodman, S. Rondeau-Gagné, J. Mei and X. Gu, Challenge and Solution of Characterizing Glass Transition Temperature for Conjugated Polymers by Differential Scanning Calorimetry, J. Polym. Sci., Part B: Polym. Phys., 2019, 57(23), 1635–1644, DOI:10.1002/polb.24889.
- S. E. Root, S. Savagatrup, C. J. Pais, G. Arya and D. J. Lipomi, Predicting the Mechanical Properties of Organic Semiconductors Using Coarse-Grained Molecular Dynamics Simulations, Macromolecules, 2016, 49(7), 2886–2894, DOI:10.1021/acs.macromol.6b00204.
- J. Munshi, T. Chien, W. Chen and G. Balasubramanian, Elasto-morphology of P3HT:PCBM bulk heterojunction organic solar cells, Soft Matter, 2020, 16(29), 6743–6751, 10.1039/D0SM00849D.
- V. M. Nazarychev, A. V. Lyulin, S. V. Larin, A. A. Gurtovenko, J. M. Kenny and S. V. Lyulin, Molecular dynamics simulations of uniaxial deformation of thermoplastic polyimides, Soft Matter, 2016, 12, 3972–3981, 10.1039/C6SM00230G.
- S. E. Root, N. E. Jackson, S. Savagatrup, G. Arya and D. J. Lipomi, Modelling the morphology and thermomechanical behaviour of low-bandgap conjugated polymers and bulk heterojunction films, Energy Environ. Sci., 2017, 10, 558–569, 10.1039/C6EE03456J.
- N. R. Tummala, C. Bruner, C. Risko, J.-L. Brédas and R. H. Dauskardt, Molecular-Scale Understanding of Cohesion and Fracture in P3HT:Fullerene Blends, ACS Appl. Mater. Interfaces, 2015, 7(18), 9957–9964, DOI:10.1021/acsami.5b02202.
- N. R. Tummala, S. G. Aziz, V. Coropceanu and J.-L. Bredas, Characterization of the structural, mechanical, and electronic properties of fullerene mixtures: a molecular simulations description, J. Mater. Chem. C, 2018, 6(14), 3642–3650, 10.1039/C7TC03820H.
- S. Shanbhag and M. Kröger, Primitive Path Networks Generated by Annealing and Geometrical Methods: Insights into Differences, Macromolecules, 2007, 40(8), 2897–2903, DOI:10.1021/ma062457k.
- R. S. Hoy, K. Foteinopoulou and M. Kröger, Topological analysis of polymeric melts: Chain-length effects and fast-converging estimators for entanglement length, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031803, DOI:10.1103/PhysRevE.80.031803.
- M. Kröger, J. D. Dietz, R. S. Hoy and C. Luap, The Z1+ package: Shortest multiple disconnected path for the analysis of entanglements in macromolecular systems, Comput. Phys. Commun., 2023, 283, 108567, DOI:10.1016/j.cpc.2022.108567.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Charge Transport in Organic Semiconductors, Chem. Rev., 2007, 107(4), 926–952, DOI:10.1021/cr050140x.
- J. Cornil, D. Beljonne, J. P. Calbert and J. L. Brédas, Interchain Interactions in Organic π-Conjugated Materials: Impact on Electronic Structure, Optical Response, and Charge Transport, Adv. Mater., 2001, 13(14), 1053–1067, DOI:10.1002/1521-4095(200107)13:14<1053::AID-ADMA1053>3.0.CO;2-7.
- S. M. Gali, C. Quarti, Y. Olivier, J. Cornil, L. Truflandier, F. Castet, L. Muccioli and D. Beljonne, Impact of structural anisotropy on electro-mechanical response in crystalline organic semiconductors, J. Mater. Chem. C, 2019, 7(15), 4382–4391, 10.1039/C8TC06385K.
- V. Bhat, B. Ganapathysubramanian and C. Risko, Rapid Estimation of the Intermolecular Electronic Couplings and Charge-Carrier Mobilities of Crystalline Molecular Organic Semiconductors through a Machine Learning Pipeline, J. Phys. Chem. Lett., 2024, 15(28), 7206–7213, DOI:10.1021/acs.jpclett.4c01309.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03618b |
| This journal is © The Royal Society of Chemistry 2024 |