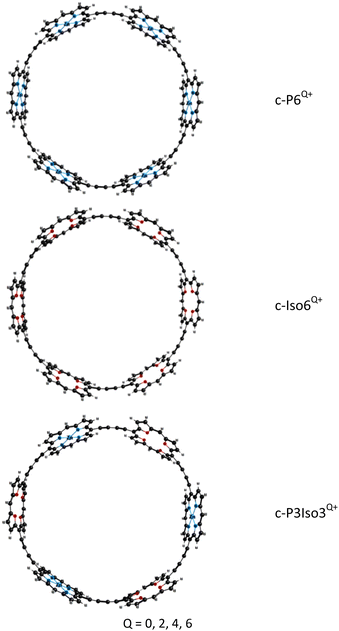Insight into magnetically induced ring currents and photophysics of six-porphyrin nanorings†
Lenara I.
Valiulina
 *,
Victor N.
Cherepanov
and
Kirill
Khoroshkin
*,
Victor N.
Cherepanov
and
Kirill
Khoroshkin
Department of Optics and Spectroscopy, Tomsk State University, Tomsk, 634050, Russia. E-mail: valiulina-lenara@mail.ru
First published on 5th August 2024
Abstract
The series of nanorings based on Zn–porphyrins and tetraoxa-isophlorins in different oxidation states (Q = 0, 2+, 4+, 6+) have been studied studied computationally at density functional theory level (DFT) using BHandHLYP functional combined with def2-SVP basis sets. Magnetically induced ring currents of nanorings have been calculated using the GIMIC method and the Ampère–Maxwell integration scheme. Ring current calculations show that neutral nanorings sustain equal diatropic and paratropic currents of 8 nA T−1, resulting in zero net ring current strengths. The charged nanorings sustain strong ring currents with tropicity depending on the oxidation state Q. Among the considered nanorings, the nanoring composed of 6 isophlorins c-Iso66+ is the most aromatic with a ring current of IGIMIC = 81.6 nA T−1. The structure c-P62+ with a ring current of IGIMIC = 54.9 nA T−1 can be considered as the most aromatic among the synthesized porphyrin nanorings. Spin–orbit coupling matrix elements, oscillator strengths, and excitation energies calculated at the CAM-B3LYP/def2-SVP level of theory were used to estimate rate constants for radiative and nonradiative processes. The algorithm based on X–H approximation were used to calculate the internal conversion rates (kIC). The main channel for the deactivation of the excitation energy in the studied nanorings is the process of internal conversion. The deactivation of excited energy occurs due to the vibrations of certain groups of C–H bonds in the nanorings. The nanoring c-Iso6 has magnetically allowed low-lying transitions that contributes significantly to the paratropic ring current, resulting in strong local antiaromaticity in the tetraoxa-isophlorin units.
Introduction
Aromaticity is one of the important concepts in organic chemistry, which determines the distinctive properties of fully conjugated cyclic molecules. Although emerged as a concept for simple monocyclic hydrocarbons, aromaticity is now being considered for more complex systems, including expanded porphyrins, fullerenes, sandwich compounds, nanorings, and Möbius conjugated molecules.1–8 Currently, aromaticity is defined as the manifestation of electron delocalization in closed 2D- or 3D-circuits, resulting in energy lowering, bond lengths equalization, special chemical behavior, and specific magnetic and spectroscopic properties.9Defining aromaticity unambiguously is challenging due to its multifaceted nature.10–12 Among various criteria, the magnetic criterion is one of the most reliable determinants of aromaticity.9,13,14 The main magnetic feature of aromatic compounds is sustaining ring currents when placed under an external magnetic field. According to the ring-current model, there are two types of currents: diatropic and paratropic. Diatropic ring currents flow in such a way as to generate a magnetic field that opposes the external field inside the ring. Paratropic ring currents flow in the reverse direction, which induces a magnetic field that strengthens the external field. Diatropic ring currents have the classical direction according to Lenz's law, whereas paratropic ring currents are a purely quantum mechanical effect. Molecules sustaining a strong diatropic ring current are classified as aromatic, whereas molecules possessing a strong paratropic ring current are referred to as antiaromatic. Nonaromatic molecules also sustain ring currents; however, the strengths of diatropic and paratropic ring currents are equal and therefore cancel each other.15,16
Aromatic ring currents can be indirectly measured using NMR spectroscopy as a magnetic shielding or modeled through quantum chemical methods, which are more representative. Theoretical methods allow to visualize the electron delocalization and ring current distribution and to quantify the aromaticity. The degree of molecular aromaticity is estimated by ring current strengths (in nA T−1). Ring current strengths can be calculated by integrating the magnetically induced ring current density passing through a plane that is perpendicular to molecular rings or obtained from Ampère–Maxwell's law.17–19 Additionally, there are several techniques to quantify ring currents based on NICS, magnetizabilities and NMR shielding calculations.20–25
It is well known that as conjugation in molecules expands, the energy gap between the frontier molecular orbitals (HOMO–LUMO) decreases as well as the molecular hardness.26–28 As a result, large conjugated macrocycles suffer out-of-plane distortions that prevent efficient conjugation. The distorted conjugated system prevents electron delocalization, making large macrocycles nonaromatic with zero ring currents. Therefore, it is difficult to find large (anti)aromatic macrocycles sustaining strong ring currents.
Recently synthesized belt-shaped porphyrin nanorings have gathered great interest due to peculiar geometries, unique conjugation pathways and unexpected aromatic character.5,29–32 Because of the lack of end-group effects, the properties of porphyrin nanorings differ significantly from linear oligomers. The special electronic structure and charge transfer properties make porphyrin nanorings especially attractive for electronic, spintronic, and optoelectronic devices.33,34 Novel porphyrin nanoring complexes (c-PN) have been synthesized by combining the N number of Zn–porphyrins with butadiyne or ethyne linkers into a ring. It is reported that the synthesis of π-conjugated macrocycles consists of 5–50 porphyrin units with diameters of 2–20 nm (c-PN, N = 5–50).35,36
Studies on c-P6 showed the absence of global electron delocalization in the neutral porphyrin nanoring. However, oxidation and reduction, as well as the electron excitation of the ring, leads to global ring currents, resulting in the global aromaticity of these structures. Such interesting local to global shift upon charge modification has been also discussed for medium- and large-sized carbon nanobelts.37–39 NICS and ACID analyses (at the B3LYP/6-31G* level of theory) for c-P6Q systems in different oxidation states (Q) demonstrate antiaromaticity for the Q = ±4 states and aromaticity for the Q = ±6 states.5,40,41
It is known that hybrid density functional approximations with a low percentage (<50%) of HF exchange (the B3LYP among them) are prone to some delocalization errors that result in the overestimation of the aromaticity/antiaromaticity.42,43 In previously reported works,44,45 using various aromaticity descriptors (NICS, ACID, HOMA, FLU, etc.), the authors conclude that the B3LYP description of c-P66+ enhances the aromaticity of this species and may also affect the antiaromaticity of c-P64+. In another work, the authors also concluded that c-P66+ is only weakly aromatic and the antiaromaticity of c-P64+ is not as pronounced as previously reported.5,46 However, the experimental 1H NMR spectra of c-P6·T6 in different oxidation states (Q) indicate the presence of global aromatic and antiaromatic ring currents in these species.47,48 The use of template T6 in the experimental study is associated with two aspects. The template T6 holds the porphyrin nanoring from structural distortions. It is also used as a marker to establish the global aromaticity of the nanoring. Global ring currents lead to the magnetic shielding of the T6 template protons, which can be experimentally observed in the NMR spectra.47–49 Moreover, the experimentally measured magnetizability of the antiaromatic porphyrin nanoring with template c-P6·T64+ provides for the first time experimental evidence for paramagnetism in closed-shell system. A high paramagnetic susceptibility exaltation (χmol = 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm cm3 mol−1) of c-P6·T64+ is associated with a strong paratropic ring current induced in this structure.50
000 ppm cm3 mol−1) of c-P6·T64+ is associated with a strong paratropic ring current induced in this structure.50
The induced ring currents in such large molecular systems resemble the persistent currents observed in mesoscopic metal rings under an external magnetic field.51,52 The direction of persistent currents in mesoscopic rings oscillates as a function of the field strength. If the nature of aromatic ring currents in molecules is similar to the persistent currents, then at sufficiently large fields (B = 104 T) or in strongly (anti)aromatic rings (with a diameter of 10–20 nm), field-induced changes will be observed in chemical reactivity, NMR spectrum, as well as in the vibrational and electronic spectra.23 Thus, large conjugated systems such as porphyrin nanorings are promising structures for testing this hypothesis. This stimulates further synthesis and studies of aromatic ring currents in large porphyrin nanorings.
In this work, we have computationally investigated the ring current strengths of the synthesized c-P6, c-P62+, c-P64+, and c-P66+. We have also considered the aromaticity of a series of novel nanorings with tetraoxa-isophlorins: c-Iso6 and c-P3Iso3 structures, as well as their dication (c-Iso62+ and c-P3Iso32+), tetracation (c-Iso64+ and c-P3Iso34+) and hexacation (c-Iso66+ and c-P3Iso36+). Free-base tetraoxa-isophlorin is an air-stable synthesized antiaromatic molecules with strong paratropic ring currents.53 The study of arrays and sheets based on isophlorin molecules has been previously reported.50 The study has shown that isophlorin arrays and sheets are characterized by the unusual topology of the ring currents and mixed aromatic–antiaromatic nature. Alternating local diatropic and paratropic ring currents in isophlorin arrays prevent global electron delocalization, resulting in a size-independent HOMO–LUMO energy gap.50 To our knowledge, studies on isophlorin-based nanorings have not been reported previously. Therefore, it is interesting to investigate the electron delocalization in nanorings based on antiaromatic isophlorins. Additionally, we performed calculations of the photophysical characteristics of the studied molecules. We believe that the calculation of the magnetically induced ring current strengths will reveal the aromaticity of porphyrin nanoring c-P6Q+ as well as novel nanorings.
Computational methods
The molecular structure of c-P6Q+, c-Iso6Q+ and c-P3Iso3Q+ in different oxidation states (Q = 0, 2, 4, 6) were optimized using density functional theory (DFT) at the BHandHLYP level.54,55 The Karlsruhe def2-SVP basis sets were employed in all calculations.56 The hybrid BHandHLYP functional with 50% HF exchange and 50% B88 exchange is recommended for modeling the magnetic properties, as shown in a recent benchmark.57 Nuclear magnetic resonance (NMR) shielding tensors were calculated at the same level of theory (BHandHLYP/def2-SVP). The optimization and NMR calculations were performed with the Gaussian 09 software package.58The spatial arrangement of the π-conjugated system in the studied nanorings is characterized by a non-planar conformation involving multiple rings. Because of the unusual geometry and electron conjugation, the structural descriptor of aromaticity, such as the popular HOMA (Harmonic Oscillator Model of Aromaticity) index,59 is not appropriate for studying the global electron delocalization in large belt-shaped nanorings. The ring current descriptors are a more reliable approach to indicate the presence of electron delocalization and aromaticity of porphyrin nanorings.
The GIMIC method was used for calculating the magnetically induced current densities and for integrating the ring current strengths.15,17,18 The density matrix and the magnetically perturbed density matrices obtained in the GIAO NMR shielding calculations as well as basis sets information were used as the input data for GIMIC calculations. Numerically integrating the current density flux passing through the plane placed perpendicularly to the chemical bond estimates the strength of magnetically induced ring current susceptibility (I, nA T−1). Further, we used ring current strength to denote magnetically induced ring current susceptibility (I, nA T−1). The integrating plane was placed perpendicularly to the chemical bond C–C of the butadiene linkers to calculate the global ring current strength. The magnetic field is oriented along the z axis, which is perpendicular to the plane of the butadiene linkers. The magnitude of the ring current strengths is used for assessing and quantifying the degree of aromaticity. The GIMIC method was chosen because it is a reliable tool for directly calculating the magnetically induced ring currents, as shown in numerous studies.7,16,60–64 The ring current strengths were also estimated by the Ampère–Maxwell integration scheme.19 This scheme involves integrating the zz component of the magnetic shielding tensor calculated in discrete points along the z axis, which is perpendicular to the molecular plane.
Currently, calculations of the rate constants of the non-radiative electronic process are the most important and difficult part in the study of photophysics of molecules.65 The algorithm based on the X–H approximation was used to calculate the internal conversion rates (kIC).65 According to the X–H approximation, the acceptors of the energy of the excited electronic state in the process of internal conversion are X–H vibrational modes. Previously, this algorithm has demonstrated good results for various classes of molecules, including organic, organometallic structures, and molecular clusters.65
The rate constants for the intersystem crossing (kISCj) between Si and the j-th triplet state (Tj) were obtained using the following expression:66
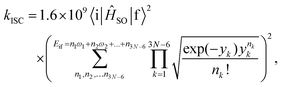 | (1) |
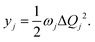 | (2) |
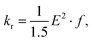 | (3) |
The TDDFT electronic structure data calculations at the CAM-B3LYP/def2-SVP level of theory were performed for evaluating the photophysical rates using Gaussian 09 software package.54,68 The matrix elements of the spin–orbit coupling were calculated with the computer program MolSOC.69
Results and discussion
Molecular structures
We have analyzed the synthesized porphyrin nanoring c-P6Q+ without the aryl groups and the template because it reduces computational costs without changing the aromaticity of these compounds. The aryl groups were replaced with hydrogen atoms. The molecular structures of the studied nanorings are presented in Fig. 1.Porphyrin nanoring c-P6Q+ consists of 6 Zn–porphyrins linked by butadiene moieties (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C
C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C). The molecular structures of the novel nanoring c-Iso6Q+ were obtained from c-P6Q+ by replacing all Zn–porphyrin units with tetraoxa-isophlorin molecules. The nanoring c-P3Iso3Q+ consists of alternating Zn–porphyrin and tetraoxa-isophlorin units linked by butadiene bridges. The obtained optimized structures of c-P6Q+ and c-Iso6Q+ belong to the D6h point group. The exception is c-Iso64+, which belongs to the D2h point group. The structures of the c-P3Iso3Q+ nanoring belong to the D3h point group. The Cartesian coordinates of the optimized molecular structures are given as the ESI.†
C). The molecular structures of the novel nanoring c-Iso6Q+ were obtained from c-P6Q+ by replacing all Zn–porphyrin units with tetraoxa-isophlorin molecules. The nanoring c-P3Iso3Q+ consists of alternating Zn–porphyrin and tetraoxa-isophlorin units linked by butadiene bridges. The obtained optimized structures of c-P6Q+ and c-Iso6Q+ belong to the D6h point group. The exception is c-Iso64+, which belongs to the D2h point group. The structures of the c-P3Iso3Q+ nanoring belong to the D3h point group. The Cartesian coordinates of the optimized molecular structures are given as the ESI.†
Ring current strengths calculation
The ring current strength is a reliable indicator of (anti)aromaticity in molecules. The GIMIC method enables obtaining not only the net ring current but also the distribution of diatropic and paratropic ring currents in it. According to the theory of magnetically induced ring currents, diatropic currents have a positive sign, while paratropic currents have a negative sign. The calculated strengths of the global magnetically induced ring currents for the investigated nanorings are given in Table 1. Ring current strengths obtained from the Ampère–Maxwell integration scheme are indicated as IA–M, while the GIMIC ring current strengths are denoted as IGIMIC. We begin our discussion with the results of the ring current calculations for the porphyrin nanoring c-P6Q+ as well as novel nanoring structures c-P3Iso3Q+ and c-Iso6Q+, then consider the global aromaticity of the porphyrin nanoring c-P6Q+ (Q = 4, 6) (section Global aromaticity of tetracation (4+) and hexacation (6+) porphyrin nanoring (c-P6)).| Nanoring | Q | I A–M, nA T−1 | I GIMIC, nA T−1 | ||
|---|---|---|---|---|---|
| Diatropic | Paratropic | Net | |||
| c-P6 | 0 | −0.2 | 7.6 | −7.9 | −0.3 |
| 2+ | 52.6 | 54.9 | 0.0 | 54.9 | |
| 4+ | −21.5 | 0.1 | −22.7 | −22.6 | |
| 6+ | 1.7 | 7.9 | −6.2 | 1.7 | |
| c-Iso6 | 0 | −0.2 | 7.9 | −8.1 | −0.2 |
| 2+ | 38.3 | 40.1 | 0.0 | 40.1 | |
| 4+ | −2.3 | 6.6 | −9.2 | −2.6 | |
| 6+ | 78.3 | 81.6 | 0.0 | 81.6 | |
| c-P3Iso3 | 0 | −0.1 | 7.7 | −7.9 | −0.2 |
| 2+ | 61.0 | 64.0 | 0.0 | 64.0 | |
| 4+ | 50.7 | 53.1 | 0.0 | 53.1 | |
| 6+ | −8.6 | 3.4 | −12.5 | −9.1 | |
The calculated ring current strengths obtained by the Ampère–Maxwell integration scheme are in good agreement with GIMIC ring currents calculations. The differences in the predicted ring current strengths obtained by two methods do not exceed 3.3 nA T−1.
The aromaticity of the investigated nanorings is dependent on the oxidation states Q. The induced diatropic and paratropic ring currents in the neutral nanorings have almost identical magnitude (about 8 nA T−1). This results in zero net ring current strengths and nonaromatic character of the neutral nanorings. Nanorings with Q = 2 are strongly aromatic, which is consistent with the experimental NMR spectra.70 The aromaticity of these molecules is caused by purely strong diatropic ring currents. The degree of aromaticity according to the Ampère–Maxwell integration scheme for nanorings Q = 2 changes in the following order: c-Iso62+ (38.3 nA T−1) < c-P62+ (52.6 nA T−1) < c-P3Iso32+ (61.0 nA T−1). The GIMIC calculations predict the same trend.
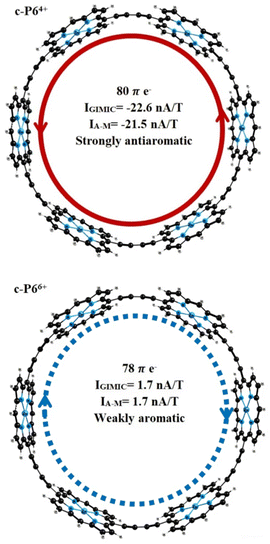
The change in the oxidation state to Q = 4 leads to a change in the aromaticity of the structures c-P6 and c-Iso6. The c-P64+ is strongly antiaromatic with a paratropic ring current of IA–M = −21.5 nA T−1 (IGIMIC = −22.6 nA T−1). The c-Iso64+ is much less antiaromatic. The induced ring current does not exceed −3 nA T−1. The ring with 3 Zn–porphyrins and 3 tetraoxa-isophlorins (c-P3Iso34+) sustains a strong diatropic ring current of IA–M = 50.7 nA T−1 (IGIMIC = 53.1 nA T−1), making it strongly aromatic. For nanorings c-P6Q+ and c-Iso6Q+ with Q = 6, ring current calculations yield global net diatropic ring currents. The structure c-P66+ is weakly aromatic with a ring current of 1.7 nA T−1, calculated using both the GIMIC method and Ampère–Maxwell scheme. Nanoring c-Iso66+ is the most aromatic among the other nanorings considered in this work. The net ring current for this structure is IA–M = 78.3 nA T−1. GIMIC calculations for c-Iso66+ predict a global pure diatropic current of 81.6 nA T−1. Replacing 3 Zn–porphyrin units with 3 tetraoxa-isophlorins leads to a change in the character of aromaticity. According to the calculated ring current strengths, the structure c-P3Iso36+ is antiaromatic with a net paratropic ring current of IA–M = −8.6 nA T−1 (IGIMIC = −9.1 nA T−1).
Previously, the GIMIC method was utilized to estimate ring currents in porphyrin nanorings with templates c-P6·T6Q+.45,70 The calculations were performed using BLYP35 and CAM-B3LYP functionals with a combination of 6-31G* basis sets. Porphyrin nanoring template c-P6·T62+ according to ring current calculations is aromatic. However, the results obtained at the same level of theory (BLYP35/6-31G*) in two works differ in the ring current prediction (5.6 nA T−1 and 60.3 nA T−1).45,70 The calculated ring current strength for c-P6·T62+ using the CAM-B3LYP functional is 58.4 nA T−1,45 which is close to the ring current strength for the structure without the template c-P62+ obtained in this work (54.9 nA T−1). For nanoring P6·T64+, ring current calculations lead to the global paratropic ring currents of −60/−74.2 nA T−1 and −7.4 nA T−1 at the BLYP35/6-31G* and CAM-B3LYP/6-31G* levels of theory, respectively.45,70 For nanoring P6·T66+, BLYP35/6-31G* ring current calculations lead to the global diatropic ring currents of 6.8/6.9 nA T−1.45,70 The CAM-B3LYP/6-31G* calculations predict that P6·T66+ is nonaromatic with zero ring current. It seems that the functional BLYP35 overestimates paratropic ring currents in the antiaromatic porphyrin nanoring with templates c-P6·T64+. The functional BLYP3571 consists of 35% HF exchange, which is not enough to correctly estimate paratropic ring currents. As was reported previously, functionals with less HF exchange overestimate paratropic ring currents in antiaromatic molecules.43 The template in porphyrin nanoring does not strongly affect the aromaticity of c-P6Q+. According to ring current calculations, the porphyrin nanorings with template c-P6·T62+ and c-P6·T66+ are slightly more aromatic than without it. The template provides a frame to hold the nanoring from structural distortions, increasing efficient conjugation.
Global aromaticity of tetracation (4+) and hexacation (6+) porphyrin nanoring (c-P6)
The size of porphyrin nanorings limits high-precision ab initio calculations. Therefore, all available theoretical calculations are performed at the density functional theory. Because the results of DFT calculations significantly depend on the functional used, the global (anti)aromaticity of porphyrin nanorings (c-P64+, c-P66+) is controversial. Various approaches have been utilized to quantify ring current strengths for c-P64+ and c-P66+.5,40,41,44–48 Different ring current descriptors of aromaticity for porphyrin nanorings are collected in Table 2.| Ring current descriptors | c-P64+ | c-P66+ |
|---|---|---|
| a Based on experimental NMR chemical shifts.48 b B3LYP/6-31G*.48 c LC-ωhPBE/6-31G*.48 d LC-ωhPBE/6-31G*.46 e BHandHLYP/6-31G*.46 f BHandHLYP/def2-SVP results of this work. | ||
| n π e− | 80 | 78 |
| I NMR | 44.4 | −15.6 |
I
3D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NICS NICS
|
595.0 | −79.7 |
I
3D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NICS NICS
|
40.4 | −13.1 |
| I ICLOC,Sav | 44.4 | −11.7 |
| I CTOCD-DZ2 | 43.4 | −12.4 |
| I ICLOC,Sav | 22.5 | −0.9 |
| I CTOCD-DZ2 | 22.6 | −2.0 |
| I GIMIC | −22.6 | 1.7 |
| I A–M | −21.5 | 1.7 |
Theoretical descriptors INMR, I3D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NICS, IICLOC,Sav indirectly estimate the ring current based on the current loop model and the Biot–Savart law. The indices of the ring current strength (I) indicate which parameter or method was used to calculate the current strengths (NMR −Δδ changes in the NMR chemical shift in (anti)aromatic molecules compared with nonaromatic references);25 3D NICS – 3D NICS scan in the molecular center of gravity;25 ICLOC, Sav – infinitely thin circular loop of current with effective average radius (Sav), which combines two observables magnetizability and shielding at the center of the loop;23 CTOCD-DZ2 – continuous transformation of the origin of the current density-diamagnetic zero.22 The signed current strengths indices (INMR, I3D
NICS, IICLOC,Sav indirectly estimate the ring current based on the current loop model and the Biot–Savart law. The indices of the ring current strength (I) indicate which parameter or method was used to calculate the current strengths (NMR −Δδ changes in the NMR chemical shift in (anti)aromatic molecules compared with nonaromatic references);25 3D NICS – 3D NICS scan in the molecular center of gravity;25 ICLOC, Sav – infinitely thin circular loop of current with effective average radius (Sav), which combines two observables magnetizability and shielding at the center of the loop;23 CTOCD-DZ2 – continuous transformation of the origin of the current density-diamagnetic zero.22 The signed current strengths indices (INMR, I3D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NICS, IICLOC,Sav, ICTOCD-DZ2) are set such that a positive sign of the value indicates diatropic ring currents and aromaticity, whereas a negative sign refers to paratropic ring currents and antiaromaticity. The ring current strengths (IGIMIC, IA–M) for diatropic and paratropic currents have signs opposite to those indicated above. Therefore, different ring current descriptors and functionals presented in Table 2 are consistent with each other in predicting the tropicity of the dominant current. The tropicity of the calculated ring currents and the character of aromaticity correspond to the prediction of Hückel's rule (4n/4n + 2). It is clearly seen that the choice of the functional significantly affects the calculated magnitude of the ring currents in porphyrin nanorings.44,45 The most inconsistent values are observed for the B3LYP functional, which predicts extremely large currents for both c-P64+ and c-P66+.
NICS, IICLOC,Sav, ICTOCD-DZ2) are set such that a positive sign of the value indicates diatropic ring currents and aromaticity, whereas a negative sign refers to paratropic ring currents and antiaromaticity. The ring current strengths (IGIMIC, IA–M) for diatropic and paratropic currents have signs opposite to those indicated above. Therefore, different ring current descriptors and functionals presented in Table 2 are consistent with each other in predicting the tropicity of the dominant current. The tropicity of the calculated ring currents and the character of aromaticity correspond to the prediction of Hückel's rule (4n/4n + 2). It is clearly seen that the choice of the functional significantly affects the calculated magnitude of the ring currents in porphyrin nanorings.44,45 The most inconsistent values are observed for the B3LYP functional, which predicts extremely large currents for both c-P64+ and c-P66+.
Ring current strengths (IGIMIC) calculated with GIMIC methods and estimated by the Ampère–Maxwell integration scheme (IA–M) are in good agreement with the values obtained by other methods (ICTOCD-DZ2, IICLOC,Sav) using the same functional (BHandHLYP). The BHandHLYP calculations of the ring current predict that the c-P64+ is strongly antiaromatic with global paratropic ring current of more than −21 nA T−1. According to the ring current criterion, the c-P66+ can be considered as weakly aromatic or even nonaromatic because it sustains a weak net diatropic ring current of 1.7 nA T−1 (Fig. 2). Because BHandHLYP (with 50% HF exchange) is recommended for modeling nuclear magnetic shieldings, magnetizabilities, ring current strengths, and other magnetic properties, we can rely on the ring current strengths obtained.57
Photophysics of neutral nanorings
We have considered neutral systems because charged nanorings are characterized by a set of low-lying electronic states and would not have pronounced photophysical characteristics. Photophysical rate constants of radiative and nonradiative transfer of the energy of the excited electronic state play an important role in understanding the luminescent properties of molecules. The luminescence of a molecule is quantified by the quantum yield. For fluorescence, the quantum yield is determined by the following expression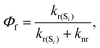 | (4) |
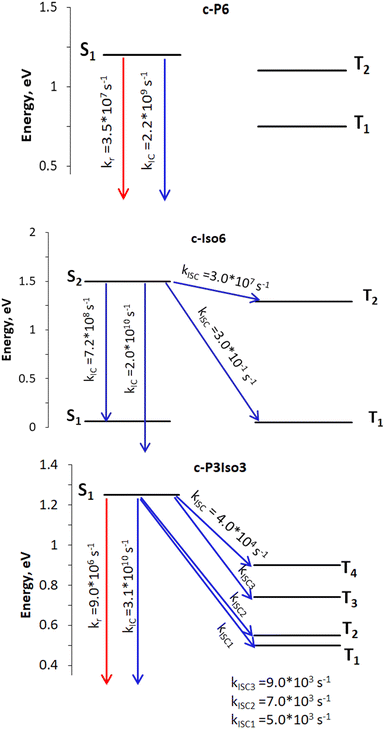 | ||
| Fig. 3 Rate constants: the red arrows represent radiative process, whereas the blue ones indicate nonradiative deactivation channels. The open-ended arrows illustrate transitions to the S0 state. | ||
| Nanoring | k r, s−1 | k ISC, s−1 | k IC, s−1 | Φ f |
|---|---|---|---|---|
| a Experimental value measured at 1050 nm.31 | ||||
| c-P6 | 3.5 × 107![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
0.0 (S1 → T1) | 2.2 × 109 (S1 → S0) | 0.016/0.018a |
| 0.0 (S1 → T2) | ||||
| c-Iso6 | — | 3.0 × 10−1 (S2 → T1) | 2.0 × 1010 (S2 → S0) | — |
| 3.0 × 107 (S2 → T2) | 7.2 × 108 (S2 → S1) | |||
| c-P3Iso3 | 9 × 106 | 5.0 × 103 (S1 → T1) | 3.1 × 1010 (S1 → S0) | 0.0003 |
| 7.0 × 103 (S1 → T2) | ||||
| 9.0 × 103 (S1 → T3) | ||||
| 4.0 × 104 (S1 → T4) | ||||
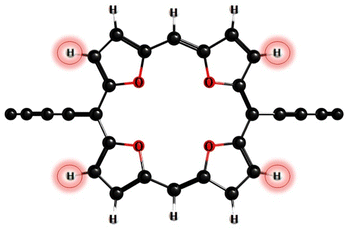
According to photophysical calculations, the rate of the internal conversion process dominates the decay of the singlet excited state for all nanorings. The used algorithm based on X–H approximation enables analyzing specific X–H vibrational modes that accept the energy in the internal conversion process. In c-P3Iso3, the acceptors of the excitation energy are C–H vibrational modes located on tetraoxa-isophlorin units. In the c-Iso6 nanoring, the excitation energy is distributed on vibrations of C–H bonds in the pyrrole units, mostly to the C–H bonds located parallel to butadiene linkers (Fig. 4). Thus, replacing the hydrogen atom in C–H acceptor bonds with appropriate substituents may decrease the internal conversion rate and increase the luminescence quantum yield of c-P3Iso3 and c-Iso6 nanorings.
Conclusions
Magnetic properties and photophysics have been studied computationally for a set of nanorings based on Zn–porphyrins and tetraoxa-isophlorins. The ring current strengths were obtained at the DFT level (BHandHLYP/def2-SVP) using the GIMIC method and the Ampère–Maxwell integration scheme. Ring currents in tetraoxa-isophlorin nanorings have been obtained for the first time. Ring current calculations show that charged nanorings based on isophlorin sustain strong ring currents. The nanoring c-Iso66+ is the most aromatic among the structures studied in this work (IGIMIC = 81.6 nA T−1).Controversial antiaromaticity/aromaticity of c-P64+/c-P66+ is associated with the use of DFT functionals with different amounts of HF exchange. To correctly estimate the contributions of diatropic and paratropic ring current in molecules, a functional with a large amount of HF exchange (>40%) is recommended to use.57 The BHandHLYP functional used in this work with 50% HF exchange predicts that c-P64+ is strongly antiaromatic with a ring current of −22 nA T−1. The nanoring c-P66+ sustains a weak diatropic ring current of 1.7 nA T−1; thus, it is only weakly aromatic or even nonaromatic based on the ring current criterion. Our ring current calculations confirm the aromaticity predictions obtained previously.44–46 According to the ring current strengths obtained, the nanoring c-P62+ can be considered as the largest aromatic molecules (IGIMIC = 54.9 nA T−1) among the synthesized porphyrin nanorings.
Rate constants for radiative and nonradiative processes were obtained by calculating the spin–orbit coupling matrix elements, oscillator strengths, and excitation energies at the CAM-B3LYP/def2-SVP level of theory. The nanoring c-Iso6 is characterized by low-lying singlet excited states with a large transition dipole moment of 7 a.u. These magnetically allowed low-lying transitions contribute significantly to the local paratropic ring current. However, the neutral nanoring c-Iso6 is globally nonaromatic. This is explained by the fact that low-lying excitations are localized on each isophlorin unit, leading to strong local antiaromaticity (IGIMIC = −636 nA T−1). To induce global ring currents, excitations should be delocalized throughout the macrocycle. The calculated rate constants indicate that the deactivation of excitation energy occurs through internal conversion channels. For nanorings c-P6 and c-P3Iso3, the radiative rate is certain orders of magnitude smaller than the rate of internal conversion; therefore, the quantum yields for these structures are low. The calculated quantum yields for c-P6 (0.016) is in good agreement with the experimental value (0.018). Thus, the used X–H algorithm correctly estimates the rate constants of the studied nanorings. Different nanorings have specific C–H vibrational modes that accept the energy in the internal conversion process. Therefore, replacing the hydrogen atoms in these specific C–H bonds with different substitution groups may decrease the rate of the internal conversion process. Because internal conversion is the main channel of excitation-energy decay, decreasing its rate may increase the fluorescence quantum yield of the studied nanoring.
Author contributions
L. V. and V. Ch. suggested current density and photophysics studies of the novel nanorings based on isophlorins. L. V. and K. Kh. performed calculations. All authors discussed the results and contributed to the final manuscript.Data availability
The data supporting this article have been included as part of the ESI.† The code for magnetically induced ring current calculations can be found at https://gimic.readthedocs.io/en/latest/index.html. The information about the code for matrix elements of the spin–orbit coupling calculation can be found at S. G. Chiodo, M. Leopoldini, Comput. Phys. Commun., 2014, 185, 676–683. (https://doi.org/10.1016/j.cpc.2013.10.014). The information about the algorithm based on the XH approximation is available at R. R. Valiev, R. T. Nasibullin, V. N. Cherepanov, A. Kurtsevich, D. Sundholm and T. Kurtén, Phys. Chem. Chem. Phys., 2021, 23, 6344. (DOI: https://doi.org/10.1039/D1CP00257K).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Russian Science Foundation under grant no. 24-23-00278. We acknowledge computational resource SKIF Cyberia. We are grateful to R. Valiev for useful discussions.Notes and references
- J.-Y. Shin, K. S. Kim, M.-Ch Yoon, J. M. Lim, Z. S. Yoon, A. Osuka and D. Kim, Chem. Soc. Rev., 2010, 39, 2751–2767 RSC.
- O. E. Bakouri, D. W. Szczepanik, K. Jorner, R. Ayub, P. Bultinck, M. Solà and H. Ottosson, J. Am. Chem. Soc., 2022, 144, 8560–8575 CrossRef PubMed.
- F.-X. Pan, L.-J. Li, Y.-J. Wang, J.-C. Guo, H.-J. Zhai, L. Xu and Z.-M. Sun, J. Am. Chem. Soc., 2015, 137, 10954–10957 CrossRef CAS PubMed.
- M. Bühl and A. Hirsch, Chem. Rev., 2001, 101, 1153–1184 CrossRef PubMed.
- M. D. Peeks, T. D. W. Claridge and H. L. Anderson, Nature, 2017, 541, 200–203 CrossRef CAS PubMed.
- S. M. Kopp, H. Gotfredsen, J.-R. Deng, T. D. W. Claridge and H. L. Anderson, J. Am. Chem. Soc., 2020, 142, 19393–19401 CrossRef CAS PubMed.
- A. Mahmood, M. Dimitrova, L. N. Wirz and D. Sundholm, J. Phys. Chem. A, 2022, 126, 1936–1945 CrossRef CAS PubMed.
- D. Ajami, O. Oeckler, A. Simon and R. Herges, Nature, 2003, 426, 819–821 CrossRef CAS PubMed.
- Z. Chen, Ch. S. Wannere, C. Corminboeuf, R. Puchta and P. R. von Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- K. Jug and A. M. Köster, J. Phys. Org. Chem., 1991, 4, 163–169 CrossRef CAS.
- M. Solà, Front. Chem., 2017, 5, 22 Search PubMed.
- G. Merino, M. Solà, I. Fernández, C. Foroutan-Nejad, P. Lazzeretti, G. Frenking, H. L. Anderson, D. Sundholm, F. P. Cossío, M. A. Petrukhina, J. Wu, J. I. Wu and A. Restrepo, Chem. Sci., 2023, 14, 5569–5576 RSC.
- J. A. N. F. Gomes and R. B. Mallion, Chem. Rev., 2001, 101, 1349–1384 CrossRef CAS PubMed.
- R. Gershoni-Poranne and A. Stanger, Chem. Soc. Rev., 2015, 44, 6597–6615 RSC.
- D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678 CAS.
- D. Sundholm, M. Dimitrova and R. J. F. Berger, Chem. Commun., 2021, 57, 12362 RSC.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- R. J. F. Berger, M. Dimitrova, R. T. Nasibullin, R. V. Valiev and D. Sundholm, Phys. Chem. Chem. Phys., 2022, 24, 624 RSC.
- R. Zanasi, P. Lazzeretti, M. Malagoli and F. Piccinini, J. Chem. Phys., 1995, 102, 7150 CrossRef CAS.
- P. Fowler, R. Zanasi, B. Cadioli and E. Steiner, Chem. Phys. Lett., 1996, 251, 132–140 CrossRef CAS.
- E. Steiner, P. W. Folwler, A. Soncini and L. W. Jenneskens, Faraday Discuss., 2007, 135, 309–323 RSC.
- S. Pelloni, G. Monaco, R. Zanasi and P. Lazzeretti, AIP Conf. Proc., 2012, 1456, 114–118 CrossRef CAS.
- G. Monaco and R. Zanasi, Chem. Phys. Lett., 2013, 588, 247–252 CrossRef CAS.
- M. Jirásek, H. L. Anderson and M. D. Peeks, Acc. Chem. Res., 2021, 54, 3241–3251 CrossRef PubMed.
- J. L. Bredas, R. Silbey, D. S. Boudreaux and R. R. Chance, J. Am. Chem. Soc., 1983, 105, 6555–6559 CrossRef CAS.
- C. H. Choi and M. Kertesz, J. Chem. Phys., 1998, 108, 6681–6688 CrossRef CAS.
- R. Gershoni-Poranne, A. P. Rahalkar and A. Stanger, Phys. Chem. Chem. Phys., 2018, 20, 14808–14817 RSC.
- M. Hoffman, C. J. Wilson, B. Odell and H. L. Anderson, Angew. Chem., Int. Ed., 2007, 46, 3122–3125 CrossRef PubMed.
- M. Hoffman, J. Kärnbratt, M.-H. Chang, L. M. Herz, B. Albinsson and H. L. Anderson, Angew. Chem., Int. Ed., 2008, 47, 4993–4996 CrossRef.
- R. Haver, L. Tejerina, H.-W. Jiang, M. Richaus, M. Jirásek, I. Grübner, H. J. Eggimann, L. M. Herz and H. L. Anderson, J. Am. Chem. Soc., 2019, 141, 7965–7971 CrossRef CAS PubMed.
- M. Rickhaus, M. Jirásek, L. Tejerina, H. Gotfredsen, M. D. Peeks, R. Haver, H.-W. Jiang, T. D. W. Claridge and H. L. Anderson, Nat. Chem., 2020, 12, 236–241 CrossRef CAS PubMed.
- C. Maeda, S. Toyama, N. Okada, K. Takaishi, S. Kang, D. Kim and T. Ema, J. Am. Chem. Soc., 2020, 142, 15661–15666 CrossRef CAS PubMed.
- S. Gao, Z. Yang, Y. Wang, G. Zhang and Y. Hu, JOM, 2020, 72, 3149–3159 CrossRef CAS.
- P. Liu, Y. Hisamune, M. D. Peeks, B. Odell, J. Gong, L. M. Herz and H. L. Anderson, Angew. Chem., Int. Ed., 2016, 55, 8358–8362 CrossRef CAS PubMed.
- P. S. Bols and H. L. Anderson, Acc. Chem. Res., 2018, 51, 2083–2092 CrossRef CAS PubMed.
- N. Toriumi, A. Muranaka, E. Kayahara, S. Yamago and M. Uchiyama, J. Am. Chem. Soc., 2015, 137(1), 82–85 CrossRef CAS PubMed.
- C. Liu, Y. Ni, X. Lu, G. Li and J. Wu, Acc. Chem. Res., 2019, 52, 2309–2321 CrossRef CAS PubMed.
- A. Muñoz-Castro, Phys. Chem. Chem. Phys., 2018, 20, 3433–3437 RSC.
- M. D. Peeks, M. Jirásek, T. D. W. Claridge and H. L. Anderson, Angew. Chem., Int. Ed., 2019, 58, 15717–15720 CrossRef CAS PubMed.
- M. D. Peeks, J. Q. Gong, K. McLoughlin, T. Kobatake, R. Haver, L. M. Herz and H. L. Anderson, J. Phys. Chem. Lett., 2019, 10, 2017–2022 CrossRef CAS PubMed.
- P. Mori-Sanchez, A. J. Cohen and W. Yang, Phys. Rev. Lett., 2008, 100, 146401 CrossRef PubMed.
- R. R. Valiev, I. Benkyi, Y. V. Konyshev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2018, 122, 4756–4767 CrossRef CAS PubMed.
- I. Casademont-Reig, R. Guerrero-Avilés, E. Ramos-Cordoba, M. Torrent-Sucarrat and E. Matito, Angew. Chem., Int. Ed., 2021, 60, 24080–24088 CrossRef CAS PubMed.
- I. Casademont-Reig, L. Soriano-Agueda, E. Ramos-Cordoba, M. Torrent-Sucarrat and E. Matito, Angew. Chem., Int. Ed., 2022, 61, e202206836 CrossRef CAS PubMed.
- A. Landi, F. F. Summa and G. Monaco, Chemistry, 2021, 3, 991–1004 CrossRef CAS.
- J.-R. Deng, D. Bradley, M. Jirásek, H. L. Anderson and M. D. Peeks, Angew. Chem., Int. Ed., 2022, 61, e202201231 CrossRef CAS PubMed.
- M. Jirásek, M. Rickhaus, L. Tejerina and H. L. Anderson, J. Am. Chem. Soc., 2021, 143, 2403–2412 CrossRef PubMed.
- D. M. Carey, P. L. Rodríguez-Kessler and A. Muñoz-Castro, Int. J. Quantum Chem., 2021, 121, e26500 CrossRef.
- R. R. Valiev, G. V. Baryshnikov, R. T. Nasibullin, D. Sundholm and H. Ågren, J. Phys. Chem. C, 2020, 124, 21027–21035 CrossRef CAS.
- D. Loss and P. Goldbart, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 13762 CrossRef PubMed.
- A. C. Bleszynski-Jayich, W. E. Shanks, B. Peaudecerf, E. Ginossar, F. von Oppen, L. Glazman and J. G. E. Harris, Science, 2009, 326, 272–275 CrossRef CAS PubMed.
- J. S. Reddy and V. G. Anand, J. Am. Chem. Soc., 2008, 130, 3718–3719 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Lehtola, M. Dimitrova, H. Fliegl and D. Sundholm, J. Chem. Theory Comput., 2021, 17, 1457–1468 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery Jr, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian 09, Revision A.02, Gaussian, Inc., Pittsburgh, PA, 2016 Search PubMed.
- T. M. Krygowski and M. K. Cyranski, Chem. Rev., 2001, 101, 1385–1420 CrossRef CAS.
- D. Sundholm and H. Fliegl, in Handbook of Porphyrin Science, ed. K. M. Kadish, K. M. Smith and R. Guilard, World Scientific, 2022, vol. 46 Search PubMed.
- R. R. Valiev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2015, 119, 1201–1207 CrossRef CAS PubMed.
- R. R. Valiev and V. N. Cherepanov, Int. J. Quantum Chem., 2013, 113, 2563–2567 CrossRef CAS.
- R. R. Valiev, H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2018, 20, 17705–17713 RSC.
- R. R. Valiev, H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2015, 17, 14215–14222 RSC.
- R. R. Valiev, R. T. Nasibullin, V. N. Cherepanov, A. Kurtsevich, D. Sundholm and T. Kurtén, Phys. Chem. Chem. Phys., 2021, 23, 6344 RSC.
- R. R. Valiev, G. Hasan, V.-T. Salo, J. Kubečka and T. Kurten, J. Phys. Chem. A, 2019, 123, 6596–6604 CrossRef CAS PubMed.
- S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, J. Phys. Chem. Lett., 2004, 393, 51–57 CrossRef CAS.
- S. G. Chiodo and M. Leopoldini, Comput. Phys. Commun., 2014, 185, 676–683 CrossRef CAS.
- D. Bradley, M. Jirásek, H. L. Anderson and M. D. Peeks, Chem. Sci., 2023, 14, 1762–1768 RSC.
- M. Renz, K. Theilacker, Ch Lambert and M. Kaupp, J. Am. Chem. Soc., 2009, 131, 16292–16302 CrossRef CAS PubMed.
- R. R. Valiev, H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2017, 19, 25979–25988 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: The Cartesian coordinates of the optimized molecular structures are reported. See DOI: https://doi.org/10.1039/d4cp02547d |
| This journal is © the Owner Societies 2024 |