Theoretical study on the mechanochemical reactivity in Diels–Alder reactions
Received
14th September 2023
, Accepted 27th November 2023
First published on 6th December 2023
Abstract
Mechanochemical reactions sometimes give different yields from those under solvent conditions, and such mechanochemical reactivities depend on the reactions. This study theoretically elucidates what governs mechanochemical reactivities, taking the Diels–Alder reactions as an example. Applying mechanical force can be regarded as the deformation of molecules, and the deformation in an orthogonal direction to a reaction mode can lower the reaction barrier. Here, we introduce a dimensionless cubic force constant, a mechanochemical reaction constant. It tells us how easily the deformation can lower a reaction barrier and enables us to compare the mechanochemical reactivities of different reactions. The constants correlate positively with the yields of the mechanochemical Diels–Alder reactions.
1 Introduction
Mechanochemistry deals with chemical phenomena, such as chemical reactions, caused by mechanical action.1 In the ball milling method, hard balls and powder samples are placed in a mill and ground together to apply a mechanical force to the powder samples. Instead of grinding, uniform pressure2 or polymer chains' tensile stress3 can also be used as mechanical action sources. In recent years, the mechanochemical synthesis of organic molecules has received particular attention. The reason is that it is ecological and economical because no solvent or catalyst is required.4 It is also of potential interest from a fundamental point of view. In mechanochemical reactions, chemical reactions that should not proceed under conventional solvent conditions often undergo unexpectedly, or reaction yields can improve. For example, Wang et al. reported that a high-speed vibration milling technique bridges buckminsterfullerenes, yielding a dumb-bell-shaped C120.5 Hickenboth et al. reported that polymeric substituents generate mechanical stress in cyclic compounds, facilitating ring-opening reactions upon being subjected to ultrasound.6 The Woodward–Hoffmann rule cannot explain the observed stereoselectivity.
It is still unclear what governs mechanochemical reaction yields. Take the Diels–Alder reactions as an example (Fig. 1 and Table 1). Watanabe et al. reported the mechanochemical Diels–Alder reaction between anthracene derivatives and p-benzoquinone.7 Though anthracene does not react under mechanochemical conditions (Scheme 1), introducing one or two methyl groups makes anthracene mechanochemically reactive (Scheme 2).7 On the other hand, Zhang et al., McKissic et al., and Gonnet et al. reported the other mechanochemical Diels–Alder reactions, including cyclopentadiene + maleic anhydride or maleimide derivatives,8 anthracene derivatives + maleic anhydride,9 and diphenylfulvene + maleimide (Schemes 3–5),10 with higher yields. These reactions (1)–(5) are similar, but their mechanochemical yields are entirely different, as shown in Table 1.
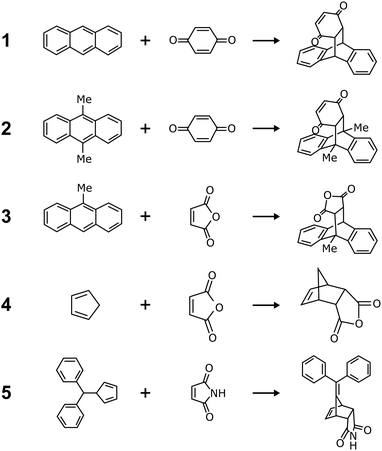 |
| | Fig. 1 The reported mechanochemical Diels–Alder reactions. Scheme 1: anthracene + p-benzoquinone.7 Scheme 2: 9,10-dimethylanthracene + p-benzoquinone.7 Scheme 3: cyclopentadiene + maleic anhydride.8 Scheme 4: 9-methylanthracene + maleic anhydride.9 Scheme 5: diphenylfulvene + maleimide.10 Their yields are listed in Table 1. | |
Table 1 The reported maximum yields of the mechanochemical Diels–Alder reactions (1)–(5). Reaction schemes are shown in Fig. 1
| Scheme |
1 |
2 |
3 |
4 |
5 |
| Yield |
0.007 |
0.267 |
≤0.828 |
0.949 |
0.9210 |
How can mechanochemical conditions be treated theoretically? Theoretical approaches to mechanochemistry are now emerging.11 We here assume the ball milling method. During grinding, random external forces are applied to individual molecules inside and at the interfaces of the micro powders. Applying an external force is equivalent to deforming the molecule from its equilibrium structure and balancing the external and internal forces. The molecular structure deforms when an external force is applied in a specific direction at a particular moment. Thus, mechanochemical reactions can be regarded as reactions between distorted (more rigorously, vibrationally excited) molecules. Luty et al. discussed the impact of mechanical force on the electronic structure of reactant molecules via structural deformation, i.e., the inverse Jahn–Teller effect.12 Ribas-Arino et al. proposed that a mechanical force can alter a reaction barrier by modifying the potential energy surface. This can be regarded as a Legendre transformation from a displacement to a force.13 They explained the facilitation of the ring-opening reaction of cis-1,2-dimethylbenzocyclobutene under a mechanochemical condition.
Recently, dibenzophenazine was synthesized with a high yield of over 99% by the ball milling method.14 Kinetic and calorimetric experiments suggested that two reaction pathways are involved in this reaction.15,16 Our density functional theory (DFT) calculations found the stepwise reaction as the lowest energy path and the concerted reaction as a higher energy path.17 However, the highest energy point of the latter is the higher-order saddle point with two or more imaginary frequencies; hence, it is not acceptable as a reaction path. The extra imaginary frequency comes from the instability of the plane-symmetric conformation in one of the reactants. We clarified that an external force easily deforms this molecule, the plane-symmetric conformation becomes stable, and the higher-order saddle point of the concerted reaction pathway changes to the transition state (TS; the first-order saddle point). This result demonstrates a mechanism by which mechanical action opens a new reaction pathway.
We also studied the Diels–Alder reaction of diphenylfulvene and maleimide. The product of this reaction has two stereoisomers called endo- and exo-isomers. Although the reaction can proceed in organic solvents, the ball milling method improves the selectivity of the endo form.10 We considered the possibility that the reactants are distorted and the reaction barrier is changed by applying an external force.18 The reaction barrier variability is characterized by the cubic force constant, which is a derivative of the curvature of the reaction curve concerning another normal coordinate (deformational coordinate). The constant indicates how much the curvature of the reaction curve is changed by the deformation in the direction of a normal mode. When reactants are distorted, the reaction barrier increases if the reaction curve bends more steeply, and the reaction barrier decreases if the reaction curve bends more loosely. Comparing the endo- and exo-formation pathways, we found a difference in the magnitudes of the cubic force constants. When deformed, the reaction barrier of the endo-type path was significantly lower than that of the exo-type pathway.
Felts et al. reported that functional groups such as C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O are mechanically cleaved from chemically modified graphene sheets when atomic force microscope tips apply the force of nano Newton.19 Though it is difficult to observe the mechanical force applied to each molecule during ball milling directly, the mechanical forces of nano Newtons seem to be needed to undergo mechanochemical reactions. This is consistent with our previous study:18 mechanical forces of (sub-)nano Newtons are needed to vary the reaction barriers.
O are mechanically cleaved from chemically modified graphene sheets when atomic force microscope tips apply the force of nano Newton.19 Though it is difficult to observe the mechanical force applied to each molecule during ball milling directly, the mechanical forces of nano Newtons seem to be needed to undergo mechanochemical reactions. This is consistent with our previous study:18 mechanical forces of (sub-)nano Newtons are needed to vary the reaction barriers.
These previous works imply that mechanochemical reactivities of various reactions depend on the change in the curvatures of their reaction curves. The present study aims to theoretically clarify the origin of the difference in the yields of the mechanochemical Diels–Alder reactions by introducing a quantity describing mechanochemical reactivities.
2 Theory
A random force is applied to each reactant molecule during grinding because of the interfacial stacking of microcrystalline grains. Any external force acting on a molecule can be divided into components along normal modes, similar to an internal force. Let us suppose that the applied force is mechanically balanced with the internal force,| | 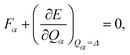 | (1) |
where Qα denotes a normal coordinate of mode α, and E represents the potential energy. The application of the force Fα for mode α is equivalent to making a structural deformation of Qα = Δ.
We here focus on forces orthogonal to the reaction mode.18 If the deformation in the direction orthogonal to the reaction mode considerably lowers the reaction barrier, such a reaction pathway is mechanochemically favorable. The potential energy E can be expanded around the TS in terms of the reaction coordinate Qs:
| | 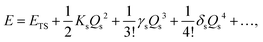 | (2) |
where
ETS is the potential energy at the TS.
Ks,
γs, and
δs are quadratic, cubic, and quartic force constants for the reaction mode, respectively. By definition,
Ks is negative, and
δs is positive. As shown in
Fig. 2, the deformation can lower the reaction barrier when the absolute value of the potential energy curvature
Ks becomes smaller. Note that the change of the higher-order derivatives is ignored here for simplicity. In this case, the decrease in the reaction barrier depends on the feasibility of variation in the curvature by deformation in mode
α, which can be evaluated by a third-order mixed derivative, a cubic force constant
K(1)s,α,
| | 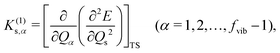 | (3) |
where
fvib denotes the vibrational degrees of freedom, and the superscript (1) means the first derivative concerning
Qα. Herein, we can introduce a cubic effective mode
ueff, which is the deformational mode
ueff such that the curvature variation is maximum,
| | 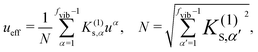 | (4) |
where
N denotes a normalization factor, and
uα is a vibrational vector for mode
α. The cubic force constant
K(1)s,eff for the cubic effective mode
ueff is given by
N.
K(1)s,eff characterizes the maximum curvature variation due to the application of a random force.
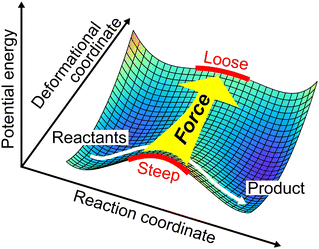 |
| | Fig. 2 Role of a force in a direction orthogonal to the reaction mode. A reaction barrier is lowered when the force changes the curvature of a reaction curve at the TS. | |
If a reaction barrier is very high in a particular reaction, the magnitude of K(1)s,eff loses its importance. A dimensionless quantity that does not depend on the energy scale is required to compare the mechanochemical reactivities of different reactions. With the frequency ωs of the reaction mode, Ks is written as
Note that
ωs is a purely imaginary number. As a result,
E can be rewritten by
| | 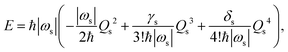 | (6) |
in which the energy of
ħ|
ωs| is factored out. We here introduce a dimensionless reaction coordinate
qs,
| | 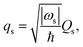 | (7) |
and thus
| | 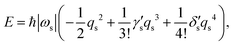 | (8) |
where
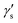
and
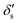
are dimensionless cubic and quartic force constants for the reaction mode,
| | 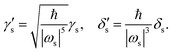 | (9) |
As with the reaction coordinate, a dimensionless normal coordinate can also be introduced as
| |  | (10) |
The energy term, including the third-order mixed derivative
K(1)s,α, can be nondimensionalized as
| | 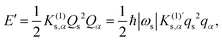 | (11) |
where a dimensionless third-order mixed derivative
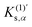
is given by
| | 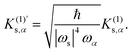 | (12) |
Similarly,
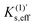
for the cubic effective mode can also be obtained.
| | 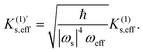 | (13) |
 means the degree of the maximum curvature variation due to a random force and is independent of the energy scale. We hereafter call
means the degree of the maximum curvature variation due to a random force and is independent of the energy scale. We hereafter call  a mechanochemical reaction constant (MRC),
a mechanochemical reaction constant (MRC),
3 Computational methods
Geometry optimizations and vibrational analyses based on DFT calculations were performed for the reactants, TSs, and products of the Diels–Alder reactions (1)–(4) in a vacuum. The reactants, TS, and product of the reaction (5) in a vacuum are available in our previous study.18 Subsequently, anharmonic vibrational analyses were performed for the TSs to obtain the cubic force constants for the reaction mode and other normal modes. All the DFT calculations were performed at the B3LYP/6-311G(d,p) level of theory using the Gaussian 09, Rev. D.01 program package.20 Furthermore, as per eqn (4) and (13), the cubic effective mode ueff and its dimensionless cubic force constant  were calculated for each TS.
were calculated for each TS.
4 Results and discussion
Fig. 3 shows the obtained reaction profiles of the Diels–Alder reactions (1)–(5). The transition states and their reaction modes are shown in Fig. 4. Diene and dienophile regions approach each other as usual in each reaction mode. All the reactions have reaction barriers with 0.6–1.1 eV, which are not too high compared with thermal energy. Additionally, we found that reaction (1), with a mechanochemical yield of almost zero, has the highest barrier, and reaction (4), with a high yield, has the lowest barrier. This result implies a weak correlation between the reaction barriers and mechanochemical yields. However, such a correlation is violated for reactions (2)–(5).
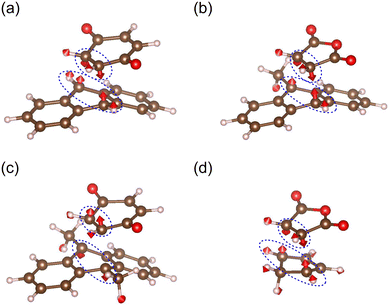 |
| | Fig. 4 The obtained transition states with the reaction modes: the Diels–Alder reactions (a) 1, (b) 2, (c) 3, and (d) 4. The frequencies of these modes are 472i, 451i, 435i, and 461i cm−1, respectively. The blue dotted circles indicate the significant components of the vibrational vectors. The transition state of the reaction (5) is available in our previous study.18 | |
We subsequently calculated MRCs for the Diels–Alder reactions (1)–(5), as shown in Fig. 5. We found that the obtained MRCs correlate positively with the yields of the mechanochemical Diels–Alder reactions well. This indicates that the maximum curvature variation due to the application of a random force determines the yields of the mechanochemical Diels–Alder reactions. It should also be noted that there are other factors than intra-molecular properties in general. For example, if the packing structures of the reactants in the solid state are different, they might have non-negligible effects on mechanochemical reactivities. We must be careful of other factors to compare mechanochemical reactivities if reaction types or reactant structures are entirely different.
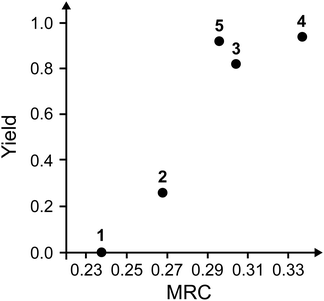 |
| | Fig. 5 The calculated mechanochemical reaction constants and the previously reported yields of the mechanochemical Diels–Alder reactions.7–10 | |
As shown in Fig. 5, reaction (1), with the highest reaction barrier, has a small MRC, whereas reaction (4), with the lowest one, has a large MRC. According to the third-order perturbation theory, a cubic force constant is given by the sum of its primary and mixing terms. The primary term depends only on the total electron density in the ground state. In contrast, the mixing term depends on the excited and ground states, in which their energy gaps are denominators. An unstable transition state generally has a narrow energy gap between occupied and unoccupied molecular orbitals, yielding minor stabilization due to orbital interaction. As a result, the mixing terms are different between reactions (1) and (4). This is one of the reasons why the MRCs differ. For enhancing/suppressing mechanochemical reactivities, MRCs should be increased/decreased by molecular design. One can introduce substituents, for example, and change the mixing terms by varying occupied and unoccupied orbital levels, leading to the control of MRCs.
Reaction (5) correlates slightly less with MRC than the other reactions. In contrast to reactions (1)–(4), only the diene (one of the reactants) of reaction (5) is neither a monocyclic ring nor a fused one. This means that the number of low-frequency modes in the transition state of reaction (5) is greater than those of reactions (1)–(4). The deformations (vibrational excitations) that are effective for the reaction are more accessible along these low-frequency modes. This could be one of the reasons that only the experimental yield of reaction (5) is higher than predicted.
Fig. 6 shows the calculated cubic effective modes for the Diels–Alder reactions (1)–(4). All the modes mainly consist of C–H stretchings. This is similar with the previously reported cubic effective mode of reaction (5).18 One plausible reason for this is that the C–H stretching modes assist in the conversion of sp2 → sp3 in carbons around the reactive regions. The curvatures are expected to change considerably if these modes are partially excited during mechanical grinding. In fact, as for reaction (5), we already confirmed that the reaction barrier is significantly lowered by deformation along the C–H stretching mode by calculating potential energy surfaces along the reaction and cubic effective modes.18
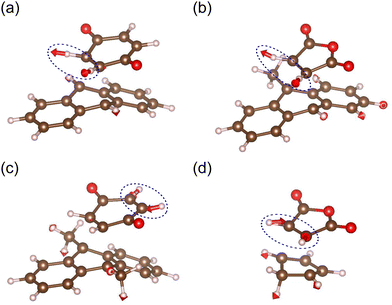 |
| | Fig. 6 The obtained cubic effective modes of the Diels–Alder reactions (a) 1, (b) 2, (c) 3, and (d) 4. The blue dotted circles indicate the significant components of the vibrational vectors. The cubic effective mode of reaction (5) is available in our previous study.18 | |
5 Conclusion
We found that a dimensionless cubic force constant, i.e., a mechanochemical reaction constant, governs the mechanochemical reactivities of the Diels–Alder reactions. This constant represents how easily the deformation can lower a reaction barrier and does not depend on the energy scale. The calculated mechanochemical reaction constants correlate positively with the yields of the mechanochemical Diels–Alder reactions well. Evaluation of the constants before experiments could enable us to predict the yields of mechanochemical Diels–Alder reactions. The present theory should be verified for various mechanochemical reactions, including the other Diels–Alder ones, in the near future.
Author contributions
W. S., L. G., and N. H. conducted DFT calculations and calculated MRCs and cubic effective modes. T. S., N. H., and M. B. supervised this work. All the authors participated in the discussion and the writing of the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We used the supercomputer of ACCMS, Kyoto University; the SuperComputer System, Institute for Chemical Research, Kyoto University; the supercomputer system at the information initiative center, Hokkaido University, Sapporo, Japan. This work was supported by JSPS Summer Program; Special Project by the Institute for Molecular Science (IMS program 22-IMS-C065).
Notes and references
- G.-W. Wang, Chem. Soc. Rev., 2013, 42, 7668–7700 RSC.
- M. K. Beyer and H. Clausen-Schaumann, Chem. Rev., 2005, 105, 2921–2948 CrossRef CAS PubMed.
- S. L. Potisek, D. A. Davis, N. R. Sottos, S. R. White and J. S. Moore, J. Am. Chem. Soc., 2007, 129, 13808–13809 CrossRef CAS PubMed.
- M. Baron, Waste Biomass Valorization, 2012, 3, 395–407 CrossRef.
- G.-W. Wang, K. Komatsu, Y. Murata and M. Shiro, Nature, 1997, 387, 583–586 CrossRef CAS.
- C. R. Hickenboth, J. S. Moore, S. R. White, N. R. Sottos, J. Baudry and S. R. Wilson, Nature, 2007, 446, 423–427 CrossRef CAS PubMed.
- H. Watanabe and M. Senna, Tetrahedron Lett., 2005, 46, 6815–6818 CrossRef CAS.
- Z. Zhang, Z.-W. Peng, M.-F. Hao and J.-G. Gao, Synlett, 2010, 2895–2898 CrossRef CAS.
- K. S. McKissic, J. T. Caruso, R. G. Blairb and J. Mack, Green Chem., 2014, 16, 1628–1632 RSC.
- L. Gonnet, A. Chamayou, C. André-Barrès, J.-C. Micheau, B. Guidetti, T. Sato, M. Baron, M. Baltas and R. Calvet, ACS Sustainable Chem. Eng., 2021, 9, 4453–4462 CrossRef CAS.
- J. G. Hernández and C. Bolm, J. Org. Chem., 2017, 82, 4007–4019 CrossRef PubMed.
- T. Luty, P. Ordon and C. J. Eckhardt, J. Chem. Phys., 2002, 117, 1775–1785 CrossRef CAS.
- J. Ribas-Arino, M. Shiga and D. Marx, Angew. Chem., Int. Ed., 2009, 48, 4190–4193 CrossRef CAS PubMed.
- L. Carlier, M. Baron, A. Chamayou and G. Couarraze, Tetrahedron Lett., 2011, 52, 4686–4689 CrossRef CAS.
- L. Carlier, M. Baron, A. Chamayou and G. Couarraze, Powder Technol., 2013, 240, 41–47 CrossRef CAS.
- P. F. M. Oliveira, N. Haruta, A. Chamayou, B. Guidetti, M. Baltas, K. Tanaka, T. Sato and M. Baron, Tetrahedron, 2017, 73, 2305–2310 CrossRef CAS.
- N. Haruta, P. F. M. de Oliveira, T. Sato, K. Tanaka and M. Baron, J. Phys. Chem. C, 2019, 123, 21581–21587 CrossRef CAS.
- W. Sakai, L. Gonnet, N. Haruta, T. Sato and M. Baron, J. Phys. Chem. A, 2023, 127, 5790–5794 CrossRef CAS PubMed.
- J. R. Felts, A. J. Oyer, S. C. Hernández, K. E. Whitener Jr., J. T. Robinson, S. G. Walton and P. E. Sheehan, Nat. Commun., 2015, 6, 6467 CrossRef CAS PubMed.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  cd,
Naoki
Haruta
cd,
Naoki
Haruta
 ab,
Tohru
Sato
*ab and
Michel
Baron
ab,
Tohru
Sato
*ab and
Michel
Baron
 c
c

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O are mechanically cleaved from chemically modified graphene sheets when atomic force microscope tips apply the force of nano Newton.19 Though it is difficult to observe the mechanical force applied to each molecule during ball milling directly, the mechanical forces of nano Newtons seem to be needed to undergo mechanochemical reactions. This is consistent with our previous study:18 mechanical forces of (sub-)nano Newtons are needed to vary the reaction barriers.
O are mechanically cleaved from chemically modified graphene sheets when atomic force microscope tips apply the force of nano Newton.19 Though it is difficult to observe the mechanical force applied to each molecule during ball milling directly, the mechanical forces of nano Newtons seem to be needed to undergo mechanochemical reactions. This is consistent with our previous study:18 mechanical forces of (sub-)nano Newtons are needed to vary the reaction barriers.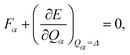
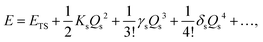
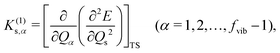
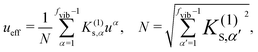

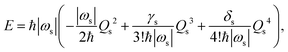
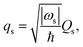
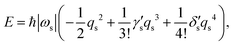
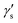 and
and 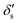 are dimensionless cubic and quartic force constants for the reaction mode,
are dimensionless cubic and quartic force constants for the reaction mode,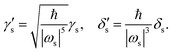

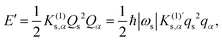
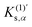 is given by
is given by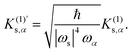
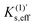 for the cubic effective mode can also be obtained.
for the cubic effective mode can also be obtained.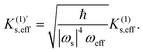
 means the degree of the maximum curvature variation due to a random force and is independent of the energy scale. We hereafter call
means the degree of the maximum curvature variation due to a random force and is independent of the energy scale. We hereafter call  a mechanochemical reaction constant (MRC),
a mechanochemical reaction constant (MRC), were calculated for each TS.
were calculated for each TS.




