Photocatalytic proton reduction by a computationally identified, molecular hydrogen-bonded framework

Abstract

We show that a hydrogen-bonded framework, TBAP-α, with extended π-stacked pyrene columns has a sacrificial photocatalytic hydrogen production rate of up to 3108 μmol g⁻¹ h⁻¹. This is the highest activity reported for a molecular organic crystal. By comparison, a chemically-identical but amorphous sample of TBAP was 20–200 times less active, depending on the reaction conditions, showing unambiguously that crystal packing in molecular crystals can dictate photocatalytic activity. Crystal structure prediction (CSP) was used to predict the solid-state structure of TBAP and other functionalised, conformationally-flexible pyrene derivatives. Specifically, we show that energy–structure–function (ESF) maps can be used to identify molecules such as TBAP that are likely to form extended π-stacked columns in the solid state. This opens up a methodology for the a priori computational design of molecular organic photocatalysts and other energy-relevant materials, such as organic electronics.

---

Introduction

The de novo design of solid-state energy materials is challenging because function is defined by features that span multiple length scales. One example is photocatalytic solar fuels production, where the catalytic activity can depend on a range of factors such as optical gap, electronic energy levels, surface area, particle size, and hydrophilicity.^1–8 Organic materials are promising candidates for photocatalytic hydrogen production, but predicting the best combination of properties is difficult because the underlying structure–activity rules are poorly understood. So far, most studies involving heterogeneous organic photocatalysts have been conducted on carbon nitride materials or amorphous conjugated polymers,⁹ where insolubility and lack of long-range order make thorough structural characterization difficult. Consequently, it is hard to deconvolute the structure–activity relationships in organic photocatalysts where the extended packing is poorly defined.

Molecular organic crystals have highly ordered structures that can be prepared in a modular way using solution-processable units. This makes molecular crystals attractive candidates for studying the effect of secondary structure on photocatalytic activity, since it is possible to compare materials that are chemically identical and that differ only in terms of their solid-state packing. By contrast, such structural comparisons are challenging for amorphous polymers and extended organic networks, such as covalent–organic frameworks (COFs), which often have only moderate crystallinity: for example, there are only a handful of single crystal structures reported in the literature for COFs,^10,11 and none of those materials have been shown to have photocatalytic activity. On the other hand it is relatively straightforward to grow high-quality single crystals of organic molecules. Until now, however, there are no examples of appreciable photocatalytic hydrogen evolution from molecular organic crystals.

We showed previously that amorphous pyrene-containing polymer networks can produce hydrogen photochemically from water in the presence of a sacrificial hole scavenger.¹² Recently, Lotsch et al. reported that a more crystalline material, a 2-D pyrene-based COF,¹³ shows higher photochemical activity. While this material has in-plane conjugation, out-of-plane conjugation between the close-packed organic layers was also invoked as an important structural feature for high photocatalytic activity. Through-plane conjugation is a relatively common feature of pyrene-containing materials and pyrene itself has been described as “the fruit fly of photochemists”¹⁴ because it is known to have interesting packing-related photophysical properties for organic electronics. Here, we chose three pyrene-based molecules; tetraphenylpyrene (TPhP), 1,3,6,8-tetrapyridin-4-yl pyrene (TPyP), and 1,3,6,8-tetra(4′-carboxyphenyl)pyrene (TBAP) (Fig. 1), which all form stable crystalline solids, to investigate the effect of molecular structure and extended crystal packing on photocatalytic hydrogen production rate.

Fig. 1 Chemical structures of TPhP, TPyP and TBAP.

In its native α-form, pyrene has a herringbone-type crystal packing arrangement, and this α-polymorph transforms to the structurally-related β-polymorph below 163 °C.¹⁵ By crystallising pyrene from CH₂Cl₂ at pressures > 0.3 GPa, it is possible to obtain the denser γ-polymorph, which features aligned π-stacked columns of pyrene molecules.¹⁶ However, this structure was reported to dissolve in the crystallisation solvent during decompression, making it impossible for us to access this π-stacked polymorph for photochemical experiments. The pyrene derivative, TPhP, crystallises from CH₂Cl₂/n-hexane,¹⁷ to produce a solid that also lacks π–π stacking interactions between pyrene molecules. This is because the phenyl groups frustrate the packing of pyrene cores.

Here, we use TPyP and TBAP to also investigate the effect of pyridyl and benzoic acid groups on the extended packing of pyrene cores. Hydrogen bonding has been shown to have the potential to frustrate dense packing of organic molecules, and to generate electrostatically-stabilised, low-density, hydrogen bonded organic frameworks (HOFs).^18–20 Similarly, labile C–H⋯N bonding interactions in molecular crystals, comprising pyridyl functionalised molecules, have been used to stabilise low density crystal packings.²¹ Hence, TPyP and TBAP both feature functional groups that have the potential to direct low-density, porous crystal packings with extended π-stacks, which is attractive for organic photocatalysts.

When we started this study, there were no reported structures of either TPyP or TBAP in their native uncoordinated states, even though these molecules have been used as struts in metal–organic frameworks (MOFs).^22–24 A crystal structure of TBAP was subsequently published while this study was in progress.²⁵

Molecular crystals are not subject to the same intuitive design rules associated with materials such as MOFs^26–28 and COFs,^29–31 because the crystallisation of organic molecules is governed by an interplay of many weak intra- and intermolecular interactions. It therefore remains a significant challenge to design, from first principles, new organic molecular crystals that feature porosity and/or extended π-conjugation. Porosity is also much less common in organic crystals because of their strong preference for close packing.³² At the atomistic level, discovering a new material involves substantiating a stable minimum on the free energy surface defined by chemical composition and the relative positions of atoms within an extended solid.³³ Traditionally, the search for new functional molecular materials has been led by knowledge-guided experiment. However, the role of computation in materials discovery has evolved rapidly in the past few years, from explanatory post-analysis of new materials to genuinely predictive methods that can be applied in advance of, or in tandem with, experiment. Such computationally-led approaches^34–36 promise to accelerate experimental searches and to unearth materials that might otherwise have remained undiscovered.³⁷ One area where this applies is the design of porous materials, which have applications in gas storage,^38–41 separation,^42–44 and organic catalysis,⁴⁵ as well as photocatalytic water splitting.^46–48 For example, we have developed computational methods for crystal structure prediction (CSP) to generate energy–structure–function (ESF) maps,^36,49 that have been used to target the discovery of highly porous hydrogen-bonded-frameworks (HOFs)³⁶ and organic semiconductors.^50,51 These ESF maps summarize the energetic distribution of stable crystal structures available to a given molecule, along with simulated properties relevant to the desired function.

No prior knowledge is required about the crystal packing of a candidate molecule because these approaches are based on ab initio structure prediction. However, to be reliable, the CSP method must fully explore the configurational space of available crystal packings; this is a high dimensional problem including molecular positions, orientation, and unit cell dimensions, as well as flexible intramolecular degrees of freedom. The associated computational expense has meant that most applications of CSP for the discovery of functional materials have been limited to rigid molecules,^{36,40,50–52} where a lack of conformational freedom leads to a reduced search space. TPhP, TPyP and TBAP are conformationally flexible and in this study, we have implemented a CSP method that accounts for this flexibility during structure searching, thus expanding the scope of CSP in the de novo design of functional materials. Specifically, we performed CSP calculations with TPhP, TPyP and TBAP, to determine whether these molecules were likely to form porous or π-stacked structures that could increase their photocatalytic activity for hydrogen production from water.

Results and discussion

Crystal structure landscapes

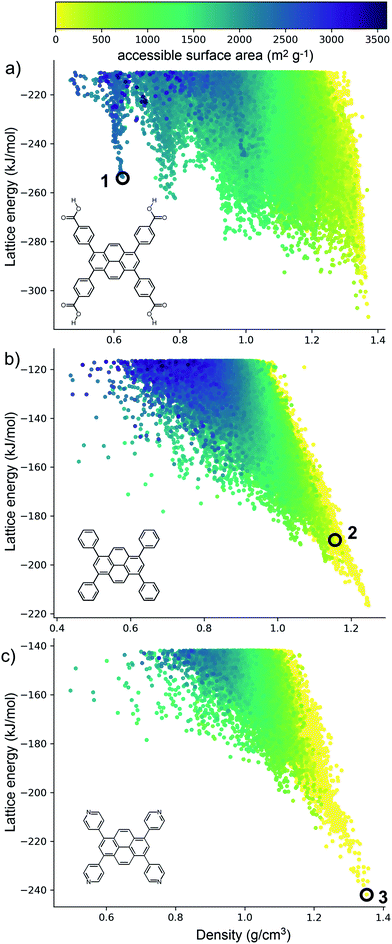
The crystal structure landscapes of TPhP and TPyP (Fig. 2b and c) are similar and show the usual strong correlation between energetic stability and crystal density. We calculated the accessible surface area for all predicted crystal structures, and this showed a lack of porous structures in stable regions of the energy landscape for these two molecules. Thus, we can decide a priori that neither molecule is a promising candidate for the formation of porous solids.

Fig. 2 Energy-density distributions of predicted crystal structures (a) TBAP, (b) TPhP and (c) TPyP. Each point corresponds to a distinct crystal structure, coloured by calculated accessible surface area (m² g⁻¹), and calculated using a 1.2 Å probe radius. The observed crystal structures are labelled.

By contrast, the computed crystal energy landscape for TBAP (Fig. 2a) contains several regions of low-energy, low-density predicted structures that fall well below the bulk energy-density trend. These low energy ‘spikes’ are reminiscent of those on the landscapes of the triptycene benzimidazolone molecule, T2,³⁶ and also trimesic acid,³⁷ both of which corresponded to experimentally accessible porous structures. These spikes correspond to isolated, deep basins on the lattice energy surface, separated by a high energy barrier from regions of the lattice energy surface corresponding to dense structures. The most prominent of these spikes has a density of ca. 0.6 g cm⁻³; the lowest energy structure in this spike, 1 (Fig. 2a) has a lattice energy 57 kJ mol⁻¹ above the dense global minimum on the TBAP landscape.

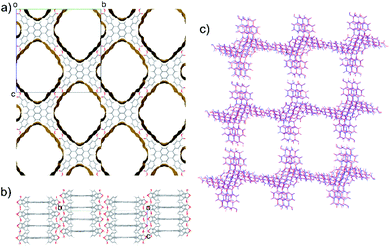
TBAP structure 1 features 2-dimensional sheets with rhomboid voids held open by acid–acid hydrogen bonds between TBAP molecules (Fig. 3). These sheets are stacked to form infinite pyrene columns (Fig. 3b) and parallel channels that run perpendicular to the hydrogen-bonded sheets. A second spike at a density of ca. 0.75 g cm⁻³ features similar structures containing one-dimensional channels between π-stacked pyrene columns, but with some collapsed channels (ESI, Fig. S1†). Thus, the CSP results suggested that TBAP had the potential for the construction of porous frameworks, like MOFs^22–24 but without the inclusion of metals. During the course of this study, although after these calculations, structure 1 was in fact reported independently by another research group,²⁵ confirming our prediction.

Fig. 3 Predicted porous structure of TBAP. (a) Viewed down the channels with voids with the surface indicating the solvent accessible surface (probe radius 1.2 Å) and (b) viewed perpendicular to the channels, showing the pyrene π-stacking. (c) An overlay of the predicted crystal structure 1 (red) and the experimental crystal structure TBAP-α (blue).

Using ESF maps to search for candidate photocatalysts

Although porosity has been linked to increased photocatalytic hydrogen evolution activity for conjugated organics polymers and polymeric carbon nitride,^47,53 many of the most active organic photocatalysts are in fact non-porous.^5,54 This indicates that photocatalytic hydrogen evolution activity is not determined by a single factor: it is dependent on many variables.⁸ There is, however, compelling evidence that certain recurrent structural motifs are more desirable than others. In particular, studies involving COFs^13,55 indicate that extended π–π stacking is linked to increased photocatalytic hydrogen evolution activity. ESF maps offer a method to search for such structural motifs systematically, particularly as predictions are now tractable for more complex molecules and can often be performed on a timescale that is much faster than the associated experiments (i.e., synthesis and crystallisation of a new candidate molecule coupled with photocatalytic measurements).

Fig. 4 shows ESF maps that summarize the propensity of TPhP, TPyP, and TBAP to crystallise to form extended π–π stacks with significant overlap between the pyrene cores. In this analysis, we define an extended π–π stack as four or more nearly co-parallel molecules with limits on the separation between centres of mass (see ESI, Section 1.4 for details†). Due to the translational symmetry, this is equivalent to infinite stacks in almost all cases. All three of these molecules have similar energetic distributions of stacked versus unstacked structures. Note that many unstacked structures are hidden in Fig. 4 (see ESI, Fig. S66†). In all three cases, the low-energy edge of the energy-density distribution is dominated by structures containing π-stacked columns. One key difference is the presence of low-energy spikes on the TBAP landscape, discussed above, which are not present for TPhP or TPyP. The structures within these deep basins on the lattice energy surface all show extended π–π stacking; that is, these regions of enhanced stability are explicitly linked to π–π stacking. We would therefore predict a priori that TBAP is a more promising candidate for π-stacked HOFs than either of its two structural analogues, TPhP or TPyP.

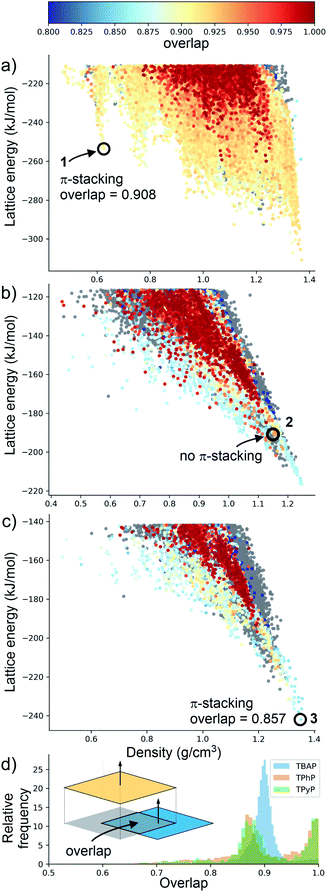Fig. 4 Energy-density distributions of predicted crystal structures. (a) TBAP, (b) TPhP and (c) TPyP. Coloured data points are structures containing extended stacks of coplanar molecules (see ESI for details†) and are coloured by the extent of molecular overlap between stacked molecules (inset, part D). Structures without stacking are shown in grey, but stacked data points are plotted on top of unstacked ones, thus hiding many of the unstacked structures (see ESI, Fig. S66†). Annotations in A–C refer to the observed crystal structures. (d) Histogram of the degree of molecular overlap in predicted crystal structures with extended stacks. Note that the histograms are transparent, so that overlapping regions appear dark green.

Charge transport is highly sensitive to small changes in molecular packing, which dictates the electronic coupling between molecules. We therefore developed methods to analyse geometric parameters within predicted crystal structures that display extended π-stacked columns. The distribution of predicted structures in Fig. 4 is coloured according to the geometric overlap of neighbouring stacked molecules, which was calculated from the projection of their planes of best fit (Fig. 4d and ESI†). This geometric measure of stacking overlap is used as a proxy for overlap of frontier molecular orbitals and is correlated with efficient charge transport and exciton dissociation in π-conjugated materials.^56–58

From a predictive point of view, the distribution of π-overlap on the ESF maps is important. Experimentally accessible structures are expected to be found either near the lattice energy global minimum or, in the case of porous structures that are stabilised by solvent inclusion during crystal growth, along the low energy ‘leading edge’ of the energy-density distribution. All three molecules have predicted structures with nearly perfect π–π overlap (overlap ≈ 1, Fig. 4d), but these occur in high energy regions of their crystal structure landscapes, away from the global energy minimum and leading edge of the ESF maps. The structures in experimentally accessible regions are those with overlaps in the range 0.85–0.95, where TBAP structures show significantly higher overlap than TPhP and TPyP (blue peak in histogram; Fig. 4d). This difference stems from the carboxylic acid groups in TBAP, which direct the molecule into crystal packings that favour π-stacks with strong π–π overlap. This demonstrates a global, predictable preference for TBAP to adopt favourable packing for charge transport compared to TPhP and TPyP, which may enhance charge-transport to the interface with water and the hole scavenger. While the global energy minima structures for both TPhP and TPyP also show π-stacking with a reasonable degree of overlap (0.863 and 0.857, respectively), an experimentally known structure of TPhP¹⁷ that sits well above the global energy minimum displays no π-stacking, suggesting that these more ‘optimal’ structures may be kinetically difficult to access, at least for TPhP.

Crystallisation experiments

Crystallisation of TPhP. We sublimed the P2₁2₁2₁ α-polymorph of TPhP under vacuum at 425 °C, which is the same polymorph as that reported from recrystallisation using CH₂Cl₂/n-hexane.¹⁷ The crystal packing in TPhP-α closely matches a predicted structure from the computed crystal structure landscape, 2 (Fig. 2b). The geometric agreement between these structures is excellent (ESI, Fig. S2†), but this structure is predicted to lie above the global minimum energy structure. The energetic ranking of this structure might reflect limitations of the force field and rigid-molecule approach adopted in the CSP, but it might also indicate that more thermodynamically stable crystal structures of TPhP exist.

Crystallisation of TPyP. Due to its poor solubility, we were unable to crystallise TPyP from solvent. We therefore sublimed TPyP under vacuum at 450 °C to afford a solvent-free structure, TPyP-α, which crystallised in the monoclinic space group P2₁/n (ESI, Fig. S3†). TPyP-α is reproduced accurately by the predicted global minimum energy crystal structure, 3 (Fig. 2c and ESI, Fig. S4†) and features close-packed, interdigitated, columnar stacks of TPyP molecules, which are packed 3.95 Å apart along the crystallographic a axis.

Crystallisation of TBAP. TBAP was crystallised by vapour diffusion of CHCl₃ into a saturated N,N-dimethylformamide (DMF) solution. The crystallisation solvent was then exchanged with acetone, and the acetone was subsequently removed from the crystal pores at 120 °C under dynamic vacuum (ESI, Fig. S5–S15 and Table S5†). The desolvated crystal structure, TBAP-α, which has C2/m symmetry is in excellent agreement with the predicted low-density TBAP structure, 1 (Fig. 2a and 3c). The crystal structure of TBAP-α, as determined at 25 °C, had a packing distance between pyrene cores of 3.93 Å, which is slightly longer than 3.85 Å reported for the γ-polymorph of pyrene recorded at 0.3 GPa and 25 °C.¹⁶ We carried out sorption measurements to estimate the surface area of TBAP-α, which was found to match our ESF map predictions (Brunauer–Emmett–Teller surface area, SA_BET = 2001–2270 m² g⁻¹, ESI, Fig. S19–S22;† ESF map prediction = 2273 m² g⁻¹). This is also in agreement with the report by Yin et al.²⁵

These three crystalline solids, TPhP-α, TPyP-α, TBAP-α, display different π–π stacking modes of pyrene cores, and the TBAP-α structure features a high surface area. These three crystalline solids are therefore good candidates to investigate the effect of crystal structure on photocatalytic activity in molecular crystals.

Photocatalysis experiments

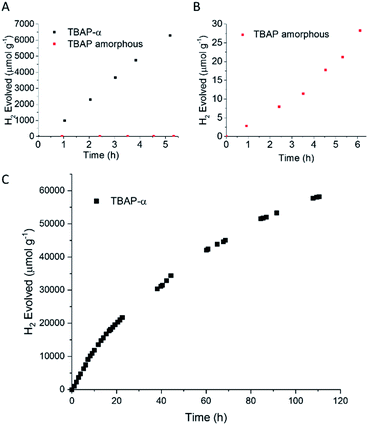
TPhP-α, TPyP-α, TBAP-α have light absorption onsets well into the visible region (Fig. S34†). We therefore tested activity for sacrificial photocatalytic hydrogen production under visible light (λ > 420 nm, 300 W Xe light source) with 1 wt% platinum co-catalyst, using ascorbic acid as the sacrificial hole-scavenger. TBAP-α was by far the most active material under these conditions with an initial hydrogen evolution rate (HER) of 1293 μmol g⁻¹ h⁻¹ (Table 1). This is the first example of a crystalline porous HOF that shows appreciable photocatalytic hydrogen evolution from water under sacrificial conditions, challenging the paradigm that covalent networks such as COFs or extended polymer chains are required. These photocatalytic rates are significantly higher than for amorphous pyrene-based conjugated microporous polymers (CMPs) (HER_{λ>420 nm} = 174 μmol g⁻¹ h⁻¹ using diethylamine as the hole-scavenger).¹² The external quantum efficiency (EQE) of TBAP-α was estimated to be 4.1% at 420 nm using monochromatic light from a LED source, which is higher than many conjugated polymer catalysts such as a benzodithiophene-bipyridine CMP, PCP4e (EQE_{350 nm} = 0.34% using triethylamine/water mixtures)⁸ and a tricyano-benzene-centered phenylenevinylene-co-terphenylene polymer network, OB-POP-3, (EQE_{420 nm} = 2.0% using water triethanolamine mixtures),⁵⁹ but lower than dibenzo[b,d]thiophene-CMP S-CMP3 (EQE_{420 nm} = 13.2%, using water/methanol/triethylamine mixtures),⁴⁷ and certain linear conjugated polymers, such as poly(dibenzo[b,d]thiophene) P10 (EQE_{420 nm} = 11.6%, using water/methanol/triethylamine mixtures).⁵⁴ At 470 nm, the EQE for TBAP-α is reduced to 1.2% and no significant activity is observed at 595 nm. As such, the photocatalytic efficiency follows the absorption profile of TBAP-α (ESI, Fig. S28†).

Table 1 Photocatalytic activity of the materials

Material	Hole-scavenger	pH	HER^a (μmol h^−1 g^−1)
a Catalyst (25 mg) loaded with 1 wt% Pt, from in situ photodeposition of H2PtCl6, suspended in water and scavenger (25 mL), irradiated with a 300 W Xe light source fitted with a λ > 420 nm filter. The HER was determined over five hours. b HER calculated over 20 hours. c Material fully or partially dissolved under these conditions.
TPhP-α	Ascorbic acid 0.1 M	2.6	2^b
TPyP-α^c	Ascorbic acid 0.1 M	2.6	18
TBAP-α	Ascorbic acid 0.1 M	2.6	1293
Amorphous TBAP	Ascorbic acid 0.1 M	2.6	6
TPyP-α	Ascorbic acid 0.1 M	7	<0.1
TBAP-α	Ascorbic acid 0.1 M	7	3108
Amorphous TBAP	Ascorbic acid 0.1 M	7	156
TPhP-α	Triethylamine 5 vol%	11.5	6
TPyP-α	Triethylamine 5 vol%	11.5	40
TBAP-α^c	Triethylamine 5 vol%	11.5	<0.1

---

No hydrogen production is observed in the dark or in the absence of the TBAP-α. When D₂O was used as the proton source, D₂ production was mostly observed (ESI, Fig. S29†), with a small amount of H₂, probably due to H–D exchange with protons in the non-deuterated ascorbic acid.⁶⁰ Essentially no CO production is observed under these conditions (ESI, Fig. S31†). Taken together, these observations lead us to conclude that the hydrogen production process is indeed photocatalytic.

TPyP-α was much less active and produced hydrogen at a rate of just 18 μmol g⁻¹ h⁻¹, although the basic pyridyl groups in TPyP meant that a significant proportion of the TPyP-α catalyst (>50 wt%) dissolved in the acidic medium during this measurement. Consequently, a direct comparison between the HER activity of TPyP-α and TBAP-α in ascorbic acid is not possible. TPhP-α is stable in ascorbic acid but had an even lower HER of 2 μmol g⁻¹ h⁻¹.

To allow for a direct comparison between TBAP-α and TPyP-α, we tested the materials in a 0.1 M ascorbic acid solution adjusted to pH 7 with NaOH, where neither material dissolves. Under these conditions, TPyP-α produced no measurable amount of hydrogen over a five-hour period. By contrast, TBAP-α was even more active with a HER of 3108 μmol g⁻¹ h⁻¹ (ESI, Fig. S24†). This large change in HER can be rationalised by considering the driving forces of the two half reactions occurring in the system. Density functional theory (DFT)^61,62 calculations performed on isolated molecules immersed in water at pH 2.6 (the expected pH of 0.1 M ascorbic acid solution, Fig. S48†) suggest that all three materials should have a large driving force for proton reduction and reasonable driving force for the overall oxidation of ascorbic acid. The driving force for the initial one-hole oxidation of ascorbic acid is very small for TBAP and TPyP and actually slightly negative for TPhP. Thus, we might expect the oxidation of the scavenger to be rate limiting in these systems, accounting for the increased activity of TBAP-α when changing the pH level from pH 2.6 to pH 7, because the driving force for ascorbic acid oxidation increases. This change also reduces the driving force for proton reduction, however, even at pH 7, the driving force for proton reduction remains large (>1.5 V) and, crucially, larger than that for ascorbic acid oxidation (0.9 V for the 2-hole and 0.5 V for the intermediate one-hole oxidation). This does not explain the decrease in rate of TPyP-α when changing the pH level from pH 2.6 to pH 7, but we note that the partial dissolution of the material and the influence of protonation on the substrate electronics under acidic conditions could play a role.

When 5 vol% triethylamine in water solution was used as the sacrificial system, TBAP-α was found to dissolve and no measurable hydrogen was produced under visible light irradiation. TPyP-α and TPhP-α were both stable in 5% triethylamine but had low HERs of 40 and 6 μmol g⁻¹ h⁻¹, respectively. None of the materials produced hydrogen when tested in a 5 vol% TEA solution adjusted to pH 7.

At first glance, these results could suggest that porosity is the dominant factor for hydrogen evolution, because the porous TBAP-α structure greatly outperforms the non-porous analogues, even though TPyP-α also contains significantly overlapped π-stacking. This may however be an oversimplification. As evident from water sorption isotherms, TBAP-α has no significant water uptake between partial pressures of 0.2–0.6 (Fig. S52†). There is significant water uptake at higher relative pressure, which might suggest water adsorption but could also indicate water molecules condensing on the crystal surfaces or between crystals. We note that this wetting behaviour may be different in the presence of the sacrificial agent, ascorbic acid, and in this respect, water sorption isotherms may not reflect the photocatalysis conditions.

Perhaps more significantly, it is unclear that the platinum cocatalyst, which is possibly the site for proton reduction, actually resides in the pores of the TBAP HOF. This raises additional doubts that porosity alone can account for the superior performance of this material. In the absence of added Pt co-catalyst, TBAP-α had a dramatically reduced rate of 59 μmol g⁻¹ h⁻¹. It is possible that residual palladium from synthesis acts as the active site in this case. Pd levels by ICP-MS were found to be below the 10 ppm detection level of the instrument but we note that very low concentration can be sufficient to give limited photocatalytic activity.⁶³ The addition of 1 wt% Pt was found to give the highest catalytic activity, while increasing the loading to 4 wt% appeared to reduce HER (ESI, Table S6†), perhaps due to reduced light absorption or recombination.^64,65 Element analysis (ICP-MS; ESI, Table S6†) and STEM imaging were employed to confirm that in situ photo deposition of platinum had been successful (Fig. 5 and ESI Fig. S54†). Platinum nanoparticles of between 2 and 15 nm formed on both TBAP-α and amorphous TBAP. It was noted that the distribution of Pt in the samples with 1 wt% Pt was generally more even, and that larger, less well-dispersed clusters could be observed at the higher 4 wt% Pt loading (Fig. 5 and ESI, Fig. S54†).

Fig. 5 STEM images of TBAP-α in (A) BF mode and (B) HADF mode, with 1 wt% photodeposited Pt in (C) BF mode and (D) HADF mode and with 4 wt% photodeposited Pt in (E) BF mode and (F) HADF mode.

Photolysis experiments using 4 wt% Pt were repeated for three different batches of TBAP-α and showed good reproducibility between batches (ESI Fig. S23†). The PXRD patterns and sorption isotherms of the three batches were also very similar (ESI Fig. S19–S22†) with BET surface areas of 2001, 2270 and 2074 m² g⁻¹. Likewise, static light scattering showed only modest variations in the particle size distribution between batches (average diameters of 9.25–15.52 μm, ESI Fig. S62 and Table S9†).

To investigate further, we conducted photocatalysis experiments using large (13 nm by DLS, ESI Fig. S55†) pre-made platinum nanoparticles as the co-catalyst source, rather than photodeposition of Pt from solution. These pre-made Pt particles are too large to fit within the 1.9 × 2.1 nm TBAP-α nanopores and, hence, if these pores are the main sites for hydrogen evolution, then we might expect to see a very large decrease in rate compared to materials with photodeposited Pt particles, which might be small enough to form within the pore channels. This was not observed. The rate with the pre-formed nanoparticles was 813 μmol g⁻¹ h⁻¹; that is, only around 37% lower than for the photodeposited Pt sample under those catalysis conditions (1293 μmol g⁻¹ h⁻¹). ICP-MS analysis indicated the Pt contents were similar for both the photodeposited and the pre-made Pt materials and STEM imaging showed deposition had occurred in both cases.

Scanning electron microscopy imaging also indicated the inaccessibility of the TBAP-α pores: even the small, photodeposited Pt particles appeared to reside on the crystal surface, rather than within the pore channels (ESI, Fig. S57†). At present, it is not possible to state the precise role that micropores in TBAP-α play in the photocatalytic process, although the location of the Pt cocatalyst instead suggests that the external crystal surface is very important. It is conceivable that hole scavenging can occur within the pore channels, even if the main sites for photocatalytic hydrogen production are on the crystal surface; if so, then charge transport of the holes and electrons in the material would be important, which might explain the benefit of the extended π-stacks in TBAP-α.

Visible light absorption is also an important aspect of photocatalysis, and the three materials do show different absorption onsets in the solid state. These were determined to be 504, 477 and 449 nm for TBAP-α, TPyP-α and TPhP-α, respectively. However, based on experience with other materials, we would not expect this degree of blueshift to give the large, order-of-magnitude, change in photocatalytic activity between TBAP-α and the other two materials.

While the two π-stacked materials do outperform the non-π-stacking TPhP-α, the blue-shifted optical gap (ESI, Fig. S34†), lower wettability (ESI, Fig. S63 and S65†) and smaller driving force (ESI, Fig. S48†) of TPhP-α, relative to TPyP-α, could also contribute to the differences in HER between these two materials. As such, we cannot conclude that TPyP-α outperforms TPhP-α solely due to more optimal π-stacking.

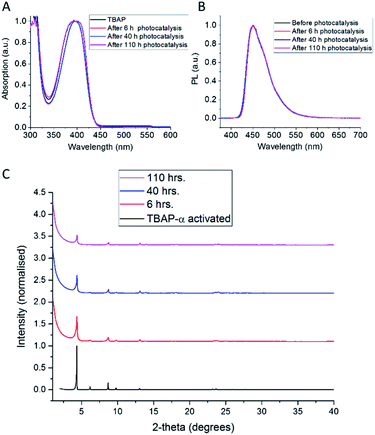
The photocatalytic activity of TBAP-α was also investigated over a longer-term experiment and a slow loss of activity was observed over time (Fig. 6c); the rate reduced to 653 μmol g⁻¹ h⁻¹ after 20 hours, to 369 μmol g⁻¹ h⁻¹ after 60 hours and 156 μmol g⁻¹ h⁻¹ after 110 hours of photolysis. While this points to long-term instability, the sustained photochemical production of hydrogen at these rates over 110 hours is remarkable when one considers that TBAP-α is a molecular HOF where the framework is held together by hydrogen bonds and van der Waals interactions, which are weak in comparison to bonded frameworks such as CMPs and COFs.

Fig. 6 (A) Time-course of hydrogen evolution for TBAP-α (black symbols) and TBAP amorphous (red symbols) (25 mg) loaded with 1 wt% Pt, from photodeposition of H₂PtCl₆, dispersed in ascorbic acid solution (25 mL, 0.1 M) illuminated with a 300 W Xe light source fitted with a λ > 420 nm cut-off filter. (B) Expanded plot showing activity for amorphous TBAP. (C) Extended run over 110 hours. The solution was degassed at 6, 11, 18, 40, 67 and 90 hours.

The observed loss of activity is accompanied by a gradual decrease in crystallinity, as evident from a drop in X-ray peak intensity (Fig. 7c). No changes in the solution UV-vis spectrum (Fig. 7a) were observed after 110 hours photolysis; also, the photoluminescence spectrum (Fig. 7b) and the solution ¹H NMR spectrum (ESI, Fig. S32†) remain unchanged. This suggests that the loss of catalytic activity is connected to changes in the TBAP packing, rather than any chemical degradation. Consequently, amorphous TBAP, isolated from the photocatalysis experiments after filtration, could be used to regenerate TBAP-α, after re-crystallisation from DMF/CHCl₃.

Fig. 7 (A) UV-vis and (B) PL (λ_exc = 360 nm) in DMSO solution and (C) PXRD of TBAP-α loaded with 1 wt% Pt, after photocatalysis experiments performed in ascorbic acid (0.1 M), illuminated with a 300 W Xe light source fitted with a λ > 420 nm cut-off filter. After photocatalysis experiments, the samples were collected by filtration and air-dried before analysis.

It was thought that the loss in crystallinity of TBAP-α we observed during the photocatalysis experiments in aqueous solutions may be reduced by decreasing the polarity of the reaction medium. TBAP-α was therefore also tested using a 9 : 1 mixture of MeCN : water (Fig. S71†). In this case, the initial HER of 358 μmol g⁻¹ h⁻¹ remained approximately linear over the whole 118 hour experiment, with TBAP-α producing hydrogen at a rate of 347 μmol g⁻¹ h⁻¹ over hours 102–118, very close to the initial rate. This improved performance in the MeCN : water dispersant was also accompanied by a slower drop in the TBAP-α crystallinity over the experiment (Fig. S71†), as compared to the fully aqueous system (Fig. 7). We ascribe the lower rate in the MeCN : water medium to the smaller driving force for scavenger oxidation expected in this system as well as the fact that photodeposition of platinum appeared to occur less efficiently, with only 0.05 wt% Pd measured by ICP-MS (Table S6†).

To test the link between crystallinity and HER further, we deliberately produced amorphous material by the rapid precipitation of TBAP from a basic solution (ESI, general methods and Fig. S33†). We found that this amorphous TBAP had a very poor photocatalytic activity (Table 1 and Fig. 6b); with 1 wt% photodeposited Pt, the rate was 6 μmol g⁻¹ h⁻¹ (after an induction period). This rate is over 200 times lower than the rates observed for crystalline TBAP-α under equivalent conditions. This rationalises the steady loss of activity that is observed for TBAP-α as the crystallinity is reduced during photocatalysis. Amorphous TBAP under equivalent conditions but without added Pt produced no measurable hydrogen over 5 hours of irradiation.

DFT^61,62 calculations that consider (i) an isolated TBAP molecule immersed in water, and; (ii) a stacked column of TBAP molecules from the TBAP-α structure suggest that the effect of packing on the TBAP potentials should be small (see ESI, Section 1.5, Table S8, Fig. S49 and S50†), in keeping with the similarity of the absorption spectra for amorphous and crystalline analogues. These DFT calculations also suggest that TBAP-α and its amorphous counterpart should both have the required driving force for proton reduction and ascorbic acid oxidation.

Like TBAP-α, the amorphous TBAP material also showed better activity when tested at pH 7; HER increased to 156 μmol g⁻¹ h⁻¹, (ESI, Fig. S24†), which is consistent with an increased driving-force for ascorbic acid oxidation as discussed above. This rate for amorphous TBAP is still 20-times lower than that of crystalline material under equivalent conditions (3108 μmol g⁻¹ h⁻¹), again suggesting that crystallinity and the packing of TBAP units is the dominant factor in the photocatalytic activity of this systems.

Time-correlated single photon counting (TCSPC) was employed to investigate the lifetime of the excited state in these materials. TBAP-α and amorphous TBAP suspended in water showed almost identical TCSPC spectra, when excited at 405 nm with average lifetimes of 2.12 and 2.13 ns, respectively. When using an aqueous suspension in ascorbic acid (0.1 M) significantly reduced fluorescence lifetimes were observed for both crystalline and amorphous TBAP (ESI, Fig. S47†). Even though TCSPC can only be used to study emissive states, these results suggest that exciton generation is similar for the amorphous and crystalline TBAP and that ascorbic acid is an effective hole scavenger for both materials.

By contrast, TPhP-α in ascorbic acid solution showed no significant quenching of the excited state lifetime (ESI, Fig. S69†). Similarly, neither TPhP-α nor TPyP-α showed a significant reduction in excited state lifetime in the presence of TEA (ESI, Fig. S70†). This indicates that poor interaction with the ascorbic acid or TEA hole scavenger might limit the activity of TPhP-α and TPyP-α for proton reduction in comparison to TBAP-α.

Taking these various experimental observations and DFT calculations together, we suggest that the dramatic difference in catalytic activity for crystalline and amorphous TBAP might be explained, at least in part, by restricted charge/exciton transport in the amorphous material to the active sites on the catalyst surface.⁴⁷ While the exciton quenching kinetics by the hole scavenger between amorphous TBAP and TBAP-α appear to be similar, it is possible that transfer of a subsequent electron or electron polaron to a Pt active site is aided by interlayer conjugation in the crystalline HOF, which does not exist in the amorphous analogue. Materials with a higher degree of order and closer π–π stacking have been shown previously to have higher charge-carrier mobilities; for example, in conjugated polymers such as poly(thiophene-thieno[3,2-b]thiophene)⁶⁶ and poly(cyclopentadithiophene-benzothiadiazole).⁶⁷ Given this apparent benefit of extended π-stacked pyrene units, the low activity of TPyP-α, which has an overlap close to that of TBAP-α (0.86 vs. 0.91) is somewhat surprising. It is possible that in the case of TPyP-α, inefficient hole scavenging (as observed by TCSPC) prevents efficient generation of polarons from excitons reducing the amount of hydrogen that can be produced.⁵⁴ Thus, any potential increase in charge-carrier mobility due to the packing of TPyP-α in the crystal is less relevant due to the low quantity of polarons generated.

Conclusions

In summary, we report here the first example of a molecular crystalline HOF with high photocatalytic activity. The porous, hydrogen-bonded structure of TBAP-α was anticipated using CSP methods and ESF maps. TBAP-α has high photocatalytic activity for proton reduction under sacrificial conditions, while the amorphous TBAP material has an activity that is up to 200 times lower over the first 5 hours of photolysis. To our knowledge, this is the first example where two different solid phases of the same organic materials have been studied for photocatalysis, i.e. where the solids are chemically identical and differ only in their solid-state packings, and it allows us to deconvolute the effects of molecular structure and crystal structure. The huge difference in catalytic activity for crystalline and amorphous forms of the same molecule shows unambiguously that solid-state crystal packing can have a large effect on photocatalytic activity. Detailed comparisons of the activities and crystal structures of TBAP, TPyP and TPhP suggest that π-stacked columns with strong π–π overlap are a desirable packing motif. The specific role of porosity in the photocatalytic activity of TBAP-α is less clear, but porosity is, in general, a desirable feature for heterogeneous catalysis and it also opens up other opportunities, such as doping or dye sensitization.⁶⁸

While it is not yet possible to predict photocatalytic activity directly from crystal structure alone, CSP has strong potential to guide the discovery of new molecular building blocks by searching for crystal structure landscapes that contain stable structures with useful features, such as extended columns of π-stacked molecules with good overlap of the molecular faces. This is also useful for other energy materials, such as organic electronics.

Looking forward, CSP and ESF maps could be used to find other molecular systems that combine properties such as microporosity and π–π stacking. By extension, CSP could also be used to search for other packing motifs as our understanding of structure–activity relationships for organic photocatalysts expands. Because the computational search methods require no experimental input, this applies to hypothetical candidate molecules that have not yet been synthesised. Increasingly, these CSP calculations are much faster than experimental techniques such as molecular synthesis and crystallisation screens, allowing us to focus experimental resources on the most promising systems.

Experimental

Crystal structure prediction

TPhP, TPyP and TBAP all have multiple low-energy conformers, which required us to expand our CSP and ESF map methodology to consider the ensemble of possible conformers to ensure that the crystal packing arrangements are comprehensively sampled and that experimentally realizable structures are not missed.^69,70 For conformationally flexible molecules, it is not obvious which form will crystallise experimentally; indeed, observed crystal structures are sometimes based on molecular conformers that have high energies in the gas phase.⁷¹ This means that a wide range of conformers must be considered during CSP.

Conformers for each molecule were generated using a mixed torsional/low-mode sampling method^72,73 implemented in Schrödinger's Maestro package,⁷⁴ with energies modelling using the OPLS2005 force field.⁷⁵ All unique conformers were then re-optimised using dispersion-corrected DFT, at the B3LYP-D3/6-311G(d,p) level of theory, leading to 4 conformers for each of TPhP and TPyP, differing in the orientation of phenyl and pyridyl groups with respect to the pyrene core, and 28 conformers TBAP, where orientations of the carboxylic acid groups expand the conformational space.

All conformers were used as starting points for CSP, which was performed with low discrepancy sampling of crystal packing variables, using the Global Lattice Energy Explorer software.⁷⁶ Crystal structures were generated in the 25 most common space groups with one molecule in the asymmetric unit, then lattice energy minimised with molecular geometries fixed at their gas phase DFT geometries. Intermolecular interactions within the predicted crystal structures were calculated using the FIT atom–atom force field⁷⁷ combined with atomic multipole electrostatics. Total energies were calculated as a sum of the force field intermolecular energy and the dispersion corrected DFT energy of the molecular conformer. All lattice energy calculations were performed with the DMACRYS crystal structure modelling software,⁷⁸ and structures up to 100 kJ mol⁻¹ above the global minimum were kept, as highly porous structures can occupy very high energy regions of the lattice energy landscape.^36,79 This led to CSP landscapes with relatively large numbers of hypothetical structures; for example, for TBAP, the 28 conformers led to a CSP landscape with over 100 000 independent hypothetical crystal structures within 100 kJ mol⁻¹ of the global minimum in the 25 space groups studied (Fig. 2a). Full details of the crystal structure prediction methods are provided in the ESI.†

All CSP data, including predicted crystal structures, energies, accessible surface areas and stacking analysis, can be accessed at https://doi.org/10.5258/SOTON/D1015.

DFT potential calculations

The vertical ionization potential (IP) and electron affinity (EA) of TBAP, TPhP and TPyP were calculated using a ΔDFT approach. First the ground state geometry of each as an isolated molecule was optimised using the B97-3c approach by Grimme and co-workers.⁶² Next the energy of each of the molecules in its neutral (E(N)), cation (E(N − 1)) and anionic (E(N + 1)) state were obtained from single-point calculations using the B3LYP functional^80–83 and the 6-31G** basis-set.^84,85 Finally, IP and EA were calculated from:

IP = −(E(N) − E(N − 1)) − 4.44

EA = −(E(N + 1) − E(N)) − 4.44

where all energies are in eV and the subtraction by 4.44 converts the calculated IP and EA from the vacuum to the standard hydrogen electrode scale. The B3LYP single-point calculations were performed using Gaussian16 (ref. 86) and employed the PCM solvation model⁸⁷ to describe the aqueous environment of the molecules near the molecular solid–solution interface. The B97-3c calculations were performed using Turbomole 7.3 (ref. 88) and employed no solvation model as to as closely as possible match the computational set-up of the periodic DFT calculations on TBAP-α.

In the case of TBAP the IP and EA values were also calculated using an alternative strategy, starting from the crystal structure of TBAP-α. Initially, the experimental crystal structure of TBAP-α is energy minimised in a periodic DFT calculation using the B97-3c approach as implemented in Crystal17.⁸⁹ Subsequently, three cluster models were cut out of the DFT optimised crystal structure, corresponding to one monomer, one monomer (1C) with a molecule above and below it, as well as the phenyl groups of the laterally adjacent molecules (1C+, see Fig. S49†), and an analogous structure with a tetramer in the centre (4C+). The IP and EA values of the three cluster models were calculated in the same way as for the isolated molecules discussed above, other than that in the last two cases we used the ONIOM QM/MM approach⁹⁰ and described the molecule (fragments) around the monomer and tetramer using the UFF forcefield.⁹¹

All DFT optimised cluster models have been uploaded as electronic supplementary information.

Synthesis

Synthesis of 1,3,6,8-tetra(4′-carboxyphenyl)pyrene (TBAP). TBAP was synthesised according to literature routes.²²¹H NMR (400 MHz, DMSO-d₆): δ (ppm) = 8.20 (s, 4H), 8.15 (d, 8H, J = 8.0 Hz), 8.07 (s, 2H), 7.84 (d, 8H, J = 8.0 Hz). HR-MS calcd for [C₄₄H₂₆O₈ + H]⁺m/z = 683.1706; found: m/z = 683.1716. Anal. calcd for C₄₄H₂₆O₈: C, 77.41; H, 3.84; found: C, 76.06; H, 3.80.

Synthesis of 1,3,6,8-tetraphenylpyrene (TPhP). TPhP was synthesised according to a literature route.¹⁷¹H NMR (400 MHz, CDCl₃): δ (ppm) = 8.18 (s, 4H), 7.99 (s, 2H), 7.72 (d, J = 7.5 Hz, 8H), 7.61–7.63 (m, 8H), 7.54 (t, J = 7.5 Hz, 4H). HR-MS calcd for [C₄₀H₂₆ + H]⁺m/z = 507.2113; found: m/z = 507.2109. Anal. calcd for C₄₀H₂₆: C, 94.83; H, 5.17; found: C, 94.36; H, 5.04.

Synthesis of 1,3,6,8-tetrapyridin-4-yl pyrene (TPyP). 1,3,6,8-Tetrabromopyrene (1.04 g, 2 mmol), 4-pyridinylboronic acid (983 mg, 8 mmol), N,N-dimethylformamide (200 mL) and K₂CO₃ (50 mL) were added to a flask and degassed by N₂ bubbling for 30 minutes. [Pd(PPh₃)₄] (40 mg, 0.035 mmol) was added and the solution was degassed for a further 10 minutes before heating to 145 °C for 48 hours. After cooling the mixture was poured into water (1 L) and stirred for 30 minutes. The precipitate was collected by filtration and washed with, water (100 mL), methanol (mL) and dichloromethane (100 mL) before drying under vacuum. The product was obtained as a green solid (986 mg, 1.92 mmol, 96%). ¹H NMR (400 MHz, acetic acid-d₄): δ (ppm) = 9.08 (d, J = 6.0 Hz, 8H), 8.41 (s, 4H), 8.36 (s, 2H), 8.17 (d, J = 6.0 Hz, 8H). HR-MS calcd for [C₃₆H₂₂N₄ + H]⁺m/z = 511.1923; found: m/z = 511.1922. Anal. calcd for C₃₆H₂₂N₄: C, 84.68; H, 4.34; N, 10.97; found: C, 84.37; H, 4.31; N, 10.73.

Crystallisation, solvent exchange and activation of TBAP-α. 500 mg of as-synthesised TBAP was covered by DMF (40 mL) in a large vial. The mixture was sonicated for 10 min and left overnight so all remaining undissolved material settled at the bottom of the vial. 20 mL of the supernatant solution was the filtered into two 40 mL vial using a 0.45 μm PTFE syringe filter to remove any particulates. For batches 1 and 3, the 40 mL vials were capped with a septum that had been pierced using a needle and these vials were placed in a sealed chamber containing chloroform. For batch 2, the 40 mL sample vials were left uncapped and placed in a sealed chamber containing chloroform. Vapour diffusion of chloroform into the TBAP solution was carried out for until the vials containing the TBAP material were nearly full of solvent. Most of the solvent was then removed via syringe, until the level of solvent was just above the TBAP crystals. Acetone (10 mL) was then injected into the solution and subsequently removed via syringe. This process was repeated twice more, and enough acetone was then added to fill the vial completely. This solvent was removed and then replenished every 12 hours for 5 days, which yielded the solvent exchanged the TBAP·x (acetone) solvate (Fig. S9 and S10†), the yellow crystalline material was filtered off and allowed to dry under ambient conditions. The solid was then evacuated at 120 °C for 14 hours to give the activated material (Fig. S12 and S18†). Complete removal of the solvent was confirmed by the absence of resonances relating to DMF, CHCl₃, or acetone in the ¹H NMR spectra of the activated sample (Fig. S11†).

Generation of amorphous TBAP phase. As synthesised TBAP was fully dissolved 2 M KOH (aq.). The aq. solution was then placed in an ice bath for 10 minutes, and excess concentrated HCl (aq.) was added in one portion to neutralise the solution and rapidly precipitate the TBAP material. The TBAP material was collected by filtration and washed with copious amounts of water. The filtrate was then suspended in water (20 mL), sonicated for 1 hour, and re-filtered to ensure all remaining salts were washed out. This process was repeated three times in total. The amorphous TBAP sample was dried under vacuum at 120 °C and a PXRD pattern of the amorphous material was recorded, see Fig. S33.†

Sublimation of TPhP and TPyP. Crystals of TPhP were obtained by sublimation at 425 °C and pressure of 5 × 10⁻⁴ hPa. Crystals of TPyP were obtained by sublimation at 450 °C and pressure of 5 × 10⁻⁴ hPa.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the Engineering and Physical Sciences Research Council (EPSRC, EP/N004884/1), the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC through grant agreement numbers 321156 (ERC-AG-PE5-ROBOT) and 307358 (ERC-stG-2012-ANGLE), and the Leverhulme Research Centre for Functional Materials Design for funding. We thank Diamond Light Source for access to beamlines I19 (CY21726). We thank the Advanced Light Source, supported by the Director, Office of Science, Office of Basic Energy Sciences, of the US Department of Energy under contract no. DE-AC02-05CH11231, and thank Simon J. Teat for his assistance during this experiment. We acknowledge the use of the IRIDIS High Performance Computing Facility, and associated support services at the University of Southampton, and the ARCHER UK National Supercomputing Service, via our membership of the UK's HEC Materials Chemistry Consortium funded by EPSRC (EP/L000202, EP/R029431), in the completion of this work. The authors acknowledge the EPSRC UK National Mass Spectrometry Facility at Swansea University. Dr Jan-Gerrit Brandenburg and Prof. Furio Cora are kindly acknowledged for useful discussion.

References

1. G. Zhang, Z.-A. Lan and X. Wang, Angew. Chem., Int. Ed., 2016, 55, 15712.
2. J. Wen, J. Xie, X. Chen and X. Li, Appl. Surf. Sci., 2017, 391, 72.
3. S. Chen, T. Takata and K. Domen, Nat. Rev. Mater., 2017, 2, 17050.
4. L. Li, Z. Cai, Q. Wu, W. Y. Lo, N. Zhang, L. X. Chen and L. Yu, J. Am. Chem. Soc., 2016, 138, 7681.
5. C. Yang, B. C. Ma, L. Zhang, S. Lin, S. Ghasimi, K. Landfester, K. A. I. Zhang and X. Wang, Angew. Chem., Int. Ed., 2016, 55, 9202.
6. G. Zhang, G. Li, Z.-A. Lan, L. Lin, A. Savateev, T. Heil, S. Zafeiratos, X. Wang and M. Antonietti, Angew. Chem., Int. Ed., 2017, 56, 13445.
7. R. S. Sprick, C. M. Aitchison, E. Berardo, L. Turcani, L. Wilbraham, B. M. Alston, K. E. Jelfs, M. A. Zwijnenburg and A. I. Cooper, J. Mater. Chem. A, 2018, 6, 11994.
8. Y. Bai, L. Wilbraham, B. J. Slater, M. A. Zwijnenburg, R. S. Sprick and A. I. Cooper, J. Am. Chem. Soc., 2019, 141, 9063.
9. Y.-G. Huang, Y. Shiota, M.-Y. Wu, S.-Q. Su, Z.-S. Yao, S. Kang, S. Kanegawa, G.-L. Li, S.-Q. Wu, T. Kamachi, K. Yoshizawa, K. Ariga, M.-C. Hong and O. Sato, Nat. Commun., 2016, 7, 11564.
10. D. Beaudoin, T. Maris and J. D. Wuest, Nat. Chem., 2013, 5, 830.
11. T. Ma, E. A. Kapustin, S. X. Yin, L. Liang, Z. Zhou, J. Niu, L. H. Li, Y. Wang, J. Su, J. Li, X. Wang, W. D. Wang, W. Wang, J. Sun and O. M. Yaghi, Science, 2018, 361, 48.
12. R. S. Sprick, J. X. Jiang, B. Bonillo, S. Ren, T. Ratvijitvech, P. Guiglion, M. A. Zwijnenburg, D. J. Adams and A. I. Cooper, J. Am. Chem. Soc., 2015, 137, 3265.
13. L. Stegbauer, S. Zech, G. Savasci, T. Banerjee, F. Podjaski, K. Schwinghammer, C. Ochsenfeld and B. V. Lotsch, Adv. Energy Mater., 2018, 8, 1703278.
14. T. M. Figueira-Duarte and K. Müllen, Chem. Rev., 2011, 111, 7260.
15. Y. Kai, F. Hama, N. Yasuoka and N. Kasai, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 1263.
16. F. P. A. Fabbiani, D. R. Allan, S. Parsons and C. R. Pulham, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 826.
17. X. Feng, H. Tomiyasu, J. Y. Hu, X. Wei, C. Redshaw, M. R. J. Elsegood, L. Horsburgh, S. J. Teat and T. Yamato, J. Org. Chem., 2015, 80, 10973.
18. Y. He, S. Xiang and B. Chen, J. Am. Chem. Soc., 2011, 133, 14570.
19. Z. Bao, D. Xie, G. Chang, H. Wu, L. Li, W. Zhou, H. Wang, Z. Zhang, H. Xing, Q. Yang, M. J. Zaworotko, Q. Ren and B. Chen, J. Am. Chem. Soc., 2018, 140, 4596.
20. I. Hisaki, Y. Suzuki, E. Gomez, Q. Ji, N. Tohnai, T. Nakamura and A. Douhal, J. Am. Chem. Soc., 2019, 141, 2111.
21. H. Yamagishi, H. Sato, A. Hori, Y. Sato, R. Matsuda, K. Kato and T. Aida, Science, 2018, 361, 1242.
22. K. C. Stylianou, R. Heck, S. Y. Chong, J. Bacsa, J. T. A. Jones, Y. Z. Khimyak, D. Bradshaw and M. J. Rosseinsky, J. Am. Chem. Soc., 2010, 132, 4119.
23. P. Li, N. A. Vermeulen, X. Gong, C. D. Malliakas, J. F. Stoddart, J. T. Hupp and O. K. Farha, Angew. Chem., Int. Ed., 2016, 55, 10358.
24. S. B. Kalidindi, S. Nayak, M. E. Briggs, S. Jansat, A. P. Katsoulidis, G. J. Miller, J. E. Warren, D. Antypov, F. Corà, B. Slater, M. R. Prestly, C. Martí-Gastaldo and M. J. Rosseinsky, Angew. Chem., Int. Ed., 2015, 54, 221.
25. Q. Yin, P. Zhao, R. J. Sa, G. C. Chen, L. Jian, T. F. Liu and R. Cao, Angew. Chem., Int. Ed., 2018, 57, 7691.
26. K. Adil, Y. Belmabkhout, R. S. Pillai, A. Cadiau, P. M. Bhatt, A. H. Assen, G. Maurin and M. Eddaoudi, Chem. Soc. Rev., 2017, 46, 3402.
27. O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705.
28. G. Férey, C. Mellot-Draznieks, C. Serre, F. Millange, J. Dutour, S. Surblé and I. Margiolaki, Science, 2005, 309, 2040.
29. C. S. Diercks and O. M. Yaghi, Science, 2017, 355, 585.
30. N. Huang, P. Wang and D. Jiang, Nat. Rev. Mater., 2016, 1, 16068.
31. S. J. Lyle, P. J. Waller and O. M. Yaghi, Trends Chem., 2019, 1, 172.
32. A. I. Kitaigorodskii, Acta Crystallogr., 1965, 18, 585.
33. M. Jansen and J. C. Schön, Angew. Chem., Int. Ed., 2006, 45, 3406.
34. Y. Ma, M. Eremets, A. R. Oganov, Y. Xie, I. Trojan, S. Medvedev, A. O. Lyakhov, M. Valle and V. Prakapenka, Nature, 2009, 458, 182.
35. M. S. Dyer, C. Collins, D. Hodgeman, P. A. Chater, A. Demont, S. Romani, R. Sayers, M. F. Thomas, J. B. Claridge, G. R. Darling and M. J. Rosseinsky, Science, 2013, 340, 847.
36. A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Nature, 2017, 543, 657.
37. P. Cui, D. P. McMahon, P. R. Spackman, B. M. Alston, M. A. Little, G. M. Day and A. I. Cooper, Chem. Sci., 2019, 10, 9988.
38. W. Wang, M. Zhou and D. Yuan, J. Mater. Chem. A, 2017, 5, 1334.
39. C. A. Trickett, A. Helal, B. A. Al-Maythalony, Z. H. Yamani, K. E. Cordova and O. M. Yaghi, Nat. Rev. Mater., 2017, 2, 17045.
40. J. T. A. Jones, T. Hasell, X. Wu, J. Bacsa, K. E. Jelfs, M. Schmidtmann, S. Y. Chong, D. J. Adams, A. Trewin, F. Schiffman, F. Cora, B. Slater, A. Steiner, G. M. Day and A. I. Cooper, Nature, 2011, 474, 367.
41. E. O. Pyzer-Knapp, H. P. G. Thompson, F. Schiffmann, K. E. Jelfs, S. Y. Chong, M. A. Little, A. I. Cooper and G. M. Day, Chem. Sci., 2014, 5, 2235.
42. Z. Kang, L. Fan and D. Sun, J. Mater. Chem. A, 2017, 5, 10073.
43. M. S. Denny, J. C. Moreton, L. Benz and S. M. Cohen, Nat. Rev. Mater., 2016, 1, 16078.
44. A. G. Slater, P. S. Reiss, A. Pulido, M. A. Little, D. L. Holden, L. Chen, S. Y. Chong, B. M. Alston, R. Clowes, M. Haranczyk, M. E. Briggs, T. Hasell, G. M. Day and A. I. Cooper, ACS Cent. Sci., 2017, 3, 734.
45. Y.-B. Zhou and Z.-P. Zhan, Chem.–Asian J., 2018, 13, 9.
46. E. Jin, Z. Lan, Q. Jiang, K. Geng, G. Li, X. Wang and D. Jiang, Chem, 2019, 5, 1632.
47. R. S. Sprick, Y. Bai, A. A. Y. Guilbert, M. Zbiri, C. M. Aitchison, L. Wilbraham, Y. Yan, D. J. Woods, M. A. Zwijnenburg and A. I. Cooper, Chem. Mater., 2019, 31, 305.
48. V. S. Vyas, V. W. H. Lau and B. V. Lotsch, Chem. Mater., 2016, 28, 5191.
49. G. M. Day and A. I. Cooper, Adv. Mater., 2018, 30, 1704944.
50. J. Yang, S. De, J. E. Campbell, S. Li, M. Ceriotti and G. M. Day, Chem. Mater., 2018, 30, 4361.
51. J. E. Campbell, J. Yang and G. M. Day, J. Mater. Chem. C, 2017, 5, 7574.
52. B. Rice, L. M. LeBlanc, A. Otero-de-la-Roza, M. J. Fuchter, E. R. Johnson, J. Nelson and K. E. Jelfs, Nanoscale, 2018, 10, 1865.
53. X. Wang, K. Maeda, X. Chen, K. Takanabe, K. Domen, Y. Hou, X. Fu and M. Antonietti, J. Am. Chem. Soc., 2009, 131, 1680.
54. M. Sachs, R. S. Sprick, D. Pearce, S. A. J. Hillman, A. Monti, A. A. Y. Guilbert, N. J. Brownbill, S. Dimitrov, X. Shi, F. Blanc, M. A. Zwijnenburg, J. Nelson, J. R. Durrant and A. I. Cooper, Nat. Commun., 2018, 9, 4968.
55. L. Stegbauer, K. Schwinghammer and B. V. Lotsch, Chem. Sci., 2014, 5, 2789.
56. J. L. Bredas, J. P. Calbert, D. A. da Silva Filho and J. Cornil, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804.
57. K. J. Thorley and C. Risko, J. Mater. Chem. C, 2016, 4, 3825.
58. B. Gao, H. Yao, B. Jang, J. Zhu, R. Yu, Y. Cui, F. Wang, J. Hou, H. Y. Woo and J. Hou, J. Mater. Chem. A, 2018, 6, 2664.
59. S. Bi, Z.-A. Lan, S. Paasch, W. Zhang, Y. He, C. Zhang, F. Liu, D. Wu, X. Zhuang, E. Brunner, X. Wang and F. Zhang, Adv. Funct. Mater., 2017, 27, 1703146.
60. M. Schwarze, D. Stellmach, M. Schröder, K. Kailasam, R. Reske, A. Thomas and R. Schomäcker, Phys. Chem. Chem. Phys., 2013, 15, 3466.
61. P. Guiglion, A. Monti and M. A. Zwijnenburg, J. Phys. Chem. C, 2017, 121, 1498.
62. J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104.
63. J. Kosco, M. Sachs, R. Godin, M. Kirkus, L. Francas, M. Bidwell, M. Qureshi, D. Anjum, J. R. Durrant and I. McCulloch, Adv. Energy Mater., 2018, 8, 1802181.
64. K. Maeda, X. Wang, Y. Nishihara, D. Lu, M. Antonietti and K. Domen, J. Phys. Chem. C, 2009, 113, 4940.
65. B. Ohtani, K. Iwai, S.-I. Nishimoto and S. Sato, J. Phys. Chem. B, 1997, 101, 3349.
66. I. McCulloch, M. Heeney, C. Bailey, K. Genevicius, I. MacDonald, M. Shkunov, D. Sparrowe, S. Tierney, R. Wagner, W. Zhang, M. L. Chabinyc, R. J. Kline, M. D. McGehee and M. F. Toney, Nat. Mater., 2006, 5, 328.
67. Y. Yamashita, F. Hinkel, T. Marszalek, W. Zajaczkowski, W. Pisula, M. Baumgarten, H. Matsui, K. Müllen and J. Takeya, Chem. Mater., 2016, 28, 420.
68. X. Wang, L. Chen, S. Y. Chong, M. A. Little, Y. Wu, W.-H. Zhu, R. Clowes, Y. Yan, M. A. Zwijnenburg, R. S. Sprick and A. I. Cooper, Nat. Chem., 2018, 10, 1180.
69. G. M. Day, W. D. S. Motherwell and W. Jones, Phys. Chem. Chem. Phys., 2007, 9, 1693.
70. A. V. Kazantsev, P. G. Karamertzanis, C. C. Pantelides and C. S. Adjiman, Comput.-Aided Chem. Eng., 2010, 28, 817.
71. H. P. G. Thompson and G. M. Day, Chem. Sci., 2014, 5, 3173.
72. I. Kolossváry and W. C. Guida, J. Comput. Chem., 1999, 20, 1671.
73. I. Kolossváry and W. C. Guida, J. Am. Chem. Soc., 1996, 118, 5011.
74. L. L. C. Schrodinger, MacroModel, Version 9.0, 2011.
75. W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657.
76. D. H. Case, J. E. Campbell, P. J. Bygrave and G. M. Day, J. Chem. Theory Comput., 2016, 12, 910.
77. D. S. Coombes, S. L. Price, D. J. Willock and M. Leslie, J. Phys. Chem., 1996, 100, 7352.
78. S. L. Price, M. Leslie, G. W. A. Welch, M. Habgood, L. S. Price, P. G. Karamertzanis and G. M. Day, Phys. Chem. Chem. Phys., 2010, 12, 8478.
79. D. P. McMahon, A. Stephenson, S. Y. Chong, M. A. Little, J. T. A. Jones, A. I. Cooper and G. M. Day, Faraday Discuss., 2018, 211, 383.
80. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200.
81. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
82. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
83. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623.
84. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213.
85. W. J. Hehre and W. A. Lathan, J. Chem. Phys., 1972, 56, 5255.
86. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Gaussian, Inc., Wallingford CT, 2016.
87. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.
88. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91.
89. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360.
90. S. Dapprich, I. Komáromi, K. S. Byun, K. Morokuma and M. J. Frisch, J. Mol. Struct.: THEOCHEM, 1999, 1, 461.
91. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 1919802–1919809. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ta00219d

‡ These authors contributed equally to this work.

---