Dihydrogen intermolecular contacts in group 13 compounds: H⋯H or E⋯H (E = B, Al, Ga) interactions?

Abstract

A systematic theoretical analysis of homopolar dihydrogen interactions in group 13 compounds is presented here. Ab initio calculations and structural analysis allow us to demonstrate that interactions involving B–H⋯H–B contacts are comparable in strength to the previously studied C–H⋯H–C ones, yet attractive and important for the stabilization of dimers of large molecules. We have also shown that a polyhedral skeleton enhances the B–H⋯H–B interaction strength with respect to non-polyhedral compounds, and it has also been proven that Al–H⋯H–Al and Ga–H⋯H–Ga interactions can be attractive in some cases. If H⋯E (B, Al and Ga) short contacts are present, the interaction is significantly strengthened, especially for Al and Ga. In general, H⋯H interactions combined with associated H⋯E (B, Al and Ga) short contacts are responsible for the stability of a large number of dimers of group 13 compounds and may play an important role in the packing of their crystal structures.

---

Introduction

During the last few decades, it has been observed that weak intermolecular interactions play an important role in determining the structure and reactivity of several families of compounds.^1–5 Dihydrogen contacts are a type of intermolecular interaction that involves two hydrogen atoms with the same (X–H⋯H–X) or different polarities (X–H⋯H–Y).⁶ Usually, the term dihydrogen bond is reserved for the second case whereas the first one is referred to as dihydrogen interaction.⁷ While X–H^δ+⋯^δ−H–Y dihydrogen bonds have an electrostatic contribution due to the opposite charge of the two hydrogen atoms, the homopolar X–H^δ+⋯^δ+H–X dihydrogen interactions are generally classified as weak and governed by dispersion. The dihydrogen bonding of heteropolar units such as C–H⋯H–B⁸ or N–H⋯H–B^9,10 has been widely studied and many experimental^11,12 and theoretical^13–16 works can be found in the literature. However, homopolar contacts have attracted less attention and only in recent years has there been an increase in the number of publications on the subject. For example, the surprising strength of some C–H⋯H–C contacts was for the first time evaluated via a theoretical analysis,^17,18 and confirmed experimentally by the stabilization of alkanes with very long C–C bonds.¹⁹ On the other hand, in group 13 compounds, B–H⋯H–B interactions have been observed in boron hydrides and complex metal hydrides²⁰ and lyotropic lamellar phases of carborane-cage amphiphiles,²¹ and they seem to play an important role in the design of materials for hydrogen storage.²² Descending down the group 13, Al–H⋯H–Al intramolecular contacts have been found in several polymorphs of the crystal structure of alane,²³ whereas short Ga–H⋯H–Ga contacts can be found only in a handful of structures and, to our knowledge, there is no theoretical work in the literature devoted to them. However, short heteropolar N–H⋯H–Ga contacts have been detected, for example, in the crystal structure of methylamine-gallane.²⁴ Homopolar dihydrogen contacts have not been observed in compounds of the two heaviest elements of group 13, In and Tl.

From a theoretical point of view, dihydrogen bonding has been approached in several ways. The quantum theory of atoms in molecules (AIM) has been used by McGrady and Wolstenholme to prove the existence of a bond path typical of attractive interactions between two hydrogen atoms of the same polarity.²⁰ The electron localization function (ELF) can be also employed to find and characterize dihydrogen bonds.²⁵ Modern Valence Bond (VB)¹⁸ and, especially, Molecular Orbital (MO)-based methods have been widely used to investigate the nature of C–H⋯H–C interactions (see section 2.1 in ref. 1 for a comprehensive account of theoretical methods that take into account dispersion forces).

In this work, we undertake a combined structural and systematic ab initio analysis of intermolecular E–H⋯H–E contacts in group 13 compounds, focusing on those with a homopolar character. E⋯H (B, Al and Ga) short contacts will also be evaluated since they are often associated with dihydrogen contacts. Since Hartree–Fock theory completely neglects dispersion, we have employed second-order Møller–Plesset (MP2) perturbation theory combined with a large basis set to capture the non-covalent nature of the interaction. This theoretical approach has been extensively tested and compared to high level calculations such as CCSD(T)/CBS, giving very good results for the study of H⋯H contacts in alkanes¹⁷ and other families of compounds.²⁶ We have studied small boranes, as well as larger arachno, nido and closo polyhedral boranes, and also Al and Ga hydrides. The heaviest elements of group 13, In and Tl, have been excluded in the present study, because these atoms are affected by relativistic effects²⁷ and, thus, their hydrides behave differently from those of the lighter elements of the group (B, Al and Ga).

Structural evidence

Boron hydrides

We have searched the Cambridge Structural Database (CSD)²⁸ for E–H⋯H–E (E = B, Al, Ga, In and Tl) contacts shorter than twice the van der Waals radius of hydrogen²⁹ plus 25%, i.e. 3 Å, in order to have a global picture of the occurrence of these interactions. B–H⋯H–B contacts were the most numerous ones with 3542 hits (Fig. 1a). We have also analyzed the B–H⋯H angles associated with those contacts. Since angles smaller than 80° are unlikely due to steric hindrance, values for B–H⋯H angles range from 80° to 180° and show a clear maximum at around 115° (Fig. 1b). This is similar to what was found for R₃C–H⋯H–CR₃ contacts, where the C–H⋯H angle presents a peak at 125°.¹⁸

Fig. 1 (a) Distribution of B–H⋯H–B distances shorter than 5 Å as found in the CSD. The blue bars represent all B–H⋯H–B contacts, the transparent bars with grey outline represent only the contacts involving two hexacoordinate B atoms, and the solid grey bars correspond to all the crystal structures excluding artificially fixed B–H bond lengths and R < 5%. (b) Distribution of the B–H⋯H angles for the H⋯H contacts (a) within the van der Waals peak (i.e., shorter than 3.5 Å) in blue, and the same distribution for the two distinct angles α and β (Fig. 2) in the 3 : 1 contacts between B₃H₃ and H–B groups. See the ESI† for the angular distribution of other contact topologies and ref. 29 for a more detailed definition of the van der Waals peak concept.

As for the quality of the analysed data, it is important to assess how the positions of the H atoms have been determined in the corresponding crystal structures. We have only found three examples of neutron diffraction structures, containing 37 short B–H⋯H–B contacts (CSD refcodes FUYYIH02,³⁰ KOMZAN,³¹ SOHZIZ³²), which exclude the possibility of a meaningful statistical analysis. However, X-ray structures can also be useful, especially when the H positions have been refined. On the other hand, structures where the H atoms have been artificially placed at fixed distances (1.1 and 1.12 Å in the case of B–H) can introduce relatively large errors in the averaged H⋯H distances. In Fig. 1a, we compare the H⋯H distances obtained with and without the inclusion of this set of structures with fixed hydrogens, obtaining similar results. In both cases, the van der Waals peak can be adjusted to a Gaussian function centred at 2.91 Å ± 0.02. This can be due to the fact that the geometrical parameters associated with the interaction topologies, with B–H⋯H angles around 115°, compensate in part the error introduced by the fixed bond lengths. Only in the case of linear topologies (B–H⋯H angles close to 180°) would the error in the H⋯H distance be added.

An 84% of all the B–H⋯H–B short contacts was found to correspond to the crystal structures of polyhedral boranes. This is evidenced by the data analysis shown in Fig. 1a, where the B–H⋯H–B contacts shorter than 5 Å are presented. The blue bars represent the frequency of all B–H⋯H–B contacts, while the grey bars represent the subset of contacts in which both B atoms involved in the interaction are hexacoordinated, which is the most common coordination number for the B atom in polyhedral boranes. Within the remaining 16%, borane adducts with Lewis bases like amines and phosphines are abundant. In the crystal structures of these compounds, B–H⋯H–B interactions coexist with heteropolar dihydrogen interactions such as N–H⋯H–B, which are usually shorter and contribute to a considerable extent to the stabilization of the crystal structure. For example, a methylamine-borane crystal shows N–H⋯H–B contacts as short as 2.13 Å, whereas the B–H⋯H–B ones are at a distance of 2.97 Å.³³ Another interesting case is the crystal structure of 1-aza-closo-dodecaborane, in which two short N–H⋯H–B (1.99–2.57 Å) and two B–H⋯H–B (2.70–2.97 Å) intermolecular contacts can be found.³⁴

The situation changes for polyhedral boranes, where B–H⋯H–B contacts usually predominate over other possible heteropolar dihydrogen interactions. The clusters of closo type, especially the derivatives of the neutral species dicarbadodecaborane (C₂H₁₂B₁₀), are able to establish mainly B–H⋯H–B interactions only between terminal hydrogen atoms (H_t–H_t). For example, a carborane dimer found in the crystal structure of a mixed ytterbium(II) complex – dicarbadodecaborane (CSD refcode QEQFUN)³⁵ presents three B–H⋯H–B short contacts (2.60–2.65 Å) with a 1 : 3 interaction topology (Fig. 2). However, this is not strictly a homopolar dihydrogen bond since the B–H units involved in the interactions in each monomer have different polarities due to the relative positions of the two carbon atoms. Arachno and nido clusters have, in addition, bridging hydrogen atoms that can establish short contacts with terminal hydrogens (H_t⋯H_b) or other bridging ones (H_b⋯H_b).

Fig. 2 Interaction topology of the 1,2-dicarbadodecaborane dimer as found in the crystal structure of bis(η⁵-pentamethyl-cyclopentadienyl)-ytterbium(II) 1,2-dicarbadodecaborane (QEQFUN).³⁵ The B–H⋯H–B short contacts at 2.60–2.70 Å are shown as multi-band cylinders.

It must be noted that the three H⋯H contacts shown in Fig. 2 correspond to distances in the range 2.60–2.65 Å, slightly longer than twice the van der Waals radius of hydrogen (2.40 Å),³⁶ but still within the van der Waals peak shown in Fig. 1a. On the other hand, the corresponding H⋯B distances (3.00–3.04 Å) are slightly shorter than the sum of van der Waals radii (3.11 Å). This means that the dispersion forces holding the two molecules together involve not only H⋯H, but also B⋯H interactions, that may be as strong or even more important, as was already commented upon in our previous study of C–H⋯H–C contacts.¹⁷ In what follows, thus, it must be understood that reference to E–H⋯H–E interactions will refer to the combined effect of H⋯H and H⋯E interactions.

The angular distribution of the short B–H⋯H–B contacts in the crystal structures of closo boranes (i.e., those contained within the van der Waals peak of Fig. 1a, with H⋯H ≤ 3.5 Å) is shown in Fig. 1b, where one can appreciate a narrow peak centered at around 110°–120°, and a broader one centered at around 150°. In our example structure, (Fig. 2) the two B–H⋯H angles associated with the 1 : 3 interaction topology, α and β, present values in the ranges 129–167° and 100–103°, respectively, and a structural database search for those types of contacts involving six-coordinated boron atoms (1) shows the presence of two distinct peaks corresponding to the two sets of B–H⋯H angles, α and β, whose distributions are centered at around 130 and 99°, respectively (Fig. 1b). Other contact topologies, such as 2 and 3 present a distribution that is more similar to the overall distribution, with all topologically independent sets of B–H⋯H angles (γ, δ, τ and ω in 2–4) presenting sharp maxima at around 110° followed by a shoulder that extends all the way to 180° (see Fig. S1 in the ESI†). The interaction topology 1 : 1 that involves one BH group from each molecule (4) is less common and only a few examples can be found among the family of polyboranes.

In the nido structures, the situation is somewhat more convoluted because of the lower symmetry. Hence, these boranes can establish contacts involving terminal and/or bridging hydrogen atoms (H_t⋯H_t, H_t⋯H_b and H_b⋯H_b). Moreover, there are more relative orientations of the two interacting molecules, which we broadly identify as involving B–H groups from the bottom (b), the sides (s) or the face (f) of the nest (5). We will therefore classify somewhat crudely, the interaction topologies in dimers of nido boranes as b–f, f–f, b–b, s–s…

It is worth pointing out that we have observed a B–H⋯H–B intermolecular distance of 2.28 Å between dodecaborate anions in the lithium salt, Li₂(B₁₂H₁₂),³⁷ which is shorter than those found between neutral molecules. This fact could be in part attributed to the Coulombic attraction caused on two neighboring anions by an intervening cation, since the contacts become longer as the size of the intervening cation increases, with a practically linear dependence on the ionic radius of the alkaline cation (2.42, 2.51, 2.64 and 2.73 Å for the Na,³⁸ K,³⁹ Rb³⁹ and Cs⁴⁰ salts, respectively).

Aluminium hydrides

As for the Al hydrides, alane is found experimentally as a polymer with the formula (AlH₃)_n that presents several polymorphic crystal structures based on vertex- and/or edge-sharing AlH₆ octahedra,⁴¹ while molecular Al₂H₆ has only been isolated in solid hydrogen due to its instability.⁴² Only 21 structures with Al–H⋯H–Al intermolecular short contacts (H⋯H < 3 Å) were found. We have observed first that, in general, aluminium tends to form very short Al–H⋯Al contacts (1.77–2.34 Å) that indicate incipient formation of Al–H–Al bridges, consistent with the fact that these contacts appear only for four-coordinated Al atoms. Other contacts appear only at distances above 3.10, with a van der Waals peak centered at 3.45 Å, in agreement with a van der Waals radii sum of 3.45 Å (see Fig. S2 in the ESI†). For instance, in the crystal structure of dimethylamine-alane,⁴³ the two Al⋯H–Al distances (d₁ in Fig. 3) are 2.07 Å, resulting in a trigonal bipyramidal environment around Al. There are, however, a few examples where actual Al–H⋯H–Al contacts can be found. For example, in the crystal structure of aluminium tris(tetrahydroborate) methylamine, there are contacts between bridging hydrogen atoms (H_b⋯H_b at 2.78 Å) and between one bridging and one terminal hydrogen atom (H_b⋯H_t at 2.55 Å).⁴⁴ Also in the crystal structure of an aluminium–nitrogen cluster, Al–H⋯H–Al intermolecular contacts at 2.85 Å coexist with C–H⋯H–Al heteropolar ones at 2.77 Å.⁴⁵ Therefore there is a clear tendency of the Al(μ-H)₂Al core to go beyond the formation of diborane type structures in such a way that the Al atoms become pentacoordinated with d₁ = d₂ (Fig. 3).^46–51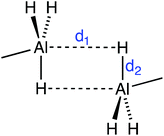

Fig. 3 Representation of the two short Al–H⋯Al contacts (dashed lines) as found in dimers of some AlH₃ adducts with Lewis bases, for example dimethylamine-alane.⁴³

Gallium hydrides

Digallane, H₂Ga(μ-H)₂GaH₂, was prepared and characterized for the first time in 1989 after several years of search,^52,53 but, to date, no crystal structure for this compound has been reported. Its structure, however, has been determined in the gas phase by electron diffraction,⁵³ and also the structure of the related compound, Me₂Ga(μ-H)₂GaMe₂, is known in the gas phase.⁵⁴ Our CSD survey yielded 13 structures with Ga–H⋯H–Ga intermolecular contacts shorter than 3 Å. In 10 of the structures, C–H⋯H–Ga⁵⁵ or N–H⋯H–Ga⁴³ heteropolar dihydrogen contacts are found along with the Ga–H⋯H–Ga ones. A larger number of structures (35) were found with Ga⋯H–Ga contacts at distances around the sum of the van der Waals radii (3.52 Å). In our CSD survey, only one structure was found with a short In–H⋯H–In contact (CSD refcode SITNAK10),⁵⁶ which corresponds also to the only short In⋯H contact, 2.96 Å, to be compared with a van der Waals sum of 3.63 Å. Finally, no Tl–H⋯H–Tl short intermolecular contacts were found in our CSD survey.

It is worth remarking that we are aware of the fact that among the thousands of structures taken into account here for statistical purposes, not all the E–H⋯H–E short contacts correspond to dihydrogen interactions. Some H⋯H short distances are the consequence of other types of intermolecular interactions, e.g. hydrogen bonds, B–H⋯π, Al⋯donor, etc. In the next section, we focus on those particular H⋯H contacts that are not accompanied by any other interaction and, thus, can be considered as actual dihydrogen interactions.

Computational results

Dimers of EH₃ molecules

In this section we present the results of our computational analysis of several existing and hypothetical dimers of the group 13 hydrides, comparing the results with experimental references when possible. We start by looking at the dimers of trivalent hydrides of the type EH₃, in order to evaluate the energetics of the simplest possible homopolar B–H⋯H–B interactions, even if such molecules are unlikely to be found in crystal structures since the formation of diborane type dimers (6) is strongly favored (Table 1). Since InH₃ and TlH₃ are unstable and their corresponding dihydrides, In₂H₆ and Tl₂H₆, have been the subject of solely theoretical studies to date,⁵⁷ we have decided not to include them in the present analysis. The results of calculations on the dimers of EH₃ (E = B, Al, Ga) hydrides with several topologies (6, 7a–7d) are presented in Table 1.

Table 1 Intermolecular distances and dissociation energies (D) for group 13 trivalent hydride dimers. BSSE-corrected dissociation energies (D) are given in kJ mol⁻¹. The dissociation energies of the diborane-type E₂H₆ dimers into two EH₃ monomers are given for comparison. Experimental dissociation energies for diborane and dialane are given in parenthesis, and the sum of van der Waals radii is given in square brackets

Hydride	Topology	E⋯H calc. (Å)	H⋯H calc. (Å)	D
B2H6	6			179.32 (146^58–247^59)
BH3	7a	4.055	2.868	0.30
	7b	3.627	3.202	0.41
	7c	4.021	3.294	0.46
	7d	3.797 [3.11]	3.388 [2.40]	0.75
Al2H6	6			150.39 (138^60)
AlH3	7b	3.927	3.431	0.23
	7c	4.102	5.076	−0.16
	7d	3.492 [3.45]	3.106 [2.40]	5.19
Ga2H6	6			105.53
GaH3	7a	4.736	3.160	−0.11
	7b	3.869	3.375	0.36
	7c	4.675	3.684	0.08
	7d	3.656 [3.52]	3.244 [2.40]	3.77

---

We note that dimers with topologies 7a, 7b and 7c are not likely and the very low dissociation energies indicate that they are held together by nothing else than very weak dispersion forces.⁶¹ However, these very weak interactions could play a role in the stabilization of supramolecular assemblies when working cooperatively, as previously observed in alkanes. It must be stressed that the topology 7a, which allows for only one H⋯H interaction, corresponds to very weak attractive or even repulsive interaction and yields optimized H⋯H and E⋯H distances significantly longer than the corresponding sum of van der Waals radii.²⁹ Interestingly, for topology 7d, dissociation energies are significantly larger than for other topologies and follow the trend Al > Ga > B (Fig. 4). For this topology, the Al⋯H and Ga⋯H distances are much closer to the van der Waals sum than the B⋯H one. In fact, it is clearly seen that the dissociation energy increases as the E⋯H contact distance approaches the van der Waals distance, again pointing to a possible role of the E⋯H interactions in the intermolecular dissociation energy (Fig. 4). On the other hand, the calculated H⋯H distances are longer than the van der Waals distance (2.40 Å) but similar to those found in alkane dimers with considerably strong interactions (dissociation energy for methane dimer is 1.75 kJ mol⁻¹ with a H⋯H distance of 3.165 Å).¹⁷ Also hypothetical E⋯E interactions may favor stronger attractive intermolecular interactions. Such contacts appear at distances clearly shorter than the sum of the van der Waals radii for both Al and Ga (E⋯E = 3.99 and 4.17 Å, radii sum = 4.50 and 4.64 Å, respectively) with topology 7d (Fig. 4).

In order to gain further insight into the intermolecular interactions, we have carried out an analysis of the electron density of the EH₃ dimers with topology 7d by means of the AIM method. For the BH₃ dimer, only a bond critical point (BCP) was found in a bond path between the two B atoms, suggesting the absence of an attractive H⋯H interaction. However, for AlH₃ and GaH₃, four BCPs are found in each dimer associated with four H⋯H bond paths corresponding to the four H⋯H contacts. The electron densities at these BCPs (0.0042 for Al and 0.0032 for Ga) are similar to those reported for CH⋯HC contacts¹⁷ and the positive values of the Laplacian are characteristic of closed-shell interactions.

Fig. 4 Dissociation energy as a function of the difference between the E⋯H (E = B, Al and Ga) intermolecular distance and the sum of the van der Waals radii in EH₃ dimers with interaction topology 2 : 2 (7d).

Thus, the relatively large dissociation energies calculated for AlH₃ and GaH₃ dimers with topology 7d can be due to the combination of H⋯H dihydrogen and E⋯H (E = Al, Ga) interactions. It is worth remarking that our goal here is to evaluate the strength of noncovalent interactions (7a–d) rather than to compare them with the covalent bonded dimers (6). It is clear that the formation of a covalent 3c–2e bond will be strongly preferred when possible (see the large values of D in Table 1). Only when there is no possibility of covalent bonding, noncovalent interactions, several orders of magnitude weaker, could participate in the stabilization of crystal structures.

Dimers of diborane and digallane

In our calculations, diborane and digallane also appear to be capable of forming supramolecular dimers with the formula E₄H₁₂ (E = B and Ga). Both terminal and bridging hydrogen atoms are able to establish dihydrogen contacts where two different intermolecular interactions can be distinguished (8a and 8b). The first one (8a) is observed in the crystal structure of diborane⁶² and involves two terminal hydrogen atoms at 2.74 Å, while in the same crystal structure, the contacts between a terminal and a bridging hydrogen atom (8b) are still shorter (2.58 Å). In an earlier crystal structure of diborane,⁶³ a short contact occurs only between a terminal and a bridging hydrogen atom at 2.73 Å (8b). The 8b topology implies a heteropolar dihydrogen interaction due to the different character of the two hydrogen atoms, which makes us expect a stronger attraction. The existence of the terminal–bridging interaction has been recently detected in an AIM analysis of several boron hydrides.⁶⁴

Geometry optimizations were carried out for dimers of diborane, dialane and digallane in topologies, 8a and 8b. While diborane and digallane resulted in stable dimers (Fig. 5 and Table 2), no supramolecular dimers were found for dialane (see below). Key intermolecular distances and dissociation energies for diborane and digallane shown in Table 2 indicate that the E–H⋯H–E terminal–terminal interactions are similarly weak for B and Ga. The terminal–bridging interaction topology 8b led to different results for diborane and digallane, as can be seen in Fig. 5. The optimized diborane dimer presents three terminal–bridging H⋯H interactions (2.711–2.875 Å) and two short B–H⋯B contacts involving both terminal (3.204 Å) and bridging (3.057 Å) hydrogen atoms. In turn, the interaction topology of digallane after geometry optimization shows two H⋯H contacts (H_t⋯H_t at 2.900 Å, H_t⋯H_b at 2.937 Å) and two shorter Ga⋯H–Ga contacts (2.880 Å). The latter interaction can be responsible for the quite larger dissociation energy of the digallane dimer 8b compared to the diborane analogue (Table 2). This is consistent with the natural atomic charges calculated by means of a NPA analysis of the H_t⋯H_b digallane dimer (Fig. 5). In such a structure, Ga and terminal H atoms involved in the interaction present atomic charges of 0.957 and −0.319, respectively, whereas analogous atoms in diborane show atomic charges of 0.021 and −0.038.

Fig. 5 Optimized structures of dimers of diborane (above) and digallane (below) with terminal–bridging interaction topologies. Short H⋯H and E⋯H contacts are shown as multi-band cylinders and dashed lines, respectively. Natural atomic charges are given next to each atom.

Table 2 Intermolecular distances (in Å) and dissociation energies for group 13 dimers of E₂H₆ molecules with terminal–terminal and terminal–bridge interaction topologies 8a and 8b. BSSE-corrected dissociation energies (D) are given in kJ mol⁻¹

Hydride	Topology	E⋯H calc.	H⋯H calc.	H⋯H exp.	D
a An extra Ht⋯Ht contact at 2.900 Å appears after the geometry optimization of Ht⋯Hb interaction topology (white and blue multi-band cylinders in Fig. 5).
B2H6	8a	3.894	2.740	2.74^62	0.64
	8b	3.204 (Ht), 3.057 (Hb)	2.711	2.73^63	4.53
Ga2H6	8a	4.385	2.861	—	0.57
	8b	2.880	2.937^a	—	8.58

---

It is also interesting to observe how the natural atomic charges are modified when forming dimers with respect to the monomers. In diborane, terminal H atoms have charges of −0.037 while the same atom's charge is −0.043 when involved in an H⋯H contact in the dimer. However bridging H and B atoms show the same charge both in the monomer and dimer. In digallane, charges for Ga, terminal H and bridging H are 0.942, −0.295 and −0.351, respectively. These charges are significantly modified in the atoms that establish interactions in the dimer, as can be seen in Fig. 5. Therefore, it seems plausible that an electrostatic effect, together with a small amount of charge transfer is contributing to the large dissociation energy observed in the digallane dimer. The different nature of the bridging hydrogen atoms in diborane and digallane is also worth noting. While their charges are slightly positive in diborane (0.043–0.045), they present a more hydridic character in digallane (natural charge of −0.351), in good agreement with the lower electronegativity of Ga relative to B and H.

Taking the four data sets in Table 2, a clear correlation appears between the shortest E⋯H distance in each dimer and its dissociation energy (Fig. 6), while no correlation at all can be found between the H⋯H distance and the dissociation energy. This latter fact does not mean that H⋯H interactions are irrelevant. In fact, an AIM analysis of the four dimers in Table 2 shows that BCPs are found between hydrogen atoms and no bond path appears that indicates an E⋯H (E = B, Ga) interaction. A dimer with topology 8a presents a BCP between two terminal hydrogen atoms (ρ = 0.0026), both for B and Ga. For topology 8b, the (B₂H₆)₂ dimer shows two BCPs (ρ = 0.0037, 0.0041) between the terminal and bridging hydrogen atoms while the (Ga₂H₆)₂ dimer shows only one BCP (ρ = 0.0092) between two terminal hydrogens (the bond path corresponds to the stripped cylinder in Fig. 5).

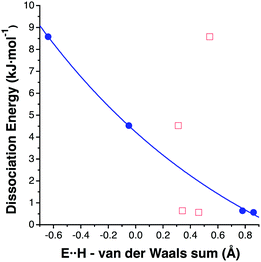Fig. 6 Dissociation energy as a function of the difference between the H⋯H (red squares) and E⋯H (blue circles) intermolecular distances and the sum of the corresponding van der Waals radii in (E₂H₆)₂ (E = B and Ga) dimers, with the optimized structures shown in Fig. 5.

In the case of dialane, optimizations starting from either interaction topology led to dimerization of the molecule, resulting in a tetranuclear structure Al₄H₁₂ (see Fig. S4 in the ESI†). The new formed tetramer showed all three Al–Al distances very close to 2.6 Å, and H⋯H contacts between the original molecules, of both terminal–terminal (H_t⋯H_t) and terminal–bridge (H_t⋯H_b) nature, with distances of 2.29 Å and 2.39 Å, respectively. The dissociation energy was calculated to be as high as 87.5 kJ mol⁻¹. The tendency of aluminium to form short Al–H⋯Al bonds in alane derivatives has been discussed above and previously stated to be greater than that of gallium. For example, dimethylamine-alane presents an Al–H⋯Al distance of 2.07 Å between neighbouring molecules in its crystal structure while in dimethylamine-gallane, the shortest Ga–H⋯Ga distance is 2.89 Å, both with the same topology.⁶⁵

Dimers of arachno and nido polyboranes

Let us now try to extend our analysis to some representative members of the large and important family of polyhedral boron compounds, which includes carboranes and metallacarboranes.⁶⁶ First, we look at three neutral boranes, the arachno B₄H₁₀ and the nido B₅H₁₉ and B₁₀H₁₄ boranes, whose crystal structures have been reported in the literature.^67–70 The geometries of these three compounds were directly retrieved from their crystal structures, finding two different conformations between molecular units that are associated to two different H⋯H interaction patterns for each of them. Then, the two dimeric topologies were fully optimized for each case (Fig. 7). All calculated dissociation energies were positive (see results in Table 3) and, thus, we have identified the interactions between monomers as attractive. The dissociation energies of the dimers of B₁₀H₁₄ are remarkably high, with H⋯H contacts between bridging hydrogen atoms as short as 2.23 Å. We have observed that, in general, H⋯H contacts involving one bridging and one terminal hydrogen atom (i.e. non-homopolar interactions) are shorter than those involving two terminal or two bridging hydrogen atoms. We note that, in general, the molecules of nido and arachno boranes in their crystal structures tend to arrange in such a way that the number of terminal–bridging interactions are maximized. In fact, these interactions are expected to be more energetic than the terminal–terminal ones due to the different character, acidic and hydridic, of the two H atoms involved. Our calculated H⋯H distances are in very good agreement with the experimental values. In the combined X-ray and neutron diffraction structure of dodecaborane (CSD refcode FUYYIH02),³⁰ we find H_t⋯H_t and H_t⋯H_b contacts at 2.55 and 2.41 Å, respectively. Other dodecaborane derivatives also present H_t⋯H_b contacts at 2.41–2.46 Å (CSD refcode CCOBOR⁷¹) and H_t⋯H_t ones at 2.43–2.50 Å (CSD refcode PIJTUX⁷²).

Fig. 7 Optimized geometries and shortest H⋯H contacts in dimers of an arachno and two nido polyboranes. The short intermolecular contacts are shown as striped cylinders, blue and white for H_t⋯H_t, grey and white for H_t⋯H_b, and red and white for H_b⋯H_b contacts. Topological code: b–f = bottom–face, b–s = bottom–side, b–b = bottom–bottom.

Table 3 Number of calculated short B⋯H (<3.890 Å) and H⋯H (<3.000 Å) contacts between two terminal H_t⋯H_t, two bridging H_b⋯H_b or one terminal and one bridging H_t⋯H_b hydrogen atoms in nido and arachno borane dimers. Interaction topologies involve the bottom (b), face (f) or side (s) of the monomers. The minimum and maximum contact distances are given in parenthesis (Å) for all cases; BSSE-corrected dissociation energies (D) are given in kJ mol⁻¹

Borane	Topol.	B⋯H	Ht⋯Ht	Ht⋯Hb	Hb⋯Hb	D
We consider contacts not exceeding the sum of the van der Waals radii by 25%. The van der Waals radii proposed by Alvarez^29 are 1.20 Å for hydrogen and 1.91 Å for boron.
B4H10	b–f	11 (3.154–3.671)	3 (2.771–2.862)	3 (2.339–2.572)	—	8.82
	b–s	11 (2.998–3.704)	1 (2.906)	3 (2.551–2.695)	1 (2.616)	8.03
B5H9	b–f	8 (3.157–3.433)	—	4 (2.392)	—	11.72
	b–s	16 (3.015–3.596)	—	6 (2.517–2.700)	—	16.53
B10H14	b–f	24 (3.103–3.712)	2 (2.497)	4 (2.329–2.406)	—	27.14
	b–b	22 (2.833–3.875)	2 (2.945–2.966)	5 (2.384–2.685)	3 (2.235–2.856)	22.91

---

In all three cases the back to face (b–f) arrangement of a dimer that is found in the crystal packing appears to be stable toward dissociation and the dissociation energy increases with the size of the borane. The distribution of B–H⋯H angles in these optimized structures follows the same general pattern seen in Fig. 1b. Optimization of dimers with the topology found for sideways interactions in the crystal structures, however, lead to other topologies that imply more hydrogen atoms into the intermolecular interaction. For instance, B₅H₉ gives a bottom to side topology for a dimer (Fig. 7) that can be described as resulting from the tilting one of the molecules from the b–f geometry, in such a way that two more H⋯H short contacts are introduced without disrupting the 4 : 1 contacts, therefore increasing the dissociation energy from 11.7 to 16.5 kJ mol⁻¹. Obviously, we cannot pretend the interaction topology to be the same as that found in the solid state, because in the latter case somewhat weaker interactions can be compensated by the possibility of extending them in one or two dimensions. It is nevertheless rewarding that in the three cases studied here the b–f interactions that correspond to the minima for the dimers are consistent with those found in one direction of the crystal structure. In this way, our results clearly indicate that (i) those interactions are attractive and (ii) they increase with the size of the borane. The latter result is consistent with our previous finding that the C–H⋯H–C interactions between polyhedranes are enhanced by (a) the degree of substitution of the supporting C atom and (b) the loss of pyramidality of the C–H group as the size of the polyhedron increases.¹⁷

Dimers of closo dicarbadodecaborane

Unfortunately, most of the members of the closo polyboranes family are charged species, which makes them unsuitable for a computational study of noncovalent intermolecular interactions that are undoubtedly much weaker than ionic forces. A neutral species of this family is the icosahedral 1,2-closo-dicarbadodecaborane, in which two B–H units are substituted by C–H ones. We present in Table 4 the geometrical parameters of four selected dimers of dicarbadodecaborane retrieved from four different CSD crystal structures. The dissociation energies (D in Table 4) are calculated on the geometry of only two interacting molecules (omitting all others) with the desired interaction topology as found in the crystal structures without further optimization. We are aware that more molecules may be present in the unit cell of each crystal structure that contribute to the stabilization of the ensemble and, thus, the calculated dimers may not be minima of the potential energy surface. However, in this way, by avoiding geometrical rearrangements like those observed in the optimization of nido polyborane dimers, we can have a picture of the interaction strength between two molecules as they are found in a crystal structure.

Table 4 Experimental geometrical parameters and calculated dissociation energies (D in kJ mol⁻¹) for the dimers of closo polyhedral boranes with topologies 1 : 3 (1), 2 : 2 (2), 1 : 2 (3) and 1 : 1 (4)

Refcode	Topology	H⋯H (Å)	Angles (°)	D
QEQFUN^35	1	2.60, 2.64, 2.65	α = 156.7, 133.6, 129.1	8.70
			β = 102.8, 102.2, 99.9
TOKGIJ^73	2	2.50	γ = δ = 129.5	6.85
BEZTUW^74	3	2.66, 2.86	τ = 132.2, 132.4	10.34
			ω = 114.8, 121.1
TUQTEE^75	4	2.90	φ = 129.8	4.26

---

The calculated dissociation energies for dicarbadodecaborane dimers with topologies 1 : 3 (1) and 2 : 2 (2) are close to those found for dimers of arachno B₄H₁₀ with a similar number of H⋯H interactions (Tables 3 and 4). Large nido dimers like B₁₀H₁₄ present larger dissociation energies than the closo dicarbadodecaborane because the former can establish much more H⋯H and B⋯H contacts (for the latter, see Table 3). The dicarbadodecaborane dimer with 1 : 2 interaction topology (BEZTUW) shows in its crystal structure two heteropolar C–H⋯H–B contacts at 2.97 and 2.99 Å, in addition to the two B–H⋯H–B ones, which might also contribute to the total dissociation energy of 10.34 kJ mol⁻¹. On the other hand, the dissociation energy for TUQTEE, 4.26 kJ mol⁻¹, with only one H⋯H interaction (2.90 Å) is much larger than those obtained for the 1 : 1 dimers of BH₃ and B₂H₆, 0.30 and 0.64 kJ mol⁻¹, respectively. This magnification of the dissociation energy by a polyhedral skeleton was already observed for alkanes, among which the dimer of dodecahedrane C₂₀H₂₀ presented a dissociation energy of 4.14 kJ mol⁻¹, in contrast with the minute 0.52 kJ mol⁻¹ found for methane with the same 1 : 1 interaction topology.¹⁷ An explanation to this remarkable behaviour is that E–H⋯H–E interactions in large systems (e.g. dimers of polyhedral alkanes or boranes) are stabilized by a different mechanism than those of small ones (e.g. CH₄ or BH₃ dimers). While the latter are governed by interactions between oscillating dipoles E^δ+–H^δ−⋯H^δ+–E^δ− and E^δ−–H^δ+⋯H^δ−–E^δ+ and, thus, the stabilization can be attributed to “classic” dispersion, the great stability of larger dimers can be explained in terms of a reorganization of the bonding electrons of two E–H bonds to create alternative H⋯H and E⋯E “bonds” and also to the charge transfer between the two interacting units to establish long-range E⋯H interactions.¹⁸

Conclusions

We have carried out a systematic theoretical study of homopolar dihydrogen interactions in group 13 compounds. Several families of compounds containing E–H (E = B, Al and Ga) interacting units have been analysed, from the smallest trivalent hydrides EH₃ to the larger polyhedral boranes. B–H⋯H–B contacts are by far the most abundant ones and involve small dissociation energies, comparable to those associated to previously studied C–H⋯H–C contacts.¹⁷ In some cases, B–H⋯H–B interactions, combined with B–H⋯B ones, can be associated to surprisingly large dissociation energies, as for example in the calculated dimer of the nido polyborane B₁₀H₁₄ (D = 27.14 kJ mol⁻¹). We have identified two factors that strengthen the interaction: (a) the presence of a polyhedral skeleton associated to the E–H interacting unit (for example, a 1 : 1 H⋯H interaction is one order of magnitude larger in a dicarbadodecaborane dimer than in a diborane one) and, (b) a high number of H⋯H and E⋯H contacts between two monomers working cooperatively. This cooperative character of the intermolecular contacts was previously found in alkanes,¹⁷ and now also observed in boron hydrides. We note that the 2 : 2 staggered (7d) and the 3 : 3 staggered topologies are the most stable ones for EH₃ and CH₄ noncovalent dimers, respectively, but for E = B the dissociation energy is almost negligible. In general, the calculated dissociation energies are larger for interaction topologies that involve multiple H⋯H and E⋯H short contacts (7d and 8b) for B, Al and Ga. This is in good agreement with the experimental data, since in many crystal structures, the real scenario is a combination of several short contacts of H⋯H, H⋯E and even E⋯E types, all contributing to the global stability. Based on our theoretical analysis, we have observed that the strength of the interaction within group 13 follows the trend Al > Ga > B, with Al showing a remarkable tendency to form very short Al⋯H bonds.

Computational details

All calculations were done with the Gaussian09 package.⁷⁶ Geometry optimizations were carried out at the MP2 level of theory with the 6-311++G(3df,3pd) basis set for all atoms. Single point calculations on dimers of closo polyhedral boranes directly obtained from crystal structures were performed at the MP2/6-311+G(d,p) level. Dissociation energies were corrected for the BSSE by the counterpoise method.⁷⁷ The following structures were characterized as true minima after diagonalization of the Hessian matrix: diborane (B₂H₆), alane (Al₂H₆), digallane (Ga₂H₆), diborane (B₂H₆)₂ and digallane (Ga₂H₆)₂ dimers with terminal–bridging interaction topology, (B₄H₁₀)₂ with both bottom–side and bottom–face interaction topologies and (B₅H₉)₂ with bottom–face interaction topology. Other hypothetical dimers and those coming from crystal structure optimizations, even if they are not real minima, have been analysed to further investigate different possibilities of interaction topologies and geometries that can be found in the solid state. Atomic charges were calculated via the Natural Population Analysis (NPA) implemented in Gaussian09. The AIM analysis was performed on the MP2 electron density by means of AIMAll software.⁷⁸ Crystal structures were retrieved from the Cambridge Structural Database (version 5.38 + 1 update). Only structures with 3D coordinates determined, not disordered, and with R < 5% were allowed in searches.

Acknowledgements

J. E. thanks the Generalitat the Catalunya and the European Commission (FP7) for a Beatriu de Pinós-Marie Curie fellowship (BP-A2-00022). The authors thank the CSUC for the allocation of computing facilities, and MINECO for financial support through grant CTQ2015-64579-C3-1-P.

References

1. J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296.
2. D. Braga, G. R. Desiraju, J. S. Miller, A. G. Orpen and S. L. Price, CrystEngComm, 2002, 4, 500–509.
3. J. Cerny and P. Hobza, Phys. Chem. Chem. Phys., 2007, 9, 5291–5303.
4. J. C. Stendahl, M. S. Rao, M. O. Guler and S. I. Stupp, Adv. Funct. Mater., 2006, 16, 499–508.
5. H. Suezawa, T. Yoshida, Y. Umezawa, S. Tsuboyama and M. Nishio, Eur. J. Inorg. Chem., 2002, 3148–3155.
6. R. H. Crabtree, P. E. M. Siegbahn, O. Eisenstein and A. L. Rheingold, Acc. Chem. Res., 1996, 29, 348–354.
7. V. I. Bakhmutov, Dihydrogen Bonds: Principles, Experiments and Applications, John Wiley & Sons Inc., Hoboken NJ, 2008.
8. E. J. Juárez-Pérez, R. Núñez, C. Viñas, R. Sillanpää and F. Teixidor, Eur. J. Inorg. Chem., 2010, 2385–2392.
9. I. Alkorta, F. Blanco and J. Elguero, J. Phys. Chem. A, 2010, 114, 8457–8462.
10. X. Chen, J.-C. Zhao and S. G. Shore, Acc. Chem. Res., 2013, 46, 2666–2675.
11. R. Custelcean and J. E. Jackson, Chem. Rev., 2001, 101, 1963–1980.
12. J. G. Planas, C. Viñas, F. Teixidor, A. Comas-Vives, G. Ujaque, A. Lledós, M. E. Light and M. B. Hursthouse, J. Am. Chem. Soc., 2005, 127, 15976–15982.
13. T. Richardson, S. de Gala, R. H. Crabtree and P. E. M. Siegbahn, J. Am. Chem. Soc., 1995, 117, 12875–12876.
14. H. Cybulski, M. Pecul, J. Sadlej and T. Helgaker, J. Chem. Phys., 2003, 119, 5094–5104.
15. T. Kar and S. Scheiner, J. Chem. Phys., 2003, 119, 1473–1482.
16. S. J. Grabowski, W. A. Sokalski and J. Leszczynski, J. Phys. Chem. A, 2005, 109, 4331–4341.
17. J. Echeverría, G. Aullón, D. Danovich, S. Shaik and S. Alvarez, Nat. Chem., 2011, 3, 323–330.
18. D. Danovich, S. Shaik, F. Neese, J. Echeverría, G. Aullón and S. Alvarez, J. Chem. Theory Comput., 2013, 9, 1977–1991.
19. P. R. Schreiner, L. V. Chernish, P. A. Gunchenko, E. Y. Tikhonchuk, H. Hausmann, M. Serafin, S. Schlecht, J. E. P. Dahl, R. M. K. Carlson and A. A. Fokin, Nature, 2011, 477, 308–311.
20. D. J. Wolstenholme, J. L. Dobson and G. S. McGrady, Dalton Trans., 2015, 44, 9718–9731.
21. D. Brusselle, P. Bauduin, L. Girard, A. Zaulet, C. Viñas, F. Teixidor, I. Ly and O. Diat, Angew. Chem., Int. Ed., 2013, 52, 12114–12118.
22. D. J. Wolstenholme, K. T. Traboulsee, Y. Hua, L. A. Calhoun and G. S. McGrady, Chem. Commun., 2012, 48, 2597–2599.
23. P. Sirsch, F. N. Che, J. T. Titah and G. S. McGrady, Chem. – Eur. J., 2012, 18, 9476–9480.
24. S. Marchant, C. Y. Tang, A. J. Downs, T. M. Greene, H. J. Himmel and S. Parsons, Dalton Trans., 2005, 3281–3290.
25. N. K. V. Monteiro and C. L. Firme, J. Phys. Chem A, 2014, 118, 1730–1740.
26. A. Krapp, G. Frenking and E. Uggerud, Chem. – Eur. J., 2008, 14, 4028–4038.
27. P. Pyykkö, in Annual Review of Physical Chemistry, ed. M. A. Johnson and T. J. Martinez, 2012, vol. 63, pp. 45–64.
28. F. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388.
29. S. Alvarez, Dalton Trans., 2013, 42, 8617–8636.
30. R. Brill, H. Dietrich and H. Dierks, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1971, 27, 2003–2018.
31. S.-A. Khan, J. H. Morris, M. Harman and M. B. Hursthouse, J. Chem. Soc., Dalton Trans., 1992, 119–126.
32. P. M. B. Piccoli, J. A. Cowan, A. J. Schultz, T. F. Koetzle, G. P. A. Yap and S. Trofimenko, J. Mol. Struct., 2008, 890, 63–69.
33. M. E. Bowden, I. W. M. Brown, G. J. Gainsford and H. Wong, Inorg. Chim. Acta, 2008, 361, 2147–2153.
34. B. Tinant, J. P. Declercq, G. Lepropre and J. Fastrez, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1994, 50, 1982–1985.
35. M. Schultz, C. J. Burns, D. J. Schwartz and R. A. Andersen, Organometallics, 2000, 19, 781–789.
36. B. Cordero, V. Gómez, A. E. Platero-Prats, M. Reves, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832–2838.
37. J.-H. Her, M. Yousufuddin, W. Zhou, S. S. Jalisatgi, J. G. Kulleck, J. A. Zan, S.-J. Hwang, R. C. BowmanJr and T. J. Udovic, Inorg. Chem., 2008, 47, 9757.
38. J.-H. Her, W. Zhou, V. Stavila, C. M. Brown and T. J. Udovic, J. Phys. Chem. C, 2009, 113, 11187.
39. I. Tiritiris and T. Schleid, Z. Anorg. Allg. Chem., 2003, 629, 1390.
40. I. Tiritiris, T. Schleid, K. Mueller and W. Preetz, Z. Anorg. Allg. Chem., 2000, 626, 323.
41. J. Graetz and J. J. Reilly, J. Alloys Compd., 2006, 424, 262–265.
42. L. Andrews and X. F. Wang, Science, 2003, 299, 2049–2052.
43. C. Y. Tang, R. A. Coxall, A. J. Downs, T. M. Greene and S. Parsons, J. Chem. Soc., Dalton Trans., 2001, 2141–2147.
44. K. N. Semenenko, E. B. Lobkovskii, B. L. Tarnopolskii and M. A. Simonov, J. Struct. Chem., 1976, 17, 915–917.
45. G. Perego, M. Cesari, G. Del Piero, A. Balducci and E. Cernia, J. Organomet. Chem., 1975, 87, 33–41.
46. V. K. Bel'sky, A. I. Sizov, B. M. Bulychev and G. L. Soloveichik, J. Organomet. Chem., 1985, 280, 67–80.
47. P. C. Andrews, M. G. Gardiner, C. L. Raston and V.-A. Tolhurst, Inorg. Chim. Acta, 1997, 259, 249–255.
48. M. Veith, T. Kirs and V. Huch, Z. Anorg. Allg. Chem., 2013, 639, 312–318.
49. C. Cui, H. W. Roesky, M. Noltemeyer and H.-G. Schmidt, Organometallics, 1999, 18, 5120–5123.
50. H. S. Isom, A. H. Cowley, A. Decken, F. Sissingh, S. Corbelin and R. J. Lagow, Organometallics, 1995, 14, 2400–2406.
51. U. Dümichen, T. Gelbrich and J. Sieler, Z. Anorg. Allg. Chem., 2001, 627, 1915–1920.
52. A. J. Downs, M. J. Goode and C. R. Pulham, J. Am. Chem. Soc., 1989, 111, 1936–1937.
53. C. R. Pulham, A. J. Downs, M. J. Goode, D. W. H. Rankin and H. E. Robertson, J. Am. Chem. Soc., 1991, 113, 5149–5162.
54. P. L. Baxter, A. J. Downs, M. J. Goode, D. W. H. Rankin and H. E. Robertson, J. Chem. Soc., Dalton Trans., 1990, 2873–2881.
55. J. Lorberth, R. Dorn, W. Massa and S. Wocadlo, Z. Naturforsch. B Chem. Sci., 1993, 48, 224–226.
56. N. S. Hosmane, K.-J. Lu, A. K. Saxena, H. Zhang, J. A. Maguire, A. H. Cowley and R. D. Schluter, Organometallics, 1994, 13, 979–988.
57. B. Vest, K. Klinkhammer, C. Theirfeldert, M. Lein and P. Schwerdtfeger, Inorg. Chem., 2009, 48, 7953.
58. A. B. Burg and Y.-C. Fu, J. Am. Chem. Soc., 1966, 88, 1147–1151.
59. P. S. Ganguli and H. A. McGee, J. Chem. Phys., 1969, 50, 4658–4660.
60. D. J. Goebbert, H. Hernandez, J. S. Francisco and P. G. Wenthold, J. Am. Chem. Soc., 2005, 127, 11684–11689.
61. R. Hoffmann, P. V. R. Schleyer and H. F. Schaefer, Angew. Chem., Int. Ed., 2008, 47, 7164–7167.
62. D. Mullen and E. Hellner, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 3816–3822.
63. H. W. Smith and W. N. Lipscomb, J. Chem. Phys., 1965, 43, 1060–1064.
64. D. J. Wolstenholme, E. J. Fradsham and G. S. McGrady, CrystEngComm, 2015, 17, 7623–7627.
65. C. Y. Tang, R. A. Coxall, A. J. Downs, T. M. Greene and S. Parsons, Dalton Trans., 2001, 2141.
66. P. Farrás, E. J. Juárez-Pérez, M. Lepsik, R. Luque, R. Nuñez and F. Teixidor, Chem. Soc. Rev., 2012, 41, 3445–3463.
67. E. B. Moore, R. E. Dickerson and W. N. Lipscomb, J. Chem. Phys., 1957, 27, 209.
68. C. E. Nordman and W. N. Lipscomb, J. Chem. Phys., 1953, 21, 1856.
69. P. T. Brain, C. A. Morrison, S. Parsons and D. W. H. Rankin, J. Chem. Soc., Dalton Trans., 1996, 4589.
70. D. Forster, C. B. Hubschle, P. Luger, T. Hugle and D. Lentz, Inorg. Chem., 2008, 47, 1874.
71. J. R. Pipal and R. N. Grimes, Inorg. Chem., 1977, 16, 3251–3255.
72. F. Meyer, P. Paetzold and U. Englert, Chem. Ber., 1994, 127, 93.
73. M. G. Davidson, T. G. Hibbert, J. A. K. Howard, A. Mackinnon and K. Wade, Chem. Commun., 1996, 2285–2286.
74. Y. Nie, H. Pritzkow and W. Siebert, Eur. J. Inorg. Chem., 2004, 2004, 2425–2433.
75. R. J. Blanch, M. Williams, G. D. Fallon, M. G. Gardiner, R. Kaddour and C. L. Raston, Angew. Chem., Int. Ed. Engl., 1997, 36, 504–506.
76. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
77. F. B. van Duijneveldt, J. G. C. M. van Duijneveldt-van de Rijdt and J. H. van Lenthe, Chem. Rev., 1994, 94, 1873–1885.
78. T. A. Keith, AIMAll (Version 16.08.17), TK Gristmill Software, Overland Park KS, USA, 2016 (http://aim.tkgristmill.com).

---

Footnote

† Electronic supplementary information (ESI) available: Angular distribution of B–H⋯H–B intermolecular contacts, distribution of Al⋯H distances, structure of Al₄H₁₂, Cartesian coordinates of all calculated dimers characterized as true minima and thermochemical properties of selected dimers. See DOI: 10.1039/c6dt02854c

---