Open Access Article
Open Access ArticleAxonal tension contributes to consistent fold placement
Xincheng
Wang
 a,
Shuolun
Wang
a and
Maria A.
Holland
a,
Shuolun
Wang
a and
Maria A.
Holland
 *ab
*ab
aDepartment of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, IN 46556, USA. E-mail: maria-holland@nd.edu
bBioengineering Graduate Program, University of Notre Dame, Notre Dame, IN 46556, USA
First published on 15th March 2024
Abstract
Cortical folding is a critical process during brain development, resulting in morphologies that are both consistent and distinct between individuals and species. While earlier studies have highlighted important aspects of cortical folding, most existing computational models, based on the differential growth theory, fall short of explaining why folds tend to appear in particular locations. The axon tension hypothesis may provide insight into this conundrum; however, there has been significant controversy about a potential role of axonal tension during the gyrification. The common opinion in the field is that axonal tension is inadequate to drive gyrification, but we currently run the risk of discarding this hypothesis without comprehensively studying the role of axonal tension. Here we propose a novel bi-layered finite element model incorporating the two theories, including characteristic axonal tension in the subcortex and differential cortical growth. We show that axon tension can serve as a perturbation sufficient to trigger buckling in simulations; similarly to other types of perturbations, the natural stability behavior of the system tends to determine some characteristics of the folding morphology (e.g. the wavelength) while the perturbation determines the location of folds. Certain geometries, however, can interact or compete with the natural stability of the system to change the wavelength. When multiple perturbations are present, they similarly compete with each other. We found that an axon bundle of reasonable size will overpower up to a 5% thickness perturbation (typical in the literature) and determine fold placement. Finally, when multiple axon tracts are present, even a slight difference in axon stiffness, representing the heterogeneity of axonal connections, is enough to significantly change the folding pattern. While the simulations presented here are a very simple representation of white matter connectivity, our findings point to urgent future research on the role of axon connectivity in cortical folding.
1 Introduction
Brain development is a protracted procedure, during which the brain transforms from small and smooth to large and folded.1 The resulting ridge-shaped folds are called gyri, while the fissures are called sulci. During gestational weeks 16–27, deep primary folds grow outward rapidly in specific locations – maintaining some consistency not only between individuals but also across species.2,3 Following the primary folds, the secondary and tertiary folds emerge during weeks 23–37,4 with more variation in their location, size, and orientation.5Understanding the role of physical forces during the formation of the brain's convoluted surface has been of great interest for decades.6,7 Early studies of brain development assumed that the driving force was compressive stress from the rigid constraint of the skull, regulating the expansion of the brain tissue to optimize the available space.1 However, this theory was contradicted by experimental studies on sheep.8 Another important hypothesis is the differential growth theory, which suggests that different growth rates in the cortex and subcortex, or in different layers of the cortex, would lead to folding as the outer layer reaches critical stress and becomes unstable.9 Early studies developed simple theoretical models,10 while later works have performed increasingly complex simulations of cortical growth and folding.11,12 However, one limitation of these theories is that, by themselves, they fail to explain the consistency in the location of the primary folds.1,2
The questions about the conserved locations of primary folds might be answered with the help of another competing – and controversial – theory. The axonal tension hypothesis states that axons pull strongly connected regions close together, forming a gyrus, while weakly connected areas drift apart, forming sulci.13 It further suggests that this tension-driven folding leads to globally compact wiring. A prominent role for axon tension makes sense, considering that axons, the primary processes that extend from each neuron, make up the majority of the interior white matter of the brain. Groups of hundreds of parallel axons form axonal bundles or tracts, connecting different regions of the brain, both radially and circumferentially. The axon tension theory is specifically supported by the evidence that axons exist in a state of tension in vitro,14 with linear force–displacement response, axial viscosity, stretch-driven growth,15,16 and active retraction, with axial tension measured around 30 to 40 μdyne (300 to 400 pN). Additionally, a recent diffusion tensor imaging (DTI) study found that axon microstructure matures prior to the formation of folds, potentially helping to initialize cortical folding.17
Despite this evidence of axon behavior, experimental results have challenged the wholesale acceptance of the axonal tension hypothesis. For example, residual stress cutting experiments in the brains of adult mice18 and developing ferrets19 show that sustained tension exists in the subcortex, which may significantly impact the folding process. However, three main conclusions challenge the tension-based folding hypothesis: (1) the subcortical axonal tension is far away from the folding region, (2) the circumferential axonal tension around the gyri is too weak to pull the tissue directly, and (3) the observed orientation of residual stress in gyri does not match the model's predictions.19 Their experiments and simulations suggest that differential growth primarily drives folding, while allowing that axonal tension may still be a constraint that affects cortical folding.
In other studies, axon connection has been found to scale with cortical folding across species,20,21 leading researchers to extend the original axon–tension theory to propose that axonal tension causes white matter folding, influencing gray matter folding in turn. Recently, Van Essen has reformulated the original tension-based morphogenesis theory, incorporating more forces at both cellular and tissue scales that promote folding.22 Pushing back on critiques of his theory,19 he noted that ex vivo experiments might not capture in vivo tension, which could be affected by slicing or tissue edema. He also calls for a simulation framework capable of modeling key neurobiological features in the cortical tissue, such as axons that are orientated at different angles and even cross.23 Currently, there is still a gap in understanding how axonal tension is involved during gyrification. For example, what level of axonal tension exists in vivo? Is this level of tension capable of triggering cortical folding? How does the axon network wire during the folding process?
White matter is particularly interesting in light of the open questions about the relationship between brain structure and function.24 It has been observed that abnormal white matter connectivity is found in various neurological disorders, which frequently coincide with atypical folding patterns within the brain. Of course, these relationships could be causal or simply correlative. Regardless, a deeper understanding of the role of white matter connectivity in cortical folding has far-reaching implications for our understanding of the brain's structure and function.
From a macroscopic perspective, the inner white matter and the outer gray matter form a bi-layered system, and the folding process in the cortex layer can be categorized as an instability problem. Instability theory has been heavily used in the study of gyrification; however, it can only predict the critical conditions and wavelength of the cortical folds, not the precise location of folds. Instead, numerical simulations are often used to understand certain features of the post-buckling analysis. However, finite element simulations require some type of perturbation that induces symmetry breaking and determines fold placement.25–30 There are several approaches available to introduce the imperfections in the finite element simulations, such as applying a small perturbation in thickness, growth, curvature, or stiffness.31–33 While axonal tension has been relatively less studied than these other sources of perturbation, it is a plausible source of heterogeneous forces that could break symmetry.
Recently, finite element simulations have made promising advances in understanding the process of brain development.34–39 Simulations can not only provide quantitative information about stress, for instance, which is difficult to measure experimentally, but when combined with experiments, they can help to identify and evaluate potential mechanisms of folding.40,41 However, the complexity of brain tissue is a challenge for the accuracy of finite element models. In addition to multiple cell types, complex mechanical behavior,42 and highly heterogeneous structure and properties,43,44 there is also an issue of scale. This is particularly relevant for axons whose length exceeds the dimensions of typical finite elements, challenging the assumption of local behavior.
Despite the wide variety and increasing complexity of finite element models of cortical folding, the mechanical role of axons has generally been overlooked, and only a few models have incorporated axon fibers when modeling the white matter tissue. The first model of cortical folding to incorporate axonal growth15 represented axon orientations as directions of transversely isotropic growth and found that axon arrangement affected the resulting morphology. However, a limitation of that study was that each point in the model could only have a single axonal orientation, meaning that distributed fiber anisotropy45–47 or intersections between multiple axonal bundles couldn't be captured. More recently, the role of heterogeneous axonal distribution has been explored using the embedded element method in both 2D48 and 3D domains;49 however, these models were limited to straight, radially aligned axons without prestretch. Another recent model has focused on how the patterns of axons seen in the brain emerge as a result of their stretch-driven growth.50 Although the resulting fiber distribution is consistent with experimental data, the computational model doesn't consider phenomena like widespread crossing fibers.23
In this paper, we introduce a novel model of cortical folding incorporating both the differential growth and axon tension hypotheses (Section 2). We assume that these mechanisms contribute to cortical folding concurrently, with the differential growth serving as the main driver of gyrification and the subcortical axon tension as a slight perturbation during the initiation of folding. Our model incorporates axon orientation and homeostatic tension, allowing us to investigate the effects of these features on brain development. Using our model, we are specifically interested in testing several hypotheses put forward in the foundational paper on the axon tension hypothesis:13 first, that axon tension works to draw strongly connected regions closer together, while allowing less-connected regions to drift apart; and second, that axon tension tends to result in globally-optimized wiring patterns (Section 3).
2 Methodology
2.1 Kinematics of cortical growth
We simulate brain tissue growth using the finite growth theory based on nonlinear continuum mechanics. To capture the large deformation during the cortical folding, we introduce the deformation mapping φ. The particle X in the reference configuration moves to x = φ(X, t) in the current configuration after time t. The deformation gradient of this mapping F is given by,| F = Δφ, | (1) |
| F = Fe·Fg, | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F > 0, can similarly be decomposed into J = JeJg, where Jg and Je are the determinants of Fg and Fe, respectively.
F > 0, can similarly be decomposed into J = JeJg, where Jg and Je are the determinants of Fg and Fe, respectively.
As in previous works,40 we model the substrate as a purely elastic material (i.e., Fg = I), while the gray matter experiences in-plane area growth defined by
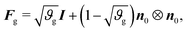 | (3) |
The inverse of the growth tensor is
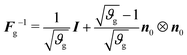 | (4) |
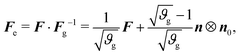 | (5) |
Assuming that the cortex grows roughly linearly with time t,34 we adopt a linear growth rate, such that
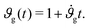 | (6) |
2.2 Constitutive equations
We model the cortex and the subcortex tissue as compressible neo-Hookean materials with strain energy density function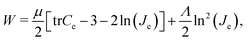 | (7) |
| β = μc/μs. | (8) |
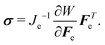 | (9) |
div![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ = 0. σ = 0. | (10) |
2.3 Computational model of axonal tension
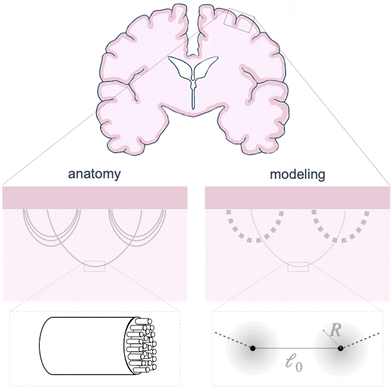
The circumferential fibers in the subcortical region can be divided into short- and long-association fibers, which connect neighboring gyri and distant cortical areas in the same hemisphere, respectively. Short-association fibers (3 mm to 30 mm52) are also called U-fiber because they form a “U” shape around a sulcus, connecting neighboring cortical areas.53,54 U-Fibers are prominent in superficial brain tissue across species, including humans, monkeys, and ferrets,53,55 and have been thought to play a crucial role in brain development, aging, and plasticity. Reductions in U-fiber density are associated with multiple brain disorders.56 To model these fibers in the brain, we discretize longer axon tracts as a series of shorter connector elements that are attached to the white matter subcortex via surfaced-based coupling constraints in Abaqus/Standard.57 The connector element, CONN2D2, acts as a straight wire connection between two nodes with linear or nonlinear force–displacement relationships. We approximate the U-fiber shape (Fig. 1), which is typical of axon connectivity in the subcortex, by connecting multiple elements end to end.Here, we consider linear elastic connector behavior, where the magnitude of tension along a connector is
T = K(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0), 0), | (11) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and the reference length
and the reference length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. The geometrical length is the Euclidean distance between two connector nodes when creating the model, and the reference length specifies the resting length of the axon. The stretch ratio λ of the connector is defined as
0. The geometrical length is the Euclidean distance between two connector nodes when creating the model, and the reference length specifies the resting length of the axon. The stretch ratio λ of the connector is defined as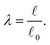 | (12) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) =
= ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, there is no stretch along the axial direction, representing a stress-free state; λaxon > 1 implies that the axon is under a state of stretch. The stiffness of the connector elements, K, is an extrinsic quantity, with dimensions of force per length change. However, when measured experimentally, it is more common to determine the intrinsic stiffness with dimensions of force per cross-sectional area; for instance, the shear modulus μ is an intrinsic quantity. To find the intrinsic stiffness of axons, we need Young's modulus, cross-sectional area, and initial length. The Young's modulus, assuming a nearly incompressible material, can be found as
0, there is no stretch along the axial direction, representing a stress-free state; λaxon > 1 implies that the axon is under a state of stretch. The stiffness of the connector elements, K, is an extrinsic quantity, with dimensions of force per length change. However, when measured experimentally, it is more common to determine the intrinsic stiffness with dimensions of force per cross-sectional area; for instance, the shear modulus μ is an intrinsic quantity. To find the intrinsic stiffness of axons, we need Young's modulus, cross-sectional area, and initial length. The Young's modulus, assuming a nearly incompressible material, can be found as| E ≈ 3μaxon. | (13) |
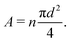 | (14) |
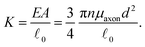 | (15) |
Each connector element connects two nodes, which play multiple roles. They serve as the hinge connections to adjacent connectors and act as the coupling points for the connector–substrate interaction, governed by surface-based coupling constraints in Abaqus.57 For the surface-based coupling constraints, we chose the distributing coupling constraint, where the connector tension T is transmitted to n nearby substrate nodes within a specified influence radius R (Fig. 1) via a weighted function,
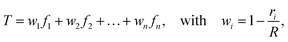 | (16) |
2.4 Finite element bi-layered model
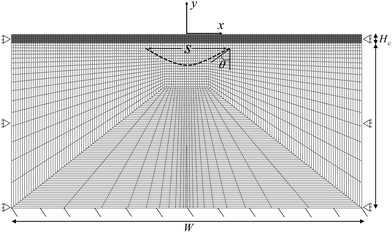
We implement our computational model in ABAQUS/Standard. The simulation domain is a 2D rectangle with dimension W × H, composed of a cortical layer with thickness Hc and shear modulus μc, and a subcortical substrate with thickness Hs and shear modulus μs. The default value of all parameters are provided in Table 1. We discretize the domain with 4795 hybrid elements CPE4H (Fig. 2). All solutions presented here are the converged solutions checked by a mesh sensitivity test.| Variable | Description | Value and unit | Source/comment |
|---|---|---|---|
| a Indicates values that are calculated; otherwise the values are given in the relevant source. | |||
| ϑ g | The total growth of the cortex layer | 1.23 | |
| W | Width of the bi-layered model | 80 mm | |
| H c | Thickness of the cortex tissue | 2 mm | |
| H s | Thickness of the subcortex tissue | 38 mm | |
| μ c | Shear modulus of the cortex | 0.1 kPa | Holland et al.34 |
| v | Poisson's ratio of the materials | 0.46 | Holland et al.34 |
| β | Stiffness ratio between the cortex and the subcortex | 3 | Holland et al.34 |
| λ | Stretch ratio of axon tracts | 2 | Dennerll et al.14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 0 |
Reference length of the axon segment | 65 μm | |
| d | Average diameter of myelinated axons | 1 μm | Liewald et al.64 |
| μ axon | Shear modulus of myelinated axon | 12 kPa | Bernal et al.65 |
| R | Coupling constraint influence radius | 1.0 mm | Chosen based on mesh sensitivity test |
| n | Number of the paralleled axons in the bundle | 3.45 × 105 | Chavoshnejad et al.48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| a | Second-order geometrical parameter | 1/130 mm | Riley et al.58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| b | First-order geometrical parameter | −7 mm | Riley et al.58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| l | Sinusoidal perturbation wavelength | 4 mm | Diab et al.60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| ξ/Hc | Relative thickness perturbation amplitude | 2.5–5% | Auguste et al.62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
The bottom surface is fixed, and roller boundary conditions are applied to the left and right edges of the rectangle. In addition, we apply a frictionless self-contact interaction to the top surface of the cortex, which prevents self-penetration.
To model the axon tracts, we approximate their geometry with parabola equations,
| y = ax2 + b | (17) |
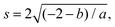 and the tangent at the right intersection is
and the tangent at the right intersection is 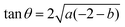 . From histology images,58 we estimate s ≈ 24.5 mm and tan
. From histology images,58 we estimate s ≈ 24.5 mm and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ ≈ 0.8. Solving the equations, we obtain the geometrical parameters
θ ≈ 0.8. Solving the equations, we obtain the geometrical parameters 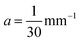 and b = −7 mm.
and b = −7 mm.
In this work, we predominantly focus on the effect of a single axon bundle. However, we also briefly consider the effects of multiple bundles, where two additional tracts are placed symmetrically around the primary tract, centered around the ends of the primary tract. As different axon tracts may have different stiffnesses, we quantify this by the stiffness ratio η,
| η = K1/K2, | (18) |
We also consider the role of local thickness changes, as another plausible source of perturbations in a numerical simulation. This is achieved by slightly altering the y-position of nodes along the cortical–subcortical interface in a sinusoidal form,60–63
u2 = ξ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos(2πX1/l), for −l/4 ≤ X1 ≤ l/4 cos(2πX1/l), for −l/4 ≤ X1 ≤ l/4 | (19) |
When comparing two folding morphologies, we quantify the differences via the mean squared displacements ψ for each of the m = 800 nodes on the top surface of the cortex layer,
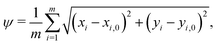 | (20) |
3 Results and discussion
3.1 Critical strain in presence of axonal tension
The first goal of this study is to confirm that small amounts of axonal tension can serve as a perturbation of the bi-layered system. Here, we compare the theoretical critical strain of a perfect bilayered system66 with our simulations of a bilayer with a single axon tract. For comparison, we identify the buckling points visually, and calculate the critical strain as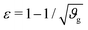 . Both approaches show that higher cortical–subcortical stiffness ratios correlate with lower critical strains, meaning the system is increasingly prone to instability (Fig. 3). By comparing our simulation results with the theoretical prediction, we found that our model is less stable, consistent with axonal tension serving as a perturbation. Furthermore, when testing with three different axonal tract stiffness values (10 N m−1, 150 N m−1 and 300 N m−1), we found that higher axon stiffnesses further decreased stability slightly.
. Both approaches show that higher cortical–subcortical stiffness ratios correlate with lower critical strains, meaning the system is increasingly prone to instability (Fig. 3). By comparing our simulation results with the theoretical prediction, we found that our model is less stable, consistent with axonal tension serving as a perturbation. Furthermore, when testing with three different axonal tract stiffness values (10 N m−1, 150 N m−1 and 300 N m−1), we found that higher axon stiffnesses further decreased stability slightly.
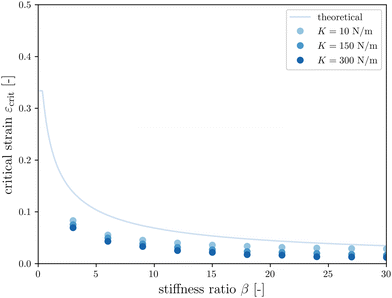 | ||
Fig. 3 Critical strain 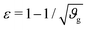 vs. cortical–subcortical stiffness ratio. Theoretical results are taken from Holland et al.66 vs. cortical–subcortical stiffness ratio. Theoretical results are taken from Holland et al.66 | ||
3.2 Influence of the axon geometry
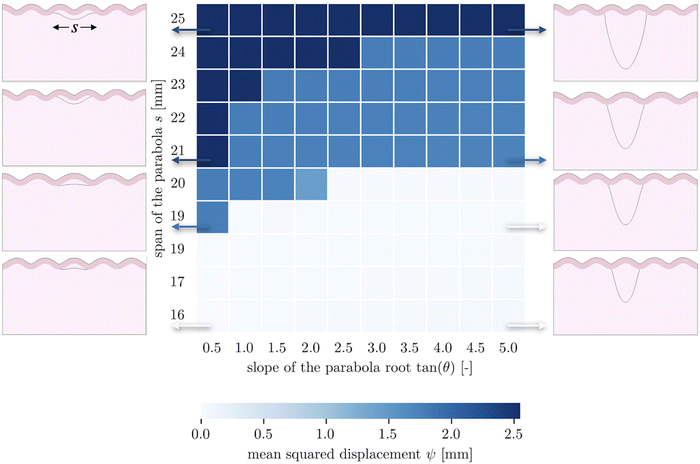
The second goal of this study is to understand how the arrangement of axons affects cortical morphology. We theorize that alterations in axon geometry would lead to a different distribution of axonal tension on the white matter, thus influencing the cortical folding pattern. To test this, we consider a single axon bundle with a stiffness of 150 N m−1 (representing approximately 3.4 × 105 axons), with different initial geometries. Since we use parabola equations to characterize the axon arrangement, the span of the curve and the tangent at intersections can be changed easily. This allows us to approximate radial axons, with a near-infinite tangent, as have been studied elsewhere,48 and to compare them with axons that act at an angle. Note that because of the biased mesh density, we increase the value of the influence radius to 1.5 mm in the case when the axon tract is placed close to the bottom of the model.Given a cortical–subcortical stiffness ratio of 3, the system is predicted to buckle into wavelengths of 15.6 mm; given the dimensions of our model, this is likely to translate into a wave number of 5 (or wavelength of 16 mm).66 When exploring the parameter space of span and slope, we found that nearly all of the resulting folding patterns matched this wavelength. Simulations with a small span (16 mm) and a large span (25 mm) showed different patterns with the same wavelength, with a sulcus and a gyrus in the middle, respectively (Fig. 4). Interestingly, in these regimes, the morphology was not sensitive to the insertion angle. However, in an intermediate range, a third morphology with different wavelength emerges at moderate slopes.
These patterns appear to reflect the competition between the natural stability of the system and the effect of axon tension. Naturally, the system tends to form five folds, and many axon configurations can be accommodated by such undulations, with the axon either spanning a single fold in the case of short spans, or two folds in the case of long spans. However in the middle, the span is such that it falls awkwardly relative to the natural wavelength of the system – tending to connect something like sulcal walls instead of sulci themselves. At shallow angles, these sulcal walls are pulled together fairly efficiently, while at steeper angles it is more energetically favorable for the axonal insertion points to form true sulci, which entails changing the wavelength. In short, both the initial axon span and the initial axonal tension orientation interact with the system stability to determine the folding morphology.
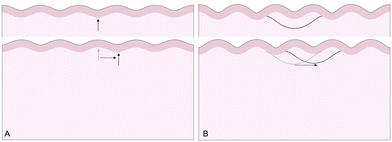
3.3 Influence of axonal tension vs. thickness perturbation
The third goal of this study is to compare the influence of axonal tension with other perturbations. Slight heterogeneities, for instance in thickness, curvature, stiffness, or growth, can change the location of gyral and sulcal folds throughout the brain and are potential explanations for the consistent location of primary folds throughout the brain.2 Here, we compare axonal tension against a small change in local cortical thickness. Initially, we apply both perturbations in two locations (in the center and slightly off-center) and observe the effect on folding morphology (Fig. 5). In both cases, a sulcus emerges in the center of the domain when the perturbation is located in the middle. Similarly, when the perturbation is shifted to the right by half of a wavelength, the location of the folds shifts accordingly, and a gyrus is instead located at the center. Thus, while the system properties (i.e. the cortical–subcortical stiffness ratio) determine the resulting wavelength, the location of the perturbation determines the phase shift of the folding pattern.We are further interested in the pote competition between these two perturbations – if they are applied such that they tend to form folds in different locations, which perturbation will dominate under which conditions? To answer this question, we apply both perturbations in a single model, with the thickness perturbation in the center of the model and the axon tract shifted half of a wavelength to the right. We run 100 simulations with varying combinations of thickness perturbation magnitude and axonal stiffness. The benchmark case is taken to be the case of (ξ/Hc = 0.05, K = 10 N m−1), where the thickness perturbation is the greatest and the axonal tension is the weakest (Fig. 6). That is, low values of ψ suggest that the resulting morphology resembles that driven by the thickness perturbation.
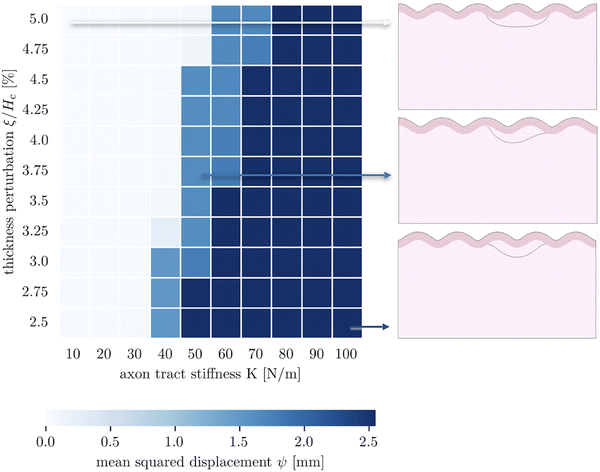 | ||
| Fig. 6 Parametric studies of thickness perturbation versus major axon tract stiffness 10 N m−1 ≤ K1 ≤ 100 N m−1. | ||
The 100 simulations result in three distinct folding morphologies. As expected, simulations with low levels of axonal tension (K ≲ 30 N m−1) deviate only slightly from the benchmark case, with a sulcus forming in the center (Fig. 6, top), indicating that the thickness perturbation strongly dominates. At the other extreme, when the axon tension is the strongest, the folding pattern is markedly different, with a gyrus forming in the center (Fig. 6, bottom), suggesting that the axonal tension determines the folding pattern. In between, there are some combinations of thickness and tension that result in an in-between, asymmetrical pattern, where neither a gyrus nor a sulcus is located at the center (Fig. 6, middle). Interestingly, it seems that the resulting pattern depends more on the axonal stiffness than the magnitude of the thickness perturbation, and that an axon tension of only 80 N m−1 is sufficient to overpower a thickness perturbation of 5%.
3.4 Influence of the varying axonal density
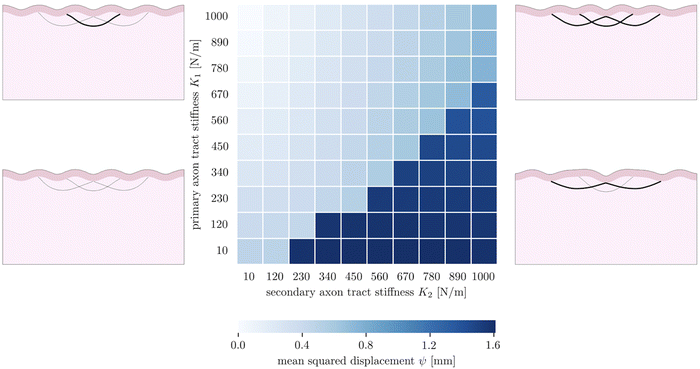
The fourth goal of this study is to investigate the effect of varying axonal density throughout the brain. This heterogeneous density had previously been theorized to drive cortical folding,13,67 specifically predicting that strongly connected regions would be drawn together as adjacent sulci, while loosely connected regions would be allowed to drift apart as adjacent gyri. In our model, axon density is represented by the stiffness of the axon fiber bundles, which is proportional to the number of axons they contain. In previous sections, we simplified axonal connectivity to a single axon tract. However, in reality, there are many axon bundles in every region of the brain, with complex crossing, bending, and kissing patterns.68 To capture the influence of multiple axon tracts, we extend the model by introducing two additional secondary fiber tracts along with the original primary tract, and vary the tract stiffnesses from 10 N m−1 to 1000 N m−1, so that there is a stiffness difference between the primary tract and the secondary tracts. We limit the total growth of the cortical layer to 1.2. The benchmark case is taken to be the case of (K1 = 1000 N m−1, K2 = 10 N m−1).The resulting simulations (7) reveal that the primary and secondary axon tracts compete to determine the placement of folds; the “winner” is able to draw its connected cortex into adjacent sulci, forming a gyrus, while the “loser” is forced to span a longer distance to connect two gyri. Thus the simulations fall into two main configurations, with one dominated by the primary axon tract when it is stiffer, and the other dominated by the secondary tracts when they are stiffer. Interestingly, in the case of equal stiffnesses, the primary tract dominates over the secondary tracts; we hypothesize this is because that configuration is closer to the system's natural instability pattern. In each case, the role of strongly connected axon tracts is consistent with the axonal tension hypothesis, which predicts that strong axonal tension will draw sulci together, forming a gyrus between them.
3.5 Axon wiring length change during the growth
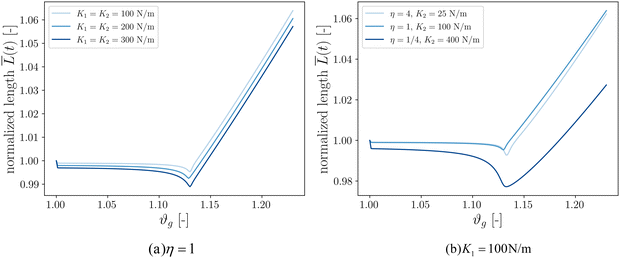
Our final goal was to test another predicted result of the axon tension hypothesis – that it will result in globally efficient wiring of the brain,13 minimizing the physical connection cost and maximizing topological efficiency.69 To test this theory, we use the three-tract model and measure the total axonal length throughout the simulation. To amplify the wiring length change, we increase the cortical–subcortical stiffness ratio β from 3 to 5 in this section. We define the normalized total wiring length as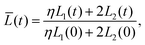 | (21) |
When simulating three tracts with equal stiffnesses (Fig. 8a), the wiring length decreases slightly after instability before increasing steadily. This is because axon tracts are passively deformed by the large deformation of the cortex tissue. These results suggest that higher axon stiffness will result in more compact wiring because the axons resist deformation more strongly. However, in this case the difference is slight, as seen in the very similar resulting morphologies (Fig. 7).
 | ||
| Fig. 7 Parametric studies of three axon tracts with varying density, consisting of one primary tract with stiffness K1 and two secondary tracts with stiffness K2. | ||
We additionally simulate three tracts of different stiffnesses by varying the axon tract stiffness ratio η from 1/4 to 4 while keeping K1 = 100 N m−1 (Fig. 8b). As in the previous case, the total length decreases to some extent before increasing at a steady rate. The cases of η = 1 and η = 4 denote primary axon tracts that are equal to or four times stiffer than the secondary axon tracts, respectively. The wiring length changes of these two cases are similar (Fig. 7), with primary axons connecting adjacent sulci. In contrast, the case of η = 1/4 shows more compact global wiring, because the stronger secondary axon tracts control the folding and connect adjacent sulci. These results point to a second factor influencing wiring efficiency: when there is a disparity in the axon stiffnesses, one can overpower the other to achieve a more efficient configuration. However, when all the tracts are equally stiff (Fig. 8a and η = 1 in Fig. 8b), the competition between them results in the least efficient wiring.
These results show that variations in axon placement and density can affect the global wiring in the final folded morphology. Of course, the real connectome of the brain is hugely more complex than the simplified version considered here, which allows for even more interactions between different axonal bundles of different strengths.
4 Limitations and future improvements
In this study, we implemented a simplified model of axon connectivity with discrete axon tracts. However, several limitations in our model point towards potential future research. First, we assume the time-independent elastic behavior in axons. This fails to capture the viscoelastic70,71 and growing15 behavior of axons. While viscoelasticity is likely not so relevant on the timescales of growth (days and weeks), growth could play a very significant role in the mechanical forces exerted on the cortex by axons.Secondly, the geometry of our model is significantly simplified compared to the complex architecture of the brain. A rectangular domain, while omitting the heterogeneous curvature seen in the actual brain, is a common domain for initial simulations of cortical folding.11,15,72 Furthermore, the connectivity of axons throughout the brain is incredibly complex, and here we have used a stereotypical arrangement of only three axon tracts. While this is a simplification, our model is capable of representing fiber bundles with varying cross-sections along its length, although this study has focused on the mechanics of homogeneous axon fiber bundles. We believe our model provides a strong foundation for future work to investigate increasingly complex fiber architectures, ideally based on histology or DTI data,73–75 in more realistic three-dimensional domains.
Thirdly, reliable experimental material properties for various components of brain tissue are difficult to find, particularly in vivo. We estimated the axon tract stiffnesses based on the number of parallel axons in a tract.64,65 Additionally, we use a cortical–subcortical stiffness ratio of β = 3 in our simulations, which is likely slightly higher than the physiological value, due to convergence issues in Abaqus/Standard. One way around this would be to solve the governing equations explicitly instead, which would likely expand the possible range of physical properties. There are spaces for improvement, such as more accurate axon arrangement and axon tract stiffness value. However, it is worth to note that here we focus on capturing the essential physics and assessing the central hypothesis.
Last but not least, computational models alone are unable to prove hypotheses. While we have shown that the observed folding behavior aligns with certain predictions, we can't rule out other explanations. Further research in this area, including experimental data on the in vivo properties of axons, histology and DTI data for axon distributions, and simulations using increasingly complex geometrical models, is necessary to understand the role of axon tension in cortical development more fully.
5 Conclusion
The hypothesis that axonal tension influences cortical folding has been proposed for decades. However, due to conflicting experimental data and computational results, the role of axonal tension during brain development is still under debate. While a few recent computational models have considered the mechanical influence of white matter anisotropy, these models have fallen short of modeling axon fibers' various orientations at different positions. Here, we present a 2D bi-layered finite element model of the developing brain incorporating the mechanical stimuli of typical subcortical axon tract connections via connector elements. We simplify the complex fiber architecture to first study the role of a single axon tract, later expanding to investigate three fiber bundles of differing axonal density. We have demonstrated the potential for axonal tension to serve as a symmetry-breaking perturbation in cortical folding that could help determine the location of cortical folds. In direct comparisons with thickness perturbations, both were shown to determine the placement of folds while the wavelength of the system remained unchanged. When in competition, however, fairly low levels of axon tension (80 N m−1, representing around 1.8 × 105 axons) were found to be more influential than thickness perturbations of 5%, which have been used in previous studies. While our simulations are significantly simplified representations of axon connectivity, we did explore the effect of multiple competing axon tracts, finding that even a slight difference in the density of axonal connections is enough to significantly change the folding pattern. This study is highly relevant to fundamental questions regarding brain structure and function. In normal cortical development, recent neuroimaging studies point out the consistent spatial placement of gyral peaks in macaque brains and the gyral hinges in human brains.76,77 It has also been found that subcortical axonal connections are one of the possible factors controlling the locations of cortical landmarks.78 Furthermore, abnormal white matter connectivity has been identified in various neurological disorders79,80 and is often found to be associated with abnormal folding. While the mechanics of altered neural connectivity are still unclear, our model and future work in the area may help understand axon tension's role during brain development.Data availability
The code to run the described simulations, along with select results, are available at the online repository https://github.com/mholla/axon_tension.Conflicts of interest
There are no conflicts of interest.Acknowledgements
MAH and XW acknowledge support from the National Science Foundation (NSF) under grant CMMI 2144412.References
- W. Welker, in Why Does Cerebral Cortex Fissure and Fold? Cerebral Cortex, ed. E. G. Jones, A. R. Peters, E. G. Jones and A. Peters, Springer US, Boston, MA, 1990, Vol. 8B, pp. 3–136 DOI:10.1007/978-1-4615-3824-0_1.
- N. Demirci, F. Jafarabadi, X. Wang, S. Wang and A. M. Holland, Consistency and variation in the placement of cortical folds: a perspective, Brain Multiphysics, 2023, 5, 100080, DOI:10.1016/j.brain.2023.100080.
- S. Rana, R. Shishegar, S. Quezada, L. Johnston, D. W. Walker and M. Tolcos, The subplate: a potential driver of cortical folding?, Cereb. Cortex, 2019, 29(11), 4697–4708, DOI:10.1093/cercor/bhz003.
- I. Smart and G. McSherry, Gyrus formation in the cerebral cortex in the ferret. I. Description of the external changes, J. Anat., 1986, 146, 141 CAS.
- W. E. L. G. Clark, Deformation patterns in the cerebral cortex, Printed at the Oxford University Press by John Johnson, 1945 Search PubMed.
- P. Bayly, L. Taber and C. Kroenke, Mechanical forces in cerebral cortical folding: a review of measurements and models, J. Mech. Behav. Biomed. Mater., 2014, 29, 568–581, DOI:10.1016/j.jmbbm.2013.02.018.
- K. Garcia, C. Kroenke and P. Bayly, Mechanics of cortical folding: stress, growth and stability, Philos. Trans. R. Soc., B, 2018, 373(1759), 20170321, DOI:10.1098/rstb.2017.0321.
- D. H. Barron, An experimental analysis of some factors involved in the development of the fissure pattern of the cerebral cortex, J. Exp. Zool., 1950, 113(3), 553–581, DOI:10.1002/jez.1401130304.
- D. P. Richman, R. M. Stewart, J. Hutchinson and V. S. Caviness Jr, Mechanical Model of Brain Convolutional Development: Pathologic and experimental data suggest a model based on differential growth within the cerebral cortex, Science, 1975, 189(4196), 18–21, DOI:10.1126/science.1135626.
- R. Raghavan, W. Lawton, S. Ranjan and R. Viswanathan, A continuum mechanics-based model for cortical growth, J. Theor. Biol., 1997, 187(2), 285–296, DOI:10.1006/jtbi.1997.0450.
- P. Bayly, R. Okamoto, G. Xu, Y. Shi and L. Taber, A cortical folding model incorporating stress-dependent growth explains gyral wavelengths and stress patterns in the developing brain, Phys. Biol., 2013, 10(1), 016005, DOI:10.1088/1478-3975/10/1/016005.
- T. Tallinen, J. Y. Chung, J. S. Biggins and L. Mahadevan, Gyrification from constrained cortical expansion, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(35), 12667–12672, DOI:10.1073/pnas.1406015111.
- D. Van Essen, A tension-based theory of morphogenesis and compact wiring in the central nervous system, Nature, 1997, 385(6614), 313–318, DOI:10.1038/385313a0.
- T. Dennerll, H. Joshi, V. Steel, R. Buxbaum and S. Heidemann, Tension and compression in the cytoskeleton of PC-12 neurites. II: Quantitative measurements, J. Cell Biol., 1988, 107(2), 665–674, DOI:10.1083/jcb.107.2.665.
- M. A. Holland, K. E. Miller and E. Kuhl, Emerging brain morphologies from axonal elongation, Ann. Biomed. Eng., 2015, 43(7), 1640–1653, DOI:10.1007/s10439-015-1312-9.
- D. Bray, Mechanical tension produced by nerve cells in tissue culture, J. Cell Sci., 1979, 37(1), 391–410, DOI:10.1007/s12195-012-0223-1.
- S. Wilson, D. Christiaens, H. Yun, A. Uus, L. Cordero-Grande, V. Karolis, A. Price, M. Deprez, J. D. Tournier and M. Rutherford, et al. Dynamic changes in subplate and cortical plate microstructure precede the onset of cortical folding in vivo. bioRxiv, 2023, 2023–10 DOI:10.1101/2023.10.16.562524.
- G. Xu, P. V. Bayly and L. A. Taber, Residual stress in the adult mouse brain, Biomech. Model. Mechanobiol., 2009, 8(4), 253–262, DOI:10.1007/s10237-008-0131-4.
- G. Xu, A. K. Knutsen, K. Dikranian, C. D. Kroenke, P. V. Bayly and L. A. Taber, Axons pull on the brain, but tension does not drive cortical folding, J. Biomech. Eng., 2010, 132(7), 071013, DOI:10.1115/1.4001683.
- S. Herculano-Houzel, B. Mota, P. Wong and J. H. Kaas, Connectivity-driven white matter scaling and folding in primate cerebral cortex, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(44), 19008–19013, DOI:10.1073/pnas.1012590107.
- B. Mota and S. Herculano-Houzel, How the cortex gets its folds: an inside-out, connectivity-driven model for the scaling of mammalian cortical folding, Front. Neuroanat., 2012, 6(3), 00003, DOI:10.3389/fnana.2012.
- D. C. Van Essen, A 2020 view of tension-based cortical morphogenesis, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(52), 32868–32879, DOI:10.1073/pnas.2016830117.
- D. C. Van Essen, Biomechanical models and mechanisms of cellular morphogenesis and cerebral cortical expansion and folding, Semin. Cell Dev. Biol., 2022, 140, 90–104, DOI:10.1016/j.semcdb.2022.06.007.
- S. E. Dos Santos, M. Medeiros, J. Porfirio, W. Tavares, L. Pessôa, L. Grinberg, R. E. Leite, R. E. Ferretti-Rebustini, C. K. Suemoto and W. Jacob Filho, et al., Similar microglial cell densities across brain structures and mammalian species: implications for brain tissue function, J. Neurosci., 2020, 40(24), 4622–4643, DOI:10.1523/JNEUROSCI.2339-19.2020.
- Y. Cao and J. W. Hutchinson, From wrinkles to creases in elastomers: the instability and imperfection-sensitivity of wrinkling, Proc. R. Soc. A, 2012, 468(2137), 94–115, DOI:10.1098/rspa.2011.0384.
- B. Li, Y. P. Cao, X. Q. Feng and H. Gao, Mechanics of morphological instabilities and surface wrinkling in soft materials: a review, Soft Matter, 2012, 8(21), 5728–5745, 10.1039/C2SM00011C.
- E. Kuhl, Growing matter: a review of growth in living systems, J. Mech. Behav. Biomed. Mater., 2014, 29, 529–543, DOI:10.1016/j.jmbbm.2013.10.009.
- Y. Yang, C. Fu and F. Xu, A finite strain model predicts oblique wrinkles in stretched anisotropic films, Int. J. Eng. Sci., 2020, 155, 103354, DOI:10.1016/j.ijengsci.2020.103354.
- A. D. Bakiler and A. Javili, Understanding the role of interfacial mechanics on the wrinkling behavior of compressible bilayer structures under large plane deformations, Math. Mech. Solids, 2023, 28(3), 748–772, DOI:10.1177/10812865221094833.
- W. Z. Huang, B. Li and X. Q. Feng, Mechanobiological tissue instability induced by stress-modulated growth, Soft Matter, 2023,(4), 708–722, 10.1039/D2SM01195F.
- J. Y. Sun, S. Xia, M. W. Moon, K. H. Oh and K. S. Kim, Folding wrinkles of a thin stiff layer on a soft substrate, Proc. R. Soc. A, 2012, 468(2140), 932–953, DOI:10.1098/rspa.2011.0567.
- T. Zhang, M. J. Razavi, X. Li, H. Chen, T. Liu and X. Wang, Mechanism of consistent gyrus formation: an experimental and computational study, Sci. Rep., 2016, 6(1), 37272, DOI:10.1038/srep37272.
- S. Budday, P. Steinmann, A. Goriely and E. Kuhl, Size and curvature regulate pattern selection in the mammalian brain, Extreme Mech. Lett., 2015, 4, 193–198, DOI:10.1016/j.eml.2015.07.004.
- M. Holland, S. Budday, A. Goriely and E. Kuhl, Symmetry breaking in wrinkling patterns: Gyri are universally thicker than sulci, Phys. Rev. Lett., 2018, 121(22), 228002, DOI:10.1103/PhysRevLett.121.228002.
- M. Darayi, M. E. Hoffman, J. Sayut, S. Wang, N. Demirci, J. Consolini and M. A. Holland, Computational models of cortical folding: a review of common approaches, J. Biomech., 2022, 139, 110851, DOI:10.1016/j.jbiomech.2021.110851.
- F. Jafarabadi, S. Wang and M. A. Holland, A Numerical Study on the Influence of Cerebrospinal Fluid Pressure on Brain Folding, J. Appl. Mech., 2023, 90(7), 071006, DOI:10.1115/1.4057020.
- R. Balouchzadeh, P. V. Bayly and K. E. Garcia, Effects of stress-dependent growth on evolution of sulcal direction and curvature in models of cortical folding, Brain Multiphys., 2023, 4, 100065, DOI:10.1016/j.brain.2023.100065.
- P. Chavoshnejad, L. Chen, X. Yu, J. Hou, N. Filla, D. Zhu, T. Liu, G. Li, M. J. Razavi and X. Wang, An integrated finite element method and machine learning algorithm for brain morphology prediction, Cereb. Cortex, 2023, bhad208, DOI:10.1093/cercor/bhad208.
- J. Weickenmeier, Exploring the multiphysics of the brain during development, aging, and in neurological diseases, Brain Multiphysics, 2023, 4, 100068, DOI:10.1016/j.brain.2023.100068.
- S. Wang, N. Demirci and M. A. Holland, Numerical investigation of biomechanically coupled growth in cortical folding, Biomech. Model. Mechanobiol., 2021, 20(2), 555–567, DOI:10.1007/s10237-020-01400-w.
- S. Wang, K. Saito, H. Kawasaki and M. A. Holland, Orchestrated neuronal migration and cortical folding: a computational and experimental study, PLoS Comput. Biol., 2022, 18(6), e1010190, DOI:10.1371/journal.pcbi.1010190.
- A. Goriely, M. G. Geers, G. A. Holzapfel, J. Jayamohan, A. Jérusalem, S. Sivaloganathan, W. Squier, J. A. Dommelen, S. van, Waters and E. Kuhl, Mechanics of the brain: perspectives, challenges, and opportunities, Biomech. Model. Mechanobiol., 2015, 14(5), 931–965, DOI:10.1007/s10237-015-0662-4.
- Y. Feng, R. J. Okamoto, R. Namani, G. M. Genin and P. V. Bayly, Measurements of mechanical anisotropy in brain tissue and implications for transversely isotropic material models of white matter, J. Mech. Behav. Biomed. Mater., 2013, 23, 117–132, DOI:10.1016/j.jmbbm.2013.04.007.
- C. Walter, R. Balouchzadeh, K. E. Garcia, C. D. Kroenke, A. Pathak and P. V. Bayly, Multi-scale measurement of stiffness in the developing ferret brain, Sci. Rep., 2023, 13(1), 20583, DOI:10.1038/s41598-023-47900-4.
- T. C. Gasser, R. W. Ogden and G. A. Holzapfel, Hyperelastic modelling of arterial layers with distributed collagen fibre orientations, J. R. Soc., Interface, 2006, 3(6), 15–35, DOI:10.1098/rsif.2005.0073.
- N. Nguyen, N. Nath, L. Deseri, E. Tzeng, S. S. Velankar and L. Pocivavsek, Wrinkling instabilities for biologically relevant fiber-reinforced composite materials with a case study of neo-Hookean/Ogden–Gasser–Holzapfel bilayer, Biomech. Model. Mechanobiol., 2020, 19, 2375–2395, DOI:10.1007/s10237-020-01345-0.
- A. Mirandola, A. Cutolo, A. Carotenuto, N. Nguyen, L. Pocivavsek, M. Fraldi and L. Deseri, Toward new scaling laws for wrinkling in biologically relevant fiber-reinforced bilayers, J. Appl. Phys., 2023, 134(15), 154702, DOI:10.1063/5.0161150.
- P. Chavoshnejad, X. Li, S. Zhang, W. Dai, L. Vasung, T. Liu, T. Zhang, X. Wang and M. J. Razavi, Role of axonal fibers in the cortical folding patterns: A tale of variability and regularity, Brain Multiphys., 2021, 2, 100029, DOI:10.1016/j.brain.2021.100029.
- P. Chavoshnejad, L. Vallejo, S. Zhang, Y. Guo, W. Dai, T. Zhang and M. J. Razavi, Mechanical hierarchy in the formation and modulation of cortical folding patterns, Sci. Rep., 2023, 13(1), 13177, DOI:10.1038/s41598-023-40086-9.
- K. E. Garcia, X. Wang and C. D. Kroenke, A model of tension-induced fiber growth predicts white matter organization during brain folding, Nat. Commun., 2021, 12(1), 1–13, DOI:10.1038/s41467-021-26971-9.
- E. K. Rodriguez, A. Hoger and A. D. McCulloch, Stress-dependent finite growth in soft elastic tissues, J. Biomech., 1994, 27(4), 455–467, DOI:10.1016/0021-9290(94)90021-3.
- A. Schüz and V. Braitenberg, The human cortical white matter: quantitative aspects of cortico-cortical long-range connectivity, Cortical areas: Unity and diversity, 2002, 377–385 Search PubMed.
- M. Yoshino, K. Saito, K. Kawasaki, T. Horiike, Y. Shinmyo and H. Kawasaki, The origin and development of subcortical U-fibers in gyrencephalic ferrets, Mol. Brain, 2020, 13(1), 1–9, DOI:10.1186/s13041-020-00575-8.
- M. Yoshino, Y. Shiraishi, K. Saito, N. Kameya, T. Hamabe-Horiike, Y. Shinmyo, M. Nakada, N. Ozaki and H. Kawasaki, Distinct subdivisions of subcortical U-fiber regions in the gyrencephalic ferret brain, Neurosci. Res. Lett., 2023, 200, 1–7, DOI:10.1016/j.neures.2023.10.004.
- M. Catani, F. Dell’Acqua, F. Vergani, F. Malik, H. Hodge, P. Roy, R. Valabregue and M. T. De Schotten, Short frontal lobe connections of the human brain, Cortex, 2012, 48(2), 273–291, DOI:10.1016/j.cortex.2011.12.001.
- E. Kirilina, S. Helbling, M. Morawski, K. Pine, K. Reimann, S. Jankuhn, J. Dinse, A. Deistung, J. R. Reichenbach and R. Trampel, et al., Superficial white matter imaging: Contrast mechanisms and whole-brain in vivo mapping, Sci. Adv., 2020, 6(41), eaaz9281, DOI:10.1126/sciadv.aaz9281.
- M. Smith, ABAQUS/Standard User's Manual, Version 6.9, 2009 Search PubMed.
- K. Riley, D. O’Neill and S. Kralik, Subcortical U-fibers: signposts to the diagnosis of white matter disease, Neurographics, 2018, 8(4), 234–243, DOI:10.3174/ng.1700048.
- K. Oishi, H. Huang, T. Yoshioka, S. H. Ying, D. S. Zee, K. Zilles, K. Amunts, R. Woods, A. W. Toga and G. B. Pike, et al., Superficially located white matter structures commonly seen in the human and the macaque brain with diffusion tensor imaging, Brain Connectivity, 2011, 1(1), 37–47, DOI:10.1089/brain.2011.0005.
- M. Diab, T. Zhang, R. Zhao, H. Gao and K. S. Kim, Ruga mechanics of creasing: from instantaneous to setback creases, Proc. R. Soc. A, 2013, 469(2157), 20120753, DOI:10.1098/rspa.2012.0753.
- R. Zhao, T. Zhang, M. Diab, H. Gao and K. S. Kim, The primary bilayer ruga-phase diagram I: Localizations in ruga evolution, Extreme Mech. Lett., 2015, 4, 76–82, DOI:10.1016/j.eml.2015.04.006.
- A. Auguste, J. Yang, L. Jin, D. Chen, Z. Suo and R. C. Hayward, Formation of high aspect ratio wrinkles and ridges on elastic bilayers with small thickness contrast, Soft Matter, 2018, 14(42), 8545–8551, 10.1039/C8SM01345D.
- H. Jin, A. K. Landauer and K. S. Kim, Ruga mechanics of soft-orifice closure under external pressure, Proc. R. Soc. A, 2021, 477(2249), 20210238, DOI:10.1098/rspa.2021.0238.
- D. Liewald, R. Miller, N. Logothetis, H. J. Wagner and A. Schüz, Distribution of axon diameters in cortical white matter: an electron-microscopic study on three human brains and a macaque, Biol. Cybernetics, 2014, 108, 541–557, DOI:10.1007/s00422-014-0626-2.
- R. Bernal, P. A. Pullarkat and F. Melo, Mechanical properties of axons, Phys. Rev. Lett., 2007, 99(1), 018301, DOI:10.1103/PhysRevLett.99.018301.
- M. Holland, B. Li, X. Feng and E. Kuhl, Instabilities of soft films on compliant substrates, J. Mech. Phys. Solids, 2017, 98, 350–365, DOI:10.1016/j.jmps.2016.09.012.
- C. C. Hilgetag and H. Barbas, Role of mechanical factors in the morphology of the primate cerebral cortex, PLoS Comput. Biol., 2006, 2(3), e22, DOI:10.1371/journal.pcbi.0020022.
- D. Shastin, S. Genc, G. D. Parker, K. Koller, C. M. Tax, J. Evans, K. Hamandi, W. P. Gray, D. K. Jones and M. Chamberland, Surface-based tracking for short association fibre tractography, NeuroImage, 2022, 260, 119423, DOI:10.1016/j.neuroimage.2022.119423.
- E. Bullmore and O. Sporns, The economy of brain network organization, Nat. Rev. Neurosci., 2012, 13(5), 336–349, DOI:10.1038/nrn3214.
- L. M. Wang and E. Kuhl, Mechanics of axon growth and damage: a systematic review of computational models, Semin. Cell Dev. Biol., 2022, 140, 13–21, DOI:10.1016/j.semcdb.2022.04.019.
- H. Oliveri and A. Goriely, Mathematical models of neuronal growth, Biomech. Model. Mechanobiol., 2022, 21(1), 89–118, DOI:10.1007/s10237-021-01539-0.
- M. Darayi and M. A. Holland, Surface pressure reduces stability in bilayered systems under compression, Int. J. Non Linear Mech., 2020, 127, 103589, DOI:10.1016/j.ijnonlinmec.2020.103589.
- Y. Assaf and O. Pasternak, Diffusion tensor imaging (DTI)-based white matter mapping in brain research: a review, J. Mol. Neurosci., 2008, 34(1), 51–61, DOI:10.1007/s12031-007-0029-0.
- C. Zhang and S. Ji, Sex differences in axonal dynamic responses under realistic tension using finite element models, J. Neurotrauma, 2023, 40, 2217–2232, DOI:10.1089/neu.2022.0512.
- S. Saeidi, M. P. Kainz, M. Dalbosco, M. Terzano and G. A. Holzapfel, Histology-informed multiscale modeling of human brain white matter, Sci. Rep., 2023, 13(1), 19641, DOI:10.1038/s41598-023-46600-3.
- T. Zhang, H. Chen, M. J. Razavi, Y. Li, F. Ge, L. Guo, X. Wang and T. Liu, Exploring 3-hinge gyral folding patterns among HCP Q3 868 human subjects, Human Brain mapping, 2018, 39(10), 4134–4149, DOI:10.1002/hbm.24237.
- S. Zhang, P. Chavoshnejad, X. Li, L. Guo, X. Jiang, J. Han, L. Wang, G. Li, X. Wang and T. Liu, et al., Gyral peaks: novel gyral landmarks in developing macaque brains, Human Brain Mapping, 2022, 43(15), 4540–4555, DOI:10.1002/hbm.25971.
- M. J. Razavi, T. Liu and X. Wang, Mechanism exploration of 3-hinge gyral formation and pattern recognition, Cerebral Cortex Commun., 2021, 2(3), tgab044, DOI:10.1093/texcom/tgab044.
- S. H. Ameis and M. Catani, Altered white matter connectivity as a neural substrate for social impairment in Autism Spectrum Disorder, Cortex, 2015, 62, 158–181, DOI:10.1016/j.cortex.2014.10.014.
- Y. Jiang, D. Yao, J. Zhou, Y. Tan, H. Huang, M. Wang, X. Chang, M. Duan and C. Luo, Characteristics of disrupted topological organization in white matter functional connectome in schizophrenia, Psychol. Med., 2022, 52(7), 1333–1343, DOI:10.1017/S0033291720003141.
| This journal is © The Royal Society of Chemistry 2024 |