Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Responsive CO2 capture: predictive multi-objective optimisation for managing intermittent flue gas and renewable energy supply†
Oliver J.
Fisher
 a,
Lei
Xing
a,
Lei
Xing
 *a,
Xingjian
Tian
b,
Xin Yee
Tai
a and
Jin
Xuan
*a,
Xingjian
Tian
b,
Xin Yee
Tai
a and
Jin
Xuan
 *a
*a
aSchool of Chemistry and Chemical Engineering, Faculty of Engineering and Physical Sciences, University of Surrey, UK. E-mail: l.xing@surrey.ac.uk; j.xuan@surrey.ac.uk
bSchool of Chemistry and Chemical Engineering, Jiangsu University, Zhenjiang 212013, China
First published on 22nd December 2023
Abstract
The drive for efficiency improvements in CO2 capture technologies continues to grow, with increasing importance given to the need for flexible operation to adapt to the strong fluctuations in the CO2-rich flue gas flow rate and CO2 concentration. Using renewable energy can improve the environmental benefit of CO2 capture technologies; however, renewable energy resources often suffer from the challenge of non-uniform power generation as a result of weather and seasonal variations. In this work, we aimed to dynamically self-optimise the CO2 capture process in a renewable energy system via enhanced weathering of calcite with fresh water in a packed bubble column (PBC) reactor, in which CO2 from flue gas produced by a power plant is converted into bicarbonate and stored in the ocean. Data-driven surrogate dynamic models of the PBC reactor are developed to predict the reactor CO2 capture rate (CR) and power consumption (PC) and are trained using the data generated by physics-based models. Two deep learning models are considered to capture the dynamics of the PBC reactor: a long short-term memory network (LSTM); and a two-stage multilayer perceptron network (MLP). Data-driven models based on LSTM were developed to predict wind energy (R2: 0.908) and inlet flue gas CO2 concentration (R2: 0.981) using publicly available datasets. A multi-objective NSGA-II genetic algorithm is then applied that utilised the inlet flue gas CO2 concentration and wind energy predictions to pre-emptively self-optimise the reactor process conditions (i.e., superficial liquid flow rate and superficial gas flow rate) to maximise the carbon capture rate and minimise non-renewable energy consumption. The results should that by using the dynamic modelling and predictive multi-objective optimisation framework proposed within this study, the PCB reactor CR increased by an average of 16.7% over a one-month operation, whilst simultaneously reducing the proportion of now-renewable energy consumed from an average of 92.9% to an average of 56.6%. Overall, this study demonstrates the effectiveness of a dynamic data-driven modelling and multi-objective optimisation approach to increase the operational flexibility of CO2 capture reactors to adapt to strong fluctuations in flue gas and intermittent renewable energy supply.
1. Introduction
The rapid process of industrialisation and shifting lifestyles, accompanied by a rising pattern of energy consumption, has led to a significant surge in the demand for power. Carbon dioxide emissions from power plants account for approximately 35% of global greenhouse emissions,1 responsible for over 34 billion tonnes of CO2 emissions per year.2 Although renewable energy generation has been rapidly growing, the sheer scale of current power sector emissions highlights the urgent need for nations to address their power-related emissions in order to align with global climate objectives. Carbon capture and storage (CCS) is viewed as a key technology in the transition to net zero, which involves capturing and storing carbon emissions from industrial and power generation processes. While multiple industrial-scale CCS projects are operational, capturing and storing over a million tons of CO2 annually, the high energy costs associated with the solvent-based CO2 scrubbing methods utilised in these systems hinder their broad deployment.3 Despite the high energy cost, CCS recognised internationally as a key technology for mitigating climate change and achieving net zero. The UK has set out the approach to delivering four CCS low carbon industrial clusters capturing 20–30 MtCO2 per year by 2030 (ref. 4) and in 2023 announced £20 billion investment program for carbon capture projects.5 The U.S. Department of Energy (DOE) announced up to $1.2 billion to advance the development of two commercial-scale direct air capture facilities in Texas and Louisiana.6 In November 2022, the European Commission adopted a proposal (COM/2022/672) for an EU-wide voluntary framework to certify carbon removals, with the aim to boost innovative industrial carbon removal technologies, such as bioenergy with carbon capture and storage (BECCS) or direct air carbon capture and storage (DACCS).7 In the pursuit of a sustainable future, the collective efforts to harness CCS technology underscore its pivotal role in achieving net-zero emissions.Emerging CCS technologies demonstrate significant improvements in efficiency and energy cost over the current solvent base methods. The technologies under development include: membrane separation processes; adsorbent based systems; advanced amine; aqueous ammonia scrubbing; and cryogenic separation.8 Of these technologies, adsorbent based methods offer have the potential to function as more efficient and cost effective alternatives to solvent CCS processes for selectively removing CO2 from large, stationary sources including power stations.9 An adsorbent is typically a porous substance with a significant surface area that can attract and retain other substances on its surface through intermolecular forces. Enhanced weathering (EW) is a CCS adsorbent process that uses crushed alkaline minerals is capable of accelerating the natural weathering process, which is known to convert Gt of atmospheric CO2 per year into bicarbonate stored in the ocean.10 Incorporating alkaline minerals into chemical reactors operating under controllable conditions provides a means to harness this inherent natural process with increased efficiency in carbon capture rates, milder reaction conditions and less impact on the environment than the other CCS technologies.11 Alongside enhanced weathering (EW), other promising methods have emerged, such as direct air capture (DAC),12 bioenergy with CO2 capture and storage (BECCS),13 afforestation and reforestation (AR),14 photochemical CO2 conversion,15 electrochemical reduction.16 Recently added to this list are innovative methods like CO2 capture using water- and amine-based nanofluids17 and metal–organic frameworks (MOFs).18 Among these, EW is particularly notable for its use of crushed alkaline minerals and chemical contactors to significantly accelerate the natural weathering process. Typically, this process converts atmospheric and concentrated CO2 into bicarbonate, stored in the ocean, at a impressive capacity of gigatonnes of CO2 annually, without the involvement of environmentally harmful chemical solutions and harsh operating conditions.11,19–21 Additionally, these chemical reactors can be integrated with DAC systems, transforming concentrated CO2 into bicarbonate for storage in the ocean, thereby optimising the EW process. The compromise of using EW for CCS is the cost and space required for building the infrastructure, as well as the energy and water consumption during operation.21 Modelling has proved an effective tool for the design and optimisation of EW reactors.11,19–21 By developing experimentally validated physics-based mechanistic models then using these models to generate data to train machine learning surrogate models, it enables multi-variable optimisation to maximise their CO2 capture rate, while simultaneously minimising water and energy consumption. Machine learning surrogate models are used as an efficient way to perform multi-variable and multi-objective optimisation, that significantly reduces computational time and resources while maintaining high prediction accuracy.
Previous studies modelling EW reactors have focused on the steady-state operation of the chemical reactors.11,19–21 Although several parameters, e.g., packing materials size, packed bed height and porosity, reactant and products concentration and CO2 capture rate, have been dynamically studied, the operating conditions, e.g., gas and liquid velocity, CO2 inlet concentrations etc., were fixed as constants. While these studies provide insights into the reactor's performance in steady-state operating conditions, they do not fully address the dynamic changes that occur when the concentration and flow rate of the incoming CO2 stream fluctuate over time, which is a common occurrence in real-world flue gas scenarios. Whereas dynamic machine learning models excel in handling time-dependent data and evolving patterns and can learn from historical process data and adapt to real-time changes, enabling them to predict how the reactor's behaviour will evolve over time. Power plants are increasingly requiring flexible operation to balance the intermittent electricity supply from renewable energy resources and ensure consistent energy supply to the grid.22,23 As CCS is integrated with power plants, it is vital that the technology does not compromise their ability to respond to flexible power output. Therefore, CCS systems require the development of dynamic machine learning models that can dynamically adjust their predictions and control strategies in response to these demands, enhancing the reactor's stability and robustness. Furthermore, these models should address the economic and environmental challenges of CCS technologies, aiming to establish its feasibility as a viable choice for power producers. Of particular significance is the need to mitigate energy consumption, a well-recognised barrier associated with CCS technology.3 Employing renewable energy has the potential to enhance the environmental advantages of CO2 capture technologies, yet renewable energy resources frequently suffer from the challenge of non-uniform power generation as a result of weather and seasonal variations. Considering these challenges, the development of dynamic control methodologies becomes imperative.
As computational resources have advanced and control algorithms refined, model predictive control (MPC) has gained popularity in various industries, including petrochemical, biotechnical, electrical and mechanical processes.24 By utilising dynamic models, MPC enables the control system to account for time-varying conditions and respond to changes, ensuring the efficient operation of processes like CO2 capture within integrated power plants. Model predictive control offers advantages over traditional control methods due to its predictive nature, constraint handling, and optimisation capabilities.25 Previous studies have shown that the implementation of the MPC formulation proves to be a very good option to enable the flexible operation of integrated power generation capture plants.26–30 One study showed that the MPC control strategy can quickly adapt to any disturbance applied to the capture plant, which is essential for the profitable operation of decarbonised power plants.30 Furthermore, MPC have been demonstrated to perform significantly better in terms of close-loop settling time, integral squared error and compliance of operational and environmental constraints when compared to conventional control strategies.26 Previous studies have developed dynamic models of CCS systems built using physics-based models hosted on process simulation software.26–30 Dynamic systems can be extremely complex with intricate interactions and feedback loops. Machine learning can capture these complexities without requiring explicit formulation of differential equations, making it suitable for scenarios where deriving analytical models is challenging. The integration of machine learning has empowered MPC with more accurate models of chemical systems, enabling it to excel in nonlinear and dynamic systems.31 Furthermore, machine learning models can adapt to changes in the system behaviour as new data becomes available. The disadvantage of using machine learning include: a lack of interpretability; failure to generalise beyond the training data; and the availability and quality of data. Hybrid approaches, such as by developing machine learning surrogate models from existing physics base models, can leverage the strengths of both methods. Machine learning also offers the potential to extend the capabilities of MPC to include forecasting external system variable to improve the control performance. External system variables, such as renewable energy supply, upstream processes, and other external factors, can have a direct impact on the behaviour of the system being controlled. By integrating forecasts of these variables into the MPC framework, the controller can make more informed and proactive decisions.
Using machine learning dynamic models within MPC introduces uncertainties due to various factors such as model errors, noisy measurements, and changes in the underlying system dynamics.32 Measuring uncertainty is a crucial to chemical engineering, yet when using machine learning to model chemical system, the models often predict just a single point value (e.g., the predicted CO2 capture rate). The standard procedure is to evaluate the models' ability to make new predictions using unseen test data and providing error scores for the models' overall ability to fit the unseen data. However, this does not provide a specific estimation of the uncertainty associated to that point prediction. Prediction intervals, on the other hand, provide a range of plausible values for the predictions, thereby incorporating uncertainty estimation. Conformal prediction is a well-established framework that offers a principled approach for generating prediction intervals with provable validity guarantees.33 The use of conformal prediction within reaction chemistry and engineering modelling field is limited. However, by estimating the uncertainty, conformal prediction offers engineers valuable insights into the reliability of the model's output, enabling engineers to make informed choices based on the level of uncertainty associated with each prediction. This knowledge can help to make machine learning models more interoperable, a key challenge to their widespread use within chemical engineering.34
In this study, a MPC framework is proposed aimed at optimising the rate of CO2 capture and the energy consumption in an EW reactor designed to capture CO2 emissions from the flue gas of a coal power plant. Two methods to dynamically model the system are evaluated against a steady model of the system. To enhance the framework's capabilities, a technique for integrating forecasts of external system variables into the multi-objective optimisation algorithm is developed. Moreover, the framework's functionality is extended by employing conformal prediction to assess the uncertainty associated with the outputs of the dynamic models. This also includes utilising conformal prediction to evaluate the uncertainty linked to the solutions obtained through multi-objective optimisation. Notably, to the best of the authors knowledge, this application of conformal prediction to multi-objective optimisation solutions has not been previously documented. While the framework was developed and demonstrated within the context of an EW reactor, its applicability extends to other CCS technologies and the wider reaction chemistry and engineering applications. The overarching aim is to enable flexible and efficient operation, thereby contributing to the practical implementation of CCS in pursuit of net-zero emissions targets.
2. Methods and materials
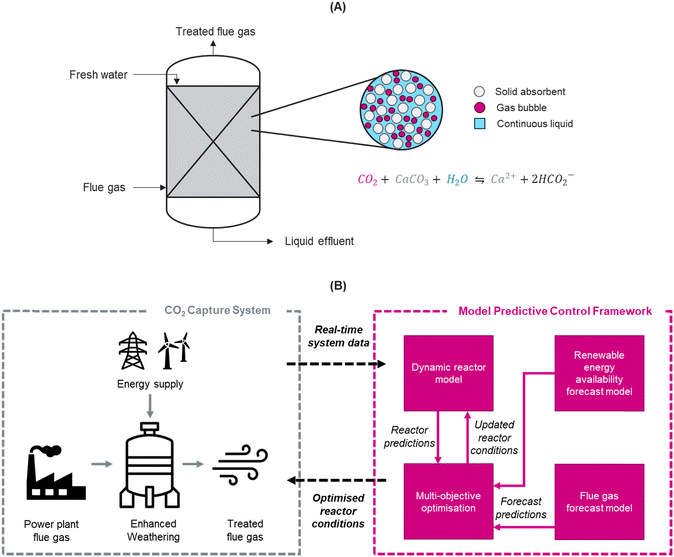
2.1 The enhanced weathering CO2 capture reactor and system
The power plant flue gas is directed into the EW packed bubble column (PBC) reactor, shown in Fig. 1(A), where efficient removal of CO2 takes place before the treated flue gas is either released to the atmosphere or subjected to additional treatment. To ensure a sustainable power supply, the reactor's electricity demand is primarily met by renewable wind energy, with grid electricity serving as a backup during periods of intermittent wind availability. However, the variable CO2 concentration in the flue gas and the intermittent nature of renewable power sources introduce challenges that compromise the CO2 capture rate and environmental benefits associated with enhanced weathering reactors. Fig. 1(B) illustrates the schematic representation of model predictive control framework developed for the CO2 capture system investigated in this study.In response to these challenges, a multi-objective predictive optimisation framework was developed aimed at proactively optimising the reactor conditions, specifically the superficial gas and liquid flow rates. This optimisation strategy aims to concurrently maximise the CO2 capture rate and minimise non-renewable energy consumption. To achieve this, the framework utilises a multi-target dynamic reactor model that predicts CO2 capture rate and the power consumption of the reactor using real-time input data encompassing the incoming flue gas CO2 concentration and reactor operating conditions. These predictions then feed into a multi-objective optimisation genetic algorithm that finds the optimal reactor conditions (superficial gas and liquid flow rates) to simultaneously maximise CO2 capture rate and minimise non-renewable energy consumption in response to the system variables, i.e., availability of renewable energy and flue gas concentration. To further enhance the framework's utility, its capabilities were extended from adaptive optimisation based on real-time data to predictive optimisation. This extension involves the development of time-series models capable of forecasting the system variables and utilise these predictions to pre-emptively optimise the reactor conditions.
2.2 Reactor-scale dynamic multi-physics simulation
The detailed mechanistic models of a packed bubble column (PBC)-based enhanced weathering system for CO2 removal have been developed previously.11,19,20 The accuracy of these models was confirmed through experimental validation, focusing on the calcite dissolution rate11,13 and dynamic CO2 removal efficiency.14 These validations were conducted using both fresh water and seawater, thereby demonstrating the robustness and reliability of the developed models. To avoid redundancy, only the key governing equations and descriptions are provided.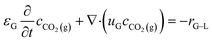 | (1) |
Similarly, a time-dependent expression for aqueous species i in the packed bed is given as
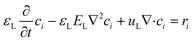 | (2) |
The Dirichlet boundary and Danckwerts' boundary conditions35 are adopted for eqn (1) and (2), respectively, leading to the following expression:
at![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gas gas![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) inlet, x = 0, cCO2(g) = cCO2(g),inlet inlet, x = 0, cCO2(g) = cCO2(g),inlet | (3) |
at![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) liquid liquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) inlet: x = Hbed, uLci,inlet = uLci − DL,i ∇ci inlet: x = Hbed, uLci,inlet = uLci − DL,i ∇ci | (4) |
at![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) liquid liquid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) outlet: x = 0, ∇ci = 0 outlet: x = 0, ∇ci = 0 | (5) |
at![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gas gas![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) outlet, x = Hbed, ∇cCO2(g) = 0 outlet, x = Hbed, ∇cCO2(g) = 0 | (6) |
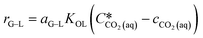 | (7) |
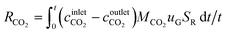 | (8) |
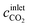 and
and 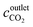 (mol m−3) are the CO2 concentration at the inlet and outlet, respectively. t (h) is the required time to dissolve a required mass of calcite, which is also the period of computational process.
(mol m−3) are the CO2 concentration at the inlet and outlet, respectively. t (h) is the required time to dissolve a required mass of calcite, which is also the period of computational process.
This requires mechanical energy, consisting of gas flowing and water pumping over a time period t, and is expressed as
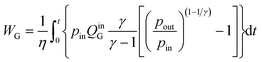 | (9) |
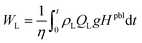 | (10) |
The total energy consumption for maintaining gas and liquid flows is thus
| Etotal = WG + WL | (11) |
2.3 Dynamic data-driven surrogate models
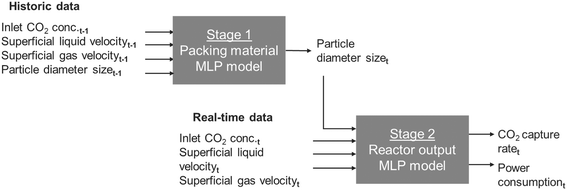
In multi-objective optimisation, conducting a substantial number of simulation runs can be prohibitively expensive and time-consuming due to the high computational cost involved.11 To address this challenge, data-driven surrogate models were developed as an alternative approach. These surrogate models offer a computationally efficient means of predicting reactor performance compared to the complex mechanistic simulation model presented in section 2.2. By leveraging these surrogate models, the optimisation process becomes more streamlined, enabling effective exploration of multiple variables while reducing computational burden and saving valuable time. Two deep learning models were developed to capture the dynamics of the EW reactor: a two-stage multilayer perceptron network (2-stage MLP); and a long short-term memory network (LSTM).A MLP is a type of artificial neural network that consists of multiple layers of interconnected neurons.42 It is a feedforward neural network, meaning that information flows only in one direction, from the input layer through hidden layers to the output layer. In contrast to conventional industrial packed bed reactors, mineral particles dissolve during the CO2 capture process, leading to changes in packing structure and interfacial areas over the course of the operation.11 Direct measurement of the packing material's size during operation is unfeasible. Therefore, to capture this dynamic a two-stage MLP model was proposed, as outlined in Fig. 2. The first stage is a model that predicts the deterioration to packing material caused by the previous timestamp. The second stage then predicts CO2 capture rate and the power consumption of the reactor using the incoming flue gas CO2 concentration, reactor operating conditions and packing material size predicted in stage 1.
An alternative to the two-stage approach, is a long short-term memory network (LSTM), which is a type of recurrent neural network that excels in capturing and processing sequential data, such as time series.43 The architecture of an LSTM network consists of a series of interconnected memory cells, which are organised into a recurrent structure. Each memory cell is equipped with three essential components: an input gate, a forget gate, and an output gate. These gates regulate the flow of information into, out of, and within the memory cell. The key innovation of LSTM lies in its ability to selectively remember or forget information over extended sequences, enabling it to capture both short-term and long-term dependencies within the data. Given the LSTM's capability to capture temporal information, the inclusion of specific details regarding the packing material, as implemented in the two-stage approach, becomes redundant as this data is inherently assimilated and encoded within the LSTM's temporal understanding. The performance of the dynamic models was evaluated in comparison to a steady-state MLP model. The MLP model solely relied on the incoming CO2 concentration and reactor conditions to predict the CO2 capture rate and power consumption. Unlike the dynamic models, the MLP model did not consider any information about the reactor dynamics.
The 2-stage MLP and LSTM models were developed using a dataset of 1001 datapoints, which simulated a 42-day operation of the EW PCB reactors with data recorded every 30 minutes. Synthetic data representing the CO2 concentration in flue gas from coal-fired power plants was created using the method and data provided in.44 The optimum Latin hypercube sampling method (OLHS)45 was used to generate random sample points for the reactor operating conditions within the standard operating range outlined in.11 The dynamic mechanistic simulation model was used to determine the CO2 capture rate, reactor power consumption, and particle size deterioration in these conditions.
The data set with 1001 samples was divided into 70% as training data, and the remaining 30% as testing data. The testing data was formed with the last 150 recorded hours, never seen by the models during the training and validation. The training data was normalised the by scaling them ranging from 0 to 1 through the minimum–maximum scaler procedure. The normalised weights were then used to normalise the testing data. The training data is then further partitioned into multiple training and validation data sets using cross validation, which splits the data into multiple folds of training and validation dataset. Each of the folds is given an opportunity to be used as a held back validation set whilst all other folds collectively are used as a training dataset. The purpose of cross-validation is to reduce the risk of overfitting the data during the hyperparameter optimisation. A hyperparameter is an adjustable algorithm parameter that must be either manually or automatically tuned in order to obtain a model with optimal performance. The withheld testing data was then used to evaluate the final models to provide an unbiased evaluation of the models' predictive capabilities.
2.4 Time-series forecasting models
In this study, two Bi-LSTM models were developed to forecast short-term CO2 concentration in flue gas from a coal plant and the availability of power from a micro wind turbine (with a capacity below 100 W) specifically designed to power the carbon capture reactor. Recently, Bi-LSTM (bi-directional long short-term memory), an extension of LSTM model with an additional backward training step has gained a lot of interest in the prediction of sequential data.46–49 By incorporating a bidirectional structure, each cell of LSTM enables to learn the data from both past and future directions. For instance, Tai et al. adopted Bi-LSTM to understand the intermittency of renewable energy, ultimately optimising the energy management in the electrochemical CO2 reduction reaction.49 The synthetic coal fire plant emission data created in section 2.3 was used to train the flue gas CO2 concentration forecast model and historical wind turbine data sourced from ref. 49 was used to train the wind power availability forecast model.2.5 Model evaluation and uncertainty quantification
The assessment of predictive capabilities among different models was subjected to statistical evaluation using three key metrics: the coefficient of determination (R2), the normalised root of mean squared error (nRMSE), and the mean absolute percentage error (MAPE). R2, which represents the squared value of the sample correlation coefficient between observed and predicted values, serves as an indicator of the extent to which the model can account for the variance in the data.50 On the other hand, nRMSE quantifies the normalised magnitude of the mean square error,51 while MAPE measures the absolute percentage of the errors.52 The ideal model from a statistical perspective is characterised by an R2 value approaching one, simultaneously minimising nRMSE and MAPE.Inductive conformal prediction was employed to determine precise levels of confidence in new predictions. The training data was further randomly partitioned into 90% training data and 10% calibration data. The models were then trained using the new training data as outlined in section 2.3. The predicted values from the calibration data set were then predicted using the trained models. The nonconformity measurers (α-values) for all the calibration examples were then generated. Nonconformity measurers how different a new example is from old examples and can be generated as the absolute difference between the actual value and the predicted value for the calibration set.33 Next the α-values are sorted in ascending order to generate nonconformity scores, which provides understand of the distribution of uncertainty across a set of predictions. The prediction interval can be defined based on the distribution of nonconformity scores from the calibration set. For example, you can select a threshold or quantile level (e.g., 95% quantile) to form the prediction interval around the predicted value for the test data point. The prediction interval is constructed based on the distribution derived from these nonconformity scores originating from the calibration set. By selecting a predetermined threshold or quantile level (for instance, the 95% quantile), a prediction interval can be established around the predicted value for the test data point.
2.6 Multi-objective optimisation
A multi-objective optimisation formulation strategy was designed to use the non-dominated sorting genetic algorithm (NSGA-II) to find the best solution for two objectives. The first objective is to maximise the CO2 capture rate and the second is to minimise the non-renewable energy resources. The estimation of the CO2 capture rate was conducted through the utilisation of data-driven surrogate models, denoted as G1, which were described in section 2.3. The objective constrained to ensure that the capture rate remains above zero in order to guarantee that the reactor is consistently configured to seize a portion of the CO2 emissions emitted by the coal-fired power plant. The NSGA-II is committed to minimising all objectives; therefore, the first objective was computed as follows:| min f1 = −g1(y1, x1, x2) | (12) |
The reactor's electricity demand is primarily met by renewable wind energy, with non-renewable grid electricity serving as a backup during periods of intermittent wind availability. The power consumption of the reactor, as evaluated by data-driven surrogate models denoted as G2, was optimised in order to minimise the reliance on non-renewable energy sources. The goal of the reactors is to maximise the capture of CO2 emissions while minimising the utilisation of non-renewable energy sources. To achieve this, a constraint was imposed to ensure that the proportion of non-renewable energy supply remains greater than or equal to zero, thereby ensuring the optimal utilisation of available renewable energy for CO2 capture.
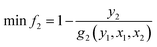 | (13) |
Overall, the multi-objective optimisation problem can be presented as below:
| min(F) = min {f1, f2} | (14) |
| f1 ≥ 0, f2 ≥ 0 | (15) |
| 0.0001 ≤ x1 ≤ 0.01, 0.0001 ≤ x2 ≤ 0.01 | (16) |
3. Results and discussion
3.1 Necessity of dynamic models
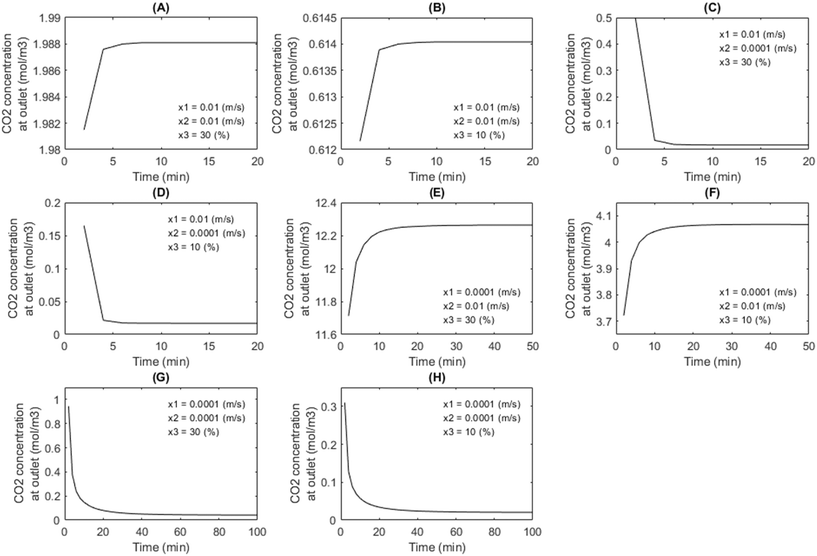
When altering the set point of reactor conditions, e.g., changing incoming flue gas CO2 concentration and velocity, the packed bubble column reactor requires time to stabilise and reach equilibrium. If the reactor conditions again shift before equilibrium is attained, relying solely on steady-state models would result in inaccurate performance predictions. This is because steady-state models assume that the system remains in a stable, equilibrium state. If the reactor frequently experiences transient behaviour and does not return to equilibrium, steady-state models may not accurately capture the system's dynamics.To investigate how long the reactor returns to equilibrium, eight different scenarios were investigated by altering permutations of the maximum and minimum values of superficial liquid velocity, superficial gas velocity, and CO2 inlet concentration. As shown in Fig. 3, in most scenarios, the required time to reach equilibrium is less than 30 minutes. However, in case G and H, when both the superficial velocities of liquid and gas are 1 × 10−4 ms−1, the time significantly increases to approximately one hour, indicating the great impact of superficial liquid velocity on the reaction equilibrium. Within this study, the reactor conditions and/or flue gas condition fluctuate every 30 minutes. When the reactor is operating under superficial velocities of liquid and gas close to 1 × 10−4 ms−1, it is experiencing transient behaviour and does not return to equilibrium before the next change. In these situations, a steady-state model may not accurately capture the system's dynamics and a dynamic modelling approach would be more appropriate method for capturing these transient responses.
3.2 Evaluation of the data-driven surrogate models
Two deep learning models were developed to capture the dynamics of the PBC reactor: a two-stage multilayer perceptron network (2-stage MLP); and a long short-term memory network (LSTM). The models' predictions were compared against the “actual” values obtained through directly solving the dynamic mechanistic simulation model. The standard correlation coefficient (R2), normalised root-mean-square deviation (nRMSE) and mean average percentage error were investigated to evaluate the predictive accuracy of the data driven surrogate models and the results are presented in Table 1.| Model | Data | CO2 capture rate | Power consumption | ||||
|---|---|---|---|---|---|---|---|
| R 2 | nRMSE | MAPE | R 2 | nRMSE | MAPE | ||
| Steady state MLP | Training | 0.98 | 0.02 | 10.71 | 0.96 | 0.04 | 6.51 |
| Testing | 0.96 | 0.04 | 20.42 | 0.90 | 0.07 | 10.05 | |
| 2-Stage MLP | Training | 0.99 | 0.02 | 7.16 | 1.00 | 0.01 | 2.45 |
| Testing | 0.99 | 0.03 | 9.87 | 0.98 | 0.03 | 7.22 | |
| LSTM | Training | 0.99 | 0.01 | 7.97 | 0.98 | 0.02 | 5.00 |
| Testing | 0.99 | 0.03 | 21.74 | 0.92 | 0.06 | 9.73 | |
The importance of incorporating system dynamics in models is evident in the superior generalisation ability exhibited by the dynamic models as compared to the steady-state models. From the results in Table 1, it can be inferred that both dynamic models we able to accurately able to predict CO2 capture rate, achieving higher R2 (>0.99), low nRMSE (<0.03) in contrast to the steady state model (R2: 0.96 and rRMSE 0.04). Notably, the MAPE of the 2-stage MLP model signifies an average percentage deviation of 7.16% between the predicted and actual values, which is significantly lower compared to the steady-state model (20.42) and LSTM model (21.74). This reduction in MAPE emphasises the accuracy of the 2-stage MLP model in predicting the CO2 capture rate, thus highlighting the model's competence in capturing the EW-reactor dynamics. The LSTM models shows a higher MAPE during testing (21.74), suggesting that the model may have had more difficulty capturing the target output accurately compared to 2-stage MLP model.
The results in Table 1 show that all models accuracy decreased when predicting the reactors power consumption when compared to predicting CO2 capture rate. This was particularly true for the steady state MLP and LSTM models that have a larger difference in their training and testing statistically error metrics, indicating their decreased ability to generalise to unseen data. However, the benefit of including dynamic information was again demonstrated by the superior performance of the 2-stage MLP model, which achieved a high R2 (0.98) and low nRMSE (0.03) and MAPE (7.22) of the 2-stage MLP model when evaluated on unseen testing data. When contrasted with prior research involving the construction of steady-state models for forecasting power consumption in EW reactors (with R2 values of 0.89 (ref. 11) and 0.96 (ref. 19)), the dynamic models formulated in this investigation attained superior precision, recording an R2 value of 0.98. These results are in agreement previous work that has demonstrated the benefit of capturing knowledge of the reactor dynamics when modelling chemical reactors.54 To the best of the authors knowledge, this work is the first to proposes a method to capture the deterioration of packing material size in a dynamic machine learning model. The benefit of this approach is demonstrated by the observed disparity in performance between the LSTM and 2-stage MLP models, which could be attributed to the LSTM model's inherent complexity, which renders it more susceptible to challenges during the training process, particularly in terms of overfitting.55
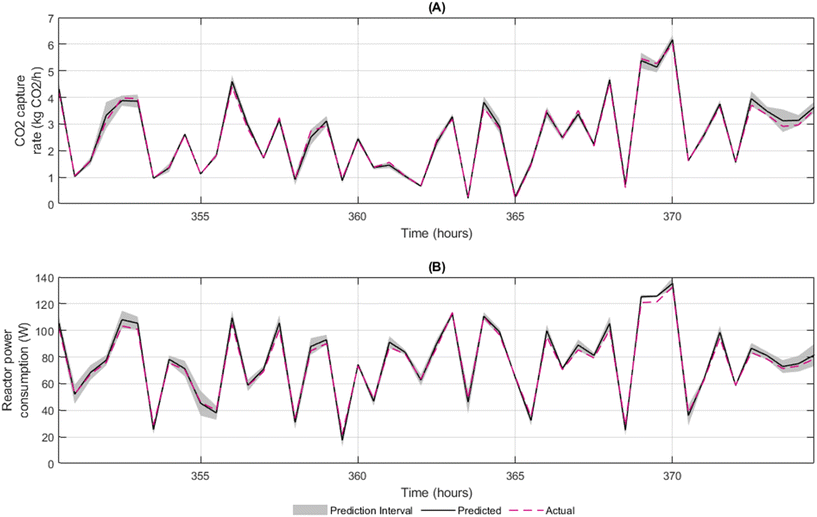
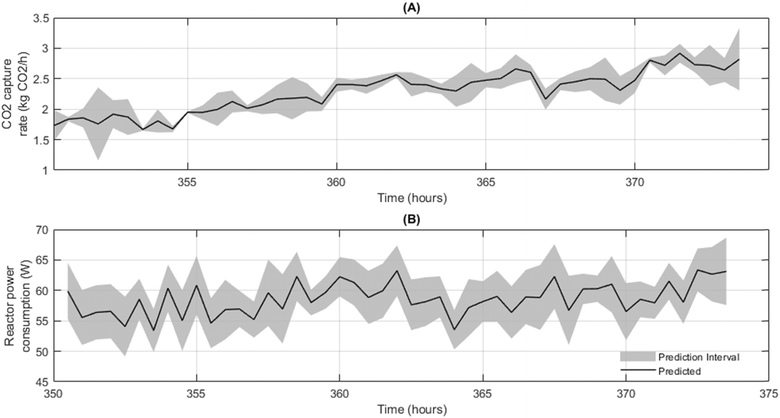
Fig. 4 presents the results of using conformal prediction applied to the 2-stage MLP models, to assess the predictive uncertainty associated with their predictions over a 24-hour operation of the reactors using unseen data. Additional results for using the models to make predictions for alternative 24-operation of reactor operation are presented in the ESI† (Fig. S1–S4). The alpha value chosen for this analysis was 0.05, corresponding to a 95% confidence level. By examining the resulting prediction intervals, insights into the models' performance and reliability were made. For the CO2 capture model predictions (Fig. 4A), the conformal prediction algorithm generated prediction intervals that exhibited a narrow range. Furthermore, the actual values are consistently within the prediction intervals for this time period. This indicates that during these periods, the model's uncertainty estimates align closely with the true variability of the data, enhancing the credibility of the model's predictive capabilities. This consistency reinforces the model's capacity to capture and quantify uncertainty, thus providing decision-makers with a reliable tool for assessing the potential outcomes of the CCS technology's CO2 capture rate predictions. There are instances where actual power consumption values deviate from the prediction intervals (e.g. 368.5–370 hours) suggest a level of unpredictability not observed in the CO2 capture rate predictions. These disparities may stem from the intricate interplay of factors influencing power consumption, such as varying operational conditions, energy demands, and fluctuations in equipment efficiency.21 Unlike the CO2 rate, which might be influenced by more stable chemical processes, power consumption can be influenced by a wider array of dynamic and complex variables.
3.3 Evaluation of time-series models
The performance of the LSTM models in forecasting short-term CO2 concentration in flue gas from the coal plant and wind energy from a micro turbine was statistically evaluated using unseen testing data and the results are presented in Table 2. This is to assess the accuracy and performance of the models in predicting CO2 concentration and power availability. Both the testing and training results showed good agreement in Table 1, indicating the models' ability to generalise well to unseen data.| Model | Data | R 2 | nRMSE | MAPE |
|---|---|---|---|---|
| CO2 | Training | 0.99 | 0.02 | 1.93 |
| Testing | 0.97 | 0.04 | 2.54 | |
| Wind energy | Training | 0.89 | 0.05 | 16.41 |
| Testing | 0.83 | 0.07 | 18.89 |
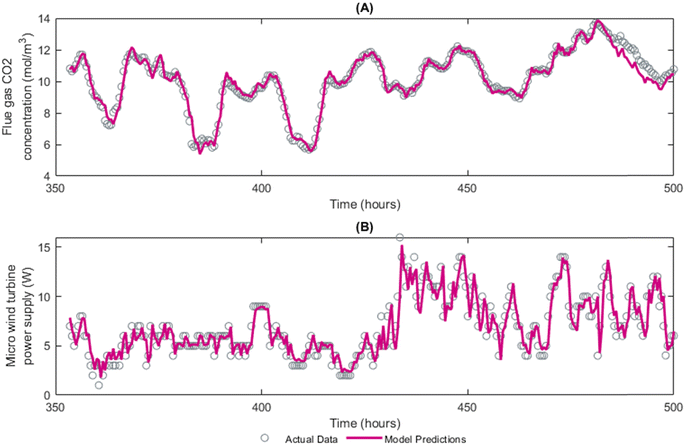
For the flue gas CO2 LSTM model, the testing results revealed a R2 value of 0.97, indicating a strong correlation between the predicted and actual CO2 concentration values. The nRMSE was 0.04, reflecting a small deviation between the predicted and actual values and the MAPE of 2.54 suggests that, on average, the model predictions deviated by 2.54% from the actual CO2 concentrations. Similarly, the wind turbine energy LSTM model demonstrated satisfactory performance. The R2 value of 0.83 indicated a reasonably good fit between the predicted and actual wind energy values. The nRMSE of 0.07 suggests a moderate level of accuracy, while the MAPE of 18.89 indicates an average percentage deviation of 18.89% between the predicted and actual wind energy values. These results are consistent with other studies that have used LSTM modelling techniques to forecast wind power from turbines.55,56 Wind power forecasting is a difficult task due to the influence of many factors, including weather, wind speed and temporal variability.56
When integrating the LSTM models into a multi-objective optimisation framework aimed at maximising the CO2 capture rate and minimising non-renewable power consumption, the observed model errors have important implications. The flue gas CO2 LSTM model strong performance enables precise estimation of the CO2 capture rate, contributing to effective decision-making for maximising the capture of CO2 emissions from the coal plant. However, the wind energy LSTM model exhibited relatively higher error rates compared to the flue gas CO2 LSTM model. This discrepancy suggests that the wind energy predictions may be less reliable, introducing uncertainties when incorporating them into the optimisation framework. The higher errors in wind energy forecasting could lead to suboptimal decisions regarding the utilisation of non-renewable power sources.
Fig. 5 presents a visual comparison of the actual data and the model predictions for the testing dataset. The plot showcases good agreement between the two, with the model predictions (shown as a solid line) closely tracking the actual CO2 concentration and wind turbine power output (represented by the scattered data points). This alignment reinforces the reliability of the LSTM models in capturing the complex behaviours of the two time series, validating their potential applicability in real-world scenarios. However, Fig. 5(A) does highlight that the LSTM model consistently overestimates the CO2 concentration for the last 20 hours of the recorded data. One possible explanation for the consistently higher CO2 concentration predictions in the final 20 hours could be a shift in the underlying dynamics of the system. This suggested that the patterns and behaviours governing the CO2 concentration may have changed during this period, rendering the trained LSTM models less effective in capturing these new dynamics. Factors such as variations in plant operation, atmospheric conditions, or other external influences could contribute to this shift. To address this issue and improve the accuracy of the predictions, retraining of the LSTM models may be necessary. If this solution was to be deployed in an industrial setting the use of online learning would be recommended to ensure the model is continuously updated and adapted as new data becomes available in a streaming or online fashion.57
3.4 Predictive multi-objective optimisation of enhanced weathering system
A multi-objective optimisation genetic algorithm was then developed with the twin goals to find the optimal reactor conditions to maximise the CO2 capture rate and minimise the proportion of non-renewable energy consumed by the EW-reactor. The ability of the predictive optimisation framework was evaluated using the unseen testing data, representing 150 hours operation of the reactor. Once the predicted optimal values of the studied reactor conditions are obtained, they are validated by the simulated results of physics-based simulation models. The simulated values are the results obtained by solving the mechanistic simulation model using the predicted optimal values. The results from validating the predicted optimal results using the simulated values is reported in Table 3. The predicted CO2 capture rate and power consumption good agreement with the simulated values, demonstrating the effective and reliable prediction of the model predictive control framework developed in this study.| Output | R 2 | nRMSE | MAPE |
|---|---|---|---|
| CO2 capture rate | 0.95 | 0.05 | 13.27 |
| Power consumption | 0.93 | 0.04 | 14.01 |
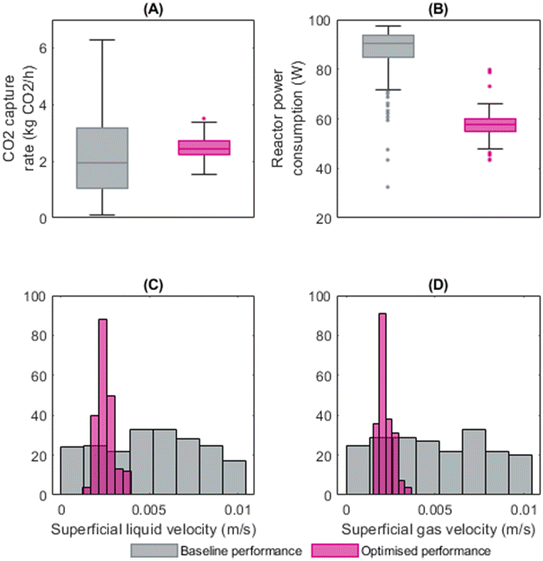
The results presented in Fig. 6(A) indicates that the multi-objective optimisation led to an average increase in the CO2 capture rate of the reactor by 16.7% compared to the baseline. Furthermore, the method also reduced the variability associated with CO2 capture rate, resulting in a more consistent and stable operation of the reactors, as shown by narrow interquartile range in the box plot in Fig. 6(A). The increased capture rate signifies a more efficient utilisation of resources and a reduction in the release of CO2 into the atmosphere. Prior to the implementation of the predictive optimisation framework, Fig. 6(B) shows the reactors were consuming an average of 92.9% non-renewable energy. However, with the application of the framework, this proportion decreased significantly, reaching an average of 56.6%. The results highlight the potential of using predictive optimisation techniques to improve the performance and sustainability of industrial processes. By leveraging predictive models and optimisation algorithms, it becomes possible to identify optimal operating conditions that maximise desirable outcomes such as CO2 capture while simultaneously minimising the consumption of non-renewable energy.
The superficial liquid and gas velocities of the EW reactor operate between 0.0001 and 0.01 m s−1. Past investigations have employed genetic algorithms to ascertain optimal operational conditions for EW reactors configured to either maximise CO2 capture rates or minimise power consumption, utilising a CO2 inlet concentration of 20%.11 This present study extends the scope of the prior research by determining optimal operational conditions that simultaneously maximise the CO2 capture rate and minimise proportion of non-renewable power consumption, encompassing a range CO2 inlet concentration (5.67–13.71%) throughout a 150-hour testing operation. As depicted in Fig. 6(C), the optimal superficial liquid velocity during this period is observed to range between 0.0015 and 0.0040 m s−1, with a median velocity of 0.0024 m s−1. Notably, this optimal range is closer to the previously established optimum superficial liquid velocity deduced for minimising power consumption (0.00106 m s−1), rather than maximising CO2 capture rates (0.01 m s−1).11 This observation suggests that the influence of liquid velocity on reactor power consumption outweighs its impact on CO2 capture rates. Fig. 6(D) reveals that the optimised superficial gas velocity lies between 0.0015 and 0.036 m s−1, with a median velocity of 0.0021 m s−1. This range surpasses the optimal superficial gas velocities identified in the earlier study for optimising both CO2 capture rates (0.001 m s−1) and power consumption (0.0007 m s−1). This deviation might be attributed to this study exploration of lower CO2 inlet concentrations (5.67–13.71%) compared to the previous study's concentration of 20%.
The MOO framework's ability to dynamically adjust reactor operating conditions to attain optimal outcomes introduces an additional layer of complexity, where the uncertainty of individual model predictions interacts to shape the overall outcome uncertainty. The framework proposed in this study, integrates the uncertainty calculated using conformal prediction for each distinct model to establish prediction intervals for the optimal CO2 capture rate and power consumption determined by the MOO algorithm, as depicted in Fig. 7. The prediction intervals associated with the MOO framework tend to exhibit greater variability compared to those of individual component models, such as the CO2 capture rate and power consumption dynamic models (Fig. 4, section 3.2). This increased interval width reflects the intricate interplay of various predictions within the MOO framework. Similarly, the reactor power consumption prediction intervals larger which can be explained as it includes the wind energy forecasting model within the MOO framework, which had a lower accuracy (R2: 0.82) when compared to other models. The application of conformal prediction to this framework provides a robust mechanism for quantifying the uncertainty associated with the MOO's decisions, enabling more informed and well-grounded choices in the pursuit of optimising both CO2 capture rates and power consumption within a dynamically evolving system.
4. Conclusion
Carbon capture and storage (CCS) technologies play a pivotal role in mitigating the environmental impact of power plants and facilitating the transition to a net-zero emission future. Nevertheless, the formidable energy costs associated with CCS technologies and the demand for flexible operational strategies present barriers to their widespread adoption. This study aimed to address these challenges by developing an integrated framework that harnesses recent advancements in machine learning and model predictive control. The work focused on increasing the CO2 capture rate of an innovative CCS adsorbent technology known as enhanced weathering (EW), while concurrently reducing its reliance on non-renewable power sources.Dynamic models of the EW reactor treating flue gas emitted from a coal power plant were developed to predict CO2 capture rate and power consumption during a 500-hour operation. A two-stage multilayer perceptron network dynamic modelling method was proposed. The model exhibited remarkable predictive accuracy for both desired outcomes, attaining R2 values of 0.99 and 0.98 for CO2 capture rate and power consumption, respectively. This performance surpassed that of traditional long short-term memory (LSTM) modelling techniques, which yielded R2 values of 0.99 and 0.92 for CO2 capture rate and power consumption, respectively. The dynamic models were used within a model predictive control framework that utilises the ensured the efficient operation CO2 capture system. Additional, machine learning models were developed to extend the capabilities of MPC framework to include forecasting external system variable to improve the control performance. Forecasting models based on LSTM were developed to predict wind energy (R2: 0.908) and inlet flue gas CO2 concentration (R2: 0.981) using publicly available datasets. A multi-objective NSGA-II genetic algorithm is then applied that utilised the inlet flue gas CO2 concentration and wind energy predictions to pre-emptively self-optimise the reactor process conditions (i.e., superficial liquid flow rate and superficial gas flow rate) to maximise the carbon capture rate and minimise non-renewable energy consumption. The dynamic modelling and MPC framework, as proposed in this study, culminated in a substantial average increase of 16.7% in the CO2 capture rate within a month-long operation of the EW reactor. Simultaneously, the framework reduced the average non-renewable energy consumption from 92.9% to 56.6%.
Overall, this study has demonstrated the effectiveness of the proposed model predictive control framework. By integrating real-time data, dynamic prediction models, and a multi-objective optimisation genetic algorithm, the framework successfully optimises reactor conditions to maximise CO2 capture rate while minimising non-renewable energy consumption. The incorporation of forecasting methodologies enables proactive optimisation, providing valuable insights into future conditions. The research contributes to the efficient control of CO2 capture systems and offers significant environmental benefits.
Conflicts of interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.Acknowledgements
The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: this work was supported by the Engineering and Physical Sciences Research Council (EPSRC) under grant number EP/W018969/1.References
- United Nations, Facts and Figures, 2023, https://www.un.org/en/actnow/facts-and-figures#:~:text=Theenergysupplysector(electricity,overhalfofallelectricity, (accessed August 20, 2023) Search PubMed.
- World Nuclear Association, Carbon Dioxide Emissions From Electricity, 2022, https://www.world-nuclear.org/information-library/energy-and-the-environment/carbon-dioxide-emissions-from-electricity.aspx#:~:text=Just20%25offinalenergy,tonnes(Gt)peryear, (accessed August 20, 2023) Search PubMed.
- D. M. D'Alessandro, B. Smit and J. R. Long, Carbon dioxide capture: Prospects for new materials, Angew. Chem., Int. Ed., 2010, 49, 6058–6082, DOI:10.1002/anie.201000431.
- Department for Energy Security and Net Zero, CCUS Net Zero Investment Roadmap, London, UK, 2023 Search PubMed.
- HM Teasury, Spring Budget 2023, London, UK, 2023 Search PubMed.
- The White House, Investing In America, 2023, https://www.whitehouse.gov/invest/?utm_source=invest.gov, (accessed August 22, 2023) Search PubMed.
- European Commission, Directorate-General for Climate Action, Proposal for a Regulation of the European Parliament and of the Council establishing a Union certification framework for carbon removals, Brussels, 2022 Search PubMed.
- B. L. Salvi and S. Jindal, Recent developments and challenges ahead in carbon capture and sequestration technologies, SN Appl. Sci., 2019, 1, 885, DOI:10.1007/s42452-019-0909-2.
- X. Gao, S. Yang, L. Hu, S. Cai, L. Wu and S. Kawi, Carbonaceous materials as adsorbents for CO2 capture: synthesis and modification, Carbon Capture Sci. Technol., 2022, 3, 100039, DOI:10.1016/j.ccst.2022.100039.
- J. Hartmann, A. J. West, P. Renforth, P. Köhler, C. L. De La Rocha, D. A. Wolf-Gladrow, H. H. Dürr and J. Scheffran, Enhanced chemical weathering as a geoengineering strategy to reduce atmospheric carbon dioxide, supply nutrients, and mitigate ocean acidification, Rev. Geophys., 2013, 51, 113–149, DOI:10.1002/rog.20004.
- L. Xing, H. Jiang, S. Wang, V. J. Pinfield and J. Xuan, Data-driven surrogate modelling and multi-variable optimization of trickle bed and packed bubble column reactors for CO2 capture via enhanced weathering, Chem. Eng. J., 2023, 454, 139997, DOI:10.1016/j.cej.2022.139997.
- J. K. Stolaroff, D. W. Keith and G. V. Lowry, Carbon dioxide capture from atmospheric air using sodium hydroxide spray, Environ. Sci. Technol., 2008, 42, 2728–2735, DOI:10.1021/es702607w.
- J. Strefler, N. Bauer, F. Humpenöder, D. Klein, A. Popp and E. Kriegler, Carbon dioxide removal technologies are not born equal, Environ. Res. Lett., 2021, 16, 074021, DOI:10.1088/1748-9326/ac0a11.
- J. Sheng, X. Han and H. Zhou, Spatially varying patterns of afforestation/reforestation and socio-economic factors in China: a geographically weighted regression approach, J. Cleaner Prod., 2017, 153, 362–371, DOI:10.1016/j.jclepro.2016.06.055.
- S. Yin, K. Zhong, Q. Yu, Z. Wang, Q. Li, Z. Feng, H. Du, J. Yang, Y. Hua, X. Zhu and H. Xu, Boosting CO2 capture and its photochemical conversion on bismuth surface, Phys. Status Solidi A, 2021, 218, 2000671, DOI:10.1002/pssa.202000671.
- Z. Yang, D. Li, H. Xiang, S. Cheng, E. Yu and A. Yang, Modeling and upscaling analysis of gas diffusion electrode-based electrochemical carbon dioxide reduction systems, ACS Sustainable Chem. Eng., 2021, 9, 351–361, DOI:10.1021/acssuschemeng.0c07387.
- C. Yuan, Y. Wang, F. Baena-Moreno, R. Zhang, H. Zhou and Z. Zhang, Review and perspectives of CO2 absorption by water- and amine-based nanofluids, Energy Fuels, 2023, 37, 8883–8901, DOI:10.1021/acs.energyfuels.3c00874.
- T. R. Menezes, K. M. C. Santos, T. S. L. Silva, K. S. Santos, A. L. Ramos, G. R. Borges, E. Franceschi, C. Dariva, J. F. De Conto, S. M. Egues and C. C. Santana, Carbon dioxide and methane capture in metal-organic framework MIL-101(Cr) at high pressure, Gas Sci. Eng., 2023, 119, 205136, DOI:10.1016/j.jgsce.2023.205136.
- H. Jiang, S. Wang, L. Xing, V. J. Pinfield and J. Xuan, Machine learning based techno-economic process optimisation for CO2 capture via enhanced weathering, Energy AI, 2023, 12, 100234, DOI:10.1016/j.egyai.2023.100234.
- L. Xing, H. Pullin, L. Bullock, P. Renforth, R. C. Darton and A. Yang, Potential of enhanced weathering of calcite in packed bubble columns with seawater for carbon dioxide removal, Chem. Eng. J., 2022, 431, 134096, DOI:10.1016/j.cej.2021.134096.
- L. Xing, R. C. Darton and A. Yang, Enhanced weathering to capture atmospheric carbon dioxide: Modeling of a trickle-bed reactor, AIChE J., 2021, 67, e17202, DOI:10.1002/aic.17202.
- J. Rúa, M. Bui, L. O. Nord and N. Mac Dowell, Does CCS reduce power generation flexibility? A dynamic study of combined cycles with post-combustion CO2 capture, Int. J. Greenhouse Gas Control, 2020, 95, 102984, DOI:10.1016/j.ijggc.2020.102984.
- J. Asadi and P. Kazempoor, Techno-economic analysis of membrane-based processes for flexible CO2 capturing from power plants, Energy Convers. Manage., 2021, 246, 114633, DOI:10.1016/j.enconman.2021.114633.
- W. Chen, T. Zheng, M. Chen and X. Li, Improved nonlinear model predictive control based on genetic algorithm, in Advanced Model Predictive Control, ed. T. Zheng, IntechOpen, Rijeka, 2011, ch. 3, DOI:10.5772/18778.
- M. Schwenzer, M. Ay, T. Bergs and D. Abel, Review on model predictive control: an engineering perspective, Int. J. Adv. Manuf. Technol., 2021, 117, 1327–1349, DOI:10.1007/s00170-021-07682-3.
- M. Hossein Sahraei and L. A. Ricardez-Sandoval, Controllability and optimal scheduling of a CO2 capture plant using model predictive control, Int. J. Greenhouse Gas Control, 2014, 30, 58–71, DOI:10.1016/j.ijggc.2014.08.017.
- Z. He, M. H. Sahraei and L. A. Ricardez-Sandoval, Flexible operation and simultaneous scheduling and control of a CO2 capture plant using model predictive control, Int. J. Greenhouse Gas Control, 2016, 48, 300–311, DOI:10.1016/j.ijggc.2015.10.025.
- B. Decardi-Nelson, S. Liu and J. Liu, Improving flexibility and energy efficiency of post-combustion CO2 capture plants using economic model predictive control, Processes, 2018, 6, 135, DOI:10.3390/pr6090135.
- X. Wu, M. Wang, J. Shen, Y. Li, A. Lawal and K. Y. Lee, Flexible operation of coal fired power plant integrated with post combustion CO2 capture using model predictive control, Int. J. Greenhouse Gas Control, 2019, 82, 138–151, DOI:10.1016/j.ijggc.2018.12.004.
- E. D. Mehleri, N. Mac Dowell and N. F. Thornhill, Model Predictive Control of Post-Combustion CO2 Capture Process integrated with a power plant, in 12 International Symposium on Process Systems Engineering and 25 European Symposium on Computer Aided Process Engineering, ed. K. V Gernaey, J. K. Huusom and R. Gani, Elsevier, 2015, pp. 161–166, DOI:10.1016/B978-0-444-63578-5.50022-0.
- K. Zarzycki and M. Ławryńczuk, LSTM and GRU neural networks as models of dynamical processes used in predictive control: A comparison of models developed for two chemical reactors, Sensors, 2021, 21, 5625, DOI:10.3390/s21165625.
- R. Soloperto, M. A. Müller, S. Trimpe and F. Allgöwer, Learning-based robust model predictive control with state-dependent uncertainty, IFAC-Pap., 2018, 51, 442–447, DOI:10.1016/j.ifacol.2018.11.052.
- U. Norinder, L. Carlsson, S. Boyer and M. Eklund, Introducing conformal prediction in predictive modeling. A transparent and flexible alternative to applicability domain determination, J. Chem. Inf. Model., 2014, 54, 1596–1603, DOI:10.1021/ci5001168.
- M. R. Dobbelaere, P. P. Plehiers, R. Van de Vijver, C. V. Stevens and K. M. Van Geem, Machine learning in chemical engineering: Strengths, weaknesses, opportunities, and threats, Engineering, 2021, 7, 1201–1211, DOI:10.1016/j.eng.2021.03.019.
- P. V. Danckwerts, Continuous flow systems. Distribution of residence times, Chem. Eng. Sci., 1995, 50, 3857–3866, DOI:10.1016/0009-2509(96)81811-2.
- A. H. G. Cents, D. W. F. Brilman and G. F. Versteeg, CO2 absorption in carbonate/bicarbonate solutions: The Danckwerts-criterion revisited, Chem. Eng. Sci., 2005, 60, 5830–5835, DOI:10.1016/j.ces.2005.05.020.
- L. N. Plummer and E. Busenberg, The solubilities of calcite, aragonite and vaterite in CO2-H2O solutions between 0 and 90°C, and an evaluation of the aqueous model for the system CaCO3-CO2-H2O, Geochim. Cosmochim. Acta, 1982, 46, 1011–1040, DOI:10.1016/0016-7037(82)90056-4.
- J. G. G. Maldonado, D. Bastoul, S. Baig, M. Roustan and G. Hébrard, Effect of solid characteristics on hydrodynamic and mass transfer in a fixed bed reactor operating in co-current gas–liquid up flow, Chem. Eng. Process.: Process Intesif., 2008, 47, 1190–1200, DOI:10.1016/j.cep.2007.02.013.
- J. H. P. Collins, A. J. Sederman, L. F. Gladden, M. Afeworki, J. Douglas Kushnerick and H. Thomann, Characterising gas behaviour during gas–liquid co-current up-flow in packed beds using magnetic resonance imaging, Chem. Eng. Sci., 2017, 157, 2–14, DOI:10.1016/j.ces.2016.04.004.
- K. Akita and F. Yoshida, Gas holdup and volumetric mass transfer coefficient in bubble columns. Effects of liquid properties, Ind. Eng. Chem. Process Des. Dev., 1973, 12, 76–80, DOI:10.1021/i260045a015.
- P. V. Danckwerts, Significance of liquid-film coefficients in gas absorption, Ind. Eng. Chem., 1951, 43, 1460–1467, DOI:10.1021/ie50498a055.
- S. Kim, MATLAB Deep learning with machine learning, neural networks and artificial intelligence, Apress, 1st edn, 2017, DOI:10.1007/978-1-4842-2845-6.
- X. Yuan, L. Li, Y. Wang, C. Yang and W. Gui, Deep learning for quality prediction of nonlinear dynamic processes with variable attention-based long short-term memory network, Can. J. Chem. Eng., 2020, 98, 1377–1389, DOI:10.1002/cjce.23665.
- Y. Hu and Y. Shi, Estimating CO2 emissions from large scale coal-fired power plants using OCO-2 observations and emission inventories, Atmosphere, 2021, 12, 811, DOI:10.3390/atmos12070811.
- N. Pholdee and S. Bureerat, An efficient optimum Latin hypercube sampling technique based on sequencing optimisation using simulated annealing, Int. J. Syst. Sci., 2015, 46, 1780–1789, DOI:10.1080/00207721.2013.835003.
- F. R. Alharbi and D. Csala, Wind speed and solar irradiance prediction using a bidirectional long short-term memory model based on neural networks, Energies, 2021, 14, 6501, DOI:10.3390/en14206501.
- Q. Sun, M. V. Jankovic, L. Bally and S. G. Mougiakakou, Predicting blood glucose with an lstm and bi-lstm based deep neural network, in 2018 14th Symposium on Neural Networks and Applications (NEUREL), IEEE, 2018, pp. 1–5 Search PubMed.
- S. Siami-Namini, N. Tavakoli and A. S. Namin, The performance of LSTM and BiLSTM in forecasting time series, in 2019 IEEE International Conference on Big Data (Big Data), 2019, pp. 3285–3292, DOI:10.1109/BigData47090.2019.9005997.
- X. Y. Tai, L. Xing, Y. Zhang, Q. Fu, O. Fisher, S. D. R. Christie and J. Xuan, Dynamic optimisation of CO2 electrochemical reduction processes driven by intermittent renewable energy: Hybrid deep learning approach, Digital Chemical Engineering, 2023, 9, 100123, DOI:10.1016/j.dche.2023.100123.
- M. H. Abbas, R. Norman and A. Charles, Neural network modelling of high pressure CO 2 corrosion in pipeline steels, Process Saf. Environ. Prot., 2018, 119, 36–45, DOI:10.1016/j.psep.2018.07.006.
- M. Dalmau, N. Atanasova, S. Gabarrón, I. Rodriguez-Roda and J. Comas, Comparison of a deterministic and a data driven model to describe MBR fouling, Chem. Eng. J., 2015, 260, 300–308, DOI:10.1016/j.cej.2014.09.003.
- R. J. Hyndman and A. B. Koehler, Another look at measures of forecast accuracy, Int. J. Forecast., 2006, 22, 679–688, DOI:10.1016/j.ijforecast.2006.03.001.
- H. K. Singh and K. Deb, Investigating the equivalence between PBI and AASF scalarization for multi-objective optimization, Swarm Evol. Comput., 2020, 53, 100630, DOI:10.1016/j.swevo.2019.100630.
- P. Petsagkourakis, I. O. Sandoval, E. Bradford, D. Zhang and E. A. del Rio-Chanona, Reinforcement learning for batch bioprocess optimization, Comput. Chem. Eng., 2020, 133, 106649, DOI:10.1016/J.COMPCHEMENG.2019.106649.
- F. Shahid, A. Zameer and M. Muneeb, A novel genetic LSTM model for wind power forecast, Energy, 2021, 223, 120069, DOI:10.1016/j.energy.2021.120069.
- Z. Li, X. Luo, M. Liu, X. Cao, S. Du and H. Sun, Short-term prediction of the power of a new wind turbine based on IAO-LSTM, Energy Rep., 2022, 8, 9025–9037, DOI:10.1016/j.egyr.2022.07.030.
- M. Chandrasekaran, M. Muralidhar, C. M. Krishna and U. S. Dixit, Online machining optimization with continuous learning, in Computational Methods for Optimizing Manufacturing Technology: Models and Techniques, 2012, pp. 85–110 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3re00544e |
| This journal is © The Royal Society of Chemistry 2024 |