Diffusiophoresis of a spherical particle in porous media
Siddharth
Sambamoorthy
 and
Henry C. W.
Chu
and
Henry C. W.
Chu
 *
*
Department of Chemical Engineering, University of Florida, Gainesville, FL 32611, USA. E-mail: h.chu@ufl.edu
First published on 17th January 2023
Abstract
Recent experiments by Doan et al. (Nano Lett., 2021, 21, 7625–7630) demonstrated and measured colloid diffusiophoresis in porous media but existing theories cannot predict the observed colloid motion. Here, using regular perturbation method, we develop a mathematical model that can predict the diffusiophoretic motion of a charged colloidal particle driven by a binary monovalent electrolyte concentration gradient in a porous medium. The porous medium is modeled as a Brinkman medium with a constant Darcy permeability. The linearized Poisson–Boltzmann equation is employed to model the equilibrium electric potential distribution that is driven out-of-equilibrium under diffusiophoresis. We report three key findings. First, we demonstrate that colloid diffusiophoresis could be drastically hindered in a porous medium due to the additional hydrodynamic drag compared to diffusiophoresis in a free electrolyte solution. Second, we show that the variation of the diffusiophoretic motion with respect to a change in the electrolyte concentration in a porous medium could be qualitatively different from that in a free electrolyte solution. Third, our results match quantitatively with experimental measurements, highlighting the predictive power of the present model. The mathematical model developed here could be employed to design diffusiophoretic colloid transport in porous media, which are central to applications such as nanoparticle drug delivery and enhanced oil recovery.
1 Introduction
Diffusiophoresis is the deterministic motion of particles induced by a surrounding concentration gradient of solutes.1–4 Diffusiophoresis comprises an electrophoretic component due to the electric field induced by a disparity in the diffusivities of the ionic solutes, and a chemiphoretic component due to the osmotic pressure gradient associated with the solute concentration gradient. Motivated by manufacturing colloidal coatings for vehicles, Prieve et al.5,6 pioneered a theory to predict the diffusiophoretic motion of a colloidal particle in a concentration gradient of electrolytes, the so-called log-sensing relation U = M∇log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n, where the mobility M relates the particle diffusiophoretic velocity U and gradient of the natural logarithm of the solute concentration n. Since then, much work has been done to characterize the diffusiophoretic mobility of rigid particles in various solutes,7–12 the mobility of drops and soft particles,13–20 and the mobility in confined environments.21–23 In addition to develop fundamental theories for diffusiophoresis, progress has been made in devising new applications using diffusiophoresis, ranging from mixing and separation of colloids,9,24–40 enhanced oil recovery,41–43 drug delivery,44,45 to water and surface cleaning.46–48 The strengths of diffusiophoresis are prominent in two aspects. First, diffusiophoresis can generate a significant colloid motion on the microscale. For instance, the diffusivity of a typical ionic solute D ∼ M ∼ 10−9 m s−2 and the length of the solute gradient L ∼ n/∇n ∼
n, where the mobility M relates the particle diffusiophoretic velocity U and gradient of the natural logarithm of the solute concentration n. Since then, much work has been done to characterize the diffusiophoretic mobility of rigid particles in various solutes,7–12 the mobility of drops and soft particles,13–20 and the mobility in confined environments.21–23 In addition to develop fundamental theories for diffusiophoresis, progress has been made in devising new applications using diffusiophoresis, ranging from mixing and separation of colloids,9,24–40 enhanced oil recovery,41–43 drug delivery,44,45 to water and surface cleaning.46–48 The strengths of diffusiophoresis are prominent in two aspects. First, diffusiophoresis can generate a significant colloid motion on the microscale. For instance, the diffusivity of a typical ionic solute D ∼ M ∼ 10−9 m s−2 and the length of the solute gradient L ∼ n/∇n ∼  10−3 m, giving U
10−3 m, giving U 10−6 m s−1. Second, diffusiophoresis can transport colloids into dead-end pores,49–51 which cannot be achieved by traditional means such as pressure pumping due to the zero volumetric fluid flow in the pore by conservation of mass.
10−6 m s−1. Second, diffusiophoresis can transport colloids into dead-end pores,49–51 which cannot be achieved by traditional means such as pressure pumping due to the zero volumetric fluid flow in the pore by conservation of mass.
However, the majority of work in the literature focuses on diffusiophoresis in a free electrolyte solution and a theory for predicting colloid diffusiophoresis in an electrolyte-filled porous medium is lacking. Porous media are ubiquitous in artificial and natural settings. For instance, tumor interstitia are filled with biohydrogels which hinder nanoparticle drug delivery.44,52,53 Distinct from transport in a free electrolyte solution, colloids experience friction and retardation as they travel through a porous medium. As a proof of concept of a novel nanoparticle drug delivery protocol in biological systems, recently Doan et al.45 demonstrated and measured diffusiophoresis of nanoparticles in a porous hydrogel. Specifically, they constructed microfluidic dead-end pores filled with collagen hydrogel and an electrolyte solution, mimicking tumor interstitia. They then generated an electrolyte concentration gradient across the dead-end pores by flowing an electrolyte solution of a different concentration past the opening of the pores. Because of the high aspect ratio of the dead-end pores, they assumed that the nanoparticle displacement x(t) and electrolyte concentration field n(x,t) are one-dimensional and follow the integrated log-sensing relation, 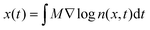 . They extracted the mobility by fitting this relation to a theoretically deduced n(x,t) and an experimentally measured x(t).
. They extracted the mobility by fitting this relation to a theoretically deduced n(x,t) and an experimentally measured x(t).
Despite the success in inferring the mobility, the experiment45 suffers from several drawbacks. First, it requires tracking the nanoparticle displacement which is subject to thermal fluctuations and demands averaging over multiple experiments to minimize statistical errors. Second, it requires a long time (up to days) to prepare the gel- and electrolyte-filled dead-end pores and to observe sufficiently large nanoparticle displacements for inferring the mobility. Third, and most importantly, the experiments cannot predict the particle diffusiophoretic motion (mobility). Hence, there is a need for a predictive theory for the colloid diffusiophoretic mobility in a porous medium, analogous to that for colloid diffusiophoresis in a free electrolyte solution.6
In this work, we develop a mathematical model that can predict the diffusiophoretic colloid mobility in a porous medium. The model considers a charged colloidal particle undergoing diffusiophoresis in a porous medium subject to a spatially uniform concentration gradient of a binary monovalent electrolyte. We invoke the Debye–Huckel approximation, which is accurate to model the electric potential of a charged particle in many practical cases, where ϕ ≤ 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mV at room temperature.54 To account for the frictional force exerted by the porous network on the fluid and particle motion, the porous medium is modeled as a Brinkman medium55 with a constant Darcy permeability. We report three key findings. First, we show that, compared to diffusiophoresis in a free electrolyte solution, colloid diffusiophoresis could be significantly hampered in porous media due to friction, as reflected in a decrease in the magnitude of the mobility. Second, we demonstrate that the variation of the mobility with electrolyte concentration could be altered qualitatively by the presence of porous media. Third, our model predictions make quantitative agreements with experiments45 with no fitting parameters.
mV at room temperature.54 To account for the frictional force exerted by the porous network on the fluid and particle motion, the porous medium is modeled as a Brinkman medium55 with a constant Darcy permeability. We report three key findings. First, we show that, compared to diffusiophoresis in a free electrolyte solution, colloid diffusiophoresis could be significantly hampered in porous media due to friction, as reflected in a decrease in the magnitude of the mobility. Second, we demonstrate that the variation of the mobility with electrolyte concentration could be altered qualitatively by the presence of porous media. Third, our model predictions make quantitative agreements with experiments45 with no fitting parameters.
The rest of this article is outlined as follows. In Section 2, we formulate the problem by first presenting the governing equations and boundary conditions for the fluid and ion transport as well as the electric potential distribution of the charged colloidal particle and the surrounding electrolyte-filled porous media. Then, we conduct a regular perturbation in the imposed electrolyte concentration gradient to obtain a set of ordinary differential equations that determine the diffusiophoretic mobility of the particle. In Section 3, we present our results and elaborate on the three above-mentioned key findings. In Section 4, we summarize this study and offer ideas for future work.
2 Problem formulation
Consider a non-conducting particle of radius a and constant surface charge q (or constant surface potential ζ) in a static porous medium with a constant Darcy permeability l2 (l is the Brinkman screening length), subject to a spatially uniform concentration gradient of a binary monovalent electrolyte ∇n∞i, where i = 1 and i = 2 are the cationic and anionic species, respectively (Fig. 1). Due to symmetry, the particle translates with a constant diffusiophoretic velocity U parallel to ∇n∞i along the z-direction. The velocity U is an unknown to be determined. A reference frame moving with U is adopted.In the steady state, conservation of individual species requires that
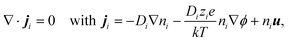 | (1) |
| −ε∇2ϕ = ρ = z1en1 + z2en2, | (2) |
| ∇·u = 0 0 = −∇p + η∇2u − ρ∇ϕ − ηl−2(u + U), | (3) |
To specify the problem, eqn (1)–(3) should be accompanied with boundary conditions at the particle surface and at location far from the particle. At the particle surface, r = a, no hydrodynamic slip and no penetration of the solvent require that
| u = 0. | (4) |
No penetration of the ionic species requires that
| n·ji = 0, | (5) |
| −n·ε∇ϕ = q or ϕ = ζ. | (6) |
At location far from the particle, r → ∞, it requires that
| u → −U and p → p∞, | (7) |
| ni → n∞i + ∇n∞i·r, | (8) |
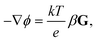 | (9) |
We linearize eqn (1)–(9) to probe typical regimes of diffusiophoresis, where the electrolyte gradient at the size of the particle is much smaller than the background concentration. To this end, we define a small parameter α = |G|a ≪ 1 and perform a regular perturbation analysis for the dependent variables
 | (10) |
2.1 Leading order perturbation
The leading order perturbation concerns the equilibrium condition where there is no electrolyte concentration gradient and therefore no fluid flow, u0 = 0. In other words, the momentum eqn (3) does not provide useful information at the leading order perturbation. Hence, only the perturbed eqn (1) and (2) and their boundary conditions are presented below.The leading order ion conservation and Poisson equation are
| ∇·(−∇n0i − zin0i∇ϕ0) = 0, | (11) |
| ∇2ϕ0 = −(κa)2(z1n01 + z2n02), | (12) |
| n·(−∇n0i − zin0i∇ϕ0) = 0, | (13) |
 | (14) |
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) and
and ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) denote the non-dimensionalized particle surface charge and surface potential, respectively. The leading order boundary conditions far from the particle, r → ∞, are
denote the non-dimensionalized particle surface charge and surface potential, respectively. The leading order boundary conditions far from the particle, r → ∞, are| n0i → n∞i and ϕ0 → 0. | (15) |
Integrating eqn (11) and applying eqn (15) yields the Boltzmann distribution of the ionic species, n0i = n∞i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ziϕ0). Substituting this result in eqn (12) furnishes the nonlinear Poisson–Boltzmann equation, which can be linearized using the Debye–Huckel approximation as ∇2ϕ0 = (κa)2ϕ0. Utilizing eqn (14) and (15), the spherically symmetric equilibrium electric potential for a particle with a constant surface charge or a constant surface potential can be obtained, respectively, as
exp(−ziϕ0). Substituting this result in eqn (12) furnishes the nonlinear Poisson–Boltzmann equation, which can be linearized using the Debye–Huckel approximation as ∇2ϕ0 = (κa)2ϕ0. Utilizing eqn (14) and (15), the spherically symmetric equilibrium electric potential for a particle with a constant surface charge or a constant surface potential can be obtained, respectively, as
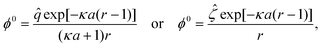 | (16) |
 | (17) |
2.2 O(α) perturbation
The O(α) equations can be simplified and converted to a set of ordinary differential equations by introducing the ψ1i potential, n1i = −zin0i(ψ1i + ϕ1),60 and exploiting symmetry of the problem to write the dependent variables as61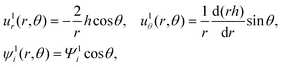 | (18) |
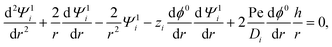 | (19) |
 | (20) |
 | (21) |
The O(α) boundary conditions far from the particle, r→∞, are
| Ψ11 → (β − 1)r, Ψ12 → (β + 1)r, | (22) |
 | (23) |
 | (24) |
Eqn (22) and (23) are set at r → ∞. To have a well-defined boundary value problem in a finite domain, we follow prior work59,60 and set the computational domain to a sphere of radius R which is concentric to the particle and completely encloses the particle. At a sufficiently large R, the electric potential decays to zero asymptotically as (1/r)exp(−κar). A value R = 1 + 20/(κa) suffices. We solve eqn (19) in this asymptotic limit, where terms associated with derivatives of ϕ0 vanish, and obtain the following expressions in replacement of eqn (22)
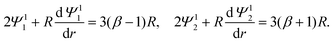 | (25) |
 | (26) |
 | (27) |
 | (28) |
 | (29) |
3 Results and discussion
In this section, we present the diffusiophoretic mobility of a particle in porous media filled with an electrolyte solution. In Section 3.1, we present results for porous media filled with potassium chloride (KCl) solution. Note that electrophoresis is negligible in a KCl solution due to the small diffusivity ratio, β = −0.02. Thus, we follow prior work18,59,62,63 and assume β = 0 so that diffusiophoresis is solely due to chemiphoresis. This enables understanding of chemiphoresis in porous media. In Section 3.2, we present results for porous media filled with sodium chloride (NaCl) solution, which has a large diffusivity ratio, β = −0.21. Both electrophoresis and chemiphoresis contribute significantly to particle diffusiophoresis. In Section 3.3, we compare our modeling predictions with experiments.3.1 Diffusiophoresis in porous media with KCl solution
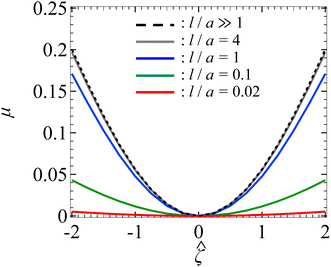
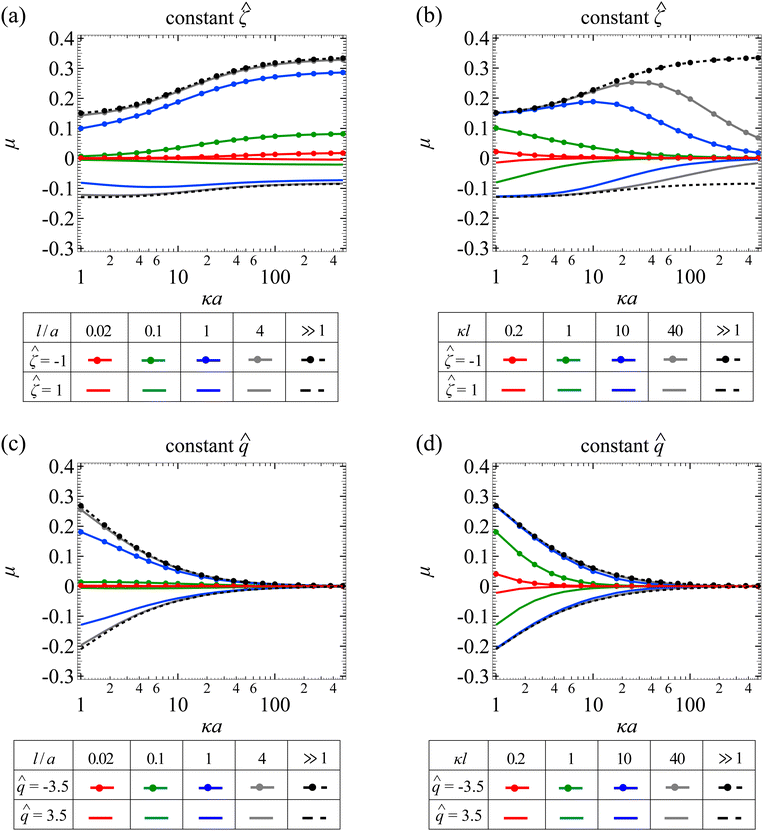
Let us start by examining colloid diffusiophoresis in porous media filled with a KCl solution. Fig. 2 shows the variation of the non-dimensionalized diffusiophoretic mobility with the non-dimensionalized particle surface potential for different ratios of the Brinkman screening length to particle radius, l/a. The ratio of the particle radius to Debye length is set as κa = 10. Physically, l/a can be interpreted as a permeability parameter. Namely, a large l/a(≫1) represents a free electrolyte solution whereas a small l/a(≪1) represents a weakly permeable porous medium filled with the electrolyte. As an overview of the figure, the mobility is positive, meaning that the particle is driven up the electrolyte concentration gradient under chemiphoresis. This is because the imposed electrolyte gradient generates a chemiosmotic flow over the particle surface from region of high to low electrolyte concentration, and the particle is moving in the opposite direction under chemiphoresis.1–4In Fig. 2, the dashed line recovers the particle mobility in a free electrolyte solution.18,59 The mobility is symmetric with respect to the sign of the particle surface potential, which is due to the absence of electrophoresis. The solid lines show the mobility in porous media with different permeabilities. The mobility is still an even function of the particle surface potential, since electrophoresis is still absent. Also, at a fixed ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) , the mobility decreases as l/a decreases. This could be understood as follows. Lowering l/a implies a lower permeability of the electrolyte solution in the porous medium. Thus, there is a weaker chemiosmotic flow past the particle and, consequently, particle chemiphoresis is weakened as reflected in a smaller particle mobility. Alternatively, one could understand this observation by recognizing that the porous medium introduces additional hydrodynamic drag to the particle, which scales as (a/l)2,55,64 as shown in eqn (20). Thus, decreasing l/a lowers the mobility.
, the mobility decreases as l/a decreases. This could be understood as follows. Lowering l/a implies a lower permeability of the electrolyte solution in the porous medium. Thus, there is a weaker chemiosmotic flow past the particle and, consequently, particle chemiphoresis is weakened as reflected in a smaller particle mobility. Alternatively, one could understand this observation by recognizing that the porous medium introduces additional hydrodynamic drag to the particle, which scales as (a/l)2,55,64 as shown in eqn (20). Thus, decreasing l/a lowers the mobility.
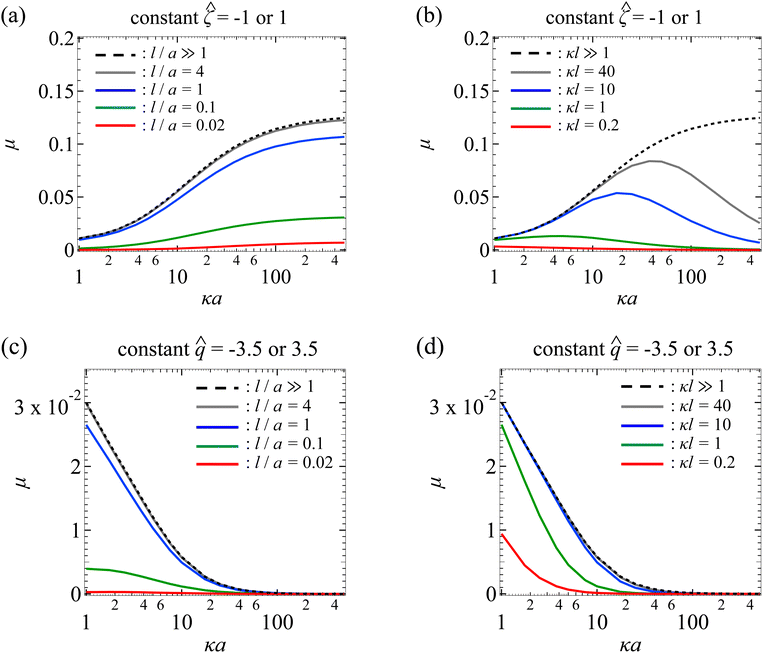
Next, Fig. 3(a) shows the variation of the non-dimensionalized diffusiophoretic mobility with κa for different l/a. The non-dimensionalized particle surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = −1. As an overview of the figure, a line of fixed l/a can be interpreted as fixing the permeability of the porous medium, l, and the size of the particle, a. Thus, at a fixed l/a, increasing κa implies increasing κ, which can be achieved in practice by increasing the bulk electrolyte concentration n∞ (recall that
= −1. As an overview of the figure, a line of fixed l/a can be interpreted as fixing the permeability of the porous medium, l, and the size of the particle, a. Thus, at a fixed l/a, increasing κa implies increasing κ, which can be achieved in practice by increasing the bulk electrolyte concentration n∞ (recall that  ).
).
In Fig. 3(a), the dashed line recovers the particle mobility in a free electrolyte solution.18,59 The mobility increases as κa increases. This is because, as noted in the above paragraph, increasing κa implies an increasing bulk ion concentration. Hence, there are more ions that contribute to a stronger chemiosmotic flow and therefore stronger chemiphoresis, as reflected in a larger mobility. The mobility plateaus as κa ≫ 1, since the chemiosmotic flux saturates in the limit of a vanishingly thin electric double layer. The solid lines show the mobility in porous media with different permeabilities. At a fixed κa, the mobility decreases as l/a decreases, consistent with the explanation provided in Fig. 2. On a different note, we have conducted separate computations and confirmed that the mobility of a particle with a constant surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/char_e102.gif) ;= 1 is the same as that shown in Fig. 3(a) for
;= 1 is the same as that shown in Fig. 3(a) for ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = −1. This is again due to the absence of electrophoresis.
= −1. This is again due to the absence of electrophoresis.
Fig. 3(b) shows the variation of the non-dimensionalized diffusiophoretic mobility with κa for different ratios of the Brinkman screening length to Debye length κl. The non-dimensionalized particle surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = −1. As an overview of the figure, a line of fixed κl can be interpreted as fixing the permeability of the porous medium, l, and the concentration of the solution, κ. Thus, at a fixed κl, increasing κa implies increasing the particle radius a, which can be achieved in practice by using particles of different sizes. The dashed line recovers the particle mobility in a free electrolyte solution.18,59
= −1. As an overview of the figure, a line of fixed κl can be interpreted as fixing the permeability of the porous medium, l, and the concentration of the solution, κ. Thus, at a fixed κl, increasing κa implies increasing the particle radius a, which can be achieved in practice by using particles of different sizes. The dashed line recovers the particle mobility in a free electrolyte solution.18,59
In Fig. 3(b), the solid lines show the mobility in porous media with different κl. For κl ≥ 1, the mobility first increases and then decreases with increasing κa, distinct from the response in a free electrolyte solution. To understand this non-monotonic response, let us consider the (grey) line with κl = 40 as an example. Before the mobility rises to a peak, the particle radius, a, is small compared to the mesh size of the porous medium (∼l). For instance, at κa = 10, a/l = 1/4. Physically, the hindrance due to the porous medium is not felt by the particle. The resulting reduction in mobility is insignificant compared to the enhancement to the mobility due to increasing κa. Thus, before attaining the peak which corresponds to a/l ∼ O(1), the mobility increases with increasing κa. Beyond the peak where a/l > O(1), the mobility decreases with increasing κa. This is because the hindrance due to the porous medium outweighs the enhancement due to increasing κa, leading to an overall decrease in the mobility as κa increases.
In Fig. 3(b), a peak is not exhibited for κl < 1 (red line). This is because a/l > O(1) for the entire range of κa shown in the figure. Thus, the hindrance due to the porous medium and the resulting reduction in mobility dominate the enhancement due to increasing κa. On a different note, at a fixed κa, lowering κl decreases the mobility. This is because lowering κl at a fixed κa implies lowering l/a, which increases the hydrodynamic drag to the particle and thus lowers the mobility, as explained in Fig. 2. As an additional remark, we have conducted separate computations and confirmed that the mobility of a particle with a constant surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = 1 is identical to that shown in Fig. 3(b) for
= 1 is identical to that shown in Fig. 3(b) for ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = −1.
= −1.
Next, let us turn our focus to Fig. 3(c) which shows the variation of the non-dimensionalized diffusiophoretic mobility with κa for different l/a. Here, the non-dimensionalized particle surface charge is fixed ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = −3.5 instead of the surface potential. Particles of a constant surface charge are more practically relevant in some cases,63,65,66 although prior work has focused on particles of a constant surface potential.8,18,20,59,62 For a particle with a constant surface charge, its surface potential decreases with increasing κa [eqn (17)]. In Fig. 3(c), the maximum non-dimensionalized potential |
= −3.5 instead of the surface potential. Particles of a constant surface charge are more practically relevant in some cases,63,65,66 although prior work has focused on particles of a constant surface potential.8,18,20,59,62 For a particle with a constant surface charge, its surface potential decreases with increasing κa [eqn (17)]. In Fig. 3(c), the maximum non-dimensionalized potential |![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) | = 1.7 occurs at κa = 1, which justifies the use of the Debye–Huckel approximation to compute the electric potential accurately.54
| = 1.7 occurs at κa = 1, which justifies the use of the Debye–Huckel approximation to compute the electric potential accurately.54
In Fig. 3(c), the dashed line shows the particle mobility in a free electrolyte solution. Going from top to bottom of the figure, at a fixed κa, the mobility decreases as l/a decreases, which is consistent with the explanation given in Fig. 2. Going from left to right of the figure, for a line of constant l/a, the mobility is maximum when κa is the smallest and decreases to zero on approaching the limit κa ≫ 1. This trend follows from the relation between the particle surface charge and surface potential [eqn (17)], where the latter vanishes in the limit of κa ≫ 1 and so does the mobility. On a different note, we have conducted separate computations and confirmed that the mobility of a particle with a constant surface charge ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = 3.5 is identical to that shown in Fig. 3(c) for
= 3.5 is identical to that shown in Fig. 3(c) for ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = −3.5.
= −3.5.
Next, let us look at Fig. 3(d) that shows the variation of the non-dimensionalized diffusiophoretic mobility with κa for different κl. The non-dimensionalized particle surface charge ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = −3.5. The dashed line shows the particle mobility in a free electrolyte solution. Going from top to bottom of the figure, at a fixed κa, the mobility decreases as l/a decreases, which is consistent with the explanation provided in Fig. 2. Going from left to right of the figure, for a line of constant l/a, the mobility decreases from a maximum when κa is the smallest to zero on approaching the limit κa ≫ 1. We have conducted separate computations and confirmed that the mobility of a particle with a constant surface charge
= −3.5. The dashed line shows the particle mobility in a free electrolyte solution. Going from top to bottom of the figure, at a fixed κa, the mobility decreases as l/a decreases, which is consistent with the explanation provided in Fig. 2. Going from left to right of the figure, for a line of constant l/a, the mobility decreases from a maximum when κa is the smallest to zero on approaching the limit κa ≫ 1. We have conducted separate computations and confirmed that the mobility of a particle with a constant surface charge ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = 3.5 is the same as that shown in Fig. 3(d) for
= 3.5 is the same as that shown in Fig. 3(d) for ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = −3.5.
= −3.5.
3.2 Diffusiophoresis in porous media with NaCl solution
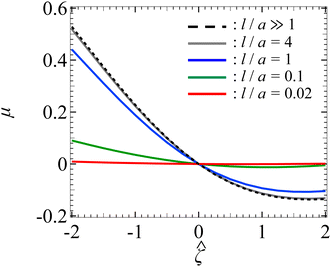
Let us turn to examine colloid diffusiophoresis in porous media filled with a NaCl solution. Fig. 4 shows the variation of the non-dimensionalized diffusiophoretic mobility with the non-dimensionalized particle surface potential for different l/a and κa = 10. The dashed line recovers the particle mobility in a free electrolyte solution.18,59 Distinct from Fig. 2 for KCl solution, here the particle mobility in a NaCl solution is asymmetric with respect to the sign of the particle surface potential due to the presence of electrophoresis. Specifically, because of the difference in the diffusivity between the sodium and chloride ions, an electric field is induced to maintain bulk electroneutrality in the imposed electrolyte gradient. This electric field induces electrophoretic motion of the particle, where a negatively (positively) charged particle is driven up (down) the electrolyte gradient. However, chemiphoresis is also present and it drives a particle up the electrolyte gradient, regardless of the sign of the particle surface potential. Hence, electrophoresis and chemiphoresis are both driving a negatively charged particle up the electrolyte gradient whereas they are acting in the opposite direction on a positively charged particle. As a result, for a positively charged particle where electrophoresis outweighs chemiphoresis, the particle is driven down the electrolyte gradient as reflected in a negative mobility. In contrast, for a negatively charged particle, the mobility is positive and has a larger magnitude compared to a positively charged particle that has the same magnitude of surface potential.In Fig. 4, the solid lines show the mobility in porous media with different permeabilities. At a fixed ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) , the magnitude of the mobility decreases as l/a decreases. This aligns with the explanation given in Fig. 2, where a small l/a implies a low permeability of the electrolyte solution in the porous medium. Hence, there is a weaker chemiosmotic and electroosmotic flow past the particle. As a result, particle diffusiophoresis is weakened as reflected in a smaller particle mobility. Also, the asymmetry of the mobility with respect to the sign of the particle surface potential persists in the presence of a porous medium. This implies that varying the permeability of the porous medium only impacts the magnitude of the particle diffusiophoretic motion but not its direction.
, the magnitude of the mobility decreases as l/a decreases. This aligns with the explanation given in Fig. 2, where a small l/a implies a low permeability of the electrolyte solution in the porous medium. Hence, there is a weaker chemiosmotic and electroosmotic flow past the particle. As a result, particle diffusiophoresis is weakened as reflected in a smaller particle mobility. Also, the asymmetry of the mobility with respect to the sign of the particle surface potential persists in the presence of a porous medium. This implies that varying the permeability of the porous medium only impacts the magnitude of the particle diffusiophoretic motion but not its direction.
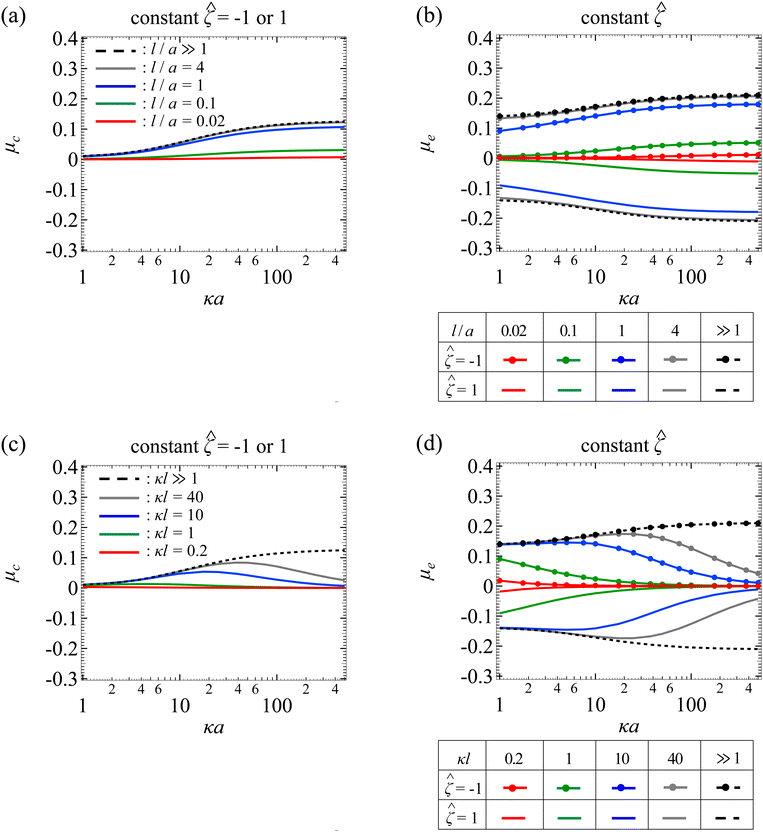
Fig. 5(a) shows the variation of the non-dimensionalized diffusiophoretic mobility with κa for different l/a. Let us first examine the upper quadrant of the figure, which corresponds to a particle with a constant non-dimensionalized surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = −1. Recall that the diffusiophoretic mobility comprises the chemiphoretic and electrophoretic component and, from Fig. 4, they both drive a negatively charged particle up the electrolyte gradient. This is confirmed by Fig. 7(a) and (b) in Appendix A, where we compute the chemiphoretic and electrophoretic mobilities, and they are positive for the entire range of κa. In Fig. 5(a), the dashed line recovers the particle mobility in a free electrolyte solution.18,59 The mobility increases as κa increases, since there are more ions contributing to stronger diffusiophoresis. The mobility plateaus in the limit of thin electric double layer, κa ≫ 1, due to the saturation of diffusioosmotic flux. The solid lines show the mobility in porous media with different permeabilities. At a fixed κa, lowering l/a decreases the magnitude of the mobility but does not change its sign, consistent with the explanation provided in Fig. 4.
= −1. Recall that the diffusiophoretic mobility comprises the chemiphoretic and electrophoretic component and, from Fig. 4, they both drive a negatively charged particle up the electrolyte gradient. This is confirmed by Fig. 7(a) and (b) in Appendix A, where we compute the chemiphoretic and electrophoretic mobilities, and they are positive for the entire range of κa. In Fig. 5(a), the dashed line recovers the particle mobility in a free electrolyte solution.18,59 The mobility increases as κa increases, since there are more ions contributing to stronger diffusiophoresis. The mobility plateaus in the limit of thin electric double layer, κa ≫ 1, due to the saturation of diffusioosmotic flux. The solid lines show the mobility in porous media with different permeabilities. At a fixed κa, lowering l/a decreases the magnitude of the mobility but does not change its sign, consistent with the explanation provided in Fig. 4.
Let us turn our focus to the lower quadrant of Fig. 5(a), which corresponds to a particle with ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = 1. Recall from Fig. 4 that electrophoresis drives the particle down the electrolyte gradient and outweighs chemiphoresis that drives the particle up the electrolyte gradient. This is confirmed by Fig. 7(a) and (b) in Appendix A where, at particular l/a and κa, electrophoresis induces a negative mobility that has a larger magnitude relative to the positive mobility generated by chemiphoresis. In Fig. 5(a), the dashed line recovers the particle mobility in a free electrolyte solution.18,59 As κa increases, the mobility decreases in magnitude and then plateaus. The solid lines show the mobility in porous media with different permeabilities. Notably, for l/a < 1, the magnitude of the diffusiophoretic mobility increases with κa monotonically, which is qualitatively different from that in a free electrolyte solution. This is due to the fact that porous media weaken the chemiphoretic and electrophoretic mobilities to different extents at different l/a and κa. Physically, this implies that particle diffusiophoresis in response to a change in the electrolyte concentration (
= 1. Recall from Fig. 4 that electrophoresis drives the particle down the electrolyte gradient and outweighs chemiphoresis that drives the particle up the electrolyte gradient. This is confirmed by Fig. 7(a) and (b) in Appendix A where, at particular l/a and κa, electrophoresis induces a negative mobility that has a larger magnitude relative to the positive mobility generated by chemiphoresis. In Fig. 5(a), the dashed line recovers the particle mobility in a free electrolyte solution.18,59 As κa increases, the mobility decreases in magnitude and then plateaus. The solid lines show the mobility in porous media with different permeabilities. Notably, for l/a < 1, the magnitude of the diffusiophoretic mobility increases with κa monotonically, which is qualitatively different from that in a free electrolyte solution. This is due to the fact that porous media weaken the chemiphoretic and electrophoretic mobilities to different extents at different l/a and κa. Physically, this implies that particle diffusiophoresis in response to a change in the electrolyte concentration ( ) in a porous medium could be qualitatively different from that in a free electrolyte solution.
) in a porous medium could be qualitatively different from that in a free electrolyte solution.
Next, let us look at Fig. 5(b) that shows the variation of the non-dimensionalized diffusiophoretic mobility with κa for different κl. Let us first inspect the upper quadrant of the figure, which corresponds to a particle with a constant non-dimensionalized surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = −1. The dashed line recovers the particle mobility in a free electrolyte solution.18,59 The solid lines show the mobility in porous media with different κl. Compared to Fig. 3(b), the diffusiophoretic mobility still increases and then decreases with increasing κa, although this trend occurs only for κl > 1 because of the electrophoretic contribution to the diffusiophoretic mobility. We show the chemiphoretic and electrophoretic mobility in Fig. 7(c) and (d) in Appendix A for reference. For κl ≤ 1, the diffusiophoretic mobility decreases monotonically as κa increases. The lower quadrant of the figure corresponds to a particle with
= −1. The dashed line recovers the particle mobility in a free electrolyte solution.18,59 The solid lines show the mobility in porous media with different κl. Compared to Fig. 3(b), the diffusiophoretic mobility still increases and then decreases with increasing κa, although this trend occurs only for κl > 1 because of the electrophoretic contribution to the diffusiophoretic mobility. We show the chemiphoretic and electrophoretic mobility in Fig. 7(c) and (d) in Appendix A for reference. For κl ≤ 1, the diffusiophoretic mobility decreases monotonically as κa increases. The lower quadrant of the figure corresponds to a particle with ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = 1. Due to a competition between chemiphoresis and electrophoresis, for all κl, the magnitude of the diffusiophoretic mobility decreases monotonically as κa increases.
= 1. Due to a competition between chemiphoresis and electrophoresis, for all κl, the magnitude of the diffusiophoretic mobility decreases monotonically as κa increases.
Fig. 5(c) shows the variation of the non-dimensionalized diffusiophoretic mobility with κa for different l/a. The non-dimensionalized particle surface charge is fixed instead of the surface potential. The upper and lower quadrant of the figure correspond to a particle with ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = −3.5 and
= −3.5 and ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = 3.5, respectively. Although electrophoresis is present here, it only alters quantitatively the variation of the diffusiophoretic mobility with κa compared to that in a purely chemiphoretic system [Fig. 3(c)]. Specifically, regardless of the sign of the particle surface charge, the following trends persist. First, at a fixed κa, the magnitude of the mobility decreases as l/a decreases. Second, at a fixed l/a, the mobility decreases monotonically to zero on approaching the limit κa ≫ 1.
= 3.5, respectively. Although electrophoresis is present here, it only alters quantitatively the variation of the diffusiophoretic mobility with κa compared to that in a purely chemiphoretic system [Fig. 3(c)]. Specifically, regardless of the sign of the particle surface charge, the following trends persist. First, at a fixed κa, the magnitude of the mobility decreases as l/a decreases. Second, at a fixed l/a, the mobility decreases monotonically to zero on approaching the limit κa ≫ 1.
Fig. 5(d) shows the variation of the non-dimensionalized diffusiophoretic mobility with κa for different κl. The upper and lower quadrant of the figure correspond to a particle with ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = −3.5 and
= −3.5 and ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = 3.5, respectively. Same as the conclusion drawn from Fig. 5(c), the presence of electrophoresis does not alter qualitatively the variation of the diffusiophoretic mobility compared to that in a purely chemiphoretic system [Fig. 3(d)]. At a fixed κa, the magnitude of the mobility decreases as κl decreases. At a fixed κl, the mobility decreases as κa increases.
= 3.5, respectively. Same as the conclusion drawn from Fig. 5(c), the presence of electrophoresis does not alter qualitatively the variation of the diffusiophoretic mobility compared to that in a purely chemiphoretic system [Fig. 3(d)]. At a fixed κa, the magnitude of the mobility decreases as κl decreases. At a fixed κl, the mobility decreases as κa increases.
3.3 Comparison with experiments
As noted in Section 1, recent experiments measured the nanoparticle diffusiophoretic mobility in porous media.45 In this section, we compare our modeling predictions with experimental measurements. Before discussing the results, we state the justifications for the comparison. First, our model assumes a weak electrolyte concentration gradient, |∇n∞i/n∞i|a ≪ 1. This condition is satisfied and can be confirmed by substituting relevant parameters from experiments as stated below. Second, our model computes the diffusiophoretic mobility of a single particle, excluding particle–particle hydrodynamic and electrostatic interactions. Neglecting these interactions is justified given the dilute particle suspension employed in experiments, since hydrodynamic disturbance and electric field due to a particle decay rapidly as 1/r3 and in an exponential manner, respectively.58 Third, our model neglects particle interactions with physical confinements, e.g., the dead-end pore walls in experiments. Neglecting this effect is justified so long as the particle is far from the confinement.
Fig. 6(a) shows the variation of the dimensional diffusiophoretic mobility with the concentration of the collagen gel (the porous medium). The collagen gel concentration, w, relates to the permeability via l2 = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 854w−1.442,52 where the units for l and w in this relation are nm and mg mL−1, respectively. In experiments,45 a concentration gradient of potassium acetate of cin = 1
854w−1.442,52 where the units for l and w in this relation are nm and mg mL−1, respectively. In experiments,45 a concentration gradient of potassium acetate of cin = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mM to cout = 0.025
mM to cout = 0.025![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mM over a distance of 800 μm is imposed to drive particles of radius 100
mM over a distance of 800 μm is imposed to drive particles of radius 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm and surface potential 60
nm and surface potential 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mV into a gel-filled dead-end pore. Utilizing these experimental parameters, we compute the mobilities with our model (line) and show them alongside the experimental measurements (circle). Our model predictions capture the experimental data qualitatively, where increasing the collagen concentration decreases the mobility due to the larger hydrodynamic drag to particle. Furthermore, our model predictions are in close quantitative agreement with experiments. We attribute the discrepancy to the large particle surface potential, 60
mV into a gel-filled dead-end pore. Utilizing these experimental parameters, we compute the mobilities with our model (line) and show them alongside the experimental measurements (circle). Our model predictions capture the experimental data qualitatively, where increasing the collagen concentration decreases the mobility due to the larger hydrodynamic drag to particle. Furthermore, our model predictions are in close quantitative agreement with experiments. We attribute the discrepancy to the large particle surface potential, 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mV, which violates the range of validity of the Debye–Huckel approximation in our model formulation, namely, |ζ| ≤ 50
mV, which violates the range of validity of the Debye–Huckel approximation in our model formulation, namely, |ζ| ≤ 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mV at room temperature.54
mV at room temperature.54
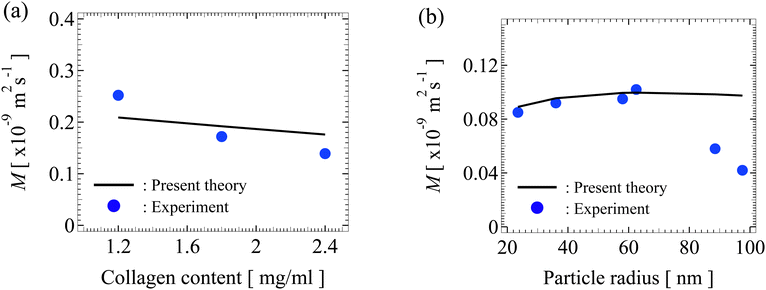 | ||
Fig. 6 (a) Variation of the dimensional diffusiophoretic mobility M with the concentration of the collagen gel. A concentration gradient of potassium acetate of cin = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mM to cout = 0.025 mM to cout = 0.025![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mM over a distance of 800 μm is imposed to drive particles of radius a = 100 mM over a distance of 800 μm is imposed to drive particles of radius a = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm and surface potential 60 nm and surface potential 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mV into a gel-filled dead-end pore. (b) Variation of M with a. A concentration gradient of sodium chloride of cin = 150 mV into a gel-filled dead-end pore. (b) Variation of M with a. A concentration gradient of sodium chloride of cin = 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mM to cout = 15 mM to cout = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mM over a distance of 800 μm is imposed to drive particles of surface potential −21 mM over a distance of 800 μm is imposed to drive particles of surface potential −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mV into a gel-filled dead-end pore. The gel concentration is 2.4 mV into a gel-filled dead-end pore. The gel concentration is 2.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mg mL−1. Solid line: predictions by present work. Circle: experimental measurements by Doan et al.45 mg mL−1. Solid line: predictions by present work. Circle: experimental measurements by Doan et al.45 | ||
Fig. 6(b) shows the variation of the dimensional diffusiophoretic mobility with the particle radius. In experiments,45 a concentration gradient of NaCl of cin = 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mM to cout = 15
mM to cout = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mM over a distance of 800 μm is imposed to drive particles of surface potential −21
mM over a distance of 800 μm is imposed to drive particles of surface potential −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mV into a gel-filled dead-end pore. The gel concentration is 2.4
mV into a gel-filled dead-end pore. The gel concentration is 2.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mg mL−1. Again, utilizing these experimental parameters, we compute the mobilities with our model (line) and show them alongside the experimental measurements (circle). Since the particle potential is within the range of validity of the Debye–Huckel approximation, here our model predictions match excellently with experiments. We propose an explanation for the discrepancy between our model and experiments in the two data points on the right as follows. As noted in experiments,45 the significantly lower mobility of the two data points may be due to the strong particle-gel interactions. Specifically, although the net charge of the gel was reported as zero in experiments, we conjecture that any residue net charge of the gel will alter the electric potential distribution around the charged particle, which may in turn lower the particle mobility.57,58 This effect is weak when the particle is small compared to the gel mesh but is more prominent when the two are comparable in size. Also, a charged gel will induce diffusioosmosis, which will alter the particle mobility in a non-trivial manner. Note that accounting for these effects requires a significant extension of the present model, including modification of the Poisson equation, the induced electric potential gradient, and consideration of a diffusioosmotic flow generated by porous media, which is beyond the scope of this work on particle diffusiophoresis in uncharged porous media but warrants future work.
mg mL−1. Again, utilizing these experimental parameters, we compute the mobilities with our model (line) and show them alongside the experimental measurements (circle). Since the particle potential is within the range of validity of the Debye–Huckel approximation, here our model predictions match excellently with experiments. We propose an explanation for the discrepancy between our model and experiments in the two data points on the right as follows. As noted in experiments,45 the significantly lower mobility of the two data points may be due to the strong particle-gel interactions. Specifically, although the net charge of the gel was reported as zero in experiments, we conjecture that any residue net charge of the gel will alter the electric potential distribution around the charged particle, which may in turn lower the particle mobility.57,58 This effect is weak when the particle is small compared to the gel mesh but is more prominent when the two are comparable in size. Also, a charged gel will induce diffusioosmosis, which will alter the particle mobility in a non-trivial manner. Note that accounting for these effects requires a significant extension of the present model, including modification of the Poisson equation, the induced electric potential gradient, and consideration of a diffusioosmotic flow generated by porous media, which is beyond the scope of this work on particle diffusiophoresis in uncharged porous media but warrants future work.
4 Conclusions
In this work, we have utilized the regular perturbation method to develop a mathematical model for predicting the diffusiophoretic mobility of a colloidal particle driven by a binary monovalent electrolyte concentration gradient in a porous medium. Our model is applicable to particles with surface potential |ζ| ≤ 50 mV at room temperature. To demonstrate our model, we have computed and analyzed the diffusiophoretic mobility of a particle in porous media filled with potassium chloride solution, where chemiphoresis dominates and electrophoresis is negligible. We have shown that, compared to diffusiophoresis in a free electrolyte solution, the particle mobility could be significantly hampered in porous media due to additional hydrodynamic drag. Because of the absence of electrophoresis, the mobility is the same regardless of the sign of the particle surface charge. We have further computed and analyzed the diffusiophoretic mobility of a particle in porous media filled with sodium chloride solution, where chemiphoresis and electrophoresis both contribute to diffusiophoresis. The presence of porous media could still significantly weaken the particle mobility. However, since the chemiphoretic and electrophoretic components are weakened to different extents, the variation of the diffusiophoretic mobility with respect to a change in the electrolyte concentration in a porous medium could be qualitatively different from that in a free electrolyte solution.We have also compared our model predictions with experiments and demonstrated excellent agreements within the scope of the model. There are discrepancies between our model predictions and experiments when assumptions of the model are violated, such as highly charged particles and charged porous media. This suggests future work to extend the present model to incorporate a net charge of the porous media and account for the modified, fully nonlinear Poisson–Boltzmann equation.
Conflicts of interest
There are no conflicts of interest to declare.Appendix A: chemiphoretic and electrophoretic components of diffusiophoretic mobility in porous media with NaCl solution
Diffusiophoretic mobility, μ, could be expressed as a sum of its chemiphoretic, μc, and electrophoretic components, μe, that is, μ = μc + μe. In Section 3.2, we utilized this fact to explain the variation of μ in Fig. 5(a) and (b). In this appendix, we discuss how we compute μc and μe, the variation of μc and μe, and that their sum indeed equals to μ.Recall that μe arises from the electric field due to the difference in ion diffusivities, represented by the diffusivity ratio β. Terms that depend on β reside in eqn (25) only in the overall calculation of μ [solving eqn (19) and (20) subject to eqn (25), (27) and (28)]. Thus, we exploit the linearity of the equations12,15 and separate eqn (25) into a part which depends on β and is associated with μe, and a part which does not depend on β and is associated with μc. In other words, μe can be calculated by replacing eqn (25) with
 | (30) |
 | (31) |
Fig. 7(a) shows the variation of μc with κa for different l/a. The physical interpretations are the same as Fig. 3(a) so we do not repeat them here. Fig. 7(b) shows the variation of μe with κa for different l/a. The upper and lower quadrant of the figure correspond to a particle with ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = −1 and
= −1 and ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = 1, respectively. As κa increases, the mobility increases in magnitude and then plateaus due to saturation of the electroosmotic flux in the limit κa ≫ 1. At a fixed κa, lowering l/a decreases the magnitude of the mobility due to the additional hydrodynamic drag by the porous media. Note that the mobility is symmetric with respect to the sign of the particle surface potential, that is, the mobility is symmetric about the κa axis. This is because of the fact that oppositely charged particles subject to the same electric field are driven into motion with the same speed but in the opposite direction. On a different note, when adding up μc and μe from Fig. 7(a) and (b), the result indeed recovers the diffusiophoretic mobility, μ, in Fig. 5(a), where Fig. 5(a) is obtained directly using eqn (25).
= 1, respectively. As κa increases, the mobility increases in magnitude and then plateaus due to saturation of the electroosmotic flux in the limit κa ≫ 1. At a fixed κa, lowering l/a decreases the magnitude of the mobility due to the additional hydrodynamic drag by the porous media. Note that the mobility is symmetric with respect to the sign of the particle surface potential, that is, the mobility is symmetric about the κa axis. This is because of the fact that oppositely charged particles subject to the same electric field are driven into motion with the same speed but in the opposite direction. On a different note, when adding up μc and μe from Fig. 7(a) and (b), the result indeed recovers the diffusiophoretic mobility, μ, in Fig. 5(a), where Fig. 5(a) is obtained directly using eqn (25).
Fig. 7(c) shows the variation of μc with κa for different κl. The physical interpretations are the same as Fig. 3(b) so we do not repeat them here. Fig. 7(d) shows the variation of μe with κa for different κl. The upper and lower quadrant of the figure correspond to a particle with ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = −1 and
= −1 and ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = 1, respectively. The dashed lines correspond to the mobility in a free electrolyte solution. The mobility increases in magnitude and then plateaus due to saturation of the electroosmotic flux in the limit κa ≫ 1. The solid lines correspond to the mobility in porous media, which varies non-monotonically with κa. This is owing to the competition between the enhancement of the mobility due to the electroosmotic flux and the weakening of the mobility due to hindrance by the porous media. On a different note, at a fixed κa, lowering κl decreases the mobility, since this corresponds to lowering l/a and increasing hydrodynamic drag. By the same reasoning as Fig. 7(b), the mobilities in the two quadrants in Fig. 7(d) are equal in magnitude but opposite in sign. Finally, when adding up Fig. 7(c) and (d), the result indeed recovers the diffusiophoretic mobility, μ, in Fig. 5(b).
= 1, respectively. The dashed lines correspond to the mobility in a free electrolyte solution. The mobility increases in magnitude and then plateaus due to saturation of the electroosmotic flux in the limit κa ≫ 1. The solid lines correspond to the mobility in porous media, which varies non-monotonically with κa. This is owing to the competition between the enhancement of the mobility due to the electroosmotic flux and the weakening of the mobility due to hindrance by the porous media. On a different note, at a fixed κa, lowering κl decreases the mobility, since this corresponds to lowering l/a and increasing hydrodynamic drag. By the same reasoning as Fig. 7(b), the mobilities in the two quadrants in Fig. 7(d) are equal in magnitude but opposite in sign. Finally, when adding up Fig. 7(c) and (d), the result indeed recovers the diffusiophoretic mobility, μ, in Fig. 5(b).
Acknowledgements
H. C. W. Chu acknowledges the startup funding support from the Division of Sponsored Programs, Department of Chemical Engineering, and Herbert Wertheim College of Engineering at University of Florida. We thank the anonymous referees for providing useful comments.References
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef
.
- H. J. Keh, Curr. Opin. Colloid Interface Sci., 2016, 24, 13–22 CrossRef CAS
.
- D. Velegol, A. Garg, R. Guha, A. Kar and M. Kumar, Soft Matter, 2016, 12, 4686–4703 RSC
.
- S. Marbach and L. Bocquet, Chem. Soc. Rev., 2019, 48, 3102–3144 RSC
.
- D. C. Prieve, Adv. Colloid Interface Sci., 1982, 16, 321–335 CrossRef CAS
.
- D. C. Prieve, J. L. Anderson, J. P. Ebel and M. E. Lowell, J. Fluid Mech., 1984, 148, 247–269 CrossRef CAS
.
- J. F. Brady, J. Fluid Mech., 2011, 667, 216–259 CrossRef CAS
.
- T. Chiang and D. Velegol, J. Colloid Interface Sci., 2014, 424, 120–123 CrossRef CAS PubMed
.
- N. Shi, R. Nery-Azevedo, A. I. Abdel-Fattah and T. M. Squires, Phys. Rev. Lett., 2016, 117, 258001 CrossRef PubMed
.
- A. Gupta, B. Rallabandi and H. A. Stone, Phy. Rev. Fluids, 2019, 4, 043702 CrossRef
.
- P. B. Warren, S. Shin and H. A. Stone, Soft Matter, 2019, 15, 278–288 RSC
.
- H. Ohshima, Colloid Polym. Sci., 2021, 299, 1877–1884 CrossRef CAS
.
- J. C. Baygents and D. A. Saville, PhysicoChem. Hydrodyn., 1988, 10, 543–560 CAS
.
- J. Lou and E. Lee, J. Phys. Chem. C, 2008, 112, 12455–12462 CrossRef CAS
.
- P. Y. Huang and H. J. Keh, J. Phys. Chem. B, 2012, 116, 7575–7589 CrossRef CAS PubMed
.
- W. Fang and E. Lee, J. Colloid Interface Sci., 2015, 459, 273–283 CrossRef CAS PubMed
.
- F. Yang, S. Shin and H. A. Stone, J. Fluid Mech., 2018, 852, 37–59 CrossRef CAS
.
-
E. Lee, Theory of electrophoresis and diffusiophoresis of highly charged colloidal particles, Elsevier, New York, 2019 Search PubMed
.
- S. Majhi and S. Bhattacharyya, Colloids Surf., A, 2022, 648, 129272 CrossRef CAS
.
- H. Ohshima, Colloid Polym. Sci., 2022, 300, 153–157 CrossRef CAS
.
- P. Y. Chen and H. J. Keh, J. Colloid Interface Sci., 2005, 286, 774–791 CrossRef CAS PubMed
.
- Y. C. Chang and H. J. Keh, J. Colloid Interface Sci., 2008, 322, 634–653 CrossRef CAS PubMed
.
- H. C. Chiu and H. J. Keh, Electrophoresis, 2017, 38, 2468–2478 CrossRef CAS PubMed
.
- B. Abecassis, C. Cottin-Bizonne, C. Ybert, A. Ajdari and L. Bocquet, New J. Phys., 2009, 11, 075022 CrossRef
.
- J. Palacci, B. Abecassis, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 104, 138302 CrossRef PubMed
.
- J. Deseigne, C. Cottin-Bizonne, A. D. Stroock, L. Bocquet and C. Ybert, Soft Matter, 2014, 10, 4795–4799 RSC
.
- R. Volk, C. Mauger, M. Bourgoin, C. Cottin-Bizonne, C. Ybert and F. Raynal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 013027 CrossRef CAS PubMed
.
- A. Banerjee, I. Williams, R. N. Azevedo, M. E. Helgeson and T. M. Squires, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8612–8617 CrossRef CAS PubMed
.
- C. Mauger, R. Volk, N. Machicoane, M. Bourgoin, C. Cottin-Bizonne, C. Ybert and F. Raynal, Phy. Rev. Fluids, 2016, 1, 034001 CrossRef
.
- S. M. Friedrich, J. M. Burke, K. J. Liu, C. F. Ivory and T. Wang, Nat. Commun., 2017, 8, 1213 CrossRef PubMed
.
- V. Shukla, R. Volk, M. Bourgoin and A. Pumir, New J. Phys., 2017, 19, 123030 CrossRef
.
- F. Raynal, M. Bourgoin, C. Cottin-Bizonne, C. Ybert and R. Volk, J. Fluid Mech., 2018, 847, 228–243 CrossRef CAS
.
- H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, Soft Matter, 2020, 16, 238–246 RSC
.
- T. J. Shimokusu, V. G. Maybruck, J. T. Ault and S. Shin, Langmuir, 2020, 36, 7032–7038 CrossRef CAS PubMed
.
- M. K. Rasmussen, J. N. Pedersen and R. Marie, Nat. Commun., 2020, 11, 2337 CrossRef CAS PubMed
.
- H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, J. Fluid Mech., 2021, 917, A52 CrossRef CAS
.
- H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, Soft Matter, 2022, 18, 1896–1910 RSC
.
- R. E. Migacz and J. T. Ault, Phy. Rev. Fluids, 2022, 7, 034202 CrossRef
.
- R. Volk, M. Bourgoin, C. Brehier and F. Raynal, J. Fluid Mech., 2022, 948, A42 CrossRef CAS
.
- B. E. McKenzie, H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, J. Fluid Mech., 2022, 949, A17 CrossRef CAS
.
- N. Shi and A. Abdel-Fattah, Phy. Rev. Fluids, 2021, 6, 053103 CrossRef
.
- H. Tan, A. Banejee, N. Shi, X. Tang, A. Abdel-Fattah and T. M. Squires, Sci. Adv., 2022, 7, eabh0638 CrossRef PubMed
.
- S. W. Park, J. Lee, H. Yoon and S. Shin, Energy Fuels, 2021, 35, 4885–4892 CrossRef CAS
.
- S. Shin, V. S. Doan and J. Feng, Phys. Rev. Appl., 2019, 12, 024014 CrossRef CAS
.
- V. S. Doan, S. Chun, J. Feng and S. Shin, Nano Lett., 2021, 21, 7625–7630 CrossRef CAS PubMed
.
- S. Shin, J. T. Ault, P. B. Warren and H. A. Stone, Phys. Rev. X, 2017, 4, 041038 Search PubMed
.
- H. Lee, J. Kim, J. Yang, S. W. Seo and S. J. Kim, Lab Chip, 2018, 18, 1317–1724 Search PubMed
.
- S. Shim, M. Baskaran, E. H. Thai and H. A. Stone, Lab Chip, 2021, 17, 3387–3400 RSC
.
- A. Kar, T. Chiang, I. O. Rivera, A. Sen and D. Velegol, ACS Nano, 2015, 9, 746–753 CrossRef CAS PubMed
.
- S. Shin, E. Um, B. Sabass, J. T. Ault, M. Rahimi, P. B. Warren and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 257–261 CrossRef CAS PubMed
.
- J. T. Ault, P. B. Warren, S. Shin and H. A. Stone, Soft Matter, 2017, 13, 9015–9023 RSC
.
- S. Ramanujan, A. Pluen, T. D. McKee, E. B. Brown, Y. Boucher and R. K. Jain, Biophys. J., 2002, 83, 1650–1660 CrossRef CAS PubMed
.
- M. Grossman, N. Ben-Chetrit, A. Zhuravlev, R. Afik, E. Bassat, I. Solomonov, Y. Yarden and I. Sagi, Cancer Res., 2016, 76, 4249–4258 CrossRef CAS PubMed
.
-
H. Ohshima, Theory of colloid and interfacial electric phenomena, Elsevier, New York, 2006 Search PubMed
.
- H. C. Brinkman, Appl. Sci. Res., 1947, 1, 27–34 Search PubMed
.
- S. A. Allison, Y. Xin and H. Pei, J. Colloid Interface Sci., 2007, 313, 328–337 CrossRef CAS PubMed
.
- F. Li and R. J. Hill, J. Colloid Interface Sci., 2013, 394, 1–12 CrossRef CAS PubMed
.
- R. J. Hill, Soft Matter, 2016, 12, 8030–8048 RSC
.
- D. C. Prieve and R. Roman, J. Chem. Soc., Faraday Trans. 2, 1987, 1287–1306 RSC
.
- R. W. O’Brien and L. R. White, J. Chem. Soc., Faraday Trans. 2, 1978, 1607–1626 RSC
.
- R. W. O’Brien and R. J. Hunter, Can. J. Chem., 1981, 81, 1878–1887 CrossRef
.
- H. J. Keh and Y. K. Wei, Langmuir, 2000, 16, 5289–5294 CrossRef CAS
.
- R. F. Stout and A. S. Khair, Phy. Rev. Fluids, 2017, 2, 014201 CrossRef
.
- R. J. Phillips, W. M. Deen and J. F. Brady, AIChE J., 1989, 35, 1761–1769 CrossRef CAS
.
- A. Garg, C. A. Cartier, K. J. M. Bishop and D. Velegol, Langmuir, 2016, 32, 11837–11844 CrossRef CAS PubMed
.
- B. M. Alessio, S. Shim, E. Mintah, A. Gupta and H. A. Stone, Phy. Rev. Fluids, 2021, 6, 054201 CrossRef
.
| This journal is © The Royal Society of Chemistry 2023 |