Open Access Article
Open Access ArticleAn in solution adsorption characterization technique based on the response to an external magnetic field of porous paramagnetic materials: application on supramolecular metal–adenine frameworks containing heterometallic heptameric clusters†
Jon
Pascual-Colino‡
 a,
Rubén
Pérez-Aguirre‡
ab,
Garikoitz
Beobide
a,
Rubén
Pérez-Aguirre‡
ab,
Garikoitz
Beobide
 ac,
Oscar
Castillo
ac,
Oscar
Castillo
 *ac,
Imanol
de Pedro
b,
Antonio
Luque
*ac,
Imanol
de Pedro
b,
Antonio
Luque
 ac,
Sandra
Mena-Gutiérrez
ac,
Sandra
Mena-Gutiérrez
 a and
Sonia
Pérez-Yáñez
a and
Sonia
Pérez-Yáñez
 cd
cd
aDepartamento de Química Orgánica e Inorgánica, Facultad de Ciencia y Tecnología, Universidad del País Vasco/Euskal Herriko Unibertsitatea, UPV/EHU, Apartado 644, E-48080 Bilbao, Spain. E-mail: oscar.castillo@ehu.eus
bCITIMAC, Facultad de Ciencias, Universidad de Cantabria, E-39005 Santander, Spain
cBCMaterials, Basque Center for Materials, Applications and Nanostructures, UPV/EHU Science Park, E-48940 Leioa, Spain
dDepartamento de Química Orgánica e Inorgánica, Facultad de Farmacia, Universidad del País Vasco/Euskal Herriko Unibertsitatea, UPV/EHU, E-01006 Vitoria-Gasteiz, Spain
First published on 18th January 2023
Abstract
Herein we explore the opportunities arising from combining magnetic properties and porosity in metal–organic materials. In this sense, we have prepared an adenine based homometallic wheel-shaped heptameric [Cu7(μ-adeninato)6(μ3-OH)6(μ-OH2)4]2+ entity containing two metal coordination environments: CuO6 at the core of the wheel with an unusually modest Jahn–Teller distortion and six peripheral CuN2O4 with a more pronounced elongation. The difference in the coordination environments of this compound facilitates the selective replacement of the central metal position by other metal centers (ZnII, NiII, CoII and CrIII) and boosts the magnetic properties of the homometallic heptameric entity. The nature of the central metal modulates the complex net of ferro- and antiferromagnetic superexchange pathways within the heptameric entity to tune the total spin (ST = 3 (Cu6Zn), 5/2 (Cu6Cu), 2 (Cu6Ni), 3/2 (Cu6Co), and 9/2 (Cu6Cr)). No evidence of single-molecule magnet behavior has been observed at 2 K, but at room temperature, where these compounds are still in the paramagnetic regime, the attraction force exerted by an external magnetic field (H) on particles immersed in a liquid is enough to keep them attached to an electromagnet pole. The 4S(S + 1) value of the central metal follows a linear dependence with respect to the 1/[H·∇(H)] value at which the particles are detached from the pole of the electromagnet. There is also a linear dependence of the H·∇(H) term with respect to the adsorbate mass incorporated inside the pores of the paramagnetic adsorbent which has allowed performing straightforward sorption selectivity experiments on Cu6Cu directly in solution, which are based on a property of the adsorbent and not as usually based on an indirect assessment of the adsorbate remaining in solution.
Introduction
There is great interest in developing polynuclear transition metal entities with a high total magnetic spin state as they are potential sources of single-molecule magnets and also show a broad scope of potential applications.1–5 In these efforts, one of the most successful strategies relies on the combination of a central paramagnetic metal atom connected to an external collection of surrounding paramagnetic metal centers through bridging ligands with a great ability to mediate strong magnetic interactions (cyanido, oxalato, oxido, and hydroxido).6 A very successful strategy has been capping growing metal oxide entities with carboxylic ligands to limit its polymerization. The first example of this kind of material is the Mn12–acetate species, a prototypical single molecule magnet.7 There are some other examples following this approach but they are limited to oxophilic transition metals such as manganese and iron, providing in this way very robust polynuclear discrete entities with single molecule magnet behaviour coming from the great anisotropy of these ions.8 On the other hand, the anti–anti coordination mode of the carboxylate is similar and can be replaced by the μ-κN3:κN9 coordination mode of the adenine nucleobase providing access to a similar capping approach but in less oxophilic transition metals such as those at the right end of d-block. We have proved that the use of the adenine nucleobase with copper under basic conditions promotes the formation of heptanuclear discrete copper-hydroxido entities capped by the adeninato ligands ([Cu7(μ-adeninato)6(μ3-OH)6(μ-OH2)6]2+).9–11 The coordination environment of the central position with a reduced Jahn–Teller distortion makes it suitable for metal replacement allowing us to obtain a family of heptameric entities: [Cu6M(μ-adeninato)6(μ3-OH)6(μ-OH2)4]SO4 with MII: Cu and Ni, and [Cu6M(μ-adeninato)6(μ3-OH)6(μ-OH2)6](SO4)x with MII (with x = 1): Zn, Co and MIII (with x = 1.5): Cr.Coming back to the magnetic properties, it is well known that bridging ligands play a key role in determining the strength and nature of the superexchange magnetic interaction, but the nature of these interactions can also be modulated by the careful selection of the paramagnetic centers. In this sense, the antiferromagnetic interactions for overlapping magnetic orbitals can flip to the ferromagnetic nature when those magnetic orbitals are orthogonal.12,13 In fact, in this work we use extensively this strategy to obtain a great variety of magnetically ordered ground state total spins: from 3/2 to 9/2.
Usually, the reported studies on this kind of material are focused on the analysis of their magnetic ordering that takes place well below room temperature.6,14 However, the generation of a high total magnetic spin state does not necessarily imply a single-molecule magnet behaviour as great magnetic anisotropy is required among other parameters.15 Instead of that, we herein address the challenge of using the room temperature paramagnetic response of this kind of compound towards an external magnetic field to prompt a driven motion of its particles while immersed in a liquid and even to accomplish sensing through the quantification of this response. Related to the latter, recently we have reported the use of the compound [Cu6Cr(μ-adeninato)6(μ3-OH)6(μ-OH2)6](SO4)1.5, Cu6Cr, to capture anti-inflammatory anionic drugs from aqueous effluents and to quantify them through this new magnetic sensing approach.16 In this work, we are focused on performing a more specific sorption selectivity study using a broader selection of adsorbates. It is also aimed to determine experimentally the dependence that the response toward an external magnetic field has with respect to the paramagnetic centers incorporated in the heptameric entity as within the [Cu6M(μ-adeninato)6(μ3-OH)6(μ-OH2)6](SO4)x compounds all other parameters that could have an impact on this response are almost equalized.
Experimental
Synthetic procedures
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio under continuous stirring and heating. Thereafter, it was added to an aqueous solution of 20 mL of copper(II) sulfate pentahydrate (0.8 mmol, 0.200 g). The appearance of a bluish suspension was observed at pH = 2.9. The suspension was redissolved by adding sulfuric acid dropwise to pH = 1.8. Then, 1 M sodium hydroxide was added dropwise obtaining a new dark blue suspension (pH = 10.1) that was placed in a small beaker and introduced into an Erlenmeyer flask containing a 1/5 (v/v) sulfuric acid solution. The vapor diffusion taking place inside the closed Erlenmeyer flask acidified the solution slowly. After four days, blue cubic crystals of Cu6Cu were obtained (pH = 9.1). Yield: 60%. Main IR features (cm−1; KBr pellets): 3430vs, 3420sh, 1640s, 1605vs, 1545s, 1465m, 1400m, 1305m, 1275m, 1200m, 1150m, 1110m, 1030w, 935w.
1 ratio under continuous stirring and heating. Thereafter, it was added to an aqueous solution of 20 mL of copper(II) sulfate pentahydrate (0.8 mmol, 0.200 g). The appearance of a bluish suspension was observed at pH = 2.9. The suspension was redissolved by adding sulfuric acid dropwise to pH = 1.8. Then, 1 M sodium hydroxide was added dropwise obtaining a new dark blue suspension (pH = 10.1) that was placed in a small beaker and introduced into an Erlenmeyer flask containing a 1/5 (v/v) sulfuric acid solution. The vapor diffusion taking place inside the closed Erlenmeyer flask acidified the solution slowly. After four days, blue cubic crystals of Cu6Cu were obtained (pH = 9.1). Yield: 60%. Main IR features (cm−1; KBr pellets): 3430vs, 3420sh, 1640s, 1605vs, 1545s, 1465m, 1400m, 1305m, 1275m, 1200m, 1150m, 1110m, 1030w, 935w.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio), heating it up under continuous stirring until a green solution was obtained. To that, 20 mL of an aqueous solution of copper(II) sulfate pentahydrate (0.8 mmol, 0.200 g) was added, obtaining a bluish suspension with pH = 3.3 which was acidified with sulfuric acid until it was completely dissolved (pH = 2.1) into a light green solution. Thereafter, triethylamine was added until the formation of a blue-green suspension at pH = 9.5 which was transferred to a crystallizer covered with a sealing film. After two days, rectangular blue crystals were obtained. Yield: 55%. Main IR features (cm−1; KBr pellets): 3335vs, 3200sh, 1640s, 1600vs, 1545s, 1465m, 1395m, 1305m, 1275m, 1200m, 1150m, 1110m, 1030w, 935w.
1 volume ratio), heating it up under continuous stirring until a green solution was obtained. To that, 20 mL of an aqueous solution of copper(II) sulfate pentahydrate (0.8 mmol, 0.200 g) was added, obtaining a bluish suspension with pH = 3.3 which was acidified with sulfuric acid until it was completely dissolved (pH = 2.1) into a light green solution. Thereafter, triethylamine was added until the formation of a blue-green suspension at pH = 9.5 which was transferred to a crystallizer covered with a sealing film. After two days, rectangular blue crystals were obtained. Yield: 55%. Main IR features (cm−1; KBr pellets): 3335vs, 3200sh, 1640s, 1600vs, 1545s, 1465m, 1395m, 1305m, 1275m, 1200m, 1150m, 1110m, 1030w, 935w.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio), heating under continuous stirring. After 10 minutes, the reaction mixture was left to temper, obtaining a blue suspension with pH = 3.78 which was left stirring for one hour (the colour turns to violet). Then, sodium hydroxide (1 M) was added dropwise until a pH value of 10.1 is reached. Finally, the resulting suspension was placed into a crystallizer covered with a sealing film and left in a fridge at 6 °C. After five days, blue needle-shaped crystals were obtained. Yield: 65%. Main IR features (cm−1; KBr pellets): 3335vs, 3200sh, 1640s, 1600vs, 1545s, 1465m, 1395m, 1305m, 1275m, 1200m, 1150m, 1110m, 1030w, 935w.
1 volume ratio), heating under continuous stirring. After 10 minutes, the reaction mixture was left to temper, obtaining a blue suspension with pH = 3.78 which was left stirring for one hour (the colour turns to violet). Then, sodium hydroxide (1 M) was added dropwise until a pH value of 10.1 is reached. Finally, the resulting suspension was placed into a crystallizer covered with a sealing film and left in a fridge at 6 °C. After five days, blue needle-shaped crystals were obtained. Yield: 65%. Main IR features (cm−1; KBr pellets): 3335vs, 3200sh, 1640s, 1600vs, 1545s, 1465m, 1395m, 1305m, 1275m, 1200m, 1150m, 1110m, 1030w, 935w.
Characterization
Results and discussion
Crystal structure determination
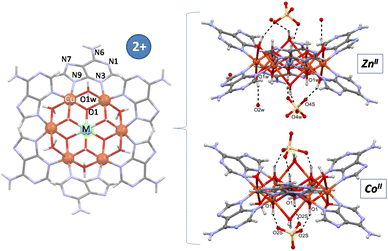
Single crystal X-ray diffraction data allowed us to elucidate the crystal structure of the compounds.§ In previous works we have designed and characterized several supramolecular metal–organic frameworks containing a wheel shaped heptameric [Cu7(μ-adeninato)6(μ3-OH)6(μ-OH2)6]2+ entity whose positive charge is counterbalanced by inorganic (sulfate) or organic species (theobrominate, terephthalate and benzoate).9–11 Both types of counterions can play a role in the supramolecular forces (hydrogen-bonding and π-stacking interactions) that govern the overall crystal packing but they have little impact on the magnetic behaviour, which is greatly dominated by the superexchange pathways within the discrete heptameric entities and only at very low temperatures (below 5 K) some differences arise from the far more weaker superexchange pathways involving the dissimilar supramolecular interactions. A closer analysis of the discrete heptameric [Cu7(μ-adeninato)6(μ3-OH)6(μ-OH2)6]2+ entity revealed the presence of two types of metal coordination environments, a Cu(OH)6 chromophore at the core of the wheel with an unusually modest Jahn–Teller distortion and the six peripheral CuN2(OH)2(Ow)2 environments with the common and pronounced Jahn–Teller distortion affecting the coordinated water molecules. This feature suggested us the possibility of replacing central copper(II) by other transition metal ions with a usually more regular coordination environment, in this way, to tune the magnetic properties of the heptameric entity. A recent work in which this central position was replaced by a CrIII atom (Cu6Cr) confirms the suitability of this approach.16 Now, we report herein four compounds, the homometallic [Cu7(μ-adeninato-κN3:κN9)6(μ3-OH)6(μ-OH2)4](SO4)·nH2O compound (Cu6Cu), and heterometallic [Cu6M(μ-adeninato-κN3:κN9)6(μ3-OH)6(μ-OH2)6](SO4)·nH2O; MII: Zn (Cu6Zn), Ni (Cu6Ni), Co (Cu6Co). Fig. 1 shows a schematic representation of the discrete heptameric units in which the connectivity is essentially identical, in such a way that a central [MII(OH)6]4− or [MIII(OH)6]3− core (Cu6Cr) is connected to the six copper(II) metal centers comprising the external ring. The peripheral copper atoms are further connected among them through the double μ-H2O and six μ-adeninato-κN3:κN9 bridges. It is necessary to note that in homometallic Cu6Cu, two water molecules, labelled as * in Fig. 1, are not present owing to the arrangement of the adjacent adeninato ligands that precludes their attachment.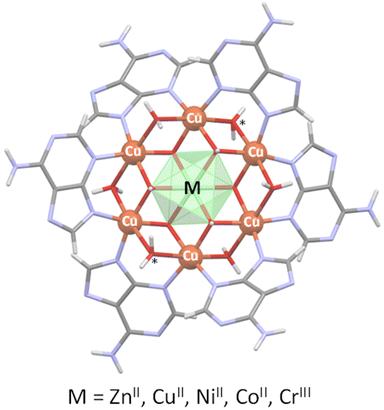 | ||
| Fig. 1 Heptameric clusters depicting the targeted replacement of the central metal center. Symbol “*” indicates the absent coordination water molecules in compound Cu6Cu. | ||
Regarding the self-assembly of the heptameric cations in the crystal packing, two basic arrangements are observed (Fig. 2). Each entity, in the trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) cCu6Zn and Cu6Co compounds, is six-connected by means of π–π interactions (comprising its six adeninato ligands) to three upper and to three lower ones to give a pcu topology with a 412·63 point symbol.27 In Cu6Cu and Cu6Cr compounds, the complex entities are four connected by single π–π stacking interactions with two adjacent polynuclear entities and by double π–π stacking interactions with another two ones that require the interacting entities to be perpendicularly oriented among them.
cCu6Zn and Cu6Co compounds, is six-connected by means of π–π interactions (comprising its six adeninato ligands) to three upper and to three lower ones to give a pcu topology with a 412·63 point symbol.27 In Cu6Cu and Cu6Cr compounds, the complex entities are four connected by single π–π stacking interactions with two adjacent polynuclear entities and by double π–π stacking interactions with another two ones that require the interacting entities to be perpendicularly oriented among them.
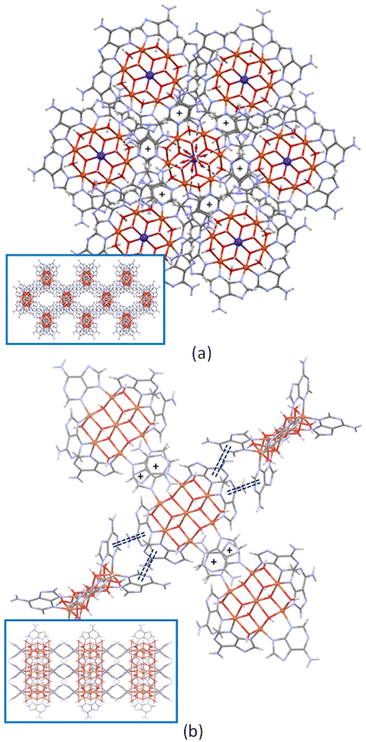 | ||
| Fig. 2 Details of the π-stacking interactions (+ symbol and double dashed lines) in compounds Cu6Zn (a) and Cu6Cu (b). The insets show a projection of the crystal packing. | ||
However, there is a subtle difference on the single π–π stacking interaction: the face exposed by the adeninato ligands for this interaction is at the side of the hydroxido ligand bridging the same metal centers in Cu6Cr whereas it employs the other face in Cu6Cu. This fact is at the bottom of their different space group and topology. Cu6Cu and Cu6Ni crystallize in the orthorhombic Cccm space group and present an sql/Shubnikov tetragonal plane net topology with a 44·62 point symbol, whereas Cu6Cr belongs to the monoclinic C2/c space group and it shows a cds CdSO4 like topology with a 65·8 point symbol.27
The sulfate anions are inserted in the cavities left by the π–π arrangement of the discrete heptameric entities and do not play a crucial role in directing the crystal packing, but provide mere counterbalance of the charge of the cationic entities. Each sulfate anion in Cu6Co, with a S–O bond lying in a three-fold axis, is hydrogen bonded like a tripod to three OH groups of the heptameric cation, whereas in the isostructural Cu6Zn compound the disposition of the sulfate anion differs, with only one of the sulfate O-atoms placed on the ternary axis (Fig. 3). In the Cu6Cr compound, the sulfate arrangement is similar to Cu6Zn, but the total site occupancy for each sulfate is set to 1/2 to counterbalance the charge of the complex entity.
The above-described supramolecular assembling of cations and anions in all the compounds leads to a three-dimensional crystal packing with channels that occupy a very significant percentage of the total unit cell volume: from 32% (Cu6Cu) to 51% (Cu6Zn). These channels are occupied by crystallization water molecules. The innocent structural role of the sulfate anions, the high tendency of the heptameric cation to form crystal networks sustained by supramolecular adeninato⋯adeninato π–π interactions, and the intrinsic porosity of the these networks suggest the insertion of other guest molecules as feasible, as corroborated by the fact that the trigonal Cu6Zn and Cu6Co compounds present the same space group and a very similar cell parameters to those of the previously reported [Cu7(μ-adeninato-κN3:κN9)6(μ3-OH)6(μ-OH2)6](NHEt3)2(SO4)2·23H2O compound, whereas monoclinic Cu6Cr is isostructural with the [Cu7(μ-adeninato-κN3:κN9)6(μ3-OH)6(μ-OH2)6](NHEt3)2(SO4)2·42H2O compound.9 Both compounds show the co-crystallization of the (NHEt3)2(SO4) salt inside the channels of the supramolecular network of the heptameric cations without modifying it.
Magnetic characterization
Fig. 4 shows the thermal dependence of the χMT product measured at 1 kOe after cooling without an applied magnetic field (ZFC) and the magnetization curves at 2 K for compounds Cu6M. Data corresponding to previously published Cu6Cr have been included for comparative purposes.16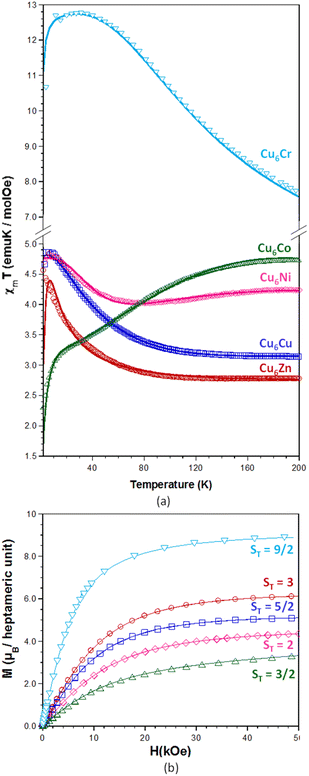 | ||
| Fig. 4 (a) Thermal evolution of the χMT products with the best fitting theoretical models depicted as a continuous line. (b) Magnetization curves at 2 K. | ||
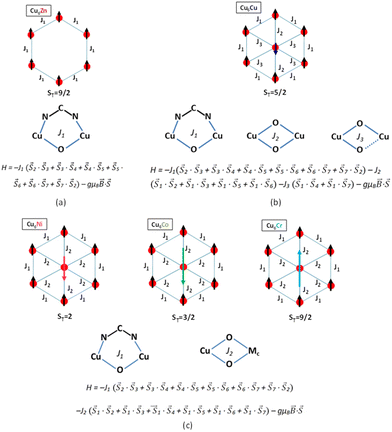
The experimental χMT values at 300 K agree with those values calculated for magnetically non interacting six Cu(II) and one central MIII or MII atoms, indicating that these compounds are still within the paramagnetic regime at room temperature with the exception of compound Cu6Cr which shows a slightly higher and not constant value of χMT near room temperature. On the other hand, the thermal evolution of the χMT products and the ST value observed in the magnetization curves make clear that compounds Cu6Zn and Cu6Cr are ferromagnetic whereas compounds Cu6Cu, Cu6Ni and Cu6Co are ferrimagnetic, in good agreement with the magnetic ordering and magnetic superexchange pathways depicted in Fig. 5.
Moreover, a slight decrease of the χMT product to below 5 K happens, which has been attributed to the presence of very weak intermolecular antiferromagnetic superexchange pathways mediated by the supramolecular interactions that hold the heptameric entities together. In the case of compound Cu6Co, which presents a more accused decrease, this behaviour can be explained by the presence of a ground state zero-field splitting of cobalt(II) ion due to its great orbital contribution28–30 that it is added to the previously described intermolecular antiferromagnetic interactions. The magnetization curves at 2 K do not show hysteresis indicative of the absence of single-molecule magnet behaviour up to this temperature, despite the non-zero spin ground state. A fitting of the χMT curves above 10 K was performed using the MagProp software tool distributed with the DAVE.31 The resulting magnetic coupling constants (Table 1) for the superexchange magnetic pathways depicted in Fig. 5 are in concordance with the expectations on the magnetic topology inferred from the saturation magnetization of Cu6M clusters. The magnetic data fitting of Cu6Co has not been performed because the complexity of the cobalt(II) magnetic behaviour would require the introduction of additional parameters that would lead to an over parametrization of the system.
| J 1 | J 2 | J 3 | zJ’ | S T (2 K) | |
|---|---|---|---|---|---|
| a J 1–3 (cm−1). | |||||
| Cu6Zn | +18 | — | — | −0.36 | 3 |
| Cu6Cu | +97 | −212 | +49 | −0.03 | 5/2 |
| Cu6Ni | +47 | −31 | — | — | 2 |
| Cu6Cr | +80 | +50 | — | −0.02 | 9/2 |
In all compounds, the external superexchange interaction between the CuII ions bridged by μ-adeninato and μ3-OH bridges (J1) results in ferromagnetic values. Usually, the presence of both non-linear NCN bridges and wide angle μ-hydroxido bridges (ca. 104°) cause strong antiferromagnetic couplings.32,33 However, the coexistence of these two types of bridges connecting the same metal centers counterbalances their effects.34–36 In fact, the splitting of the molecular magnetic orbitals is reversed for each type of bridging ligand (orbital counter-complementarity), thus leading to an almost negligible energy difference between them and, as a consequence, to the observed ferromagnetic interaction.
The radial magnetic pathway J2, involving double short coordination bond distance μ-OH bridges, depends on the nature of the central metal ion. In Cu6Zn, the diamagnetic nature of Zn(II) simplifies the magnetic superexchange pathways solely to external J1 and thus, it provides a ferromagnetic compound with ST = 3. In compounds Cu6Ni, Cu6Co and Cu6Cr with paramagnetic metal centers, the nature of the magnetic orbitals determines the parallel or antiparallel alignment between the magnetic spins of the peripheral and central paramagnetic centres. In the case of Cu6Cr, a total spin of 9/2 results from a ferromagnetic interaction of the central chromium(III) ion with the ferromagnetically coupled Cu6-ring. The ferromagnetic nature of this coupling is expectable considering the orbital orthogonality taking place between copper(II) (eg) and chromium(III) (t2g) magnetic orbitals. In compounds Cu6Co and Cu6Ni, the presence of eg symmetry magnetic orbitals ensures an efficient overlap through the hydroxido bridges and an antiferromagnetic coupling leading to ST = 3/2 and 2, respectively.37–40 The superexchange magnetic pathways in Cu6Cu are more complex due to the Jahn–Teller tetragonal elongation present in the central copper(II) atom. The simplest Hamiltonian describing the magnetic behaviour of this compound involves an additional third superexchange magnetic pathway (J3; see Fig. 5b). J3 involves a mixture of equatorial–equatorial (short–short) and equatorial–axial (short–long) coordinated μ-OH bridges, whereas, as previously stated J2 presents only an equatorial–equatorial (short–short) arrangement of the bridging hydroxide ligands. The antiferromagnetic nature of J2 agrees with that stated by Hatfield et al. for symmetrically double bridged hydroxido dinuclear complexes, in which angles larger than 98.5° promote an antiferromagnetic coupling.41 On the other hand, the weak ferromagnetic J3 interaction is related to the orthogonality between the magnetic orbitals imposed by the combination of symmetric and asymmetric μ-OH bridges. According to previous results, copper(II) centres bridged by this arrangement of the hydroxide bridges usually show a ferromagnetic behaviour with J values ranging from +10 to +90 cm−1.42 As a consequence of the presence of these three magnetic pathways, a spin frustration situation arises as there is no optimal spin ordering within the heptameric entity that could fulfill all the magnetic interaction preferences. The relative strength of these pathways: |J2(antiferromagnetic)|, |J1(ferromagnetic)| > |J3(ferromagnetic)| determines a ST = 5/2 ground state as observed in its magnetization curve at 2 K.
Magnetic sustentation experiments
As previously stated, these compounds establish complex magnetic interactions at low temperatures, but at room temperature they are well placed in the paramagnetic regime as it can be deduced from their χMT product at room temperature with the exception of Cu6Cr as mentioned previously. Therefore, the attraction force exerted by a relatively strong external magnetic field (i.e. that of magnets or electromagnets) on the particles of the samples is not strong enough to overcome the earth gravity attraction under normal conditions and, as a consequence, no displacement takes place on these particles. Contrarily, under attenuated gravity force, such as it occurs for particles suspended in a liquid, the magnetic field attraction is capable to sustain the particles avoiding their deposition at the bottom and even to induce their motion upon magnetic field shifts (Fig. 6). In this sense, a double pole electromagnet was employed in order to get fine control over the applied magnetic field. The equation that accounts for the attraction between the paramagnetic particles and the magnetic field is: F = ∇(m·H), where the gradient ∇ is the change of the quantity m·H per unit distance (m: magnetic dipole of the particle and H: external magnetic field), and the direction is that of the maximum increase of m·H. If m is aligned with H, as it is the case for paramagnetic particles, the gradient brings the particles towards the regions of maximum H-field.The paramagnetic nature of the particles implies that their magnetic dipole is related to the external magnetic field and assuming the particles are small, it can be considered constant and taken away from the gradient (eqn (1)):
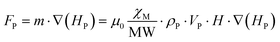 | (1) |
The magnetic force on the particles is not uniform on the whole surface of the pole but it becomes the maximum at the edge, because of the maximum magnetic field gradient placed there. Therefore, the particles are going to accumulate preferentially at this position where the magnetic attraction force is opposite to the gravitation force (Fig. 6).
The use of an electromagnet that allows dialling the magnetic field at the expense of the experimentalist facilitates determining the critical magnetic field at which the particles fall from the pole bottom edge. The molecular susceptibility can be estimated, in a first approximation, using spin-only expression depicted using eqn (2):
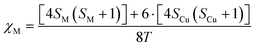 | (2) |
Considering eqn (1) and (2), and having in mind that the buoyancy force exerted by the solvent on the particles applies only to the compound framework (not to the volume occupied by the pores of the material, as the solvent molecules placed there freely exchange with the solution molecules), the mentioned critical magnetic field can be calculated from the following expression (3):
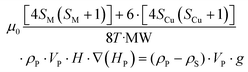 | (3) |
| Formula | MW (g mol−1) | ρ P (cm3 g−1) | 4SM (SM + 1) | |
|---|---|---|---|---|
| Cu6Zn | [Cu6Zn(C5H4N5)6(OH)6(OH2)6](SO4) | 1557 | 2.09 | 0 |
| Cu6Cu | [Cu6Cu(C5H4N5)6(OH)6(OH2)4](SO4) | 1520 | 2.08 | 3 |
| Cu6Ni | [Cu6Ni(C5H4N5)6(OH)6(OH2)4](SO4) | 1515 | — | 8 |
| Cu6Co | [Cu6Co(C5H4N5)6(OH)6(OH2)6](SO4) | 1551 | 2.11 | 15 |
| Cu6Cr | [Cu6Cr(C5H4N5)6(OH)6(OH2)6](SO4)1.5 | 1592 | 2.18 | 15 |
Accepting those two approximations implies that now there are only two variables: 4SM(SM + 1) and H·∇(HP). The remaining parameters in the formula can be simplified into A and B constant terms (eqn (4) and (5)) to lead to eqn (6):
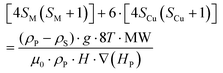 | (4) |
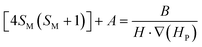 | (5) |
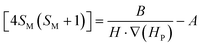 | (6) |
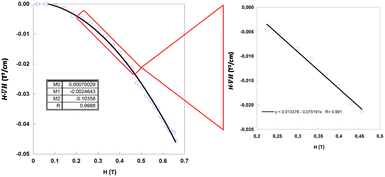
Therefore, the experimental points at which the particles detach from the pole must fit to a straight line in a 4SM(SM + 1) vs 1/[H·∇(HP)] plot. In order to check the validity of these equations, the magnetic field and its gradient were measured on the pole surface of the electromagnet at different current I values. Fig. 7 depicts the magnetic field measured along the plane corresponding to the surface of the magnetic pole in the vertical z-axis. The magnetic data were fitted to a fourth order polynomial expression, and ∇H and H·∇H were computed. The particles are sustained at the position where the upwards force is maximum; according to eqn (1), it corresponds to the position of the most negative H·∇H product: close to the lower end of the pole. Fig. 8 shows the dependence of the most negative H·∇H product for each current value with the magnetic field measured in the center of the pole.
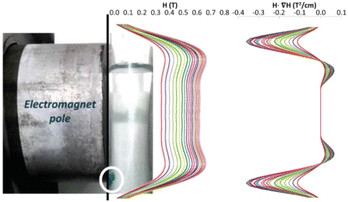 | ||
| Fig. 7 Magnetic field profile [H and H·∇(H)] on the electromagnet pole along the dashed line. The different colours refer to the applied intensity current: increasing from 0.0 to 2.5 A (step: 0.1 A). | ||
From the experimental data shown in the 4SM(SM + 1) vs 1/[H·∇(HP)] plot (Fig. 9a), the values lie in a straight line with a positive slope as predicted with the exception of Cu6Co and Cu6Cr. The first one is probably due to the well-known orbital contribution of CoII that significantly deviates the spin-only susceptibility towards greater values. The second exception corresponds to Cu6Cr whose magnetic coupling regime is closer to room temperature and it makes the spin only susceptibility calculation less realistic. It is noteworthy that at magnetic fields above 0.4 T, there is a linear relationship between ∇H and H (Fig. 9b); as a consequence the experimental data, all of them lying within this H region show also a linear correlation between 4SM(SM + 1) and 1/H.
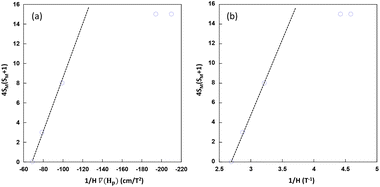 | ||
| Fig. 9 Spin-term dependence with respect to 1/[H·∇(HP)] (a) and 1/H (b) values at which the particles are detached from the electromagnet pole when submerged in MeOH. | ||
Once it has been observed that these sustentation experiments provide a characteristic value for each compound depending on the total spin of the metal centers, it can be extended to the quantification of adsorbed molecules within the channels of these materials. Any increase of the particle weight (due to a sorption phenomenon for example) will have a profound effect on the subtle balance between the magnetic attraction, gravity and buoyancy forces that determine the critical magnetic field at which the particles are detached from the poles of the electromagnet. Therefore, according to eqn (1)–(4) the modification of this critical value towards higher magnetic fields will indicate the sorption of the adsorbate molecules within the pores of the material. It has been exemplified by placing 15 mg of Cu6Cu in 2 mL of an aqueous solution containing 15 mg of different adsorbates (or 15 μL if the adsorbate is liquid) for 12 hours at room temperature (25 °C) while gently stirred. Afterwards, the critical magnetic field is determined by placing these particles in a test tube attached to the pole of the electromagnet and containing distilled water. A film describing the experiment is provided in the ESI.†
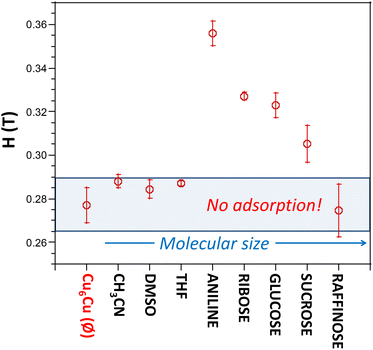
The results are depicted in Fig. 10, where we can observe that Cu6Cu presents both the selectivity based on the chemical nature of the adsorbates and also a size exclusion based selectivity. Chemical nature selectivity is observed for CH3CN, DMSO and THF which provide negligible deviation with respect to the pristine Cu6Cu compound (value indicated as Ø). These molecules are small enough to get into the pores of this material but do not interact strong enough to be adsorbed. In fact, the presence of adeninato molecules in the periphery of the heptameric entities makes this material well suited to strongly interact with molecules able to establish strong hydrogen bonding or π-stacking interactions. It becomes clear when observing a strong increase of the critical magnetic field measured for aniline, ribose and glucose. Besides, using a disaccharide (sucrose) and a trisaccharide (raffinose), the size exclusion selectivity becomes evident, with no sorption at all for raffinose. A detailed study of the size and shape compatibility between the main void present in this compound (11.4 × 6.9 × 5.9 Å) and those of the adsorbate molecules helps understanding the different sorption capacity of Cu6Cu toward the saccharides (Fig. S16†). The shapes of ribose (8.7 × 6.8 × 5.2 Å) and glucose (9.9 × 7.4 × 5.2 Å) monosaccharides fit relatively well inside this void leading to a high sorption capacity. In the case of sucrose disaccharide (11.2 × 9.1 × 6.7 Å), its dimensions are close or even slightly greater than the dimensions of the main void. However due to the flexibility of the supramolecular architecture and the conformational flexibility of sucrose it can accommodate into these voids but at the cost of a lower sorption capacity towards this adsorbate. Finally, in the case of raffinose trisaccharide (15.7 × 10.7 × 8.7 Å), its dimensions are far above those of the main void and no sorption is observed.
As is below described, the equations governing this phenomena (eqn 7, 8, 9 and 10) indicate a linear correlation between the adsorbed mass of guest molecules and the H·∇(H) product, in such a way that the greater the deviation with respect to the pristine critical magnetic value, the greater the mass of adsorbates captured by the porous material. To demonstrate this relation, we must separate the magnetic attraction force, gravitation and buoyancy in terms accounting for the framework of the compound (the heptameric entity plus the sulfate counterions) and for the adsorbates. The solvent molecules placed in the channels are not taken into consideration as previously stated.
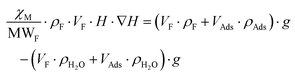 | (7) |
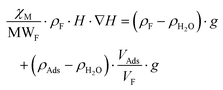 | (8) |
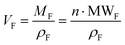 and
and 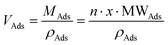 , then
, then 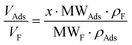 (n being the times the framework formula is repeated in the particle and x is the relative ratio between the adsorbed guest molecules and the compound framework formula). As a consequence eqn (8) transforms into eqn (9):
(n being the times the framework formula is repeated in the particle and x is the relative ratio between the adsorbed guest molecules and the compound framework formula). As a consequence eqn (8) transforms into eqn (9):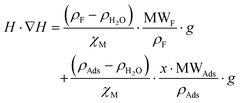 | (9) |
In this latter equation, as all parameters except “H·∇H” and “x·MWAds” are constants (we assume that the ρ values of the different adsorbates are nearly the same), the above equation can be simplified to:
| H·∇H = A + B·x·MWAds = A + B·MAds | (10) |
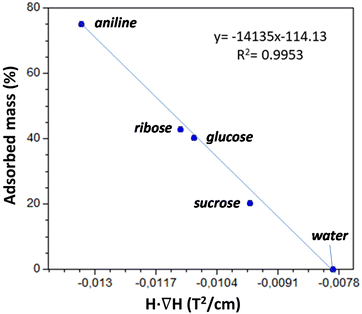 | ||
| Fig. 11 Linear correlation between the adsorbed mass percentage and the H·∇(H) value at which the particles of the adsorbent are detached from the electromagnet pole. | ||
Conclusions
In summary, we have shown that it is possible to exploit the coordination environment diversity present in homometallic polynuclear entities to incorporate selected metal centers and tailor in this way the magnetic properties of the resulting heterometallic compounds. The room temperature magnetic response of these porous materials in the presence of external magnetic fields is strong enough to provide a novel sorption characterization technique. In this sense, the magnetic sustentation experiments that allow determining the minimum magnetic field required to attach these particles to the electromagnet pole provide a straightforward parameter that can be related to the amount of unpaired electrons and also to the density of the material. We have analyzed in depth the first of these parameters observing a linear correlation between 4SM(SM + 1) and 1/[H·∇(HP)] that can provide a new method to estimate the susceptibility value of a compound if its density is known.In a previous work, we exploited the variation of the second parameter (density) to monitor how [Cu6Cr(μ-adeninato-κN3:κN9)6(μ3-OH)6(μ-OH2)6]3+ was able to capture an increasing amount of ibuprofen and naproxen anti-inflammatory drugs.16 In this work, we have gone further being able to demonstrate the sorption selectivity of compound Cu6Cu which showed a selectivity based on both the chemical nature of the adsorbate and its size. Finally, we just emphasize that this study has been performed directly in solution based on a property of the adsorbent and not as usually based on an indirect assessment by measuring the adsorbate remaining in solution.
Author contributions
The manuscript was written through contributions of all authors. These authors (R. P.-A., S. M.-G and J. P.-C.) contributed equally. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been funded by Eusko Jaurlaritza/Gobierno Vasco (IT1291-19; IT1722-22; ELKARTEK program KK-2022/00109), Ministerio de Universidades and the European Union-Next Generation EU (marsa21/52, R. P. A.), and Ministerio de Ciencia e Innovación (PID2019-108028GB-C21). Technical and human support provided by SGIker (UPV/EHU, MICINN, GV/EJ, ESF) is also acknowledged.References
- K. S. Pedersen, J. Bendix and R. Clerac, Single-molecule magnet engineering: building-block approaches, Chem. Commun., 2014, 50, 4396–4415 RSC.
- D. Maniaki, E. Pilichos and S. P. Perlepes, Coordination Clusters of 3d-metals that behave as single-molecule magnets (SMMs): synthetic routes and strategies, Front. Chem., 2018, 6, 461 CrossRef CAS PubMed.
- L. Bogani and W. Wernsdorfer, Molecular spintronics using single-molecule magnets, Nat. Mater., 2008, 7, 179–186 CrossRef CAS PubMed.
- F. D. Natterer, K. Yang, W. Paul, P. Willke, T. Choi, T. Greber, A. J. Heinrich and C. P. Lutz, Reading and writing single-atom magnets, Nature, 2017, 543, 226–228 CrossRef CAS PubMed.
- A. Dey, P. Bag, P. Kalita and V. Chandrasekhar, Heterometallic CuII–LnIII complexes: Single molecule magnets and magnetic refrigerants, Coord. Chem. Rev., 2021, 432, 213707 CrossRef CAS.
- D. Shao and X.-Y. Wang, Development of single-molecule magnets, Chin. J. Chem., 2020, 38, 1005–1018 CrossRef CAS.
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Magnetic bistability in a metal-ion cluster, Nature, 1993, 365, 141–143 CrossRef CAS.
- A. Zabala-Lekuona, J. M. Seco and E. Colacio, Single-molecule magnets: from Mn12-ac to dysprosium metallocenes, a travel in time, Coord. Chem. Rev., 2021, 441, 2139842 CrossRef.
- R. Pérez-Aguirre, G. Beobide, O. Castillo, I. de Pedro, A. Luque, S. Pérez-Yáñez, J. Rodríguez-Fernández and P. Román, 3D magnetically ordered open supramolecular architectures based on ferrimagnetic Cu/adenine/hydroxide heptameric wheels, Inorg. Chem., 2016, 55, 7755–7763 CrossRef PubMed.
- J. Pascual-Colino, G. Beobide, O. Castillo, I. da Silva, A. Luque and S. Pérez-Yáñez, Porous supramolecular architectures based on π-stacking interactions between discrete metal-adenine entities and the non-DNA theobromine/caffeine nucleobases, Cryst. Growth Des., 2018, 18, 3465–3476 CrossRef CAS.
- J. Pascual-Colino, G. Beobide, O. Castillo, P. Lodewyckx, A. Luque, S. Pérez-Yáñez, P. Román and L. F. Velasco, Adenine nucleobase directed supramolecular architectures based on ferrimagnetic heptanuclear copper(II) entities and benzenecarboxylate anions, J. Inorg. Biochem., 2020, 202, 110865 CrossRef CAS PubMed.
- O. Kahn, Y. Pei and Y. Journaux, Orthogonality of the magnetic orbitals and ferromagnetic interaction, Mol. Cryst. Liq. Cryst., 1989, 176, 429–441 CrossRef CAS.
- T. Glaser, H. Theil, I. Liratzis, T. Weyhermüller and E. Bill, Ferromagnetic coupling by orthogonal magnetic orbitals in a heterodinuclear (CuIIVIV) = O complex and in a homodinuclear CuIICuII complex, Inorg. Chem., 2006, 45, 4889–4891 CrossRef CAS PubMed.
- W. Cai, J. D. Bocarsly, A. Gomez, R. J. Letona Lee, A. Metta-Magaña, R. Seshadri and L. Echegoyen, High blocking temperatures for DyScS endohedral fullerene single-molecule magnets. High blocking temperatures for DyScS endohedral fullerene single-molecule magnets, Chem. Sci., 2020, 11, 13129–13136 RSC.
- J. Cirera, E. Ruiz, S. Álvarez, F. Neese and J. Kortus, How to build molecules with large magnetic anisotropy, Chem. – Eur. J., 2009, 15, 4078–4087 CrossRef CAS PubMed.
- R. Pérez-Aguirre, B. Artetxe, G. Beobide, O. Castillo, I. de Pedro, A. Luque, S. Pérez-Yáñez and S. Wutke, Ferromagnetic supramolecular metal-organic frameworks for active capture and magnetic sensing of emerging drug pollutants, Cell Rep. Phys. Sci., 2021, 2, 100421 CrossRef.
- A. Earnshaw, in Introduction to Magnetochemistry, Academic Press, London, 1968 Search PubMed.
- CrysAlis PRO, Agilent Technologies, UK Ltd, Yarnton, England, 2011 Search PubMed.
- A. Altomare, M. Cascarano, C. Giacovazzo and A. Guagliardi, Completion and refinement of crystal structures with SIR92, J. Appl. Crystallogr., 1993, 26, 343–350 CrossRef.
- L. J. Farrugia, WinGX suite for small-molecule single-crystal crystallography, J. Appl. Crystallogr., 1999, 32, 837–838 CrossRef CAS.
- G. M. Sheldrick, A short history of SHELX, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- J. Cepeda, O. Castillo, J. P. García-Terán, A. Luque, S. Pérez-Yáñez and P. Román, Supramolecular architectures and magnetic properties of self-assembled windmill-like dinuclear copper(II) complexes with purine ligands, Eur. J. Inorg. Chem., 2009, 2344–2353 CrossRef CAS.
- S. Pérez-Yáñez, G. Beobide, O. Castillo, J. Cepeda, A. Luque and P. Román, Structural diversity in a copper(II)/isophthalato/9-methyladenine system. From one- to three-dimensional metal-biomolecule frameworks, Cryst. Growth Des., 2013, 13, 3057–3067 CrossRef.
- P. Van der Sluis and A. L. Spek, BYPASS: an effective method for the refinement of crystal structures containing disordered solvent regions, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46, 194–201 CrossRef.
- A. L. Spek, Single-crystal structure validation with the program PLATON, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- J. Rodríguez-Carvajal, FULLPROF 2000, Version 2.5d, Laboratoire Léon Brillouin (CEA-CNRS), Centre d’Études deSaclay, Gif sur Yvette Cedex, Grenoble, France, 2003 Search PubMed.
- V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Applied topological analysis of crystal structures with the program package ToposPro, Cryst. Growth Des., 2014, 14, 3576–3586 CrossRef CAS.
- J. Krzystek, S. A. Zvyagin, A. Ozarowski, A. T. Fiedler, C. T. Brunold and J. Telser, Definitive spectroscopic determination of zero-field splitting in high-spin cobalt(II), J. Am. Chem. Soc., 2004, 126, 2148–2155 CrossRef CAS PubMed.
- J. Kobak, A. Bogucki, T. Smoleński, M. Papaj, M. Koperski, M. Potemski, P. Kossacki, A. Golnik and W. Pacuski, Direct determination of the zero-field splitting for a single Co2+ ion embedded in a CdTe/ZnTe quantum dot, Phys. Rev. B, 2018, 97, 045305 CrossRef CAS.
- M. Idešicová, J. Titiš, J. Krzystek and R. Boča, Zero-field splitting in pseudotetrahedral Co(II) complexes: a magnetic, high-frequency and -field EPR, and computational study, Inorg. Chem., 2013, 52, 9409–9417 CrossRef PubMed.
- R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, DAVE: a comprehensive software suite for the reduction, visualization, and analysis of low energy neutron spectroscopic data, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358 CrossRef CAS PubMed.
- D. Sonnenfroh and R. W. Kreilick, Exchange coupling in copper dimers with purine ligands, Inorg. Chem., 1980, 19, 1259–1262 CrossRef CAS.
- L. Cañadillas-Delgado, O. Fabelo, J. Pasán, F. S. Delgado, F. Lloret, M. Julve and C. Ruiz-Pérez, Unusual (μ-aqua)bis(μ-carboxylate) bridge in homometallic M(II) (M = Mn, Co and Ni) two-dimensional compounds based on the 1,2,3,4-butanetetracarboxylic acid: synthesis, structure, and magnetic properties, Inorg. Chem., 2007, 46, 7458–7465 CrossRef PubMed.
- S. Pérez-Yáñez, O. Castillo, J. Cepeda, J. P. García-Terán, A. Luque and P. Román, Analysis of the interaction between adenine nucleobase and metal–malonato complexes, Eur. J. Inorg. Chem., 2009, 3889–3899 CrossRef.
- Y. Nishida and S. Kida, Crystal structures and magnetism of binuclear copper(II) complexes with alkoxide bridges. Importance of orbital complementarity in spin coupling through two different bridging groups, J. Chem. Soc., Dalton Trans., 1986, 2633–2640 RSC.
- V. McKee, M. Zvagulis and C. A. Reed, Further insight into magnetostructural correlations in binuclear copper(II) species related to methemocyanin: x-ray crystal structure of 1,2-.mu.-nitrito complex, Inorg. Chem., 1985, 24, 2914–2919 CrossRef CAS.
- Y. Z. Zheng, M. L. Tong, W. Xue, W. X. Zhang, X. M. Chen, F. Grandjean and G. J. Long, A “star” antiferromagnet: a polymeric iron(III) acetate that exhibits both spin frustration and long-range magnetic ordering, Angew. Chem., 2007, 119, 6188–6192 CrossRef.
- K. C. Mondal, V. Mereacre, G. E. Kostakis, Y. Lan, C. E. Anson, I. Prisecaru and A. K. Powell, A strongly spin-frustrated FeIII7 complex with a canted intermediate spin ground state of S = 7/2 or 9/2, Chem. – Eur. J., 2015, 21, 10835–10842 CrossRef CAS PubMed.
- W. E. Hatfield, Superexchange interactions in copper(II) complexes, ACS Symp. Ser., 1974, 5, 108–141 CrossRef CAS.
- D. L. Lewis, K. T. McGregor, W. E. Hatfield and D. J. Hodgson, Preparation and structural and magnetic characterization of beta-di-u-hydroxo-bis[2-(2-dimethylaminoethyl)pyridine]dicopper(II) perchlorate, Inorg. Chem., 1974, 13, 1013–1019 CrossRef CAS.
- V. H. Crawford, H. W. Richardson, J. R. Wasson, D. J. Hodgson and W. E. Hatfield, Relation between the singlet-triplet splitting and the copper-oxygen-copper bridge angle in hydroxo-bridged copper dimers, Inorg. Chem., 1976, 15, 2107–2110 CrossRef CAS.
- J. Tercero, E. Ruiz, S. Alvarez, A. Rodríguez-Fortea and P. Alemany, Density functional study of magnetostructural correlations in cubane complexes containing the Cu4O4 core, J. Mater. Chem., 2006, 16, 2729–2735 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Films describing the magnetic sustentation experiment, details of FTIR spectroscopic data, thermogravimetric measurements, X-ray photoelectronic spectroscopy data, and crystallographic and structural data. CCDC 2153696–2153698. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2qi01994a |
| ‡ These authors contributed equally. |
§ Crystallographic data. Cu6Zn: crystal system: trigonal; space group: R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c; cell parameters: a = b = 19.108(1) Å, c = 43.046(3) Å and V = 13611(2) Å3. Cu6Cu: crystal system: orthorhombic; space group: Cccm; cell parameters: a = 10.5080(3) Å, b = 24.8920(8) Å, c = 27.0312(9) Å, and V = 7070.4(4) Å3. Cu6Co: crystal system: trigonal; space group: R c; cell parameters: a = b = 19.108(1) Å, c = 43.046(3) Å and V = 13611(2) Å3. Cu6Cu: crystal system: orthorhombic; space group: Cccm; cell parameters: a = 10.5080(3) Å, b = 24.8920(8) Å, c = 27.0312(9) Å, and V = 7070.4(4) Å3. Cu6Co: crystal system: trigonal; space group: R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c; cell parameters: a = b = 19.058(3) Å, c = 43.157(9) Å and V = 13 c; cell parameters: a = b = 19.058(3) Å, c = 43.157(9) Å and V = 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 575(5) Å3. See the ESI† for further details. 575(5) Å3. See the ESI† for further details. |
| This journal is © the Partner Organisations 2023 |