Enabling quantitative analysis of complex polymer blends by infrared nanospectroscopy and isotopic deuteration†
Nathaniel
Prine
 a,
Zhiqiang
Cao
b,
Song
Zhang
a,
Zhiqiang
Cao
b,
Song
Zhang
 a,
Tianyu
Li
bc,
Changwoo
Do
a,
Tianyu
Li
bc,
Changwoo
Do
 d,
Kunlun
Hong
be,
Camille
Cardinal
a,
Travis L.
Thornell
d,
Kunlun
Hong
be,
Camille
Cardinal
a,
Travis L.
Thornell
 f,
Sarah E.
Morgan
f,
Sarah E.
Morgan
 a and
Xiaodan
Gu
a and
Xiaodan
Gu
 *a
*a
aSchool of Polymer Science and Engineering, The University of Southern Mississippi, Hattiesburg, Mississippi 39406, USA. E-mail: xiaodan.gu@usm.edu
bCenter for Nanophase Materials Sciences, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
cDepartment of Materials Science and Engineering, University of Tennessee, Knoxville, Tennessee 37996, USA
dNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
eDepartment of Chemical & Biomolecular Engineering, University of Tennessee, Knoxville, Tennessee 37996, USA
fU.S. Army Engineer Research and Development Center, Vicksburg, Mississippi 39180, USA
First published on 4th April 2023
Abstract
Atomic-force microscopy coupled with infrared spectroscopy (AFM-IR) deciphers surface morphology of thin-film polymer blends and composites by simultaneously mapping physical topography and chemical composition. However, acquiring quantitative phase and composition information from multi-component blends can be challenging using AFM-IR due to the possible overlapping infrared absorption bands between different species. Isotope labeling one of the blend components introduces a new type of bond (carbon-deuterium vibration) that can be targeted using AFM-IR and responds at wavelengths sufficiently shifted toward unoccupied regions (around 2200 cm−1). In this project, AFM-IR was used to probe the surface morphology and chemical composition of three polymer blends containing deuterated polystyrene; each blend is expected to exhibit various degrees of miscibility. AFM-IR results successfully demonstrated that deuterium labeling prevents infrared spectral overlap and enables the visualization of blend phases that could not normally be distinguished by other scanning probe techniques. The nanoscale domain composition was resolved by fast infrared spectrum analysis. Overall, we presented isotope labeling as a robust approach for circumventing obstacles preventing the quantitative analysis of multiphase systems by AFM-IR.
Introduction
Understanding the morphology of polymer blends in the thin-film state is critical to developing future plastic recycling for sustainability, optoelectronic materials, chemical sensors, and functional coatings.1–3 Currently, few characterization methods can distinguish individual components while measuring relative domain composition at the nanometer scales. Traditional direct and indirect morphology characterization techniques such as small-angle X-ray scattering (SAXS),4,5 small-angle neutron scattering (SANS),6–8 and atomic-force microscopy (AFM)9,10 identify blend components based on the difference in scattering-length density (Δρ, contrast) due to varied electron or nuclei density, geometry, and energy-dissipation, respectively. However, these characterization techniques have limitations when identifying individual materials in blends possessing near-identical chemical composition and physical response.Specifically, for SAXS, measuring phase behavior for multi-component polymeric blends with similar electron density results in weak coherent elastic scattering signals. Recent development in resonant soft X-ray scattering partially addressed this problem by relying on the enhance scattering contrast using near edge absorption phenomenon.6–8 On the other hand, SANS provides finely tuned scattering contrast through isotopic labeling; however, it is limited by the requirement for large sample quantities and limited neutron instrument availability and low neutron flux. Furthermore, SAXS and SANS only provide an averaged representation of blend morphology in reciprocal space, neglecting local information such as localized domain size and size distribution.
The remaining class of techniques for interrogating surface morphology is scanning probe microscopy (SPM). SPM techniques generate contrast by detecting variations in topography and energy dissipation response to an external stimulus; however, poor contrast observed when measuring blends containing chemically and mechanically similar components plagues many SPM techniques.
Among the various SPM techniques, scattering-type scanning near-field optical microscopy (s-SNOM) has gained attention for its ability to provide high-resolution surface morphological and spectrometric information.9,10 While s-SNOM operates under ambient conditions and is suitable for inorganic materials such as photonics and 2-D materials that efficiently scatter light, it has certain limitations when applied to organic materials such as polymers, blends, and composites. For example, s-SNOM requires theoretical models to interpret data, which can complicate data analysis.11 The technique is also prone to artifacts such as band distortion and thermal drift, due to the sensitivity of s-SNOM to sample thickness and substrate induced shifting which can negatively impact data accuracy.11
Fitting into the category of SPM, Atomic force microscopy paired with infrared spectroscopy (AFM-IR) bridges many of the gaps left by other techniques by pairing nanoscale, topographical resolution with robust chemical sensitivity to provide a detailed chemical map of material surfaces.11–14 The technique works fundamentally by targeting the area underneath the AFM probe with a pulsed, tuneable infrared laser as the probe rasters across the material surface. When the tuned IR laser excites specific molecular bonds, the surface underneath the probe thermally expands. As the cantilever probe oscillates in response to the thermal expansion, the cantilever deflection is translated by a Fourier-transform algorithm to produce spectra analogous to Fourier-Transform Infrared Spectroscopy (FTIR).11,15
An infinite number of applications exist for AFM-IR in polymer science, where the conformation, crystallization, and chemical moieties influence the infrared absorption of polymer chains. Particularly in polymer composite matrices and blends, AFM-IR has found many uses.11,16 For example, Fuchs et al., used AFM-IR to monitor the degradation of a phenylphosphine oxide (PPO)-modified epoxy when exposed to atomic oxygen.17 After atomic oxygen exposure, samples containing low concentrations of PPO developed microscale nodes on the surface, indicating heterogeneous material decay. In contrast, samples containing higher concentrations of PPO maintained a comparatively homogenous surface.
In the field of stretchable electronics, Selivanova et al., used AFM-IR to investigate the distribution of a diketopyrrolopyrrole-based conjugated polymer with a low molecular weight branched polyethylene (BPE).18 AFM-IR analysis found that adding BPE induced a high degree of phase separation between the two blended materials. This observation helped determine the ideal blend ratio to produce a blend with favorable properties. Zhang et al., successfully used AFM-IR to map the distribution of a conjugated poly(diketopyrrolopyrrole) (DPP) blended with butyl rubber to correlate the performance of semiconductor composites with their morphology.16 AFM-IR images of blends with increasing levels of butyl rubber proved that the DPP-based polymer adopted a fibril-like structure within the continuous phase.16 Zheng et al., used AFM-IR to investigate the morphology of a covalently-embedded in situ rubber matrix (iRUM) which facilitated high elasticity without compromising electrical performance.19 The composition map generated by AFM-IR proved the interlocked fibril morphology and nanoscale domain sizes of the two complementary polymers.19
AFM-IR also has applications in organic photovoltaics, where device performance relies heavily on the carefully tuned morphology of conjugated polymer blends that compose the photoactive layer. For example, Zhu et al., successfully fabricated an organic solar cell achieving 16.88% power conversion efficiency using AFM-IR to understand how the photoactive blend changes with different solvents and annealing conditions.20 Therefore, AFM-IR has enabled the discovery of previously unexplored morphologies and guided the development of new materials and settled controversies relating to polymer physics.
Despite many exciting early discoveries, one apparent challenge of infrared-based techniques is distinguishing materials that absorb infrared light at similar resonance bands.11 Overlapping bands in the infrared spectrum cause thermal expansion uniformly across the sample surface, preventing the user from obtaining meaningful morphological contrast. One solution to this problem is attaching an infrared tag or selectively deuterating one of the blend components to sufficiently shift the IR absorption toward unoccupied frequency domains.11,21 To observe the distribution of ethylene(EP)-propylene(PP) copolymer dispersed in a blend of EP/PP, Rickard et al., chose to fully deuterate the copolymer instead of introducing an external molecular tag.13 In this case, the AFM-IR laser was tuned to the carbon-deuterium bond's unique resonance band, and the copolymer distribution was visualized at the micron scale. However, no quantitative blend information was acquired from these measurements, stopping short of pushing the capabilities of AFM-IR analysis. While the theoretical foundation is set for obtaining blend miscibility, no published reports use isotope labeling in conjunction with AFM-IR imaging to calculate quantitative polymer blend composition.
We first discuss the principles used in this work to study the composition and phase behavior of polymer blends. The morphology of polymer blends holds information beyond domain distribution and orientation. Even in inhomogeneous, phase-separated blends, individual phases intermix to a certain degree. These regions of intermixing are challenging to distinguish and quantify without special techniques such as resonant soft X-ray scattering (RSoXS).22 In traditional FTIR studies, the concentration of dilute solutions is calculated based on the Beer–Lambert law (eqn (1)):23,24
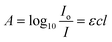 | (1) |
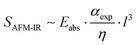 | (2) |
Centrone later highlighted the inverse proportionality of the AFM-IR signal to material thermal conductivity as a potential barrier to quantitative analysis, particularly in blends containing materials with significantly different thermal conductivity values.26 The thermal conductivity of a blend is a concentration-weighted average of the thermal conductivities of each blend component. For blend materials with different αexp/η values, the relationship between AFM-IR signal and sample concentration strongly deviates. Therefore, this correlation is only linear for blends containing materials with similar thermomechanical properties, such as polymer blends.26 Interested readers are referred to ref. 25 for a complete derivation of the linear relationship between the AFM-IR signal and sample concentration.25 Additionally, Lahiri and co-workers demonstrated that the relationship between AFM-IR signal and sample thickness remains linear for sample thickness values below 1 μm, highlighting another criterion for successful quantitative analysis of AFM-IR spectra.27 Kong et al., made notable contributions in pursuit of quantitative infrared imaging where a model sample of poly (methyl methacrylate) (PMMA) and P3HT was measured in hyperspectral mode using photo-induced force microscopy (PiFM) and principle component analysis (PCA) was used to assign principle component scores to individual pixels in the image.28 Using PCA, the presence of P3HT in PMMA aggregates was observed. PiFM and AFM-IR are similar techniques in that they both monitor probe response as a function of infrared laser absorption. PiFM is a ‘non-contact’ technique that relies on measuring the photoinduced gradient force between the probe and sample to generate contrast.28 In contrast, AFM-IR can be operated in either contact or tapping mode and directly detects rapid thermal expansion as the material responds to its resonant wavelengths of infrared energy.11 While PiFM and AFM-IR rely on different mechanisms to monitor the same chemical response, the work by Kong et al., demonstrates one of the first attempts to assign compositional scores to infrared nanospectroscopy data. However, Tang and co-workers were the first to obtain compositional values using calibration curves paired with AFM-IR analysis.29
Considering the findings from past works that paved the way for quantitative AFM-IR analysis, we perform the first in-depth, quantitative composition analysis of polymer blends containing a deuterium-labeled component. In contrast to the work by Kong et al., which utilized PCA methods, compositional AFM-IR information will be calculated using fundamental FTIR analysis methods related to the Beer–Lambert law.
In this work, we demonstrated the first in-depth morphology analysis of a complex ternary blend containing a deuterium-labeled component to bridge this fundamental gap in AFM-IR analysis. The first blend is comprised of poly(3-hexylthiophene) (P3HT) and deuterated polystyrene (dPS) and is expected to exhibit microscale phase separation. Deuterated polystyrene (dPS), polylactic acid (PLA), and polycarbonate (PC) comprise the second blend, and all demonstrate poor miscibility with one another. Lastly, a blend of dPS and protonated polystyrene (hPS) is measured to demonstrate the capability of AFM-IR to measure composition at the nanoscale in completely miscible blends. Our results indicated that isotope labeling is an effective tool for enhancing AFM-IR contrast in phase-separated and miscible blends.
Results
Three blends of deuterated with non-deuterated materials are investigated: dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P3HT, dPS
P3HT, dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PLA
PLA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PC, and dPS
PC, and dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hPS. All three blends are expected to exhibit various ranges of miscibility and spatial composition. We first demonstrate the use of deuterium labeling to generate a new resonance band sufficiently shifted away from overlapping frequencies for simplified quantitative analysis (Fig. 1a). Comparing the FTIR spectra for hPS, dPS, and P3HT in Fig. S1,† significant overlap can be observed between hPS and P3HT, obscuring each component's absorption contribution to the AFM-IR signal produced. P3HT was chosen as a proof-of-concept material because it is a well-studied and widely used semiconducting polymer, serving as a model for conjugated polymers. The blend of P3HT with dPS allows us to explore the potential of using infrared-tagged commodity plastics in optoelectronic applications. Additionally, this immiscible blend of dPS
hPS. All three blends are expected to exhibit various ranges of miscibility and spatial composition. We first demonstrate the use of deuterium labeling to generate a new resonance band sufficiently shifted away from overlapping frequencies for simplified quantitative analysis (Fig. 1a). Comparing the FTIR spectra for hPS, dPS, and P3HT in Fig. S1,† significant overlap can be observed between hPS and P3HT, obscuring each component's absorption contribution to the AFM-IR signal produced. P3HT was chosen as a proof-of-concept material because it is a well-studied and widely used semiconducting polymer, serving as a model for conjugated polymers. The blend of P3HT with dPS allows us to explore the potential of using infrared-tagged commodity plastics in optoelectronic applications. Additionally, this immiscible blend of dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P3HT (1
P3HT (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) serves as a model system to measure chemical composition because of its well-defined domains and represents a model blend of infrared-tagged commodity plastics with conjugated polymers.
1 v/v) serves as a model system to measure chemical composition because of its well-defined domains and represents a model blend of infrared-tagged commodity plastics with conjugated polymers.
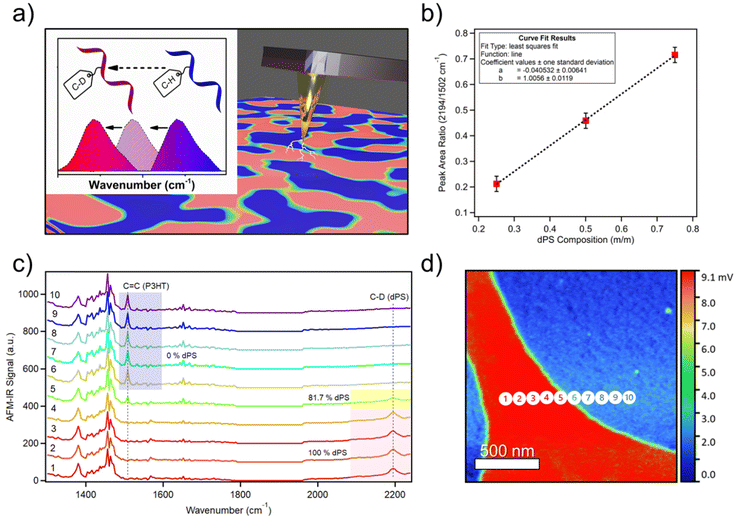 | ||
Fig. 1 Using deuterium to label polymers in multicomponent blends. (a) Deuterium labeling is used to shift FTIR resonance bands to unoccupied frequencies to distinguish blended materials using AFM-IR. (b) Calibration curve depicting the linear relationship between AFM-IR signal ratio of dPS/P3HT and chemical composition fraction of dPS. (c) AFM-IR spectra collected across the boundary of dPS/P3HT in Fig. 1d denoting in-plane P3HT carbon–carbon double bonds at 1502 cm−1 and stretching dPS carbon-deuterium bonds at 2194 cm−1. The percent of dPS composition is indicated adjacent to key spectra. (d) AFM-IR composition image acquired from dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P3HT blend highlighting dPS-rich regions in red. Numbered circles denote locations where spectra in Fig. 1c were collected. (Note, our laser does not cover 1800 to 1960 cm−1. Hence, there is no response in AFM-IR signal). P3HT blend highlighting dPS-rich regions in red. Numbered circles denote locations where spectra in Fig. 1c were collected. (Note, our laser does not cover 1800 to 1960 cm−1. Hence, there is no response in AFM-IR signal). | ||
A calibration curve (Fig. 1b) was generated by acquiring broadband spectra of dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P3HT samples of compositions ranging from 0–100% dPS (0% dPS being pure P3HT) and plotting the ratio of the AFM-IR signal intensity of the two polymers as a function of the known blend composition (raw calibration spectra found in Fig. S2a–c†) Afterward, broadband spectra were collected across the interface of dPS and P3HT, and the peak area ratios of the carbon-deuterium bond (2194 cm−1) and P3HT C
P3HT samples of compositions ranging from 0–100% dPS (0% dPS being pure P3HT) and plotting the ratio of the AFM-IR signal intensity of the two polymers as a function of the known blend composition (raw calibration spectra found in Fig. S2a–c†) Afterward, broadband spectra were collected across the interface of dPS and P3HT, and the peak area ratios of the carbon-deuterium bond (2194 cm−1) and P3HT C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds (1502 cm−1) were calculated. The dPS sample composition could then be determined using the established calibration curve on a pixel-by-pixel basis by algebraically solving the equation of the linear line (Fig. 1c). Fig. 1d depicts a 2 × 2 μm infrared image of a P3HT droplet (blue) suspended in dPS (red) with the scale bar denoting the percent composition of dPS at each location in the image. Composition measurements revealed that dPS-rich regions retain 80% dPS composition and dPS-poor regions ranged between 0–20% dPS composition.
C bonds (1502 cm−1) were calculated. The dPS sample composition could then be determined using the established calibration curve on a pixel-by-pixel basis by algebraically solving the equation of the linear line (Fig. 1c). Fig. 1d depicts a 2 × 2 μm infrared image of a P3HT droplet (blue) suspended in dPS (red) with the scale bar denoting the percent composition of dPS at each location in the image. Composition measurements revealed that dPS-rich regions retain 80% dPS composition and dPS-poor regions ranged between 0–20% dPS composition.
Larger AFM-IR images were used to measure the dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P3HT blends prepared at ratios of 1
P3HT blends prepared at ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 1
3, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 3
1, and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, where the full-size height differences of the P3HT droplets in the dPS continuous phase could be visualized (Fig. 2a–h). Fig. 2c, f, and i depict the change in dPS composition across the interface of the two materials for each blend ratio (Raw spectra included in Fig. S3a–c†). Fig. 2a and b depicts the height and IR images for dPS
1, where the full-size height differences of the P3HT droplets in the dPS continuous phase could be visualized (Fig. 2a–h). Fig. 2c, f, and i depict the change in dPS composition across the interface of the two materials for each blend ratio (Raw spectra included in Fig. S3a–c†). Fig. 2a and b depicts the height and IR images for dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hPS (1
hPS (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3). The dPS regions form elevated droplets 200–400 nm in diameter that dot the continuous phase of P3HT. Referencing Fig. 2c, the dPS composition approaches 80% while no presence of the isotope can be detected in the P3HT continuous phase. Fig. 2d and e depict the height and IR images for dPS
3). The dPS regions form elevated droplets 200–400 nm in diameter that dot the continuous phase of P3HT. Referencing Fig. 2c, the dPS composition approaches 80% while no presence of the isotope can be detected in the P3HT continuous phase. Fig. 2d and e depict the height and IR images for dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hPS (1
hPS (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Instead of droplets, the dPS composes the continuous phase in an elevated network formation. The P3HT forms droplets 2–4 μm in diameter. Referencing Fig. 2f, the dPS composition of the polystyrene network rises above 80% while the P3HT domains remain pure. Lastly, Fig. 2g and h depict the height and IR images for dPS
1). Instead of droplets, the dPS composes the continuous phase in an elevated network formation. The P3HT forms droplets 2–4 μm in diameter. Referencing Fig. 2f, the dPS composition of the polystyrene network rises above 80% while the P3HT domains remain pure. Lastly, Fig. 2g and h depict the height and IR images for dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hPS (3
hPS (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The dPS clearly composes the continuous phase with concave pits of irregular shaped P3HT 200–250 nm in diameter dotting the surface. Referencing Fig. 2i, the composition of the dPS regions remain 80% pure whereas the P3HT domains exhibit no trace of dPS. One explanation for why dPS only appears to be 80% pure instead of 100% is that it forms elevated regions in all measured blends that could mask subsurface P3HT domains. Further experiments are needed to determine of vertical phase separation plays a role in composition measurements. Our proof-of-concept P3HT and dPS blend experiment highlights the synergistic abilities of AFM-IR and deuterium labeling to study the phase behavior of polymer blends quantitatively.
1). The dPS clearly composes the continuous phase with concave pits of irregular shaped P3HT 200–250 nm in diameter dotting the surface. Referencing Fig. 2i, the composition of the dPS regions remain 80% pure whereas the P3HT domains exhibit no trace of dPS. One explanation for why dPS only appears to be 80% pure instead of 100% is that it forms elevated regions in all measured blends that could mask subsurface P3HT domains. Further experiments are needed to determine of vertical phase separation plays a role in composition measurements. Our proof-of-concept P3HT and dPS blend experiment highlights the synergistic abilities of AFM-IR and deuterium labeling to study the phase behavior of polymer blends quantitatively.
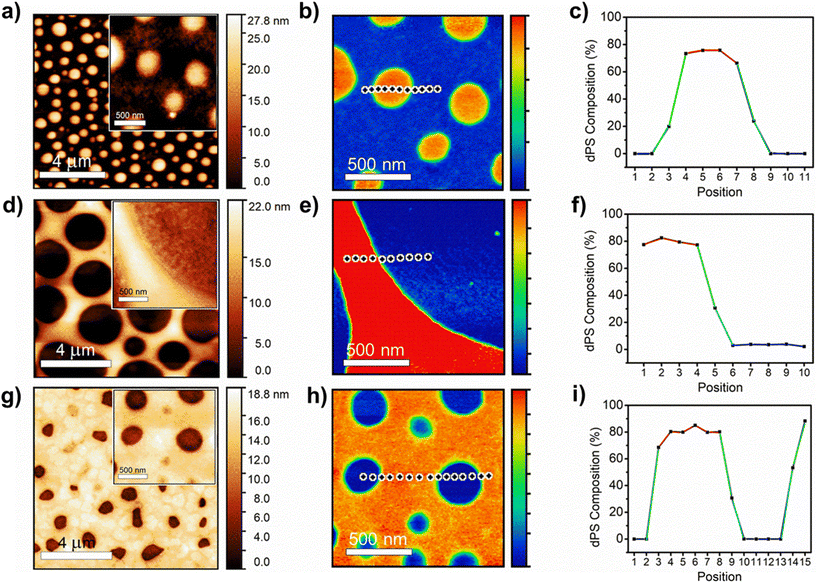 | ||
Fig. 2 Detailed height image, infrared image, and composition curve of (a–c) dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P3HT (1 P3HT (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3), (d–f) dPS 3), (d–f) dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P3HT (1 P3HT (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), and (g–i) dPS 1), and (g–i) dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P3HT (3 P3HT (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). 1). | ||
Highlighting a target material in a complex ternary blend of commodity plastics
The phase behavior in blends of commodity plastics is important to consider when attempting to compatibilize two or more polymers. Taking this capability one step further, an equal-part ternary blend of dPS, PLA, and polycarbonate (PC) was measured by AFM-IR. Single-band IR images were first collected in identical locations for each polymer (Fig. 3a–c). Comparing the IR imaging of the dPS and PLA domains reveals apparent micrometer-scale phase separation of the two materials into distinct domains. AFM-IR spectra of each pure material were acquired and IR peaks unique to each polymer were selected and targeted (dPS at 2194 cm−1, PLA at 1760 cm−1, and PC at 1502 cm−1 (Fig. 3d). Next, three spectrums were acquired, designated as point 1, point 2, and point 3 (Fig. 3e). The points corresponded well with key areas of interest in the morphology. To calculate the relative composition of each component at these three points, two calibration curves were created by preparing films of equal thickness with compositions of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 1
3, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 3
1, and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for both dPS
1 for both dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PLA blends and PC
PLA blends and PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PLA blends (see Fig. S4 and S5† for raw calibration spectra with fit curves). The AFM-IR signal was measured and plot as a function of the known composition to generate the calibration curves (Fig. S6a and b†). The chemical composition was calculated for dPS and PC based on the peak area ratio of the dPS and PLA IR peaks and the PC and PLA IR peaks. The composition of the third component (PLA) was solved for by subtraction. From these measurements, the composition of point 1, 2, and 3 were revealed.
PLA blends (see Fig. S4 and S5† for raw calibration spectra with fit curves). The AFM-IR signal was measured and plot as a function of the known composition to generate the calibration curves (Fig. S6a and b†). The chemical composition was calculated for dPS and PC based on the peak area ratio of the dPS and PLA IR peaks and the PC and PLA IR peaks. The composition of the third component (PLA) was solved for by subtraction. From these measurements, the composition of point 1, 2, and 3 were revealed.
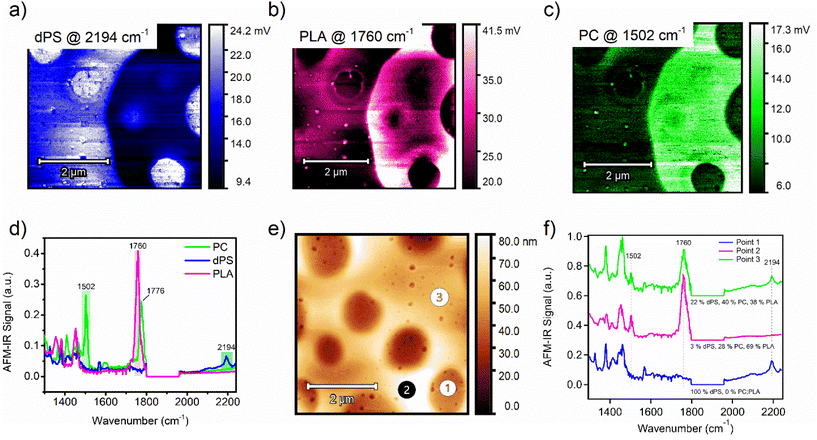 | ||
Fig. 3 (a) Single-band IR imaging of ternary blend of (a) dPS, (b) PLA, and (c) PC. (d) AFM-IR spectrums of PC (green), dPS (blue), and PLA (magenta) with highlighted peaks chosen for single-band AFM-IR scans. (e) Height image of an equal-weighted ternary blend composed of dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PLA PLA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PC. (f) AFM-IR spectra of points 1, 2, and 3 indicated in Fig. 3e, with included composition values for dPS, PLA, and PC for those points. PC. (f) AFM-IR spectra of points 1, 2, and 3 indicated in Fig. 3e, with included composition values for dPS, PLA, and PC for those points. | ||
At point 1, the composition is dominated by dPS, with no apparent PLA peak at 1760 cm−1 or PC peak at 1502 cm−1 (Fig. 3f). In contrast, point 2 trace amounts of dPS and the composition primarily favored PLA with a 69% abundance. Lastly, point 3 contained equal parts PC and PLA, with dPS in the minority. Comparing the height image to the single IR band images and the calculated composition values, it is apparent that no material is isolated to the mesas or valleys in the topography. These observations agree with previous studies showing immiscibility among these three polymers.30–32 However, it is apparent that PC and PLA occupy the same domains whereas dPS tends to strongly phase separate from both materials. This mixing behavior can be explained using the Hansen Solubility parameters of the three materials. The Hansen solubility parameter values suggest that polycarbonate and polylactic acid may have limited solubility in each other due to their different δp and δh values, but they may be partially miscible. To estimate their solubility behavior and potential for phase separation, the distance between their Hansen solubility parameter values is calculated using the following equation:
| δ2 = (δd1 − δd2)2 + (δp1 − δp2)2 + (δh1 − δh2)2 |
| δ2 = (19.1 − 18.9)2 + (7.9 − 4.6)2 + (9.3 − 7.6)2 |
| δ2 = 13.82 |
| δ2 = (22.3 − 18.9)2 + (5.8 − 4.6)2 + (4.3 − 7.6)2 |
| δ2 = 23.9 |
Nanoscale composition in isotopic, amorphous films
To further demonstrate the versatility of deuterium labeling, AFM-IR is used to probe the phase separation between deuterated PS (dPS) and protiated PS (hPS). Blends of dPS and hPS were prepared at different blend ratios with incrementally increasing dPS content and measured by AFM-IR. Broadband spectra were acquired of dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hPS films of different blend ratios (Fig. 4a), and a calibration curve was generated by plotting the ratio of the peak intensities for each polymer (2194 cm−1 for dPS and 1602 cm−1 for hPS) as a function of the known blend ratio (Fig. 4b). The height image (Fig. 4c) of the film revealed a smooth surface with no apparent features (height and IR images of 1
hPS films of different blend ratios (Fig. 4a), and a calibration curve was generated by plotting the ratio of the peak intensities for each polymer (2194 cm−1 for dPS and 1602 cm−1 for hPS) as a function of the known blend ratio (Fig. 4b). The height image (Fig. 4c) of the film revealed a smooth surface with no apparent features (height and IR images of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 3
3 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio blends exhibited similar height morphology and are included in Fig. S7†). A collection of AFM-IR spectra was collected across a 25 × 25-point matrix within the 1 × 1 μm area, and the ratio of dPS/hPS for each spectrum was calculated as the peak area ratio of 2194/1602 cm−1 corresponding to dPS's carbon-deuterium stretching and hPS carbon–hydrogen overtones. Fig. 4d depicts a composition map calculated from the 1 × 1 μm area in Fig. 4a. The relative dPS composition was mapped with a maximum composition greater than 60% and minimum composition marginally above 40%. The highly disordered blend displayed no observable phase separation size and a highly homogenous dispersion of both materials.
1 ratio blends exhibited similar height morphology and are included in Fig. S7†). A collection of AFM-IR spectra was collected across a 25 × 25-point matrix within the 1 × 1 μm area, and the ratio of dPS/hPS for each spectrum was calculated as the peak area ratio of 2194/1602 cm−1 corresponding to dPS's carbon-deuterium stretching and hPS carbon–hydrogen overtones. Fig. 4d depicts a composition map calculated from the 1 × 1 μm area in Fig. 4a. The relative dPS composition was mapped with a maximum composition greater than 60% and minimum composition marginally above 40%. The highly disordered blend displayed no observable phase separation size and a highly homogenous dispersion of both materials.
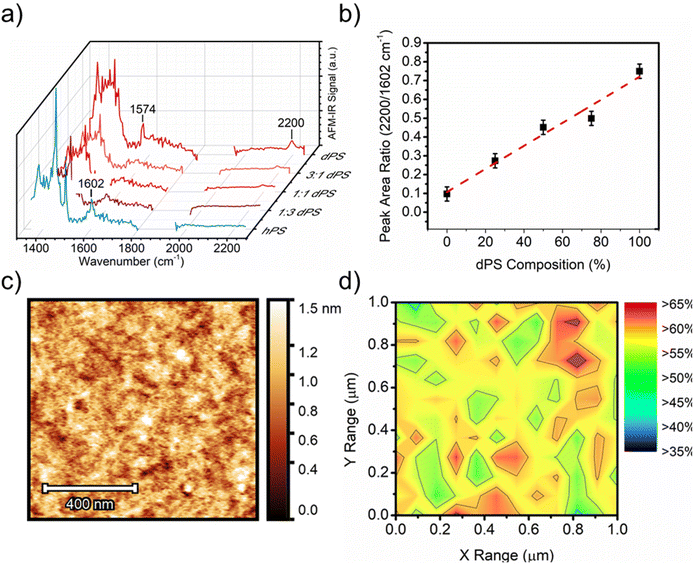 | ||
Fig. 4 Using deuterium to distinguish the isotope polymer blends. (a) Broadband AFM-IR spectrum acquired from dPS:hPS films of different blend ratios. (b) Calibration curve generated from the broadband spectra collected in (a). (c) height image of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) dPS 1 (v/v) dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hPS blend. (d) Composition map of area highlighted in Fig. 4c where percentage values indicate dPS fraction. hPS blend. (d) Composition map of area highlighted in Fig. 4c where percentage values indicate dPS fraction. | ||
Methods
Materials
All reagents were used as received without further purification unless otherwise noted. Polystyrene (Mn: 173![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, Đ: 1.06) and deuterated polystyrene-d8 (Mn: 180
000 g mol−1, Đ: 1.06) and deuterated polystyrene-d8 (Mn: 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, Đ: 1.09) were purchased from Polymer Source, Inc. Regiorandom poly(3-hexylthiophene-2,5-diyl) (60
000 g mol−1, Đ: 1.09) were purchased from Polymer Source, Inc. Regiorandom poly(3-hexylthiophene-2,5-diyl) (60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–95
000–95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) was purchased from Rieke Metals. Polycarbonate (Makrolon 2405) was purchased from Covestro. Polylactic acid in the form of Ingeo 2500HP was purchased from Natureworks, LLC.
000 g mol−1) was purchased from Rieke Metals. Polycarbonate (Makrolon 2405) was purchased from Covestro. Polylactic acid in the form of Ingeo 2500HP was purchased from Natureworks, LLC.
Film preparation
Films of hPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dPS, dPS
dPS, dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P3HT, and dPS
P3HT, and dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PLA
PLA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PC were prepared by spin-casting 10 mg mL−1 solutions in chlorobenzene onto plasma-etched silicon wafers to produce films of 90 to 120 nm thick. Thickness measurements were performed using AFM by measuring the vertical distance between the film surface and bare silicon. The surface of the sample was inspected by optical microscope to ensure no foreign debris contaminated the surface and samples were stored in sealed containers before and after measurement to avoid contamination.
PC were prepared by spin-casting 10 mg mL−1 solutions in chlorobenzene onto plasma-etched silicon wafers to produce films of 90 to 120 nm thick. Thickness measurements were performed using AFM by measuring the vertical distance between the film surface and bare silicon. The surface of the sample was inspected by optical microscope to ensure no foreign debris contaminated the surface and samples were stored in sealed containers before and after measurement to avoid contamination.
Fourier transform infrared resonance
Polymer solutions of each blend component were prepared in chlorobenzene (10 mg mL−1) and drop cast onto NaCl salt plates. Bulk infrared spectra of individual components were acquired using a Bruker Vertex 80v in transmission mode. Sixteen scans were collected for each spectrum at a spectral resolution of 4 cm−1.Atomic force microscopy – infrared spectroscopy
Spin-cast films were measured using a nanoIR3 AFM-IR from Anasys Instruments (Santa Barbara, CA) coupled to a MIRcat-QT™ quantum cascade, mid-infrared laser (frequency range of 917–1700 cm−1 and 1900–2230 cm−1 and repetition rate of 1470 kHz). AFM-IR data were collected in tapping mode using a gold-coated AFM probe (spring constant (k): 40 N m−1 and resonant frequency (fo): 300 kHz). The pulsed, mid-IR laser was tuned to resonance bands unique to each component as determined by FTIR characterization. The resolution of the spectrums in each AFM-IR spectrum is 2 cm−1. Acquired images were flattened using Analysis Studio software. Peak area and composition values for the blend of dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PLA
PLA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PC can be found in Table S1.† To reduce errors and inconsistencies in measurement and calculations, each AFM-IR spectrum was collected three times and averaged. Additionally, for phase separated blends, a collection of ten random points was selected and averaged to obtain representative spectrums of each sample blend. RMS roughness values of height images were calculated and supplied in the ESI (Table S2).†
PC can be found in Table S1.† To reduce errors and inconsistencies in measurement and calculations, each AFM-IR spectrum was collected three times and averaged. Additionally, for phase separated blends, a collection of ten random points was selected and averaged to obtain representative spectrums of each sample blend. RMS roughness values of height images were calculated and supplied in the ESI (Table S2).†
Conclusion
AFM-IR was used to measure the phase separation size, distribution, and chemical composition of two binary polymer blends (dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P3HT and dPS
P3HT and dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hPS) and one ternary blend (dPS
hPS) and one ternary blend (dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PLA
PLA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PC). Localized chemical composition was determined by comparing the IR peak area ratios acquired for each blend and comparing the peak area ratios to calibration curves generated using blends of known composition. For the first time, a multi-band infrared composition map was generated for a ternary polymer blend. This work highlights the efficacy of isotope labeling in enabling the acquisition of quantitative chemical composition in multiphase materials using AFM-IR. AFM-IR is sensitive to isotope-labeled molecules and can be used to target specific materials without significantly altering their chemical or physical properties. Combining isotope labeling with the enhanced broadband compositional measurements of AFM-IR will open new avenues towards understanding the blend dynamics of complex systems such as next-generation nanocomposites, mechanically recycled plastic wastes, multi-component optoelectronic materials and devices, and self-assembling materials.
PC). Localized chemical composition was determined by comparing the IR peak area ratios acquired for each blend and comparing the peak area ratios to calibration curves generated using blends of known composition. For the first time, a multi-band infrared composition map was generated for a ternary polymer blend. This work highlights the efficacy of isotope labeling in enabling the acquisition of quantitative chemical composition in multiphase materials using AFM-IR. AFM-IR is sensitive to isotope-labeled molecules and can be used to target specific materials without significantly altering their chemical or physical properties. Combining isotope labeling with the enhanced broadband compositional measurements of AFM-IR will open new avenues towards understanding the blend dynamics of complex systems such as next-generation nanocomposites, mechanically recycled plastic wastes, multi-component optoelectronic materials and devices, and self-assembling materials.
Author contributions
Nathaniel Prine and Camille Cardinal collected AFM-IR measurements. Zhiqiang Cao aided in the analysis of dPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hPS blends. Remaining authors provided helpful guidance and instruction in the editing of this work.
hPS blends. Remaining authors provided helpful guidance and instruction in the editing of this work.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The work presented by the authors was supported by the US Army Engineer Research and Development Center (ERDC) under PE 0603734A, Project T15, Task “Advanced Polymer Development” under ERDC BAA 18-0500 “Multifunctional Materials to Address Military Engineering” executed under Contract No. W912HZ-18-C-0022. Permission to publish was granted by the Director, Geotechnical and Structures Laboratory. Part of the research used resources at the Spallation Neutron Source and the Center for Nanophase Materials Sciences, DOE Office of Science User Facilities operated by the Oak Ridge National Laboratory.References
- H. Frey and H. R. Khan, Handbook of Thin-Film Technology, 2015, 1–5, DOI:10.1007/978-3-642-05430-3.
- P. Cheng and X. Zhan, Chem. Soc. Rev., 2016, 45, 2544–2582, 10.1039/c5cs00593k.
- A. Heeger, J. Adv. Mater., 2014, 26, 10–28, DOI:10.1002/adma.201304373.
- F. Zhao, C. Wang and X. Zhan, Adv. Energy Mater., 2018, 8, 1–34 Search PubMed.
- Z. Wang, et al. , Nat. Commun., 2021, 12, 332 CrossRef CAS PubMed.
- D. L. Ho, R. M. Briber, R. L. Jones, S. K. Kumar and T. P. Russell, Macromolecules, 1998, 31, 9247–9252 CrossRef CAS.
- L. Li, et al. , Polymer, 2019, 175, 320–328 CrossRef CAS.
- J. D. Londono, et al. , Macromolecules, 1994, 27(10), 2864–2871, DOI:10.1021/ma00088a029.
- D. H. Lim, Y. J. Kim, Y. A. Kim, K. Hwang, J. J. Park and D. Y. Kim, Structural Insight into Aggregation and Orientation of TPD-Based Conjugated Polymers for Efficient Charge-Transporting Properties , Chem. Mater., 2019, 31(13), 4629–4638, DOI:10.1021/acs.chemmater.8b04605.
- M. Chang, et al. , ACS Appl. Mater. Interfaces, 2015, 7, 14095–14103 CrossRef CAS PubMed.
- A. Dazzi and C. B. Prater, Chem. Rev., 2017, 117, 5146–5173 CrossRef CAS PubMed.
- A. Dazzi, et al. , Appl. Spectrosc., 2012, 66(12), 1365–1384, DOI:10.1366/12-06804.
- M. A. Rickard, G. F. Meyers, B. M. Habersberger, C. W. Reinhardt and J. J. Stanley, Polymer, 2017, 129, 247–251 CrossRef CAS.
- C. Policar, et al. , Angew. Chem., Int. Ed., 2011, 50, 860–864, DOI:10.1002/anie.201003161.
- A. Dazzi, R. Prazeres, F. Glotin and J. M. Ortega, Opt. Lett., 2005, 30, 2388–2390, DOI:10.1364/ol.30.002388.
- S. Zhang, et al. , Adv. Funct. Mater., 2020, 30, 2000663 CrossRef CAS.
- W. K. Fuchs, et al. , ACS Appl. Polym. Mater., 2020, 3(1), 178–190, DOI:10.1021/acsapm.0c01017.
- M. Selivanova, et al. , Macromolecules, 2019, 52, 7870–7877 CrossRef CAS.
- Y. Zheng, et al. , Nat. Commun., 2021, 12, 5701 CrossRef CAS PubMed.
- L. Zhu, et al. , Adv. Energy Mater., 2020, n/a, 1904234 CrossRef.
- S. Clède, et al. , Analyst, 2013, 138(19), 5627–5638, 10.1039/c3an00807j.
- B. A. Collins, et al. , Adv. Energy Mater., 2013, 3, 65–74, DOI:10.1002/aenm.201200377.
- D. F. Swinehart, J. Chem. Educ., 1962, 39, 333 CrossRef CAS.
- T. Mayerhöfer, A. Pipa and J. Popp, ChemPhysChem, 2019, 20, 2748–2753 CrossRef PubMed.
- A. Dazzi, F. Glotin and R. Carminati, J. Appl. Phys., 2010, 107, 124519 CrossRef.
- A. Centrone, Annu. Rev. Anal. Chem., 2015, 8, 101–126 CrossRef CAS PubMed.
- B. Lahiri, G. Holland and A. Centrone, Small, 2013, 9, 439–445 CrossRef CAS PubMed.
- J. Kong, R. Giridharagopal, J. S. Harrison and D. S. Ginger, J. Phys. Chem. Lett., 2018, 9, 3307–3314 CrossRef CAS PubMed.
- F. Tang, P. Bao and Z. Su, Anal. Chem., 2016, 88, 4926–4930 CrossRef CAS PubMed.
- A. Rudin and N. E. Brathwaite, Polym. Eng. Sci., 1984, 24, 1312–1318 CrossRef CAS.
- S. Kato, Y. Tsujita, H. Yoshimizu, T. Kinoshita and J. S. Higgins, Polymer, 1997, 38, 2807–2811 CrossRef CAS.
- K. Hamad, M. Kaseem, F. Deri and Y. G. Ko, Mater. Lett., 2016, 164, 409–412 CrossRef CAS.
- G. Zorn, F. I. Simonovsky, B. D. Ratner and D. G. Castner, Adv. Healthcare Mater., 2021, n/a, 2100894 Search PubMed.
- J. Kettle, H. Waters, Z. Ding, M. Horie and G. C. Smith, Sol. Energy Mater. Sol. Cells, 2015, 141, 139–147 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr00886j |
| This journal is © The Royal Society of Chemistry 2023 |
