Single-atom catalysts on supported silicomolybdic acid for CO₂ electroreduction: a DFT prediction

Abstract

The electrocatalytic CO₂ reduction reaction (CO₂RR) is an effective way to convert CO₂ into fuels which relies on efficient catalysts due to extreme reaction activation barriers. As a new frontier in the field of catalysis, single-atom catalysts (SACs) play an important role in the CO₂RR owing to their maximum atomic availability and unique properties. Herein, a new type of electrocatalyst combining transition metal (TM = Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag and Cd) with α-Keggin type Na₄[SiMo₁₂O₄₀] (Na₄SiMo₁₂) was investigated by density functional theory (DFT) calculations. Through comprehensive screening, TM@Na₄SiMo₁₂ (TM = Sc, Ti, V, Cr, Mn, Zn, Y, Zr, Nb and Cd) have been found to exhibit robust stability. Among them, TM@Na₄SiMo₁₂ (TM = Sc, Cr, Mn, Ti, and V) have excellent catalytic activity for the CO₂RR; in particular, the limiting potential (U_L) for CO₂RR by Cr@Na₄SiMo₁₂ is −0.23 V and the product is HCOOH. Meanwhile, Mn@Na₄SiMo₁₂ has high CO₂RR selectivity and good catalytic performance (U_L = −0.48 V). During the electrochemical CO₂RR, polyoxometalates (POMs) act as “electron sponges”, accepting and donating electrons. It is expected that the present work will spur the development of new SACs for the CO₂RR.

---

1. Introduction

The dramatic rise in carbon dioxide (CO₂) emissions into the atmosphere has caused environmental problems such as the greenhouse effect and ocean acidification.^1–3 Converting CO₂ into renewable chemical fuels is considered to be one of the most efficient solutions.^4–7 The electrocatalytic CO₂ reduction reaction (CO₂RR) has attracted extensive attention due to its mild reaction conditions, high faradaic efficiency, and environmental driving force caused by the synergistic effect with renewable energy (such as wind energy and solar energy).⁸ CO₂ is a chemically inert molecule with linear C=O bond energy up to 803 kJ mol⁻¹, meaning that it is difficult to activate. Therefore, the CO₂RR has to rely on efficient catalysts in multi-electron transfer processes for producing the target products. Many catalysts have been explored to break the strong C=O bonds, such as sulfides,^9,10 phosphates,^11,12 oxides,^13,14etc. However, the catalytic performance of these catalysts for the CO₂RR is still unsatisfactory.¹⁵ Therefore, it is of great significance to develop electrochemical CO₂RR catalysts with high selectivity and high efficiency.

Since Zhang and co-workers firstly reported a Pt₁/FeO_x single atom catalyst (SAC) in 2011,¹⁶ SACs have attracted extensive attention both in experimental and theoretical fields.^6,17–20 Due to the maximum atom utilization and unique performance, SACs show great potential in rational utilization of metal resources and the realization of atom economy.^21–23 Different from nanoparticles and metal clusters, when the dispersion of particles reaches the size of a single atom, SACs might produce many new characteristics, such as the sharp increase of surface free energy, quantum size effect, unsaturated ligand environment and metal–support interaction. Among them, the strong metal–support interaction enables the support to regulate the electronic structure of the metal atom to the greatest extent, thus affecting the adsorption behavior of reaction intermediates at the active center. Therefore, SACs can be ideal candidates for the electrochemical CO₂RR and are expected to achieve high-efficiency activation and directional CO₂ conversion.^24–27 However, there are many inevitable problems in the preparation of SACs. One of the most challenging problems is the aggregation of single atoms on the surface of the support, resulting in reduced catalyst activity or even deactivation. Therefore, the key to the synthesis of SACs is to explore a suitable support to avoid the aggregation effect of metals.

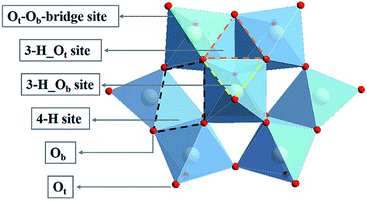
Polyoxometalates (POMs), a class of nanoscale metal oxide clusters composed of d-block transition metal (M = W, Mo, V, Nb, Ta, etc.) ions, are connected by common edge and common angle oxygen junctions.^28,29 POMs are widely investigated in the field of catalysis owing to their well-defined structures, high thermal stability and fascinating physical and chemical properties.^30–32 In the family of POMs, the best known structure of α-Keggin type has the general formula [XM₁₂O₄₀]^n– (X = P, As, Si, Ge, etc.). As shown in Fig. 1, an α-Keggin type POM is a T_d symmetric structure formed by 12 MO₆ octahedrons surrounding the central XO₄ tetrahedron. The oxygen atoms of an α-Keggin type POM can be divided into three categories: oxygen (O_a) connected to the central atom; terminal oxygen (O_t) connected to a single metal atom; and bridging oxygen (O_b) connected to three metal clusters. The exposed O atoms provide a series of coordination sites, including the single corner site, the bridge site (O_t–O_b-bridge site), the three-fold hollow site (3-H_O_t and 3-H_O_b), and the four-fold hollow site (4-H),³³ which offer the possibility of anchoring a single atom. Zhang et al. synthesis of POM supported single-atom catalysts. Low loading Pt (1 wt%) can be effectively dispersed on Keggin type phosphomolybdic acid (PMA),³⁴ and a Pt₁/PMA single-atom catalyst has been proved to have excellent catalytic performance in the hydrogenation of nitrobenzene and cyclohexanone. Notably, Pt atom exhibit strong adsorption at the 4-H site of PMA, showing a twisted square-planar geometry. In addition, Rh was also found to be deposited on the surface of phosphotungstic acid (PTA) by the self-assembly method.³⁵ When the loading amount of Rh is reduced to 0.9 wt%, Rh is located at the 4-H site of PTA together with the chemically adsorbed O₂, which can be used for CO oxidation with significantly low activation energy. Recently, Liu et al. have prepared SACs for enhancing the diborization activity of alkynes with Pt₁ stably anchored to PMA in the cavities of various metal–organic frameworks (MOFs).³⁶ These results indicate that the POM-SACs have practical application potential, providing an ideal platform for further research on SACs. However, the catalytic activity and mechanism of POM-SACs in the CO₂RR need to be clarified.

Fig. 1 Structure of an α-Keggin type polyoxometalate.

In this work, by using first principles calculations and a series of filters, we have comprehensively investigated the electrocatalytic CO₂RR activity of α-[SiMo₁₂O₄₀]⁴⁻-supported single metal catalysts in which the transition metals (Sc to Zn and Y to Cd) are from d-block elements in the periodic table. The geometric structure, stability and CO₂RR catalytic activity of the studied SACs were systematically explored. Based on the screening results, we observed that TM@Na₄SiMo₁₂ (TM = Sc, Cr, Mn, Ti and V) have high catalytic activity for the CO₂RR, and the HER is inhibited, which are expected to be potential electrocatalysts for the CO₂RR. Particularly, the limiting potential (U_L) for the CO₂RR catalyzed by Cr@Na₄SiMo₁₂ is only −0.23 V. Under the equilibrium potential of CO₂/HCOOH, Mn@Na₄SiMo₁₂ is not disturbed by H₂O. At the same time, POMs are found to play the role of electron sponge in the catalytic reaction. The present work is expected to provide valuable information for designing POM-based SACs and deepening the understanding the mechanism of the electrocatalytic CO₂RR so as to realize the effective utilization of CO₂.

2. Computational details

All geometric optimizations and single point energy calculations were performed using the Vienna Ab initio Simulation Package (VASP).^37,38 The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE)³⁹ exchange–correlation functional was chosen to describe the exchange–correlation interactions, and the DFT-D3 method was chosen to correctly describe van der Waals (vdW) interactions.⁴⁰ A plane wave cutoff energy of 450 eV was used. The geometric structure was optimized by cubic cells with a side length of 30 Å, and the Brillouin zone was sampled using only the Γ point, until the convergence criteria of energy and force were less than 10⁻⁴ eV and 0.04 eV Å⁻¹, respectively. The charge transfer was obtained based on the Bader charge analysis. To investigate the chemical bonding between the TM atom and the adsorbate, we performed crystal orbital Hamilton population (COHP) analysis,^41–43 as implemented in the LOBSTER code.⁴⁴

The adsorption energy (E_ads) was calculated using the following equation:

E_ads = E_A–S − E_S − E_A (1)

where E_A–S, E_S, and E_A are the total energies of the adsorbate–substrate (A–S) complex, the substrate (S), and the adsorbate (A), respectively.

The Gibbs free energy change (ΔG) was calculated using the computational hydrogen electrode (CHE) model developed by Nørskov et al.,⁴⁵ and is defined as:

ΔG = ΔE + ΔE_ZPE − TΔS + ΔG_pH + ΔG_U (2)

where ΔE is the difference of reaction energy, which can be directly obtained from DFT calculations. ΔE_ZPE and ΔS are the change of zero-point energy and entropy, respectively. ΔE_ZPE can be calculated by summing vibrational frequencies (ΔE_ZPE = 1/2Σhν). The entropies of gas phase molecules (CO₂, H₂, and H₂O) were obtained from the NIST database.⁴⁶T is the temperature (298.15 K). ΔG_pH is the contribution of free energy due to the change of H concentration; ΔG_pH = k_BT × ln 10 × pH, where k_B is the Boltzmann constant, and the value of pH was set to be zero in this work. ΔG_U = −neU, where n is the number of transferred electrons and U is the electrode potential relative to the standard hydrogen electrode (SHE). The U_L of the reaction is obtained by using the formula U_L = −ΔG_max/e. A conductor-like screening model (COSMO) was considered to simulate the water solvent environment throughout the whole process.⁴⁷ The energy correction of the solvent effect was implemented under an implicit solvation model (named VASP sol) developed by Hennig and colleagues.^48,49 In order to evaluate the stability of Na₄SiMo₁₂, an ab initio molecular dynamics (AIMD) simulation was performed by using the PBE functional and PAW pseudopotential. The Nose–Hoover method was used to control the temperature.⁵⁰ AIMD simulation in the NVT ensemble was carried out at 500 K with a time step of 1.0 fs for a total of 10 ps.

3. Results and discussion

3.1 Calculation model of TM@Na₄SiMo₁₂

A previous study has proved that the incorporation of counterions into the computational models is crucial to accurately reproduce the properties of polyoxoanions.⁵¹ In this work, the charge of α-[SiMo₁₂O₄₀]^4– (SiMo₁₂) was compensated by using four sodium ions to ensure the electroneutrality of the system. Based on the experimental result, we constructed a preliminary geometric model of the adsorption of Na₄SiMo₁₂ on graphene.³⁴ After optimization, the average distance between the Na₄SiMo₁₂ and graphene is 2.95 Å (Fig. 2a and c). In order to understand the interaction between Na₄SiMo₁₂ and graphene, the charge density difference of Na₄SiMo₁₂ adsorbed on graphene was analyzed and is shown in Fig. S1 of the ESI.† Herein, yellow represents the electron density accumulation region, and cyan represents the electron density depletion region. We can see the obvious electron transfer from the counterions to SiMo₁₂, indicating that the SiMo₁₂ and counterions have strong interaction, while the charge distribution on graphene is negligible, indicating that the interaction between graphene and Na₄SiMo₁₂ is weak, and that graphene plays the role of conductive support in the experiment. Thus, graphene will not be taken into account in the following calculations in order to reduce computational cost (Fig. 2b and d).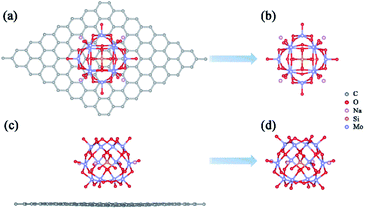

Fig. 2 Top views (a and b) and side views (c and d) of the most stable structures of Na₄SiMo₁₂ loaded with or without graphene.

Previous studies have shown that Pt atom dispersed on PMA and the most stable adsorption site is 4-H site.^34,36 In addition to the 4-H site, the other sites of the Keggin type anion, such as 3-H_O_t, 3-H_O_b, and O_t–O_b-bridge, may also trap metal atoms. Taking Sc and Y as examples, all possible adsorption sites were studied to verify the most stable adsorption site on Na₄SiMo₁₂. The optimized structures and calculated adsorption energies of the TMs (TMs = Sc and Y) on Na₄SiMo₁₂ are shown in Fig. S2 of the ESI.† It is found that the TMs prefer to anchor to the 4-H site of Na₄SiMo₁₂, which is consistent with the previous studies.^{34,36,52–55} Based on the above analysis, the calculation model of TM@Na₄SiMo₁₂ was confirmed and is shown in Fig. 3a, in which the TMs are anchored on the POM 4-H site.

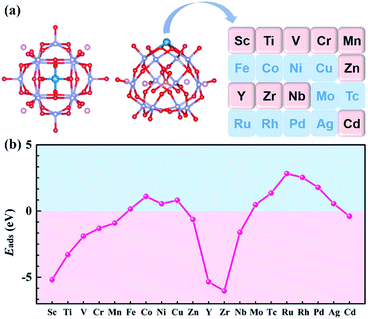Fig. 3 (a) Schematic illustration of the transition metals anchored on Na₄SiMo₁₂. (b) The adsorption energies of transition metal atoms anchored on Na₄SiMo₁₂.

3.2 Stability of TM@Na₄SiMo₁₂

For SACs, due to the high surface energy and small migration barrier of metal atoms, agglomeration can easily occur during preparation and reaction, resulting in deactivation of the catalysts. In order to evaluate the stability of the studied POM-SACs, the E_ads of single atoms anchored on the 4-H site of Na₄SiMo₁₂ was computed and the results are shown in Fig. 3b and Table S1 of the ESI.† The E_ads was calculated using the equation:⁵⁶

E_ads = E_{(TM@Na4SiMo12)} − E_(Na4SiMo12) − μ_(TM) (3)

where E_{(TM@Na4SiMo12)}, E_(Na4SiMo12) and μ_(TM) represent the total energies of the transition metal (TM) atom supported on Na₄SiMo₁₂, Na₄SiMo₁₂ substrates and the chemical potential of the TM atom calculated from the metal bulk, respectively. According to this definition, a negative E_ads means that a single metal atom is energetically favorable to be anchored on the 4-H site of Na₄SiMo₁₂. As shown in Fig. 3b, the E_ads values of TM@Na₄SiMo₁₂ (TM = Sc, Ti, V, Cr, Mn, Zn, Y, Zr, Nb and Cd) are all negative, indicating that these TMs anchored on Na₄SiMo₁₂ have high stability and may hold great promise for synthesis. However, the remaining TM atoms (TM = Fe, Co, Ni, Cu, Mo, Tc, Ru, Rh, Pd and Ag) may exist in the form of nanoparticles or aggregate in the bulk phases. The TM–O bond lengths of TM@Na₄SiMo₁₂ (TM = Sc, Ti, V, Cr, Mn, Zn, Y, Zr, Nb and Cd) are summarized in Table S2 of the ESI,† and are similar to those of the synthesized Pt@POMs reported in previous experiments.^34,36,55

The stability of Na₄SiMo₁₂ was further verified by AIMD simulation. No obvious structural deformation was observed after Na₄SiMo₁₂ was simulated at 500 K with a time step of 1.0 fs for a total of 10 ps, indicating its high thermal stability (Fig. S3 of the ESI†).

3.3 Electrochemical CO₂RR on TM@Na₄SiMo₁₂

3.3.1 CO₂ adsorption. In the following, the study focuses on whether TM@Na₄SiMo₁₂ can efficiently catalyze CO₂. The first step to initialize the reduction reaction is the CO₂ adsorption on TM@Na₄SiMo₁₂, which is often neglected in many studies. If CO₂ can be effectively captured and activated, the catalytic performance of the CO₂RR can be improved. The charge density difference, adsorption energy and charge transfer amount of CO₂ adsorption over TM@Na₄SiMo₁₂ (TM = Sc, Ti, V, Cr, Mn, Zn, Y, Zr, Nb and Cd) were computed and are shown in Fig. S4 of the ESI.† It is observed that these catalysts can effectively capture and activate CO₂ with the adsorption energy in the range of −0.30 to −0.73 eV. The O atom of CO₂ prefers to be adsorbed on TM atoms, and TM@Na₄SiMo₁₂ donate electrons to CO₂ (around 0.02–0.07e).

To further clarify the role of anchored transition metals in the catalytic cycle, the charge density difference of the system doped with transition metals was analyzed by taking Cr@Na₄SiMo₁₂ as an example (Fig. S5a of the ESI†). The charge density difference shows that the electron transfers from the anchored Cr atom to the neighboring oxygen atoms, and the Bader charge analysis (Fig. S8 of the ESI†) suggests that the Cr atom is positively charged due to losing 1.45e, and chemical bonds are formed between the Cr atom and the oxygen atoms of Na₄SiMo₁₂. The partial density of states (PDOS) of Cr@Na₄SiMo₁₂ was further analyzed and is shown in Fig. S5b of the ESI† in which the d orbitals of the Cr atom strongly hybridize with the p orbitals of adjacent O atoms near the Fermi level (E_F). The d orbitals of Cr near the Fermi level show high reactivity, which may trigger adsorption in the catalytic cycle.

3.3.2 Initial protonation steps of the CO₂RR vs. HER. The first protonation step in the electrochemical CO₂RR is the formation of carboxyl (COOH*) or formate (HCOO*) intermediates, from which various carbon-containing products are subsequently produced (Scheme 1). Under the same reaction conditions, H* can also produce competitive HER by consuming the same proton–electron pair (H⁺ + e⁻), which affects the faradaic efficiency of the CO₂RR. Therefore, we first evaluated the ΔG for COOH*, HCOO*, and H* to select catalysts that might catalyze the CO₂RR with high selectivity. Based on the Brønsted–Evans–Polanyi relation,^57,58 low free energy reactions are more selective. As shown in Fig. 4, except where TM = Cd and Zn, TM@Na₄SiMo₁₂ (TM = Sc, Ti, V, Cr, Mn, Y, Zr and Nb) are below the diagonal, indicating that these catalysts prefer to catalyze the CO₂RR rather than the HER. The calculated free energy changes for the CO₂RR on TM@Na₄SiMo₁₂ (TM = Sc, Ti, V, Cr, Mn, Y, Zr, and Nb) are presented in Table S3 of the ESI.† The ΔG for COOH* formation by candidate catalysts is much larger than those of HCOO* formation, so HCOO* is considered to be the only intermediate for subsequent hydrogenation. For catalysts with a single active site, it is unlikely to generate C2 products through the C–C coupling of C1 intermediates based on the Langmuir–Hinshelwood mechanism,^59,60 so this work only considers the generation of C1 products.

Scheme 1 All considered reaction pathways for CO₂ reduction on TM@Na₄SiMo₁₂.

Fig. 4 Free energy change (ΔG) of the first protonation step in the CO₂RR and HER on TM@Na₄SiMo₁₂.

3.3.3 HCOOH* hydrogenation vs. desorption. In order to evaluate the catalytic activity of TM@Na₄SiMo₁₂, the ΔG of HCOO* hydrogenation was computed and the limiting potential (−0.74 V) of CO₂ reduction on the Cu (211) surface is taken as the screening criterion.⁶¹ From Fig. 5a, Y, Zr and Nb@Na₄SiMo₁₂ exhibit weak catalytic activity with high ΔG values (>0.74 eV). In contrast, HCOOH* formation by TM@Na₄SiMo₁₂ (TM = Sc, Ti, V, Cr, and Mn) have lower free energies (ΔG < 0.74 eV), so they are screened as potential catalysts for further investigation.

Fig. 5 (a) The ΔG of HCOO* + e⁻ + H⁺ → HCOOH* on TM@Na₄SiMo₁₂ (TM = Sc, Ti, V, Cr, Mn, Y, Zr and Nb). The screening criterion for catalytic activity is set to ΔG < 0.74 eV (red dashed line). (b) The ΔG for HCOOH* hydrogenation (HCOOH* + e⁻ + H⁺ → HCO* + H₂O (l)) and desorption (HCOOH* → HCOOH (l) + *) on TM@Na₄SiMo₁₂ (TM = Sc, Cr, Mn, Ti and V).

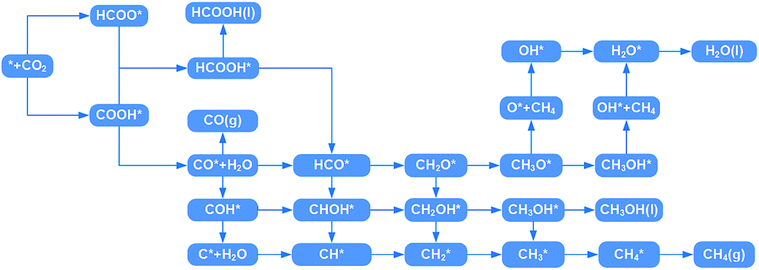
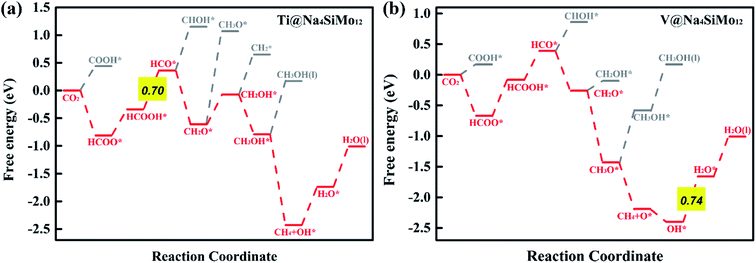
HCOOH* can be desorbed (HCOOH* → HCOOH (l) + *) from the catalyst or further hydrogenated (HCOOH* + H⁺ + e⁻ → HCO* + H₂O (l)). As shown in Fig. 5b, the HCOOH* desorption on TM@Na₄SiMo₁₂ (TM = Sc, Cr, and Mn) is easier than further hydrogenation, indicating that these three catalysts tend to produce HCOOH. In contrast, the HCO* intermediate is formed on Ti and V@Na₄SiMo₁₂ with ΔG of 0.70 eV and 0.47 eV, which are lower than the ΔG of HCOOH* desorption (0.77 eV and 0.52 eV). Therefore, the subsequent protonation process will be considered for Ti and V@Na₄SiMo₁₂.

3.3.4 CO₂RR to HCOOH on TM@Na₄SiMo₁₂ (TM = Sc, Cr, and Mn). Based on the above results, the CO₂RR on TM@Na₄SiMo₁₂ (TM = Sc, Cr, and Mn) is a 2e⁻ reaction in which the main product is HCOOH, and the calculated free energy diagrams are presented in Fig. 6. The optimal reaction path of these catalysts is CO₂ (g) → HCOO* → HCOOH* → HCOOH (l). The ΔG of each step and the structures corresponding to the optimal reaction path are shown in Table S3 and Fig. S6 of the ESI.† The potential determination steps (PDS) and U_L for the most favorable products are summarized in Table 1.

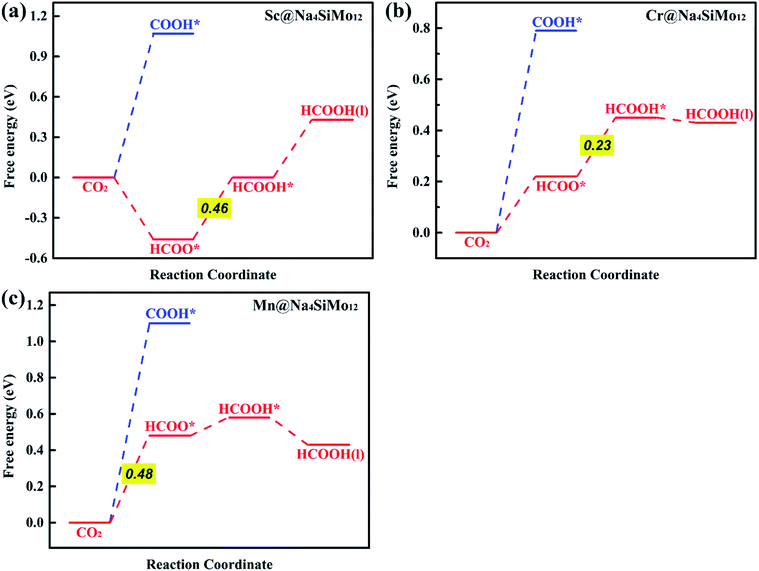Fig. 6 Calculated free energy diagrams for the electrochemical CO₂RR on (a) Sc@Na₄SiMo₁₂, (b) Cr@Na₄SiMo₁₂ and (c) Mn@Na₄SiMo₁₂.

Table 1 The calculated potential determining step (PDS) and U_L (V) for HCOOH and CH₄ formation on TM@Na₄SiMo₁₂

Metal	PDS	U L
a HCOOH production. b CH4 production.
Sc^a	HCOO* + e^− + H^+ → HCOOH*	−0.46
Cr^a	HCOO* + e^− + H^+ → HCOOH*	−0.23
Mn^a	CO2* + e^− + H^+ → HCOO*	−0.48
Ti^b	HCOOH* + e^− + H^+ → HCO* + H2O (l)	−0.70
V^b	OH* + e^− + H^+ → H2O*	−0.74

---

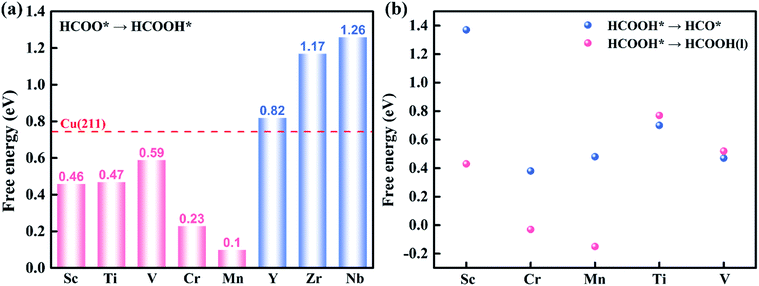
First, the H⁺ + e⁻ pair attacks the carbon atom of CO₂ to form HCOO*. It should be noted that the ΔG for CO₂ + H⁺ + e⁻ → HCOO* on Sc@Na₄SiMo₁₂ is −0.46 eV, while for Cr and Mn@Na₄SiMo₁₂, the ΔG is 0.22 eV and 0.48 eV, respectively. Afterwards, HCOO* can be further reduced to form HCOOH* on TM@Na₄SiMo₁₂ (TM = Sc, Cr and Mn) with ΔG of 0.46, 0.23, and 0.10 eV, respectively, which are less than the ΔG of HCOOH* hydrogenation to HCO*. Therefore, for TM@Na₄SiMo₁₂ (TM = Sc, Cr and Mn), HCOOH* will not undergo further hydrogenation and is released in the form of a liquid. For Sc and Cr@Na₄SiMo₁₂, the PDS is the step of HCOO* → HCOOH* with U_L of −0.46 V and −0.23 V, respectively. For Mn@Na₄SiMo₁₂, CO₂ → HCOO* is the PDS with U_L of −0.48 V.

3.3.5 CO₂RR to CH₄ on TM@Na₄SiMo₁₂ (TM = Ti and V). Different from the above catalysts, HCOOH* has strong adsorption on the surface of Ti and V@Na₄SiMo₁₂, and can be further hydrogenated with the H⁺ + e⁻ pair to obtain the HCO* intermediate. In this process, the ΔG for Ti and V@Na₄SiMo₁₂ is 0.70 and 0.47 eV, respectively. Subsequently, HCO* is hydrogenated to produce CHOH* or CH₂O*. As can be seen from Fig. 7, the CH₂O* generation on these two catalysts is an exothermic process, which is more favorable than CHOH* formation. In the next step, CH₂O* is further hydrogenated to form a CH₂OH* or CH₃O* intermediate. For Ti@Na₄SiMo₁₂, the H⁺ + e⁻ pair attacks the O atom of CH₂O* to form CH₂OH* with ΔG of 0.54 eV, which is much easier than CH₃O* formation (1.68 eV). In the following steps, the H⁺ + e⁻ pairs continuously attack the C atom of the intermediates: CH₂OH* → CH₃OH* → CH₄ + OH*, which is a continuous exothermic process with ΔG of −0.72 and −1.64 eV. Finally, the CH₄ molecule is desorbed from the catalyst surface due to the weak adsorption energy (−0.65 eV). The remaining OH* is further hydrogenated to produce an H₂O molecule with a ΔG of 0.69 eV. For the CO₂RR on Ti@Na₄SiMo₁₂, the most favorable reaction pathway is CO₂ → HCOO* → HCOOH* → HCO* → CH₂O* → CH₂OH* → CH₃OH* → CH₄ + OH* → CH₄ + H₂O, and the PDS is the step of HCOOH* → HCO* with U_L of −0.70 V.

Fig. 7 Calculated free energy diagrams for the electrochemical CO₂RR on (a) Ti and (b) V@Na₄SiMo₁₂.

For V@Na₄SiMo₁₂, once the intermediate CH₂O* is obtained, subsequent H⁺ + e⁻ pairs continue to attack the C atom until the C–O bond is broken and the CH₄ molecule is released. Due to the weak adsorption energy of CH₄ (−0.40 eV), it eventually desorbs from the surface as a product. The remaining O* undergoes two successive hydrogenation steps to produce an H₂O molecule, and the corresponding free energy changes are −0.21 eV and 0.74 eV, respectively. For V@Na₄SiMo₁₂, the most favorable reaction pathway is CO₂ → HCOO* → HCOOH* → HCO* → CH₂O* → CH₃O* → CH₄ + O* → OH* → H₂O, and the PDS is the step of OH* → H₂O with U_L of −0.74 V.

In summary, TM@Na₄SiMo₁₂ (TM = Sc, Cr, Mn, Ti and V) are promising high efficiency SACs for the electrochemical CO₂RR with low U_L, and are superior to the Cu (211) catalyst (−0.74 V).⁶¹ The competition between the H₂O and CO₂ adsorption also needs to be investigated.⁶² To further evaluate the stability of the above TM@Na₄SiMo₁₂ (TM = Sc, Cr, Mn, Ti and V) in water, we calculated the surface Pourbaix diagrams as a function of the standard hydrogen electrode (U_SHE) and pH. As shown in Fig. S9 of the ESI,† when pH = 0, TM@Na₄SiMo₁₂ (TM = Sc, Cr, Mn, Ti and V) require voltages of −0.80, −0.60, 0.43, −1.34, and −0.99 V, respectively, to protect the catalyst from being covered by OH* in water. When the actual potential is higher than the cathodic protection potential, the TM anchored on Na₄SiMo₁₂ begins to be covered by OH* in water. These catalysts are oxidized by O* when the U_SHE values increase to 0.88, −0.20, 0.66, −0.42, and −0.62 V, respectively. In this work, the equilibrium potential of CO₂/HCOOH and CO₂/CH₄ is −0.22 and −0.13 V, respectively. Therefore, the catalyst should possess a high stability in water below the equilibrium potential of CO₂/HCOOH or CO₂/CH₄. The results show that under the conditions of equilibrium potential, Mn@Na₄SiMo₁₂ will remain exposed and will not be disturbed by H₂O. In contrast, TM@Na₄SiMo₁₂ (TM = Sc, Cr, Ti and V) will be covered by OH*, affecting the performance of the CO₂RR.

It can be seen that Cr@Na₄SiMo₁₂ has a high catalytic activity for CO₂ reduction to HCOOH, while the selectivity of the CO₂RR is not good due to the competition from H₂O. In comparison, Mn@Na₄SiMo₁₂ has high selectivity and relatively good catalytic performance (U_L = −0.48 V).

3.4 Difference in the catalytic activity of TM@Na₄SiMo₁₂

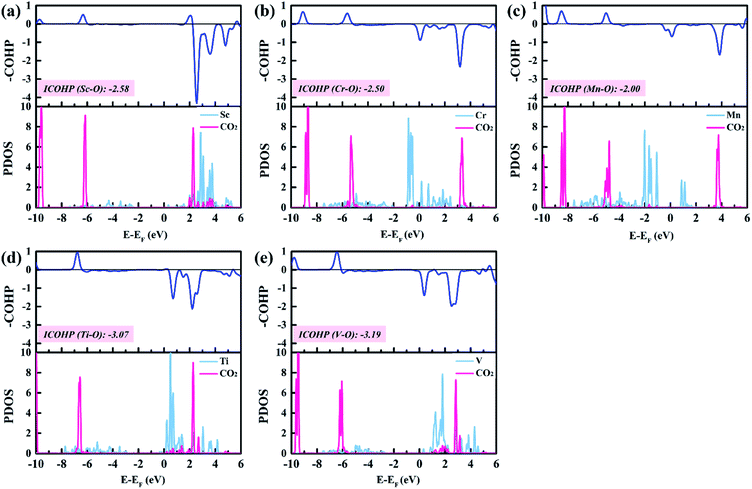
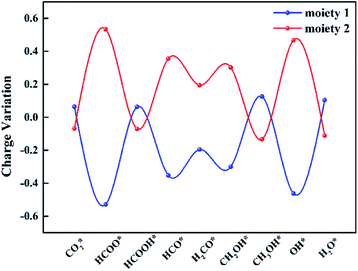
To gain insight into the catalytic performance of TM@Na₄SiMo₁₂ (TM = Sc, Cr, Mn, Ti and V), the PDOS of CO₂ adsorbed on TM@Na₄SiMo₁₂ was calculated and is shown in Fig. 8. It can be seen that Sc, Ti and V have obvious hybridization with CO₂, and the hybridization range is wide, further indicating that TM@Na₄SiMo₁₂ (TM = Sc, Ti and V) have strong interaction with CO₂. In order to evaluate the TM–O binding interaction from CO₂ adsorbed on the TM@Na₄SiMo₁₂ (TM = Sc, Cr, Mn, Ti and V), integrated-crystal orbital Hamilton population (ICOHP) analysis was performed by integrating the band states up to the highest occupied energy level to measure the bond strength (Fig. 8). Moreover, the more negative the value of ICOHP, the stronger the bonding interaction. The results show that the ICOHP values change as follows: V (−3.19) < Ti (−3.07) < Sc (−2.58) < Cr (−2.50) < Mn (−2.00), and the bonding strength order is Mn–O < Cr–O < Sc–O < Ti–O < V–O. The relationship between the ΔG of CO₂ hydrogenation to HCOO* and the ICOHP values of the TM–O bond is plotted in Fig. S7 of the ESI.† It is interesting to find an approximately linear correlation with R² of 0.75. In other words, the TM–O bond with a smaller ICOHP value is stronger, resulting in a smaller ΔG value of CO₂ → HCOO*, which also explains why the five catalysts have obvious differences in the first step of hydrogenation. In addition, we studied the relationship between the adsorption energies (E_ads) of CO₂ on the TM@Na₄SiMo₁₂ (TM = Sc, Cr, Mn, Ti and V) and the Bader charges of TMs (Fig. S8 of the ESI†). As the charge amount of transition metals increases, the E_ads of CO₂ increases, which in turn affects the catalytic performance of the CO₂RR.

Fig. 8 The PDOSs and COHPs of CO₂ on TM@Na₄SiMo₁₂ (TM = Sc, Cr, Mn, Ti and V).

To explore the role of TM@Na₄SiMo₁₂ in the electrochemical CO₂RR, Ti@Na₄SiMo₁₂ is taken as an example to analyze the charge transfer between the reaction intermediates and the catalyst through Bader charge analysis along the optimal reaction pathway. As shown in Fig. 9, the studied system was divided into two parts including adsorbed C_xH_yO_z species (moiety 1) and Ti@SiMo₁₂ (moiety 2). Counterions were not included because their charges remain essentially unchanged during the reaction. Firstly, CO₂ gains 0.07e by adsorption on Ti@SiMo₁₂, and Ti@SiMo₁₂ loses the same amount of charge. As the reaction goes on, Ti@SiMo₁₂ continuously donates and accepts electrons during the electrochemical CO₂RR, behaving as an “electron sponge”. Therefore, Ti@SiMo₁₂ acts as an electron reservoir in the electrochemical CO₂RR.

Fig. 9 Charge variation of the two moieties for Ti@Na₄SiMo₁₂ along the optical reaction pathway. Moieties 1 and 2 represent the adsorbed C_xH_yO_z species and Ti@SiMo₁₂, respectively. Negative and positive values indicate electron gain and loss.

4. Conclusions

In summary, a series of SACs with TMs (TM = Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag, and Cd) anchored on Na₄SiMo₁₂ are proposed. Counterions are introduced into the calculation model, which is crucial to accurately reproduce the properties of polyoxoanions. Based on the DFT calculations, TM@Na₄SiMo₁₂ (TM = Sc, Ti, V, Cr, Mn, Zn, Y, Zr, Nb and Cd) are found to possess good stability, and might be synthesized in the experiment. Furthermore, Sc, Cr, Mn, Ti, and V@Na₄SiMo₁₂ are predicted to be efficient catalysts for the CO₂RR due to the low U_L; in particular, CO₂RR by Cr@Na₄SiMo₁₂ has a very low U_L of −0.23 V. Mn@Na₄SiMo₁₂ has high selectivity and good catalytic performance for CO₂ reduction to HCOOH with U_L of −0.48 V. In addition, POMs act as “electron sponges” during the electrochemical CO₂RR, continuously accepting and donating electrons. This work provides valuable insights into the design of highly selective and efficient SAC electrocatalysts for the CO₂RR.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge financial support by NSFC (21571031). We acknowledge the Institute of Theoretical Chemistry, Jilin University for providing the computational resources for this work.

References

1. S. Chu and A. Majumdar, Nature, 2012, 488, 294–303.
2. M. Aresta, A. Dibenedetto and A. Angelini, Chem. Rev., 2014, 114, 1709–1742.
3. J. C. Abanades, E. S. Rubin, M. Mazzotti and H. J. Herzog, Energy Environ. Sci., 2017, 10, 2491–2499.
4. C. Costentin, M. Robert and J. –M. Savéant, Chem. Soc. Rev., 2013, 42, 2423–2436.
5. Y. Li, S. H. Chan and Q. Sun, Nanoscale, 2015, 7, 8663–8683.
6. J. Deng, H. Li, J. Xiao, Y. Tu, D. Deng, H. Yang, H. Tian, J. Li, P. Ren and X. Bao, Energy Environ. Sci., 2015, 8, 1594–1601.
7. E. V. Kondratenko, G. Mul, J. Baltrusaitis, G. O. Larrazábal and J. Pérez–Ramírez, Energy Environ. Sci., 2013, 6, 3112–3135.
8. J. Qiao, Y. Liu, F. Hong and J. Zhang, Chem. Soc. Rev., 2014, 43, 631–675.
9. Y. Chen, K. Chen, J. Fu, A. Yamaguchi, H. Li, H. Pan, J. Hu, M. Miyauchi and M. Liu, Nano Mater. Sci., 2020, 2, 235–247.
10. S. Piontek, K. junge Puring, D. Siegmund, M. Smialkowski, I. Sinev, D. Tetzlaff, B. Roldan Cuenya and U. –P. Apfel, Chem. Sci., 2019, 10, 1075–1081.
11. S. Back, J. Lim, N.-Y. Kim, Y.-H. Kim and Y. Jung, Chem. Sci., 2017, 8, 1090–1096.
12. S. Mou, T. Wu, J. Xie, Y. Zhang, L. Ji, H. Huang, T. Wang, Y. Luo, X. Xiong, B. Tang and X. Sun, Adv. Mater., 2019, 31, 1903499.
13. M. Kunitski, N. Eicke, P. Huber, J. Köhler, S. Zeller, J. Voigtsberger, N. Schlott, K. Henrichs, H. Sann, F. Trinter, L. P. H. Schmidt, A. Kalinin, M. S. Schöffler, T. Jahnke, M. Lein and R. Dörner, Nat. Commun., 2019, 10, 1.
14. J. Kim, W. Choi, J. W. Park, C. Kim, M. Kim and H. Song, J. Am. Chem. Soc., 2019, 141, 6986–6994.
15. R. Kortlever, J. Shen, K. J. P. Schouten, F. Calle-Vallejo and M. T. M. Koper, J. Phys. Chem. Lett., 2015, 6, 4073–4082.
16. H. Wei, X. Liu, A. Wang, L. Zhang, B. Qiao, X. Yang, Y. Huang, S. Miao, J. Liu and T. Zhang, Nat. Commun., 2014, 5, 5634.
17. X. Fang, Q. Shang, Y. Wang, L. Jiao, T. Yao, Y. Li, Q. Zhang, Y. Luo and H.-L. Jiang, Adv. Mater., 2018, 30, 1705112–1705118.
18. J. S. Jirkovsky, I. Panas, E. Ahlberg, M. Halasa, S. Romani and D. J. Schiffrin, J. Am. Chem. Soc., 2011, 133, 19432–19441.
19. W. Liu, L. Zhang, W. Yan, X. Liu, X. Yang, S. Miao, W. Wang, A. Wang and T. Zhang, Chem. Sci., 2016, 7, 5758–5764.
20. Y.-G. Wang, D. Mei, V.-A. Glezakou, J. Li and R. Rousseau, Nat. Commun., 2015, 6, 6511–6519.
21. Y. Chen, S. Ji, C. Chen, Q. Peng, D. Wang and Y. Li, Joule, 2018, 2, 1242–1264.
22. H. Zhang, G. Liu, L. Shi and J. Ye, Adv. Energy Mater., 2018, 8, 1701343–1701367.
23. C. Zhu, S. Fu, Q. Shi, D. Du and Y. Lin, Angew. Chem., Int. Ed., 2017, 56, 13944–13960.
24. Y. Cheng, S. Zhao, H. Li, S. He, J.-P. Veder, B. Johannessen, J. Xiao, S. Lu, J. Pan, M. F. Chisholm, S.-Z. Yang, C. Liu, J. G. Chen and S. P. Jiang, Appl. Catal., B, 2019, 243, 294–303.
25. K. Jiang, S. Siahrostami, T. Zheng, Y. Hu, S. Hwang, E. Stavitski, Y. Peng, J. Dynes, M. Gangisetty, D. Su, K. Attenkofer and H. Wang, Energy Environ. Sci., 2018, 11, 893–903.
26. Y. Pan, R. Lin, Y. Chen, S. Liu, W. Zhu, X. Cao, W. Chen, K. Wu, W.-C. Cheong, Y. Wang, L. Zheng, J. Luo, Y. Lin, Y. Liu, C. Liu, J. Li, Q. Lu, X. Chen, D. Wang, Q. Peng, C. Chen and Y. Li, J. Am. Chem. Soc., 2018, 140, 4218–4221.
27. F. Yang, P. Song, X. Liu, B. Mei, W. Xing, Z. Jiang, L. Gu and W. Xu, Angew. Chem., Int. Ed., 2018, 57, 12303–12307.
28. M. Blasco-Ahicart, J. Soriano–López, J. J. Carbó, J. M. Poblet and J. R. Galan-Mascaros, Nat. Chem., 2018, 10, 24–30.
29. X. López, J. J. Carbó, C. Bo and J. M. Poblet, Chem. Soc. Rev., 2012, 41, 7537–7571.
30. N. Mizuno and K. Kamata, Coord. Chem. Rev., 2011, 255, 2358–2370.
31. A. Proust, B. Matt, R. Villanneau, G. Guillemot, P. Gouzerh and G. Izzet, Chem. Soc. Rev., 2012, 41, 7605–7622.
32. Y.-F. Song and R. Tsunashima, Chem. Soc. Rev., 2012, 41, 7384–7402.
33. L. Vilà-Nadal, K. Peuntinger, C. Busche, J. Yan, D. Lüders, D.-L. Long, J. M. Poblet, D. M. Guldi and L. Cronin, Angew. Chem., Int. Ed., 2013, 52, 9695–9699.
34. B. Zhang, H. Asakura, J. Zhang, J. Zhang, S. De and N. Yan, Angew. Chem., Int. Ed., 2016, 55, 8319–8323.
35. B. Zhang, H. Asakura and N. Yan, Ind. Eng. Chem. Res., 2017, 56, 3578–3587.
36. Y. Liu, X. Wu, Z. Li, J. Zhang, S.-X. Liu, S. Liu, L. Gu, L. R. Zheng, J. Li, D. Wang and Y. Li, Nat. Commun., 2021, 12, 4205.
37. G. Kresse and J. Hafner, Phys. Rev. B, 1997, 55, 7539–7548.
38. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B, 1992, 46, 6671–6687.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
40. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
41. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624.
42. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
43. S. Maintz, V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567.
44. S. Maintz, V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
45. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
46. Computational Chemistry Comparison and Benchmark Database; NIST Standard Reference Database Number 101, ed. R. Johnson III, National Institute of Standards and Technology, 2015, http://www.cccbdb.nist.gov.
47. F. Neese and G. Olbrich, Chem. Phys. Lett., 2002, 362, 170–178.
48. M. Fishman, H. L. Zhuang, K. Mathew, W. Dirschka and R. G. Hennig, Phys. Rev. B, 2013, 87, 245402.
49. R. A. Ojifinni, N. S. Froemming, J. Gong, M. Pan, T. S. Kim, J. M. White, G. Henkelman and C. B. Mullins, J. Am. Chem. Soc., 2008, 130, 6801–6812.
50. G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643.
51. Z. Lang, X. Aparicio-Anglès, I. Weinstock, A. Clotet and J. M. Poblet, Inorg. Chem., 2017, 56, 3961–3969.
52. S. H. Talib, X. Yu, Q. Yu, S. Baskaran and J. Li, Sci. China Mater., 2020, 63, 1003–1014.
53. C.-G. Liu, Y.-J. Chu, L.-L. Zhang, C. Sun and J.-Y. Shi, Environ. Sci. Technol., 2019, 53, 12893–12903.
54. S. H. Talib, Z. Lu, X. Yu, K. Ahmad, B. Bashir, Z. Yang and J. Li, ACS Catal., 2021, 11, 8929–8941.
55. B. Zhang, G. Sun, S. Ding, H. Asakura, J. Zhang, P. Sautet and N. Yan, J. Am. Chem. Soc., 2019, 141, 8185–8197.
56. F. Li, H. Ai, C. Shi, K. H. Lo and H. Pan, Int. J. Hydrogen Energy, 2021, 46, 12886–12896.
57. J. N. Bronsted, Chem. Rev., 1928, 5, 231–338.
58. M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11–24.
59. M. Moses-DeBusk, M. Yoon, L. F. Allard, D. R. Mullins, Z. Wu, X. Yang, G. Veith, G. M. Stocks and C. K. Narula, J. Am. Chem. Soc., 2013, 135, 12634–12645.
60. Z. Chen, J. Zhao, J. Zhao, Z. Chen and L. Yin, Nanoscale, 2019, 11, 20777–20784.
61. A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, Energy Environ. Sci., 2010, 3, 1311–1315.
62. J. Feng, J. Ni and H. Pan, J. Mater. Chem. A, 2021, 9, 10546–10561.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta08285j

---