Partial peptide dissociation and binding groove plasticity in two major histocompatibility complex class I alleles – differences between alleles versus force field and sampling effects

Abstract

Major histocompatibility complex class I (MHC I) reports a cell's health status by presenting antigenic peptides inside its binding groove. However, MHC I binding grooves can differ largely in their plasticity, from binding grooves that are conformationally stable by themselves to those that require a high-affinity peptide to be bound to attain conformational stability. These latter MHC I alleles are dependent on the C-terminus of the peptide that stabilizes the F-pocket region of their binding grooves. It has remained unclear to what extent a peptide-MHC I complex (pMHC I) can tolerate the (intermittent) partial dissociation of high-affinity peptides, especially of the peptide's N-terminus. Using bias exchange umbrella sampling (BEUS), a technique to achieve enhanced sampling in molecular dynamics (MD) simulations, we obtained the free-energy profiles of the N-terminal dissociation of a respective high-affinity peptide from HLA-B*35:01 and HLA-B*44:02, two alleles on opposite ends of the scale regarding binding groove plasticity. The potential of mean force (PMF) for HLA-B*35:01 was calculated for two different sets of starting structures and is compared with a PMF obtained previously with a different force field to disentangle allele differences from force field and sampling effects. For both alleles, the free-energy profiles indicate that the peptide N-terminus dissociates in a substantial fraction of the pMHC I, suggesting that their crystal structures with fully bound peptides only partially capture the dynamic conformational ensemble of pMHC I in solution, and thus in the cell.

---

1 Introduction

Major histocompatibility complex class I (MHC I) presents antigenic peptides derived from the cytoplasm to patrolling cytotoxic T cells on the surface of all nucleated cells.¹ Therefore, the key structural feature of MHC I is their binding groove formed by the α₁- and α₂-domain (Fig. 1a).² Below the binding groove, the α₃-domain adopts an immunoglobulin fold,³ followed by a C-terminal membrane tether and cytosolic loop.⁴ Additional support to the binding groove is provided by a non-covalently bound immunoglobulin domain termed β₂-microglobulin.² The binding groove consists of a floor with eight β-sheets flanked by two α-helices and usually forms six pockets labeled A–F.^5–7 The binding groove can accommodate antigenic peptides consisting of 8–11 residues such that the peptide N-terminus is located in the vicinity of the A-pocket and the C-terminus is bound at the F-pocket.⁸ The peptide termini are integrated in a conserved network of hydrogen bonds, and the peptide is anchored in two binding groove pockets by the side chains of either its second or fifth and its C-terminal residue.² In the complex formed by HLA-B*35:01 with the peptide VY8(P5A), the peptide anchor residues P2 and Y8 are in close contact with Y99 in the B-pocket and S116 in the F-pocket, respectively (Fig. 1b);⁶ in the complex formed by HLA-B*44:02 with the peptide EF9, E2 and F9 are the peptide's anchor residues, and E2 closely interacts with Y99 at the bottom of the binding groove.⁹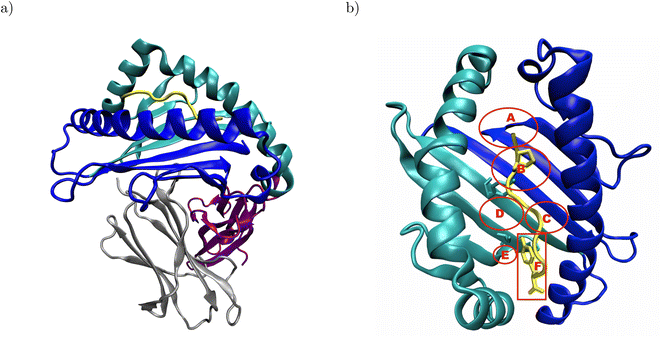

Fig. 1 Structural overview of peptide-MHC I complexes using the crystal structure of HLA-B*35:01 in complex with VY8(P5A), PDB ID: 1A1N: (a) the α₁- and α₂-domain (blue and cyan, respectively) form the binding groove, which hosts the antigenic peptide (yellow) and is supported by β₂-microglobulin (β₂m, gray). The α₃-domain (purple) attaches the MHC I to the cell surface via a membrane tether and a cytosolic loop, which were both not resolved in the crystal structure. (b) In the binding groove, the anchor residues P2 and Y8 (yellow licorice) of the antigenic peptide are in close contact with Y99 and S116 (cyan licorice) in the B- and F-pocket of the binding groove, respectively. The approximate positions of the pockets A–F are indicated in red; the backbones of both Y99 and S116 are located outside, but their side chains point into the B- and F-pocket, respectively. In the complex formed by HLA-B*44:02 and EF9, E2 and F9 are close to Y99 and D116, respectively (not shown). The α₃-domain and β₂m are omitted for clarity in panel b.

In the cell, a peptide-MHC I complex (pMHC I) has to pass three quality controls. When the MHC I encounters the antigenic peptide for the first time in the peptide loading complex in the endoplasmic reticulum (ER), it is bound by a chaperone called tapasin.^10–12 Tapasin is designed to bind MHC I tightly such that it can only be out-competed by a high-affinity peptide. To this end, it inserts a loop into the MHC I binding groove such that the loop's key leucine residue can dive into the F-pocket, which often prefers hydrophobic side chains like in HLA-B*44:02.¹³ Moreover, tapasin contacts the α₂-helix and two β-strands in the F-pocket region such that it can both stabilize the binding groove and open it slightly in order to start a molecular tug-of-war with the antigenic peptide that closes this binding groove region upon binding.^12,14 Last, tapasin forms a C-terminal interface with the α₃-domain of MHC I,^10,12 which is allosterically coupled to the F-pocket region of the binding groove.^15–17 The second quality check in the ER–Golgi intermediate compartment and the cis-Golgi involves the chaperone TAP binding protein related (TAPBPR).^18–20 Like tapasin, TAPBPR probes the interaction between the MHC I and the peptide C-terminus with the help of a loop with a key leucine residue, an N-terminal interface contacting the α₂-helix and three β-strands in the F-pocket region of the binding groove, and a C-terminal interface involving the α₃-domain of MHC I.^21–23 Finally, at the cell surface, MHC I are continuously monitored for optimal peptide cargo, and empty or sub-optimally loaded MHC I are internalized eight times faster than pMHC I containing high-affinity peptides.²⁴ Although the molecular details of that quality control remain elusive,²⁵ it is speculated that the cytosolic tail of MHC I is allosterically coupled to the F-pocket region such that the loading status of the MHC I can be communicated into the cell interior.⁴

In sum, the cellular fate of a pMHC I is determined by the plasticity of its binding groove, especially of the F-pocket region, which is significantly reduced in the presence of a high-affinity peptide. The key role of binding groove plasticity was successfully demonstrated with the help of MHC I molecules whose binding groove helices were connected by an artificial disulfide bond in the F-pocket region: they were transported to and stayed at the cell surface without an antigenic peptide bound.¹⁸ While MHC I allele HLA-B*44:02 is tapasin-dependent and requires a high-affinity peptide to be bound to pass the above cellular quality checks,²⁶ HLA-B*35:01 is tapasin-independent and can be transported to the cell surface without or with sub-optimal peptide cargo.²⁷ Consequently, HLA-B*35:01 and HLA-B*44:02 mark two opposite ends of the scale regarding their binding groove's conformational stability.

Here, we report the potential of mean force (PMF) for the N-terminal dissociation of a respective high-affinity peptide from both alleles, investigating how binding groove plasticity influences the extent to which an MHC I allele can tolerate N-terminal peptide dissociation. Moreover, the PMF for HLA-B*35:01 was calculated employing different starting structures and force fields,²⁸ allowing us to tell apart force field and sampling effects from allele differences.

2 Methods

The potentials of mean force (PMF) for the dissociation of the peptide N-terminus in the complexes formed by HLA-B*35:01 with the peptide VPLRAMTY (VY8(P5A)) and HLA-B*44:02 with the peptide EEFGRAFSF (EF9) were determined with bias exchange umbrella sampling (BEUS) simulations as implemented in GROMACS, version 5.1.4,^29–35 patched with PLUMED, version 2.3.2.³⁶ The theory of BEUS, a combination of replica exchange and umbrella sampling, has been reviewed in detail in.²⁸ Starting from the pre-processed crystal structure (PDB ID: 1A1N and 1M6O for HLA-B*35:01 and HLA-B*44:02, respectively), BEUS simulations with 24 windows, each sampling 1 μs for HLA-B*35:01 and 950 ns for HLA-B*44:02, were carried out. For HLA-B*35:01, an additional BEUS simulation with 24 windows, each sampling 1 μs, was launched from the final configurations of a BEUS simulation that had been run with AMBER99SB*-ILDNP as protein force field and TIP4P/2005 as water model,²⁸ yielding a total sampling time of 48 μs for HLA-B*35:01 and 22.8 μs for HLA-B*44:02. In all the simulations, the potential energy of the system was described by the AMBER99SB-disp force field³⁷ together with the TIP4PD water model,³⁸ with the modifications specific to AMBER99SB-disp.³⁷

For all three BEUS simulations, the PMF was computed using the weighted histogram analysis method (WHAM) as implemented in the GROMACS tool gmx wham.³⁹ Statistical errors were estimated by bootstrapping, i.e., the PMF was re-calculated for 200 new random trajectories with properly distributed and autocorrelated configurations. To assess the plasticity of the MHC I binding groove, eight distances between segments on opposite binding groove helices were computed. The position of each segment (residues 59–64 and 65–70 on the α₁-helix and residues 152–157, 158–163, 164–169, and 170–175 on the α₂-helix) was represented by the center of mass of the C_α-atoms of the respective six amino acids. Moreover, the configurational entropy of the binding groove was calculated according to the quasi-harmonic approximation as formulated by Schlitter.⁴⁰ Here, the flexible loops of the binding groove were excluded, and the covariance matrix of particle positions underlying the entropy estimate was computed for the C_α-atoms of residues 4–11, 23–36, 46–85, 93–101, 112–118, 122–126 and 137–180.

The system setup, the simulation protocol, and the analyses performed are described in more detail in the ESI.†

3 Results

In this study, three potentials of mean force (PMF) for the dissociation of the peptide N-terminus in two pMHC I were computed (Fig. 2). The two PMFs calculated for HLA-B*35:01 starting from different sets of initial configurations (black and red lines in Fig. 2a) are indistinguishable within statistical error, which is reassuring. Unexpectedly, the PMF for HLA-B*44:02 (Fig. 2b), which is known to be far more dependent on a tightly bound high-affinity peptide to exert its function in a cell than HLA-B*35:01,^26,27 also indicates that the free energy of the partially dissociated state is comparable to, if not lower than the free energy of the fully bound state. Thus, the allele-specific differences in the PMFs, which have smoothly converged and represent the free-energy profiles at equilibrium (Fig. S2†), are subtle. Therefore, we first analyze the two PMFs for HLA-B*35:01 and compare them with the PMF obtained with the AMBER99SB*-ILDNP force field²⁸ to understand how the choice of the force field and the amount of sampling affect the free-energy profile recorded. Having disentangled the influence of the simulation setup from allele-specific contributions to the PMF, we draw conclusions about differences and similarities between the two MHC I alleles HLA-B*35:01 and HLA-B*44:02.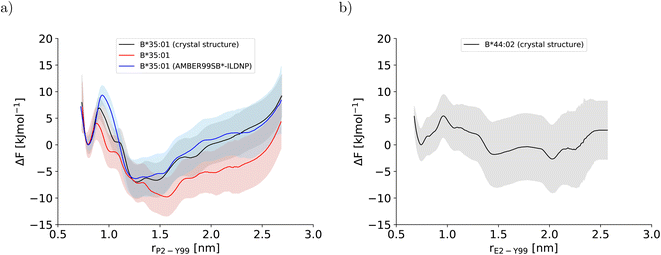

Fig. 2 Potentials of mean force along the center-of-mass distance between Y99 in the binding groove and P2 and E2 at the peptide N-terminus for (a) HLA-B*35:01 and (b) HLA-B*44:02, respectively. In (a), the PMF that was obtained with AMBER99SB*-ILDNP as protein force field and TIP4P/2005 as water model and published previously (blue line)²⁸ is included to facilitate comparisons with the PMFs obtained in this study (black and red line). The BEUS simulation yielding the PMF shown in red was started from the final configurations of the BEUS simulation with AMBER99SB*-ILDNP and TIP4P/2005.

3.1 Force field and sampling influences on the potentials of mean force

To understand the impact of the simulation setup on the PMF for the dissociation of the peptide N-terminus, this section focuses only on the two PMFs calculated for HLA-B*35:01 and compares them with the PMF obtained previously with the AMBER99SB*-ILDNP force field²⁸ (Fig. 2a). The PMF obtained from the BEUS simulation initiated from the crystal structure of HLA-B*35:01 in complex with its antigenic peptide VY8(P5A) (black line in Fig. 2a) is nearly identical to the PMF obtained with AMBER99SB*-ILDNP²⁸ (blue line in Fig. 2a), which underlines the robustness of the computational results. Apart from the barrier at r_P2–Y99 ≈ 0.9 nm separating the fully bound and the partially dissociated state, which was estimated to be approximately 2.4 kJ mol⁻¹ higher with AMBER99SB*-ILDNP, the average PMF and the statistical error nearly exactly overlap in both the fully bound and the partially dissociated state. Most importantly, both PMFs identify a fully bound free-energy minimum at r_P2–Y99 ≈ 0.8 nm, which matches the respective distance in the crystal structure,⁶ and the global minimum of the free energy at r_P2–Y99 ≈ 1.3 nm in the partially dissociated state is statistically significantly lower than the free energy of the fully bound state. The average PMF obtained from the BEUS simulation started from the final configurations of the BEUS simulation with AMBER99SB*-ILDNP²⁸ (red line in Fig. 2a) predicts the barrier between the fully bound and the partially dissociated state to be even lower by approximately 2.9 kJ mol⁻¹ compared with the BEUS simulation initiated from the crystal structure. Moreover, the global free energy minimum in the partially dissociated state has been shifted from r_P2–Y99 ≈ 1.3 nm to r_P2–Y99 ≈ 1.6 nm. Because the BEUS simulation underlying this PMF was started from the final configurations of the BEUS simulation with AMBER99SB*-ILDNP, it inherits the configurational sampling achieved in the BEUS simulation with AMBER99SB*-ILDNP via a more diverse set of starting structures compared with the simulation initiated from the crystal structure. Thus, at first glance, these differences suggest that, despite 1 μs of simulated time per umbrella window, the amount of sampling affects the free-energy profile more than the difference between the force fields (AMBER99SB*-ILDNP versus AMBER99SB-disp).

The collective motions of the pMHC I that are likely to affect the free-energy profile while being hard to sample are re-arrangements of the MHC I binding groove. In the previous BEUS simulation using the AMBER99SB*-ILDNP force field, the A-pocket region of the binding groove was found to collapse after the dissociation of the peptide N-terminus, leading to a significant reduction in binding groove volume.²⁸ Thus, a set of distances between residues at opposite sides of the binding groove is a suitable proxy for the volume of the groove. Interestingly, the average of the distances between sextets of residues on opposite binding groove helices flanking the A-pocket region does not indicate any collapse of the binding groove for the BEUS simulation with AMBER99SB-disp initiated from the crystal structure (Fig. 3). Lower average distances corresponding to lower binding groove volumes and a collapsed binding groove were only observed in the simulation with AMBER99SB-disp that was started from the final configurations of the AMBER99SB*-ILDNP simulation. Consequently, the binding groove of HLA-B*35:01 is conformationally stable with AMBER99SB-disp (it only widens very slightly after the peptide N-terminus has dissociated), and collapsed conformations of the groove, which were included in the set of final configurations of the AMBER99SB*-ILDNP simulation, artificially increase the binding groove's plasticity in the simulation with AMBER99SB-disp.

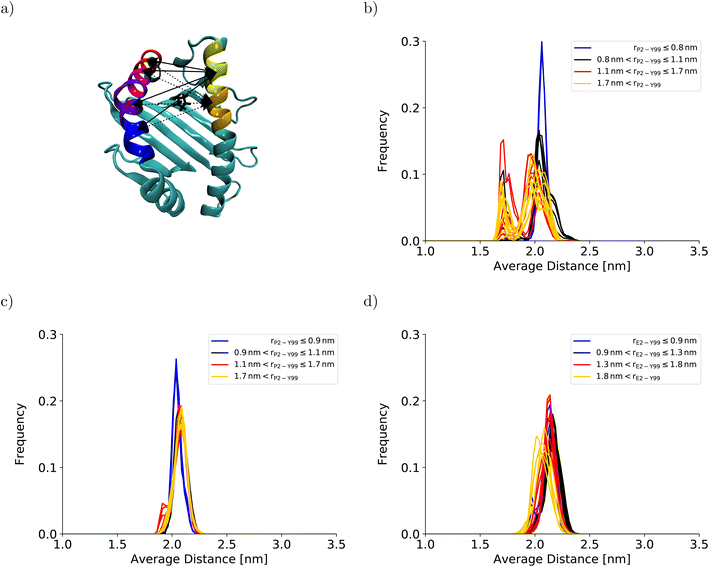Fig. 3 Binding groove plasticity as captured by sextet distances. To judge the groove's plasticity, eight pair distances between the centers of mass of the C_α-atoms of sextets of residues on opposite binding groove helices were calculated. These sextet distances were computed for residues 59–64 (yellow) and 65–70 (orange) on the α₁-helix and residues 152–157 (blue), 158–163 (violet), 164–169 (magenta), and 170–175 (red) on the α₂-helix, which are highlighted on the HLA-B*35:01 binding groove in (a). The four sextet distances including the first segment on the α₁-helix are shown as solid lines; the four sextet distances including the second segment on the α₁-helix are depicted as dotted lines. The arrows point to the correct segment; they do not indicate the exact position of the center of mass. The black licorice model illustrates the position of P2 at the peptide N-terminus. The positions of the corresponding residue sextets in the HLA-B*44:02 binding groove are highlighted in Fig. S3 in the ESI.† The distribution of the average of these eight sextet distances is shown for (b) HLA-B*35:01 (starting from the final structures of the BEUS simulation with AMBER99SB*-ILDNP²⁸), (c) HLA-B*35:01 (starting from the crystal structure), and (d) HLA-B*44:02 (starting from the crystal structure). Histograms shown in blue represent umbrella windows of the fully bound state, histograms in black belong to the barrier region of the PMF, and histograms in red and yellow belong to the adjacent and distant half of the partially dissociated state, respectively. The histograms of the individual distances are shown in Fig. S4–S11 in the ESI.†

This artificial plasticity is reflected by the configurational entropy of the binding groove (Fig. 4). For the BEUS simulation with AMBER99SB-disp initiated from the crystal structure, the increase in the binding groove's configurational entropy lowers the entropic contribution to the free energy of the pMHC I by approximately 20 kJ mol⁻¹ after crossing the barrier at r_P2–Y99 ≈ 0.9 nm, but the contribution to the free energy from the binding groove's configurational entropy is approximately constant in the partially dissociated state (Fig. 4a). In contrast, for the BEUS simulation with AMBER99SB-disp started from the final configurations of the AMBER99SB*-ILDNP simulation, the binding groove's configurational entropy artificially stabilizes the barrier region by up to 50 kJ mol⁻¹, and it provides additional stability to configurations with large distances between the peptide N-terminus and the binding groove (r_P2–Y99 ≥ 1.7 nm) in the partially dissociated state. Unfortunately, the configurational entropies could only be assigned to the value of the reaction coordinate (RC) that was targeted in the respective umbrella window. Consequently, the effect of the additional configurational entropy may be visible in the PMF for values of r_P2–Y99 that differ from the targeted value by the width of the RC distribution in the respective umbrella window (see Fig. S1†). Considering this uncertainty, the ranges of RC values in which the increase in the binding groove's configurational entropy stabilizes the pMHC I correlate well with the areas where the PMFs of the two BEUS simulations with AMBER99SB-disp deviate, i.e., for the simulation started from the final configurations of the BEUS simulation with AMBER99SB*-ILDNP, the free energies of the barrier region (0.9 nm ≤ r_P2–Y99 ≤ 1.2 nm) and of configurations with large distances (r_P2–Y99 ≥ 1.6 nm) have been lowered compared with the simulation initiated from the crystal structure.

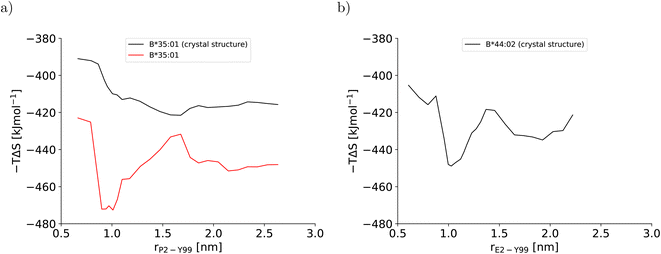Fig. 4 Configurational entropy of the binding groove obtained with the quasi-harmonic approximation (QHA) as formulated by Schlitter⁴⁰ for (a) HLA-B*35:01 and (b) HLA-B*44:02. The configurational entropy of the antigenic peptide and of the MHC I binding groove together with the antigenic peptide are shown in Fig. S12 and S13, respectively, in the ESI.†

Consequently, the differences between the PMFs obtained for the two BEUS simulations with AMBER99SB-disp are due to HLA-B*35:01 binding groove conformations that are most likely not accessible with AMBER99SB-disp alone. Thus, these differences are an implicit consequence of force field differences rather than that they reflect the impact of the amount of sampling on the free-energy profile. Most strikingly, even with the quite extensive microsecond sampling underlying these PMF calculations, the conformational stability of the HLA-B*35:01 binding groove is more a function of the force field than of the amount of simulated time, and even simulations with large differences in binding groove plasticity can lead to very similar PMFs for the dissociation of the peptide N-terminus.

3.2 N-terminal peptide dissociation in different alleles

The stable HLA-B*35:01 binding groove predicted by AMBER99SB-disp is consistent with experimental findings that this allele is both TAP- and tapasin-independent.²⁷ Furthermore, the AMBER99SB-disp force field was designed to deal with both folded and intrinsically disordered proteins equally well.³⁷ Therefore, we chose this force field to study HLA-B*44:02, which is known to have a less conformationally stable binding groove.²⁶ In the resulting PMF (Fig. 2b), the free-energy minimum of the fully bound state is located at r_E2–Y99 ≈ 0.7 nm, which is again in agreement with the crystal structure. The fully bound and the partially dissociated state are separated by a barrier at r_E2–Y99 ≈ 1.0 nm, and the partially dissociated state corresponds to a wide free-energy minimum with its lowest values between r_E2–Y99 ≈ 1.4 nm and r_E2–Y99 ≈ 2.1 nm. In contrast to the PMFs obtained for HLA-B*35:01, the free energies of RC values belonging to the partially dissociated state are not statistically significantly lower than the free energy of the fully bound state. Consequently, if the PMF is integrated, the free energy difference between the fully bound and the partially dissociated state amounts to ΔF_diss = (−6.4 ± 9.5) kJ mol⁻¹ such that it cannot be unambiguously decided from this PMF which of the two states is more stable, the fully bound or the partially dissociated one. But even for the most unfavorable free energy estimate (within the statistical error margin), the partially dissociated state still constitutes a significant minor population of approximately 20%. In contrast, both PMFs for HLA-B*35:01 clearly predict the partially dissociated state to be more stable, with ΔF_diss = (−11.3 ± 4.9) kJ mol⁻¹ for the BEUS simulation initiated from the crystal structure and ΔF_diss = (−14.3 ± 6.0) kJ mol⁻¹ for the BEUS simulation started from the final configurations of the AMBER99SB*-ILDNP simulation.

Similarly to the BEUS simulation of HLA-B*35:01 initiated from the crystal structure, the HLA-B*44:02 binding groove proves to be rather stable; only a slight tendency to explore more compact groove conformations can be observed (Fig. 3d). However, these changes are sufficient to again stabilize the barrier region by an entropic contribution to the free energy of up to 50 kJ mol⁻¹ due to an increase in the binding groove's configurational entropy (Fig. 4b), similarly to the stabilization observed in the BEUS simulation of HLA-B*35:01 started from the final configurations of the BEUS simulation with AMBER99SB*-ILDNP.

Altogether, these findings suggest that HLA-B*35:01 with its conformationally stable binding groove and HLA-B*44:02 with its conformationally more labile binding groove can both tolerate the dissociation of the peptide N-terminus to a significant extent, with the partially dissociated state being the major state for HLA-B*35:01 and at least a significantly populated state for HLA-B*44:02, too. The results suggest but do not suffice to prove (in a statistically rigorous way) that the dissociation of the peptide N-terminus becomes less favorable as the binding groove becomes more labile. However, they show that N-terminal peptide dissociation can occur even in strongly tapasin-dependent alleles like HLA-B*44:02.

4 Conclusions

In this work, the free-energy profiles for the dissociation of the N-terminus of high-affinity peptides from the binding grooves of MHC I alleles HLA-B*35:01 and HLA-B*44:02 are presented. The PMF for HLA-B*35:01 was computed using different sets of starting structures and different force fields. Regardless of the choice for these two simulation parameters, the bias exchange umbrella sampling (BEUS) simulations employed robustly and reliably yield consistent free-energy profiles within statistical error. However, important properties of the MHC I allele studied, like the plasticity of the binding groove, were found to be force field-dependent, and even if the same free-energy profile for N-terminal peptide dissociation is obtained with two different force fields, they can still predict very different binding groove plasticities for the same MHC I allele. Therefore, the BEUS simulations can reliably predict the probability of peptide N-terminus dissociation in a given pMHC I even if the alleles studied differ in their binding groove plasticity. However, large-scale conformational re-arrangements of the binding groove observed in the simulations that could provide a mechanistic link between the free energy of partial peptide dissociation and binding groove plasticity have to be interpreted with care, because they may be a consequence of the force field used rather than a property of the MHC I allele studied.

With the tapasin-independent allele HLA-B*35:01 and the highly tapasin-dependent allele HLA-B*44:02, two extremes on the scale of conformational stability were studied. Surprisingly, the N-terminus of the peptide is likely to dissociate in both alleles. Therefore, even in pMHC I complexes formed by a high-affinity peptide and an MHC I allele with a conformationally labile binding groove, the peptide may partially dissociate in a significant fraction, suggesting that the crystal structure with a fully bound peptide may not completely represent the relevant conformational ensemble of the pMHC I in solution and thus inside the cell or on the cell surface. Consequently, even pMHC I for which experimental structures could only be determined with a fully bound peptide may undergo dynamic processes that require partial peptide dissociation, like dipeptide-catalyzed exchange of the antigenic peptide⁴¹ or N-terminal processing of C-terminally bound antigenic peptides by ERAP.^42–44

Author contributions

S. W. designed the study and conducted and analysed all simulations. Both authors discussed and interpreted the data, and wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2033 – 390677874 – RESOLV.

References

1. A. W. Purcell and T. Elliott, Curr. Opin. Immunol., 2008, 20, 75–81.
2. C. A. Wright, P. Kozik, M. Zacharias and S. Springer, Biol. Chem., 2004, 385, 763–778.
3. M. Wieczorek, E. T. Abualrous, J. Sticht, M. Álvaro-Benito, S. Stolzenberg, F. Noé and C. Freund, Front. Immunol., 2017, 8, 292.
4. P. van Endert, Immunol. Rev., 2016, 272, 80–96.
5. K. L. Rock, E. Reits and J. Neefjes, Trends Immunol., 2016, 37, 724–737.
6. S. Yanaka, T. Ueno, Y. Shi, J. Qi, G. F. Gao, K. Tsumoto and K. Sugase, J. Biol. Chem., 2014, 289, 24680–24690.
7. A. C. McShan, C. A. Devlin, S. A. Overall, J. Park, J. S. Toor, D. Moschidi, D. Flores-Solis, H. Choi, S. Tripathi, E. Procko and N. G. Sgourakis, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 25602–25613.
8. S. Hulpke and R. Tampé, Trends Biochem. Sci., 2013, 38, 412–420.
9. W. A. Macdonald, A. W. Purcell, N. A. Mifsud, L. K. Ely, D. S. Williams, L. Chang, J. J. Gorman, C. S. Clements, L. Kjer-Nielsen, D. M. Koelle, S. R. Burrows, B. D. Tait, R. Holdsworth, A. G. Brooks, G. O. Lovrecz, L. Lu, J. Rossjohn and J. McCluskey, J. Exp. Med., 2003, 198, 679–691.
10. A. Blees, D. Januliene, T. Hofmann, N. Koller, C. Schmidt, S. Trowitzsch, A. Moeller and R. Tampé, Nature, 2017, 551, 525–528.
11. C. Thomas and R. Tampé, Front. Immunol., 2017, 8, 65.
12. O. Fisette, G. F. Schröder and L. V. Schäfer, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 20597–20606.
13. I. Hafstrand, E. C. Sayitoglu, A. Apavaloaei, B. J. Josey, R. Sun, X. Han, S. Pellegrino, D. Ozkazanc, R. Potens, L. Janssen, J. Nilvebrant, P.-Å. Nygren, T. Sandalova, S. Springer, A.-M. Georgoudaki, A. D. Duru and A. Achour, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 5055–5060.
14. O. Fisette, S. Wingbermühle, R. Tampé and L. V. Schäfer, Sci. Rep., 2016, 6, 19085.
15. A. Bailey, N. Dalchau, R. Carter, S. Emmott, A. Phillips, J. M. Werner and T. Elliott, Sci. Rep., 2015, 5, 14928.
16. A. van Hateren, M. Anderson, A. Bailey, J. M. Werner, P. Skipp and T. Elliott, J. Biol. Chem., 2017, 292, 20255–20269.
17. C. M. Ayres, E. T. Abualrous, A. Bailey, C. Abraham, L. M. Hellman, S. A. Corcelli, F. Noé, T. Elliott and B. M. Baker, Front. Immunol., 2019, 10, 966.
18. Z. Hein, H. Uchtenhagen, E. T. Abualrous, S. K. Saini, L. Janßen, A. Van Hateren, C. Wiek, H. Hanenberg, F. Momburg, A. Achour, T. Elliott, S. Springer and D. Boulanger, J. Cell Sci., 2014, 127, 2885–2897.
19. A. Neerincx, C. Hermann, R. Antrobus, A. van Hateren, H. Cao, N. Trautwein, S. Stevanović, T. Elliott, J. E. Deane and L. H. Boyle, Elife, 2017, 6, e23049.
20. T. Elliott and A. van Hateren, Biochemistry, 2018, 57, 1423–1425.
21. F. T. Ilca, A. Neerincx, C. Hermann, A. Marcu, S. Stevanović, J. E. Deane and L. H. Boyle, Elife, 2018, 7, e40126.
22. C. Thomas and R. Tampé, Science, 2017, 358, 1060–1064.
23. J. Jiang, K. Natarajan, L. F. Boyd, G. I. Morozov, M. G. Mage and D. H. Margulies, Science, 2017, 358, 1064–1068.
24. A. C. Adiko, J. Babdor, E. Gutiérrez-Martínez, P. Guermonprez and L. Saveanu, Front. Immunol., 2015, 6, 335.
25. S. Montealegre and P. M. van Endert, Front. Immunol., 2019, 9, 3098.
26. K. Ostermeir, S. Springer and M. Zacharias, Mol. Immunol., 2015, 63, 312–319.
27. J. Geng, A. J. Zaitouna and M. Raghavan, PLoS Pathog., 2018, 14, e1007171.
28. S. Wingbermühle and L. V. Schäfer, J. Chem. Theory Comput., 2020, 16, 4615–4630.
29. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
30. S. Páll, M. J. Abraham, C. Kutzner, B. Hess and E. Lindahl, Solving Software Challenges for Exascale, 2015, 8759, 3–27.
31. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
32. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
33. D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
34. E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model., 2001, 7, 306–317.
35. H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56.
36. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
37. P. Robustelli, S. Piana and D. E. Shaw, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E4758–E4766.
38. S. Piana, A. G. Donchev, P. Robustelli and D. E. Shaw, J. Phys. Chem. B, 2015, 119, 5113–5123.
39. J. S. Hub, B. L. de Groot and D. van der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720.
40. J. Schlitter, Chem. Phys. Lett., 1993, 215, 617–621.
41. S. K. Saini, H. Schuster, V. R. Ramnarayan, H.-G. Rammensee, S. Stevanović and S. Springer, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 202–207.
42. H. Chen, L. Li, M. Weimershaus, I. Evnouchidou, P. van Endert and M. Bouvier, Sci. Rep., 2016, 6, 28902.
43. L. Li, M. Batliwala and M. Bouvier, J. Biol. Chem., 2019, 294, 18534–18544.
44. A. Papakyriakou, E. Reeves, M. Beton, H. Mikolajek, L. Douglas, G. Cooper, T. Elliott, J. M. Werner and E. James, J. Biol. Chem., 2018, 293, 7538–7548.

---

Footnotes

† Electronic supplementary information (ESI) available: Detailed methods as well as additional plots for PMF convergence, distances between helix segments, and configurational entropies. See DOI: https://doi.org/10.1039/d2ra05324a

‡ Current affiliation: Department of Applied Physics, Science for Life Laboratory, KTH Royal Institute of Technology, Solna, Sweden.

---