Open Access Article
Open Access ArticleGeometries, molecular Rayleigh scattering, Raman and infrared frequencies of polycyclic aromatic hydrocarbons and subunits of graphite studied by DFT methods†
Freja
Hasager
 ,
Ole John
Nielsen
,
Ole John
Nielsen
 and
Kurt V.
Mikkelsen
and
Kurt V.
Mikkelsen
 *
*
Department of Chemistry, University of Copenhagen, Universitetsparken 5, 2100 Copenhagen Ø, Denmark. E-mail: kmi@chem.ku.dk
First published on 26th July 2022
Abstract
This study presents a computational investigation of geometric parameters, infrared (IR) and Raman frequencies as well as molecular Rayleigh scattering of polycyclic aromatic hydrocarbons (PAHs), used as models for subunits of larger graphitic materials. DFT functionals B3LYP, ωB97XD and M06-2X with basis sets 6-31+G(d,p), 6-311+G(d,p), aug-cc-pVDZ and aug-cc-pVTZ were utilized in different combinations in the investigation of two molecular systems: 2H-benzo(cd)pyrene and double-layered 2H-benzo(cd)pyrene. Bond lengths and angles of central carbon atoms in the different subunits varied by a maximum of 2% between systems. Calculated Raman spectra compare well with experimental and simulated Raman spectra from the literature of other PAHs, and only to some extent with experimental spectra of graphitic materials. The molecular Rayleigh scattering was found to increase by a factor of 3.5 upon addition of an extra layer to the system.
Environmental significanceWe investigate how black carbon particles can affect the climate by the direct scattering and absorption of light. Black carbon (BC) particles are strong warming agents of the same magnitude as methane and they pose a threat to human health. Emissions of these particles are estimated to be around 7500 Gg year−1 and the particles are able to travel long distances from the source areas. Basically, BC particles are systems that we need to know more about. It is important to know the photophysical properties of the BC particles in order to understand their impact on the climate. |
1 Introduction
Aerosols affect climate by the direct scattering and absorption of light and by the indirect effect of cloud interactions.1,2 Carbonaceous particles pose a threat to human health as they have been found to be the cause of cardiovascular and respiratory diseases.3,4 Ultrafine BC particles (less than 0.1 μm) and fine (less than 2.5 μm) penetrate deep into the lungs and carry with them carcinogenic polycyclic aromatic hydrocarbons causing lung cancer.3,4,5 Black carbon (BC) is a strong warming agent of the same magnitude as methane.6 The source of BC is incomplete fossil fuel combustion and biomass burning. The term soot is used mainly in the combustion community whereas BC is used in the atmospheric community. Different emission inventory methods estimated the 2000 total global BC emissions to be 7500 Gg year−1 with an uncertainty of 2000–29,000 Gg year−1.7 There is a large potential for emission reductions. BC also plays a special positive warming role in the Arctic due to deposition on snow and ice. It is well known that BC particles travel long distances from the source areas.8,9 BC particles are spherules consisting of wrinkled graphite layers forming disordered structures containing different levels of elemental carbon and they absorb strongly in the ultraviolet, visible and infrared wavelength ranges. Measurements of BC mass concentrations rely on the optical properties of BC. Real-time methods are based on measurements of optical properties: extinction, scattering and absorption in wavelength regions where interferences from other species can be minimized or completely avoided. Large uncertainties exist in the determination of aerosol induced radiative forcing used in climate models.6 Assessment of the properties of particles is thus important in understanding the climate impact of anthropogenic aerosol emissions, and hence minimizing the uncertainty in the radiative forcing from aerosols in climate models. Optical properties are also important for detection and quantification of BC. In this study graphite subunits were used to investigate properties of graphite on the molecular scale. Here, the vibrational frequencies, Raman shifts and Rayleigh scattering, as well as the geometries have been determined for two different polycyclic aromatic hydrocarbons. The investigated subunits were: 2H-benzo(cd)pyrene and a double-layer system consisting of two 2H-benzo(cd)pyrene molecules. The structures are given in Fig. 1.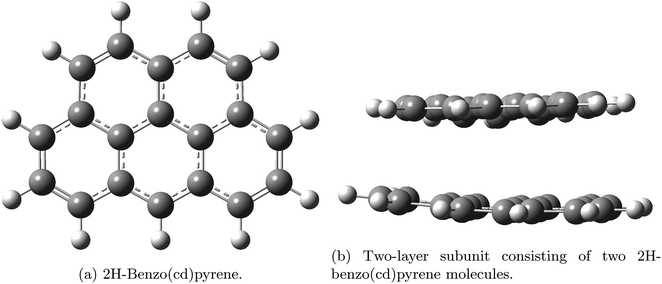 | ||
| Fig. 1 Graphite subunits investigated in this study: 2H-benzo(cd)pyrene (a) and double-layer 2H benzo(cd)pyrene (b). Gray represents carbon atoms and white represents hydrogen atoms. | ||
2 Computational approach
Graphite subunits were investigated computationally using the Gaussian16 program.10 Calculations were performed with three density functional theory (DFT) functionals: B3LYP, ωB97XD and M06-2X. The hybrid functional B3LYP was chosen, as it has previously proven useful in the study of PAHs.11,12 The ωB97XD functional has also shown to provide reliable results for PAHs13 and the Minnesota functional M06-2X has previously given excellent results for aromatic–aromatic stacking interactions.14 The DFT functionals were used in combination with the basis sets 6-31+G(d,p) and 6-311+G(d,p)15 and the correlation consistent basis sets aug-cc-pVDZ and aug-cc-pVTZ.16 Specifically, 2H-benzo(cd)pyrene was investigated using B3LYP, ωB97XD and M06-2X in combination with 6-31+G(d,p), 6-311+G(d,p), aug-cc-pVDZ, and aug-cc-pVTZ, while the double-layer subunit was investigated using B3LYP, ωB97XD and M06-2X in combination with basis sets 6-31+G(d,p) and 6-311+G(d,p). As this study presumes to model graphite subunits, diffuse functions were added only to the carbon atoms. Polarization functions were added to both hydrogen and carbon atoms.Isotropic, α, and anisotropic, β, polarizabilities were used to calculate the molecular Rayleigh scattering 〈R〉 by the relation 〈R〉 = 45α2 + 13β2.17,18
3 Results and discussion
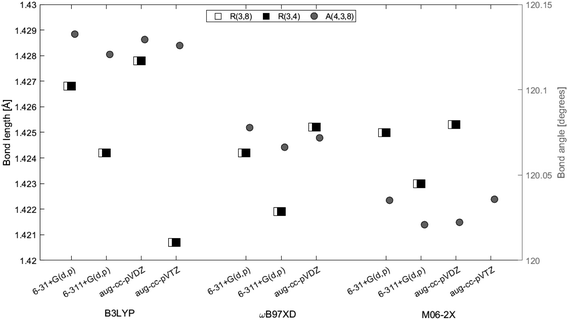
3.1 Geometry optimizations
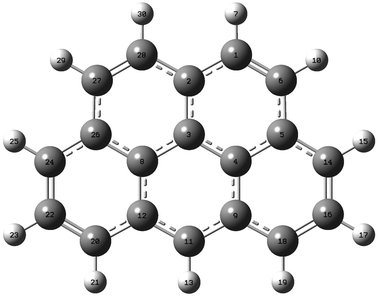 | ||
| Fig. 2 2H-Benzo(cd)pyrene optimized at the M06-2X/aug-cc-pVTZ level of theory. Labels indicate atom number. | ||
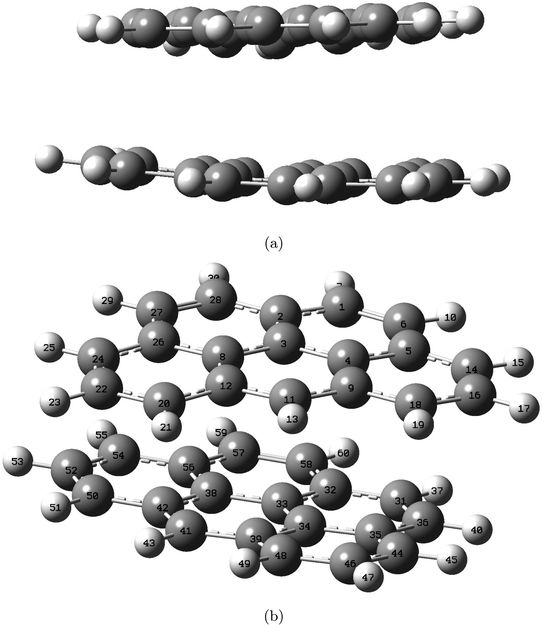 | ||
| Fig. 4 Structure of the double-layered graphite subunit optimized at the M06-2X/6-311+G(d,p) level, shown from side view (a) and top-side view (b). Labels indicate atom number. | ||
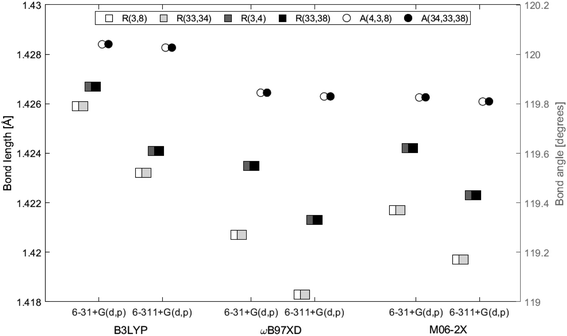
The distance between the two layers, 3.3222 Å, is estimated in GaussView6.0.16 (ref. 19) as the distance between atom 3 and 33, both located at the center in each of the two layers. In Fig. 5 the bond lengths and angles between the center atoms in the two layers are shown as a function of basis set and method. The 6-31+G(d,p) basis set systematically estimates higher values than 6-311+G(d,p) by a maximum of 0.2%. Bond lengths R(3, 4), R(3, 8) and angle A(4, 3, 8) belong to the top layer, while bond lengths R(33, 34), R(33, 38) and angle A(34, 33, 38) belong to the bottom layer. The two angles are almost identical at a given functional/basis set combination. Angles obtained by different combinations of basis set and functional only vary up to 0.2%. The greatest variation between bond lengths, regardless of basis set/functional combination, proved to be 0.6%. As for the single layer, only small variations in the optimized geometries were identified depending on level of theory and/or location in the system.
3.2 Spectral properties
IR vibrational frequencies, Raman shifts and polarizabilities were calculated for 2H-benzo(cd)pyrene utilizing functionals B3LYP, ωB97XD and M06-2X with basis sets 6-31+G(d,p), 6-311+G(d,p) and aug-cc-pVDZ. For the double-layer subunit, functionals B3LYP, ωB97XD, and M06-2X were utilized in combination with basis sets 6-31+G(d,p) and 6-311+G(d,p).The calculated IR spectra of 2H-benzo(cd)pyrene and the double-layer subunit contain major peaks in the 850–900 cm−1 range arising from the out-of-plane vibration. Thus this mode has been compared to the experimental value of 868 cm−1. Improved computational accuracy would be expected as a result of increasing basis set size and with each step up on the rungs of Jacob's ladder.21,22 In Table 1 and Fig. 7 it is seen that the frequency for 2H-benzo(cd)pyrene calculated at the M06-2X/6-311+G(d,p) level is closest to the experimental value, underestimating the experimental frequency by 1 cm−1. The calculations from ωB97XD in combination with the Pople basis sets are 2 cm−1 from the experimental value, and hence the second best determinations. The ωB97XD and M06-2X with aug-cc-pVDZ levels overestimate the frequency by 11 and 15 cm−1, respectively, while the B3LYP/aug-cc-pVDZ level yields a value 3 cm−1 above the experimental. The B3LYP method combined with 6-31+G(d,p) and 6-311+G(d,p) underestimates the frequency by 7 and 10 cm−1, respectively. The IR spectra of 2H-benzo(cd)pyrene calculated at the aug-cc-pVDZ level show that the peak in the 850–900 cm−1 range is split in two, whereas the other basis sets yield spectra with only one peak in that range, see Fig. 6a. The peak used for the aug-cc-pVDZ analysis is the high energy split, which is a possible explanation for why aug-cc-pVDZ overestimates the frequency. For the double-layer 2H-benzo(cd)pyrene the aug-cc-pVDZ basis set was not utilized. The B3LYP calculations underestimate the frequency by 3 cm−1 and 9 cm−1 for 6-31+G(d,p) and 6-311+G(d,p), respectively. Hence, the B3LYP/6-31+G(d,p) method yields the best value. Functionals ωB97XD and M06-2X with the basis set 6-31+G(d,p) overestimate the frequency by 12 cm−1 and 9 cm−1, respectively, while the ωB97XD/6-311+G(d,p) and M06-2X/6-311+G(d,p) calculations overestimate the frequency by 4 cm−1 and 6 cm−1, respectively.
| B3LYP | ωB97XD | M06-2X | |
|---|---|---|---|
| 2H-Benzo(cd)pyrene | |||
| 6-31+G(d,p) | 860.5708 | 869.8538 | 871.9956 |
| 6-311+G(d,p) | 857.9248 | 866.3583 | 867.063 |
| aug-cc-pVDZ | 870.8079 | 878.762 | 883.4537 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Double-layer | |||
| 6-31+G(d,p) | 865.2546 | 880.3031 | 877.3855 |
| 6-311+G(d,p) | 858.5925 | 871.9908 | 873.8561 |
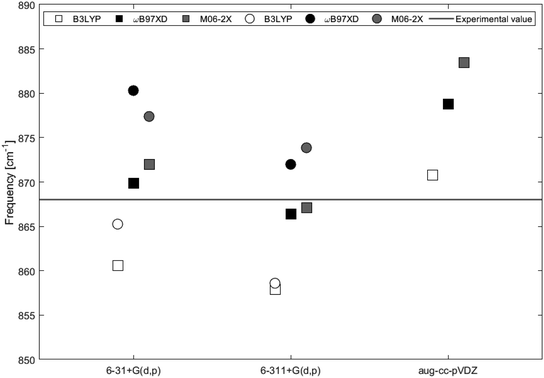 | ||
| Fig. 7 IR vibrational frequencies of the major peak for 2H-benzo(cd)pyrene (squares) and the double-layer subunit (circles) obtained by different levels of theory. The black line represents the experimental value of 868 cm−1 from Kastner et al.20 | ||
On the basis of this investigation it is concluded that the ωB97XD/6-311+G(d,p) level of theory yields reliable results for both 2H-benzo(cd)pyrene and double-layered 2H-benzo(cd)pyrene, with a maximum variation of 0.5% from the experimental value. It is expected that by increasing the size of the subunit a better calculated value would be obtained, as the graphitic material used for the experimental determination is a large multi-layer system. Comparison between the two subunits relative to the experimental value were done for frequencies obtained by B3LYP, ωB97XD and M06-2X with basis sets 6-31+G(d,p) and 6-311+G(d,p). The calculated value for 2H-benzo(cd)pyrene maximally varies 1.2% from the experimental value, and 1.4% for double-layered 2H-benzo(cd)pyrene. Hence, no improvement was observed going from the single to the double-layer subunit. It is important to note that the experimental IR features were measured for graphitic systems much larger than the two subunits investigated here. Additionally, calculations were performed for vacuum conditions, while experiments were not conducted in vacuum. This introduces some uncertainty when comparing theoretical and experimental values, as these may not be directly comparable.
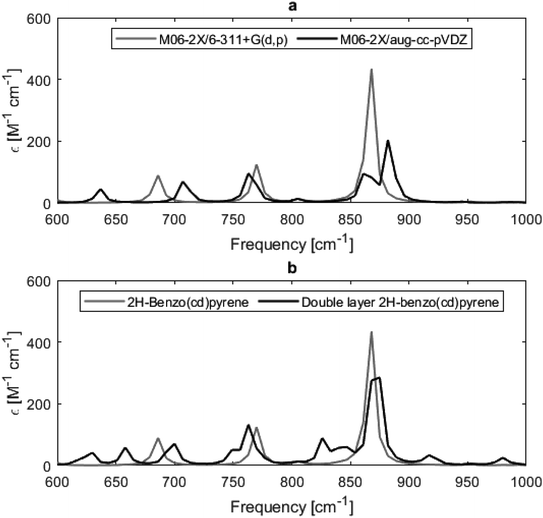
Fig. 8 shows calculated Raman spectra for 2H-benzo(cd)pyrene and the double-layer system calculated at the M06-2X/6-311+G(d,p) level. Very notable is the “missing” G′ band at 2700 cm−1 characteristic for graphitic materials. For both subunits, the spectra contain features at around 1240–1280 cm−1 and 1650–1670 cm−1 that could be associated with the D band from sp2 carbon and the G band from disorder. At around 3200 cm−1 the calculated spectra each have a medium/strong peak that arises from the C–H modes, similar to what is observed for various PAHs.11,27 The Raman spectra of these PAHs contain several features in the 1000–1500 cm−1 range. Thus, the Raman features identified here resemble PAHs better than they resemble graphite.
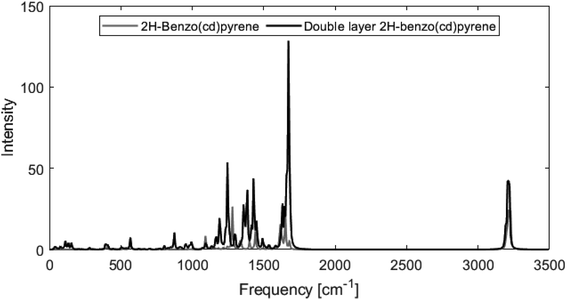 | ||
| Fig. 8 Raman spectra obtained from M06-2X/6-311+G(d,p) calculations of 2H-benzo(cd)pyrene (gray line) and the double-layer subunit (black line). | ||
From Fig. 8 it is evident that the calculated Raman spectra for 2H-benzo(cd)pyrene and the double-layer subunit look somewhat similar. The features in the double-layer spectrum are shifted a bit to the left relative to the spectrum of 2H-benzo(cd)pyrene. Both spectra contain several peaks in the 1100–1600 cm−1 range. A zoom of this range, see ESI,† shows that the double-layer subunit spectrum contains more features than the 2H-benzo(cd)pyrene spectrum, which is not surprising, as larger systems contain more vibrational modes.
Fig. 9 and Table 2 show the Raman shifts at ∼1600–1700 cm−1 arising from the C–C in-plane vibrational mode, for 2H-benzo(cd)pyrene and the double-layer subunit calculated at different levels of theory. Comparison of the shifts within the same functional but varying basis set yields a maximum variation of 1% for each of the two subunits. Comparison of the shifts between the two subunits calculated utilizing all functionals with basis sets 6-31+G(d,p) and 6-311+G(d,p) yields a maximum variation of 2% for the ωB97XD/6-31+G(d,p) determinations, and a minimum variation of 1% for the B3LYP/6-311+G(d,p) determinations. Functionals ωB97XD and M06-2X yield similar results for each of the subunits, while values calculated at the B3LYP level are generally lower.
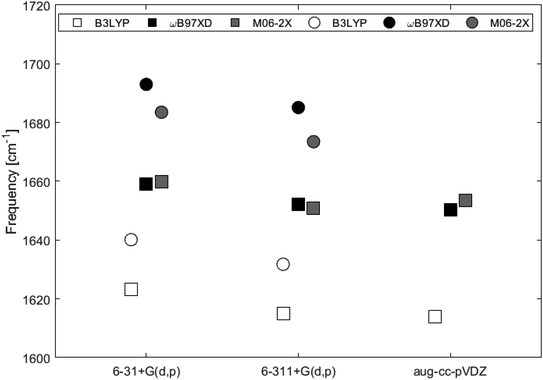 | ||
| Fig. 9 Major Raman shifts in the 1600–1700 cm−1 range calculated at different levels of theory for 2H-benzo(cd)pyrene (squares) and the double-layer subunit (circles). | ||
| B3LYP | ωB97XD | M06-2X | |
|---|---|---|---|
| 2H-Benzo(cd)pyrene | |||
| 6-31+G(d,p) | 1623.2125 | 1659.0021 | 1659.7803 |
| 6-311+G(d,p) | 1615.0978 | 1652.0413 | 1650.9097 |
| aug-cc-pVDZ | 1614.0553 | 1650.3219 | 1653.6153 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Double-layer | |||
| 6-31+G(d,p) | 1640.1342 | 1692.9805 | 1683.5198 |
| 6-311+G(d,p) | 1631.7723 | 1685.1069 | 1673.4912 |
| Isotropic | Anisotropic | |||||
|---|---|---|---|---|---|---|
| B3LYP | ωB97XD | M06-2X | B3LYP | ωB97XD | M06-2X | |
| 2H-Benzo(cd)pyrene | ||||||
| 6-31+G(d,p) | 244.92 | 234.42 | 239.05 | 230.02 | 214.86 | 225.31 |
| 6-311+G(d,p) | 243.80 | 234.33 | 237.03 | 228.85 | 214.33 | 221.21 |
| aug-cc-pVDZ | 252.18 | 243.25 | 246.25 | 232.09 | 216.72 | 225.72 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Double-layer | ||||||
| 6-31+G(d,p) | 537.34 | 481.81 | 481.03 | 164.12 | 162.58 | 171.98 |
| 6-311+G(d,p) | 528.23 | 480.39 | 476.89 | 159.46 | 162.20 | 169.57 |
4 Conclusion
DFT functionals combined with different basis sets have been used to investigate geometries, IR vibrational frequencies, Raman shifts and molecular Rayleigh scattering for two molecular systems used as model units for graphite. Geometry parameters of 2H-benzo(cd)pyrene were calculated using DFT functionals B3LYP, ωB97XD, M06-2X in combination with basis sets 6-31+G(d,p), 6-311+G(d,p) and aug-cc-pVDZ. Functionals B3LYP and M06-2X with basis set aug-cc-pVTZ were also utilized for the geometry optimization of 2H-benzo(cd)pyrene. The geometry of double-layered 2H-benzo(cd)pyrene was calculated utilizing functionals B3LYP, ωB97XD, M06-2X with basis sets 6-31+G(d,p) and 6-311+G(d,p). Bond lengths and bond angles of central atoms in the two systems proved to vary by less than 2% and 0.1%, respectively, between the systems. Thus, the configurations of atoms in these systems are not greatly affected by increasing the system size by addition of an extra layer.Theoretical IR spectra were calculated for both subunits. The functionals B3LYP, ωB97XD, M06-2X with the basis sets 6-31+G(d,p), 6-311+G(d,p) and aug-cc-pVDZ was used for 2H-benzo(cd)pyrene, while the basis sets 6-31+G(d,p) and 6-311+G(d,p) were utilized for the double-layer structure. IR spectra contained a prominent peak at ∼850–900 cm−1, arising from out-of-plane C–C vibrations. Comparison of this vibrational frequency with an experimental value of 868 cm−1 for graphitic material showed no improvement of accuracy by the addition of an extra layer of 2H-benzo(cd)pyrene to the system. It was also found that the ωB97XD/6-311+G(d,p) level of theory yields the best result for both the single- and double-layer subunits.
Calculated Raman spectra of the two subunits compared better with experimental Raman spectra of PAHs than to those of graphitic materials. Raman shifts of the C–C in-plane vibrational mode calculated using B3LYP, ωB97XD and M06-2X with basis sets 6-31+G(d,p) and 6-311+G(d,p), varied up to 1% between basis sets within a given functional for each of the two subunits, and up to 2% for comparison of the two systems within same functional/basis set combination. The most consistent results were obtained by ωB97XD and M06-2X.
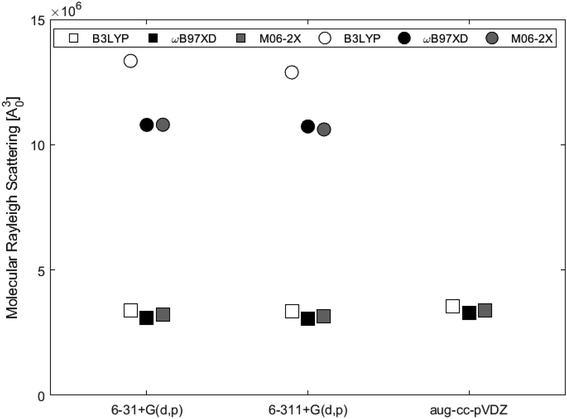
Isotropic and anisotropic polarizabilities were calculated and used to determine molecular Rayleigh scattering. Evaluation of the scattering obtained from the B3LYP, ωB97XD and M06-2X functionals with basis sets 6-31+G(d,p) and 6-311+G(d,p) for the two systems, showed that ωB97XD and M06-2X yielded similar results for each of the systems, while B3LYP estimated values about 10% and 20% higher for the single- and double-layer subunits, respectively.
In summary, it has been found that the computational methods ωB97XD, M06-2X/6-31+G(d,p), 6-311+G(d,p) are useful tools for theoretical investigations of large polycyclic aromatic hydrocarbons and consequently useful in expanding our understanding of graphitic materials on the molecular scale.
5 Conflicts of interest
There are no conflicts to declare.References
- J. Haywood and O. Boucher, Rev. Geophys., 2000, 38, 513–543 CrossRef CAS.
- J. Fan, Y. Wang, D. Rosenfeld and X. Liu, J. Atmos. Sci., 2016, 73, 4221–4252 CrossRef.
- P. M. Mannucci, S. Harari, I. Martinelli and M. Franchini, Internal and Emergency Medicine, 2015, 10, 657–662 CrossRef PubMed.
- J. S. Lighty, J. M. Veranth and A. F. Sarofim, J. Air Waste Manage. Assoc., 2000, 50, 1565–1618 CrossRef CAS PubMed.
- A. A. Koelmans, M. T. Jonker, G. Cornelissen, T. D. Bucheli, P. C. Van Noort and Ö. Gustafsson, Chemosphere, 2006, 63, 365–377 CrossRef CAS PubMed.
- G. Myhre, D. Shindell, F.-M. Bréon, W. Collins, J. Fuglestvedt, J. Huang, D. Koch, J.-F. Lamarque, D. Lee, B. Mendoza, T. Nakajima, A. Robock, G. Stephens, T. Takemura and H. Zhang, in Anthropogenic and Natural Radiative Forcing, ed. T. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P. Midgley, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013, book section 8, pp. 659–740 Search PubMed.
- T. C. Bond, S. J. Doherty, D. W. Fahey, P. M. Forster, T. Berntsen, B. J. DeAngelo, M. G. Flanner, S. Ghan, B. Kärcher and D. Koch, et al. , J. Geophys. Res.: Atmos., 2013, 118, 5380–5552 CrossRef CAS.
- E. Freud, R. Krejci, P. Tunved, R. Leaitch, Q. T. Nguyen, A. Massling, H. Skov and L. Barrie, Atmos. Chem. Phys., 2017, 17, 8101–8128 CrossRef CAS.
- K. S. Law and A. Stohl, Science, 2007, 315, 1537–1540 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- F. Negri, C. Castiglioni, M. Tommasini and G. Zerbi, J. Phys. Chem. A, 2002, 106, 3306–3317 CrossRef CAS.
- D. G. Smith and K. Patkowski, J. Chem. Theory Comput., 2012, 9, 370–389 CrossRef PubMed.
- A. Yadav and P. Mishra, Mol. Phys., 2014, 112, 88–96 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- T. Joranger, J. V. Kildgaard, S. Jørgensen, J. Elm and K. V. Mikkelsen, Phys. Chem. Chem. Phys., 2019, 21, 17274–17287 RSC.
- J. Elm, P. Norman, M. Bilde and K. V. Mikkelsen, Phys. Chem. Chem. Phys., 2014, 16, 10883–10890 RSC.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView Version 6, Semichem Inc., Shawnee Mission KS, 2019 Search PubMed.
- J. Kastner, T. Pichler, H. Kuzmany, S. Curran, W. Blau, D. Weldon, M. Delamesiere, S. Draper and H. Zandbergen, Chem. Phys. Lett., 1994, 221, 53–58 CrossRef CAS.
- S. Kurth, J. P. Perdew and P. Blaha, Int. J. Quantum Chem., 1999, 75, 889–909 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, J. Tao, V. N. Staroverov, G. E. Scuseria and G. I. Csonka, J. Chem. Phys., 2005, 123, 062201 CrossRef PubMed.
- S. Reich and C. Thomsen, Philos. Trans. R. Soc., A, 2004, 362, 2271–2288 CrossRef CAS PubMed.
- R. Vidano, D. Fischbach, L. Willis and T. Loehr, Solid State Commun., 1981, 39, 341–344 CrossRef CAS.
- M. Pimenta, G. Dresselhaus, M. S. Dresselhaus, L. Cancado, A. Jorio and R. Saito, Phys. Chem. Chem. Phys., 2007, 9, 1276–1290 RSC.
- S. Reichardt and L. Wirtz, Optical Properties of Graphene, World Scientific, 2017, pp. 85–132 Search PubMed.
- W. Maddams and I. Royaud, Spectrochim. Acta, Part A, 1990, 46, 309–314 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d1ea00105a |
| This journal is © The Royal Society of Chemistry 2022 |