Quantification anomalies in single pulse LA-ICP-MS analysis associated with laser fluence and beam size

Abstract

Laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) has undergone major improvements in recent years which have led to reduction of the analysis time, higher spatial resolution, and better sensitivity. However, quantification and accurate analysis remain one of the bottlenecks in LA-ICP-MS analysis and so far satisfactory calibration solutions are restricted to well-documented matrices and suitable internal standards. Additional uncertainties associated with laser fluence and beam size via various ablation cells and interfaces make quantification even more challenging. This work is focused on the influence of fluence, beam size and aerosol transport on quantification in single pulse LA-ICP-MS analysis via approaches based on pulse intensity, LA spot volumes, noise characteristics, etc. for different elements (As, Gd, La, Ni, Te and Zn), concentrations (between 10 and 1000 μg g⁻¹), and matrices (gelatin standards and NIST SRM 612). The findings indicate that selection of the appropriate laser fluence, just above the ablation threshold, and beam size, depending on the interface of LA and ICP-MS, are critical for reliable quantification and should be properly adjusted to avoid excessive Poisson and Flicker noise, achieve maximum sensitivity, and prevent the formation of double peaks in single pulses.

---

Introduction

Laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) is a technically advanced microanalytical method for direct sampling of solid materials and measurement of most elements of the periodic table. However, the processes involved from ablation to detection are complex; in particular, the interaction of the laser beam with the solid material, involving transient changes from solid, through liquid, into a plasma state, is not well-understood.

The provoking title of Hergenröder's presentation at the 9th European Workshop on Laser Ablation in Elemental and Isotopic Analysis (Prague, Czech Republic, 2008), “LA-ICP-MS: The astonishing story why it works (at least sometimes)”, appropriately conveys these intricacies. Elemental quantification in LA-ICP-MS, either in bulk or imaging mode, requires that the stoichiometry of the ablated material is the same as the overall stoichiometry of the particles measured by the ICP-MS. However, non-stoichiometric conversion of elements leads to elemental fractionation, which may occur during ablation, transport and/or atomization/ionization in the ICP.¹ During transport from the LA cell to the ICP-MS, particle size-segregation may occur as a result of size-dependent impaction when particles collide with the surfaces of the laser ablation cell or the interface, or due to gravitational settling.^2–4 Once entering the plasma, larger particles may not be completely atomized and ionized, resulting in further elemental fractionation.^2,4–7

Despite these drawbacks, under matrix-matched conditions, it is assumed that samples and standards with the same total elemental concentrations can be accurately quantified. However, matrix-matched standards are hardly ever available, especially for biological samples, hence a number of calibration strategies have emerged,⁸ such as homogenization of tissue and standard addition of element(s) of interest,⁹ spiking of the samples by soaking in solution (e.g. for hair samples),¹⁰ preparation of external standards in gelatin that mimic the tissue matrix,^11,12 including microdroplet standards,¹³ (in-cell or in-torch) aspiration of a standard solution during laser sampling,^14–16 and application of a “film” standard on/under a biological sample combined with total consumption (i.e. ablation of the entire depth) of the assembly.¹⁷ In addition, internal standardization protocols have been developed to compensate for instrumental drift and possible ablation differences between matrices of sample and calibration standards. These include, e.g., the use of homogeneously distributed elements in the sample^18,19 and labeling of tissue components with a metallo-intercalator.²⁰

Generally, better precision in single pulse LA-ICP-MS can be obtained by increasing signal intensity, i.e., generating more counts, implying a higher laser fluence, and/or larger beam size. In imaging applications, signal intensity can also be increased using more laser shots per measurement or pixel (=dosage). The effects of laser shot dosage on LA-ICP-MS imaging and image quality were recently discussed,²¹ while the influence of laser fluence and beam size on noise still has to be investigated.

Precision in LA-ICP-MS measurements can be evaluated by the total standard deviation (SD_t) of the signal intensity (i.e., number of counts, A), and can be divided into two components, i.e., Poisson noise (SD_P) and Flicker noise (SD_F). Poisson noise, which originates in counting statistics, is proportional to the square root of signal intensity (√A) and is important at lower signal intensities. Flicker noise is proportional to the signal intensity (q × A, where q is a factor between 0 and 1) and is associated with LA-ICP-MS settings (laser fluence, beam size, …).²² The factor q is only constant for the same settings used. Hence, when we change any of the parameters influencing the Flicker noise vide supra, the factor q also changes as this is the actual variable in the propagation of noise that we can affect and try to minimize. Total noise can therefore be expressed as

SD_t² = SD_P² + SD_F² = A + q²·A². (1)

Careful selection of operational settings can improve the precision of LA-ICP-MS analysis. A series of experiments was conducted to investigate the effects of laser fluence and beam size on the single pulse response, signal intensity, and noise. This study will help to better understand the issues that may occur if the experimental parameters (laser fluence and beam size in this case) are not optimized and how these may affect the precision of the obtained LA-ICP-MS results. The study was conducted on gelatin standards, commonly used as a standard of choice in studies of biological samples,^23–25 and NIST glass standards, commonly used in geological studies^26–28 as appropriate “general” reference standards. As and Gd were selected to be measured in all experiments, and for single peak profiles some additional elements were measured, namely La, Ni, Te and Zn.

Experimental

Materials and standards

Gelatin gels and glass standards were used as target matrices in the experiments. Silicate glass NIST SRM 612 (trace elements in glass, nominal concentration of 50 μg g⁻¹; National Institute for Standards and Technology, Gaithersburg, MD, USA) was used as a glass standard. Gelatin standards were prepared in-house following the procedure previously described by Šala et al.¹² In brief, 10% (m/v) gelatin solution was prepared by suspending gelatin (porcine-skin gelatin, type A, bloom strength 300, Sigma-Aldrich, St Louis, MO, USA) in ultra-pure water (18.2 MΩ cm), supplied by a Milli-Q water purification system and heating it up to approximately 55 °C. Subsequently, the desired amount of selected elemental ICP standard solution(s) from Merck or Sigma Aldrich was added. The mixture was then dropped onto a microscope glass slide using a micropipette and dried in a convection oven at 95 °C for one hour.

Instrumentation

In all experiments, an Analyte G2 193 nm ArF* excimer laser ablation system (Teledyne Photon Machines Inc., Bozeman, MT, USA) was used. It was equipped with a standard two-volume ablation cell HelEx II (aerosol washout time 0.5 s, full width at 1% of the maximum (FW 0.01 M)). The LA system was coupled to an ICP-MS instrument Agilent 7900x (Agilent Technologies, Santa Clara, CA, USA), either via the standard HelEx II aerosol delivery system²⁹ (HelEx in further text) or using the Aerosol Rapid Introduction System³⁰ (ARIS) for fast aerosol washout (FW 0.01 M, ca. 20 ms). Ablation cell and both aerosol delivery systems are commercially available from Teledyne Cetac Technologies. Similar behavior is expected from ablation cells and aerosol delivery systems by other vendors. A 3D interference optical profilometer (Zegage PRO HR, Zygo Corporation, PA, USA) was used to determine the volume of craters after laser ablation. The 3D information was recorded using a 50× magnification lens with a lateral resolution of 0.173 μm, and a surface topography repeatability better than 3.5 nm.

Signal intensity and noise contributions as a function of laser fluence

We investigated how the single pulse intensities and generation of Flicker and Poisson noise correlate with increasing laser fluence. In-house prepared gelatin standards and the NIST SRM 612 glass standard were used in the ARIS setup. As and Gd (10, 50, 100 and 150 μg g⁻¹ each) were measured in gelatin and NIST SRM 612 ³¹ (certified value for As 37.4 ± 2.2 μg g⁻¹, informative value for Gd 39 μg g⁻¹). These elements were selected as highly homogeneous standards and can be prepared in gelatin.¹² Gd also exhibits minimal polyatomic interferences and low background in ICP-MS analysis. As was chosen as a toxic element that may be of interest for determination in tissues. Laser fluences between 0.5 and 9 J cm⁻² were used for gelatin standards and between 1 and 9 J cm⁻² for glass standards. The data were obtained in line scanning mode with a fixed dosage of 1 (non-overlapping laser shots/craters), and integration of counts for single peaks by matching the integration time to the particle washout time and the inverse of the repetition rate. Detailed instrumental conditions used in the experiments are summarized in Table S1† (ESI). Raw data were processed with OriginLab software (OriginPro 2018, OriginLab Corporation, Northampton, MA, USA).

Influence of laser fluence and beam size on the signal intensity normalized to crater volume

To investigate whether or not the ablated volume is linearly proportional to the measured signal intensity, the accumulated counts for LA-ICP-MS single pulses, obtained at different fluences and beam sizes, were normalized to their crater volume. To enable accurate determination of the crater volumes, the scanning speed was selected in such a way that ablation craters for each laser shot were nonadjacent, i.e., scanning speed (μm s⁻¹)/repetition rate (Hz) > 2 × beam size (μm). Three different laser fluences were compared (0.5, 4 and 8 J cm⁻²) and three different beam sizes for each setup (5, 10 and 20 μm square with ARIS, 35 and 80 μm square, and 65 μm circle with HelEx). Data acquisition was performed similarly to the previous experiment. The data obtained with both setups cannot be directly compared; only data obtained with different parameters using the same setup are comparable. Other instrumental conditions used for ablation of gelatin (containing 1000 μg g⁻¹ As or Gd) are listed in Table S2† (ESI). OriginLab software was used to process the raw data.

Effect of fluence and beam size on single pulse peak profiles

Single pulse peak profiles were monitored by ablation of single spots, generated by one laser shot per spot for individual elements. Gelatin standards containing different elements (As, Gd, La, Ni, Te, and Zn) at a concentration level of 1000 μg g⁻¹ were ablated in this experiment. Additionally, As and Gd gelatin standards were prepared (20 and 100 μg g⁻¹) to evaluate if the shape of the peak profile is also influenced by the concentration or only by the ablation conditions. Laser fluences of 0.5 and 4 J cm⁻² were used with 5, 10 and 20 μm beam sizes (square) with ARIS, and 35 and 80 μm (square), and 65 μm (circle) with HelEx. Detailed conditions used are summarized in Table S3† (ESI). OriginLab software was used for data processing and peak profile depiction. Again, data using different setups cannot be compared and the experiments with both setups were performed to see if trends are similar or not.

Results and discussion

Signal intensity and noise contributions as a function of laser fluence

A major characteristic of the analytical performance is related to the signal intensity and noise as a function of the laser fluence which was investigated by single pulse LA-ICP-MS of ca. 50 μg g⁻¹ Gd in both the gelatin standard and the NIST SRM 612 glass standard, followed by retrieval of the Flicker and Poisson noise using eqn (1). From Fig. 1 it follows that for both the gelatin and NIST 612 the Flicker noise determines the overall noise as by quadratically summing the Flicker and Poisson noise, the low levels of Poisson noise negligibly affect the overall noise. Although one would expect the signal intensity to linearly increase with fluence, this is only seen in the case of the NIST 612 above an ablation threshold of ca. 3 J cm⁻², whereas for the gelatin standard we can see that for laser fluences well above the ablation threshold of approx. 0.2 J cm⁻², the signal intensities of Gd reach a plateau. The fact that the measured volumes ablated per shot as a function of the fluence for the NIST 612 (Fig. 2) follow a very similar trend as the Gd intensities vs. fluence graphs (Fig. 1), is an indication that signal intensities for the NIST are likely linked to LA processes and to a lesser extent to transport and detection phenomena for these particular LA-ICP-MS conditions.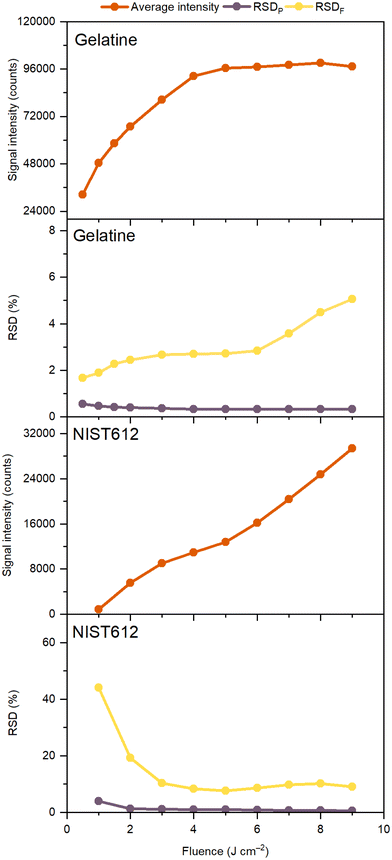

Fig. 1 Average line intensity, Poisson noise and Flicker noise as a function of fluence for single dosage experiments with ca. 50 μg g⁻¹ Gd in gelatin and NIST SRM 612 glass standards (see Table S1† for operational conditions).

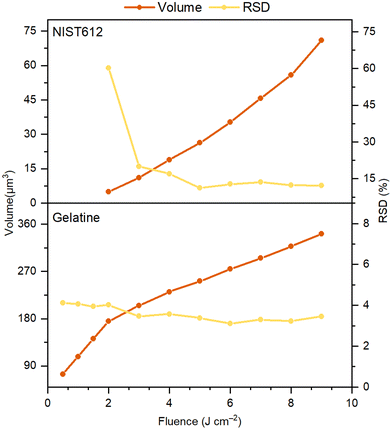Fig. 2 Average crater volumes and RSDs (based on 50 measurements) for 5 μm LA shots in gelatin and NIST 612 as a function of the fluence.

From Fig. 2 is can be seen that gelatin ablates much better than NIST 612 (5–20 times better, depending on the fluence), potentially leading to plasma shielding³² at higher fluences, resulting in lower signal intensities and plateauing as we may see in Fig. 1. The higher Flicker noise for NIST 612 compared to gelatin is most likely associated with more erratic ablation of the NIST 612, resulting in less reproducible craters, evident from the calculated RSDs in the volumes ablated per laser shot (Fig. 2). The fact that the Flicker noise for the NIST 612 is so high at low fluences is due to ablation below the ablation threshold as it levels off to ca. 10% off above 3 J cm⁻², similar to the RSDs levels for the volumes ablated. In our experiments for gelatin, ablation always took place above the ablation threshold, implying that no irregular ablation (on the account of lower fluence than ablation threshold used) took place as for the NIST 612. Nevertheless, the Flicker noise slightly increased to ca. 5% at the highest fluence, whereas the RSDs in the volumes ablated were more or less constant, slightly above 3%. This discrepancy might be caused by the much higher particle generation and throughput compared to NIST 612, suggesting that for ablation of gelatin besides LA processes also other processes play a role in determination of the Flicker noise. Similar to above experiments with Gd (Fig. 1), from Fig. S1† (ESI) we can see that for ca. 50 μg g⁻¹ As in gelatin and NIST 612 almost identical results were obtained. Additional ablation of a range of As concentrations in gelatin (10, 100 and 150 μg g⁻¹) as a function of the fluence (Fig. S2, ESI†) showed that concentration affects the signal intensity as expected, i.e., signal intensity ≈ concentration, with plateauing for all concentrations, whereas Poisson and Flicker noise are minimally affected.

Previous studies on LA-ICP-MS analysis of glass,^4–7,33 metals,⁶ and gelatin² have shown that the laser wavelength, fluence, and ablation mode are the key parameters influencing the particle size (range) generated. Using a fluence well above the material's ablation threshold considerably alters the particle size distribution, resulting in the formation of proportionally larger particles that undergo significantly more gravitational settling.³³ Additionally, it has been shown that larger particles are less likely to be completely vaporized, atomized, and ionized in the ICP.⁷ Studies have shown that the plasma source is not capable of sufficiently atomizing particles above 150 nm.⁷ If standards and samples are matrix-matched, this would merely result in lower sensitivity; however, if the matrix is not ideally matched, the concentrations in the samples may be under- or overestimated. In the remainder of the text, we will only focus on the irregular laser ablation behaviour of gelatin as an approximation for elemental quantification of biological tissues.

Influence of laser fluence and beam size on the signal intensity normalized to crater volume

We expect larger beam sizes to ideally only affect the number of particles generated, whereas higher fluences may not only result in higher particle number concentrations but also in a changed particle size distribution. Generation of larger particles may potentially result in gravitational settling and/or incomplete atomization/ionization.^2,4–7 To investigate how the fluence and beam size affect the signal intensity, we measured single pulse intensities of Gd and As in gelatin as a function of the ablation volume–normalized intensity in the ARIS and HelEx setups (Fig. 3). A constant intensity/volume ratio would imply that no analysis anomalies exist. However, Fig. 3 shows that the average intensity/volume ratio at different fluences and beam sizes is not constant in either the ARIS or HelEx setup. Regardless of the setup used or the element measured, there is a trend that the highest intensity/volume ratios are obtained for the lowest fluence, implying that some of the particles “disappear” due to transport losses or detection problems, potentially as a result of generation of larger particles or agglomeration of smaller particles. However, larger beam sizes do not necessarily lead to lower intensity/volume ratios as can be seen from the Gd and As measurements in the HelEx setup. In the ARIS setup, there is an indication of decreasing intensity/volume ratios with beam size, presumably due to overloading the ICP plasma and insufficient time for ionization due to because of much faster aerosol transport than in the HelEx cell.³⁰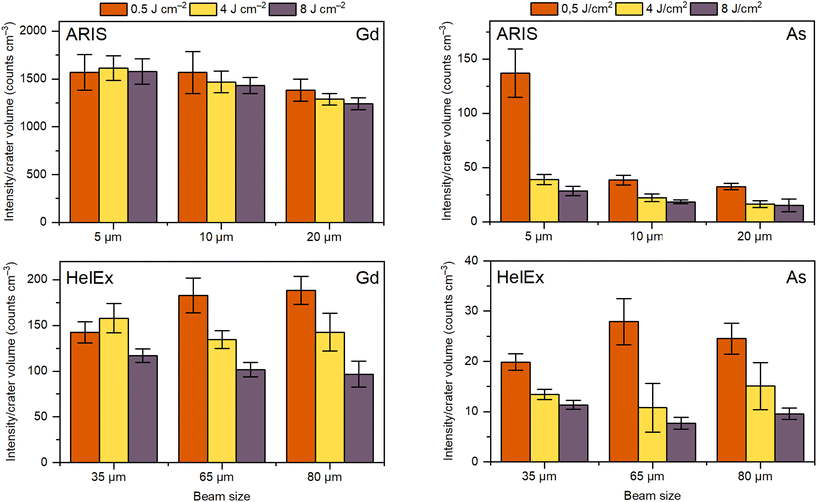

Fig. 3 Signal intensity to crater volume ratios for single pulse LA-ICP-MS of Gd and As in gelatin at different beam sizes (4, 10 and 20 μm for ARIS and 35, 65 and 80 μm for HelEx), fluences (0.5, 4 and 8 J cm⁻²) and aerosol transport setups (ARIS or HelEx) (see Table S2† for operational conditions).

Effect of fluence and beam size on single pulse peak profiles

Ablation of gelatin standards containing various elements (As, Te, Zn, Au, Gd, or La, 1000 μg g⁻¹) in the HelEx setup, using a fluence of 4 J cm⁻² and a beam size of 80 μm (square mask), led to a single pulse response showing differences in peak profiles – either single or double peak profiles were obtained, depending on the element (Fig. 4). It can be seen that the occurrence of single and double peaks was very reproducible. However, the occurrence of double peaks for As, Te, and Zn was very dependent on the fluence and beam size as with a lower fluence (0.5 J cm⁻²) and a smaller beam size (35 μm, square mask) single peaks were recorded for all measured elements in the HelEX setup, although some shouldering was observed for As (Fig. S3, ESI†), Te and Zn (data not shown). Differences seem to be the result of an excess of material ejected upon ablation since for the ARIS setup in Fig. S3† (ESI), having a much smaller overall internal volume, similar results were obtained for As at scaled-down settings (beam size 5, 10 and 20 μm), square mask at the same fluences. Consequently, at 5 and 10 μm and 0.5 J cm⁻² in the ARIS setup, a single peak was obtained for As, while at 20 μm and 0.5 J cm⁻² as well as 4 J cm⁻², regardless of the beam size, split peaks were observed. Additional Gd and As gelatin standards (20 and 100 μg g⁻¹) were used to assess whether the peak shape in the HelEx setup is affected by the concentration. The results (Fig. S4, ESI†) showed no differences in peak shape with different concentrations, which suggests that splitting of peaks is merely affected by the parameters used in the LA-ICP-MS experiment.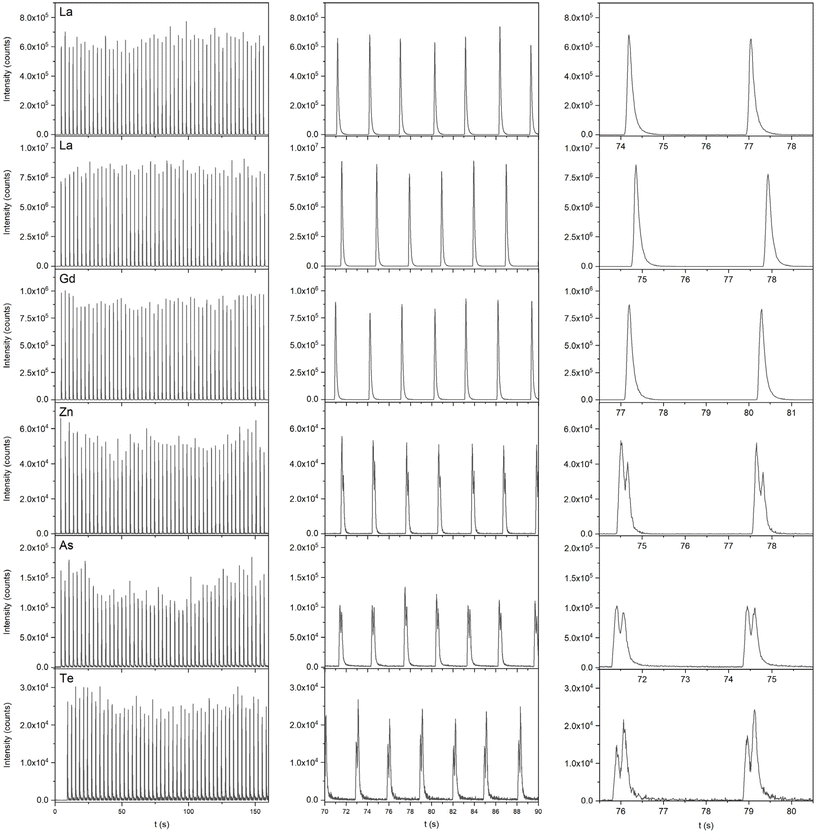

Fig. 4 Single pulse peak profiles for Ni, La, Gd (single peaks), Zn, As and Te (double peaks) – 50 pulses [left] and two zoom ins (20 [middle] and 5 s [right]) for each element that show the repeatability of the peak shape. Data were obtained using the HelEx aerosol delivery system at a fluence of 4 J cm⁻² and a beam size of 80 μm (square mask) (see Table S3† for operational conditions).

Nováková et al.⁵ demonstrated the influence of the beam size on the particle size distribution upon ablation of glass. They showed a bimodal particle size distribution, most probably related to small primary particles and large coagulates/agglomerates, regardless of the beam size, although the larger beam sizes produced proportionally more large particles than the smaller beam sizes. However, if this is the case in the present study, one would expect all elements to showcase similar behavior resulting in double peaks for every element. Niehaus et al.² on the other hand reported that at higher fluences larger particles are generated for gelatin and the embedding polymer resin Technovit (used for fixation of biological materials). Also, the efficiency/speed of the transport from the ablation cell to the ICP might be affected by the particle size. If the distribution of different elements over the particle size range varies, double peaks can appear for elements that are distributed in small and large particles, while single peaks can appear for elements that are primarily present in particles of similar size.

Conclusions

This paper is focused on quantification anomalies in single pulse LA-ICP-MS analysis caused by non-optimized laser fluence and beam size. The results from this study stress the importance of selecting the appropriate ablation parameters to minimize noise and improve the precision of the analytical results caused by differences in particle size distribution, particle agglomeration, inertial impact, gravitational settling, laminar and/or turbulent diffusion, electrostatic attraction, ion yield, degree of ionization, etc. In a series of experiments, we investigated the influence of laser fluence and beam size on signal and noise, single pulse intensity profiles, LA spot volumes, etc. The results from this study suggest that through the appropriate choice of instrumental parameters, we can circumvent (i) LA-generation of a large particle size range, (ii) elements distributing differently over the particle size range generated, (iii) issues related to particle size and transportation of generated aerosol (e.g. gravitational settling) and (iv) particle size-related ionization in the ICP.

It was shown that ablation with higher fluences (i.e., fluences well above the material's threshold) and large beam sizes (depending on the interface associated with the HelEx or ARIS setup) result in issues such as lowering the signal/ablated volume ratio, increasing the RSDs, splitting of peaks in single pulse response mode, etc. The results from the present study support the previously published findings stating that with higher fluences, larger particles are formed, whereas too large beam sizes generate an excess of aerosol particles. This can lead to impaired transport efficiency from the ablation cell into the ICP as well as poor atomization and/or ionization of the elements present in large particles, which result in the partial loss of signal. By selecting optimal parameters for the investigated material, one can considerably improve the precision and accuracy of the obtained results.

Author contributions

Ana Jerše: investigation, formal analysis, writing – original draft, visualization. Kristina Mervič: investigation, formal analysis, writing – original draft, visualization. Johannes Teun van Elteren: conceptualization, writing – review & editing, visualization. Vid Simon Šelih: writing – review & editing, funding acquisition. Martin Šala: investigation, conceptualization, writing – review & editing, visualization, data curation, supervision.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from the Slovenian Research Agency ARRS (research core funding no. P1-0034). K. M. thanks the Slovenian Research Agency for funding her PhD research.

References

1. S. Zhang, M. He, Z. Yin, E. Zhu, W. Hang and B. Huang, J. Anal. At. Spectrom., 2016, 31, 358–382.
2. R. Niehaus, M. Sperling and U. Karst, J. Anal. At. Spectrom., 2015, 30, 2056–2065.
3. H. R. Kuhn and D. Günther, Anal. Chem., 2003, 75, 747–753.
4. M. Guillong and D. Günther, J. Anal. At. Spectrom., 2002, 17, 831–837.
5. H. Nováková, M. Holá, M. Vojtíšek-Lom, J. Ondráček and V. Kanický, Spectrochim. Acta, Part B, 2016, 125, 52–60.
6. M. Holá, J. Ondráček, H. Nováková, M. Vojtíšek-Lom, R. Hadravová and V. Kanický, Spectrochim. Acta, Part B, 2018, 148, 193–204.
7. H. R. Kuhn, M. Guillong and D. Günther, Anal. Bioanal. Chem., 2004, 378, 1069–1074.
8. A. Limbeck, P. Galler, M. Bonta, G. Bauer, W. Nischkauer and F. Vanhaecke, Anal. Bioanal. Chem., 2015, 407, 6593–6617.
9. D. J. Hare, J. Lear, D. Bishop, A. Beavis and P. A. Doble, Anal. Methods, 2013, 5, 1915–1921.
10. D. La Rosa Novo, T. Van Acker, J. Belza, F. Vanhaecke and M. F. Mesko, J. Anal. At. Spectrom., 2022, 37, 775–782.
11. D. Gholap, J. Verhulst, W. Ceelen and F. Vanhaecke, Anal. Bioanal. Chem., 2012, 402, 2121–2129.
12. M. Šala, V. S. Šelih and J. T. Van Elteren, Analyst, 2017, 142, 3356–3359.
13. A. Schweikert, S. Theiner, D. Wernitznig, A. Schoeberl, M. Schaier, S. Neumayer, B. K. Keppler and G. Koellensperger, Anal. Bioanal. Chem., 2022, 414, 485–495.
14. D. Günther, H. Cousin, B. Magyar and I. Leopold, J. Anal. At. Spectrom., 1997, 12, 165–170.
15. J. J. Leach, L. A. Allen, D. B. Aeschliman and R. S. Houk, Anal. Chem., 1999, 71, 440–445.
16. C. O’ Connor, B. L. Sharp and P. Evans, J. Anal. At. Spectrom., 2006, 21, 556–565.
17. C. Austin, D. Hare, T. Rawling, A. M. McDonagh and P. Doble, J. Anal. At. Spectrom., 2010, 25, 722–725.
18. J. S. Becker, R. C. Dietrich, A. Matusch, D. Pozebon and V. L. Dressler, Spectrochim. Acta, Part B, 2008, 63, 1248–1252.
19. M. S. Jiménez, M. T. Gomez, L. Rodriguez, L. Martinez and J. R. Castillo, Anal. Bioanal. Chem., 2009, 393, 699–707.
20. D. A. Frick, C. Giesen, T. Hemmerle, B. Bodenmiller and D. Günther, J. Anal. At. Spectrom., 2015, 30, 254–259.
21. M. Šala, V. S. Šelih, C. C. Stremtan, T. Tămaş and J. T. Van Elteren, J. Anal. At. Spectrom., 2021, 36, 75–79.
22. J. T. Van Elteren, V. S. Šelih and M. Šala, J. Anal. At. Spectrom., 2019, 34, 1919–1931.
23. M. Birka, K. S. Wentker, E. Lusmöller, B. Arheilger, C. A. Wehe, M. Sperling, R. Stadler and U. Karst, Anal. Chem., 2015, 87, 3321–3328.
24. M. Costas-Rodríguez, T. Van Acker, A. A. M. B. Hastuti, L. Devisscher, S. Van Campenhout, H. Van Vlierberghe and F. Vanhaecke, J. Anal. At. Spectrom., 2017, 32, 1805–1812.
25. M. Cruz-Alonso, B. Fernandez, A. Navarro, S. Junceda, A. Astudillo and R. Pereiro, Talanta, 2019, 197, 413–421.
26. J. B. H. Andersson, L. Logan, O. Martinsson, D. Chew, E. Kooijman, M. Kielman-Schmitt, T. C. Kampmann and T. E. Bauer, Precambrian Res., 2022, 372, 106613.
27. K. Drost, D. Chew, J. A. Petrus, F. Scholze, J. D. Woodhead, J. W. Schneider and D. A. T. Harper, Geochem., Geophys., Geosyst., 2018, 19, 4631–4648.
28. H. C. Yu, K. F. Qiu, D. Chew, C. Yu, Z. J. Ding, T. Zhou, S. Li and K. F. Sun, Ore Geol. Rev., 2022, 140, 104612.
29. S. M. Eggins, R. Grün, M. T. McCulloch, A. W. G. Pike, J. Chappell, L. Kinsley, G. Mortimer, M. Shelley, C. V. Murray-Wallace, C. Spötl and L. Taylor, Quat. Sci. Rev., 2005, 24, 2523–2538.
30. T. Van Acker, S. J. M. Van Malderen, T. Van Helden, C. Stremtan, M. Šala, J. T. Van Elteren and F. Vanhaecke, J. Anal. At. Spectrom., 2021, 36, 1201–1209.
31. NIST, Certificate of Analysis Standard Reference Material 612 Trace Elements in Glass, Gaithersburg, MD, 2012.
32. X. Mao and R. Russo, Appl. Phys. A, 1997, 64(1), 1–6.
33. S. H. Jeong, O. V. Borisov, J. H. Yoo, X. L. Mao and R. E. Russo, Anal. Chem., 1999, 71, 5123–5130.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2an01172g

‡ These authors contributed equally to this work.

---