Localizing genesis in polydomain liquid crystal elastomers†
Hayden E.
Fowler
a,
Brian R.
Donovan
a,
Joselle M.
McCracken
a,
Francisco
López Jiménez
b and
Timothy J.
White
 *a
*a
aDepartment of Chemical and Biological Engineering, University of Colorado Boulder, Boulder, CO 80309, USA. E-mail: Timothy.J.White@colorado.edu
bAnn and H. J. Smead Department of Aerospace Engineering Sciences, University of Colorado Boulder, Boulder, CO 80309, USA
First published on 8th November 2019
Abstract
Programming the local orientation of liquid crystal elastomers (LCEs) is a differentiated approach to prepare monolithic material compositions with localized deformation. Our prior efforts prepared LCEs with surface-enforced spatial variations in orientation to localize deformation when the LCEs were subjected to directional load. However, because these surface alignment methods included regions of planar orientation, the deformation of these programmed LCEs is inherently directional. The absence of macroscopic orientation in polydomain LCEs results in uniform, nonlinear deformation in all axes (omnidirectional soft elasticity). Here, we exploit the distinct mechanical response of polydomain LCEs prepared with isotropic or nematic genesis. By localizing the polydomain genesis via masked photopolymerizations conducted at different temperatures, we detail the preparation of main-chain, polydomain LCEs that are homogeneous in composition but exhibit spatially localized programmability in their mechanical response that is uniform in all directions.
Introduction
Flexible electronic devices are emerging in commercial and consumer goods applications. Key considerations of these devices are robustness, weight, and comfort.1 Applications of these range from wearable devices to bio-integrated systems, in which soft and elastic materials are needed.2 One approach to increase the ruggedness of flexible electronic devices is to spatially control the elasticity of the material in order to protect fragile components on the device. The primary approaches to date3,4 include the preparation of heterogeneous systems with multimaterial compostions.5–7 However, material–material interfaces can lead to premature failure of the device.Controlling anisotropy in a homogeneous material system, such as in liquid crystal elastomers (LCEs), is an approach to prepare materials with local variation in mechanical properties absent of material–material interfaces.8,9 LCEs are lightly crosslinked polymer networks containing side-chain or main-chain mesogenic units that dictate their organization. The organization of LCEs can be disrupted by a variety of stimuli, including heat, light, and electric field.10 The stimuli-induced decrease in liquid crystalline order produces amplified and directional strain.11 This is due to a contraction of the material parallel to the liquid crystalline alignment direction. Accordingly, recent research has extensively focused on the potential utility of LCEs as stimuli-responsive actuators.12–15 Directed self-assembly by surface enforced alignment can locally organize LCEs and direct strain to realize force output as much as 20 J kg−1.16
LCEs also exhibit distinctive, anisotropic mechanical responses to load.17–20 A planarly aligned, nematic LCE exhibits a classical rubber-like response when a mechanical load is applied parallel to the nematic director. Distinctively, LCEs exhibit a nonlinear mechanical response (called soft elasticity) when the load is applied perpendicular to the nematic director.17 The nonlinearity in the deformation is associated with the reorientation of mesogenic units towards the direction of applied stress. Exploratory efforts into the utility of soft elasticity in planar LCEs realized spatially distinct deformations under application of uniform strain.8 More recently, LCEs were spatially oriented with adjacent homeotropic and planar domains that exhibited directional and omnidirectional soft elasticity, respectively.9 Both of these approaches employ planar domains, which inherently introduce directionality to the global mechanical response. LCEs prepared by surface-enforced alignment have limitations on material thickness.21
Polydomain LCEs, absent of macroscopic long-range order, are characteristically uniform to all axes of deformation. Prior research indicates that the stress–strain response of polydomain LCEs is correlated to their genesis, i.e. polymerization in either the isotropic or nematic state.22 Functionally, isotropic genesis (IG) polydomain LCEs are polymerized at a higher temperature (in the isotropic phase) than nematic genesis (NG) polydomain LCEs, which are polymerized at lower temperature (in the nematic phase). Isotropic genesis, side-chain polydomain LCEs have been shown to display softer modes than nematic genesis analogues. Similar results have been reported in main-chain polydomain LCEs.23
Here, we develop a materials chemistry and processing method to prepare main-chain, polydomain LCEs in which the genesis of formation is locally varied through spatial patterning and assimilated into a material of homogeneous chemical composition. This allows for the stress–strain response to be localized within these materials while also enabling omnidirectionality in the material deformation. By using a material of homogeneous composition, we circumvent the problem with material–material interfaces while enabling the same functionality shown in heterogeneous systems.
Results and discussion
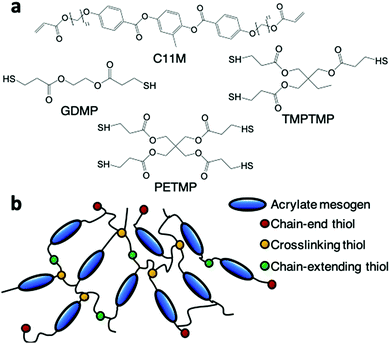
Acrylate and thiol monomers illustrated in Fig. 1a were mixed in nonstoichiometric ratios to prepare LCEs via chain extension and chain transfer reactions. The diacrylate monomer C11M is the liquid crystalline component. Upon photoinitiation, these constituents undergo acrylate homopolymerization, thiol–acrylate polymerization, and chain transfer. As detailed by Bowman et al.,24 the acrylate monomers in this reaction primarily homopolymerize. However, a thiyl radicals can chain extend through thiol–acrylate reactions. Acrylate-based radicals can undergo chain transfer reactions with the thiol monomer as well. Thiols may also act as crosslinkers. We vary the functionality of the thiol monomer from two to four as an approach to adjust the degree of crosslinking in the LCEs (GDMP is difunctional, TMPTMP is trifunctional, and PETMP is tetrafunctional). The thiol functional groups participate in one of three reactions: as chain extenders, chain ends, or crosslinking points (Fig. 1b). All compositions in this study were formulated with an acrylate-to-thiol ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8. Each LCE composition was prepared in the polydomain orientation (e.g. no macroscopic orientation) to form polymer networks with either isotropic genesis or nematic genesis. Again, isotropic genesis (IG) polydomain LCEs are polymerized at a higher temperature (in the isotropic phase) than nematic genesis (NG) polydomain LCEs. All polymerization reactions were initiated by exposure to 50 mW cm−2 of UV light (365 nm) for 10 minutes.
0.8. Each LCE composition was prepared in the polydomain orientation (e.g. no macroscopic orientation) to form polymer networks with either isotropic genesis or nematic genesis. Again, isotropic genesis (IG) polydomain LCEs are polymerized at a higher temperature (in the isotropic phase) than nematic genesis (NG) polydomain LCEs. All polymerization reactions were initiated by exposure to 50 mW cm−2 of UV light (365 nm) for 10 minutes.
The optical properties of NG and IG LCEs, regardless of the thiol used, are considerably different, as evident in Fig. 2a. Upon polymerization, the NG LCEs are opaque while the IG LCEs are transparent. The difference in optical properties is associated with domain size in these LCEs.22 Polarized optical micrographs of C11M/TMPTMP are shown in Fig. S1 (ESI†). Other formulations look similar to these. To qualify the comparison of the mechanical deformations of these LCEs, we quantified the reaction kinetics of these formulations with real-time FTIR (RTIR) to assure that the opacity of the NG LCE does not limit the conversion of the constituents during photopolymerization. Gel fractions (Table S1, ESI†) are above 90%, indicating formation of a well crosslinked network. Fig. 2b is representative of the data collected by RTIR (see also ESI,† Fig. S2–S5). In the C11M/TMPTMP composition, regardless of polymerization temperature (IG or NG), the acrylate monomer rapidly goes to full conversion upon initiation (which starts at 60 seconds). Comparatively, the conversion of the thiol reaches approximately 50%. The slight difference in reaction rate between the IG and NG polymerization reactions, evident in the slope of the conversion–time curves, is attributed to the temperature at which polymerization occurred. The overall conversion of the acrylate and thiol functional groups for each composition and genesis are summarized in Fig. 2c (from results included in ESI,† Fig. S3–S5). The conversion of acrylates for each reaction and genesis is nearly 100%. For the C11M/GDMP and C11M/TMPTMP compositions, the thiol conversion is approximately 50% for each genesis. For the C11M/PETMP composition, with the highest number of thiols per molecule of those studied, the IG polydomain LCE maintains a comparable thiol conversion, but has a 10% decreased thiol conversion in the NG LCE. We suspect this is due to the influence of thiol functionality on gel point conversion25 and relative immobilization of the developing polymer network at the lower NG polymerization temperature. DSC data are presented in Fig. S6 (ESI†). Glass transition temperatures for these materials are summarized in Table S2 (ESI†).
The data in Fig. 2 indicate that regardless of composition or genesis, the polymer networks of the LCE examined here are composed of fully converted C11M and partially converted thiol monomers (approximately 50% in nearly all cases). Accordingly, we conclude that any differences in mechanical deformation between LCEs of a given composition should be primarily associated with the genesis of the materials. The stress–strain response of each material is shown in Fig. 2d for both IG and NG. In each LCE composition, the IG LCE is initially softer than the NG LCE. This is in good agreement with previous work that documents the varied deformation of IG and NG polydomain LCEs.22 Here, in a result that is distinct from this prior examination of the deformation of side-chain LCEs,26 both NG and IG polydomain LCEs in the C11M/GDMP formulation exhibit soft elastic plateaus at low stress values. Conversely, the deformation of C11M/PETMP for both the IG and NG LCE exhibit fairly classical, rubber-like deformation. We attribute this to the significant crosslink density which may prevent cooperative reorientation. Also notable in the data presented in Fig. 2d is the crossover strain value in the C11M/TMPTMP composition where the NG LCE becomes softer than the IG LCE due to strain hardening in the IG LCE. The crossover strain value for this composition makes it a compelling candidate for localized strain applications relative to the other compositions studied.
The elastic recovery of the LCEs is also strongly dependent on thiol functionality. The recovery of these materials is visually examined as well as quantified with creep-recovery experiments in Fig. 3 (see also Fig. S7–S9, ESI†). Fig. 3a–c are photographs of the IG LCE for each formulation, viewed between crossed polarizers before deformation (i), during deformation to 64% strain (ii), immediately after release (iii), and five minutes after release (iv). For the C11M/GDMP LCE composition, the birefringence is indicative of a transition from polydomain to monodomain. Evident in Fig. 3d, large residual strain is retained in C11M/GDMP in the creep-recovery test for each genesis when the material is deformed through the minimum stress for soft elasticity (e.g. reorientation of the domains). The LCEs prepared from C11M/TMPTMP and C11M/PETMP elastically recover, regardless of genesis and magnitude of stress applied. Evident in Fig. 3b and c, the deformation of the IG LCE of these materials exhibit similar birefringence (e.g. alignment) upon deformation to 64% strain but recover both their initial length as well as their optical quality five minutes after deformation.
Local programming of regions of NG and IG in the same polydomain LCE is a differentiated and potentially advantageous approach to prepare monolithic LCEs with spatial variation in deformation. Here, we report a facile method of programming genesis in these materials by photopolymerizing local regions of these compositions at different temperatures and initiating polymerization through a photomask. This process is illustrated in Fig. 4. First, the IG regions are briefly polymerized (for 1–3 seconds) at elevated temperature (i.e. the isotropic state) with a mask covering the intended NG regions. The mask is removed, and the temperature is decreased to prepare the NG regions. The sample is uniformly exposed to complete the polymerization of the IG region as well as the NG region. This approach allows us to prepare polydomain LCEs with adjacent regions of IG and NG on the same film. Fig. 4 illustrates the preparation of an LCE monolith with complex pattern of IG and NG. The opaque region is formed by polymerization through a mask shaped as the CU buffalo. The buffalo forms the scattering NG region, surrounded by an optically clear IG boundary (transparent to a black background) as well as an inset “CU” that is also IG. The sharp interface of the IG and NG regions is evident in Fig. 4.
The localization of the mechanical deformation in these programmed LCEs is illustrated in Fig. S10 (ESI†), where half the LCE was prepared in the IG state and half in the NG state. To ensure that the adjustment to the preparation method does not significantly influence the mechanical properties, samples were cut from each side for tensile testing. Fig. S10 (ESI†) confirms the mechanical responses of materials prepared with this approach are nearly identical to those reported in Fig. 2d.
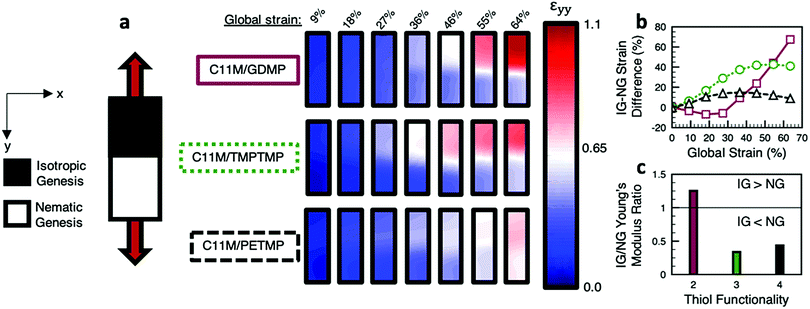
Two-dimensional digital image correlation (DIC) was used to monitor the local deformation of patterned LCE (Fig. 5a) to uniform load. The strain is represented by a color gradient from blue (low strains) to red (high strains). For LCEs prepared from C11M/TMPTMP and C11M/PETMP, the difference in strain between IG and NG regions (Fig. 5b) shows a similar trend. As global strain increases, the strain difference increases up to a maximum before plateauing and decreasing slightly. Notably, the local strain difference is comparatively less for the LCE prepared from C11M/PETMP due to the similarity of the IG and NG stress–strain behaviour in this highly crosslinked material. The LCE prepared from C11M/GDMP follows a trend unique from the other two thiol compositions studied, with the difference in local strain for the IG and NG regions initially modestly decreasing before rapidly increasing. As expected from the nascent stress–strain behaviour of this material, the difference in local strain in the IG and NG regions is more than 60% at a global strain of 60%. The initial decrease in strain localization in the LCE prepared from C11M/GDMP is likely due to the difference in Young's modulus values for the IG and NG of this material. The ratio of Young's modulus, extrapolated from the linear region of the stress–strain curves of each material, is summarized in Fig. 5c for the compositions examined here.
The LCE prepared from the C11M/TMPTMP was selected as an optimal system for further study and spatial programming. Fig. 6 illustrates the potential to arbitrarily pattern the polydomain LCE films with local variation in genesis, as demonstrated by different geometries such as in a dot array (Fig. 6a) or chevron pattern (Fig. 6b). For the dot array, the IG regions undergo significant deformation, in this case nearly 25% greater than the NG regions at 27% global strain. In the chevron pattern, the deformation in the loading axis (εyy) is similar, with local variation between IG and NG regions. However, the structure of this pattern results in shear strain differences, apparent in the accompanying measurement of εxy. The omnidirectionality of the deformation to directional strain is illustrated in a biaxial deformation in Fig. 6c. DIC confirms uniformity in the deformation with respect to each direction.
Numerical simulations were also done to compare the predicted strain mapping with the actual strain mapping. The material model was fitted to uniaxial tension experiments using a Gent hyperplastic model. This was done independently of the experimental results, only taking into account the geometry and loading of the experiment. Fig. 7 shows the agreement between simulations and experiments for IG circles on NG surroundings (Fig. 7a) and NG circles on IG surroundings (Fig. 7b), both stretched to 55% global strain.
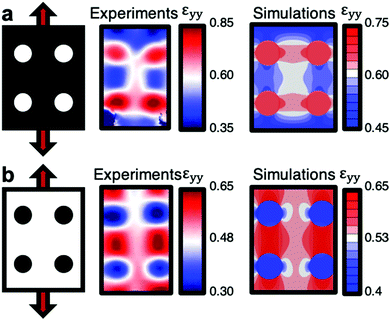 | ||
| Fig. 7 Local strain measured by DIC and predicted from numerical simulations for (a) IG circles on NG surroundings and (b) NG circles on IG surroundings. At 55% global strain. | ||
As mentioned in the discussion of Fig. 2d, the softness of the LCE prepared from C11M/TMPTMP with IG and NG inverts above 75% strain. This inversion should result in differentiated deformation above and below this value. To illustrate, we prepared elliptical IG regions of various aspect ratios patterned within the surrounding NG region (Fig. 8a). Upon deformation, the three ellipses in the programmed LCE elongate in the principle loading direction (Fig. 8c). The ellipses form circles at different strain values. This is quantified in Fig. 8b, which summarizes the aspect ratio (the aspect ratio of a circle is 1) of the IG regions as a function of strain. Visually evident in the image in Fig. 8c, the 0.385 aspect ratio ellipse forms a circle near 75% strain. This circle is retained at further stretch, in which the NG regions of the patterned polydomain LCE film begin to deform, evident in the image of the film at 90% global strain (Fig. 8c) and the plateau in aspect ratio values in Fig. 8b. Numerical simulations in Fig. 8b (solid black lines) well-match the change in aspect ratio. Simulation of the deformation of the patterned film, shown in Fig. 8c, predict the change in localization of strain from the IG ellipses to the NG surroundings, leading to the plateau in aspect ratios.
Materials and methods
Materials
Trimethylolpropane tris(3-mercaptopropionate) (TMPTMP) and pentaerythritol tetrakis(3-mercaptopropionate) (PETMP) were purchased from Sigma Aldrich. Ethylene glycol bis(3-mercaptopropionate) (GDMP) was purchased from TCI. 1,4-Bis[4-(11-acryloyloxyundecyloxy)-benzoyloxy]-2-methylbenzene (C11M) was synthesized and purchased from Synthon Chemical. The photoiniatiator bis(2,4,6-trimethylbenzoyl)-phenylphosphineoxide (I-819) was purchased from IGM.LCE fabrication
Glass slides were plasma cleaned for 5 minutes and then spin-coated with 0.125 wt% Elvamide in methanol. Coated slides were subjected to no treatment and glued together using 100 μm silicon bead spacers and Norland optical adhesive. Cells were placed on a hot plate at 110 °C. C11M, thiol, and 2.5 wt% of photoinitiator I-819 were melt mixed using a heat gun and vortex. The mixture was filled into the cells by capillary action. For isotropic genesis, cells were exposed to 365 nm light at 50 mW cm−2 for 10 min at 110 °C. To prepare nematic genesis, cells were heated to 60 °C before being exposed to light at the same conditions. After polymerization, the cells were opened, and the films were harvested.Characterization
Real-time FTIR was used to examine the reaction kinetics of monomer conversion. Prior to polymerization, mixtures were melted and placed between salt plates on a heat stage at the appropriate temperature. Data was collected approximately every one second. Values of the area under the thiol peak (2550–2600 cm−1) and acrylate peak (810 cm−1) were recorded. After one minute, samples were polymerized for four minutes with 365 nm light. Conversion was calculated using the following equation:| X = (Ainitial − Afinal)/Afinal |
Mechanical properties were measured in strips of approximately 2 mm width, 6 mm height, and 100 μm thickness. Mechanical tests were undertaken with TA Instruments’ Discovery 850 dynamic mechanical analyser (DMA). Tensile testing was performed at room temperature with a strain rate of 5% min−1. Samples were loaded into the tensile grips along the long axis. Creep recovery tests were carried out at room temperature. A constant-stress load was applied for 5 min, after which the load was removed, and the sample was allowed to relax for another 5 min. Dynamic examination of the materials was conducted using a frequency of 1 Hz and an amplitude of 30 μm. The temperature was ramped at a rate of 5 °C min−1 from −40 °C to 100 °C.
Programming genesis
Cells were prepared as described above. Black patterns were printed onto optical transparencies to create masks. The masks were placed on top of the cells at 110 °C. Polymerization was initiated with 365 nm light at approximately 8 mW cm−2 for 1–3 seconds. Subsequently, the temperature was decreased to 60 °C, the mask removed, and the entire sample was exposed to 365 nm light at 50 mW cm−2 for 10 min.Digital image correlation
2D strain mapping of local deformation was characterized with digital image correlation (DIC). Samples were airbrushed with black ink to create a speckle pattern necessary for DIC analysis. Samples were loaded into a Micro Vice sample holder (Fig. S11, ESI†) and strained at intervals of 9.1%. Biaxially stretched samples were deformed via the apparatus in Fig. S12 (ESI†). Images were taken using a Canon EOS M50 fitted with a Canon Ef-M Macro IS STM lens. DIC analysis was performed using opensource code run in Matlab.27 Strains were calculated for each image.Finite elements simulation
The numerical simulations were performed using the finite element package Abaqus. A user defined function, UHYPER, was used to model the material as a fully incompressible three-parameter Gent hyperplastic potential.28 The parameters were fitted to tensile experiments used to characterize the material, with each genesis being tested and fitted independently. The analysis used continuum solid elements with a hybrid formulation, C3D8H, to avoid locking due to incompressibility. The number of elements was chosen after a mesh refinement parametric study and ranged between 170.000 and 180.000 elements depending on the analysis.Conclusions
We have reported on a facile method of programming genesis in polydomain LCEs using a simple thiol–acrylate chemistry. Genesis and thiol functionality were varied to determine their effect on the chemistry and mechanical properties of the system. It was found that thiol functionality affected the softness and recovery of the material. Furthermore, NG and IG showed different mechanical properties for each formulation, which is in good agreement with the literature.20,21 Genesis was programmed into single homogeneous films, and it was shown that the difference in mechanical properties was retained. Strain was concentrated to the initially softer IG regions. The TMPTMP formulation was then explored further to determine that strain concentration was retained for more complicated patterns and to demonstrate control over the dimensions of programmed shapes past the inversion point, i.e. where NG becomes softer than IG. The materials properties described here could be useful in flexible, stretchable electronics, eliminating material–material interfaces of heterogeneous systems that ultimately lead to failure of the device.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors recognize financial support from the University of Colorado Boulder. H. E. F. recognizes Fellowship support from the Department of Education program “Graduate Assistantships in Areas of National Need” (GAANN).Notes and references
- S. J. Kim, K. Choi, B. Lee, Y. Kim and B. H. Hong, Annu. Rev. Mater. Res., 2015, 45, 63–84 CrossRef CAS.
- J. A. Rogers, T. Someya and Y. Huang, Science, 2010, 327, 1603–1608 CrossRef CAS.
- A. Romeo, Y. Hofmeister and S. P. Lacour, Proc. SPIE, 2014, 9083, 90831F-5 CrossRef.
- A. Romeo and S. P. Lacour, Extreme Mech. Lett., 2015, 3, 1–7 CrossRef.
- D. Kim, Z. Liu, Y. Kim, J. Wu, H. Kim, Y. Huang, K. Hwang, Y. Zhang and J. A. Rogers, Small, 2009, 5, 2841–2847 CrossRef CAS PubMed.
- N. Lu, Z. Suo and J. J. Vlassak, Acta Mater., 2010, 58, 1679–1687 CrossRef CAS.
- A. J. Baca, J. H. Ahn, Y. Sun, M. A. Meitl, E. Menard, H. S. Kim, W. M. Choi, D. H. Kim, Y. Huang and J. A. Rogers, Angew. Chem., Int. Ed., 2008, 47, 5524–5542 CrossRef CAS.
- T. H. Ware, J. S. Biggins, A. F. Shick and T. J. White, Nat. Commun., 2016, 7, 10781 CrossRef.
- A. D. Auguste, J. W. Ward, J. O. Hardin, B. A. Kowalski, T. C. Guin, J. D. Berrigan and T. J. White, Adv. Mater., 2018, 30, 1802438 CrossRef.
- T. J. White and D. J. Broer, Nat. Mater., 2015, 14, 1087–1098 CrossRef CAS.
- H. Wermter and H. Finkelmann, e-Polym., 2001, 1, 111–123 Search PubMed.
- T. H. Ware, M. E. McConney, J. J. Wie, V. P. Tondiglia and T. J. White, Science, 2015, 347, 982–984 CrossRef CAS PubMed.
- C. P. Ambulo, J. J. Burroughs, J. M. Boothby, H. Kim, M. R. Shankar and T. H. Ware, ACS Appl. Mater. Interfaces, 2017, 9, 37332–37339 CrossRef CAS.
- A. Kotikian, R. L. Truby, J. W. Boley, T. J. White and J. A. Lewis, Adv. Mater., 2018, 30, 1706164 CrossRef.
- M. Lopez-Valdeolivas, D. Liu, D. J. Broer and C. Sanchez-Somolinos, Macromol. Rapid Commun., 2018, 39, 1700710 CrossRef PubMed.
- T. C. Guin, M. J. Settle, B. A. Kowalski, A. D. Auguste, R. V. Beblo, G. W. Reich and T. J. White, Nat. Commun., 2018, 9, 2531 CrossRef.
- M. Warner, P. Bladon and E. M. Terentjev, J. Phys. II, 1994, 4, 93–102 CrossRef CAS.
- G. C. Verwey, M. Warner and E. M. Terentjev, J. Phys. II, 1996, 6, 1273–1290 CrossRef CAS.
- M. Warner and E. M. Terentjev, Prog. Polym. Sci., 1996, 21, 853–891 CrossRef CAS.
- H. Finkelmann, A. Greve and M. Warner, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 5, 281–293 CrossRef CAS.
- B. A. Kowalski, V. P. Tondiglia, T. Guin and T. J. White, Soft Matter, 2017, 13, 4335–4340 RSC.
- K. Urayama, E. Kohmon, M. Kojima and T. Takigawa, Macromolecules, 2009, 42, 4084–4089 CrossRef CAS.
- N. A. Traugutt, R. H. Volpe, M. S. Bollinger, M. O. Saed, A. H. Torbati, K. Yu, N. Dadivanyan and C. M. Yakacki, Soft Matter, 2017, 13, 7013–7025 RSC.
- N. B. Cramer and C. N. Bowman, J. Polym. Sci., Part A: Polym. Chem., 2001, 39, 3311–3319 CrossRef CAS.
- B. S. Chiou, R. J. English and S. A. Khan, Macromolecules, 1996, 29, 5368–5374 CrossRef CAS.
- J. S. Biggins, M. Warner and K. Bhattacharya, J. Mech. Phys. Solids, 2012, 60, 573–590 CrossRef CAS.
- J. Blaber, B. Adair and A. Antoniou, Exp. Mech., 2015, 55, 1105–1122 CrossRef.
- A. N. Gent, Int. J. Non-Linear Mech., 2005, 40, 165–175 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01923e |
| This journal is © The Royal Society of Chemistry 2020 |