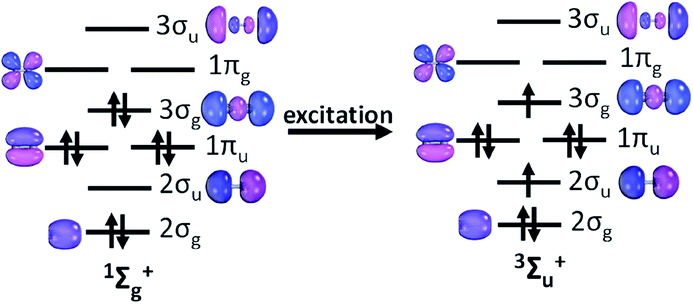Open Access Article
Open Access ArticleComprehending the quadruple bonding conundrum in C2 from excited state potential energy curves†
Ishita
Bhattacharjee
,
Debashree
Ghosh
 * and
Ankan
Paul
* and
Ankan
Paul
 *
*
School of Chemical Sciences, Indian Association for the Cultivation of Science, Jadavpur, India. E-mail: pcdg@iacs.res.in; rcap@iacs.res.in
First published on 11th June 2020
Abstract
The question of quadruple bonding in C2 has emerged as a hot button issue, with opinions sharply divided between the practitioners of Valence Bond (VB) and Molecular Orbital (MO) theory. Here, we have systematically studied the Potential Energy Curves (PECs) of low lying high spin sigma states of C2, N2, Be2 and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH using several MO based techniques such as CASSCF, RASSCF and MRCI. The analyses of the PECs for the 2S+1Σg/u (with 2S + 1 = 1, 3, 5, 7, 9) states of C2 and comparisons with those of relevant dimers and the respective wavefunctions were conducted. We contend that unlike in the case of N2 and HC
CH using several MO based techniques such as CASSCF, RASSCF and MRCI. The analyses of the PECs for the 2S+1Σg/u (with 2S + 1 = 1, 3, 5, 7, 9) states of C2 and comparisons with those of relevant dimers and the respective wavefunctions were conducted. We contend that unlike in the case of N2 and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH, the presence of a deep minimum in the 7Σ+ state of C2 and CN+ suggests a latent quadruple bonding nature in these two dimers. Our investigations reveal that the number of bonds in the ground state can be determined for 2nd row dimers by figuring out at what value of spin symmetry a purely dissociative PEC is obtained. For N2 and HC
CH, the presence of a deep minimum in the 7Σ+ state of C2 and CN+ suggests a latent quadruple bonding nature in these two dimers. Our investigations reveal that the number of bonds in the ground state can be determined for 2nd row dimers by figuring out at what value of spin symmetry a purely dissociative PEC is obtained. For N2 and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH the purely dissociative PEC appears for the septet spin symmetry as compared to that for the nonet in C2. This is indicative of a higher number of bonds between the two 2nd row atoms in C2 as compared to those of N2 and HC
CH the purely dissociative PEC appears for the septet spin symmetry as compared to that for the nonet in C2. This is indicative of a higher number of bonds between the two 2nd row atoms in C2 as compared to those of N2 and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH. Hence, we have struck a reconciliatory note between the MO and VB approaches. The evidence provided by us can be experimentally verified, thus providing the window so that the narrative can move beyond theoretical conjectures.
CH. Hence, we have struck a reconciliatory note between the MO and VB approaches. The evidence provided by us can be experimentally verified, thus providing the window so that the narrative can move beyond theoretical conjectures.
Introduction
Bonding in homodiatomic 2nd period elements constitutes the bedrock of our understanding of chemical bonding.1 Though bonding in many of these homodiatomic species is well understood, the bonding situation in C2 presents an exceptionally enigmatic scenario. A routine inspection of molecular orbitals (Hartree Fock orbitals) of C2 would suggest that the bond order of C2 is 2.0 arising from the two π bonds.2 However, decades back a typical Wiberg bond index computation conducted on C2 indicated the presence of four bonds.3 The last few years have witnessed a steep spike in interest to comprehend the state of bonding in C2.4–12 This has led to intense debate on the aspect of quadruple bonding in C2.13 Shaik and co-workers have investigated the electronic structure of C2 within the VB manifold and have concluded that the bonding in C2 is best described as a case of quadruple bond and have went on to predict that the strength of the fourth bond is approximately 12 kcal mol−1.4,5 These findings were contested by Frenking and co-workers who mainly disagreed on the approach adopted by Shaik of estimating the strength of the fourth bond.7,10 There have been several attempts by different groups which either concur or refute the presence of a fourth bond in C2. The incongruity in views from different corners arise from the multi-reference nature of the σ orbitals in C2.14 Incidentally, MO based approaches have by and large refuted the case of quadruple bonding, with some exceptions.7,10 Zhong and co-workers have tried to point out some similarities between the MO based and the VB approaches for C2 regarding a key orbital which was achieved through unitary transformation of CASSCF orbitals.15 However, their final Effective Bond Order study with the same orbitals suggested that the dimer in question has a bond order of 2.15. Alternatively, magnetic shielding studies based on MO based approaches by Karadakov et al. suggested a “bulkier” bond compared to that of acetylene.11 Nevertheless, it can be argued that there is no direct or definitive proof of the presence of four bonds in C2 from a MO standpoint. The lack of existence of reconciliation on this issue between the VB and the MO approaches still has kept the debate wide open and given the conflicting views it may not be unfair to comment that the overall understanding is still nebulous. Here we report our view point on the bonding in C2 by conducting extensive studies on potential energy curves of excited states of C2, largely covering the cases of high spin states of C2 along with similar investigations on N2 and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH. Our findings provide clinching evidence in support of the presence of quadruple bonding in C2 or rather the ability to form two bonds by electrons in orbitals in σ symmetry thus establishing reconciliation between MO and VB manifold of methods.
CH. Our findings provide clinching evidence in support of the presence of quadruple bonding in C2 or rather the ability to form two bonds by electrons in orbitals in σ symmetry thus establishing reconciliation between MO and VB manifold of methods.
The quintessential signature of bonding between two atoms lies in the presence of a well-defined discrete minimum in the potential energy curve (PEC) plotted against the interatomic distance of the two atoms. For instance, in the case of H2 ground electronic state the PEC shows the presence of a distinct minimum and has a significant dissociation energy. This is due to the presence of a σ bond arising from 1σg2 in the H2 molecule.16 If this electron pair in the bonding orbital is broken and one of the electrons is promoted to the corresponding 1σu one would find that the bonding stabilization is negated and as a result a dissociative PEC with no minimum is obtained for the 3Σu+ state. Hence one can create a high spin state corresponding to the rupture of a bond that generates a PEC without a minimum. This seemingly simple argument may be extended to multiply bonded species as well, albeit with some intrinsic limitations which are discussed later. Multiple bonding between two atoms in the ground state would certainly leave footprints on the excited state PECs. Unlike H2, N2 which is multiply bonded exhibits high spin triplet and quintet states with respective minima.17 This becomes more evident when one compares and contrasts spectra of diatomics with and without multiple bonding.18
Hence, in the multiply bonded diatomic species one may generate high spin states by breaking bonding electron pairs within the valence orbitals and promoting electrons from a particular bonding orbital to the corresponding antibonding orbital such that for a particular high spin state a set of bonding orbital/s and respective antibonding have single occupation with parallel spins. This would lead to high spin states of 2S+1Σ+ states. A step by step procedure can be adopted such that particular types of bonding may be negated by the proper choice of orbital symmetry. If specific orbitals are chosen to generate high spin electronic states, one can gradually generate electronic states which eliminate bonds one by one and reach a high spin state which would correspond to the total absence of any bonds between the two atoms resulting to a purely dissociative state. The no. of bonds in the ground state of the diatomic species would determine at which high spin state the purely dissociative PEC would be reached. For instance, in H2 which has only one bond the triplet state is purely dissociative, whereas for N2 which is known to have three bonds the septet state is purely dissociative.16,17
Results and discussion
As the bonding in C2 is suspect, we decided to investigate the nature of the PECs of high spin states of C2 and see at which spin state a purely dissociative state is obtained. A cursory estimate obtained from the primary Hartree Fock (HF) MO picture of the C2 would suggest that C2 has only two π bonds.2 The four electrons in the σ orbitals would appear not to contribute to bonding as there are two electrons in a bonding orbital and two electrons in an antibonding orbital. It must be noted that the Be2 dimer with the same σ electron population and no π electron shows a total absence of bonding at HF and CASSCF levels of theory.19 Hence, one is tempted to infer that C2 will have just two π bonds arising from the two π electrons. A full valence CASSCF calculation on the ground electronic state of C2 reveals the multireference character of C2. The dominant configuration state functions (CSFs) are with 70.9% and 13.6% contributions. The 2nd CSF may suggest that it can contribute two σ bonds in the ground electronic state of C2 (see Table 1). The no. of bonds arising from σ orbitals is the bone of contention, whereas there is no debate as to the presence of two π bonds in the ground electronic state. VB theory predictions from Shaik and others suggest that indeed two σ bonds are present. Due to the multi-reference character of C2, simple MO based electronic structure theories are inadequate to predict the no. of σ bonds. However, as discussed earlier the high spin state PECs can be investigated to gauge the bonding situation in the ground electronic state. Using a full valence CASSCF for C2, N2, CN+ and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH we have investigated the dissociation PECs for high spin Σ states (see Fig. 1(a), (b) and (c) for C2, N2 and CN+ and Fig S1 in ESI† for acetylene respectively). The high spin Σ states are created in such a way that it would have lesser number of electron pairs in bonding orbitals. Such an exercise immediately reveals that for N2 (Fig. 1(b)) and HC
CH we have investigated the dissociation PECs for high spin Σ states (see Fig. 1(a), (b) and (c) for C2, N2 and CN+ and Fig S1 in ESI† for acetylene respectively). The high spin Σ states are created in such a way that it would have lesser number of electron pairs in bonding orbitals. Such an exercise immediately reveals that for N2 (Fig. 1(b)) and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH (Fig S1†) the lowest lying 7Σu+ state is purely dissociative. This would suggest that only three electron pairs contribute to bonding in the ground electronic state and when all of them are disrupted to create a high spin state of septet symmetry it leads to a purely dissociative PEC. Intriguingly, the same exercise with C2 reveals a purely dissociative PEC is obtained for the Σ state of nonet spin symmetry, with 7Σu+ displaying a distinct minimum. The trends immediately suggest that probably the no. of electron pairs contributing to the bonding in the ground state of C2 is more compared to those for N2 and HC
CH (Fig S1†) the lowest lying 7Σu+ state is purely dissociative. This would suggest that only three electron pairs contribute to bonding in the ground electronic state and when all of them are disrupted to create a high spin state of septet symmetry it leads to a purely dissociative PEC. Intriguingly, the same exercise with C2 reveals a purely dissociative PEC is obtained for the Σ state of nonet spin symmetry, with 7Σu+ displaying a distinct minimum. The trends immediately suggest that probably the no. of electron pairs contributing to the bonding in the ground state of C2 is more compared to those for N2 and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH. Our hypothesis is based on the fact that on promoting electrons to the high spin states eliminate bonds. With that one needs to go the nonet spin state (9Σg+) for the purely dissociative state. It suggests that four bonding pairs have to be disrupted to decimate any form of bonding between the two atoms.
CH. Our hypothesis is based on the fact that on promoting electrons to the high spin states eliminate bonds. With that one needs to go the nonet spin state (9Σg+) for the purely dissociative state. It suggests that four bonding pairs have to be disrupted to decimate any form of bonding between the two atoms.
| Spin multiplicity | Major contributing CSF | Percentage |
|---|---|---|
| 1Σg+ | |2σg22σu21πux21πuy2〉 | 70.9 |
| |2σg23σg21πux21πuy2〉 | 13.6 | |
| 3Σu+ | |2σg22σu11πux21πuy23σg1〉 | 86.3 |
| |2σg21πux21πuy12σu21πgy1〉 + |2σg21πux11πuy22σu21πgx1〉 | 3.6 | |
| 5Σg+ | |2σg22σu11πux11πuy23σg11πgx1〉 + |2σg22σu11πux21πuy13σg11πgy1〉 | 81.7 |
| |2σg22σu21πux11πuy11πgx11πgy1〉 | 6.7 | |
| 7Σu+ | |2σg22σu11πux11πuy13σg11πgx11πgy1〉 | 97.8 |
| |2σg12σu11πux11πuy13σg21πgx11πgy1〉 | 0.5 | |
| 9Σg+ | |2σg12σu11πux11πuy13σg11πgx11πgy13σu1〉 | 100.0 |
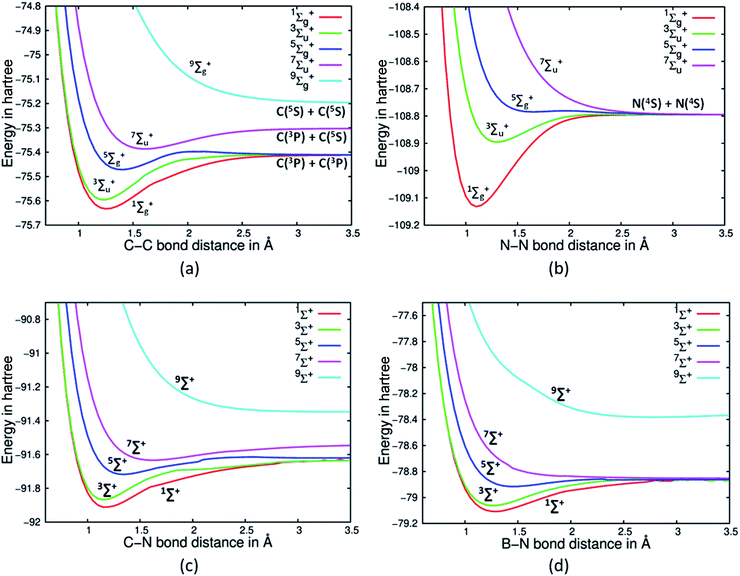 | ||
| Fig. 1 PECs corresponding to the (a) five spin states of C2, (b) four spin states of N2,17a (c) five spin states of CN+ and (d) five spin states of BN. | ||
Further inspection of the excited state PECs of C2 along with the dominant CSF at the minimum at the PEC is instructive. The lowest lying 3Σu+ is dominated by a CSF which has the presence of two π bonds (see Table 1). The electron distribution in σ orbitals in 3Σu+ space avoids any significant participation from configurations which will have simultaneous double occupation in 2σg and 3σg orbital. Also, the dissociation energy of the 3Σu+ state is lower compared to that of the 1Σg+ state by about 27 kcal mol (see ESI Table ST1†). The dominant CSF of 3Σu+ at the PEC minimum, |2σg22σu11πu43σg1〉 may be viewed as an excitation from the CSF |2σg22σ0u1πu43σg2〉 (the 2nd most important CSF present in the ground state minimum) (see Fig. 2), which is essentially breaking a bonding pair of 3σg and putting parallel spins in 3σg and 2σu. It may be argued that 3Σu+ essentially maintains 2π bonds and eliminates plausibly one σ bond, which shows up in the decrease of the dissociation energy. The 5Σg+ is riddled with strong signatures of avoided crossings. State averaging by including four low lying 5Σg+ states were used to draw up the PECs (see ESI, Section S1†). The nature of the dominant CSF suggests the elimination of only one π bond and one σ bond w.r.t that of the ground state, using the same line of argument which was employed in the previous case. The dominant CSF at the minimum of the PEC for the lowest lying septet Σ state, 7Σu+ shows a total absence of π bonding but the presence of a deep minimum indicates stability conferred from the electron pair in 2σg orbital. The dominant septet state CSF at the 7Σu+ PEC minimum shows a marked absence of π bonding, yet this is the third state which has one σ bond w.r.t that of the ground electronic state as it has parallel spins in 3σg and 2σu akin to the dominant CSF in the PEC minima of 3Σu+ and 5Σg+ states. As mentioned earlier, all of the bonding interactions are annihilated at the 9Σg+ state leading to a purely dissociative PEC. This fact is in conjunction with the fact that 7Σu+ state PEC has a distinct minimum which strongly indicates that the ground electronic state of C2 has four bonds, two σ and two π.
Though we have noted earlier that for N2 and acetylene purely dissociative state appears only when one reaches the septet spin state (7Σu+), unfortunately the corresponding 5Σg+ state PECs do not show presence of distinct minima. Further investigations reveal that the situation for the 5Σg+ state is extremely complex as it involves significant contribution from CSFs which have partially filled π and σ orbitals. Moreover, some majorly contributing CSFs also show participation from 3σu orbital. State averaging does not alleviate the problem and such issues are well documented.17b However, it must be noted that though the 5Σg+ state for N2 does not show a distinct minimum, the PEC is certainly not purely dissociative in nature. Moreover, previous studies with MRCI and Multi-Reference Coupled Cluster suggested that the 5Σg+ state of N2 does possess a shallow minimum.17a,c Furthermore, the nature of bonding in diatomic systems BN and CN+ isoelectronic to C2 were also investigated using the same stratagem. Interestingly, we do find that for CN+ the lowest four spin states display a distinct minimum on their respective PECs, while its nonet state is purely dissociative. Hence, by the extension of the same line of argument it can be suggested that CN+ has signature of quadruple bonding in agreement to the findings of Shaik and co-workers (see Fig. 1(c)).5 Contrary to the findings of Shaik et al. we find BN, which is also isoelectronic to C2, does not have a quadruple bond as suggested by the purely dissociative PEC for 7Σ+ state (see Fig. 1(d)). Our strategy of counting bonds suggests it has three bonds which conforms to the usual Lewis structure prediction.2 This difference may be ascribed to the electronegativity difference in the case of BN, which is completely absent in C2 and quite reduced in CN+. After excitation in BN to 7Σ+ (with major contributing CSF: |[core]2σ22σ*11πx11πy13σ11πx*11πy*1〉), the fourth electron pair gets mostly localized as a lone pair on the nitrogen atom in contrast to C2 where the excited electrons remain on each C atom. This may be the reason why 7Σ+ state of BN is unbound, even though VB theory shows a quadruple bond.5
One is disposed to question what happens if dynamic correlation is roped in. Does it change the scenario and the inferences derived from it? To address this question MRCI computations were conducted for C2, BN and CN+ (see ESI Fig S3–S5†). The general trends of the PECs for the different Σ states for C2 remain unaltered. The 7Σu+ state PEC still exhibited a distinct minimum and the dissociation energy was estimated to be 69 kcal mol−1 and the 9Σg+ shows pristine dissociative character. Our MRCI results on BN also suggest that the 7Σu+ state is dissociative, indicating unlike C2 it does not have a quadruple bond. Incidentally, the 7Σ+ states of C2 and BN have not been studied experimentally. Our computations suggest that the 7Σu+ state of C2 lies 9.4 eV above the ground state. Hence, the proof of existence of a minimum in the 7Σu+ for C2 and the absence of such a minimum in the equivalent case for BN is likely to corroborate our findings on quadruple bonding in these two cases. Furthermore, CN+ being an ionic species can be investigated in an ion trap.20 The case of presence of a bound 7Σ+ state can be verified experimentally.
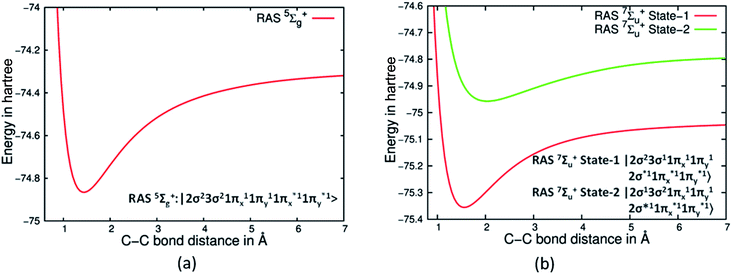
The most perplexing aspect of bonding in C2 is the question of the presence of two σ bonds, while σ bonds are distinctly absent in Be2 despite both having largely four electron population in σ orbitals (see ESI Section S2 and Fig S2†).19 We ventured to understand what would happen if we artificially prevent formation of π bonds in C2, a situation akin to Be2 where the electron population is zero in the π orbitals. We resorted to the use of the RASSCF technique which allowed us to restrict the population of π orbitals with one electron in each of them for C2, thus negating the possibility of any π bonding. Whereas, for Be2 we restricted the population of π orbitals to zero. This ensured that the dominant configurations both in Be2 and C2 would be restricted to four electrons in four σ orbitals. Such an approach helped us to examine the PECs of Be2 and C2 without any contribution to bonding from the π orbitals. Gratifyingly, we found that the RASSCF based PECs for 5Σg+ state of C2 with dominant CSFs show a distinct deep minimum, whereas for 1Σg+ Be2 was totally dissociative (see Fig S2 in ESI† and Fig. 3(a)). RASSCF studies show that on imposition of similar restrictions on the two low lying 7Σu+ states the PECs have deep minimum in each state. Further analysis reveals that this is due to the presence of a single σ bond in each of these states (see Fig. 3(b)). The dominant CSFs of these two states are |2σg23σg11πu21πg22σu1〉 and |2σg13σg21πu21πg22σu1〉 respectively, indicating that indeed two sets of σ electron pairs do give rise to two σ bonds.
Frenking and others have questioned the basis of quadruple bonding by comparing the force constants of the bond in C2 with that of HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH, with the bond in C2 being weaker than that of HC
CH, with the bond in C2 being weaker than that of HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH.7 In the light of our findings this may stand as a contradiction. Here we must reiterate that the dominant determinant of the ground state of C2 contributes only two π bonds. Hence, analysis of force constants is likely to reflect the attribute of primarily the dominant determinant of C2 and may not serve as a good metric for this purpose. The latent quadruple nature of the bond in C2 and CN+ can only be recognized through the PECs of the excited states.
CH.7 In the light of our findings this may stand as a contradiction. Here we must reiterate that the dominant determinant of the ground state of C2 contributes only two π bonds. Hence, analysis of force constants is likely to reflect the attribute of primarily the dominant determinant of C2 and may not serve as a good metric for this purpose. The latent quadruple nature of the bond in C2 and CN+ can only be recognized through the PECs of the excited states.
Though our approach possibly brings in an avenue to understand the bonding situation in C2, a probable question may arise that whether this hypothesis can be applied to comprehend the number of bonds in all diatomic systems and what are its intrinsic limitations. Naturally, one is inclined to ask whether this technique can be extended to molecules with triplet ground states like O2 and B2. Here we first discuss the case of O2 to illustrate how this approach can be tailored to address cases where the ground state is 3Σg− within the framework of traditional MO theory. In the case of the 3Σg− ground state of O2, a formal bond order of 2.0, one from σ and the other from π is assigned from the electronic distribution [core]2σg2 2σu23σg21πu41πg2. One can generate a higher spin state by breaking the bonding pair in the 3σg2 bonding orbital and promoting an electron to 3σu, thus eliminating the σ bond. In order to disrupt the bonding arising from π orbitals one needs to excite a single electron from π to π* creating a configuration of the type πu3πg3 from πu4πg2 of the ground state. This would eliminate the single π bond without ascending on the spin ladder. This is obviously different from the molecules with singlet ground state 1Σg+ that has π bonds (consider the case of N2 or HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH). Armed with this simple information one would expect to obtain 3Σu+ with a minimum (conventional bond order = 1) and a 5Σg+ with a purely dissociative curve (conventional bond order = 0) (see Fig. S6(b) and S7(b) in ESI†). Indeed the findings from the previously reported CASSCF/MRCI PECs of high spin Σ states show that the approach holds good, it must be emphasized that for triplet ground state diatomic systems arising from πu3πg3 and πu4πg2 configurations moving the bonding electron to the antibonding electron would not create a sigma state with higher spin symmetry.21 If this may seem confusing one may modify our strategy from a different viewpoint. Associated with these two configurations is a low-lying singlet 1Δg configuration. From the lowest lying singlet state bonding pairs have to be broken to create high spin sigma states and the corresponding wavefunctions and their respective PECs have to be inspected to arrive at a proper conclusion regarding the number of bonds present in them (see Fig. S8 in ESI†). This tailored strategy would yield two bonds for O2 and a single bond in B2. While our approach appears to be simple it would be prudent to add a cautionary note, particularly for the quintet states of p-block elements. As has been discussed earlier, we find that for the p-block elements the quintet Σ state PECs are fraught with multiple avoided crossings as the dominating configurations can arise from electron bond pair breaking of the σ orbital or from π orbital. One has to ensure that adequate state-averaging is conducted to reveal the true nature of the state PECs of these dimers. Admittedly, the approach has to be tested further on metal dimer systems to see whether proper inferences can be drawn from analogous high spin state PECs regarding the number of bonds in their respective ground states.
CH). Armed with this simple information one would expect to obtain 3Σu+ with a minimum (conventional bond order = 1) and a 5Σg+ with a purely dissociative curve (conventional bond order = 0) (see Fig. S6(b) and S7(b) in ESI†). Indeed the findings from the previously reported CASSCF/MRCI PECs of high spin Σ states show that the approach holds good, it must be emphasized that for triplet ground state diatomic systems arising from πu3πg3 and πu4πg2 configurations moving the bonding electron to the antibonding electron would not create a sigma state with higher spin symmetry.21 If this may seem confusing one may modify our strategy from a different viewpoint. Associated with these two configurations is a low-lying singlet 1Δg configuration. From the lowest lying singlet state bonding pairs have to be broken to create high spin sigma states and the corresponding wavefunctions and their respective PECs have to be inspected to arrive at a proper conclusion regarding the number of bonds present in them (see Fig. S8 in ESI†). This tailored strategy would yield two bonds for O2 and a single bond in B2. While our approach appears to be simple it would be prudent to add a cautionary note, particularly for the quintet states of p-block elements. As has been discussed earlier, we find that for the p-block elements the quintet Σ state PECs are fraught with multiple avoided crossings as the dominating configurations can arise from electron bond pair breaking of the σ orbital or from π orbital. One has to ensure that adequate state-averaging is conducted to reveal the true nature of the state PECs of these dimers. Admittedly, the approach has to be tested further on metal dimer systems to see whether proper inferences can be drawn from analogous high spin state PECs regarding the number of bonds in their respective ground states.
Conclusions
In summary we provide overwhelming evidence which brings out the quadruple bonding nature in C2 and CN+ with two σ and two π bonds. However, our approach indicates that BN, which is isoelectronic to C2 at the most has three bonds. Additionally, we suggest that for both CN+ and C2, a 7Σ+ state exists which has a clear distinct and deep minimum, which opens up a window for experimental verification.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AP would like to thank Professor Debashis Mukherjee and Professor Eluvathingal D. Jemmis for enlightening discussions and thoughtful inputs. AP would like to acknowledge financial support from DST SERB CRG/2019/006685. DG would like to acknowledge DST-SERB grant EMR/2017/001054 for the financial support. IB would like to acknowledge financial support in the form of a research fellowship from CSIR, Govt. of India (Award Number: 09/080(1065)/2017-EMR-I).References
- (a) R. C. Fischer and P. P. Power, Chem. Rev., 2010, 110, 3877–3923 CrossRef CAS PubMed; (b) P. R. Schreiner and H. P. Reisenauer, Angew. Chem., Int. Ed., 2009, 48, 8133–8136 CrossRef CAS PubMed.
- I. N. Levine, Quantum Chemistry, Allyn and Bacon, 2nd edn, 1974, p. 321, table 13.2 Search PubMed.
- P. V. R. Schleyer and P. Maslak, Tetrahedron Lett., 1993, 34, 6387–6390 CrossRef CAS.
- P. Su, J. Wu, J. Gu, W. Wei, S. Shaik and P. C. Hiberty, J. Chem. Theory Comput., 2011, 7, 121–130 CrossRef CAS PubMed.
- S. Shaik, D. Danovich, W. Wu, P. Su, H. S. Rzepa and P. C. Hiberty, Nat. Chem., 2012, 4, 195–200 CrossRef CAS PubMed.
- (a) S. Shaik, H. S. Rzepa and R. Hoffmann, Angew. Chem., Int. Ed., 2013, 52, 3020–3033 CrossRef CAS PubMed; (b) D. Danovich, S. Shaik, H. S. Rzepa and R. Hoffmann, Angew. Chem., Int. Ed., 2013, 52, 5926–5928 CrossRef CAS PubMed.
- G. Frenking and M. Hermann, Angew. Chem., Int. Ed., 2013, 52, 5922–5925 CrossRef CAS PubMed.
- D. Danovich, P. C. Hiberty, W. Wu, H. S. Rzepa and S. Shaik, Chem. –Eur. J., 2014, 20, 6220–6232 CrossRef CAS PubMed.
- D. W. O. Sousa and M. A. C. Nascimento, J. Chem. Theory Comput., 2016, 12, 2234–2241 CrossRef PubMed.
- M. Hermann and G. Frenking, Chem. –Eur. J., 2016, 22, 4100–4108 CrossRef CAS PubMed.
- P. B. Karadakov and J. Kirsopp, Chem. –Eur. J., 2017, 23, 12949–12954 CrossRef CAS PubMed.
- J. M. Matxain, F. Ruipérez, I. Infante, X. Lopez, J. M. Ugalde, G. Merino and M. Piris, J. Chem. Phys., 2013, 138, 151102 CrossRef PubMed.
- (a) S. Shaik, H. S. Rzepa and R. Hoffmann, Angew. Chem., Int. Ed., 2013, 52, 3020–3033 CrossRef CAS PubMed; (b) L. T. Xu and T. H. Dunning Jr, J. Chem. Theory Comput., 2014, 10, 195–201 CrossRef CAS PubMed; (c) S. Shaik, D. Danovich, B. Braida and P. C. Hiberty, Chem. –Eur. J., 2016, 22(52), 18977–18980 CrossRef CAS PubMed; (d) M. Piris, X. Lopez and J. M. Ugalde, Chem. –Eur. J., 2016, 22(12), 4109–4115 CrossRef CAS PubMed.
- P. F. Fougere and R. K. Nesbet, J. Chem. Phys., 1966, 1, 285–298 CrossRef.
- R. Zhong, M. Zhang, H. Xu and Z. Su, Chem. Sci., 2016, 7, 1028–1032 RSC.
- K. K. Lange, E. I. Tellgren, M. R. Hoffmann and T. Helgaker, Science, 2012, 337, 327–331 CrossRef CAS PubMed.
- (a) A. Engels-Putzka and M. Hanrath, Mol. Phys., 2009, 107, 143–155 CrossRef CAS; (b) R. S. Mulliken, J. Chem. Phys., 1962, 37, 809–813 CrossRef CAS; (c) H. Werner and P. J. Knowles, J. Chem. Phys., 1991, 94(2), 1264–1270 CrossRef CAS.
- (a) G. S. Scuseria, T. P. Hamilton and H. F. Schaefer III, J. Chem. Phys., 1990, 92, 568–573 CrossRef CAS; (b) W. D. Laidig, P. Saxe and R. J. Bartlett, J. Chem. Phys., 1987, 86, 887–907 CrossRef CAS.
- J. M. Matxain, F. Ruipérez and M. Piris, J. Mol. Model, 2013, 19, 1967–1972 CrossRef CAS PubMed.
- A. L. Padellec, J. B. A. Mitchell, A. Al-Khalili, H. Danared, A. Källberg, Å. Larsen, S. Rosén, M. Ugglas, L. Vikor and M. Larsson, J. Chem. Phys., 1999, 110(2), 890–901 CrossRef.
- (a) H. Liu, D. Shi, J. Sun, Z. Zhu and Z. Shulin, Spectrochim. Acta, Part A, 2014, 124, 216–229 CrossRef CAS PubMed; (b) H. Partridge, C. W. Bauschlicher Jr, S. R. Langhoff and P. R. Taylor, J. Chem. Phys., 1991, 95(11), 8292–8300 CrossRef CAS; (c) H. Lefebvre-Brion, H. P. Liebermann, J. M. Amero and G. J. Vázquez, J. Chem. Phys., 2016, 144(14), 144302 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc02336a |
| This journal is © The Royal Society of Chemistry 2020 |