An accurate potential energy surface and ring polymer molecular dynamics study of the Cl + CH4 → HCl + CH3 reaction†
Yang
Liu
 and
Jun
Li
and
Jun
Li
 *
*
School of Chemistry and Chemical Engineering, Chongqing University, Chongqing 401331, China. E-mail: jli15@cqu.edu.cn
First published on 2nd December 2019
Abstract
The reaction Cl + CH4 → HCl + CH3, a prototypical bimolecular reaction, has been established as an important proving ground for studying chemical reaction kinetics and dynamics of polyatomic molecules. In this work, a globally accurate full-dimensional potential energy surface (PES) for this reaction is developed by using the permutationally invariant polynomial neural network (PIP-NN) approach based on 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points calculated at the level of the explicitly correlated unrestricted coupled cluster single, double, and perturbative triple level with the augmented correlation corrected valence triple-zeta basis set (UCCSD(T)-F12a/AVTZ). For points in the entrance channel, spin–orbit corrections stemming from Cl(2P) are determined at the level of complete active space self-consistent field (CASSCF) with the AVTZ basis set. With this PES, thermal rate coefficients and kinetic isotope effects are computed for reactions Cl + CH4 → HCl + CH3 and Cl + CD4 → DCl + CD3 using the ring polymer molecular dynamics (RPMD) method, which can provide reliable estimations for thermal rate coefficients effectively. Generally, the agreement with the scattered experimental results is reasonably satisfactory.
000 points calculated at the level of the explicitly correlated unrestricted coupled cluster single, double, and perturbative triple level with the augmented correlation corrected valence triple-zeta basis set (UCCSD(T)-F12a/AVTZ). For points in the entrance channel, spin–orbit corrections stemming from Cl(2P) are determined at the level of complete active space self-consistent field (CASSCF) with the AVTZ basis set. With this PES, thermal rate coefficients and kinetic isotope effects are computed for reactions Cl + CH4 → HCl + CH3 and Cl + CD4 → DCl + CD3 using the ring polymer molecular dynamics (RPMD) method, which can provide reliable estimations for thermal rate coefficients effectively. Generally, the agreement with the scattered experimental results is reasonably satisfactory.
I. Introduction
Due to its significance in atmospheric chemistry,1–4 extensive theoretical5–28 and experimental29–74 investigations have been reported for the reaction, Cl + CH4 → HCl + CH3, and its isotopic analogues. This reaction is a prototypical bimolecular reaction and has been established as a benchmark system for studying chemical reaction kinetics and dynamics of polyatomic molecules,4,75 in particular, on the state-to-state and thermal rate coefficients, kinetic isotope effects (KIEs), mode-specific and bond-selective chemistry, stereodynamics, non-adiabaticity effects, and scattering resonances, etc.Theoretically, due to the chattering motion of the transfer of a light hydrogen atom between two heavy atoms (chlorine and carbon atoms), the title reaction is expected to be affected strongly by quantum tunneling and recrossing, thus presenting a challenge to transition-state theory.7,8,10,21 Therefore, its kinetics and dynamics need be treated quantum mechanically for accurate description of quantum effects, such as tunneling, recrossing and zero-point vibrational energy (ZPVE). However, for the title reaction system with six atoms, it is still impractical to perform exactly full-dimensional (12D) quantum scattering calculations. So far, all quantum mechanical computations on this reaction were based on reduced-dimensional models,9,12,19,25,76–78 by using several different potential energy surfaces (PESs), which play a key role in the reactive kinetics and dynamics. Indeed, an inaccurate PES is not expected to yield reliable results no matter how accurate the kinetics or dynamical method might be.79 For the title system, Espinosa-Garcia and Corchado and co-workers have developed several semi-empirical full-dimensional PESs with relatively simpler function forms based on ab initio results for the stationary points and some experimental measurements.8,10,14 The most recent PES from them, denoted as the RNCE PES hereafter, can reproduce the available experimental kinetics effectively.14 Using the Shepard interpolation, Castillo et al. developed a full-dimensional PES for the title system based on QCISD(T)/AVDZ calculations and scaling-all-correlation level of theory.80 In 2011, Czako and Bowman fitted a high-quality, full-dimensional global PES (denoted as CB PES hereafter) to a permutationally invariant polynomial (PIP) function form81 based on ca. 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ab initio energy points calculated by an efficient composite method, which can provide accuracy almost equivalent to all-electron CCSD(T)/aug-cc-pCVQZ.18,20 In the CB PES, spin–orbit (SO) corrections were also considered for 1600 points in the entrance channel at the level of multi-reference configuration interaction (MRCI) with Davison correction (+Q) and the augmented correlation corrected valence triple-zeta (AVTZ) basis set.20
000 ab initio energy points calculated by an efficient composite method, which can provide accuracy almost equivalent to all-electron CCSD(T)/aug-cc-pCVQZ.18,20 In the CB PES, spin–orbit (SO) corrections were also considered for 1600 points in the entrance channel at the level of multi-reference configuration interaction (MRCI) with Davison correction (+Q) and the augmented correlation corrected valence triple-zeta (AVTZ) basis set.20
In this work, we report a new full-dimensional PES for the title reaction developed by using the PIP-neural network (PIP-NN) method,82–84 which has been employed successfully to fit PESs for polyatomic reaction systems, such as OH + H2O,85 OH + HO2 → H2O + O2,86 H/OH + CH4 → H2/H2O + CH387–89 and F + CH3OH → HF + CH3O/CH2OH90 with high fidelity. About 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points were sampled and calculated at the explicitly correlated unrestricted coupled cluster single, double, and perturbative triple level with the augmented correlation corrected valence triple-zeta basis set (UCCSD(T)-F12a/AVTZ).91,92 In order for the correct description of the entrance channel within the adiabatic framework, the SO correction was calculated at the state-averaged level of complete active space self-consistent field (CASSCF) with the AVTZ basis set. Indeed, this PES has been already used to construct vibrationally and SO coupled diabatic potentials for the title reaction using an ansatz scheme by Manthe and co-workers very recently.28 Using this newly fitted PES, thermal rate coefficients for reactions Cl + CH4/CD4 → HCl/DCl + CH3/CD3 are then computed with the ring polymer molecular dynamics (RPMD) method,93 an approximate quantum mechanical approach with full dimensionality. It has been shown that the RPMD approach can efficiently provide accurate rate coefficients for several bimolecular reactions with reliable quantum effects such as ZPVE and tunneling.22,94–115 The remaining of the publication is organized as follows. The next section (Section II) details the ab initio calculations, the PES fitting, and RPMD theory briefly. Section III presents and discusses the results. A summary and conclusions are given in Section IV.
000 points were sampled and calculated at the explicitly correlated unrestricted coupled cluster single, double, and perturbative triple level with the augmented correlation corrected valence triple-zeta basis set (UCCSD(T)-F12a/AVTZ).91,92 In order for the correct description of the entrance channel within the adiabatic framework, the SO correction was calculated at the state-averaged level of complete active space self-consistent field (CASSCF) with the AVTZ basis set. Indeed, this PES has been already used to construct vibrationally and SO coupled diabatic potentials for the title reaction using an ansatz scheme by Manthe and co-workers very recently.28 Using this newly fitted PES, thermal rate coefficients for reactions Cl + CH4/CD4 → HCl/DCl + CH3/CD3 are then computed with the ring polymer molecular dynamics (RPMD) method,93 an approximate quantum mechanical approach with full dimensionality. It has been shown that the RPMD approach can efficiently provide accurate rate coefficients for several bimolecular reactions with reliable quantum effects such as ZPVE and tunneling.22,94–115 The remaining of the publication is organized as follows. The next section (Section II) details the ab initio calculations, the PES fitting, and RPMD theory briefly. Section III presents and discusses the results. A summary and conclusions are given in Section IV.
II. Theory
II.A Ab initio calculations
In this work, all electronic calculations were performed using MOLPRO.116 The geometries, energies, and harmonic frequencies of all stationary points, including the reactants, products, intermediates, and transition states, were obtained at the UCCSD(T)-F12a/AVXZ (X = D, T) levels,117 which have been recommended for developing reliable PESs since it can efficiently provide results of accuracy similar to those obtained at the UCCSD(T)/AV5Z level.117,118In the entrance channel, the ground state of the Cl(2P) atom splits by 881 cm−1 into the four-fold degenerate ground Cl(2P3/2) and twofold degenerate excited Cl*(2P1/2) SO states. The SO ground state Cl(2P3/2) lies 294 cm−1 below the non-relativistic (spin-averaged) ground state of Cl(2P), while the SO excited state Cl*(2P1/2), 587 cm−1 above, has been found to play a negligible role in the reaction with CH4.40,46 Thus, only the SO ground state was considered in this work by adding the SO correction, which can be obtained effectively in the adiabatic representation, to the ground electronic state of the title reaction system under the adiabatic framework. This strategy is similar to the CB PES for the same reaction,18,20 the PES for the F + CH4 reaction,119 and to our previous work for the F + H2O reaction.120 In particular, the SO coupling matrix elements were determined using the Breit–Pauli Hamiltonian with the unperturbed CASSCF wavefunctions.121 The SO energies were then obtained by diagonalizing the combined matrix of the electronic and SO Hamiltonians, and the SO corrections taken as the difference between the SO energies and their corresponding non-relativistic counterparts. As a compromise between efficiency and computational costs, the SO corrections in the entrance channel were calculated at the state-averaged CASSCF level with the AVTZ basis set using an active space consisting of all valence electrons, namely, (15e, 12o). The 1s, 2s, 2p orbitals of the Cl atom and the 1s orbital of the C atom were kept doubly occupied.
II.B PIP-NN fitting
Developing PESs consists of three procedures: sampling data points in the dynamically relevant configuration space, calculating their energies by the ab initio method, and fitting them to a specific function. Following our previous strategy,87,88,90 possible reaction channels were firstly surveyed to determine the ranges of the energy and configuration space. For the Cl + CH4 reaction, two reaction channels, namely the hydrogen abstraction and substitution pathways, were considered with the focus on the former with a barrier height of only ca. 7 kcal mol−1, since the barrier height of the latter is about 35 kcal mol−1 higher than the former, making it only available at very high temperatures or energies.18,20 Then we started to sample the configuration space along the two reaction pathways with other coordinates fixed at the corresponding transition states. In this way, the main feature of the PES was captured. Further for the reactant and product asymptotes, the internal coordinates were sampled in dense grids while the intramolecular coordinates were sampled with relatively sparse grids. In order to avoid sampling points of unreasonably high energy, direct dynamical calculations were also carried out at a low level of theory, e.g., B3LYP/6-31+G(d), starting from different initial conditions.
Ab initio calculations were then performed at the level of UCCSD(T)-F12a/AVTZ for the initial set of data points, and a primitive PES can be fit. To further explore regions that are not described well due to lacking points, trajectory calculations with various initial conditions were performed on this PES. In order for efficient sampling, only those points that are not close to the existing data set will be added to improve these regions. In this work, the judgement is 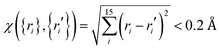 with the generalized Euclidean distance, χ, defined in terms of the internuclear distances between a new point {ri} and a data point {ri′} in the existing data set. Note that all permutationally equivalent points, namely, those configurations generated by permutations with respect to all four identical hydrogen atoms (4! = 24), were included in such screenings. The PES was also examined by checking the properties of stationary points, such as geometries, energies, and harmonic frequencies, as well as the minimum energy paths. With new points added, the PES was improved gradually. After several iterations, the outcome on the PES was converged. Finally, for points in the entrance channel, additional calculations were carried out at the CASSCF/AVTZ level to obtain their SO corrections.
with the generalized Euclidean distance, χ, defined in terms of the internuclear distances between a new point {ri} and a data point {ri′} in the existing data set. Note that all permutationally equivalent points, namely, those configurations generated by permutations with respect to all four identical hydrogen atoms (4! = 24), were included in such screenings. The PES was also examined by checking the properties of stationary points, such as geometries, energies, and harmonic frequencies, as well as the minimum energy paths. With new points added, the PES was improved gradually. After several iterations, the outcome on the PES was converged. Finally, for points in the entrance channel, additional calculations were carried out at the CASSCF/AVTZ level to obtain their SO corrections.
All ab initio points were fitted to a permutation invariant polynomial-neural network (PIP-NN) form with two hidden layers,82–84
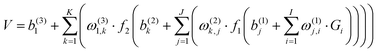 | (1) |
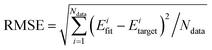 . The input layer of the NN consists of low-order PIPs, namely, symmetrized monomials of Morse-like variables of internuclear distances,
. The input layer of the NN consists of low-order PIPs, namely, symmetrized monomials of Morse-like variables of internuclear distances, 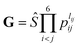 , pij = exp(−rij/α) (α = 1.0 Å), and Ŝ the symmetrization operator, which contains all the permutation operations among four identical hydrogen atoms in the system.122–124 In this work, all PIPs up to a maximum order of 5, namely,
, pij = exp(−rij/α) (α = 1.0 Å), and Ŝ the symmetrization operator, which contains all the permutation operations among four identical hydrogen atoms in the system.122–124 In this work, all PIPs up to a maximum order of 5, namely, 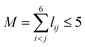 , resulting in 1052 PIP terms (I = 1052), were used as the input layer of NN to ensure the adequate permutation symmetry of the system.83
, resulting in 1052 PIP terms (I = 1052), were used as the input layer of NN to ensure the adequate permutation symmetry of the system.83
To avoid overfitting, the “early stopping” algorithm125 was employed with the entire data set divided randomly into three parts, i.e., the training (90%), validation (5%), and test (5%) sets. To minimize false extrapolation due to possible edge points randomly selected in the validation or test sets, only fits with similar RMSEs for all three sets were accepted as the final optimal PES. Besides, the absolute maximum deviation was considered for choosing the final PIP-NN PES. Several different NN architectures with two hidden layers were tested. For each architecture, 100 NN trainings with different initial fitting parameters, and different training, validation, and test sets were performed due to the non-linear fitting nature of the NN.
II.C RPMD
The RPMD rate code126 developed by Suleimanov et al. was employed to calculate the thermal rate coefficients of the Cl + CH4/CD4 reactions. Since the methodology and theoretical details are available in ref. 126 and 127, only a brief description was given here. According to the Bennett–Chandler factorization,128 the RPMD rate coefficient is expressed as:| kRPMD = kQTST(T;ξ‡)κ(t → ∞;ξ‡) | (2) |
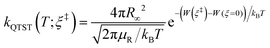 | (3) |
The second factor κ(t → ∞;ξ‡) in eqn (2) counterbalances the first factor kQTST(T;ξ‡), ensuring that the final RPMD rate coefficient does not depend on the choice of the dividing surface, a highly desirable property since it is difficult to define the dividing surface for high-dimensional systems. It is the long-time limit of a time-dependent ring-polymer transmission coefficient, accounting for recrossing at the bottleneck of the PMF. In practice, it reaches a plateau relatively fast in reactions with explicit barrier, as in the title reaction, along the minimal energy path. Technically, the transmission coefficient is calculated by sampling ring polymer trajectories starting with their centroid pinned at the bottleneck.
An extra advantage of the RPMD rate theory is that it would reduce to the classical limit when only one bead is used. In this limit, the static and dynamical components become identical to the classical transition state theory rate coefficient and the classical transmission coefficient, respectively. The quantum effects such as ZPVE and tunneling can be captured well by more beads. The following formula is used to estimate the minimal number of beads needed to account for these quantum effects:
| nmin = ħωmax/kBT | (4) |
III. Results and discussions
III.A Ab initio calculations
The reaction between Cl + CH4 has two reaction pathways, the dominated abstraction channel to HCl + CH3 and the negligible substitution channel to H + CH3Cl, as shown in Fig. 1. In this work, only the low energy pathway is reported, although the sampling covers other high energy regions. As shown in Fig. 1, there exists two van der Waals complexes between Cl and CH4, RvdW1 and RvdW2, which are expected to play some roles in reaction dynamics especially at low collision energies.18 The geometries of the stationary points, optimized at the levels of UCCSD(T)-F12a/AVDZ and UCCSD(T)-F12a/AVTZ, are presented in Fig. 2, with the harmonic frequencies listed in Table 1. Note that all the energies are relative to the spin-averaged reactant asymptote Cl(2P) + CH4 if not specified. For clarity, the high-level theoretical results on the CB PES,20 which considered counterpoise and SO corrections, are also included for comparison. For the stationary points in the entrance channel, namely, the reactants, RvdW1, RvdW2, and TS1, their energies consist of two contributions, the non-SO electronic energy at the level of UCCSD(T)-F12a/AVTZ and the SO correction calculated at the level of CASSCF(15e, 12o)/AVTZ. Generally, the results are consistent with each other. For instance, the energy differences between the current work, UCCSD(T)-F12a/AVTZ + CASSCF(15e, 12o)/AVTZ and CB PES are all less than 0.13 kcal mol−1 for these stationary points. Besides, at the level of CASSCF(15e, 12o)/AVTZ, the SO corrections of the reactant asymptote, RvdW1, RvdW2 and TS1 are −279, −231, −165, and −4 cm−1, respectively, consistent with those by MRCI + Q/AVTZ used in the CB PES.20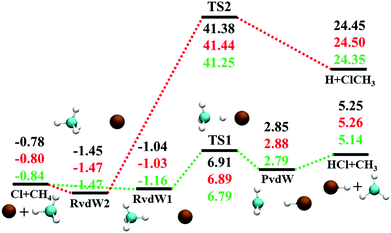 | ||
| Fig. 1 Schematic illustration of the energetics for the reaction Cl + CH4 on the lowest doublet state PES with the SO correction in the reactant channel. All energies are in kcal mol−1 and relative to the Cl(2P) + CH4 asymptote at various levels: PIP-NN PES, UCCSD(T)-F12a/AVTZ, and CB PES,20 from top to bottom. | ||
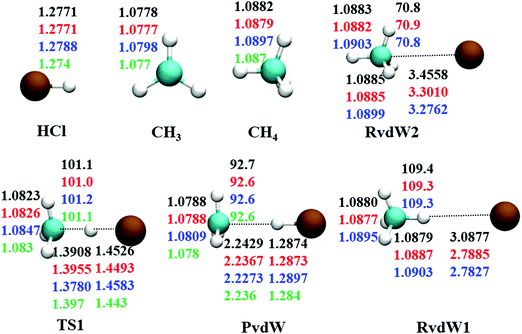 | ||
| Fig. 2 Comparison of geometries in internal coordinates (distances in Å and angles in degrees) for the stationary points. The values correspond to PIP-NN PES, UCCSD(T)-F12a/AVTZ, UCCSD(T)-F12a/AVDZ, and UCCSD(T)/AVTZ20 from top to bottom. | ||
| Species | Method | Frequencies (cm−1) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| a This work, fitted PIP-NN PES. b This work, UCCSD(T)-F12a/AVTZ. c This work, UCCSD(T)-F12a/AVDZ. d CCSD(T)/AVTZ, see ref. 20 for details. | |||||||||||||
| Cl + CH4 | PESa | 1343(t) | 1565(e) | 3028 | 3154(t) | ||||||||
| F12ab | 1344(t) | 1569(e) | 3033 | 3156(t) | |||||||||
| F12ac | 1340(t) | 1563(e) | 3032 | 3154(t) | |||||||||
| CCSD(T)d | 1351 | 1574 | 3028 | 3146 | |||||||||
| HCl + CH3 | PESa | 2983 | 517 | 1421(e) | 3118 | 3305(e) | |||||||
| F12ab | 2991 | 518 | 1421(e) | 3120 | 3304(e) | ||||||||
| F12ac | 2993 | 520 | 1419(e) | 3117 | 3301(e) | ||||||||
| CCSD(T)d | 2990 | 496 | 1419 | 3114 | 3294 | ||||||||
| RvdW1 | PESa | i57 | i53 | 32 | 1338 | 1338 | 1344 | 1565 | 1566 | 3035 | 3140 | 3151 | 3151 |
| F12ab | i135 | i109 | 58 | 1304 | 1321 | 1336 | 1549 | 1550 | 2661 | 3115 | 3157 | 3159 | |
| F12ac | i108 | i102 | 53 | 1320 | 1321 | 1338 | 1545 | 1546 | 3029 | 3144 | 3158 | 3158 | |
| RvdW2 | PESa | 53 | 60 | 62 | 1336 | 1347 | 1347 | 1572 | 1572 | 3017 | 3144 | 3144 | 3144 |
| F12ab | 71 | 155 | 165 | 1335 | 1348 | 1353 | 1572 | 1574 | 3028 | 3149 | 3150 | 3153 | |
| F12ac | i84 | i73 | 80 | 1335 | 1338 | 1341 | 1557 | 1557 | 3027 | 3145 | 3145 | 3151 | |
| PvdW | PESa | 97 | 135 | 136 | 318 | 318 | 641 | 1415 | 1415 | 2847 | 3107 | 3293 | 3293 |
| F12ab | 95 | 101 | 105 | 309 | 314 | 609 | 1418 | 1420 | 2835 | 3110 | 3294 | 3294 | |
| F12ac | 104 | 141 | 141 | 334 | 335 | 612 | 1418 | 1419 | 2828 | 3108 | 3292 | 3292 | |
| CCSD(T)d | 101 | 136 | 136 | 328 | 328 | 600 | 1419 | 1419 | 2834 | 3104 | 3285 | 3285 | |
| TS1 | PESa | i1021 | 366 | 367 | 501 | 925 | 925 | 1189 | 1438 | 1438 | 3096 | 3251 | 3251 |
| F12ab | i1006 | 359 | 361 | 505 | 924 | 925 | 1196 | 1432 | 1432 | 3088 | 3251 | 3251 | |
| F12ac | i976 | 254 | 254 | 504 | 863 | 863 | 1207 | 1428 | 1428 | 3084 | 3245 | 3245 | |
| CCSD(T)d | i1024 | 364 | 364 | 514 | 924 | 924 | 1197 | 1437 | 1437 | 3082 | 3242 | 3242 | |
III.B Potential energy surface
In total, ca. 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points were sampled and calculated at the level of UCCSD(T)-F12/AVTZ. Among them, ca. 27
000 points were sampled and calculated at the level of UCCSD(T)-F12/AVTZ. Among them, ca. 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points were located in the reactant channel, and their SO corrections were computed at the level of CASSCF(15e, 12o)/AVTZ. Then the PIP-NN method82–84 was employed to fit the PES of the title reaction system. After several tests, the final hidden layers (J and K) were chosen to be of 5 and 100 neurons, respectively, resulting in 5966 nonlinear fitting parameters with a total RMSE of 7.4 meV, which is comparable to that of H + CH4, 5.1 meV.87 Thanks to the high fidelity of the PIP-NN fitting approach, the properties of the stationary points, including the energies, geometries, and harmonic frequencies, are reproduced well on the PIP-NN PES, as shown in Fig. 1, 2, and Table 1, respectively. Note that the geometries and harmonic frequencies were calculated at the level of UCCSD(T)-F12a/AVTZ without SO correction. As can be seen in Fig. 1, for the energies of the stationary points along the abstraction channel, the largest deviation between PIP-NN PES and ab initio calculations is only 0.02 kcal mol−1. For the geometries in Fig. 2, all rigid coordinates, including bond distances and angles, are well produced with the deviations less than 0.0007 Å and 0.1°, respectively. For floppy coordinates in the weakly interacted complexes RvdW1 and RvdW2, the deviation can be as large as 0.3 Å. This is partly due to that the PIP-NN PES includes the SO correction in the reactant channel, which is not considered in the UCCSD(T)-F12a/AVTZ calculation.
000 points were located in the reactant channel, and their SO corrections were computed at the level of CASSCF(15e, 12o)/AVTZ. Then the PIP-NN method82–84 was employed to fit the PES of the title reaction system. After several tests, the final hidden layers (J and K) were chosen to be of 5 and 100 neurons, respectively, resulting in 5966 nonlinear fitting parameters with a total RMSE of 7.4 meV, which is comparable to that of H + CH4, 5.1 meV.87 Thanks to the high fidelity of the PIP-NN fitting approach, the properties of the stationary points, including the energies, geometries, and harmonic frequencies, are reproduced well on the PIP-NN PES, as shown in Fig. 1, 2, and Table 1, respectively. Note that the geometries and harmonic frequencies were calculated at the level of UCCSD(T)-F12a/AVTZ without SO correction. As can be seen in Fig. 1, for the energies of the stationary points along the abstraction channel, the largest deviation between PIP-NN PES and ab initio calculations is only 0.02 kcal mol−1. For the geometries in Fig. 2, all rigid coordinates, including bond distances and angles, are well produced with the deviations less than 0.0007 Å and 0.1°, respectively. For floppy coordinates in the weakly interacted complexes RvdW1 and RvdW2, the deviation can be as large as 0.3 Å. This is partly due to that the PIP-NN PES includes the SO correction in the reactant channel, which is not considered in the UCCSD(T)-F12a/AVTZ calculation.
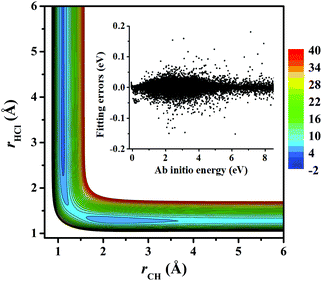
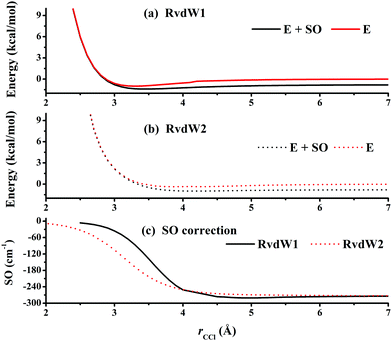
Fig. 3 represents the contour plot along the two reactive distances rCH and rHCl with other coordinates constrained at the transition state TS1. Along the reaction path, TS1 and the post-reaction complex PvdW can be clearly seen. The pre-reaction complexes RvdW1 and RvdW2 cannot be shown due to the geometric constraints. The fitting errors are also shown in the inset of the same figure. It can be seen that small errors are evenly distributed in the energy range of −0.1 to 8.5 eV, which is sufficient for high temperature simulations up to 3000 K. It should be noted that some additional points at high-energy regions were included for reliable quantum dynamical simulations in the future. Besides, we also present in Fig. 4(a and b) the non-SO (E) and the SO corrected energies (E + SO) as a function of the rCCl distance when Cl approaches CH4 at the configuration of RvdW1 or RvdW2 in the entrance channel. Clearly, the SO corrections lower the reactant asymptote by about 0.78 kcal mol−1, then start to decrease at 4–5 Å in both cases, and finally vanishes around 2.0 Å, as shown in Fig. 4(c). The PES is available from the corresponding author upon request.
III.C RPMD rate coefficients
The thermal rate coefficients of the Cl + CH4 → HCl + CH3 and Cl + CD4 → DCl + CD3 reactions were determined with the PIP-NN PES interfaced to the RPMDrate code.126 Most parameters are essentially the same as those used in ref. 22 for the same reaction but on the RNCE and CB PESs. Briefly, for the calculation of the PMF, the reaction coordinate (−0.06 to 1.10) was divided by an equal size (dξ = 0.01) with the force constant of the biasing potential of 2.72 (T/K) eV using the umbrella sampling technique. In each sampling window, 60 constrained sampling trajectories of 100 ps were carried out, before which the system was equilibrated for 20 ps with the Andersen thermostat129 for thermalization. After determining the PMF at each temperature, the transmission coefficient was computed. Specifically, a long (20 ns) mother trajectory was carried out with the ring-polymer centroid fixed at the top of PMF via the SHAKE algorithm.130 Configurations were sampled once every 2 ps to serve as the starting positions for the child trajectories used to calculate the flux-side correlation function. For each starting position, 100 separate ring polymer trajectories were spawned with different initial momenta sampled from a Boltzmann distribution. These trajectories were then propagated without constraints for 100 fs, which is sufficiently long for the transmission coefficients to reach plateau values for the title activated reaction with apparent barriers. The time step is selected to be 0.3 fs in all RPMD calculations, comparable to 0.5 fs used in the RPMD computations on the CB PES due to the expensive evaluations.22 Several tests have been performed to guarantee that the results are converged with respect to the parameters above, as shown in Fig. S1 of the ESI.†The final RPMD rate coefficients were corrected by an electronic partition function ratio of the following form,
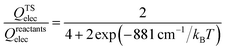 | (5) |
For Cl + CH4 → HCl + CH3, the rate coefficients were calculated at 200, 300, 400, 600, 800, 1000, 1100, 1500, and 2000 K. At each temperature, the RPMD calculations were firstly performed with one bead, which provides the classical limit. Then we performed calculations with a sufficiently large number of beads, which were estimated according to eqn (4). Specifically, the RPMD calculations were done with 32 beads for 200, 300, 400, 600 K, 16 beads for 800 K, 8 beads for 1000, 1100, 1500, 2000 K, respectively. Similar parameters were used in the work by Li et al.,22 albeit only at 600 and 1000 K on the CB PES due to the expensive evaluations of this PES. It should be noted that the evaluation of the PIP-NN PES is even much more expensive. In addition, the previous RPMD calculations were calculated at 300, 400, 600, 800, and 1000 K on the much faster RNCE PES.22
Fig. 5(a) presents the converged RPMD PMFs for the reaction Cl + CH4 → HCl + CH3. As shown, the peaks of the PMFs are all nearly at ξ = 1 within 200–3000 K for this activated reaction. With the temperature increased, the top positions show a negative shift slightly. The barriers of the PMFs are increased significantly from low to high temperatures due to the reduction in entropy from reactants to the transition state: they are 4.68, 5.68, 6.57, 7.99, 9.15, 10.12, 10.49, 11.89, and 13.22 kcal mol−1, at 200, 300, 400, 600, 800, 1000, 1100, 1500, and 2000 K, respectively. The quantum effects, including ZPVE and tunneling, are significant especially at low temperatures, and can be described well by the RPMD method. The transmission coefficient, κ(t), another important factor, is shown in Fig. 5(b). Clearly, all the transmission coefficients show a fast drop initially. After some oscillations, it becomes flat eventually. Similar behaviors have been found and discussed by Li et al. on the same reaction.22 Fig. S2–S10 of the ESI† provide additional tests on the RPMD calculations of Cl + CH4.
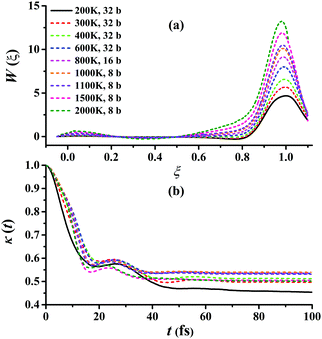 | ||
| Fig. 5 (a) Converged PMFs and (b) transmission coefficients at 200, 300, 400, 600, 800, 1000, 1100, 1500, 2000 K for the Cl + CH4 → HCl + CH3 reaction. | ||
For Cl + CD4 → DCl + CD3, the RPMD calculations were carried out at 300, 400, 600, 800, and 1000 K with 32, 32, 32, 16, and 8 beads, respectively. Fig. 6(a) presents the converged RPMD PMFs for the reaction Cl + CD4 → DCl + CD3. Similar to Cl + CH4, the barrier heights of the PMFs, all essentially at ξ = 1, are increased along with the temperature due to the decrease in the entropy from reactants to the transition state. At 300, 400, 600, 800, and 1000 K, they are 7.22, 8.05, 9.39, 10.42, 11.29 kcal mol−1, respectively. It can be seen that, the barrier heights at the same temperature are higher than those in Cl + CH4 due to the differences in the ro-vibrational energy levels, ZPVE, and tunneling effects. Fig. 6(b) presents the corresponding transmission coefficients. After initial drops, they finally reach plateau values, which are larger than those for Cl + CH4, whose recrossing effect is less significant than those in Cl + CD4. Additional comparisons and tests on the RPMD calculations of Cl + CD4 are given in Fig. S11–S15 of the ESI.†
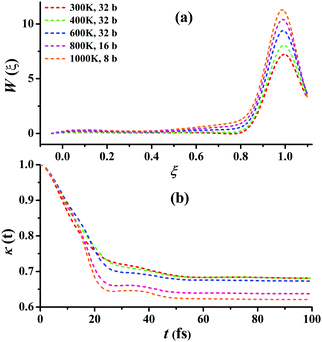 | ||
| Fig. 6 (a) Converged PMFs and (b) transmission coefficients at 300, 400, 600, 800, 1000 K for the Cl + CD4 → DCl + CD3 reaction. | ||
In Fig. 7, the RPMD rate coefficients for the Cl + CH4 reaction are compared with available experimental29–34,37,38,41,42,54,62 and theoretical results.21,22 The current results are essentially the same as those on the CB PES at 600 and 1000 K,22 since both PESs are fitted to tens of thousands of points calculated at similar ab initio levels.20 The RPMD predictions are apparently lower than other available results at low temperatures, 200–400 K, at which the barrier height can affect the low temperature rate coefficients significantly. With a reduction of only 0.22 kcal mol−1 in the barrier, the scaled RPMD results agree well with others in the entire temperature range of 200–3000 K, as shown in Fig. 7. Nonetheless, the overall agreement is reasonably good, given the fact that the experimental results are quite scattered. On the RNCE PES, the RPMD results were slightly overestimated at temperatures higher than 500 K and agreed well with experiment at low temperatures 300–500 K.22 With anharmonicity and energies calculated at advanced levels, rate coefficients of the title reaction and its isotopologues determined by the semiclassical transition state theory (SCTST) were in good agreement with experiments,21 as shown in Fig. 7. Careful scrutiny shows that SCTST results are slightly overestimated especially at temperatures above 600 K.
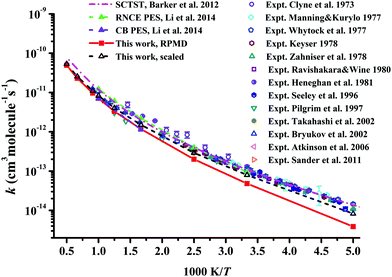 | ||
| Fig. 7 Comparison of the rate coefficients for the reaction Cl + CH4 → HCl + CH3 from available theoretical and experimental results. | ||
Similarly, Fig. 8 displays the corresponding rate coefficients for the Cl + CD4 → DCl + CD3 reaction within 300–1000 K. The RPMD results on the CB PES at 600 and 1000 K22 again are consistent with the current RPMD ones. Around room temperatures, the RPMD calculations on the PIP-NN PES are slightly lower than experiment.131–133 After reduction in the barrier by 0.22 kcal mol−1, the scaled RPMD results agree well with the scattered experimental results around 300 K. On the RNCE PES, the RPMD results22 were evidently overestimated due to the empirical nature of this PES.14 Particularly, the imaginary frequency on the RNCE PES is only i782 cm−1,14 significantly smaller than i1021 cm−1 in magnitude on the current PIP-NN PES. Interestingly, the SCTST results21 are very close to the current RPMD results for the Cl + CD4 reaction.
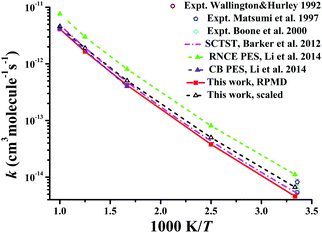 | ||
| Fig. 8 Comparison of the rate coefficients of the reaction Cl + CD4 → DCl + CD3 from available theoretical and experimental results. | ||
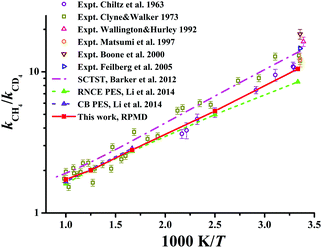 | ||
| Fig. 9 The kinetics isotopic effect (KIE) defined as kCH4/kCD4 within the temperature range of 300–1000 K. Available theoretical and experiment results are included for comparison. | ||
The KIEs, defined as the ratios between Cl + CH4 and Cl + CD4 rate coefficients, kCH4/kCD4, are displayed in Fig. 9 within 300–1000 K. Available theoretical21,22 and experimental results29,131–135 are also compared in the same figure. Clearly, experimental values differ considerably within the temperature range. The RPMD KIEs on the current PES, the CB PES, and the RNCE PES are consistent with each other at temperatures above 400 K. At temperatures between 300 and 400 K, the current RPMD KIEs, larger than those on the RNCE PES,22 are close to the lower end of the experimental data. On the contrary, the SCTST results21 are much higher, near the high end of the experiments.
IV. Conclusions
In the present work, we developed a new full-dimensional accurate PES for the reaction Cl + CH4 → HCl + CH3 based on ca. 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points calculated at the UCCSD(T)-F12a/AVTZ level with the SO corrections considered at the CASSCF/AVTZ level for ca. 27
000 points calculated at the UCCSD(T)-F12a/AVTZ level with the SO corrections considered at the CASSCF/AVTZ level for ca. 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points in the entrance channel. The full-dimensional approximate quantum mechanical approach, ring polymer molecular dynamics (RPMD), was employed to calculate the thermal rate coefficients within 200–2000 K for Cl + CH4 and 300–1000 K for Cl + CD4. The RPMD predicted results are in reasonable agreement with the experimental measurements, which are scattered. If the barrier height is reduced by only 0.22 kcal mol−1, the agreement becomes much better at temperatures below 400 K. The RPMD rate coefficients and the KIEs on the new PES are in good agreement with experiment in a large temperature range, suggesting that RPMD provides a reliable and efficient alternative to transition state theory for polyatomic reactions, for which it is still challenging to carry out rigorous quantum mechanical calculations. The previous RPMD results on the CB PES, including rate coefficients for Cl + CH4/CD4 and KIEs, are in excellent agreement with those on the current PES within 600–1000 K. As has been discussed in ref. 22, the rate coefficients on the more efficient RNCE PES were slightly overestimated within 500–1000 K for Cl + CH4, and significantly overestimated within 300–1000 K for Cl + CD4. Hence, the KIEs were significantly underestimated within 300–400 K on the RNCE PES.
000 points in the entrance channel. The full-dimensional approximate quantum mechanical approach, ring polymer molecular dynamics (RPMD), was employed to calculate the thermal rate coefficients within 200–2000 K for Cl + CH4 and 300–1000 K for Cl + CD4. The RPMD predicted results are in reasonable agreement with the experimental measurements, which are scattered. If the barrier height is reduced by only 0.22 kcal mol−1, the agreement becomes much better at temperatures below 400 K. The RPMD rate coefficients and the KIEs on the new PES are in good agreement with experiment in a large temperature range, suggesting that RPMD provides a reliable and efficient alternative to transition state theory for polyatomic reactions, for which it is still challenging to carry out rigorous quantum mechanical calculations. The previous RPMD results on the CB PES, including rate coefficients for Cl + CH4/CD4 and KIEs, are in excellent agreement with those on the current PES within 600–1000 K. As has been discussed in ref. 22, the rate coefficients on the more efficient RNCE PES were slightly overestimated within 500–1000 K for Cl + CH4, and significantly overestimated within 300–1000 K for Cl + CD4. Hence, the KIEs were significantly underestimated within 300–400 K on the RNCE PES.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was financially supported by the Chongqing Municipal Natural Science Foundation (grant no. cstc2019jcyj-msxmX0087) and the National Natural Science Foundation of China (contract no. 21573027 and 21973009). Prof. Hua Guo is thanked for helpful discussion on the work.References
- A. A. P. Pszenny, W. C. Keene, D. J. Jacob, S. Fan, J. R. Maben, M. P. Zetwo, M. Springer-Young and J. N. Galloway, Geophys. Res. Lett., 1993, 20, 699–702 CrossRef CAS.
- A. R. Douglass, M. R. Schoeberl, R. S. Stolarski, J. W. Waters, J. M. Russell III, A. E. Roche and S. T. Massie, J. Geophys. Res.: Atmos., 1995, 100, 13967–13978 CrossRef.
- M. L. Santee, L. Froidevaux, G. L. Manney, W. G. Read, J. W. Waters, M. P. Chipperfield, A. E. Roche, J. B. Kumer, J. L. Mergenthaler and J. M. Russell, J. Geophys. Res.: Atmos., 1996, 101, 18835–18859 CrossRef CAS.
- H. A. Michelsen, Acc. Chem. Res., 2001, 34, 331–337 CrossRef CAS PubMed.
- T. N. Truong, D. G. Truhlar, K. K. Baldridge, M. S. Gordon and R. Steckler, J. Chem. Phys., 1989, 90, 7137–7142 CrossRef CAS.
- K. D. Dobbs and D. A. Dixon, J. Phys. Chem., 1994, 98, 12584–12589 CrossRef CAS.
- W. T. Duncan and T. N. Truong, J. Chem. Phys., 1995, 103, 9642–9652 CrossRef CAS.
- J. Espinosa-García and J. C. Corchado, J. Chem. Phys., 1996, 105, 3517–3523 CrossRef.
- H. G. Yu and G. Nyman, Phys. Chem. Chem. Phys., 1999, 1, 1181–1190 RSC.
- J. C. Corchado, D. G. Truhlar and J. Espinosa-García, J. Chem. Phys., 2000, 112, 9375–9389 CrossRef CAS.
- L. Zhang, M.-D. Chen, M.-L. Wang and K.-L. Han, J. Chem. Phys., 2000, 112, 3710–3716 CrossRef CAS.
- S. Skokov and J. M. Bowman, J. Chem. Phys., 2000, 113, 4495–4497 CrossRef CAS.
- C. Rangel, J. Espinosa-García and J. C. Corchado, J. Phys. Chem. A, 2005, 109, 8071–8073 CrossRef CAS.
- C. Rangel, M. Navarrete, J. C. Corchado and J. Espinosa-García, J. Chem. Phys., 2006, 124, 124306 CrossRef PubMed.
- J. Sansón, J. C. Corchado, C. Rangel and J. Espinosa-García, J. Chem. Phys., 2006, 124, 074312 CrossRef PubMed.
- J. Sansón, J. C. Corchado, C. Rangel and J. Espinosa-García, J. Phys. Chem. A, 2006, 110, 9568–9574 CrossRef PubMed.
- S. J. Greaves, R. A. Rose, F. Abou-Chahine, D. R. Glowacki, D. Troya and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2011, 13, 11438–11445 RSC.
- G. Czakó and J. M. Bowman, Science, 2011, 334, 343–346 CrossRef PubMed.
- Z. Zhang, Y. Zhou, D. H. Zhang, G. Czakó and J. M. Bowman, J. Phys. Chem. Lett., 2012, 3, 3416–3419 CrossRef CAS PubMed.
- G. Czakó and J. M. Bowman, J. Chem. Phys., 2012, 136, 044307 CrossRef PubMed.
- J. R. Barker, T. L. Nguyen and J. F. Stanton, J. Phys. Chem. A, 2012, 116, 6408–6419 CrossRef CAS PubMed.
- Y. Li, Y. V. Suleimanov, W. H. Green and H. Guo, J. Phys. Chem. A, 2014, 118, 1989–1996 CrossRef CAS PubMed.
- R. Liu, F. Wang, B. Jiang, G. Czakó, M. Yang, K. Liu and H. Guo, J. Chem. Phys., 2014, 141, 074310 CrossRef PubMed.
- W. Yan and D. Wang, Chem. Phys. Lett., 2014, 603, 41–45 CrossRef CAS.
- N. Liu and M. Yang, J. Chem. Phys., 2015, 143, 134305 CrossRef PubMed.
- B. Hornung, J. N. Harvey, T. J. Preston, G. T. Dunning and A. J. Orr-Ewing, J. Phys. Chem. A, 2015, 119, 9590–9598 CrossRef CAS PubMed.
- A. J. Totenhofer, J. N. L. Connor and G. Nyman, J. Phys. Chem. B, 2016, 120, 2020–2032 CrossRef CAS PubMed.
- T. Lenzen, W. Eisfeld and U. Manthe, J. Chem. Phys., 2019, 150, 244115 CrossRef PubMed.
- M. A. A. Clyne and R. F. Walker, J. Chem. Soc., Faraday Trans. 1, 1973, 69, 1547–1567 RSC.
- R. G. Manning and M. J. Kurylo, J. Phys. Chem., 1977, 81, 291–296 CrossRef CAS.
- D. A. Whytock, J. H. Lee, J. V. Michael, W. A. Payne and L. J. Stief, J. Chem. Phys., 1977, 66, 2690–2695 CrossRef CAS.
- M. S. Zahniser, B. M. Berquist and F. Kaufman, Int. J. Chem. Kinet., 1978, 10, 15–29 CrossRef CAS.
- A. R. Ravishankara and P. H. Wine, J. Chem. Phys., 1980, 72, 25–30 CrossRef CAS.
- S. P. Heneghan, P. A. Knoot and S. W. Benson, Int. J. Chem. Kinet., 1981, 13, 677–691 CrossRef CAS.
- W. R. Simpson, T. P. Rakitzis, S. A. Kandel, A. J. Orrewing and R. N. Zare, J. Chem. Phys., 1995, 103, 7313–7335 CrossRef CAS.
- W. R. Simpson, T. P. Rakitzis, S. A. Kandel, T. LevOn and R. N. Zare, J. Phys. Chem., 1996, 100, 7938–7947 CrossRef CAS.
- J. V. Seeley, J. T. Jayne and M. J. Molina, J. Phys. Chem., 1996, 100, 4019–4025 CrossRef CAS.
- J. S. Pilgrim, A. McIlroy and C. A. Taatjes, J. Phys. Chem. A, 1997, 101, 1873–1880 CrossRef CAS.
- S. A. Kandel and R. N. Zare, J. Chem. Phys., 1998, 109, 9719–9727 CrossRef CAS.
- Z. H. Kim, A. J. Alexander, H. A. Bechtel and R. N. Zare, J. Chem. Phys., 2001, 115, 179–183 CrossRef CAS.
- K. Takahashi, O. Yamamoto and T. Inomata, Proc. Combust. Inst., 2002, 29, 2447–2453 CrossRef CAS.
- M. G. Bryukov, I. R. Slagle and V. D. Knyazev, J. Phys. Chem. A, 2002, 106, 10532–10542 CrossRef CAS.
- S. Yoon, S. Henton, A. N. Zivkovic and F. F. Crim, J. Chem. Phys., 2002, 116, 10744–10752 CrossRef CAS.
- Z. H. Kim, H. A. Bechtel and R. N. Zare, J. Chem. Phys., 2002, 117, 3232–3242 CrossRef CAS.
- S. Yoon, R. J. Holiday, E. L. Sibert III and F. F. Crim, J. Chem. Phys., 2003, 119, 9568–9575 CrossRef CAS.
- J. Zhou, J. J. Lin, B. Zhang and K. Liu, J. Phys. Chem. A, 2004, 108, 7832–7836 CrossRef CAS.
- H. A. Bechtel, Z.-H. Kim, J. P. Camden and R. N. Zare, J. Chem. Phys., 2004, 120, 791–799 CrossRef CAS PubMed.
- H. A. Bechtel, J. P. Camden, D. J. A. Brown, M. R. Martin, R. N. Zare and K. Vodopyanov, Angew. Chem., Int. Ed., 2005, 44, 2382–2385 CrossRef CAS PubMed.
- B. L. Zhang and K. P. Liu, J. Chem. Phys., 2005, 122, 101102 CrossRef PubMed.
- M. J. Bass, M. Brouard, R. Cireasa, A. P. Clark and C. Vallance, J. Chem. Phys., 2005, 123, 094301 CrossRef CAS PubMed.
- Z. H. Kim, H. A. Bechtel, J. P. Camden and R. N. Zare, J. Chem. Phys., 2005, 122, 084303 CrossRef PubMed.
- H. A. Bechtel, Z. H. Kim, J. P. Camden and R. N. Zare, Mol. Phys., 2005, 103, 1837–1846 CrossRef CAS.
- R. J. Holiday, C. H. Kwon, C. J. Annesley and F. F. Crim, J. Chem. Phys., 2006, 125, 133101 CrossRef PubMed.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Atmos. Chem. Phys., 2006, 6, 3625–4055 CrossRef CAS.
- S. Yan, Y. T. Wu, B. Zhang, X.-F. Yue and K. Liu, Science, 2007, 316, 1723–1726 CrossRef CAS PubMed.
- H. Kawamata, S. Tauro and K. Liu, Phys. Chem. Chem. Phys., 2008, 10, 4378–4382 RSC.
- Y.-T. Wu and K. Liu, J. Chem. Phys., 2008, 129, 154302 CrossRef PubMed.
- S. Yan, Y.-T. Wu and K. Liu, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12667–12672 CrossRef CAS PubMed.
- J. Riedel, S. N. Yan and K. Liu, J. Phys. Chem. A, 2009, 113, 14270–14276 CrossRef CAS PubMed.
- J. Riedel and K. Liu, J. Phys. Chem. A, 2009, 113, 4249–4254 CrossRef CAS PubMed.
- H. Kawamata and K. Liu, J. Chem. Phys., 2010, 133, 124304 CrossRef PubMed.
- S. P. Sander, J. Abbatt, J. R. Barker, J. B. Burkholder, R. R. Friedl, D. M. Golden, R. E. Huie, C. E. Kolb, M. J. Kurylo, G. K. Moortgat, V. L. Orkin and P. H. Wine, Chemical kinetics and photochemical data for use in atmospheric studies, Evaluation No. 17, JPL Publication 10-6, Pasadena, 2011.
- F. Wang, J.-S. Lin and K. Liu, Science, 2011, 331, 900–903 CrossRef CAS PubMed.
- B. L. Zhang, K. P. Liu, G. Czako and J. M. Bowman, Mol. Phys., 2012, 110, 1617–1626 CrossRef CAS.
- F. Wang, K. Liu and T. P. Rakitzis, Nat. Chem., 2012, 4, 636–641 CrossRef CAS PubMed.
- A. E. Berke, E. H. Volpa, C. J. Annesley and F. F. Crim, J. Chem. Phys., 2013, 138, 224306 CrossRef PubMed.
- F. Wang, J.-S. Lin, Y. Cheng and K. Liu, J. Phys. Chem. Lett., 2013, 4, 323–327 CrossRef CAS PubMed.
- L. M. T. Joelsson, R. Forecast, J. A. Schmidt, C. Meusinger, E. J. K. Nilsson, S. Ono and M. S. Johnson, Chem. Phys. Lett., 2014, 605, 152–157 CrossRef.
- F. Wang, H. Pan and K. Liu, J. Phys. Chem. A, 2015, 119, 11983–11988 CrossRef CAS PubMed.
- F. Wang and K. Liu, J. Chem. Phys., 2016, 145, 144305 CrossRef PubMed.
- F. Wang and K. Liu, J. Chem. Phys., 2016, 145, 144306 CrossRef PubMed.
- H. Pan, Y. Cheng and K. Liu, J. Phys. Chem. A, 2016, 120, 4799–4804 CrossRef CAS PubMed.
- H. Pan, F. Wang, G. Czako and K. Liu, Nat. Chem., 2017, 9, 1175–1180 CrossRef CAS PubMed.
- H. Pan, O. Tkac and K. Liu, J. Chem. Phys., 2018, 148, 244307 CrossRef PubMed.
- C. Murray and A. J. Orr-Ewing, Int. Rev. Phys. Chem., 2004, 23, 435–482 Search PubMed.
- G. Nyman, H. G. Yu and R. B. Walker, J. Chem. Phys., 1998, 109, 5896–5904 CrossRef CAS.
- H. G. Yu and G. Nyman, J. Chem. Phys., 1999, 110, 7233–7244 CrossRef CAS.
- F. Meng, W. Yan and D. Wang, Phys. Chem. Chem. Phys., 2012, 14, 13656–13662 RSC.
- J. Li, B. Jiang, H. Song, J. Ma, B. Zhao, R. Dawes and H. Guo, J. Phys. Chem. A, 2015, 119, 4667–4687 CrossRef CAS PubMed.
- J. F. Castillo, F. J. Aoiz and L. Banares, J. Chem. Phys., 2006, 125, 124316 CrossRef CAS PubMed.
- C. Qu, Q. Yu and J. M. Bowman, Annu. Rev. Phys. Chem., 2018, 69, 151–175 CrossRef CAS PubMed.
- B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 054112 CrossRef PubMed.
- J. Li, B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 204103 CrossRef PubMed.
- B. Jiang, J. Li and H. Guo, Int. Rev. Phys. Chem., 2016, 35, 479–506 Search PubMed.
- M. Bai, D. Lu and J. Li, Phys. Chem. Chem. Phys., 2017, 19, 17718–17725 RSC.
- Y. Liu, M. Bai, H. Song, D. Xie and J. Li, Phys. Chem. Chem. Phys., 2019, 21, 12667–12675 RSC.
- J. Li, J. Chen, Z. Zhao, D. Xie, D. H. Zhang and H. Guo, J. Chem. Phys., 2015, 142, 204302 CrossRef PubMed.
- J. Li and H. Guo, J. Chem. Phys., 2015, 143, 221103 CrossRef PubMed.
- J. Li, K. Song and J. Behler, Phys. Chem. Chem. Phys., 2019, 21, 9672–9682 RSC.
- M. L. Weichman, J. A. DeVine, M. C. Babin, J. Li, L. Guo, J. Ma, H. Guo and D. M. Neumark, Nat. Chem., 2017, 9, 950–955 CrossRef CAS PubMed.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- S. Habershon, D. E. Manolopoulos, T. E. Markland and T. F. Miller III, Annu. Rev. Phys. Chem., 2013, 64, 387–413 CrossRef CAS PubMed.
- R. Collepardo-Guevara, Y. V. Suleimanov and D. E. Manolopoulos, J. Chem. Phys., 2009, 130, 174713 CrossRef PubMed.
- Y. V. Suleimanov, R. Collepardo-Guevara and D. E. Manolopoulos, J. Chem. Phys., 2011, 134, 044131 CrossRef PubMed.
- R. Pérez de Tudela, F. J. Aoiz, Y. V. Suleimanov and D. E. Manolopoulos, J. Phys. Chem. Lett., 2012, 3, 493–497 CrossRef PubMed.
- Y. Li, Y. V. Suleimanov, M. Yang, W. H. Green and H. Guo, J. Phys. Chem. Lett., 2013, 4, 48–52 CrossRef CAS PubMed.
- Y. V. Suleimanov, R. Pérez de Tudela, P. G. Jambrina, J. F. Castillo, V. Sáez-Rábanos, D. E. Manolopoulos and F. J. Aoiz, Phys. Chem. Chem. Phys., 2013, 15, 3655–3665 RSC.
- Y. Li, Y. V. Suleimanov, J. Li, W. H. Green and H. Guo, J. Chem. Phys., 2013, 138, 094307 CrossRef PubMed.
- J. W. Allen, W. H. Green, Y. Li, H. Guo and Y. V. Suleimanov, J. Chem. Phys., 2013, 138, 221103 CrossRef PubMed.
- J. Espinosa-Garcia, A. Fernandez-Ramos, Y. V. Suleimanov and J. C. Corchado, J. Phys. Chem. A, 2014, 118, 554–560 CrossRef CAS PubMed.
- R. Pérez de Tudela, Y. V. Suleimanov, M. Menendez, F. Castillo and F. J. Aoiz, Phys. Chem. Chem. Phys., 2014, 16, 2920–2927 RSC.
- Y. Li, Y. V. Suleimanov and H. Guo, J. Phys. Chem. Lett., 2014, 5, 700–705 CrossRef CAS PubMed.
- E. Gonzalez-Lavado, J. C. Corchado, Y. V. Suleimanov, W. H. Green and J. Espinosa-Garcia, J. Phys. Chem. A, 2014, 118, 3243–3252 CrossRef CAS PubMed.
- K. M. Hickson, J.-C. Loison, H. Guo and Y. V. Suleimanov, J. Phys. Chem. Lett., 2015, 6, 4194–4199 CrossRef CAS PubMed.
- D. J. Arseneau, D. G. Fleming, Y. Li, J. Li, Y. V. Suleimanov and H. Guo, J. Phys. Chem. B, 2016, 120, 1641–1648 CrossRef CAS PubMed.
- Y. V. Suleimanov, F. Javier Aoiz and H. Guo, J. Phys. Chem. A, 2016, 120, 8488–8502 CrossRef CAS PubMed.
- M. Bai, D. Lu, Y. Li and J. Li, Phys. Chem. Chem. Phys., 2016, 18, 32031–32041 RSC.
- K. M. Hickson and Y. V. Suleimanov, J. Phys. Chem. A, 2017, 121, 1916–1923 CrossRef CAS PubMed.
- J. F. Castillo and Y. V. Suleimanov, Phys. Chem. Chem. Phys., 2017, 19, 29170–29176 RSC.
- J. X. Zuo, C. J. Xie, H. Guo and D. Q. Xie, J. Phys. Chem. Lett., 2017, 8, 3392–3397 CrossRef CAS PubMed.
- X. X. Lu, Q. Y. Meng, X. G. Wang, B. N. Fu and D. H. Zhang, J. Chem. Phys., 2018, 149, 174303 CrossRef PubMed.
- H. Wang, J. Fang, H. Yang, J. Song and Y. Li, Chem. Phys. Lett., 2019, 730, 227–233 CrossRef CAS.
- X. X. Lu, X. G. Wang, B. N. Fu and D. H. Zhang, J. Phys. Chem. A, 2019, 123, 3969–3976 CrossRef CAS PubMed.
- J. Li, Chin. J. Chem. Phys., 2019, 32, 313–318 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, et al., MOLPRO, version 2015, a package of ab initio programs, see http://www.molpro.net.
- L. Kong, F. A. Bischoff and E. F. Valeev, Chem. Rev., 2011, 112, 75–107 CrossRef PubMed.
- G. Czakó, I. Szabó and H. Telekes, J. Phys. Chem. A, 2014, 118, 646–654 CrossRef PubMed.
- G. Czakó and J. M. Bowman, Phys. Chem. Chem. Phys., 2011, 13, 8306–8312 RSC.
- J. Li, B. Jiang and H. Guo, J. Chem. Phys., 2013, 138, 074309 CrossRef PubMed.
- A. Berning, M. Schweizer, H. J. Werner, P. J. Knowles and P. Palmier, Mol. Phys., 2000, 98, 1823–1833 CrossRef CAS.
- Z. Xie and J. M. Bowman, J. Chem. Theory Comput., 2010, 6, 26–34 CrossRef CAS PubMed.
- J. N. Murrell, K. Sobie and A. J. C. Varandas, Mol. Phys., 1976, 32, 1359–1372 CrossRef CAS.
- A. Schmelzer and J. N. Murrell, Int. J. Quantum Chem., 1985, 28, 287–295 CrossRef CAS.
- L. M. Raff, R. Komanduri, M. Hagan and S. T. S. Bukkapatnam, Neural Networks in Chemical Reaction Dynamics, Oxford University Press, Oxford, 2012 Search PubMed.
- Y. V. Suleimanov, J. W. Allen and W. H. Green, Comput. Phys. Commun., 2013, 184, 833–840 CrossRef CAS.
- Y. V. Suleimanov, F. J. Aoiz and H. Guo, J. Phys. Chem. A, 2016, 120, 8488–8502 CrossRef CAS PubMed.
- D. Chandler, J. Chem. Phys., 1978, 68, 2959–2970 CrossRef CAS.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393 CrossRef CAS.
- J. P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- T. J. Wallington and M. D. Hurley, Chem. Phys. Lett., 1992, 189, 437–442 CrossRef CAS.
- Y. Matsumi, K. Izumi, V. Skorokhodov, M. Kawasaki and N. Tanaka, J. Phys. Chem. A, 1997, 101, 1216–1221 CrossRef CAS.
- G. D. Boone, F. Agyin, D. J. Robichaud, F.-M. Tao and S. A. Hewitt, J. Phys. Chem. A, 2000, 105, 1456–1464 CrossRef.
- G. Chiltz, R. Eckling, P. Goldfinger, G. Huybrechts, H. S. Johnston, L. Meyers and G. Verbeke, J. Chem. Phys., 1963, 38, 1053–1061 CrossRef CAS.
- K. L. Feilberg, D. W. T. Griffith, M. S. Johnson and C. J. Nielsen, Int. J. Chem. Kinet., 2005, 37, 110–118 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05693a |
| This journal is © the Owner Societies 2020 |